A High-Confidence Intelligent Measurement Method for Aero-Engine Oil Debris Based on Improved Variational Mode Decomposition Denoising
Abstract
:1. Introduction
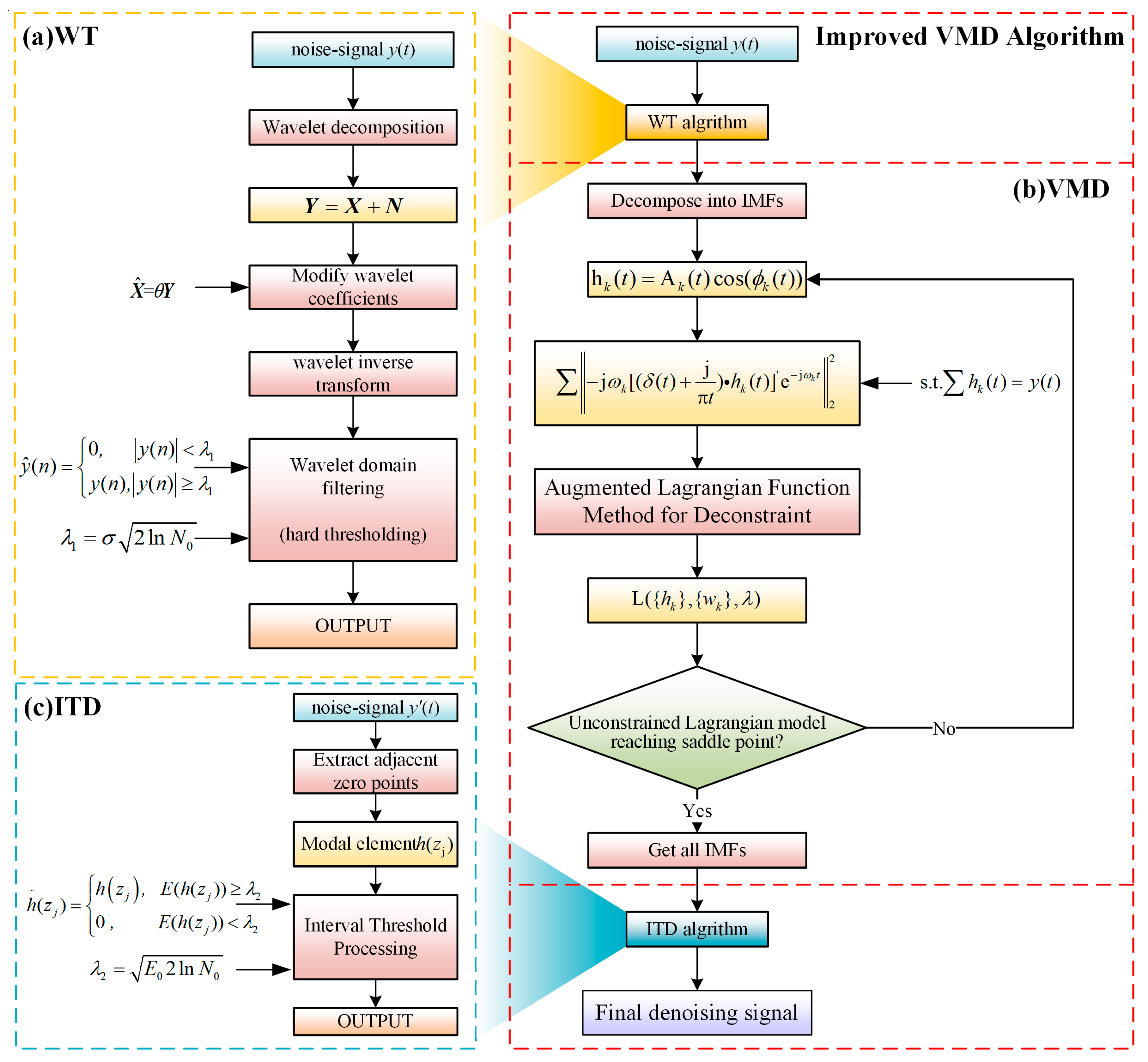
2. Improved VMD-Based Fusion Denoising Algorithm
2.1. Wavelet Transform Preprocessing
2.2. Variational Mode Decomposition
2.3. Interval Threshold Filtering for IMFs of VMD
3. Oil Debris Signal Detection Method Based on DSS-LSTM
3.1. Data Mapping Based on Deep Scattering Spectrum
3.2. Metal Debris Signal Recognition Model Based on LSTM
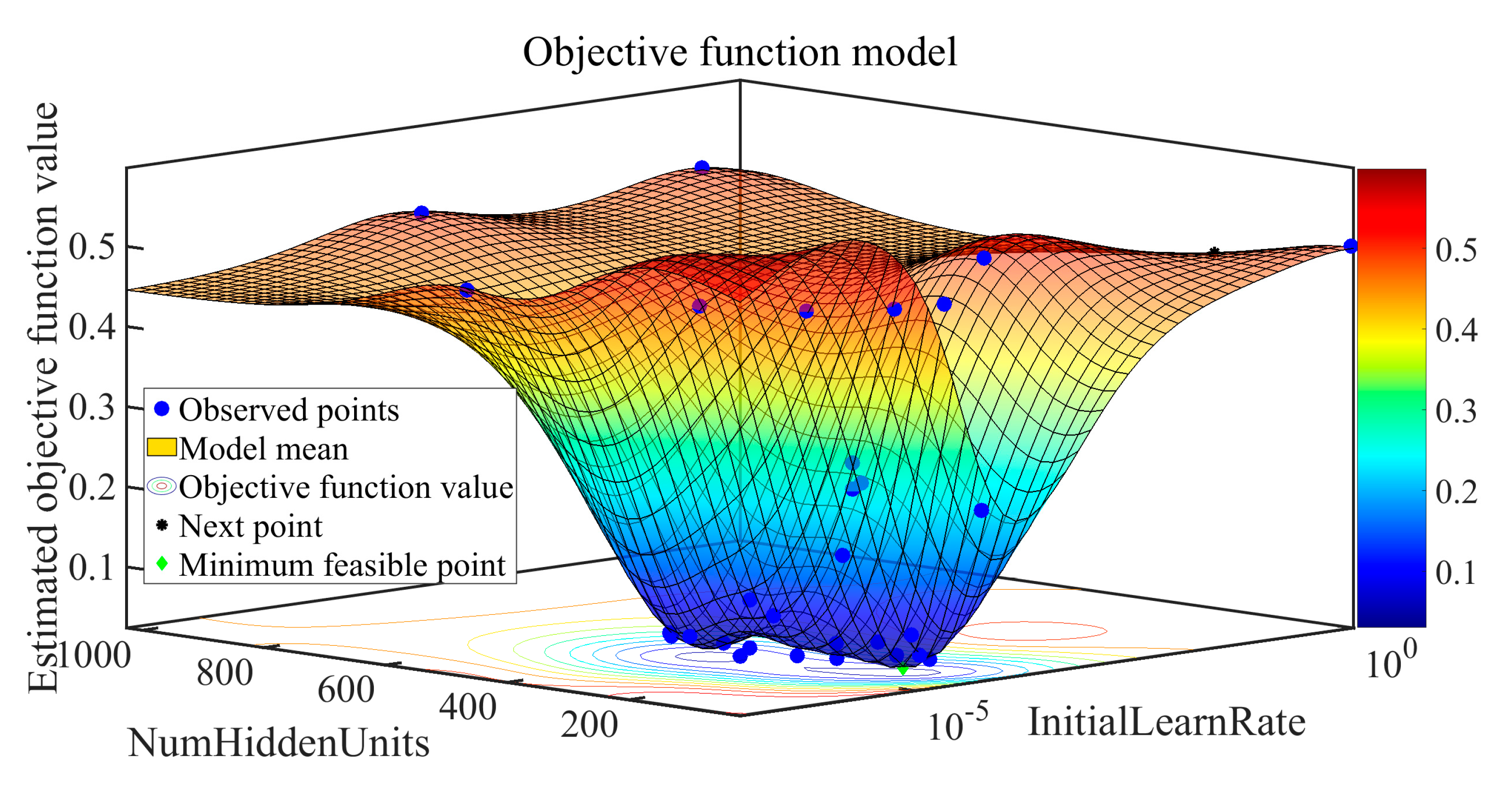
3.3. Hyperparameter Optimization Based on Bayesian Optimization
4. High-Confidence Measurement Method for Oil Debris
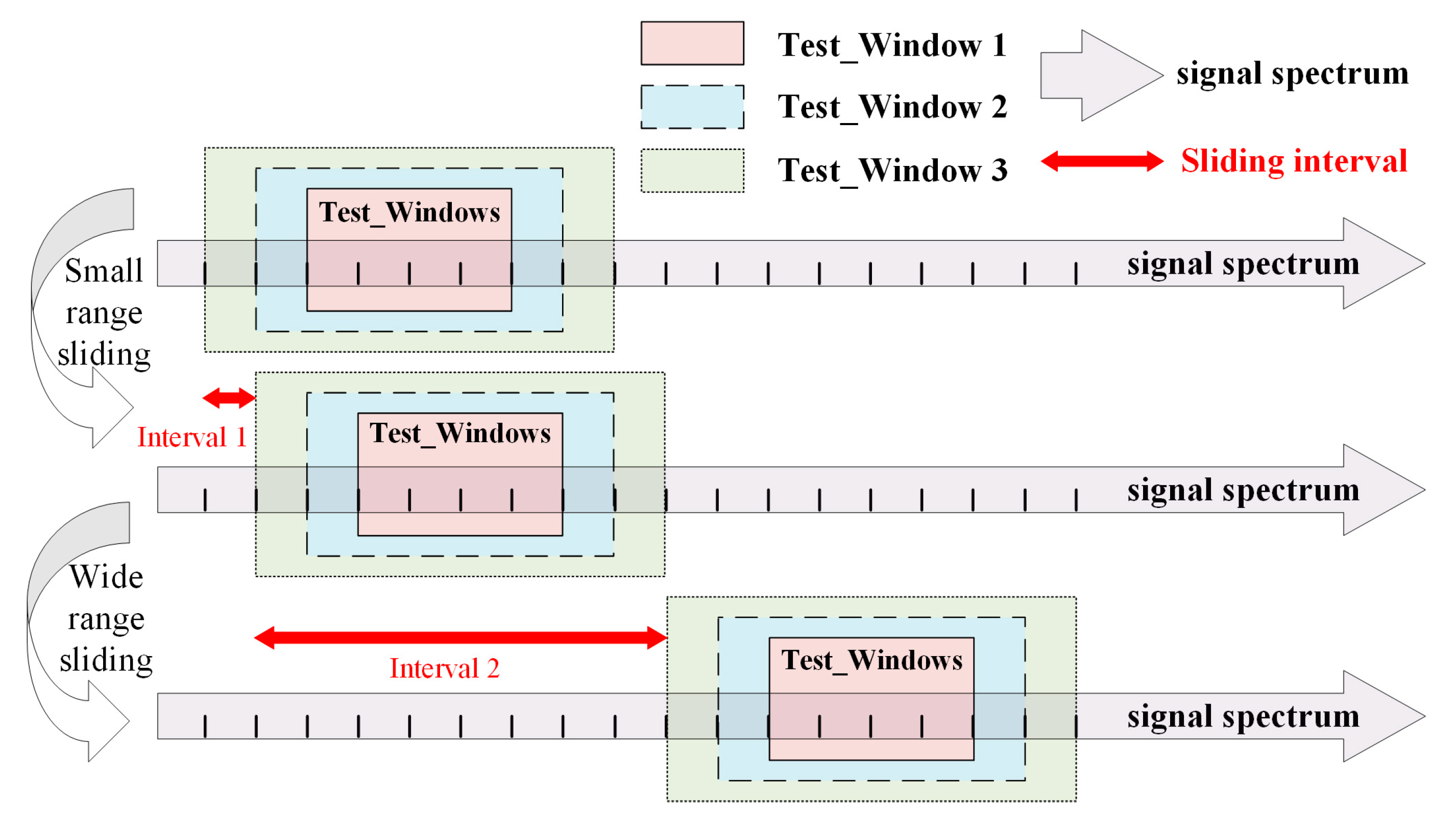
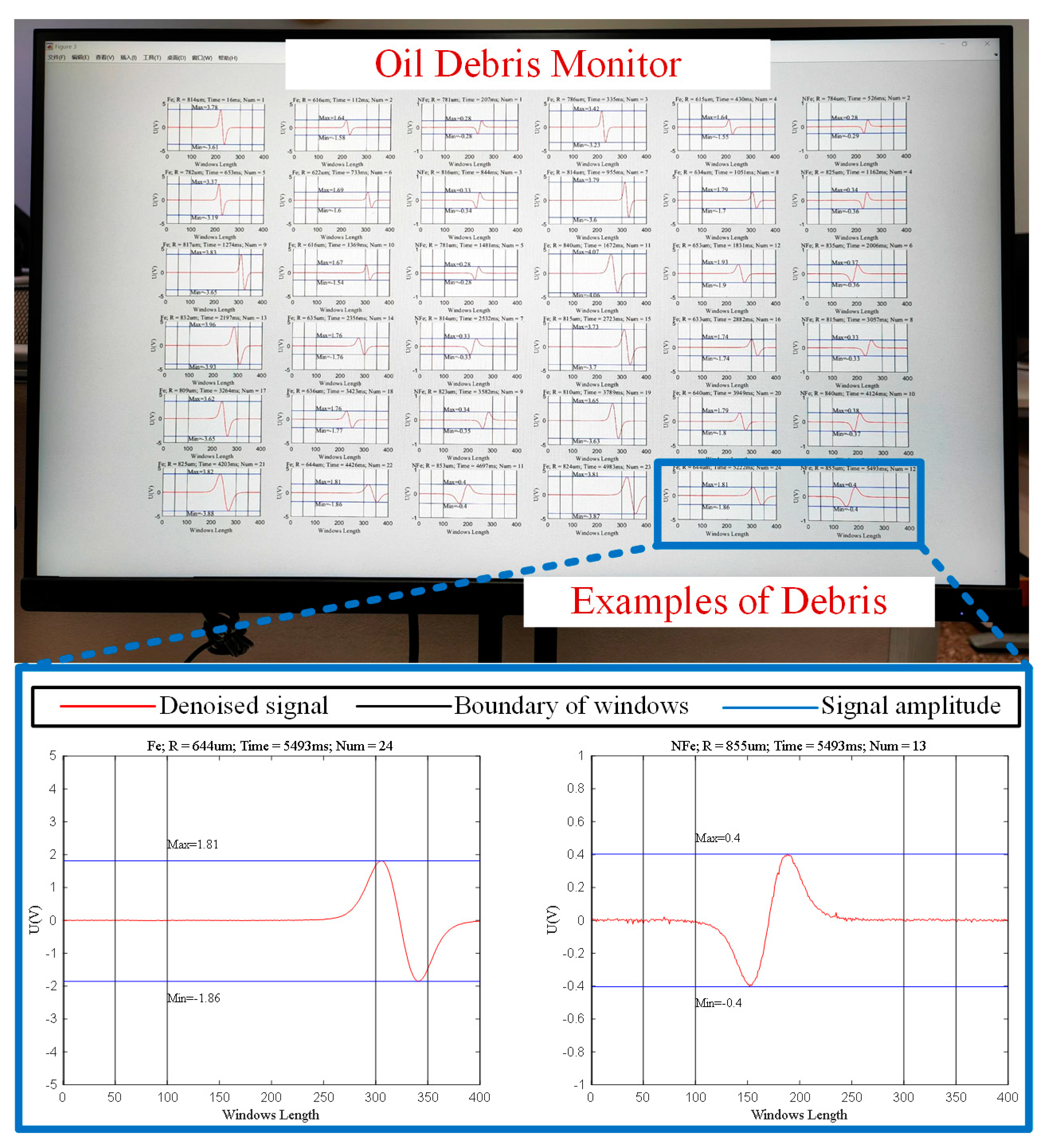
4.1. Detection Method of Multi-Window Information Fusion
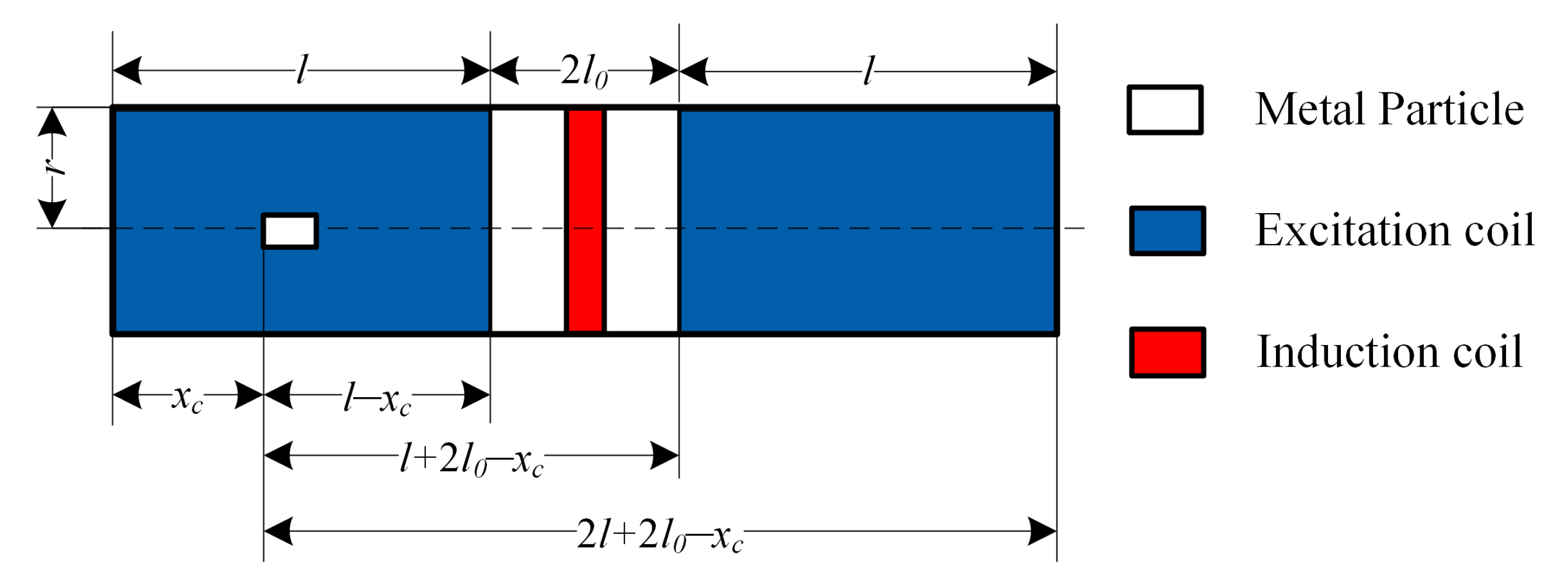
4.2. Principle of Electromagnetic Metal Debris Sensor
5. Simulation and Experimental Verification
5.1. Oil Debris Signal Denoising Simulation Experiment
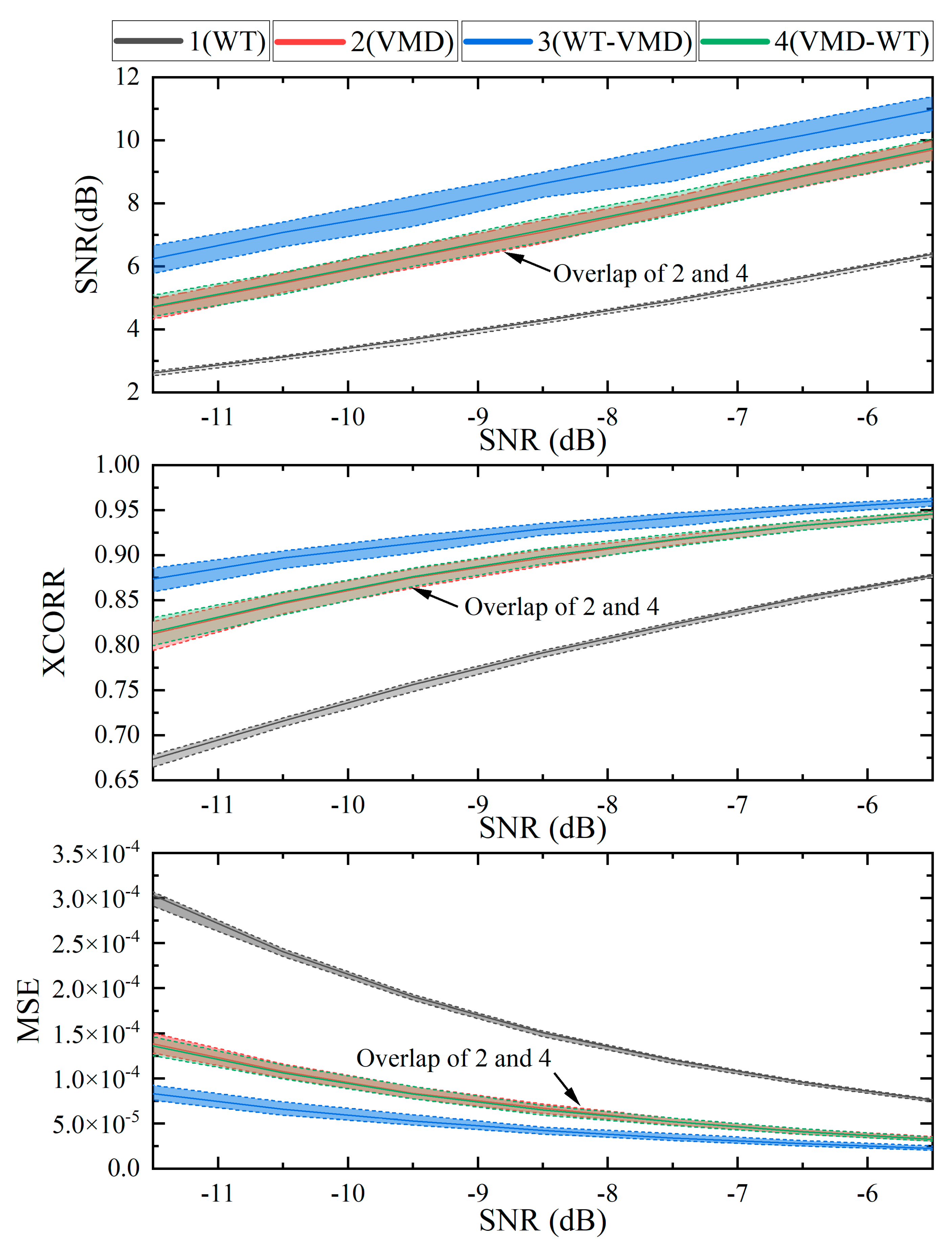
5.1.1. Comparison of Traditional Denoising Methods
5.1.2. Test of the Improved VMD Fusion Denoising Algorithm
5.2. Oil Debris Signal Denoising Simulation Experiment
5.2.1. DSS-LSTM Training Process Based on BO
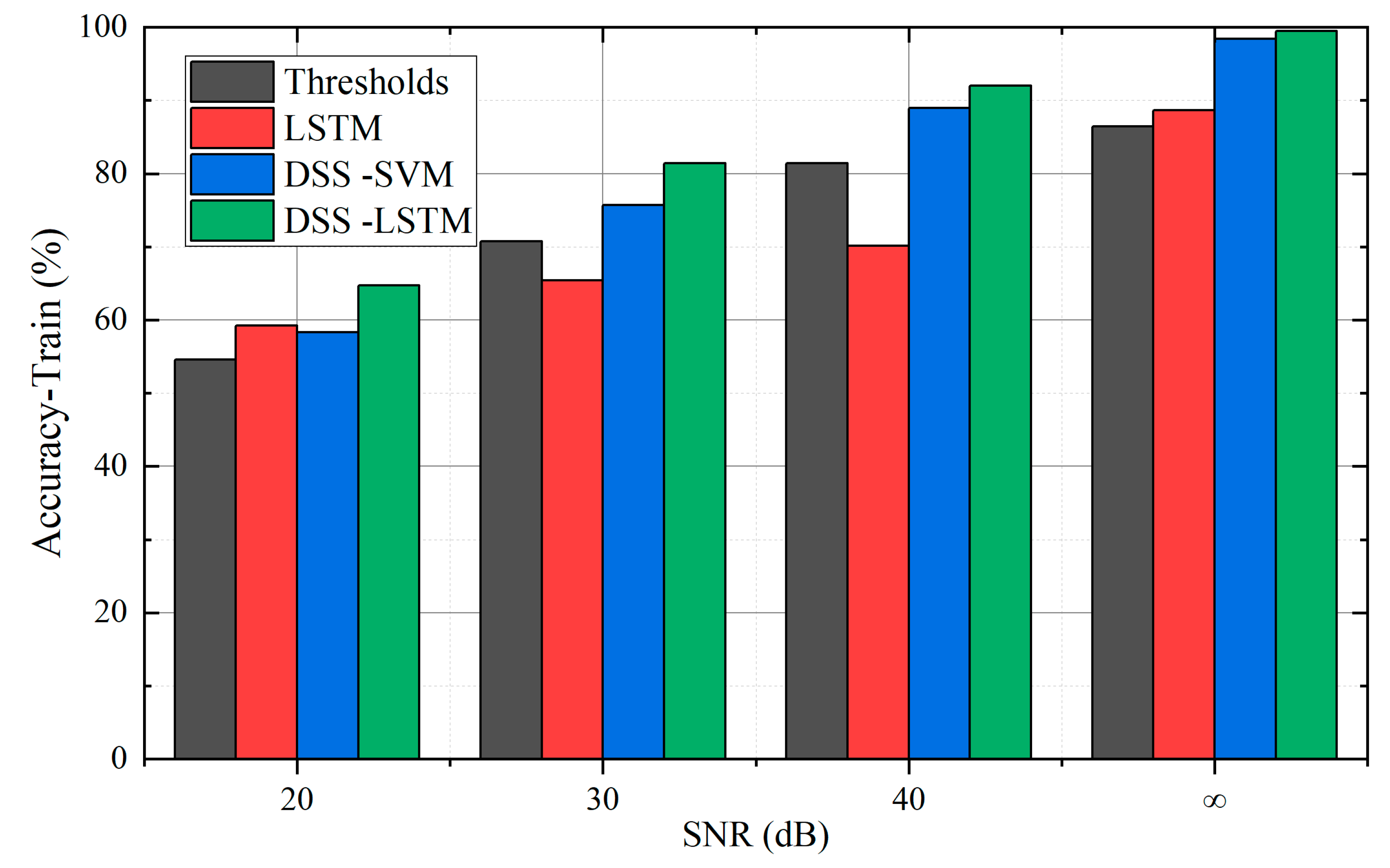
5.2.2. Comparison of Effects of Debris Classification Models
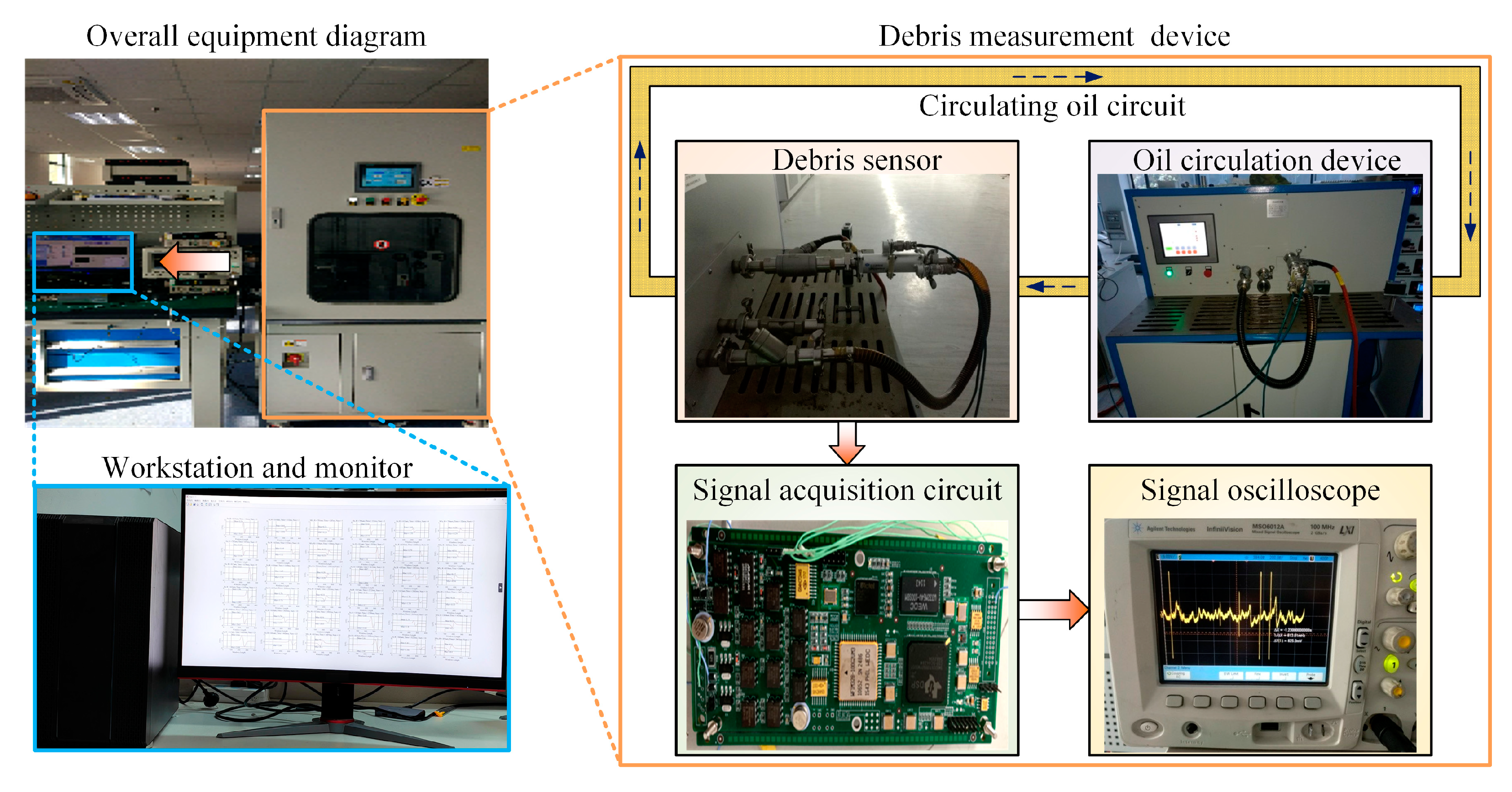
5.3. Oil Debris Signal Measurement Experiment
5.3.1. Signal Amplitude Calibration Experiment
5.3.2. Measurement Method Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wei, H.; Wenjian, C.; Shaoping, W.; Tomovic, M.M. Mechanical wear debris feature, detection, and diagnosis: A review. Chin. J. Aeronaut. 2018, 31, 867–882. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Y.; Xiang, J. An online debris sensor system with vibration resistance for lubrication analysis. Rev. Sci. Instrum. 2016, 87, 1590–1597. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Wu, H.; Du, Y.; Kwok, N.; Peng, Z. Imaged wear debris separation for on-line monitoring using gray level and integrated morphological features. Wear 2014, 316, 19–29. [Google Scholar] [CrossRef]
- Du, L.; Zhu, X.; Han, Y.; Zhao, L.; Zhe, J. Improving sensitivity of an inductive pulse sensor for detection of metallic wear debris in lubricants using parallel lc resonance method. Meas. Technol. 2013, 24, 660–664. [Google Scholar] [CrossRef]
- Wen, Z.; Yin, X.; Jiang, Z. Applications of electrostatic sensor for wear debris detecting in the lubricating oil. J. Inst. Eng. (India) Ser. C 2013, 94, 281–286. [Google Scholar] [CrossRef]
- Islam, T.; Yousuf, M.; Nauman, M. A highly precise cross-capacitive sensor for metal debris detection in insulating oil. Rev. Sci. Instrum. 2020, 91, 025005. [Google Scholar] [CrossRef]
- Chao, X.; Zhang, P.; Wang, H.; Li, Y.; Lv, C. Ultrasonic echo waveshape features extraction based on qpso-matching pursuit for online wear debris discrimination. Mech. Syst. Signal Process. 2015, 60–61, 301–315. [Google Scholar] [CrossRef]
- Du, L.; Zhe, J. An integrated ultrasonic–inductive pulse sensor for wear debris detection. Smart Mater. Struct. 2012, 22, 025003. [Google Scholar] [CrossRef]
- Zhu, X.; Du, L.; Zhe, J. A 3 × 3 wear debris sensor array for real time lubricant oil conditioning monitoring using synchronized sampling. Mech. Syst. Signal Process. 2017, 83, 296–304. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, H.; Wang, M.; Chen, H. Differentiation of nonferrous metal particles in lubrication oil using an electrical conductivity measurement-based inductive sensor. Rev. Sci. Instrum. 2018, 89, 025002. [Google Scholar] [CrossRef]
- Qiu, H.; Eklund, N.; Luo, H.; Hirz, M.; Van Der Merwe, G.; Hindle, E.; Rosenfeld, T.; Gruber, F. Fusion of vibration and on-line oil debris sensors for aircraft engine bearing prognosis. In Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 18th AIAA/ASME/AHS Adaptive Structures Conference 12th, Orlando, FL, USA, 12–15 April 2010; p. 2858. [Google Scholar] [CrossRef]
- Luo, J.; Yu, D.; Ming, L. Enhancement of oil particle sensor capability via resonance-based signal decomposition and fractional calculus. Measurement 2015, 76, 240–254. [Google Scholar] [CrossRef]
- Hong, H.; Liang, M. A fractional calculus technique for on-line detection of oil debris. Meas. Sci. Technol. 2008, 19, 055703. [Google Scholar] [CrossRef]
- Zhi, Z.; Wang, S.; Wei, H.; Tomovic, M. Aliasing signal separation of oil debris monitoring. In Proceedings of the 2016 IEEE 11th Conference on Industrial Electronics and Applications (ICIEA), Hefei, China, 5–7 June 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Fan, X.; Liang, M.; Yeap, T. A joint time-invariant wavelet transform and kurtosis approach to the improvement of in-line oil debris sensor capability. Smart Mater. Struct. 2009, 18, 085010. [Google Scholar] [CrossRef]
- Li, C.; Peng, J.; Liang, M. Enhancement of the wear particle monitoring capability of oil debris sensors using a maximal overlap discrete wavelet transform with optimal decomposition depth. Sensors 2014, 14, 6207–6228. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Du, L.; Zhe, J. An integrated lubricant oil conditioning sensor using signal multiplexing. J. Micromech. Microeng. 2014, 25, 015006. [Google Scholar] [CrossRef]
- Yu, B.; Cao, N.; Zhang, T. A novel signature extracting approach for inductive oil debris sensors based on symplectic geometry mode decomposition. Measurement 2021, 185, 110056. [Google Scholar] [CrossRef]
- Bozchalooi, I.S.; Liang, M. In-line identification of oil debris signals: An adaptive subband filtering approach. Meas. Sci. Technol. 2010, 21, 015104. [Google Scholar] [CrossRef]
- Nugraha, R.D.; He, K.; Liu, A.; Zhang, Z. Short-Term Cross-Sectional Time-Series Wear Prediction by Deep Learning Approaches. J. Comput. Inf. Sci. Eng. 2023, 23, 021007. [Google Scholar] [CrossRef]
- Wu, S.; Liu, Z.; Yu, K.; Fan, Z.; Yuan, Z.; Sui, Z.; Yin, Y.; Pan, X. A novel multichannel inductive wear debris sensor based on time division multiplexing. IEEE Sens. J. 2021, 21, 11131–11139. [Google Scholar] [CrossRef]
- Guo, J.; Zuo, H.; Zhong, Z.; Jiang, H. Foreign object monitoring method in aero-engines based on electrostatic sensor. Aerosp. Sci. Technol. 2022, 123, 107489. [Google Scholar] [CrossRef]
- Hong, W.; Li, T.; Wang, S.; Zhou, Z. A general framework for aliasing corrections of inductive oil debris detection based on artificial neural networks. IEEE Sens. J. 2020, 20, 10724–10732. [Google Scholar] [CrossRef]
- Li, X.Q.; Song, L.K.; Bai, G.C.; Li, D.G. Physics-informed distributed modeling for CCF reliability evaluation of aeroengine rotor systems. Int. J. Fatigue 2023, 167, 107342. [Google Scholar] [CrossRef]
- Li, X.Q.; Song, L.K.; Choy, Y.S.; Bai, G.C. Multivariate ensembles-based hierarchical linkage strategy for system reliability evaluation of aeroengine cooling blades. Aerosp. Sci. Technol. 2023, 138, 108325. [Google Scholar] [CrossRef]
- Aydin, F.; Durgut, R.; Mustu, M.; Demir, B. Prediction of wear performance of ZK60/CeO2 composites using machine learning models. Tribol. Int. 2023, 177, 107945. [Google Scholar] [CrossRef]
- Li, X.Q.; Song, L.K.; Bai, G.C. Deep learning regression-based stratified probabilistic combined cycle fatigue damage evaluation for turbine bladed disks. Int. J. Fatigue 2022, 159, 106812. [Google Scholar] [CrossRef]
- Deng, K.; Song, L.K.; Bai, G.C.; Li, X.Q. Improved Kriging-based hierarchical collaborative approach for multi-failure dependent reliability assessment. Int. J. Fatigue 2022, 160, 106842. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Mohammadi, M.; Ghafoor Salim, S.; Farid Hama Ali, H.; Hashim Ibrahim, H.; Nariman Abdulhamid, S.; Nejati, H.R.; Rashidi, S. Machine learning techniques to predict rock strength parameters. Rock Mech. Rock Eng. 2022, 55, 1721–1741. [Google Scholar] [CrossRef]
- Qi, T.; Wei, X.; Feng, G.; Zhang, F.; Zhao, D.; Guo, J. A method for reducing transient electromagnetic noise: Combination of variational mode decomposition and wavelet denoising algorithm. Measurement 2022, 198, 111420. [Google Scholar] [CrossRef]
- Rohan, A. Deep Scattering Spectrum Germaneness for Fault Detection and Diagnosis for Component-Level Prognostics and Health Management (PHM). Sensors 2022, 22, 9064. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Y.; Li, N.; Zhai, J.; Han, Q.; Hou, Z. A weak fault identification method of micro-turbine blade based on sound pressure signal with LSTM networks. Aerosp. Sci. Technol. 2023, 136, 108226. [Google Scholar] [CrossRef]
- Madeira, T.; Melício, R.; Valério, D.; Santos, L. Machine learning and natural language processing for prediction of human factors in aviation incident reports. Aerospace 2021, 8, 47. [Google Scholar] [CrossRef]
- Zou, L.; Zhuang, K.J.; Zhou, A.; Hu, J. Bayesian optimization and channel-fusion-based convolutional autoencoder network for fault diagnosis of rotating machinery. Eng. Struct. 2023, 280, 115708. [Google Scholar] [CrossRef]
- Sheng, H.; Chen, Q.; Zhang, T. Aircraft Engine Surge-Precursor Detection and Antisurge Control Method at Onboard Environment. AIAA J. 2022, 60, 4855–4867. [Google Scholar] [CrossRef]
- Zeng, Z.; Xu, E.; Huang, X.; Zhao, J.; Li, J. High-sensitivity, low-voltage lubricating oil wear debris sensor based on electromagnetic induction. Chin. J. Sci. Instrum. 2022, 43, 1–9. [Google Scholar] [CrossRef]
- Wang, Z.; Ding, H.; Wang, B.; Liu, D. New Denoising Method for Lidar Signal by the WT-VMD Joint Algorithm. Sensors 2022, 22, 5978. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, P.; Zhao, Y.; Sun, Y. A Denoising Method for Mining Cable PD Signal Based on Genetic Algorithm Optimization of VMD and Wavelet Threshold. Sensors 2022, 22, 9386. [Google Scholar] [CrossRef] [PubMed]
- Che, C.; Wang, H.; Fu, Q.; Ni, X. Combining multiple deep learning algorithms for prognostic and health management of aircraft. Aerosp. Sci. Technol. 2019, 94, 105423. [Google Scholar] [CrossRef]






| Methods | Advantages | Disadvantages |
|---|---|---|
| Optical | High precision; morphological information. | Low efficiency; affected by bubbles and oil transparency. |
| Resistive–capacitive | Simple structure; high measurement accuracy. | Cannot distinguish particle material and cause oil deterioration. |
| Acoustic | Distinguishes between bubbles and solid particles. | Cannot distinguish particle material; interference of flow speed, viscosity, vibration. |
| Electromagnetic | Significant flow rate and high efficiency; distinguishes between ferromagnetic and non-ferromagnetic particles. | Interference of vibration and electromagnetic noise; relatively low resolution. |
| SNR | Type | Accuracy (%) | Recall (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| All | None | Fe | NFe | All | None | Fe | NFe | ||
| 20 | Thresholds | 54.62 | 39.0 | 92.9 | 44.0 | 54.65 | 96.7 | 62.7 | 0.5 |
| LSTM | 59.21 | 44.0 | 95.2 | 40.7 | 59.28 | 68.2 | 71.7 | 31.7 | |
| DSS-SVM | 58.34 | 46.0 | 90.0 | 37.2 | 58.34 | 53.9 | 72.3 | 41.8 | |
| DSS-LSTM | 64.71 | 53.4 | 90.5 | 44.1 | 64.72 | 48.9 | 82.6 | 53.7 | |
| 30 | Thresholds | 70.76 | 52.9 | 96.7 | 58.0 | 70.75 | 88.0 | 88.4 | 27.0 |
| LSTM | 65.45 | 62.3 | 95.7 | 44.6 | 66.04 | 22.9 | 83.2 | 83.4 | |
| DSS-SVM | 75.71 | 66.5 | 96.8 | 59.2 | 76.29 | 77.7 | 87.8 | 57.6 | |
| DSS-LSTM | 81.46 | 65.3 | 96.6 | 81.8 | 81.49 | 93.1 | 97.6 | 45.7 | |
| 40 | Thresholds | 81.44 | 67.7 | 97.3 | 77.1 | 81.48 | 94.2 | 90.5 | 55.2 |
| LSTM | 70.15 | 49.6 | 100 | 73.0 | 70.89 | 100 | 89.6 | 13.7 | |
| DSS-SVM | 89.00 | 83.0 | 98.1 | 84.4 | 89.65 | 91.1 | 95.5 | 79.4 | |
| DSS-LSTM | 92.03 | 89.6 | 97.9 | 85.7 | 92.03 | 87.9 | 98.4 | 86.6 | |
| ∞ | Thresholds | 86.49 | 87.4 | 93.3 | 76.4 | 86.49 | 82.6 | 91.4 | 83.0 |
| LSTM | 88.63 | 79.4 | 100 | 85.6 | 88.65 | 90.4 | 81.2 | 98.1 | |
| DSS-SVM | 98.44 | 99.6 | 99.7 | 96.4 | 98.70 | 96.8 | 99.7 | 99.1 | |
| DSS-LSTM | 99.51 | 100 | 98.9 | 100 | 99.51 | 100 | 100 | 98.3 | |
| Metal Filing Particle Diameter (Fe) | ||||||
|---|---|---|---|---|---|---|
| 400 μm | 600 μm | 800 μm | ||||
| Speed (m/s) | Peak (V) | Trough (V) | Peak (V) | Trough (V) | Peak (V) | Trough (V) |
| 1 | 0.6483 | −0.6798 | 1.8959 | −1.9917 | 4.0680 | −4.2729 |
| 2 | 0.6315 | −0.6455 | 1.8663 | −1.9050 | 3.9286 | −3.9925 |
| 3 | 0.6251 | −0.6232 | 1.8175 | −1.8136 | 3.8367 | −3.8300 |
| 5 | 0.5790 | −0.5484 | 1.6988 | −1.6057 | 3.5926 | −3.4168 |
| Metal Filing Particle Diameter (Fe) | ||||
|---|---|---|---|---|
| 600 μm | 800 μm | |||
| Speed (m/s) | Peak (V) | Trough (V) | Peak (V) | Trough (V) |
| 1 | 1.8959 | −1.9917 | 4.0680 | −4.2729 |
| 2 | 1.8663 | −1.9050 | 3.9286 | −3.9925 |
| 3 | 1.8175 | −1.8136 | 3.8367 | −3.8300 |
| 5 | 1.6988 | −1.6057 | 3.5926 | −3.4168 |
| Accuracy (%) | Error Rate (%) | FAR (%) | Loss (%) | Fe | NFe | |||
|---|---|---|---|---|---|---|---|---|
| Accuracy (%) | Recall (%) | Accuracy (%) | Recall (%) | |||||
| Multi-windows | 99.76 | 0.24 | 0.035 | 0.24 | 99.74 | 100 | 99.78 | 99.48 |
| Single-window | 93.45 | 6.55 | 5.77 | 0.83 | 90.46 | 99.80 | 98.40 | 98.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Sheng, H.; Jin, Z.; Ding, L.; Chen, Q.; Huang, R.; Liu, S.; Li, J.; Yin, B. A High-Confidence Intelligent Measurement Method for Aero-Engine Oil Debris Based on Improved Variational Mode Decomposition Denoising. Aerospace 2023, 10, 826. https://doi.org/10.3390/aerospace10100826
Liu T, Sheng H, Jin Z, Ding L, Chen Q, Huang R, Liu S, Li J, Yin B. A High-Confidence Intelligent Measurement Method for Aero-Engine Oil Debris Based on Improved Variational Mode Decomposition Denoising. Aerospace. 2023; 10(10):826. https://doi.org/10.3390/aerospace10100826
Chicago/Turabian StyleLiu, Tong, Hanlin Sheng, Zhaosheng Jin, Li Ding, Qian Chen, Rui Huang, Shengyi Liu, Jiacheng Li, and Bingxiong Yin. 2023. "A High-Confidence Intelligent Measurement Method for Aero-Engine Oil Debris Based on Improved Variational Mode Decomposition Denoising" Aerospace 10, no. 10: 826. https://doi.org/10.3390/aerospace10100826





