Integrating GRU with a Kalman Filter to Enhance Visual Inertial Odometry Performance in Complex Environments
Abstract
:1. Introduction
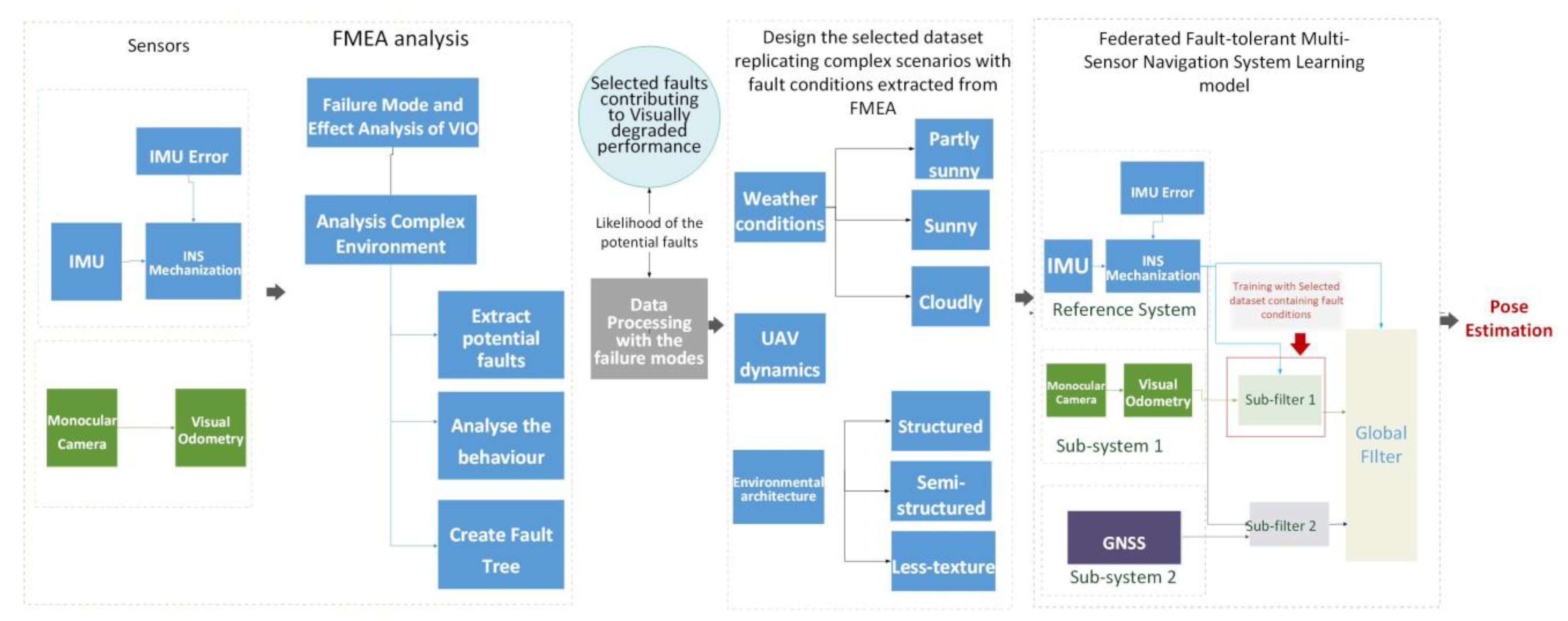
- The proposition of an FMEA-supported fault-tolerant federated GNSS/IMU/VO integrated navigation system. The FMEA execution on an integrated VINS system contributes to enhancing the system’s design, with a focus on accurate navigation during GNSS outages.
- The proposition of a GRU-based enhancement of ESKF for predicting increments of positions to update measurements of ESKF, aiming to correct visual positioning errors, leading to more accurate and robust navigation in challenging conditions.
- Performance evaluation of GRU-aided ESKF-based VIO within the fault-tolerant GNSS/IMU/VO multi-sensor navigation system. Training datasets for the GRU model are selected to replicate the failure modes extracted with fault conditions from FMEA. The verification is simulated and benchmarked on the Unreal engine, where the environment includes complex scenes of sunlight, shadow, motion blur, lens blur, no-texture, light variation, and motion variation. The validation dataset is grouped into multiple zone categories in accordance with single or multiple fault types due to environmental sensitivity and dynamic motion transitions.
- The performance of the proposed algorithm is compared with the state-of-the-art End-to-End VIO and Self-supervised VIO by testing similar datasets on the proposed algorithm.
2. Related Works
2.1. Kalman Filter for VIO
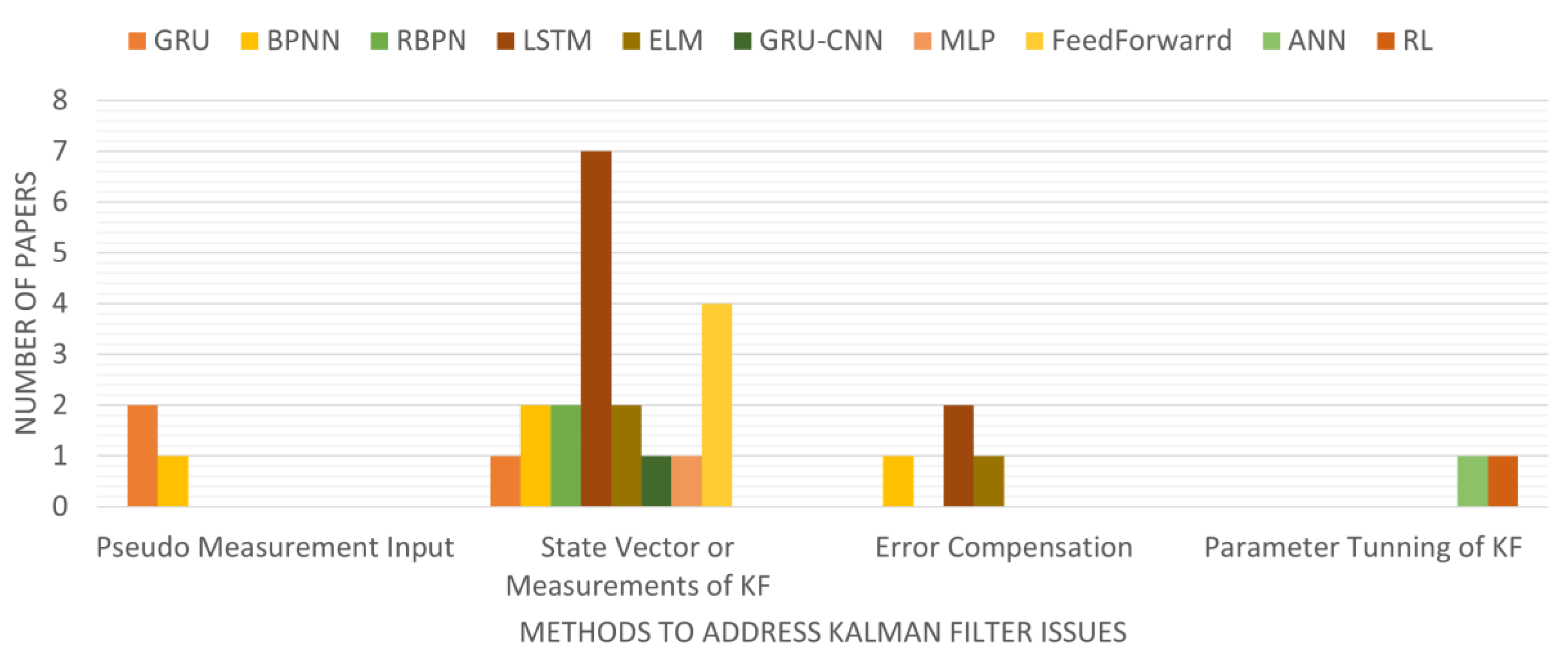
2.2. Hybrid Fusion Enhanced by AI
2.3. FMEA in VIO
3. Proposed Fault Tolerant Navigation System
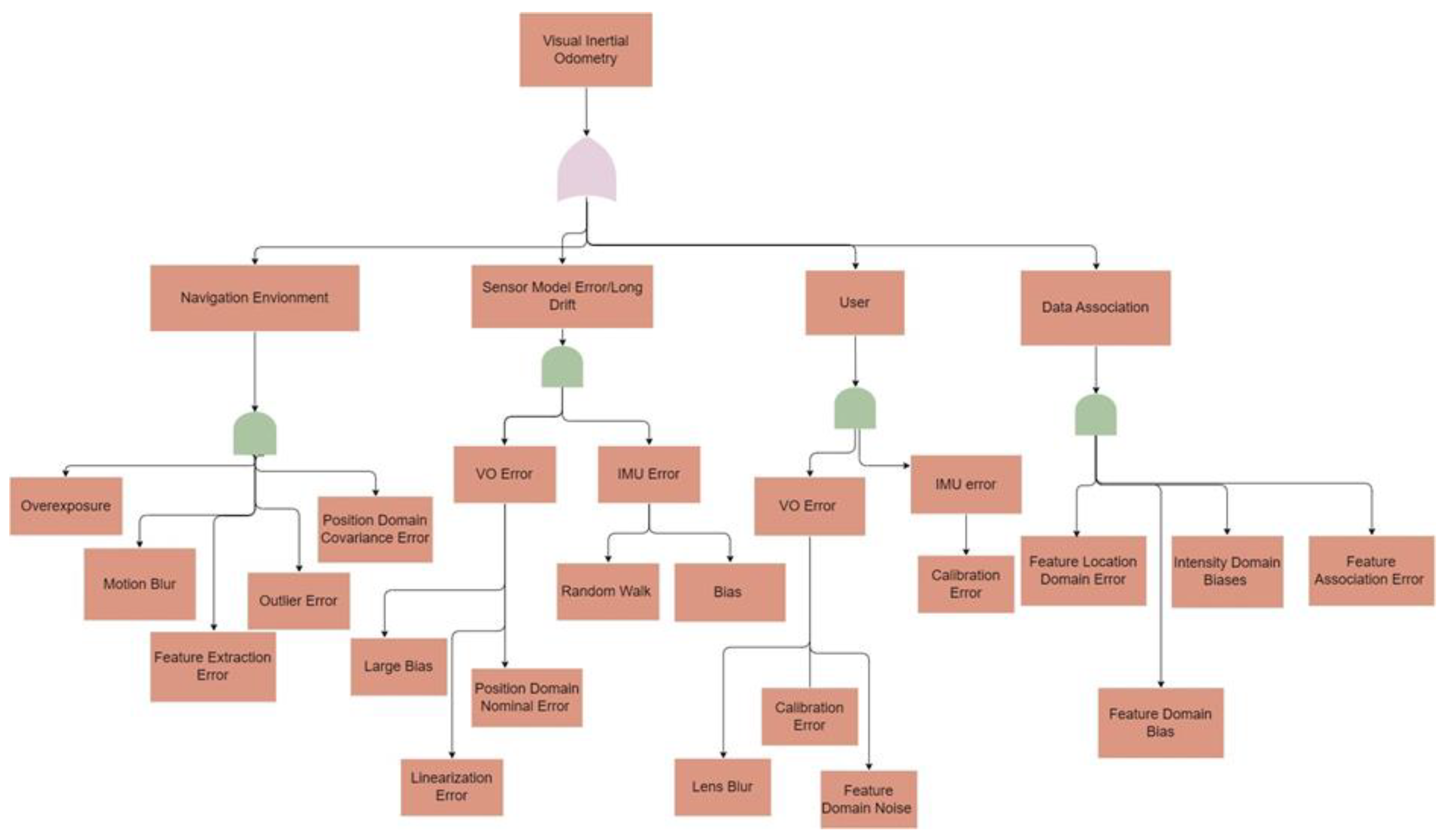
3.1. Failure Mode and Effect Analysis (FMEA)
- One common fault in the navigation environment fault event is the feature extraction error that contains deterministic biases that frequently lead to position errors.
- Another common fault in the data association failure event is the feature association error that occurs during matching 2D feature locations with 3D landmarks.
- The sensor model error/long drift failure events represent errors generated by sensor dynamics, including VO error and IMU error types.
- User failure events stand for the errors created during user operations that are normally relevant to the user calibration mistakes.
3.2. Fault-Tolerant Federated Navigation System Architecture
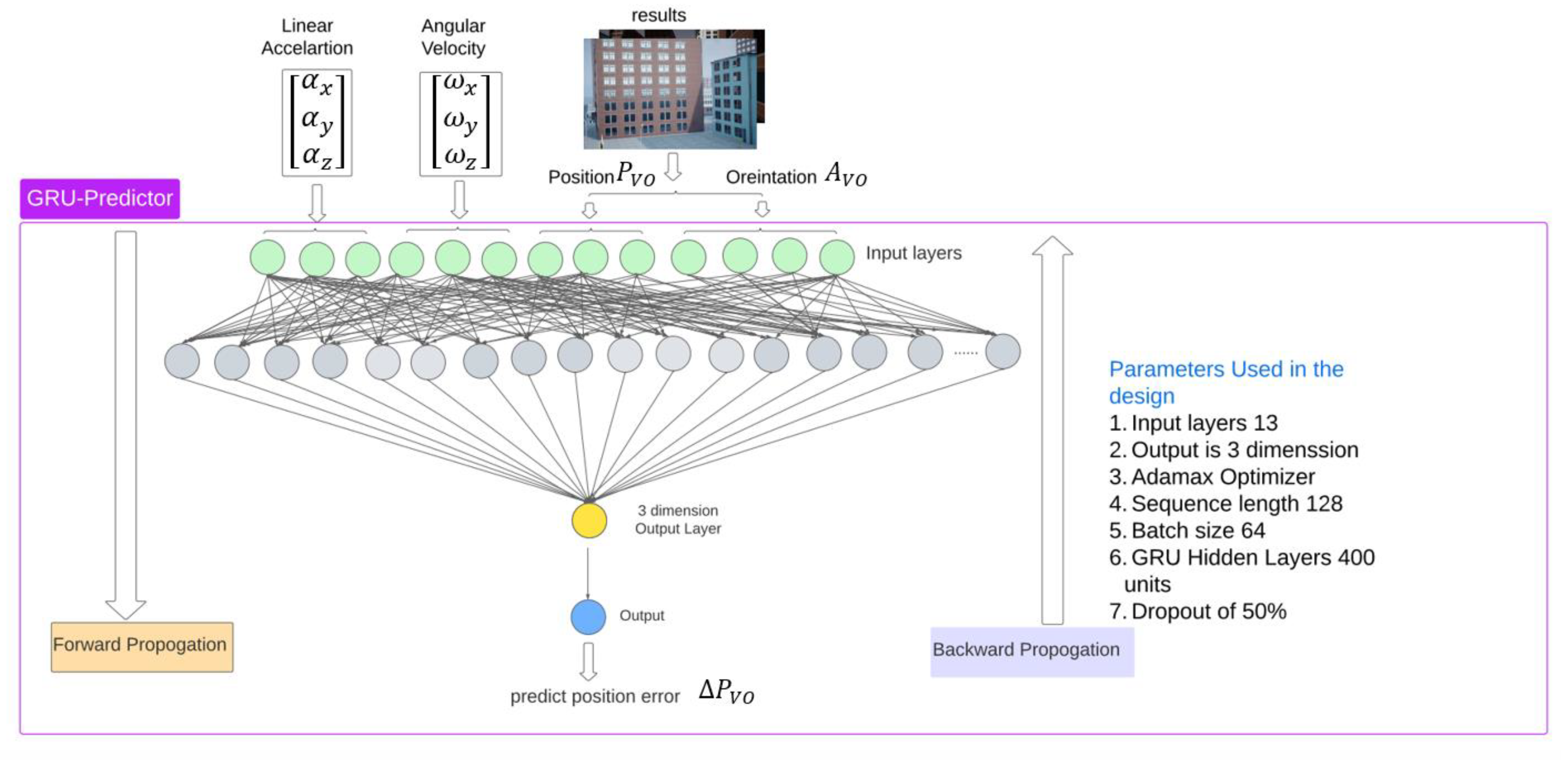
3.2.1. Proposed GRU-aided ESKF VIO Integration (Sub-Filter 1)
ESKF VIO Fusion
GRU-Aided VIO
3.2.2. EKF Based GNSS/IMU Integration (Sub-Filter 2)
3.2.3. Federated Filter for Multi-Sensor Fusion
| Algorithm 1: Algorithm of GNSS/IMU/VO Multi-Sensor Navigation System |
Initialize:
Prediction Phase:
Measurement Phase for sub-filters:
Measurement update for Global filter:
|
4. Experimental Setup
5. Test and Results
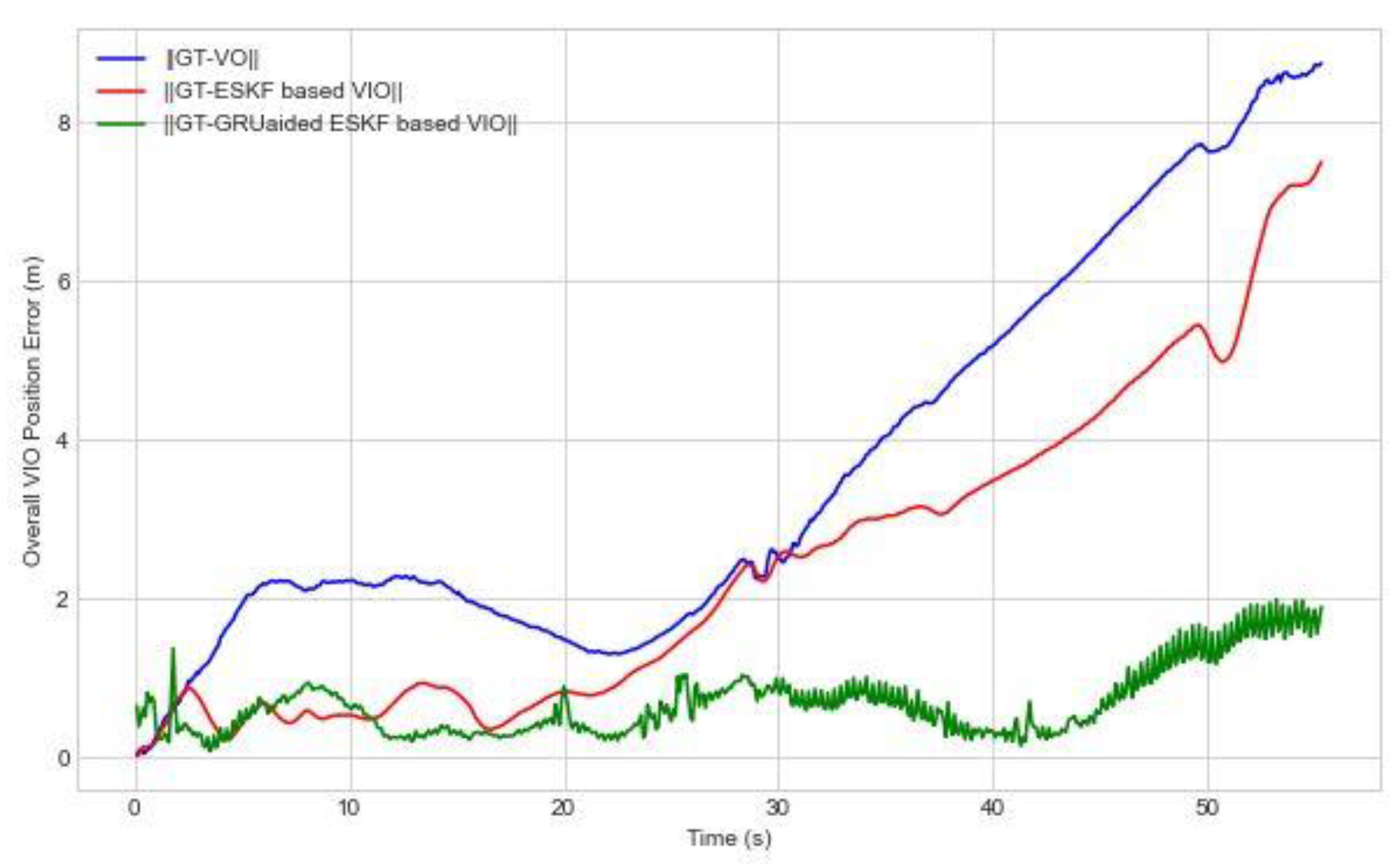
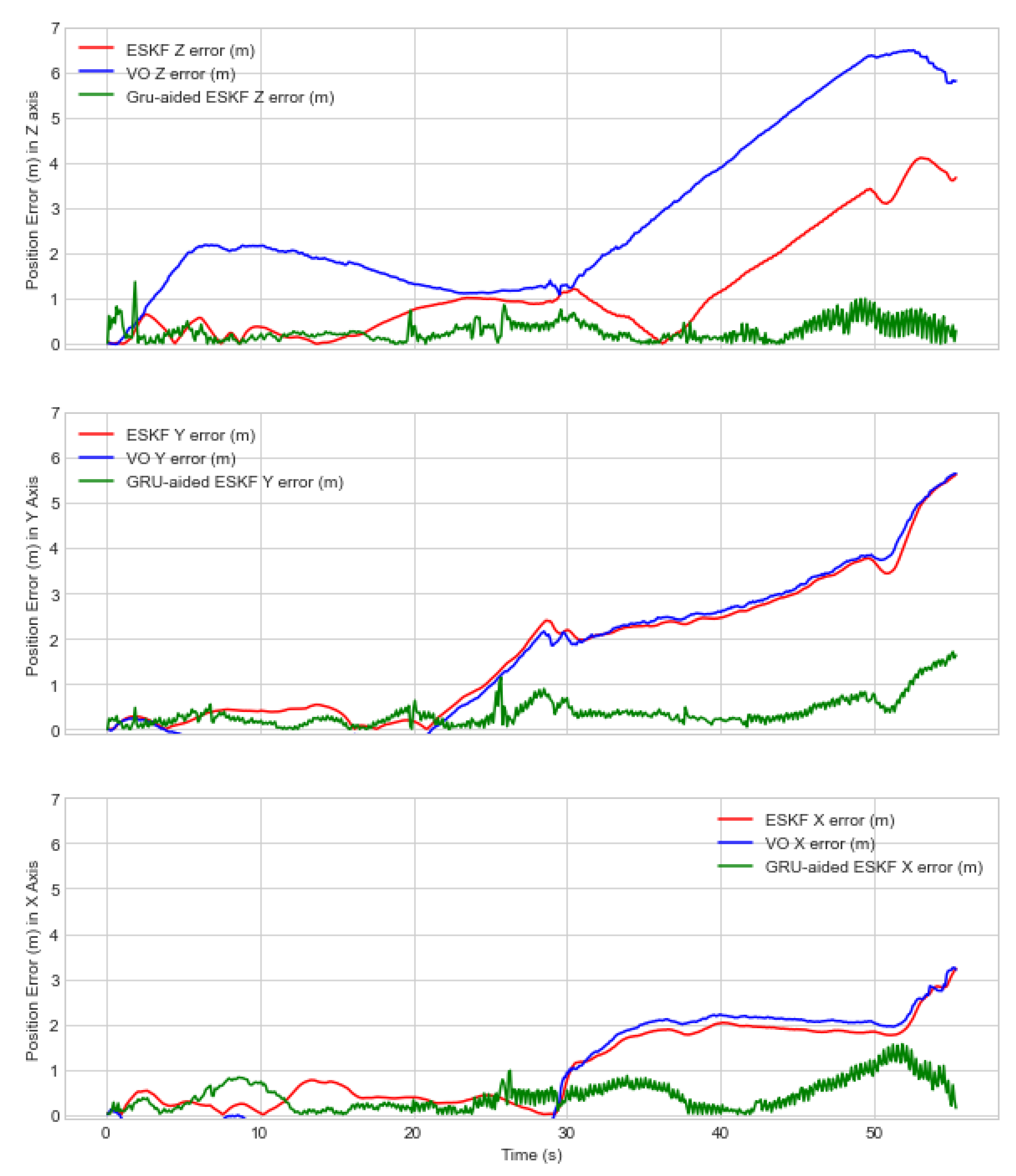
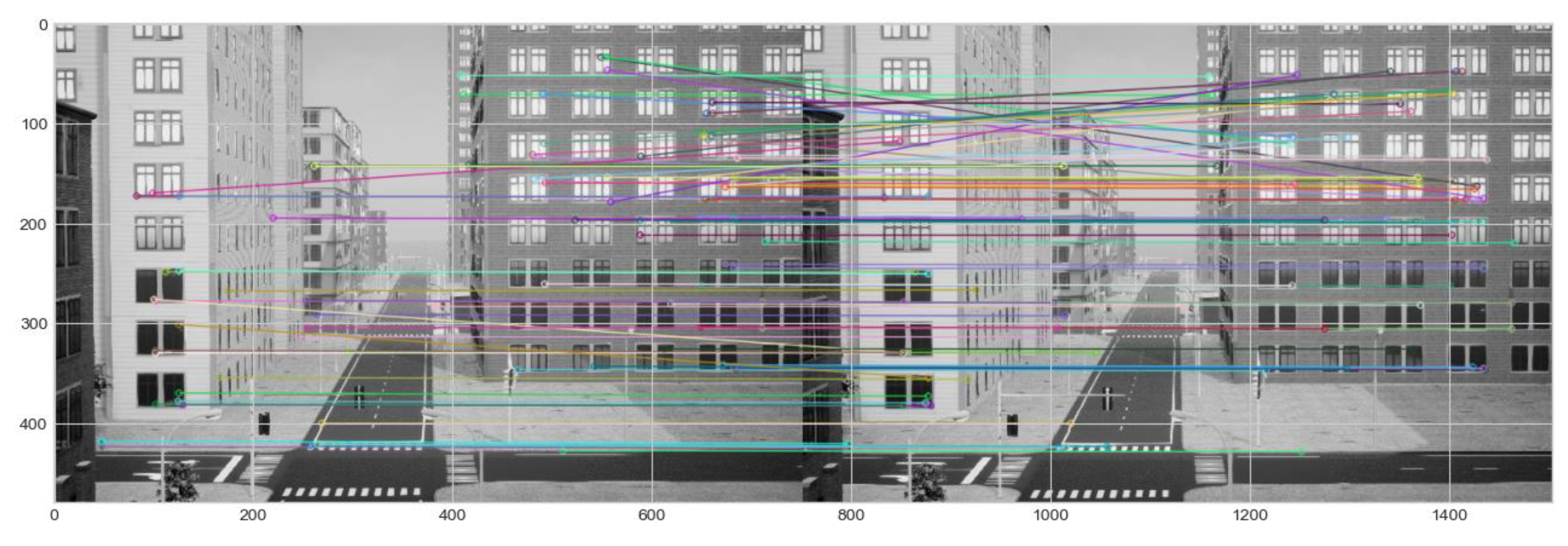
5.1. Experiment 1—Dense Urban Cynon
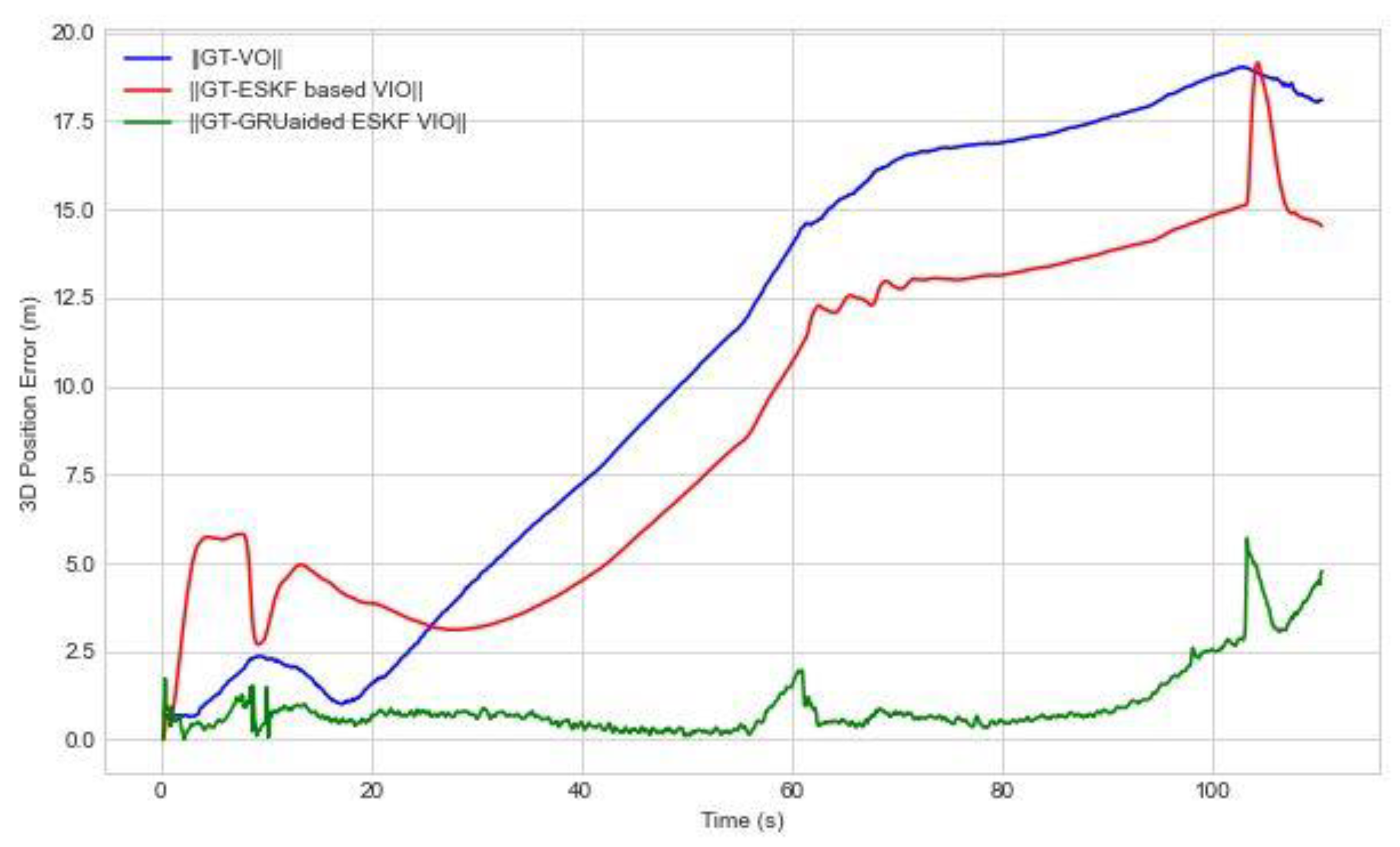
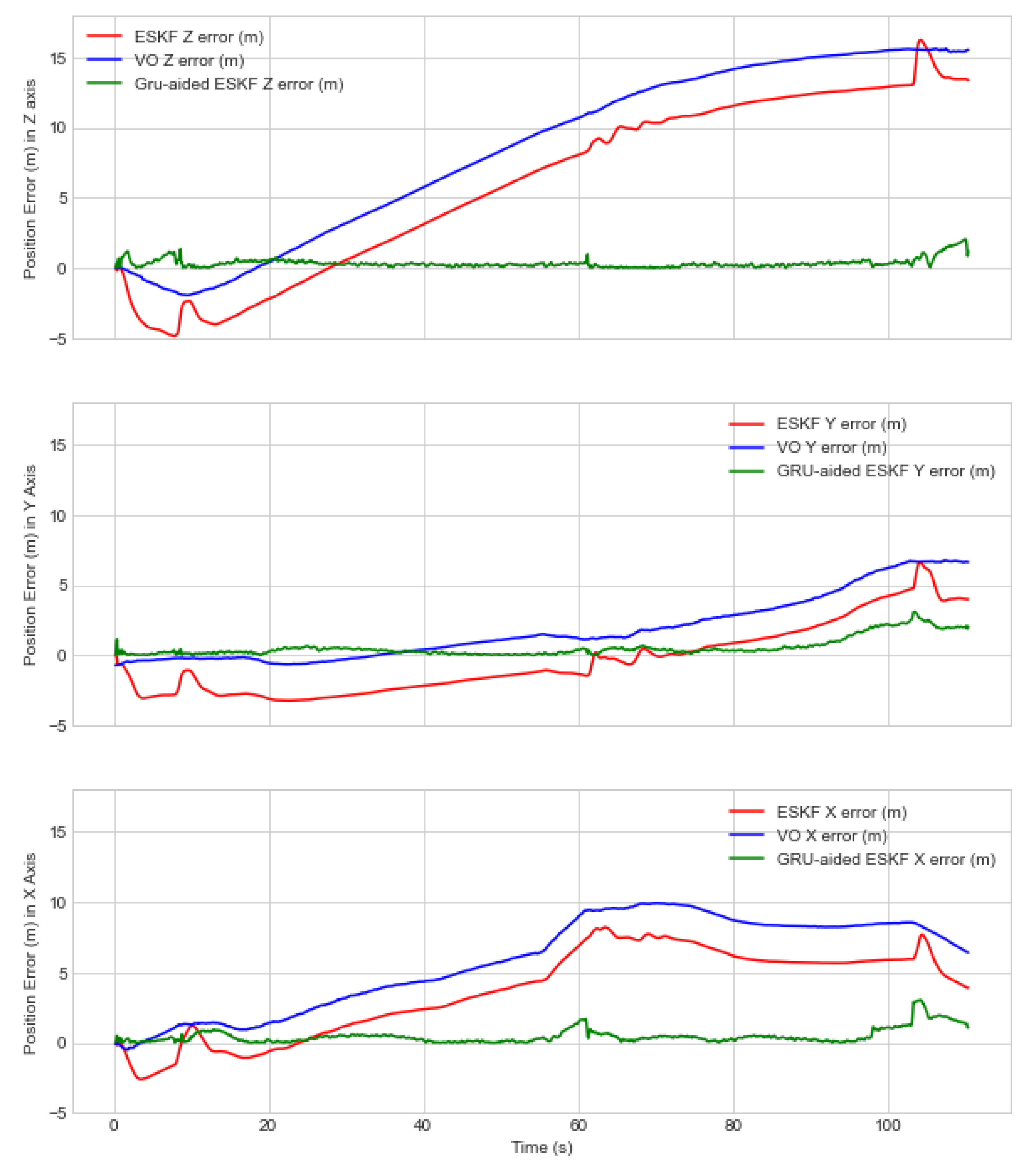
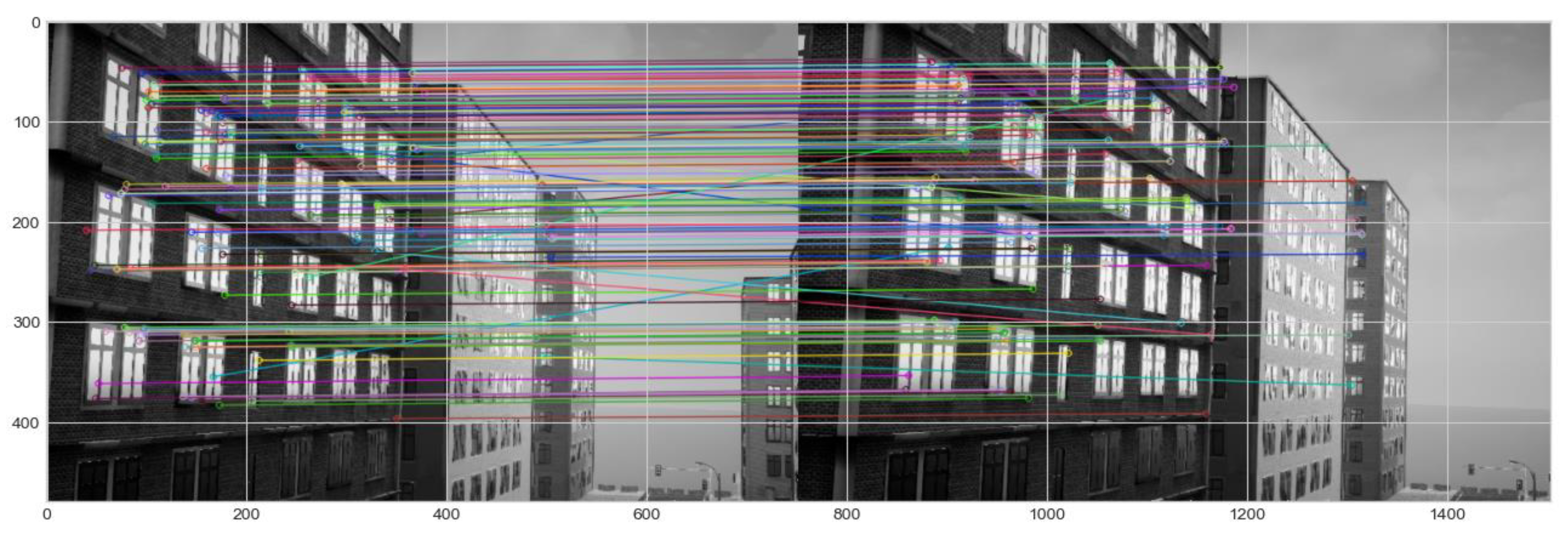
5.2. Experiment 2—Semi-Structured Urban Environment
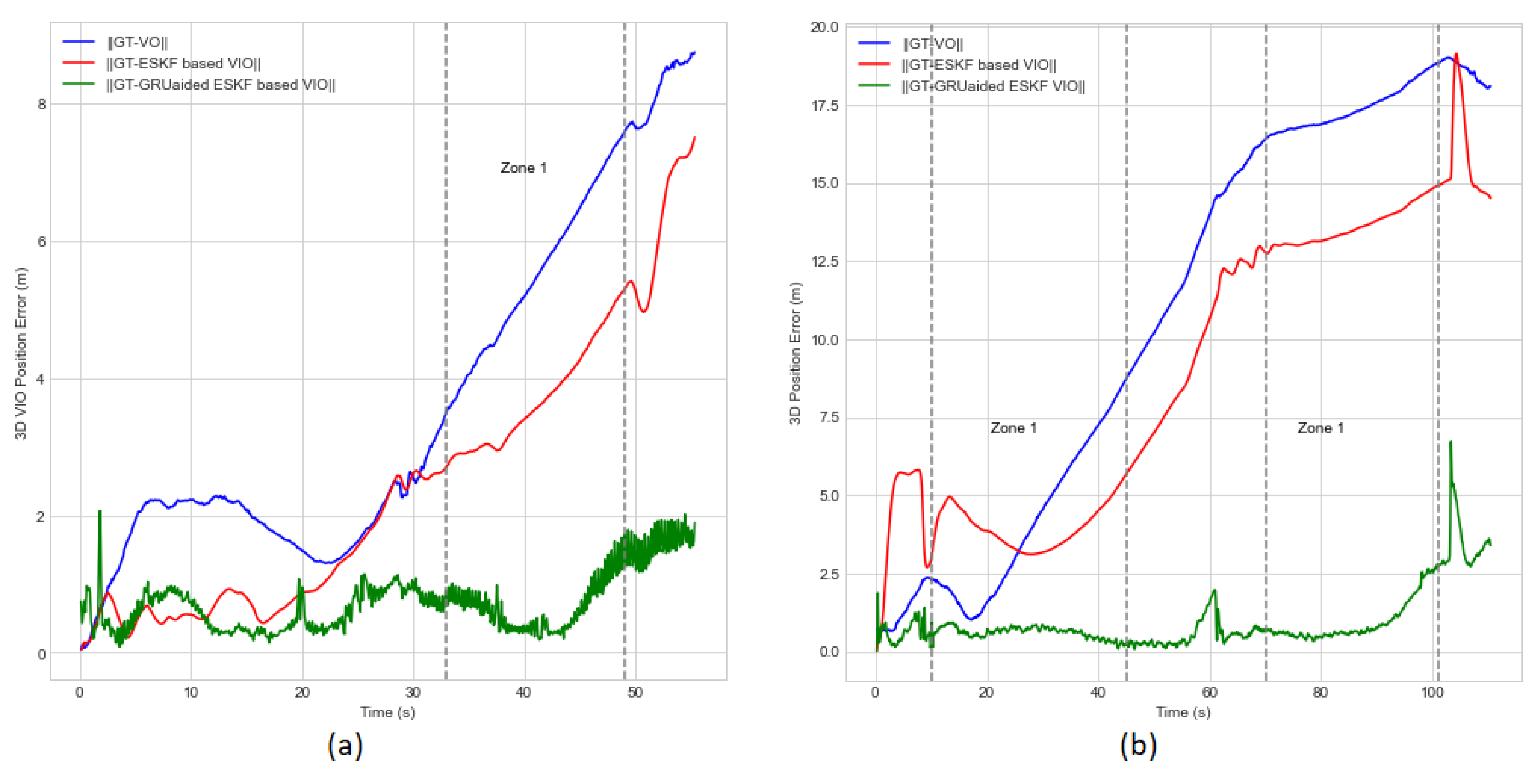
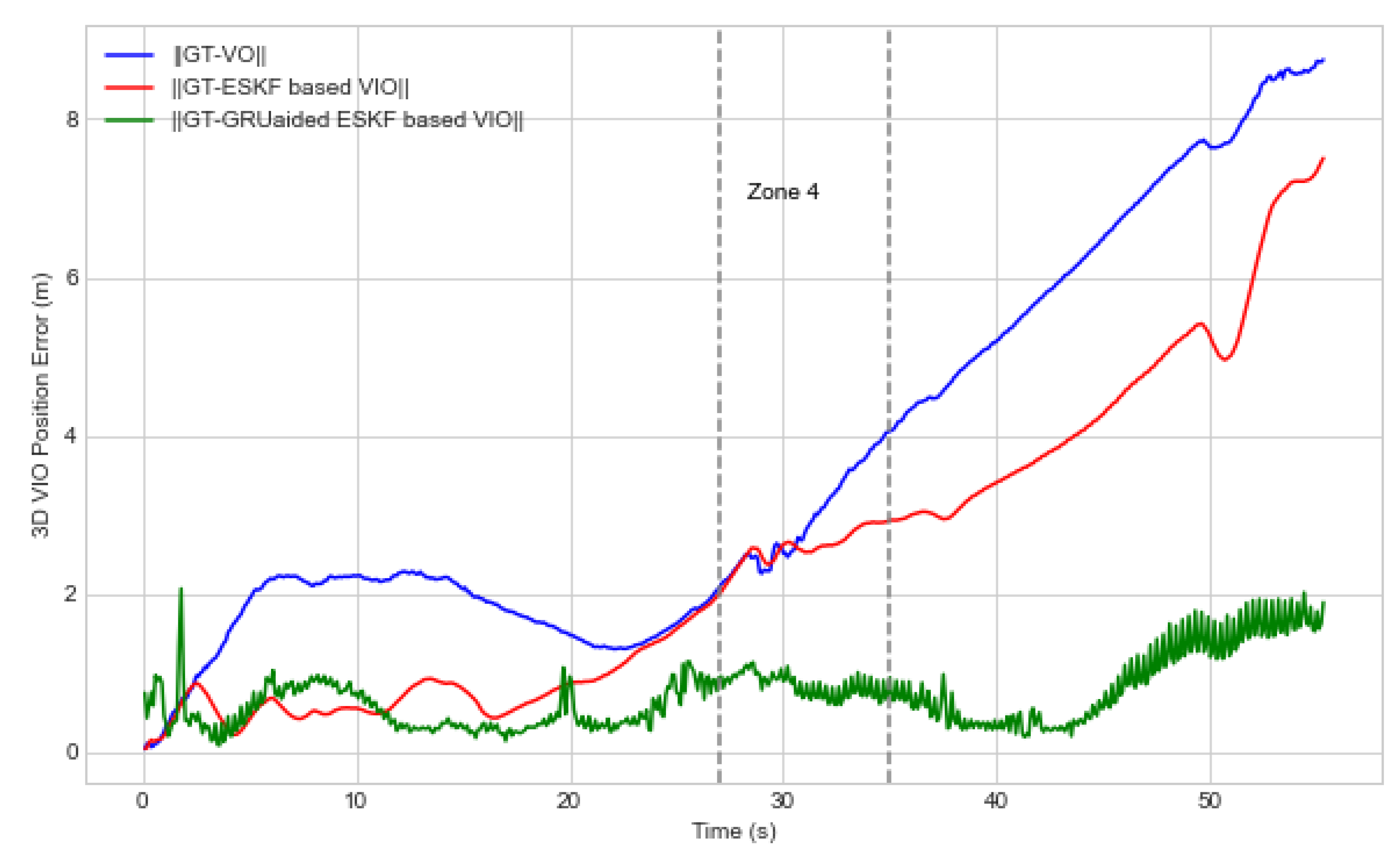
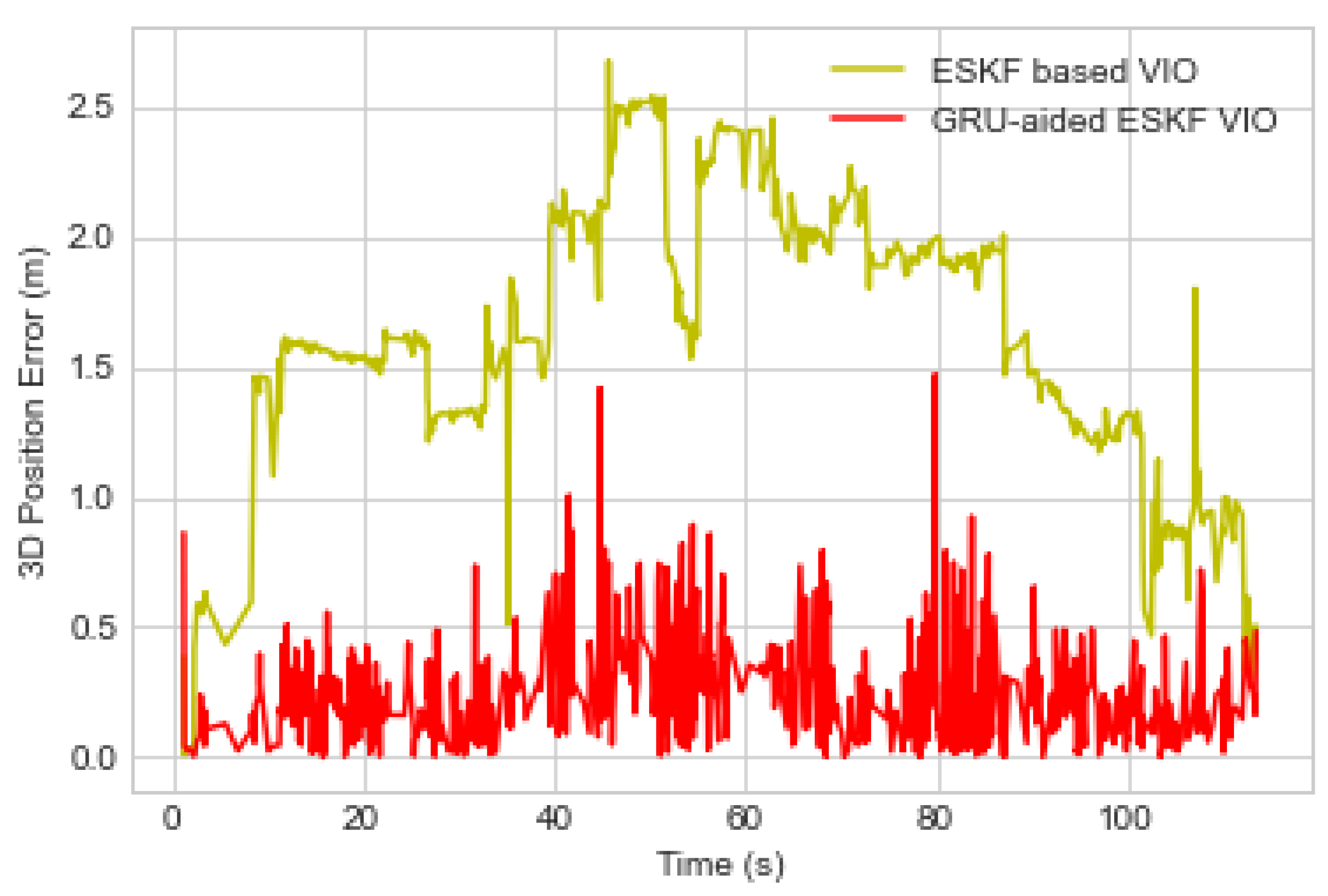
5.3. Performance Evaluation Based on Zone Categories
5.4. Performance Comparison with Other Datasets
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arafat, M.Y.; Alam, M.M.; Moh, S. Vision-Based Navigation Techniques for Unmanned Aerial Vehicles: Review and Challenges. Drones 2023, 7, 89. [Google Scholar] [CrossRef]
- Alkendi, Y.; Seneviratne, L.; Zweiri, Y. State of the Art in Vision-Based Localization Techniques for Autonomous Navigation Systems. IEEE Access 2021, 9, 76847–76874. [Google Scholar] [CrossRef]
- Afia, A.B.; Escher, A.; Macabiau, C. A Low-cost GNSS/IMU/Visual monoSLAM/WSS Integration Based on Federated Kalman Filtering for Navigation in Urban Environments. In Proceedings of the 28th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015. [Google Scholar]
- Lee, Y.D.; Kim, L.W.; Lee, H.K. A tightly-coupled compressed-state constraint Kalman Filter for integrated visual-inertial-Global Navigation Satellite System navigation in GNSS-Degraded environments. IET Radar Sonar Navig. 2022, 16, 1344–1363. [Google Scholar] [CrossRef]
- Liao, J.; Li, X.; Wang, X.; Li, S.; Wang, H. Enhancing navigation performance through visual-inertial odometry in GNSS-degraded environment. GPS Solut. 2021, 25, 50. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Mourikis, A.I.; Roumeliotis, S.I. A multi-state constraint Kalman filter for vision-aided inertial navigation. In Proceedings of the Proceedings 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 3565–3572. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodriguez, J.J.G.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual-Inertial, and Multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Geneva, P.; Eckenhoff, K.; Lee, W.; Yang, Y.; Huang, G. OpenVINS: A Research Platform for Visual-Inertial Estimation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 4666–4672. [Google Scholar] [CrossRef]
- Zhu, C.; Meurer, M.; Günther, C. Integrity of Visual Navigation—Developments, Challenges, and Prospects. Navig. J. Inst. Navig. 2022, 69, 518. [Google Scholar] [CrossRef]
- JDai, J.; Hao, X.; Liu, S.; Ren, Z. Research on UAV Robust Adaptive Positioning Algorithm Based on IMU/GNSS/VO in Complex Scenes. Sensors 2022, 22, 2832. [Google Scholar] [CrossRef]
- Wagstaff, B.; Wise, E.; Kelly, J. A Self-Supervised, Differentiable Kalman Filter for Uncertainty-Aware Visual-Inertial Odometry. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, AIM, Sapporo, Japan, 11–15 July 2022; pp. 1388–1395. [Google Scholar] [CrossRef]
- Zhai, Y.; Fu, Y.; Wang, S.; Zhan, X. Mechanism Analysis and Mitigation of Visual Navigation System Vulnerability. In China Satellite Navigation Conference (CSNC 2021) Proceedings; Springer: Singapore, 2021; Volume 773, pp. 515–524. [Google Scholar] [CrossRef]
- Markovic, L.; Kovac, M.; Milijas, R.; Car, M.; Bogdan, S. Error State Extended Kalman Filter Multi-Sensor Fusion for Unmanned Aerial Vehicle Localization in GPS and Magnetometer Denied Indoor Environments. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems, ICUAS 2022, Dubrovnik, Croatia, 21–24 June 2022; pp. 184–190. [Google Scholar] [CrossRef]
- Xiong, X.; Chen, W.; Liu, Z.; Shen, Q. DS-VIO: Robust and Efficient Stereo Visual Inertial Odometry based on Dual Stage EKF. arXiv 2019, arXiv:1905.00684. [Google Scholar]
- Fanin, F.; Hong, J.H. Visual Inertial Navigation for a Small UAV Using Sparse and Dense Optical Flow. In Proceedings of the 2019 Workshop on Research, Education and Development of Unmanned Aerial Systems (RED UAS), Cranfield, UK, 25–27 November 2019. [Google Scholar]
- Bloesch, M.; Burri, M.; Omari, S.; Hutter, M.; Siegwart, R. Iterated extended Kalman filter based visual-inertial odometry using direct photometric feedback. Int. J. Robot. Res. 2017, 36, 1053–1072. [Google Scholar] [CrossRef]
- Sun, K.; Mohta, K.; Pfrommer, B.; Watterson, M.; Liu, S.; Mulgaonkar, Y.; Taylor, C.J.; Kumar, V. Robust Stereo Visual Inertial Odometry for Fast Autonomous Flight. IEEE Robot. Autom. Lett. 2018, 3, 965–972. [Google Scholar] [CrossRef]
- Li, G.; Yu, L.; Fei, S. A Binocular MSCKF-Based Visual Inertial Odometry System Using LK Optical Flow. J. Intell. Robot. Syst. Theory Appl. 2020, 100, 1179–1194. [Google Scholar] [CrossRef]
- Yang, Y.; Geneva, P.; Eckenhoff, K.; Huang, G. Visual-Inertial Odometry with Point and Line Features. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Macau, China, 3–8 November 2019; pp. 2447–2454. [Google Scholar] [CrossRef]
- Ma, F.; Shi, J.; Yang, Y.; Li, J.; Dai, K. ACK-MSCKF: Tightly-coupled ackermann multi-state constraint kalman filter for autonomous vehicle localization. Sensors 2019, 19, 4816. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Pang, B.; Song, Y.; Yuan, X.; Xu, Q.; Li, Y. Robust Visual-Inertial Odometry Based on a Kalman Filter and Factor Graph. IEEE Trans. Intell. Transp. Syst. 2023, 24, 7048–7060. [Google Scholar] [CrossRef]
- Omotuyi, O.; Kumar, M. UAV Visual-Inertial Dynamics (VI-D) Odometry using Unscented Kalman Filter. IFAC Pap. 2021, 54, 814–819. [Google Scholar] [CrossRef]
- Sang, X.; Li, J.; Yuan, Z.; Yu, X.; Zhang, J.; Zhang, J.; Yang, P. Invariant Cubature Kalman Filtering-Based Visual-Inertial Odometry for Robot Pose Estimation. IEEE Sensors J. 2022, 22, 23413–23422. [Google Scholar] [CrossRef]
- Xu, J.; Yu, H.; Teng, R. Visual-inertial odometry using iterated cubature Kalman filter. In Proceedings of the 30th Chinese Control and Decision Conference, CCDC, Shenyang, China, 9–11 June 2018; pp. 3837–3841. [Google Scholar] [CrossRef]
- Liu, Y.; Xiong, R.; Wang, Y.; Huang, H.; Xie, X.; Liu, X.; Zhang, G. Stereo Visual-Inertial Odometry with Multiple Kalman Filters Ensemble. IEEE Trans. Ind. Electron. 2016, 63, 6205–6216. [Google Scholar] [CrossRef]
- Kim, S.; Petrunin, I.; Shin, H.-S. A Review of Kalman Filter with Artificial Intelligence Techniques. In Proceedings of the Integrated Communications, Navigation and Surveillance Conference, ICNS, Dulles, VA, USA, 5–7 April 2022; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Jwo, D.-J.; Biswal, A.; Mir, I.A. Artificial Neural Networks for Navigation Systems: A Review of Recent Research. Appl. Sci. 2023, 13, 4475. [Google Scholar] [CrossRef]
- Shaukat, N.; Ali, A.; Moinuddin, M.; Otero, P. Underwater Vehicle Localization by Hybridization of Indirect Kalman Filter and Neural Network. In Proceedings of the 2021 7th International Conference on Mechatronics and Robotics Engineering, ICMRE 2021, Budapest, Hungary, 3–5 February 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 111–115. [Google Scholar] [CrossRef]
- Shaukat, N.; Ali, A.; Iqbal, M.J.; Moinuddin, M.; Otero, P. Multi-sensor fusion for underwater vehicle localization by augmentation of rbf neural network and error-state kalman filter. Sensors 2021, 21, 1149. [Google Scholar] [CrossRef]
- Vargas-Meléndez, L.; Boada, B.L.; Boada, M.J.L.; Gauchía, A.; Díaz, V. A sensor fusion method based on an integrated neural network and Kalman Filter for vehicle roll angle estimation. Sensors 2016, 16, 1400. [Google Scholar] [CrossRef]
- Jingsen, Z.; Wenjie, Z.; Bo, H.; Yali, W. Integrating Extreme Learning Machine with Kalman Filter to Bridge GPS Outages. In Proceedings of the 2016 3rd International Conference on Information Science and Control Engineering, ICISCE 2016, Beijing, China, 8–10 July 2016; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2016; pp. 420–424. [Google Scholar] [CrossRef]
- Zhang, X.; Mu, X.; Liu, H.; He, B.; Yan, T. Application of Modified EKF Based on Intelligent Data Fusion in AUV Navigation; Application of Modified EKF Based on Intelligent Data Fusion in AUV Navigation. In Proceedings of the 2019 IEEE Underwater Technology (UT), Kaohsiung, Taiwan, 16–19 April 2019. [Google Scholar]
- Al Bitar, N.; Gavrilov, A.I. Neural_Networks_Aided_Unscented_Kalman_Filter_for_Integrated_INS_GNSS_Systems. In Proceedings of the 27th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), St. Petersburg, Russia, 25–17 May 2020; pp. 1–4. [Google Scholar]
- Miljković, Z.; Vuković, N.; Mitić, M. Neural extended Kalman filter for monocular SLAM in indoor environment. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2016, 230, 856–866. [Google Scholar] [CrossRef]
- Choi, M.; Sakthivel, R.; Chung, W.K. Neural Network-Aided Extended Kalman Filter for SLAM Problem. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 1686–1690. [Google Scholar]
- Kotov, K.Y.; Maltsev, A.S.; Sobolev, M.A. Recurrent neural network and extended Kalman filter in SLAM problem. IFAC Proc. Vol. 2013, 46, 23–26. [Google Scholar] [CrossRef]
- Chen, L.; Fang, J. A Hybrid Prediction Method for Bridging GPS Outages in High-Precision POS Application. IEEE Trans. Instrum. Meas. 2014, 63, 1656–1665. [Google Scholar] [CrossRef]
- Lee, J.K.; Jekeli, C. Neural Network Aided Adaptive Filtering and Smoothing for an Integrated INS/GPS Unexploded Ordnance Geolocation System. J. Navig. 2010, 63, 251–267. [Google Scholar] [CrossRef]
- Bi, S.; Ma, L.; Shen, T.; Xu, Y.; Li, F. Neural network assisted Kalman filter for INS/UWB integrated seamless quadrotor localization. PeerJ Comput. Sci. 2021, 7, e630. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Zhou, Y.; Huang, T. A Novel Method for AI-Assisted INS/GNSS Navigation System Based on CNN-GRU and CKF during GNSS Outage. Remote Sens. 2022, 14, 4494. [Google Scholar] [CrossRef]
- Xie, D.; Jiang, J.; Wu, J.; Yan, P.; Tang, Y.; Zhang, C.; Liu, J. A Robust GNSS/PDR Integration Scheme with GRU-Based Zero-Velocity Detection for Mass-Pedestrians. Remote Sens. 2022, 14, 300. [Google Scholar] [CrossRef]
- Jiang, Y.; Nong, X. A Radar Filtering Model for Aerial Surveillance Base on Kalman Filter and Neural Network. In Proceedings of the IEEE International Conference on Software Engineering and Service Sciences, ICSESS, Beijing, China, 16–18 October 2020; pp. 57–60. [Google Scholar] [CrossRef]
- Miao, Z.; Shi, H.; Zhang, Y.; Xu, F. Neural network-aided variational Bayesian adaptive cubature Kalman filtering for nonlinear state estimation. Meas. Sci. Technol. 2017, 28, 10500. [Google Scholar] [CrossRef]
- Li, C.; Waslander, S. Towards End-to-end Learning of Visual Inertial Odometry with an EKF. In Proceedings of the 2020 17th Conference on Computer and Robot Vision, CRV 2020, Ottawa, ON, Canada, 13–15 May 2020; pp. 190–197. [Google Scholar] [CrossRef]
- Tang, Y.; Jiang, J.; Liu, J.; Yan, P.; Tao, Y.; Liu, J. A GRU and AKF-Based Hybrid Algorithm for Improving INS/GNSS Navigation Accuracy during GNSS Outage. Remote Sens. 2022, 14, 752. [Google Scholar] [CrossRef]
- Hosseinyalamdary, S. Deep Kalman Filter: Simultaneous Multi-Sensor Integration and Modelling; A GNSS/IMU Case Study. Sensors 2018, 18, 1316. [Google Scholar] [CrossRef]
- Song, L.; Duan, Z.; He, B.; Li, Z. Application of Federal Kalman Filter with Neural Networks in the Velocity and Attitude Matching of Transfer Alignment. Complexity 2018, 2018, 3039061. [Google Scholar] [CrossRef]
- Li, D.; Wu, Y.; Zhao, J. Novel Hybrid Algorithm of Improved CKF and GRU for GPS/INS. IEEE Access 2020, 8, 202836–202847. [Google Scholar] [CrossRef]
- Gao, X.; Luo, H.; Ning, B.; Zhao, F.; Bao, L.; Gong, Y.; Xiao, Y.; Jiang, J. RL-AKF: An Adaptive Kalman Filter Navigation Algorithm Based on Reinforcement Learning for Ground Vehicles. Remote Sens. 2020, 12, 1704. [Google Scholar] [CrossRef]
- Aslan, M.F.; Durdu, A.; Sabanci, K. Visual-Inertial Image-Odometry Network (VIIONet): A Gaussian process regression-based deep architecture proposal for UAV pose estimation. Measurement 2022, 194, 111030. [Google Scholar] [CrossRef]
- Chen, C.; Lu, C.X.; Wang, B.; Trigoni, N.; Markham, A. DynaNet: Neural Kalman Dynamical Model for Motion Estimation and Prediction. IEEE Trans. Neural Networks Learn. Syst. 2021, 32, 5479–5491. [Google Scholar] [CrossRef] [PubMed]
- Yusefi, A.; Durdu, A.; Aslan, M.F.; Sungur, C. LSTM and Filter Based Comparison Analysis for Indoor Global Localization in UAVs. IEEE Access 2021, 9, 10054–10069. [Google Scholar] [CrossRef]
- Zuo, S.; Shen, K.; Zuo, J. Robust Visual-Inertial Odometry Based on Deep Learning and Extended Kalman Filter. In Proceedings of the 2021 China Automation Congress, CAC 2021, Beijing, China, 22–24 October 2021; pp. 1173–1178. [Google Scholar] [CrossRef]
- Luo, Y.; Hu, J.; Guo, C. Right Invariant SE2(3)—EKF for Relative Navigation in Learning-based Visual Inertial Odometry. In Proceedings of the 2022 5th International Symposium on Autonomous Systems, ISAS 2022, Hangzhou, China, 8–10 April 2022. [Google Scholar] [CrossRef]
- Bhatti, U.I.; Ochieng, W.Y. Failure Modes and Models for Integrated GPS/INS Systems. J. Navig. 2007, 60, 327–348. [Google Scholar] [CrossRef]
- YDu, Y.; Wang, J.; Rizos, C.; El-Mowafy, A. Vulnerabilities and integrity of precise point positioning for intelligent transport systems: Overview and analysis. Satell. Navig. 2021, 2, 3. [Google Scholar] [CrossRef]
- Burri, M.; Nikolic, J.; Gohl, P.; Schneider, T.; Rehder, J.; Omari, S.; Achtelik, M.W.; Siegwart, R. The EuRoC micro aerial vehicle datasets. Int. J. Robot. Res. 2016, 35, 1157–1163. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Zhong, Y.; Zhu, X. Cubature Kalman Filter With Both Adaptability and Robustness for Tightly-Coupled GNSS/INS Integration. IEEE Sensors J. 2021, 21, 14997–15011. [Google Scholar] [CrossRef]
- Gao, B.; Gao, S.; Zhong, Y.; Hu, G.; Gu, C. Interacting multiple model estimation-based adaptive robust unscented Kalman filter. Int. J. Control Autom. Syst. 2017, 15, 2013–2025. [Google Scholar] [CrossRef]
- Gao, G.; Zhong, Y.; Gao, S.; Gao, B. Double-Channel Sequential Probability Ratio Test for Failure Detection in Multisensor Integrated Systems. IEEE Trans. Instrum. Meas. 2021, 70, 1–14. [Google Scholar] [CrossRef]
- Gao, G.; Gao, B.; Gao, S.; Hu, G.; Zhong, Y. A Hypothesis Test-Constrained Robust Kalman Filter for INS/GNSS Integration With Abnormal Measurement. IEEE Trans. Veh. Technol. 2022, 72, 1662–1673. [Google Scholar] [CrossRef]
- Gao, B.; Li, W.; Hu, G.; Zhong, Y.; Zhu, X. Mahalanobis distance-based fading cubature Kalman filter with augmented mechanism for hypersonic vehicle INS/CNS autonomous integration. Chin. J. Aeronaut. 2022, 35, 114–128. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Zhong, Y.; Zhu, X. Cubature rule-based distributed optimal fusion with identification and prediction of kinematic model error for integrated UAV navigation. Aerosp. Sci. Technol. 2021, 109, 106447. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Zhu, X.; Zhong, Y. A Robust Cubature Kalman Filter with Abnormal Observations Identification Using the Mahalanobis Distance Criterion for Vehicular INS/GNSS Integration. Sensors 2019, 19, 5149. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Gao, B.; Zhong, Y.; Ni, L.; Gu, C. Robust Unscented Kalman Filtering With Measurement Error Detection for Tightly Coupled INS/GNSS Integration in Hypersonic Vehicle Navigation. IEEE Access 2019, 7, 151409–151421. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y. Constrained ESKF for UAV Positioning in Indoor Corridor Environment Based on IMU and WiFi. Sensors 2022, 22, 391. [Google Scholar] [CrossRef]
- Geragersian, P.; Petrunin, I.; Guo, W.; Grech, R. An INS/GNSS fusion architecture in GNSS denied environments using gated recurrent units. In Proceedings of the AIAA Science and Technology Forum and Exposition, AIAA SciTech Forum 2022, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Kourabbaslou, S.S.; Zhang, A.; Atia, M.M. A Novel Design Framework for Tightly Coupled IMU/GNSS Sensor Fusion Using Inverse-Kinematics, Symbolic Engines, and Genetic Algorithms. IEEE Sens. J. 2019, 19, 11424–11436. [Google Scholar] [CrossRef]
- Ramirez-Atencia, C.; Camacho, D. Extending QGroundControl for Automated Mission Planning of UAVs. Sensors 2018, 18, 2339. [Google Scholar] [CrossRef]
- Hernandez, G.E.V.; Petrunin, I.; Shin, H.-S.; Gilmour, J. Robust multi-sensor navigation in GNSS degraded environments. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar] [CrossRef]





| Error Sources | Fault Event | References | Error Effect |
|---|---|---|---|
| Feature Tracking Error | Navigation environment error | [45] | Motion blur |
| Outlier Error | [52] | Overexposure | |
| [12,45] | Rapid Motion | ||
| Feature Extraction Error | [10,12] | Overshoot | |
| Feature Mismatch | Data Association error | ||
| Feature Domain Bias | [52] | Lighting Variation |
| Parameter | Value |
|---|---|
| Accelerometer Bias Stability | |
| Gyroscope Bias Stability | |
| Angle Random Walk | |
| Velocity Random Walk |
| Experiment | Method | RMSE(m)-x-axis | RMSE(m)-y-axis | RMSE(m)-z-axis | RMSE(m)-Overall |
|---|---|---|---|---|---|
| 1 | VO | 1.4 | 2.3 | 3.4 | 4.3 |
| ESKF VIO | 1.3 | 2.2 | 1.6 | 3.1 | |
| GRU-aided ESKF VIO | 0.5 | 0.4 | 0.3 | 0.7 | |
| 2 | VO | 6.6 | 2.9 | 10.4 | 12.6 |
| ESKF VIO | 4.7 | 2.5 | 8.6 | 10.1 | |
| GRU-aided ESKF VIO | 0.8 | 0.9 | 0.5 | 1.3 |
| Experiment | Method | Maximum Error in x-axis (m)- | Maximum Error in y-axis (m)- | Maximum Error in z-axis (m)- | Maximum 3D Error (m)- |
|---|---|---|---|---|---|
| ESKF VIO | 3.2 | 5.6 | 4.1 | 7.5 | |
| 1 | GRU-aided ESKF VIO | 1.5 | 1.6 | 1.2 | 1.9 |
| ESKF VIO | 8.2 | 6.6 | 16.2 | 19.1 | |
| 2 | GRU-aided ESKF VIO | 5.0 | 4.4 | 3.0 | 6.8 |
| Algorithms | 3D RMSE Position Error (m) |
|---|---|
| Faulted-VO/GNSS/IMU | 1.2 |
| Faulted-VIO-ESKF/GNSS/IMU | 0.7 |
| Faulted-GRU-aided-ESKF-VIO/GNSS/IMU | 0.09 |
| Faulted-VO/Faulted-GNSS/IMU | 1.5 |
| Faulted-ESKF-VIO/Faulted-GNSS/IMU | 1.0 |
| Faulted-GRU-aided-ESKF-VIO/Faulted-GNSS/IMU | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabassum, T.E.; Xu, Z.; Petrunin, I.; Rana, Z.A. Integrating GRU with a Kalman Filter to Enhance Visual Inertial Odometry Performance in Complex Environments. Aerospace 2023, 10, 923. https://doi.org/10.3390/aerospace10110923
Tabassum TE, Xu Z, Petrunin I, Rana ZA. Integrating GRU with a Kalman Filter to Enhance Visual Inertial Odometry Performance in Complex Environments. Aerospace. 2023; 10(11):923. https://doi.org/10.3390/aerospace10110923
Chicago/Turabian StyleTabassum, Tarafder Elmi, Zhengjia Xu, Ivan Petrunin, and Zeeshan A. Rana. 2023. "Integrating GRU with a Kalman Filter to Enhance Visual Inertial Odometry Performance in Complex Environments" Aerospace 10, no. 11: 923. https://doi.org/10.3390/aerospace10110923
APA StyleTabassum, T. E., Xu, Z., Petrunin, I., & Rana, Z. A. (2023). Integrating GRU with a Kalman Filter to Enhance Visual Inertial Odometry Performance in Complex Environments. Aerospace, 10(11), 923. https://doi.org/10.3390/aerospace10110923







