Research on the Influence of the Disturbance Rejection Rate of a Roll–Pitch Seeker on Stable Tracking Characteristics
Abstract
:1. Introduction
- The stability loop of the seeker is analyzed, which adopts a semi-strap-down mode to realize the stability of the platform.
- According to the analysis of the kinematics and frame structure of the stable platform, the conditions for the seeker to completely isolate the disturbance of the attitude are obtained.
- The closed-loop tracking control model of the roll–pitch seeker is established, and the formula of the frame tracking instruction is derived. Then, the DRR model of the roll frame and pitch frame is established from the angle of frame control, and the influence of interference torque on the DRR is analyzed.
- The tracking ability of the seeker under different amounts of disturbance torque and attitude disturbance is simulated and analyzed.
2. Roll–Pitch Seeker Stability Tracking Principle
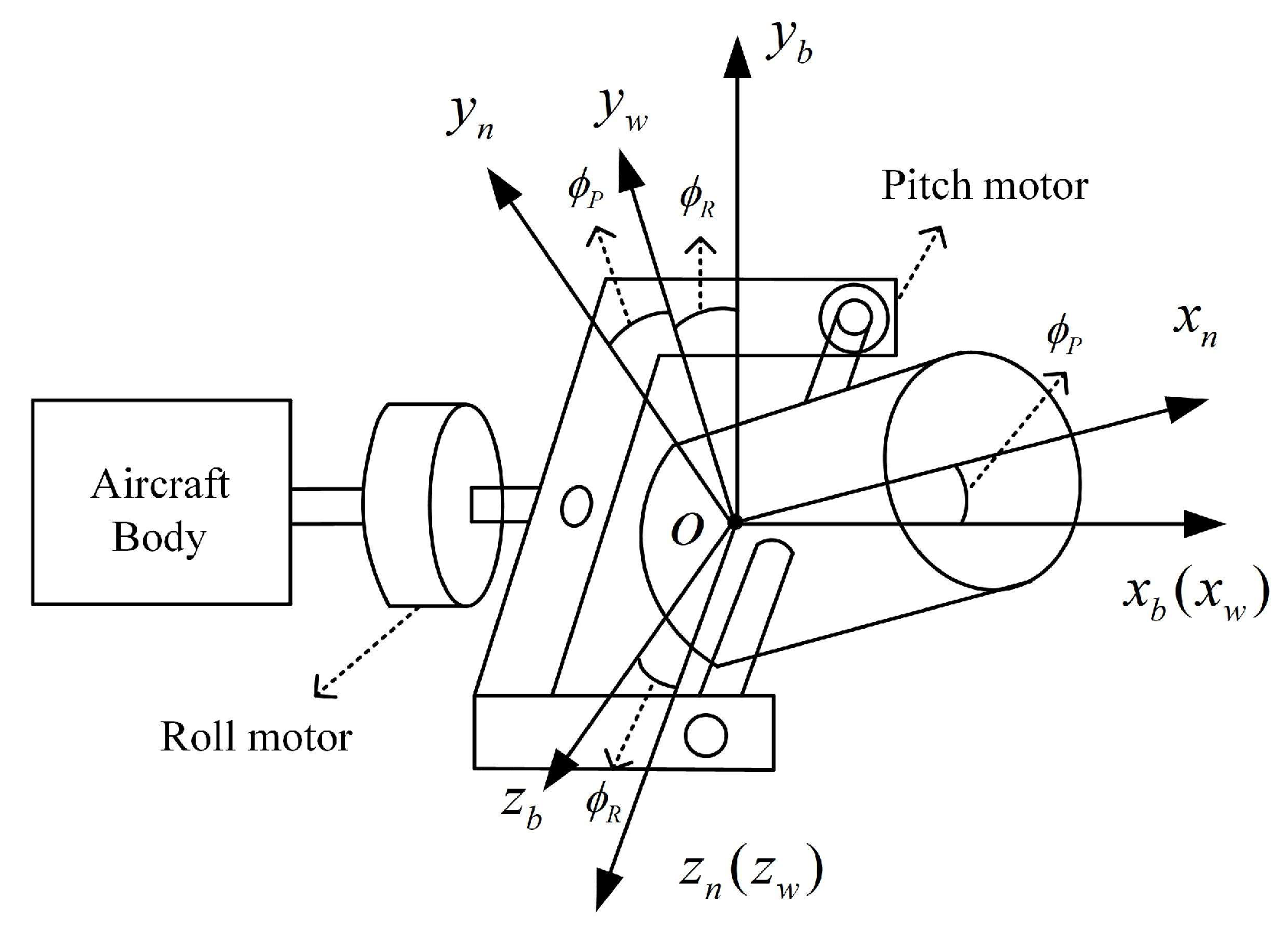
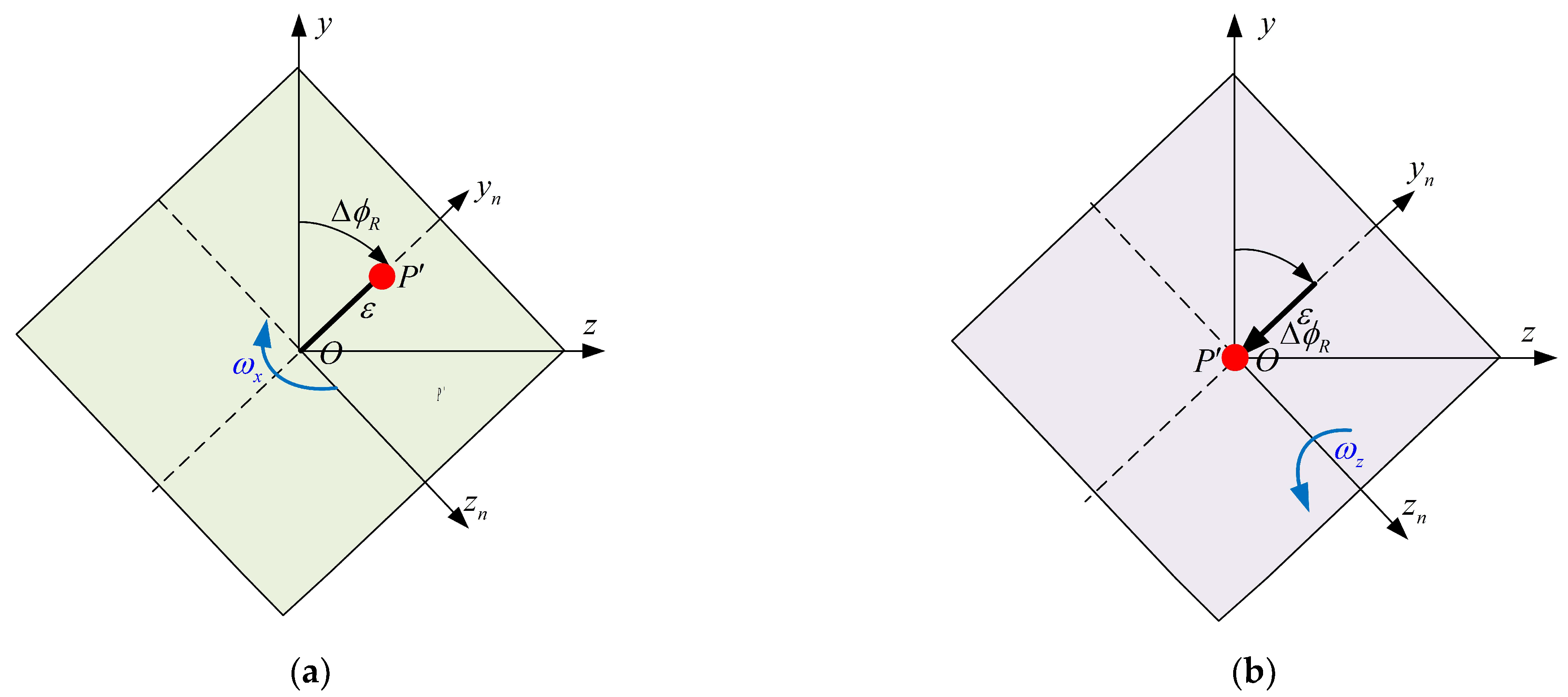
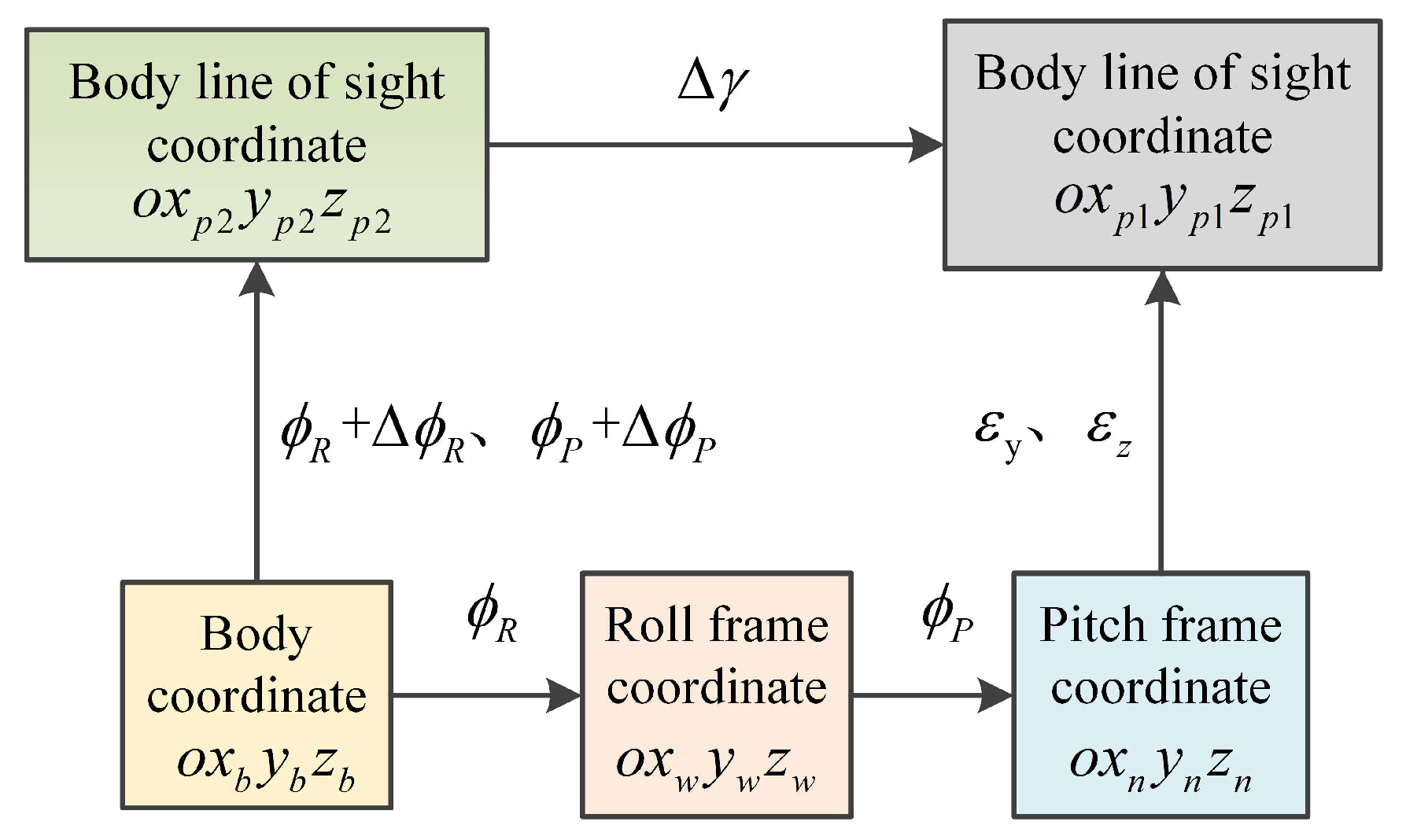
2.1. Kinematics of the Framework Stability Principle
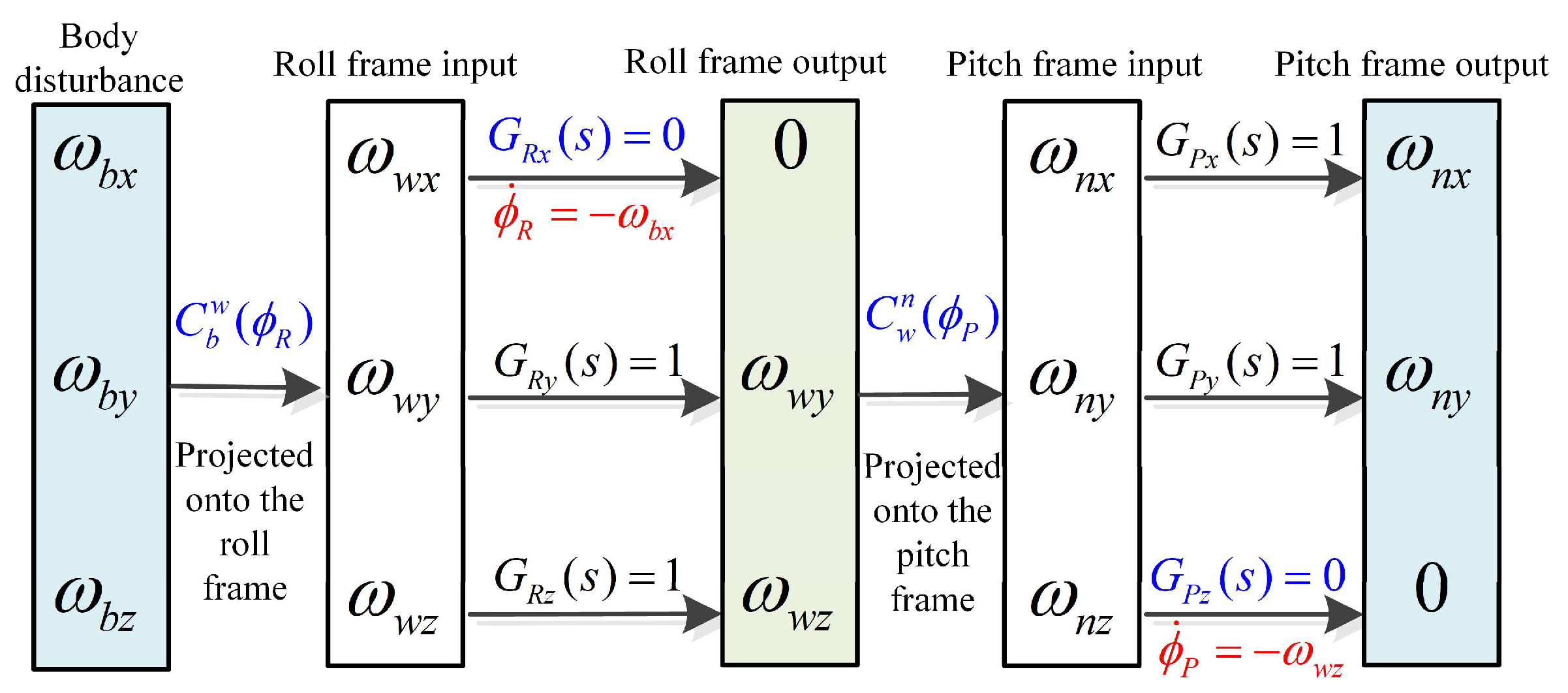
2.2. The Conditions for a Stable Platform to Completely Isolate the Disturbance of the Aircraft Attitude
3. Roll–Pitch Seeker Semi-Strap-Down Stability Control Scheme
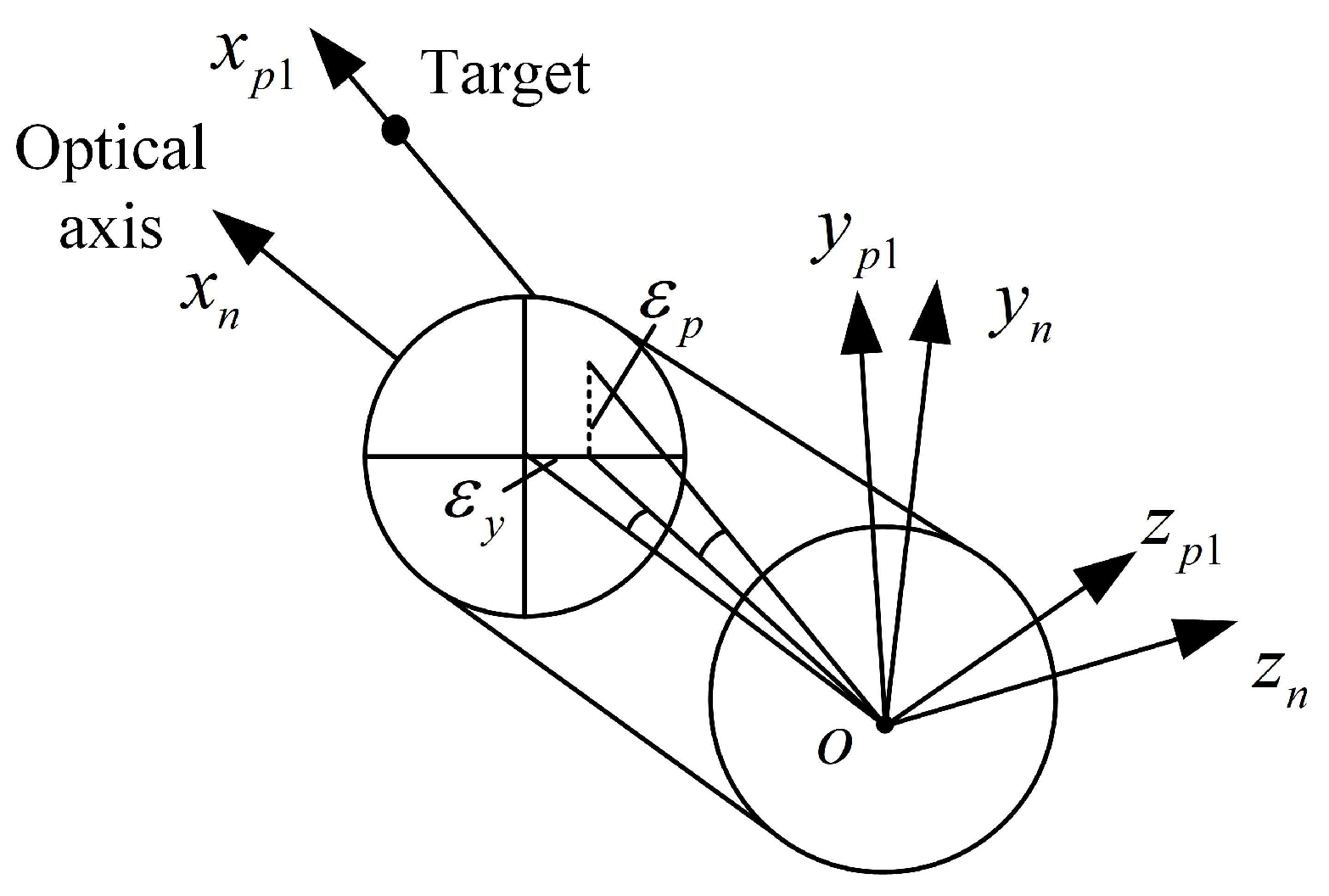
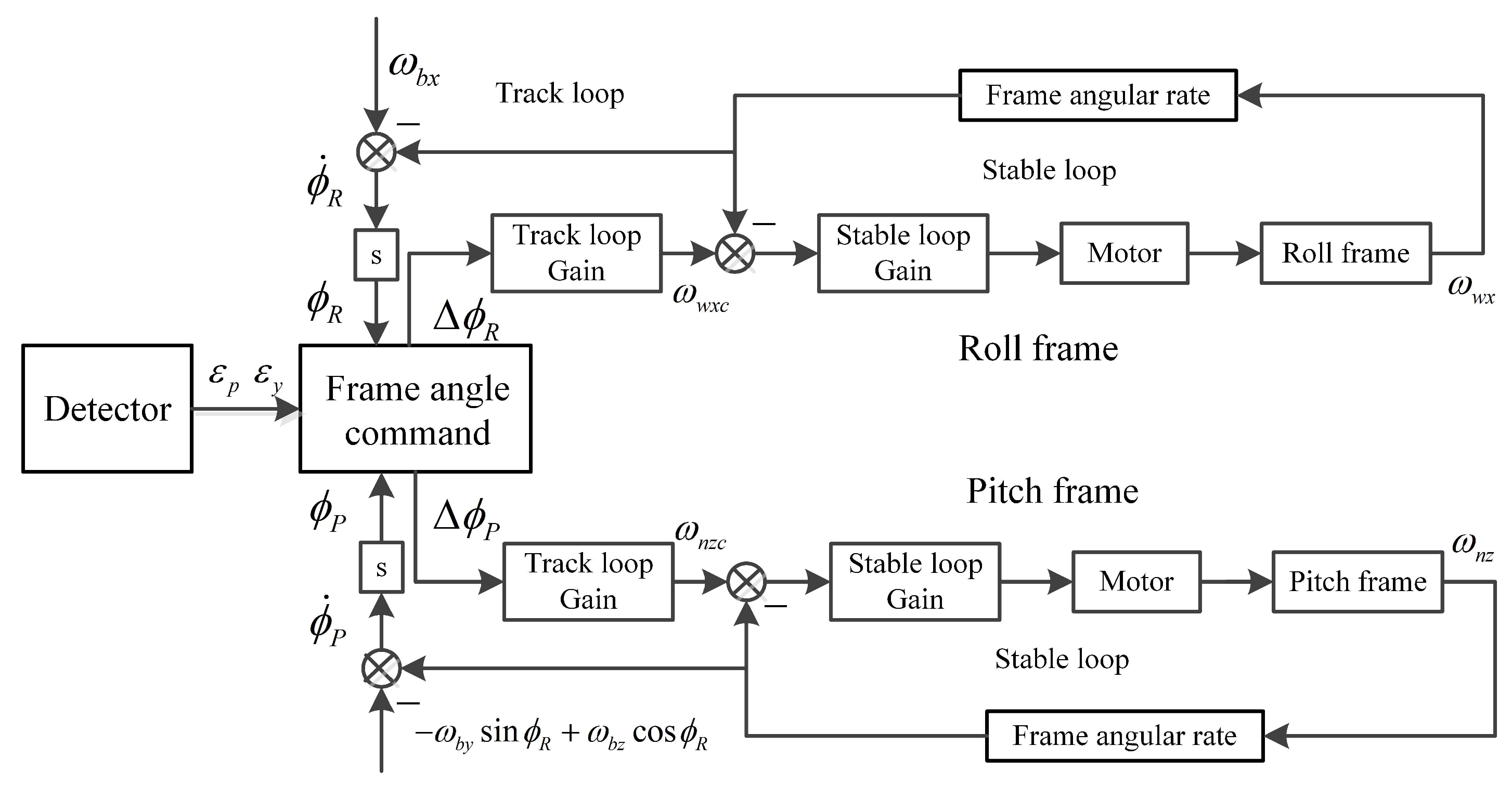
3.1. Closed-Loop Track Principle
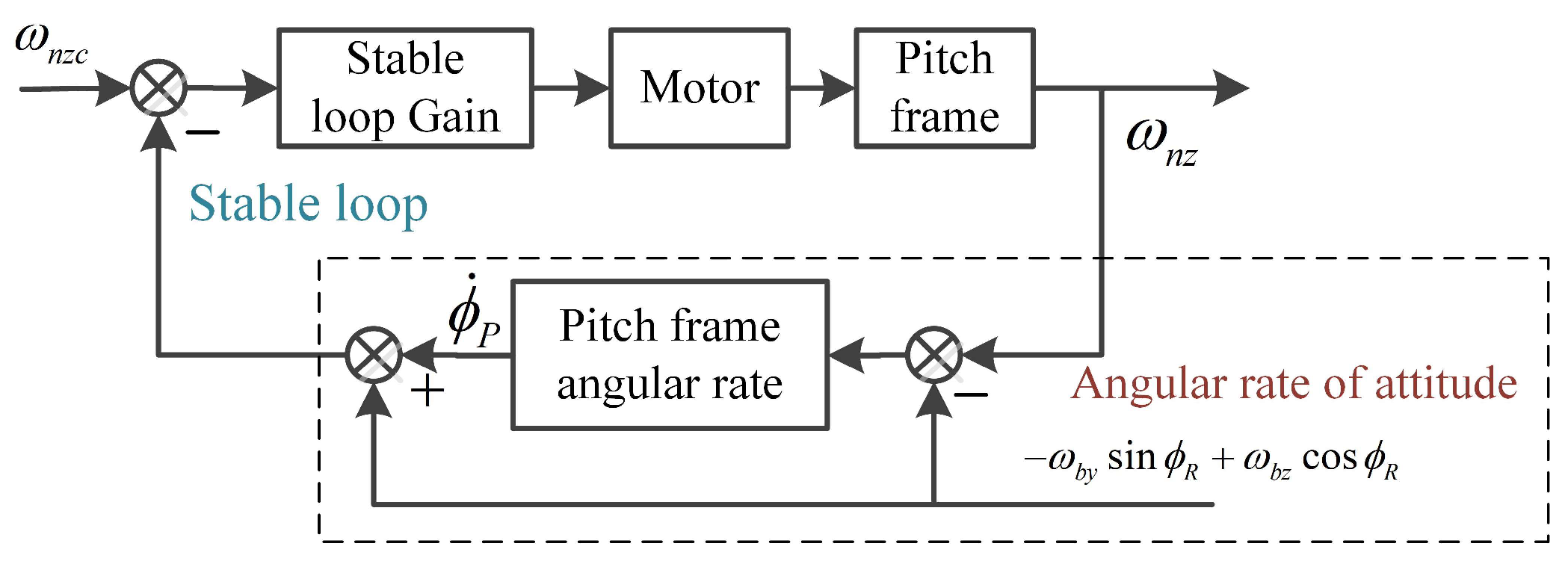
3.2. Frame Tracking Instruction Calculation
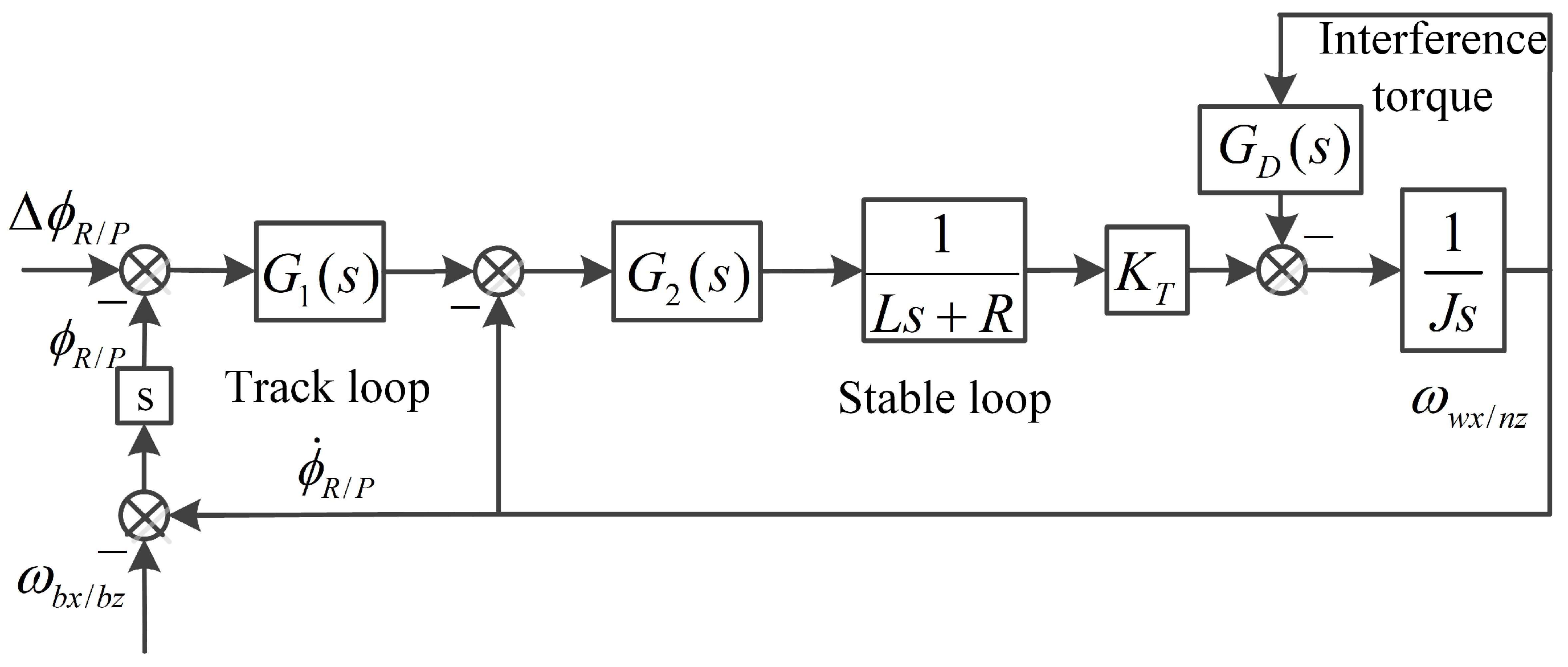
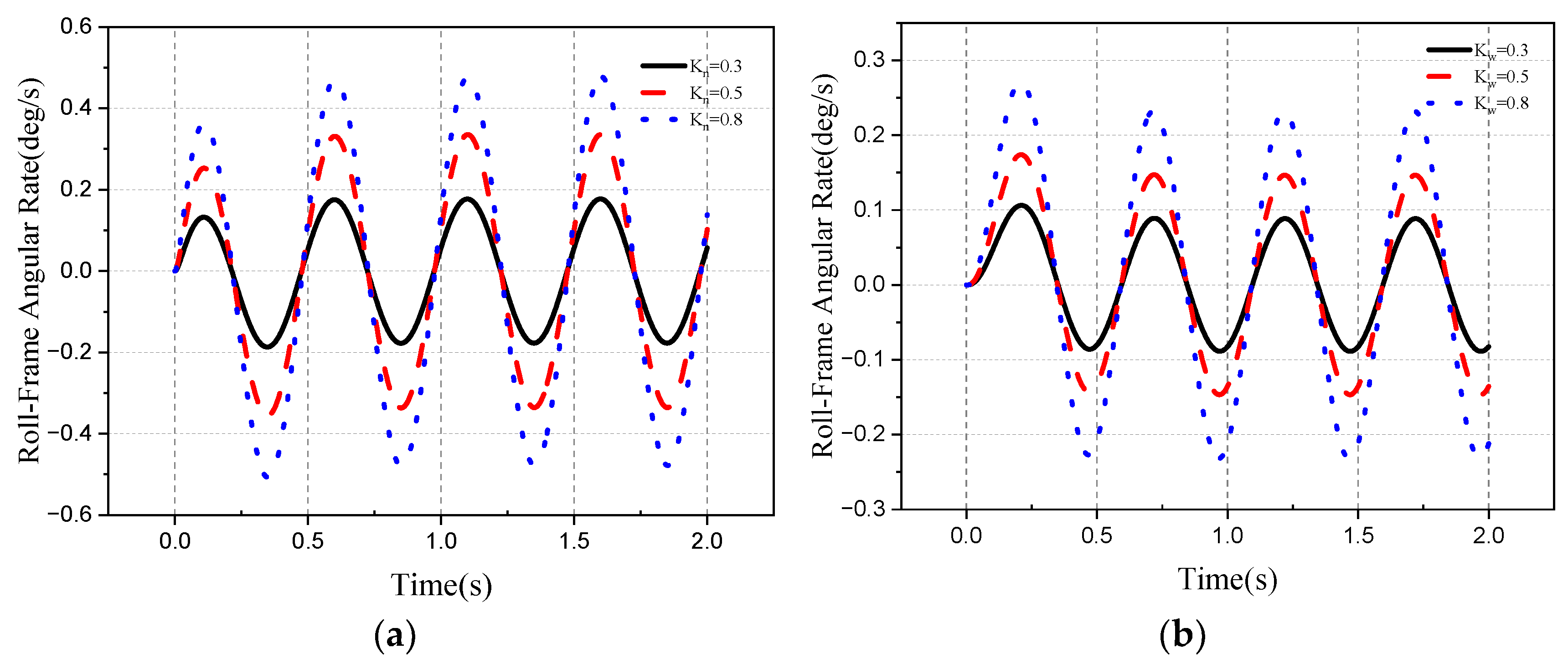
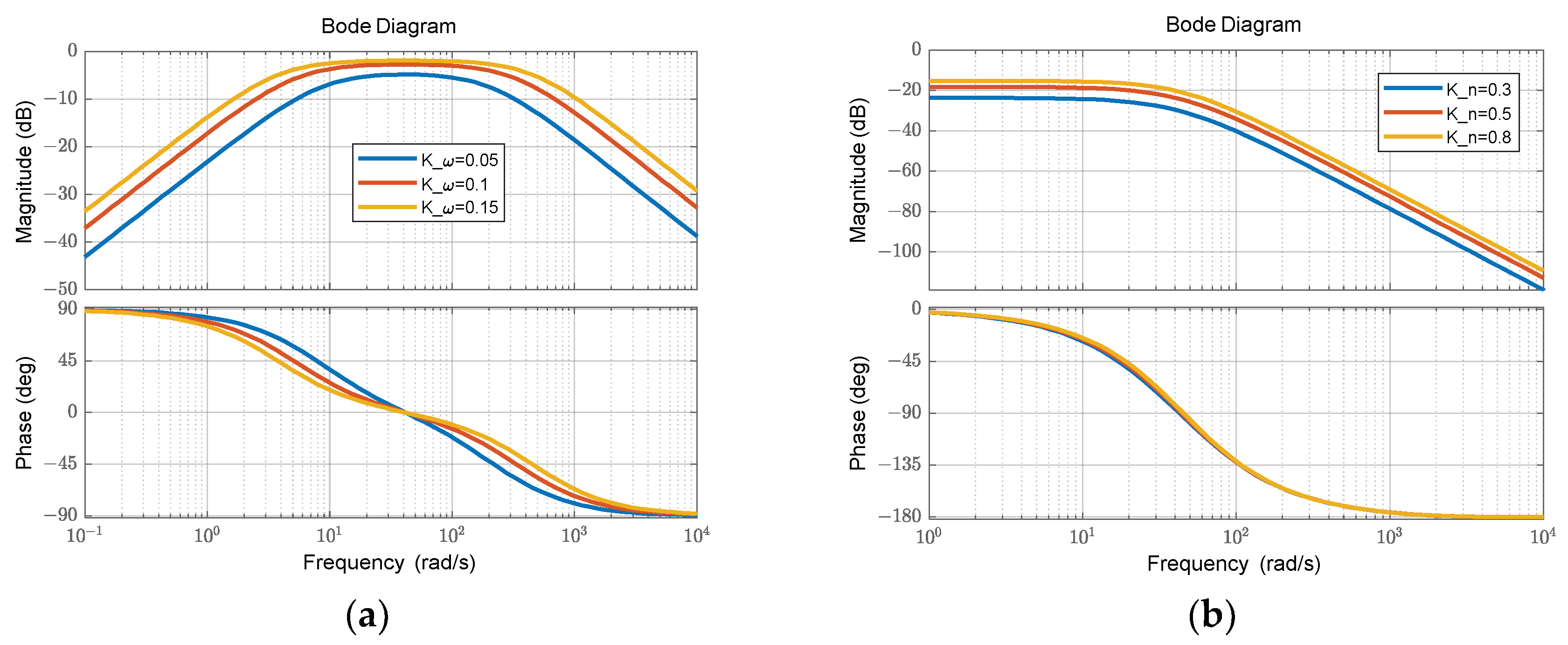
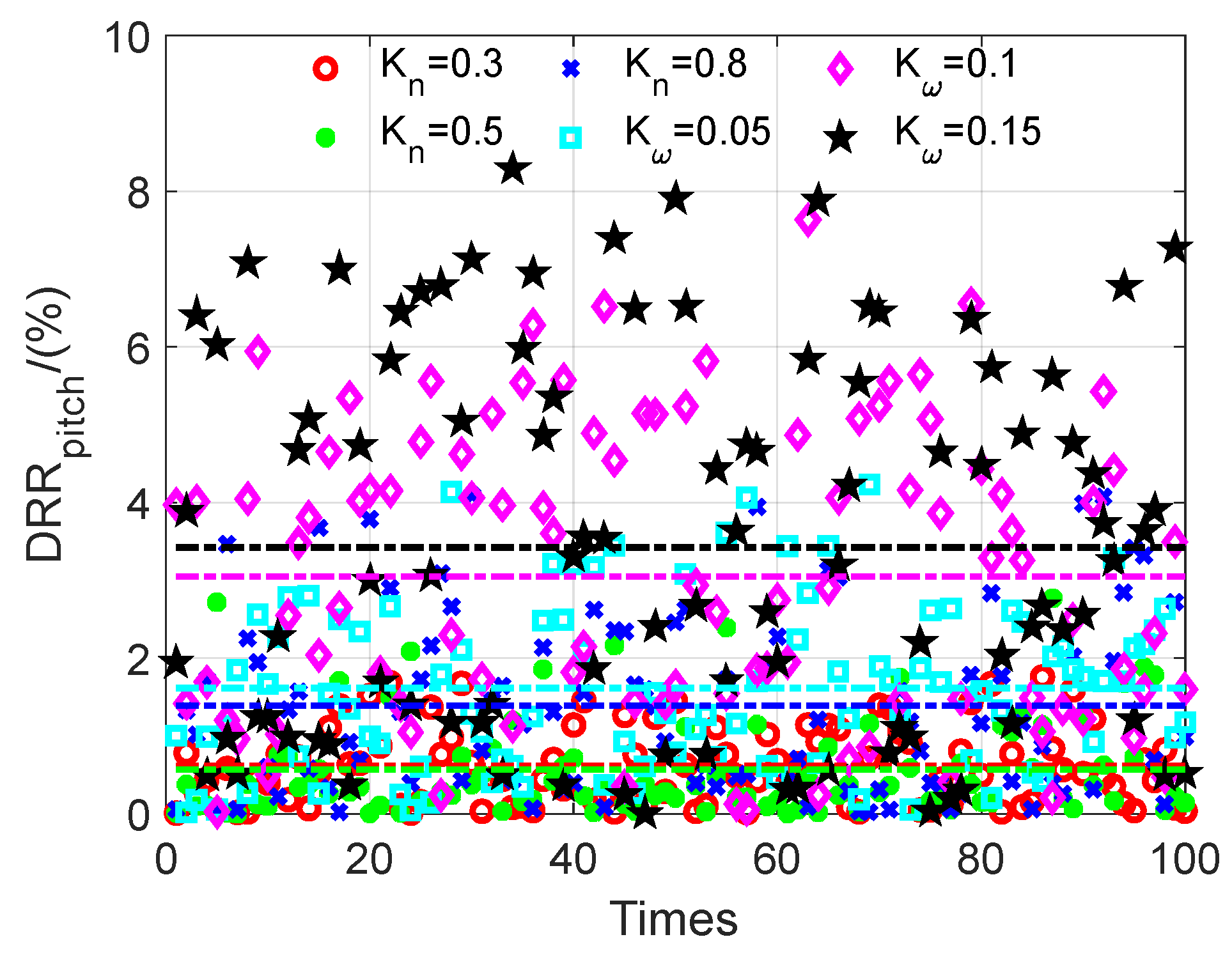
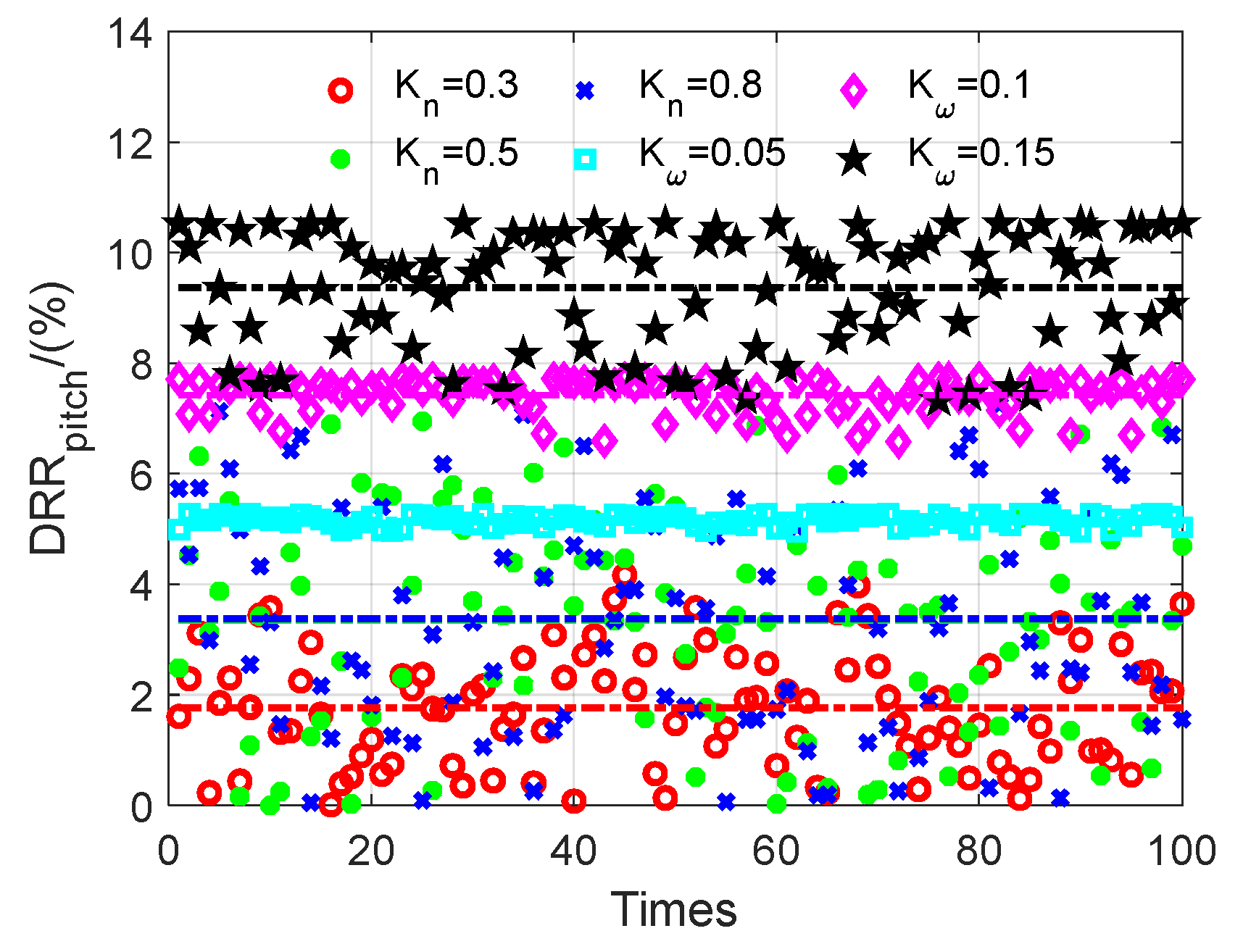
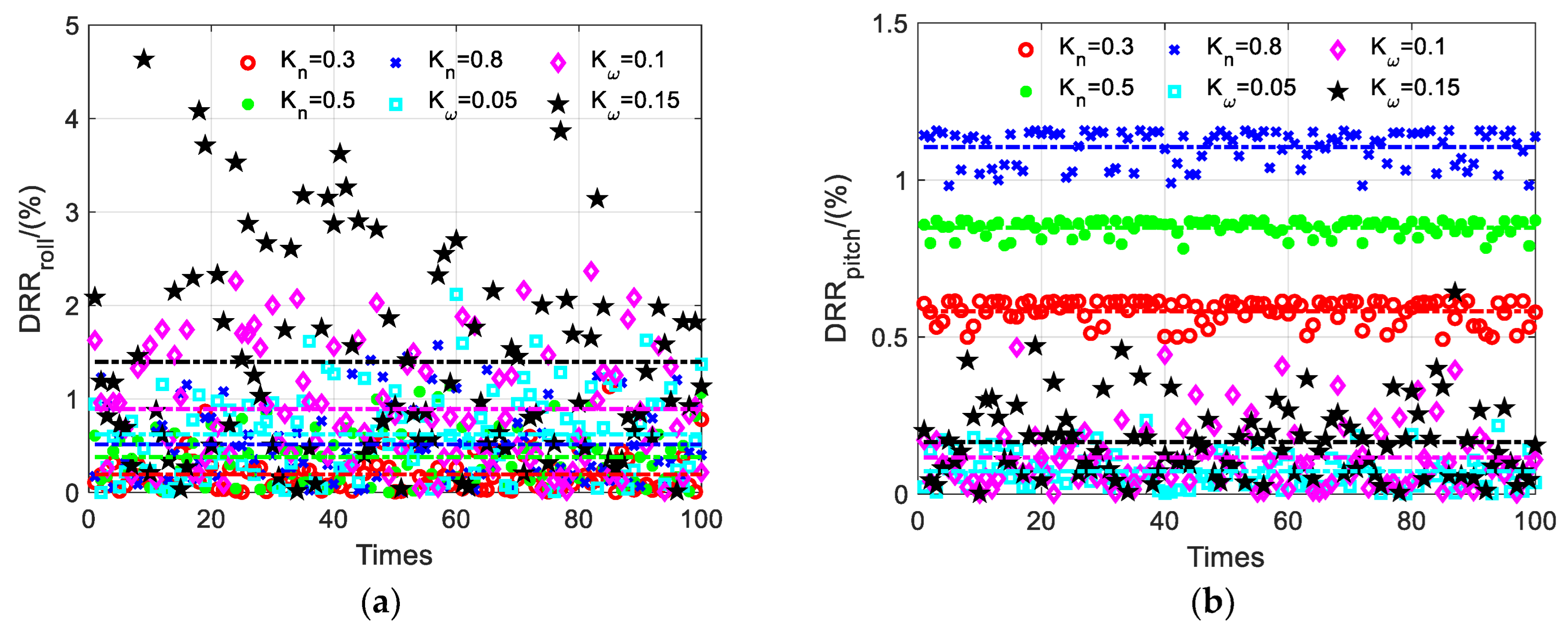
3.3. Frame Control DRR
4. Simulation
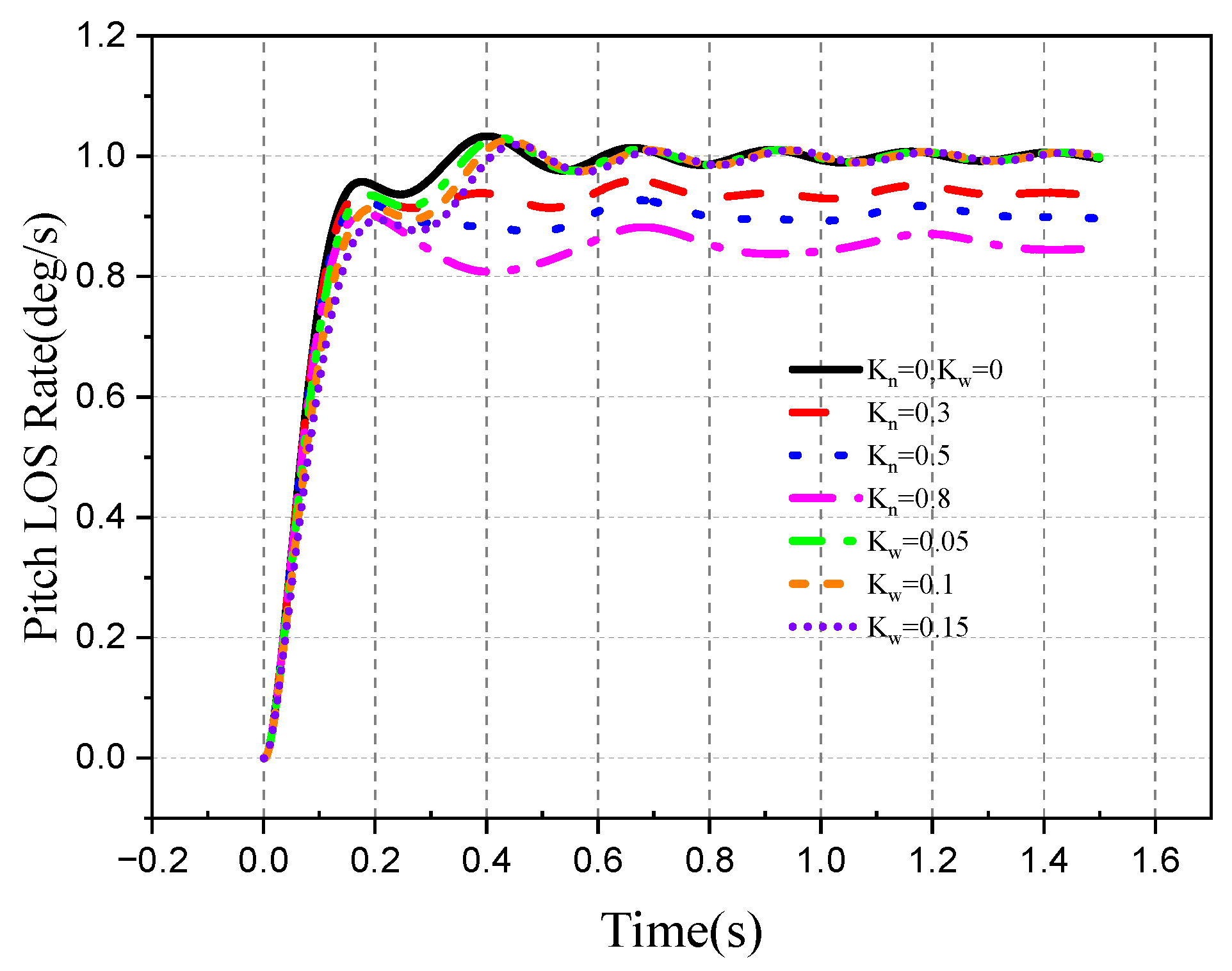
4.1. Stability of the Roll–Pitch Seeker
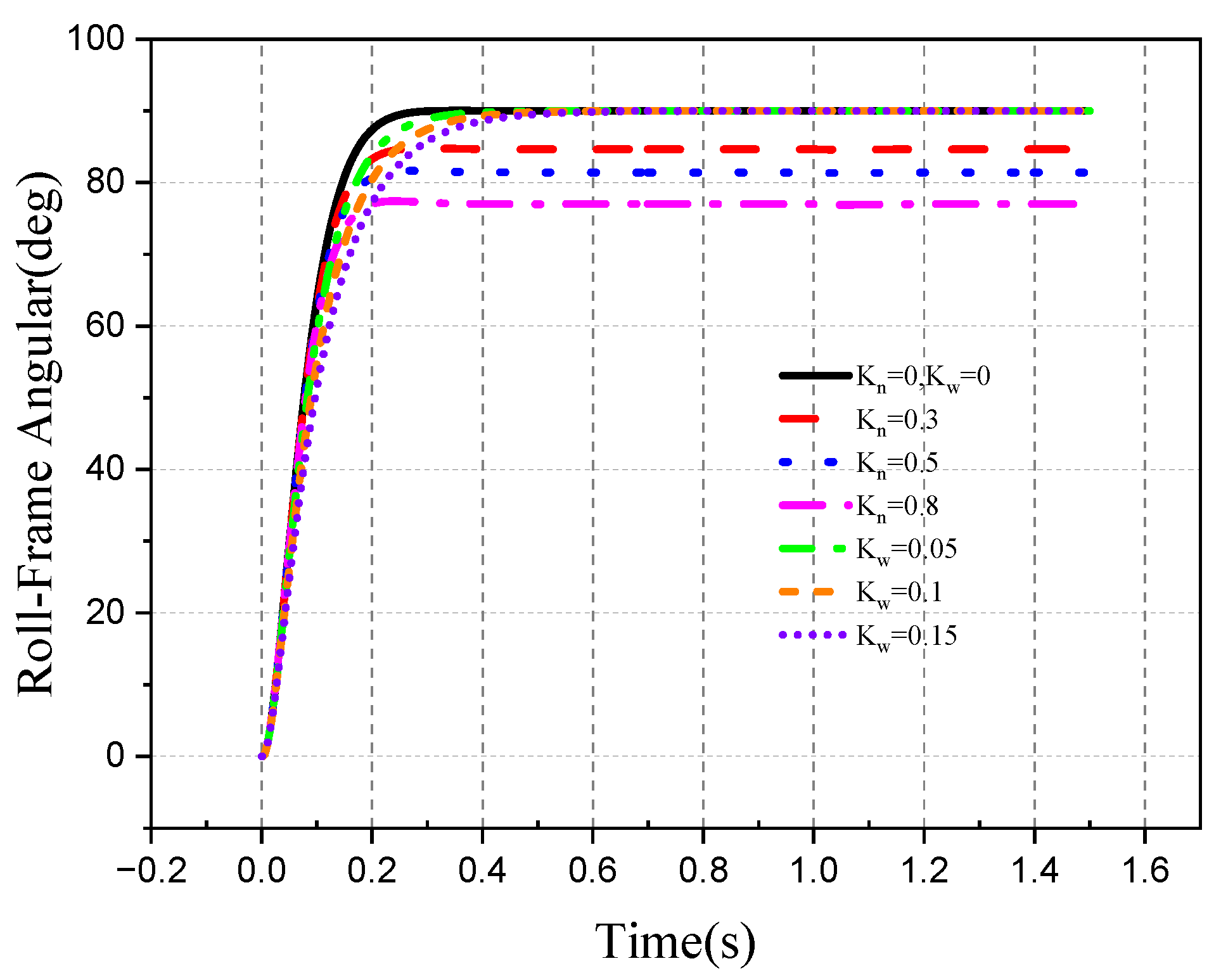
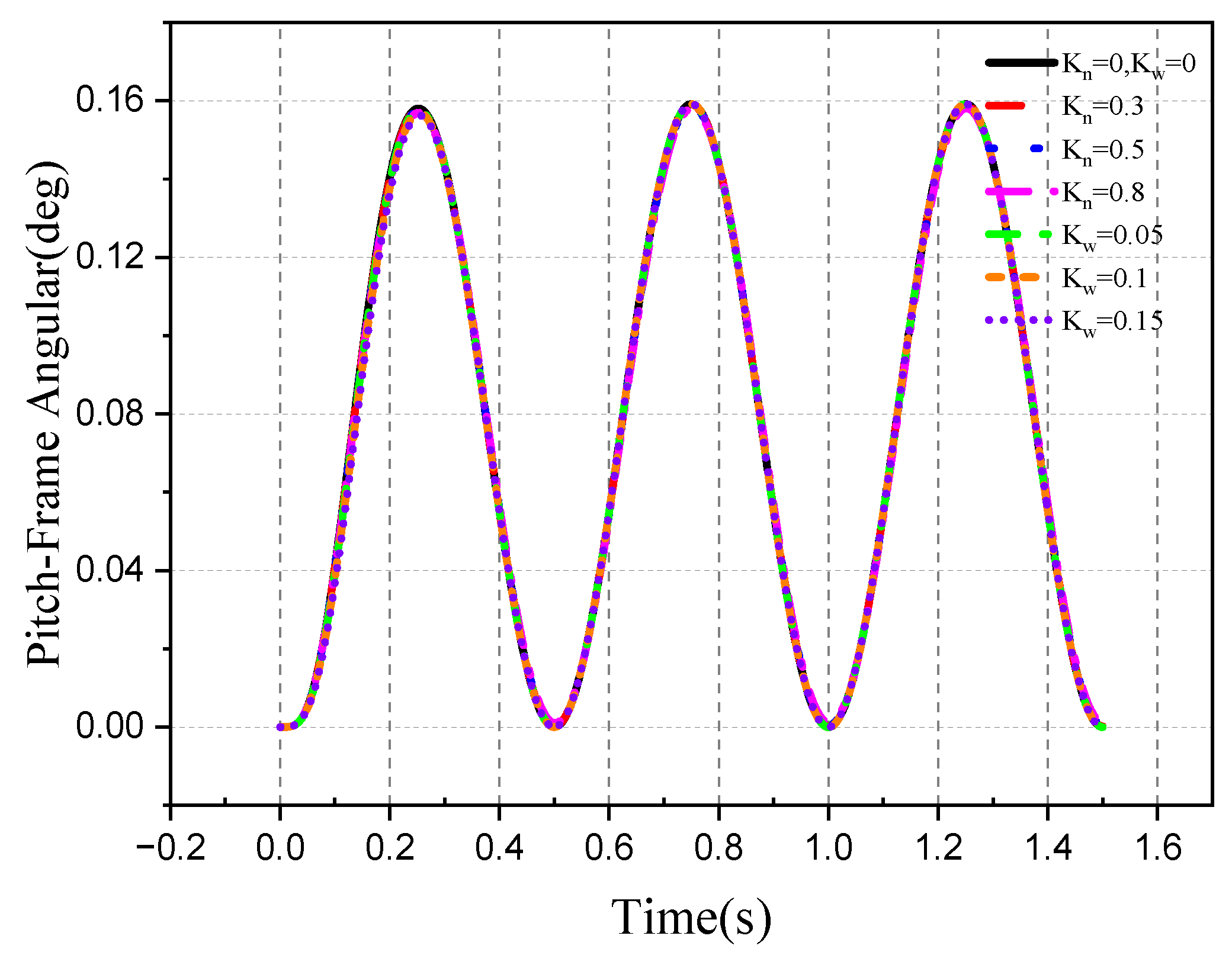
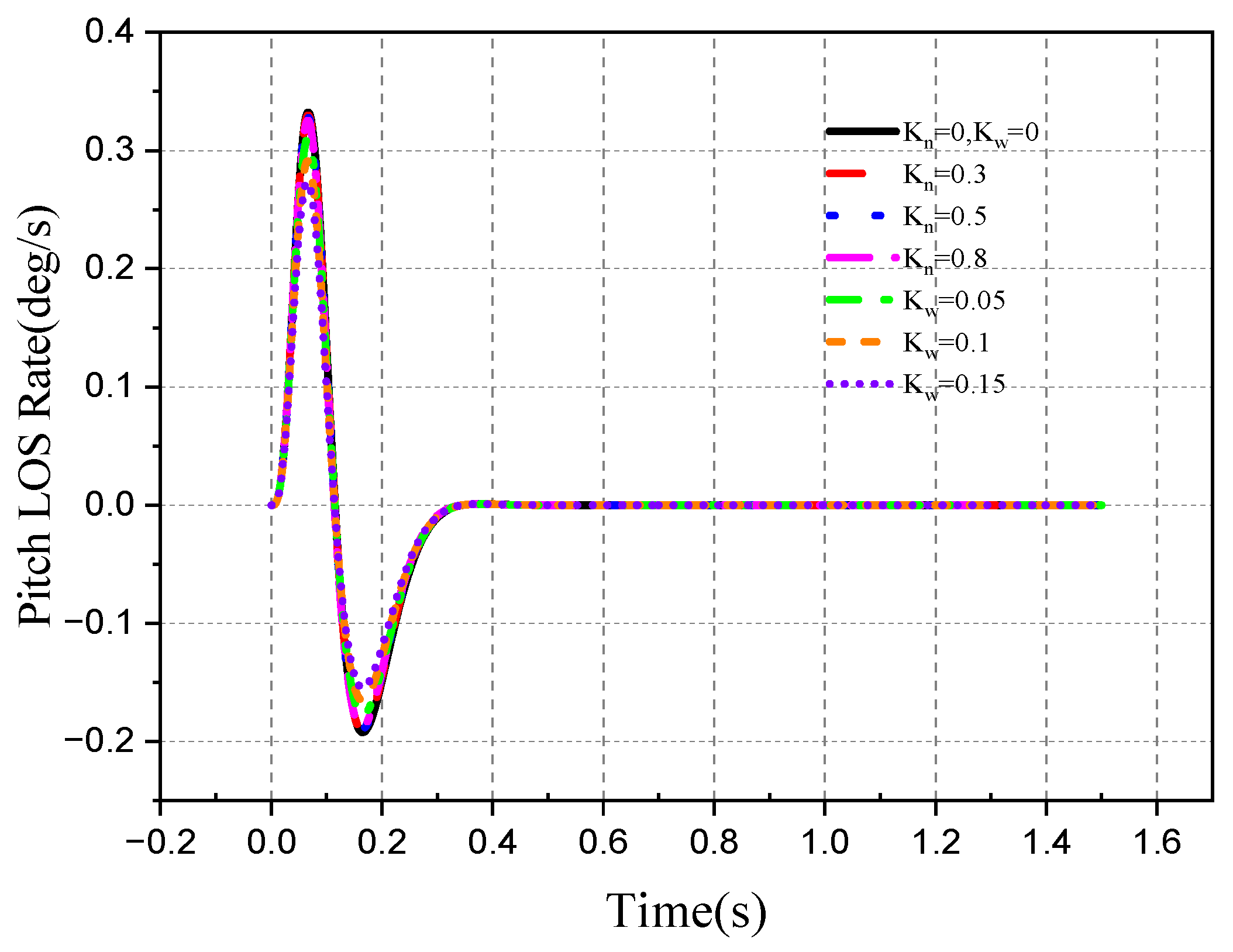
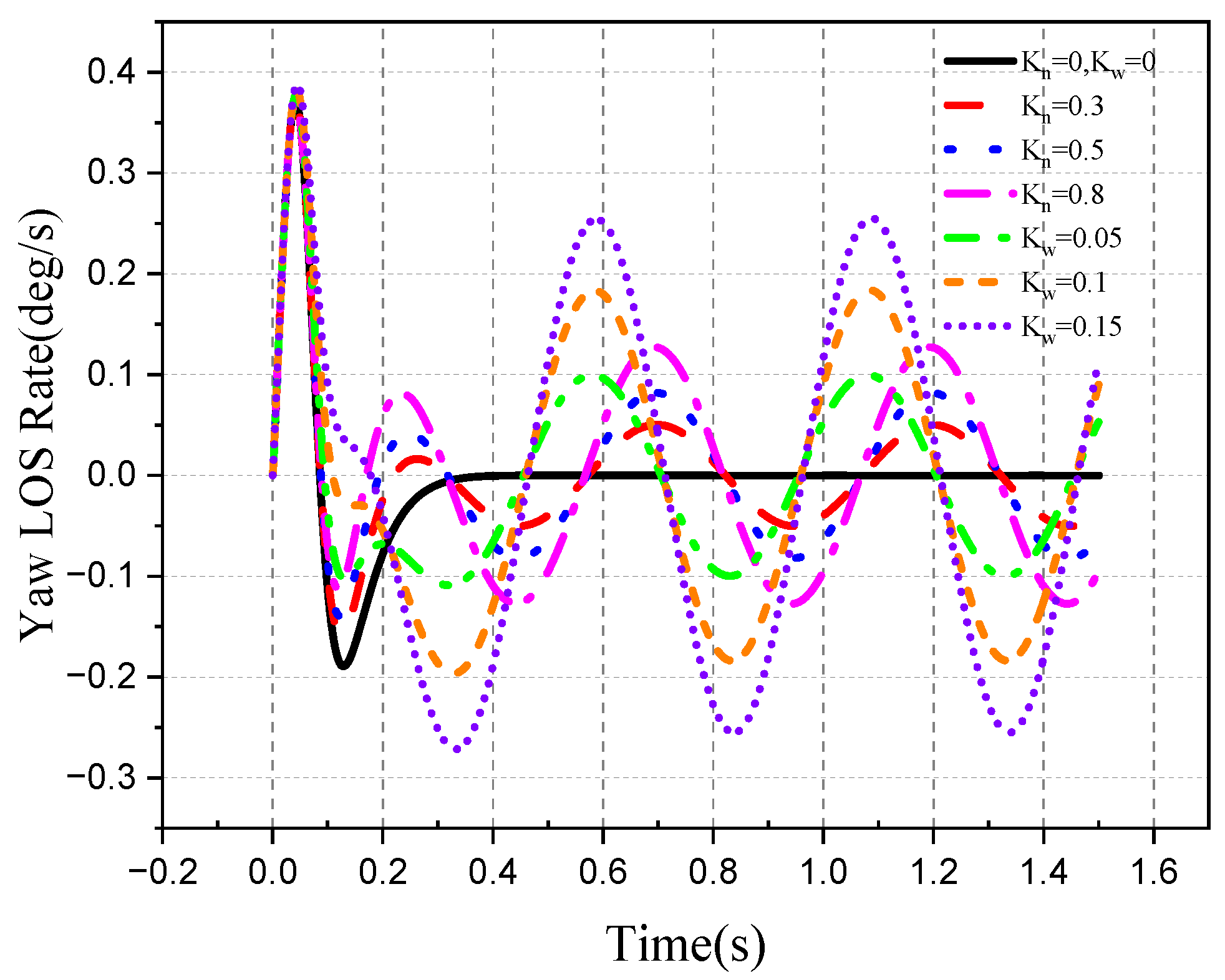
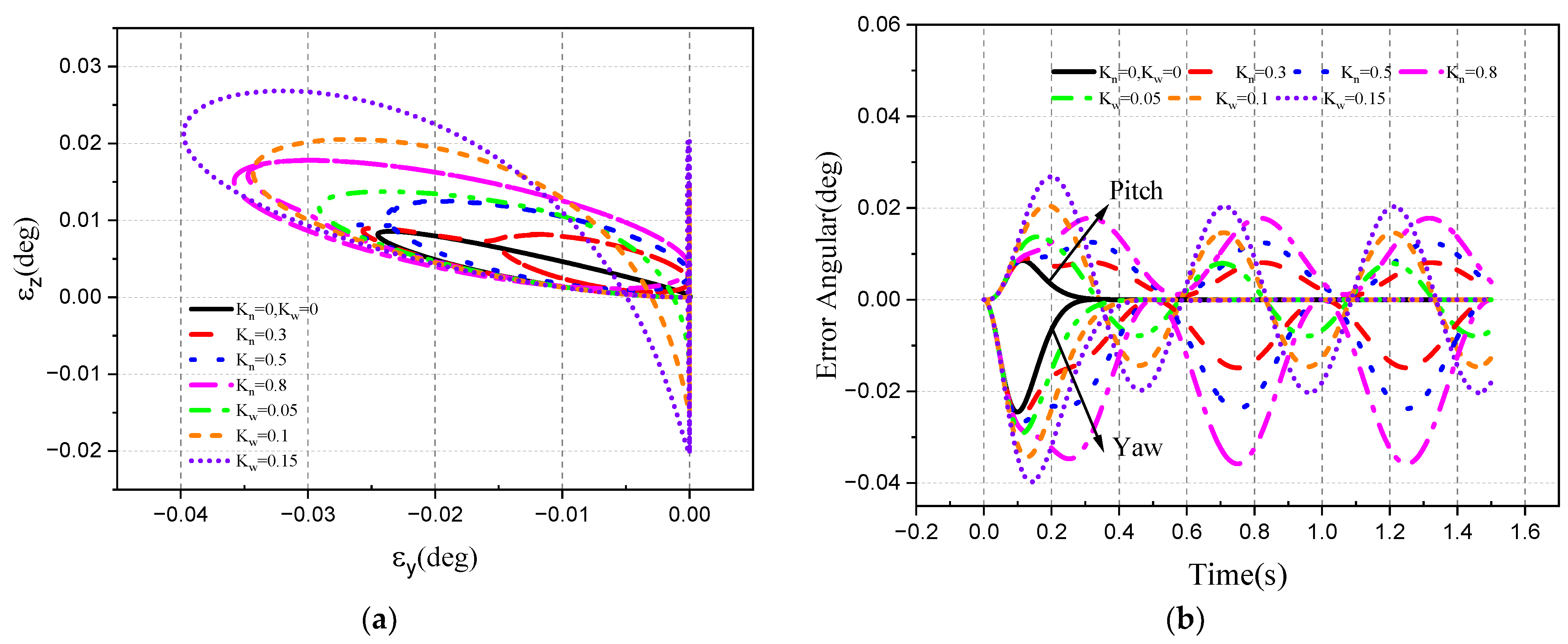
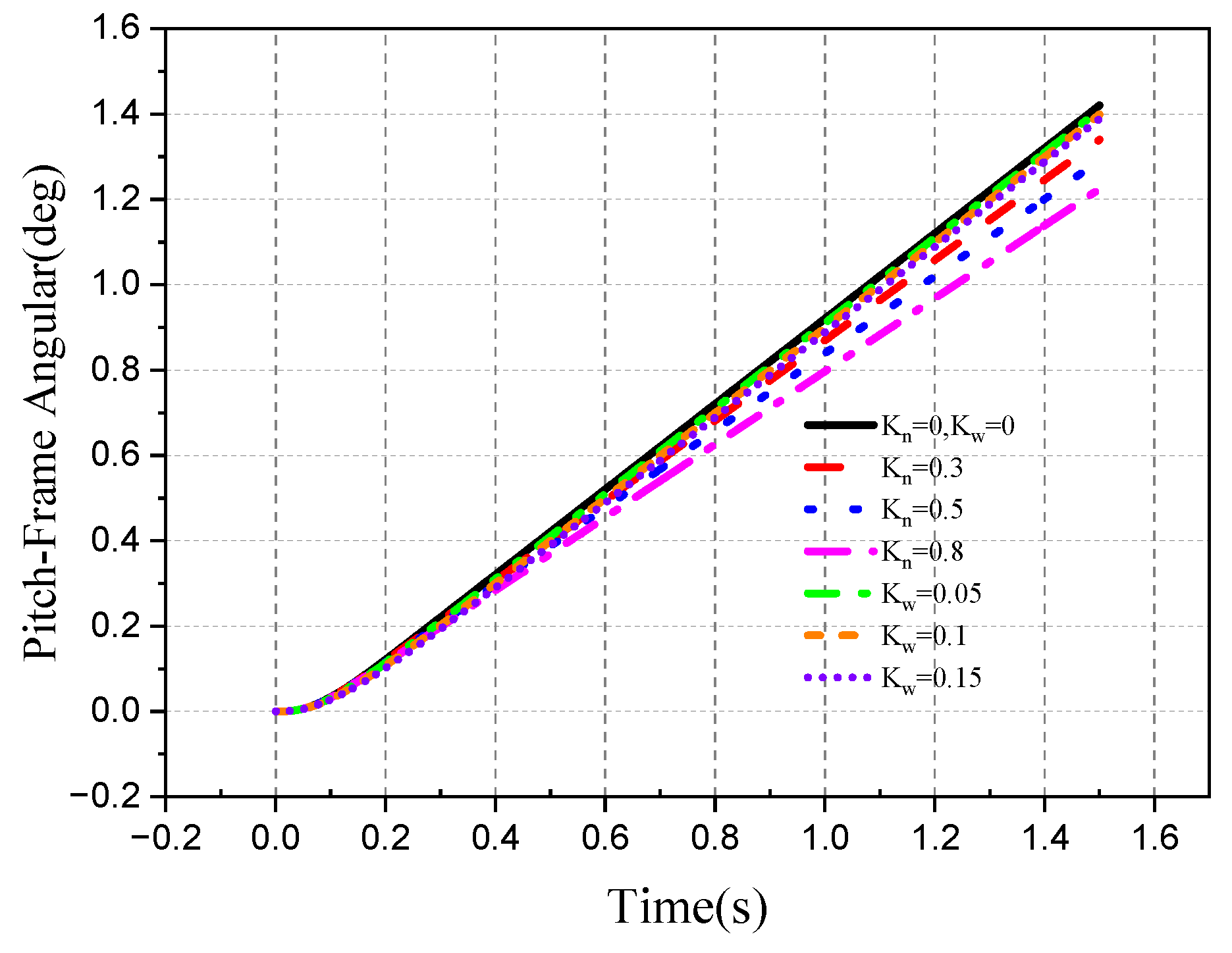
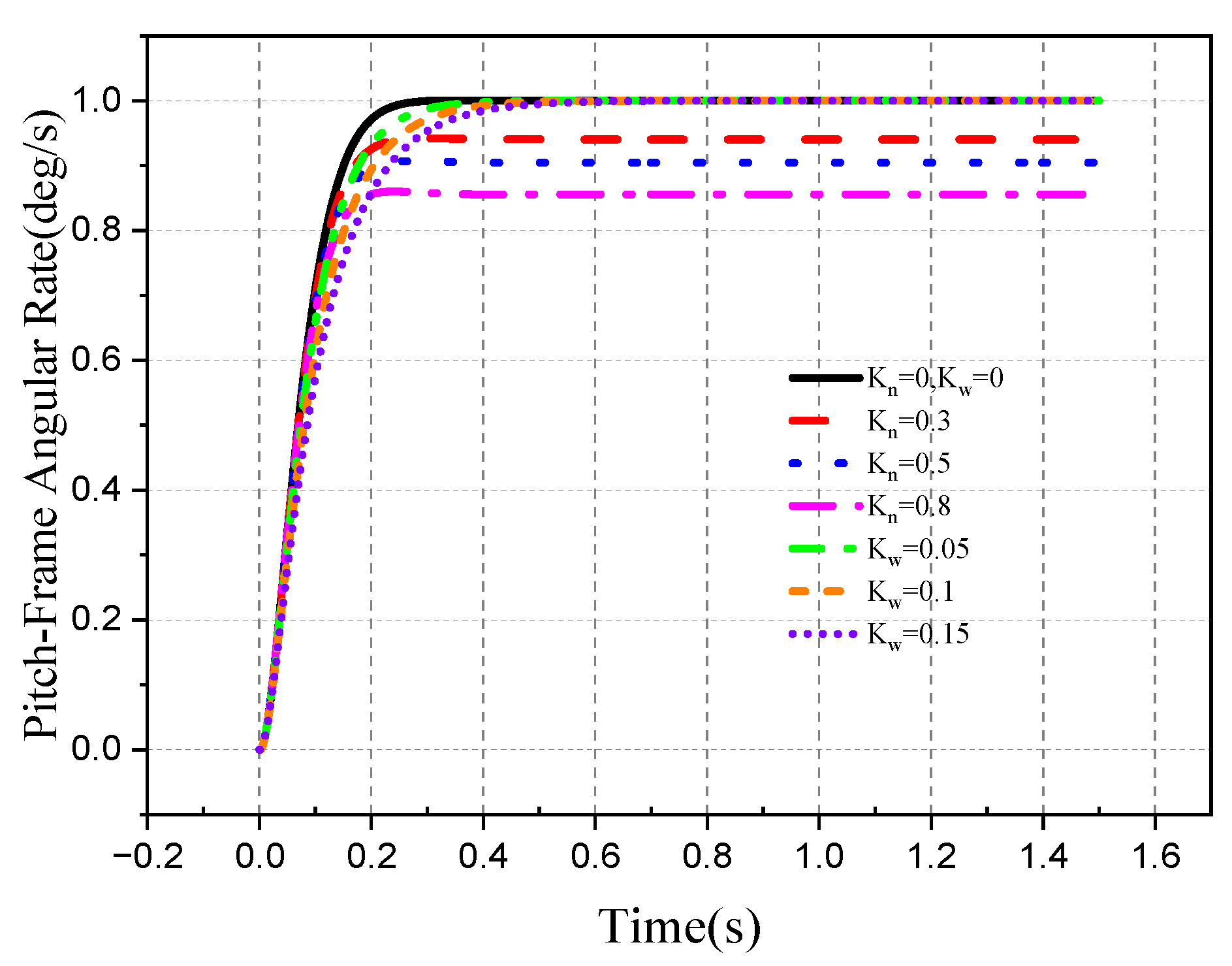
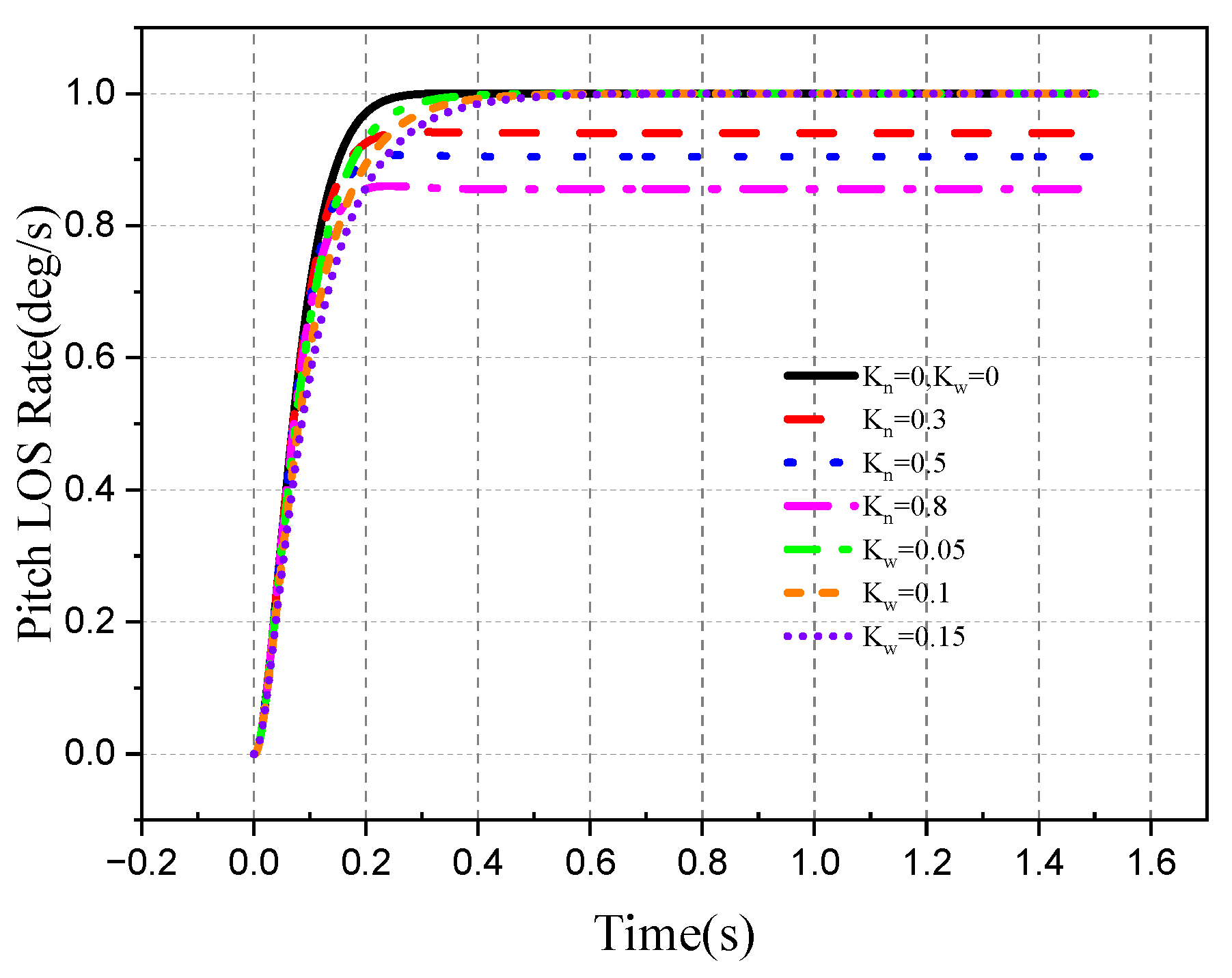
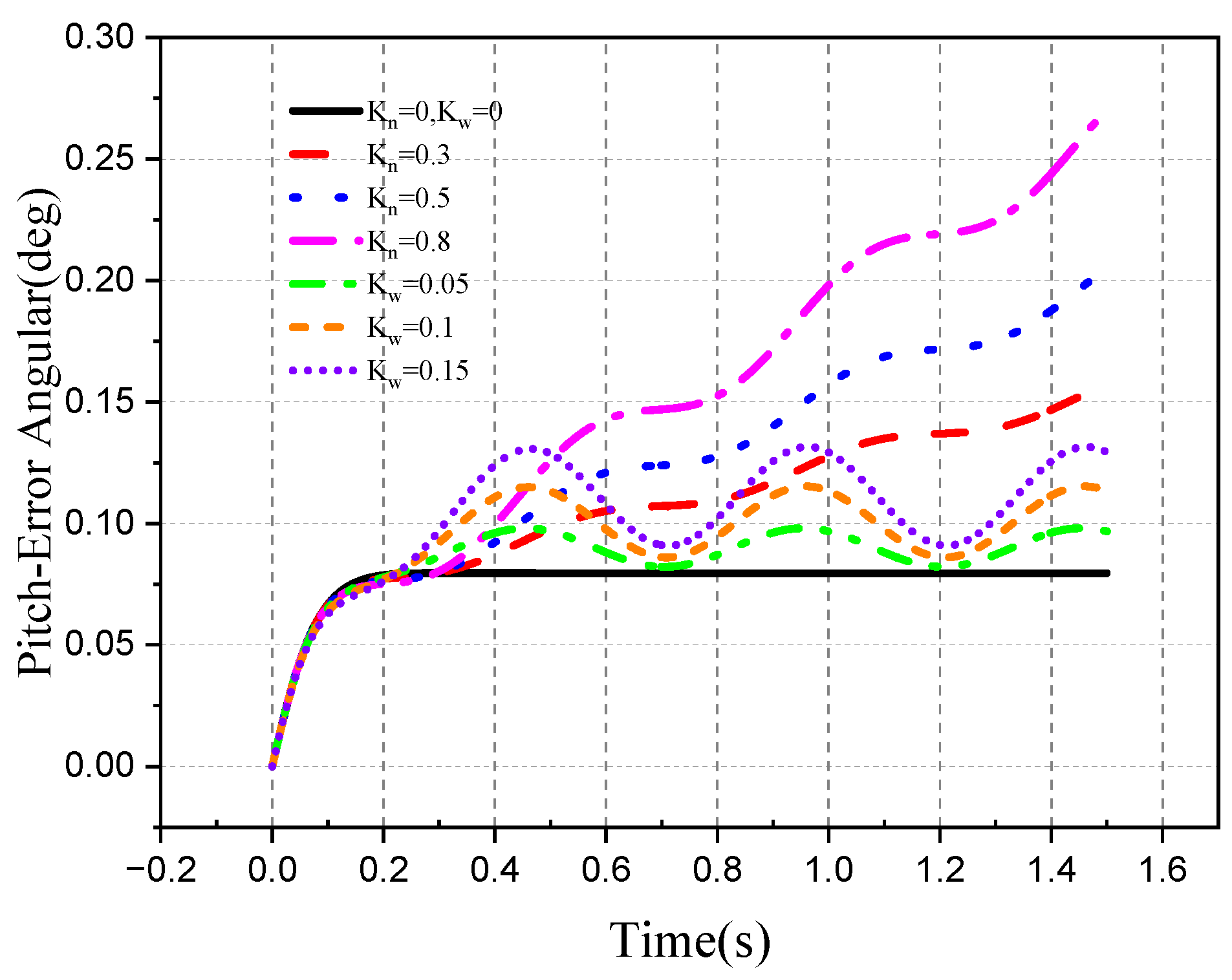
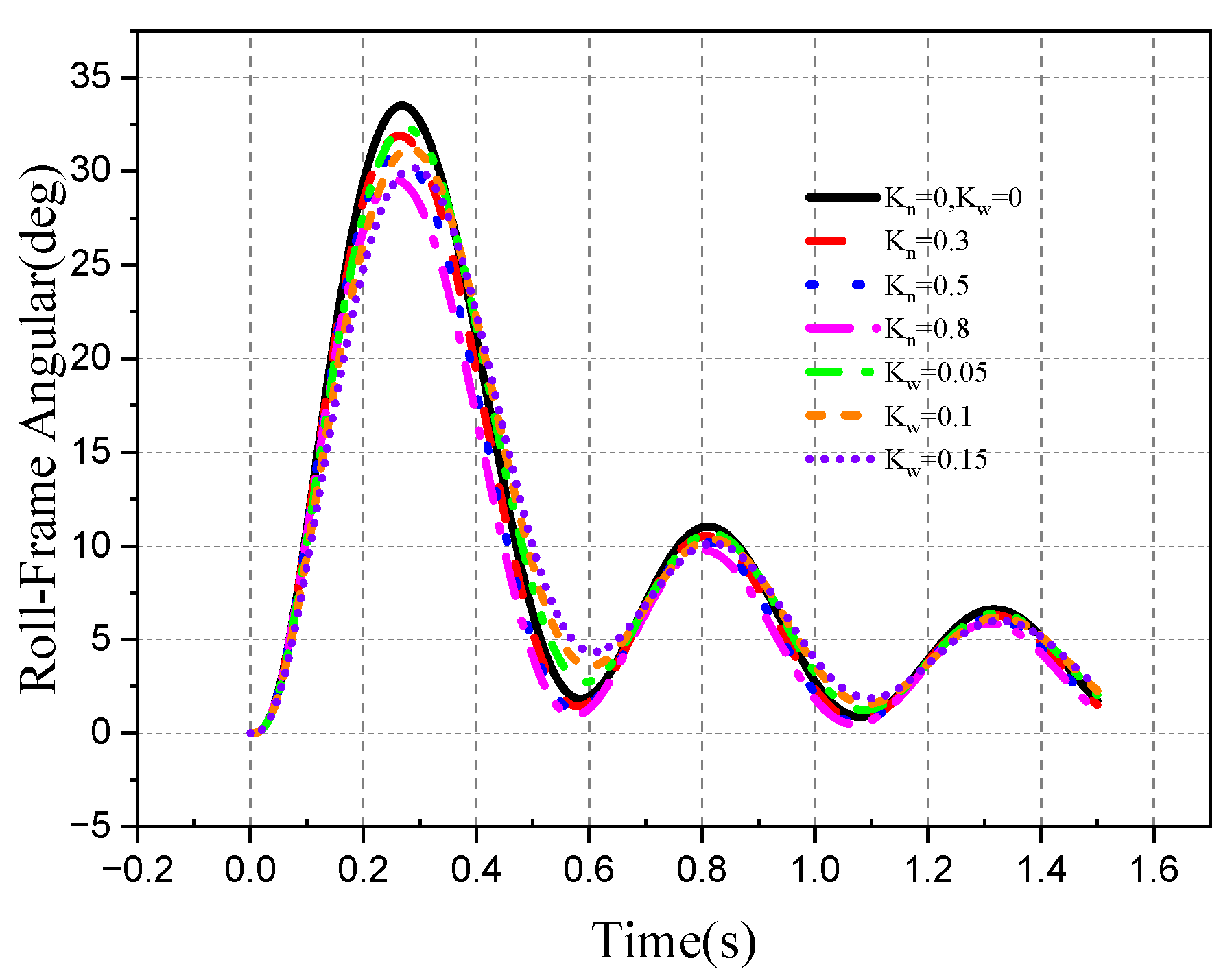
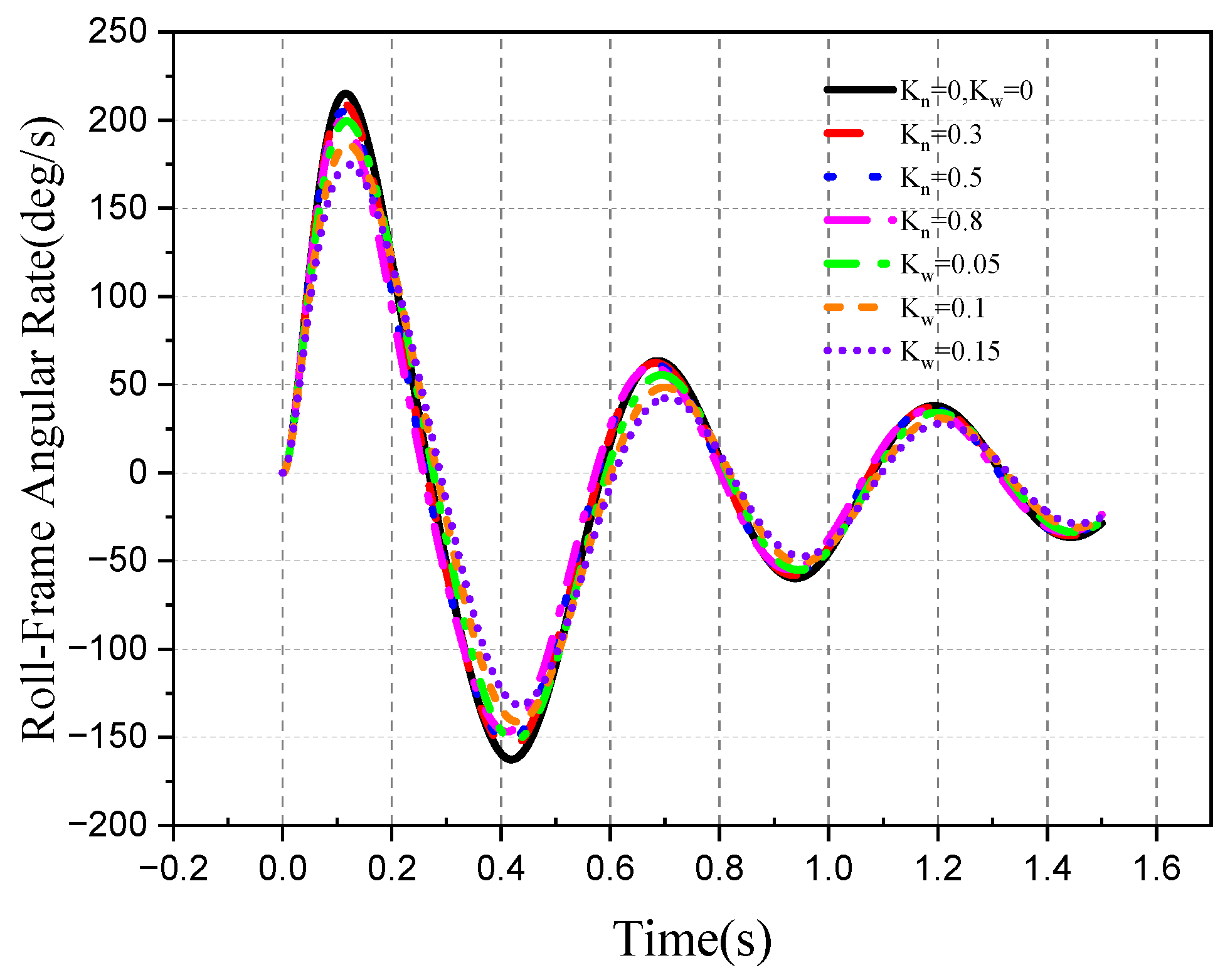
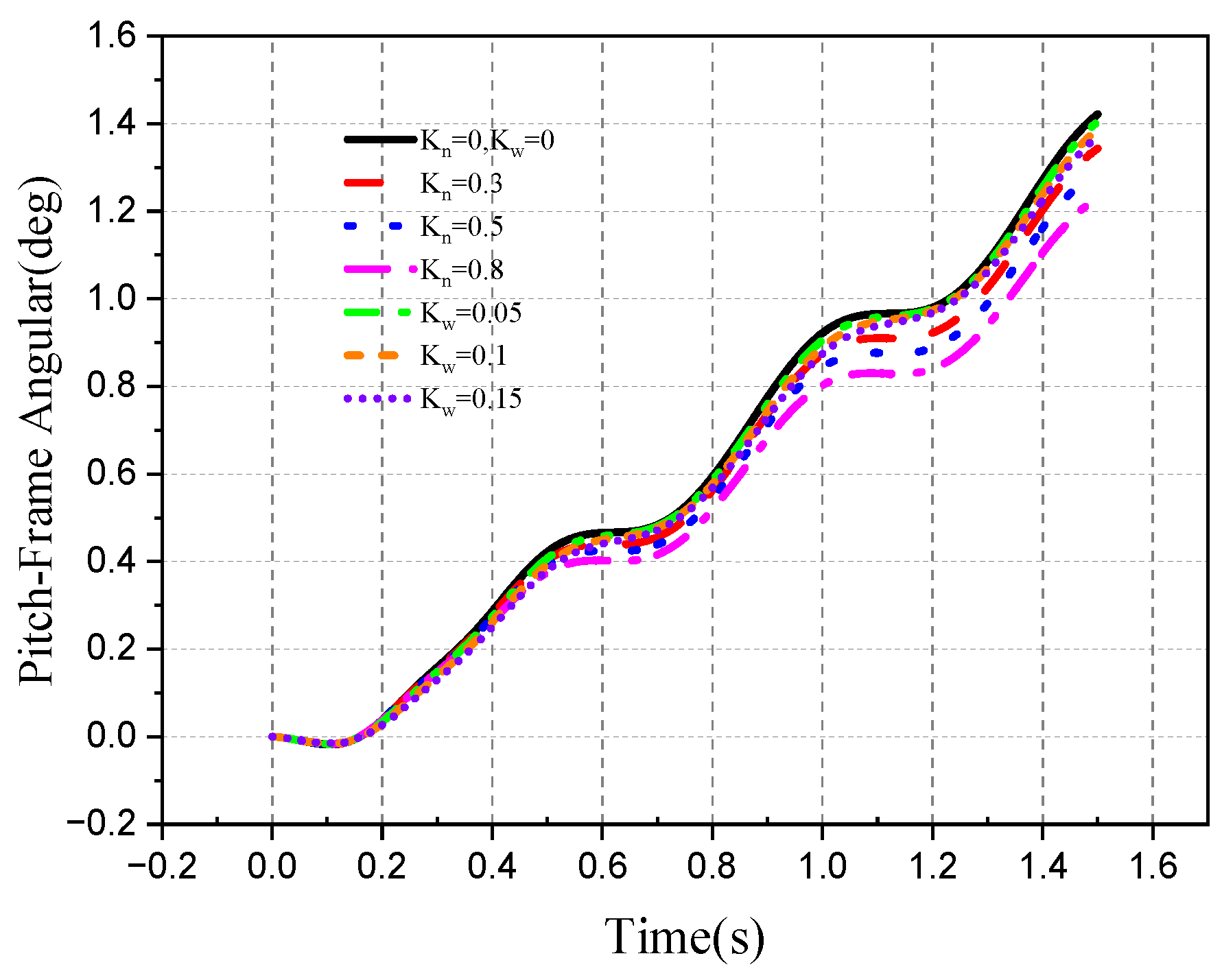
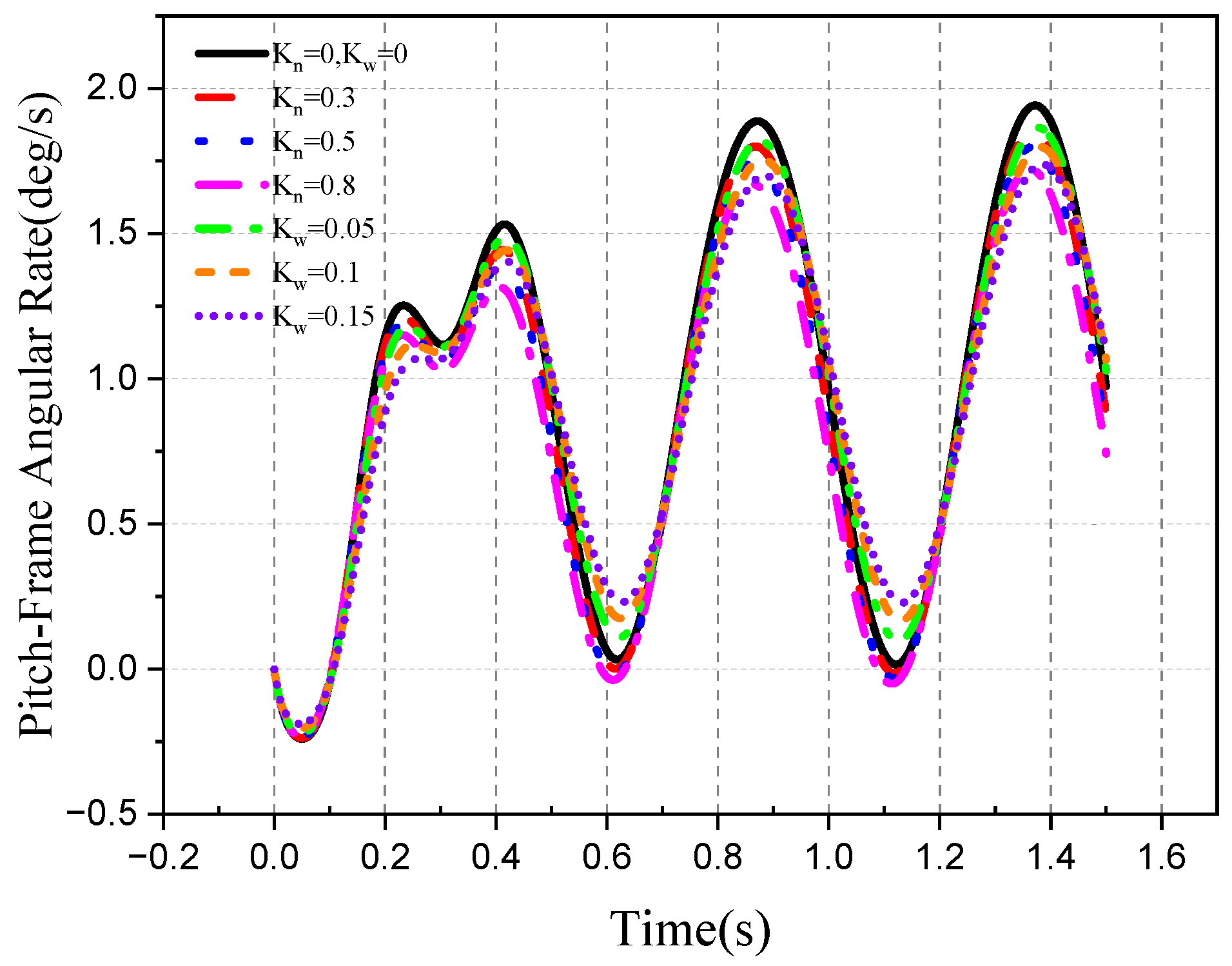
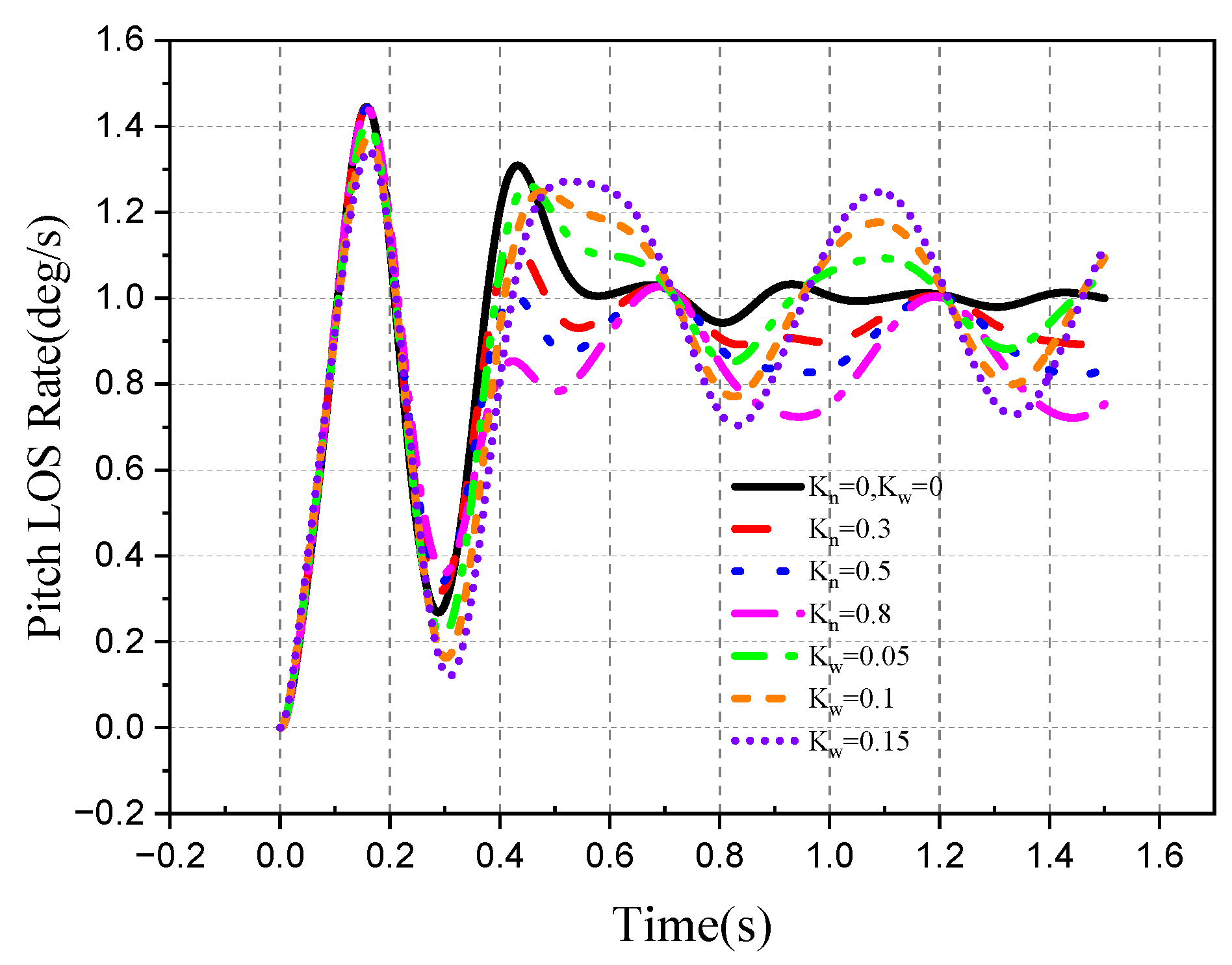
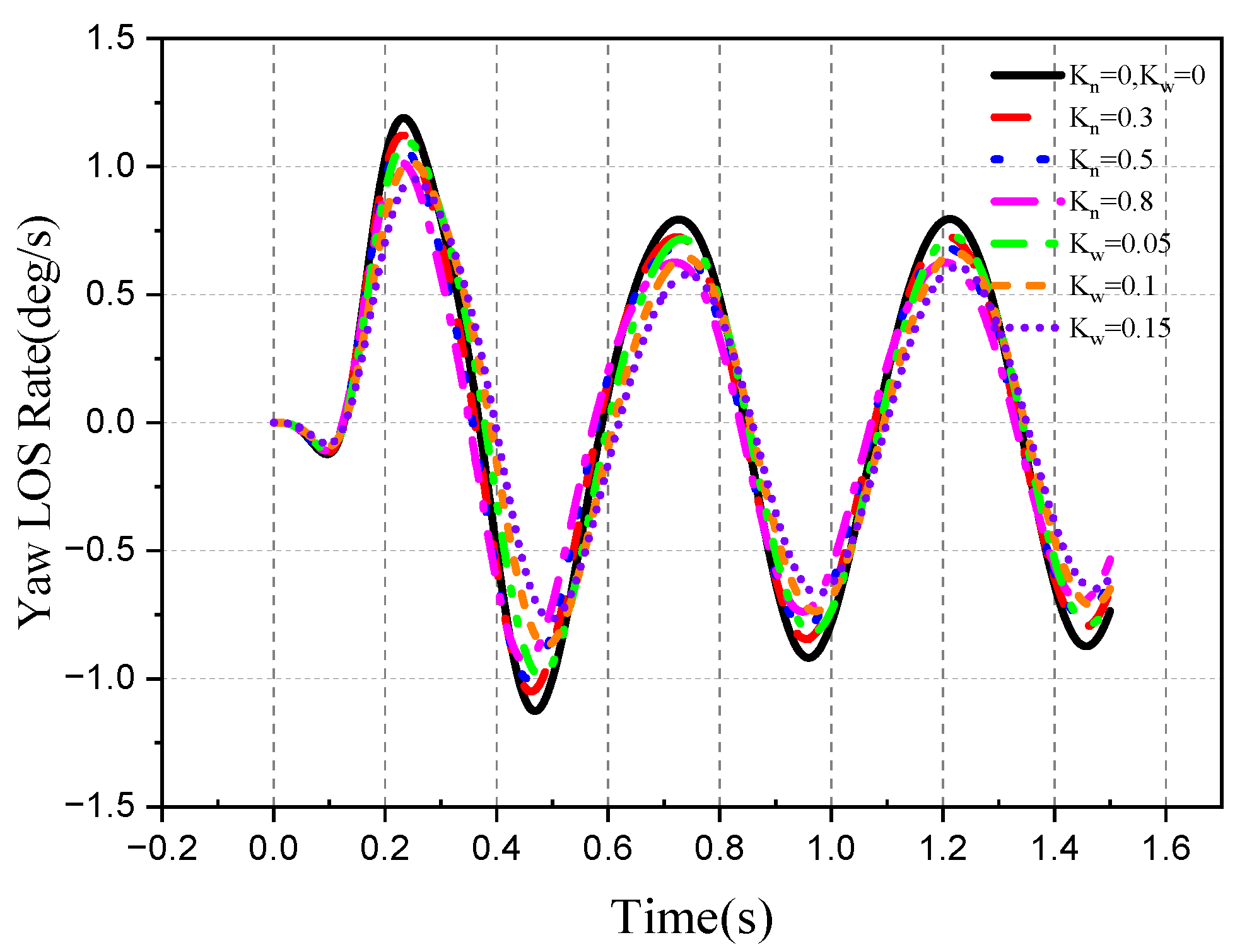
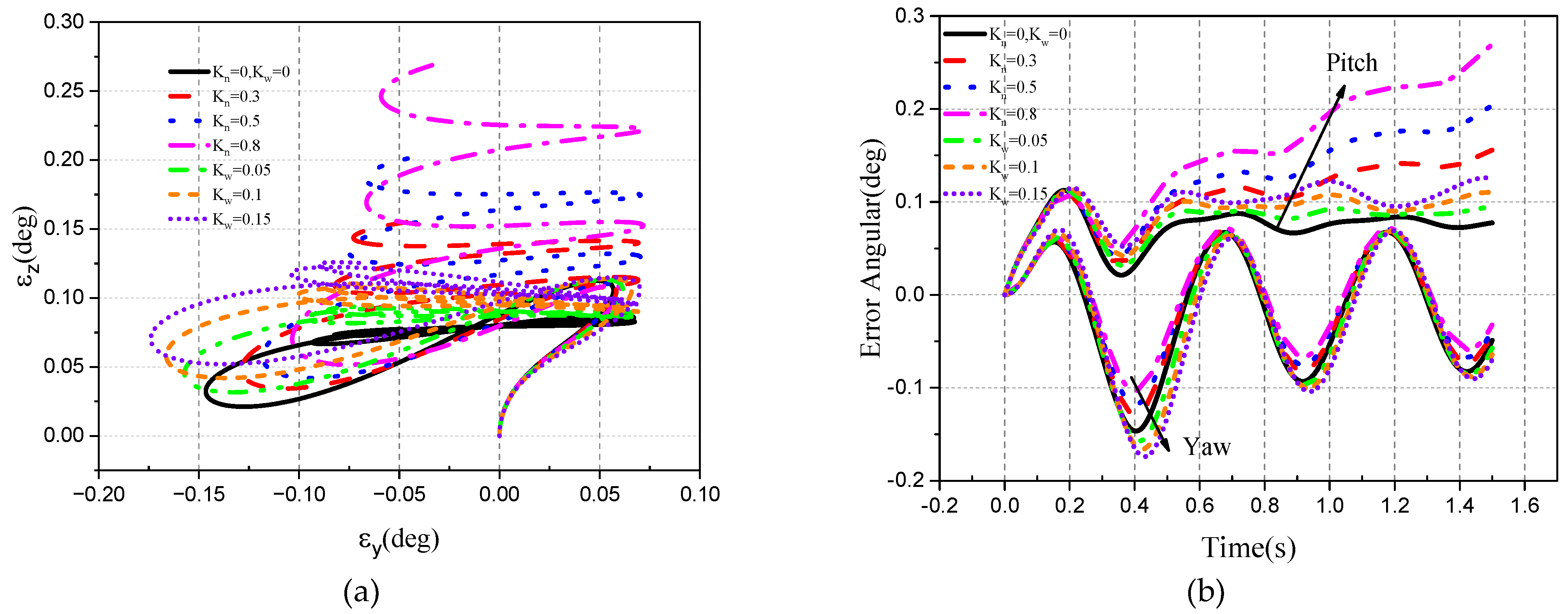
4.2. Tracking Ability of the Roll–Pitch Seeker
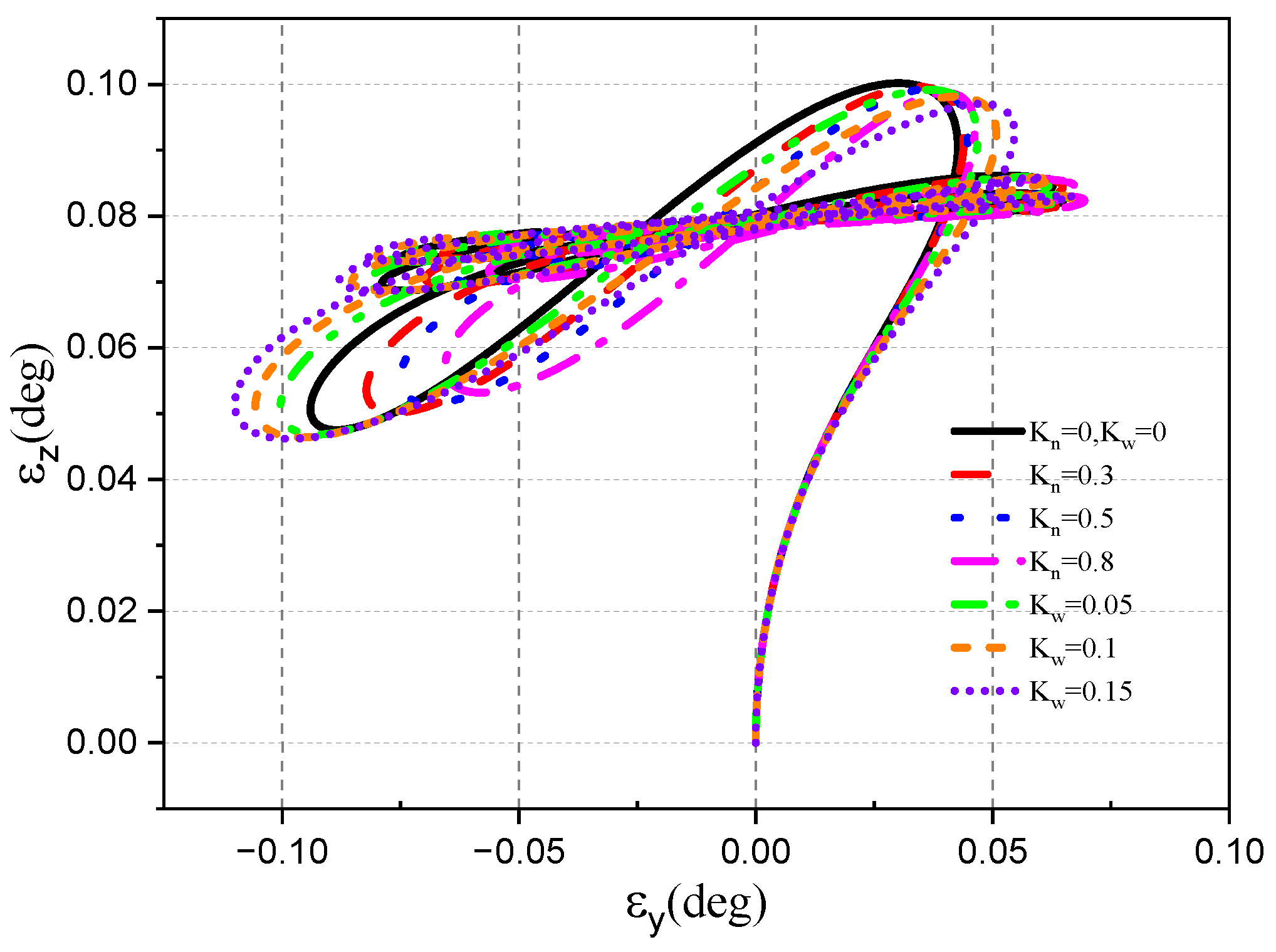
4.2.1. Target Single-Plane Motion
- The direction of the target movement is the same as the direction of the disturbance of the aircraft attitude.
- 2.
- The movement direction of the target is different from the disturbance direction of attitude.
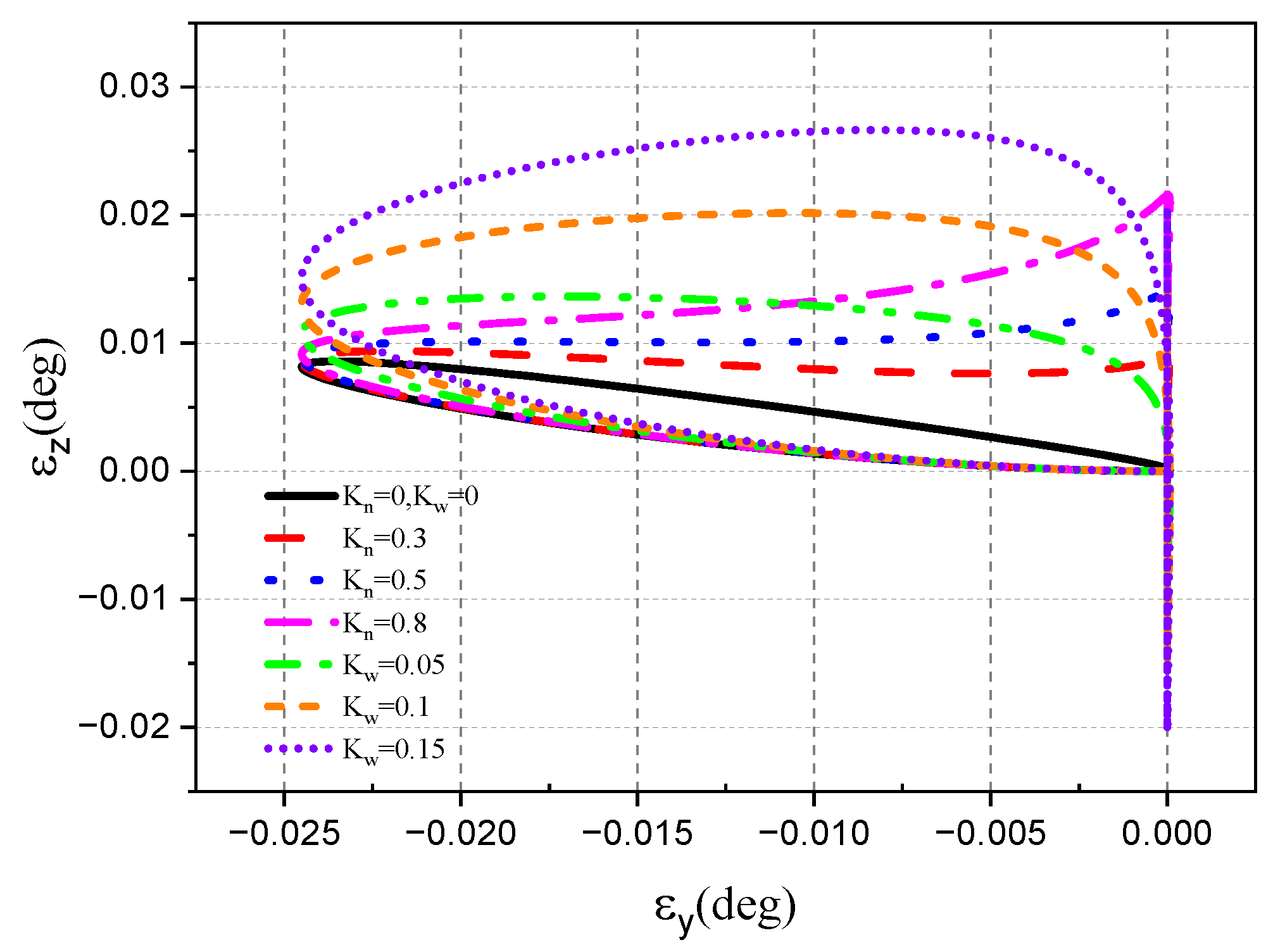
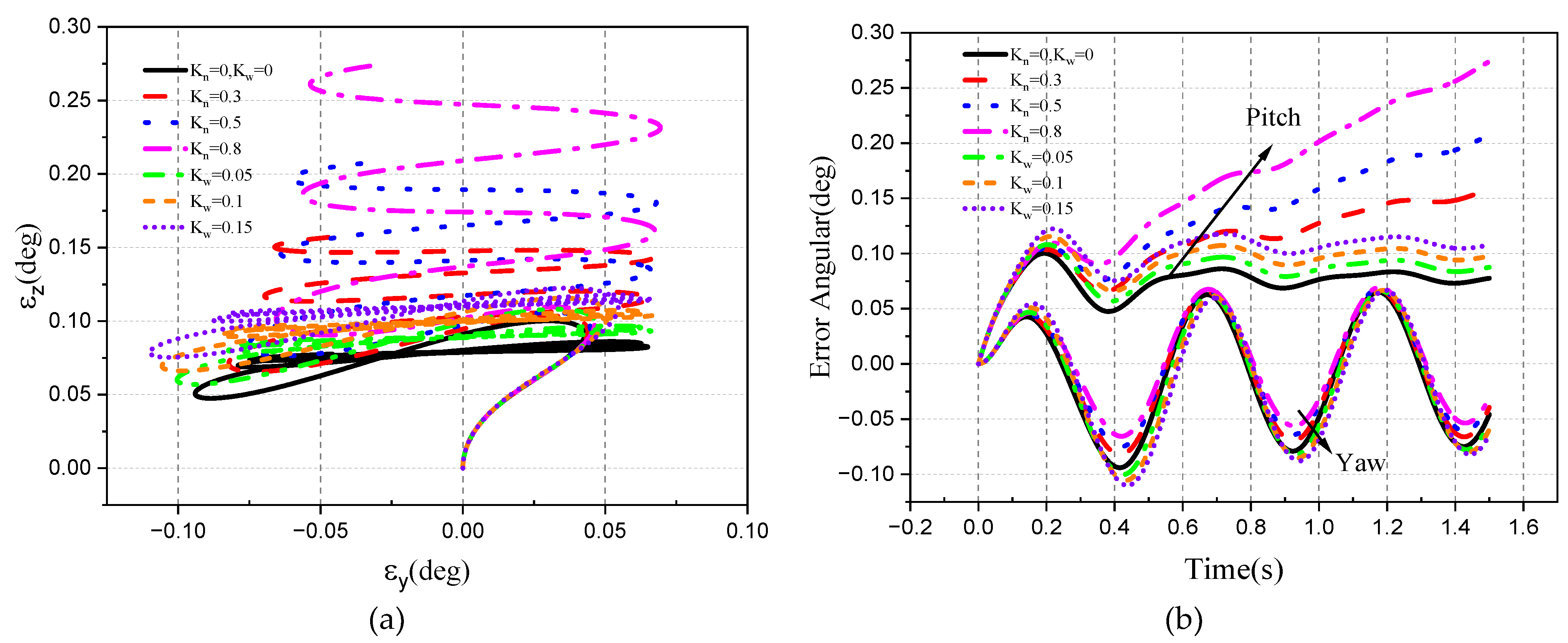
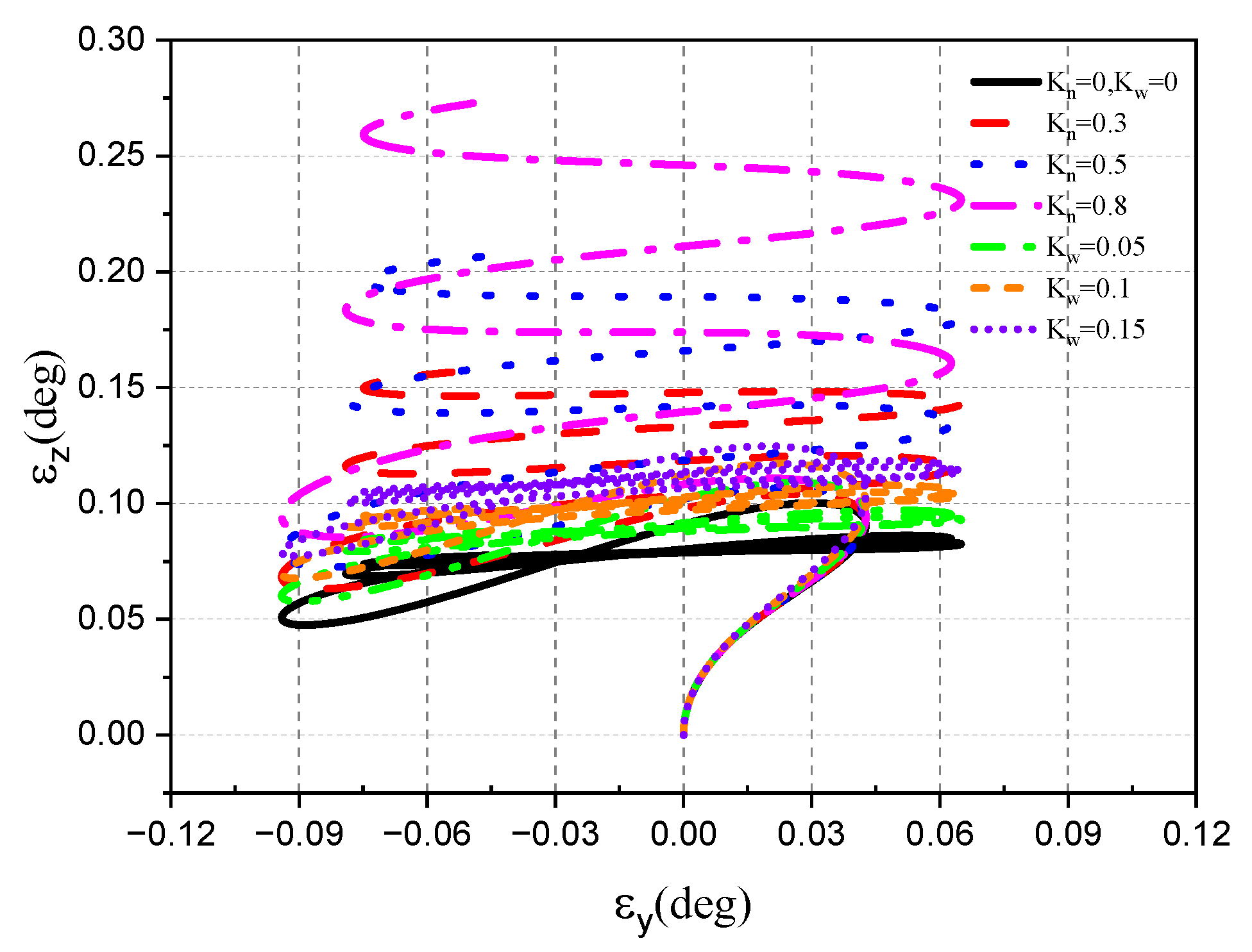
4.2.2. Target Space Motion
- Target tracking without aircraft attitude disturbance
- 2.
- Target tracking under aircraft attitude disturbance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, D.; Zheng, Y.; Xu, W.; Bai, S. An Accurate Line-of-Sight Rate Estimation Method Based on LSTM Recurrent Neural Network for Strapdown Imaging Seeker. IEEE Sens. J. 2022, 22, 21827–21836. [Google Scholar] [CrossRef]
- Dehghani, M.A.; Menhaj, M.B. Integral sliding mode formation control of fixed-wing unmanned aircraft using seeker as a relative measurement system. Aerosp. Sci. Technol. 2016, 58, 318–327. [Google Scholar] [CrossRef]
- Zhan, S.T.; Yan, W.X.; Fu, Z. Robust control of a yaw-pitch gimballed seeker. Aircr. Eng. Aerosp. Technol. 2015, 87, 83–91. [Google Scholar] [CrossRef]
- Ahi, B.; Haeri, M. A high-performance guidance filter scheme with exact dynamic modeling of a pitch-yaw gimballed seeker mechanism. Mech. Syst. Signal Proc. 2020, 144, 106857. [Google Scholar] [CrossRef]
- Li, S.; Zhong, M.; Qin, J. The Internal Model Control Design of Three-Axis Inertially Stabilized Platform for Airborne Remote Sensing. In Proceedings of the 2012 8th IEEE International Symposium on Instrumentation and Control Technology (ISICT), London, UK, 11–13 July 2012. [Google Scholar]
- Jiang, H.H.; Jia, H.G.; Wei, Q. Analysis of zenith pass problem and tracking strategy design for roll–pitch seeker. Aerosp. Sci. Technol. 2012, 23, 345–351. [Google Scholar] [CrossRef]
- Li, D.S.; Zhang, H.Q.; Zhao, Y. Research on Modeling and Simulation for Pitch/Roll Two-Axis strapdown Stabilization Platform. In Proceedings of the IEEE 2011 10th International Conference on Electronic Measurement & Instruments, Chengdu, China, 16–19 August 2011. [Google Scholar]
- Arrieta, O.; Campos, D.; Rico-Azagra, J.; Gil-Martínez, M.; Rojas, J.D.; Vilanova, R. Model-Based Optimization Approach for PID Control of Pitch–Roll UAV Orientation. Mathematics 2023, 11, 3390. [Google Scholar] [CrossRef]
- Wang, X.C.; Mo, B.; Li, X.; Liu, F.X. A line-of-sight rate estimation method for roll-pitch gimballed infrared seeker. Optik 2019, 192, 162935. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Z.C.; Yi, K.; Han, Y.; Ren, Z. Snake-Hot-Eye-Assisted Multi-Process-Fusion Target Tracking Based on a Roll-Pitch Semi-strapdown Infrared Imaging Seeker. J. Bionic Eng. 2022, 19, 1124–1139. [Google Scholar] [CrossRef]
- Wang, Y.D.; Wang, J.; He, S.M.; Shin, H.S.; Tsourdos, A. Optimal Guidance With Active Observability Enhancement for Scale Factor Error Estimation of Strapdown Seeker. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 4347–4362. [Google Scholar] [CrossRef]
- Yang, H.; Bai, X.B.; Zhang, S.F. Layout Design of Strap down Array Seeker and Extraction Method of Guidance Information. Aerospace 2022, 9, 373. [Google Scholar] [CrossRef]
- Leomanni, M.; Bianchini, G.; Garulli, A.; Quartullo, R. Sum-of-norms periodic model predictive control for space rendezvous. IEEE Trans. Control Syst. Technol. 2021, 30, 1311–1318. [Google Scholar] [CrossRef]
- Eren, U.; Prach, A.; Koçer, B.B.; Raković, S.V.; Kayacan, E.; Açıkmeşe, B. Model predictive control in aerospace systems: Current state and opportunities. J. Guid. Control Dyn. 2017, 40, 1541–1566. [Google Scholar] [CrossRef]
- Singh, K.; Gupta, P.K.; Chaurasia, D.; Kandanvli, V.K.R. Stability of Discrete-Time Delayed Systems Subject to External Interference and Generalized Overflow Nonlinearities. IEEE Trans. Ind. Appl. 2022, 58, 5353–5364. [Google Scholar] [CrossRef]
- Liu, S.X.; Du, X.; Xia, Q.L. An on-line compensation method for the disturbance rejection rate of seekers. Optik 2018, 157, 1306–1318. [Google Scholar] [CrossRef]
- Jianmei, S.; Gaohua, C.; Xianxiang, C.; Lixia, K. Stability region analysis of the parasitic loop of the semi-strapdown homing seeker. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2012, 226, 550–562. [Google Scholar] [CrossRef]
- Wen, Q.Q.; Lu, T.Y.; Xia, Q.L.; Sun, Z.D. Beam-pointing error compensation method of phased array radar seeker with phantom-bit technology. Chin. J. Aeronaut. 2017, 30, 1217–1230. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, M.C.; Liu, B.; Jia, H.G. LOS stabilization and gyro configuration analysis for roll-pitch seeker. Appl. Mech. Mater. 2013, 397, 530–535. [Google Scholar] [CrossRef]
- Li, Y.; Wen, X.H.; Li, W.; Wei, L.; Xia, Q.L. Influence of roll-pitch seeker DRR and parasitic loop on Lyapunov stability of guidance system. J. Syst. Eng. Electron. 2021, 32, 1509–1526. [Google Scholar]
- Du, X.; Lv, R.; Tu, H.F.; Jiang, C.W. The research on infrared seeker with disturbance rejection effect parasitic. Optik 2018, 170, 409–419. [Google Scholar] [CrossRef]
- Wu, D.W.; Chen, M.; Gong, H.J. Adaptive neural flight control for an aircraft with time-varying distributed delays. Neurcomputing 2018, 307, 130–145. [Google Scholar] [CrossRef]
- Naghdi, M.; Sadrnia, M.A. A novel fuzzy extended state observer. ISA Trans. 2020, 102, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ran, M.P.; Li, J.C.; Xie, L.H. A new extended state observer for uncertain nonlinear systems. Automatica 2021, 131, 109772. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, J.Z.; Shi, D.W.; Shi, L. Toward Event-Triggered Extended State Observer. IEEE Trans. Autom. Control 2018, 63, 1842–1849. [Google Scholar] [CrossRef]
- Yu, B.Q.; Shen, A.W.; Chen, B.; Luo, X.; Tang, Q.P.; Xu, J.B.; Zhu, M.F. A Compensation Strategy of Flux Linkage Observer in SPMSM Sensorless Drives Based on Linear Extended State Observer. IEEE Trans. Energy Convers. 2022, 37, 824–831. [Google Scholar] [CrossRef]
- Liu, X.; Mo, B.; Liu, F.X. Line-of-sight stabilization of roll-pitch seeker using differentiator-based disturbance compensation control. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 234, 1326–1339. [Google Scholar] [CrossRef]
- Lin, S.Y.; Lin, D.F.; Wang, W. A Novel Online Estimation and Compensation Method for Strap down Phased Array Seeker Disturbance Rejection Effect Using Extended State Kalman Filter. IEEE Access 2019, 7, 172330–172340. [Google Scholar] [CrossRef]






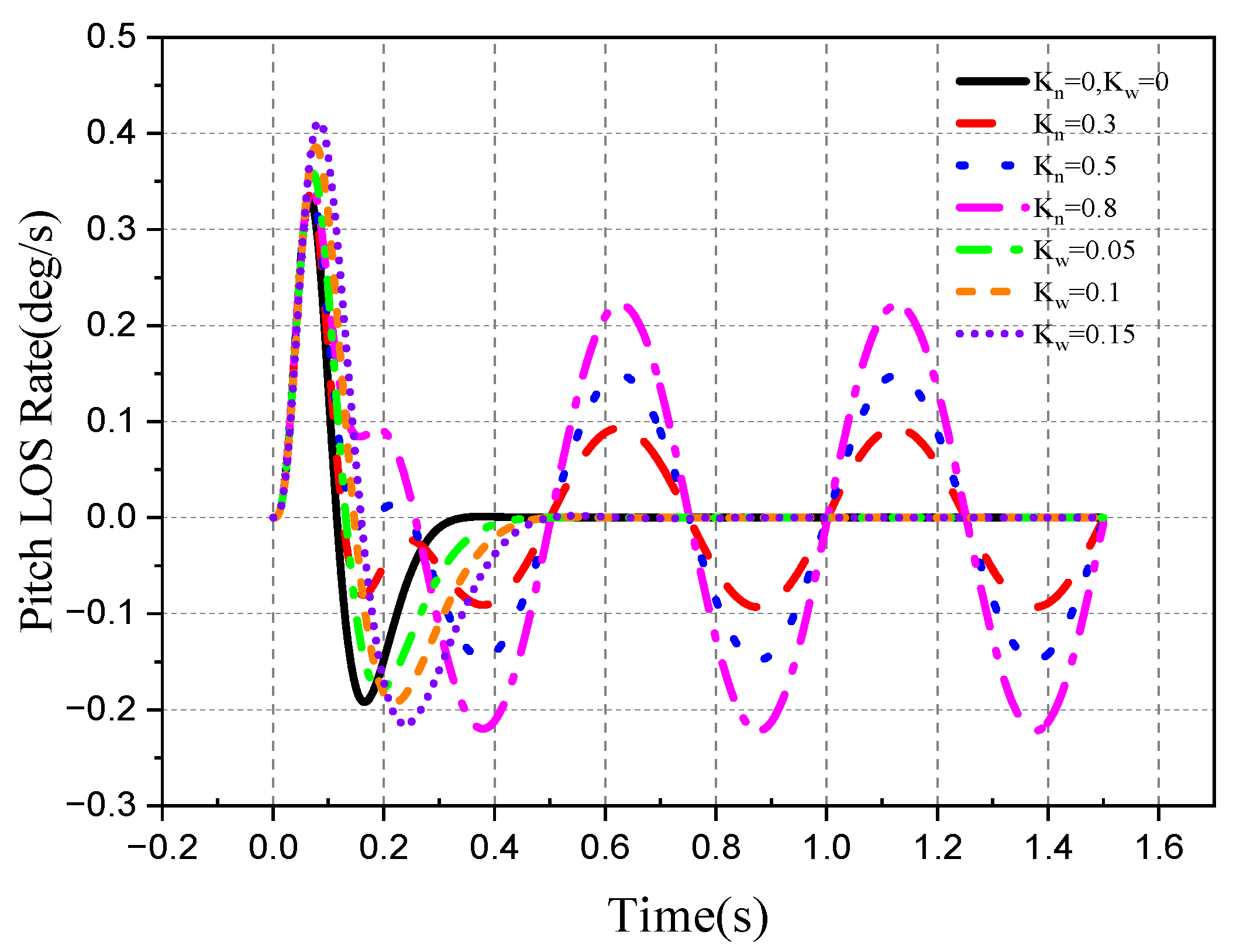


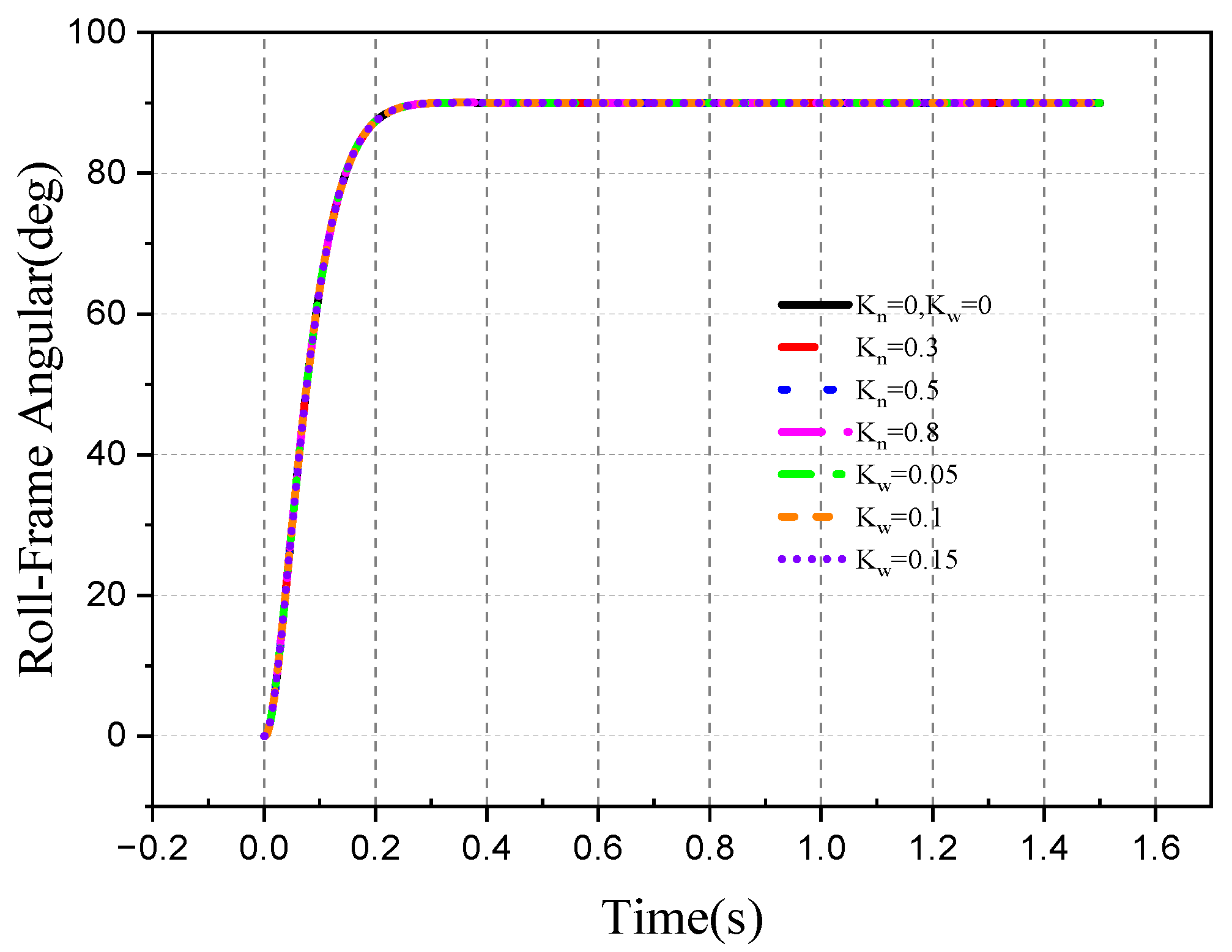

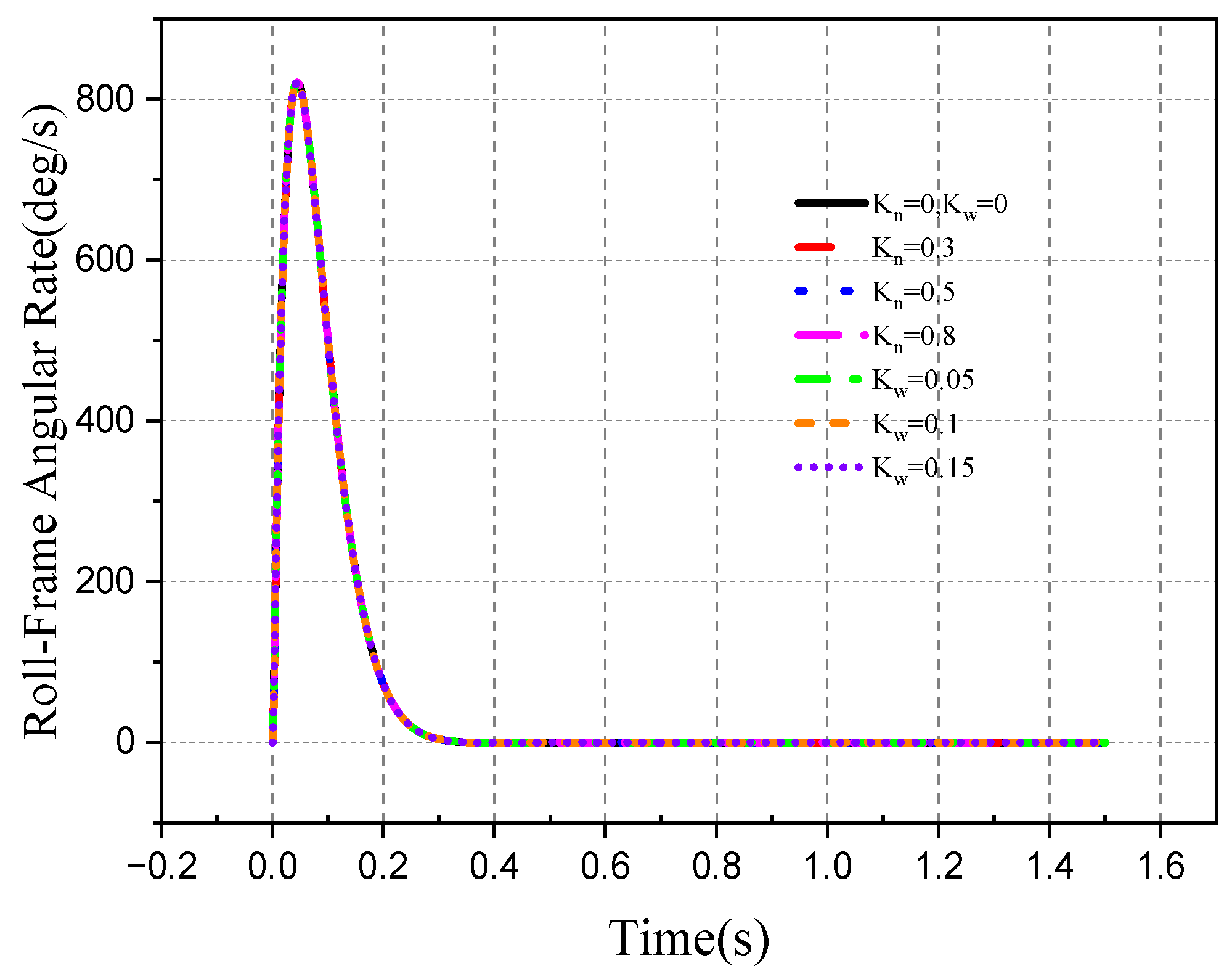
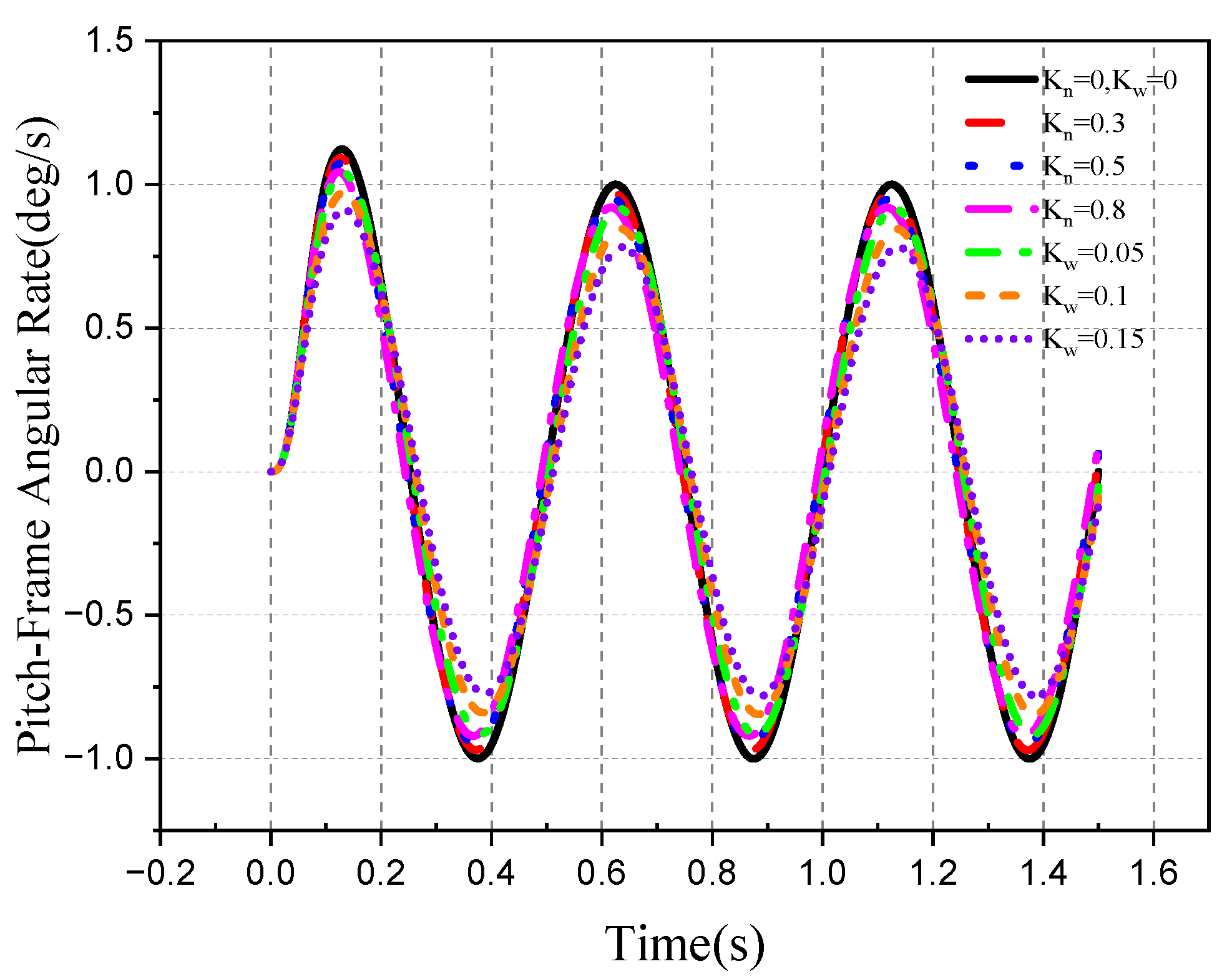










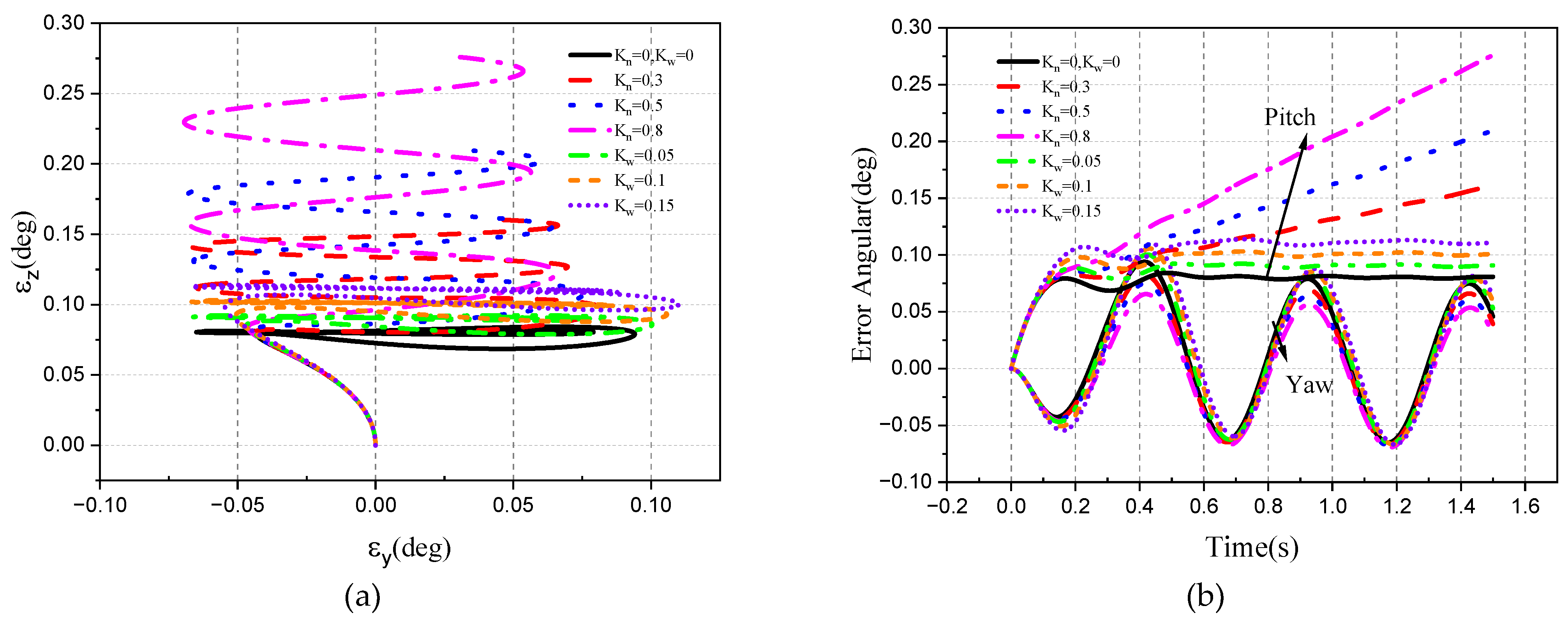

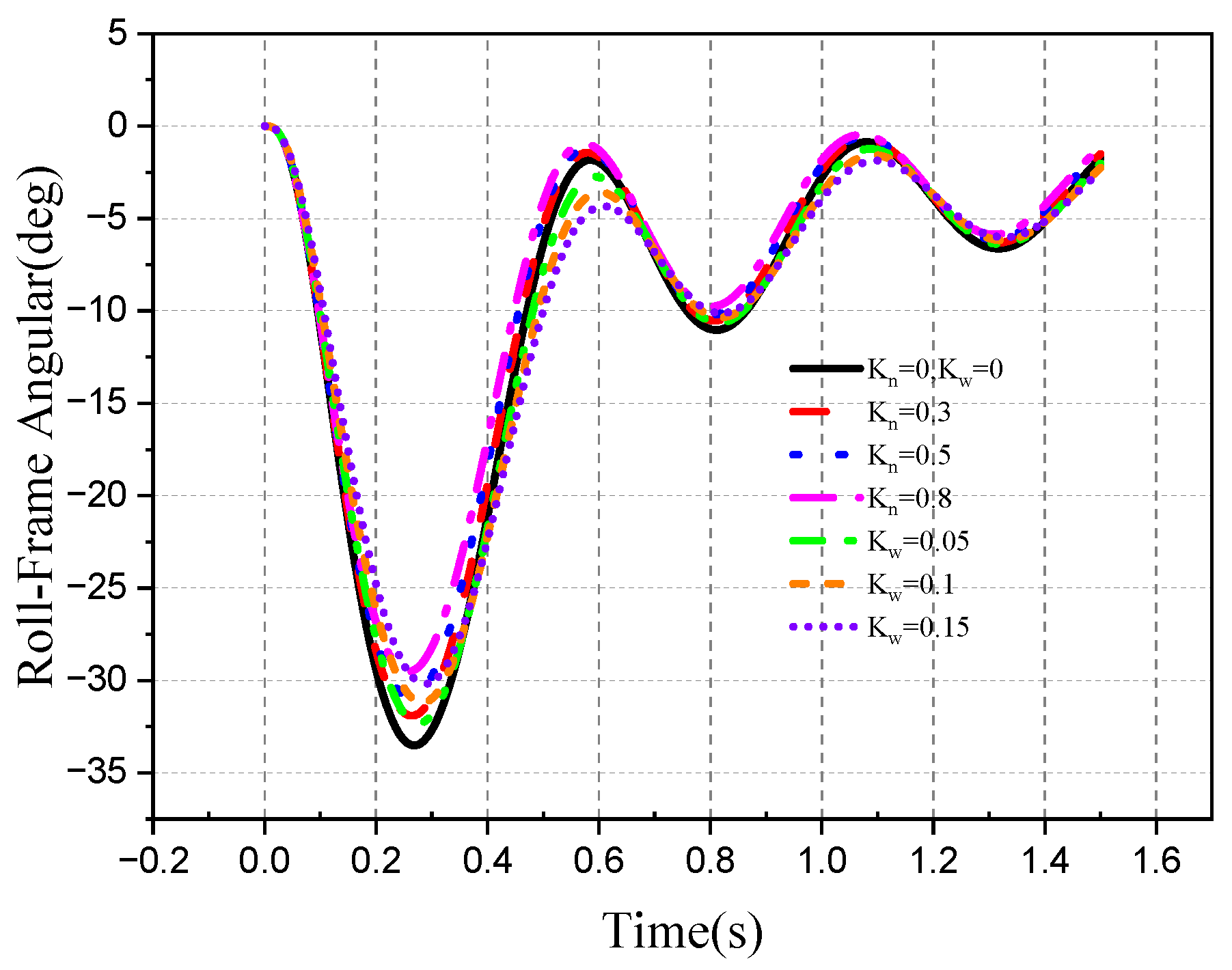

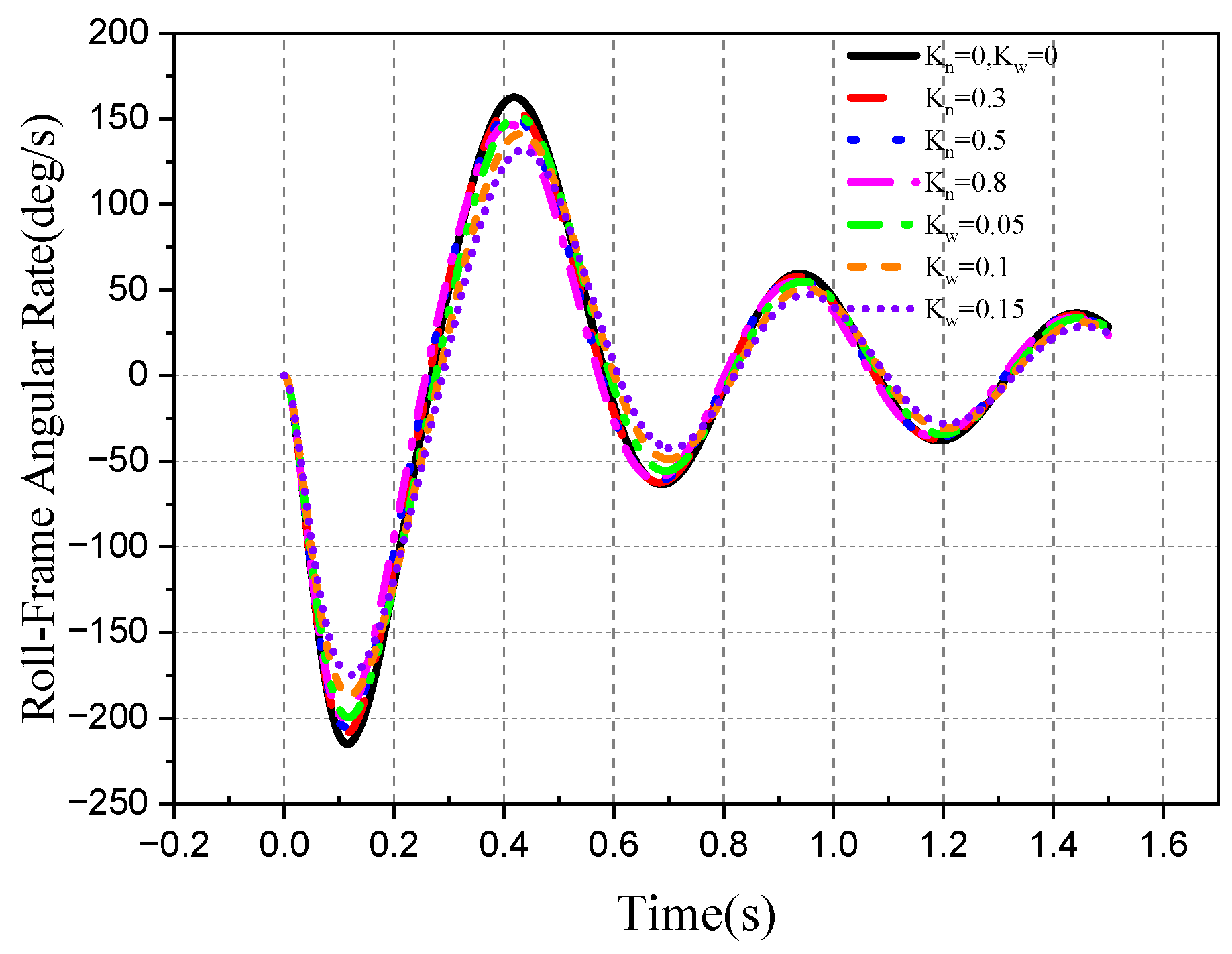
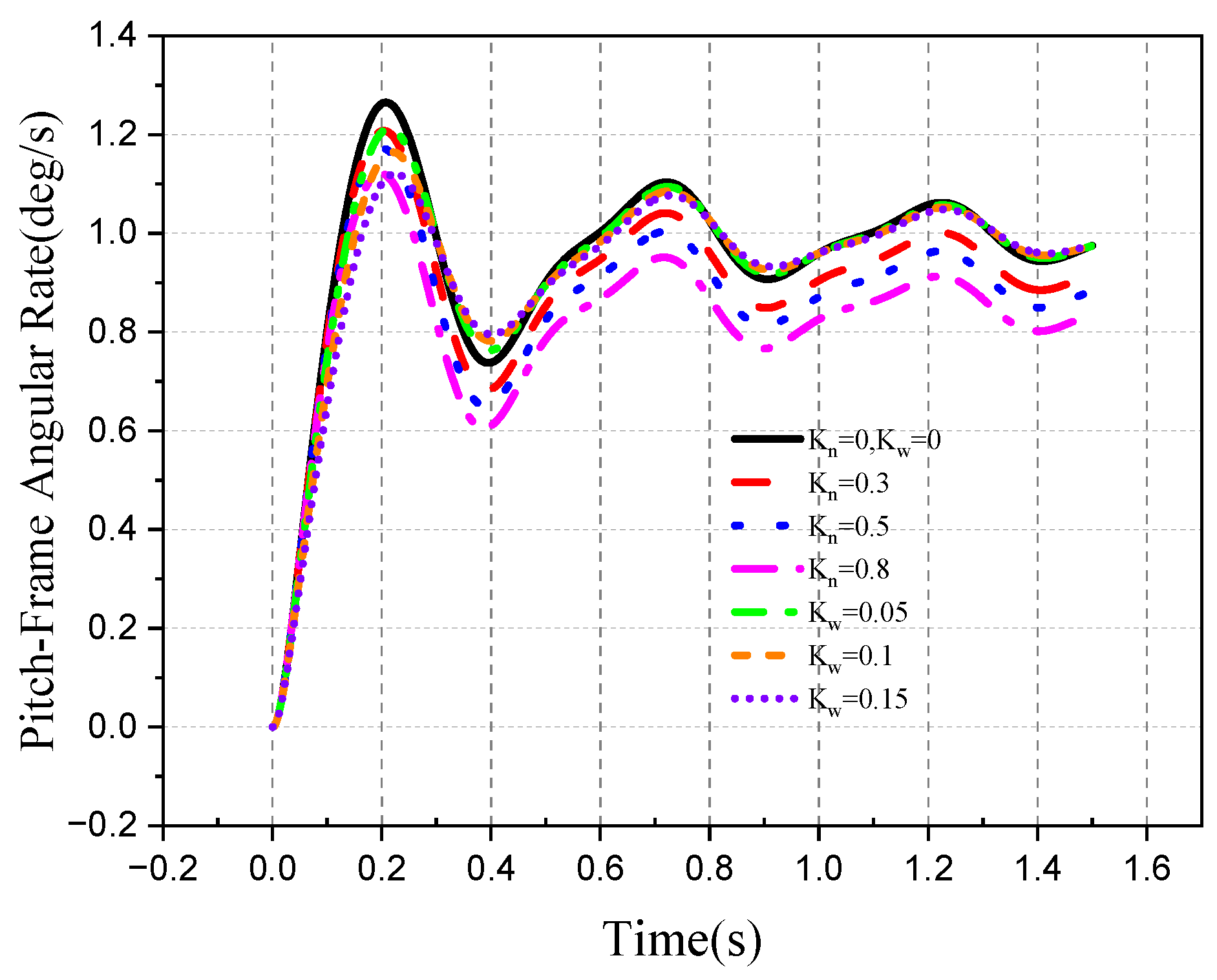

| Parameter | Roll Frame | Pitch Frame | Unit |
|---|---|---|---|
| Tracking loop gain G1 | 24 | 12 | - |
| Stable loop gain G2 | 18 | 18 | - |
| Resistance R | 13.5 | 12.5 | Ω |
| Inductance L | 0.00675 | 0.0075 | H |
| Rotational inertia J | 0.0087 | 0.00305 | Kg m2 |
| Torque coefficient KT | 0.81 | 0.28 | Nm/A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, B.; Lu, T.; Ma, Z.; Xia, Q. Research on the Influence of the Disturbance Rejection Rate of a Roll–Pitch Seeker on Stable Tracking Characteristics. Aerospace 2023, 10, 940. https://doi.org/10.3390/aerospace10110940
Xiao B, Lu T, Ma Z, Xia Q. Research on the Influence of the Disturbance Rejection Rate of a Roll–Pitch Seeker on Stable Tracking Characteristics. Aerospace. 2023; 10(11):940. https://doi.org/10.3390/aerospace10110940
Chicago/Turabian StyleXiao, Bowen, Tianyu Lu, Zeyuan Ma, and Qunli Xia. 2023. "Research on the Influence of the Disturbance Rejection Rate of a Roll–Pitch Seeker on Stable Tracking Characteristics" Aerospace 10, no. 11: 940. https://doi.org/10.3390/aerospace10110940
APA StyleXiao, B., Lu, T., Ma, Z., & Xia, Q. (2023). Research on the Influence of the Disturbance Rejection Rate of a Roll–Pitch Seeker on Stable Tracking Characteristics. Aerospace, 10(11), 940. https://doi.org/10.3390/aerospace10110940





