Characteristics of a Heat Exchanger in a Liquid Rocket Engine Using Conjugate Heat Transfer Coupling with Open-Source Tools
Abstract
:1. Introduction
2. Numerical Setup
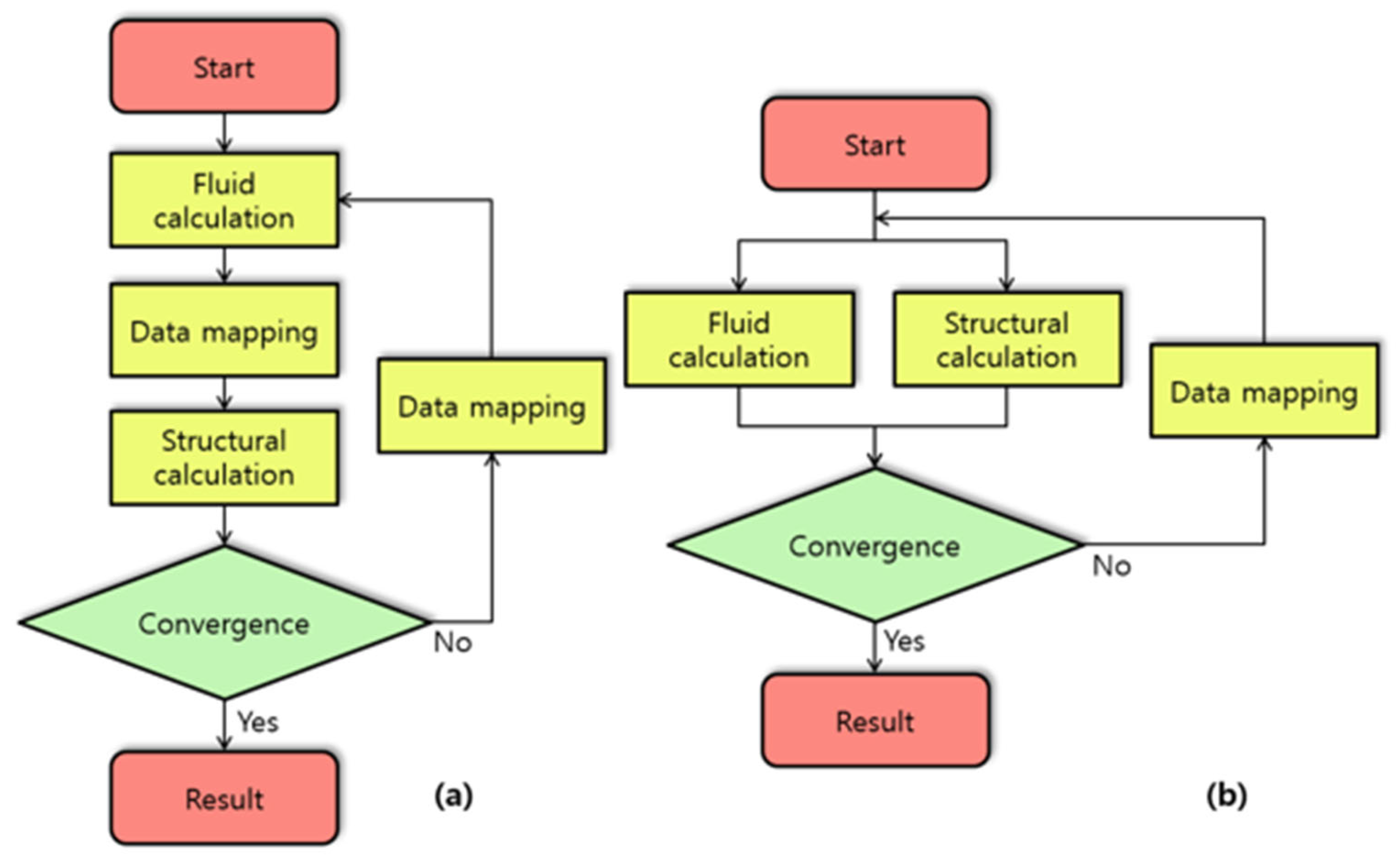
2.1. Methodology
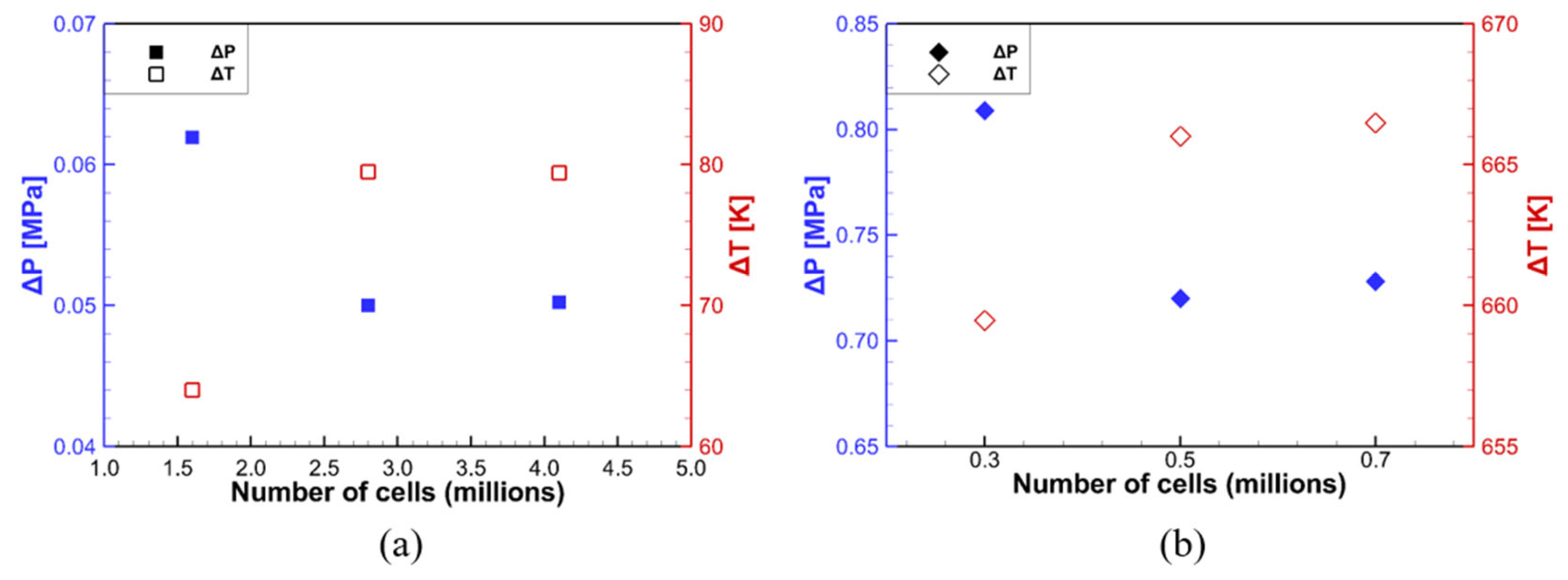
2.2. Numerical Analysis
3. Results
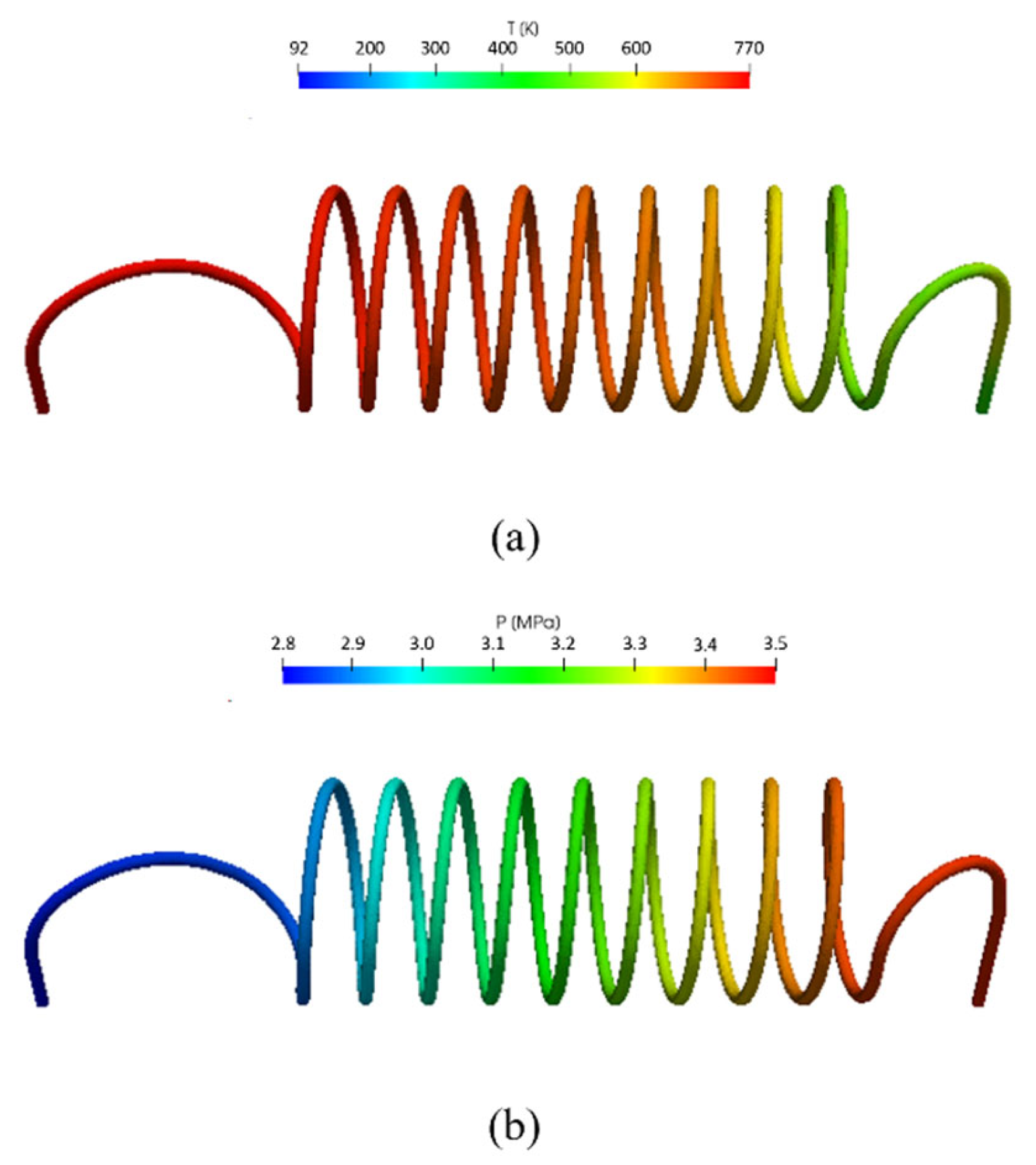
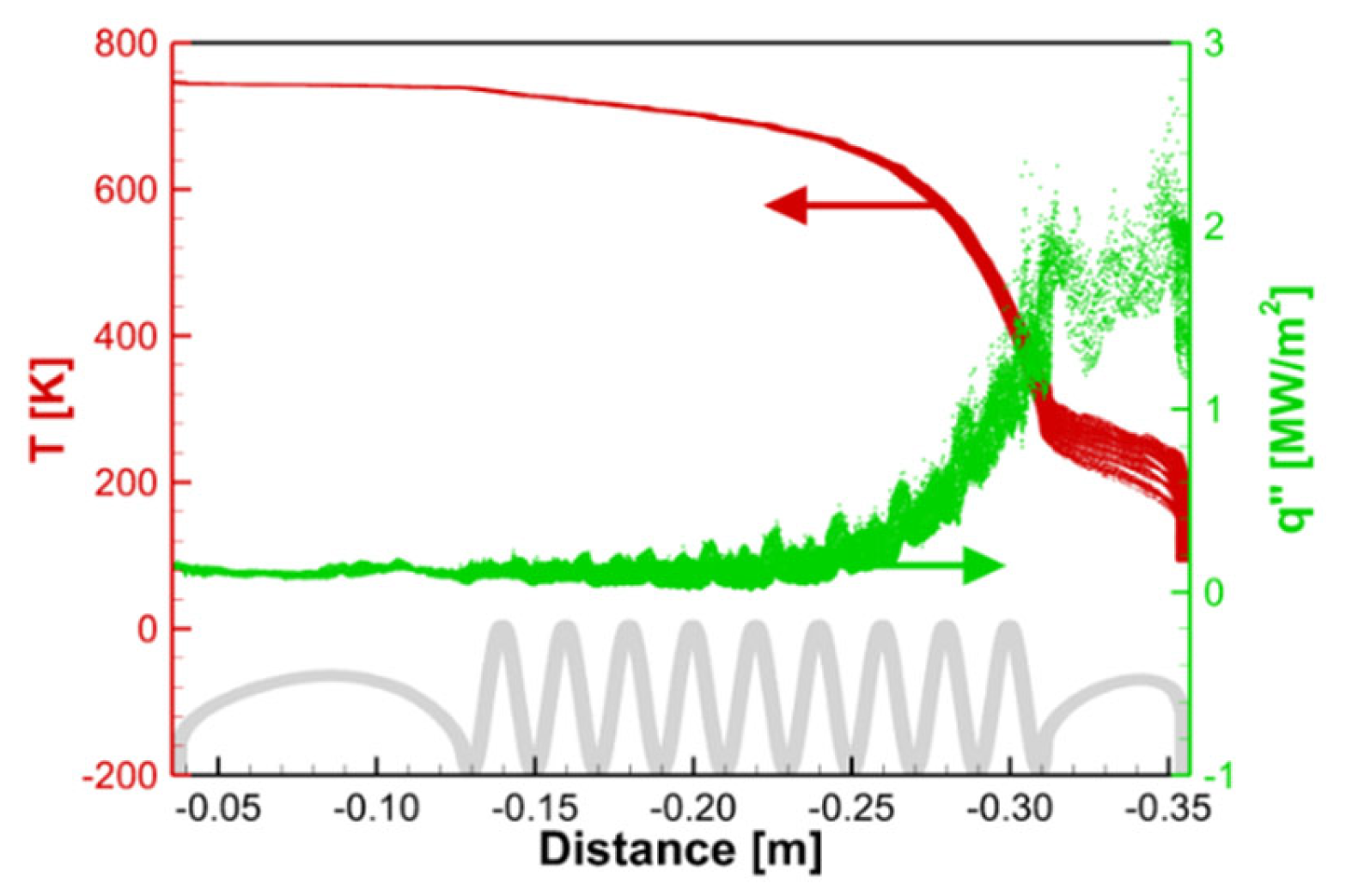
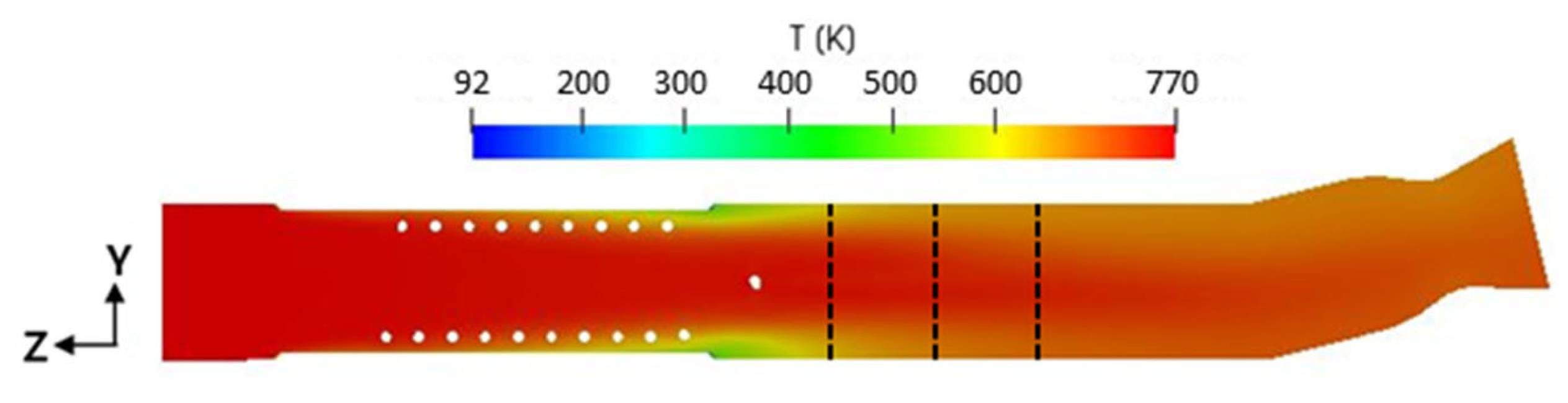
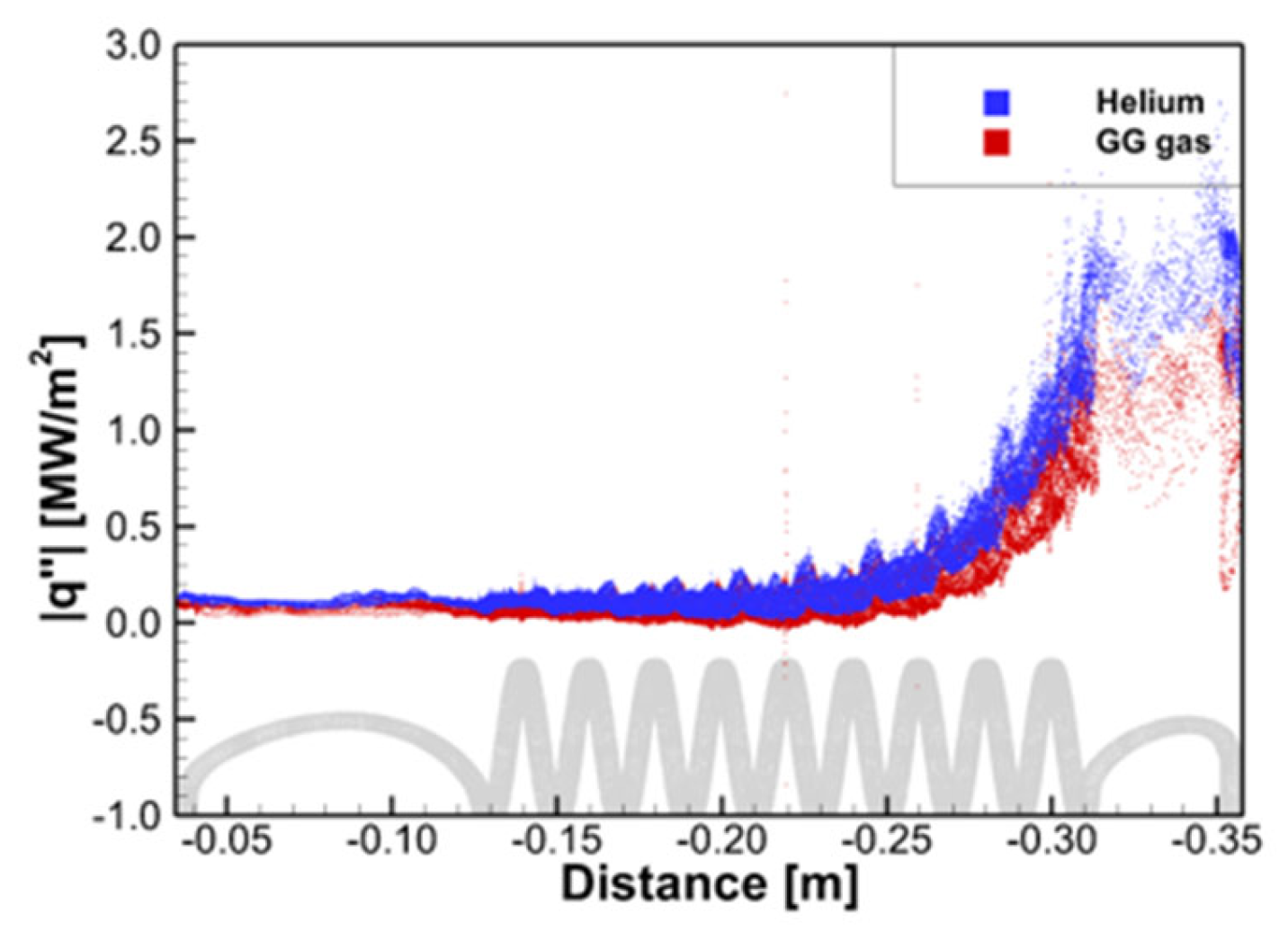
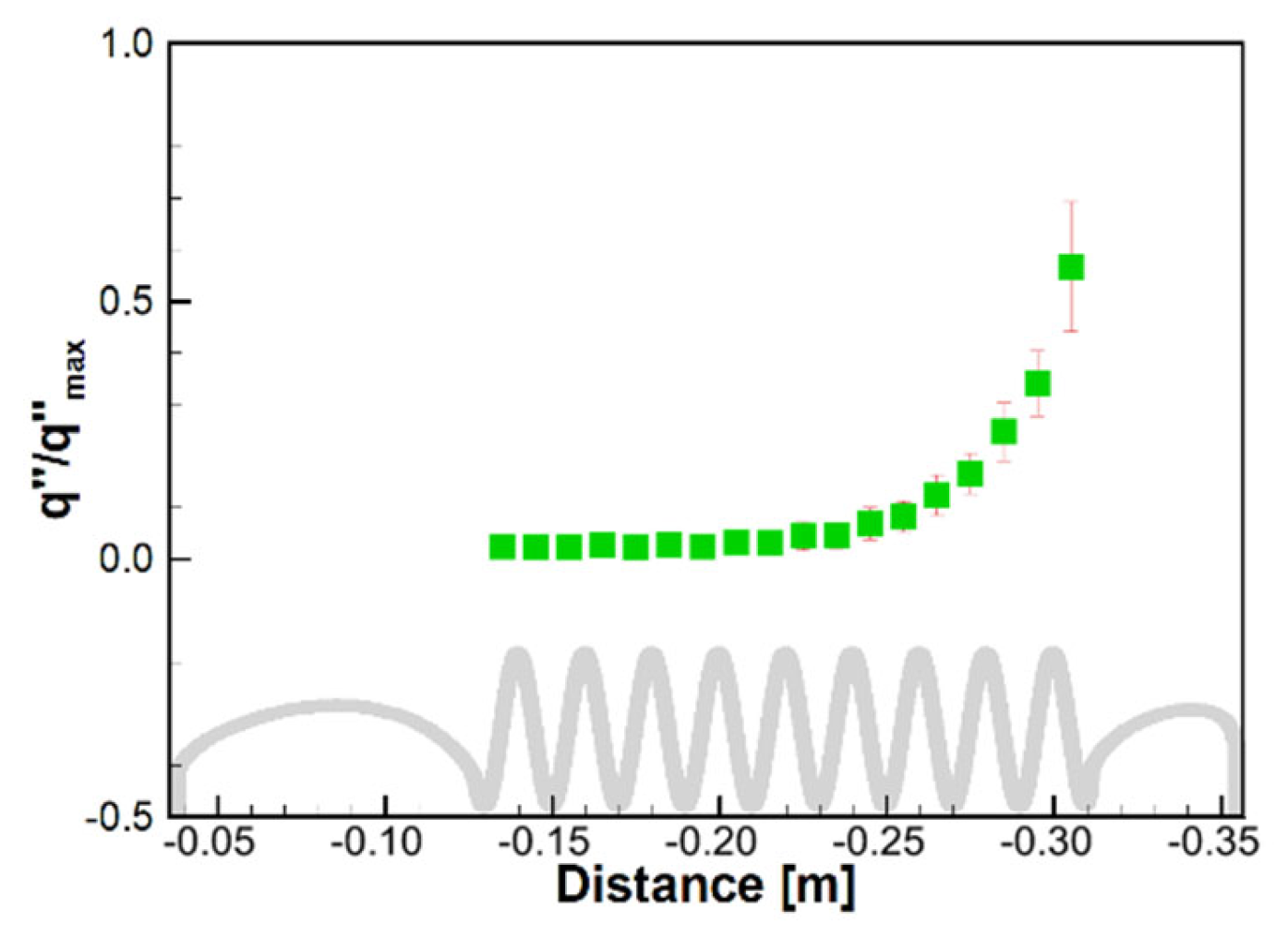
3.1. Behaviors of Helium in Helically-Coiled Tube with Nine Turns
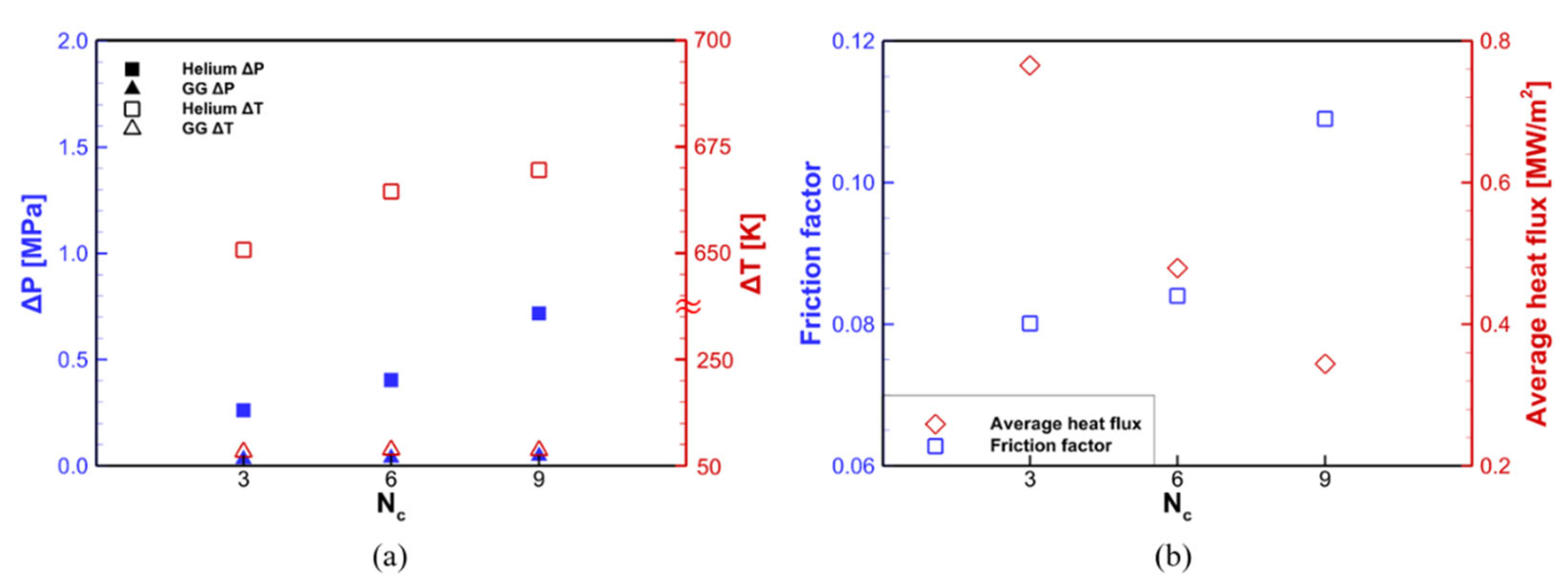
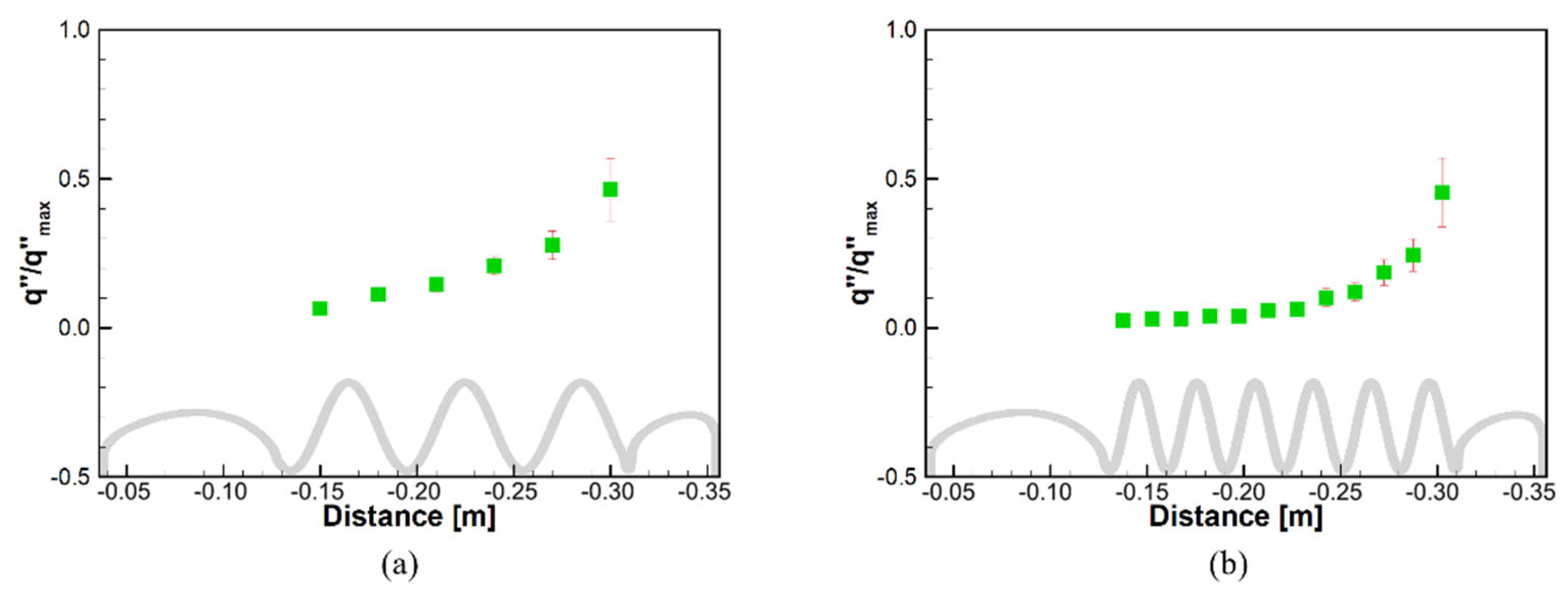
3.2. Effect of Number of Turns ()
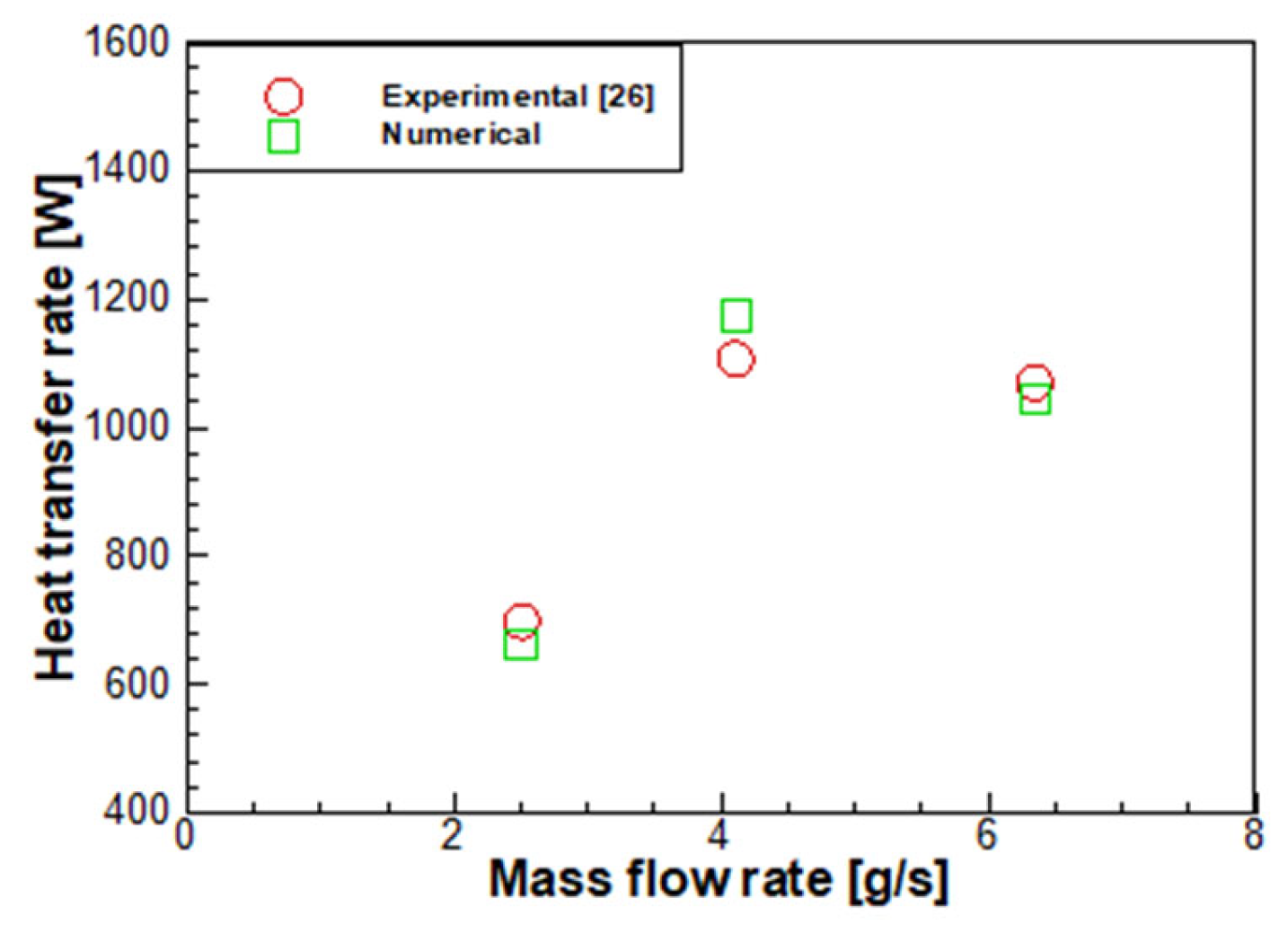
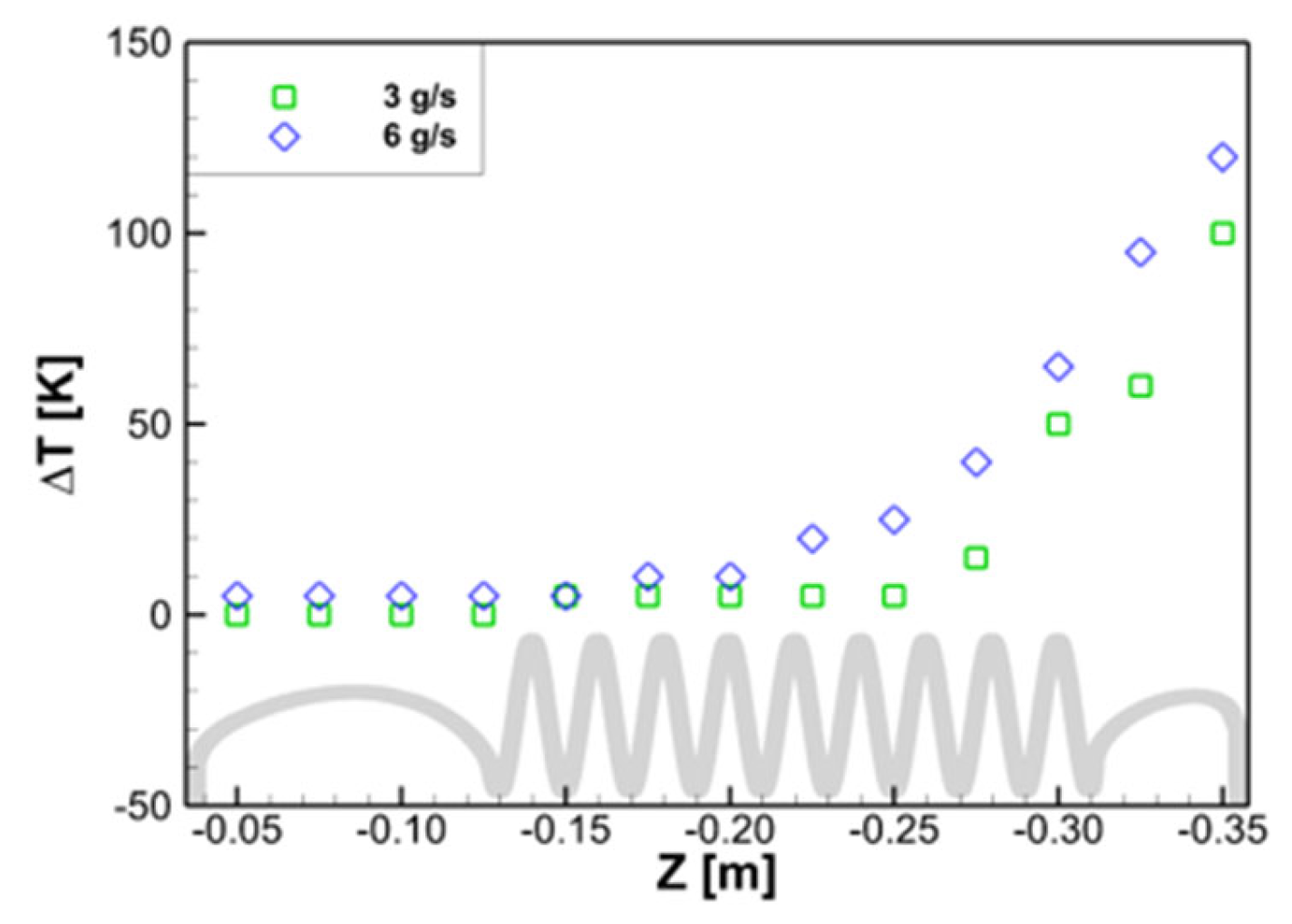
3.3. Effect of Mass Flow Rate ()
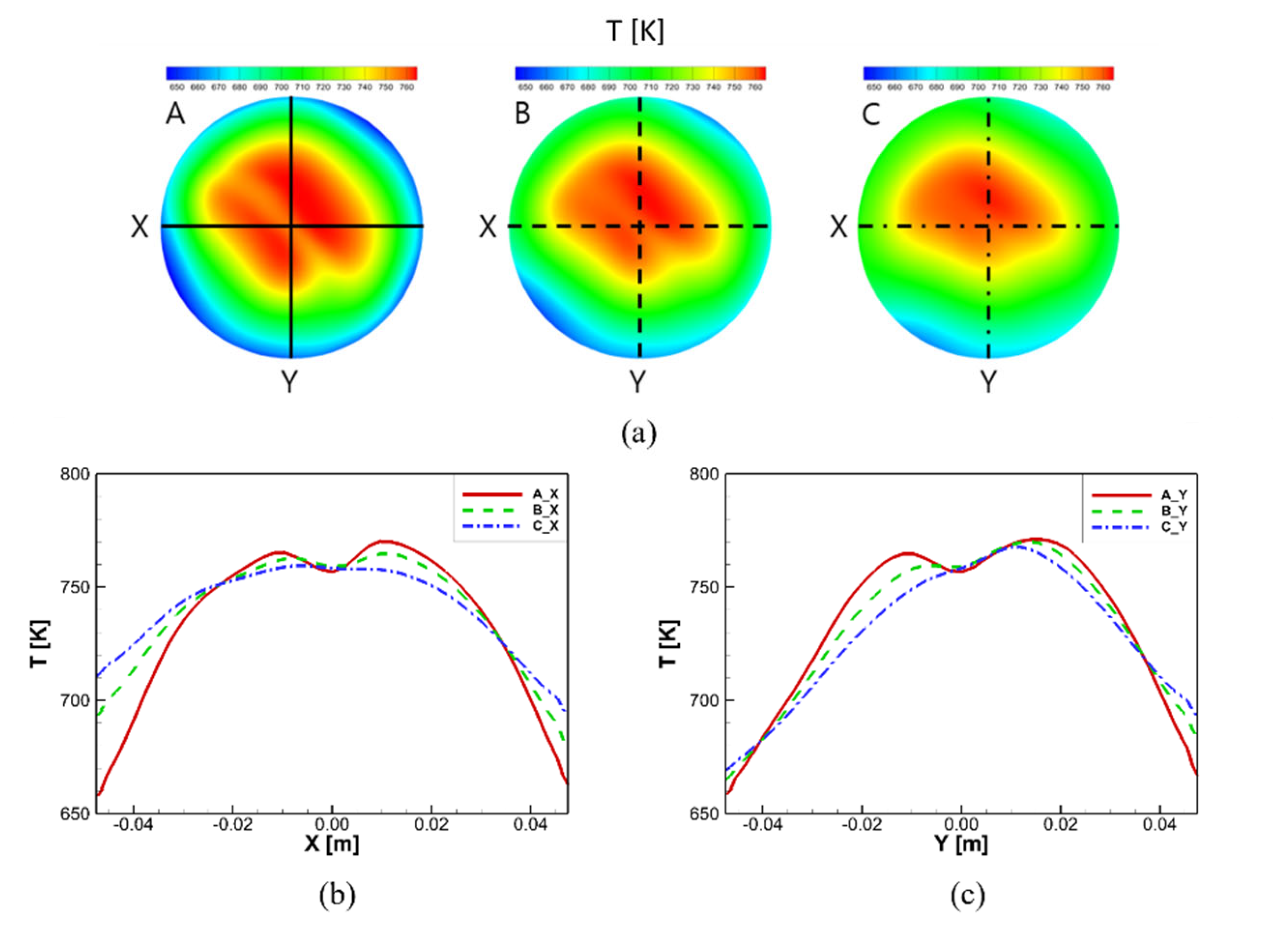
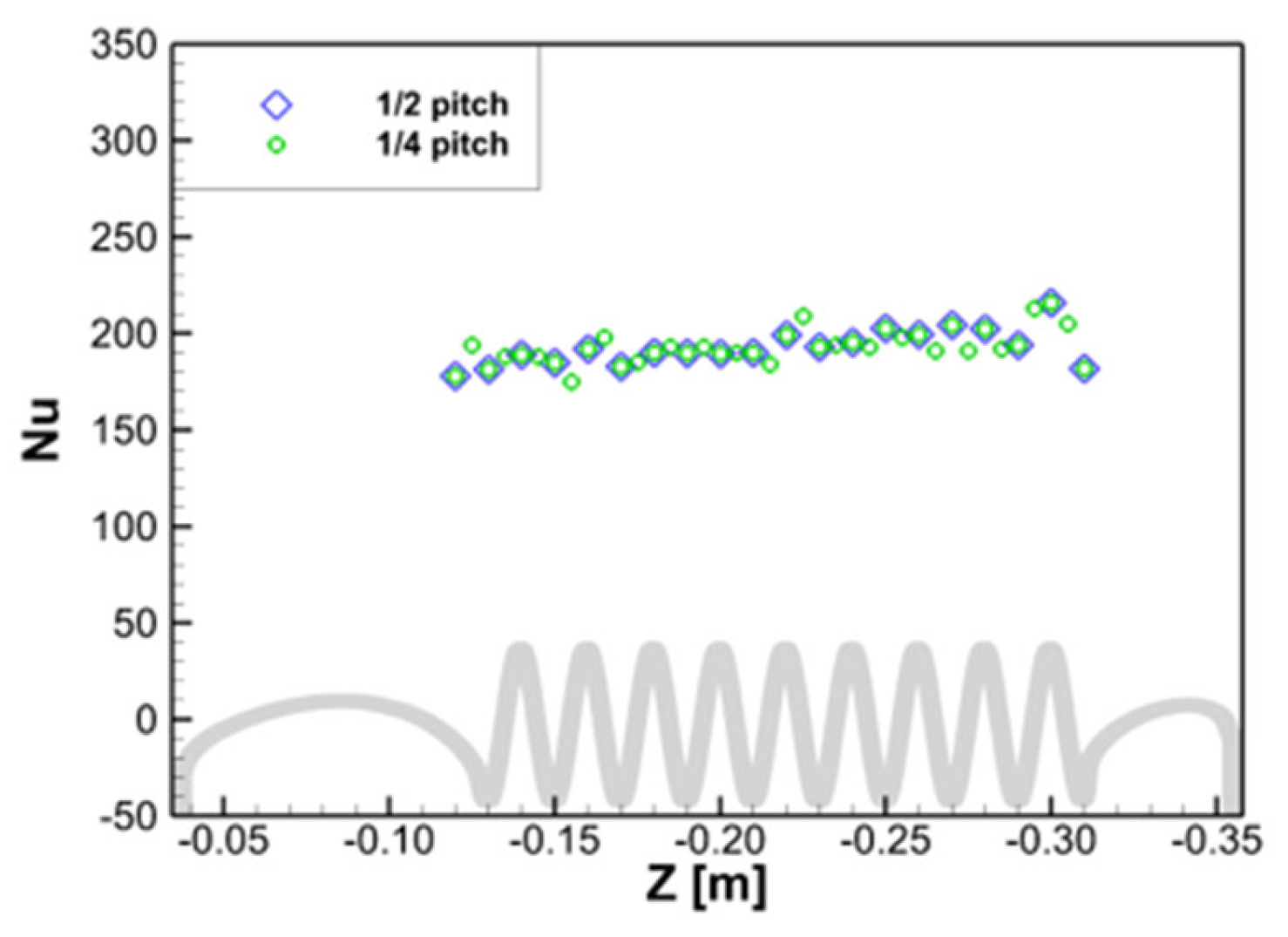
3.4. Analysis of Heat Transfer Characteristics
4. Conclusions
- (1)
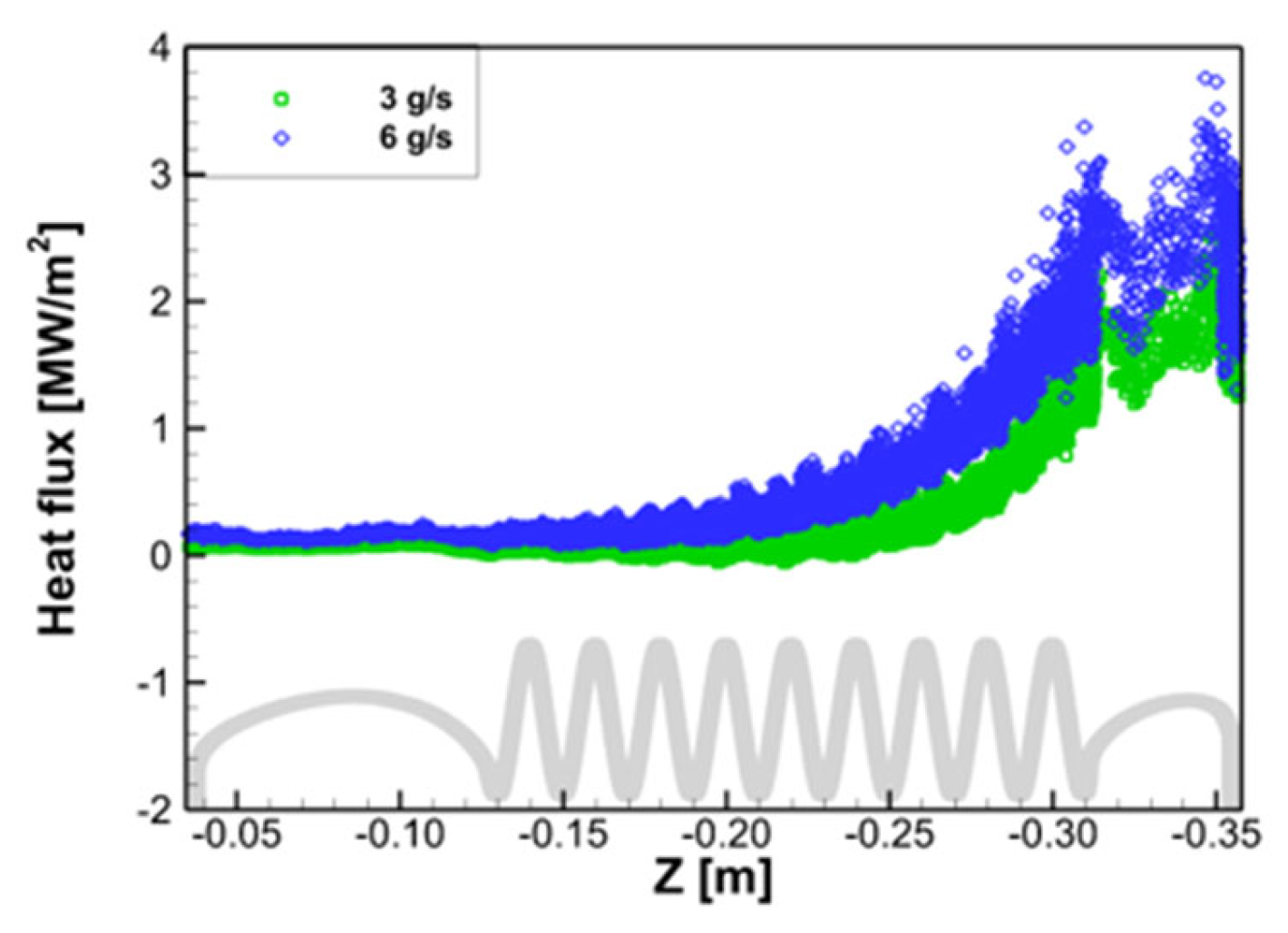
- For the baseline heat exchanger ( = 9), the characteristics of heat transfer were investigated. As the temperature difference between GG gas and helium decreased along the coiled tube, the heat flux decreased dramatically, resulting in a value of about 5% after the sixth turn of the coiled tube. Therefore, the baseline heat exchanger is overdesigned from the viewpoint of heat transfer optimality. Therefore, further numerical analysis was performed to predict the effect of on the performance of the heat exchanger;
- (2)
- In the case of = 3, the outlet temperature was 20 K lower than that in the case of = 9 due to the excessively-reduced residence time and heat transfer area. Therefore, the heat exchanger with = 3 had a small number of pitches and thus poor heat transfer performance. For = 6, the outlet temperature was 5 K lower than that for = 9, the pressure drop of helium was 0.3 MPa, and the weight of the helically-coiled tube structure was reduced by 72% compared with that for = 9. Consequently, the optimal number of turns of the coiled tube was six or more;
- (3)
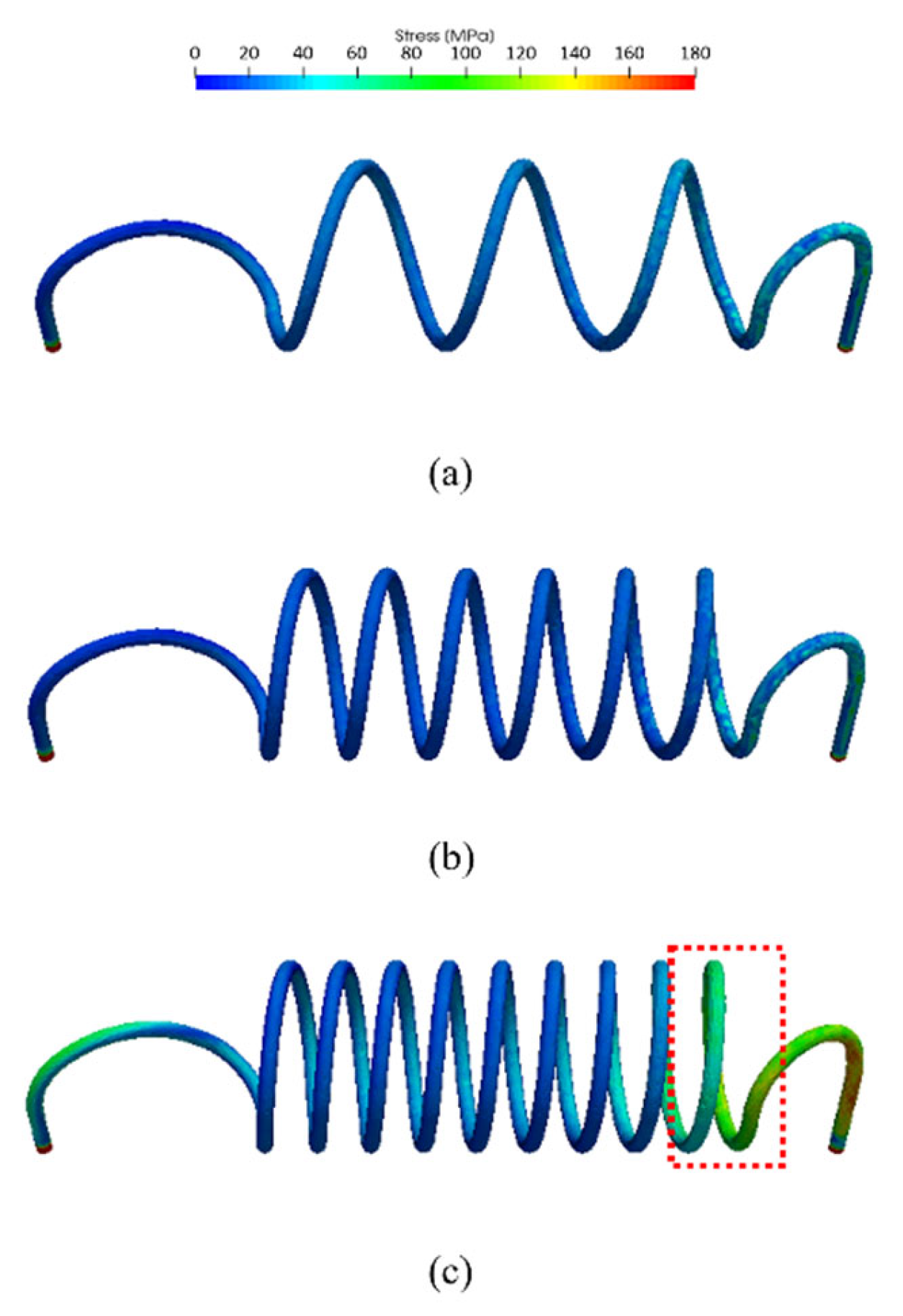
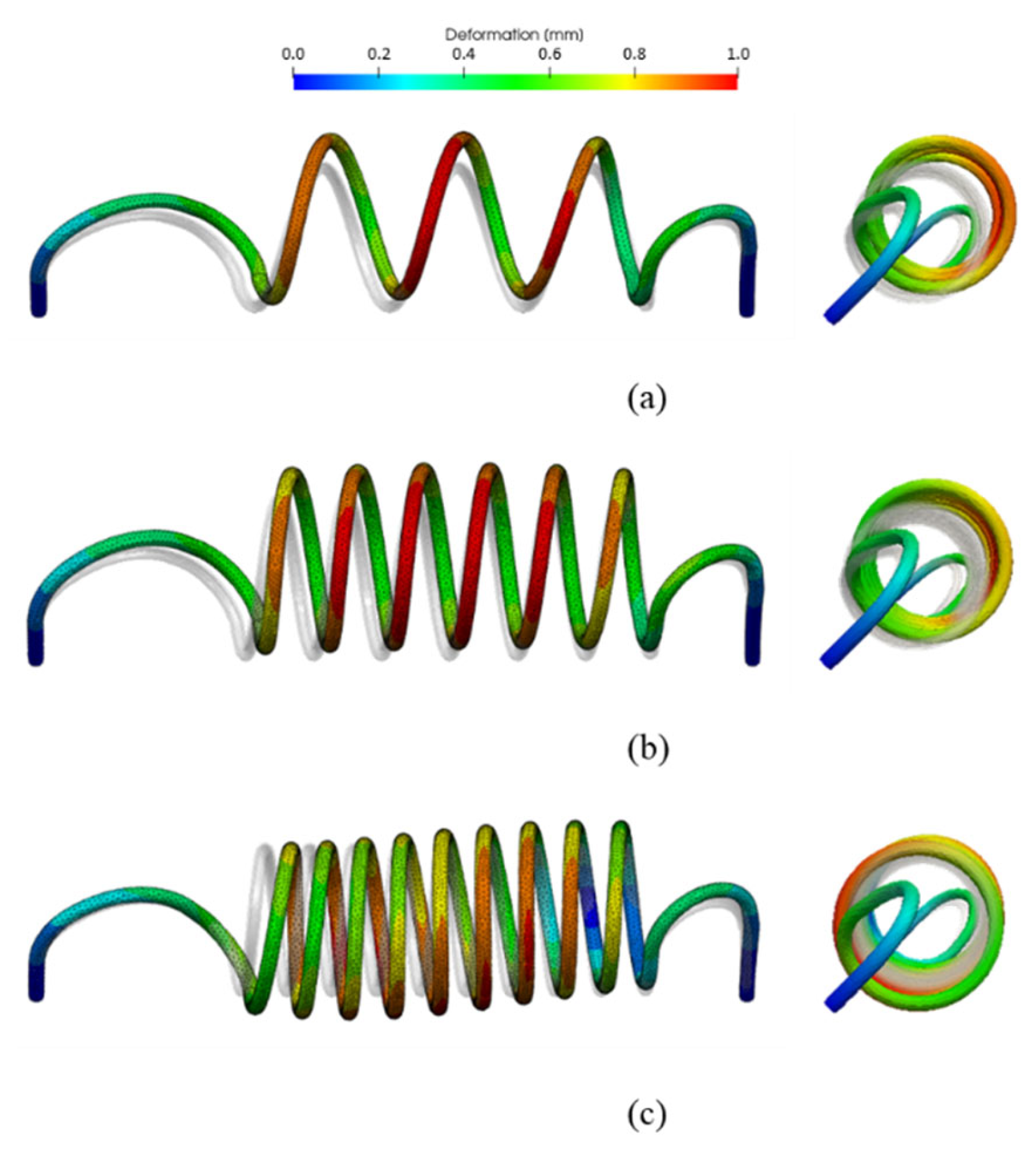
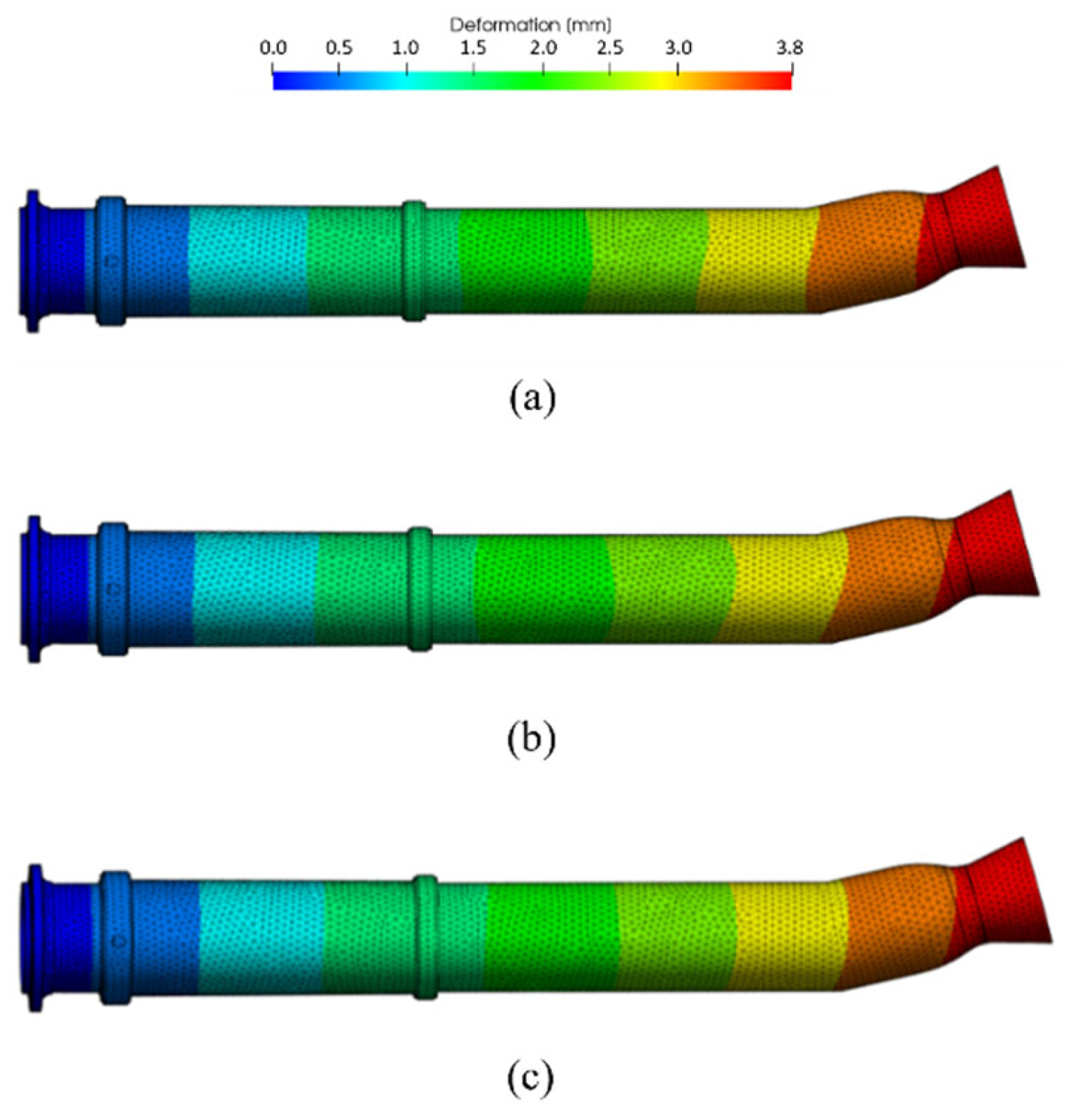
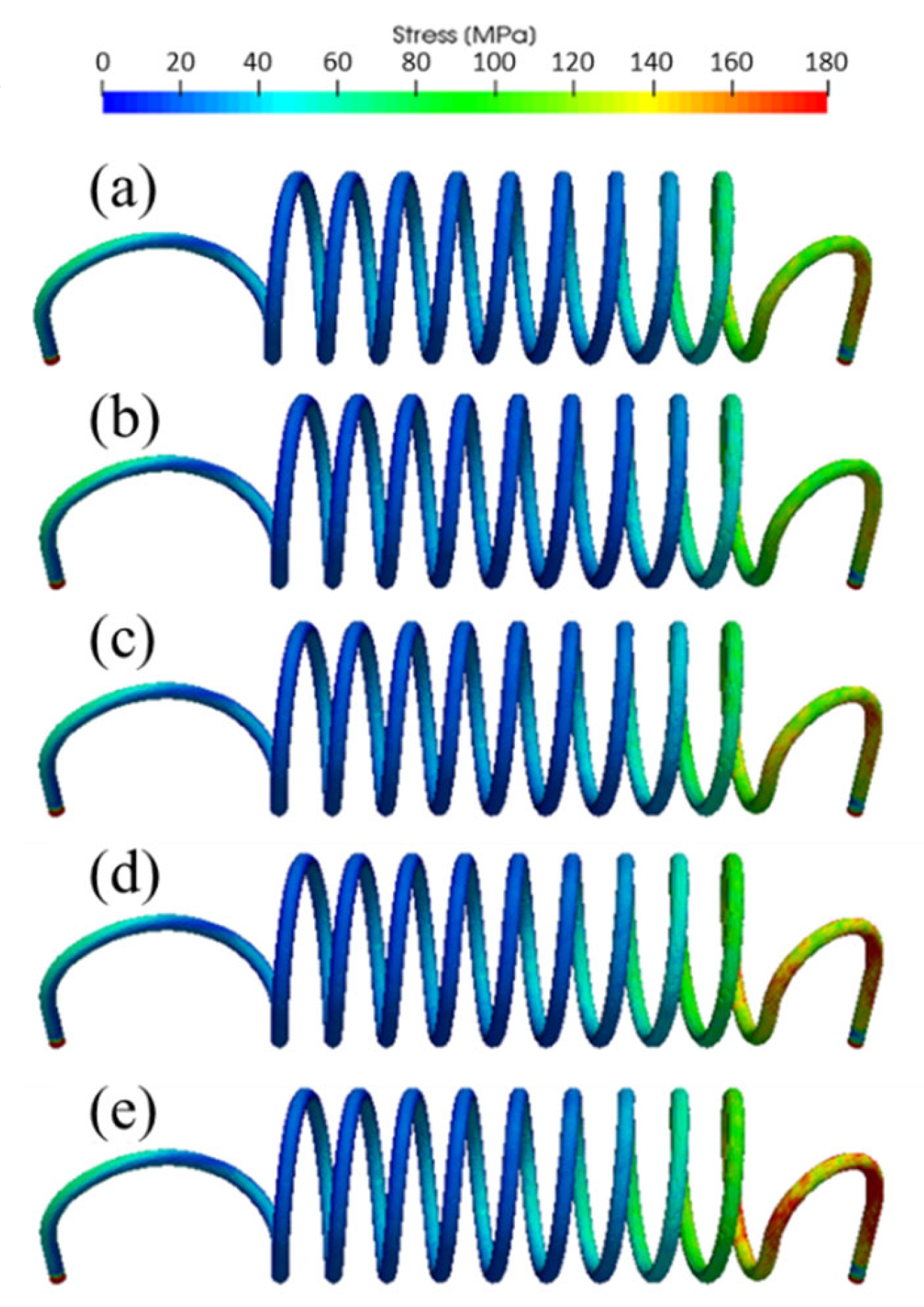
- According to the structural analysis of the helically-coiled tube, a maximum deformation of about 1 mm was predicted. This deformation could not make any structural problems, such as physical contact with the inner wall of the heat exchanger. In addition, the safety factors for thermal stress for = 3, 6, and 9 exceed 1, so the structural integrity was acceptable. At the outer casing of the heat exchanger, a maximum deformation of 3.8 mm was predicted near the outlet due to heat transfer from GG gas. However, such deformation would not cause structural problems, such as physical contact with the main nozzle of the liquid rocket engine. Considering this deformation of the outer casing of the heat exchanger, a heat exchanger with a straight body can be designed to generate higher thrust;
- (4)
- The amount of heat received from the hot GG gas increased with the mass flow rate. However, the temperature difference between the inlet and outlet of helium decreased from 670 K to 654 K. In the case of the highest flow rate (6 g/s), the outlet temperature was 8 K lower than that in the case of the design flow rate and was within the usable range. As the flow rate increased, the pressure drop of helium increased from 0.34 MPa to 2.73 MPa;
- (5)
- As the mass flow rate increased, the amount of heat received from the high-temperature GG gas tended to increase which caused an increase in the temperature difference on the right side of the helically-coiled tube. Consequently, the thermal stress was higher than that at the design flow rate and the safety factor was less than 1 at a flow rate of 4 g/s or more. Thus, a kind of design limit in safety factor was identified from the design point of view;
- (6)
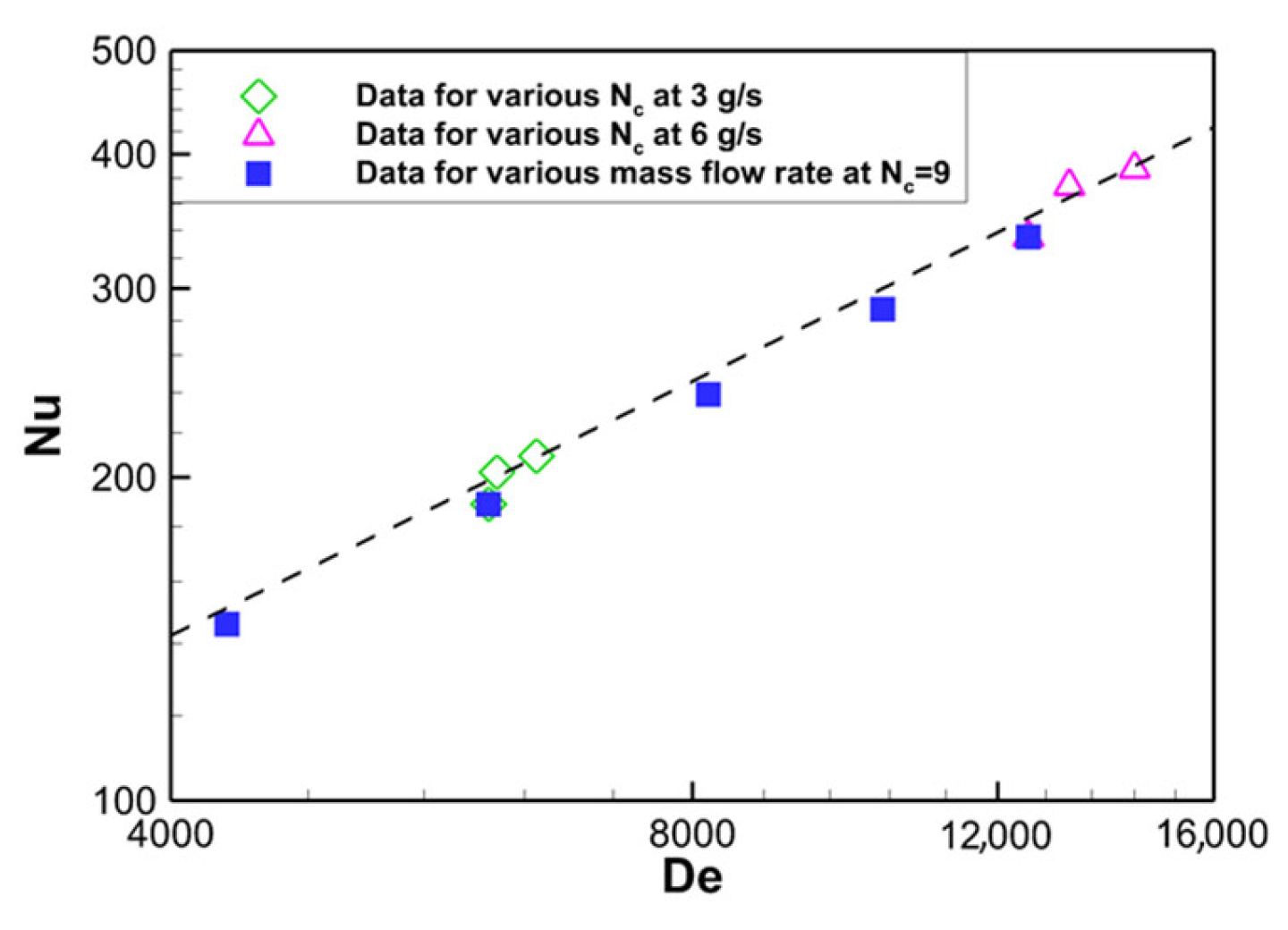
- The heat transfer characteristics according to the shape and flow rate changes of the heat exchanger were analyzed using dimensionless numbers. De and Nu increased as the of the coiled tube decreased. Moreover, De and Nu increased with the mass flow rate. The correlation of Nu and De was in the form of an exponential function and a trend was derived from these results. Nu and De showed similar trends at flow rates other than the design flow rate; therefore, their trend was related to . This exponential correlation can be used with respect to one of the thermal correlations for the design of the heat exchanger with coiled tubes in open-cycle liquid rocket engines. In the future, the effect of fluid properties, such as viscosity, will be analyzed in terms of the Prandtl number.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Available online: http://history.msfc.nasa.gov/saturn_apollo/documents/F-1_Engine.pdf (accessed on 22 September 2023).
- Available online: http://www.spacex.com/falcon9.php/ (accessed on 22 September 2023).
- Coulon, D. Vulcain-2 cryogenic engine passes first test with new nozzle extension. ESA Bull. 2000, 102, 123–124. [Google Scholar]
- Ko, J.; Cho, S.Y. Space Launch Vehicle Development in Korea Aerospace Research Institute. In Proceedings of the 14th International Conference on Space Operations, Daejeon, Republic of Korea, 16–20 May 2016; p. 2530. [Google Scholar]
- Park, J.S.; Yu, I.S.; Shin, M.K.; Oh, J.H.; Lee, H.J.; Ko, Y.S. Numerical Study on Performance Characteristics of Exhaust Gas Properties in Channel and Coil Type Heat Exchanger. Trans. Korean Soc. Mech. Eng. B 2019, 43, 1–9. [Google Scholar] [CrossRef]
- Khan, T.W.; Qamar, I. Optimum Characteristic Length of Gas Generator for Liquid Propellant Rocket Engine. Acta Astronaut. 2020, 176, 1–12. [Google Scholar] [CrossRef]
- Matsumoto, J.; Okaya, S.; Igoh, H.; Kawaguchi, J. Concept of a Self-Pressurized Feed System for Liquid Rocket Engines and Its Fundamental Experiment Results. Acta Astronaut. 2017, 133, 166–176. [Google Scholar] [CrossRef]
- Karimi, H.; Nassirharand, A.; Mohseni, M. Modeling and simulation of a class of liquid propellant engine pressurization systems. Acta Astronaut. 2010, 66, 539–549. [Google Scholar] [CrossRef]
- Karimi, H.; Nassirharand, A.; Zanj, A. Integration of modeling and simulation of warm pressurization and feed systems of liquid propulsion systems. Acta Astronaut. 2011, 69, 258–265. [Google Scholar] [CrossRef]
- Li, J.; Yu, N.; Zeng, P.; Cai, G. Design and integrated simulation of a pressurized feed system of the dual-thrust hybrid rocket motor. Sci. China Technol. Sci. 2011, 56, 989–1000. [Google Scholar] [CrossRef]
- Patankar, S.V.; Pratap, V.S.; Spalding, D.B. Prediction of laminar flow and heat transfer in helically coiled pipes. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Pergamon, Turkey, 1983; pp. 117–129. [Google Scholar]
- Etghani, M.M.; Baboli, S.A.H. Numerical investigation and optimization of heat transfer and exergy loss in shell and helical tube heat exchanger. Appl. Therm. Eng. 2017, 121, 294–301. [Google Scholar] [CrossRef]
- Li, F.; Xing, J.; Liu, Y. Thermal analysis and stress analysis of the heat-exchange pipe based on ANSYS. In Proceedings of the 2011 Fourth International Conference on Information and Computing, Phuket, Thailand, 25–27 April 2011. [Google Scholar]
- Laloui, L.; Nuth, M.; Vulliet, L. Experimental and numerical investigations of the behaviour of a heat exchanger pile. Int. J. Numer. Anal. Methods Géoméch. 2006, 30, 763–781. [Google Scholar] [CrossRef]
- John, B.; Senthilkumar, P.; Sadasivan, S. Applied and theoretical aspects of conjugate heat transfer analysis: A review. Arch. Comput. Methods Eng. 2018, 26, 475–489. [Google Scholar] [CrossRef]
- Du, Y.; Qu, Z.; Zhao, C.; Tao, W. Numerical Study of Conjugated Heat Transfer in Metal Foam Filled Double-Pipe. Int. J. Heat Mass Transf. 2010, 53, 4899–4907. [Google Scholar] [CrossRef]
- OpenFOAM Users’ Guide. Available online: https://openfoam.org/ (accessed on 22 September 2023).
- CalculiX Users’ Guide. Available online: http://www.calculix.de/ (accessed on 22 September 2023).
- preCICE Users’ Guide. Available online: https://precice.org/ (accessed on 22 September 2023).
- Bhusare, V.; Dhiman, M.; Kalaga, D.; Roy, S.; Joshi, J. CFD Simulation of a Bubble Column with and without Internals by Using OpenFOAM. Chem. Eng. J. 2017, 317, 157–174. [Google Scholar] [CrossRef]
- Yoon, T.H.; Park, S.K.; Seo, D.W.; Kim, J.S. A Study of FE Analysis Solver Comparison of Commercial and Open Source Software About the Design Review of a Bon Plate. In Proceedings of the Society of CAD/CAM Conference, Dubrovnik, Croatia, 16–19 May 2016; pp. 77–82. [Google Scholar]
- Bungartz, H.-J.; Lindner, F.; Gatzhammer, B.; Mehl, M.; Scheufele, K.; Shukaev, A.; Uekermann, B. preCICE–A Fully Parallel Library for Multi-physics Surface Coupling. Comput. Fluids 2016, 141, 250–258. [Google Scholar] [CrossRef]
- Seo, K.-S.; Nam, C.-H.; Moon, Y.-W.; Han, Y.-M. Liquid Rocket Engine Development of the Upper-Stage for the Korea Space Launch Vehicle-II. In Proceedings of the 9th European Conference For Aeronautics And Space Sciences (Eucass), Lille, France, 3–8 July 2022. [Google Scholar]
- Kim, D.; Kim, J. Simulation of a conjugate heat transfer using a preCICE coupling library. In Proceedings of the Transactions of the Korean Nuclear Society Virtual Spring Meeting, Jeju-si, Republic of Korea, 9–10 July 2020; Volume 10. [Google Scholar]
- Yau, L.C. Conjugated Heat Transfer with the Multiphysics Coupling Library preCICE; Computational Science and Engineering Technische University: München, Germany, 2016. [Google Scholar]
- Yu, I.S. A Study on Performance Prediction of Liquid Rocket Engine Heat Exchanger. Ph.D. Thesis, Chungnam National University, Daejeon, Republic of Korea, 2019; p. 2. [Google Scholar]
- Ammar, S.M.; Park, C.W. Validation of the Gnielinski correlation for evaluation of heat transfer coefficient of enhanced tubes by non-linear regression model: An experimental study of absorption refrigeration system. Int. Commun. Heat Mass Transf. 2020, 118, 104819. [Google Scholar] [CrossRef]
- Ryu, C.S.; Kim, H.J.; Choi, H.S. Structural Analysis of Gas Generator Regenerative Cooling Chamber. Trans. Korean Soc. Mech. Eng. A 2007, 31, 1046–1052. [Google Scholar] [CrossRef]
- Li, P.; Dong, H.; Xia, Y.; Hao, X.; Wang, S.; Pan, L.; Zhou, J. Inhomogeneous Interface Structure and Mechanical Properties of Rotary Friction Welded TC4 Titanium Alloy/316L Stainless Steel Joints. J. Manuf. Process. 2018, 33, 54–63. [Google Scholar] [CrossRef]
- Kalb, C.E.; Seader, J.D. Heat and Mass Transfer Phenomena for Viscous Flow in Curved Circular Tubes. Int. J. Heat Mass Transf. 1972, 15, 801–817. [Google Scholar] [CrossRef]
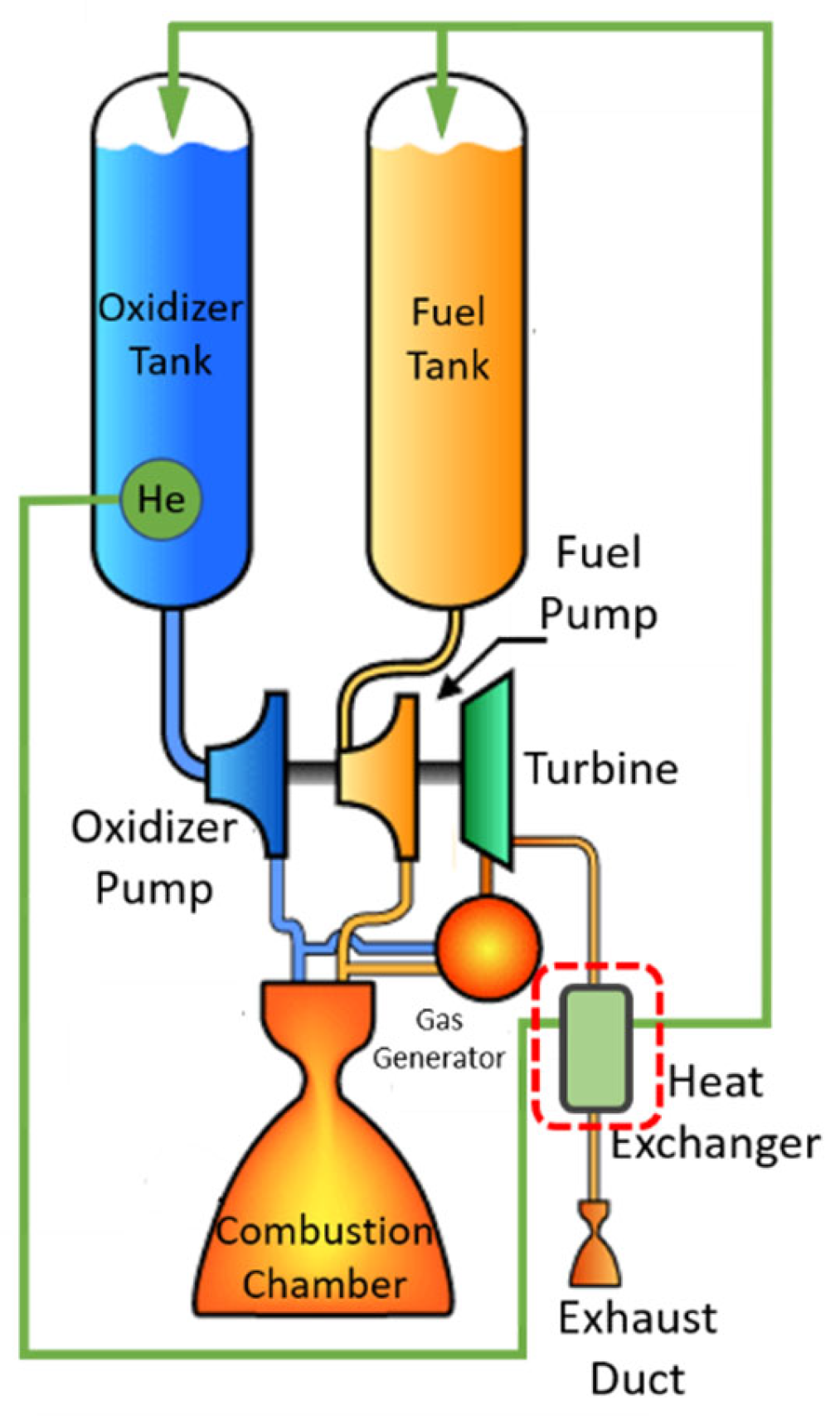
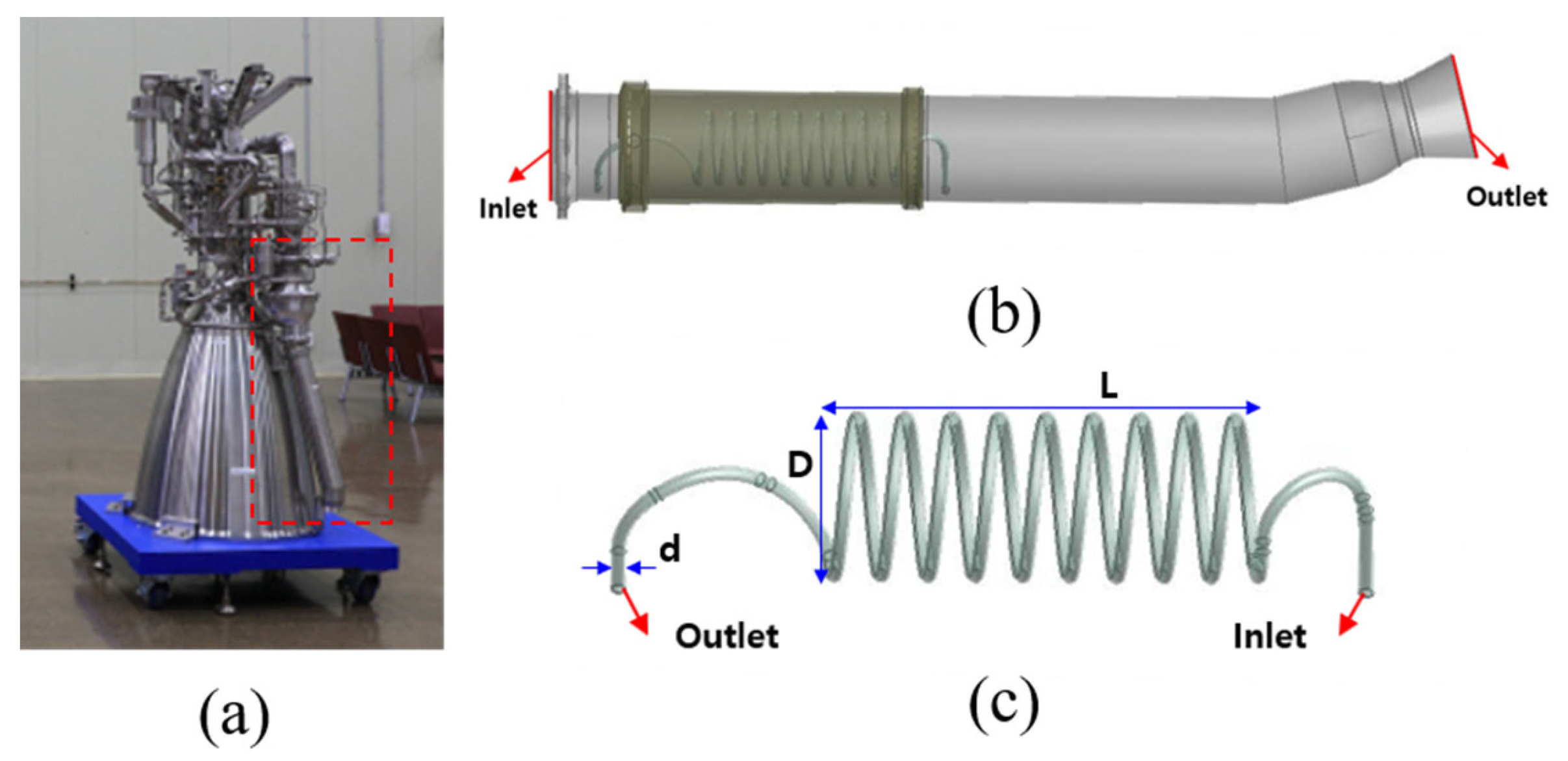
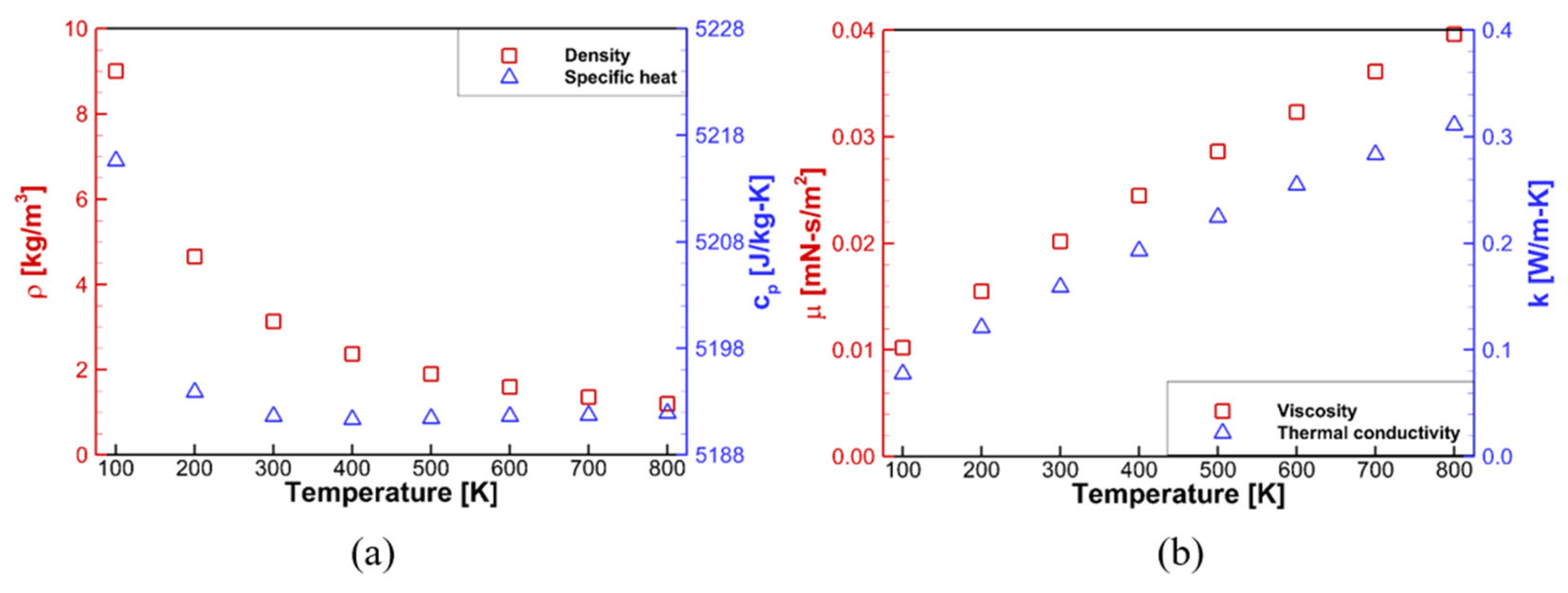
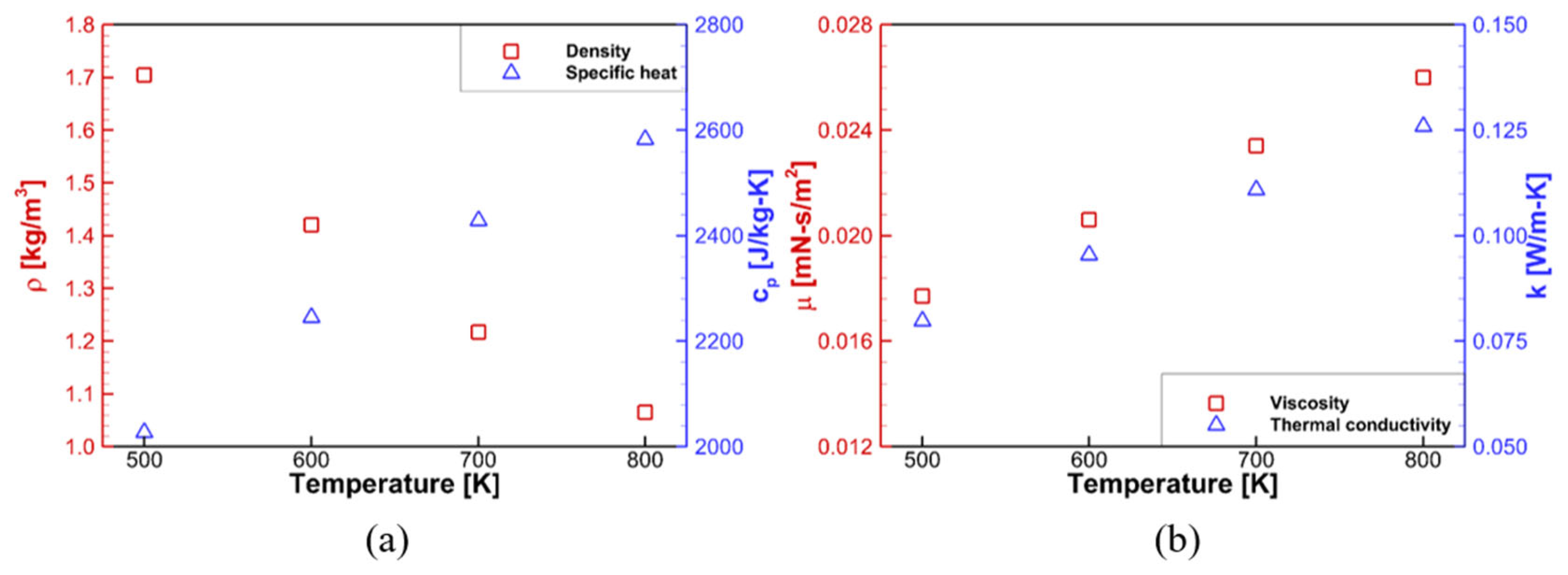

| GG Gas | Helium | |
|---|---|---|
| Fluid solver | OpenFOAM | |
| Structural solver | CalculiX | |
| Inlet Temperature [K] | 773 | 92 |
| Outlet Pressure [MPa] | 0.15 | 2.8 |
| Mass flow rate [kg/s] | 1.03 | 0.003 |
| Helium P [MPa] | 0.72 |
| GG gas P [MPa] | 0.05 |
| Helium T [K] | 666.0 |
| GG gas T [K] | 79.5 |
| 3 | 1.88 |
| 6 | 1.61 |
| 9 | 1.08 |
| [g/s] | |
|---|---|
| 2 | 1.09 |
| 3 | 1.08 |
| 4 | 0.88 |
| 5 | 0.83 |
| 6 | 0.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, W.; Jang, S.; Kim, H.-J. Characteristics of a Heat Exchanger in a Liquid Rocket Engine Using Conjugate Heat Transfer Coupling with Open-Source Tools. Aerospace 2023, 10, 983. https://doi.org/10.3390/aerospace10120983
Jeong W, Jang S, Kim H-J. Characteristics of a Heat Exchanger in a Liquid Rocket Engine Using Conjugate Heat Transfer Coupling with Open-Source Tools. Aerospace. 2023; 10(12):983. https://doi.org/10.3390/aerospace10120983
Chicago/Turabian StyleJeong, Wooseok, Seungeon Jang, and Hong-Jip Kim. 2023. "Characteristics of a Heat Exchanger in a Liquid Rocket Engine Using Conjugate Heat Transfer Coupling with Open-Source Tools" Aerospace 10, no. 12: 983. https://doi.org/10.3390/aerospace10120983
APA StyleJeong, W., Jang, S., & Kim, H.-J. (2023). Characteristics of a Heat Exchanger in a Liquid Rocket Engine Using Conjugate Heat Transfer Coupling with Open-Source Tools. Aerospace, 10(12), 983. https://doi.org/10.3390/aerospace10120983






