Mild Detonation Initiation in Rotating Detonation Engines: An Experimental Study of the Deflagration-to-Detonation Transition in a Semiconfined Flat Slit Combustor with Separate Supplies of Fuel and Oxidizer
Abstract
:1. Introduction
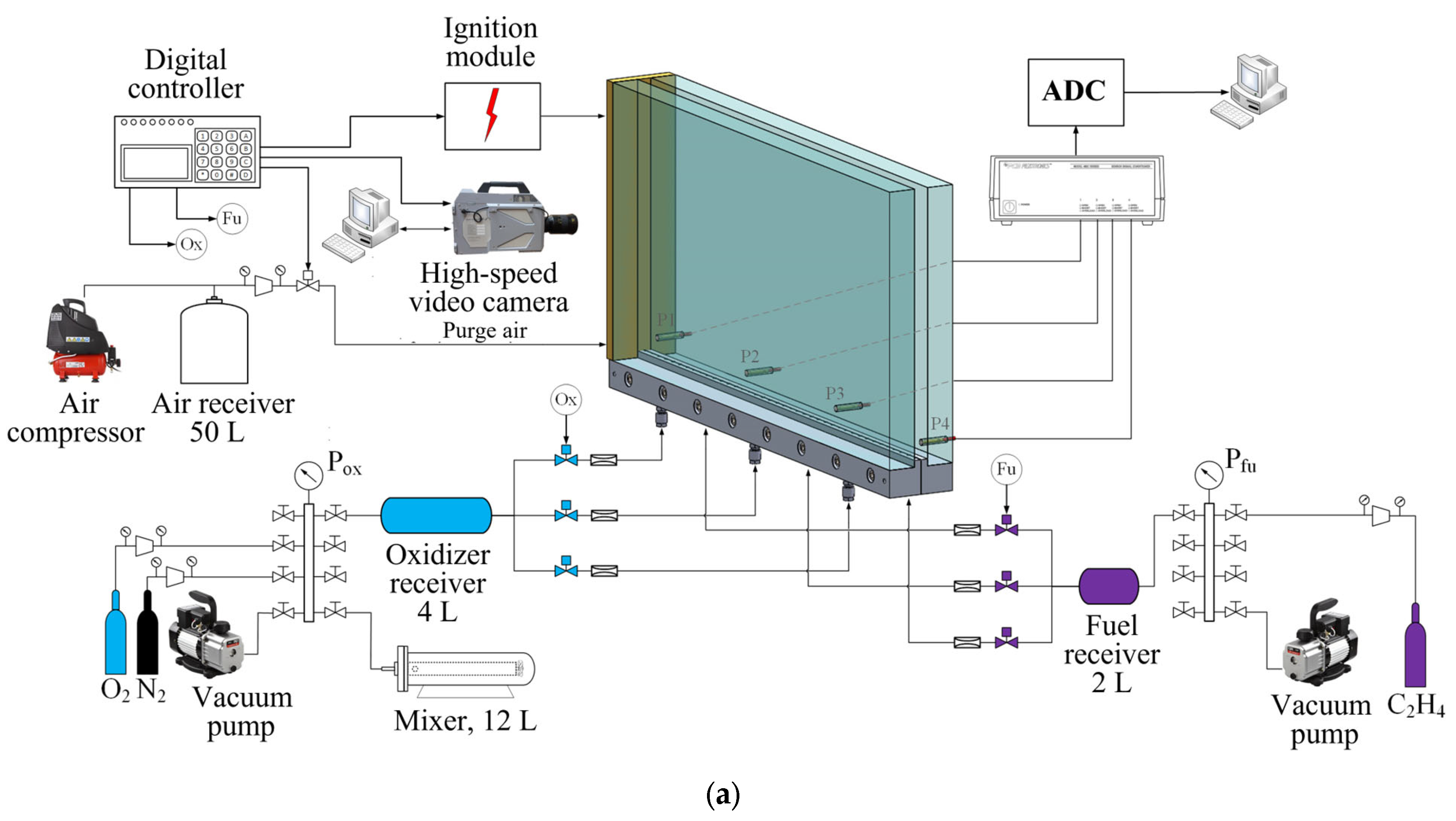
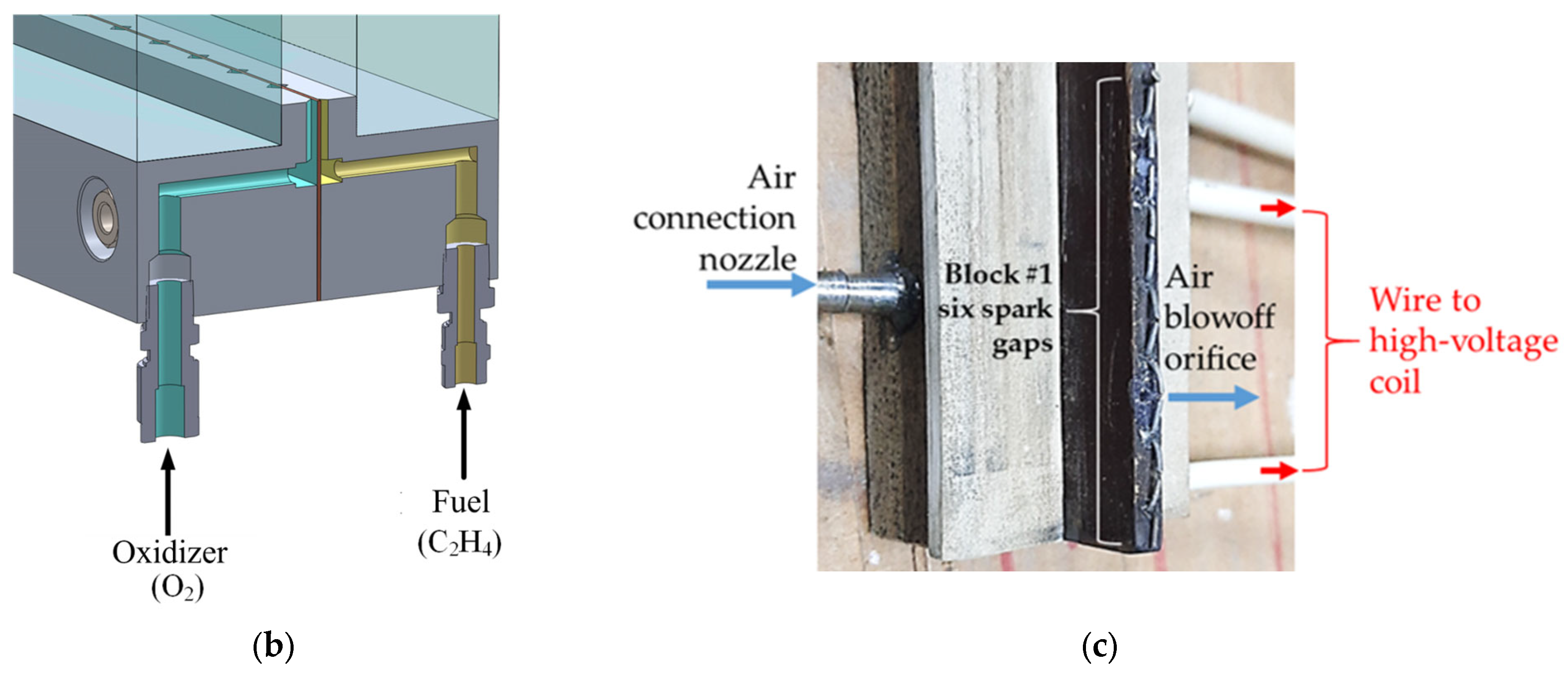
2. Materials and Methods
2.1. Experimental Setup
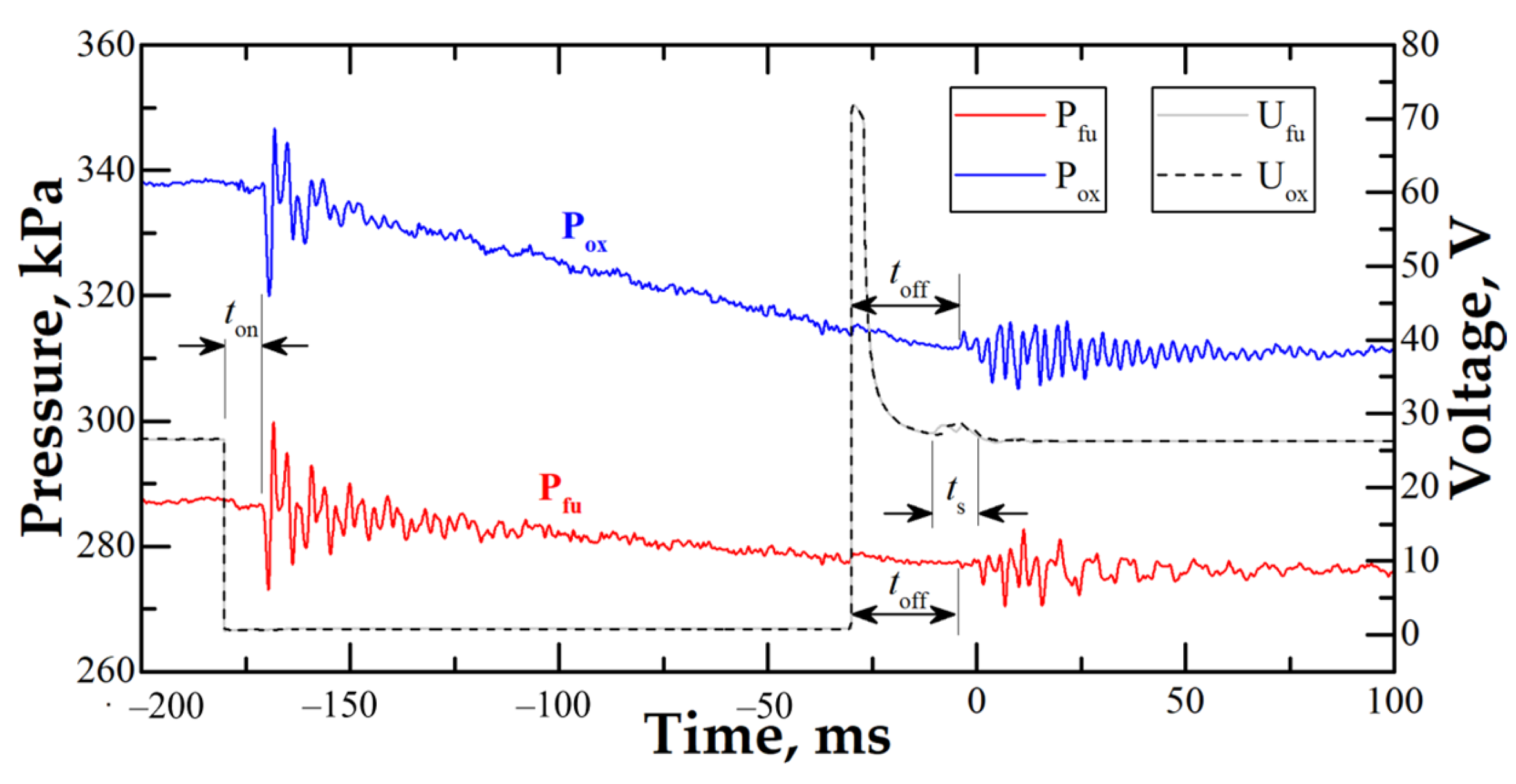
2.2. Experimental Procedure
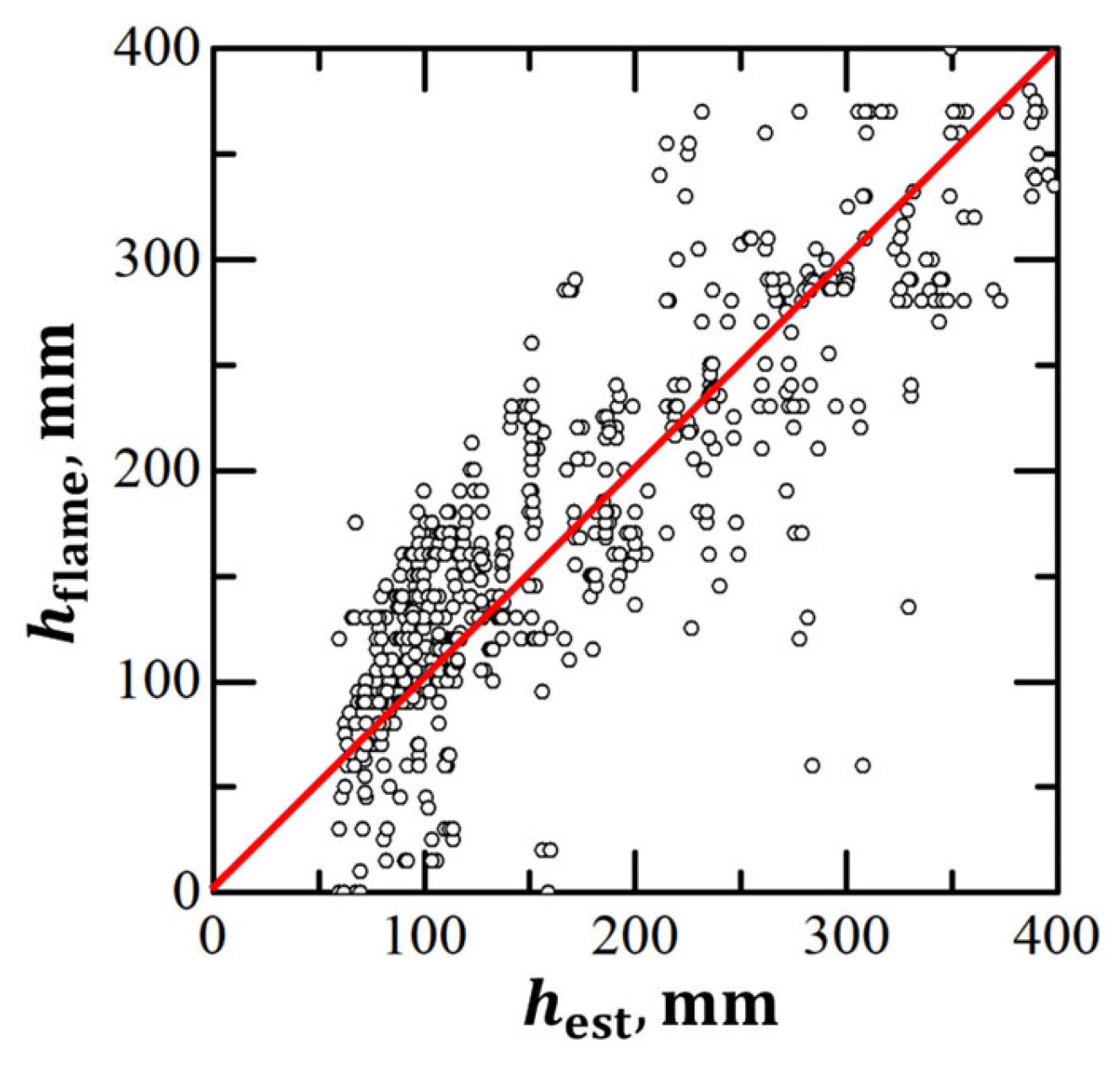
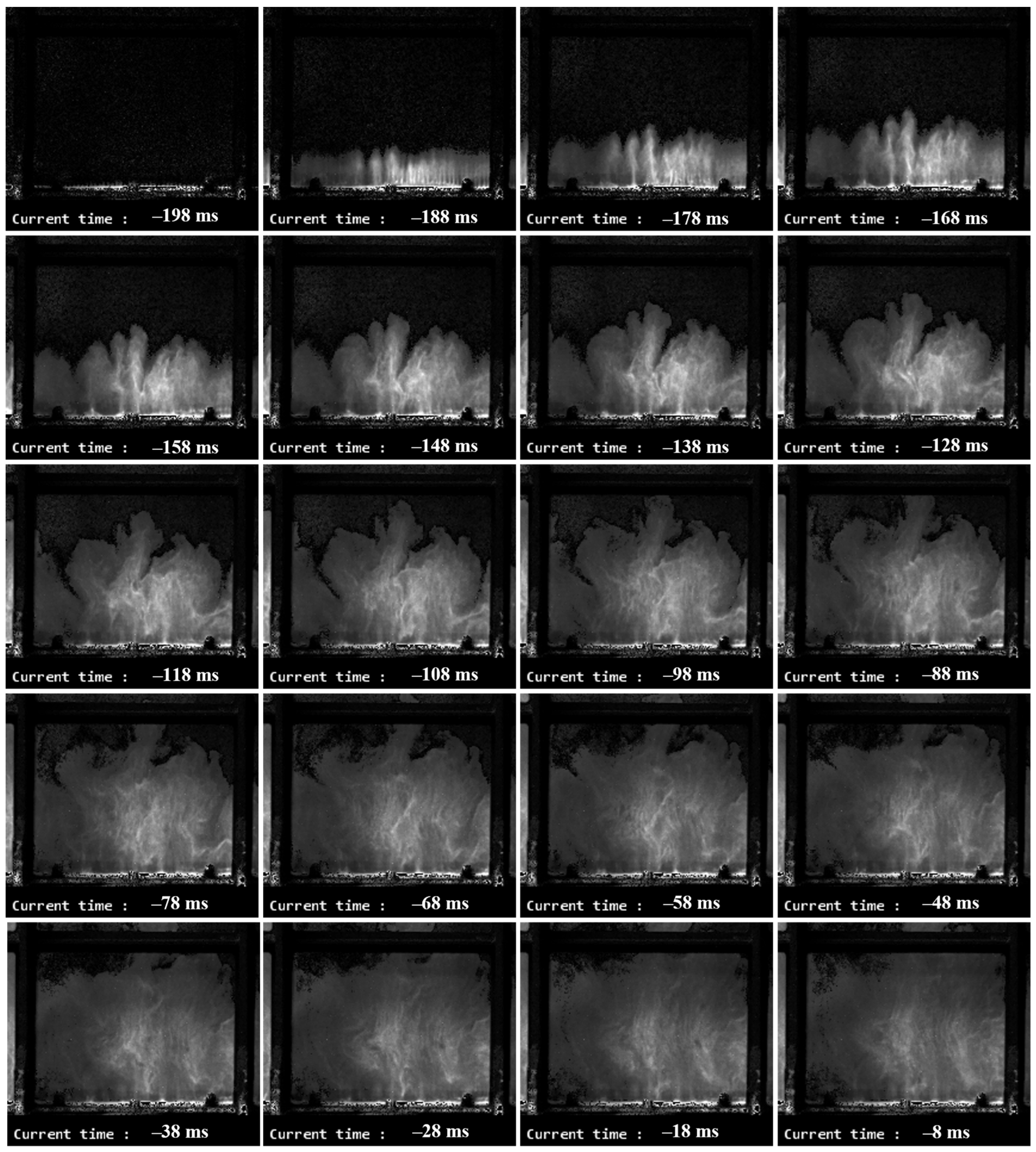
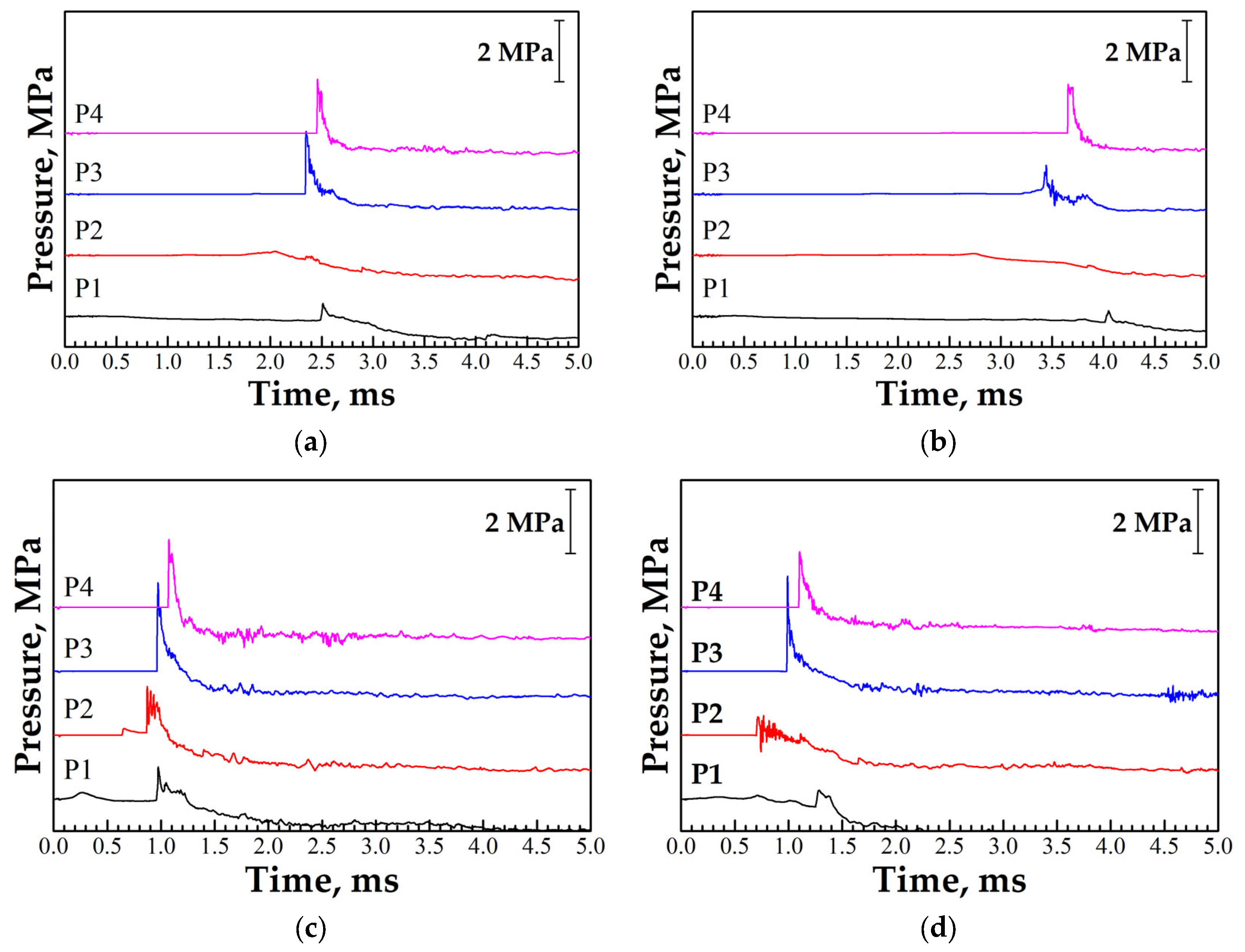
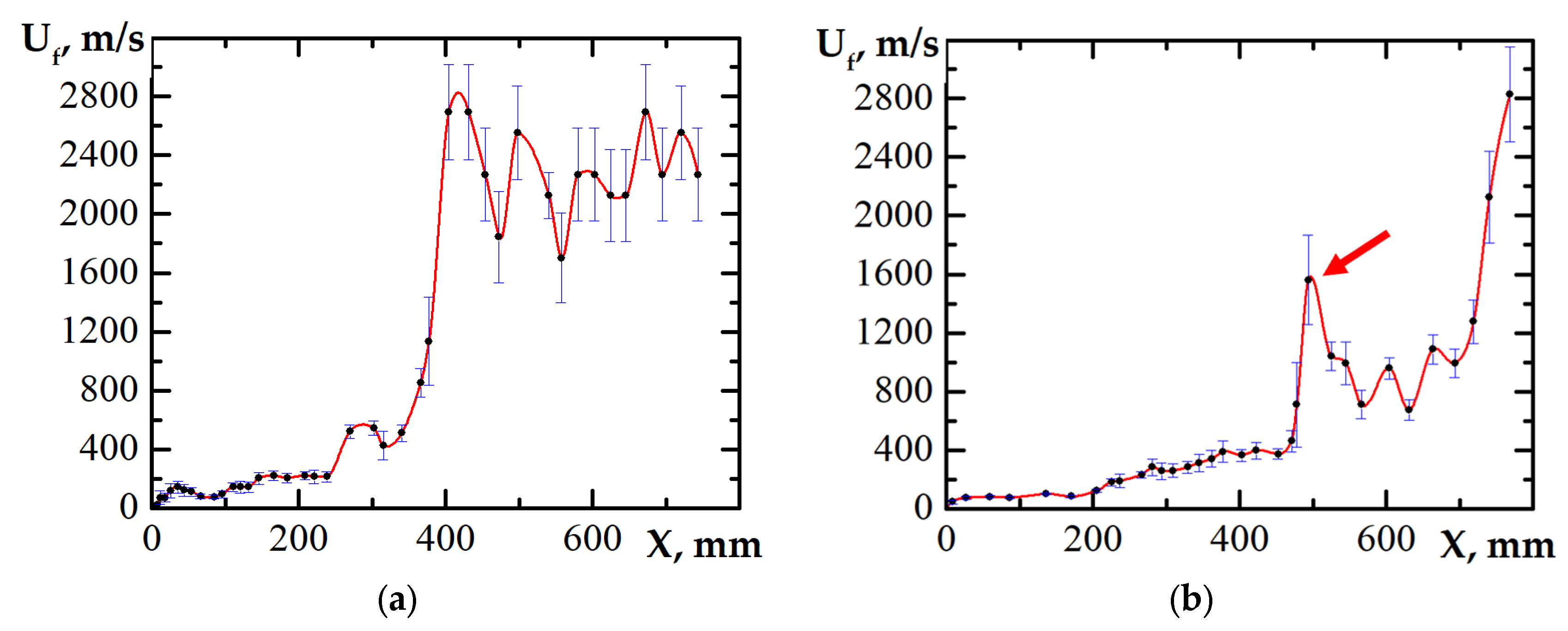
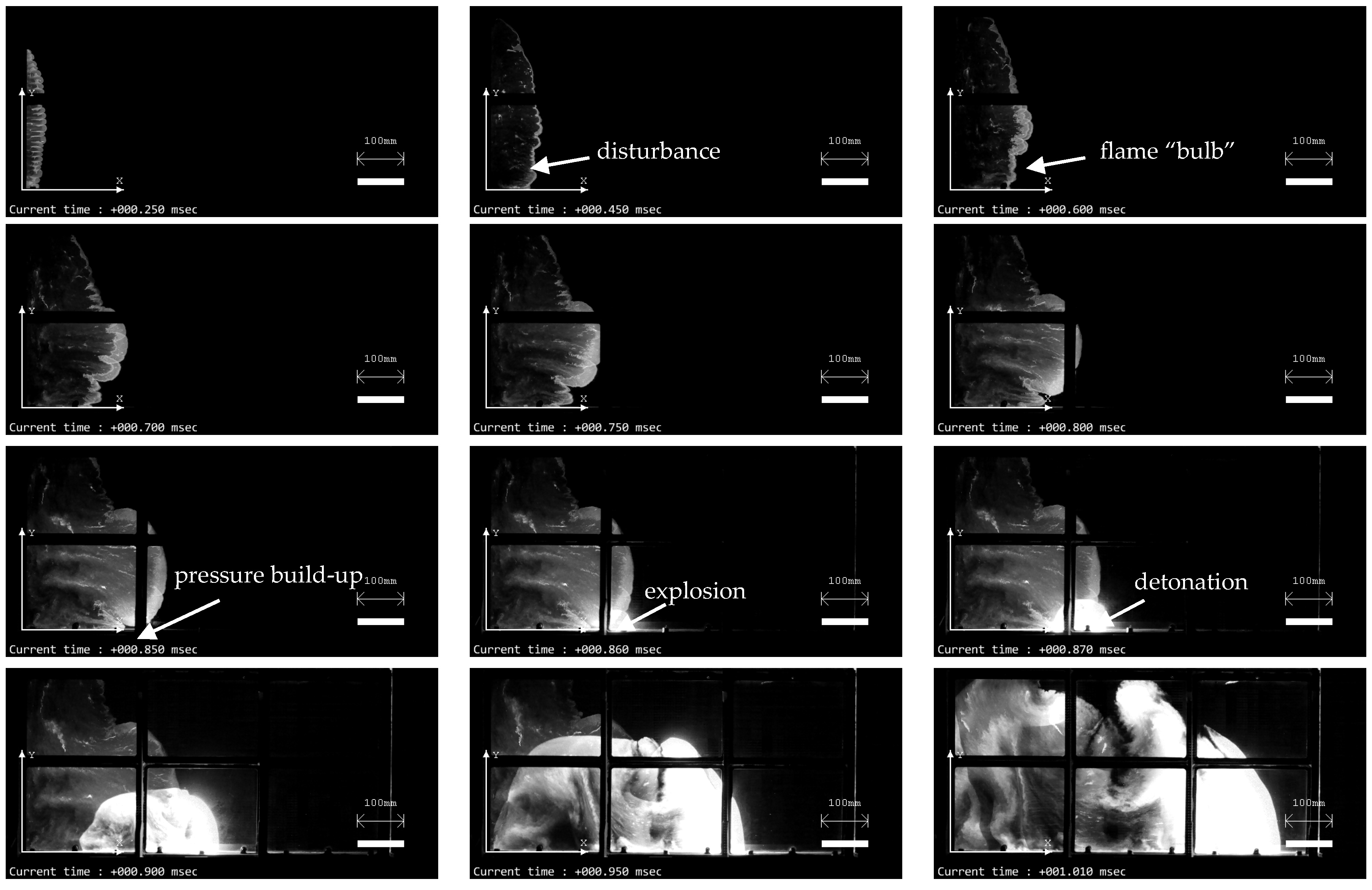
3. Results
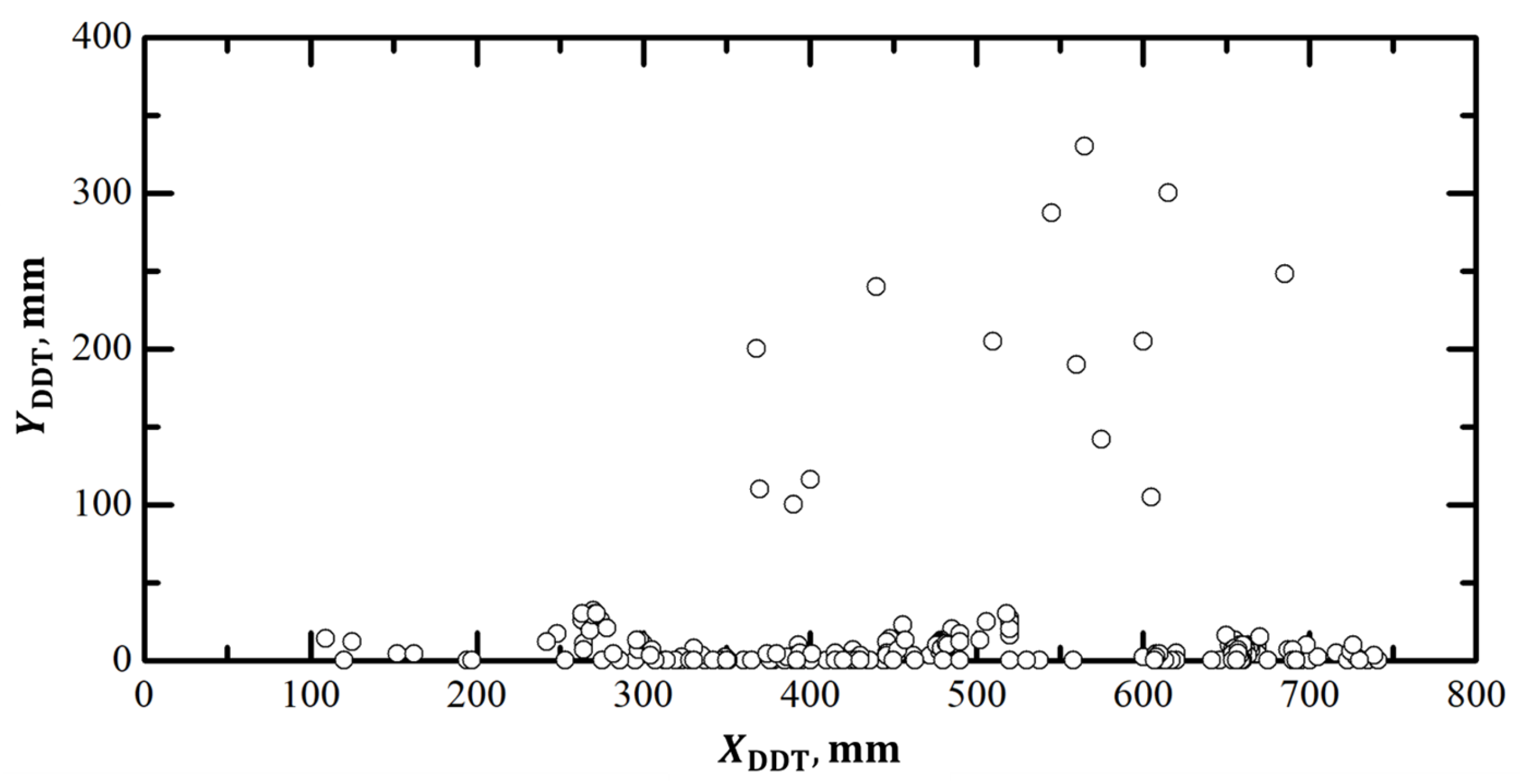
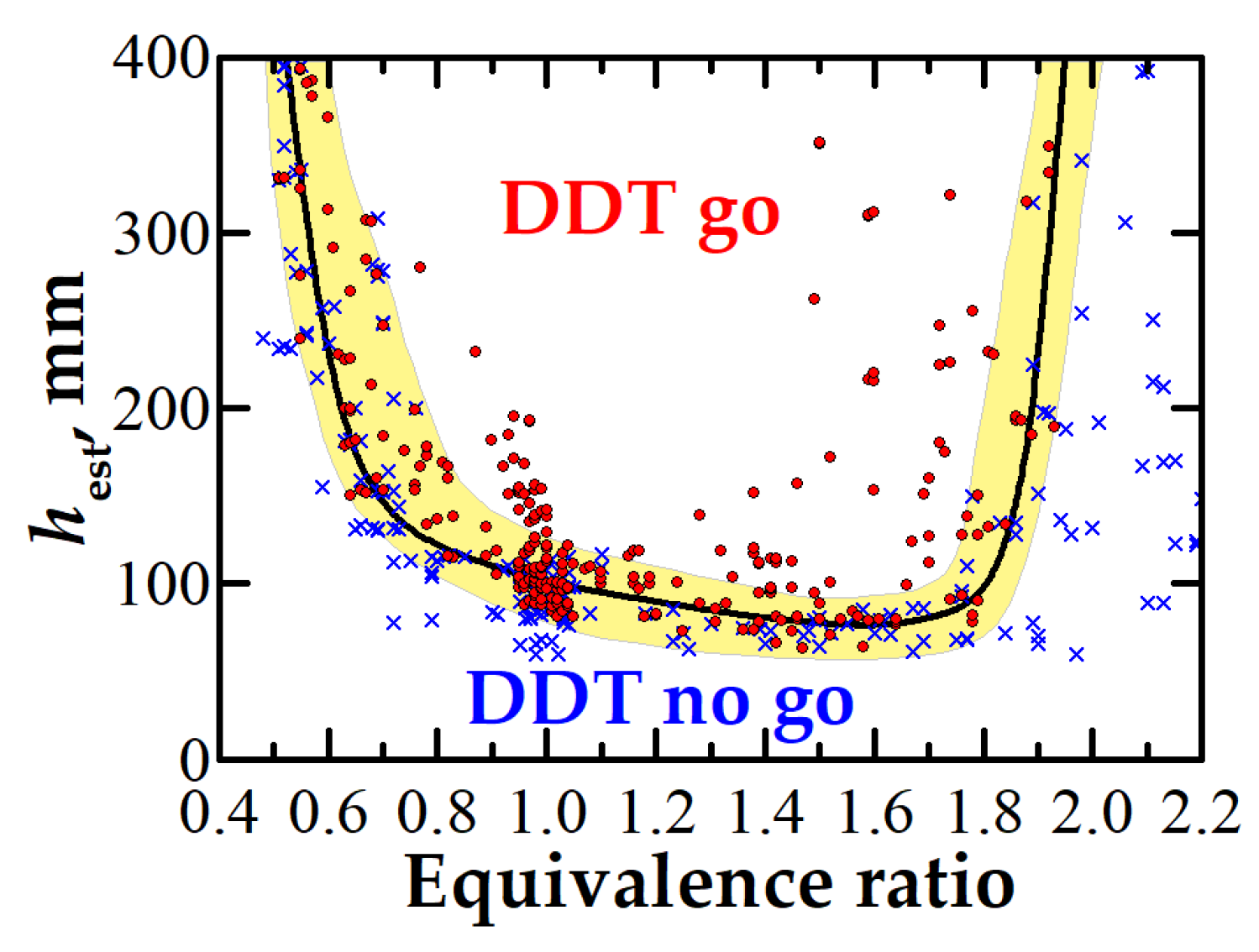
3.1. DDT Probability
3.2. Effect of Partial Ignition Failure
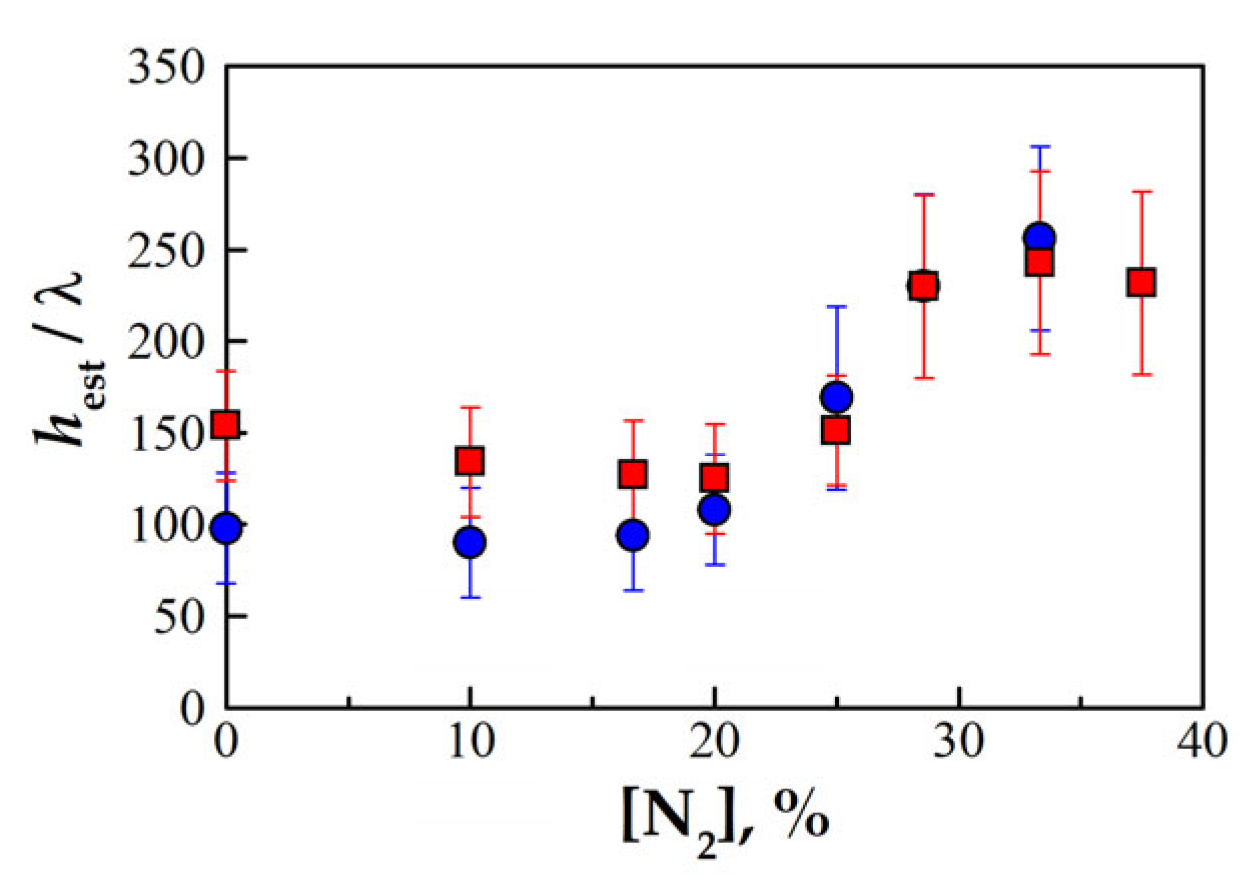
3.3. Effect of Overall Equivalence Ratio
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bykovskii, F.A.; Zhdan, S.A.; Vedernikov, E.F. Continuous spin detonations. J. Propuls. Power 2006, 22, 1204–1216. [Google Scholar] [CrossRef]
- Rankin, B.A.; Fotia, M.L.; Naples, A.G.; Stevens, C.A.; Hoke, J.L.; Kaemming, T.A.; Theuerkauf, S.W.; Schauer, F.R. Overview of Performance, Application, and Analysis of Rotating Detonation Engine Technologies. J. Propuls. Power 2017, 33, 131–143. [Google Scholar] [CrossRef]
- Zhou, R.; Wu, D.; Wang, J.-P. Progress of continuously rotating detonation engines. Chin. J. Aeronautics 2016, 29, 15–29. [Google Scholar] [CrossRef]
- Anand, V.; Gutmark, E. Rotating detonation combustors and their similarities to rocket instabilities. Prog. Energy Combust. Sci. 2019, 73, 182–234. [Google Scholar] [CrossRef]
- Wang, G.; Liu, W.; Liu, S.; Zhang, H.; Peng, H.; Zhou, Y. Experimental verification of cylindrical air-breathing continuous rotating detonation engine fueled by non-premixed ethylene. Acta Astronaut. 2021, 189, 722–732. [Google Scholar] [CrossRef]
- Heister, S.D.; Smallwood, J.; Harroun, A.; Dille, K.; Martinez, A.; Ballintyn, N. Rotating Detonation Combustion for Advanced Liquid Propellant Space Engines. Aerospace 2022, 9, 581. [Google Scholar] [CrossRef]
- Lee, J.H.S. The Detonation Phenomenon; The Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Shamshin, I.O.; Ivanov, V.S.; Aksenov, V.S.; Gusev, P.A.; Frolov, S.M. Experimental study of the initial stage of the operation process in detonation rocket and air-breathing engines. In Advances in Detonation Research; Frolov, S.M., Ed.; Torus Press: Moscow, Russia, 2022; pp. 17–20. [Google Scholar] [CrossRef]
- Voitsekhovskii, B.V. Stationary detonation. Dokl. Akad. Nauk. SSSR 1959, 129, 1254–1256. [Google Scholar]
- Sommers, W.P.; Morrison, R.B. Simulation of condensed-explosive detonation phenomena with gases. Phys. Fluids 1962, 5, 241–248. [Google Scholar] [CrossRef]
- Dabora, E.K.; Nicholls, J.A.; Morrison, R.B. The influence of a compressible boundary on the propagation of gaseous detonations. Proc. Combust. Inst. 1965, 10, 817–830. [Google Scholar] [CrossRef]
- Adams, T.G. Do weak detonation waves exist? AIAA J. 1978, 16, 1035–1040. [Google Scholar] [CrossRef]
- Ivanov, M.F.; Fortov, V.E.; Borisov, A.A. Numerical simulation of the development of a detonation in gas volumes of finite thickness. Combust. Explos. Shock Waves 1981, 17, 332–338. [Google Scholar] [CrossRef]
- Reynaud, M.; Virot, F.; Chinnayya, A. A computational study of the interaction of gaseous detonations with a compressible layer. Phys. Fluids 2017, 29, 056101. [Google Scholar] [CrossRef]
- Liu, J.C.; Liou, J.J.; Sichel, M.; Kauffman, C.W.; Nicholls, J.A. Diffraction and transmission of a detonation into a bounding explosive layer. Proc. Combust. Inst. 1988, 21, 1639–1647. [Google Scholar] [CrossRef]
- Tonello, N.A.; Sichel, M.; Kauffman, C.W. Mechanisms of detonation transmission in layered H2-O2 mixtures. Shock Waves 1995, 5, 225–238. [Google Scholar] [CrossRef]
- Oran, E.S.; Jones, D.A.; Sichel, M. Numerical simulation of detonation transmission. Proc. R. Soc. Lond. A 1992, 436, 267–297. [Google Scholar] [CrossRef]
- Ishii, K.; Kojima, M. Propagation of detonation in mixtures with concentration gradients. In Application of Detonation to Propulsion; Roy, G., Frolov, S., Shepherd, J., Eds.; Torus Press: Moscow, Russia, 2004; pp. 32–37. [Google Scholar]
- Calhoon, W.; Sinha, N. Detonation wave propagation in concentration gradients. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar] [CrossRef]
- Ishii, K.; Kojima, M. Behavior of detonation propagation in mixtures with concentration gradients. Shock Waves 2007, 17, 95–102. [Google Scholar] [CrossRef]
- Kessler, D.A.; Gamezo, V.N.; Oran, E.S. Gas-phase detonation propagation in mixture composition gradients. Phil. Trans. R. Soc. A 2012, 370, 567–596. [Google Scholar] [CrossRef]
- Houim, R.W.; Fievisohn, R.T. The influence of acoustic impedance on gaseous layered detonations bounded by an inert gas. Combust. Flame 2017, 179, 185–198. [Google Scholar] [CrossRef]
- Rudy, W.; Kuznetsov, M.; Porowski, R.; Teodorczyk, A.; Grune, J.; Sempert, K. Critical conditions of hydrogen–air detonation in partially confined geometry. Proc. Combust. Inst. 2013, 34, 1965–1972. [Google Scholar] [CrossRef]
- Kuznetsov, M.; Yanez, J.; Grune, J.; Friedrich, A.; Jordan, T. Hydrogen combustion in a flat semiconfined layer with respect to the Fukushima Daiichi accident. Nucl. Eng. Des. 2015, 286, 36–48. [Google Scholar] [CrossRef]
- Grune, J.; Sempert, K.; Haberstroh, H.; Kuznetsov, M.; Jordan, T. Experimental investigation of hydrogen–air deflagrations and detonations in semiconfined flat layers. J. Loss Prevent. Proc. Ind. 2013, 26, 317–323. [Google Scholar] [CrossRef]
- Shamshin, I.O.; Ivanov, V.S.; Aksenov, V.S.; Gusev, P.A.; Frolov, S.M. Deflagration-to-detonation transition in a semi-confined slit combustor filled with nitrogen diluted ethylene-oxygen mixture. Energies 2023, 16, 1098. [Google Scholar] [CrossRef]
- Ivanov, V.S.; Shamshin, I.O.; Frolov, S.M. Computational study of deflagration-to-detonation transition in a semi-confined slit combustor. Energies 2023, 16, 7028. [Google Scholar] [CrossRef]
- Lemcherfi, A.; Gejji, R.M.; Ayers, Z.M.; Plaehn, E.W.; Perkins, H.D.; Roy, S.; Meyer, T.R.; Fugger, C.A.; Slabaugh, C.D. Effect of injection dynamics on detonation wave propagation in a linear detonation combustor. Proc. Combust. Inst. 2023, 39, 2875–2883. [Google Scholar] [CrossRef]
- Liu, H.; Jin, D. Characteristics of injection scheme in linearized RDE. Int. J. Aeron. Space Sci. 2023, 24, 459–466. [Google Scholar] [CrossRef]
- Shi, L.; Fan, E.; Shen, H.; Wen, C.-Y.; Shang, S.; Hu, H. Numerical study of the effects of injection conditions on rotating detonation engine propulsive performance. Aerospace 2023, 10, 879. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, C.; Yang, P. Effects of ozone addition on multi-wave modes of hydrogen–air rotating detonations. Aerospace 2023, 10, 443. [Google Scholar] [CrossRef]
- Zhou, J.; Song, F.; Xu, S.; Yang, X.; Zheng, Y. Investigation of rotating detonation fueled by liquid kerosene. Energies 2022, 15, 4483. [Google Scholar] [CrossRef]
- Hansmetzger, S.; Zitoun, R.; Vidal, P. Detonation regimes in a small-scale RDE. In Proceedings of the 26th International Colloquium on the Dynamics of Explosions and Reactive Systems, Boston, MA, USA, 30 July–4 August 2017. [Google Scholar]
- Kato, Y.; Ishihara, K.; Matsuoka, K.; Kasahara, J.; Matsuo, A.; Funaki, I. Study of combustion chamber characteristic length in rotating detonation engine with convergent–divergent nozzle. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Wilhite, J.; Driscoll, R.; George, A.S.; Anand, V.; Gutmark, E.J. Investigation of a rotating detonation engine using ethylene–air mixtures. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Han, H.-S.; Lee, E.S.; Choi, J.-Y. Experimental investigation of detonation propagation modes and thrust performance in a small rotating detonation engine using C2H4/O2 propellant. Energies 2021, 14, 1381. [Google Scholar] [CrossRef]
- Taguchi, T.; Yamaguchi, M.; Matsuoka, K.; Kawasaki, A.; Watanabe, H.; Itouyama, N.; Kasahara, J.; Matsuo, A. Investigation of reflective shuttling detonation cycle by schlieren and chemiluminescence photography. Combust. Flame 2022, 236, 111826. [Google Scholar] [CrossRef]
- Nettleton, M.A. Gaseous Detonations; Chapman and Hall: London, UK, 1987. [Google Scholar]
- Matsui, H.; Lee, J.H.S. On the measure of the relative detonation hazards of gaseous fuel-oxygen and air mixtures. Proc. Combust. Inst. 1979, 17, 1269–1280. [Google Scholar] [CrossRef]
- Moen, I.O.; Donato, M.; Knystautas, R.; Lee, J.H.S. The influence of confinement on the propagation of detonations near the detonability limits. Proc. Combust. Inst. 1981, 18, 1615–1622. [Google Scholar] [CrossRef]
- Thomas, G.O. Flame Acceleration and the Development of Detonation in Fuel–Oxygen Mixtures at Elevated Temperature and Pressures. J. Hazard. Mater. 2009, 163, 783–794. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.-H.; Kuo, W.-C. Transmission of near-limit detonation wave through a planar sudden expansion in a narrow channel. Combust. Flame 2012, 159, 3414–3422. [Google Scholar] [CrossRef]
- Kawasaki, A.; Kasahara, J. A novel characteristic length of detonation relevant to supercritical diffraction. Shock Waves 2020, 30, 1–12. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Kompaneeta, A.S. The Theory of Detonation; Gostekhteorizdat Publication: Moscow, Russia, 1955. [Google Scholar]
- Monwar, M.; Yamamoto, Y.; Ishii, K.; Tsuboi, T. Detonation propagation in narrow gaps with various configurations. J. Therm. Sci. 2007, 16, 283–288. [Google Scholar] [CrossRef]
- Ishii, K.; Monwar, M. Detonation propagation with velocity deficits in narrow channels. Proc. Combust. Inst. 2011, 33, 2359–2366. [Google Scholar] [CrossRef]
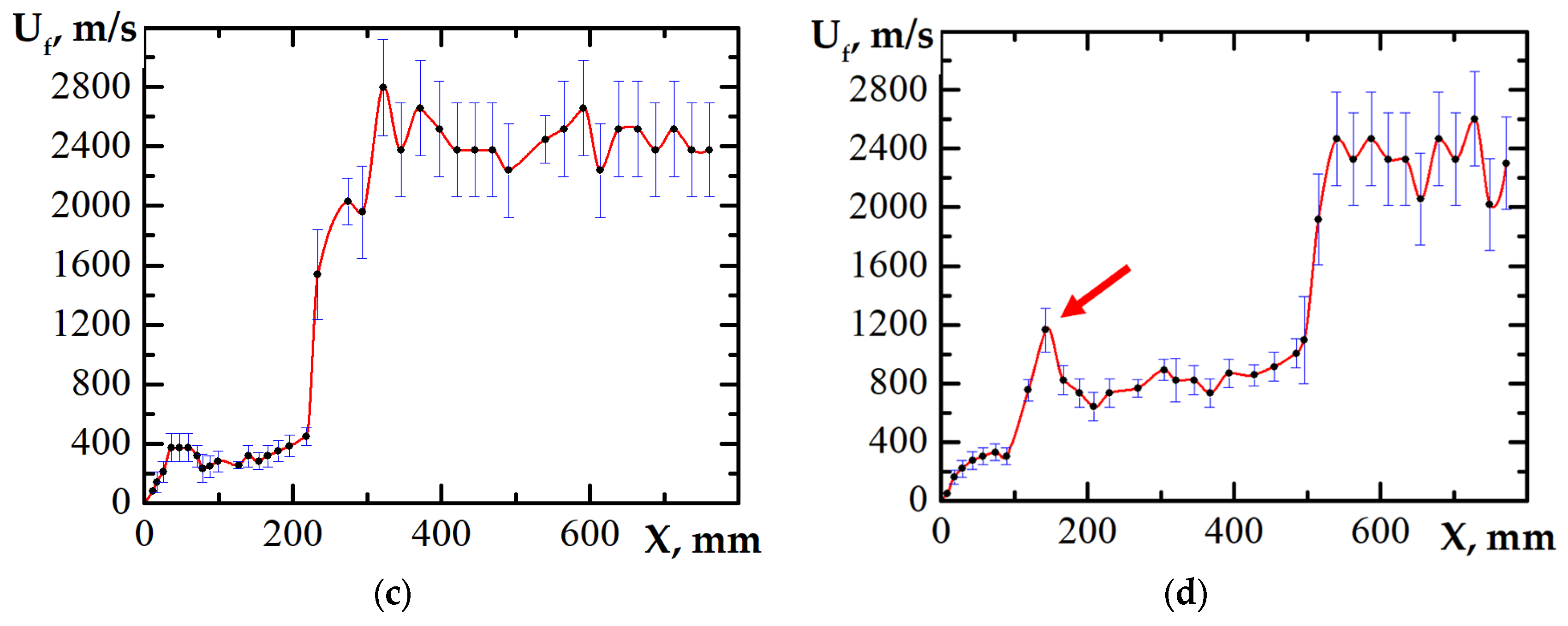



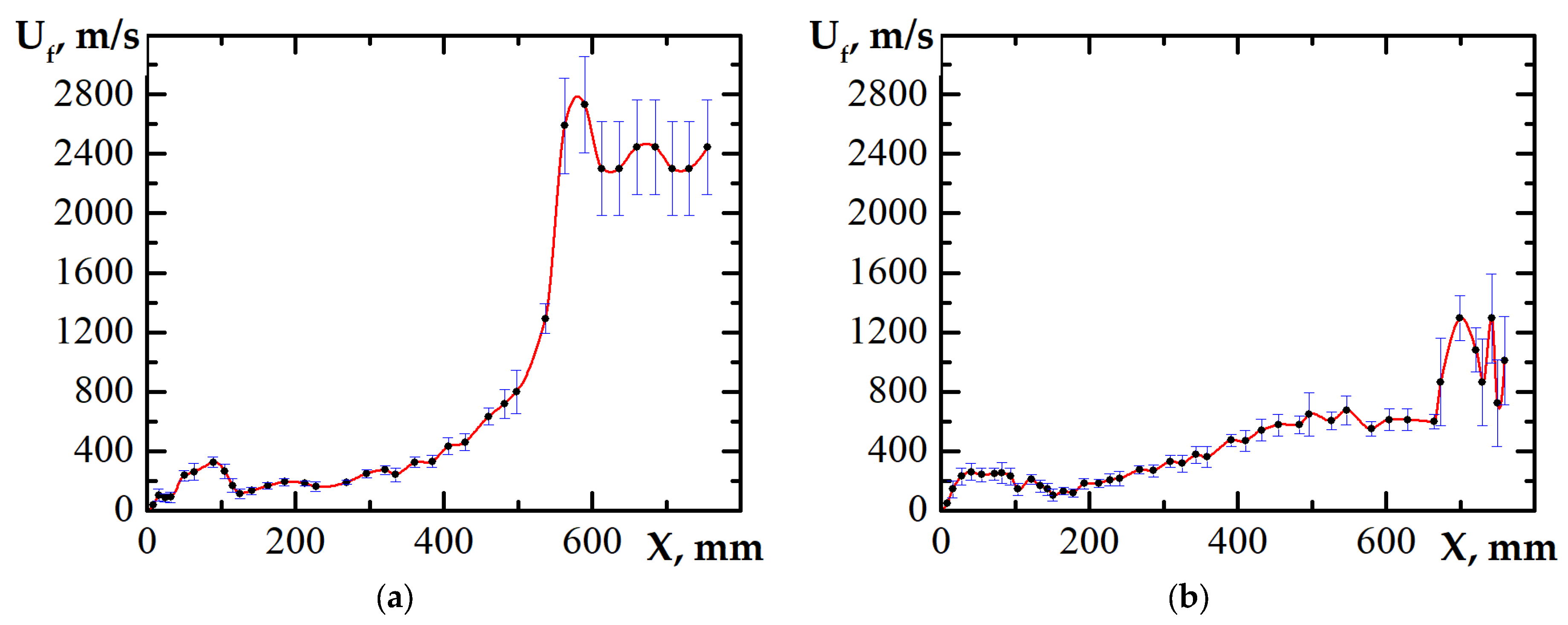
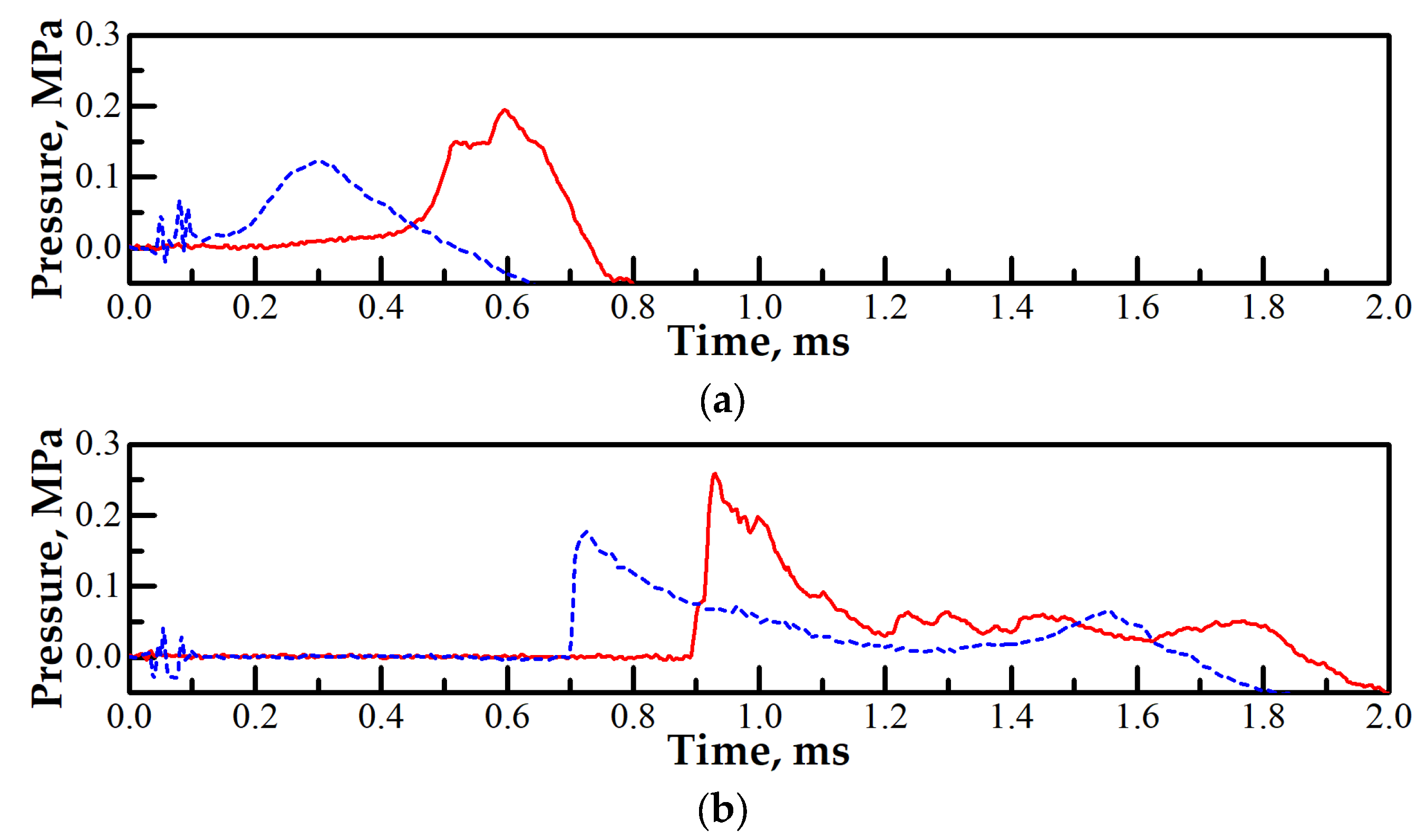
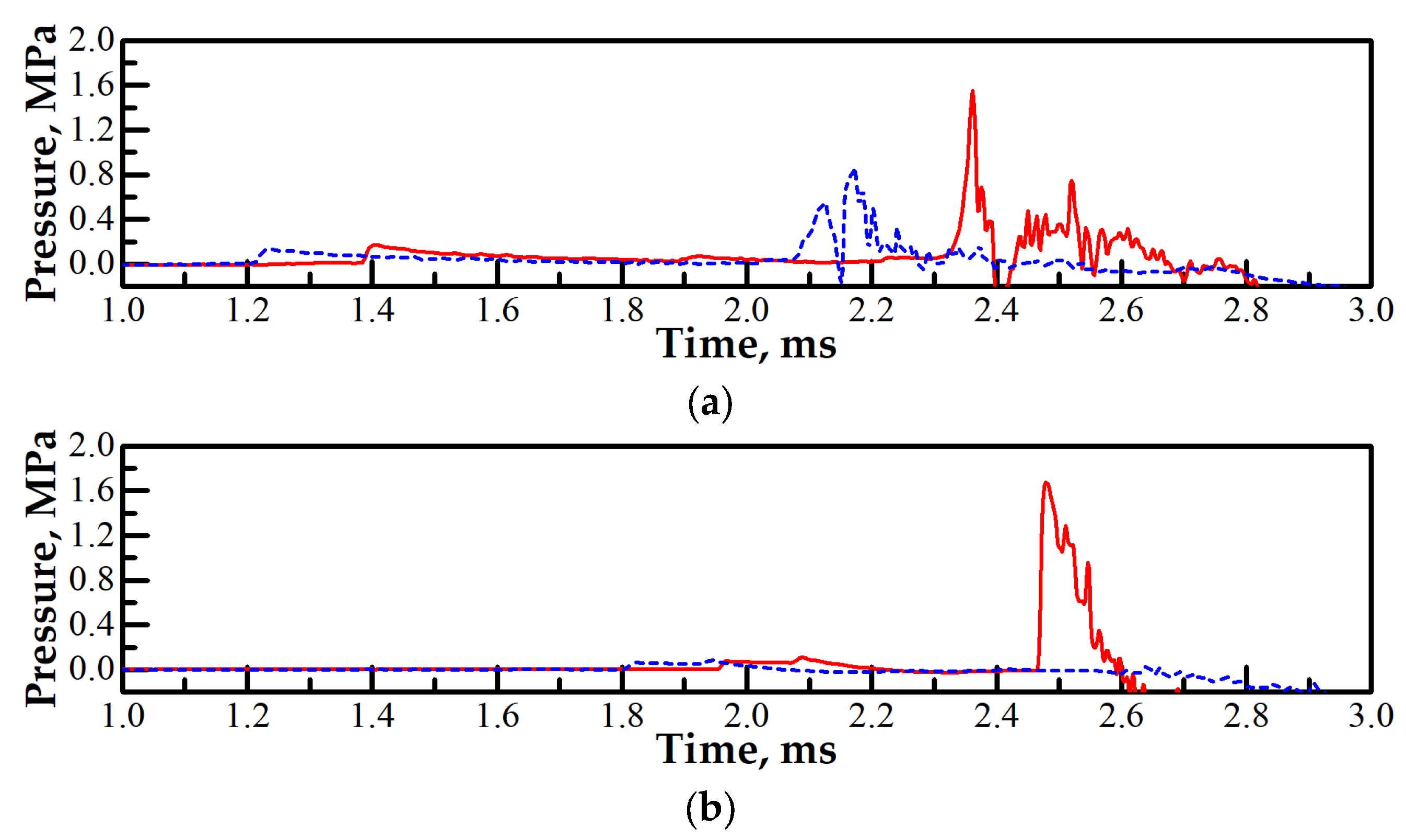



| No. | β | N2, % | , m/s | , m/s | , bar | , bar | , mm | 1, mm |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 2376 | 2372 ± 84 | 33.9 | 12.9–35.6 | 80 | 50 |
| 2 | 1/9 | 10 | 2331 | 2306 ± 86 | 32.4 | 16.4–33.5 | 95 | 65 |
| 3 | 1/5 | 16.7 | 2299 | 2365 ± 62 | 31.4 | 14.2–29.6 | 110 | 80 |
| 4 | 1/4 | 20 | 2283 | 2386 ± 83 | 30.9 | 14.2–35.1 | 120 | 110 |
| 5 | 1/3 | 25 | 2259 | 2371 ± 31 | 30.2 | 17.6–35.6 | 170 | 200 |
| 6 | 2/5 | 28.6 | 2240 | 2421 ± 128 | 29.6 | 15.8–33.7 | 270 (290) | 290 |
| 7 | 1/2 | 33.3 | 2215 | 2415 ± 0 | 28.8 | 13.5–25.9 | 290 (360) | 390 |
| 8 | 3/5 | 37.5 | 2191 | ― 4 | 28.1 | 15.7–35.3 | >400 2 | >400 2 |
| 9 | 2/3 | 40 | 2177 | ― 4 | 27.6 | 23.1–25.6 | ― 3 | >400 2 |
| No. | , mm | , mm | Number of Runs with DDT | , mm | , mm |
|---|---|---|---|---|---|
| Number of Runs in the Series | |||||
| 1 | 65 ± 3 | 127 ± 26 | 0/7 | ― | ― |
| 2 | 80 ± 3 | 94 ± 37 | 4/13 | 385 | 725 |
| 3 | 91 ± 2 | 122 ± 26 | 15/29 | 282 | 741 |
| 4 | 101 ± 4 | 128 ± 42 | 27/37 | 297 | 739 |
| 5 | 109 ± 3 | 132 ± 26 | 18/25 | 270 | 723 |
| 6 | 140 ± 2 | 196 ± 32 | 6/6 | 275 | 450 |
| 7 | 153 ± 2 | 163 ± 50 | 9/9 | 248 | 485 |
| No. | , mm | , mm | Number of Runs with DDT | , mm | , mm |
|---|---|---|---|---|---|
| Number of Runs in the Series | |||||
| 1 | 72 ± 1 | 41 ± 9 | 0/3 | ― | ― |
| 2 | 89 ± 1 | 103 ± 39 | 0/5 | ― | ― |
| 3 | 111 ± 1 | 100 ± 50 | 4/7 | 448 | 730 |
| 4 | 152 ± 1 | 191 ± 32 | 8/8 | 305 | 670 |
| 5 | 191 ± 1 | 163 ± 50 | 3/3 | 242 | 263 |
| No. | , mm | , mm | Number of Runs with DDT | , mm | , mm |
|---|---|---|---|---|---|
| Number of Runs in the Series | |||||
| 1 | 95 ± 1 | 118 ± 15 | 0/7 | ― | ― |
| 2 | 116 ± 1 | 116 ± 6 | 1/5 | ― | 641 |
| 3 | 137 ± 1 | 139 ± 9 | 2/5 | 610 | 669 |
| 4 | 186 ± 1 | 180 ± 13 | 5/5 | 482 | 656 |
| 5 | 236 ± 1 | 241 ± 8 | 5/5 | 380 | 478 |
| No. | , mm | , mm | Number of Runs with DDT | , mm | , mm |
|---|---|---|---|---|---|
| Number of Runs in the Series | |||||
| 1 | 106 ± 1 | 132 ± 8 | 0/5 | ― | ― |
| 2 | 137 ± 1 | 145 ± 18 | 2/7 | 658 | 665 |
| 3 | 187 ± 1 | 199 ± 22 | 4/8 | 650 | 726 |
| 4 | 237 ± 1 | 250 ± 18 | 7/7 | 330 | 610 |
| 5 | 284 ± 2 | 293 ± 7 | 5/5 | 392 | 608 |
| No. | , mm | , mm | Number of Runs with DDT | , mm | , mm |
|---|---|---|---|---|---|
| Number of Runs in the Series | |||||
| 1 | 127 ± 1 | 146 ± 19 | 0/8 | ― | ― |
| 2 | 172 ± 1 | 174 ± 16 | 2/7 | 482 | 664 |
| 3 | 219 ± 1 | 227 ± 9 | 1/11 | ― | 655 |
| 4 | 263 ± 2 | 288 ± 23 | 3/7 | 394 | 610 |
| 5 | 292 ± 1 | 285 ± 14 | 6/7 | 457 | 670 |
| 6 | 308 ± 1 | 326 ± 9 | 5/5 | 342 | 661 |
| 7 | 352 ± 2 | 365 ± 6 | 4/4 | 446 | 657 |
| No. | , mm | , mm | Number of Runs with DDT | , mm | , mm |
|---|---|---|---|---|---|
| Number of Runs in the Series | |||||
| 1 | 225 ± 1 | 224 ± 10 | 0/5 | ― | ― |
| 2 | 273 ± 1 | 258 ± 20 | 0/5 | ― | ― |
| 3 | 301 ± 1 | 281 ± 23 | 6/14 | 420 | 662 |
| 4 | 327 ± 1 | 304 ± 13 | 7/12 | 428 | 663 |
| 5 | 389 ± 4 | 345 ± 26 | 10/14 | 392 | 660 |
| 6 | 406 ± 6 | 358 ± 25 | 3/3 | 510 | 575 |
| No. | , mm | , mm | Number of Runs with DDT | , mm | , mm |
|---|---|---|---|---|---|
| Number of Runs in the Series | |||||
| 1 | 243 ± 1 | 226 ± 23 | 0/7 | ― | ― |
| 2 | 289 ± 1 | 280 ± 25 | 5/13 | 656 | 690 |
| 3 | 362 ± 1 | 318 ± 28 | 6/8 | 490 | 659 |
| 4 | 388 ± 2 | 329 ± 20 | 4/7 | 430 | 660 |
| No. | , mm | , mm | Number of Runs with DDT | , mm | , mm |
|---|---|---|---|---|---|
| Number of Runs in the Series | |||||
| 1 | 333 ± 1 | 320 ± 12 | 0/9 | ― | ― |
| 2 | 380 ± 3 | 346 ± 24 | 0 (5)/15 | 530 | 692 |
| 3 | 425 ± 1 | 366 ± 34 | 2/5 | 580 | 656 |
| 4 | 470 ± 1 | 384 ± 18 | 6/11 | 520 | 667 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shamshin, I.O.; Ivanov, V.S.; Aksenov, V.S.; Gusev, P.A.; Avdeev, K.A.; Frolov, S.M. Mild Detonation Initiation in Rotating Detonation Engines: An Experimental Study of the Deflagration-to-Detonation Transition in a Semiconfined Flat Slit Combustor with Separate Supplies of Fuel and Oxidizer. Aerospace 2023, 10, 988. https://doi.org/10.3390/aerospace10120988
Shamshin IO, Ivanov VS, Aksenov VS, Gusev PA, Avdeev KA, Frolov SM. Mild Detonation Initiation in Rotating Detonation Engines: An Experimental Study of the Deflagration-to-Detonation Transition in a Semiconfined Flat Slit Combustor with Separate Supplies of Fuel and Oxidizer. Aerospace. 2023; 10(12):988. https://doi.org/10.3390/aerospace10120988
Chicago/Turabian StyleShamshin, Igor O., Vladislav S. Ivanov, Viktor S. Aksenov, Pavel A. Gusev, Konstantin A. Avdeev, and Sergey M. Frolov. 2023. "Mild Detonation Initiation in Rotating Detonation Engines: An Experimental Study of the Deflagration-to-Detonation Transition in a Semiconfined Flat Slit Combustor with Separate Supplies of Fuel and Oxidizer" Aerospace 10, no. 12: 988. https://doi.org/10.3390/aerospace10120988
APA StyleShamshin, I. O., Ivanov, V. S., Aksenov, V. S., Gusev, P. A., Avdeev, K. A., & Frolov, S. M. (2023). Mild Detonation Initiation in Rotating Detonation Engines: An Experimental Study of the Deflagration-to-Detonation Transition in a Semiconfined Flat Slit Combustor with Separate Supplies of Fuel and Oxidizer. Aerospace, 10(12), 988. https://doi.org/10.3390/aerospace10120988







