Spherical Formation Tracking Control of Non-Holonomic UAVs with State Constraints and Time Delays
Abstract
:1. Introduction
- Owing to time delays and velocity constraints in the formation subsystem coupling with the tracking subsystem, a virtual-structure-like design is introduced to form a formation with time delays in the directed communication network. It is noted that the condition of the delays in assumption is weaker than these for tracking control in [37,38,39,40];
2. Preliminaries and Problem Statement
2.1. Preliminaries
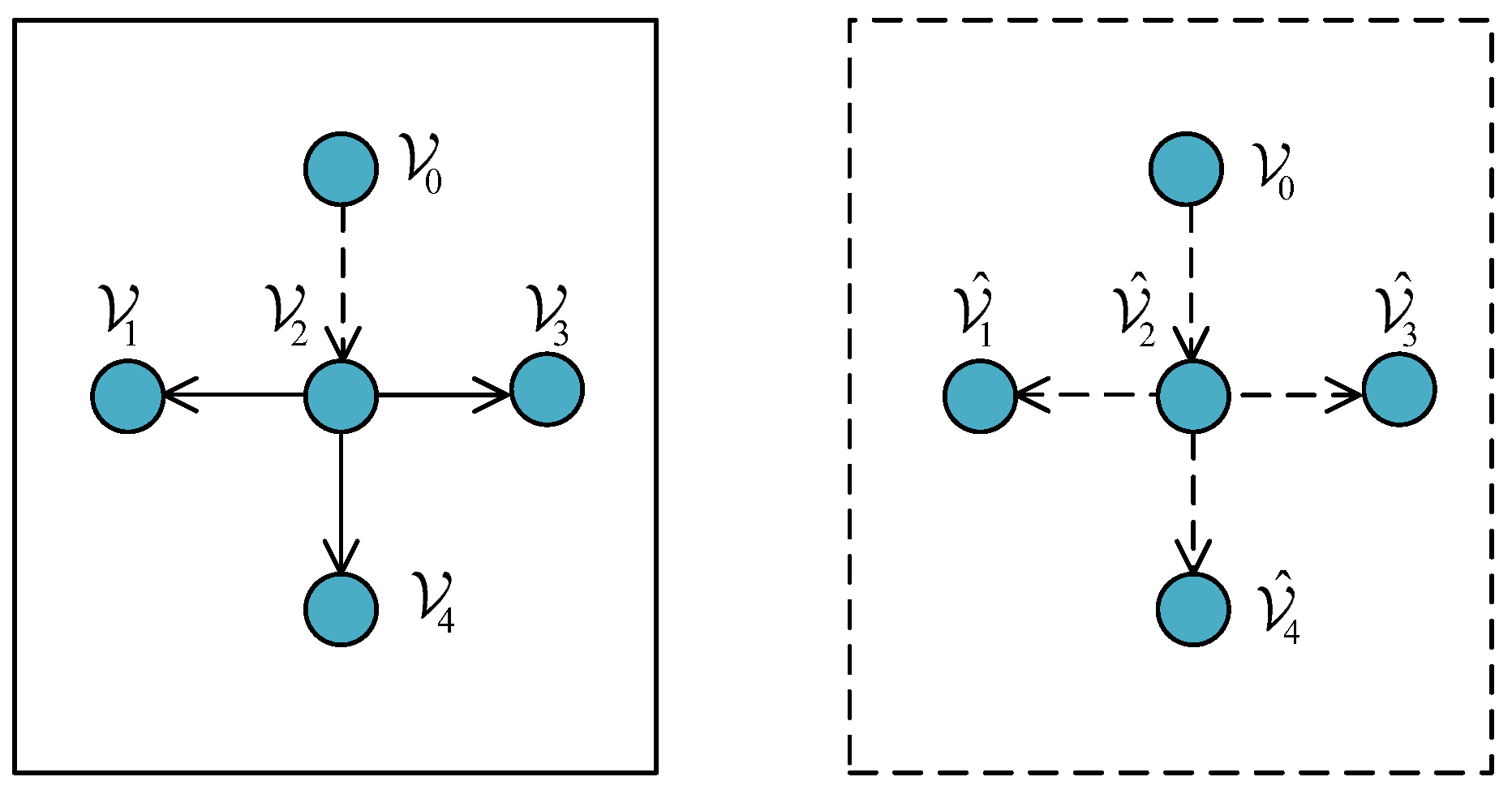
2.2. Problem Statement
- (C1)
- and ,
- (C2)
- and ,
- (C3)
- .
3. Main Results
Controller Design
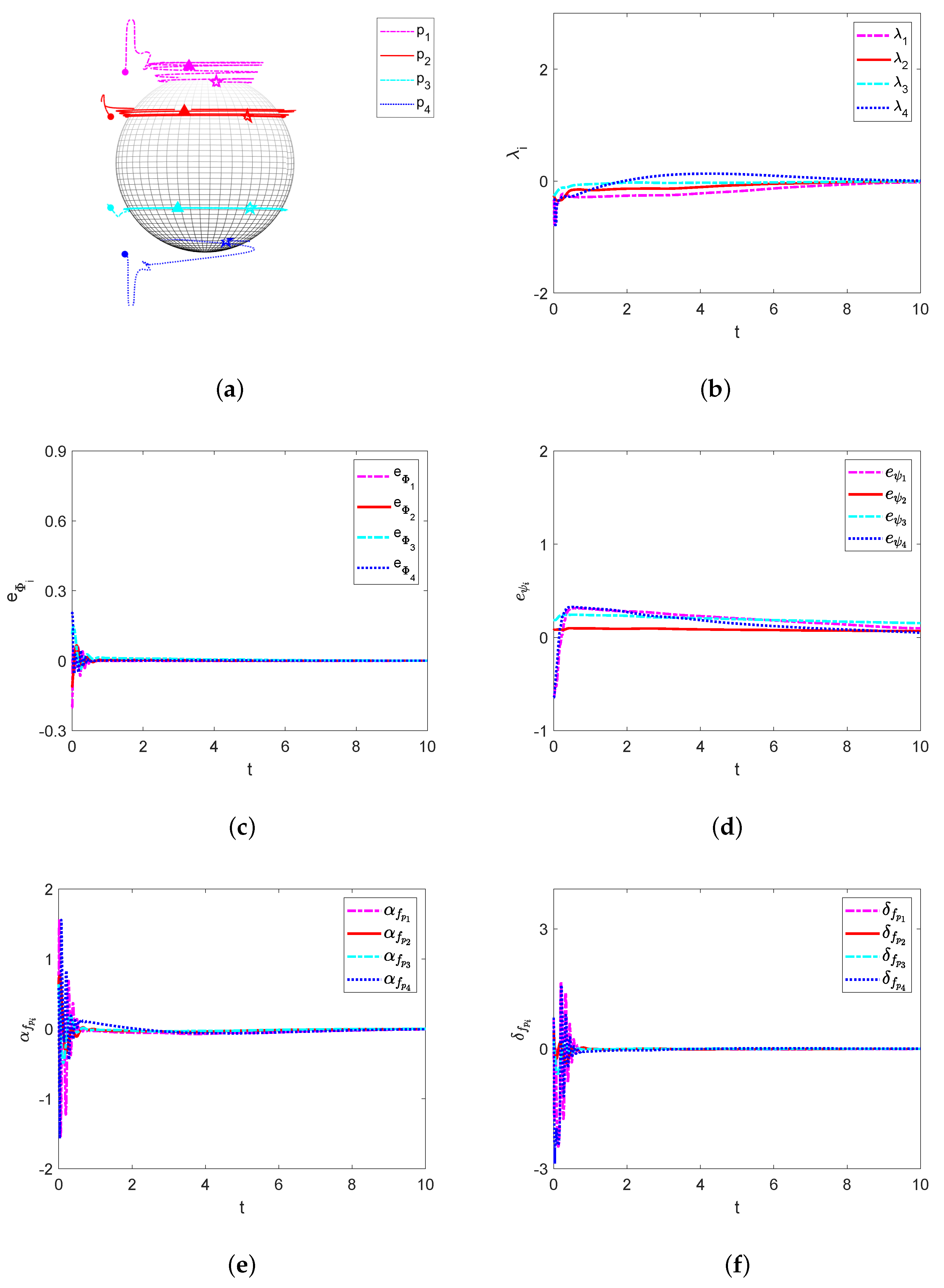
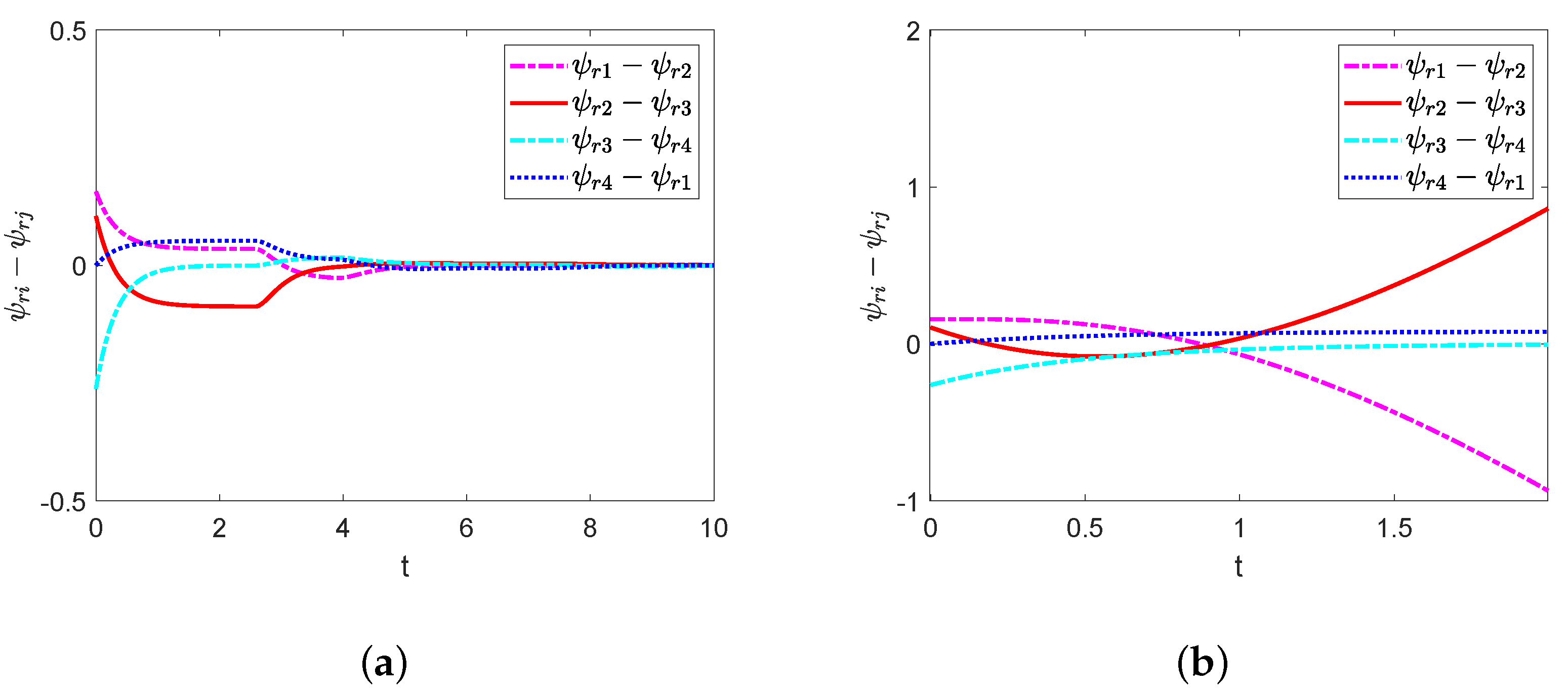
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, R.; Shi, Y.; Song, Y. Localization and circumnavigation of multiple agents along an unknown target based on bearing-only measurement: A three-dimensional solution. Automatica 2018, 94, 18–25. [Google Scholar] [CrossRef]
- Dou, L.; Song, C.; Wang, X.; Liu, L.; Feng, G. Target localization and enclosing control for networked mobile agents with bearing measurements. Automatica 2020, 118, 109022. [Google Scholar] [CrossRef]
- Lin, J.; Song, S.; You, K.; Wu, C. 3-D velocity regulation for nonholonomic source seeking without position measurement. IEEE Trans. Control Syst. Technol. 2015, 24, 711–718. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Li, C.; Guo, Y.; Ma, G.; Zhu, B. Spacecraft formation-containment flying control with time-varying translational velocity. Chin. J. Aeronaut. 2020, 33, 271–281. [Google Scholar] [CrossRef]
- Li, D.; Ma, G.; He, W.; Ge, S.; Lee, T. Cooperative circumnavigation control of networked microsatellites. IEEE Trans. Cybern. 2020, 20, 4550–4555. [Google Scholar] [CrossRef]
- Yang, J.; Liu, C.; Coombes, M.; Yan, Y.; Chen, W.H. Optimal path following for small fixed-wing UAVs under wind disturbances. IEEE Trans. Control Syst. Technol. 2021, 29, 996–1008. [Google Scholar] [CrossRef]
- Leonard, N.; Paley, D.; Lekien, F.; Sepulchre, R.; Fratantoni, D.; Davis, R. Collective motion, sensor networks, and ocean sampling. Proc. IEEE 2007, 95, 48–74. [Google Scholar] [CrossRef] [Green Version]
- Lin, P.; Qin, K.; Li, Z.; Ren, W. Collective rotating motions of second-order multi-agent systems in three-dimensional space. Syst. Control Lett. 2011, 60, 365–372. [Google Scholar] [CrossRef]
- Tan, Y.; Jin, Y. Multi-agent rotating consensus without relative velocity measurements in three-dimensional space. Int. J. Robust Nonlinear Control 2013, 23, 473–482. [Google Scholar]
- Chen, L.; Mei, J.; Li, C.; Ma, G. Distributed leader-follower affine formation maneuver control for high-order multi-agent systems. IEEE Trans. Autom. Control 2020, 65, 4941–4948. [Google Scholar] [CrossRef]
- Miao, Z.; Liu, Y.; Wang, Y.; Yi, G.; Fierro, R. Distributed estimation and control for leader-following formations of nonholonomic mobile robots. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1946–1954. [Google Scholar] [CrossRef]
- Lv, J.; Chen, F.; Chen, G. Nonsmooth leader-following formation control of nonidentical multi-agent systems with directed communication topologies. Automatica 2016, 64, 112–120. [Google Scholar]
- Han, T.; Guan, Z.; Chi, M.; Hu, B.; Li, T.; Zhang, X. Multi-formation control of nonlinear leader-following multi-agent systems. ISA Trans. 2017, 69, 140–147. [Google Scholar] [CrossRef]
- Rezaee, H.; Abdollahi, F. A decentralized cooperative control scheme with obstacle avoidance for a team of mobile robots. IEEE Trans. Ind. Electron. 2014, 61, 347–354. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, J.; Shi, X.; Jiang, C. Decentralization of virtual linkage in formation control of multi-agents via consensus strategies. Appl. Sci. 2020, 8, 2020. [Google Scholar] [CrossRef] [Green Version]
- Do, K.; Pan, J. Nonlinear formation control of unicycle-type mobile robots. Robot. Auton. Syst. 2007, 55, 191–204. [Google Scholar] [CrossRef]
- Ghabcheloo, R.; Pascoal, A.; Silvestre, C.; Kaminer, I. Coordinated path following control of multiple wheeled robots with directed communication links. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 7084–7089. [Google Scholar]
- Peng, Z.; Wang, D.; Wang, H.; Wang, W. Distributed coordinated tracking of multiple autonomous underwater vehicles. Nonlinear Dyn. 2014, 78, 1261–1276. [Google Scholar] [CrossRef]
- Zhang, F.; Leonard, N. Coordinated patterns of unit speed particles on a closed curve. Syst. Control Lett. 2007, 56, 397–407. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.Y.; Chen, K.; Astolfi, A. Adaptive formation tracking control for first-order agents with a time-varying flow parameter. IEEE Trans. Autom. Control 2021, 67, 2481–2488. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Chen, K.; Astolfi, A. Adaptive formation tracking control of directed networked vehicles in a time-varying flowfield. J. Guid. Control Dyn. 2021, 44, 1883–1891. [Google Scholar] [CrossRef]
- Zhao, S.; Dimarogonas, D.; Sun, Z.; Bauso, D. A general approach to coordination control of mobile agents with motion constraints. IEEE Trans. Autom. Control 2017, 63, 1509–1516. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.; Dong, Q.; Zhao, Y. Adaptive leader–follower formation control for swarms of unmanned aerial vehicles with motion constraints and unknown disturbances. Chin. J. Aeronaut. 2020, 33, 2972–2988. [Google Scholar] [CrossRef]
- Yu, X.; Liu, L. Distributed formation control of nonholonomic vehicles subject to velocity constraints. IEEE Trans. Ind. Electron. 2016, 63, 1289–1298. [Google Scholar] [CrossRef]
- Wang, X.; Yu, Y.; Li, Z. Distributed sliding mode control for leader-follower formation flight of fixed-wing unmanned aerial vehicles subject to velocity constraints. Int. J. Robust Nonlinear Control 2021, 31, 2110–2125. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Tian, Y.P. Coordinated path following control of multi-unicycle formation motion around closed curves in a time-invariant flow. Nonlinear Dyn. 2015, 81, 1005–1016. [Google Scholar] [CrossRef]
- Ai, X.; Chen, Y.Y.; Zhang, Y. Spherical formation tracking control of non-holonomic aircraft-like vehicles in a spatiotemporal flowfield. J. Frankl. Inst. 2020, 357, 3924–3952. [Google Scholar] [CrossRef]
- Yong, K.; Chen, M.; Wu, Q. Constrained adaptive neural control for a class of nonstrict-feedback nonlinear systems with disturbances. Neurocomputing 2018, 272, 405–415. [Google Scholar] [CrossRef]
- Liu, Y.J.; Zhao, W.; Liu, L.; Li, D.; Tong, S.; Chen, C.L.P. Adaptive neural network control for a class of nonlinear systems with function constraints on states. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Ghabcheloo, R.; Aguiar, A.; Pascoal, A.; Silvestre, C.; Kaminer, I.; Hespanha, J. Coordinated path-following in the presence of communication losses and time delays. SIAM J. Control Optim. 2009, 48, 234–265. [Google Scholar] [CrossRef] [Green Version]
- Olfati-Saber, R.; Murray, R. Consensus problems in networks of agents with switching topology and time–delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.P.; Liu, C. Consensus of multi-agent systems with diverse input and communication delays. IEEE Trans. Autom. Control 2008, 53, 2122–2128. [Google Scholar] [CrossRef]
- Li, W.; Chen, Z.; Liu, Z. Leader-following formation control for second-order multiagent systems with time-varying delay and nonlinear dynamics. Nonlinear Dyn. 2013, 72, 803–812. [Google Scholar] [CrossRef]
- Li, T.; Li, Z.; Shen, S.; Fei, S. Extended adaptive event-triggered formation tracking control of a class of multi-agent systems with time-varying delay. Neurocomputing 2018, 316, 386–398. [Google Scholar] [CrossRef]
- Liu, K.; Xie, G.; Wang, L. Containment control for second-order multi-agent systems with time-varying delays. Syst. Control Lett. 2014, 67, 24–31. [Google Scholar] [CrossRef]
- Wang, F.; Ni, Y.; Liu, Z.; Chen, Z. Fully distributed containment control for second-oder multi-agent systems with communication delay. ISA Trans. 2020, 99, 123–139. [Google Scholar] [CrossRef]
- Li, D.; Liu, L.; Liu, Y.J.; Tong, S.; Chen, C.L.P. Adaptive NN control without feasibility conditions for nonlinear state constrained stochastic systems with unknown time delays. IEEE Trans. Cybern. 2019, 49, 4485–4494. [Google Scholar] [CrossRef]
- Li, D.P.; Li, D.J. Adaptive neural tracking control for an uncertain state constrained robotic manipulator with unknown time-varying delays. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 2219–2228. [Google Scholar] [CrossRef]
- Sun, W.; Wu, Y.; Lv, X. Adaptive neural network control for full-state constrained robotic manipulator with actuator saturation and time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3331–3342. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Q. Event-triggered adaptive neural network control for stochastic nonlinear systems with state constraints and time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Ren, W.; Cao, Y. Distributed Coordination of Multi-Agent Networks; Springer: London, UK, 2011. [Google Scholar]
- Khalil, H. Nonlinear Systems, 2nd ed.; Pearson Education Limited: Prentice Hall, Upper Saddle River, NJ, USA, 1996. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, X.; Zhang, Y.; Chen, Y.-Y. Spherical Formation Tracking Control of Non-Holonomic UAVs with State Constraints and Time Delays. Aerospace 2023, 10, 118. https://doi.org/10.3390/aerospace10020118
Ai X, Zhang Y, Chen Y-Y. Spherical Formation Tracking Control of Non-Holonomic UAVs with State Constraints and Time Delays. Aerospace. 2023; 10(2):118. https://doi.org/10.3390/aerospace10020118
Chicago/Turabian StyleAi, Xiang, Ya Zhang, and Yang-Yang Chen. 2023. "Spherical Formation Tracking Control of Non-Holonomic UAVs with State Constraints and Time Delays" Aerospace 10, no. 2: 118. https://doi.org/10.3390/aerospace10020118





