DNS Study on Turbulent Transition Induced by an Interaction between Freestream Turbulence and Cylindrical Roughness in Swept Flat-Plate Boundary Layer
Abstract
1. Introduction
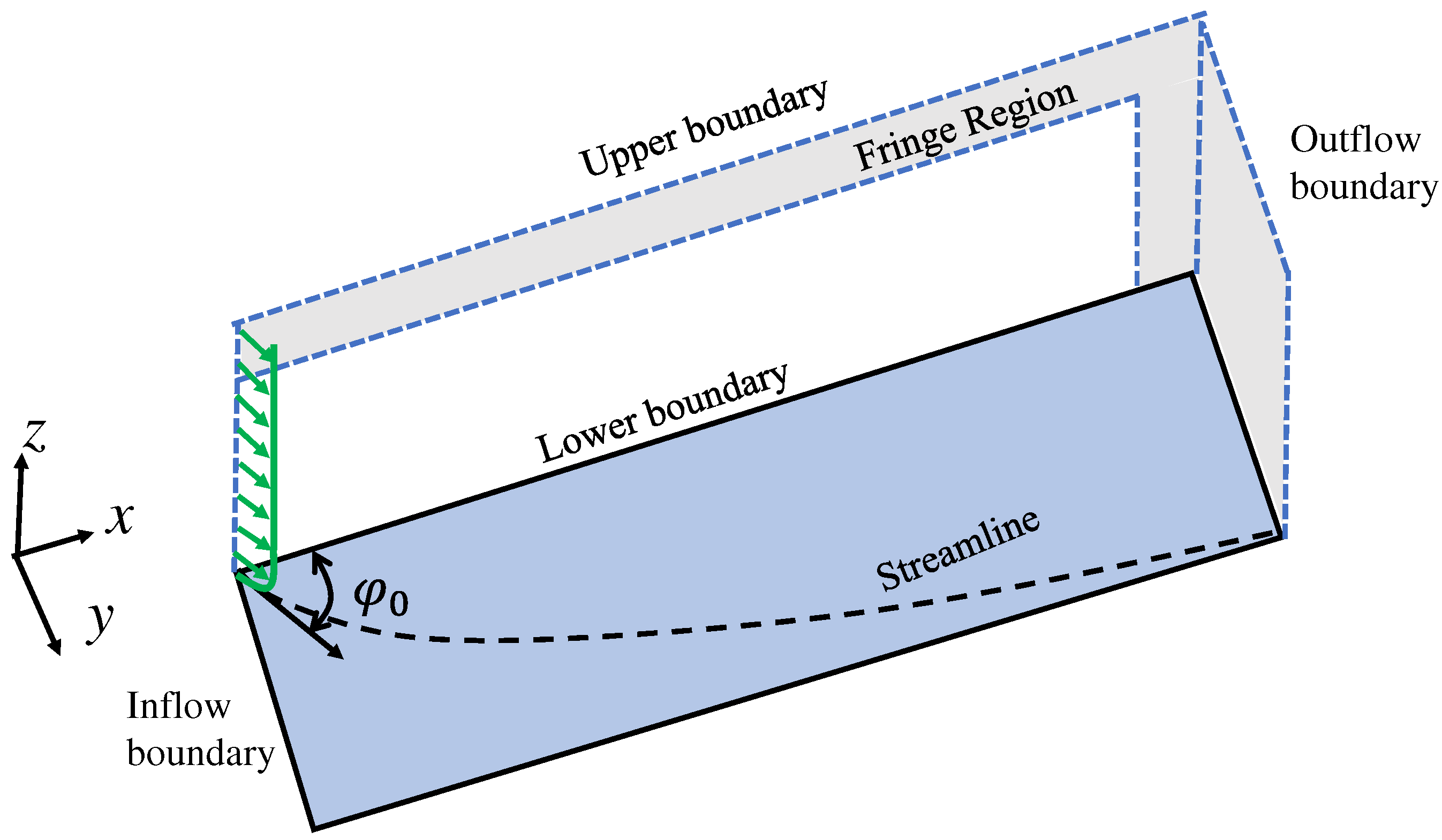
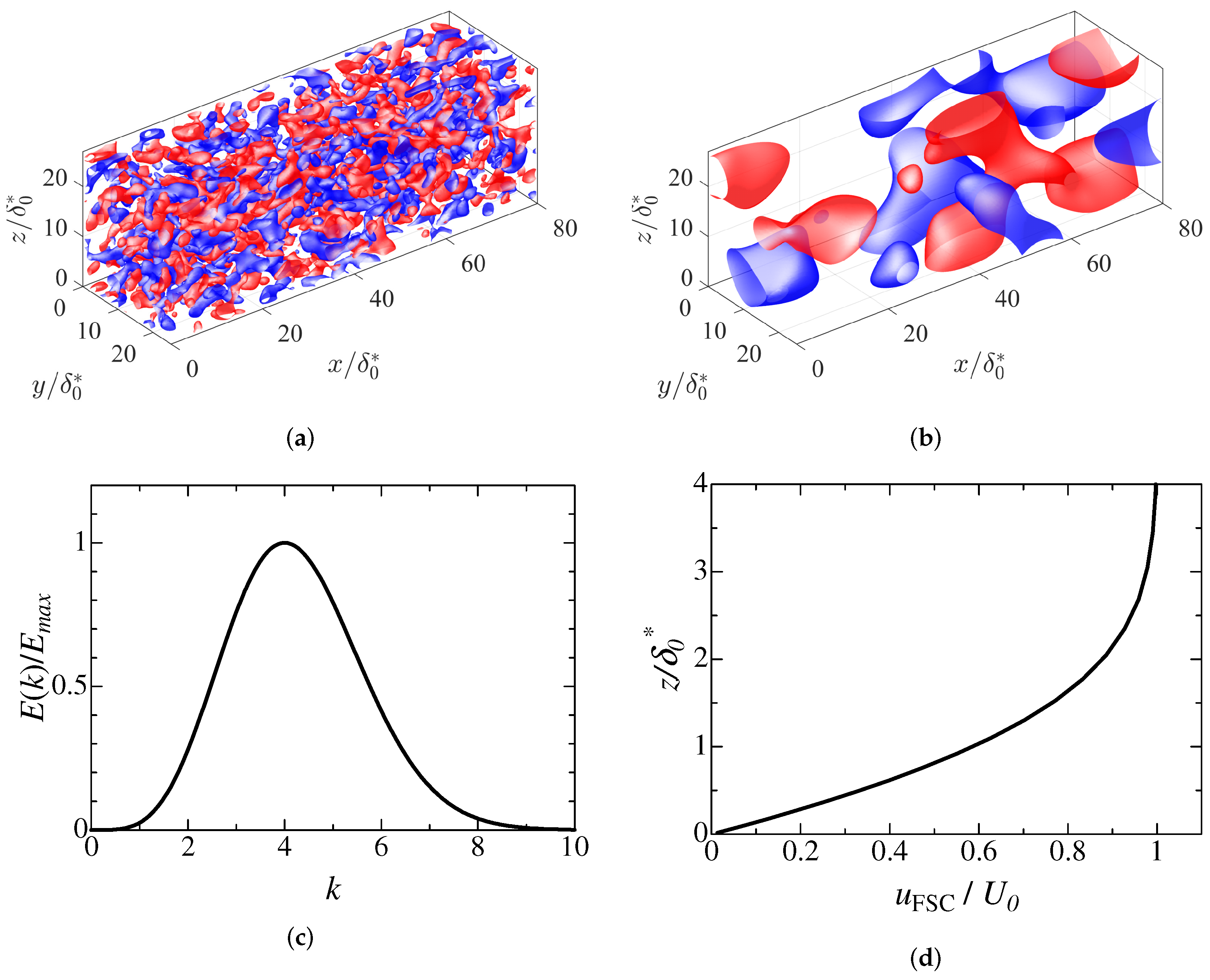
2. Numerical Setup and Method
3. Results
3.1. Roughness Height Dependency without Freestream Turbulence
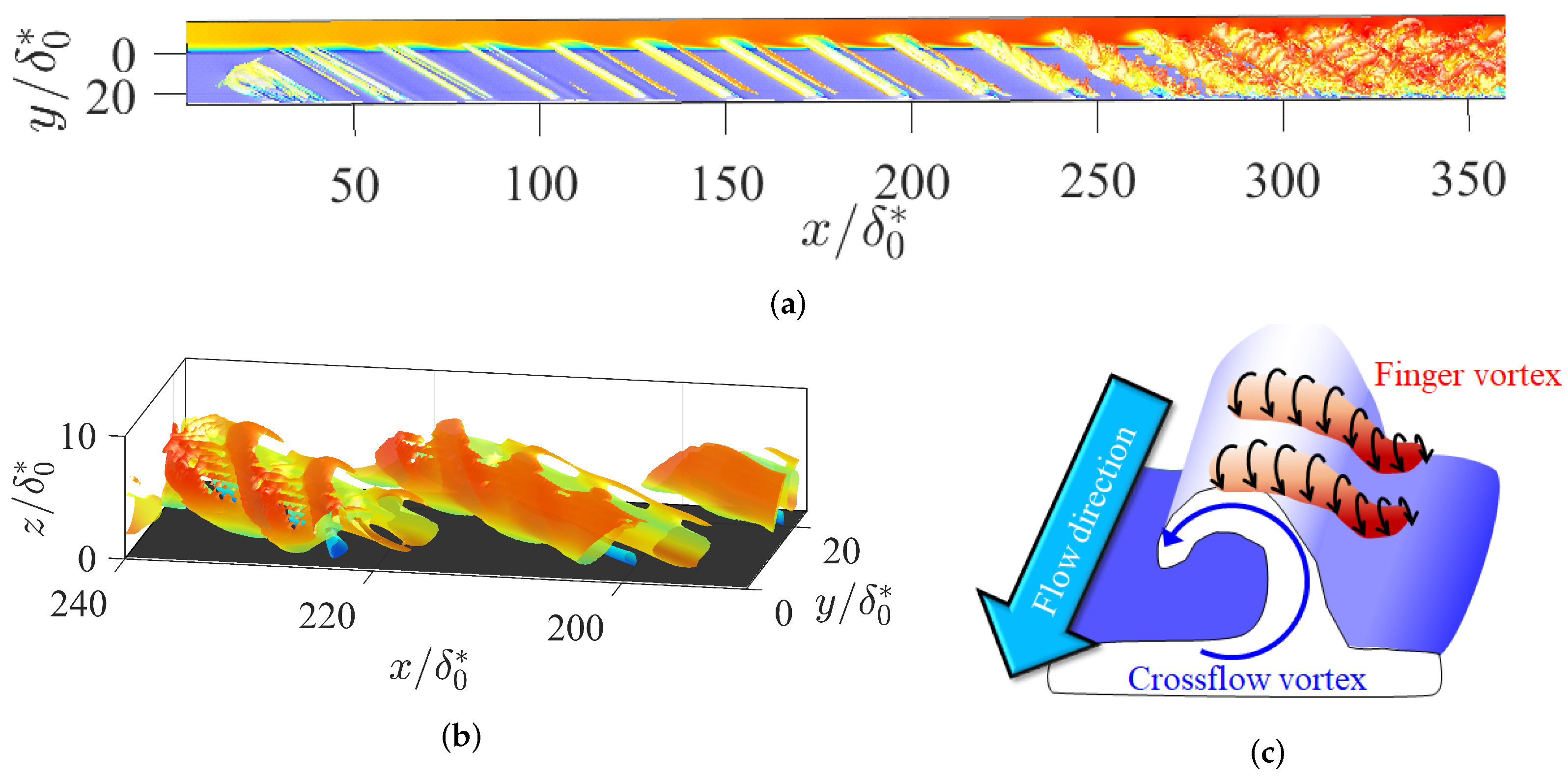
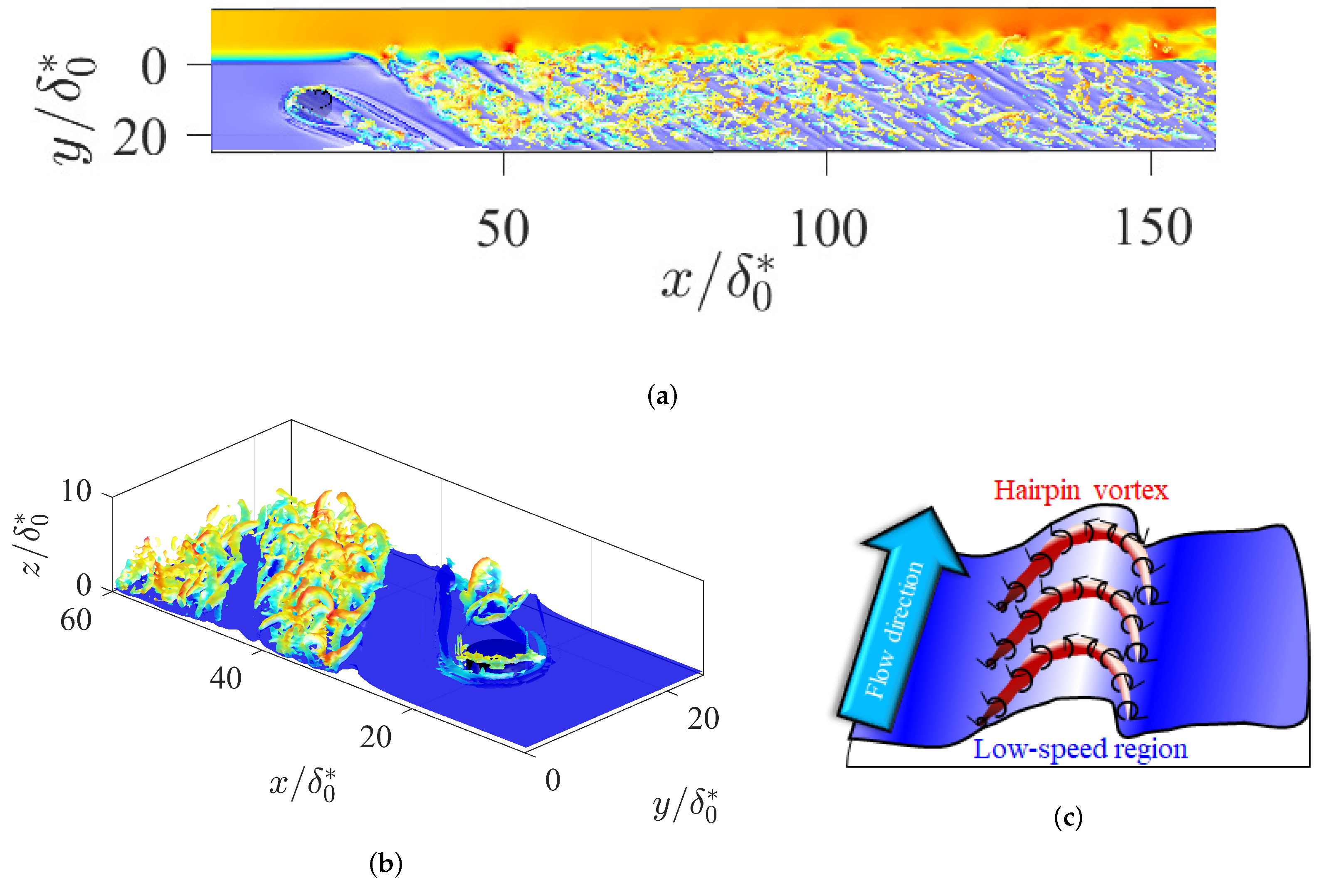
3.2. Different Transition Process
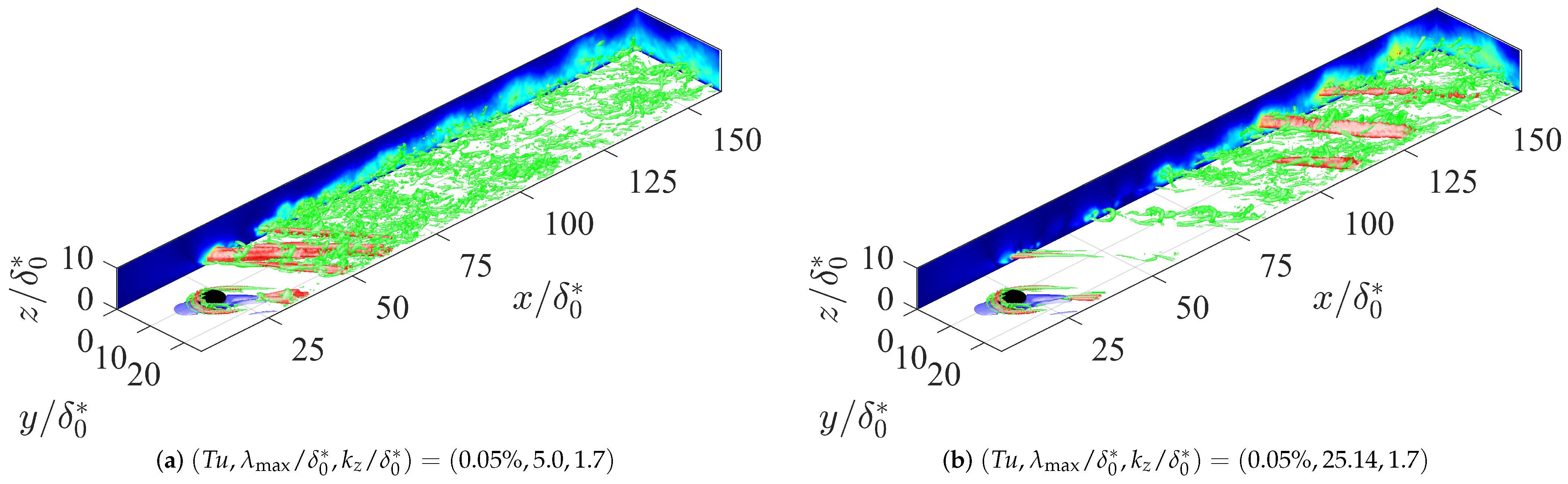
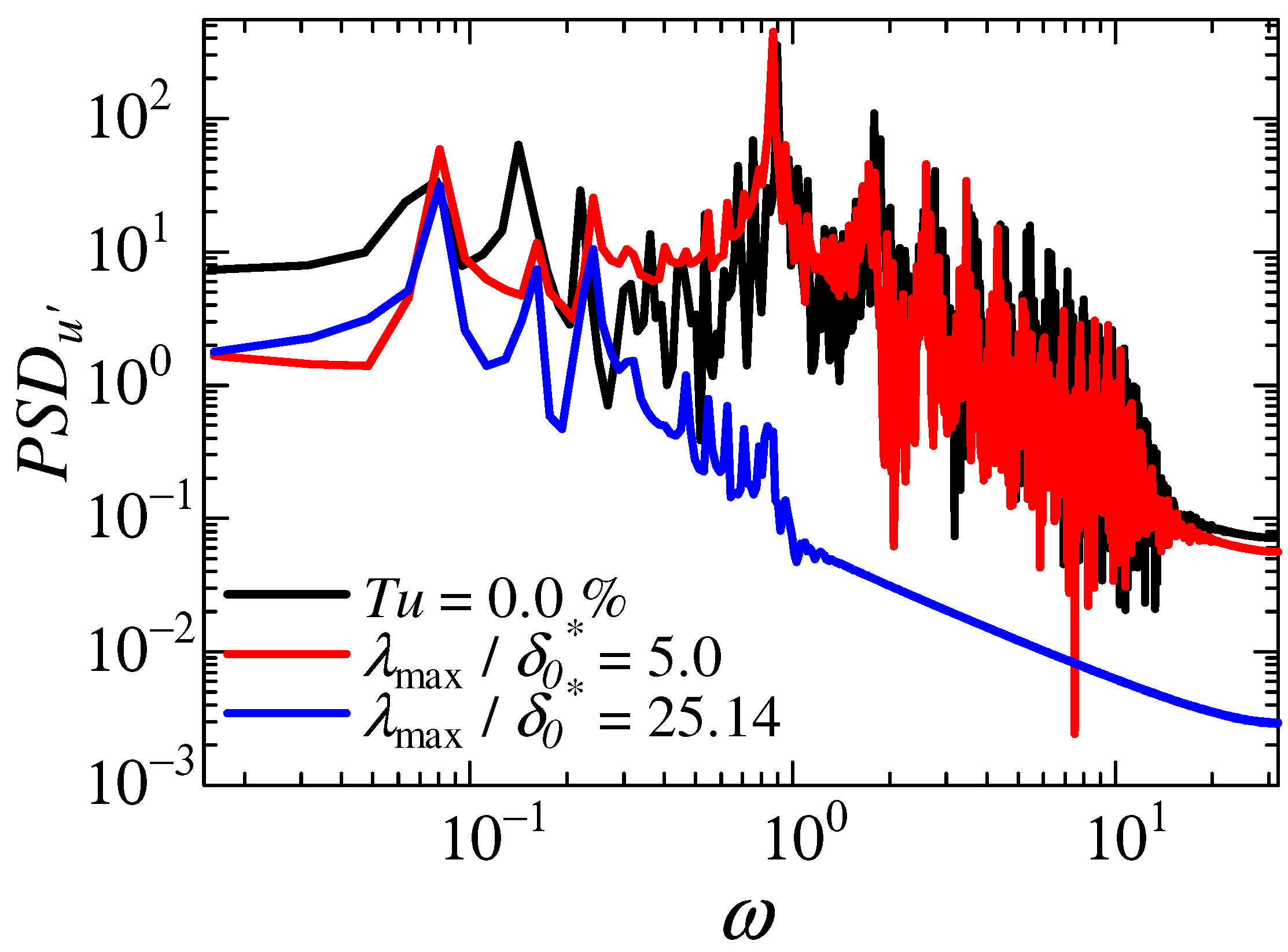
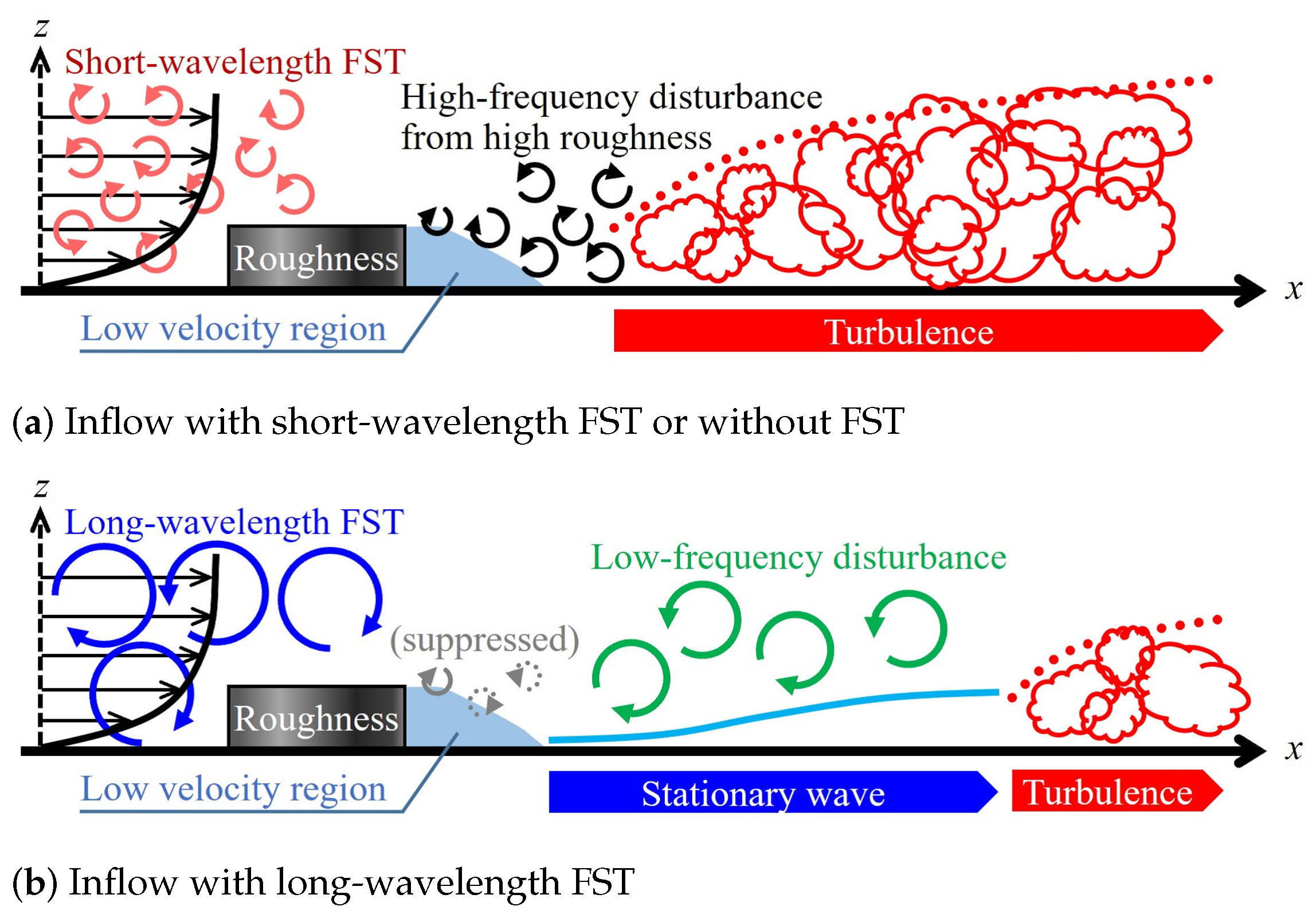
3.3. Transition Mechanisms with Freestream Turbulence
3.4. Disturbance from High Roughness Upper Edge
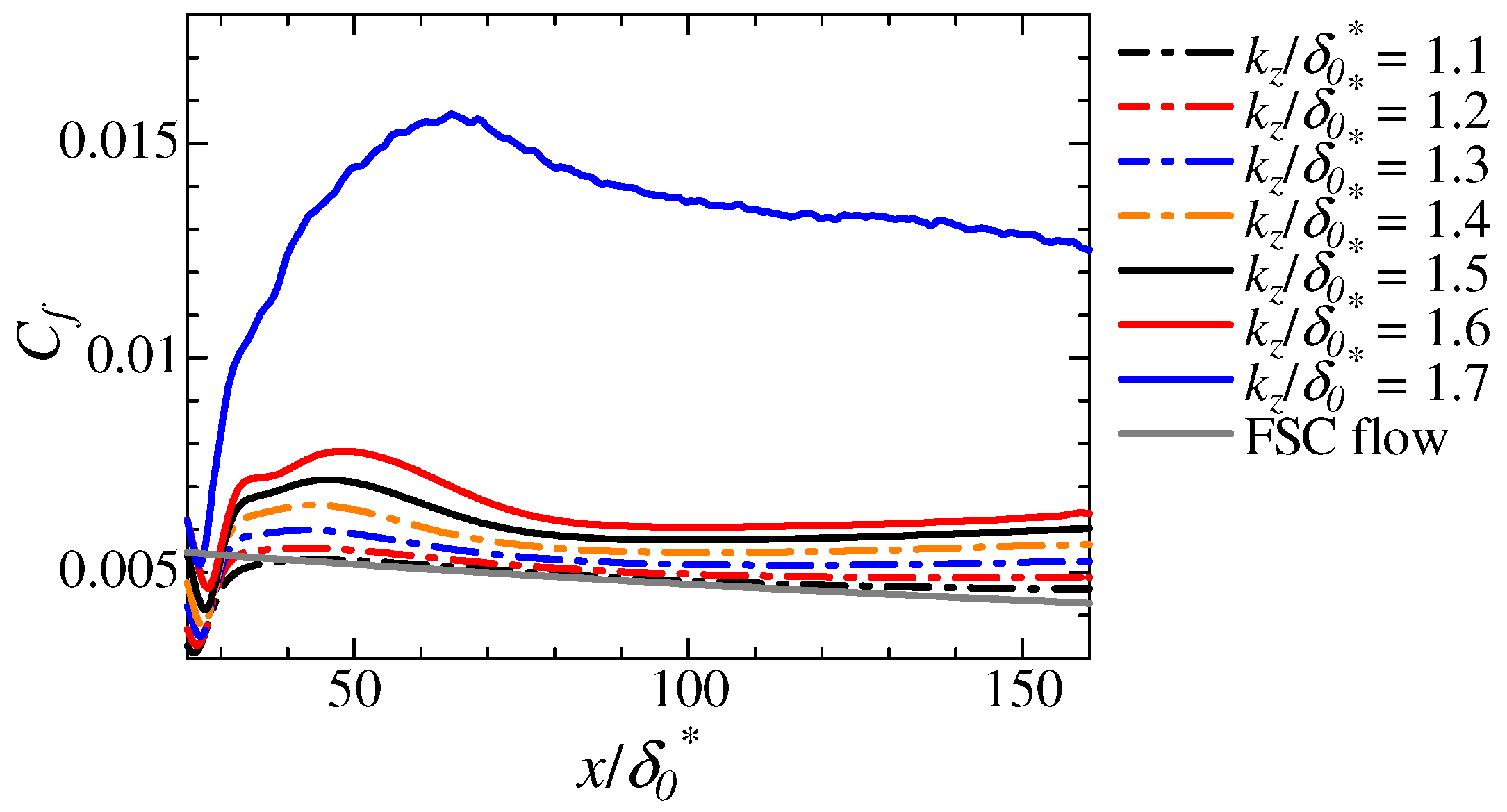
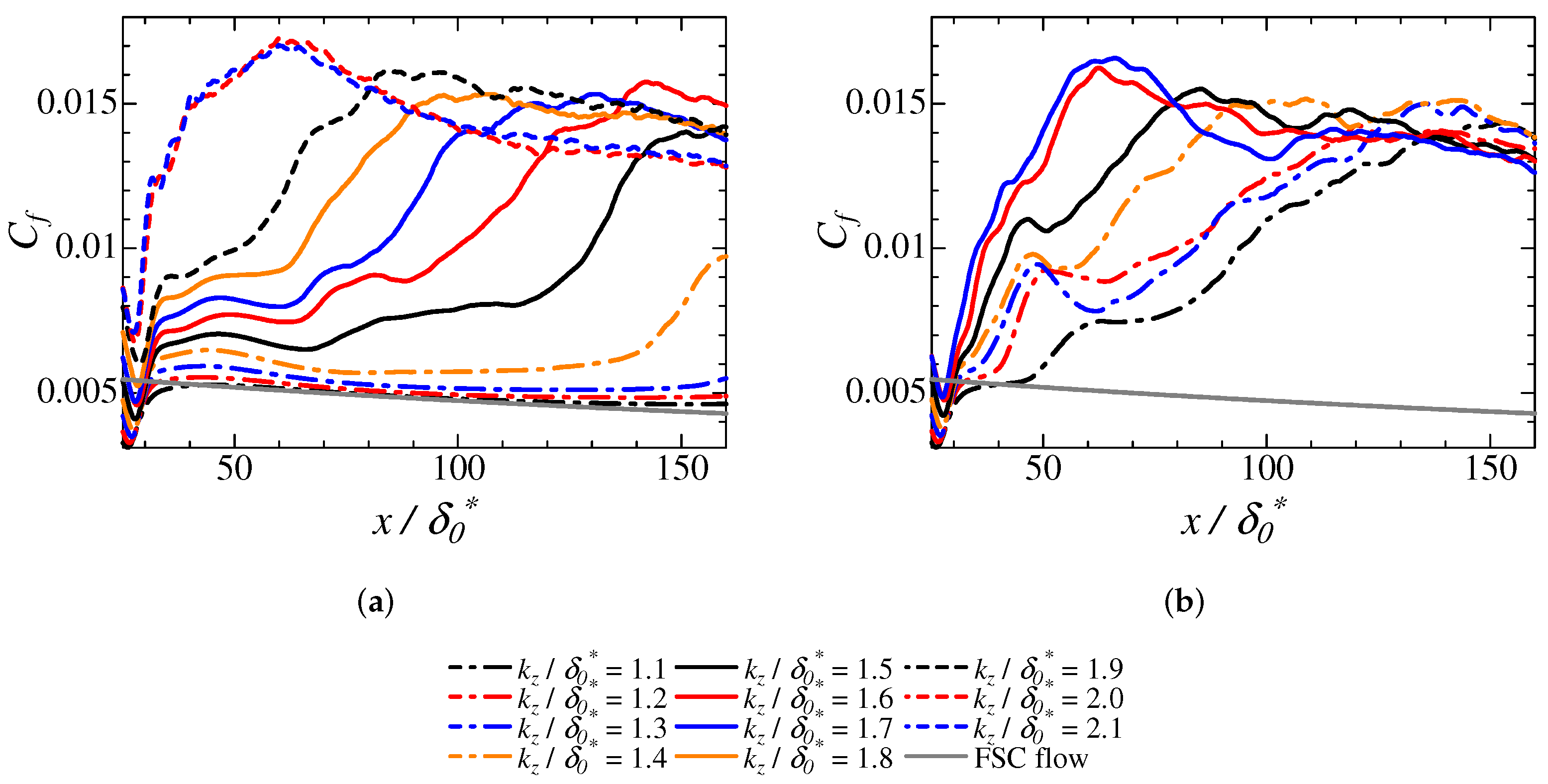
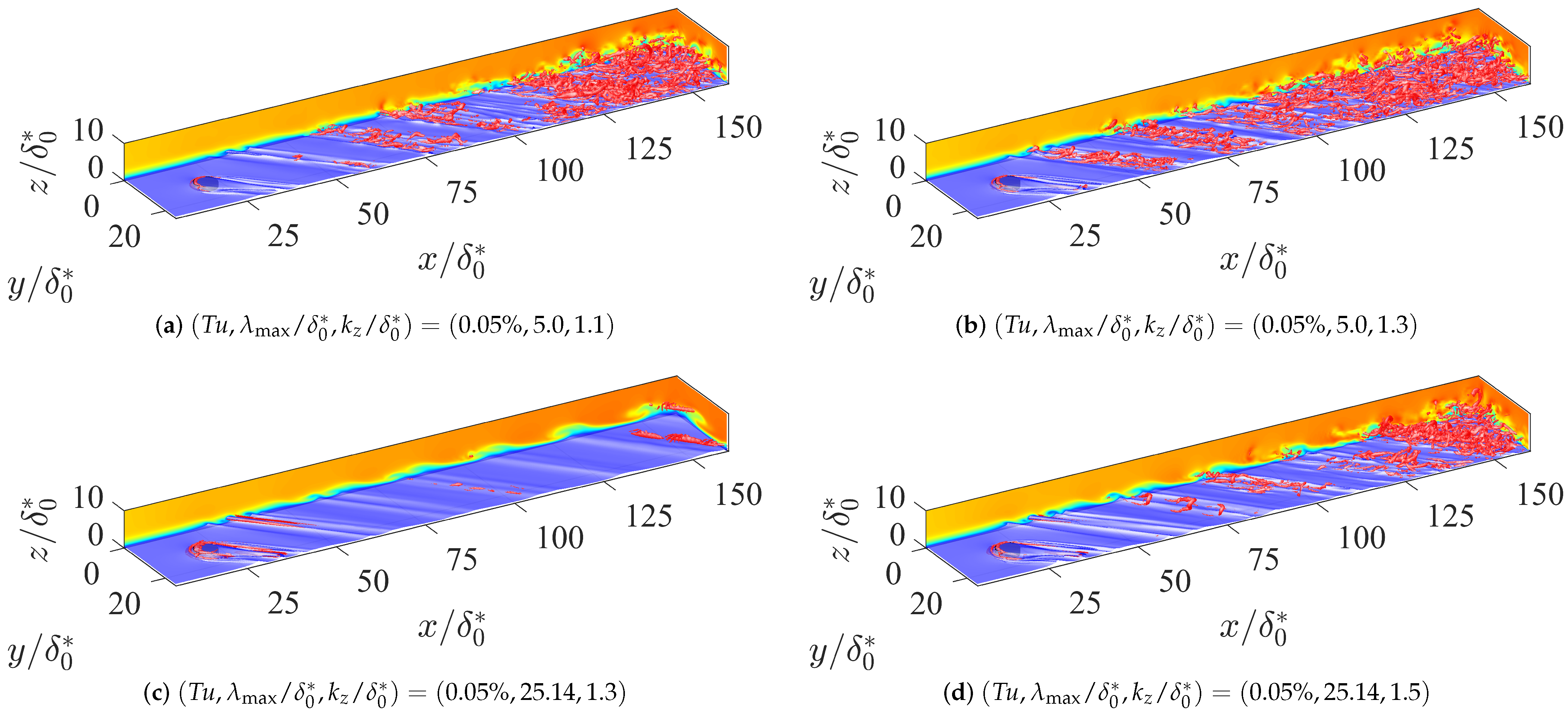
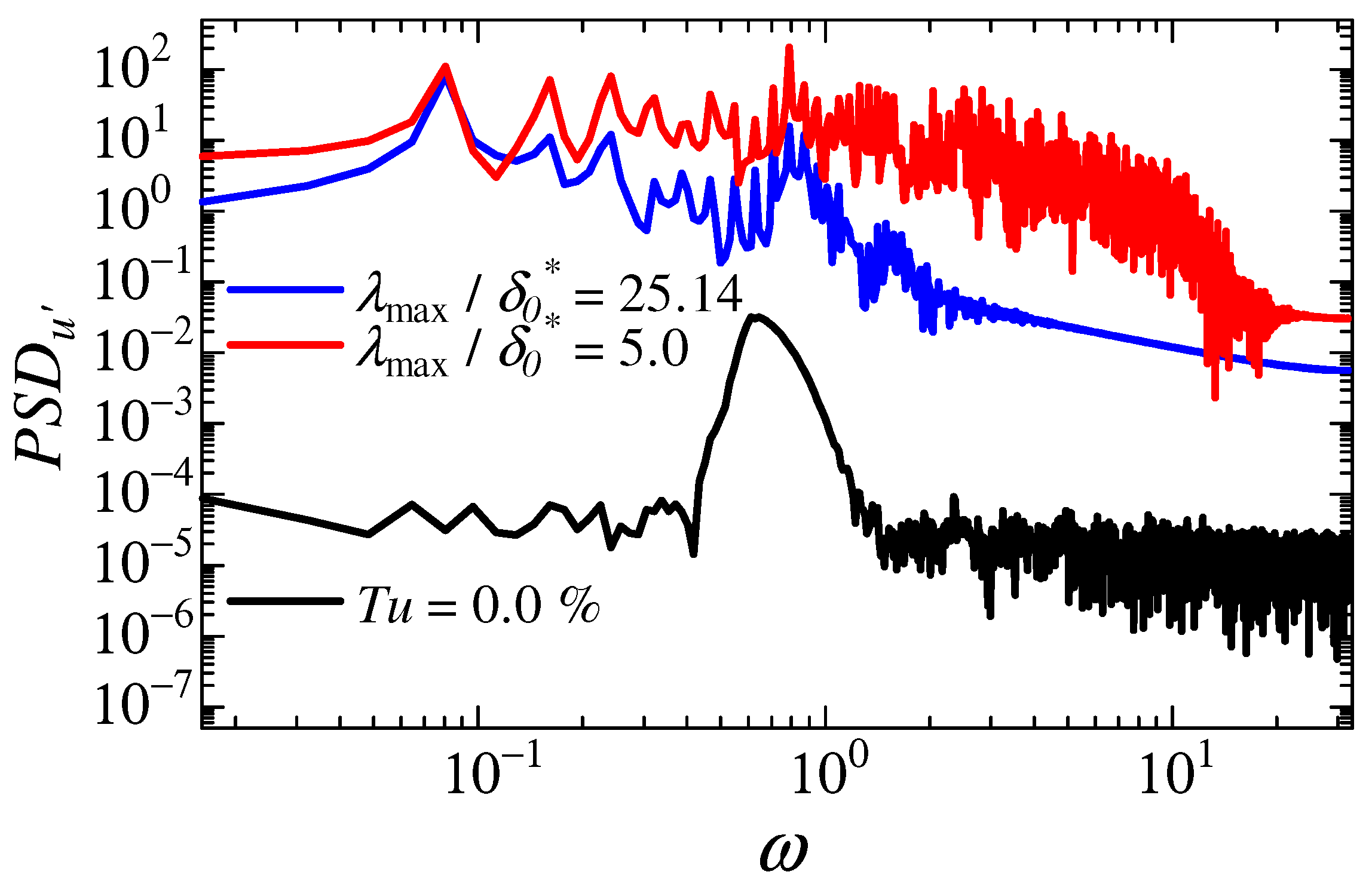
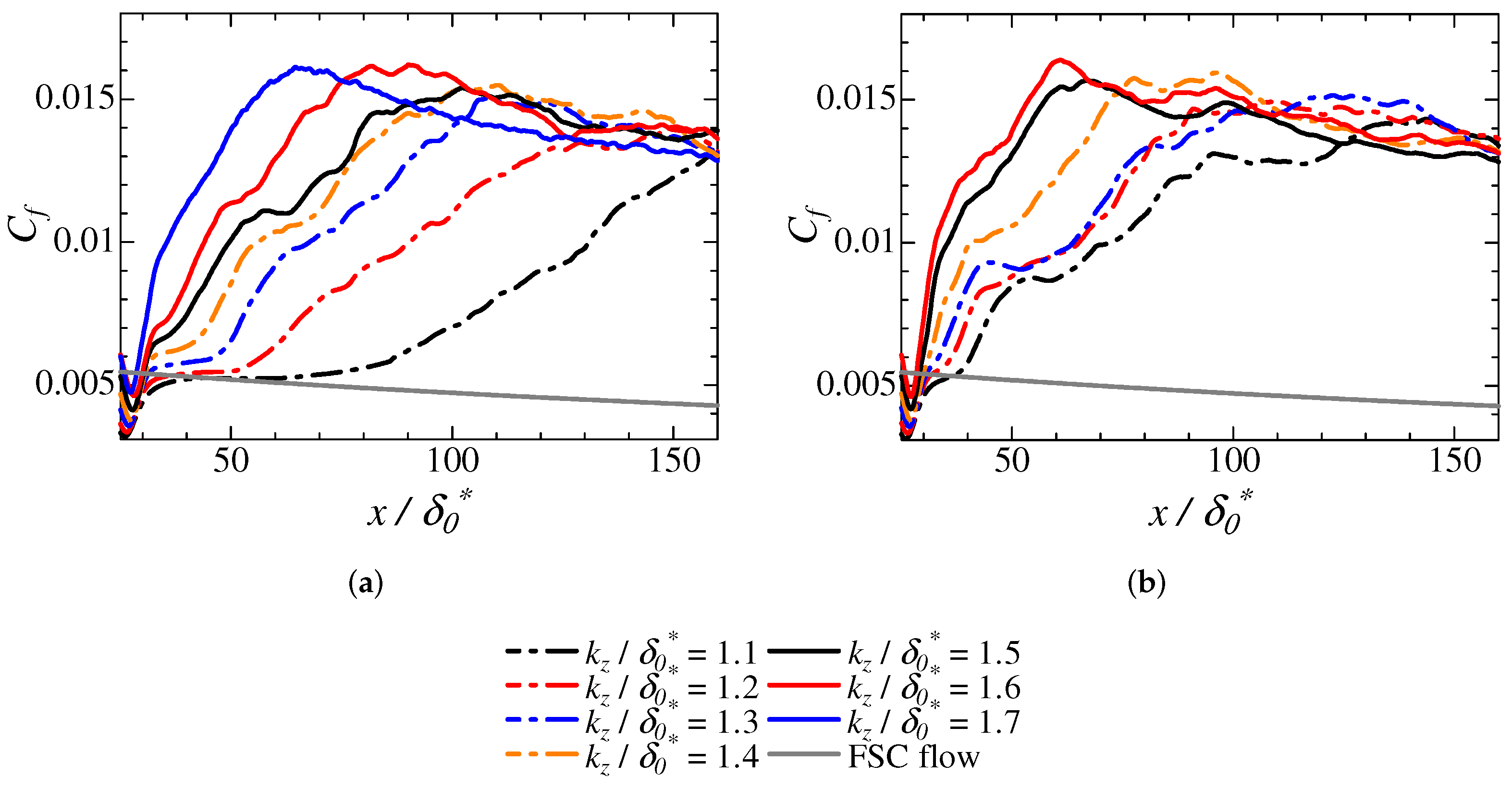
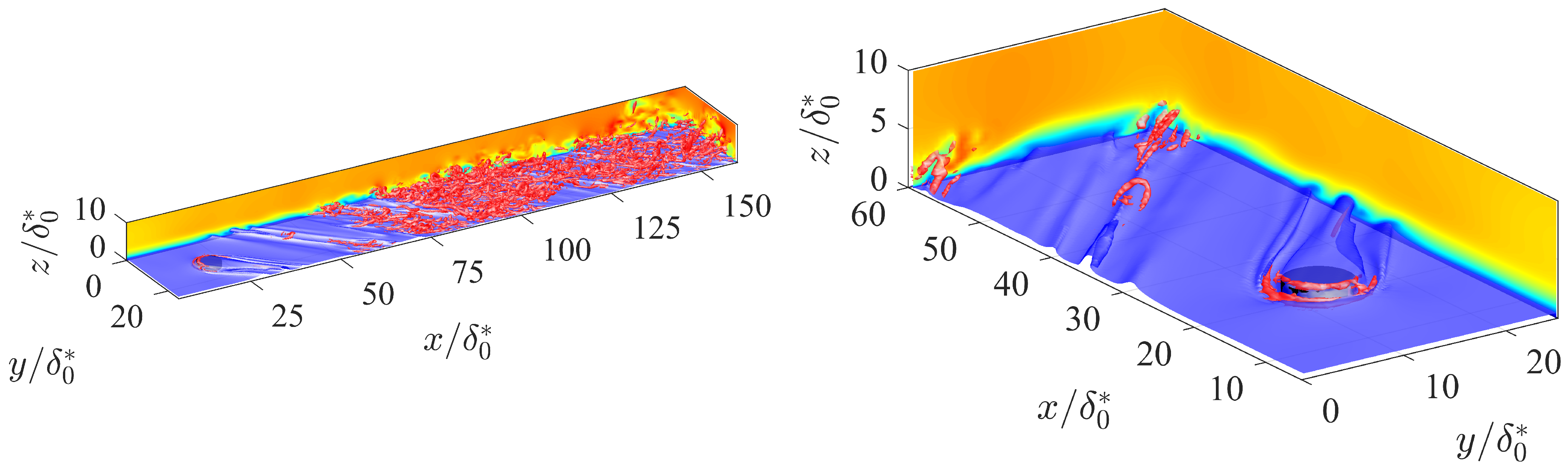
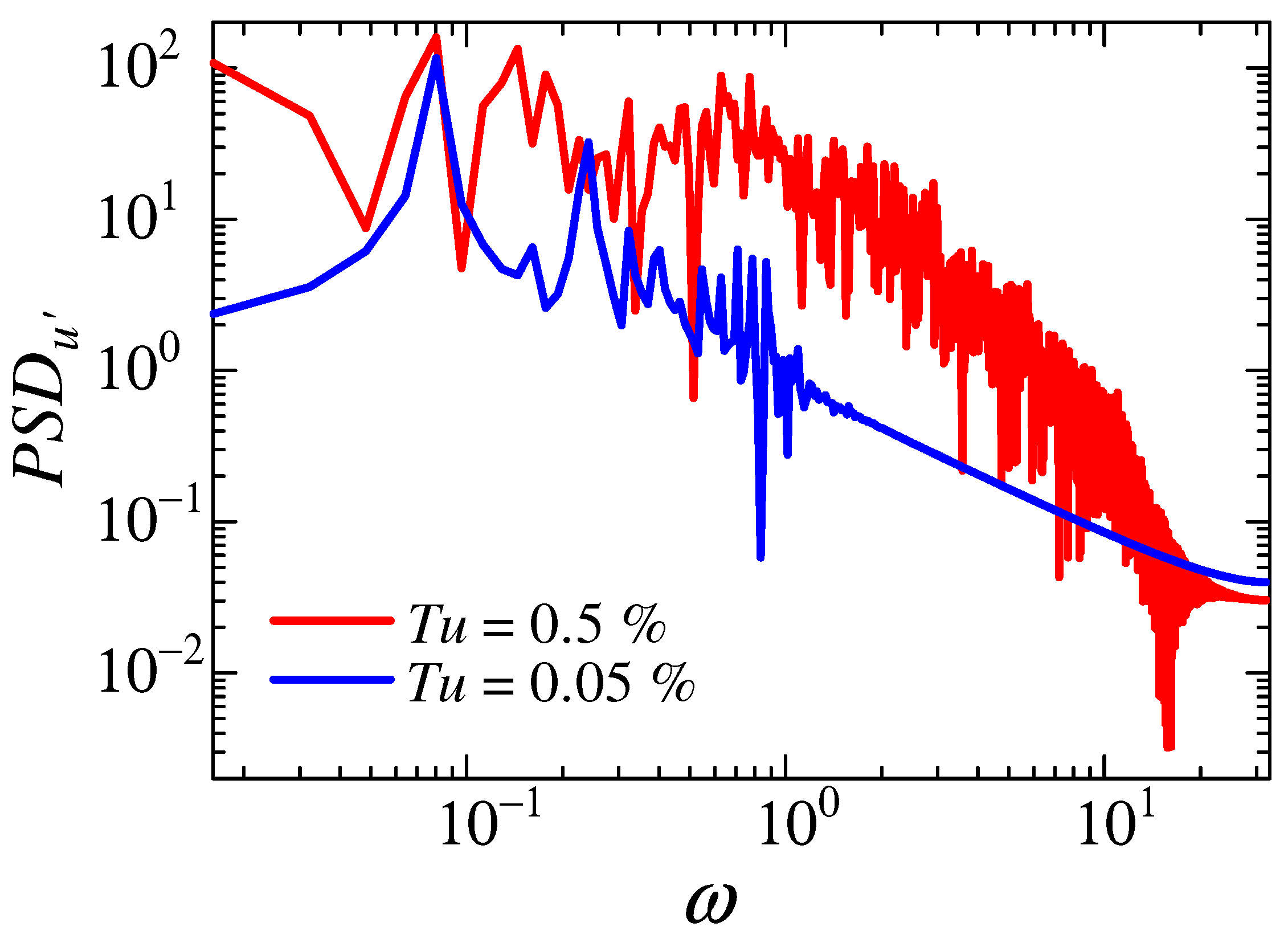
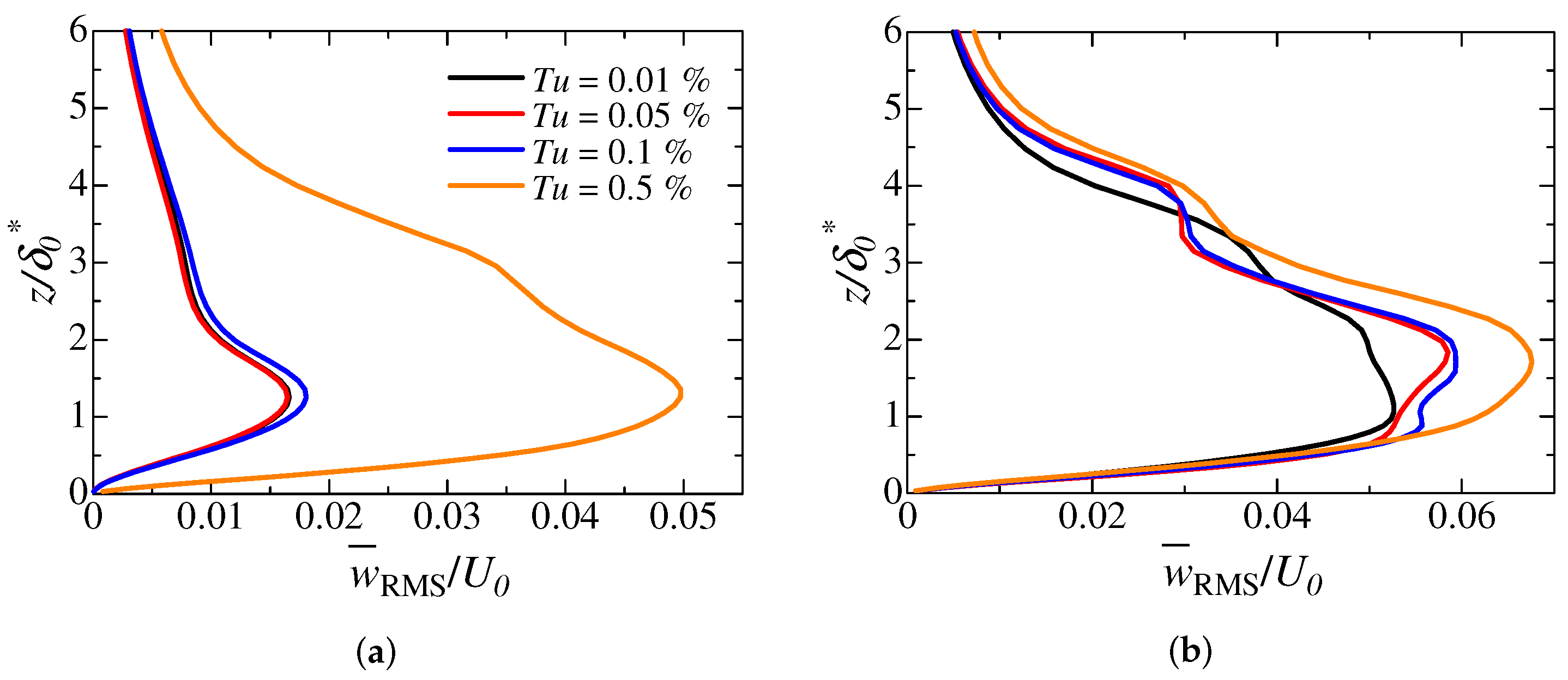
3.5. Turbulent Intensity Dependence on Transition Mechanisms
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Friction coefficient, | |
| Energy spectrum as a function of k | |
| k | Wave number |
| Roughness height | |
| Size of the main computational domain of DNS in x, y, and z | |
| Size of the disturbance box size in x, y, and z | |
| m | Acceleration parameters for the FSC solution |
| Number of grid points for the main computational domain in x, y, and z | |
| Number of grid points for the disturbance box in x, y, and z | |
| Power spectrum density of the chordwise disturbance velocity | |
| Q | Second invariant of the velocity gradient tensor normalized by and |
| Reynolds number, | |
| Roughness Reynolds number, | |
| Critical for immediate transition | |
| Time step | |
| Turbulence intensity of FST, | |
| u, v, w | Velocity in chordwise, spanwise, and wall-normal directions |
| , | External chordwise and spanwise velocities at the inlet |
| Wall-parallel velocity at the roughness height and location | |
| x, y, z | Coordinates in the chordwise, spanwise, and wall-normal directions |
| Displacement thickness at the inlet | |
| Kinematic viscosity | |
| Wavelength | |
| Streamline angle on the wall surface | |
| Wall-shear stress | |
| Disturbance component | |
| Nondimensionalized by and | |
| Time-averaged value | |
| RMS value | |
| Spanwise-averaged RMS value, | |
| External velocity at inlet | |
| Maximum value |
Abbreviations
| CFV | Crossflow vortex |
| DNS | Direct numerical simulation |
| FSC | Falkner–Skan–Cooke |
| FST | Freestream turbulence |
| RMS | Root-mean-square |
References
- Denham, C.L.; Patil, M.; Roy, C.J.; Alexandrov, N. Framework for estimating performance and associated uncertainty for modified aircraft configurations. Aerospace 2022, 9, 490. [Google Scholar] [CrossRef]
- Buntov, M.Y.; Makeev, P.V.; Ignatkin, Y.M.; Glazkov, V.S. Numerical modeling of the walls perforation influence on the accuracy of wind tunnel experiments using two-dimensional computational fluid dynamics model. Aerospace 2022, 9, 478. [Google Scholar] [CrossRef]
- Jiménez-Portaz, M.; Chiapponi, L.; Clavero, M.; Losada, M.A. Air flow quality analysis of an open-circuit boundary layer wind tunnel and comparison with a closed-circuit wind tunnel. Phys. Fluids 2020, 32, 125120. [Google Scholar] [CrossRef]
- Guissart, A.; Romblad, J.; Nemitz, T.; Tropea, C. Small-scale atmospheric turbulence and its impact on laminar-to-turbulent transition. AIAA J. 2021, 59, 3611–3621. [Google Scholar] [CrossRef]
- Kohama, Y. Some expectation on the mechanism of cross-flow instability in a swept wing flow. Acta Mech. 1987, 66, 21–38. [Google Scholar] [CrossRef]
- Saric, W.S.; Reed, H.L.; White, E.B. Stability and transition of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 2003, 35, 413–440. [Google Scholar] [CrossRef]
- Yakeno, A.; Obayashi, S. Propagation of stationary and traveling waves in a leading-edge boundary layer of a swept wing. Phys. Fluids 2021, 33, 094111. [Google Scholar] [CrossRef]
- Lin, P.; Wu, J.; Lu, L.; Xiong, N.; Liu, D.; Su, J.; Liu, G.; Tao, Y.; Wu, J.; Liu, X. Investigation on the Reynolds number effect of a flying wing model with large sweep angle and small aspect ratio. Aerospace 2022, 9, 523. [Google Scholar] [CrossRef]
- Chen, X.; Xi, Y.; Ren, J.; Fu, S. Cross-flow vortices and their secondary instabilities in hypersonic and high-enthalpy boundary layers. J. Fluid Mech. 2022, 947, A25. [Google Scholar] [CrossRef]
- Brynjell-Rahkola, M.; Shahriari, N.; Schlatter, P.; Hanifi, A.; Henningson, D.S. Stability and sensitivity of a cross-flow-dominated Falkner-Skan-Cooke boundary layer with discrete surface roughness. J. Fluid Mech. 2017, 144, 830–850. [Google Scholar] [CrossRef]
- Loiseau, J.C.; Robinet, J.C.; Cherubini, S.; Leriche, E. Investigation of the roughness-induced transition: Global stability analyses and direct numerical simulations. J. Fluid Mech. 2014, 760, 175–211. [Google Scholar] [CrossRef]
- Högberg, M.; Hennigson, D. Secondary instability of a cross-flow vortices in Falkner-Skan-Cooke boundary layer. J. Fluid Mech. 1998, 368, 339–357. [Google Scholar] [CrossRef]
- Malik, M.R.; Li, F.; Choudhari, M.M.; Chang, C.L. Secondary instability of a cross-flow vortices and swept-wing boundary-layer transition. J. Fluid Mech. 1999, 399, 85–115. [Google Scholar] [CrossRef]
- Bonfigli, G.; Kloker, M. Secondary instability of crossflow vortices: Validation of the stability theory by direct numerical simulation. J. Fluid Mech. 2007, 583, 229–272. [Google Scholar] [CrossRef]
- Wassermann, P.; Kloker, M. Mechanisms and passive control of crossflow-vortex-induced transition in a three-dimensional boundary layer. J. Fluid Mech. 2002, 456, 49–84. [Google Scholar] [CrossRef]
- Kurz, B.E.H.; Kloker, J.M. Mechanisms of flow tripping by discrete roughness elements in a swept-wing boundary layer. J. Fluid Mech. 2016, 796, 158–194. [Google Scholar] [CrossRef]
- Ishida, T.; Tsukahara, T.; Tokugawa, N. Parameter effects of spanwise-arrayed cylindrical roughness elements on transition in the Falkner–Skan–Cooke boundary layer. Trans. Jpn. Soc. Aeronaut. Space Sci. 2022, 65, 84–94. [Google Scholar] [CrossRef]
- Ishida, T.; Ohira, K.; Hosoi, R.; Tokugawa, N.; Tsukahara, T. Numerical and experimental analysis of three-dimensional boundary-layer transition induced by isolated cylindrical roughness elements. Int. J. Aeronaut. Space Sci. 2022, 23, 649–659. [Google Scholar] [CrossRef]
- Örlü, R.; Tillmark, N.; Alfredsson, P.H. Measured Critical Size of Roughness Elements; Technical Report by KTH Royal Institude of Technology: Stockholm, Sweden, 2021. [Google Scholar]
- Zoppini, G.; Westerbeek, S.; Ragni, D.; Kotsonis, M. Receptivity of crossflow instability to discrete roughness amplitude and location. J. Fluid Mech. 2022, 939, A33. [Google Scholar] [CrossRef]
- Saric, W.S.; Reed, H.L.; Kerschen, E.J. Boundary-layer receptivity to freestream disturbance. Annu. Rev. Fluid Mech. 2002, 34, 291–319. [Google Scholar] [CrossRef]
- Deyhle, H.; Bippes, H. Disturbance growth in an unstable three-dimensional boundary layer and its dependence on environmental conditions. J. Fluid Mech. 1996, 316, 73–113. [Google Scholar] [CrossRef]
- Downs, R.S.; White, E.B. Free-stream turbulence and the development of cross-flow disturbances. J. Fluid Mech. 2013, 735, 347–380. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Hanifi, A.; Hennigson, D.S. Effect of freestream turbulence on roughness-induced crossflow instability. Procedia IUTAM 2015, 14, 303–310. [Google Scholar] [CrossRef]
- Vincentiis, L.D.; Henningson, D.S.; Hanifi, A. Transition in an infinite swept-wing boundary layer subject to surface roughness and free-stream turbulence. J. Fluid Mech. 2022, 931, A24. [Google Scholar] [CrossRef]
- Huai, X.; Joslin, R.D.; Piomellt, U. Large-eddy simulation of boundary-layer transition on a swept wedge. J. Fluid Mech. 1999, 381, 357–380. [Google Scholar] [CrossRef]
- Bose, S.T.; Park, G.I. Wall-modeled large-eddy simulation for complex turbulent flows. Annu. Rev. Fluid Mech. 2018, 50, 535–561. [Google Scholar] [CrossRef]
- Chen, J.; Dong, S.; Chen, X.; Yuan, X.; Xu, G. Stationary cross-flow breakdown in a high-speed swept-wing boundary layer. Phys. Fluids 2021, 33, 024108. [Google Scholar] [CrossRef]
- De Vanna, F.; Baldan, G.; Picano, F.; Benini, E. Effect of convective schemes in wall-resolved and wall-modeled LES of compressible wall turbulence. Comput. Fluids 2023, 250, 105710. [Google Scholar] [CrossRef]
- Brynjell-Rahkola, M.; Schlatter, P.; Hanifi, A.; Henningson, D.S. Global stability analysis of a roughness wake in a Falkner-Skan-Cooke boundary layer. Procedia IUTAM 2015, 14, 192–200. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Tempelmann, D.; Hanifi, A.; Henningson, D.S. Stabilization of a swept-wing boundary layer by distributed roughness elements. J. Fluid Mech. 2013, 718, R1. [Google Scholar] [CrossRef]
- Owen, M.; Frendi, A. Towards the understanding of humpback whale tubercles: Linear stability analysis of a wavy flat plate. Fluids 2020, 5, 212. [Google Scholar] [CrossRef]
- Saric, W.S.; Carpenter, A.L.; Reed, H.L. Passive control of transition in three-dimensional boundary layers, with emphasis on discrete roughness elements. Philos. Transitions R. Soc. A 2011, 369, 1352–1364. [Google Scholar] [CrossRef]
- Cooke, J.C. The boundary layer of a class of infinite yawed cylinders. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1950; Volume 46, pp. 645–648. [Google Scholar] [CrossRef]
- Fadlun, E.; Verzicco, R.; Orlandi, P.; Mohd-Yusof, J. Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 2000, 161, 35–60. [Google Scholar] [CrossRef]
- Muths, S.; Bhushan, S. Comparison between temporal and spatial direct numerical simulations for bypass transition flows. J. Turbul. 2020, 21, 311–354. [Google Scholar] [CrossRef]
- Watanabe, D.; Maekawa, H. Rapid growth of unsteady finite-amplitude perturbations in a supersonic boundary-layer flow. In Ninth International Symposium on Turbulence and Shear Flow Phenomena; Begel House Inc.: Melbourne, Australia, 2015; Volume 3B-4. [Google Scholar] [CrossRef]
- Brandt, L.; Schlatter, P.; Henningson, D.S. Transition in boundary layers subject to free-stream turbulence. J. Fluid Mech. 2004, 517, 167–198. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Serpieri, J.; Kotsonis, M. Three-dimensional organisation of primary and secondary crossflow instability. J. Fluid Mech. 2016, 799, 200–245. [Google Scholar] [CrossRef]
- Casacuberta, J.; Groot, K.J.; Hickel, S.; Kotsonis, M. Secondary instabilities in swept-wing boundary layers: Direct Numerical Simulations and BiGlobal stability analysis. In AIAA SCITECH 2022 Forum; AIAA: San Diego, CA, USA, 2022; p. 2330. [Google Scholar] [CrossRef]
- Bucci, M.A.; Puckert, D.K.; Andriano, C.; Loiseau, J.C.; Cherubini, S.; Robinet, J.C.; Rist, U. Roughness-induced transition by quasi-resonance of a varicose global mode. J. Fluid Mech. 2018, 836, 167–191. [Google Scholar] [CrossRef]
- Von Doenhoff, A.E.; Braslow, A.L. The effect of distributed surface roughness on laminar flow. In Boundary Layer and Flow Control; Lachmann, G., Ed.; Pergamon: Amsterdam, The Netherlands, 1961; pp. 657–681. [Google Scholar] [CrossRef]
- Robinson, S.K. Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 1991, 23, 601–639. [Google Scholar] [CrossRef]
- Vaid, A.; Vadlamani, N.R.; Malathi, A.S.; Gupta, V. Dynamics of bypass transition behind roughness element subjected to pulses of free-stream turbulence. Phys. Fluids 2022, 34, 114110. [Google Scholar] [CrossRef]




| m | |||||||
|---|---|---|---|---|---|---|---|
| Short domain | 337.9 | ||||||
| Long domain | 337.9 |
| 342 | 401 | 491 | 538 | 583 | 666 | 717 | 810 | 867 | 967 | 1030 | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | – | – | – | – | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | – | – | – | – | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | – | – | – | – | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | – | – | – | – | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | – | – | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | – | – | – | – | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | – | – | – | – | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | – | – | – | – | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | – | – | – | – | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | – | – | – | – | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | – | – | – | – | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | – | – | – | – | |||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | – | – | – | – | |||
| 0.01–0.5% | 2.514–25.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakagawa, K.; Tsukahara, T.; Ishida, T. DNS Study on Turbulent Transition Induced by an Interaction between Freestream Turbulence and Cylindrical Roughness in Swept Flat-Plate Boundary Layer. Aerospace 2023, 10, 128. https://doi.org/10.3390/aerospace10020128
Nakagawa K, Tsukahara T, Ishida T. DNS Study on Turbulent Transition Induced by an Interaction between Freestream Turbulence and Cylindrical Roughness in Swept Flat-Plate Boundary Layer. Aerospace. 2023; 10(2):128. https://doi.org/10.3390/aerospace10020128
Chicago/Turabian StyleNakagawa, Kosuke, Takahiro Tsukahara, and Takahiro Ishida. 2023. "DNS Study on Turbulent Transition Induced by an Interaction between Freestream Turbulence and Cylindrical Roughness in Swept Flat-Plate Boundary Layer" Aerospace 10, no. 2: 128. https://doi.org/10.3390/aerospace10020128
APA StyleNakagawa, K., Tsukahara, T., & Ishida, T. (2023). DNS Study on Turbulent Transition Induced by an Interaction between Freestream Turbulence and Cylindrical Roughness in Swept Flat-Plate Boundary Layer. Aerospace, 10(2), 128. https://doi.org/10.3390/aerospace10020128







