Non-Intersecting Diverging Runways Separation under Emergency Avoidance Situation
Abstract
:1. Introduction
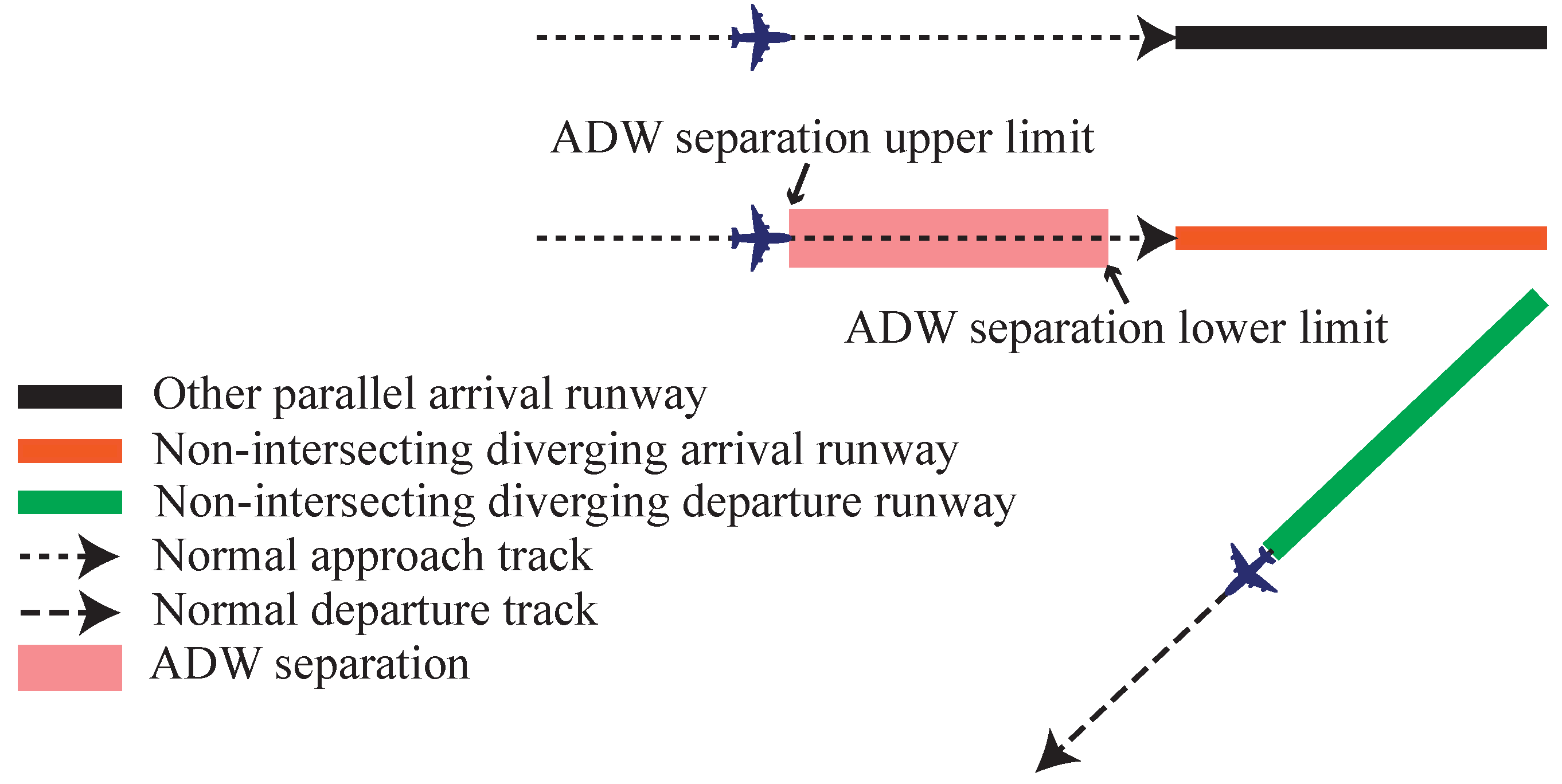
2. Models and Methods
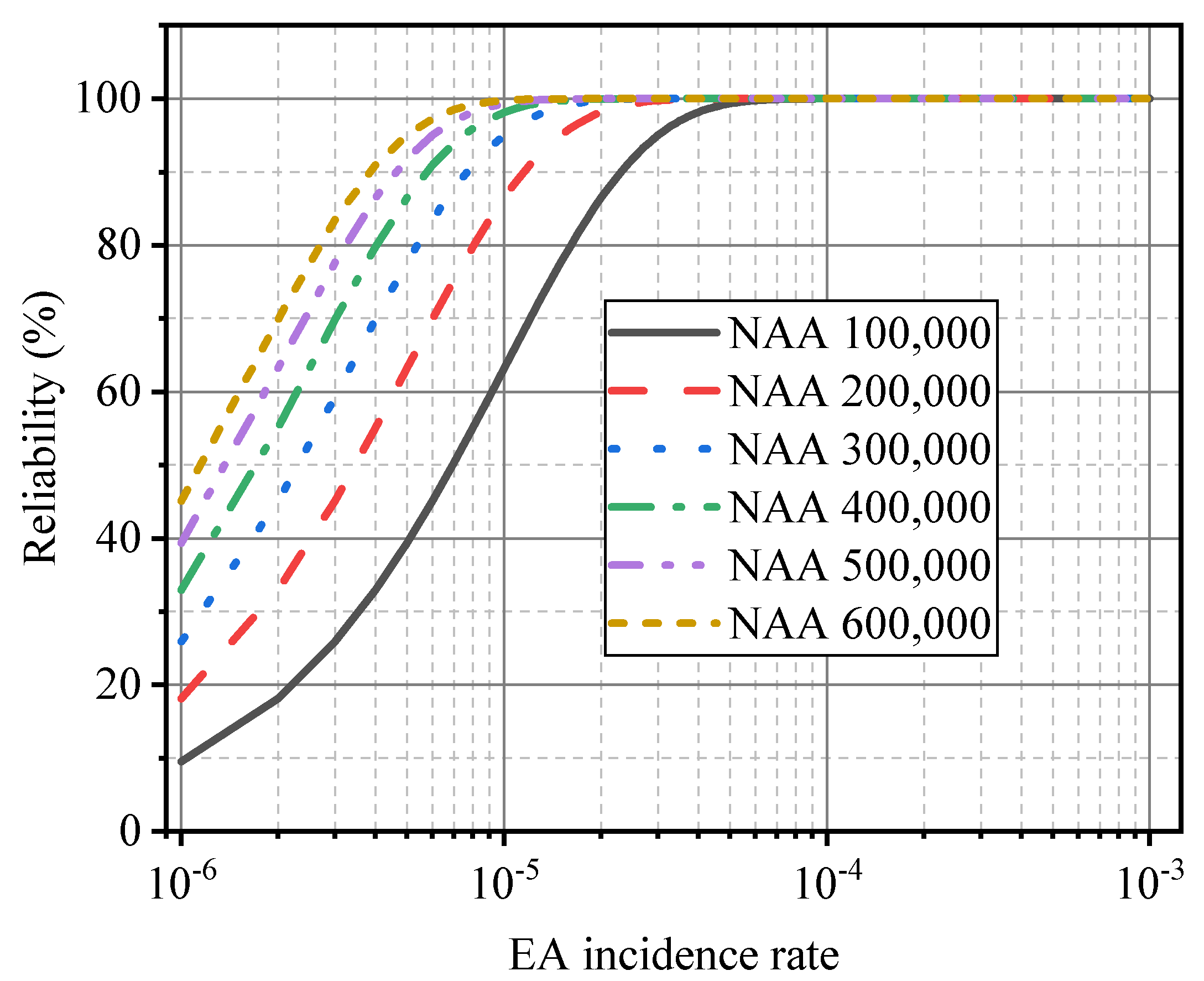
2.1. EA Incidence Rate and Required CP
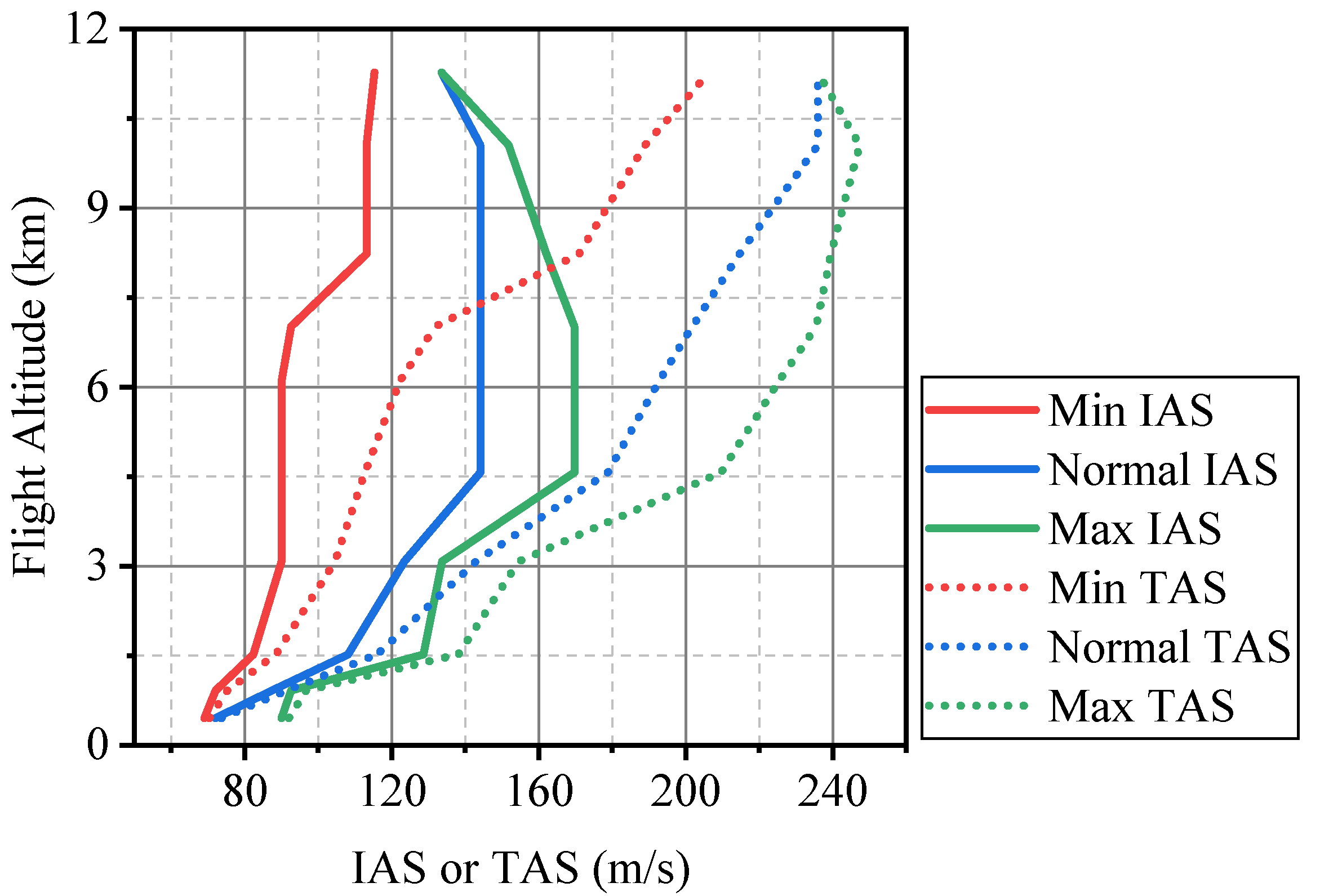
2.2. Computer-Simulated Aircraft Nominal Trajectory
2.3. CP Calculation
- For aircraft and , first calculate the Euclidean distance between the centroids of the two aircraft. If the distance is greater than, or equal to, , it is impossible for the two aircraft to collide anyway; otherwise, the next step of judgment is performed.
- According to the dynamic position and attitude of aircraft and , the established 3D convex hulls of the aircraft are updated. If the 3D convex hulls do not intersect, it is absolutely impossible for the two aircraft to collide; otherwise, proceed to the next step.
- Finally, compare whether the actual 3D models of aircraft and intersect to determine whether the two aircraft collide.
| Algorithm 1 Calculate CP of two aircraft. |
|
3. Case Study and Results
3.1. Parameter Settings
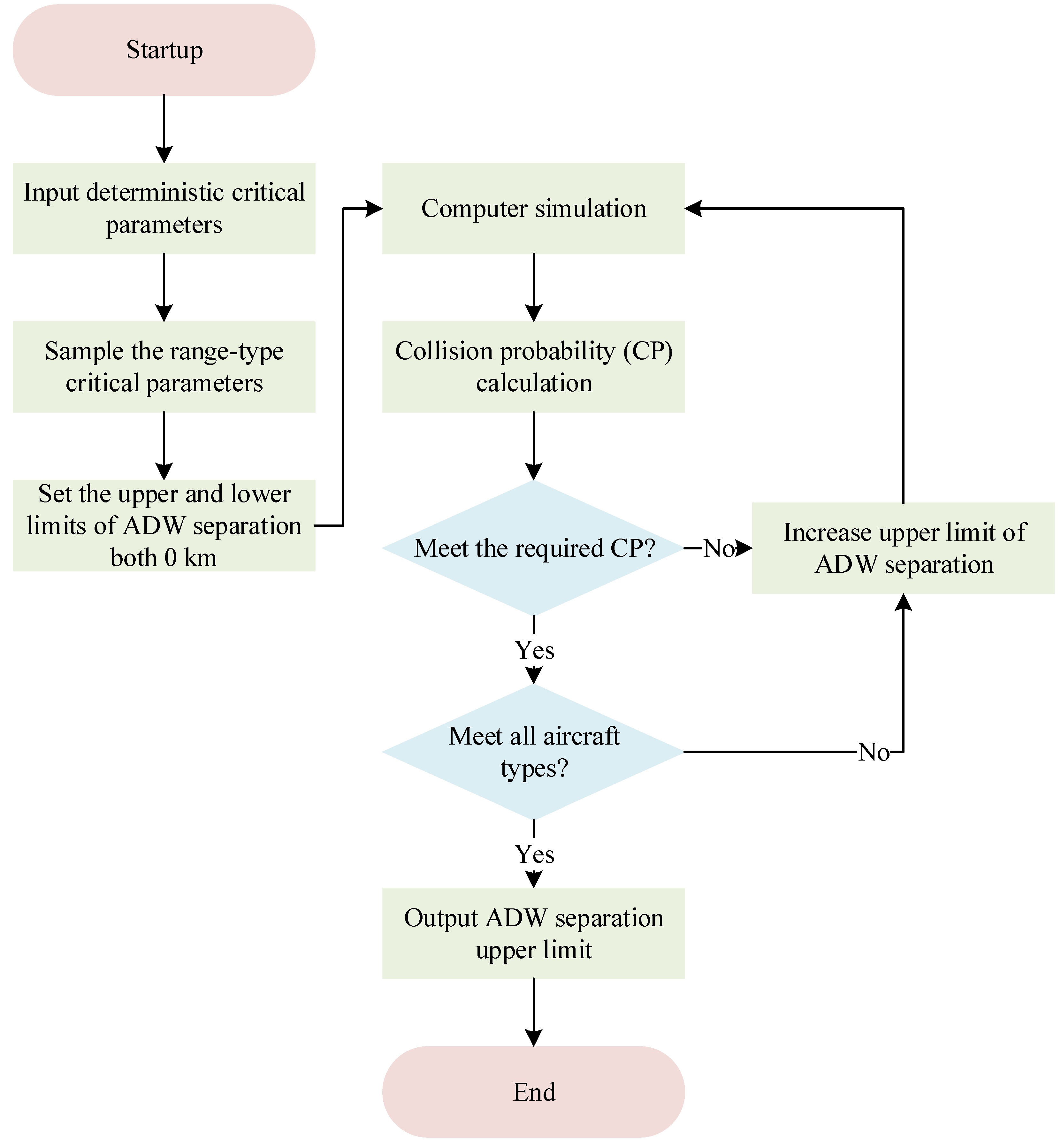
3.2. Calculation Process
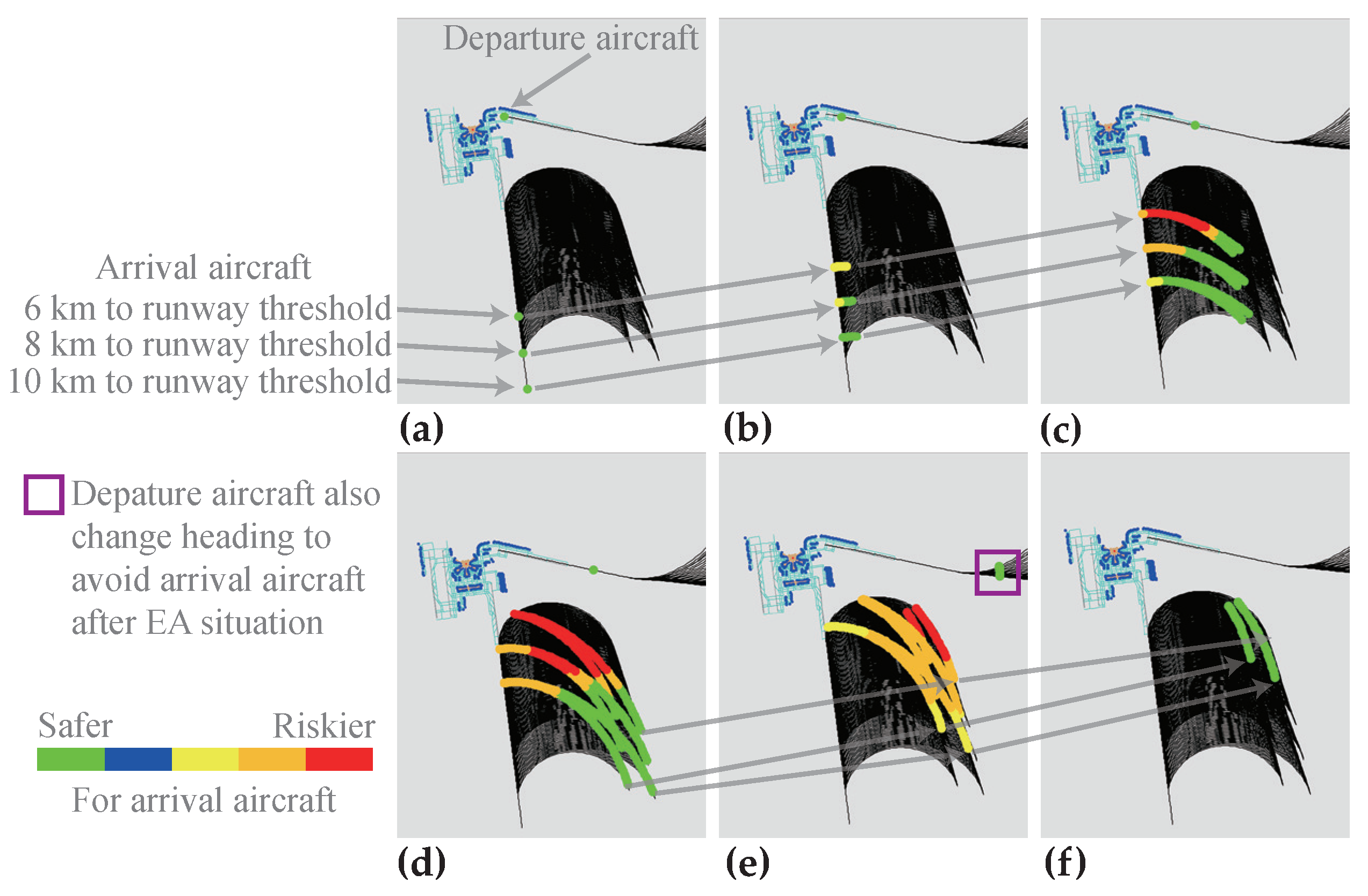
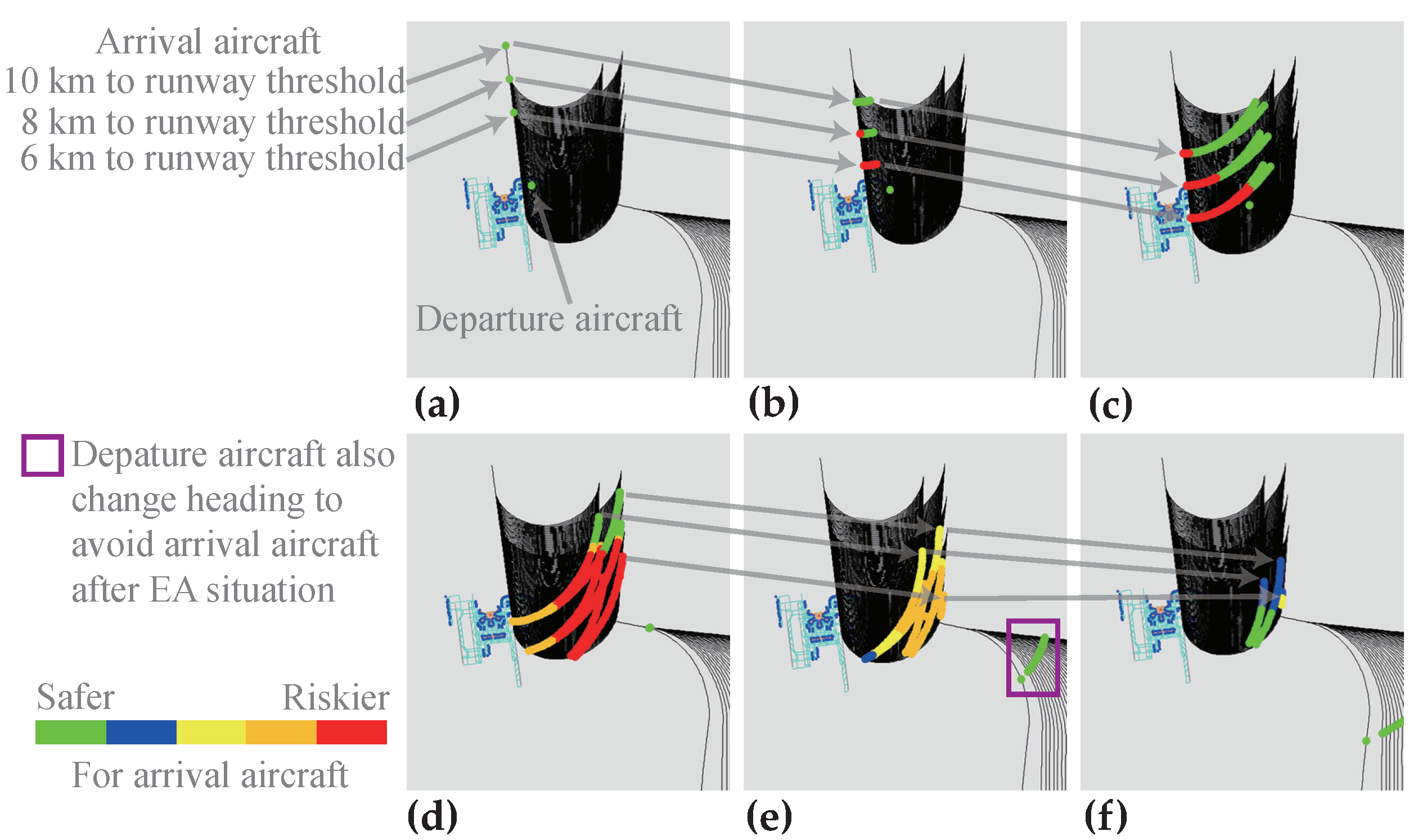
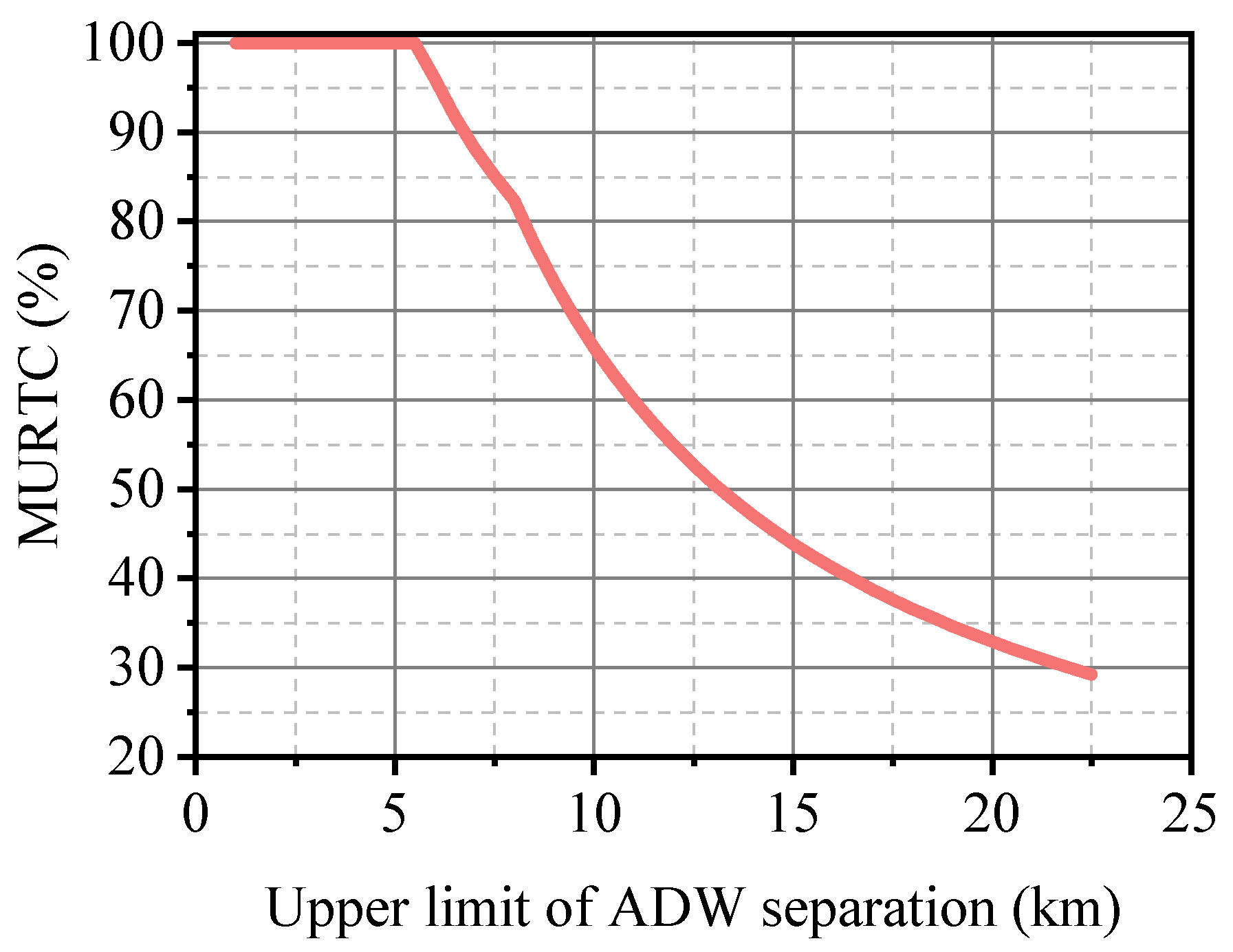
3.3. Result Analysis
4. Discussion and Conclusions
- A calculation method for EA incidence rate was proposed for airports where EA has never occurred. From the reliability perspective, the quantitative calculation determines the value of the EA incidence rate.
- The combination of computer simulation and CP calculation not only considers the complex representation of aircraft performance and control behavior, but also combines the mathematical method of probability analysis. A more accurate output result, close to the actual operation, can be ensured within a reasonable time range.
- Whether a collision occurs between aircraft is no longer based on whether the traditional standard geometric collision volumes (usual cuboids) intersect. Instead, this paper combined computer-aided 3D design [22] and other technologies to carry out high-precision digital 3D models of the aircraft’s shapes. The Boolean operations [25] of the constructive solid geometry were then used to more accurately analyze whether a collision between aircraft during the simulation process occurs. In the meantime, the calculation speed of 3D graphics operation was appropriately dealt with.
- The established models and methods were applied to the NID runway configuration of PKX. Then the influence of different range-type parameters on the ADW separation results was analyzed, providing a quantitative reference for policy-related or normative parameter constraints.
- Under the constraints of an EA maximum speed limit of 200 kt (102.9 m/s) and an EA minimum climb rate of 10%, PKX does not need to set ADW separation for northward operation, and the ADW separation for southward operation is from 3.2 km to 7.1 km. This result was approved by the Civil Aviation Administration of China and applied to PKX, significantly enhancing MURTC under the premise of satisfying TLS.
- Refining the parameter granularity of computer simulation, and analyzing the probability distribution of parameters related to aircraft performance and control behavior through the analysis of a large amount of historical data (such as actual trajectories, airborne equipment, and control voice records). Conducting real-life experiments with control simulators and flight simulators. This has extremely stringent requirements for the breadth and accuracy of data sources, and the data sources available at the time of writing were incapable of supporting such a level of data analysis.
- In this paper, the uncertainty of aircraft position was considered in the calculation of CP. However, methods like the Tunnel Gaussian Process [3] and others [4] can also calibrate the distribution of various aircraft performance parameters. Based on the probability distribution of each parameter, using the Monte Carlo simulation method to randomize each parameter’s value and repeatedly performing tens of billions or even hundreds of billions of simulation hours of deduction should be considered. In this way, the relationship between CP and TLS could be more rigorously demonstrated on the premise of satisfying statistical significance at the extremely small magnitude threshold of the accident rate. Such a large-scale and time-consuming simulation deduction necessitates the utilization of multiple high-performance computers, parallel computing [26], and cloud computing [27] in order to be completed in a reasonable amount of time.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| AIP | Aeronautical information publication |
| ADW | Arrival and departure window |
| ADWS | Arrival and departure window separation |
| CP | Collision probability |
| EA | Emergency avoidance |
| IAS | Indicated airspeed |
| ICAO | International Civil Aviation Organization |
| ISA | International standard atmosphere |
| MURTC | Maximum utilization of runway theoretical capacity |
| NAA | Number of arrival aircraft |
| NID | Non-intersecting diverging |
| PKX | Beijing Daxing Airport |
| TAS | True airspeed |
| TLS | Target level of safety |
References
- ICAO. Safety Management Manual; ICAO: Montreal, QC, Canada, 2018. [Google Scholar]
- ICAO. Operating Procedures and Practices for Regional Monitoring Agencies in Relation to the Use of a 300 m (1000 ft) Vertical Separation Minimum between FL 290 and FL 410 Inclusive; ICAO: Montreal, QC, Canada, 2010. [Google Scholar]
- Goh, S.K.; Singh, N.P.; Lim, Z.J.; Alam, S. Interpretable Tracking and Detection of Unstable Approaches Using Tunnel Gaussian Process. IEEE Trans. Aerosp. Electron. Syst. 2022; early access. [Google Scholar] [CrossRef]
- Singh, N.P.; Goh, S.K.; Alam, S. Real-time unstable approach detection using sparse variational gaussian process. In Proceedings of the 2020 International Conference on Artificial Intelligence and Data Analytics for Air Transportation (AIDA-AT), Singapore, 3–4 February 2020; pp. 1–10. [Google Scholar]
- Wang, L.; Zhong, L. Study on the method of dividing arrival-departure window for closely spaced parallel runway. Flight Dyn. 2020, 38, 18. [Google Scholar]
- Kullstam, P.A. Parallel Runway Spacing. Navigation 1972, 19, 19–28. [Google Scholar] [CrossRef]
- Hsu, D. The Evaluation of Aircraft Collision Probabilities at Intersecting Air Routes. J. Navig. 1981, 34, 78–102. [Google Scholar] [CrossRef]
- Blom, H.; Bakker, G.; Blanker, P.; Daams, J.; Everdij, M.; Klompstra, M. Accident Risk Assessment for Advanced ATM; National Aerospace Laboratory NLR: Rotterdam, The Netherlands, 1999. [Google Scholar]
- Campos, L.M.; Marques, J.M. On probabilistic risk of aircraft collision along air corridors. Aerospace 2021, 8, 31. [Google Scholar] [CrossRef]
- Mitici, M.; Blom, H.A.P. Mathematical Models for Air Traffic Conflict and Collision Probability Estimation. IEEE Trans. Intell. Transp. Syst. 2019, 20, 1052–1068. [Google Scholar] [CrossRef] [Green Version]
- Reich, P.G. Analysis of long-range air traffic systems: Separation standards—I. J. Navig. 1966, 19, 88–98. [Google Scholar] [CrossRef]
- Reich, P.G. Analysis of long-range air traffic systems: Separation standards—II. J. Navig. 1966, 19, 169–186. [Google Scholar] [CrossRef]
- Reich, P.G. Analysis of long-range air traffic systems: Separation standards—III. J. Navig. 1966, 19, 331–347. [Google Scholar] [CrossRef]
- Bakker, G.J.; Blom, H.A.P. Air Traffic Collision Risk Modelling. In Proceedings of the 32nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 15–17 December 1993; pp. 1464–1469. [Google Scholar] [CrossRef]
- Endoh, S. Aircraft Collision Models. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1982. [Google Scholar]
- Blom, H.A.; Krystul, J.; Bakker, G.; Klompstra, M.B.; Obbink, B.K. Free flight collision risk estimation by sequential MC simulation. In Stochastic Hybrid Systems; Taylor and Francis Group: Abingdon, UK, 2007; pp. 249–281. [Google Scholar]
- Matthews, R.A. The science of murphy’s law. Sci. Am. 1997, 276, 88–91. [Google Scholar] [CrossRef]
- Sulov, V. Iteration vs recursion in introduction to programming classes: An empirical study. Cybern. Inf. Technol. 2016, 16, 63–72. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.A.; Stoller, S.D. From recursion to iteration: What are the optimizations? In Proceedings of the 2000 ACM SIGPLAN Workshop on Partial Evaluation and Semantics-Based Program Manipulation, Boston, MA, USA, 22–23 January 1999; pp. 73–82. [Google Scholar]
- Gracey, W. Measurement of Aircraft Speed and Altitude; National Aeronautics and Space Administration Hampton Va Langley Research Center: Hampton, VA, USA, 1980. [Google Scholar]
- Cavcar, M. The international standard atmosphere. Anadolu Univ. Turk. 2000, 30, 1–6. [Google Scholar]
- Piegl, L.A. Ten challenges in computer-aided design. Comput.-Aided Des. 2005, 37, 461–470. [Google Scholar] [CrossRef]
- Stein, A.; Geva, E.; El-Sana, J. CudaHull: Fast parallel 3D convex hull on the GPU. Comput. Graph. 2012, 36, 265–271. [Google Scholar] [CrossRef]
- Tee, Y.Y.; Zhong, Z.W. Modelling and simulation studies of the runway capacity of Changi Airport. Aeronaut. J. 2018, 122, 1022–1037. [Google Scholar] [CrossRef]
- Zhou, Q.; Grinspun, E.; Zorin, D.; Jacobson, A. Mesh arrangements for solid geometry. ACM Trans. Graph. TOG 2016, 35, 39. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.L.; Sun, G.Z.; Zhang, Y.Q.; Mo, Z.Y. Study on parallel computing. J. Comput. Sci. Technol. 2006, 21, 665–673. [Google Scholar] [CrossRef]
- Surbiryala, J.; Rong, C.; Soc, I.C. Cloud Computing: History and Overview. In Proceedings of the 3rd IEEE International Conference on Cloud and Fog Computing Technologies and Applications (IEEE Cloud Summit), Washington, DC, USA, 8–10 August 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Khallouli, W.; Huang, J. Cluster resource scheduling in cloud computing: Literature review and research challenges. J. Supercomput. 2021, 78, 6898–6943. [Google Scholar]

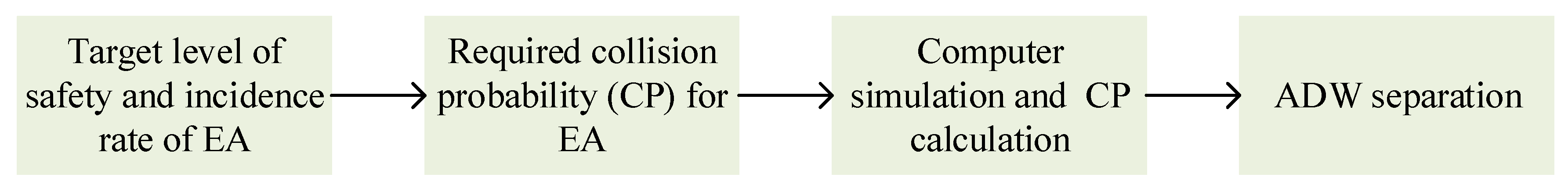
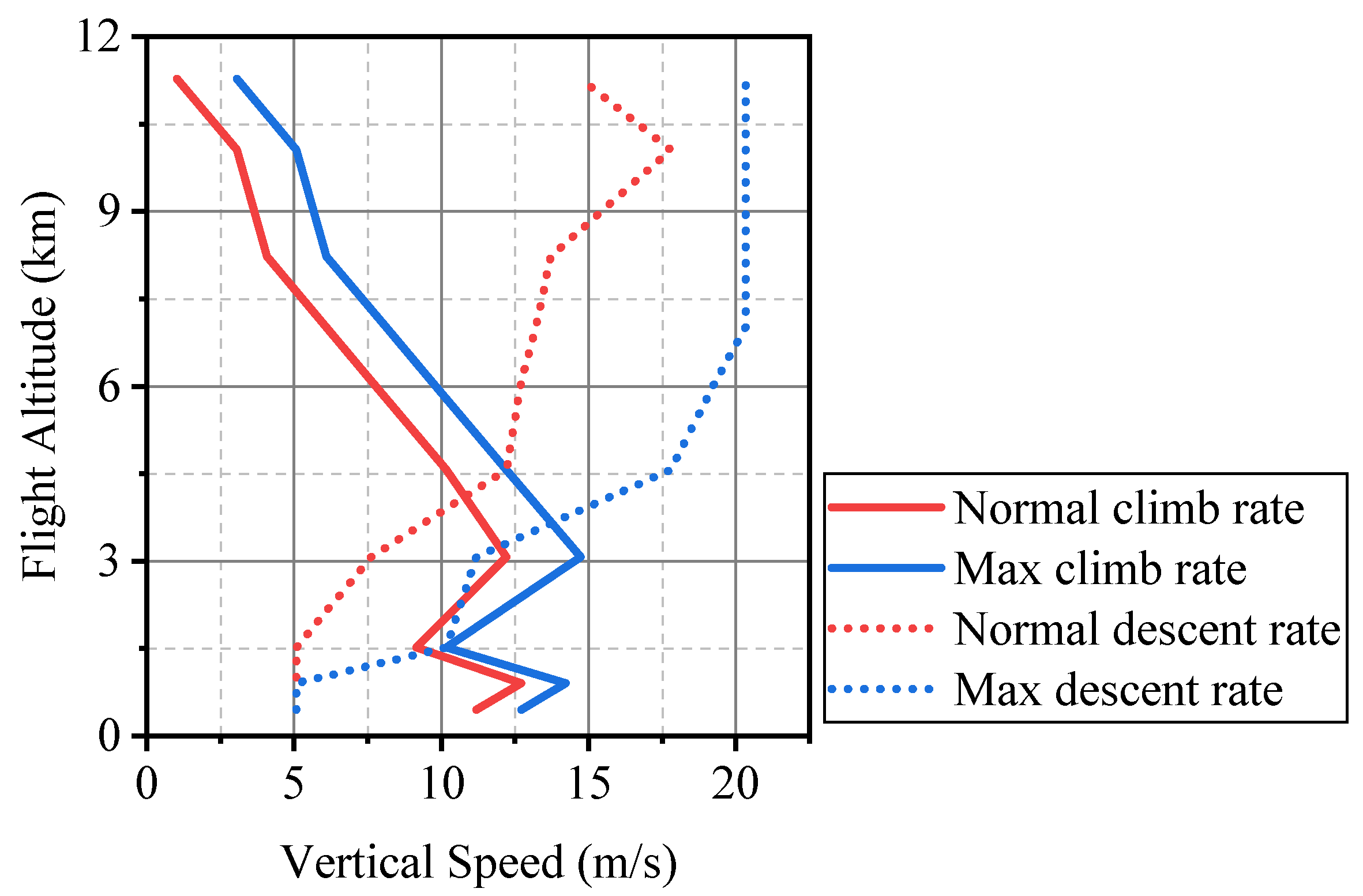


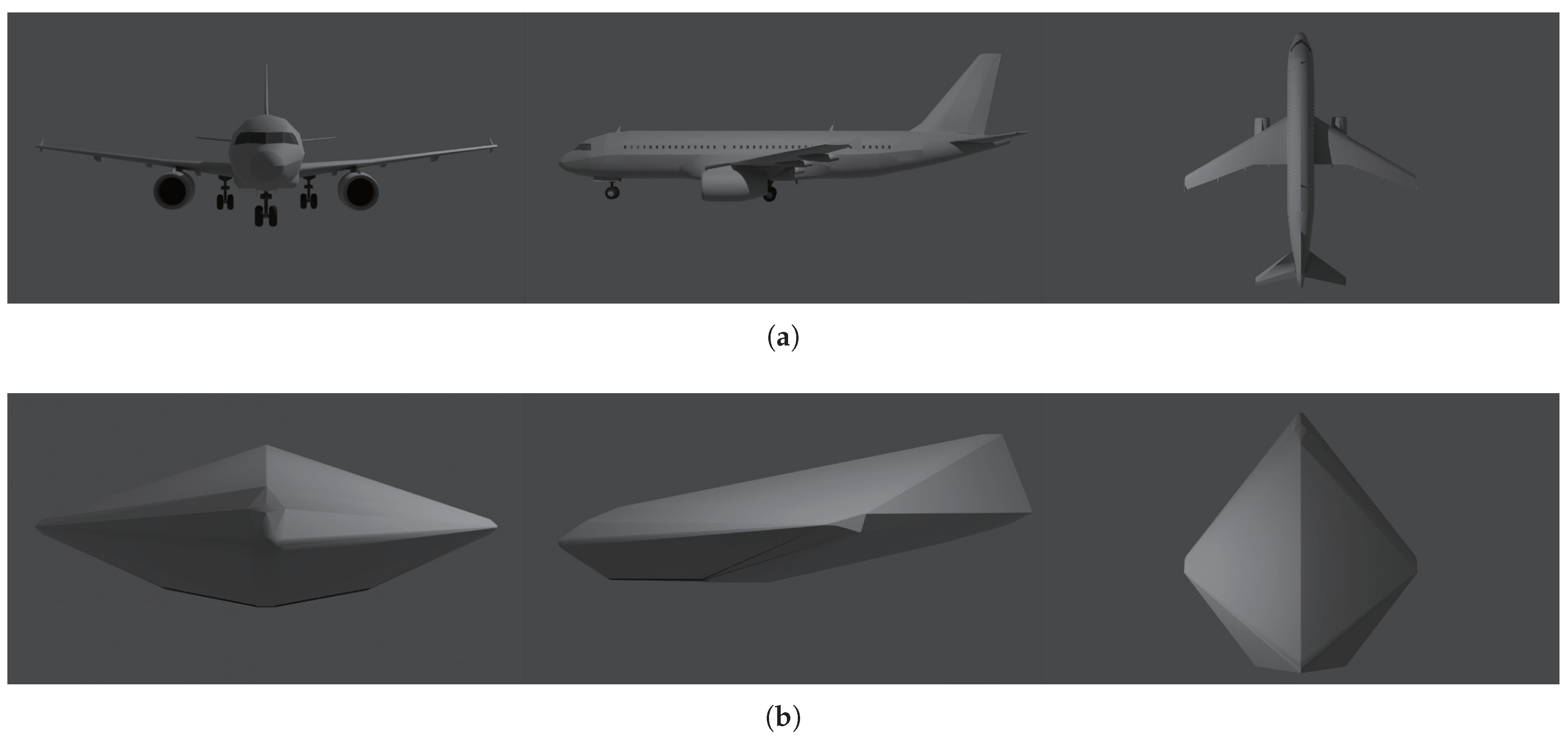



| Description | Parameter | Source |
|---|---|---|
| Acceleration of take-off roll | 1.7 m/s to 2.5 m/s | Historical data analysis, expert experience |
| Acceleration from the lift-off of the aircraft to the retraction of the landing gear | 0.8 m/s | Historical data analysis, expert experience |
| Acceleration after retracting the landing gear | 1.2 m/s | Historical data analysis, expert experience |
| Normal departure climb gradient | 4.5% | AIP data |
| Description | Parameter | Source |
|---|---|---|
| Maximum speed limit under EA situation | 200 kt (102.9 m/s) or 230 kt (118.3 m/s) | Procedure design specifications, expert experience |
| Duration of controller’s command to arrival aircraft under EA situation | 8 s | Expert experience |
| Duration of pilot read-back command of arrival aircraft under EA situation | 4 s | Expert experience |
| Duration from the time the pilot begins operating the arrival aircraft until the aircraft begins to change the attitude | 8 s | Expert experience |
| Turn slope under EA situation | 25° | Procedure design specifications, expert experience |
| Climb rate under EA situation | 0.0% to 20.0% | Expert experience |
| Acceleration under EA situation | 1.2 m/s | Historical data analysis, expert experience |
| Normal approach glide angle | 3° | AIP data |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Hu, M.; Zhao, Z.; Hu, Y.; Peng, Y. Non-Intersecting Diverging Runways Separation under Emergency Avoidance Situation. Aerospace 2023, 10, 131. https://doi.org/10.3390/aerospace10020131
Li C, Hu M, Zhao Z, Hu Y, Peng Y. Non-Intersecting Diverging Runways Separation under Emergency Avoidance Situation. Aerospace. 2023; 10(2):131. https://doi.org/10.3390/aerospace10020131
Chicago/Turabian StyleLi, Changcheng, Minghua Hu, Zheng Zhao, Yuxin Hu, and Ying Peng. 2023. "Non-Intersecting Diverging Runways Separation under Emergency Avoidance Situation" Aerospace 10, no. 2: 131. https://doi.org/10.3390/aerospace10020131
APA StyleLi, C., Hu, M., Zhao, Z., Hu, Y., & Peng, Y. (2023). Non-Intersecting Diverging Runways Separation under Emergency Avoidance Situation. Aerospace, 10(2), 131. https://doi.org/10.3390/aerospace10020131







