Effects of Inlet Swirl Distortion on a Multi-Stage Compressor with Inlet Guide Vanes and Stall Margin Enhancement Method
Abstract
:1. Introduction
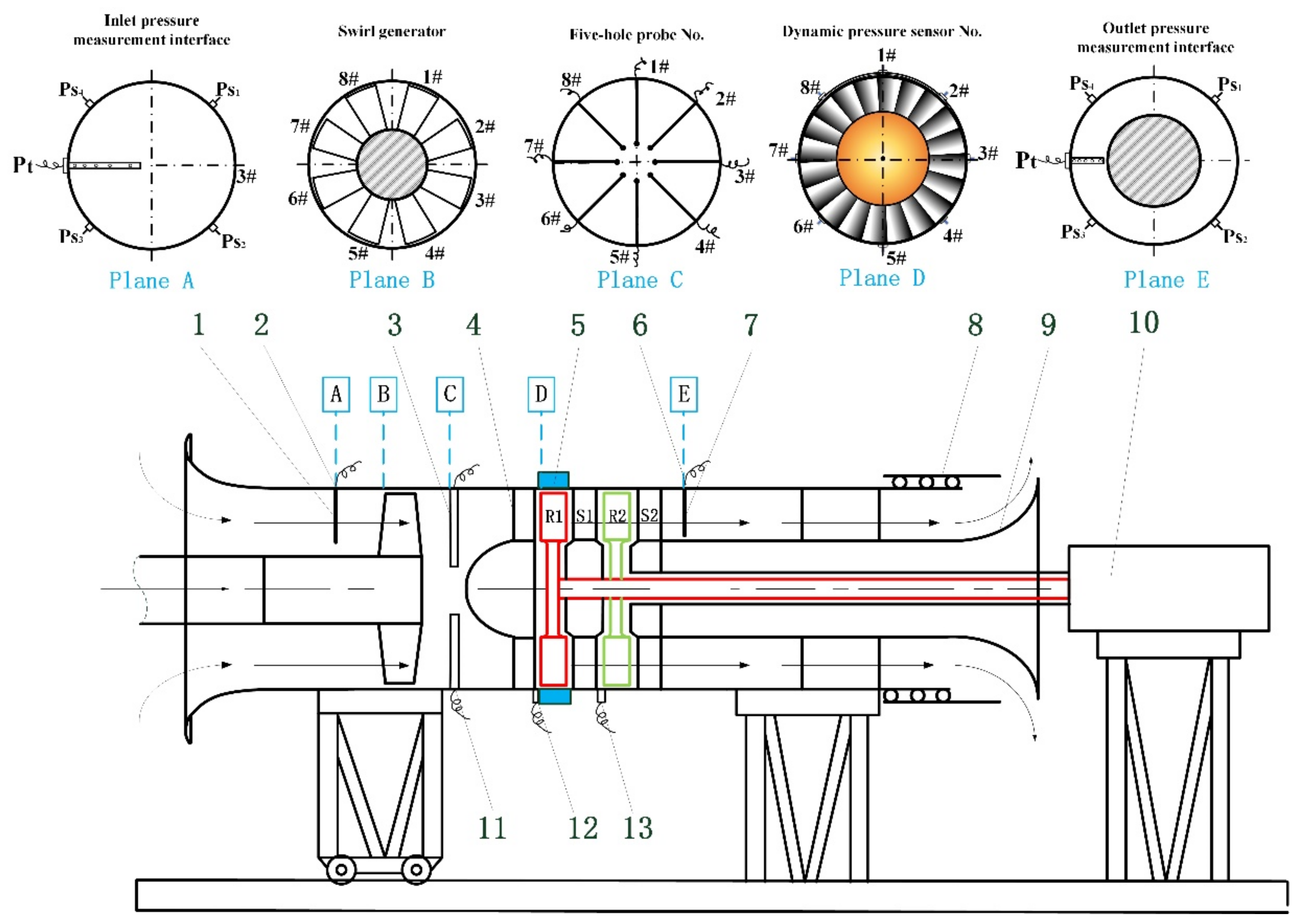
2. Experimental Facility and Sensors Equipment
2.1. Two-Stage Compressor TA66
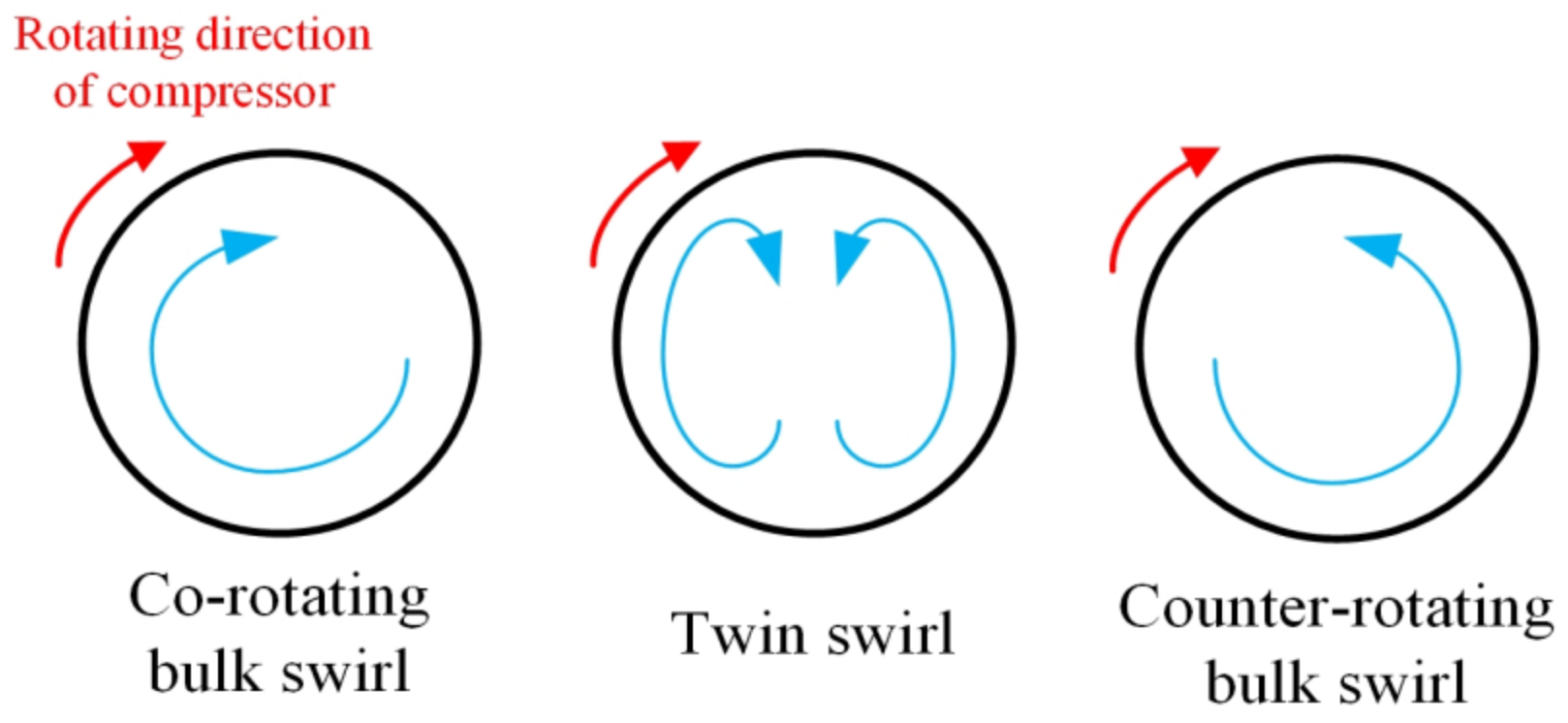
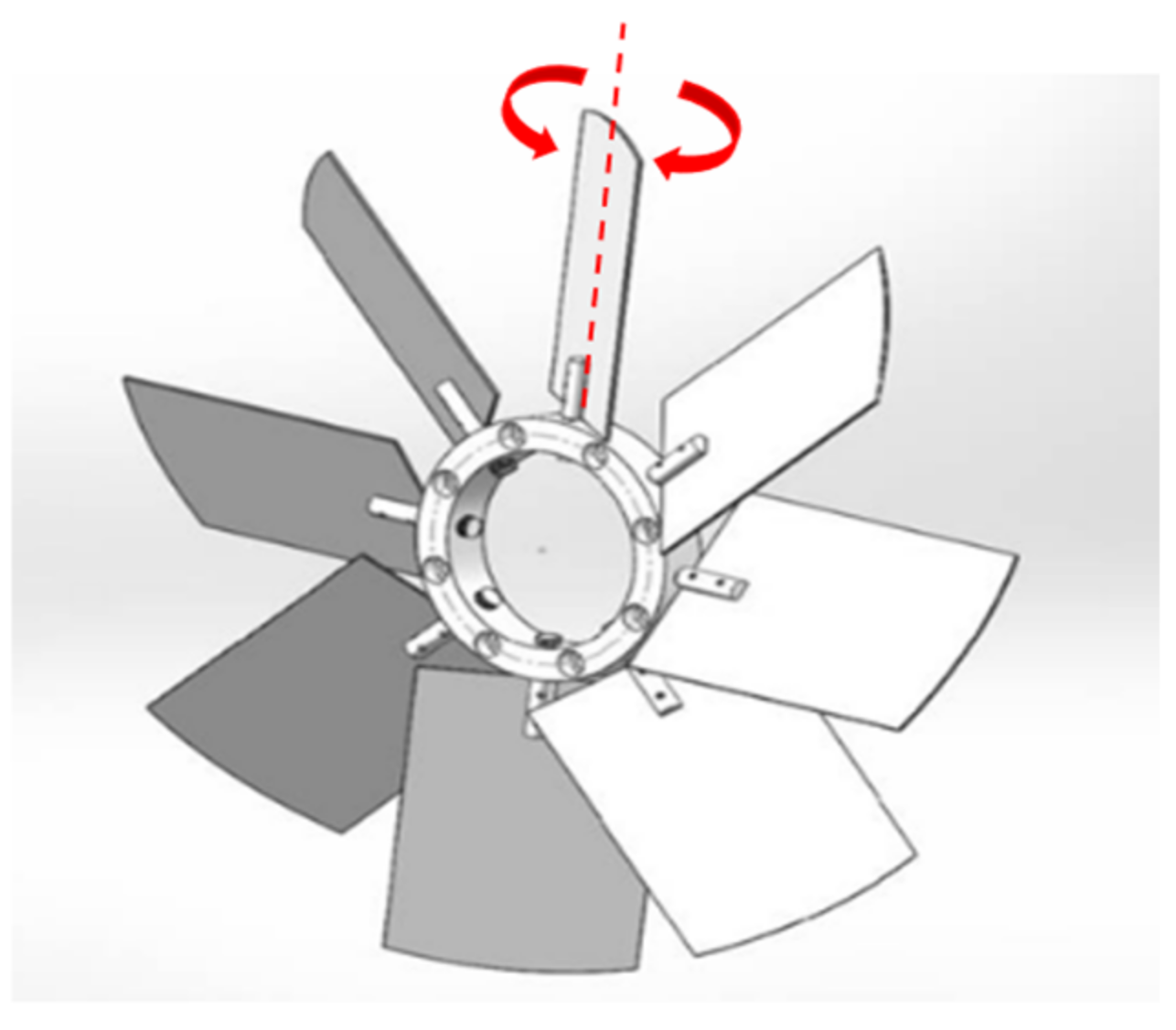
2.2. Swirl Distortion Generator
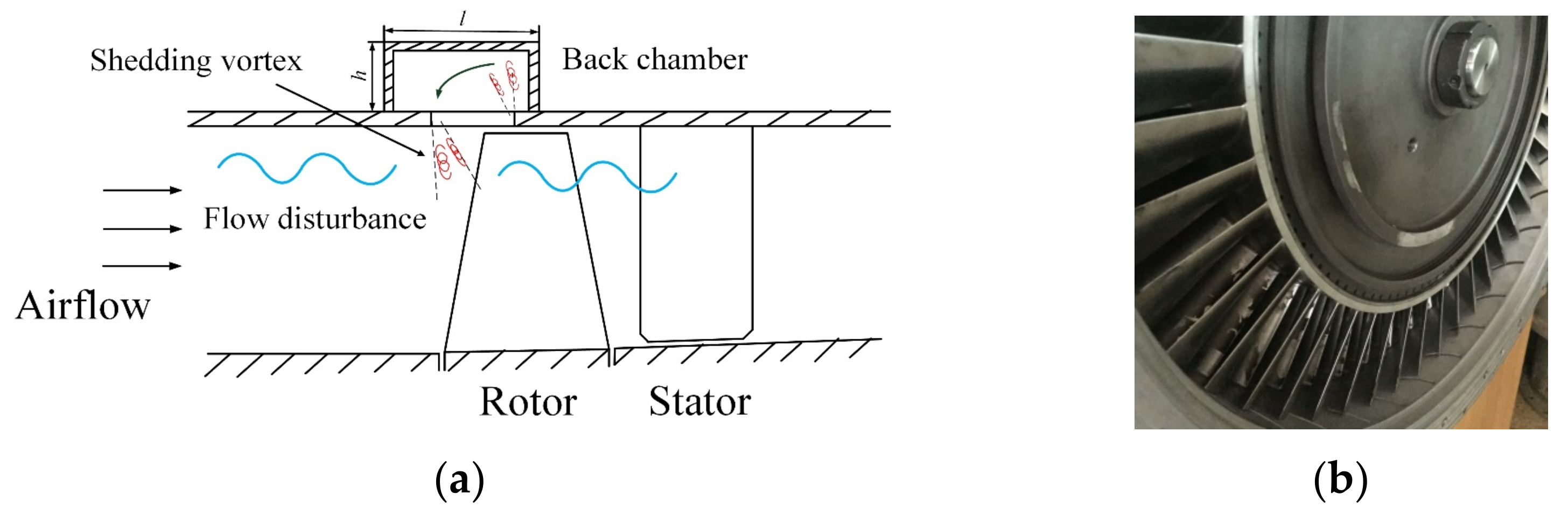
2.3. Stall Precursor-Suppressed (SPS) Casing Treatment
3. Experimental Results
3.1. Physical Parameters
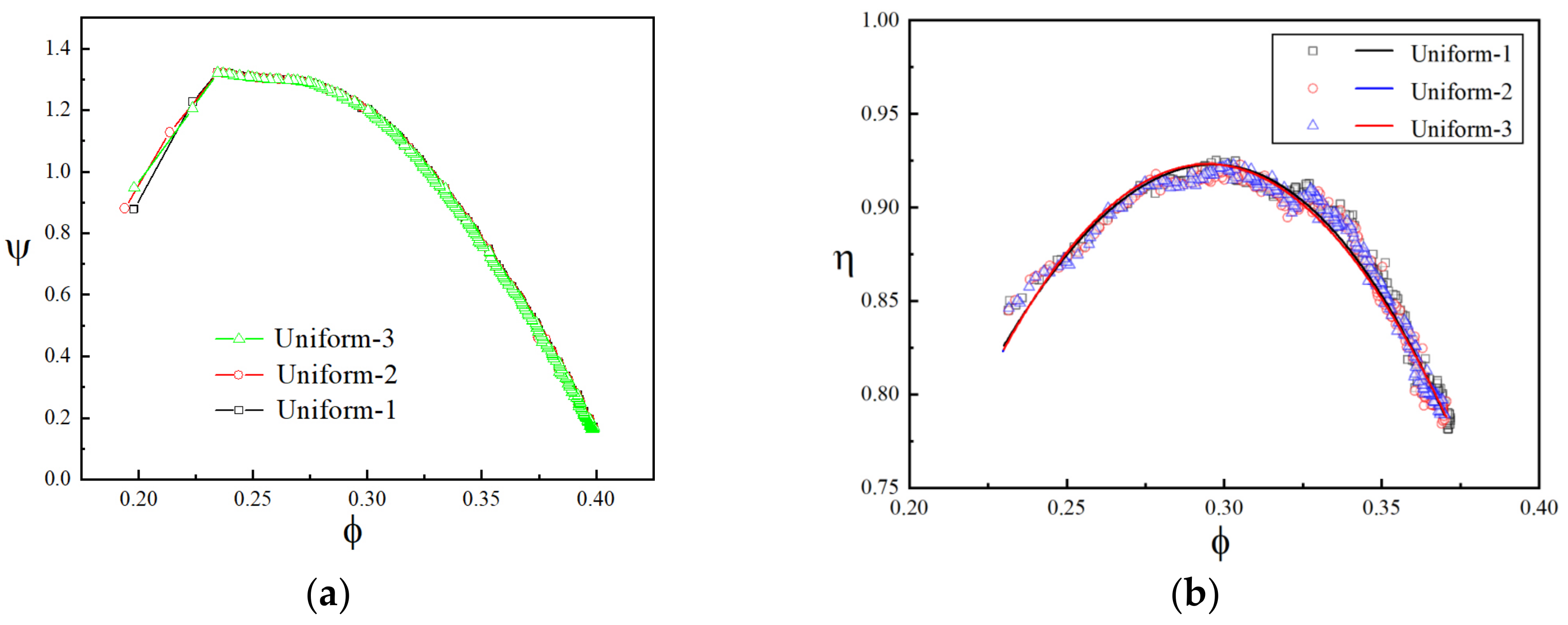
3.2. Experimental Repeatability
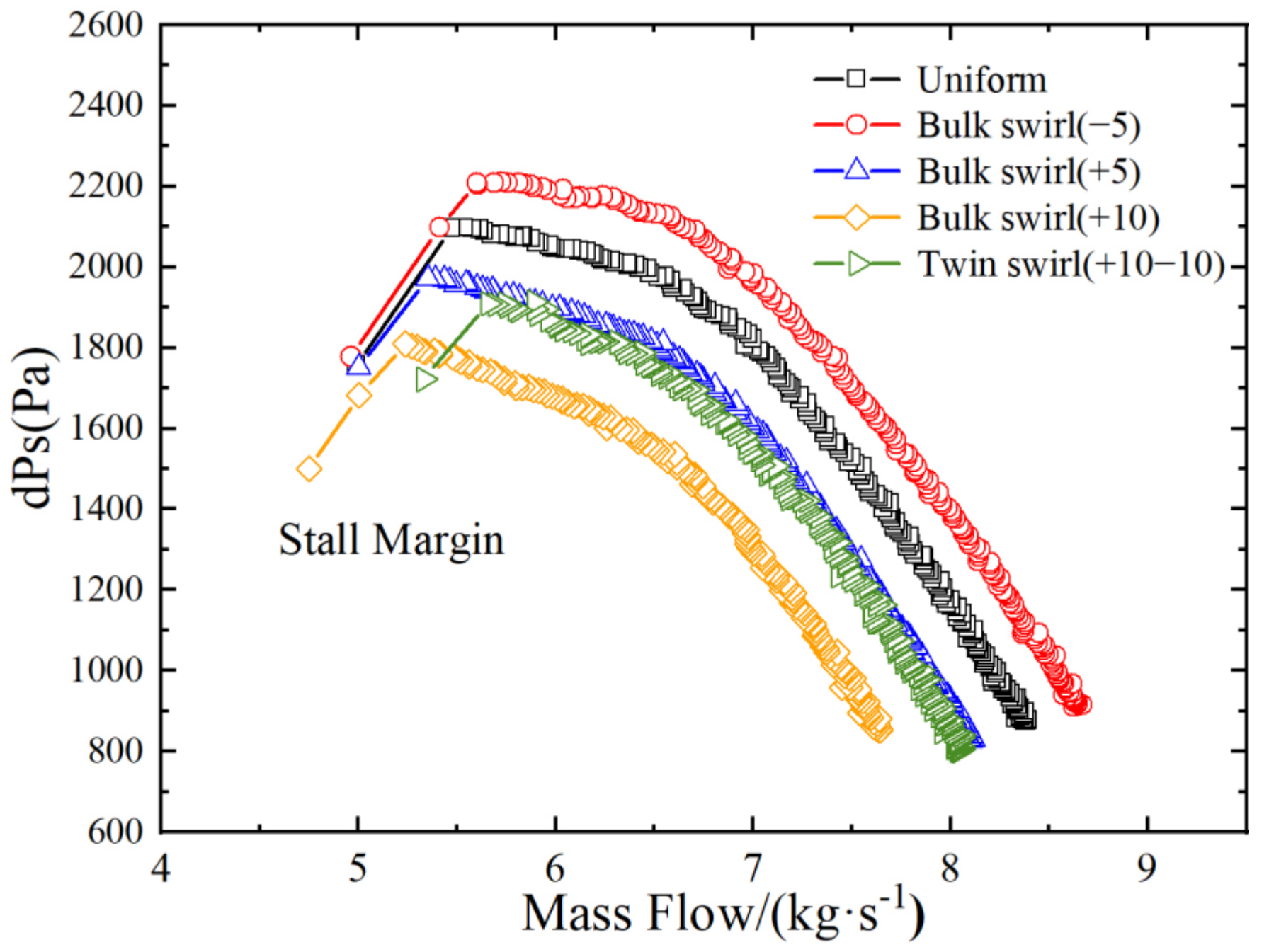
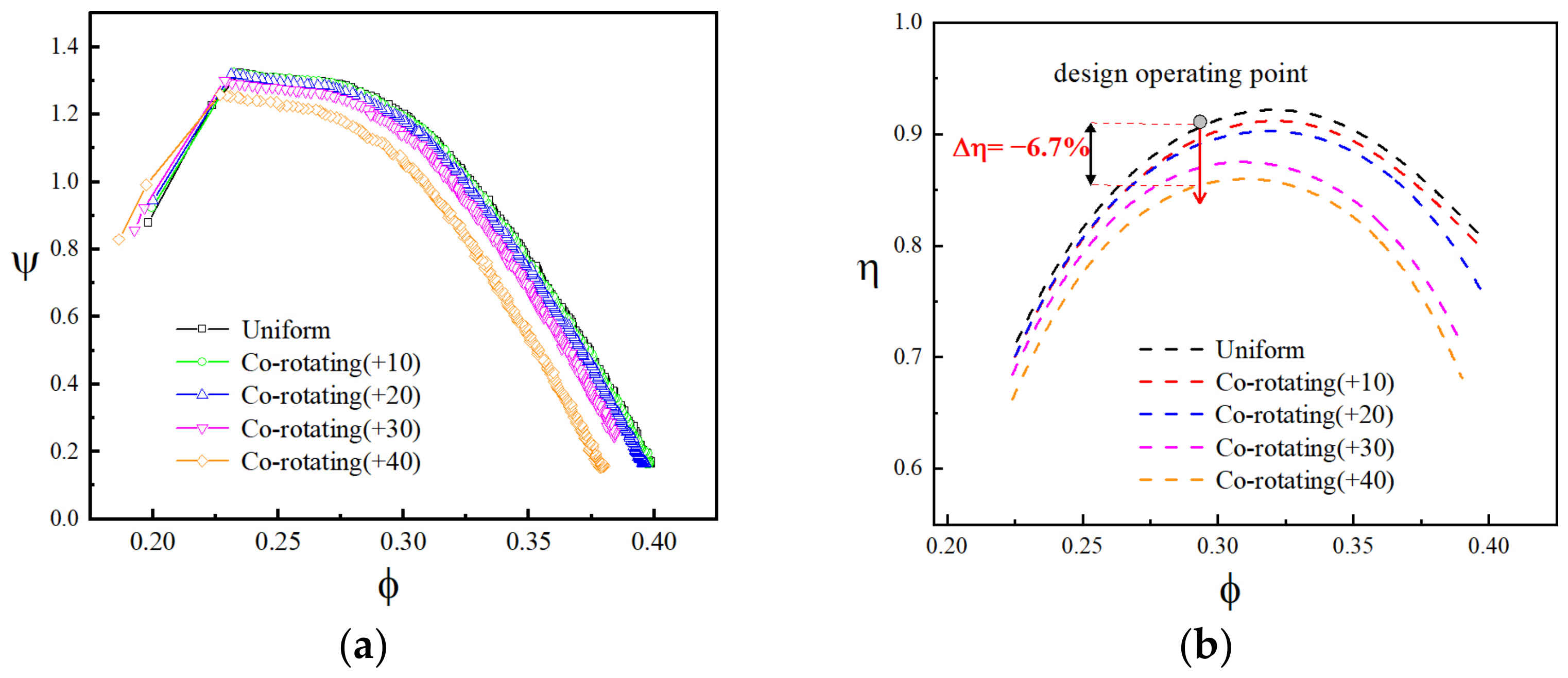
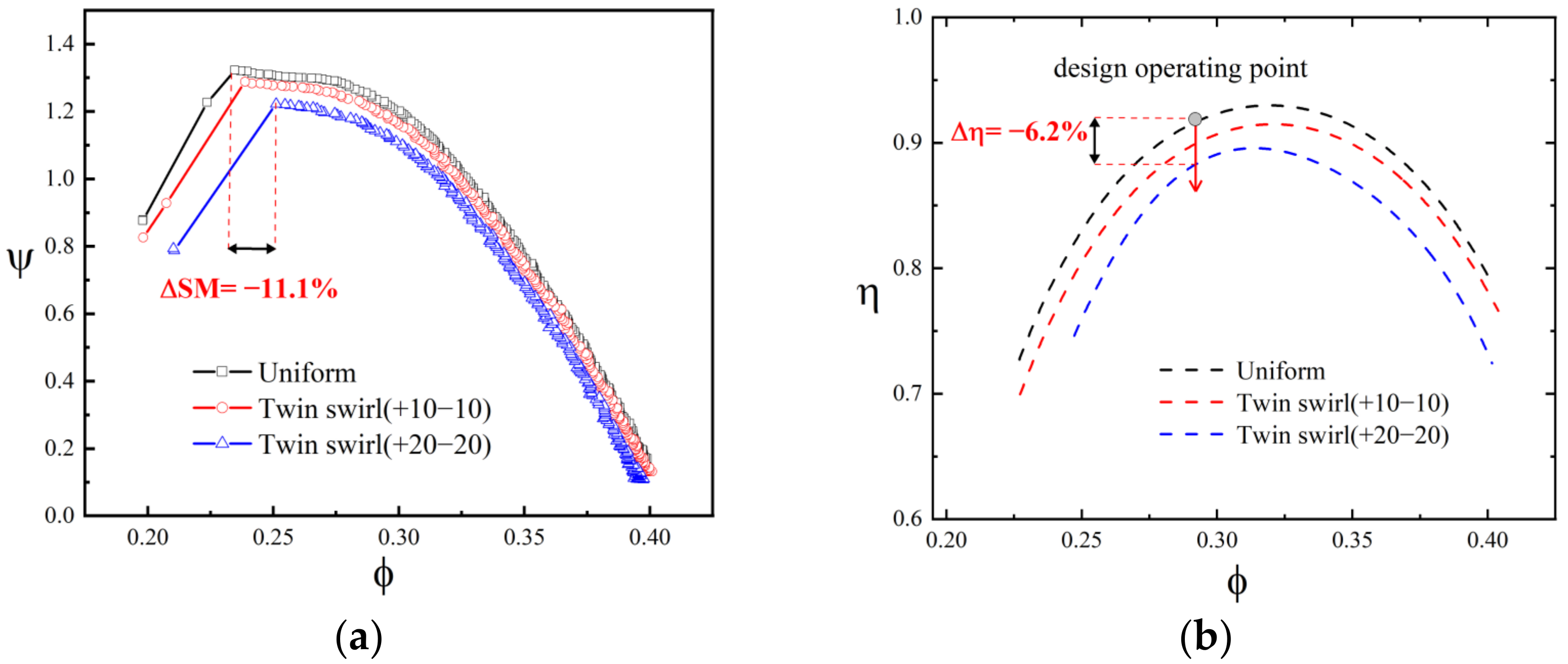
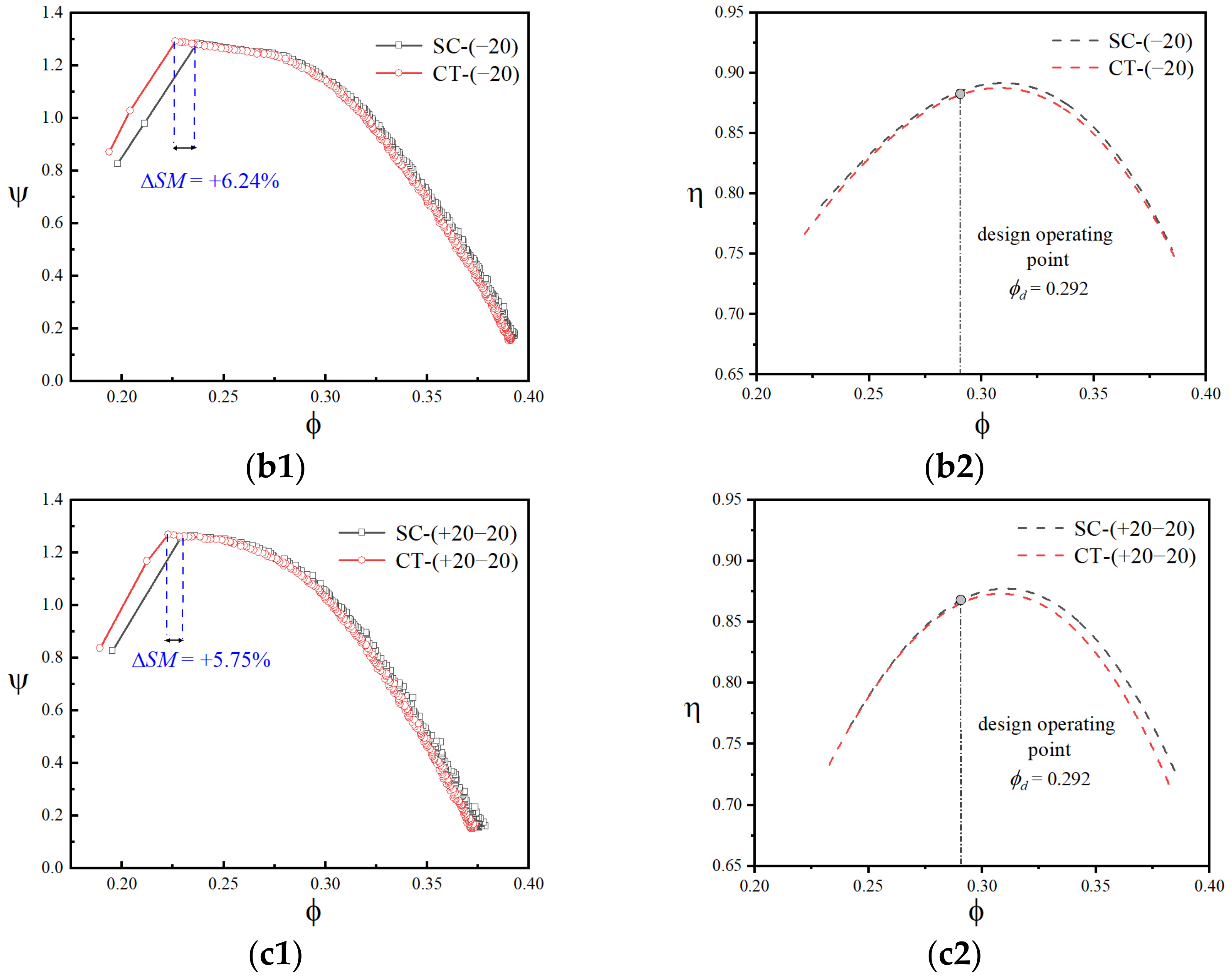
3.3. The Influence of Inlet Swirl Distortion on the TA66 with an IGV
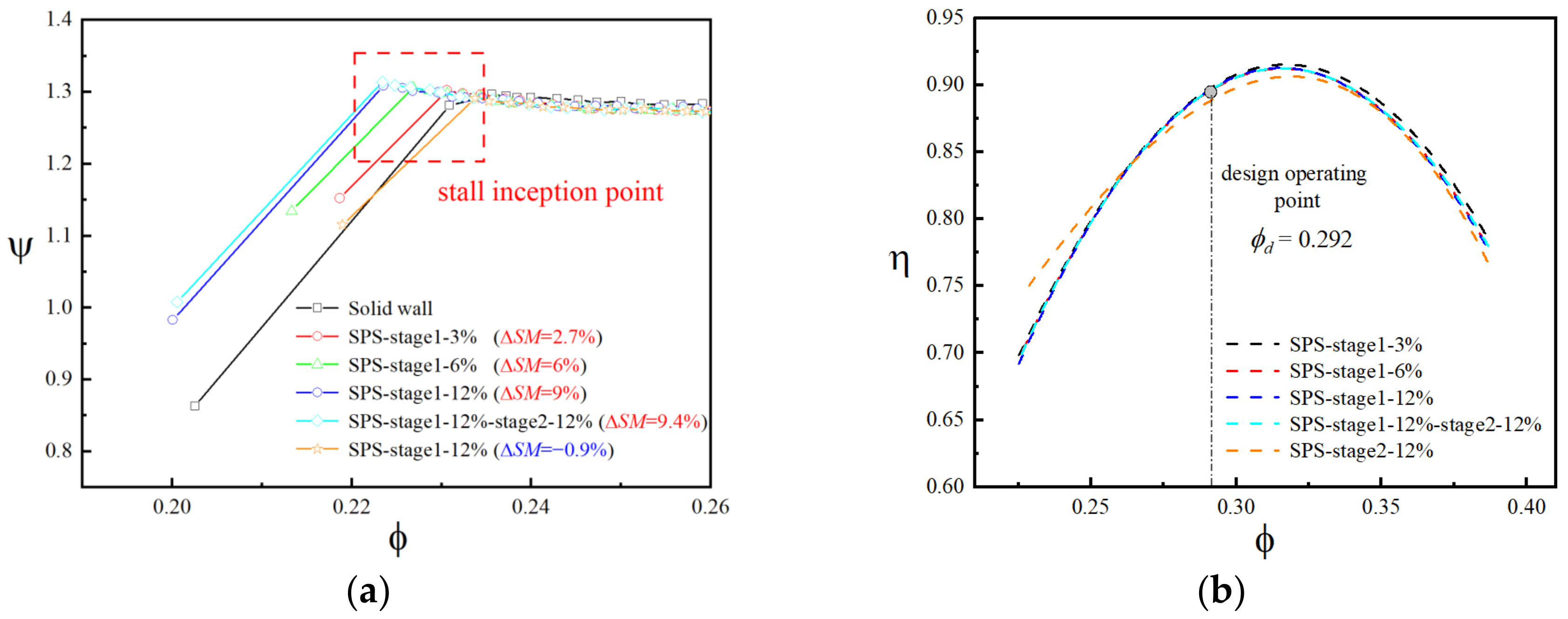
3.4. Stall Margin Enhancement of SPS Casing Treatment
4. Conclusions
- (1)
- For the multi-stage compressor with an IGV installed, under the inlet bulk swirl distortion with low intensity, there was almost no negative influence on the compressive capability and stall margin of the compressor. When the distortion intensity further increased, there was still a decrease in the compressive capability and obvious additional efficiency loss.
- (2)
- Under the inlet twin swirl distortion, even with the installation of an IGV, there still existed a significantly negative influence on the multi-stage compressor, especially the stall margin. This might have been caused by the accompanying total pressure distortion induced by the twin swirl flow. The inlet twin swirl distortion could be avoided by adjusting the geometric parameters of the S-duct in engineering.
- (3)
- The best strategy for the installation of SPS casing treatment is to install it in the first stage to guarantee sufficient stall margin improvement and minimum efficiency loss. In this way, it can improve the stall margin of the compressor with no change in the characteristic curves and no additional efficiency loss under various types of inlet swirl distortions.
- (4)
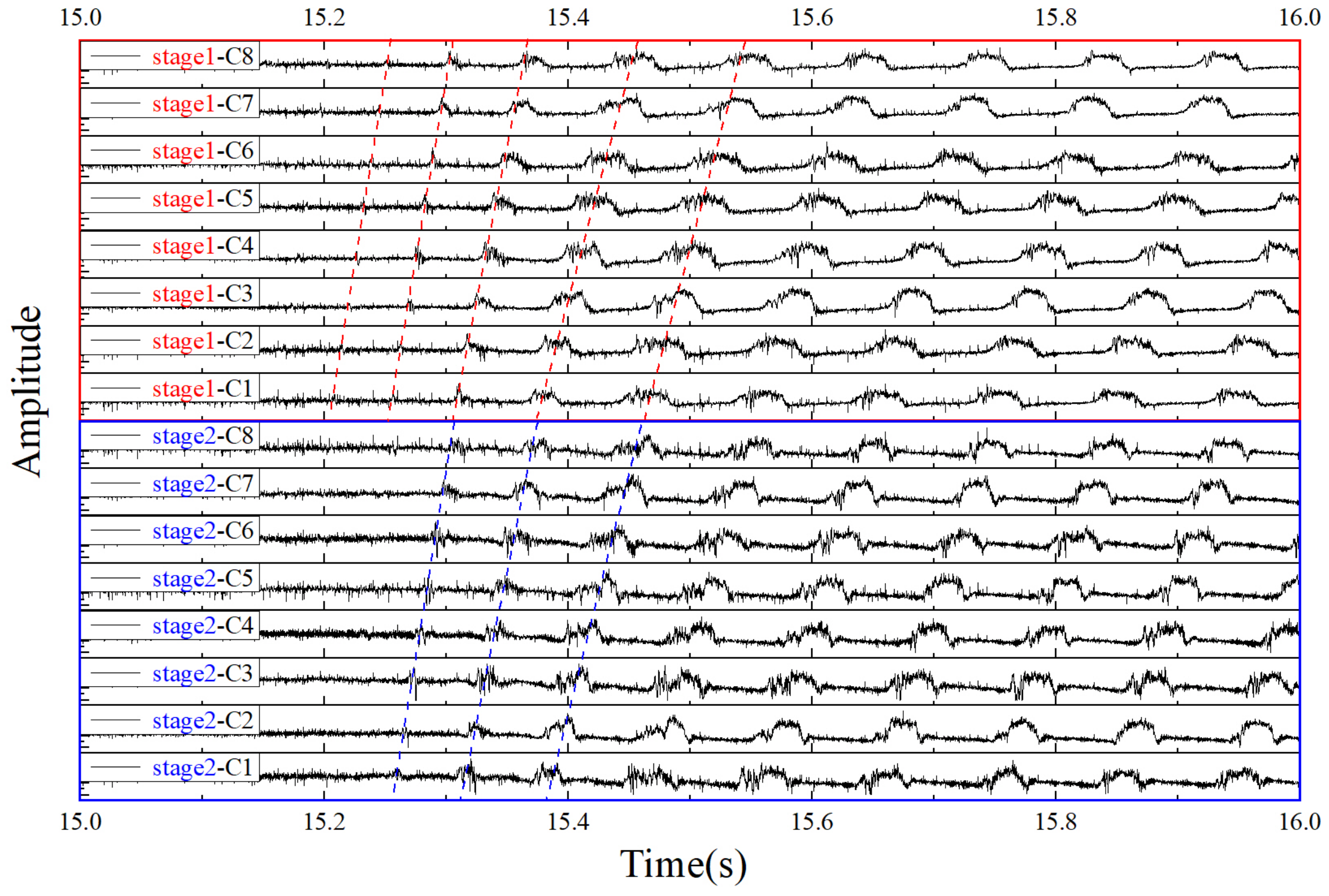
- The mechanism of SPS casing treatment was verified by the dynamic pressure signals and PSD analysis to absorb the pressure perturbation energy and suppress the nonlinear amplification of the pressure perturbation, including the stall precursors, to delay the occurrence of rotating stall.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goldsmith, E.L. Intake Aerodynamics; Blackwell Science: Oxford, UK, 1985. [Google Scholar]
- Manas, M.P.; Pradeep, A.M. Stall Inception in a Contra-Rotating Fan under Radially Distorted Inflows. Aerosp. Sci. Technol. 2020, 105, 105909. [Google Scholar] [CrossRef]
- Tamaki, T.; Nagano, S. Effects of Inlet Distortions on a Multi-Stage Compressor<149>transonic Flow Pressure Distortion. In Proceedings of the AIAA 4th International Symposium on Air Breathing Engines, Orlando, FL, USA, 1–6 April 1979. [Google Scholar]
- Gil-Prieto, D.; Zachos, P.K.; MacManus, D.G.; McLelland, G. Unsteady Characteristics of S-Duct Intake Flow Distortion. Aerosp. Sci. Technol. 2019, 84, 938–952. [Google Scholar] [CrossRef]
- Stocks, C.P.; Bissinger, N.C. Design and Development of the Tornado Engine Air Intake. In Proceedings of the AGARD Conference Proceedings, Turin, Italy, 29 September–3 October 1981. [Google Scholar]
- Sheoran, Y.; Bouldin, B.; Krishnan, P.M. Compressor Performance and Operability in Swirl Distortion. J. Turbomach. 2011, 134, 1–13. [Google Scholar] [CrossRef]
- Kapoor, K.; Anderson, B.; Reddy, D. A Comparative Study of Full Navier-Stokes and Reduced Navier-Stokes Analyses for Separating Flows within a Diffusing Inlet S-Duct. In Proceedings of the 29th Joint Propulsion Conference and Exhibit, Monterey, CA, USA, 28–30 June 1993. [Google Scholar]
- Anderson, B.H.; Reddy, D.R.; Kapoor, K. Study on Computing Separating Flows within a Diffusion Inlet S-Duct. J. Propuls. Power 1994, 10, 661–667. [Google Scholar] [CrossRef]
- Verma, A.; Jang, H.; Mahesh, K. The Effect of an Upstream Hull on a Propeller in Reverse Rotation. J. Fluid Mech. 2012, 704, 61–88. [Google Scholar] [CrossRef]
- Milidonis, K.; Semlitsch, B.; Hynes, T. Effect of Clocking on Compressor Noise Generation. AIAA J. 2018, 56, 4225–4231. [Google Scholar] [CrossRef]
- Inlet, A.; Distortion, S. AIR5686—A Methodology for Assessing Inlet Swirl Distortion; SAE International: Warrendale, PA, USA, 2017. [Google Scholar] [CrossRef]
- Pazur, W.; Fottner, L. The Influence of Inlet Swirl Distortions on the Performance of a Jet Propulsion Two-Stage Axial Compressor. J. Turbomach. 1991, 113, 233. [Google Scholar] [CrossRef]
- Schmid, N.R.; Leinhos, D.C.; Fottner, L. Steady Performance Measurements of a Turbofan Engine with Inlet Distortions Containing Co- And Counterrotating Swirl from an Intake Diffuser for Hypersonic Flight. J. Turbomach. 2001, 123, 379–385. [Google Scholar] [CrossRef]
- Rademakers, R.P.M.; Bindl, S.; Niehuis, R. Effects of Flow Distortions as They Occur in S-Duct Inlets on the Performance and Stability of a Jet Engine. J. Eng. Gas Turbines Power 2016, 138, 1–10. [Google Scholar] [CrossRef]
- Dong, X.; Sun, D.; Li, F.; Jin, D.; Gui, X.; Sun, X. Effects of Stall Precursor-Suppressed Casing Treatment on a Low-Speed Compressor with Swirl Distortion. J. Fluids Eng. Trans. ASME 2018, 140, 1091–1101. [Google Scholar] [CrossRef]
- Sheoran, Y.; Bouldin, B. A Versatile Design of a Controlled Swirl Distortion Generator for Testing Gas Turbine Engines. In Proceedings of the ASME Turbo Expo, Berlin, Germany, 9–13 June 2008; Volume 1, pp. 81–92. [Google Scholar]
- Sheoran, Y.; Bouldin, B.; Krishnan, P.M. Advancements in the Design of an Adaptable Swirl Distortion Generator for Testing Gas Turbine Engines. In Proceedings of the ASME Turbo Expo, Orlando, FL, USA, 8–12 June 2009; Volume 1, pp. 23–32. [Google Scholar]
- Chue, R.; Hynes, T.P.; Greitzer, E.M.; Tan, C.S.; Longley, J.P. Calculations of Inlet Distortion Induced Compressor Flow Field Instability. Int. J. Heat Fluid Flow 1989, 10, 211–223. [Google Scholar] [CrossRef]
- Greitzer, E.M.; Moore, F.K. A Theory of Post-Stall Transients in Axial Compression Systems: Part II—Application. J. Eng. Gas Turbines Power 1986, 108, 68–76. [Google Scholar] [CrossRef]
- Dong, X.; Sun, D.; Li, F.; Sun, X. Stall Margin Enhancement of a Novel Casing Treatment Subjected to Circumferential Pressure Distortion. Aerosp. Sci. Technol. 2018, 73, 239–255. [Google Scholar] [CrossRef]
- Takata, H.; Tsukuda, Y. Stall Margin Improvement by Casing Treatment—Its Mechanism and Effectiveness. J. Eng. Power Trans. ASME 1977, 99, 121–133. [Google Scholar] [CrossRef]
- Kroeckel, T.; Hiller, S.J.; Jeschke, P. Application of a Multistage Casing Treatment in a High Speed Axial Compressor Test Rig. In Proceedings of the Proceedings of the ASME Turbo Expo, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Sun, D.; Liu, X.; Jin, D.; Gui, X.; Sun, X. Theory of Compressor Stability Enhancement Using Novel Casing Treatment, Part II: Experiment. J. Propuls. Power 2014, 30, 1236–1247. [Google Scholar] [CrossRef]
- Sun, X.; Sun, D.; Liu, X.; Yu, W.; Wang, X. Theory of Compressor Stability Enhancement Using Novel Casing Treatment, Part I: Methodology. J. Propuls. Power 2014, 30, 1224–1235. [Google Scholar] [CrossRef]
- Dong, X.; Sun, D.; Li, F.; Jin, D.; Gui, X.; Sun, X. Effects of Rotating Inlet Distortion on Compressor Stability with Stall Precursor-Suppressed Casing Treatment. J. Fluids Eng. Trans. ASME 2015, 137, 1–15. [Google Scholar] [CrossRef]
- McDougall, N.M.; Cumpsty, N.A.; Hynes, T.P. Stall Inception in Axial Compressors. J. Turbomach. 1990, 112, 116–123. [Google Scholar] [CrossRef]
- Hoopes, K.M.; O’Brien, W.F. The Streamvane© Method: A New Way to Generate Swirl Distortion for Jet Engine Research. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013; pp. 1–11. [Google Scholar] [CrossRef]
- Frohnapfel, D.J.; Todd Lowe, K.; O’Brien, W.F. Experimental Quantification of Fan Rotor Effects on Inlet Swirl Using Swirl Distortion Descriptors. J. Eng. Gas Turbines Power 2018, 140, 1–8. [Google Scholar] [CrossRef]
- Wellborn, S.R.; Wellborn, B.A.; Okiishi, T.H. Study of the Compressible Flow in a Diffusing S-Duct. J. Propuls. Power 1994, 10, 668–675. [Google Scholar] [CrossRef]
- Williams, J.E.F. Review Lecture—Anti-Sound. Proc. R. Soc. London. A. Math. Phys. Sci. 1984, 395, 63–88. [Google Scholar] [CrossRef]
- Jing, X.; Sun, X. Effect of Plate Thickness on Impedance of Perforated Plates with Bias Flow. AIAA J. 2000, 38, 1573–1578. [Google Scholar] [CrossRef]
- Wetgt, H.J.; Paduano, J.D.; Fréchette, L.G.; Epstein, A.H.; Greitzer, E.M.; Bright, M.M.; Strazisar, A.J. Active Stabilization of Rotating Stall and Surge in a Transonic Single Stage Axial Compressor. In Proceedings of the ASME Turbo Expo, Orlando, FL, USA, 2–5 June 1997; Volume 4. [Google Scholar]
- Jing, X.; Wang, X.; Sun, X. Broadband Acoustic Liner Based on the Mechanism of Multiple Cavity Resonance. AIAA J. 2007, 45, 2429–2437. [Google Scholar] [CrossRef]




| Structural parameters | |||||
| IGV | 1-Rotor | 1-Stator | 2-Rotor | 2-Stator | |
| Blade number | 38 | 47 | 45 | 47 | 45 |
| Installation angle with axis direction | 0° | 60° | 10° | 60° | 10° |
| Diameter (mm) | 600 | ||||
| Aspect ratio | 1.69 | ||||
| Blade ratio | 0.7 | ||||
| Performance parameters at the operating point | |||||
| Mass rate (kg/s) | 7.25 | Rotating speed (rpm) | 3000 | ||
| Flow coefficient | 0.267 | Pressure rise coefficient | 1.176 | ||
| Rated power (kW) | 16 | Efficiency | 0.92 | ||
| Pressure ratio | 1.056 | Static pressure rise (Pa) | 4600 | ||
| Tip clearance (mm) | 0.6–0.8 | Tangential velocity at blade tip (m/s) | 94.2 | ||
| Rotor–stator gap (mm) | 8–20 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Sun, D.; Dong, X.; Sun, X. Effects of Inlet Swirl Distortion on a Multi-Stage Compressor with Inlet Guide Vanes and Stall Margin Enhancement Method. Aerospace 2023, 10, 141. https://doi.org/10.3390/aerospace10020141
Fang Y, Sun D, Dong X, Sun X. Effects of Inlet Swirl Distortion on a Multi-Stage Compressor with Inlet Guide Vanes and Stall Margin Enhancement Method. Aerospace. 2023; 10(2):141. https://doi.org/10.3390/aerospace10020141
Chicago/Turabian StyleFang, Yibo, Dakun Sun, Xu Dong, and Xiaofeng Sun. 2023. "Effects of Inlet Swirl Distortion on a Multi-Stage Compressor with Inlet Guide Vanes and Stall Margin Enhancement Method" Aerospace 10, no. 2: 141. https://doi.org/10.3390/aerospace10020141
APA StyleFang, Y., Sun, D., Dong, X., & Sun, X. (2023). Effects of Inlet Swirl Distortion on a Multi-Stage Compressor with Inlet Guide Vanes and Stall Margin Enhancement Method. Aerospace, 10(2), 141. https://doi.org/10.3390/aerospace10020141





