Aerodynamic Design Optimization and Analysis of Ducted Fan Blades in DEP UAVs
Abstract
:1. Introduction
2. Initial Rotor Design
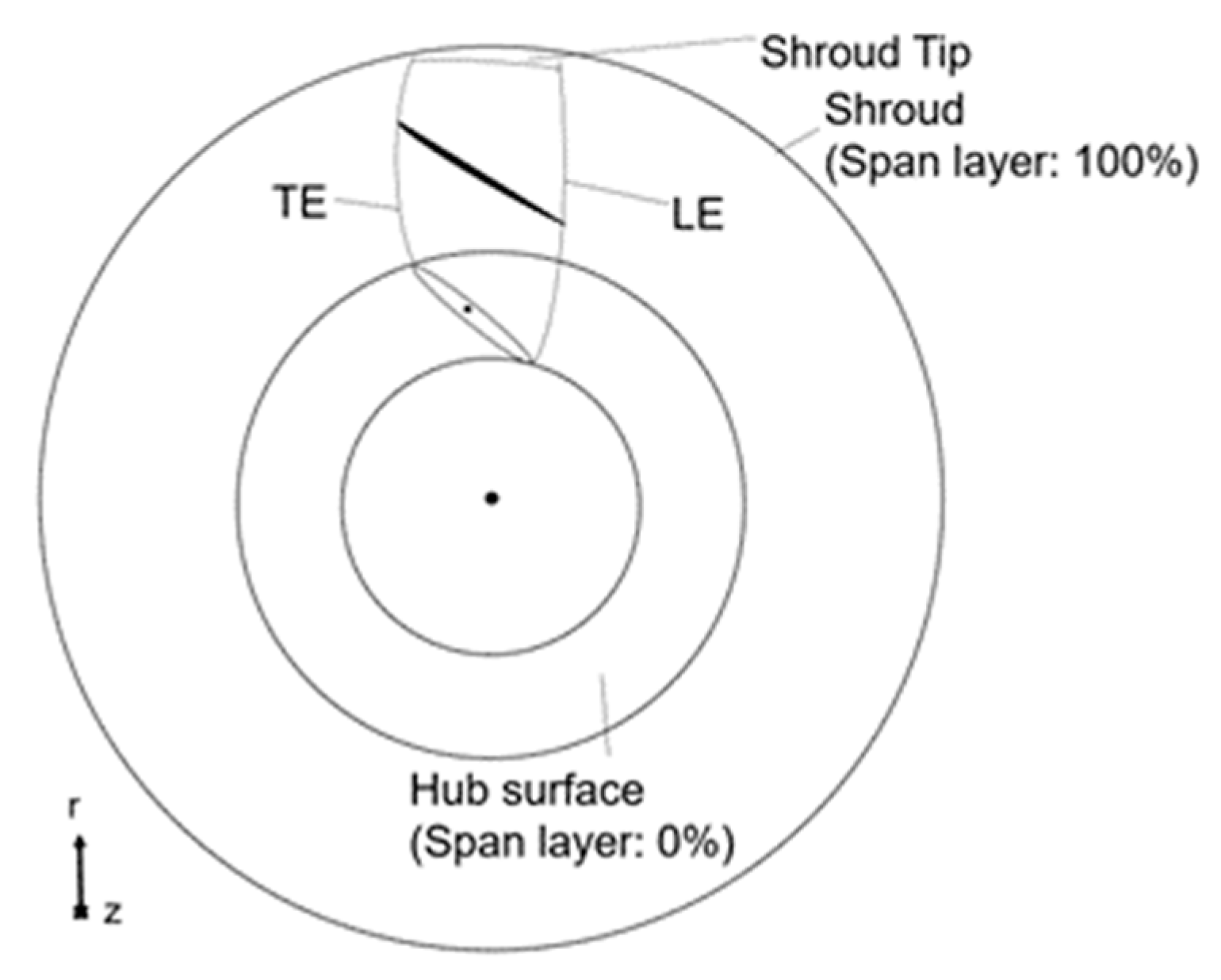
2.1. Initial Model Building
2.2. Numerical Simulation and Results
3. Blade Aerodynamic Optimization
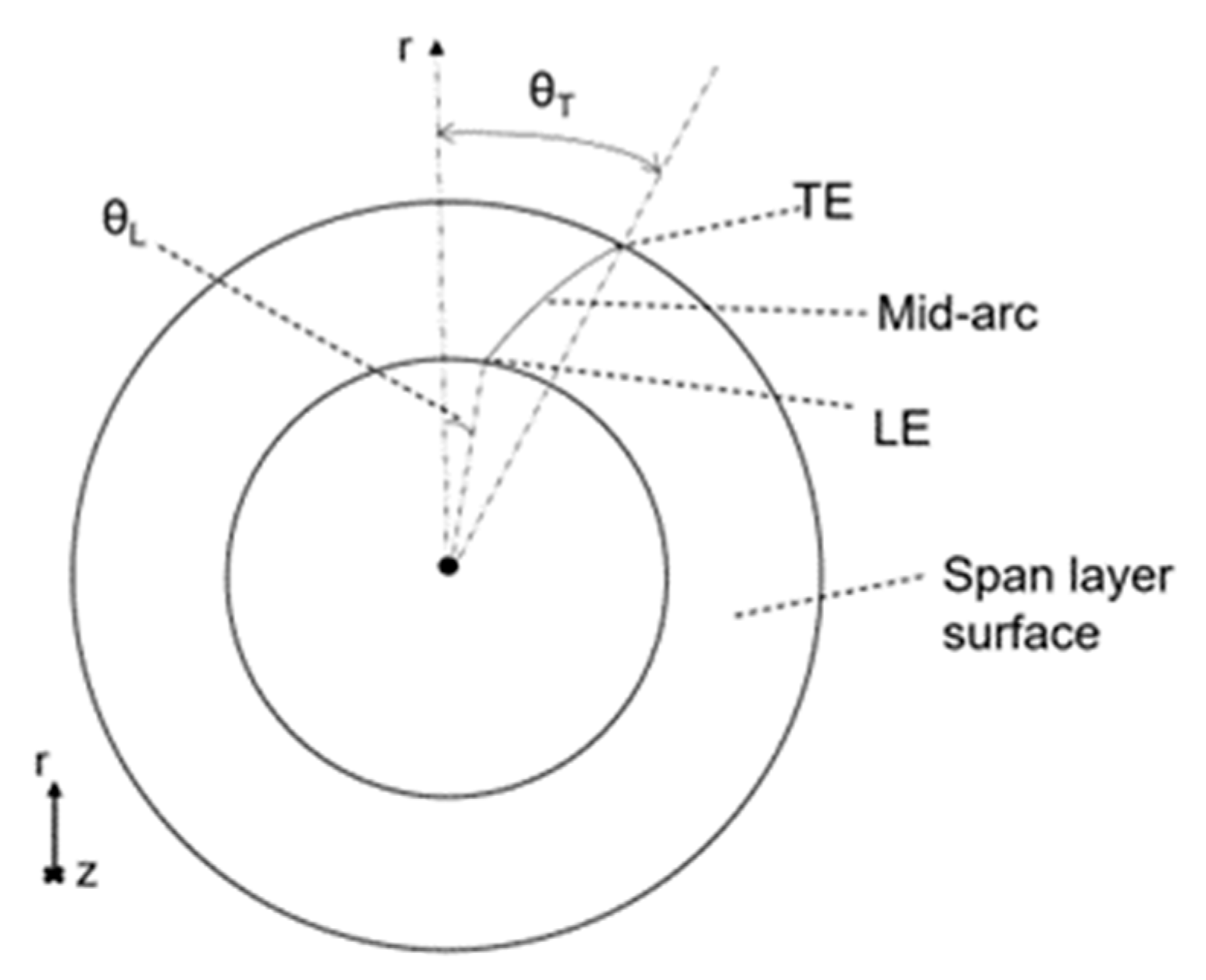
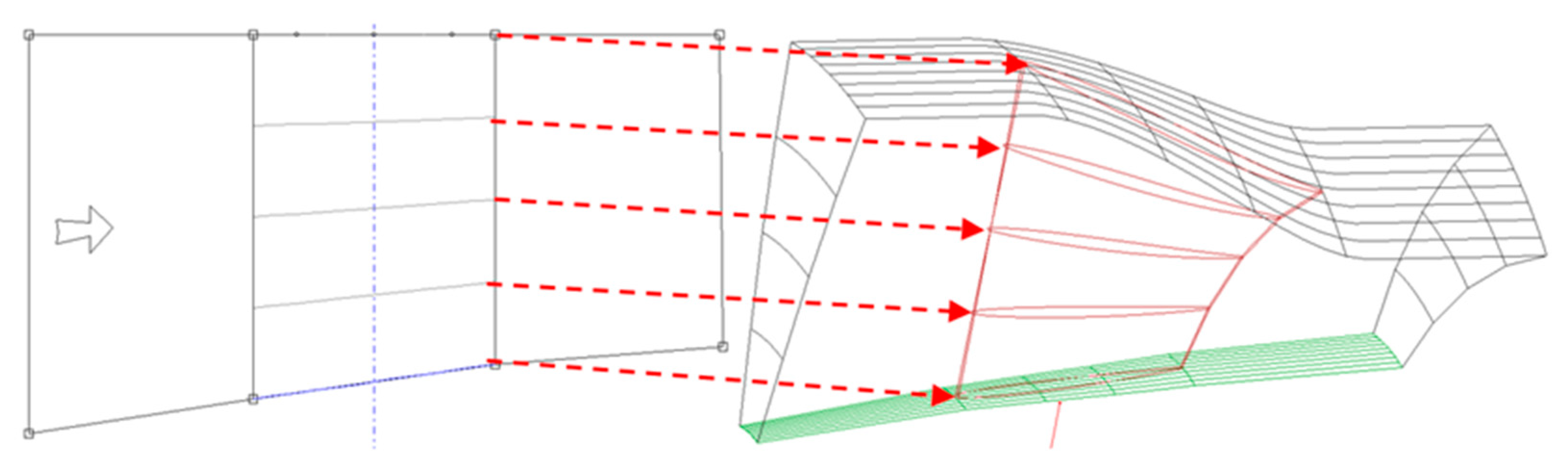
3.1. Blade Parameterization
3.2. Optimization Method
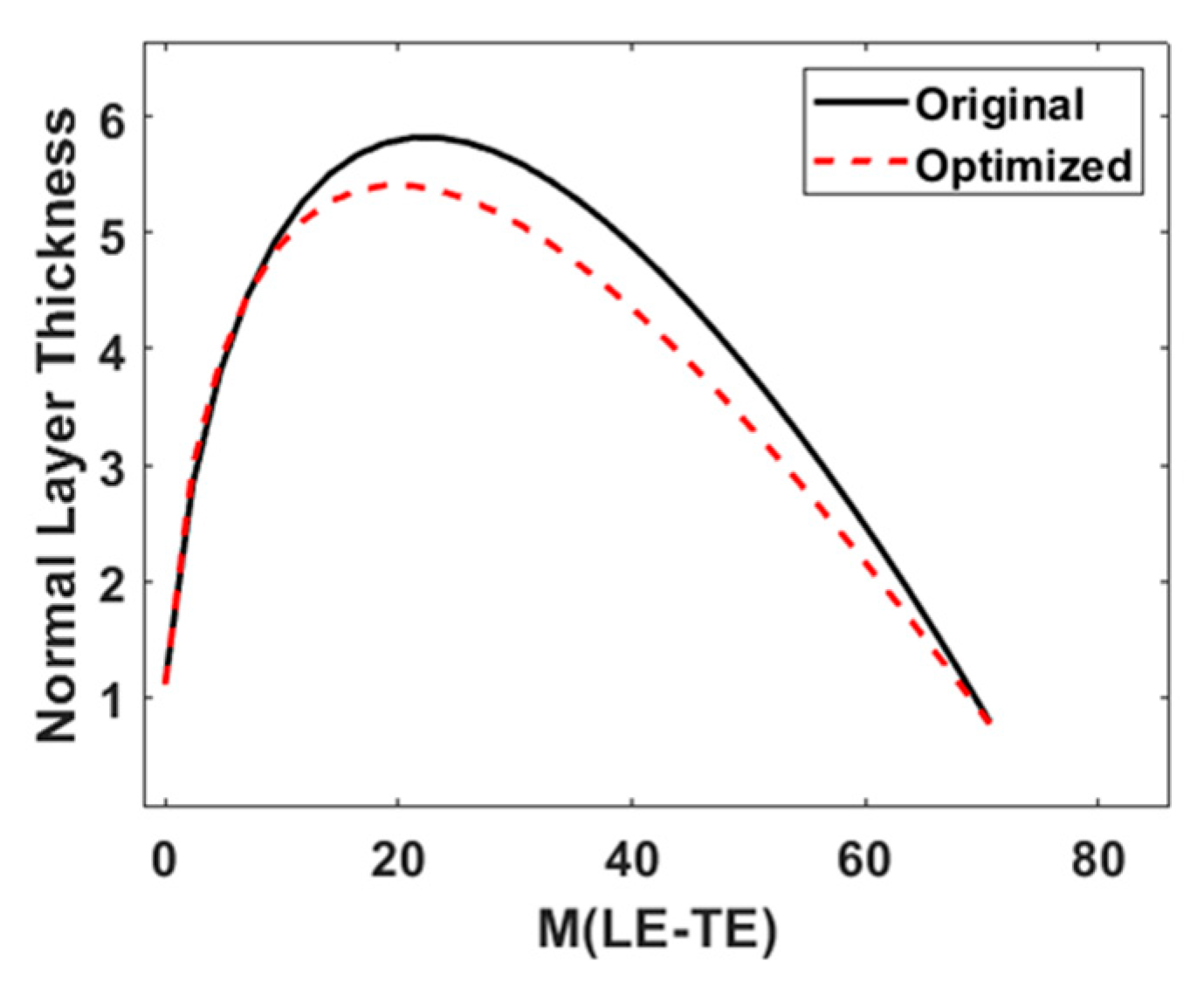
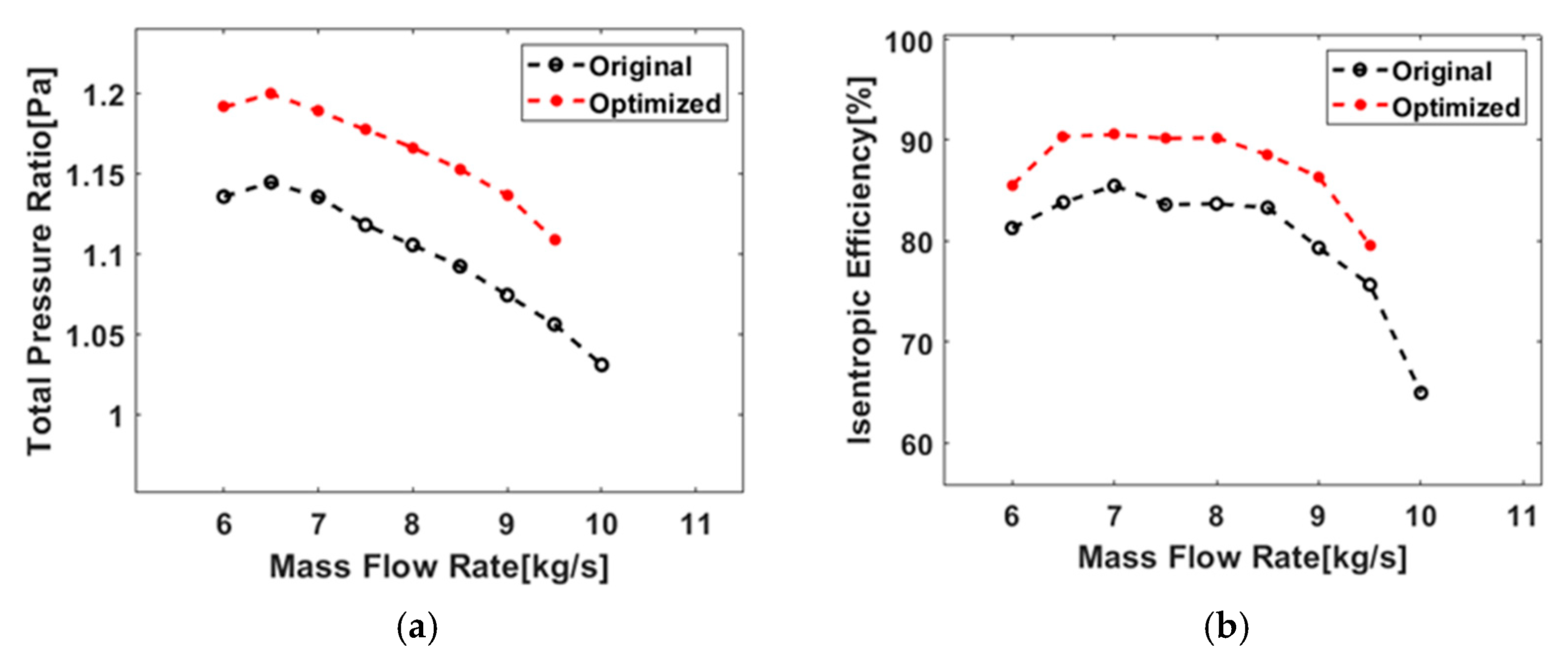
4. Analysis of Optimization Results
4.1. Results
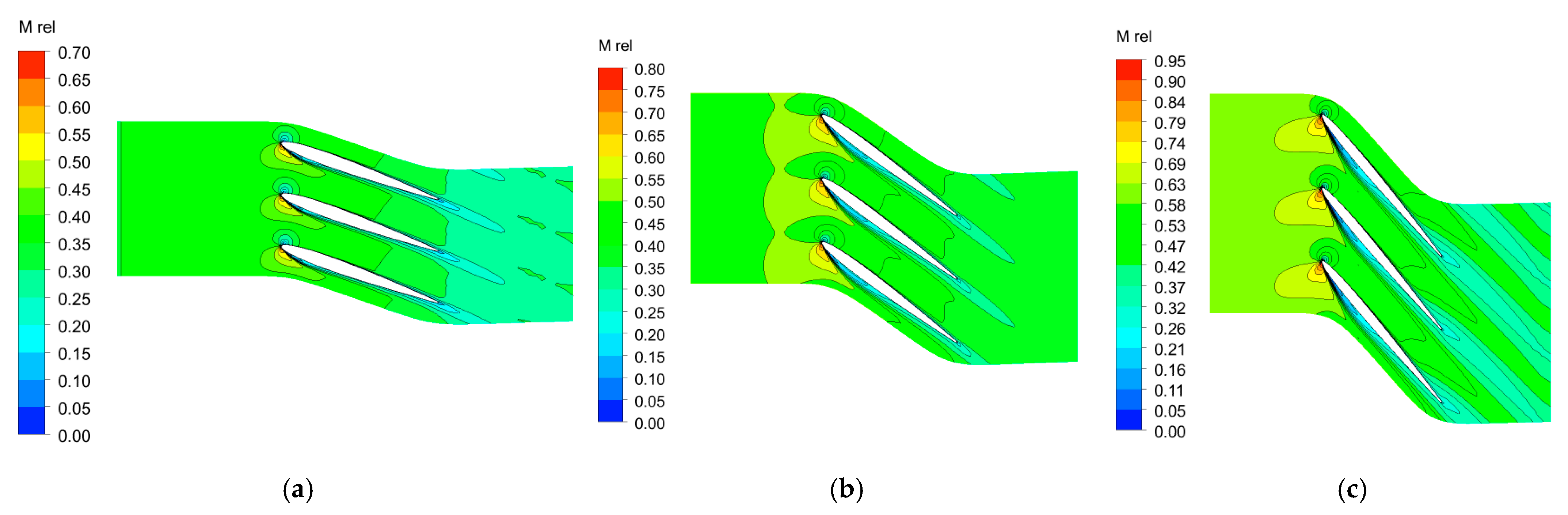
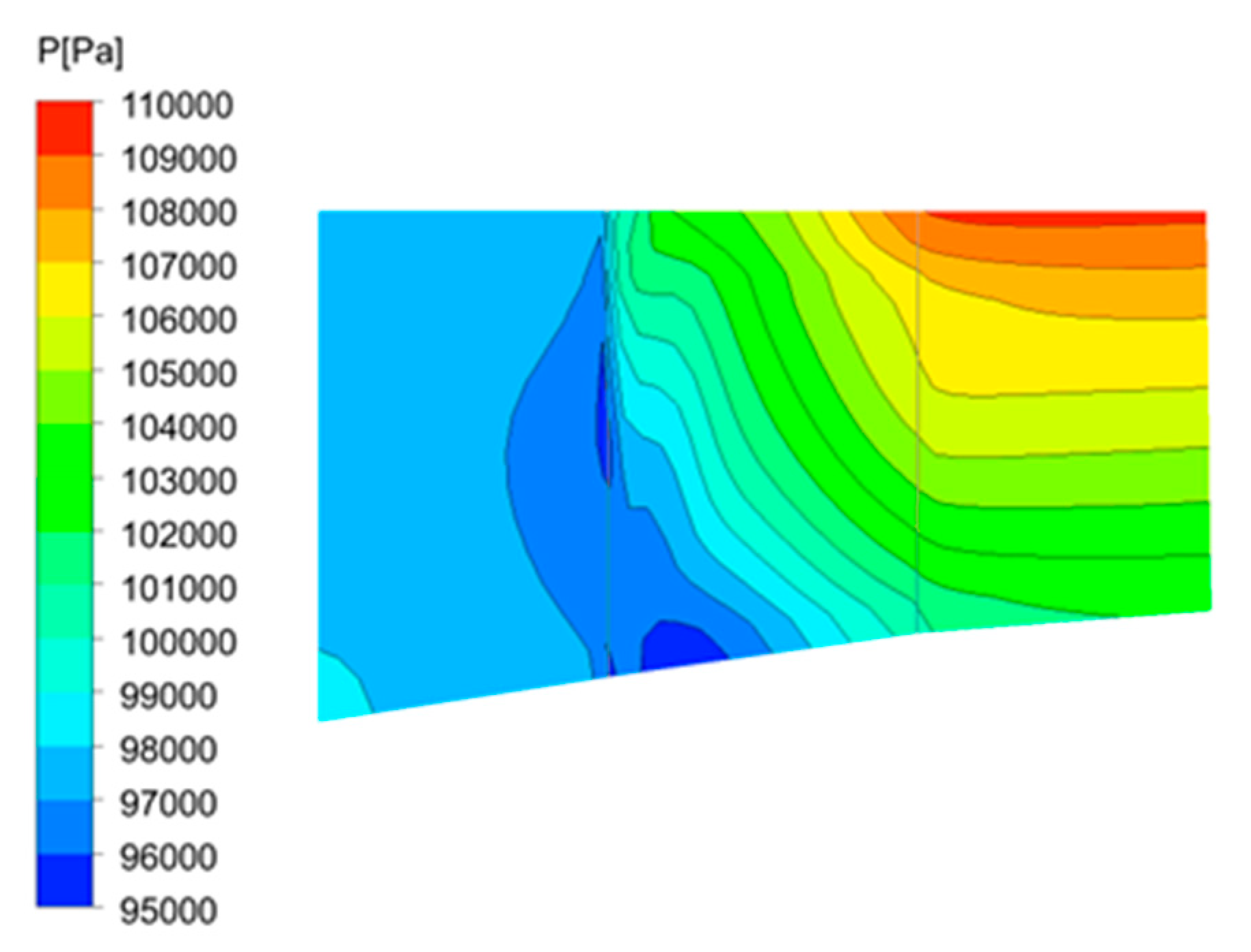
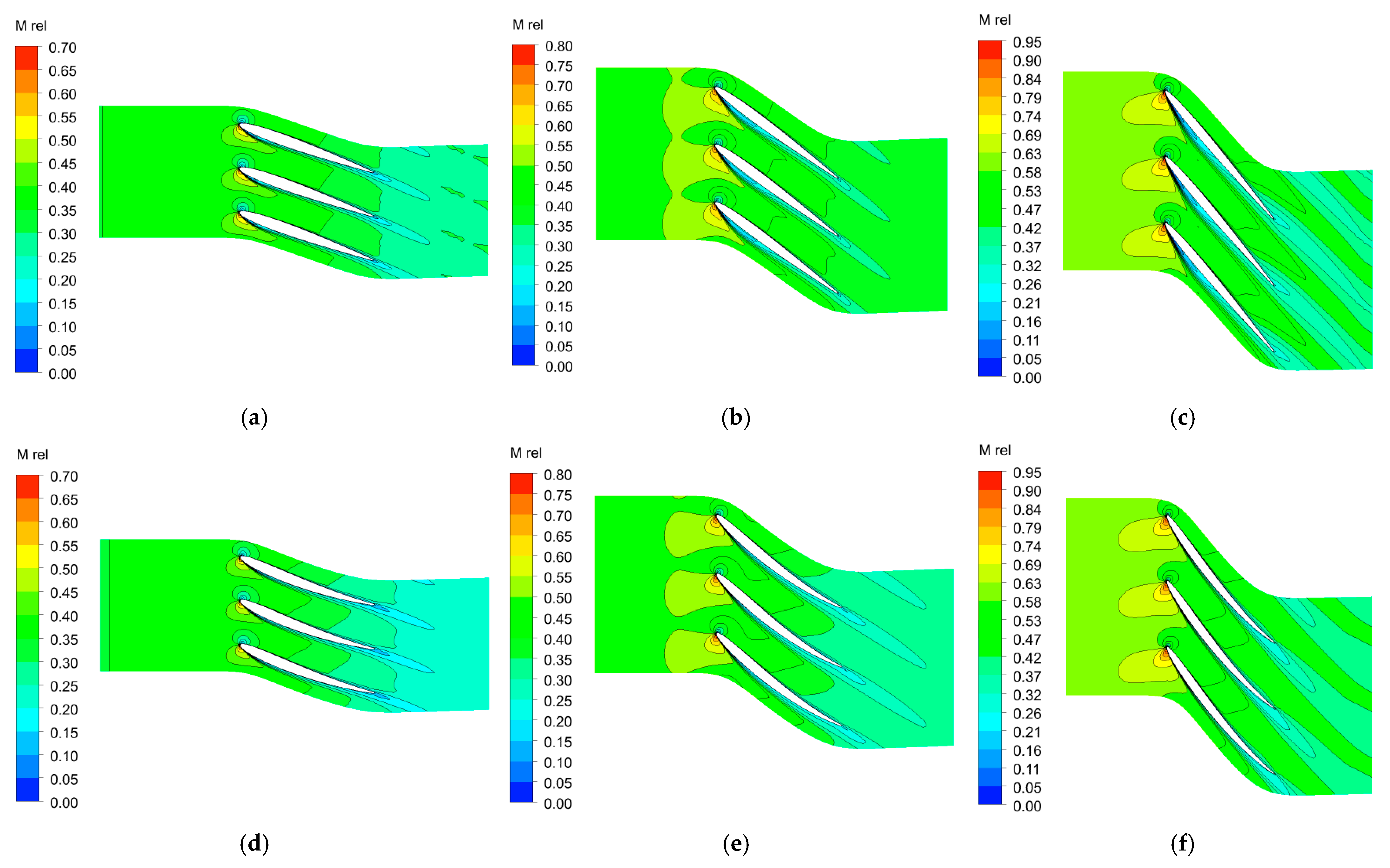
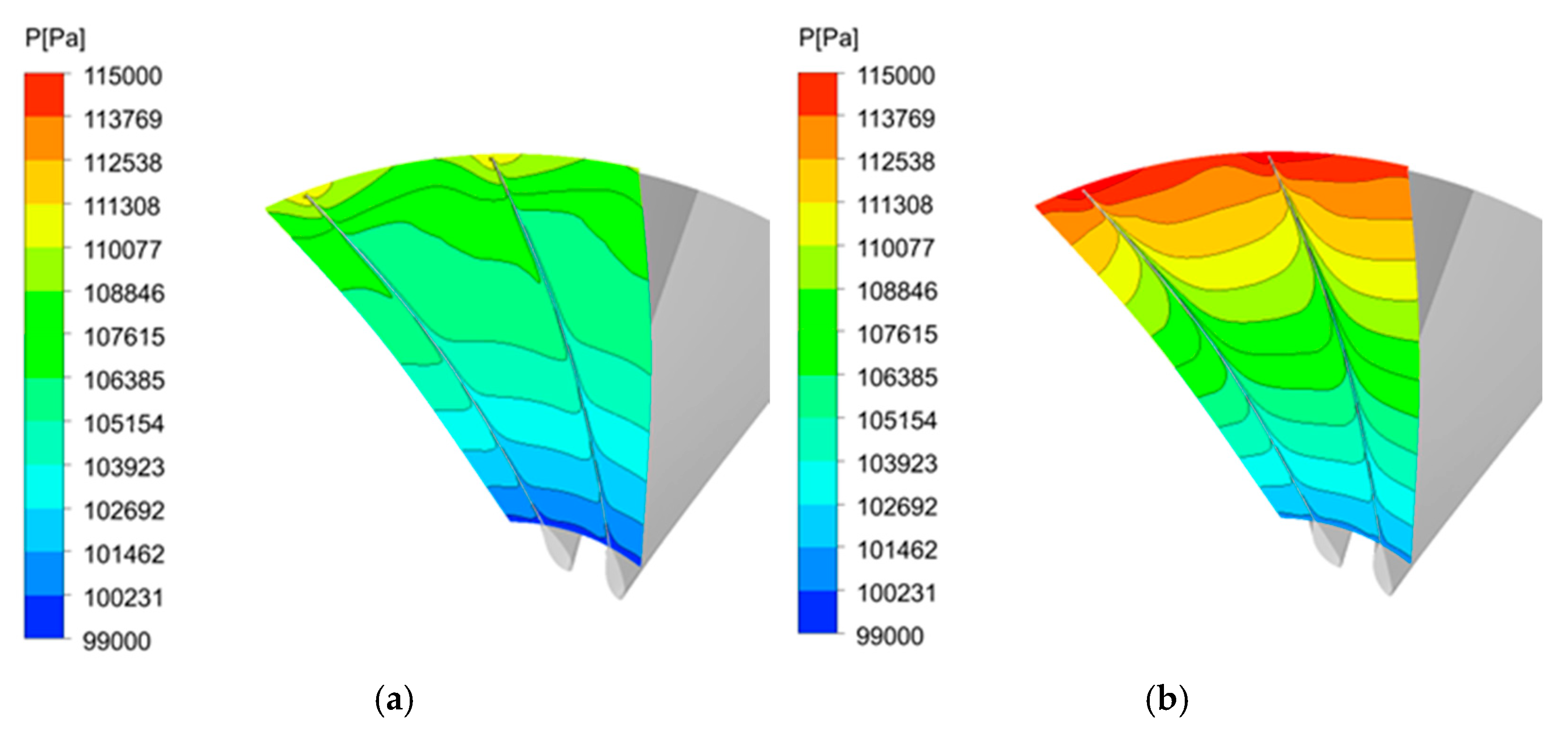
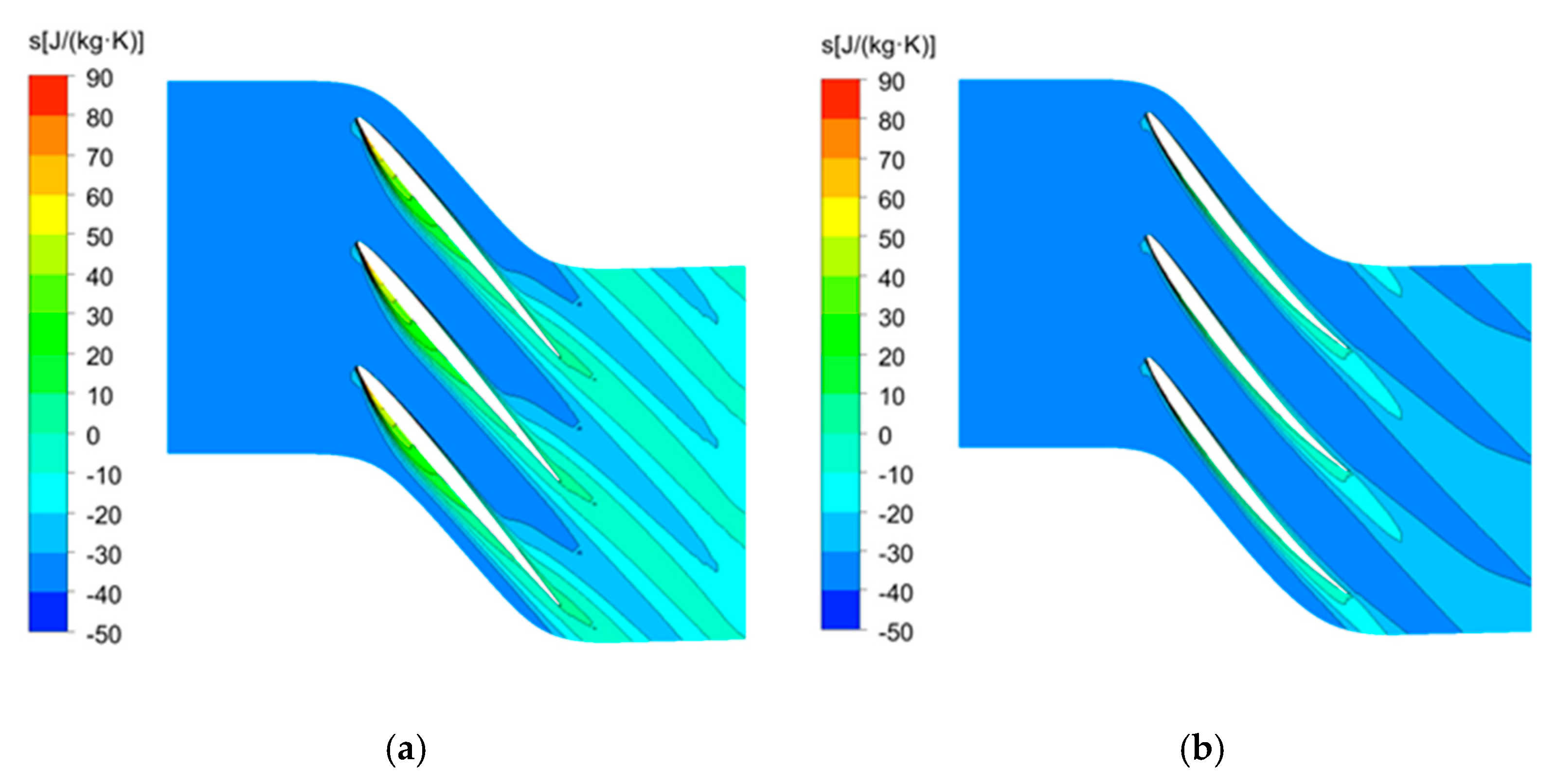
4.2. Flow Field and Performance Analyses
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krein, A.; Williams, G. Flightpath 2050: Europe’s vision for aeronautics. In Innovation for Sustainable Aviation in a Global Environment: Proceedings of the Sixth European Aeronautics Days; Knörzer, D., Szodruch, J., Eds.; IOS Press BV: Amsterdam, The Netherlands, 2012; pp. 63–71. [Google Scholar]
- Owen, B.; Lee, D.S.; Lim, L. Flying into the future: Aviation emissions scenarios to 2050. Environ. Sci. Technol. 2010, 44, 2255–2260. [Google Scholar] [CrossRef]
- Köhler, J.; Jeschke, P. Conceptual design and comparison of hybrid electric propulsion systems for small aircraft. CEAS Aeronaut. J. 2021, 12, 907–922. [Google Scholar] [CrossRef]
- Wheeler, P.; Sirimanna, T.S.; Bozhko, S.; Haran, K.S. Electric/hybrid-electric aircraft propulsion systems. Proc. IEEE 2021, 109, 1115–1127. [Google Scholar] [CrossRef]
- Jansen, R.; Duffy, K.P.; Brown, G. Partially turboelectric aircraft drive key performance parameters. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017; p. 4702. [Google Scholar]
- Martin, P.; Tung, C. Performance and Flowfield Measurements on a 10-Inch Ducted Rotor Vtol Uav; BiblioGov: Washington, DC, USA, 2013. [Google Scholar]
- Brelje, B.J.; Martins, J.R.R.A. Electric, hybrid, and turboelectric fixed-wing aircraft: A review of concepts, models, and design approaches. Prog. Aerosp. Sci. 2019, 104, 1–19. [Google Scholar] [CrossRef]
- Wang, X.Y. A review of NASA’s first All-Eletric X-plane, the X57 Maxwell. Aerosp. Power 2020, 2, 29–32. [Google Scholar]
- Aurora Flight Sciences. Available online: http://www.aurora.aero/lightningstrike (accessed on 24 May 2018).
- Murphy, P.C.; Landman, D. Experiment design for complex VTOL aircraft with distributed propulsion and tilt wing. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Dallas, TX, USA, 5–9 January 2015; p. 0017. [Google Scholar]
- Lilium. Available online: https://lilium.com/technology (accessed on 24 May 2018).
- Kim, H.D.; Perry, A.T.; Ansell, P.J. A review of distributed electric propulsion concepts for air vehicle technology. In Proceedings of the 2018 AIAA/IEEE EATS, Cincinnati, OH, USA, 12–14 July 2018; pp. 1–21. [Google Scholar]
- Huang, J. Survey on design technology of distributed electric propulsion aircraft. Acta A Aeronaut. Astronaut. Sin. 2021, 42, 624037–624054. [Google Scholar]
- Nalianda, D.; Singh, R. Turbo-electric distributed propulsion–opportunities, benefits and challenges. Aircr. Eng. Aerosp. Technol. Int. J. 2014, 86, 543–549. [Google Scholar] [CrossRef]
- Deere, K.A.; Viken, J.K.; Viken, S.; Carter, M.B.; Wiese, M.; Farr, N. Computational analysis of a wing designed for the X-57 distributed electric propulsion aircraft. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017; p. 3923. [Google Scholar]
- Bacchini, A.; Cestino, E. Electric VTOL configurations comparison. Aerospace 2019, 6, 26. [Google Scholar] [CrossRef]
- Borer, N.K.; Patterson, M.D.; Viken, J.K.; Moore, M.D.; Clarke, S.; Redifer, M.E.; Christie, R.J.; Stoll, A.M.; Dubois, A.; Bevirt, J.; et al. Design and performance of the NASA SCEPTOR distributed electric propulsion flight demonstrator. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016; p. 3920. [Google Scholar]
- Gallimore, S.J. Axial flow compressor design. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1999, 213, 437–449. [Google Scholar] [CrossRef]
- Saravanamuttoo, H.I.H.; Rogers, G.F.C.; Cohen, H. Gas Turbine Theory, 3rd ed.; Longman Scientific & Technical: Harlow, UK, 2001; pp. 138–219. [Google Scholar]
- Boyce, M.P. Gas Turbine Engineering Handbook, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2011; pp. 303–355. [Google Scholar]
- Karpowitz, D. Bezier curve fitting method for existing turbine blade design. J. Appl. Eng. Math. 2005, 1, 1. [Google Scholar]
- Song, P.; Sun, J.; Wang, K. Blade shape optimization of transonic axial flow fan in terms of sectional profiles and stacking line. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: Düsseldorf, Germany, 2014; Volume 45615, p. V02BT39A016. [Google Scholar]




| Design Parameters | |
|---|---|
| Design Total Pressure Ratio | 1.1 |
| Design Isentropic Efficiency | 90% |
| Design Diameter | about 300 mm |
| Design Parameters | |
|---|---|
| Hub/Shroud | 0.33 |
| Number of Blades | 19 |
| Shroud Tip | 1 mm |
| Inlet Blade Angle | 20° |
| Outlet Blade Angle | 60° |
| Rotating Speed | about 14,600 r/min |
| Design Parameters | |
|---|---|
| Rotation Speed | 14,650 r/min |
| Mass Flow Rate | 6.42 kg/s |
| Inlet Volume Flow Rate | 5.24 m3/s |
| Input Power | 93,024.80 W |
| Reference Radius | 0.11 m |
| Inlet Flow Coefficient | 0.64 |
| Exit Flow Coefficient | 0.52 |
| Total Pressure Ratio | 1.14 |
| Total Temperature Ratio | 1.05 |
| Total Isentropic Efficiency | 83.84% |
| Total Polytropic Efficiency | 84.17% |
| Control Layers | Control Points | θ | Thickness Distribution |
|---|---|---|---|
| 0 | 2,3 | ±10.0% | ±5.0%, ±10.0% |
| 50% | 2,3 | ±10.0% | - |
| 100% | 2,3 | ±10.0% | - |
| Total Pressure Ratio | Total Isentropic Efficiency | |
|---|---|---|
| Design Goal | 1.10 | 90.00% |
| Origin Blade | 1.14 | 83.84% |
| Optimized Blade | 1.20 | 90.37% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Liu, K. Aerodynamic Design Optimization and Analysis of Ducted Fan Blades in DEP UAVs. Aerospace 2023, 10, 153. https://doi.org/10.3390/aerospace10020153
Li H, Liu K. Aerodynamic Design Optimization and Analysis of Ducted Fan Blades in DEP UAVs. Aerospace. 2023; 10(2):153. https://doi.org/10.3390/aerospace10020153
Chicago/Turabian StyleLi, Huiling, and Kun Liu. 2023. "Aerodynamic Design Optimization and Analysis of Ducted Fan Blades in DEP UAVs" Aerospace 10, no. 2: 153. https://doi.org/10.3390/aerospace10020153
APA StyleLi, H., & Liu, K. (2023). Aerodynamic Design Optimization and Analysis of Ducted Fan Blades in DEP UAVs. Aerospace, 10(2), 153. https://doi.org/10.3390/aerospace10020153





