Integrated Guidance-and-Control Design for Three-Dimensional Interception Based on Deep-Reinforcement Learning
Abstract
:1. Introduction
- (1)
- Multiple constraints were satisfied in the guidance field to attack the target accurately, and the effectiveness and feasibility are verified by the random initialization of the missile and target states.
- (2)
- The convergence speed and guidance accuracy were effectively improved by introducing the convergence factor of the angular velocity of the target line-of-sight.
- (3)
- The deep dual filter (DDF) method was introduced when designing the DRL algorithm, guaranteeing better performance under the same training burden.
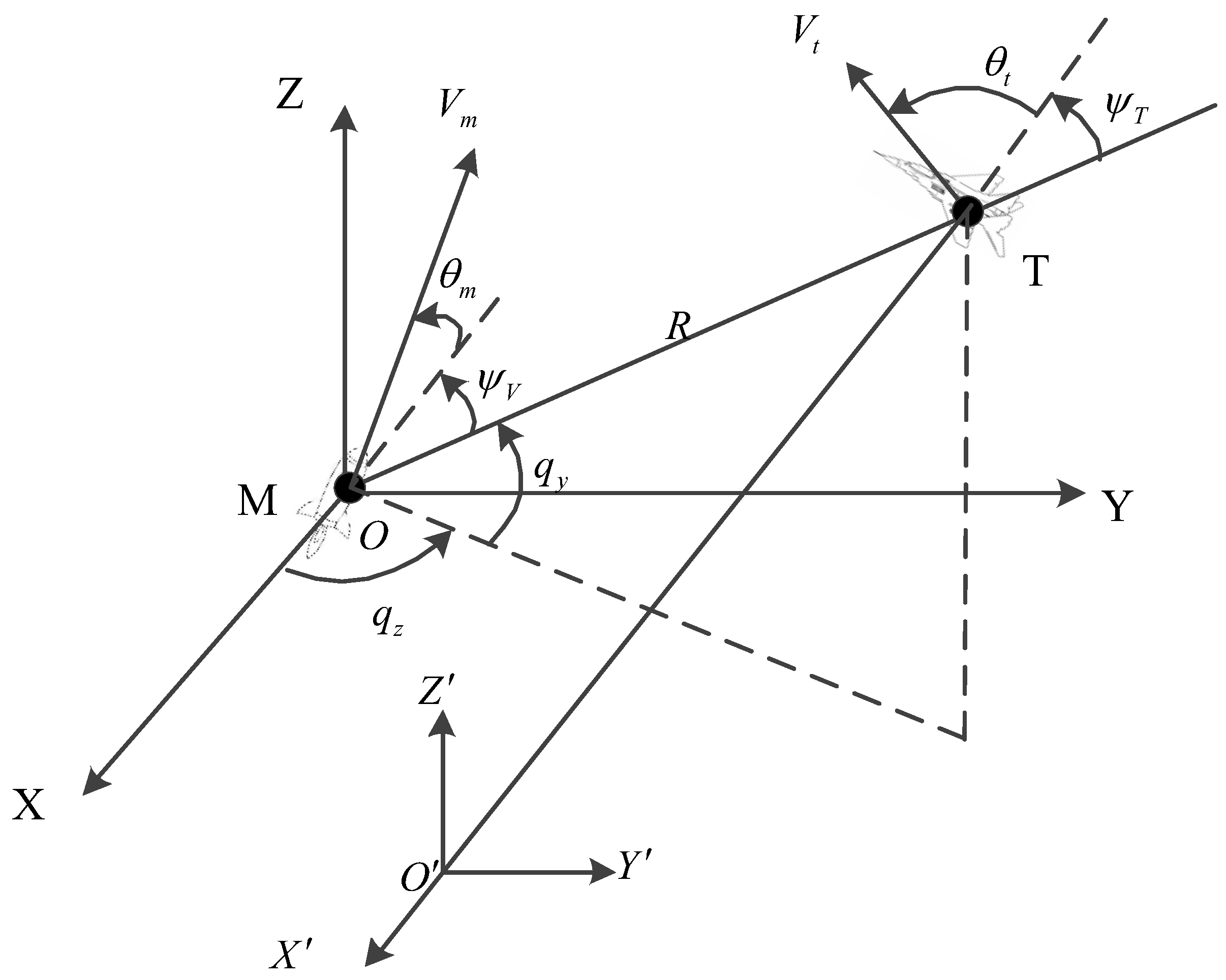
2. Three-Dimensional IGC Model
2.1. Missile-Dynamics Equations
2.2. Aerodynamic Parameters
3. Deep-Reinforcement-Learning Algorithms
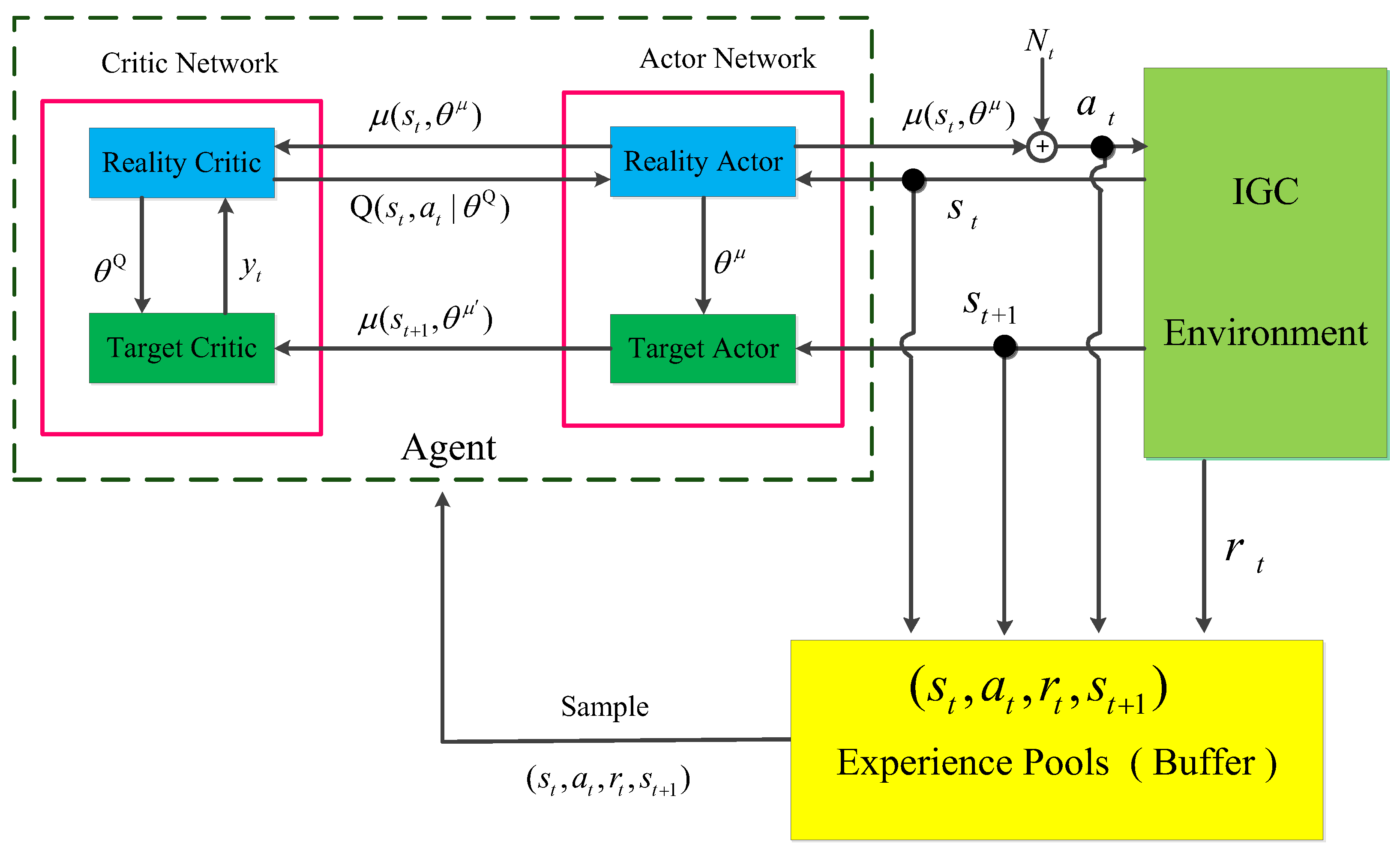
3.1. DDPG Algorithm Framework
3.2. DDPG Algorithm Flow
| Algorithm 1: DDPG |
| 1: Initialize critic network parameters and randomly |
| 2: Initialize the respective Target-Network parameters , |
| 3: Initialize the Experience Pools (Buffer) for storing empirical information |
| 4: for episode = 1: Max Episode do |
| 5: Obtain the initialized state |
| 6: for t = 1: Max Step do |
| 7: Select action , where is a Gaussian perturbation |
| 8: Execute to obtain the corresponding reward and the next state |
| 9: The tuple formed by the above process is stored in Buffer |
| 10: Sample a random minibatch of transitions from Buffer |
| 11: Calculate the temporal-difference error |
| 12: Update critic by minimizing the loss: |
| 13: Update the Critic-Network using gradient descent: |
| 14: Update the target networks: |
| 15: end for |
| 16: end for |
4. Modeling the Reinforcement-Learning Problem
4.1. Reinforcement Learning Environment
4.2. Reward Function
4.3. Training Scheme
4.4. Creating the Networks
- (1)
- (2)
- (3)
5. Simulation Results and Analysis
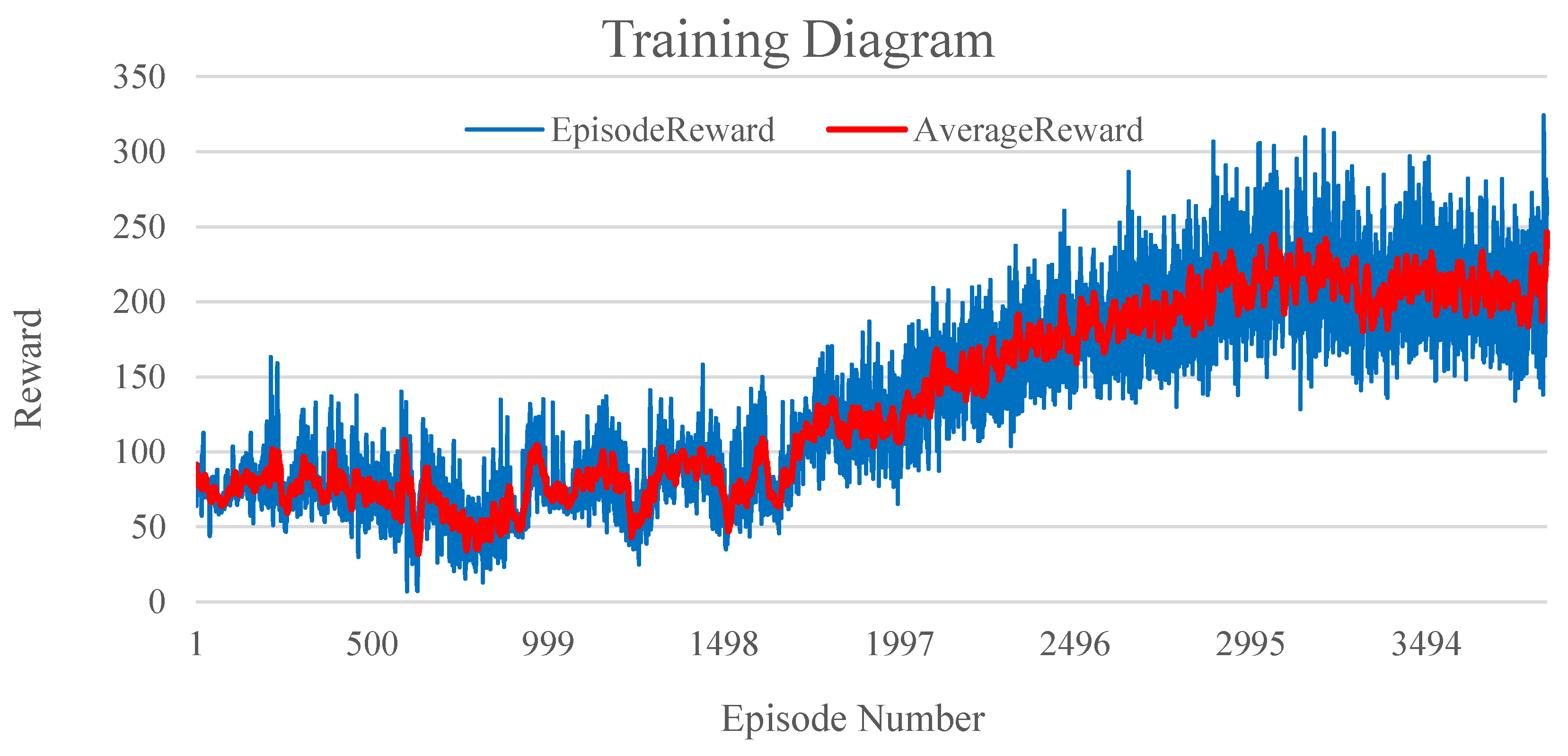
5.1. Training Results
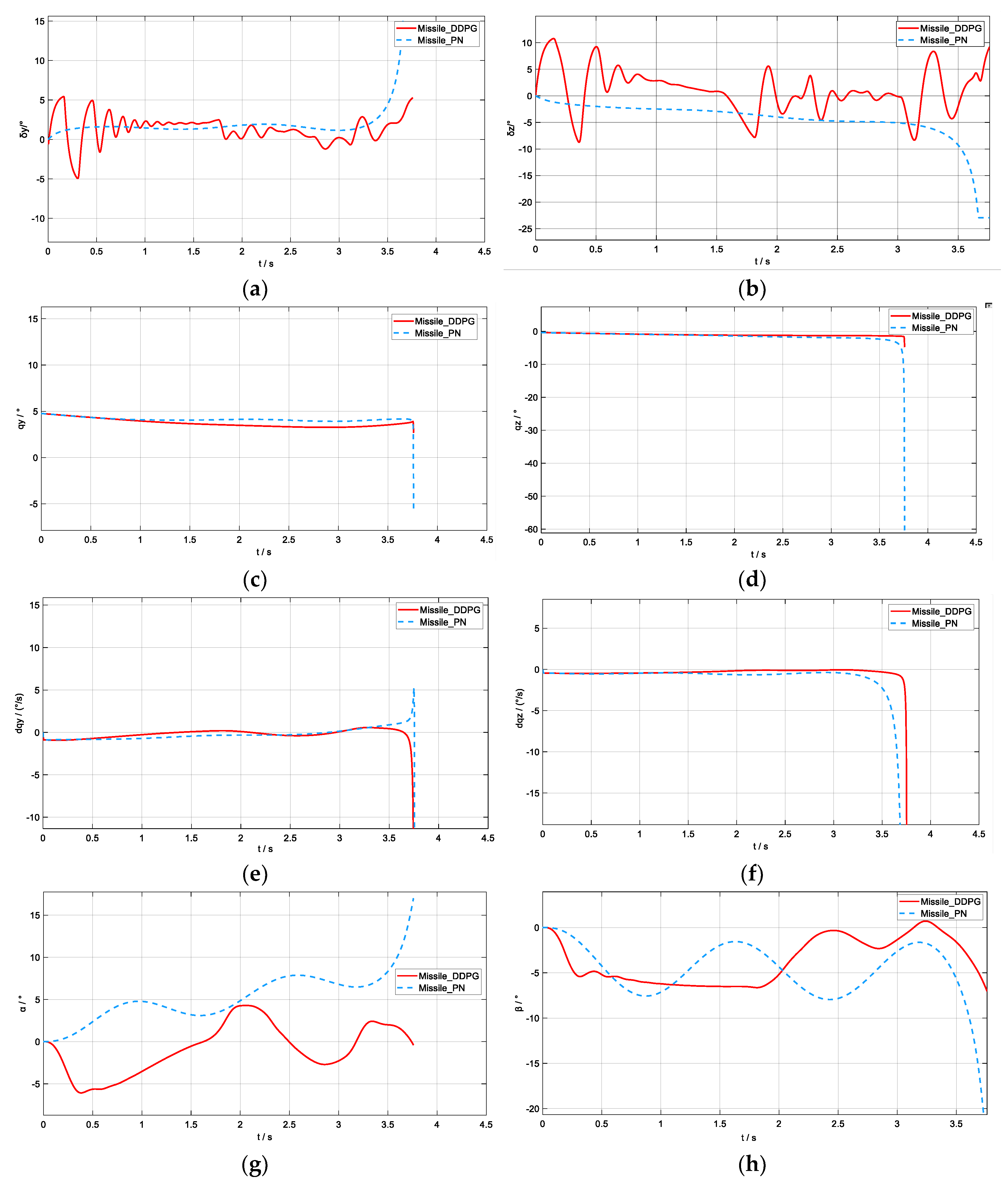
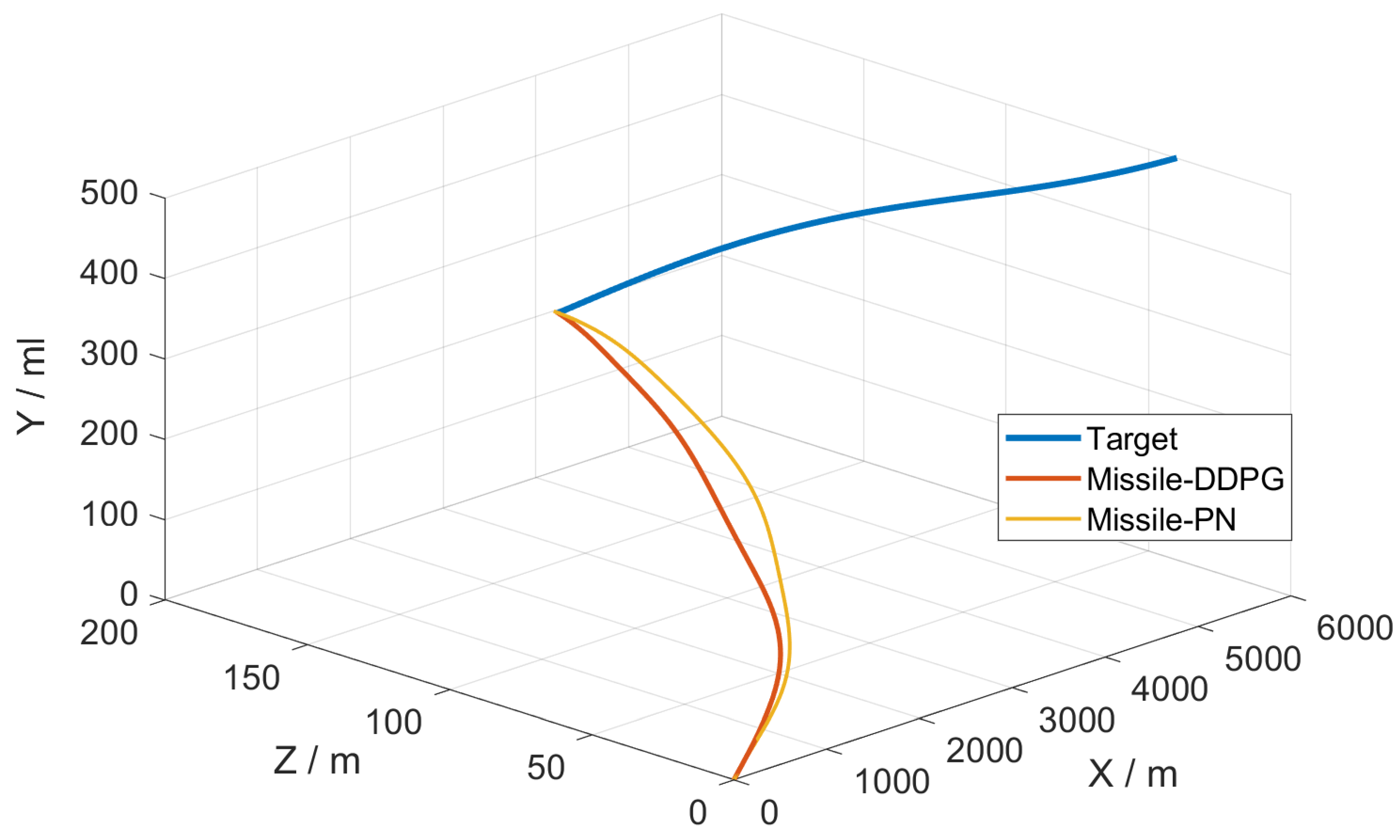
5.2. Simulation Verification
- (1)
- The target was at the farthest initial distance from the missile.
- (2)
- The target had the maximum initial velocity and acceleration.
- (3)
- The missile had the minimum initial velocity.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Williams, D.E.; Friedland, B.; Richman, J. Integrated Guidance and Control for Combined Command/Homing Guidance. In Proceedings of the American Control Conference IEEE, Atlanta, GA, USA, 5–17 June 1988. [Google Scholar]
- Cho, N.; Kim, Y. Modified pure proportional navigation guidance law for impact time control. J. Guid. Control Dyn. 2016, 39, 852–872. [Google Scholar] [CrossRef]
- He, S.; Lee, C. Optimal proportional-integral guidance with reduced sensitivity to target maneuvers. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2568–2579. [Google Scholar] [CrossRef]
- Asad, M.; Khan, S.; Ihsanullah; Mehmood, Z.; Shi, Y.; Memon, S.A.; Khan, U. A split target detection and tracking algorithm for ballistic missile tracking during the re-entry phase. Def. Technol. 2020, 16, 1142–1150. [Google Scholar] [CrossRef]
- Yanushevsky, R. Modern Missile Guidance, 1st ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2007; pp. 12–19. [Google Scholar]
- Ming, C.; Wang, X.; Sun, R. A novel non-singular terminal sliding mode control-based integrated missile guidance and control with impact angle constraint. Aerosp. Sci. Technol. 2019, 94, 105368. [Google Scholar] [CrossRef]
- Wang, J.; Liu, L.; Zhao, T.; Tang, G. Integrated guidance and control for hypersonic vehicles in dive phase with multiple constraints. Aerosp. Sci. Technol. 2016, 53, 103–115. [Google Scholar] [CrossRef]
- Ai, X.L.; Shen, Y.C.; Wang, L.L. Adaptive integrated guidance and control for impact angle constrained interception with actuator saturation. Aeronaut. J. 2019, 123, 1437–1453. [Google Scholar] [CrossRef]
- Padhi, R.; Kothari, M. Model predictive static programming: A computationally efficient technique for suboptimal control design. Int. J. Innov. Comput. Inf. Control Ijicic 2009, 5, 23–35. [Google Scholar]
- Guo, B.Z.; Zhao, Z.L. On convergence of the nonlinear active disturbance rejection control for mimo systems. SIAM J. Control Optim. 2013, 51, 1727–1757. [Google Scholar] [CrossRef]
- Zhao, C.; Huang, Y. ADRC based input disturbance rejection for minimum-phase plants with unknown orders and/or uncertain relative degrees. J. Syst. Sci. Complex. 2012, 25, 625–640. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Li, S.; She, Y. Recent advances in contact dynamics and post-capture control for combined spacecraft. Prog. Aerosp. Sci. 2021, 120, 100678. [Google Scholar] [CrossRef]
- Gaudet, B.; Furfaro, R. Adaptive Pinpoint and Fuel Efficient Mars Landing Using Reinforcement Learning. IEEE/CAA J. Autom. Sin. 2014, 1, 397–411. [Google Scholar]
- Gaudet, B.; Linares, R.; Furfaro, R. Deep reinforcement learning for six degree-of-freedom planetary landing. Adv. Space Res. 2020, 65, 1723–1741. [Google Scholar] [CrossRef]
- Gaudet, B.; Furfaro, R.; Linares, R. Reinforcement learning for angle-only intercept guidance of maneuvering targets. Aerosp. Sci. Technol. 2020, 99, 105746. [Google Scholar] [CrossRef]
- Wu, M.-Y.; He, X.-J.; Qiu, Z.-M.; Chen, Z.-H. Guidance law of interceptors against a high-speed maneuvering target based on deep Q-Network. Trans. Inst. Meas. Control 2020, 44, 1373–1387. [Google Scholar] [CrossRef]
- He, S.; Shin, H.-S.; Tsourdos. Computational missile guidance: A deep reinforcement learning approach. J. Aerosp. Inf. Syst. 2021, 18, 571–582. [Google Scholar] [CrossRef]
- Pei, P.; Chen, Z. Integrated Guidance and Control for Missile Using Deep Reinforcement Learning. J. Astronaut. 2021, 42, 1293–1304. (In Chinese) [Google Scholar]
- Qinhao, Z.; Baiqiang, A.; Qinxue, Z. Reinforcement learning guidance law of Q-learning. Syst. Eng. Electron. 2019, 40, 67–71. [Google Scholar]
- Scorsoglio, A.; Furfaro, R.; Linares, R. Actor-critic reinforcement learning approach to relative motion guidance in near-rectilinear orbit. Adv. Astronaut. Sci. 2019, 168, 1737–1756. [Google Scholar]
- Fu, Z.; Zhang, K.; Gan, Q. Integrated Guidance and Control with Input Saturation and Impact Angle Constraint. Discret. Dyn. Nat. Soc. 2020, 2020, 1–19. [Google Scholar] [CrossRef]
- Kang, C. Full State Constrained Stochastic Adaptive Integrated Guidance and Control for STT Missiles with Non-Affine Aerodynamic Characteristics-ScienceDirect. Inf. Sci. 2020, 529, 42–58. [Google Scholar]
- Tian, J.; Xiong, N.; Zhang, S.; Yang, H.; Jiang, Z. Integrated guidance and control for missile with narrow field-of-view strapdown seeker. ISA Trans. 2020, 106, 124–137. [Google Scholar] [CrossRef]
- Jiang, S.; Tian, F.Q.; Sun, S.Y. Integrated guidance and control of guided projectile with multiple constraints based on fuzzy adaptive and dynamic surface-ScienceDirect. Def. Technol. 2020, 16, 1130–1141. [Google Scholar] [CrossRef]
- Zhang, D.; Ma, P.; Wang, S.; Chao, T. Multi-constraints adaptive finite-time integrated guidance and control design. Aerosp. Sci. Technol. 2020, 107, 106334. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with deep reinforcement learning. arXiv 1312, arXiv:1312.5602. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 1509, arXiv:1509.02971. [Google Scholar]



| 0.1 | 0.02 | 0.2 | 0.1 | 20 | 50 |
| Parameter Name | Min | Max |
|---|---|---|
| Target’s initial position | 4000 | 6000 |
| Missile’s initial velocity | 900 | 1100 |
| Target’s initial speed (Negative direction) | 00 | 700 |
| Initial acceleration in the y-direction of the target | 0 | 30 (Negative and positive directions) |
| Network Layer | Actor-Network | Critic Network | ||
|---|---|---|---|---|
| Number of Units | Activation Function | Number of Units | Activation Function | |
| Input layer | 10 | —— | 12 | —— |
| Hidden layer 1 | 64 | Relu | 64 | Relu |
| Hidden layer 2 | 100 | Relu | 100 | Relu |
| Hidden layer 3 | 100 | Relu | 100 | Relu |
| Output layer | 1 | tanh | 1 | Linear |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Maximum number of segments | 5000 | Sampling time | |
| Actor learning rate | Noise variance | ||
| Critic learning rate | Noise-variance decay rate | ||
| Discount factor | 0.99 | Minimum sample size | 64 |
| Target network smoothing factor | Experience buffer size |
| Algorithm | Min | Max | Average | Variance |
|---|---|---|---|---|
| DDPG | 0.06 | 4.17 | 1.97 | 1.08 |
| PN | 1.37 | 172 | 14.16 | 17.11 |
| Change Mode and Percentage | Positive Pull-Off | Negative Pull-Off | ||||
|---|---|---|---|---|---|---|
| 10% | 20% | 30% | 10% | 20% | 30% | |
| DDPG | 0.45 | 0.52 | 0.60 | 0.76 | 0.95 | 1.15 |
| PN | 3.02 | 4.01 | 5.0 | 11.42 | 18.03 | 22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Wu, M.; Chen, Z.; Liu, X. Integrated Guidance-and-Control Design for Three-Dimensional Interception Based on Deep-Reinforcement Learning. Aerospace 2023, 10, 167. https://doi.org/10.3390/aerospace10020167
Wang W, Wu M, Chen Z, Liu X. Integrated Guidance-and-Control Design for Three-Dimensional Interception Based on Deep-Reinforcement Learning. Aerospace. 2023; 10(2):167. https://doi.org/10.3390/aerospace10020167
Chicago/Turabian StyleWang, Wenwen, Mingyu Wu, Zhihua Chen, and Xiaoli Liu. 2023. "Integrated Guidance-and-Control Design for Three-Dimensional Interception Based on Deep-Reinforcement Learning" Aerospace 10, no. 2: 167. https://doi.org/10.3390/aerospace10020167
APA StyleWang, W., Wu, M., Chen, Z., & Liu, X. (2023). Integrated Guidance-and-Control Design for Three-Dimensional Interception Based on Deep-Reinforcement Learning. Aerospace, 10(2), 167. https://doi.org/10.3390/aerospace10020167






