Development and Calibration of a Three-Directional High-Energy Particle Detector for FY-3E Satellite
Abstract
:1. Introduction
2. Main Technical Indexes
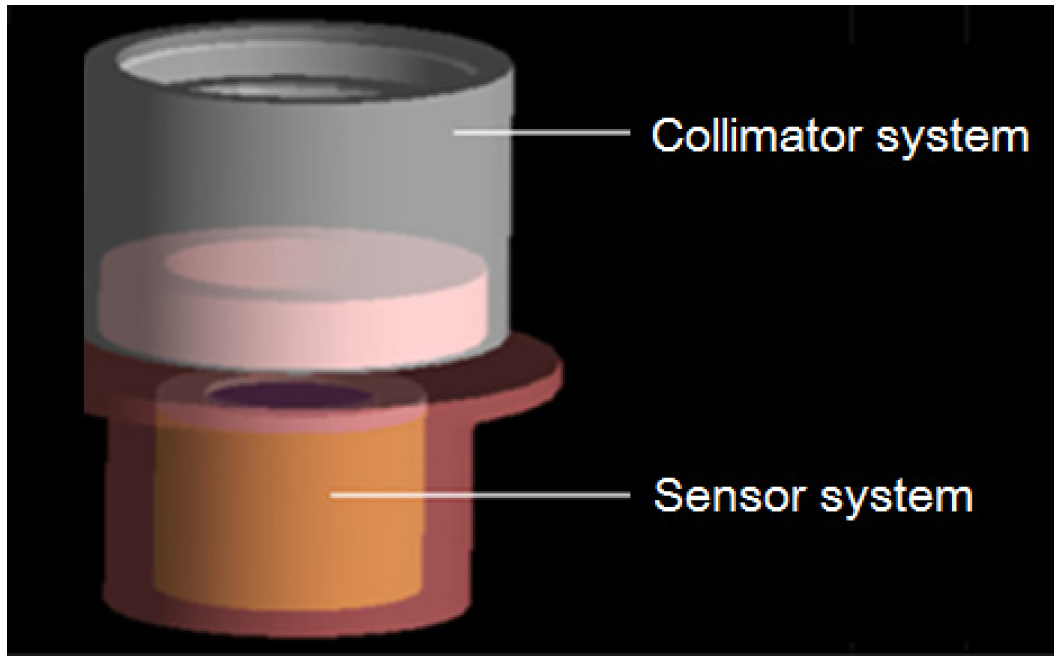
3. System Composition
4. Instrument Design
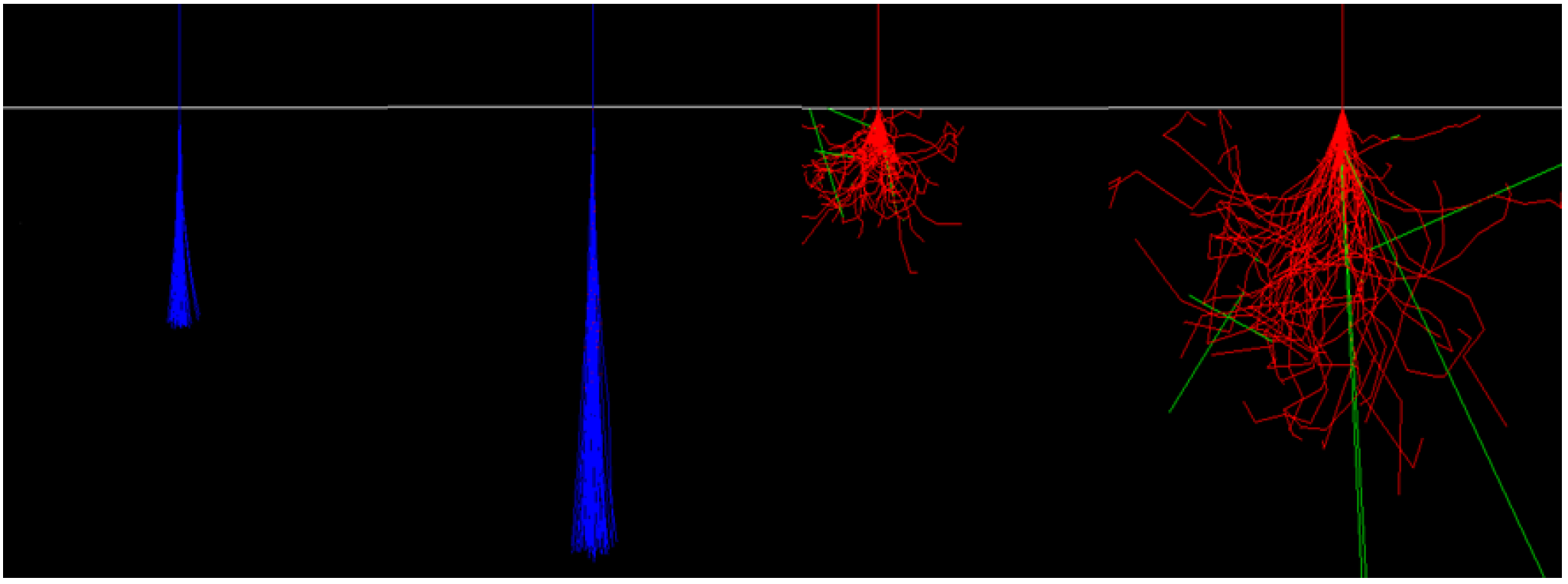
4.1. Fundamental Principle
4.2. Detailed Designs
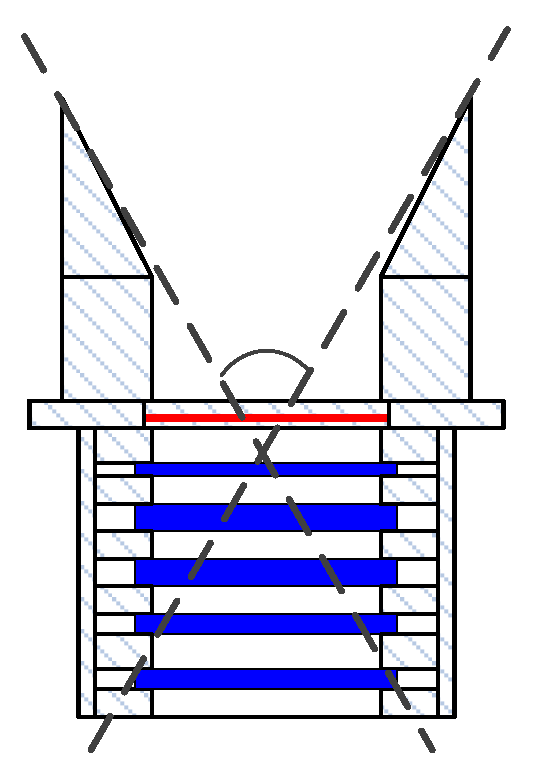
4.2.1. Design of Collimator System
- High-energy electron collimation design
- High-energy proton collimation design
4.2.2. Design of Sensor System
4.2.3. Design of Logical Working Modes
- High-energy proton detection logic
- High-energy electron detection logic
4.2.4. Design of Geometric Factor
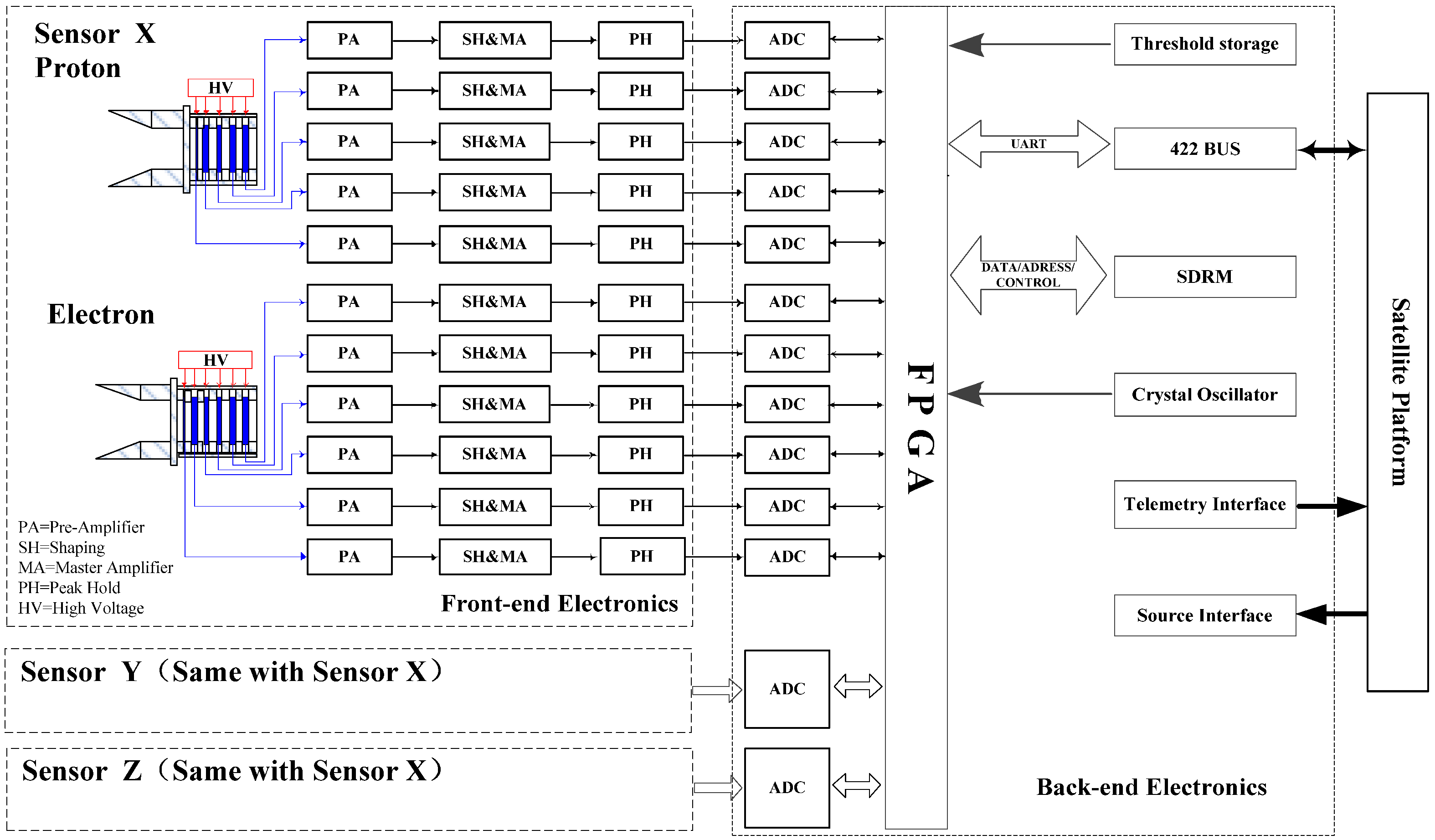
4.2.5. Electronics Design
5. Ground-Based Calibrations
5.1. Energy Calibration
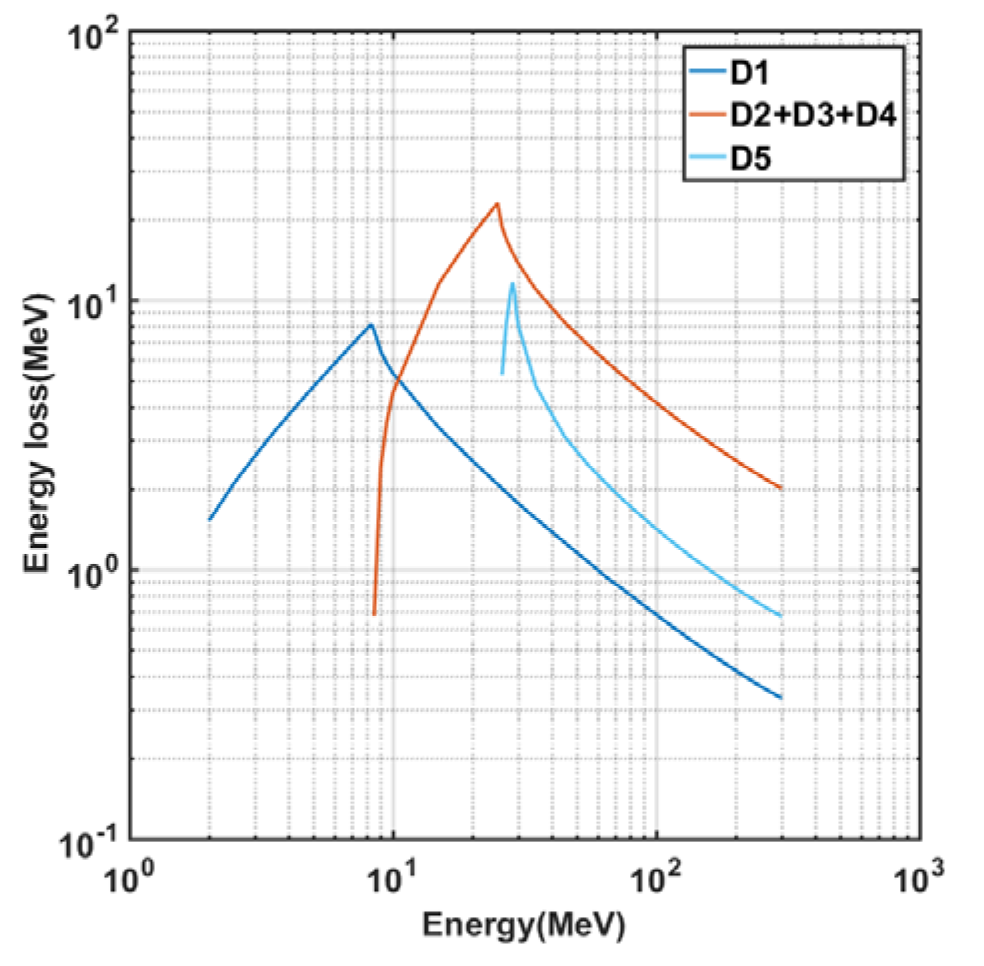
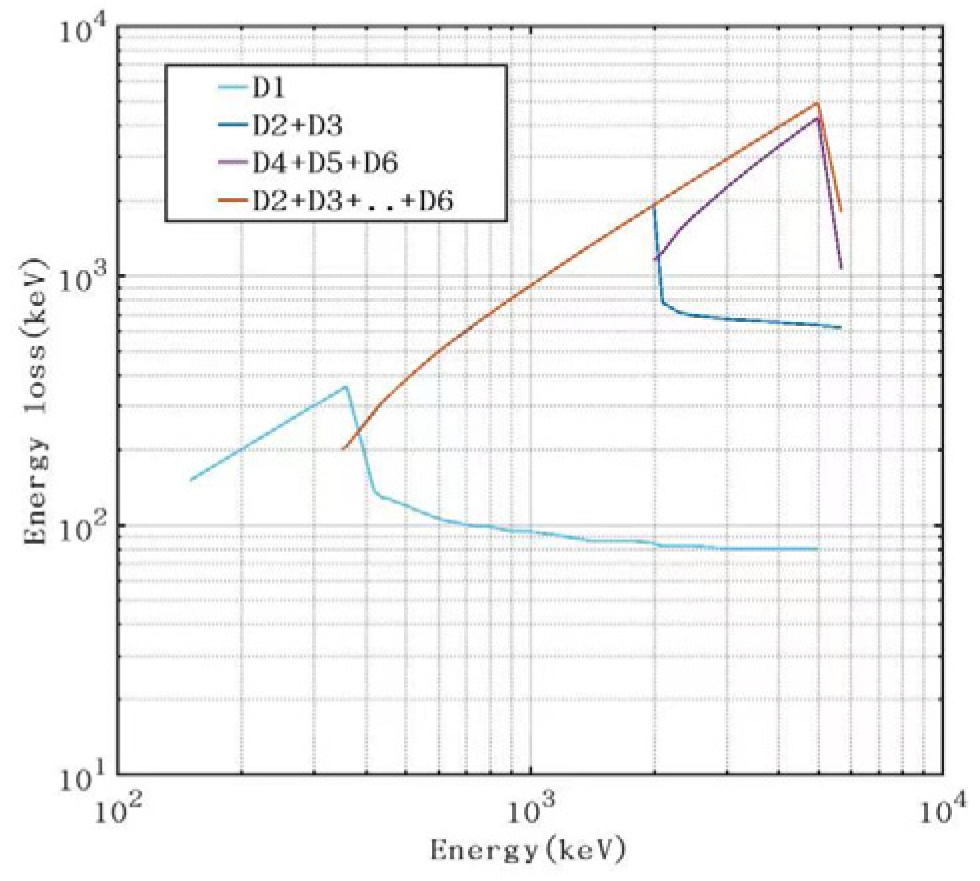
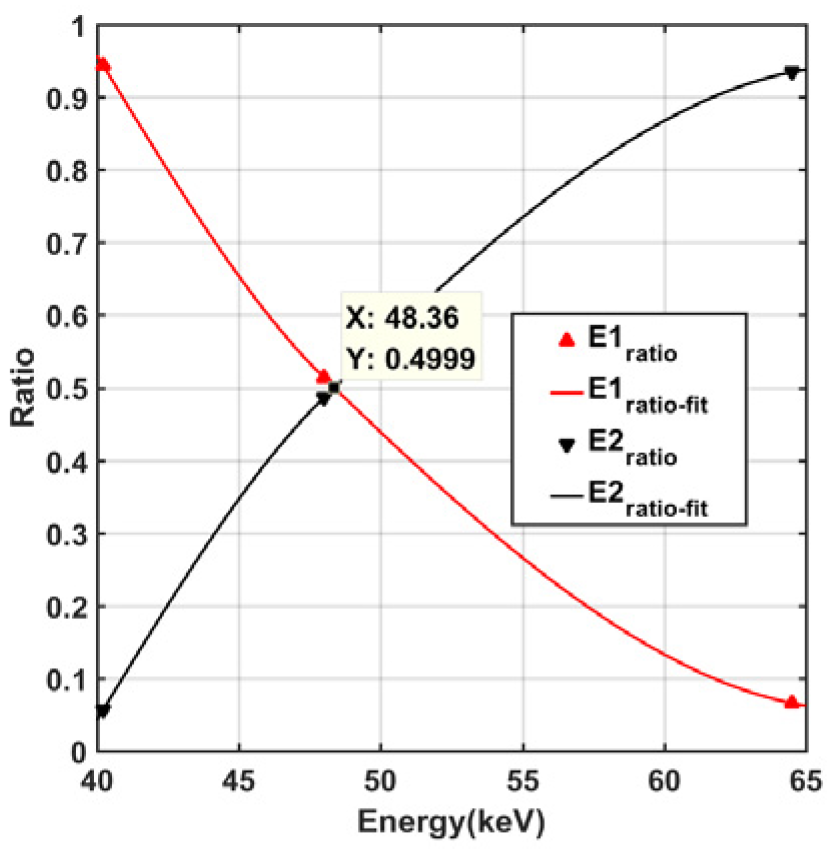
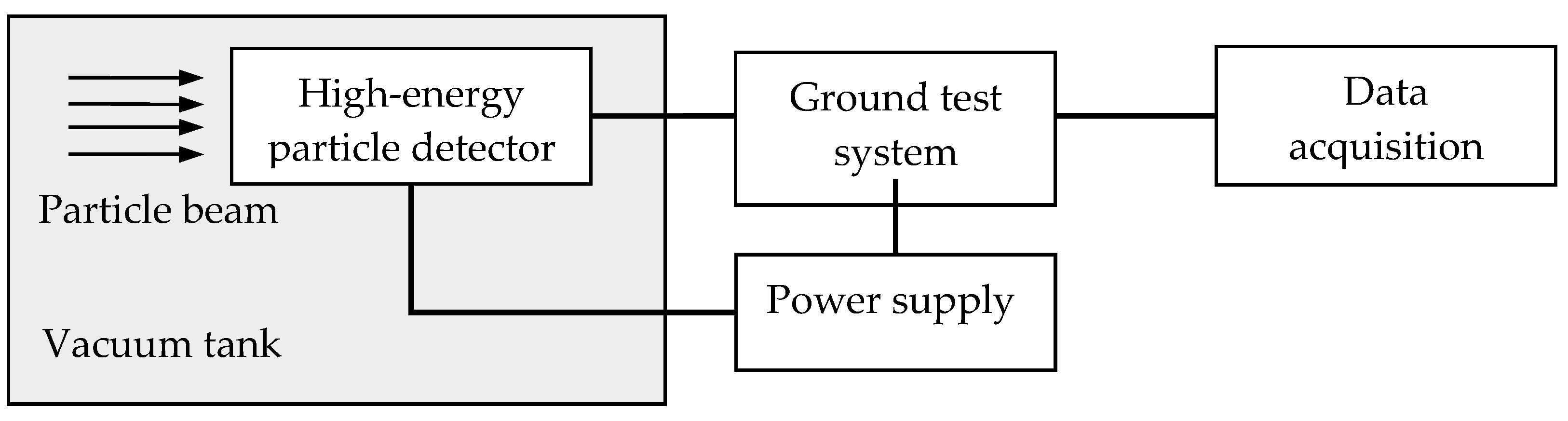
5.1.1. Calibration Methods
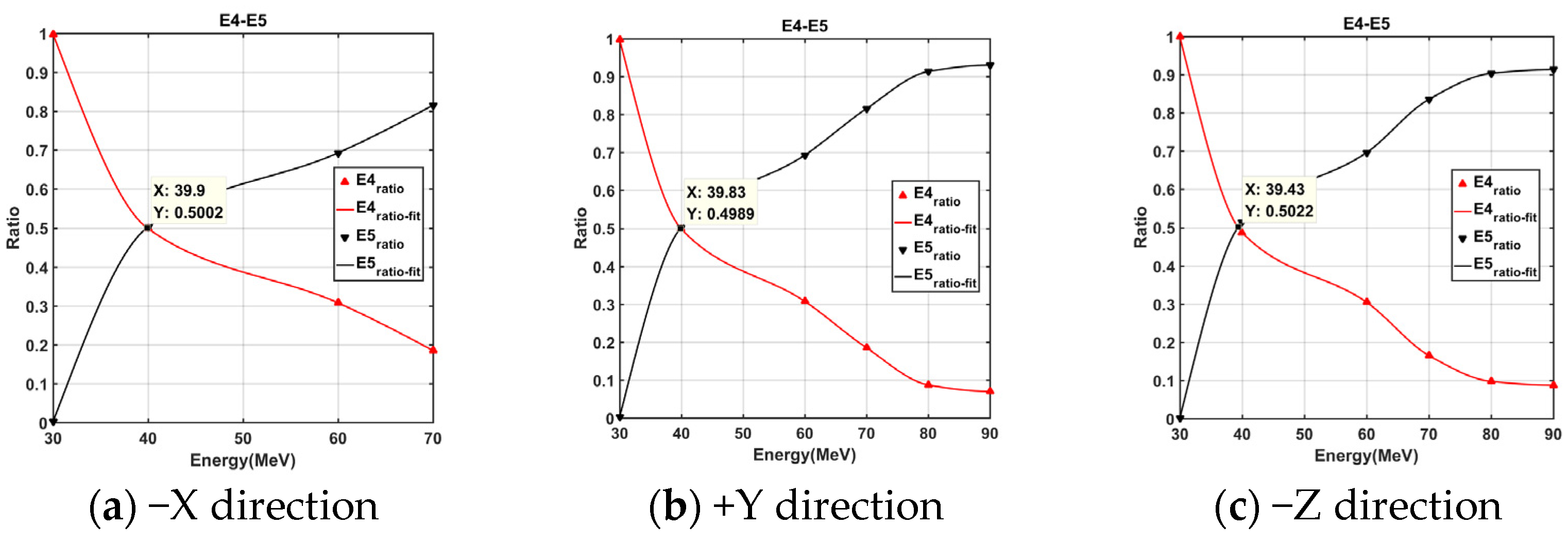
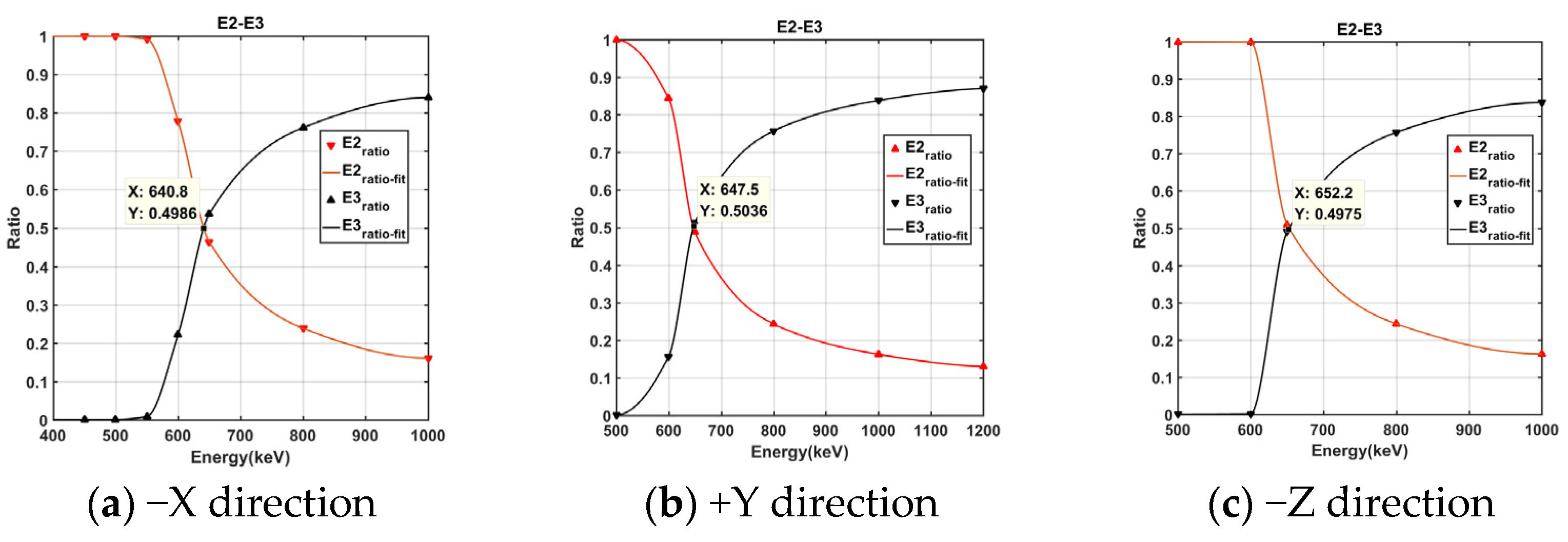
5.1.2. Calibration Results
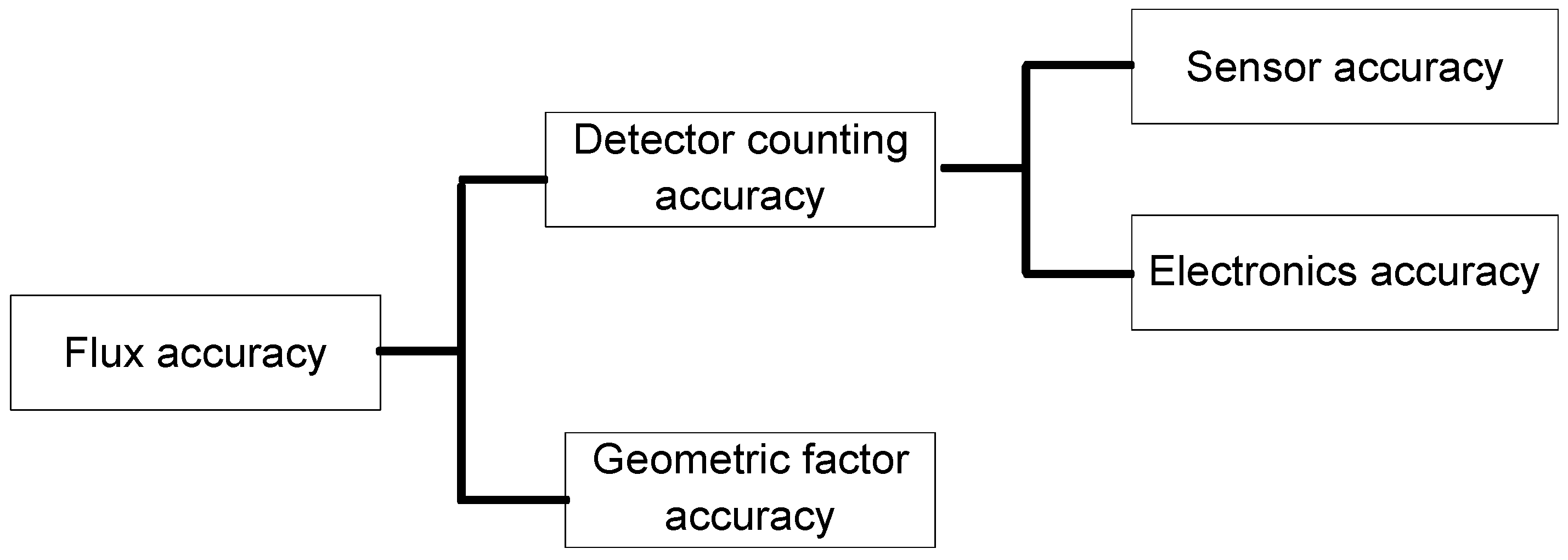
5.2. Flux Accuracy Calibration
5.2.1. Calibration Methods
5.2.2. Calibration Results
5.3. Sensitivity Calibration
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xian, D. FengYun NO. 3—Li Ming Satellite. Satell. Appl. 2022, 1, 70. [Google Scholar]
- He, X.Y.; Cai, X.F.; Zhu, Y.P.; Zhang, L. China’s Fengyun polar orbit meteorological satellite and its application progress. Adv. Meteorol. Sci. Technol. 2021, 11, 34–39. [Google Scholar]
- China successfully launched Fengyun NO. 3 E satellite. Infrared 2021, 42, 54. Available online: http://www.xinhuanet.com/tech/2021-07/05/c_1127622185.htm (accessed on 23 December 2022).
- Gao, H.; Tang, S.H.; Han, X.Z. China’s Fengyun (FY) meteorological satellites, development and applications. Sci. Technol. Rev. 2021, 39, 9–22. [Google Scholar]
- Zhang, P.; Xu, Z.; Guan, M.; Xie, L.; Xian, D.; Liu, C. Progress of Fengyun Meteorological Satellites Since 2020. Chin. J. Space Sci. 2022, 42, 724–732. [Google Scholar] [CrossRef]
- Wang, C.Q.; Zhang, X.; Zhang, L.G.; Zhang, R.Y.; Jin, L.Q.; Sun, Y.Q.; Jing, T.; Zhang, K.Y.; Zhang, H.X.; Chang, Z. Space Radiation Environment Observations and Applications Based on GEO Satellites. Aerosp. Shanghai 2017, 34, 85–95. [Google Scholar]
- Feng, Y.J.; Hua, G.X.; Liu, S.F. Summary of research on radiation resistance of aerospace electronics. J. Astronaut. 2007, 05, 1071–1080. [Google Scholar]
- Zhu, G.W.; Li, B.Q.; Wang, S.J.; Liang, J.B.; Zhang, W.; Huang, H.J.; Shen, S.Z.; Zhai, Y.Y.; Sun, Y.Q.; Ye, Z.H. Analysis of influence of solar proton events on the space radiation environment of solar synchronous orbit. Chin. J. Space Sci. 2002, 22, 58–64. [Google Scholar]
- Xue, Y.X.; Yang, S.S.; Ba, D.D.; An, H.; Liu, Q.; Shi, H.; Cao, Z. Analysis of spacecraft faults or anomalies by space radiation environment. Vacuun Low Temp. 2012, 18, 63–70. [Google Scholar]
- di Stefano, I.; Cappuccio, P.; Iess, L. The BepiColombo solar conjunction experiments revisited. Class. Quantum Gravity 2021, 38, 055002. [Google Scholar] [CrossRef]
- Turyshev, S.G.; Toth, V.T. The Pioneer Anomaly. Living Rev. Relativ. 2010, 13, 4. [Google Scholar] [CrossRef]
- Jordan, J.F.; Madrid, G.A.; Pease, G.E. Effects of Major Errors Sources on Planetary Spacecraft Navigation Accuracies. J. Spacecr. Rocket. 1972, 9, 196–204. [Google Scholar] [CrossRef]
- Asmar, S.W.; Armstrong, J.W.; Iess, L.; Tortora, P. Spacecraft Doppler tracking: Noise budget and accuracy achievable in precision radio science observations. Radio Sci. 2005, 40, 1–9. [Google Scholar] [CrossRef]
- Xue, B.S.; Ye, Z.H. Study on the long-term prediction method of solar proton events. Manned Spacefl. 2007, 4, 47–53. [Google Scholar]
- Xue, B.S.; Ye, Z.H. Forecast of the enhancement of relativistic electron at the geo-synchronous orbit. Chin. J. Space Sci. 2004, 24, 283–288. [Google Scholar]
- Wang, S. Current situation and trend of solar-terrestrial system research. J. Geophys. 1996, 4, 449–450. [Google Scholar]
- Yang, X.C.; Wang, S.J.; Liang, J.B.; Shen, G.H. Electron orientation detection design on sun-synchronous orbit. J. Astronaut. 2012, 33, 281–284. [Google Scholar]
- Vincenzo, V.; Francesco, P.; Alessandro, S. The High-Energy Particle Detector on board of the CSES mission. EPJ Web Conf. 2017, 136, 01007. [Google Scholar]
- Jo, G.B.; Sohn, J.; Choi, C.R.; Yi, Y.; Min, K.W.; Kang, S.B.; Na, G.W.; Shin, G.H. Development of High Energy Particle Detector for the Study of Space Radiation Storm. J. Astron. Space Sci. 2014, 31, 277–283. [Google Scholar] [CrossRef]
- Le, G.M.; Ye, Z.H. The Study of Space Distribution Configuration of the Radbelt Protons with High Energy. Chin. J. Space Sci. 2003, 23, 278–285. [Google Scholar]
- Buhler, P.; Desorgher, L.; Zehnder, A.; Daly, E.; Adams, L. Observations of the low earth orbit radiation environment from MIR. Radiat. Meas. 1996, 26, 917–921. [Google Scholar] [CrossRef] [PubMed]
- Lazutin, L.L.; Kuznetsov, S.N.; Podorol’skii, A.N. Dynamics of the radiation belt formed by solar protons during magnetic storms. Geomagn. Aeron. 2007, 47, 175–184. [Google Scholar] [CrossRef]
- Chen, G.F.; Ye, Z.H.; Zhu, G.W.; Shen, S.Z.; Liang, J.B.; Huang, H.J. Variation of proton in inner radiation belt during solar proton events. Chin. J. Geophys. 1993, 04, 428–433. [Google Scholar]
- Wissing, J.M.; Bornebusch, J.P.; Kallenrode, M.-B. Variation of energetic particle precipitation with local magnetic time. Adv. Space Res. 2007, 41, 1274–1278. [Google Scholar] [CrossRef]
- Ye, Z.H. Space Particle Radiation Detection Technology; Beijing Science Press: Beijing, China, 1986; pp. 77–78. [Google Scholar]
- Jiao, W.X. Space Exploration; Peking University Press: Beijing, China, 2002. [Google Scholar]
- Wimmer Schweingruber, R.F.; Janitzek, N.P.; Pacheco, D.; Cernuda, I.; Lara, F.E.; Gómez-Herrero, R.; Mason, G.M.; Allen, R.C.; Xu, Z.G.; Carcaboso, F.; et al. First year of energetic particle measurements in the inner heliosphere with Solar Orbiter’s Energetic Particle Detector. Astron. Astrophys. 2021, 656, A22. [Google Scholar] [CrossRef]
- Rodriguez Pacheco, J.; Wimmer Schweingruber, R.F.; Mason, G.M.; Ho, G.C.; Sánchez-Prieto, S.; Prieto, M.; Martín, C.; Seifert, H.; Andrews, G.B.; Kulkarni, S.R.; et al. The Energetic Particle Detector. Energetic particle instrument suite for the Solar Orbiter mission. Astron. Astrophys. 2019, 642, A7. [Google Scholar] [CrossRef]
- Hou, D.H.; Zhang, S.Y.; Zhang, X.X.; Zong, W. Design and research of collimator for space high-energy electron detector. J. Vac. Sci. Technol. 2020, 40, 965–970. [Google Scholar]
- Zhang, S.Y.; Wang, S.J. Design and research of deflection magnet in spaceborne particle detector. Chin. J. Geophys. 2007, 03, 684–690. [Google Scholar]
- Zhang, S.Y.; Zhang, X.G.; Wang, C.Q.; Shen, G.H.; Jing, T.; Zhang, B.Q.; Sun, Y.Q.; Zhu, G.W.; Liang, J.B.; Zhang, X.X.; et al. Calculation of geometric factors of space high-energy proton detector of FY-3 satellite. Sci. Sin. 2014, 44, 2479–2486. [Google Scholar]
- Douglass, M.; Bezak, E. Physical Modelling of Proton and Heavy Ion Radiation using Geant4. EPJ Web Conf. 2012, 35, 04001. [Google Scholar] [CrossRef]
- Khoo, L.Y.; Li, X.; Selesnick, R.S.; Schiller, Q.; Zhang, K.; Zhao, H.; Hogan, B.; Cantilina, J.T.; Sims, A.; Bauch, E.; et al. On the Challenges of Measuring Energetic Particles in the Inner Belt: A Geant4 Simulation of an Energetic Particle Detector Instrument, REPTile-2. J. Geophys. Res. Space Phys. 2022, 127, e2021JA030249. [Google Scholar] [CrossRef]
- Beretta, M.; Biassoni, M.; Gironi, L.; Maino, M.; Nastasi, M.; Pagnanini, L.; Pozzi, S. Monte Carlo simulation of particle detector data stream. Eur. Phys. J. Plus 2021, 136, 89. [Google Scholar] [CrossRef]
- Yando, K.; Millan, R.M.; Green, J.C.; Evans, D.S. A Monte Carlo simulation of the NOAA POES medium energy proton and electron detector instrument. J. Geophys. Res. Space Phys. 2011, 116, 10231. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Zhang, X.G.; Wang, C.Q.; Shen, G.; Jin, T.; Zhang, B.; Sun, Y.; Zhu, G.; Liang, J.; Zhang, X.; et al. The geometric factor of high energy protons detector on FY-3 satellite. Sci. China Earth Sci. 2014, 57, 2558–2566. [Google Scholar] [CrossRef]
- Babu, E.M.; Tyssøy, H.N.; SmithJohnsen, C.; Maliniemi, V.; Salice, J.A.; Millan, R.M.; Richardson, I.G. Determining Latitudinal Extent of Energetic Electron Precipitation Using MEPED On-Board NOAA/POES. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030489. [Google Scholar] [CrossRef]
- Sandanger, M.I.; Glesnes Ødegaard, L.K.; Tyssøy, H.N.; Stadsnes, J.; Søraas, F.; Oksavik, K.; Aarsnes, K. In-flight calibration of NOAA POES proton detectors—Derivation of the MEPED correction factors. J. Geophys. Res. Space Phys. 2015, 120, 9578–9593. [Google Scholar] [CrossRef]
- Belhaj, M.; Dadouch, S. A simple method for energy calibration of keV incident electron beam using a contactless electrostatic voltmeter probe. Rev. Sci. Instrum. 2021, 92, 083301. [Google Scholar] [CrossRef]
- Maier, D.; Limousin, O. Energy calibration via correlation. Nucl. Inst. Methods Phys. Res. A 2016, 812, 43–49. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.Y.; Liang, X.H.; Xu, Y.B.; Peng, W.; He, J.; Guo, D.; Gong, K.; Liu, Y.; An, Z.; Zhang, D.; et al. Result of proton beam energy calibration of GECAM satellite charged particle detector. Radiat. Detect. Technol. Methods 2021. prepublish. [Google Scholar] [CrossRef]
- He, Z.Y.; Steckmeyer, J.C.; Kerambrun, A. Time and energy calibration of silicon telescope with secondary beam. Nucl. Tech. 1993, 16, 705–709. [Google Scholar]






| Item | Energy Range | Detection Field | Sensitivity |
|---|---|---|---|
| High-energy protons | 3~300 MeV | 40° | 5% (ΔN/N) |
| High-energy electrons | 0.15–5.7 MeV | 30° | 5% (ΔN/N) |
| Energy Channel | Energy Range | Logical Working Modes |
|---|---|---|
| P1 | 3–5 MeV | |
| P2 | 5–10 MeV | |
| P3 | 10–26 MeV | |
| P4 | 26–40 MeV | |
| P5 | 40–100 MeV | |
| P6 | 100–300 MeV |
| Energy Channel | Energy Range | Logical Working Modes |
|---|---|---|
| E1 | 0.15–0.35 MeV | |
| E2 | 0.35–0.65 MeV | |
| E3 | 0.65–1.20 MeV | |
| E4 | 1.2–2.0 MeV | |
| E5 | 2.0–5.7 MeV | |
| E6 | 3.0–5.7 MeV |
| Energy Range (MeV) | Flux (cm2ssr) | FY-3E Satellite Maximum (Counts/s) |
|---|---|---|
| 3–5 | 1 × 101–3 × 103 | 1 × 103 |
| 5–10 | 1 × 101–2 × 103 | 6 × 102 |
| 10–26 | 1 × 101–1 × 103 | 3 × 102 |
| 26–40 | 1 × 101–6 × 102 | 2 × 101 |
| 40–100 | 1 × 101–1 × 103 | 3 × 102 |
| 100–300 | 1 × 101–1 × 103 | 3 × 102 |
| Energy Range (MeV) | Flux (cm2ssr) | FY-3E Satellite Maximum (Counts/s) |
|---|---|---|
| 0.15–0.35 | 5 × 105–106 | 4 × 104 |
| 0.35–0.65 | 1 × 103–4 × 105 | 2 × 104 |
| 0.65–1.20 | 1 × 103–5 × 104 | 2 × 102 |
| 1.20–2.0 | 1 × 103–1 × 104 | 5 × 101 |
| 2.0–5.7 | 1 × 103–1 × 104 | 5 × 101 |
| Electronic Counting Error | Sensor Counting Error | Geometric Factor Error | Flux Error | |
|---|---|---|---|---|
| Error | 0.95% | 4.8% | 3% | 8.75% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, G.; Zhang, X.; Wang, J.; Huang, C.; Li, J.; Zhang, S.; Zhang, X.; Yang, Y.; Zhang, P.; Sun, Y. Development and Calibration of a Three-Directional High-Energy Particle Detector for FY-3E Satellite. Aerospace 2023, 10, 173. https://doi.org/10.3390/aerospace10020173
Shen G, Zhang X, Wang J, Huang C, Li J, Zhang S, Zhang X, Yang Y, Zhang P, Sun Y. Development and Calibration of a Three-Directional High-Energy Particle Detector for FY-3E Satellite. Aerospace. 2023; 10(2):173. https://doi.org/10.3390/aerospace10020173
Chicago/Turabian StyleShen, Guohong, Xiaoxin Zhang, Jinhua Wang, Cong Huang, Jiawei Li, Shenyi Zhang, Xianguo Zhang, Yong Yang, Pengfei Zhang, and Yueqiang Sun. 2023. "Development and Calibration of a Three-Directional High-Energy Particle Detector for FY-3E Satellite" Aerospace 10, no. 2: 173. https://doi.org/10.3390/aerospace10020173
APA StyleShen, G., Zhang, X., Wang, J., Huang, C., Li, J., Zhang, S., Zhang, X., Yang, Y., Zhang, P., & Sun, Y. (2023). Development and Calibration of a Three-Directional High-Energy Particle Detector for FY-3E Satellite. Aerospace, 10(2), 173. https://doi.org/10.3390/aerospace10020173






