A Large Neighborhood Search Algorithm with Simulated Annealing and Time Decomposition Strategy for the Aircraft Runway Scheduling Problem
Abstract
1. Introduction
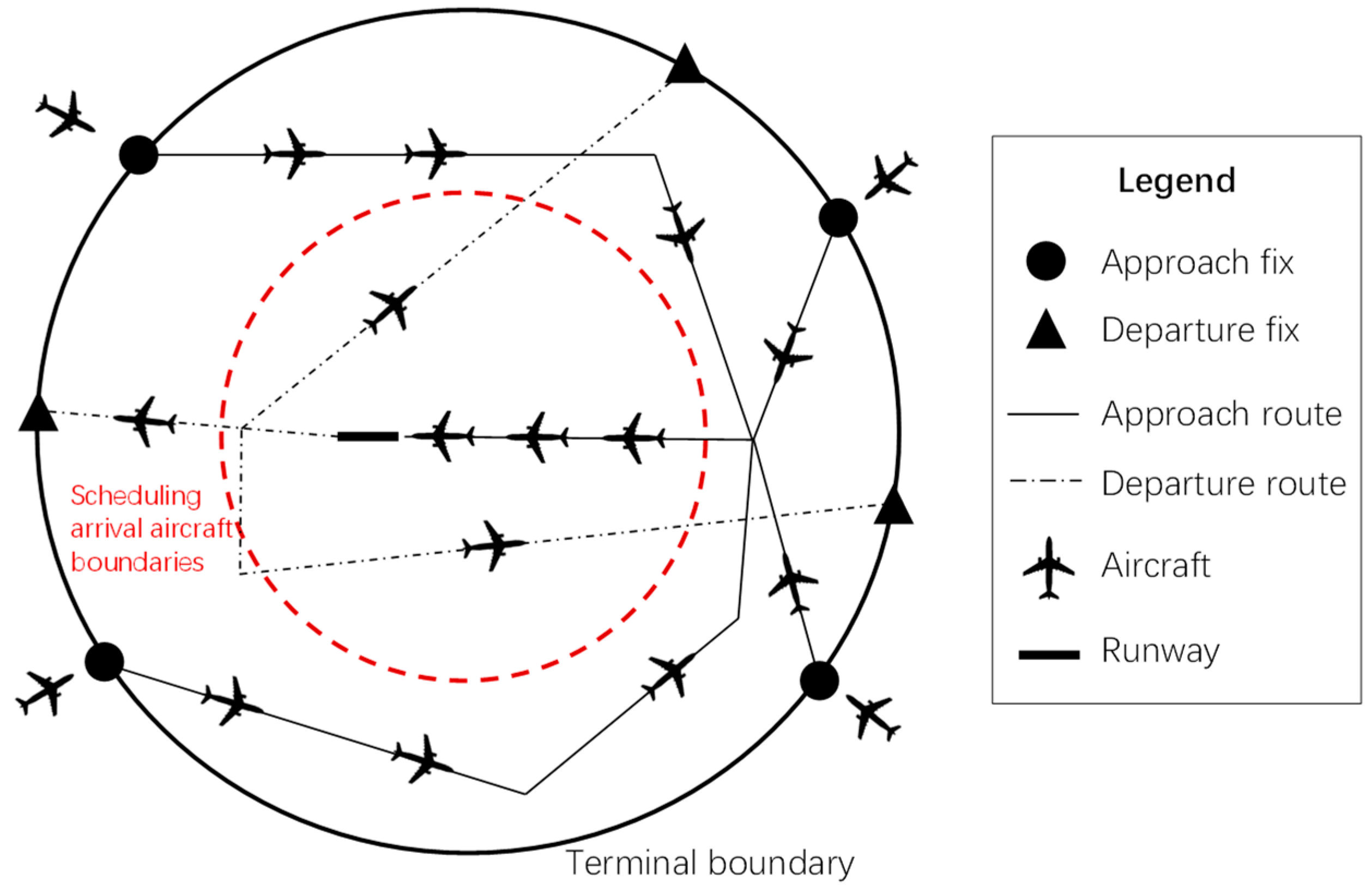
1.1. Problem Description
1.2. Literature Review
- (1)
- This research aims to improve the neighborhood construction method, which is one of the cores of the simulated annealing algorithm. We propose the large neighborhood search simulated annealing algorithm (SALNS). The breaking process, reorganization process, and local search process are introduced to improve the efficiency of the algorithm operations. Combining the large neighborhood search with a simulated annealing algorithm can fully utilize the advantages of both.
- (2)
- We aim to combine the RHC framework with the SALNS algorithm, and propose the RHC-SALNS algorithm to further improve the efficiency of the algorithm for solving ARSP models.
1.3. Organisation of the Paper
2. Mathematical Model
2.1. Notations
2.2. Constraints
2.2.1. Safety Separation Constraints
2.2.2. Time Window Constraints
2.2.3. Runway Occupancy Time Constraints
2.2.4. Flight Turnaround Constraint
2.3. Objectives
| the voyage of aircraft i is consecutive | |
| otherwise | |
| the type of aircraft i is super | |
| the type of aircraft i is heavy | |
| the type of aircraft i is medium | |
| the type of aircraft i is light | |
| i is an arrival (departing) aircraft at airport arrival (departing) peaks | |
| otherwise |
3. The Proposed Method
3.1. Algorithm Design
- Step 1: Initialize the algorithm initial temperature , algorithm termination temperature , cooling coefficient , number of internal cycles , number of non-updating generations , and maximum number of non-updating generations ; encode and generate the initial solution (see Section 3.2, Section 3.3 for details), and then .
- Step 2: Calculate the objective function value of the current initial solution and make the optimal solution , and the optimal solution objective function value is .
- Step 3: If , execute Step 4; otherwise, make and execute Step 7.
- Step 4: The initial solution is broken (see Section 3.4.1 for details), reorganized (see Section 3.4.2 for details), and locally searched (see Section 3.4.3 for details) to generate the neighborhood solution .
- Step 5: Calculate the objective function value of the neighborhood solution ; accept the neighborhood solution according to the Metropolis criterion, .
- Step 6: If , then make , , , and return to Step 3.
- Step 7: . If the solution under the current temperature is the same as the solution under previous temperature, then .
- Step 8: If , or , stop the algorithm and output the optimal solution and the objective function value ; otherwise, return to Step 3.
3.2. Code
3.3. Initialisation
- Step 1: Randomly distribute the aircraft to all runways.
- Step 2: Based on the runway allocation result of Step 1, the aircraft sequence of each runway is initialized to first-come-first-served. Take one of the runways as an example; select the aircraft with the smallest expected runway usage time as the first to use that runway.
- Step 3: The aircraft that is closest to the last assigned aircraft in terms of runway usage time is not scheduled as the next aircraft to use the runway. Repeat until all the aircraft are scheduled.
- Step 4: Based on the generated aircraft sequence above, the runway usage time of the aircraft is assigned according to the constraints in Section 2.2.
| Algorithm 1. Initial solution generation method |
| be the number of aircraft and be the number of runways; |
| be the safety separation between aircraft and aircraft ; |
| 3: Set The solution after the breaking and reorganization process; |
| 4: Sort the aircraft based on their estimated runway usage times , and add them to , where |
| 5: while do |
| 6: Randomly select a runway from and add to ; |
| 7: ; |
| 8: end while |
| 9: while do |
| 10: for each two aircraft and belong to |
| 11: If then assign to ; |
| 12: Else assign to ; |
| 13: end if |
| 14: ; |
| 15: end while |
| 16: Return the generated solution |
3.4. Large Neighborhood Search
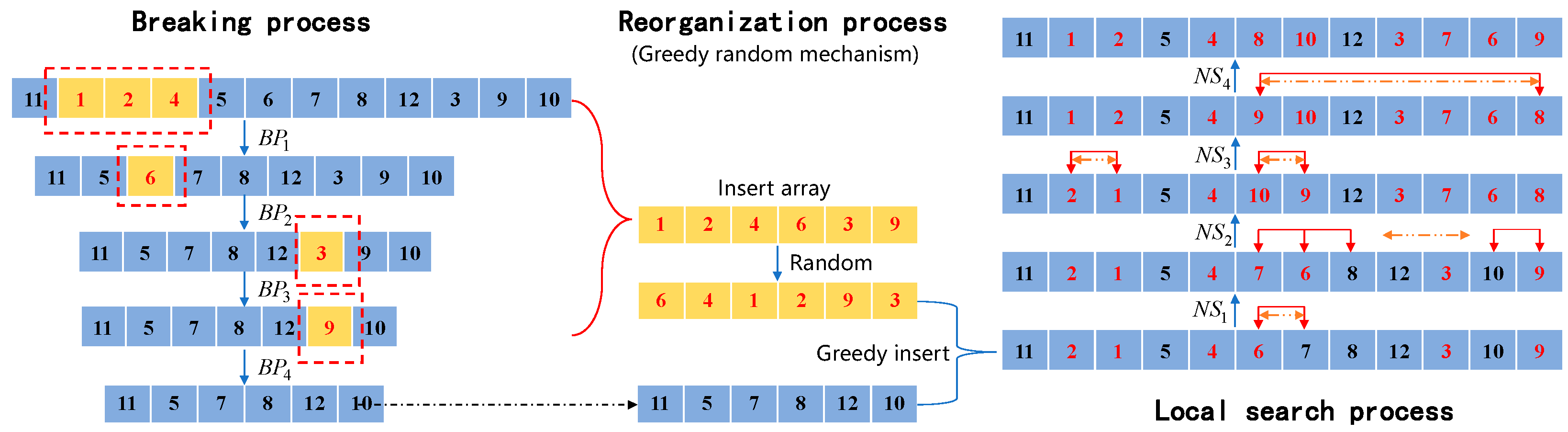
3.4.1. Breaking Process
- Step 1: Select a random aircraft as the root.
- Step 2: Calculate the maximum number of removed aircraft , , where ⌈ ⌉ denotes upward rounding and is the probability of adjacent breaking.
- Step 3: Randomly select the number of aircraft , is a random number between .
- Step 4: Remove the root aircraft and the closest aircraft from the root aircraft from the original sequence and add them to the Insert array.
- Step 1: Calculate the cost of aircraft delay savings for each aircraft after it is removed from the aircraft queue: , .
- Step 2: Calculate the maximum number of removed aircraft , , where ⌈ ⌉ denotes upward rounding and is the probability of maximum saving breaking.
- Step 3: Randomly select the number of removed aircraft , is a random number between .
- Step 4: Randomly select aircraft according to the roulette method, where the larger the , the greater the chance of the aircraft being selected for removal. Then, removal the selected Q2 aircraft to the insert array.
- Step 1: Calculate the maximum number of removed aircraft , , where ⌈ ⌉ denotes upward rounding and is the probability of random breaking.
- Step 2: Randomly select the number of removed aircraft , is a random number between .
- Step 3: Randomly select aircraft, remove all the selected aircraft, and add them to the insert array.
- Step 1: Generate a random number between .
- Step 2: If , then randomly remove an aircraft from the aircraft sequence and add it to the insert array. is the single point breaking probability.
| Algorithm 2. Breaking process |
| 1: Let be the number of the proposed breaking process; |
| 2: ; |
| 3: The solution after the initial solution generation process; |
| 4: while do |
| 5: Performs the initial solution breaking process using ; |
| 6: Put the breaking aircraft into the Insert array |
| 7: ; |
| 8: end while |
| 9: and Insert array |
3.4.2. Reorganization Process
- Step 1: Randomly disorder the aircraft to be inserted in the Insert array.
- Step 2: If there is no point to be inserted, end; otherwise, find the aircraft positions available for insertion on each runway according to the aircraft runway usage time constraint in Section 2.2.
- Step 3: Calculate the increase in cost for all positions available for insertion, randomly select the position with the smallest or second smallest cost, and return to Step 2.
| Algorithm 3. Reorganization process |
| 1: Let be the number of the breaking aircraft; |
| 2: The solution after the breaking process; |
| 3: Randomly disrupt the aircraft in the insert array; |
| 4: while do |
| 5: the positions on each runway available for aircraft according to the safety interval and the time window constraint in Section 2.2; |
| 6: Calculate the insertion cost of each insertable point and sort them in ascending order |
| 7: Randomly insert the aircraft at the insertion point and ; |
| 8: ; |
| 9: end while |
| 10: Return as |
3.4.3. Local Search Process
| Algorithm 4. Local search process |
| 1: Let be the number of the local search process; |
| 2: Set ; |
| 3: The solution after the breaking and reorganization process; |
| 4: while do |
| 5: Generates a neighborhood of using ; |
| 6: If then |
| 7: ; |
| 8: ; |
| 9: else |
| 10: ; |
| 11: end if |
| 12: end while |
| 13: Return |
3.5. Time Decomposition Approach
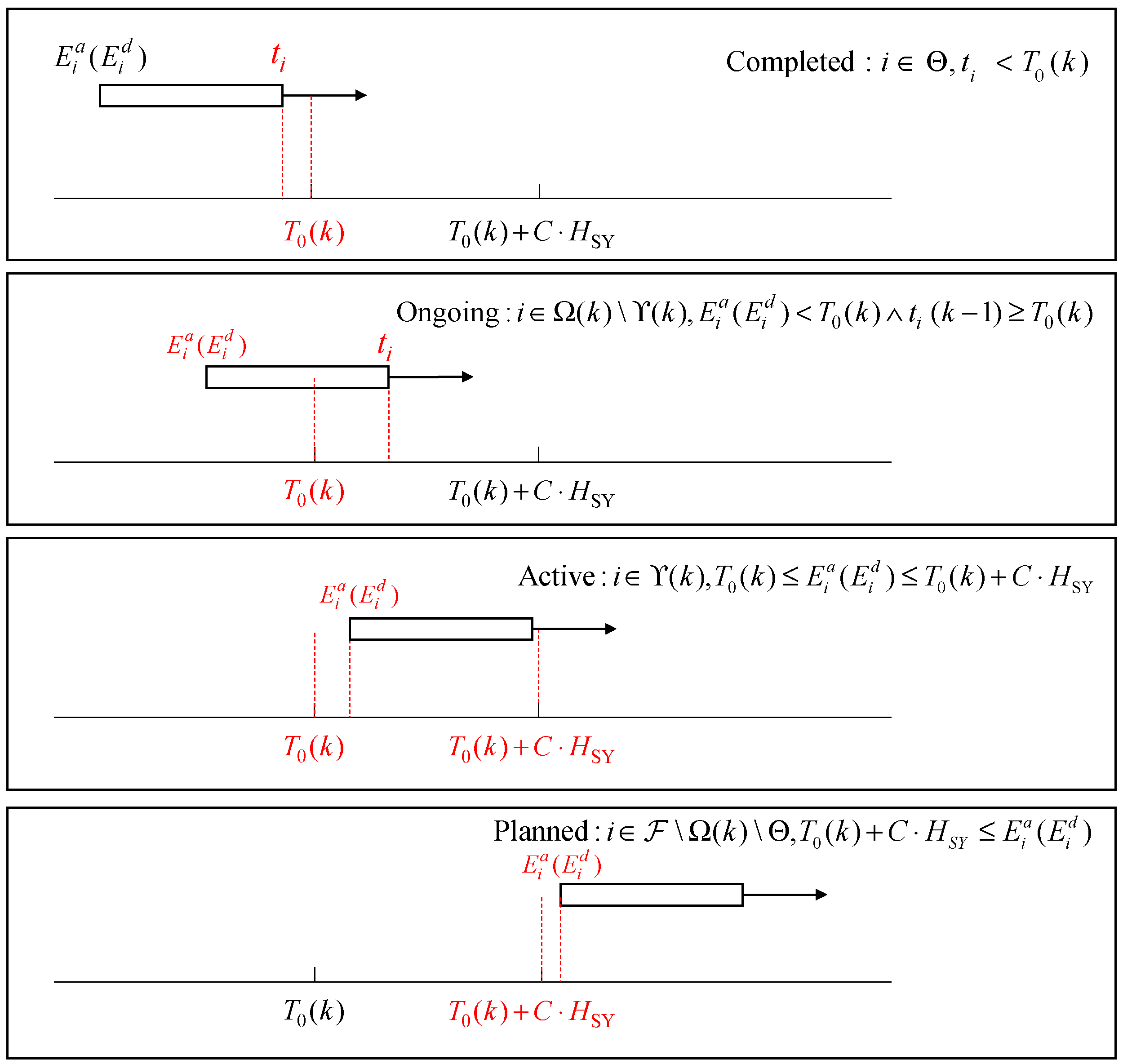
3.5.1. Aircraft Status Classification
3.5.2. Receding Horizon Control Strategy
- Step 1: Generate the initial aircraft queue in the order of the values of and ; set the of the first aircraft to if the first aircraft ; set the of the first aircraft to if the first aircraft . Let = 0; set the value of ; initialize , , and .
- Step 2: After the completion of the stage of aircraft scheduling, those aircraft with are put into the set . is calculated with reference to Equation (10).Freeze the existing scheduling results of those aircraft with, put them into the set , and update the constraints with reference to Equation (11).Let . Put the aircraft which is in into . Put the aircraft which is in into .
- Step 3: The aircraft that, in , is optimally scheduled in the stage using the SALNS algorithm with reference to Equation (12), where
- Step 4: Let ; if , go to Step 5. Otherwise, go to Step 2.
- Step 5: Calculate with reference to Equation (13).
| Algorithm 5. RHC-SALNS |
| Require: matrix, , for aircraft its , maximum acceptable delay time . For aircraft its , maximum acceptable delay time . 1: Generate initial parameter value, set , 2: , ; 3: while do 4: use SALNS algorithm schedule aircraft runway operation 5: set choose from which 6: 7: calculate 8: 9: set choose from which 10: 11: for in 12: reset constraints ; 13: end for 14: set choose from which 15: 16: set choose from which 17: 18: set ; 19: ; 20: end while 21: |
4. Experimental Results and Comparisons
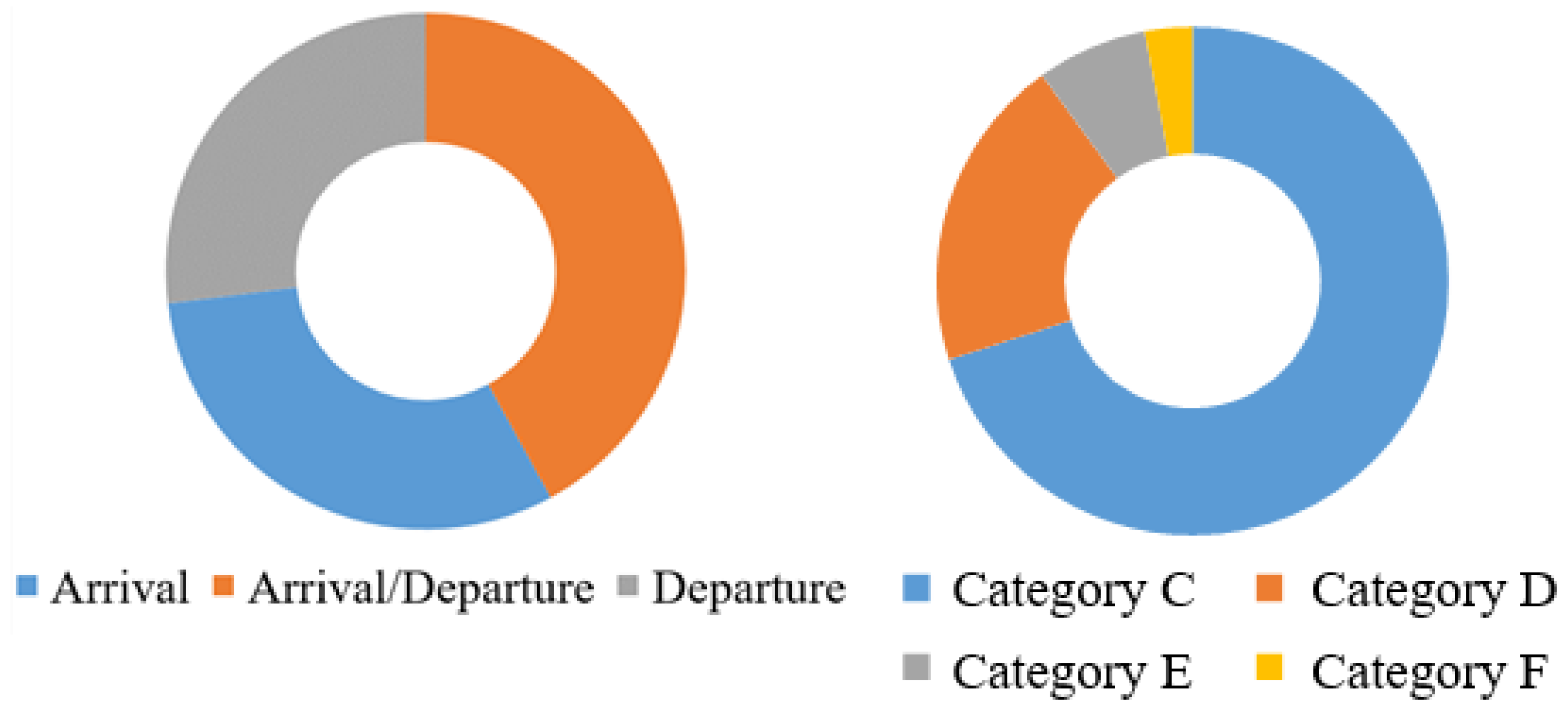
4.1. Experimental Setup
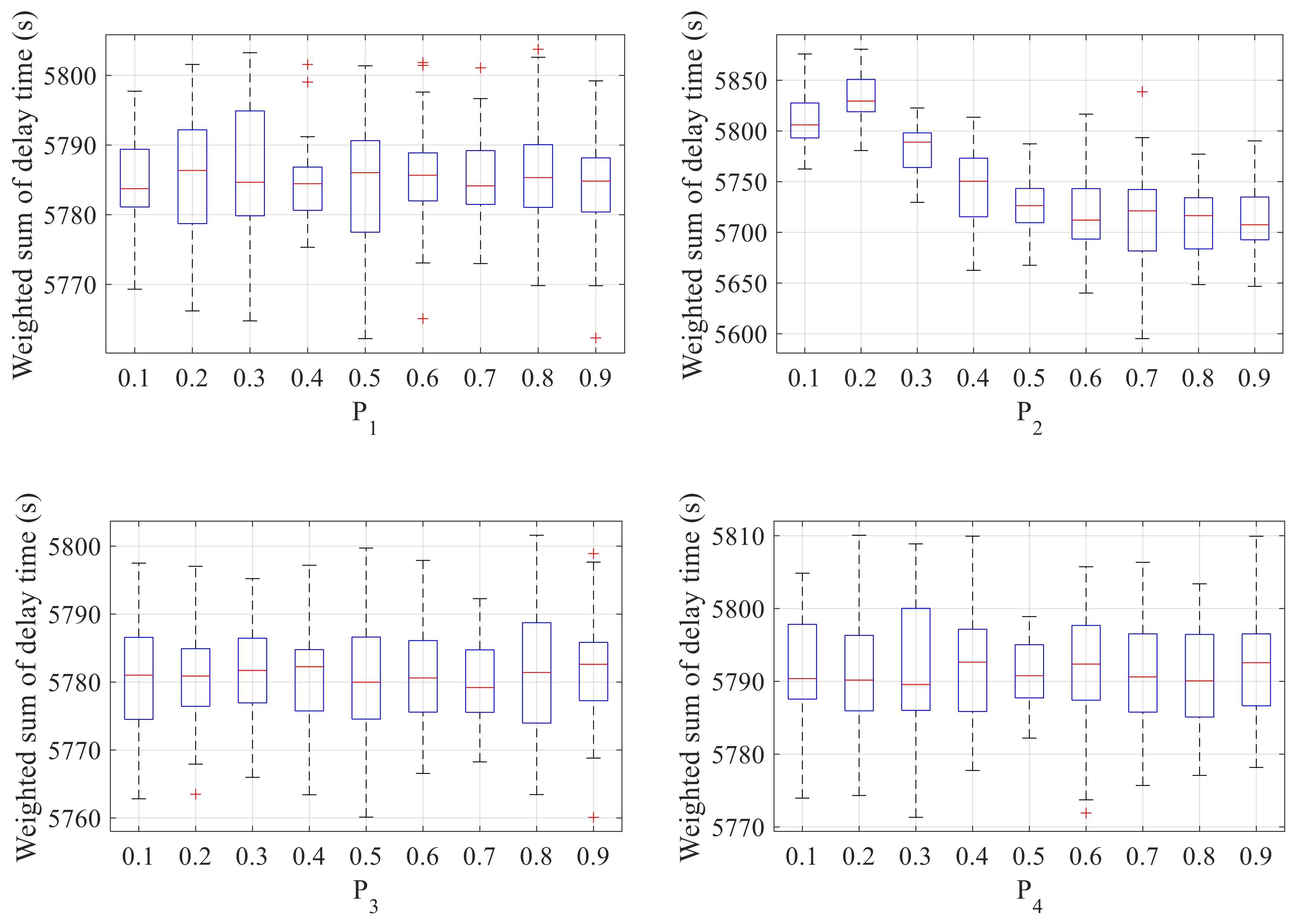
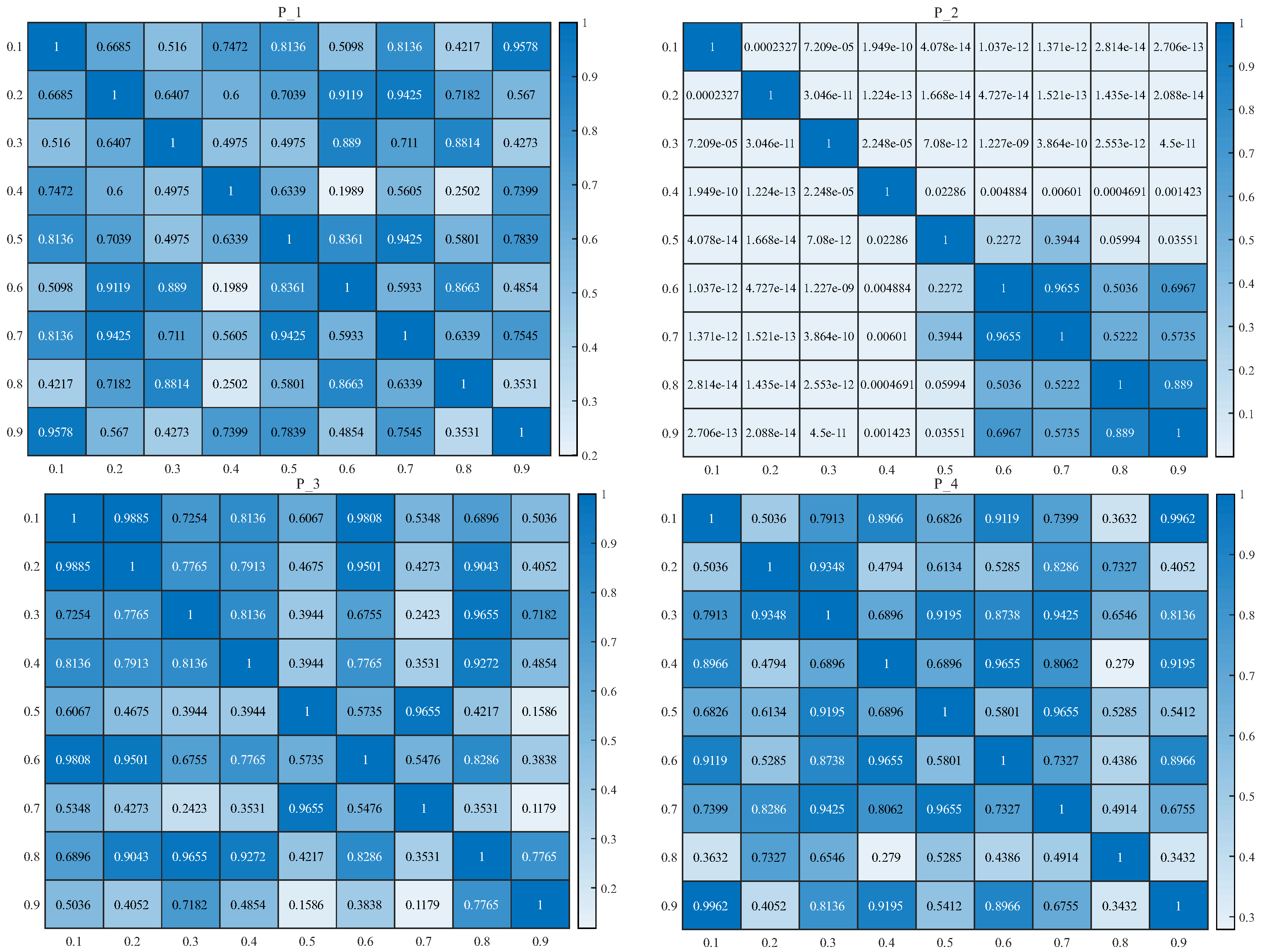
4.2. SALNS Parameters Sensitivity Analysis
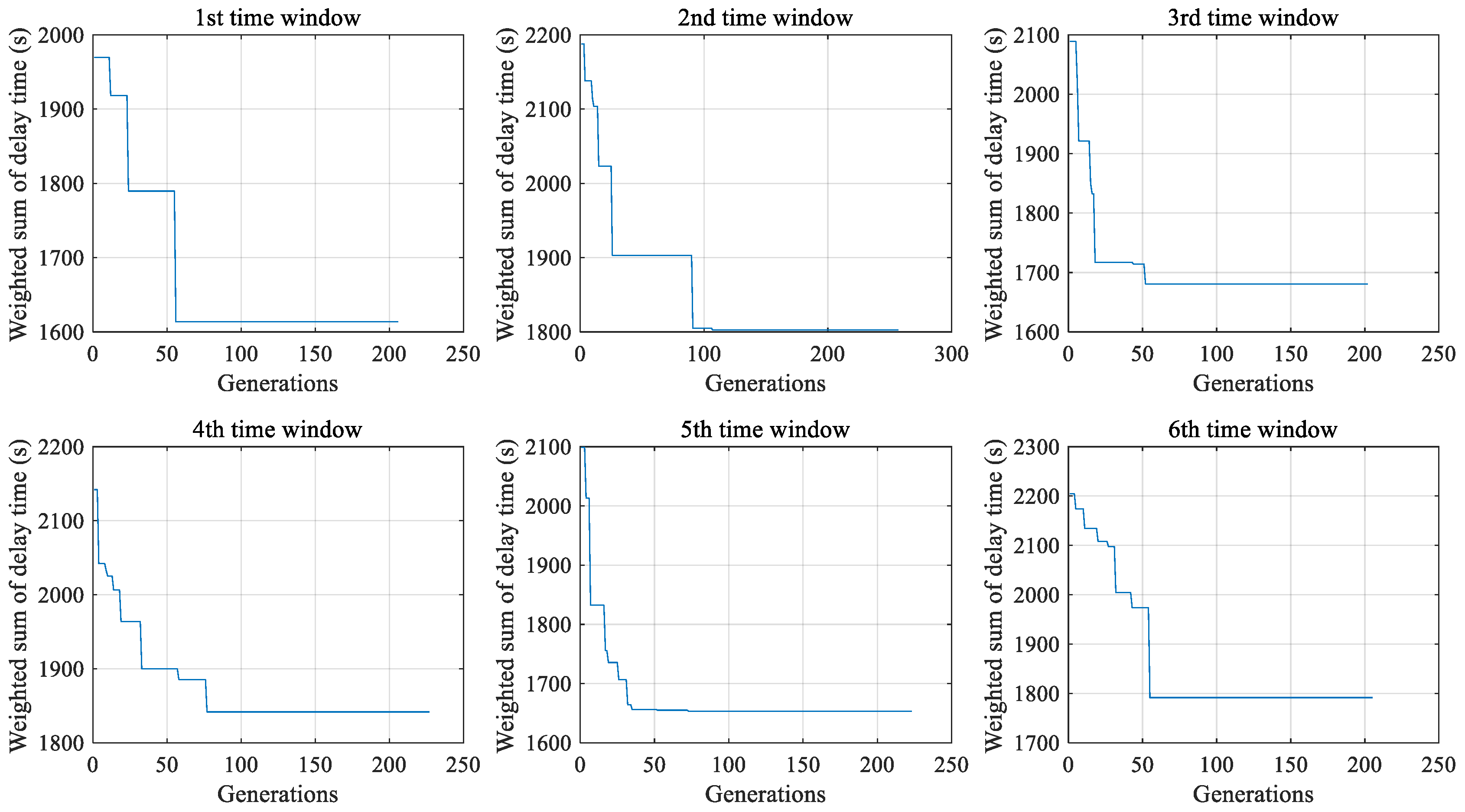
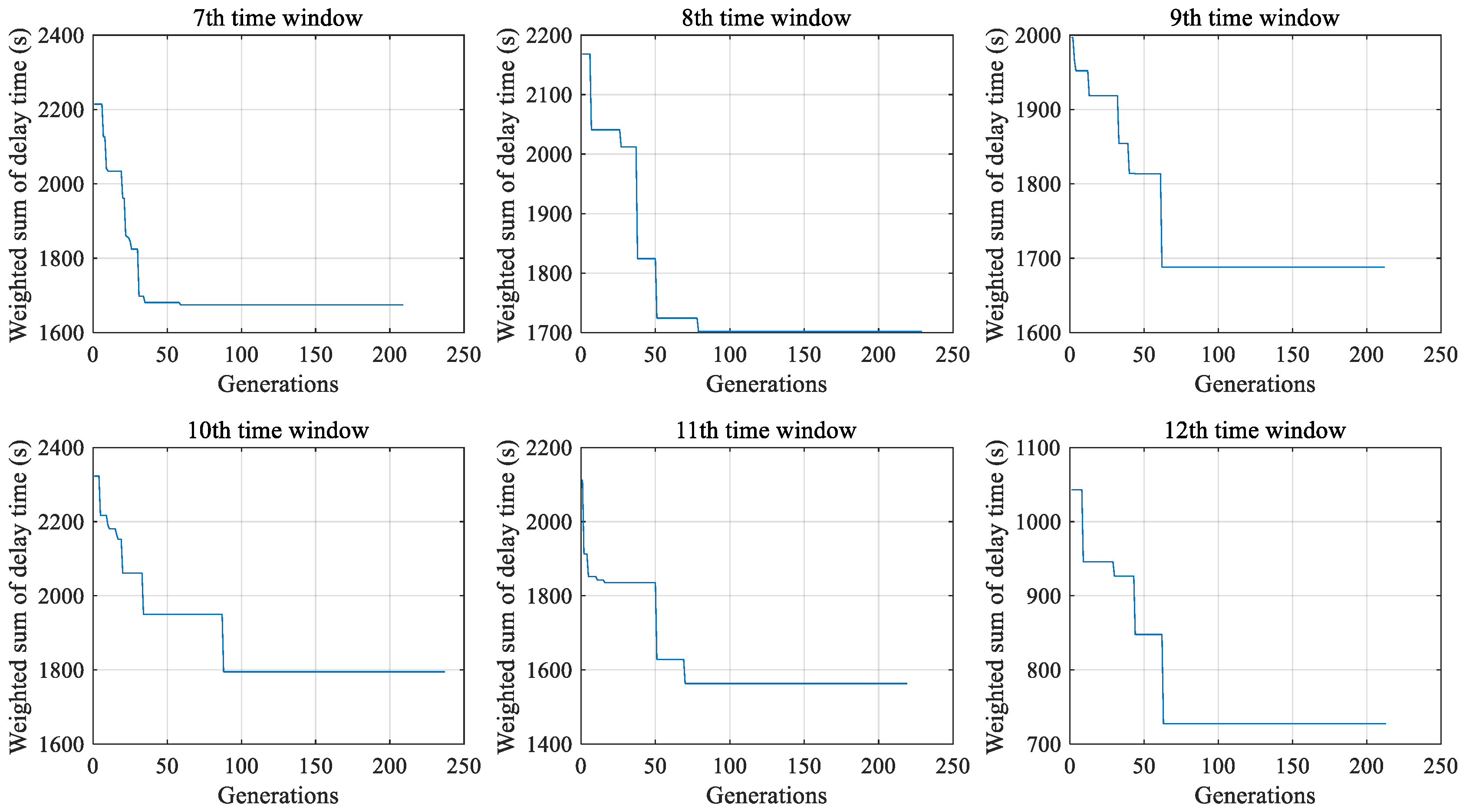
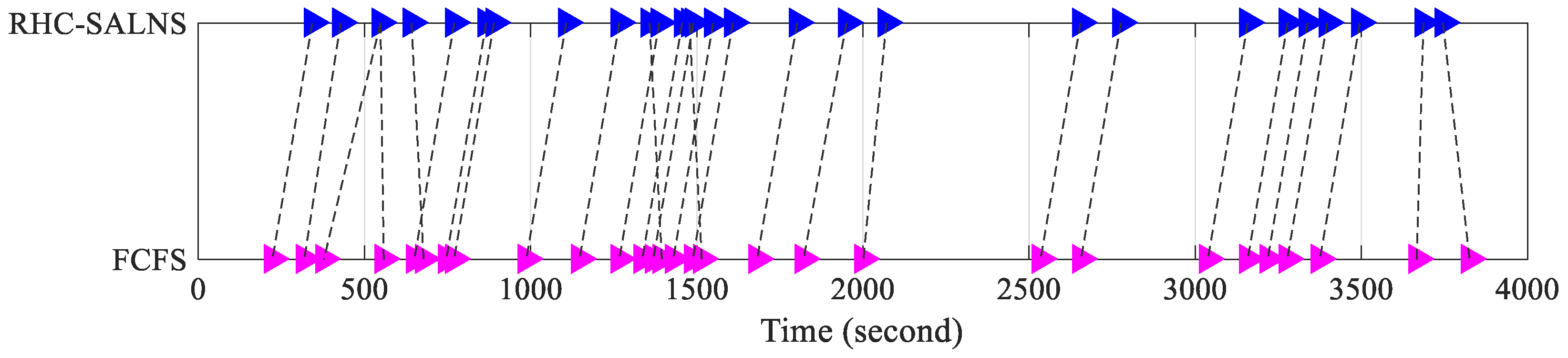
4.3. Receding Horizon Control Analysis
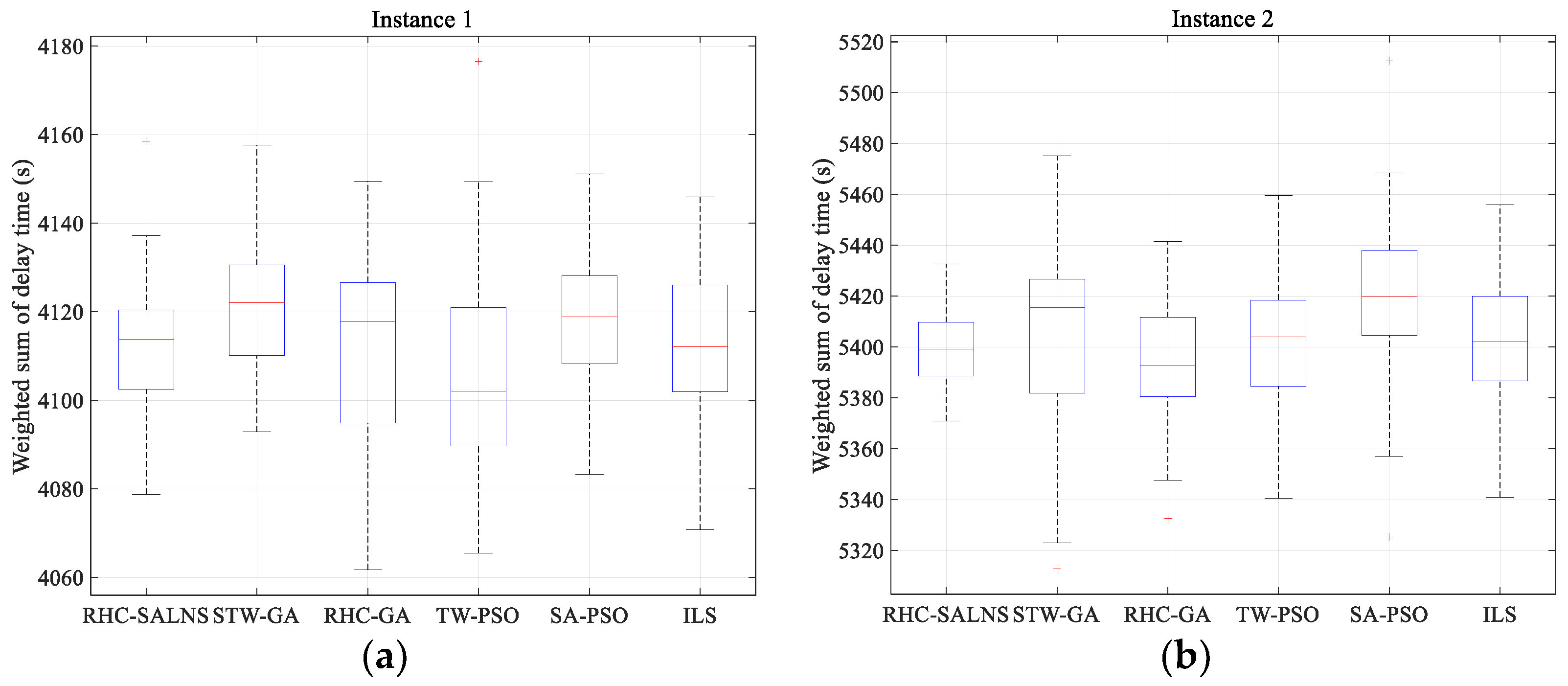
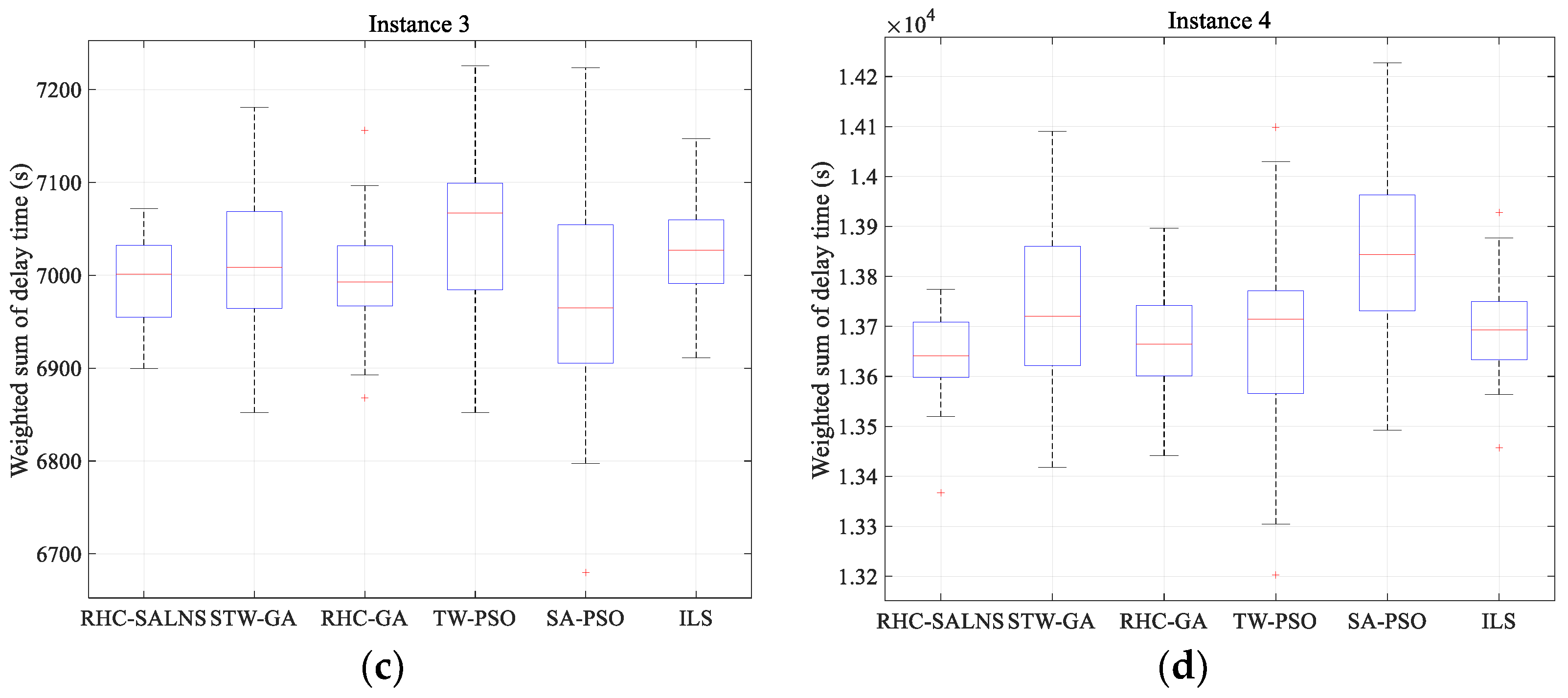
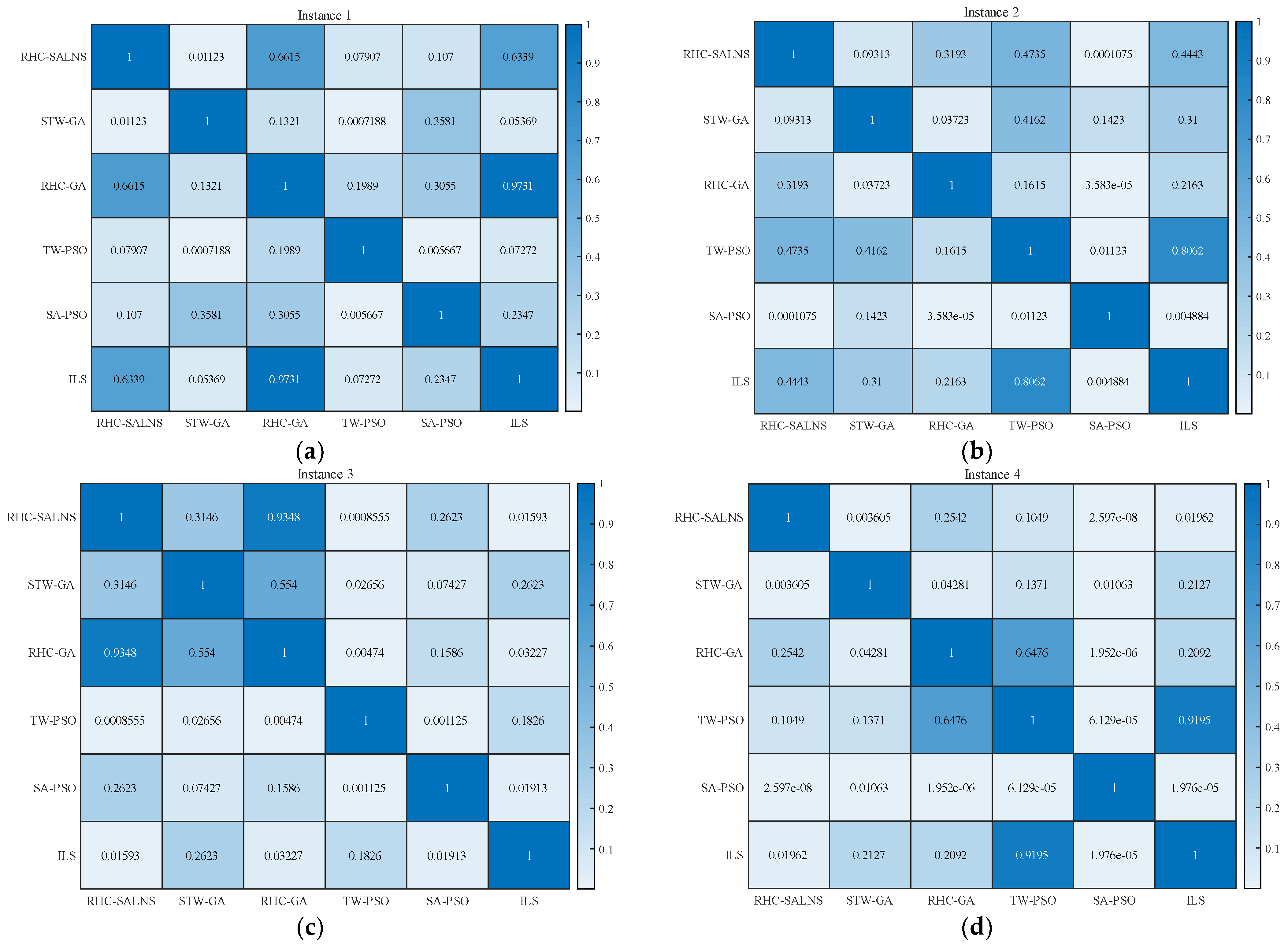
4.4. RHC-SALNS Compared to State of the Art Methodologies
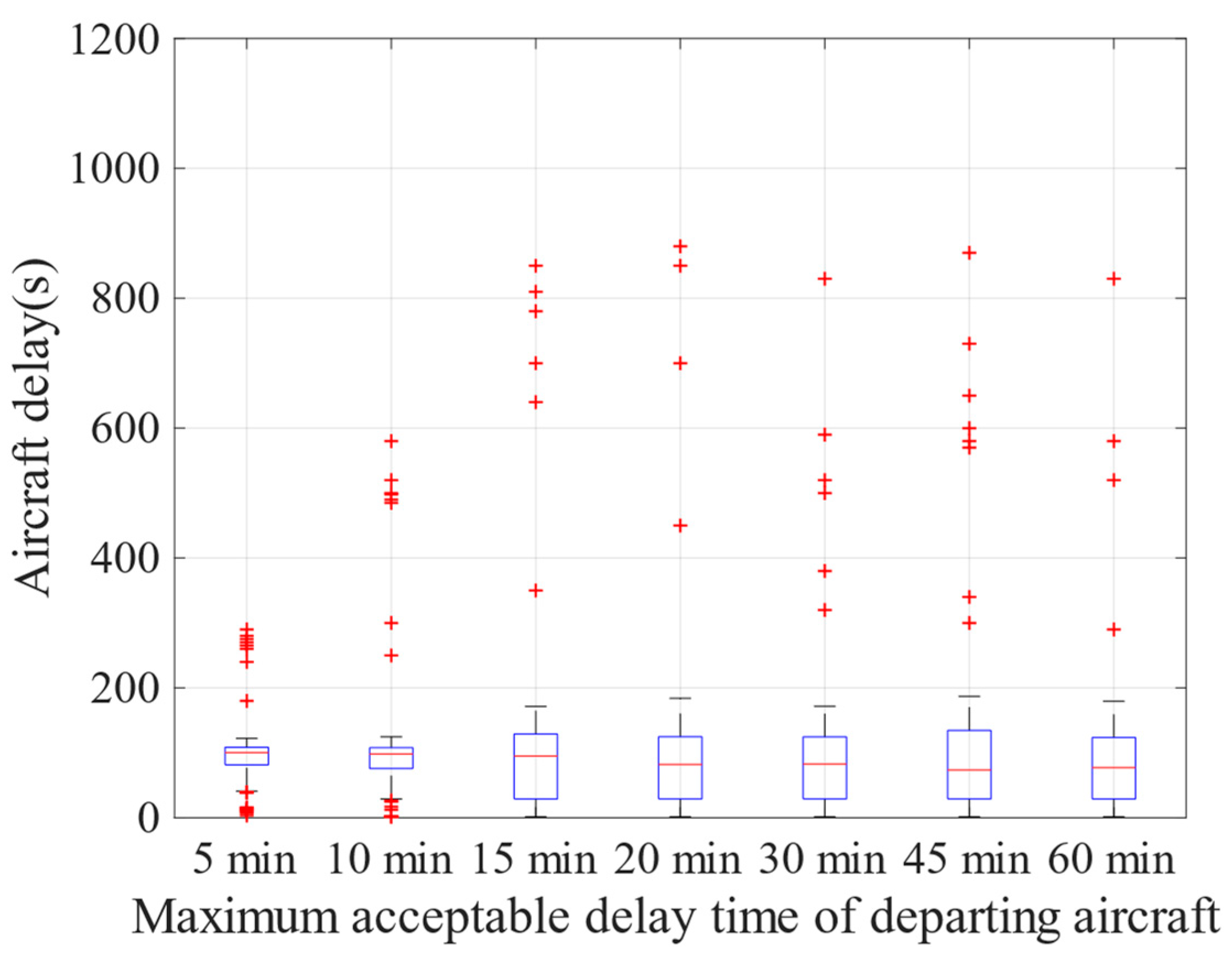
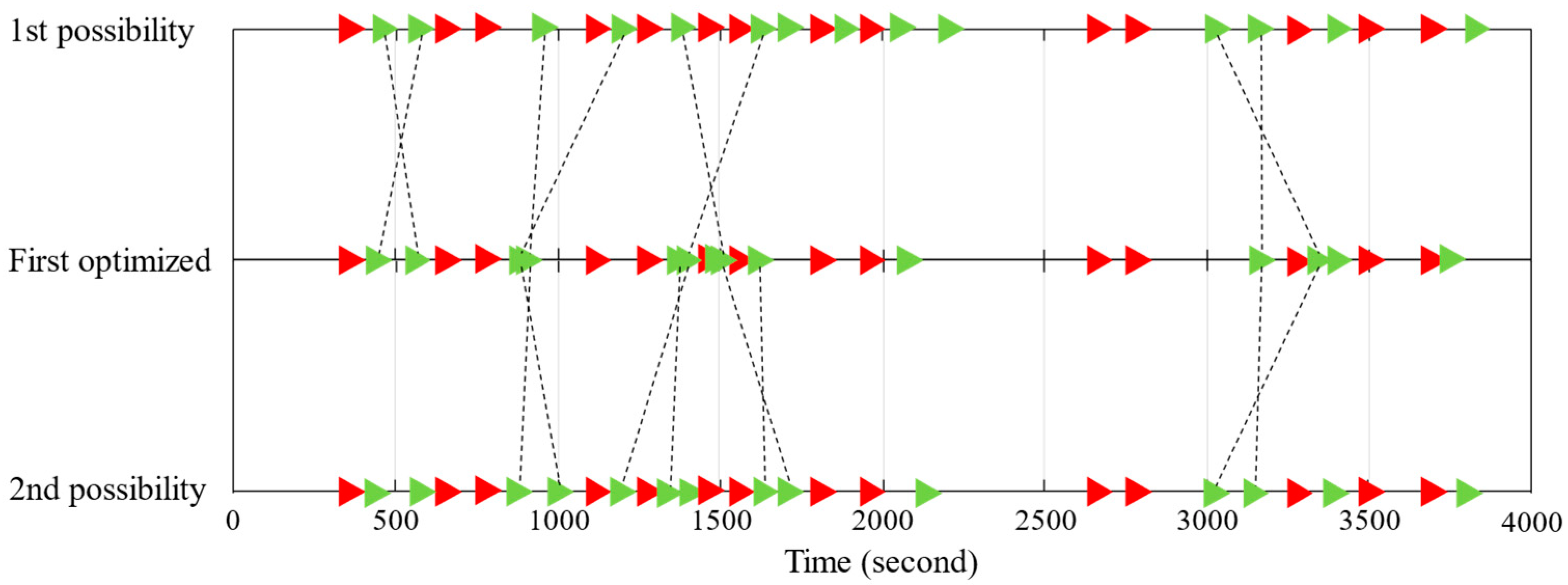
4.5. Analysis of Scheduling Results for Application
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| The set of aircraft that requiring scheduled during the planning time period | |
| The set of runways available for aircraft, where , | |
| The set of arrival aircraft that land at the airport and stay until planning time period, | |
| The set of departing aircraft that are parked at the airport at the beginning of the planning time period, | |
| The set of arrival-departing aircraft, | |
| The number of aircraft | |
| The number of runways | |
| The safety separation between aircraft i and aircraft | |
| Maximum acceptable delay time of arrival aircraft , | |
| Maximum acceptable delay time of departing aircraft , | |
| Runway occupancy time of aircraft , | |
| 1 if departing aircraft and arrival aircraft are a pair of connected aircraft, 0 otherwise, | |
| The minimum connection time between the takeoff time of departing aircraft and landing time of arrival aircraft , | |
| The estimated landing time of aircraft , | |
| The estimated takeoff time of aircraft , | |
| Extremely large values, applied to simplified the model | |
| Delay constraint weights of arrival aircraft | |
| The allocated runway usage time of aircraft , | |
| is 1 if the aircraft uses the runway , 0 otherwise, | |
| is 1 if aircraft uses the runway before aircraft , 0 otherwise. | |
| Algorithm initial temperature | |
| Algorithm termination temperature | |
| Cooling coefficient | |
| Number of internal cycles | |
| Maximum number of non-updating generations | |
| Initial solution | |
| Neighborhood solution | |
| Objective function value of the current initial solution | |
| Optimal solution | |
| Number of algorithm iterations | |
| Maximum number of removed aircraft | |
| Probability of adjacent breaking | |
| Probability of maximum saving breaking | |
| Probability of random breaking | |
| Probability of single point breaking | |
| The length of an operating interval | |
| The length of receding horizon | |
| The beginning time of the receding horizon at the kth operating interval | |
| The scheduled runway usage time of aircraft is in the interval after the kth optimization scheduling stage | |
| The set of aircraft participating in the optimization scheduling of the stage | |
| The set of aircraft that have completed scheduling after the completion of the kth optimization scheduling stage | |
| The set of aircraft that have not completed scheduling after the completion of the kth optimization scheduling stage | |
| The set of aircraft that or in interval | |
| Estimated take-off time is at the kth operating stage | |
| Estimated landing time is at the kth operating stage |
Abbreviations
| ARSP | Aircraft runway scheduling problem |
| RHC | Receding horizon control |
| SA | Simulated annealing algorithm |
| SALNS | Large neighborhood search simulated annealing algorithm |
| RHC-SALNS | Large neighborhood search algorithm combined with simulated annealing and the receding horizon control strategy |
| ATFM | Air traffic flow management |
| FCFS | The runway scheduling concept of first-come-first-served |
| TSP | Traveling salesman problem |
| TRP | Traveling repairman problem |
| MIP | Mixed integer programming |
| PFSP | Permutation flow shop scheduling problem |
| ILS | Iterated local search algorithm |
| SA-PSO | Simulated annealing particle swarm algorithm |
| STW-GA | Sliding time window algorithm with the dual-structured chromosome genetic algorithm |
| TW-PSO | Sliding time window algorithm with the particle swarm optimization algorithm |
References
- Boeing. Commercial Market Outlook 2019–2038. 2019. Available online: https://www.boeing.com/commercial/market/commercial-market-outlook/ (accessed on 30 January 2023).
- Sölveling, G.; Clarke, J.-P. Scheduling of airport runway operations using stochastic branch and bound methods. Transp. Res. Part C Emerg. Technol. 2014, 45, 119–137. [Google Scholar] [CrossRef]
- Hancerliogullari, G.; Rabadi, G.; Al-Salem, A.H.; Kharbeche, M. Greedy algorithms and metaheuristics for a multiple runway combined arrival-departure aircraft sequencing problem. J. Air Transp. Manag. 2013, 32, 39–48. [Google Scholar] [CrossRef]
- Mas, Q.G. The Research of Flight Sequencing of Air Traffic Management; Civil Aviation University of China: Tianjin, China, 2014. [Google Scholar]
- Bennell, J.A.; Mesgarpour, M.; Potts, C.N. Airport runway scheduling. 4OR 2011, 9, 115–138. [Google Scholar] [CrossRef]
- Xu, X.; Huang, B. Study of Fuzzy Integrated Judge Method Applied to the Aircraft Sequencing in the Terminal Area. Acta Aeronaut. Astronaut. Sin. 2001, 22, 259–261. [Google Scholar]
- Pohl, M. Runway Scheduling During Winter Operations—Models, Methods, and Applications. Doctoral Dissertation, Technische Universität München, Munich, Germany, 2020. [Google Scholar]
- Ratcliffe, S. Congestion in terminal areas. J. Navig. 1964, 17, 183–186. [Google Scholar] [CrossRef]
- Carr, G.C.; Erzberger, H.; Neuman, F. Airline arrival prioritization in sequencing and scheduling. In Proceedings of the 2nd USA/Europe Air Traffic Management R&D Seminar, Orlando, FL, USA, 1–4 December 1998. [Google Scholar]
- Bennell, J.A.; Mohammad, M.; Potts, C.N. Airport runway scheduling. Ann. Oper. Res. 2013, 204, 249–270. [Google Scholar] [CrossRef]
- Kjenstad, D.; Mannino, C.; Nordlander, T.E.; Schittekat, P.; Smedsrud, M. Optimizing AMAN-SMAN-DMAN at Hamburg and Arlanda airport. In Proceedings of the SESAR Innovation Days (SID), Stockholm, Sweden, 27 November 2013. [Google Scholar]
- Heidt, A.; Helmke, H.; Kapolke, M.; Liers, F.; Martin, A. Robust runway scheduling under uncertain conditions. J. Air Transp. Manag. 2016, 56, 28–37. [Google Scholar] [CrossRef]
- Kjenstad, D.; Mannino, C.; Schittekat, P.; Smedsrud, M. Integrated surface and departure management at airports by optimization. In Proceedings of the 5th International Conference on Modeling, Simulation and Applied Optimization (ICMSAO), Hammamet, Tunisia, 28–30 April 2013; pp. 1–5. [Google Scholar]
- Donohue, G.L. A macroscopic air transportation capacity model: Metrics and delay correlation. In New Concepts and Methods in Air Traffic Management; Springer: Berlin/Heidelberg, Germany, 2001; pp. 45–62. [Google Scholar]
- Chen, X. Research on Capacity Evaluation and Optimization Methods at Airport Airside; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2007. [Google Scholar]
- Balakrishnan, H.; Chandran, B.G. Algorithms for scheduling runway operations under constrained position shifting. Oper. Res. 2010, 58, 1650–1665. [Google Scholar] [CrossRef]
- Yin, J.; Ma, Y.; Hu, Y.; Han, K.; Yin, S.; Xie, H. Delay, throughput and emission tradeoffs in airport runway scheduling with uncertainty considerations. Netw. Spat. Netw. Spat. Econ. 2021, 21, 85–122. [Google Scholar] [CrossRef]
- Avella, P.; Boccia, M.; Mannino, C.; Vasilyev, I. Time-indexed formulations for the runway scheduling problem. Transp. Sci. 2017, 51, 1196–1209. [Google Scholar] [CrossRef]
- D’Ariano, A.; Pacciarelli, D.; Pistelli, M.; Pranzo, M. Real-time scheduling of aircraft arrivals and departures in a terminal maneuvering area. Networks 2015, 65, 212–227. [Google Scholar] [CrossRef]
- Beasley, J.E.; Krishnamoorthy, M.; Sharaiha, Y.M.; Abramson, D. Scheduling aircraft landings—The static case. Transp. Sci. 2000, 34, 180–197. [Google Scholar] [CrossRef]
- Bertsimas, D.; Frankovich, M. Unified optimization of traffic flows through airports. Transp. Sci. 2016, 50, 77–93. [Google Scholar] [CrossRef]
- Ceberio, J.; Mendiburu, A.; Lozano, J.A. Introducing the mallows model on estimation of distribution algorithms. In Proceedings of the International Conference on Neural Information Processing, Shanghai, China, 13–17 November 2011. [Google Scholar]
- Lieder, A.; Briskorn, D.; Stolletz, R. A dynamic programming approach for the aircraft landing problem with aircraft classes. Eur. J. Oper. Res. 2015, 243, 61–69. [Google Scholar] [CrossRef]
- Wei, M.; Sun, B.; Wu, W.; Jing, B. A multiple objective optimization model for aircraft arrival and departure scheduling on multiple runways. Math. Biosci. Eng. 2020, 17, 5545–5560. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Sbihi, M.; Delahaye, D. Optimization of departure runway scheduling incorporating arrival crossings. Int. Trans. Oper. Res. 2021, 28, 615–637. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, J.; Zhou, W. Bi-level Programming Model for Joint Scheduling of Arrival and Departure Flight Based on Traffic Scenario. Trans. Nanjing Univ. Aeronaut. Astronaut. 2021, 38, 671–684. [Google Scholar]
- De Maere, G.; Atkin, J.A.D.; Burke, E.K. Pruning rules for optimal runway sequencing. Transp. Sci. 2018, 52, 898–916. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, M.; Zhang, Y.; Gao, M. An Uncertainty Analysis of Arrival Aircraft Schedule Based on Monte-Carlo Simulation. J. Transp. Inf. Saf. 2016, 34, 22–28. [Google Scholar]
- Zhang, J.; Ge, T.; Zheng, Z. Collaborative Arrival and Departure Sequencing for Multi-airport Terminal Area. J. Transp. Syst. Eng. Inf. Technol. 2017, 17, 197–204. [Google Scholar]
- Zhang, J.; Yang, W. The Optimization Based on Priority for a Mixed Arrival Departure Aircraft Sequencing Problem. Oper. Res. Manag. Sci. 2018, 27, 115–121. [Google Scholar]
- Salehipour, A.; Modarres, M.; Naeni, L.M. An efficient hybrid meta-heuristic for aircraft landing problem. Comput. Oper. Res. 2013, 40, 207–213. [Google Scholar] [CrossRef]
- Sabar, N.R.; Kendall, G. An iterated local search with multiple perturbation operators and time varying perturbation strength for the aircraft landing problem. Omega 2015, 56, 88–98. [Google Scholar] [CrossRef]
- Wang, S.; Yang, Y.; Wu, X.; Liu, H. Research on Optimization Mathematical Model of Arrival Flight Scheduling. J. Sichuan Univ. (Eng. Sci. Ed.) 2015, 47, 113–120. [Google Scholar]
- Mas, Q.L. Study on Multi-Runway Aircraft Optimal Scheduling Method Based on Improved Genetic Algorithm; Chongqing University: Chongqing, China, 2019. [Google Scholar]
- Zhang, J.; You, L.; Yang, C. Arrival sequencing and scheduling based on multi-objective Imperialist competitive algorithm. Acta Aeronaut. Astronaut. Sin. 2021, 42, 475–487. [Google Scholar]
- Wang, L.; Lin, Y. Aircraft Sequencing Modeling and Algorithm for Shared Waypoints in Airport Group. J. Transp. Inf. Saf. 2021, 39, 93–99+136. [Google Scholar]
- Ji, X.-P.; Cao, X.-B.; Du, W.-B.; Tang, K. An evolutionary approach for dynamic single-runway arrival sequencing and scheduling problem. Soft Comput. 2017, 21, 7021–7037. [Google Scholar] [CrossRef]
- Hu, X.-B.; Chen, W.-H. Receding horizon control for aircraft arrival sequencing and scheduling. IEEE Trans. Intell. Transp. Syst. 2005, 6, 189–197. [Google Scholar] [CrossRef]
- Clarke, J.; Solak, S.; Chang, Y.; Ren, L.; Vela, A. Air traffic flow management in the presence of uncertainty. In Proceedings of the 8th USA/Europe Air Traffic Seminar (ATM’09), Napa, CA, USA, 29 June–2 July 2009; Volume 2. [Google Scholar]
- Zhang, Q.; Hu, M.; Shi, S.; Yang, J. Optimization algorithm of flight takeoff and landing on mutirunways. J. Traffic Transp. Eng. 2012, 12, 63–68. [Google Scholar]
- Lieder, A.; Stolletz, R. Scheduling aircraft take-offs and landings on interdependent and heterogeneous runways. Transp. Res. Part E Logist. Transp. Rev. 2016, 88, 167–188. [Google Scholar] [CrossRef]
- Ng, K.K.H.; Lee, C.K.M.; Chan, F.T.; Qin, Y. Robust aircraft sequencing and scheduling problem with arrival/departure delay using the min-max regret approach. Transp. Res. Part E Logist. Transp. Rev. 2017, 106, 115–136. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Federal Aviation Administration Order JO 7110.65X. Air Traffic Control. 2017. Available online: https://www.faa.gov/regulationspolicies/orders/notices/index.cfm/go/document.current/documentNumber/7110.65 (accessed on 30 January 2023).
- ICAO: Doc 8643 (Aircraft Type Designators). Available online: https://www.icao.int/publications/doc8643 (accessed on 30 January 2023).
- Malik, W.; Lee, H.; Jung, Y.C. Runway scheduling for Charlotte Douglas International airport. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016; pp. 1–11. [Google Scholar]
- Steinbrunn, M.; Moerkotte, G.; Kemper, A. Heuristic and randomized optimization for the join ordering problem. VLDB J. 1997, 6, 191–208. [Google Scholar] [CrossRef]
- Atkin, J.A.D.; Burke, E.K.; Greenwood, J.S.; Reeson, D. Hybrid metaheuristics to aid runway scheduling at London Heathrow airport. Transp. Sci. 2007, 41, 90–106. [Google Scholar] [CrossRef]
- Furini, F.; Persiani, C.A.; Toth, P. Aircraft sequencing problems via a rolling horizon algorithm. In Proceedings of the International Symposium on Combinatorial Optimization, Athens, Greece, 19–21 April 2012. [Google Scholar]
- Xiao, M.; Cai, K.; Abbass, H.A. Hybridized encoding for evolutionary multi-objective optimization of air traffic network flow: A case study on China. Transp. Res. Part E Logist. Transp. Rev. 2018, 115, 35–55. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. In Breakthroughs in Statistics; Kotz, S., Johnson, N., Eds.; Springer Series in Statistics; Springer: New York, NY, USA, 1992; pp. 196–202. [Google Scholar]
- Wen, X.; Huo, J. Research Based on Dynamic Priority for a Multi-runway Mixed Arrival-Departure Aircraft Scheduling Problem. Ind. Eng. Manag. 2021, 26, 1–8. [Google Scholar]
- Ikli, S.; Mancel, C.; Mongeau, M.; Olive, X.; Rachelson, E. The aircraft runway scheduling problem: A survey. Comput. Oper. Res. 2021, 132, 105336. [Google Scholar] [CrossRef]





| Sets | |
| The set of aircraft that requiring scheduled during the planning time period | |
| The set of arrival aircraft that land at the airport and stay until planning time period: | |
| The set of departing aircraft that are parked at the airport at the beginning of the planning time period: | |
| The set of arriving-departing aircraft: , | |
| The set of runways available for aircraft, where , | |
| Parameters | |
| The estimated landing time of aircraft: , | |
| The estimated takeoff time of aircraft: , | |
| The minimum runway usage separation time between aircraft: , | |
| Maximum acceptable delay time of arrival aircraft : | |
| Maximum acceptable delay time of departing aircraft : | |
| Runway occupancy time of aircraft : | |
| 1 if departing aircraft and arrival aircraft are a pair of connected aircraft, 0 otherwise: | |
| The minimum connection time between the takeoff time of departing aircraft and landing time of arrival aircraft: , | |
| Extremely large values, applied to simplify the model | |
| Variables | |
| The allocated runway usage time of aircraft: , | |
| is 1 if the aircraft uses the runway , 0 otherwise: | |
| is 1 if aircraft uses the runway before aircraft , 0 otherwise: |
| J | Arrival (Departing) at Peaks (1) | Otherwise (2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R | Super (1) | Heavy (2) | Medium (3) | Light (4) | Super (1) | Heavy (2) | Medium (3) | Light (4) | ||
| O | ||||||||||
| Consecutive (1) | 1 | 2 | 5 | 11 | 3 | 6 | 12 | 22 | ||
| Inconsecutive (2) | 7 | 11.5 | 19 | 30.5 | 12.5 | 20 | 31.5 | 48 | ||
| Instance Name | Number of Aircraft | Time Duration (Second) |
|---|---|---|
| Instance 1 | 150 | 13,200 |
| Instance 2 | 200 | 21,600 |
| Instance 3 | 250 | 25,200 |
| Instance 4 | 500 | 46,800 |
| Algorithm Framework | Parameters | Value |
|---|---|---|
| LNS | ||
| 0.2 | ||
| 0.6 | ||
| 0.3 | ||
| 0.4 | ||
| SA | ||
| 200 | ||
| 10,000 | ||
| 0.1 | ||
| 0.96 | ||
| 150 |
| Instance | Algorithm | Parameter Setting | Total Execution Time(s) | Objective Value(s) | Execution Time per Aircraft(s) |
|---|---|---|---|---|---|
| Instance 2 | SALNS | - | 2110 | 6270 | 10.55 |
| RHC-SALNS | , | 253.0 | 5345 | 1.27 | |
| RHC-SALNS | , | 204.35 | 5638 | 1.02 | |
| RHC-SALNS | , | 492.72 | 5494 | 2.46 | |
| RHC-SALNS | , | 364.8 | 5512 | 1.82 | |
| Instance 3 | SALNS | - | 2938 | 7756 | 10.95 |
| RHC-SALNS | , | 300.12 | 6971 | 1.20 | |
| RHC-SALNS | , | 243.6 | 6774 | 0.97 | |
| RHC-SALNS | , | 567.39 | 7018 | 2.27 | |
| RHC-SALNS | , | 398.2 | 7084 | 1.59 | |
| Instance 4 | SALNS | - | 4557 | 15,164 | 11.54 |
| RHC-SALNS | , | 571.4 | 13,691 | 1.14 | |
| RHC-SALNS | , | 411.21 | 13,664 | 0.82 | |
| RHC-SALNS | , | 1072.53 | 13,535 | 2.15 | |
| RHC-SALNS | , | 742.75 | 14,565 | 1.49 |
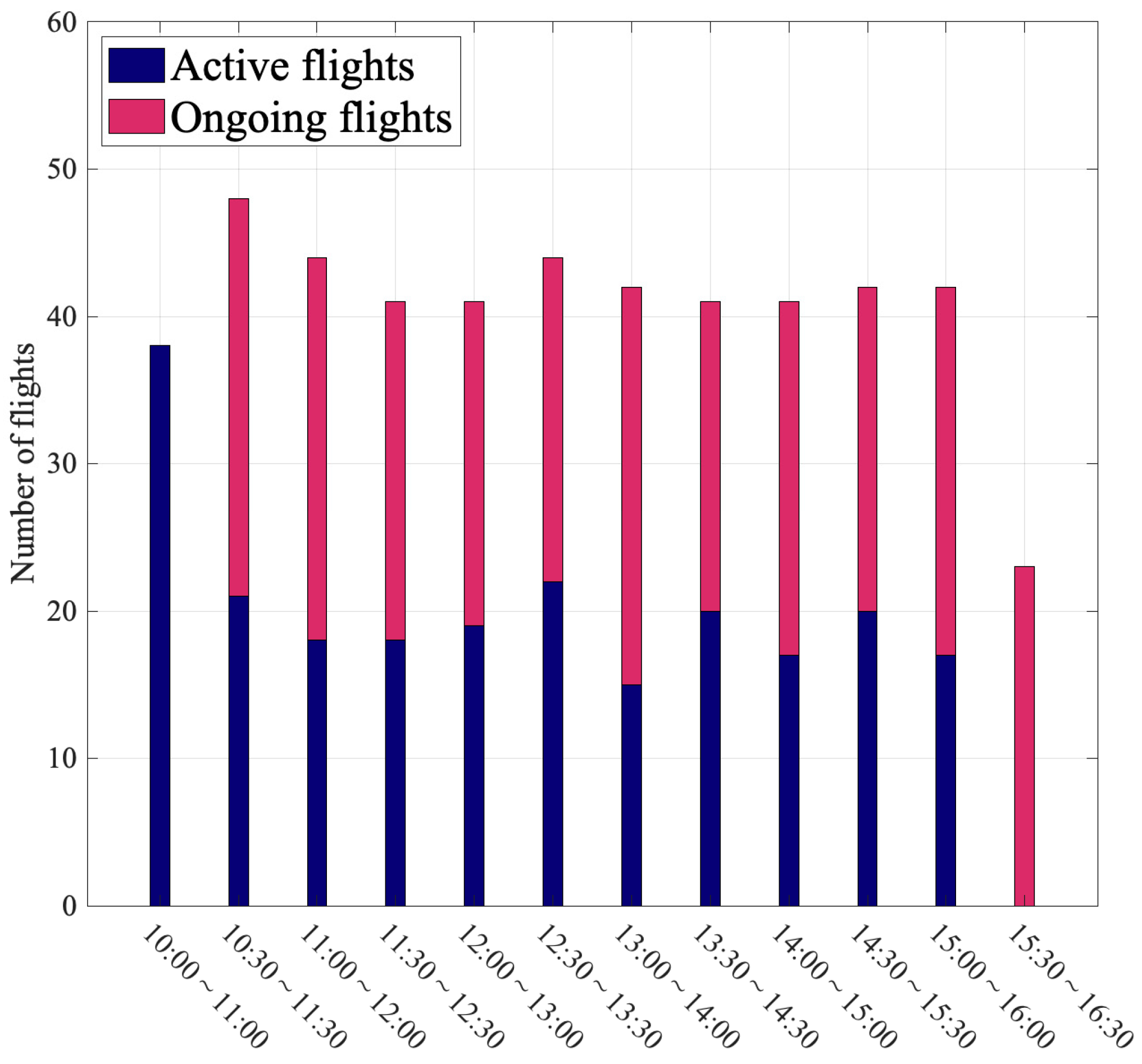
| Parameter Setting | Time Horizon | Active Aircraft | Ongoing Aircraft | Total Aircraft | Execution Time(s) | Objective Value(s) |
|---|---|---|---|---|---|---|
| 10:00–11:00 | 38 | 0 | 38 | 22.25 | 1565 | |
| 10:30–11:30 | 21 | 27 | 48 | 28.22 | 1667 | |
| 11:00–12:00 | 18 | 26 | 44 | 18.83 | 1826 | |
| 11:30–12:30 | 18 | 23 | 41 | 22.97 | 1543 | |
| 12:00–13:00 | 19 | 22 | 41 | 18.25 | 1763 | |
| 12:30–13:30 | 22 | 22 | 44 | 24.56 | 1745 | |
| 13:00–14:00 | 15 | 27 | 42 | 20.08 | 1821 | |
| 13:30–14:30 | 20 | 21 | 41 | 26.84 | 1649 | |
| 14:00–15:00 | 17 | 24 | 41 | 20.79 | 1923 | |
| 14:30–15:30 | 20 | 22 | 42 | 20.17 | 1687 | |
| 15:00–16:00 | 17 | 25 | 42 | 21.51 | 1785 | |
| 15:30–16:30 | 0 | 23 | 23 | 8.54 | 759 |
| Instance | Algorithm | Average(s) | STD | Execution Time per Aircraft (s) |
|---|---|---|---|---|
| Instance 1 | RHC-SALNS | 4112.3 | 15.8 | 1.21 |
| STW-GA | 4121.1 | 13.8 | 1.18 | |
| RHC-GA | 4111.5 | 23.3 | 1.37 | |
| TW-PSO | 4106.6 | 24.8 | 1.43 | |
| SA-PSO | 4117.7 | 13.9 | 1.20 | |
| ILS | 4113.2 | 17.2 | 1.37 | |
| Instance 2 | RHC-SALNS | 5399.4 | 14.8 | 1.27 |
| STW-GA | 5405.8 | 36.9 | 2.07 | |
| RHC-GA | 5394.2 | 23.3 | 1.34 | |
| TW-PSO | 5402.9 | 28.8 | 1.26 | |
| SA-PSO | 5419.2 | 31.4 | 1.45 | |
| ILS | 5400.7 | 28.6 | 2.12 | |
| Instance 3 | RHC-SALNS | 6995.0 | 46.1 | 1.20 |
| STW-GA | 7011.9 | 68.8 | 3.81 | |
| RHC-GA | 6999.8 | 57.2 | 2.30 | |
| TW-PSO | 7049.2 | 78.7 | 3.24 | |
| SA-PSO | 6978.1 | 114.9 | 2.49 | |
| ILS | 7024.6 | 55.2 | 3.05 | |
| Instance 4 | RHC-SALNS | 13640.7 | 76.8 | 1.14 |
| STW-GA | 13747.2 | 162.0 | 4.23 | |
| RHC-GA | 13665.1 | 95.6 | 2.54 | |
| TW-PSO | 13667.4 | 185.7 | 3.70 | |
| SA-PSO | 13850.8 | 180.1 | 2.81 | |
| ILS | 13693.3 | 89.2 | 3.12 |
| Average Departing Delay Time(s) | STD | |
|---|---|---|
| 5 min | 122.8 | 68.15 |
| 10 min | 126.8 | 134.51 |
| 15 min | 114.14 | 180.17 |
| 20 min | 109.7 | 159.35 |
| 30 min | 108.6 | 139.16 |
| 45 min | 104.58 | 174.72 |
| 60 min | 107.46 | 137.82 |
| Instance | Execution Time per Aircraft(s) | Average Objective Value |
|---|---|---|
| Instance 2 | 1.47 s | 5582.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, J.; Hu, M.; Liu, Y.; Yin, J. A Large Neighborhood Search Algorithm with Simulated Annealing and Time Decomposition Strategy for the Aircraft Runway Scheduling Problem. Aerospace 2023, 10, 177. https://doi.org/10.3390/aerospace10020177
Su J, Hu M, Liu Y, Yin J. A Large Neighborhood Search Algorithm with Simulated Annealing and Time Decomposition Strategy for the Aircraft Runway Scheduling Problem. Aerospace. 2023; 10(2):177. https://doi.org/10.3390/aerospace10020177
Chicago/Turabian StyleSu, Jiaming, Minghua Hu, Yingli Liu, and Jianan Yin. 2023. "A Large Neighborhood Search Algorithm with Simulated Annealing and Time Decomposition Strategy for the Aircraft Runway Scheduling Problem" Aerospace 10, no. 2: 177. https://doi.org/10.3390/aerospace10020177
APA StyleSu, J., Hu, M., Liu, Y., & Yin, J. (2023). A Large Neighborhood Search Algorithm with Simulated Annealing and Time Decomposition Strategy for the Aircraft Runway Scheduling Problem. Aerospace, 10(2), 177. https://doi.org/10.3390/aerospace10020177






