Time-Varying Aeroelastic Modeling and Analysis of a Rapidly Morphing Wing
Abstract
:1. Introduction
2. Aeroelastic Modeling of the Rotating Variable Swept Wing
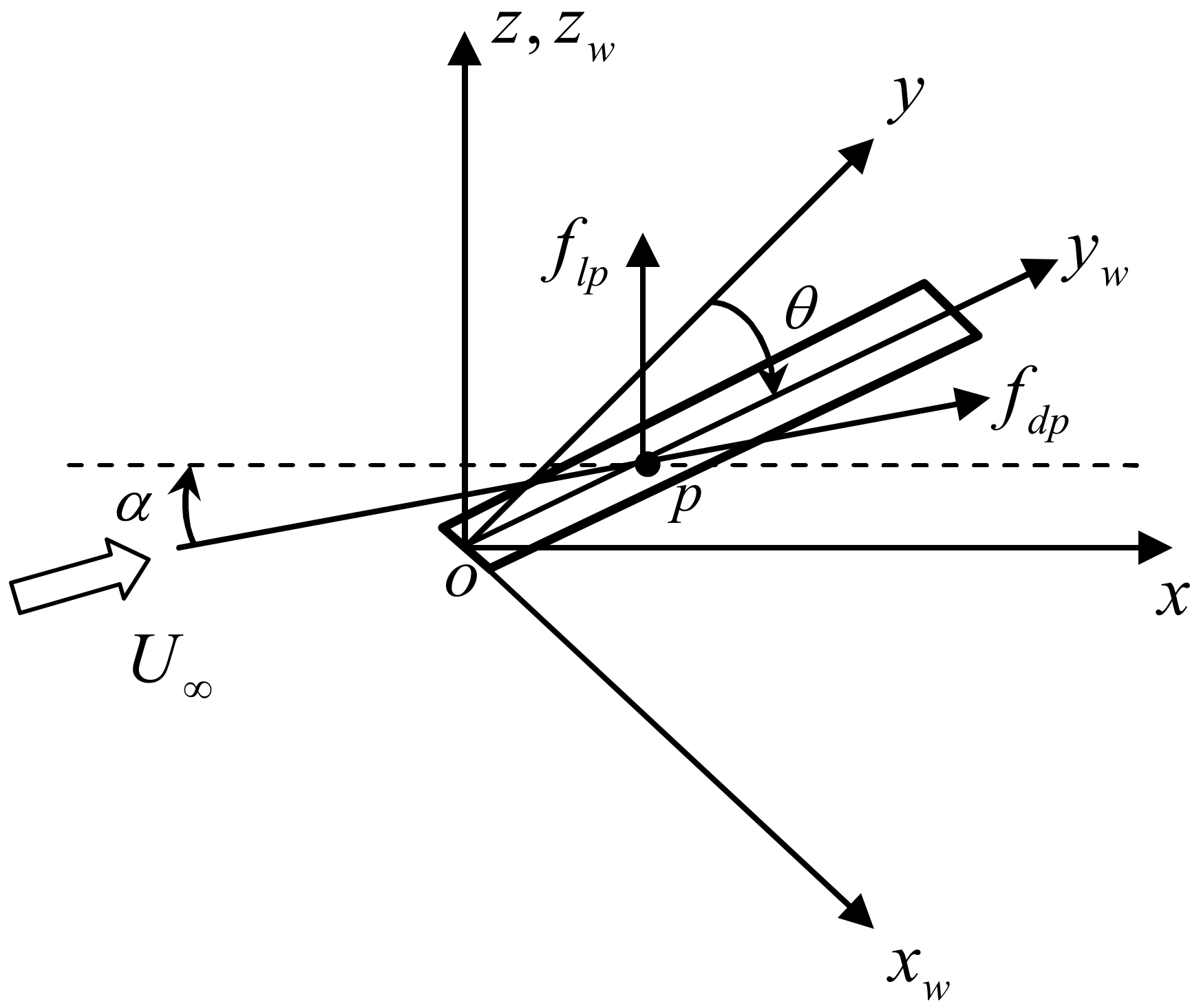
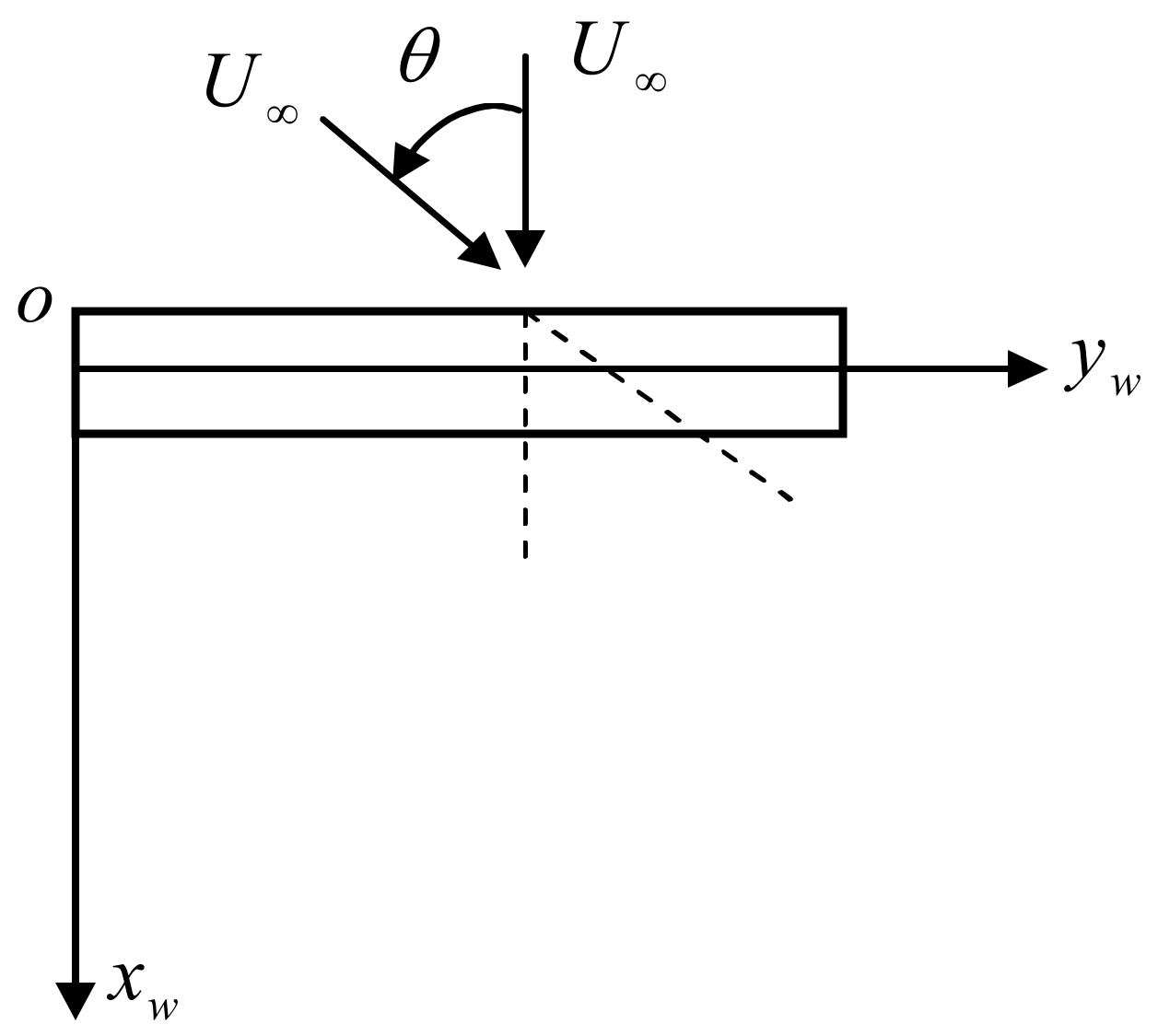
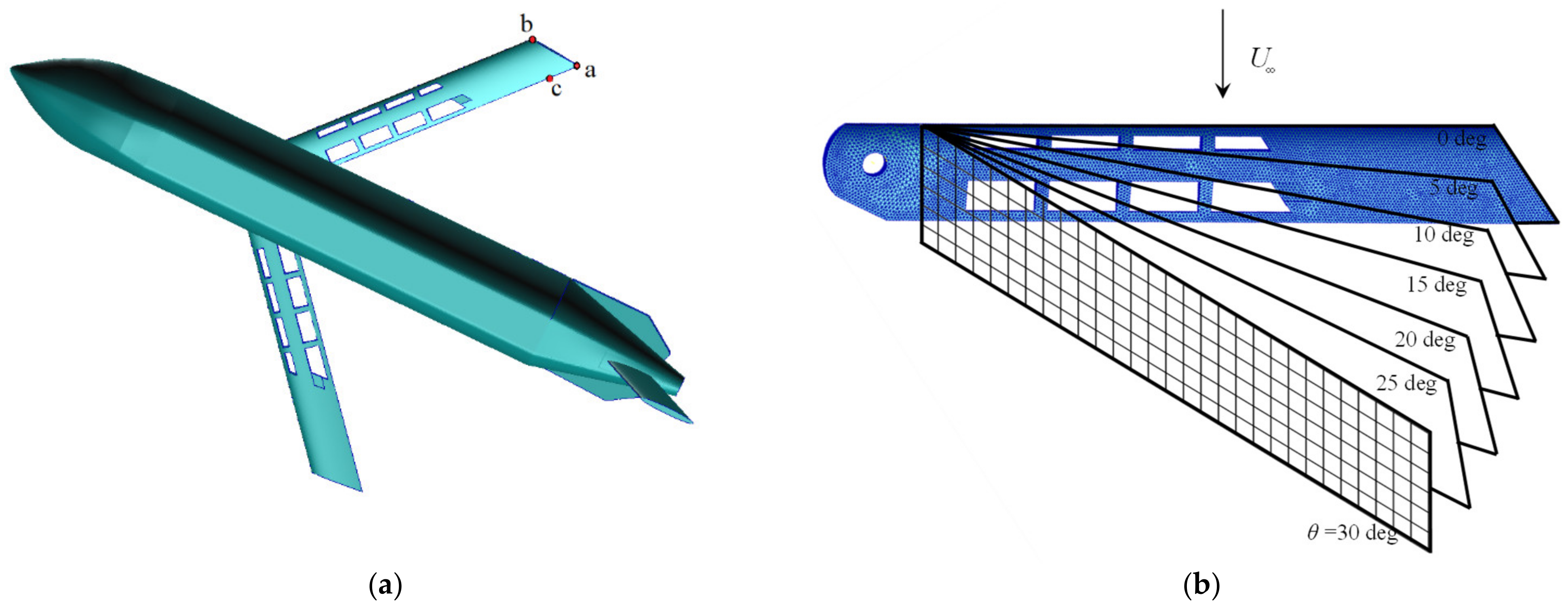
2.1. Description of the Motion of the Wing
2.2. Structural Dynamic Modeling of a Variable Swept Wing
2.3. Generalized Unsteady Aerodynamic Forces
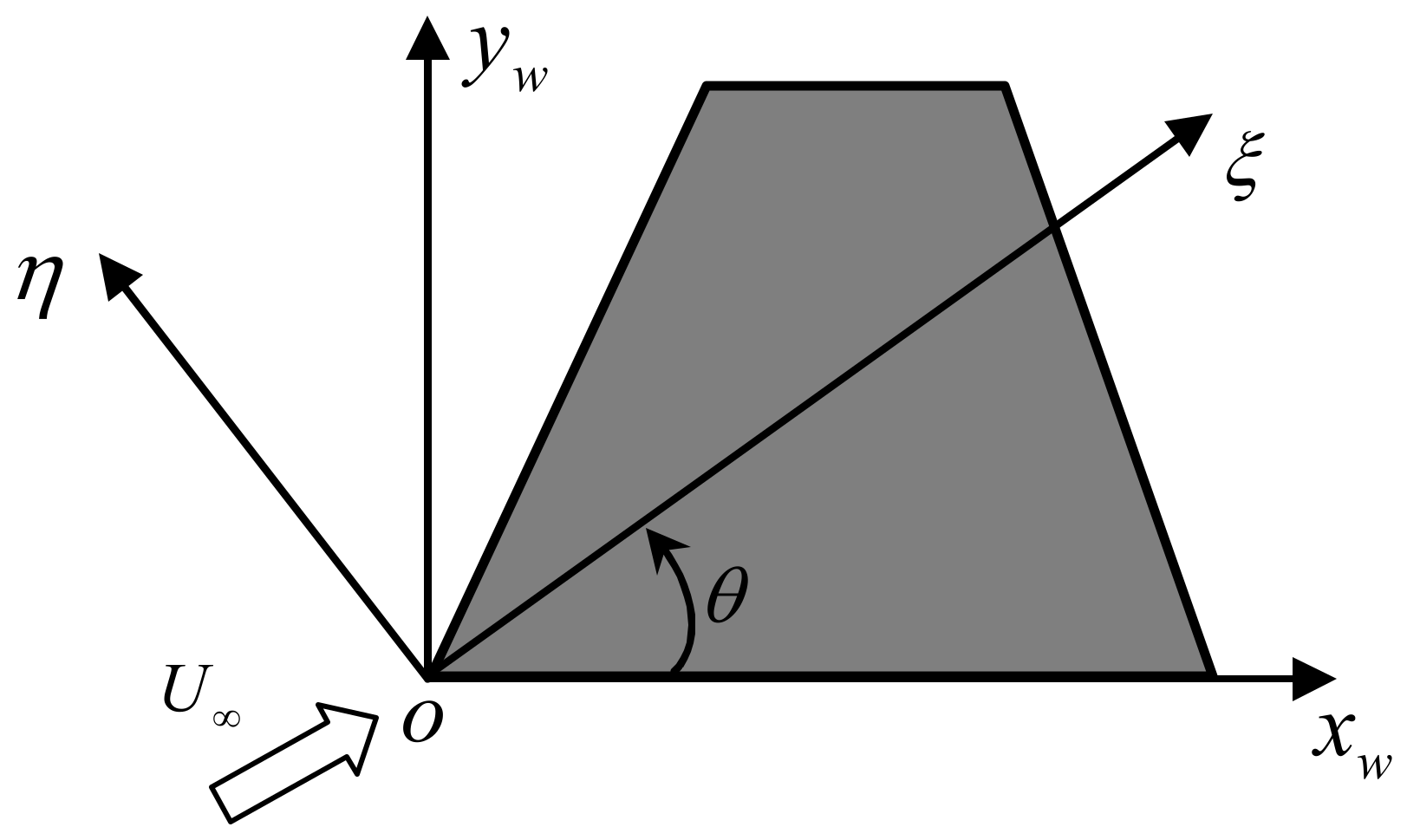
2.4. Nonlinear and Time-Varying Aeroelastic Equations of the Variable Swept Wing
2.5. Several Issues on Numerical Simulations
2.5.1. Double Numerical Integrations
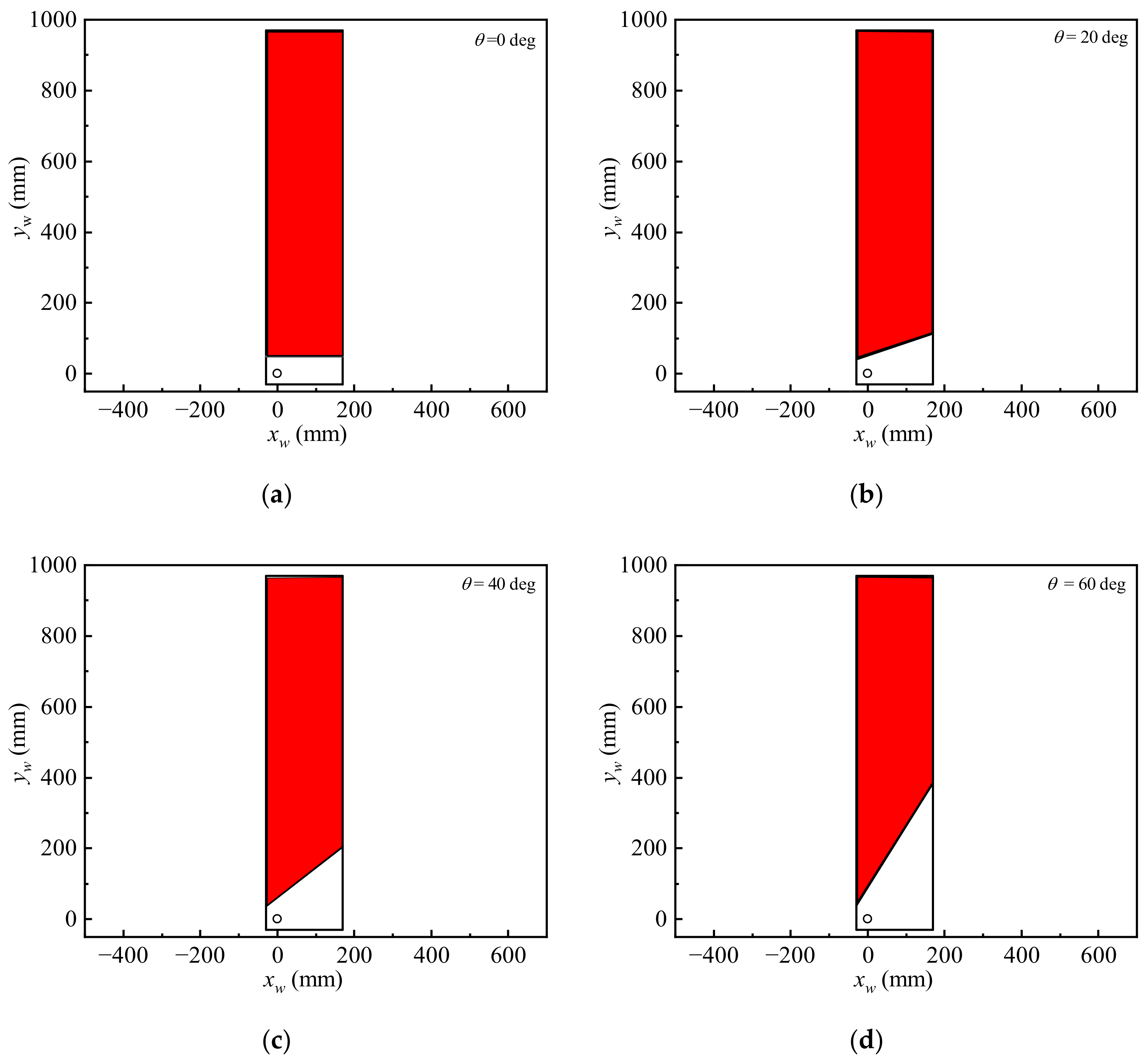
2.5.2. Time-Varying Lifting Surface
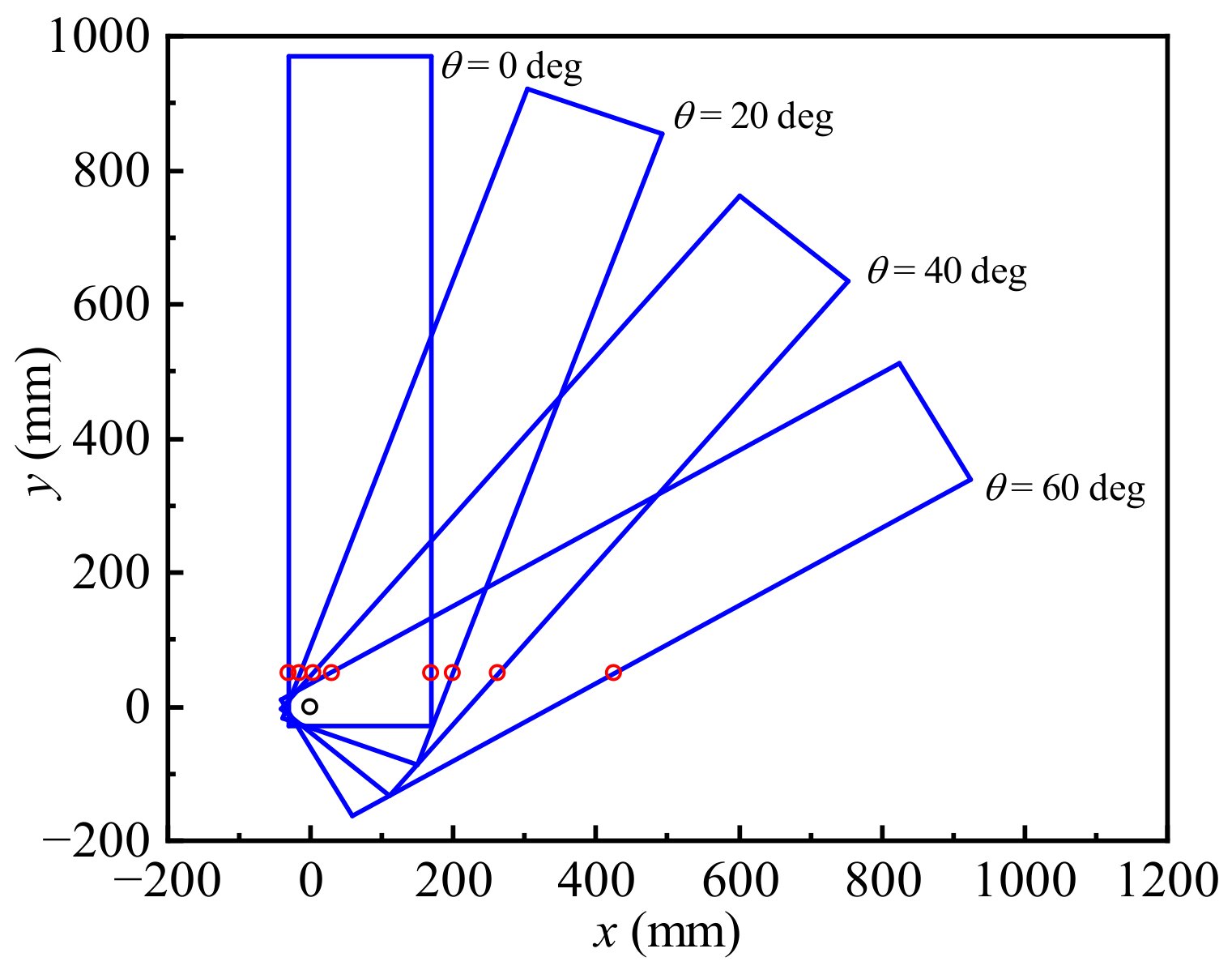
3. Numerical Simulations
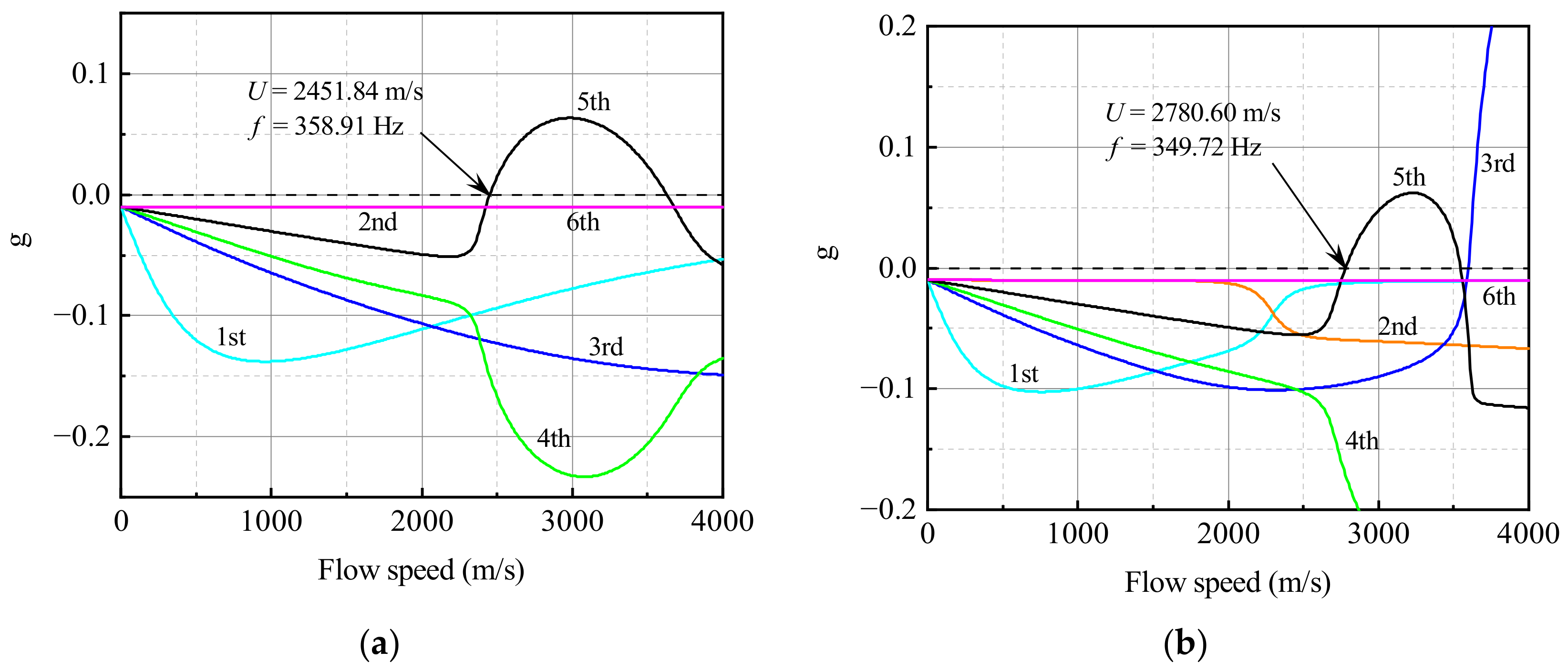
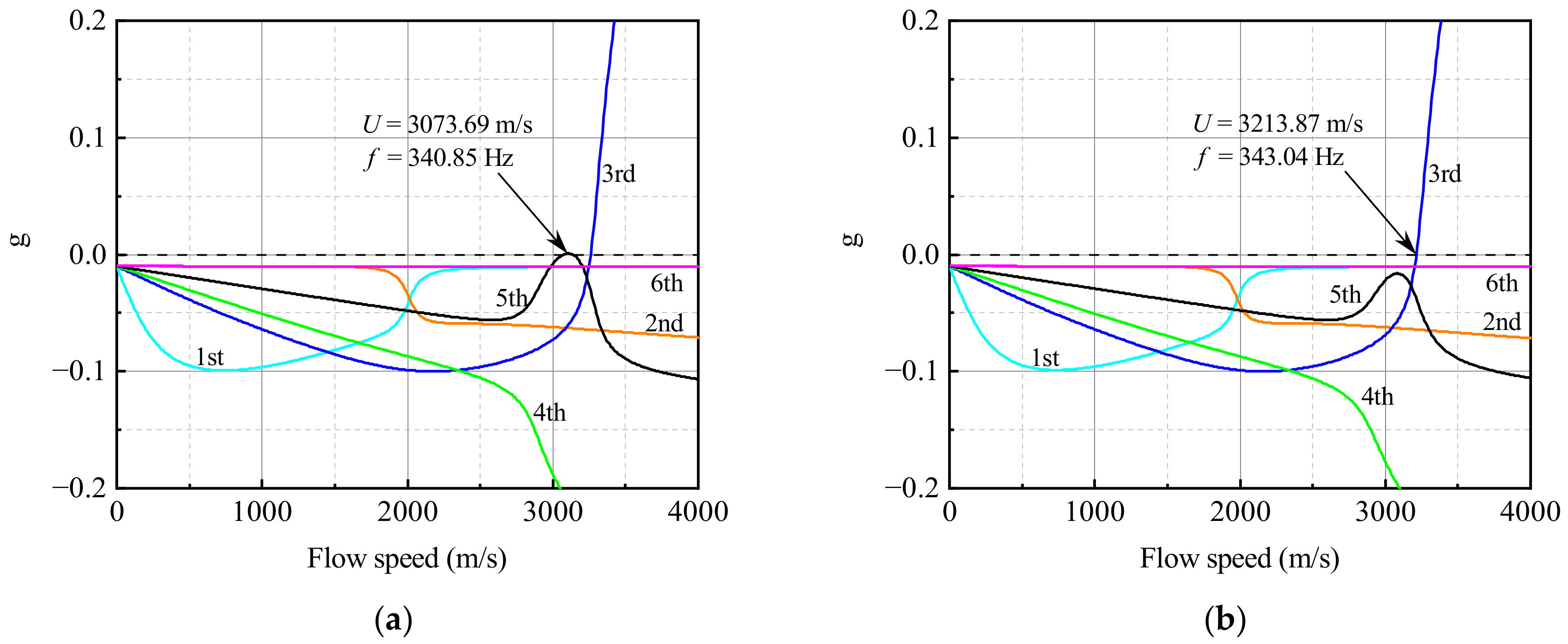
3.1. Flutter Analysis
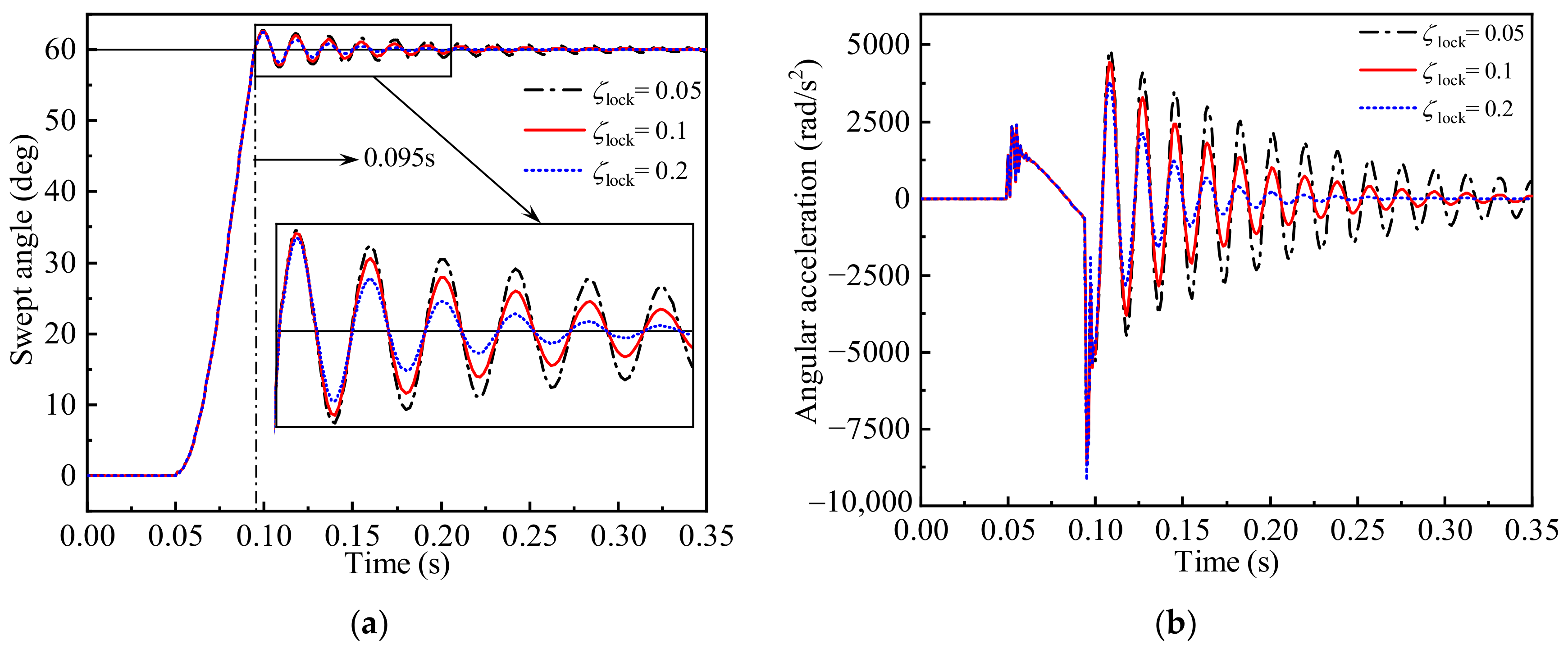
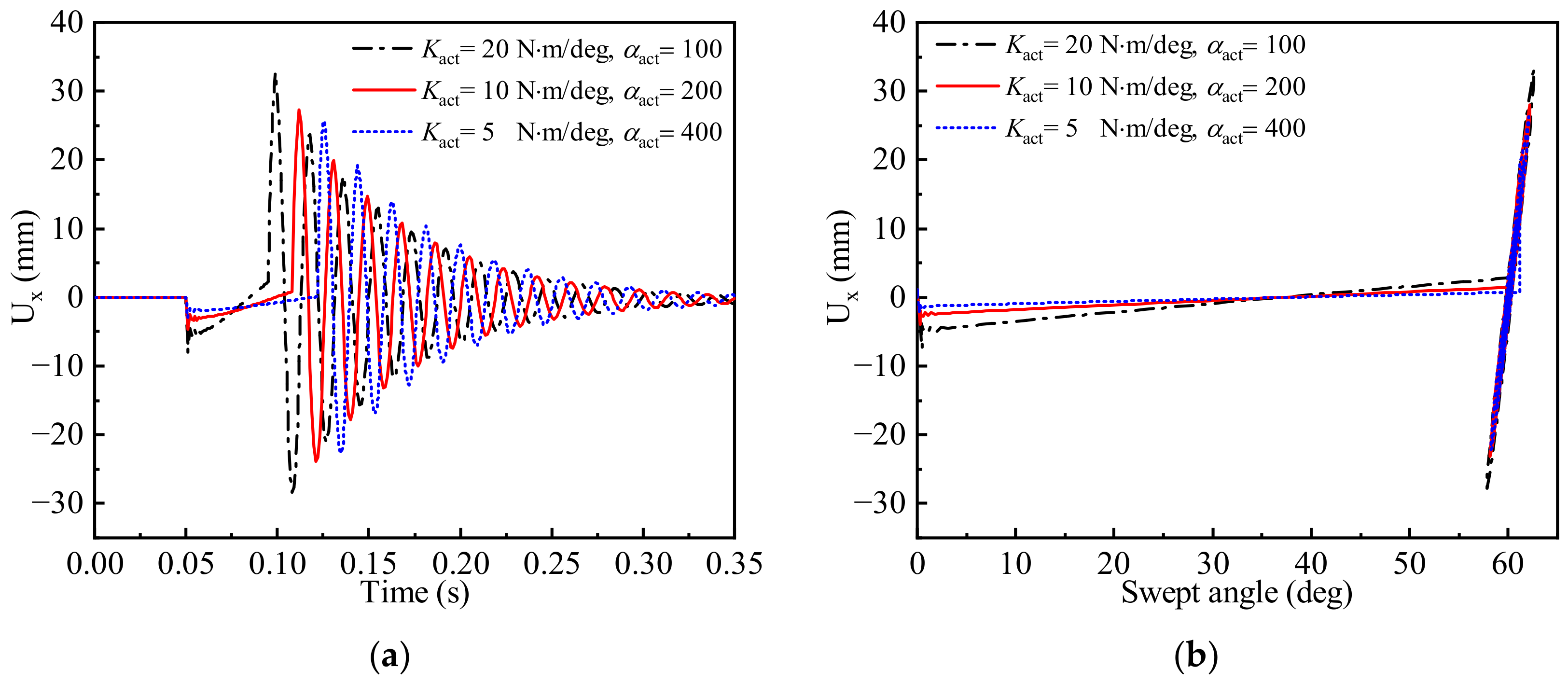
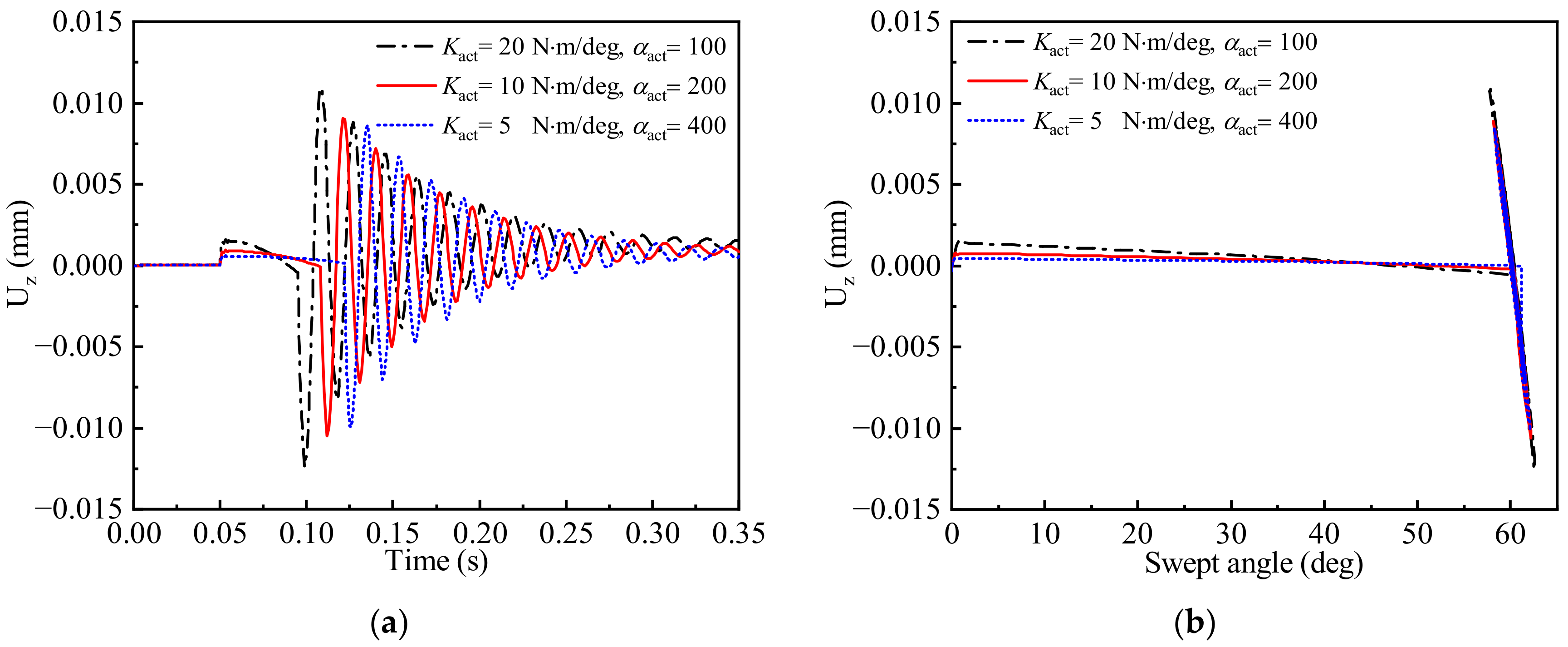
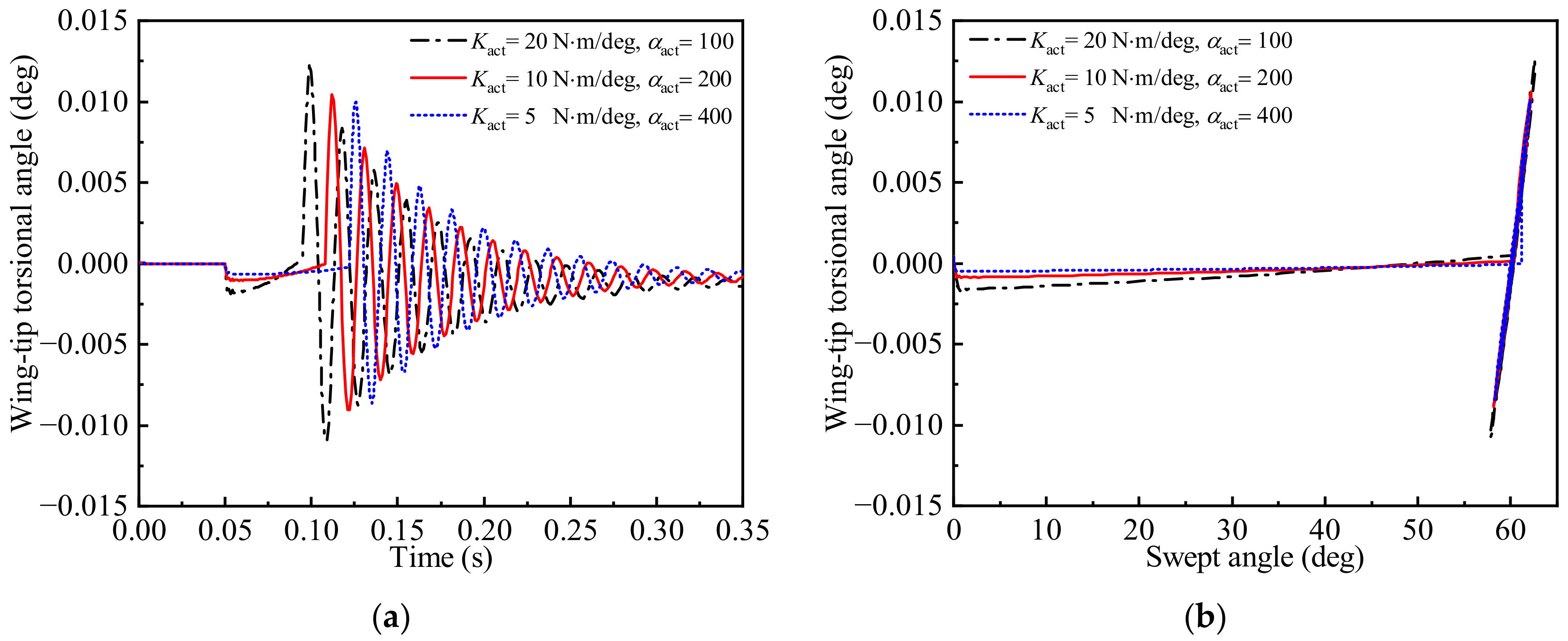
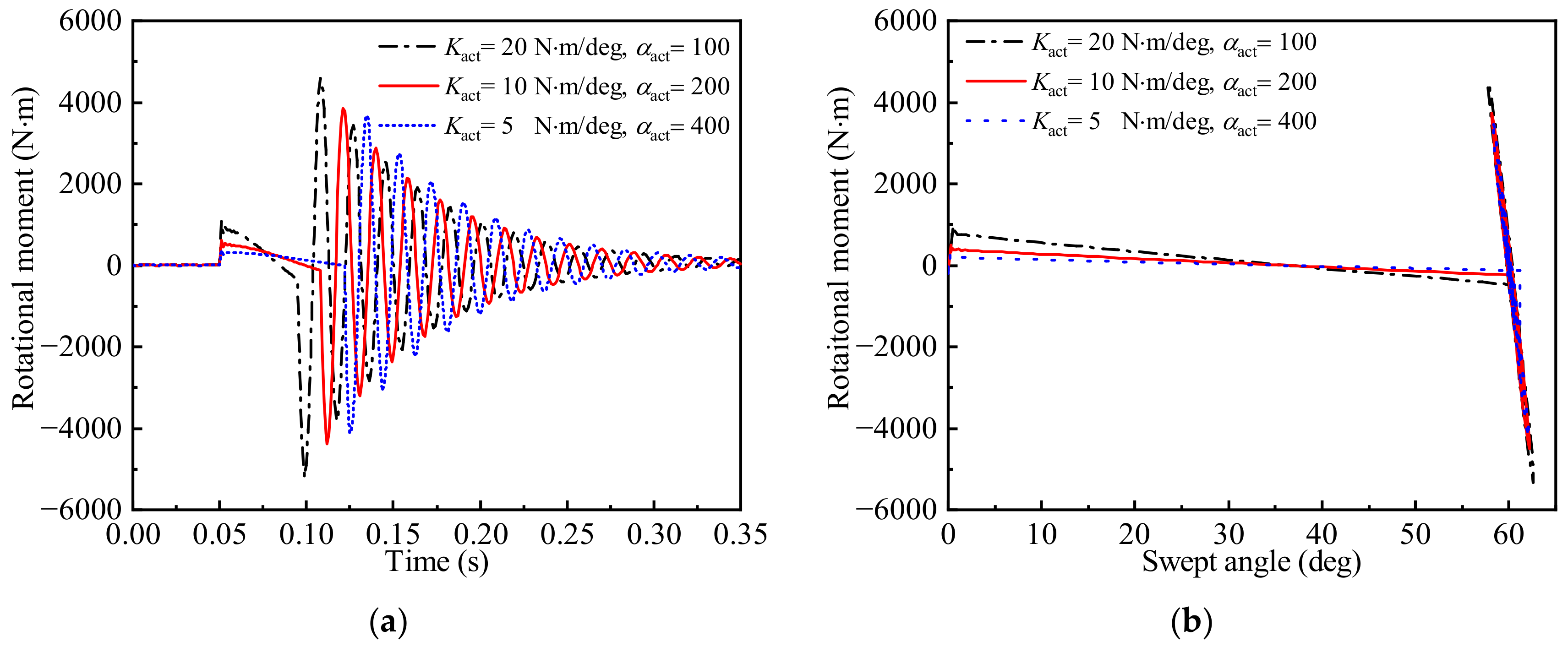
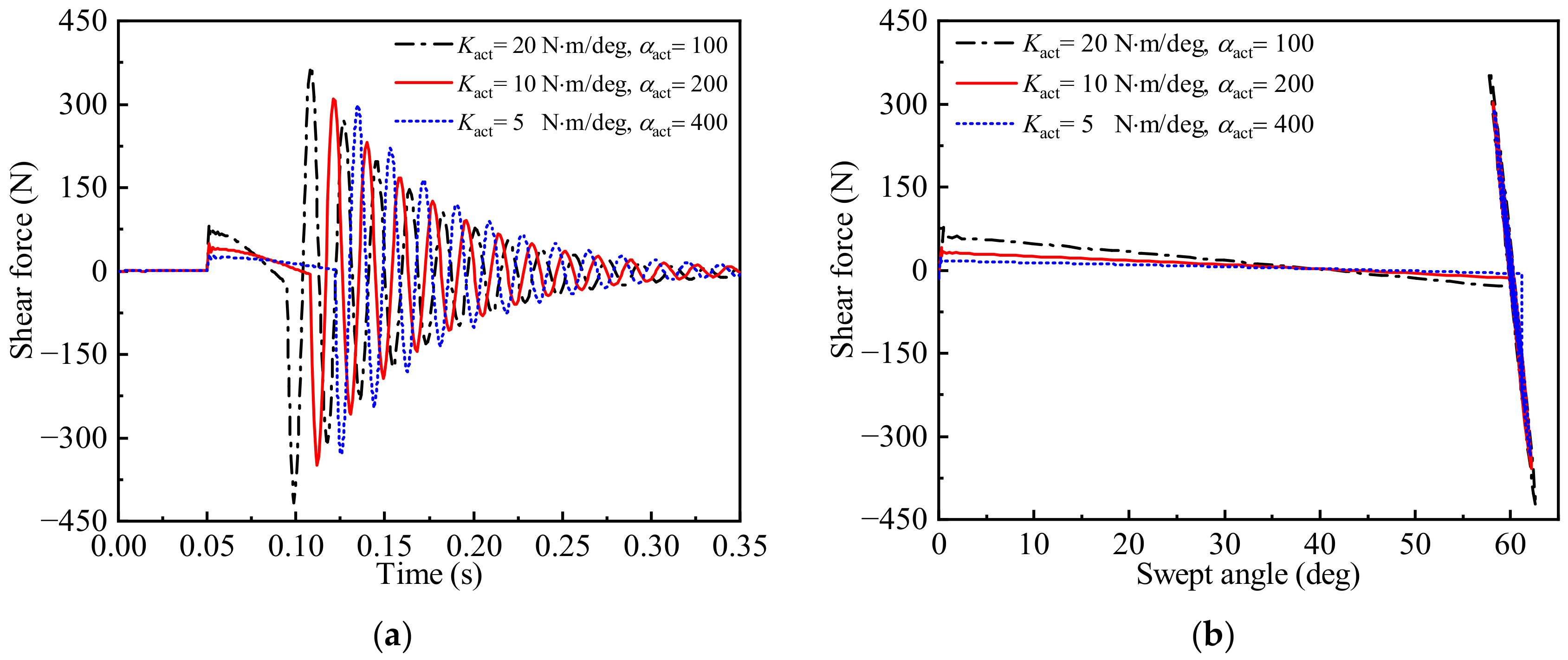
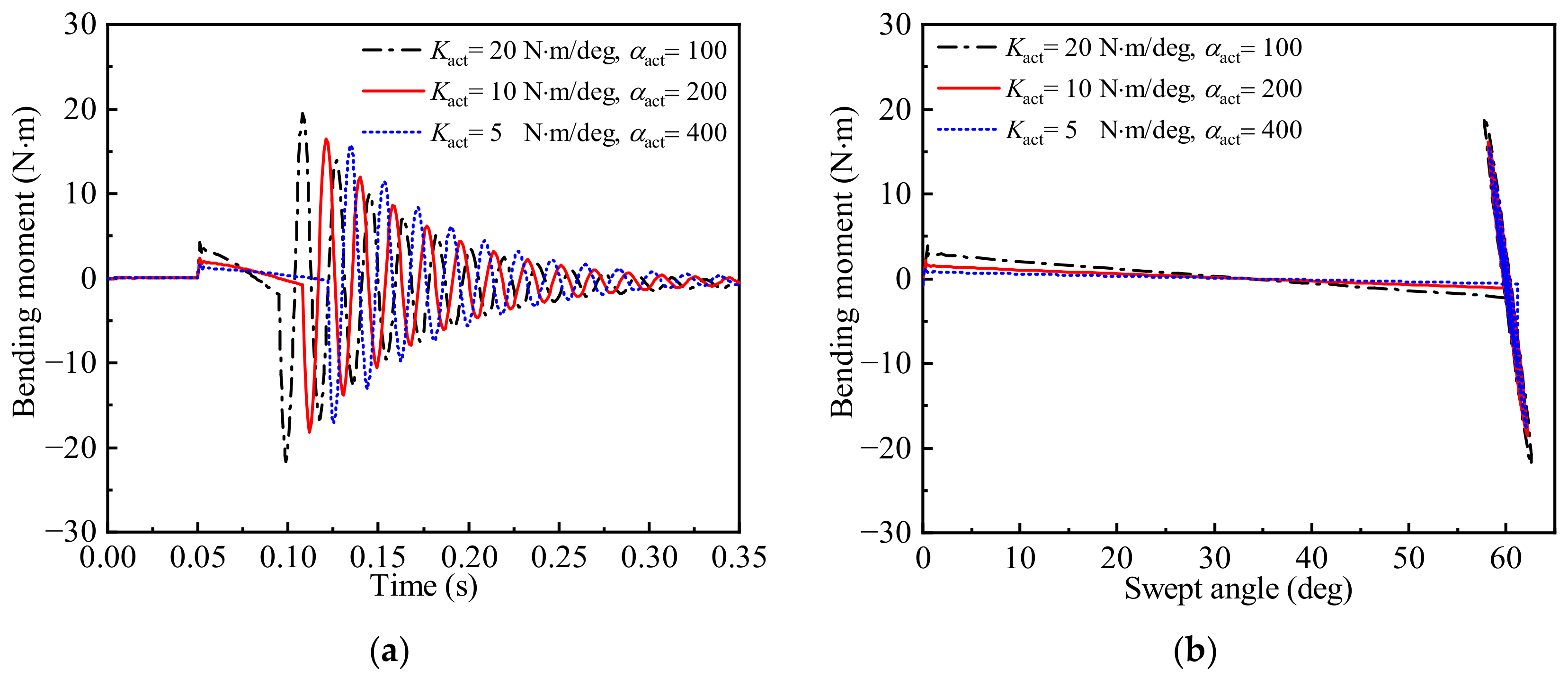
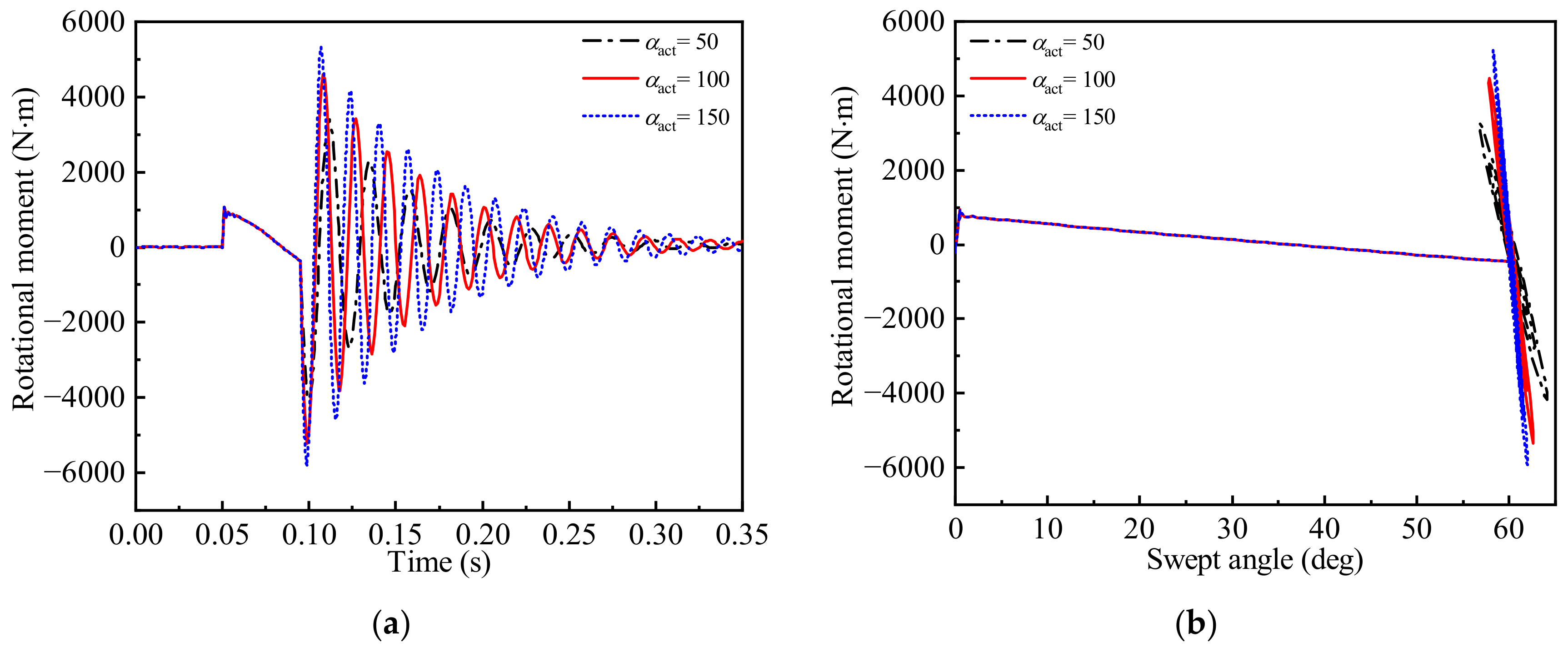
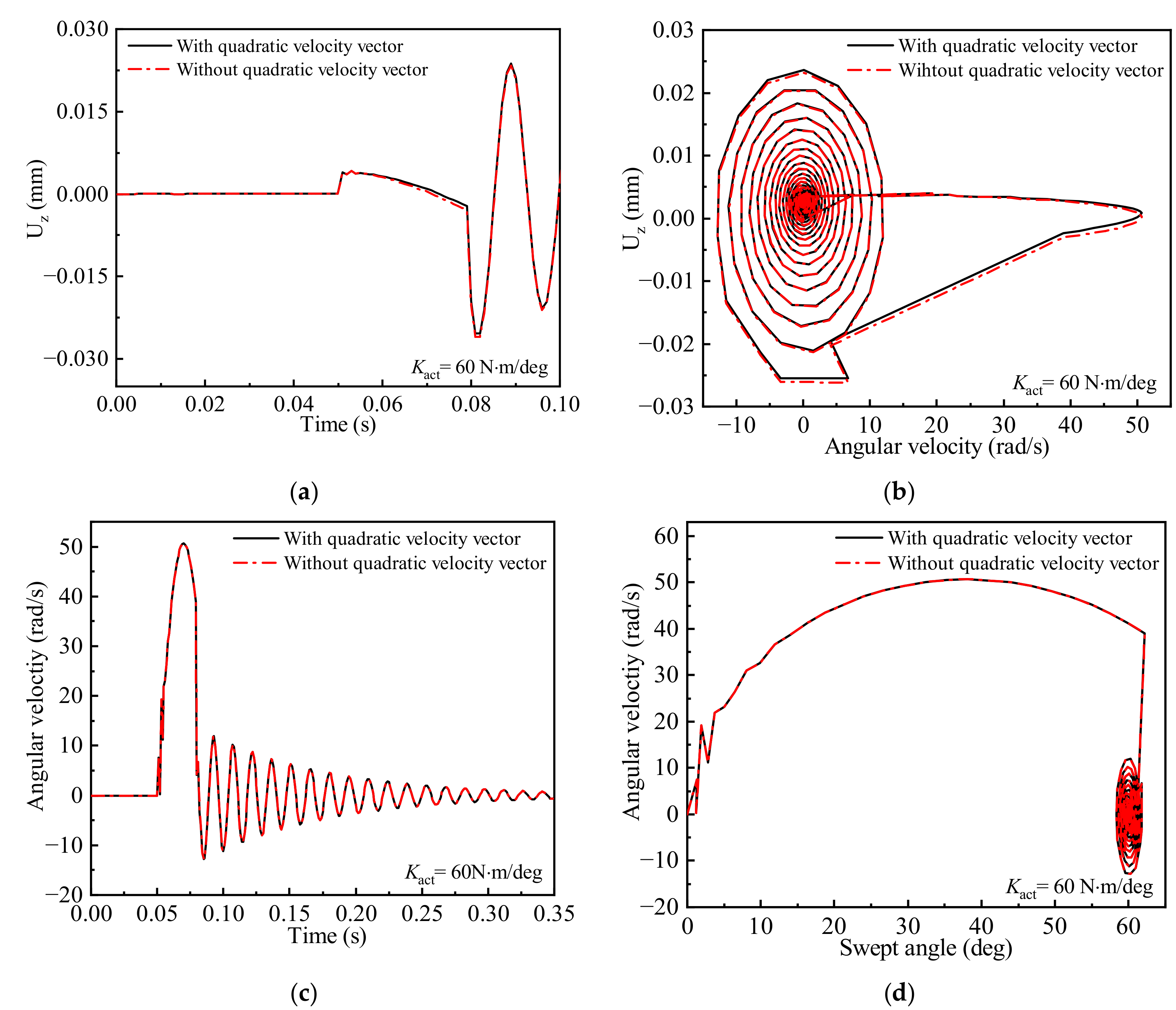
3.2. Time-Varying Aeroelastic Responses
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| the transformation matrix | |
| the damping coefficients in the rotation | |
| the damping coefficients in the locking phase | |
| modal damping matrix | |
| the drag coefficient | |
| the constant moment | |
| the quadratic velocity vector | |
| the generalized unsteady aerodynamic forces (GAF) | |
| the aerodynamic force vector | |
| the lift force | |
| the drag force | |
| the correction factor | |
| , | the spline matrix |
| the airfoil thickness | |
| the displacement vector at the interpolation points | |
| the slope vector at the interpolation points | |
| the torsional spring constant | |
| the modal stiffness matrix | |
| the nominal stiffness coefficient | |
| the lumped mass | |
| the time-varying mass matrix | |
| the Mach number | |
| the number of the finite element nodes | |
| the number of the finite element nodes | |
| the modal coordinate vector | |
| the modal aerodynamic force | |
| the modal shapes | |
| the skew symmetric matrix | |
| the vibration mode | |
| the kinetic energy | |
| the position vector of the node | |
| the elastic potential energy | |
| the strain energy | |
| the global FEM displacement vector | |
| the preloaded spring angle | |
| the max rotation angle | |
| the sweep angle | |
| the static angle of attack | |
| the leading edge sweep angle |
References
- Cui, E. Research statutes development trends and key technical problems of near space flying vehicles. Adv. Mech. 2009, 39, 658. [Google Scholar]
- Weisshaar, T.A. Morphing Aircraft Systems: Historical Perspectives and Future Challenges. J. Aircr. 2013, 50, 337–353. [Google Scholar] [CrossRef]
- Ajaj, R.M.; Beaverstock, C.S.; Friswell, M.I. Morphing aircraft: The need for a new design philosophy. Aerosp. Sci. Technol. 2016, 49, 154–166. [Google Scholar] [CrossRef] [Green Version]
- Andersen, G.; Cowan, D.; Piatak, D. Aeroelastic Modeling, Analysis and Testing of a Morphing Wing Structure. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007. [Google Scholar]
- Kuder, I.K.; Arrieta, A.F.; Raither, W.E.; Ermanni, P. Variable stiffness material and structural concepts for morphing applications. Prog. Aerosp. Sci. 2013, 63, 33–55. [Google Scholar] [CrossRef]
- Dayyani, I.; Shaw, A.D.; Flores, E.S.; Friswell, M.I. The mechanics of composite corrugated structures: A review with applications in morphing aircraft. Compos. Struct. 2015, 133, 358–380. [Google Scholar] [CrossRef] [Green Version]
- Chu, L.; Li, Q.; Gu, F.; DU, X.; He, Y.; Deng, Y. Design, modeling, and control of morphing aircraft: A review. Chin. J. Aeronaut. 2022, 35, 220–246. [Google Scholar] [CrossRef]
- Dai, P.; Yan, B.; Huang, W.; Zhen, Y.; Wang, M.; Liu, S. Design and aerodynamic performance analysis of a variable-sweep-wing morphing waverider. Aerosp. Sci. Technol. 2020, 98, 105703. [Google Scholar] [CrossRef]
- Li, Y.; Yi, L.; Ao, Y.; Ma, L.; Wang, Y. Simulation analysis the aerodynamic characteristics of variable sweep wing missile. J. Phys. 2020, 1570, 012073. [Google Scholar] [CrossRef]
- Xia, W.; Wang, W.; Zhang, W. The Optimal Sweep Angle Design of a Morphing Firebee Drone in a Cruise Mission. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021. [Google Scholar]
- Chen, X.; Li, C.; Gong, C.; Gu, L.; Da Ronch, A. A study of morphing aircraft on morphing rules along trajectory. Chin. J. Aeronaut. 2020, 34, 232–243. [Google Scholar] [CrossRef]
- Dai, P.; Yan, B.; Liu, S.; Liu, R.; Wang, M. Longitudinal Tracking Control for a Morphing Waverider Using Adaptive Super Twisting Control. IEEE Access 2021, 9, 59692–59702. [Google Scholar] [CrossRef]
- Dai, P.; Yan, B.; Liu, R.; Liu, S.; Wang, M. Modeling and Nonlinear Model Predictive Control of a Variable-Sweep-Wing Morphing Waverider. IEEE Access 2021, 9, 63510–63520. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, H. Prediction of transient responses of a folding wing during the morphing process. Aerosp. Sci. Technol. 2013, 24, 89–94. [Google Scholar] [CrossRef]
- Zhao, A.; Zou, H.; Jin, H.; Wen, D. Structural design and verification of an innovative whole adaptive variable camber wing. Aerosp. Sci. Technol. 2019, 89, 11–18. [Google Scholar] [CrossRef]
- Ajaj, R.M.; Parancheerivilakkathil, M.S.; Amoozgar, M.; Friswell, M.I.; Cantwell, W.J. Recent developments in the aeroelasticity of morphing aircraft. Prog. Aerosp. Sci. 2021, 120, 100682. [Google Scholar] [CrossRef]
- Li, W.; Jin, D. Flutter suppression and stability analysis for a variable-span wing via morphing technology. J. Sound Vib. 2017, 412, 410–423. [Google Scholar] [CrossRef]
- Lovera, M.; Novara, C.; dos Santos, P.L.; Rivera, D. Guest Editorial Special Issue on Applied LPV Modeling and Identification. IEEE Trans. Control. Syst. Technol. 2011, 19, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Lee, L.H.; Poolla, L. Identification of linear parameter-varying systems using nonlinear programming. J. Dyn. Syst. Meas. Control 1999, 121, 71–78. [Google Scholar] [CrossRef] [Green Version]
- Mocsányi, R.D.; Takarics, B.; Vanek, B. Grid and Polytopic LPV Modeling of Aeroelastic Aircraft for Co-design. IFAC-PapersOnLine 2020, 53, 5725–5730. [Google Scholar] [CrossRef]
- Wang, D.; Zhu, W. Advances in modeling and control of linear parameter varying systems. Acta Automat. Sin. 2021, 47, 780. [Google Scholar]
- Boef, P.D.; Tóth, R.; Schoukens, M. On Behavioral Interpolation in Local LPV System Identification. IFAC-PapersOnLine 2019, 52, 20–25. [Google Scholar] [CrossRef]
- Lovera, M.; Bergamasco, M.; Casella, F. LPV Modelling and Identification: An Overview; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Balas, G.J. Linear, parameter-varying control and its application to a turbofan engine. Int. J. Robust Nonlinear Control 2002, 12, 763–796. [Google Scholar] [CrossRef]
- Zhang, L.; Yue, C.; Zhao, Y. Parameter-varying aeroelastic modeling and analysis for a variable-sweep wing. Chin. J. Theor. Appl. Mech. 2021, 53, 3134. [Google Scholar]
- Poussot-Vassal, C.; Roos, C. Generation of a reduced-order LPV/LFT model from a set of large-scale MIMO LTI flexible aircraft models. Control Eng. Pract. 2012, 20, 919–930. [Google Scholar] [CrossRef]
- Amsallem, D.; Farhat, C. An Online Method for Interpolating Linear Parametric Reduced-Order Models. SIAM J. Sci. Comput. 2011, 33, 2169–2198. [Google Scholar] [CrossRef]
- Caigny, J.D.; Pintelon, R. Interpolated modeling of LPV systems. IEEE. Trans. Contr. Syst. Technol. 2014, 22, 2232. [Google Scholar] [CrossRef] [Green Version]
- Selitrennik, E.; Moti, K.; Levy, Y. Computational aeroelastic simulation of rapidly morphing air vehicles. J. Aircr. 2012, 49, 1675. [Google Scholar] [CrossRef]
- Shabana, A.A. Dynamics of Multibody Systems; Cambridge University Press: New York, NY, USA, 1998. [Google Scholar]
- Liu, D.D.; Yao, Z.X.; Sarhaddi, D.; Chavez, F. From Piston Theory to a Unified Hypersonic-Supersonic Lifting Surface Method. J. Aircr. 1997, 34, 304–312. [Google Scholar] [CrossRef]
- Harder, R.L.; Desmarais, R.N. Interpolation using surface splines. J. Aircr. 1972, 9, 189–191. [Google Scholar] [CrossRef]





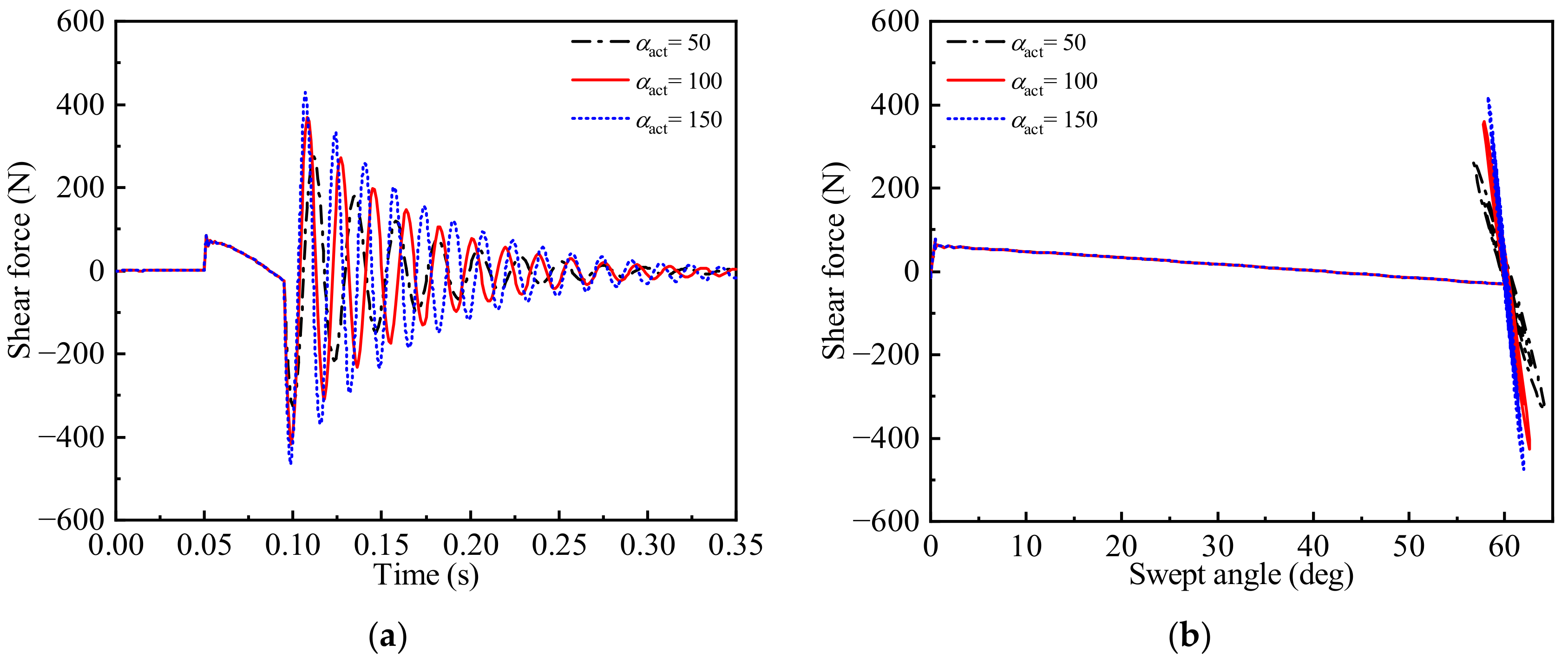
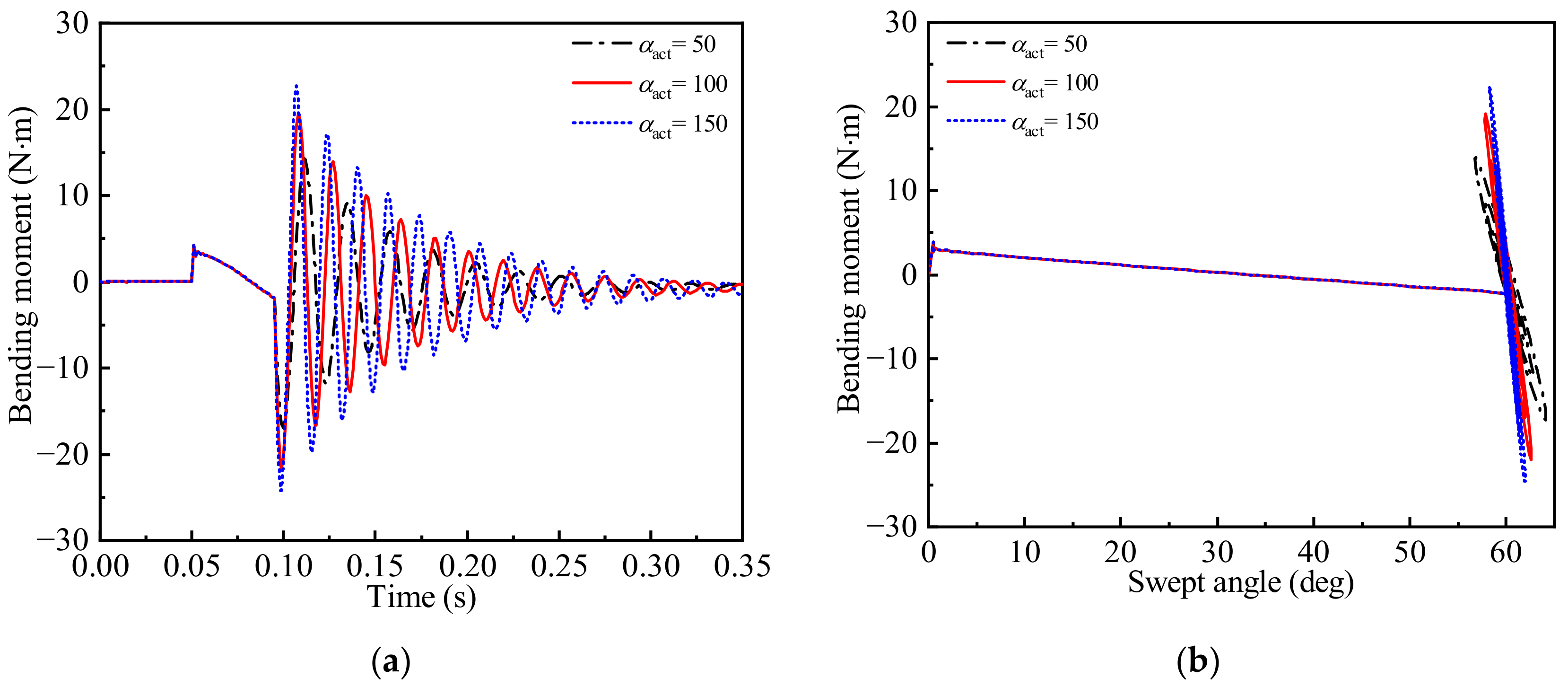
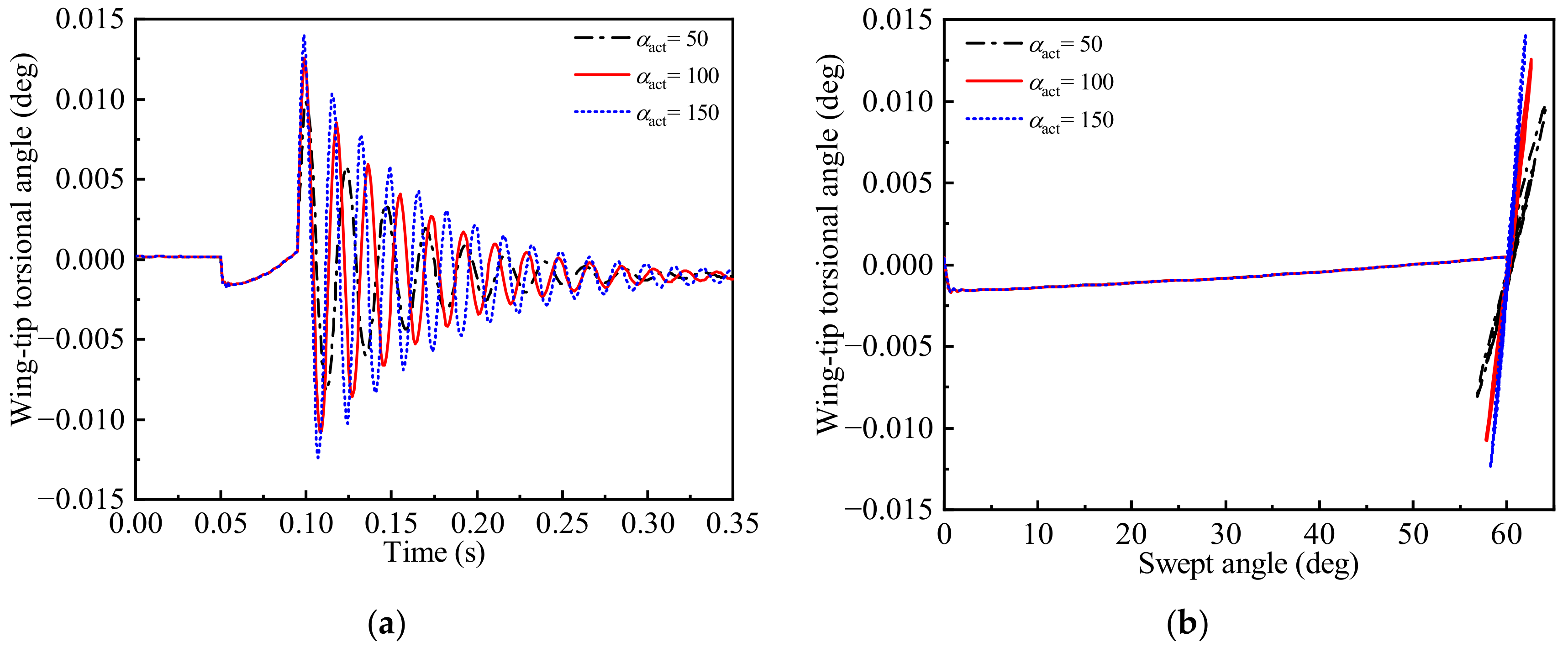
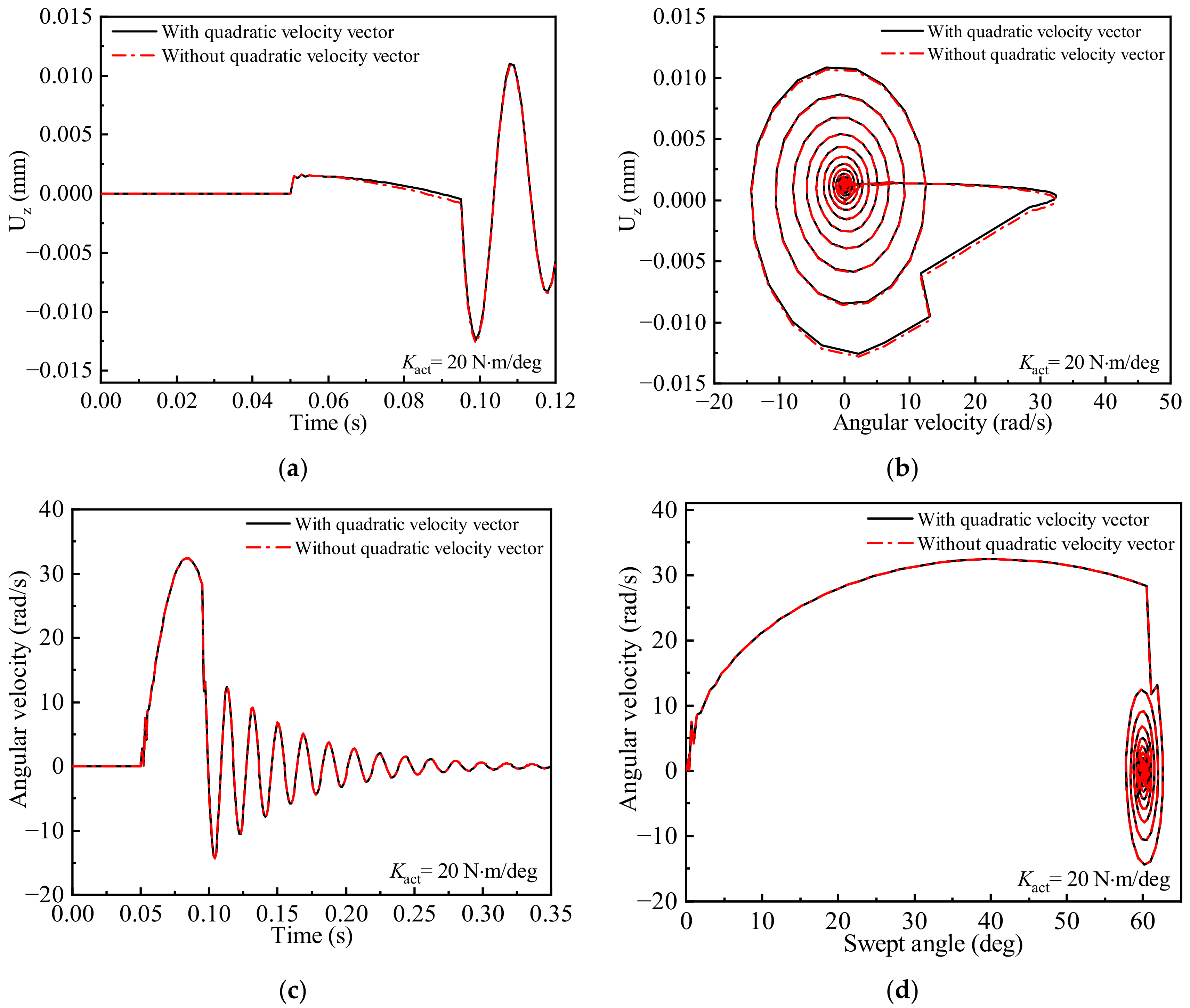
| Order | Frequency (Hz) | Mode Shape |
|---|---|---|
| Mode 1 | 14.34 | 1st vertical bending |
| Mode 2 | 81.89 | 1st in-plane bending |
| Mode 3 | 117.43 | 2nd vertical bending |
| Mode 4 | 204.65 | 1st torsion |
| Mode 5 | 363.33 | 3rd vertical bending |
| Mode 6 | 544.56 | 2nd torsion |
| Mode 7 | 682.44 | 4th vertical bending |
| Mode 8 | 909.84 | 3rd torsion |
| Mode 9 | 1049.79 | 5th vertical bending |
| Mode 10 | 1245.86 | 4th torsion |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhao, Y. Time-Varying Aeroelastic Modeling and Analysis of a Rapidly Morphing Wing. Aerospace 2023, 10, 197. https://doi.org/10.3390/aerospace10020197
Zhang L, Zhao Y. Time-Varying Aeroelastic Modeling and Analysis of a Rapidly Morphing Wing. Aerospace. 2023; 10(2):197. https://doi.org/10.3390/aerospace10020197
Chicago/Turabian StyleZhang, Liqi, and Yonghui Zhao. 2023. "Time-Varying Aeroelastic Modeling and Analysis of a Rapidly Morphing Wing" Aerospace 10, no. 2: 197. https://doi.org/10.3390/aerospace10020197
APA StyleZhang, L., & Zhao, Y. (2023). Time-Varying Aeroelastic Modeling and Analysis of a Rapidly Morphing Wing. Aerospace, 10(2), 197. https://doi.org/10.3390/aerospace10020197





