Space-Time Finite Element Method for Fully Intrinsic Equations of Geometrically Exact Beam
Abstract
:1. Introduction
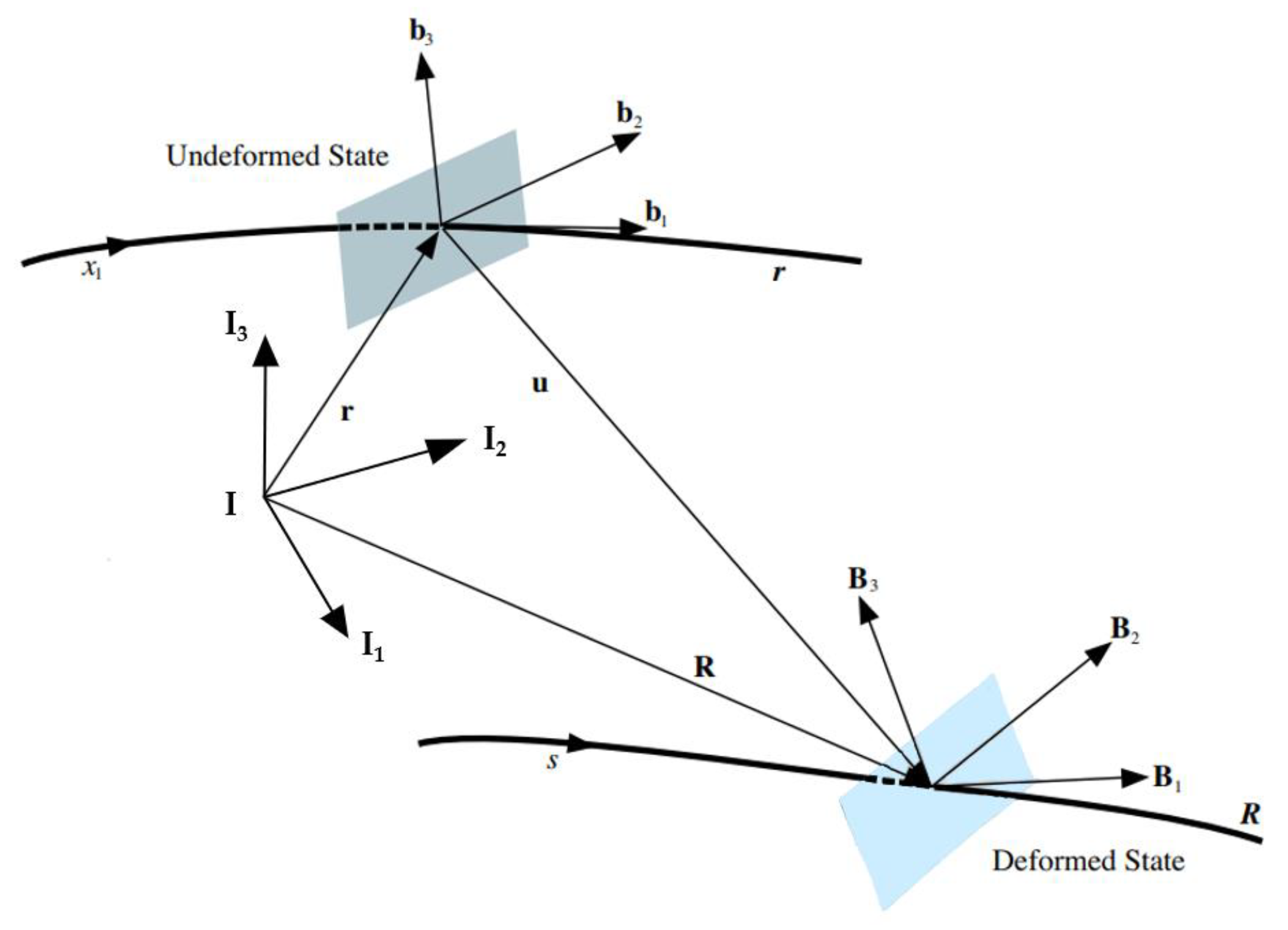
2. Fully Intrinsic Beam Equations of Geometrically Exact Beam
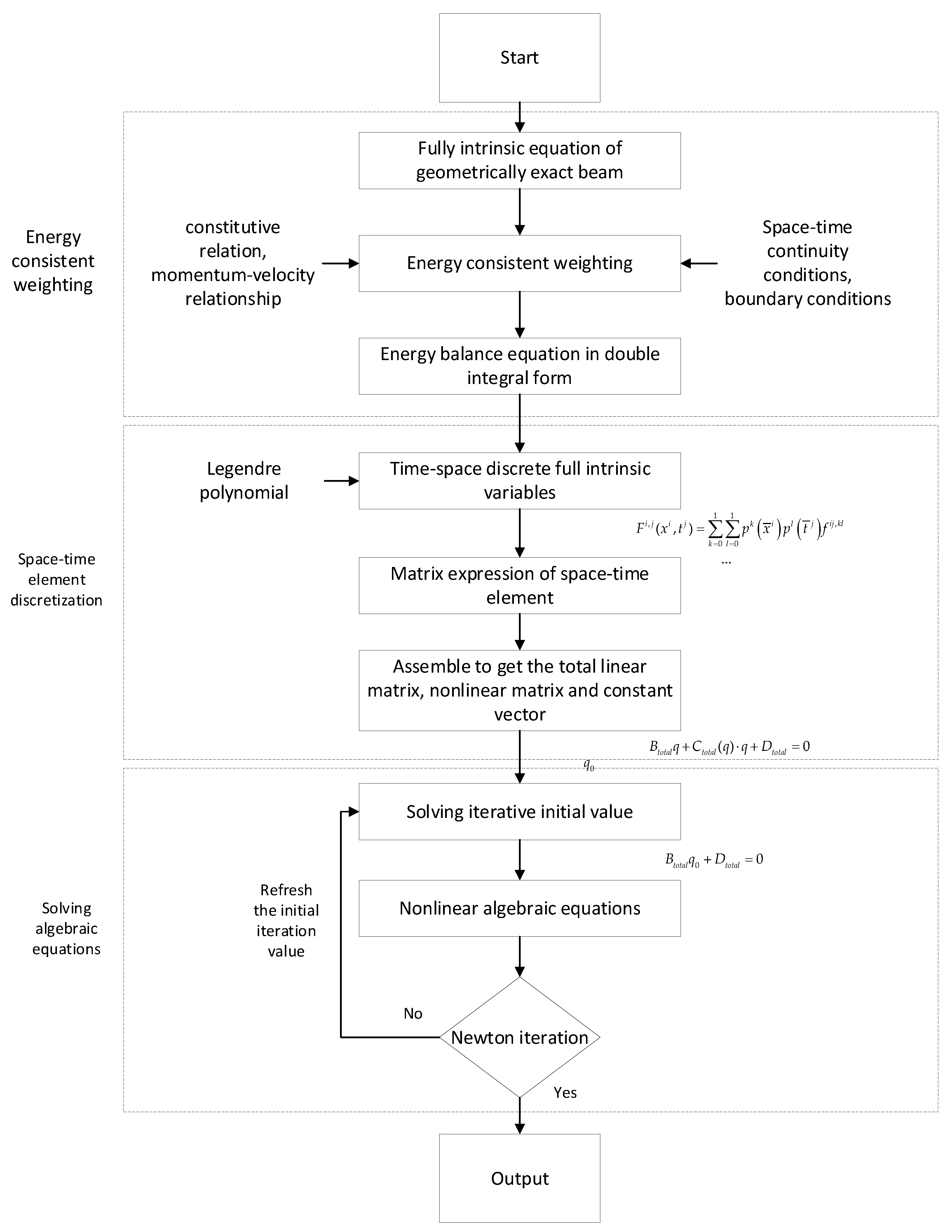
3. Space-Time Finite Element Method of Fully Intrinsic Equations
3.1. Continuous Energy Weighting Method
3.2. Legendre Polynomial Interpolation
3.3. Constant Cross-Section, Curvature
3.4. Matrix Assembly
3.5. Post Process
3.6. Process of Simulation
- (1)
- For a single space-time unit, consider the continuity of , , , and in space. Meanwhile, consider the continuity of , , and in time. The unit needs special continuity operation at the space-time boundary conditions, see Formulas (8) and (10), and Formulas (9) and (11).
- (2)
- Combined with the constitutive relation, momentum-velocity relation and continuity condition, a set of energy balance equations in the form of a double integral of time and space is derived from the full intrinsic equations by using the weighted margin technique.
- (3)
- In the process of integral, the Legendre interpolation polynomial is used as a discrete function of intrinsic quantity. The specific expressions of linear matrix, nonlinear matrix, time-connected matrix, spatial connected matrix, and constant vector of single space-time element are derived based on the Galerkin approximation.
- (4)
- In the dimensionality of space and time, the coefficient matrix of a single space-time unit derived in the previous step can be assembled into a total coefficient matrix. Thus, the final discrete equations will be expressed as .
- (5)
- For the derivation of nonlinear algebraic equations, solve equation of as the iteration start value. Then the Newton iteration method was used to get the convergent solution.
- (6)
- After obtaining the convergence solution, in addition to extracting the intrinsic quantity, the displacement response at any point can be obtained by applying its generalized strain through the post-processing process.
4. Numerical Results
4.1. Static Analysis and Modal Calculation of the Cantilever Beam
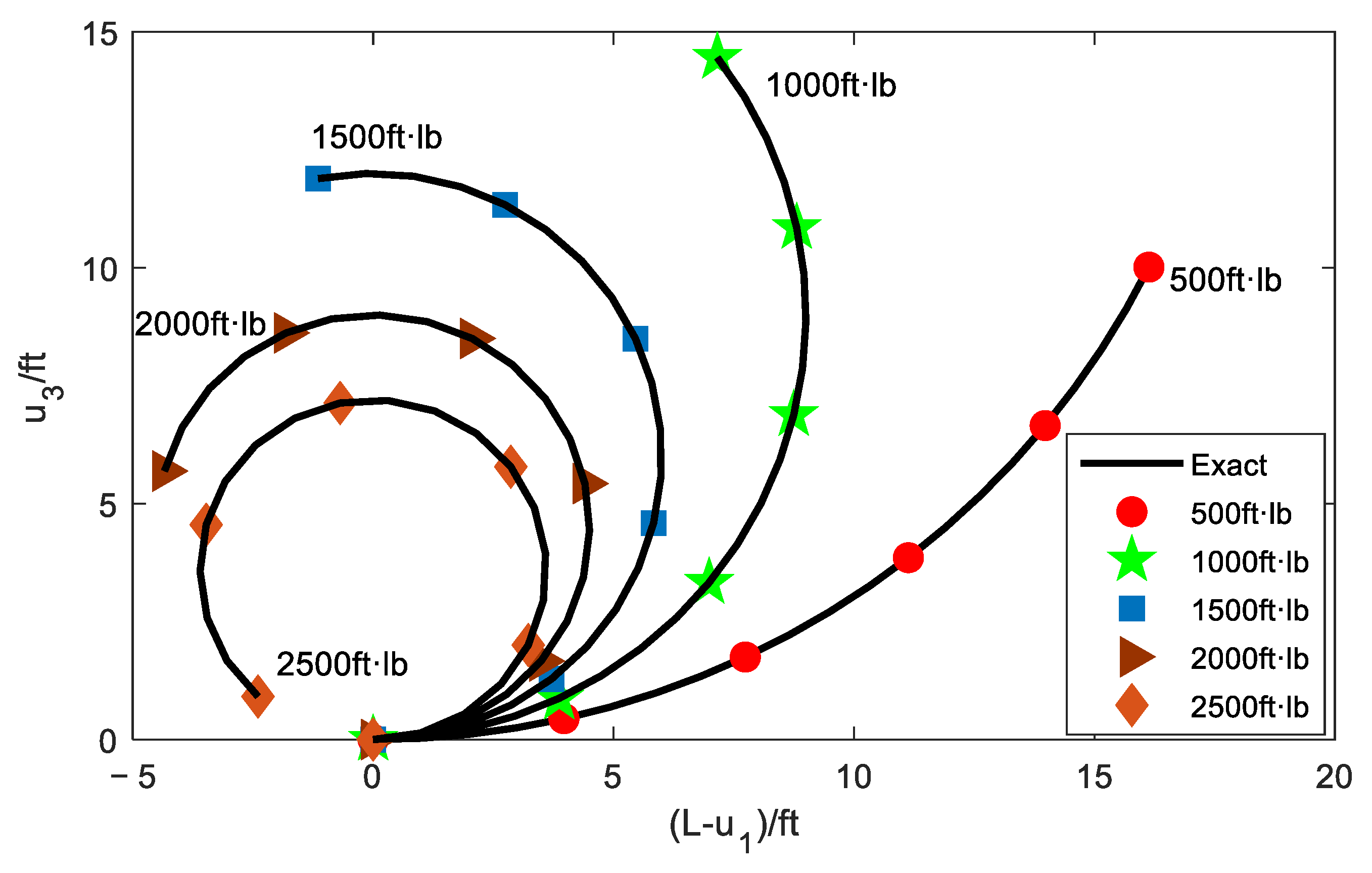
4.2. Cantilever Subjected to a Follower Force at the Tip
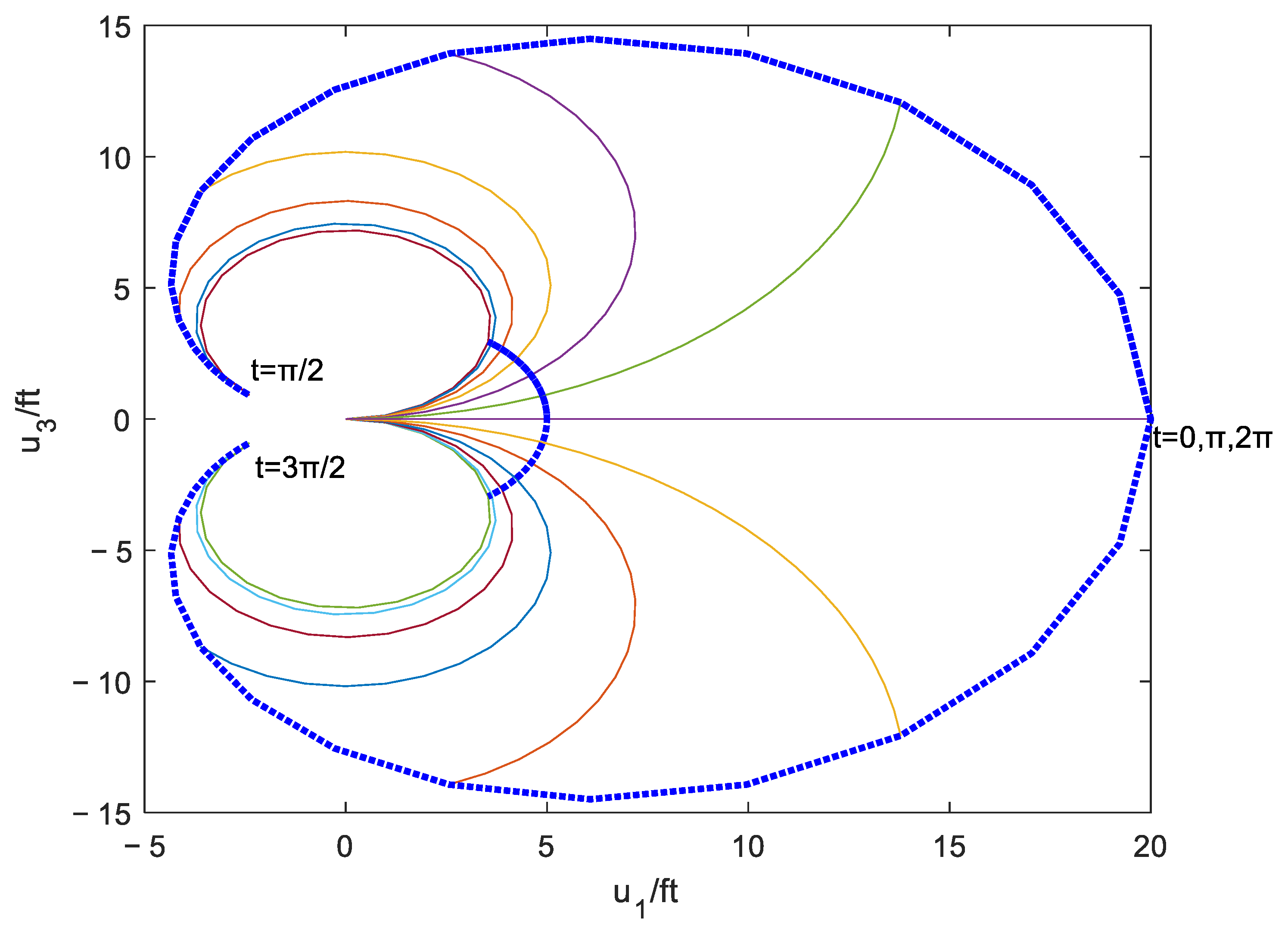
4.3. The Rotating Cantilever Subjected to a Periodic Follower Force at the Tip
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| I | Inertial coordinate system |
| Basis vector of the undeformed coordinate system | |
| Basis vector of the deformed coordinate system | |
| r | The relative position of undeformed beam section in I |
| R | The relative position of deformed beam section in I |
| u | Displacement vector of reference line |
| The observed quantity in B | |
| Antisymmetric matrix associated with a column matrix; Equation (3) | |
| Cross-sectional force vector | |
| Cross-sectional moment vector | |
| Cross-sectional linear velocity vector | |
| Cross-sectional angular velocity vector | |
| Cross-sectional force strain vector | |
| Cross-sectional moment strain vector | |
| Cross-sectional linear momentum vector | |
| Cross-sectional angular momentum vector | |
| Distributed applied force vector | |
| Distributed applied moment vector | |
| k | The initial bending and torsion of the beam |
| R, S, T | Cross-sectional flexibility coefficient matrices; Equation (4) |
| G, I, K | Cross-sectional inertia coefficient matrices; Equation (6) |
| Mass per unit length | |
| identity matrix | |
| The position offsets in b2,b3 from reference line to cross-sectional mass centroid | |
| Cross-sectional mass moments of inertia | |
| L | Length of beam |
| Length of i th beam element | |
| T | Periodic time |
| Length of j th time element | |
| n | Number of segments discretized in spatial direction |
| m | Number of segments discretized in temporal direction |
| i th (space) and j th (time) space-time element | |
| Relative variable of Eij | |
| Linear velocity and angular velocity of beam root | |
| Force and moment at the free end of the beam | |
| Legendre interpolation polynomial | |
| Legendre interpolation polynomial about space and time | |
| k th (space) and l th (time) unknown variable of Eij | |
| Space integral coefficient of α th legendre interpolation polynomial | |
| Space integral coefficient of α,k,p th legendre interpolation polynomial | |
| Space integral coefficient of α,k,p th legendre interpolation polynomial | |
| Time integral coefficient of β th legendre interpolation polynomial | |
| Time integral coefficient of β,l th legendre interpolation polynomial | |
| Time integral coefficient of β,l,q th legendre interpolation polynomial | |
| Space-time element linear array | |
| Space-time element nonlinear array | |
| Constant vector | |
| Unknown quantity of the space-time unit | |
| Unknown quantity of the space-time unit and | |
| Unknown quantity of the space-time unit and | |
| Connection matrix of space-time element in space and time | |
| Coefficient matrix of the final equation |
Appendix A
Appendix B
Appendix C
References
- Bauchau, O.A.; Kang, N.K. A Multibody Formulation for Helicopter Structural Dynamic Analysis. J. Am. Helicopter Soc. 1993, 38, 3–14. [Google Scholar] [CrossRef]
- Hodges, D.H. A Mixed Variational Formulation Based on Exact Intrinsic Equations for Dynamics of Moving Beams. Int. J. Solids Struct. 1990, 26, 1253–1273. [Google Scholar] [CrossRef]
- Hodges, D.H.; Shang, X.; Carlos, C. Finite Element Solution of Nonlinear Intrinsic Equations for Curved Composite Beams. J. Am. Helicopter Soc. 1996, 41, 313–321. [Google Scholar] [CrossRef]
- Hodges, D.H. Geometrically Exact, Intrinsic Theory for Dynamics of Curved and Twisted Anisotropic Beams. AIAA J. 2003, 41, 1131–1137. [Google Scholar] [CrossRef]
- Hodges, D.H. Nonlinear Composite Beam Theory; AIAA: Reston, VA, USA, 2006. [Google Scholar]
- Green, A.E.; Laws, N. A General Theory of Rods. Proceed. R. Soc. 1966, 293, 145–155. [Google Scholar]
- Hegemier, G.A.; Nair, S. A Nonlinear Dynamical Theory for Heterogeneous, Anisotropic, Elasticrods. AIAA J. 1977, 15, 8–15. [Google Scholar] [CrossRef]
- Patil, M.J.; Hodges, D.H. Flight dynamics of highly flexible flying wings. J. Aircr. 2006, 43, 1790–1799. [Google Scholar] [CrossRef] [Green Version]
- Sotoudeh, Z.; Hodges, D.H. Modeling Beams with Various Boundary Conditions Using Fully Intrinsic Equations. J. Appl. Mech. 2011, 78, 031010. [Google Scholar] [CrossRef]
- Sotoudeh, Z.; Hodges, D.H. Incremental method for structural analysis of joined-wing aircraft. J. Aircr. 2011, 48, 1588–1601. [Google Scholar] [CrossRef]
- Sotoudeh, Z.; Hodges, D.H.; Chang, C.S. Validation Studies for Aeroelastic Trim and Stability of Highly Flexible Aircraft. J. Aircr. 2010, 47, 1240–1247. [Google Scholar] [CrossRef]
- Patil, M.J.; Althoff, M. Energy-consistent, Galerkin approach for the nonlinear dynamics of beams using intrinsic equations. J. Vib. Control. 2011, 17, 1748–1758. [Google Scholar] [CrossRef]
- Patil, M.J.; Hodges, D.H. Variable-order finite elements for nonlinear, fully intrinsic beam equations. J. Mech. Mater. Struct. 2011, 6, 479–493. [Google Scholar] [CrossRef] [Green Version]
- Khaneh Masjedi, P.; Ovesy, H.R. Chebyshev collocation method for static intrinsic equations of geometrically exact beams. Int. J. Solids Struct. 2015, 54, 183–191. [Google Scholar] [CrossRef]
- Bellman, R.; Casti, J. Differential quadrature and long-term integration. J. Math. Anal. Appl. 1971, 34, 235–238. [Google Scholar] [CrossRef] [Green Version]
- Amoozgar, M.R.; Shahverdi, H. Analysis of Nonlinear Fully Intrinsic Equations of Geometrically Exact Beams Using Generalized Differential Quadrature Method. Acta Mech. 2016, 227, 1265–1277. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Y. Differential Quadrature Method for Fully Intrinsic Equations of Geometrically Exact Beams. J. Aerosp. 2022, 9, 596. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Hulbert, G.M. Space-time finite element methods for elastodynamics: Formulations and error estimates. J. Comput. Methods Appl. Mech. Eng. 1988, 66, 339–363. [Google Scholar] [CrossRef]
- Oden, J.T. A general theory of finite elements. II. Applications. Int. J. Numer. Meth. Eng. 1969, 1, 247–259. [Google Scholar] [CrossRef]
- Bajer, C.L. Triangular and tetrahedral space-time finite elements in vibration analysis. J. Numer. Methods Eng. 1986, 23, 2031–2048. [Google Scholar] [CrossRef]
- Hulbert, G.M. Time Finite Element Methods for Structural Dynamics. Int. J. Numer. Eng. 1992, 33, 307–331. [Google Scholar] [CrossRef] [Green Version]
- Griebel, M.; Oeltz, D.; Vassilevski, P. Space-time approximation with sparse grids. J. Sci. Comput. 2006, 28, 701–727. [Google Scholar] [CrossRef]
- Tezduyar, T.E.; Sathe, S.; Cragin, T.; Nanna, B.; Conklin, B.S.; Pausewang, J.; Schwaab, M. Modelling of fluid–structure interactions with the space-time finite elements: Arterial fluid mechanics. Int. J. Numer. Meth. Fluids 2007, 54, 901–922. [Google Scholar] [CrossRef]
- Yang, Y.; Chirputkar, S.; Alpert, D.N.; Eason, T.; Spottswood, S.; Qian, D. Enriched space-time finite element method: A new paradigm for multiscaling from elastodynamics to molecular dynamics. Int. J. Numer. Meth. Eng. 2012, 92, 115–140. [Google Scholar] [CrossRef]
- Bause, M.; Radu, F.A.; Köcher, U. Space-time finite element approximation of the Biot poroelasticity system with iterative coupling. J. Comput. Methods Appl. Mech. Eng. 2017, 320, 745–768. [Google Scholar] [CrossRef] [Green Version]
- Steinbach, O.; Yang, H. Comparison of algebraic multigrid methods for an adaptive space-time finite-element discretization of the heat equation in 3d and 4d. J. Numer. Linear Algebra Appl. 2018, 25, e2143. [Google Scholar] [CrossRef]
- Moore, S.E. A stable space-time finite element method for parabolic evolution problems. J. Calcolo 2018, 55, 18. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.; Fujisawa, K.; Murakami, A.; Sasakawa, S. A methodology to control numerical dissipation characteristics of velocity based time discontinuous Galerkin space-time finite element method. J. Numer. Methods Eng. 2022, 123, 5517–5545. [Google Scholar] [CrossRef]
- Johnson, C. Discontinuous Galerkin finite element methods for second order hyperbolic problems. J. Comput. Meth. Appl. Mech. Eng. 1993, 107, 117–129. [Google Scholar] [CrossRef]
- Shaw, S. An a priori error estimate for a temporally discontinuous Galerkin space-time finite element method for linear elasto- and visco-dynamics. J. Comput. Methods Appl. Mech. Eng. 2019, 351, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Gong, C.Y.; Bao, W.M. A parallel algorithm for the Riesz fractional reaction–diffusion equation with explicit finite difference method. J. Fract. Calc. Appl. Anal. 2013, 16, 654–669. [Google Scholar] [CrossRef]
- Yu, W.; Hodges, D.H. Generalized Timoshenko theory of the variational asymptotic beam sectional analysis. J Am. Helicopter Soc. 2005, 50, 46–55. [Google Scholar] [CrossRef]
- Yu, W.; Hodges, D.H.; Volovoi, V.V.; Cesnik, C.E.S. On Timoshenko-like modeling of initially curved and twisted composite beams. J. Solids Struct. 2002, 39, 5101–5121. [Google Scholar] [CrossRef]
- Hopkins, A.S.; Ormiston, R.A. An Examination of Selected Problems in Rotor Blade Structural Mechanics and Dynamics. J. Am. Helicopter Soc. 2006, 51, 104–119. [Google Scholar] [CrossRef] [Green Version]
- Argyris, J.; Symeonidis, S. Nonlinear finite element analysis of elastic systems under nonconservative loading-natural formulation. Part I. Quasistatic problems. J. Comput. Methods Appl. Mech. Eng. 1981, 26, 75–123. [Google Scholar] [CrossRef]


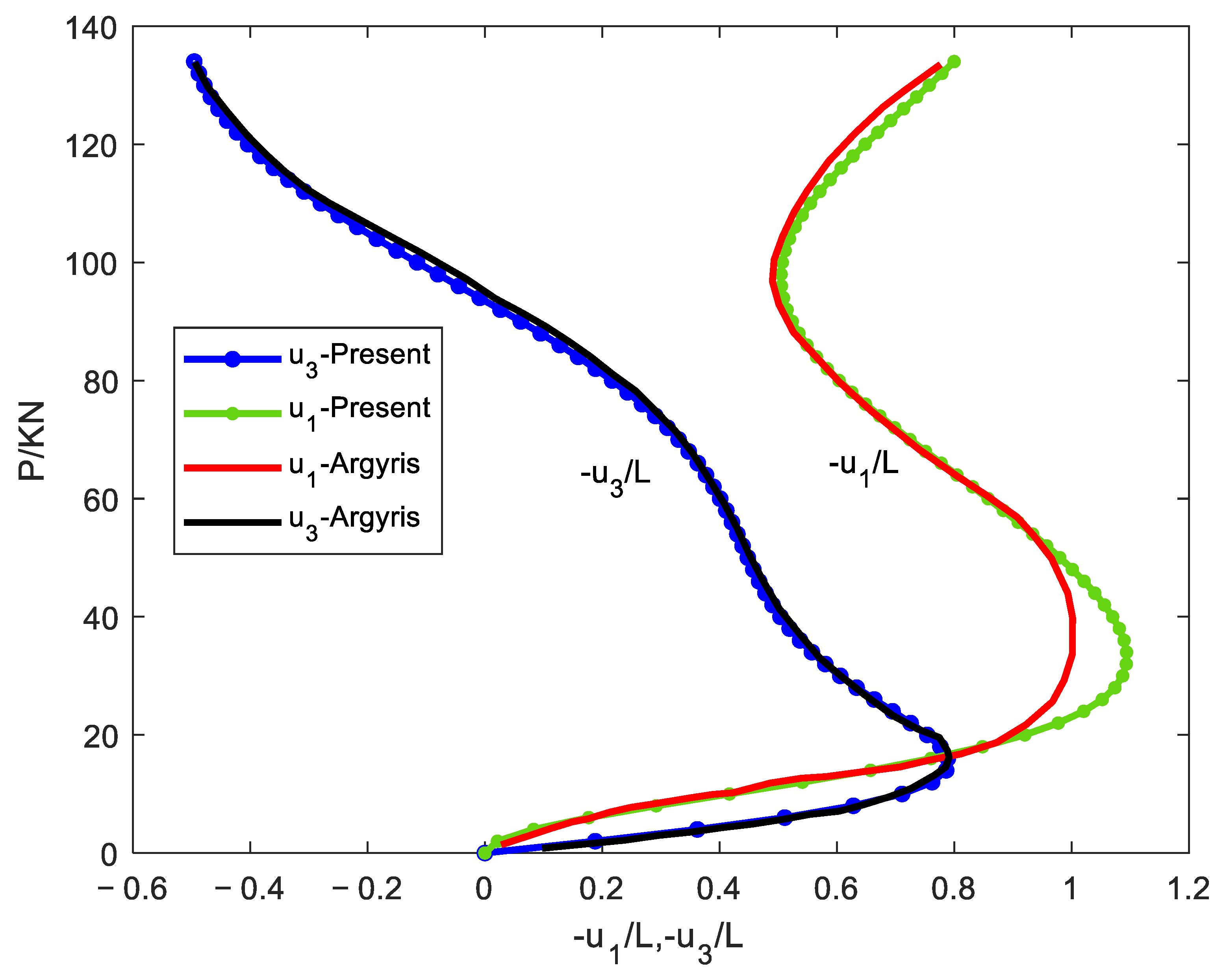
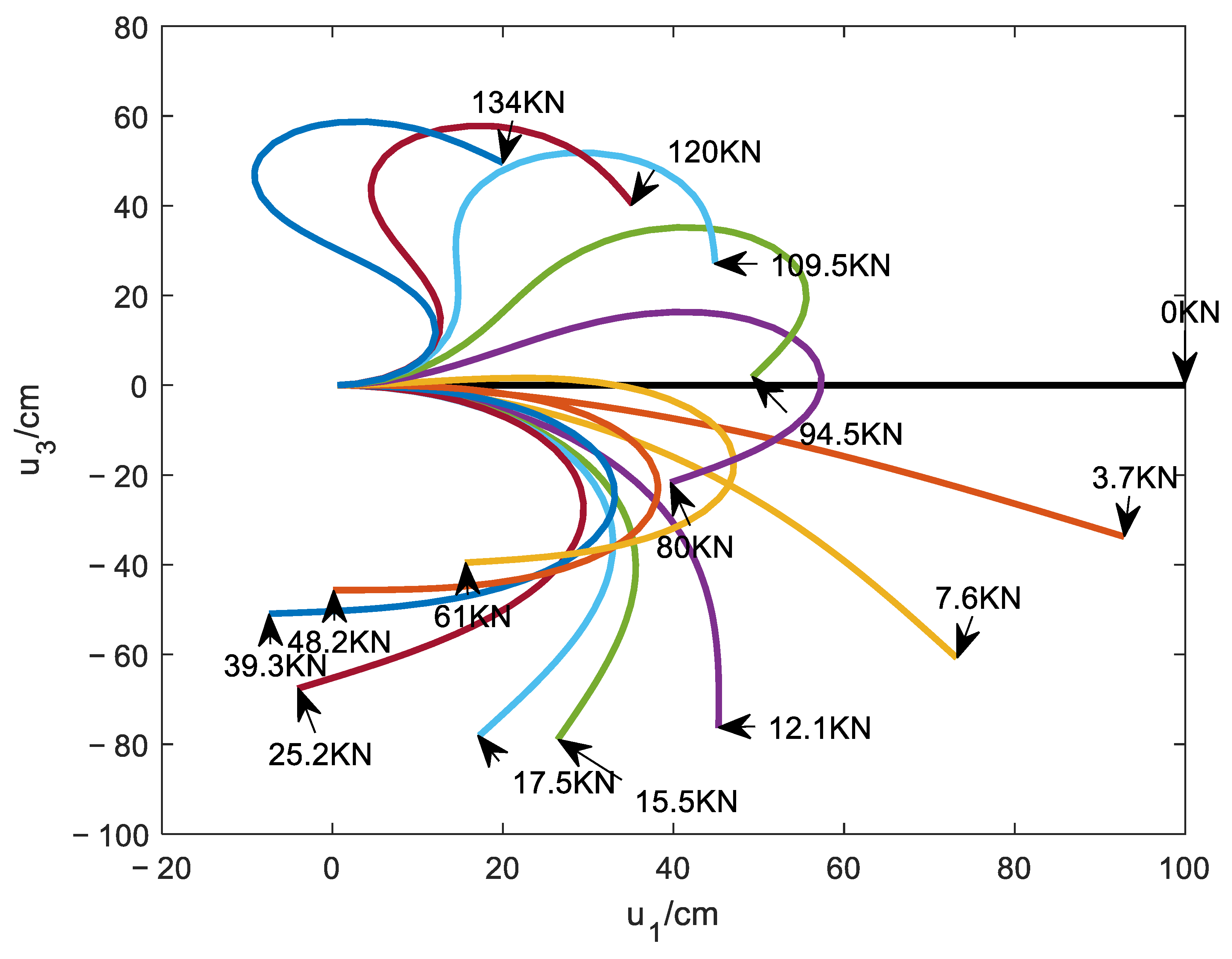
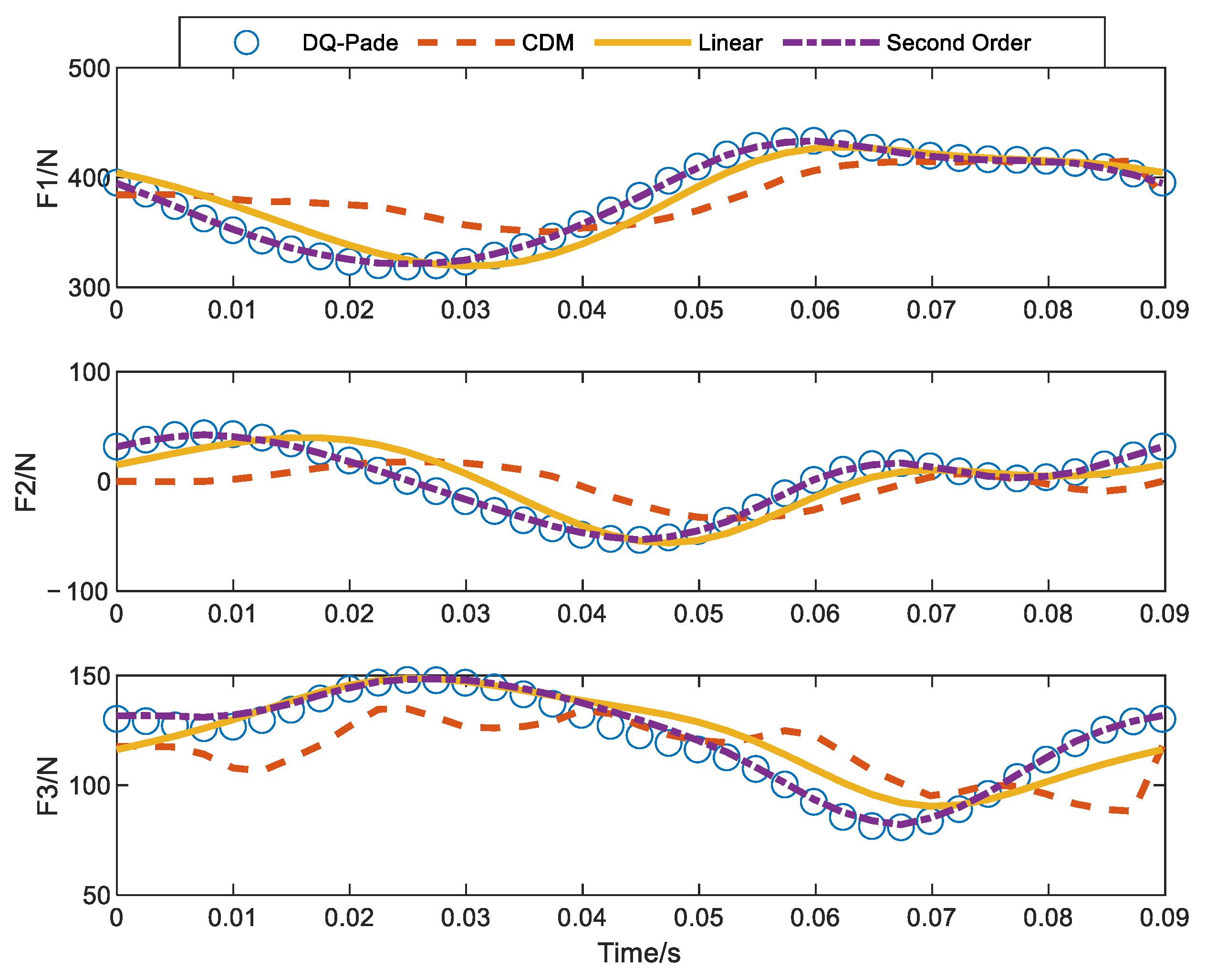
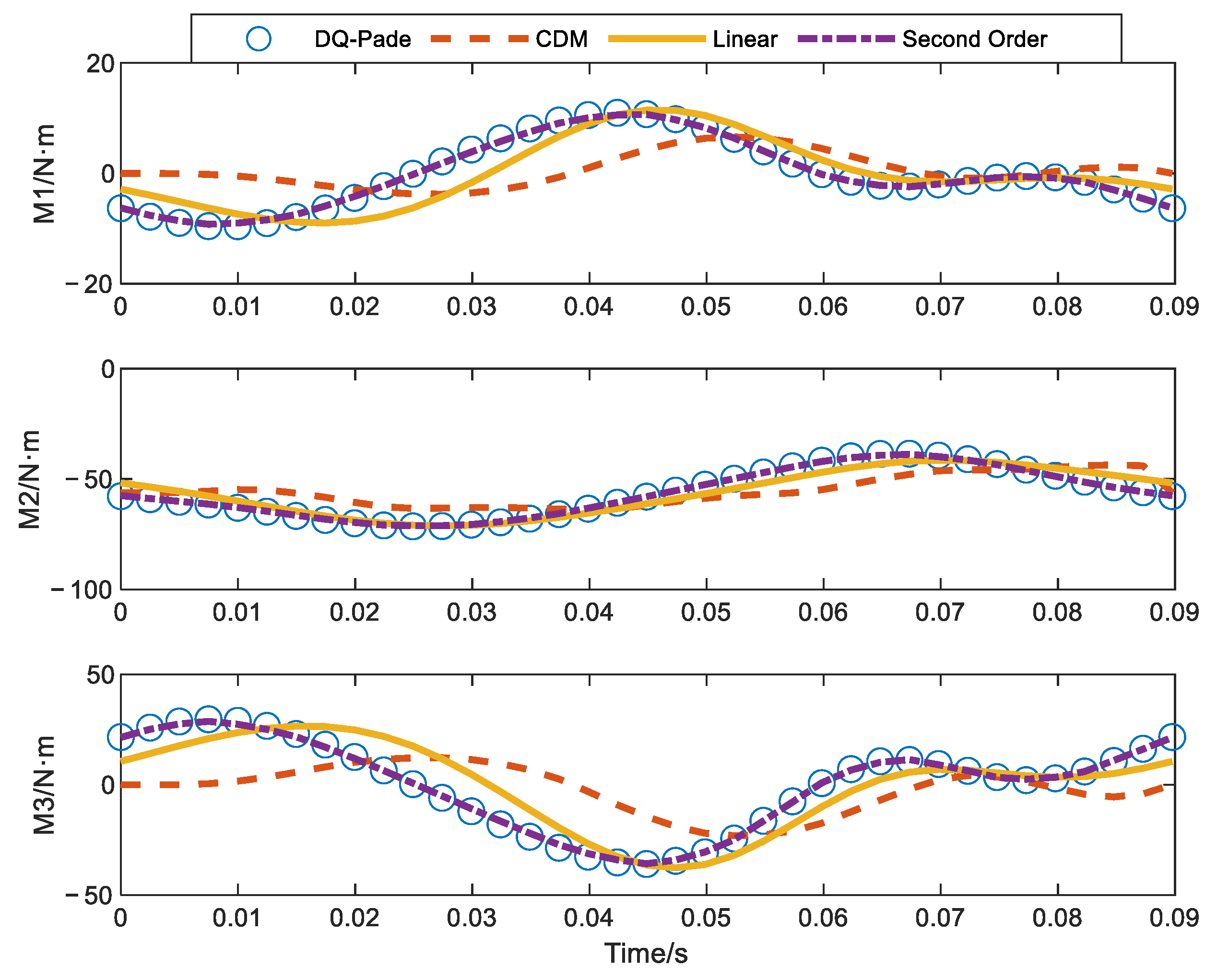
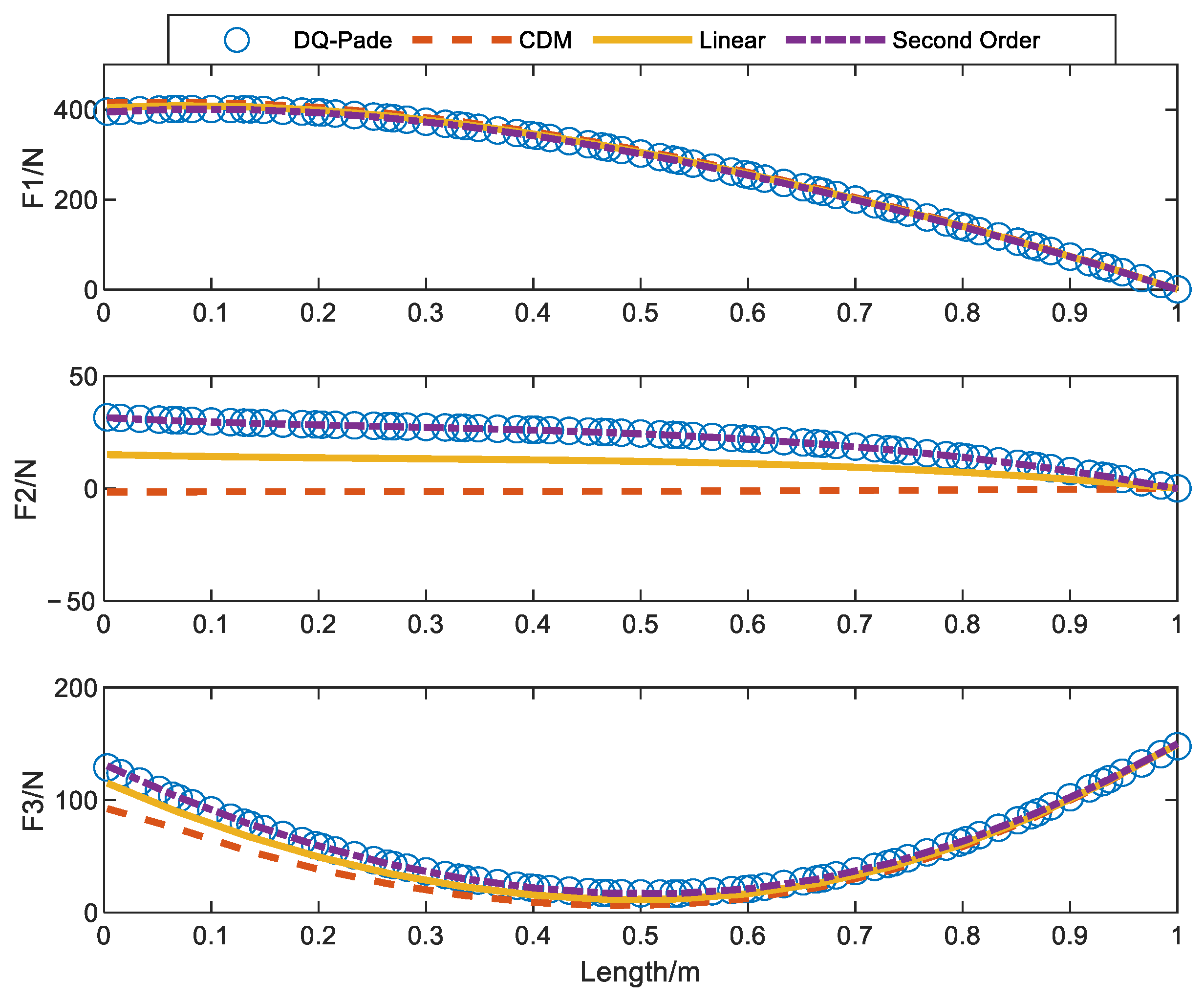
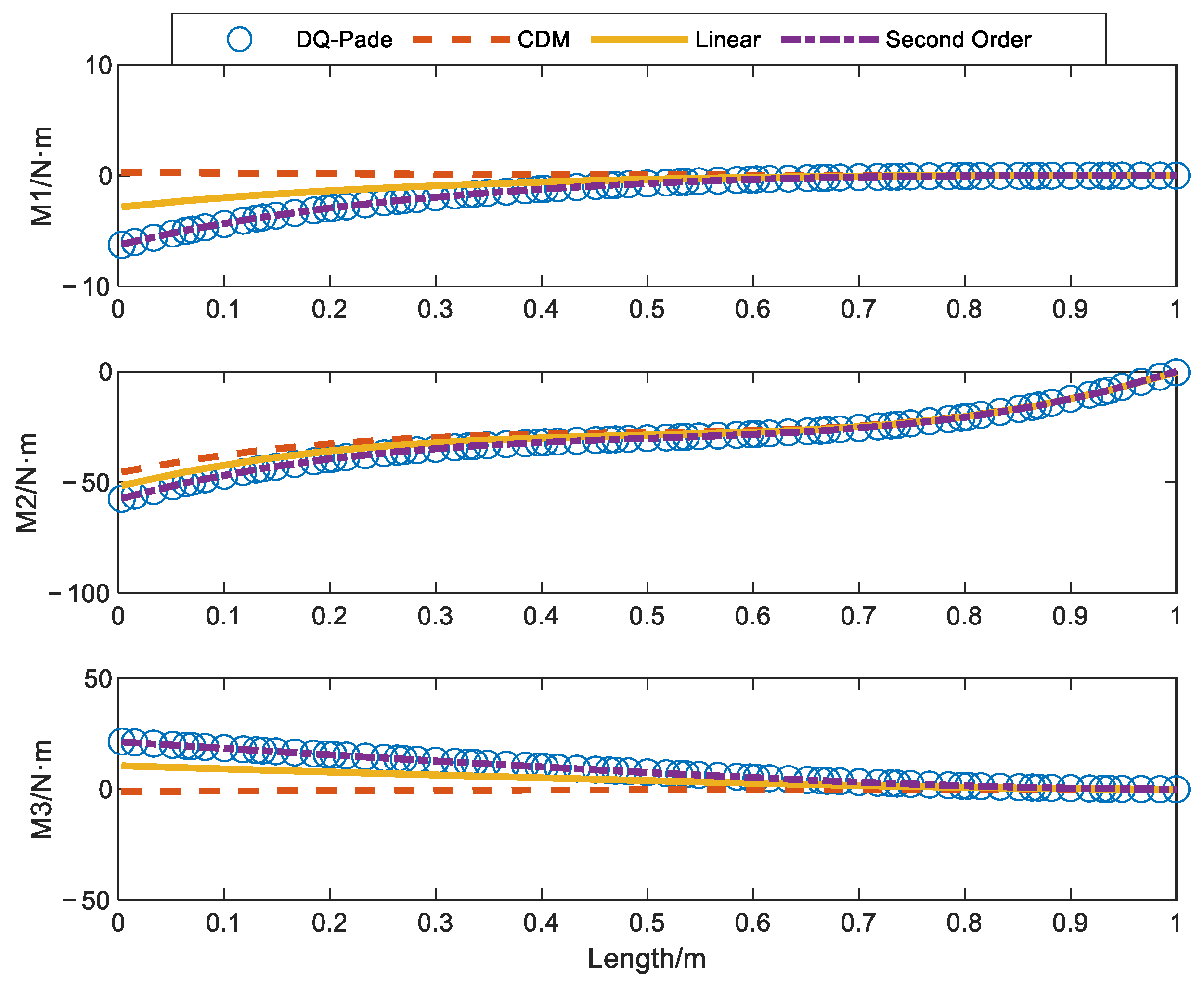
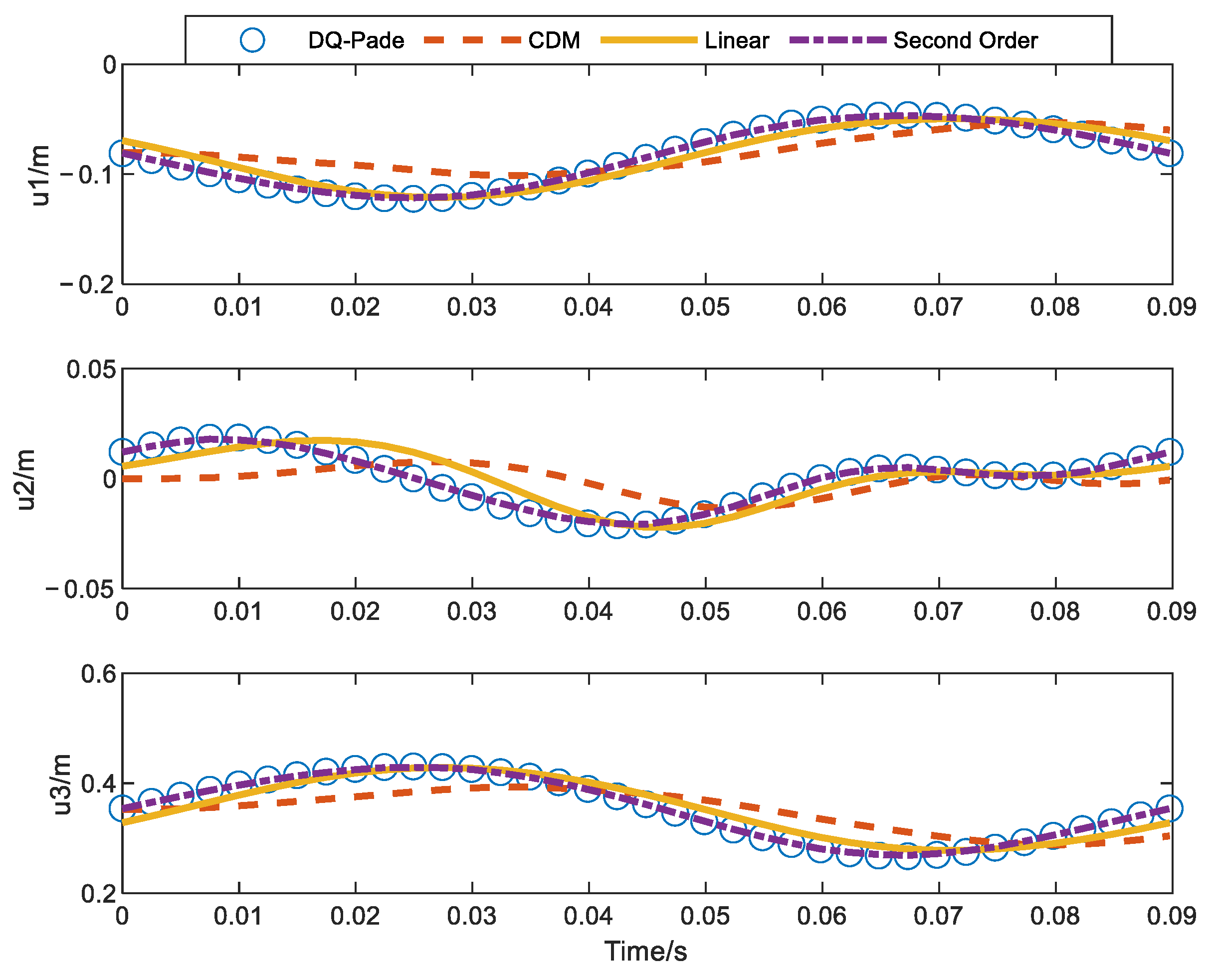
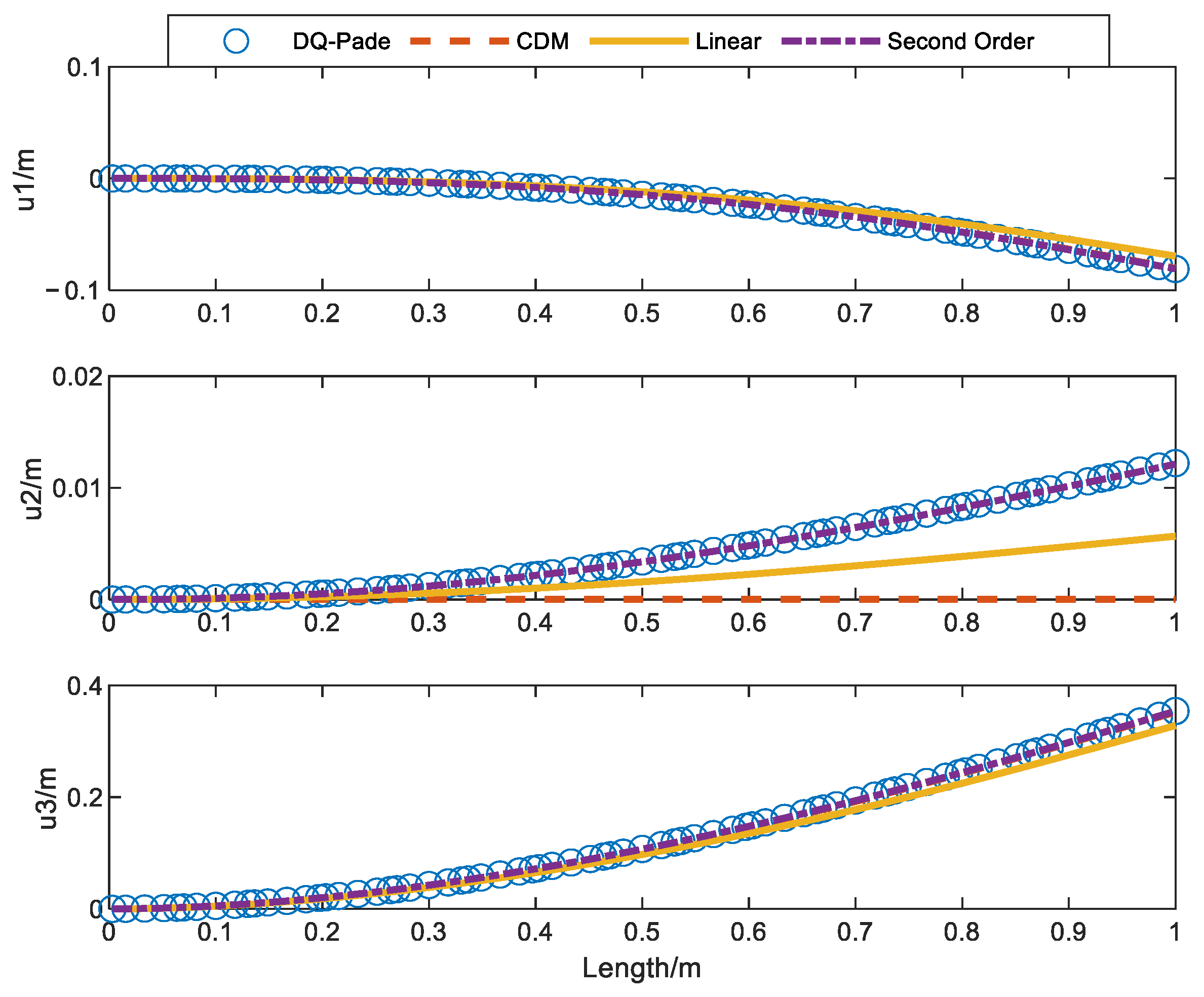
| No. of Units | 2 | 3 | 4 | 5 | 10 | 20 | |
|---|---|---|---|---|---|---|---|
| 500 N.m | Exact | 10.01401161 | |||||
| STFEM | 10.01401208 | 10.01401181 | 10.01401166 | 10.01401158 | 10.01401158 | 10.01401158 | |
| Error | 4.74 × 10−8 | 2.00 × 10−8 | 0.50 × 10−8 | 0.26 × 10−8 | 0.26 × 10−8 | 0.26 × 10−8 | |
| 2500 N.m | Exact | 0.91168936 | |||||
| STFEM | 0.91174717 | 0.91165092 | 0.91167167 | 0.91168341 | 0.91168634 | 0.91168896 | |
| Error | 6.34 × 10−5 | 4.22 × 10−5 | 1.94 × 10−5 | 0.65 × 10−5 | 0.33 × 10−5 | 4.39 × 10−7 | |
| Parameter | Value |
|---|---|
| Mass per unit length | |
| Moment of inertia per unit length | |
| Moment of inertia per unit length | |
| Moment of inertia per unit length | |
| Extensional rigidity | |
| Shear rigidity | |
| Shear rigidity | |
| Torsional rigidity | |
| Bending rigidity | |
| Bending rigidity (chordwise) |
| DQ-Pade | Second-Order Format | Linear Format (Space × Time) | |||
|---|---|---|---|---|---|
| 10 × 24 | 15 × 36 | 15 × 48 | 15 × 60 | 15 × 72 | |
| 130.1947 | 130.7331 | 113.8371 | 122.1947 | 127.3349 | 129.8467 |
| Error | 0.41% | 12.56% | 6.14% | 2.19% | 0.26% |
| CPU time/s | 68.63 | 21.76 | 37.90 | 77.17 | 162.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Hu, X.; Liu, Y. Space-Time Finite Element Method for Fully Intrinsic Equations of Geometrically Exact Beam. Aerospace 2023, 10, 92. https://doi.org/10.3390/aerospace10020092
Chen L, Hu X, Liu Y. Space-Time Finite Element Method for Fully Intrinsic Equations of Geometrically Exact Beam. Aerospace. 2023; 10(2):92. https://doi.org/10.3390/aerospace10020092
Chicago/Turabian StyleChen, Lidao, Xin Hu, and Yong Liu. 2023. "Space-Time Finite Element Method for Fully Intrinsic Equations of Geometrically Exact Beam" Aerospace 10, no. 2: 92. https://doi.org/10.3390/aerospace10020092
APA StyleChen, L., Hu, X., & Liu, Y. (2023). Space-Time Finite Element Method for Fully Intrinsic Equations of Geometrically Exact Beam. Aerospace, 10(2), 92. https://doi.org/10.3390/aerospace10020092





