In-Plane Libration Suppression of a Two-Segment Tethered Towing System
Abstract
:1. Introduction
- (1)
- With the elasticity of the tethers, the equilibrium configurations of a two-segment tethered towing system with constant thrust are obtained and the stabilities of equilibria are proved.
- (2)
- An in-plane sliding mode controller is designed to suppress the librations of the in-plane angles of the system.
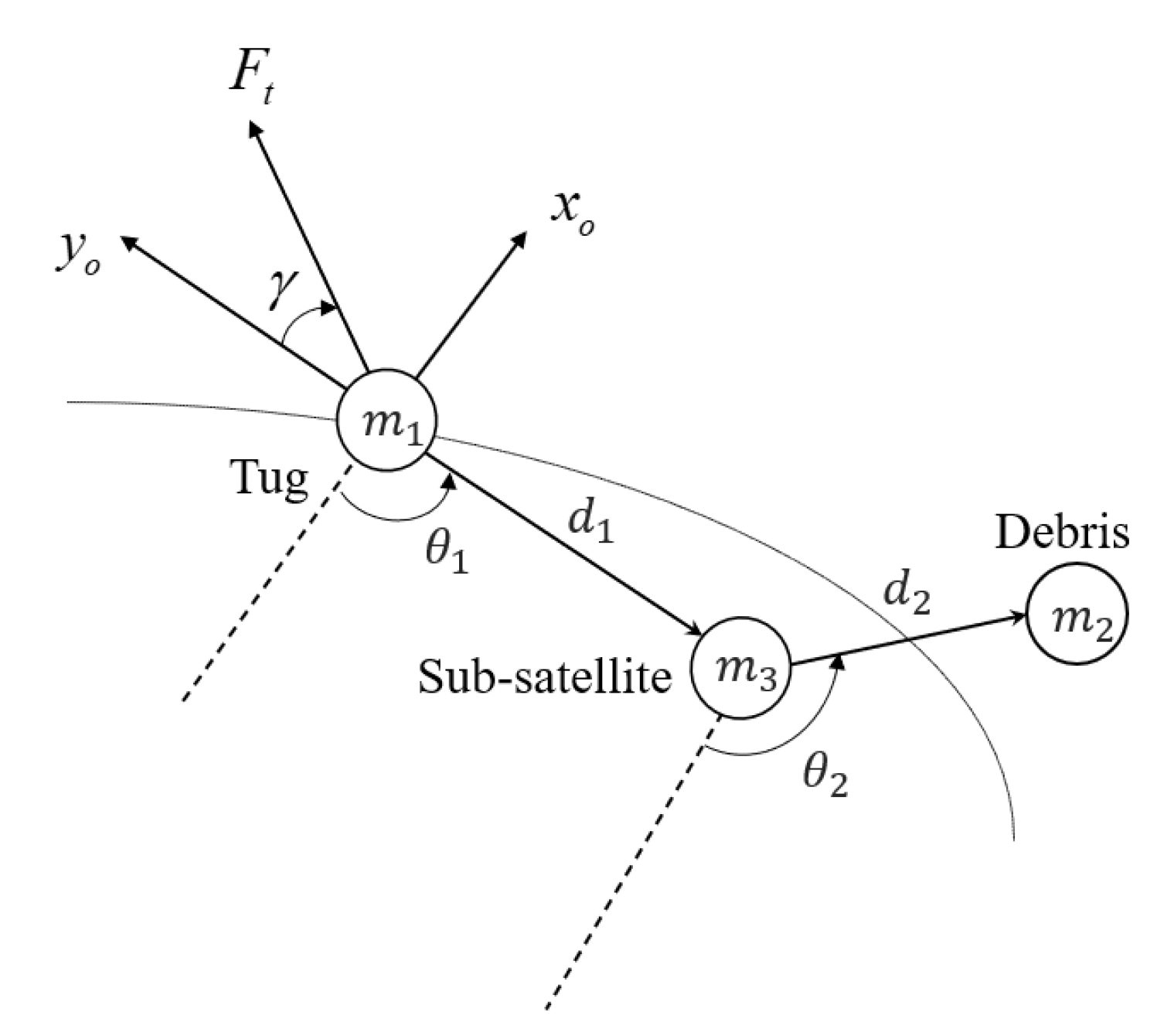
2. Problem Formulation
3. Equilibria and Stability Analysis
3.1. Equilibrium Configurations of the System
3.2. Stability of Equilibrium Configuration
4. Libration Controller Design
5. Simulation Results
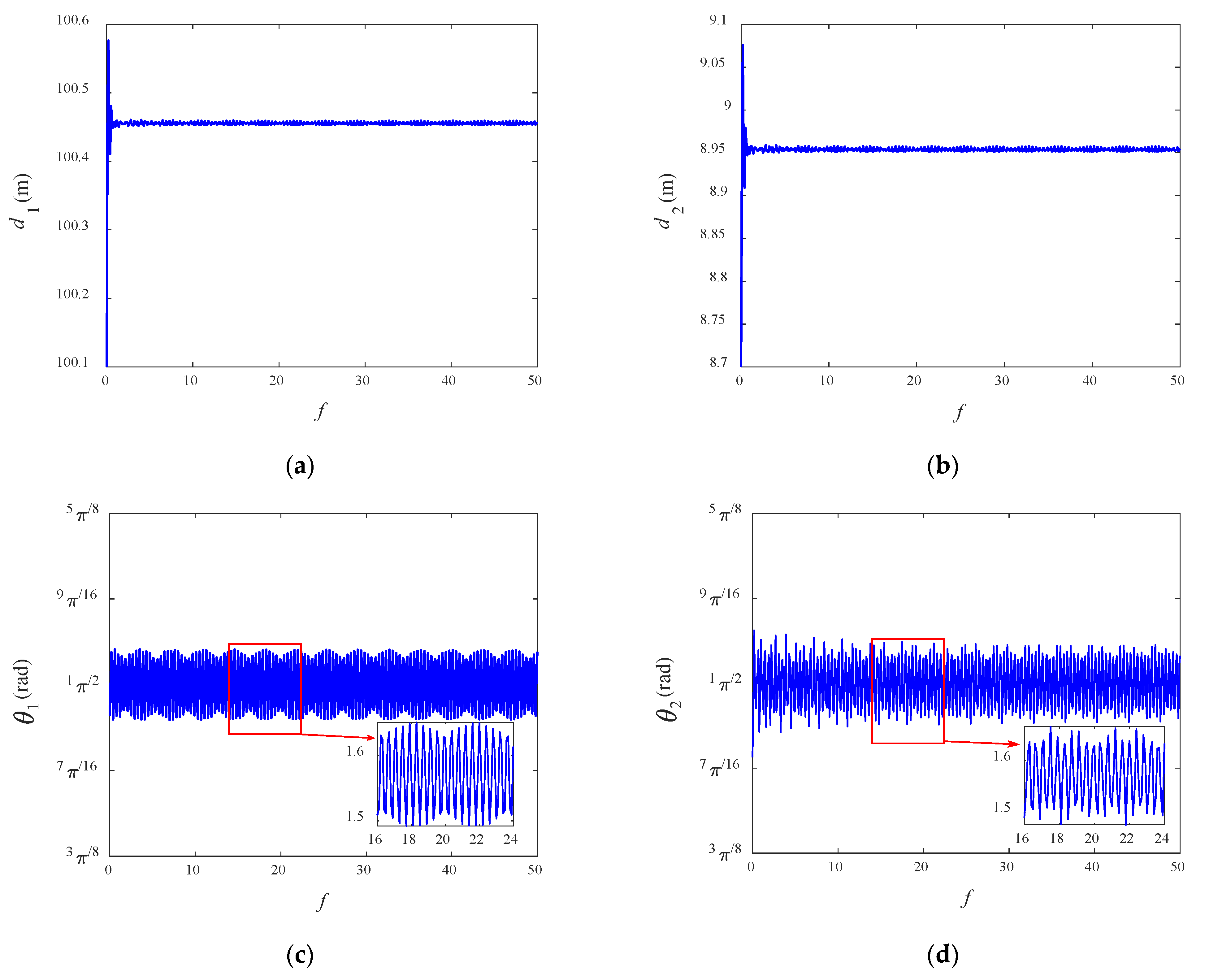
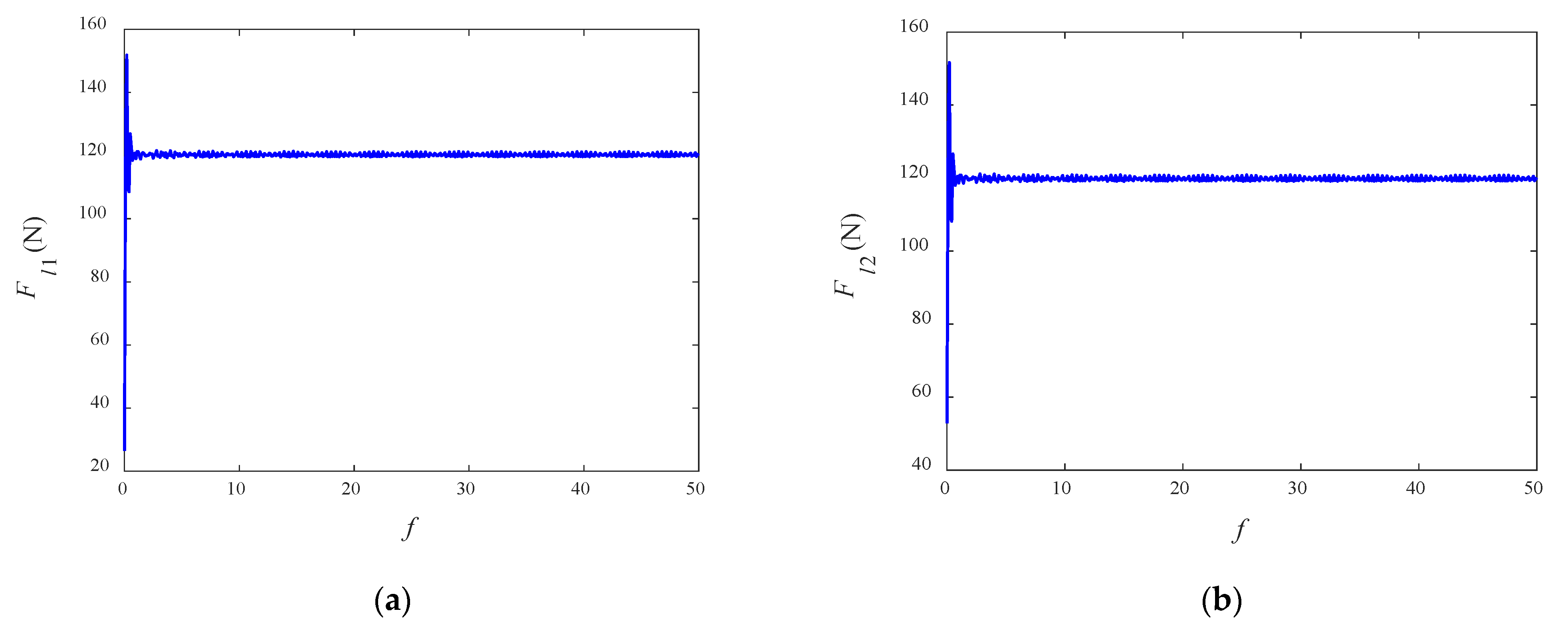
5.1. Simulations for Equilibrium Configuration
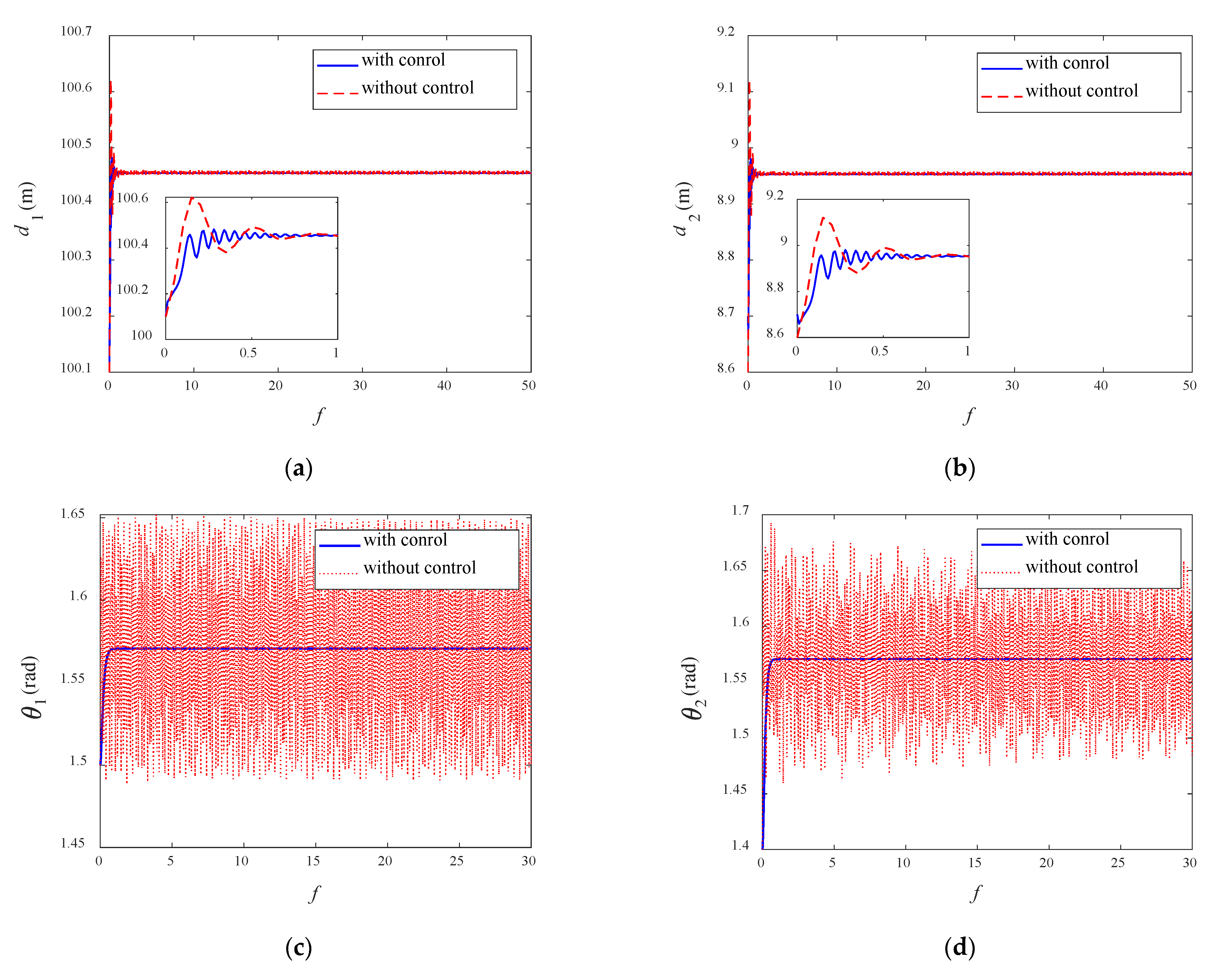
5.2. Simulations for Libration Controller
6. Conclusions
- (1)
- Seven sets of equilibrium configurations are given. The configuration in which the tug, sub-satellite, and debris remain in a straight line along the local horizontal is stable.
- (2)
- An in-plane libration controller is designed. According to the Lyapunov function, the system will converge to the sliding surface asymptotically. The system will reach the equilibrium asymptotically with the action of the designed libration controller. It can be seen from the Monte Carlo results that the control can converge within a short time.
- (3)
- It can be found from the simulation results that the librations in the direction of tether length can be effectively suppressed with the suppression of the oscillations of the in-plane angles. This is attributed to the coupling characteristics between in-plane angles and the tether length. As a result, the system under the action of the designed controller can reach the desired state while the librations of in-plane angles are effectively suppressed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Muelhaupt, T.J.; Sorge, M.E.; Morin, J.; Wilson, R.S. Space traffic management in the new space era. J. Space Saf. Eng. 2019, 6, 80–87. [Google Scholar] [CrossRef]
- Shan, M.; Guo, J.; Gill, E. Deployment dynamics of tethered-net for space debris removal. Acta Astronaut. 2017, 132, 293–302. [Google Scholar] [CrossRef]
- Botta, E.M.; Sharf, I.; Misra, A.K. Contact dynamics modeling and simulation of tether nets for space-debris capture. J. Guid. Control Dyn. 2017, 40, 110–123. [Google Scholar] [CrossRef]
- Botta, E.M.; Sharf, I.; Misra, A.K.; Teichmann, M. On the simulation of tether-nets for space debris capture with vortex dynamics. Acta Astronaut. 2016, 123, 91–102. [Google Scholar] [CrossRef]
- Benvenuto, R.; Lavagna, M.; Salvi, S. Multibody dynamics driving GNC and system design in tethered nets for active debris removal. Adv. Space Res. 2016, 58, 45–63. [Google Scholar] [CrossRef]
- Sharf, I.; Thomsen, B.; Botta, E.M.; Misra, A.K. Experiments and simulation of a net closing mechanism for tether-net capture of space debris. Acta Astronaut. 2017, 139, 332–343. [Google Scholar] [CrossRef]
- Yue, S.; Li, M.; Zhao, Z.; Du, Z.; Wu, C.; Zhang, Q. Parameter Analysis and Experiment Validation of Deployment Characteristics of a Rectangular Tether-Net. Aerospace 2023, 10, 115. [Google Scholar] [CrossRef]
- Lv, S.; Zhang, H.; Zhang, Y.; Ning, B.; Qi, R. Design of an integrated platform for active debris removal. Aerospace 2022, 9, 339. [Google Scholar] [CrossRef]
- Mark, C.P.; Kamath, S. Review of active space debris removal methods. Space Policy 2019, 47, 194–206. [Google Scholar] [CrossRef]
- Stadnyk, K.; Ulrich, S. Validating the Deployment of a Novel Tether Design for Net-Based Orbital Debris Removal Missions. In Proceedings of the AIAA SciTech Forum and Exposition, Orlando, FL, USA, 6–10 January 2020; pp. 592–611. [Google Scholar]
- Jung, W.; Mazzoleni, A.P.; Chung, J. Dynamic analysis of a tethered satellite system with a moving mass. Nonlinear Dyn. 2014, 75, 267–281. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Guirao, J.L.G.; Hobiny, A.; Alzahrani, F. Dynamics of a tethered satellite with variable mass. Discret. Contin. Dyn. Syst. Ser. S 2015, 8, 1035–1045. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Guirao, J.L.G.; Vera, J.A. Dynamics of a dumbbell satellite under the zonal harmonic effect of an oblate body. Commun. Nonlinear Sci. 2015, 20, 1057–1069. [Google Scholar] [CrossRef] [Green Version]
- Pang, Z.; Jin, D.; Yu, B.; Wen, H. Nonlinear normal modes of a tethered satellite system of two degrees of freedom under internal resonances. Nonlinear Dyn. 2016, 85, 1779–1789. [Google Scholar] [CrossRef]
- Aslanov, V.S.; Ledkov, A.S. Dynamics of towed large space debris taking into account atmospheric disturbance. Acta Astronaut. 2014, 225, 2685–2697. [Google Scholar] [CrossRef]
- Aslanov, V.S.; Yudintsev, V.V. Dynamics, analytical solutions and choice of parameters for towed space debris with flexible appendages. Adv. Space Res. 2015, 55, 660–667. [Google Scholar] [CrossRef]
- Aslanov, V.S.; Yudintsev, V.V. The motion of tethered tug–debris system with fuel residuals. Adv. Space Res. 2015, 56, 1493–1501. [Google Scholar] [CrossRef]
- Aslanov, V.S.; Misra, A.K.; Yudintsev, V.V. Chaotic attitude motion of a low-thrust tug-debris tethered system in a keplerian orbit. Acta Astronaut. 2017, 139, 419–427. [Google Scholar] [CrossRef]
- Aslanov, V.S.; Yudintsev, V.V. Chaos in tethered tug–debris system induced by attitude oscillations of debris. J. Guid. Control Dyn. 2019, 42, 1630–1637. [Google Scholar] [CrossRef]
- Aslanov, V.S. Stability of a pendulum with a moving mass: The averaging method. J. Sound Vib. 2019, 445, 261–269. [Google Scholar] [CrossRef]
- Lim, J.; Chung, J. Dynamic analysis of a tethered satellite system for space debris capture. Nonlinear Dyn. 2018, 94, 2391–2408. [Google Scholar] [CrossRef]
- Shan, M.; Shi, L. Comparison of tethered post-capture system models for space debris removal. Aerospace 2022, 9, 33. [Google Scholar] [CrossRef]
- Qi, R.; Misra, A.K.; Zuo, Z. Active debris removal using double-tethered space-tug system. J. Guid. Control Dyn. 2017, 40, 722–730. [Google Scholar] [CrossRef]
- Hovell, K.; Ulrich, S. Attitude stabilization of an unknown and spinning target spacecraft using a visco-elastic tether. In Proceedings of the 13th Symposium on Advanced Space Technologies in Robotics and Automation, Noordwijk, The Netherlands, 11–13 May 2015; pp. 1–8. [Google Scholar]
- Hovell, K.; Ulrich, S. Attitude stabilization of an uncooperative spacecraft in an orbital environment using visco-elastic tethers. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–8 January 2016; pp. 1343–1358. [Google Scholar]
- Hovell, K.; Ulrich, S. Experimental validation for tethered capture of spinning space debris. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017; pp. 626–644. [Google Scholar]
- Hovell, K.; Ulrich, S. Postcapture dynamics and experimental validation of subtethered space debris. J. Guid. Control Dyn. 2018, 41, 519–525. [Google Scholar] [CrossRef]
- Yang, K.Y.; Misra, A.K.; Zhang, J.; Qi, R.; Lu, S.; Liu, Y. Dynamics of a debris towing system with hierarchical tether architecture. Acta Astronaut. 2020, 177, 891–905. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Guirao, J.L.G.; Hobiny, A.; Alzahrani, F. Stability of equilibria points for a dumbbell satellite when the central body is oblate spheroid. Discret. Contin. Dyn. Syst. S 2015, 8, 1047–1054. [Google Scholar] [CrossRef]
- Hu, W.; Song, M.; Deng, Z. Energy dissipation/transfer and stable attitude of spatial on-orbit tethered system. J. Sound Vib. 2018, 412, 58–73. [Google Scholar] [CrossRef]
- Lian, X.; Liu, J.; Zhang, J.; Wang, C. Chaotic motion and control of a tethered-sailcraft system orbiting an asteroid. Commun. Nonlinear Sci. Numer. Simul. 2019, 77, 203–224. [Google Scholar] [CrossRef]
- Liu, J.F.; Qu, W.L.; Yuan, L.H.; Cui, N.G. Nonlinear dynamics of a space tethered system in the elliptic earth-moon restricted three-body system. J. Aerosp. Eng. 2019, 32, 04018139. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Huang, H. Effect of mass variation on dynamics of tethered system in orbital maneuvering. Acta Astronaut. 2018, 146, 15–23. [Google Scholar] [CrossRef]
- Jin, D.P.; Hu, H.Y. Optimal control of a tethered subsatellite of three degrees of freedom. Nonlinear Dyn. 2006, 46, 161–178. [Google Scholar] [CrossRef]
- Sun, X.; Zhong, R. Switched propulsion force libration control for the low-thrust space tug system. Aerosp. Sci. Technol. 2018, 80, 281–287. [Google Scholar] [CrossRef]
- Wen, H.; Zhu, Z.H.; Jin, D.; Hu, H. Constrained tension control of a tethered space-tug system with only length measurement. Acta Astronaut. 2016, 119, 110–117. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, Z.; Zhang, Q.; Zeng, M.; Li, S. Dynamics and control of a tethered space-tug system using Takagi-Sugeno fuzzy methods. Aerosp. Sci. Technol. 2019, 87, 289–299. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, K.; Qi, R. Dynamics and offset control of tethered space-tug system. Acta Astronaut. 2018, 142, 232–252. [Google Scholar] [CrossRef]
- Kang, J.; Zhu, Z.H.; Santaguida, L.F. Analytical and experimental investigation of stabilizing rotating uncooperative target by tethered space tug. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2426–2437. [Google Scholar] [CrossRef]
- Razzaghi, P.; Al Khatib, E.; Bakhtiari, S. Sliding mode and SDRE control laws on a tethered satellite system to de-orbit space debris. Adv. Space Res. 2019, 64, 18–27. [Google Scholar] [CrossRef]
- Chu, Z.; Di, J.; Cui, J. Hybrid tension control method for tethered satellite systems during large tumbling space debris removal. Acta Astronaut. 2018, 152, 611–623. [Google Scholar] [CrossRef]
- Xu, S.; Sun, G.; Ma, Z.; Li, X. Fractional-order fuzzy sliding mode control for the deployment of tethered satellite system under input saturation. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 747–756. [Google Scholar] [CrossRef]
- Xu, S.; Wen, H.; Huang, Z.; Jin, D. A fuzzy control scheme for deployment of space tethered system with tension constraint. Aerosp. Sci. Technol. 2020, 106, 106143. [Google Scholar] [CrossRef]
- Kang, J.; Zhu, Z.H.; Wang, W.; Li, A.; Wang, C. Fractional order sliding mode control for tethered satellite deployment with disturbances. Adv. Space Res. 2017, 59, 263–273. [Google Scholar] [CrossRef]
- Li, X.; Sun, G.; Shao, X. Discrete-time pure-tension sliding mode predictive control for the deployment of space tethered satellite with input saturation. Acta Astronaut. 2020, 170, 521–529. [Google Scholar] [CrossRef]
- Li, X.; Sun, G.; Han, S.; Shao, X. Fractional-order nonsingular terminal sliding mode tension control for the deployment of space tethered satellite. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2759–2770. [Google Scholar] [CrossRef]
- Li, X.; Sun, G.; Xue, C. Fractional-order deployment control of space tethered satellite via adaptive super-twisting sliding mode. Aerosp. Sci. Technol. 2022, 121, 107390. [Google Scholar] [CrossRef]
- Liu, E.; Yang, Y.; Yan, Y. Spacecraft attitude tracking for space debris removal using adaptive fuzzy sliding mode control. Aerosp. Sci. Technol. 2020, 107, 106310. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Control, 3rd ed.; Pearson: New York, NY, USA, 2015; pp. 133–139. [Google Scholar]


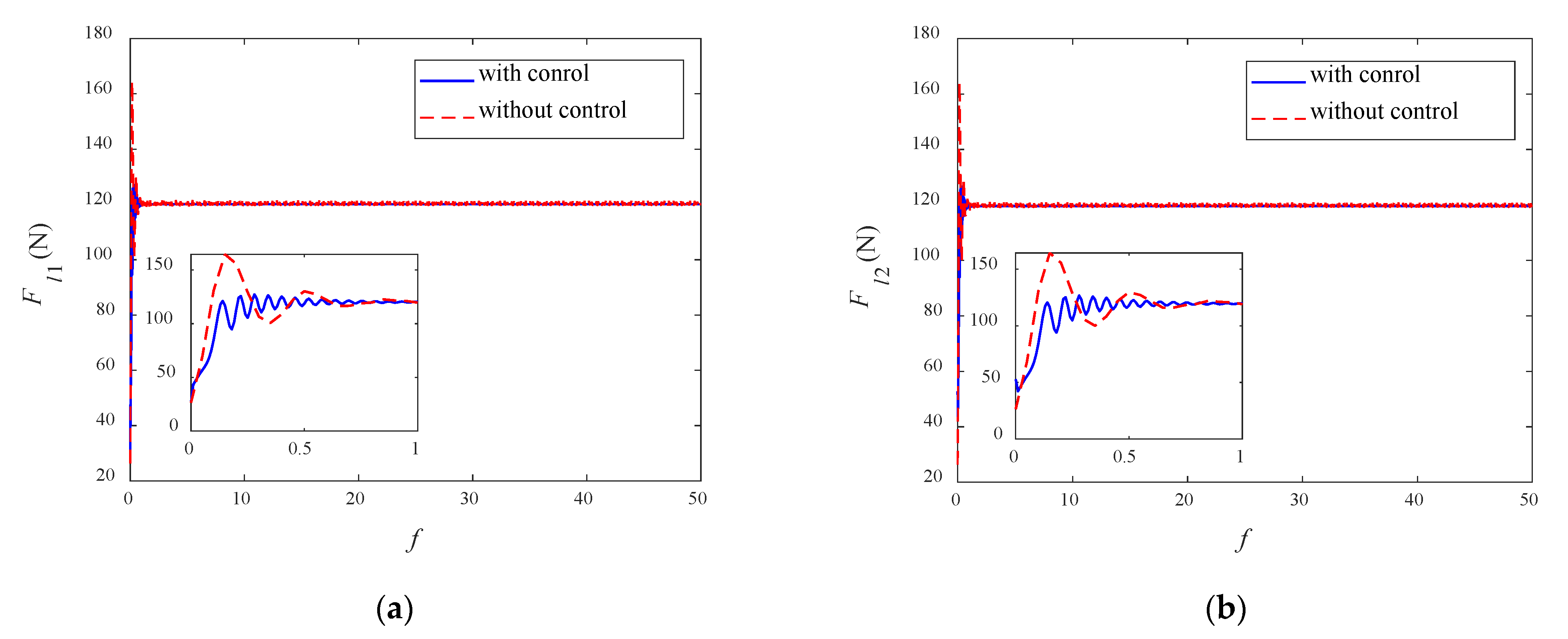
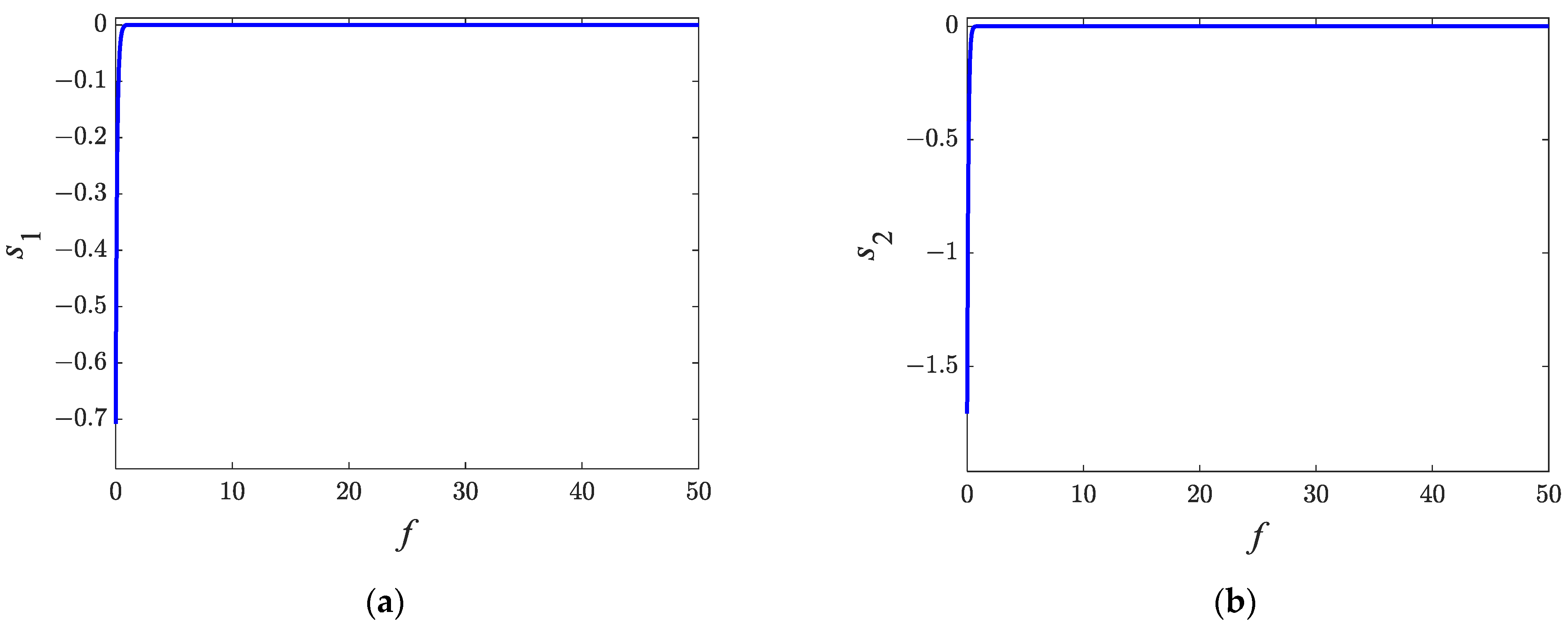
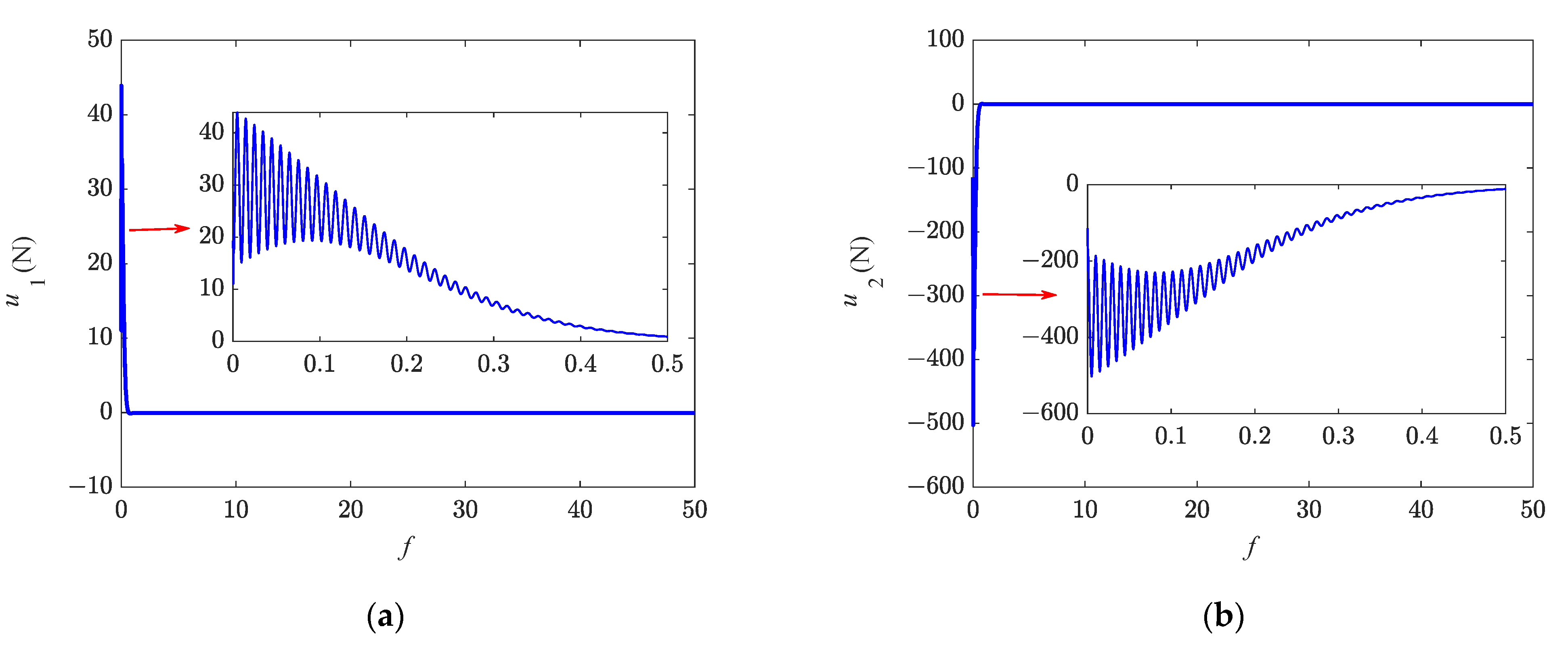
| Variables | Maximum Value without Control | Maximum Value with Control |
|---|---|---|
| 100.621 (m) | 100.482 (m) | |
| 9.121 (m) | 8.980 (m) | |
| 1.6519 (rad) | 1.5708 (rad) | |
| 1.6930 (rad) | 1.5708 (rad) | |
| 130.146 (N) | 125.297 (N) | |
| 129.745 (N) | 124.850 (N) |
| Number | Settling Time | Number | Settling Time | ||||
|---|---|---|---|---|---|---|---|
| 1 | 5.3113 | 2.7763 | 0.85 | 26 | 5.0009 | 4.3501 | 0.77 |
| 2 | 4.8808 | 2.6520 | 0.87 | 27 | 9.1271 | 3.7823 | 0.89 |
| 3 | 3.9296 | 1.6403 | 0.82 | 28 | 1.0997 | 4.3210 | 0.79 |
| 4 | 1.1259 | 2.9257 | 0.78 | 29 | 5.9695 | 3.4041 | 0.86 |
| 5 | 17.5118 | 2.6065 | 0.97 | 30 | 13.4755 | 3.6302 | 0.98 |
| 6 | 4.5052 | 2.6899 | 0.84 | 31 | 0.9988 | 4.3829 | 0.72 |
| 7 | 3.9099 | 2.1041 | 0.87 | 32 | 18.5756 | 4.1907 | 1 |
| 8 | 23.4981 | 2.8793 | 1.03 | 33 | 1.2196 | 4.2315 | 0.71 |
| 9 | 9.7099 | 3.6143 | 0.93 | 34 | 2.1536 | 4.1356 | 0.87 |
| 10 | 2.9807 | 2.9669 | 0.84 | 35 | 2.8406 | 3.5581 | 0.74 |
| 11 | 9.0193 | 1.7830 | 0.91 | 36 | 5.4548 | 2.1753 | 0.85 |
| 12 | 22.0454 | 3.8974 | 1.03 | 37 | 20.7834 | 2.2356 | 1 |
| 13 | 10.2877 | 1.0020 | 0.91 | 38 | 21.7675 | 3.8868 | 1.03 |
| 14 | 3.0421 | 3.9762 | 0.67 | 39 | 6.7766 | 3.8235 | 0.83 |
| 15 | 12.9003 | 3.2324 | 0.94 | 40 | 3.2731 | 2.4333 | 0.69 |
| 16 | 18.3562 | 3.5349 | 1 | 41 | 15.2439 | 2.4094 | 0.97 |
| 17 | 4.3885 | 2.5658 | 0.84 | 42 | 4.5732 | 3.3041 | 0.83 |
| 18 | 23.1578 | 2.1886 | 1.04 | 43 | 3.2812 | 2.1940 | 0.78 |
| 19 | 2.0496 | 2.8360 | 0.73 | 44 | 3.6449 | 4.2722 | 0.80 |
| 20 | 12.4655 | 1.3433 | 0.93 | 45 | 13.9039 | 3.0007 | 0.97 |
| 21 | 4.7030 | 1.6657 | 0.84 | 46 | 5.8025 | 3.1464 | 0.81 |
| 22 | 17.4816 | 2.0840 | 0.98 | 47 | 5.2472 | 3.6166 | 0.84 |
| 23 | 12.4809 | 1.1169 | 0.94 | 48 | 5.3351 | 3.9363 | 0.79 |
| 24 | 5.6282 | 1.9968 | 0.84 | 49 | 17.3646 | 2.7448 | 0.99 |
| 25 | 2.4166 | 2.1073 | 0.83 | 50 | 14.0092 | 2.4622 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Chen, W.; Chen, T.; Kang, J. In-Plane Libration Suppression of a Two-Segment Tethered Towing System. Aerospace 2023, 10, 286. https://doi.org/10.3390/aerospace10030286
Chen S, Chen W, Chen T, Kang J. In-Plane Libration Suppression of a Two-Segment Tethered Towing System. Aerospace. 2023; 10(3):286. https://doi.org/10.3390/aerospace10030286
Chicago/Turabian StyleChen, Shouxu, Weidong Chen, Ti Chen, and Junjie Kang. 2023. "In-Plane Libration Suppression of a Two-Segment Tethered Towing System" Aerospace 10, no. 3: 286. https://doi.org/10.3390/aerospace10030286
APA StyleChen, S., Chen, W., Chen, T., & Kang, J. (2023). In-Plane Libration Suppression of a Two-Segment Tethered Towing System. Aerospace, 10(3), 286. https://doi.org/10.3390/aerospace10030286






