Aerodynamic Thermal Simulation and Heat Flux Distribution Study of Mechanical Expansion Reentry Vehicle
Abstract
:1. Introduction
2. Methods
2.1. Numerical Model
2.2. Numerical Model Verification
3. Structure Model and Simulation Analysis of Initial Condition
3.1. Geometric Modeling
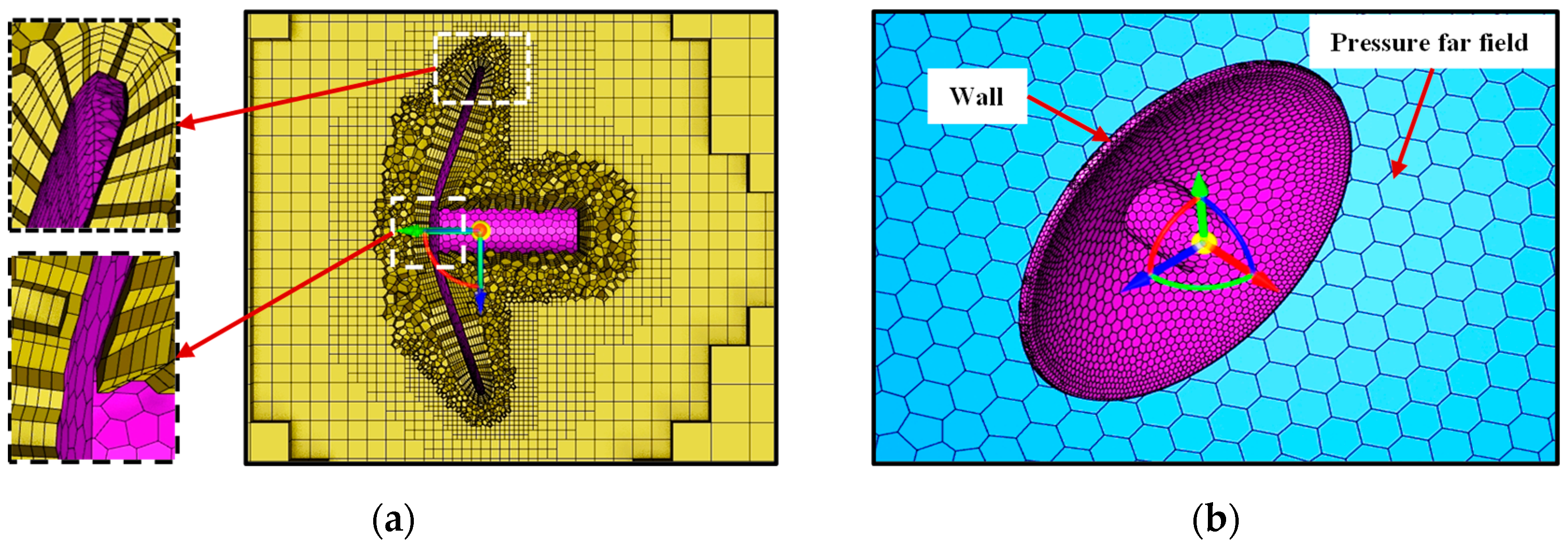
3.2. Mesh Model and Boundary Conditions
3.3. Mesh Independence Verification
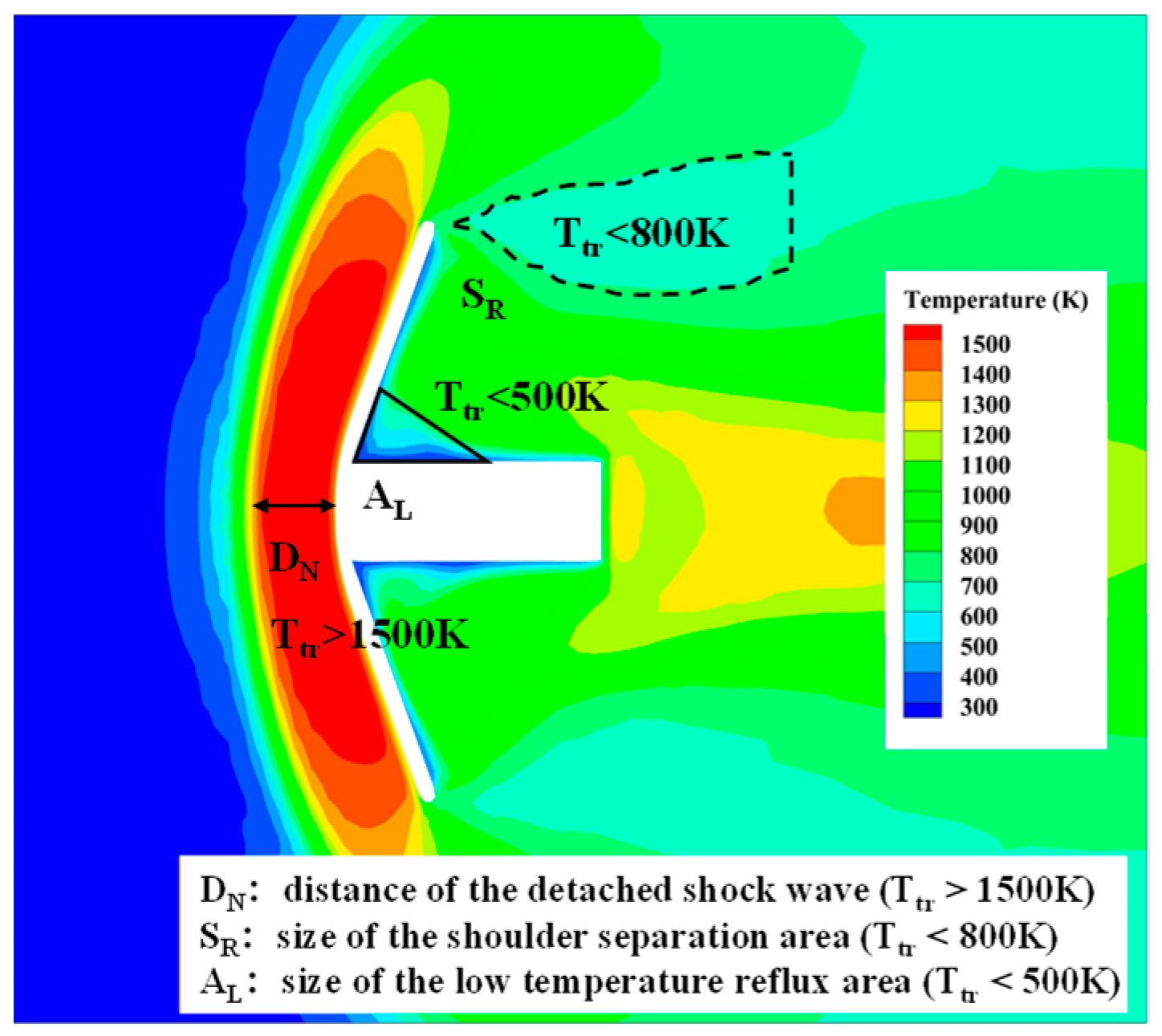
3.4. Simulation Results and Analysis of Initial Condition
4. Results and Analysis of Different Structural and Flight Parameters
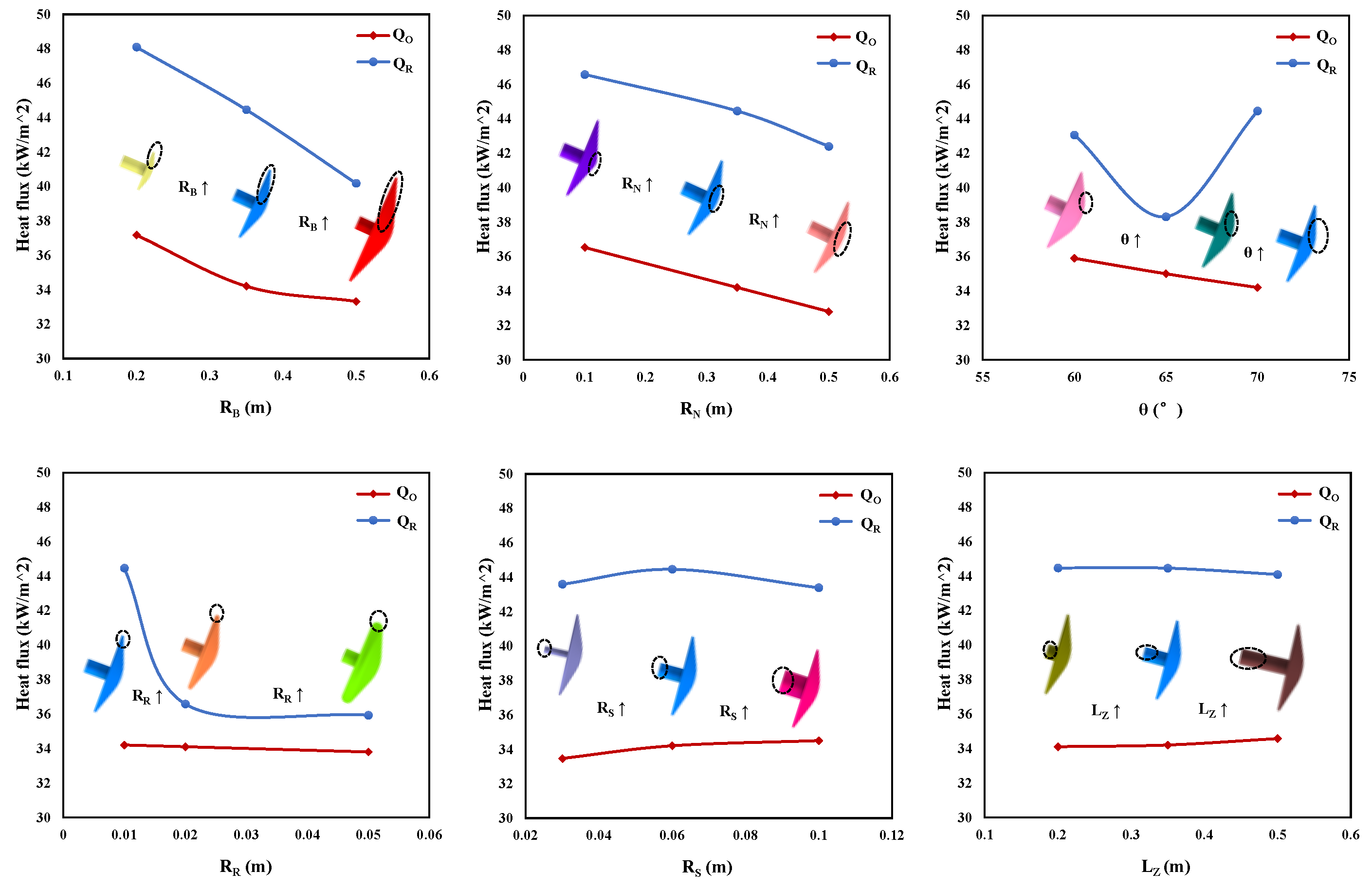
4.1. Influence of Different Structural Parameters
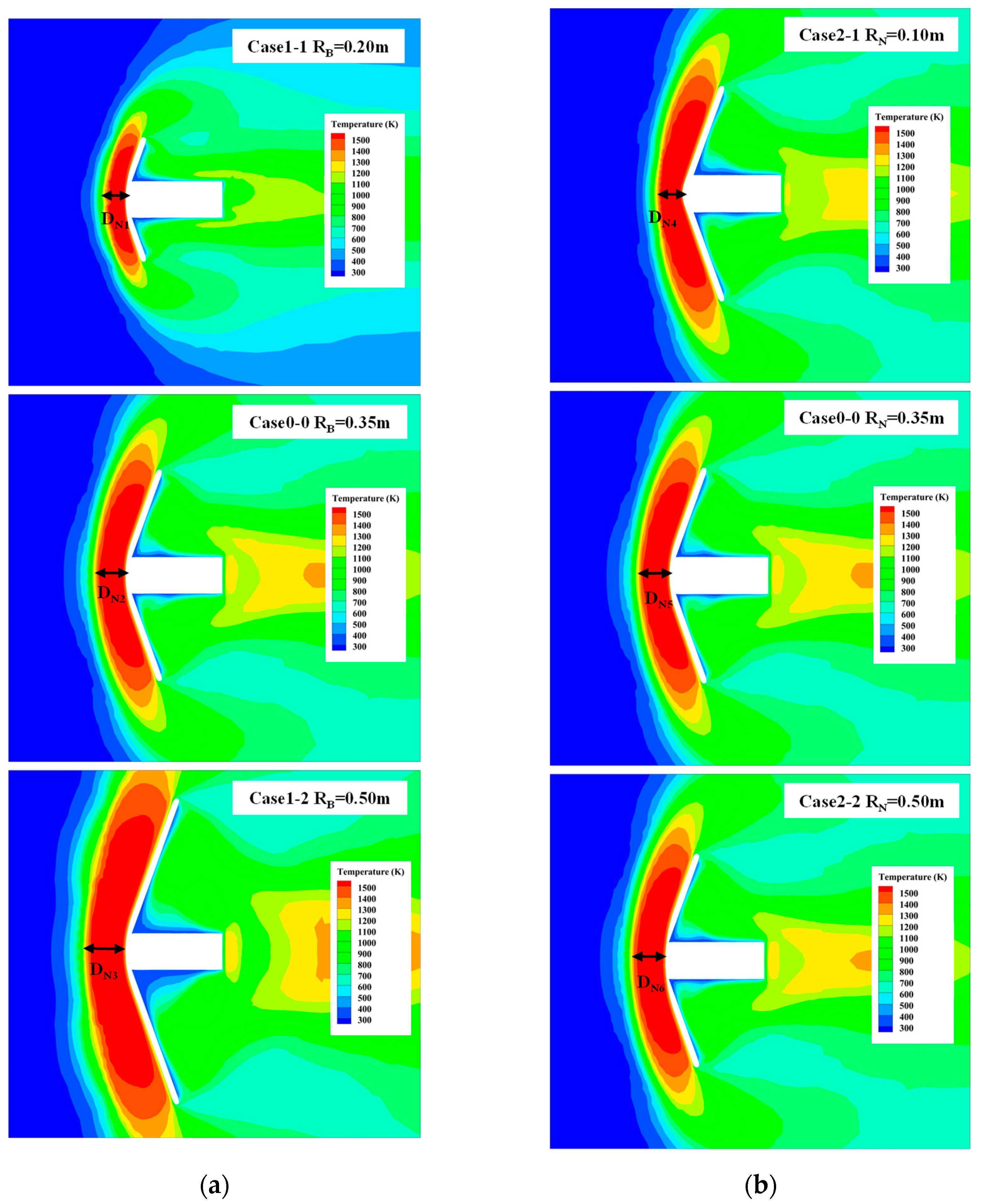
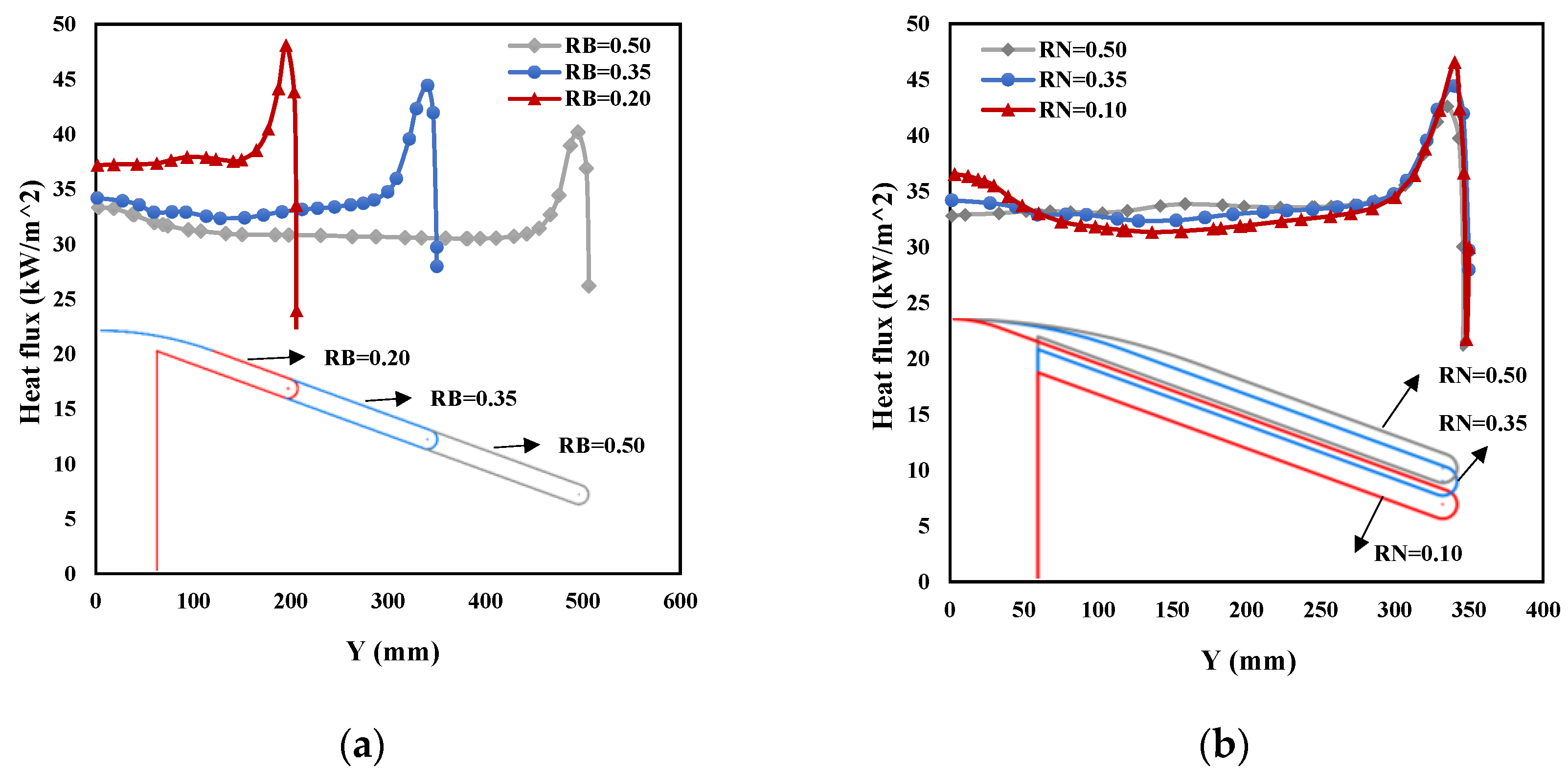
4.1.1. Influence of RB and RN
4.1.2. Influence of θ and RR
4.1.3. Influence of RS and LZ
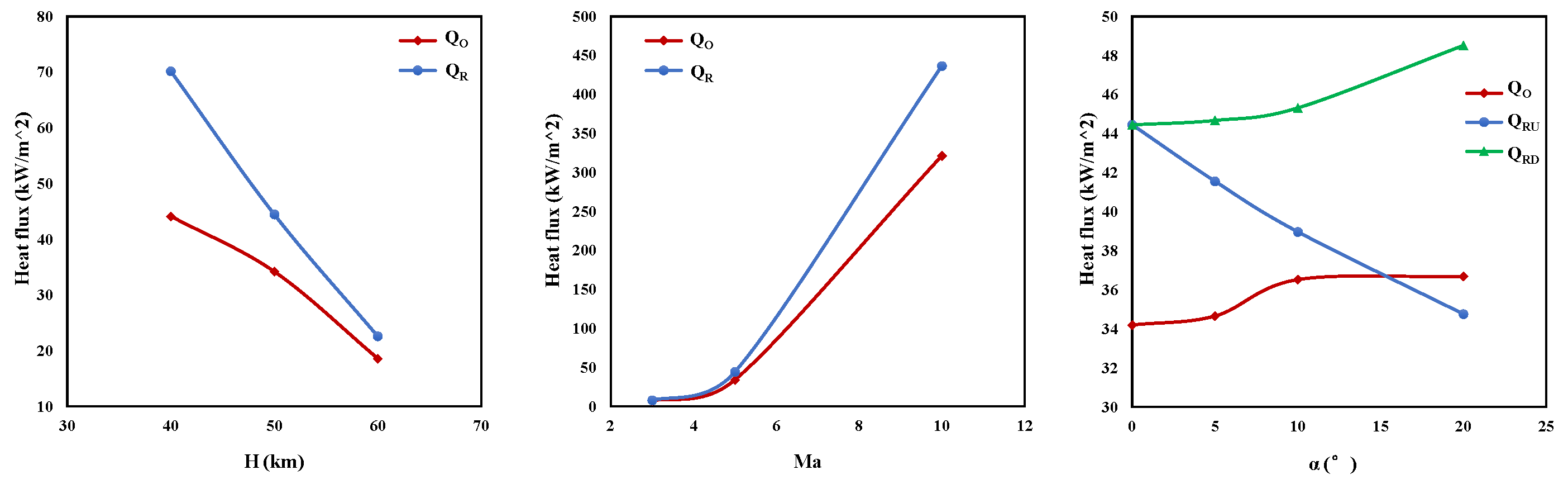
4.2. Influence of Different Flight Parameters
4.2.1. Influence of H and Ma
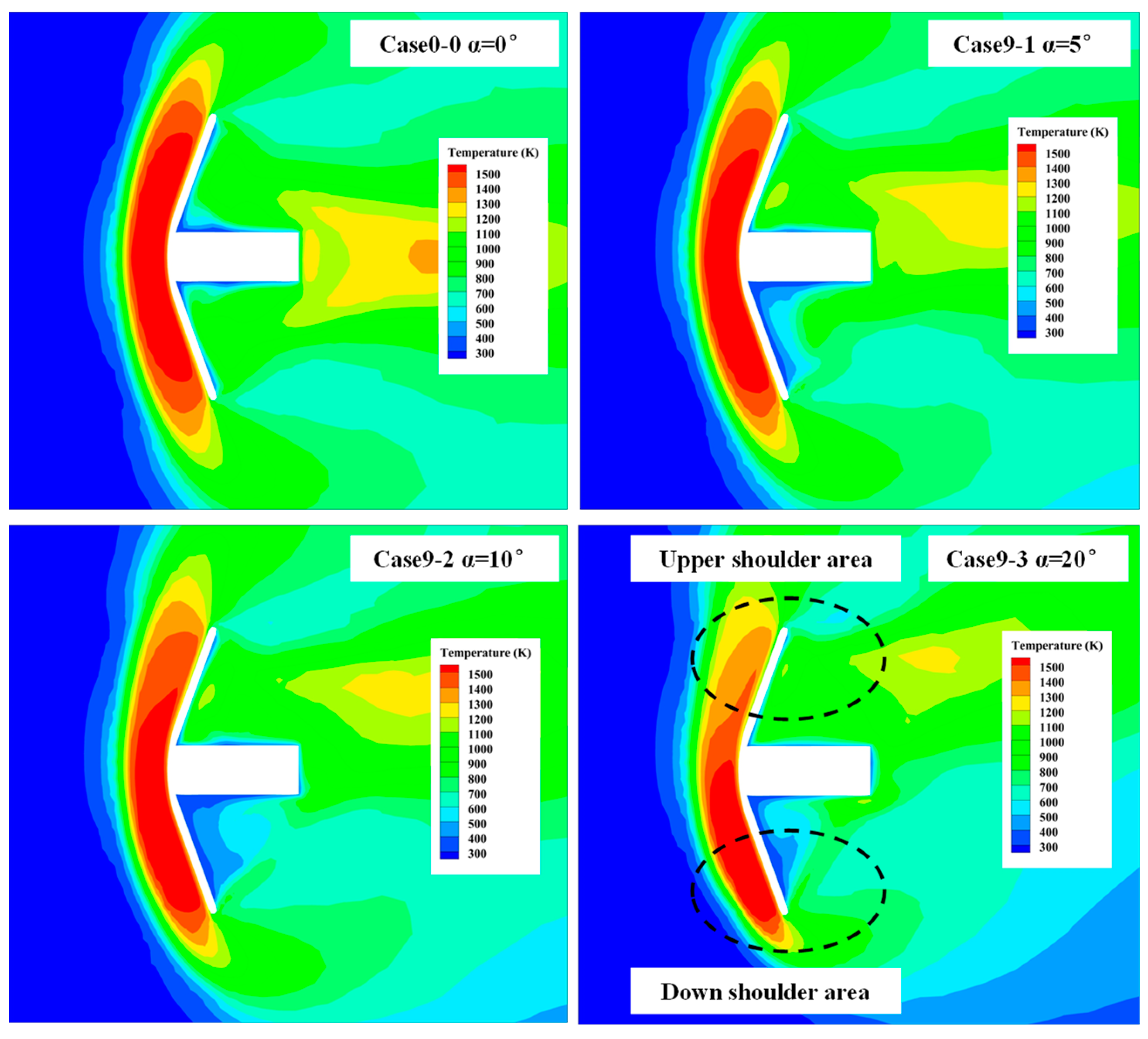
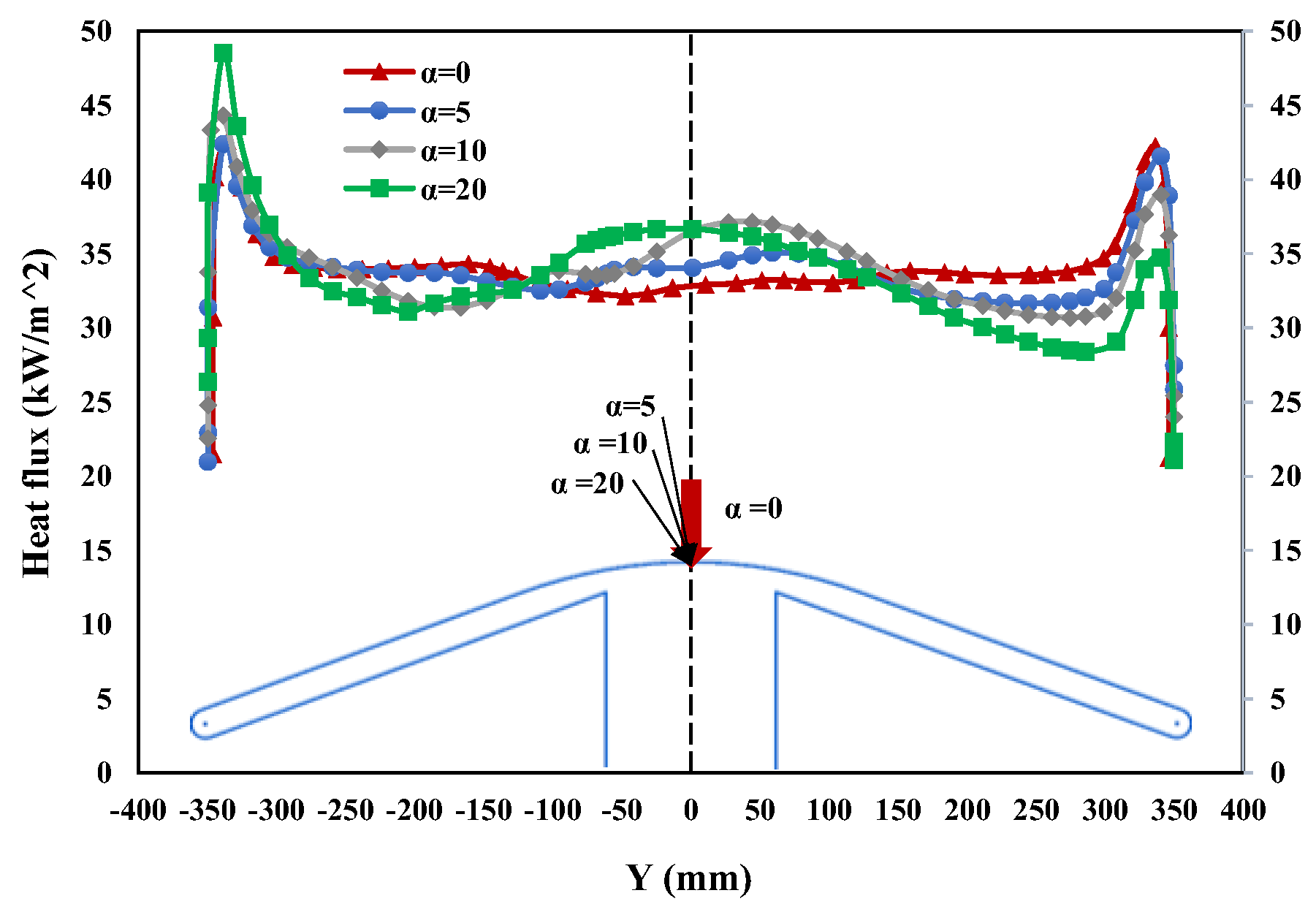
4.2.2. Influence of α
4.3. Summary of Influence
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, S.; Huang, W. Achievements and prospects of China’s spacecraft recovery and landing Technology in the past 60 years. Space Return Remote Sens. 2018, 39, 70–78. [Google Scholar]
- Otsu, H. Aerodynamic Characteristics of Re-Entry Capsules with Hyperbolic Contours. Aerospace 2021, 8, 287. [Google Scholar] [CrossRef]
- Zhang, P.; Li, X.; Bai, L.; Shang, M.; Zhang, H.; Hou, X. Review of Expanded Pneumatic Deceleration Technology for Semi-rigid Machinery. Space Return Remote Sens. 2016, 37, 1–9. [Google Scholar]
- Friz, P.D. Parametric Cost Estimates of Four 20 Ton Payload Mars EDL Vehicle Concepts. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- D’Souza, S.N.; Okolo, W.; Nikaido, B.; Yount, B.; Tran, J.; Margolis, B.; Smith, B.; Cassell, A.; Johnson, B.; Hibbard, K.; et al. Developing an Entry Guidance and Control Design Capability Using Flaps for the Lifting Nano-ADEPT. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar]
- Saranathan, H.; Saikia, S.; Grant, M.J.; Longuski, J.M. Trajectory Optimization with Adaptive Deployable Entry and Placement Technology Architecture. In Proceedings of the 11th International Planetary Probe Workshop, Pasadena, CA, USA, 16–20 June 2014. [Google Scholar]
- Wercinski, P.; Smith, B.; Battazzo, Y.; Kruger, C.; Brivkalns, C.; Makino, A.; Cassell, A.; Dutta, S.; Ghassemi, S. ADEPT sounding rocket one (SR-1) flight experiment overview. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017. [Google Scholar]
- O’Driscoll, D.S.; Bruce, P.J.K.; Santer, M. Design and Dynamic Analysis of Rigid Foldable Aeroshells for Atmospheric Entry. J. Spacecr. Rocket. 2021, 58, 741–753. [Google Scholar] [CrossRef]
- Smith, B.; Venkatapathy, E.; Wercinski, P.; Yount, B.; Prabhu, D.; Gage, P.; Glaze, L.; Baker, C. Venus In Situ Explorer Mission design using a mechanically deployed aerodynamic decelerator. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013. [Google Scholar]
- Yang, X.; Wang, J.; Zhou, Y.; Sun, K. Assessment of Radiative Heating for Hypersonic Earth Reentry Using Nongray Step Models. Aerospace 2022, 9, 219. [Google Scholar] [CrossRef]
- Saikia, S.J.; Saranathan, H.; Grant, M.J.; Longuskiet, J.M. Trajectory optimization for adaptive deployable entry and placement technology (ADEPT). In Proceedings of the Astrodynamics Specialist Conferences, San Diego, CA, USA, 4–7 August 2014. [Google Scholar]
- Griffin, M.D.; French, J.R. Space Vehicle Design, 2nd ed.; American Institute of Aeronautics & Astronautics: Reston, VA, USA, 2004; Volume 279. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, L.; Cao, X.; Zhang, Z. Prediction method of peak Thermal Load for reentry returner. Aerosp. Return Remote Sens. 2019, 40, 25–32. [Google Scholar]
- Zhang, M. Numerical Simulation of Aero-Thermal Environment for Earth Re-Entry/Outer Planet Entry Vehicle. Master’s Thesis, Shandong University, Jinan, China, 2017. [Google Scholar]
- Liu, F.; Yuan, J. Discussion on the calculation formula of stagnation heat flow in non-equilibrium Martian atmosphere. Manned Spacefl. 2018, 24, 582–589. [Google Scholar]
- Hergert, J.; Brock, J.; Stern, E. Free-Flight Trajectory Simulation of the ADEPT Sounding Rocket Test Using US3D. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Viviani, A.; Pezzella, G.; Borrelli, S. Effect of Finite Rate Chemical Models on the Aerothermodynamics of Reentry Capsules. In Proceedings of the 15th Proceeding of AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008. [Google Scholar]
- Alkandry, H.; Boyd, D. Numerical Study of Hypersonic Wind Tunnel Experiments for Mars Entry Aeroshells. In Proceedings of the 41th Thermophysics Conference, San Antonio, TX, USA, 22–25 June 2009. [Google Scholar]
- Bisceglia, S.; Ranuzzi, G. Real Gas Effects on a Planetary Reentry Capsule. In Proceedings of the 13th AIAA/CIRA International Space Planes and Hypersonics Systems and Technologies, Capua, Italy, 16–20 May 2005. [Google Scholar]
- Maciel, E. Three-Temperature Model Applied to Thermochemical Non-Equilibrium Reentry Flows in 2D—Seven Species. Fluid Dyn. 2022, 12, 35. [Google Scholar]
- Viviani, A.; Golia, C.; Pezzella, G. Analysis of thermochemical modeling and surface catalyticity in space vehicles reentry. In Proceedings of the International Congress of The Aeronautical Sciences, Anchorage, AK, USA, 14–19 September 2008. [Google Scholar]
- Liu, M. Numerical Simulation of Apollo-Like Re-Entry Vehicle. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2014. [Google Scholar]
- Matsunaga, M.; Takahashi, Y.; Oshima, N.; Yamada, K. Aerodynamic Heating Prediction of an Inflatable Reentry Vehicle in a Hypersonic Wind Tunnel. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar]
- Dejarnette, F.R.; Hamilton, H.H.; Weilmuenster, K.J.; Cheatwood, F.M. A Review of Some Approxmate Methods Used in Aerodynamic Heating Analyses. J. Thermophys. Heat Transf. 1987, 1, 5–12. [Google Scholar] [CrossRef]
- Kimmel, R.L.; Adamczak, D.W. HIFiRE-1 flight trajectory estimation and initial experimental results. In Proceedings of the 17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, San Francisco, CA, USA, 11–14 April 2011; AIAA: Reston, VA, USA, 2011. [Google Scholar]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J.A. A new k-e eddy viscosity model for high Reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Ocokoljic, G.; Rasuo, B.; Kozic, M. Supporting system interference onaerodynamic characteristics of an aircraft model in a low-speed wind tunnelAerosp. Sci. Technol. 2017, 64, 133–146. [Google Scholar]
- Wilcox, D.C. Turbulence modeling for CFD: DCW industries La Canada. Ca DCW Ind. 1998, 2, 103–217. [Google Scholar]
- Kimmel, R.L.; Adamczak, D.W. HIFiRE-l preliminary aerothermodynamics measurements. In Proceedings of the 41th AIAA Fluid Dynamics Conference and Exhibit, Honolulu, HI, USA, 27–30 June 2011; AIAA: Reston, VA, USA, 2011. [Google Scholar]
- Yentsch, R.J.; Gaitonde, D.V.; Kimmel, R.L. Performance of turbulence modeling in simulation of the HIFiRE-1 flight test. J. Spacecr. Rocket. 2014, 51, 117–127. [Google Scholar] [CrossRef]
- Takahashi, Y.; Ha, D.; Yamada, K.; Abe, T. Numerical Simulation of Flow Field around an Inflatable Reentry Vehicle during a Demonstration Flight. In Proceedings of the AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Saidi, N.; Cerdoun, M.; Khalfallah, S.; Toufik, B. Numerical investigation of the surface roughness effects on the subsonic flow around a circular cone-cylinder. Aerosp. Sci. Technol. 2020, 107, 106271. [Google Scholar] [CrossRef]
- Casseau, V.; Palharini, R.; Scanlon, T.; Brown, R. A Two-Temperature Open-Source CFD Model for Hypersonic Reacting Flows, Part One: Zero-Dimensional Analysis. Aerospace 2016, 3, 34. [Google Scholar] [CrossRef] [Green Version]
- Gnoffo, P.A.; Gupta, R.N.; Shinn, J.L. Conservation Equations and Physical Models for Hypersonic Air Flows in Thermal and Chemical Nonequilibrium; NASA: Washington, DC, USA, 1989. [Google Scholar]
- Chen, L.; Xia, J. Study on the Leading Edge of a Hypersonic Vehicle Using the Aero-Thermoelastic Coupling Method. Aerospace 2022, 9, 835. [Google Scholar] [CrossRef]
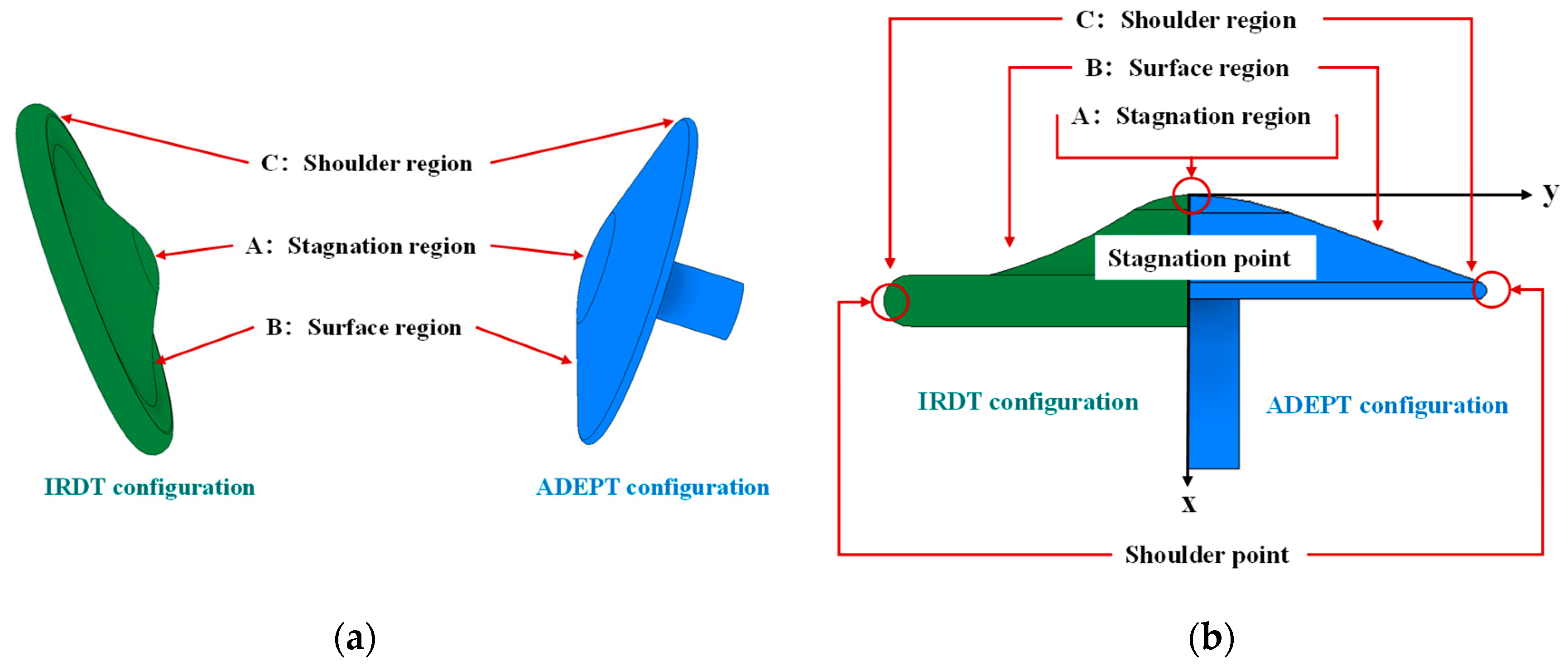
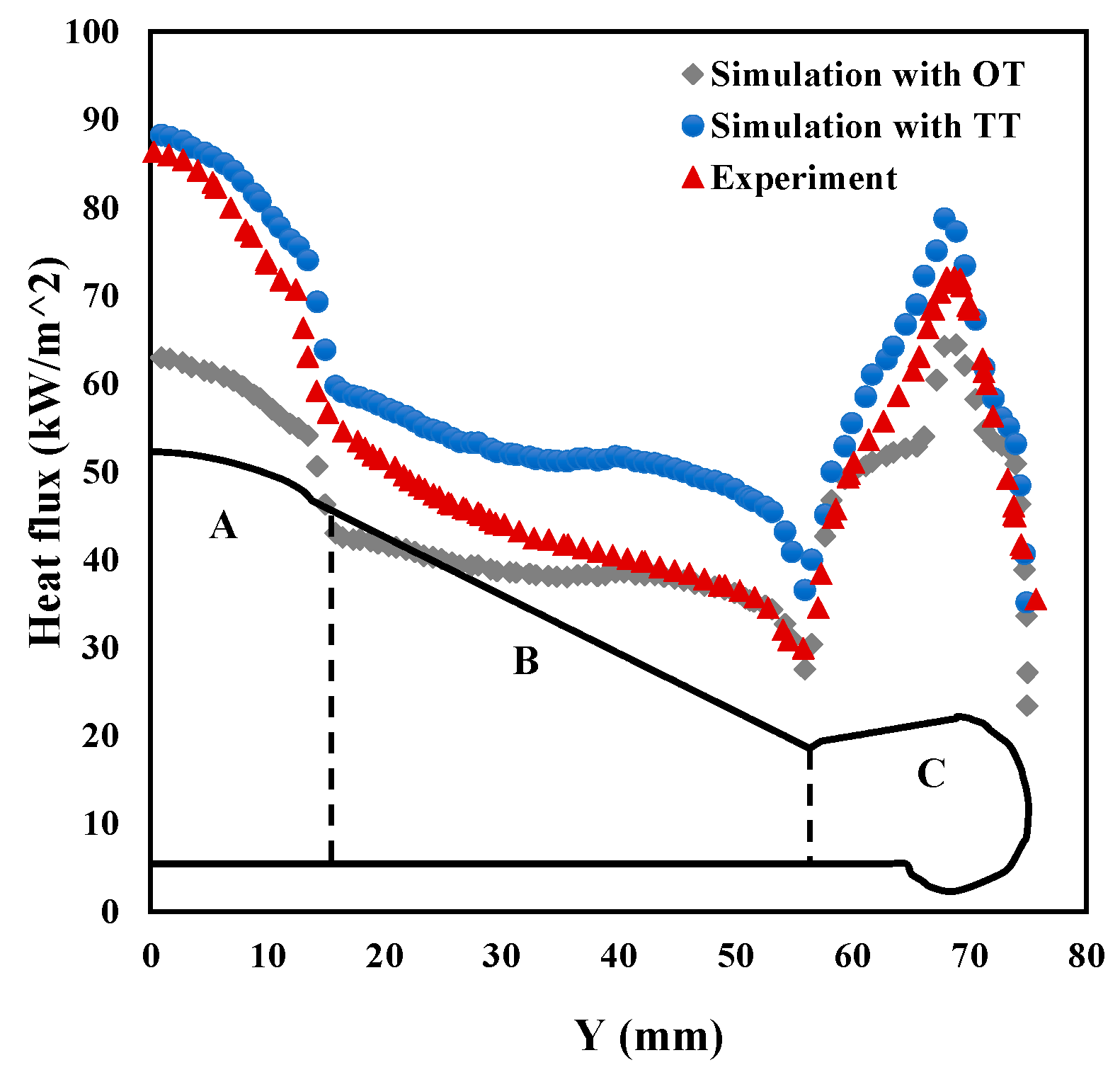
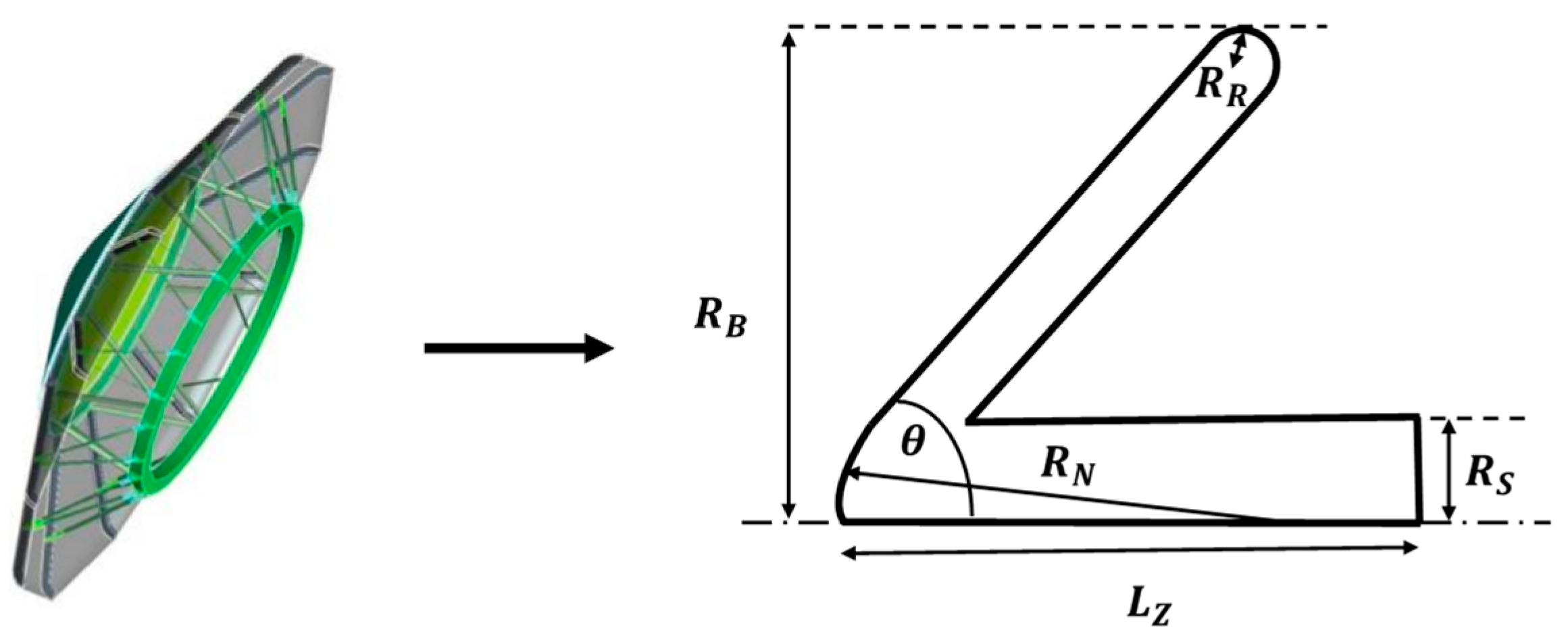
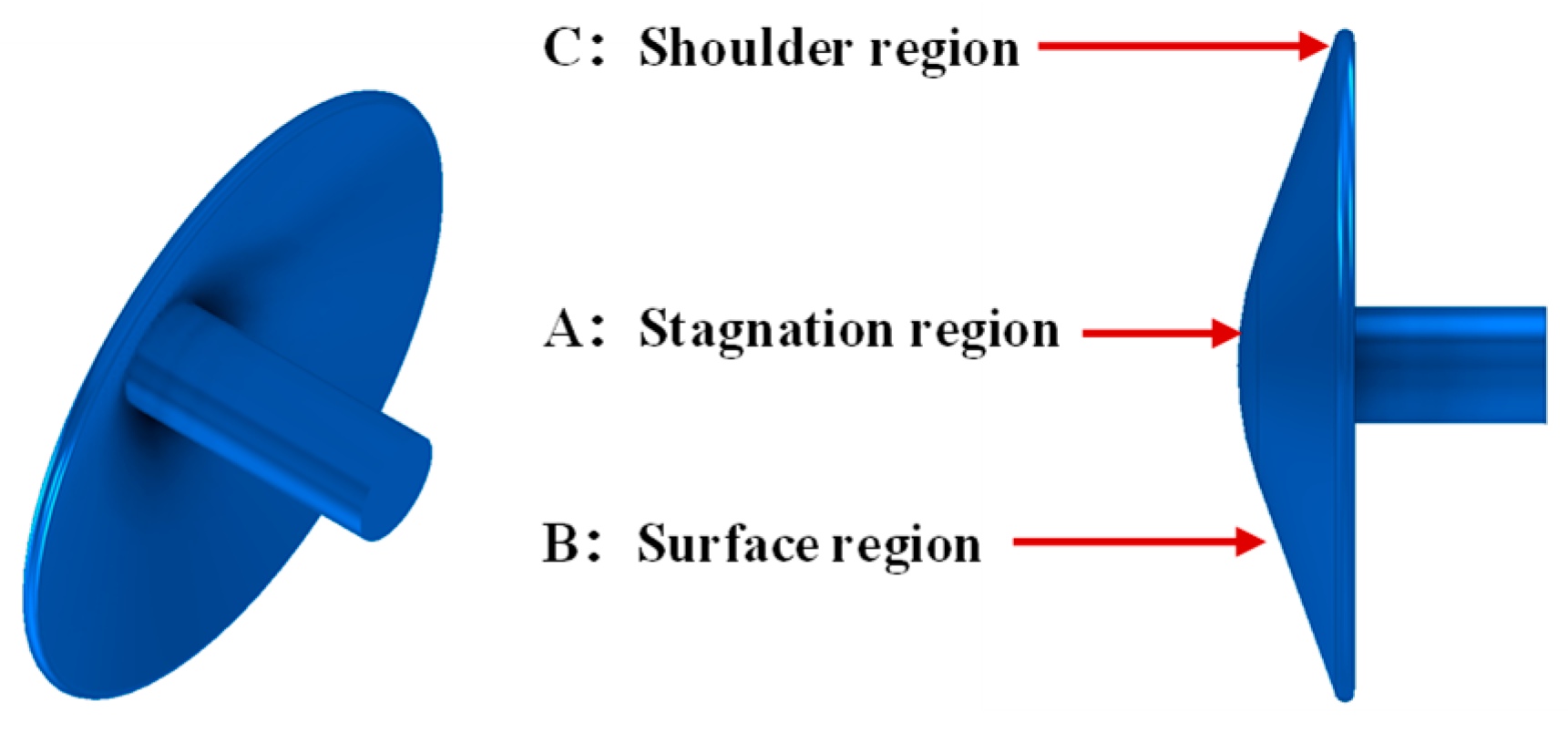



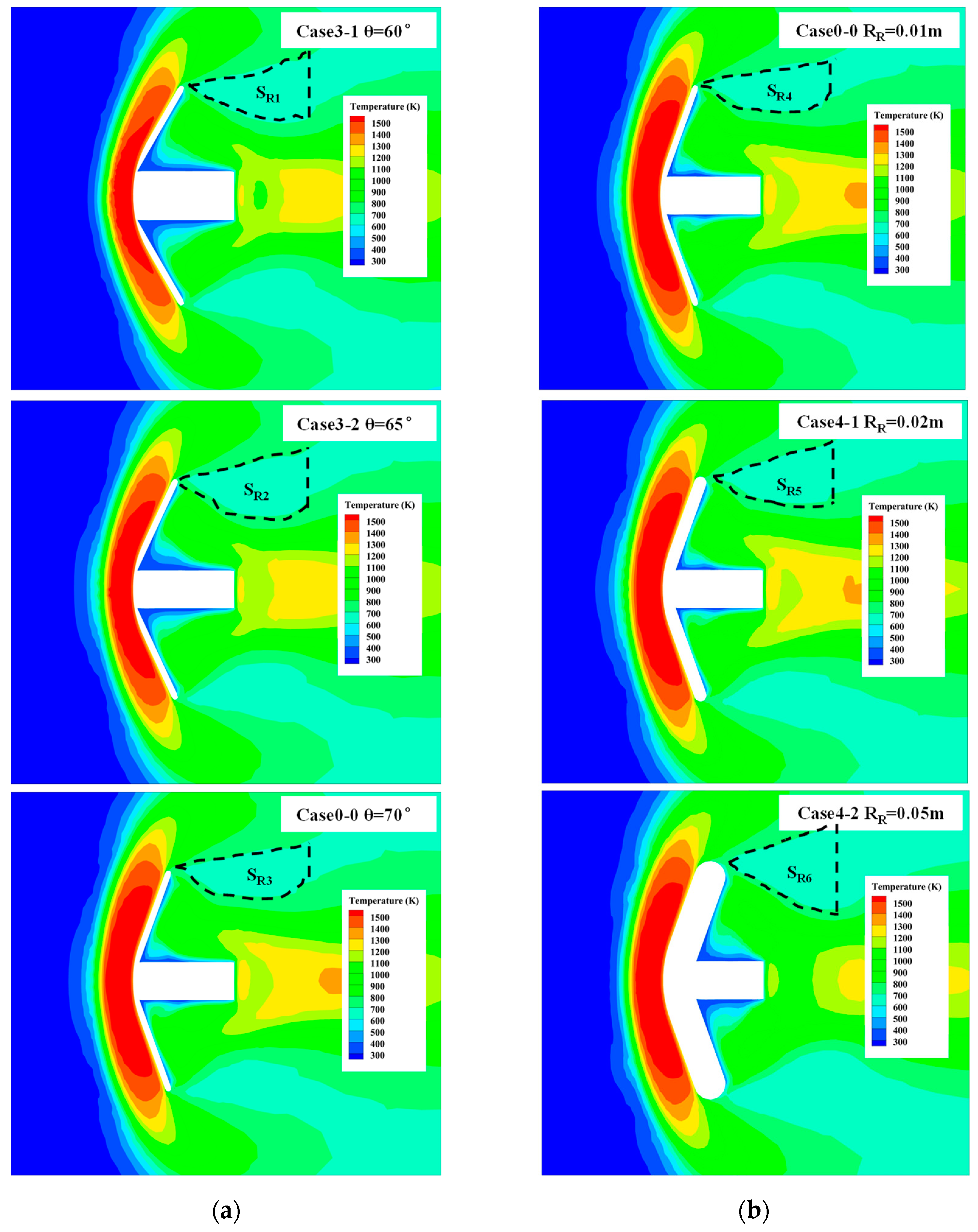
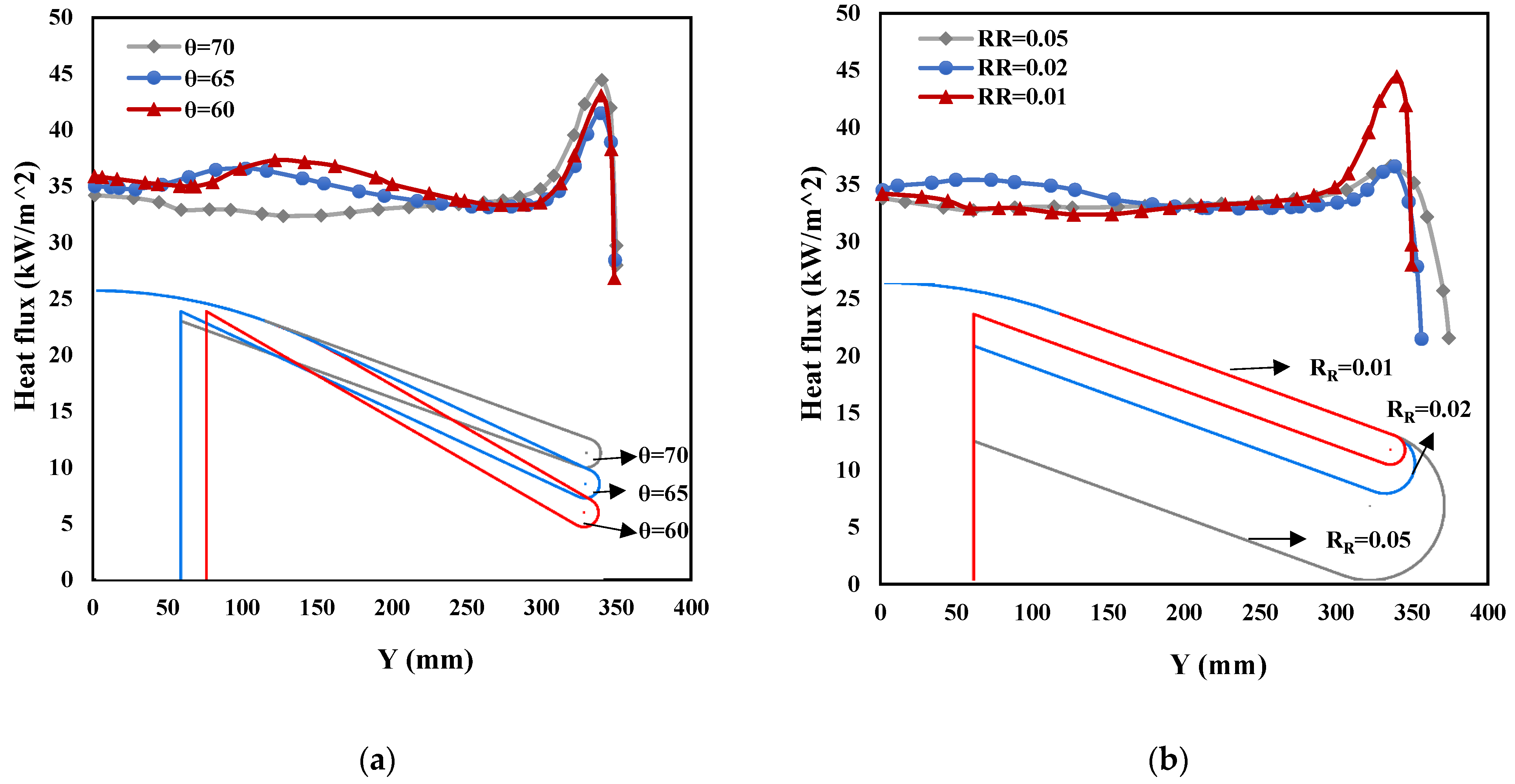

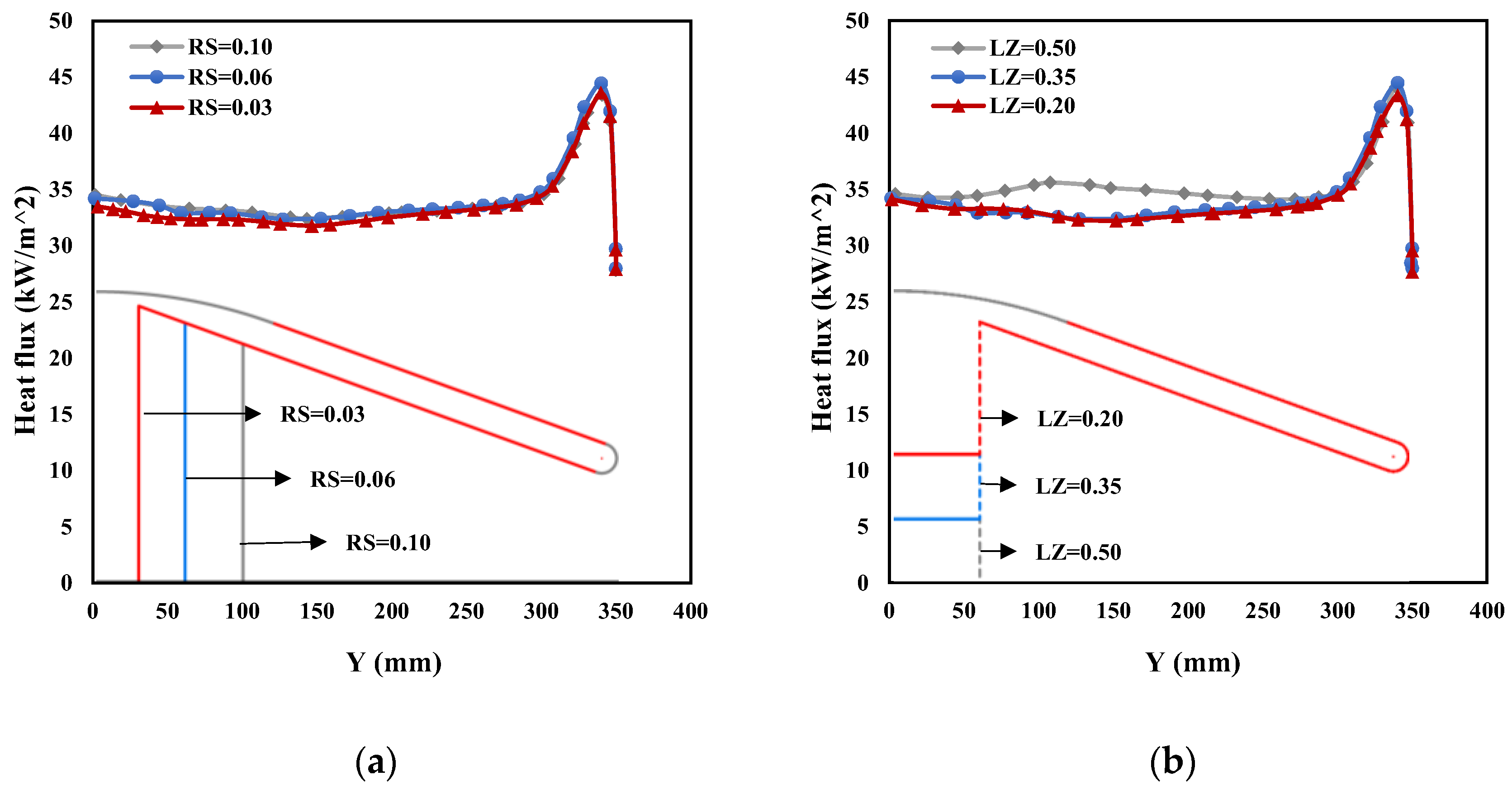

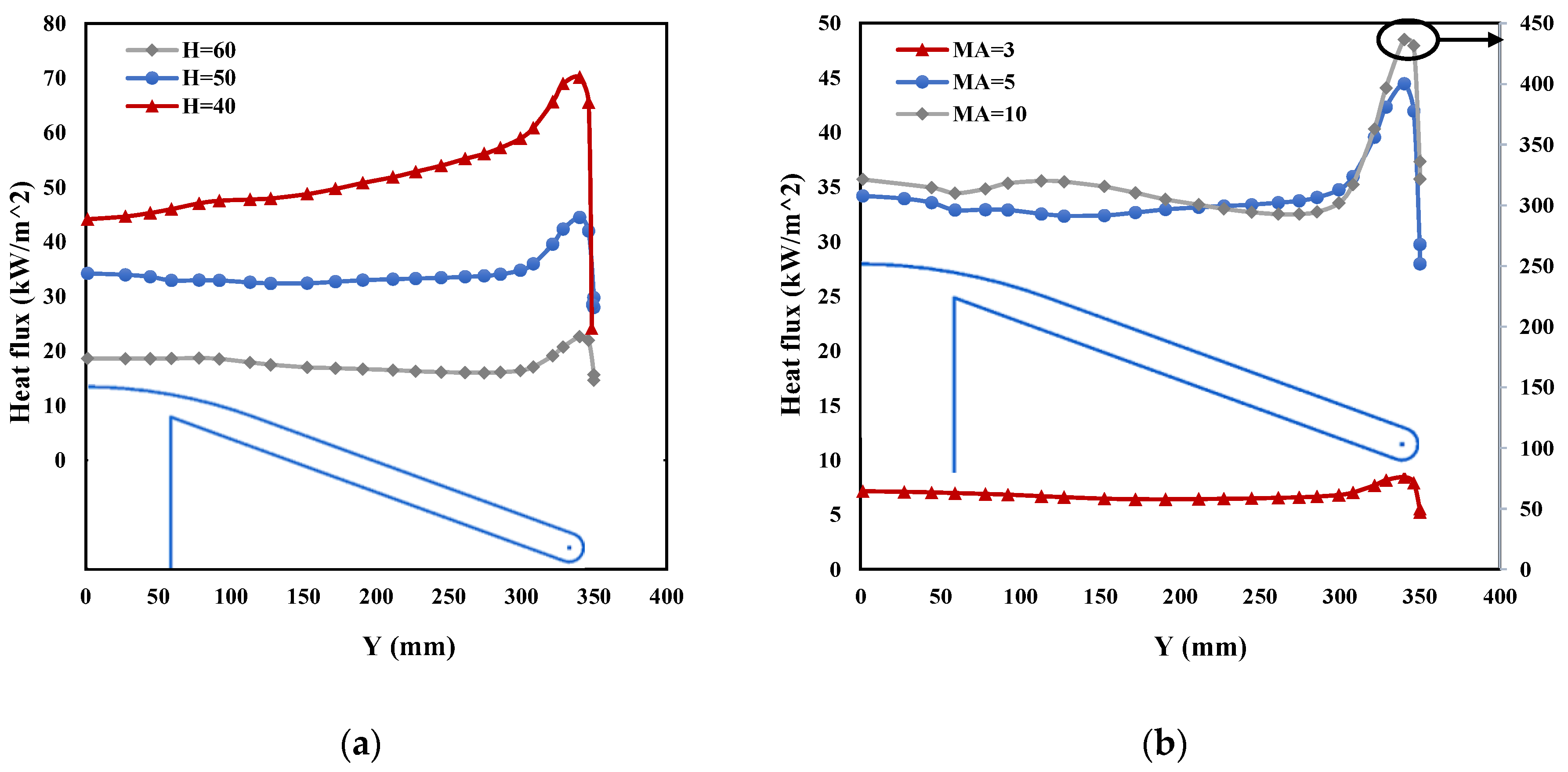
| Parameter | Meaning | Initial Value |
|---|---|---|
| RB (m) | Expansion radius | 0.35 |
| RN (m) | Nose cone radius | 0.35 |
| θ (°) | Half cone angle | 70 |
| RR (m) | Shoulder radius | 0.01 |
| RS (m) | Base radius | 0.06 |
| LZ (m) | Total length | 0.35 |
| H (m) | Flight altitude | 50 |
| Ma | Flight Mach number | 5 |
| α (°) | Flight attack angle | 0 |
| Ma∞ | Re∞ (/m) | T∞ (K) | ρ∞ (kg/m3) | Tω (K) |
|---|---|---|---|---|
| 5.0 | 6.5 × 104 | 270.65 | 1.03 × 10−3 | 300 |
| Mesh Number (Million) | First Layer Height Δy (m) | Stagnation Heat Flux QO (kW/m2) |
|---|---|---|
| 0.30 | 0.0101 | 119.69 |
| 0.75 | 0.0042 | 67.07 |
| 1.50 | 0.0015 | 51.25 |
| 3.00 | 0.00065 | 48.89 |
| Case | RB (m) | RN (m) | θ (°) | RR (m) | RS (m) | LZ (m) |
|---|---|---|---|---|---|---|
| Case 0-0 | 0.35 | 0.35 | 70 | 0.01 | 0.06 | 0.35 |
| Case 1-1 | 0.20 | 0.35 | 70 | 0.01 | 0.06 | 0.35 |
| Case 1-2 | 0.50 | 0.35 | 70 | 0.01 | 0.06 | 0.35 |
| Case 2-1 | 0.35 | 0.10 | 70 | 0.01 | 0.06 | 0.35 |
| Case 2-2 | 0.35 | 0.50 | 70 | 0.01 | 0.06 | 0.35 |
| Case 3-1 | 0.35 | 0.35 | 60 | 0.01 | 0.06 | 0.35 |
| Case 3-2 | 0.35 | 0.35 | 65 | 0.01 | 0.06 | 0.35 |
| Case 4-1 | 0.35 | 0.35 | 70 | 0.02 | 0.06 | 0.35 |
| Case 4-2 | 0.35 | 0.35 | 70 | 0.05 | 0.06 | 0.35 |
| Case 5-1 | 0.35 | 0.35 | 70 | 0.01 | 0.03 | 0.35 |
| Case 5-2 | 0.35 | 0.35 | 70 | 0.01 | 0.10 | 0.35 |
| Case 6-1 | 0.35 | 0.35 | 70 | 0.01 | 0.06 | 0.20 |
| Case 6-2 | 0.35 | 0.35 | 70 | 0.01 | 0.06 | 0.50 |
| Case | H (km) | Ma | α (°) |
|---|---|---|---|
| Case 0-0 | 50 | 5 | 0 |
| Case 7-1 | 40 | 5 | 0 |
| Case 7-2 | 60 | 5 | 0 |
| Case 8-1 | 50 | 3 | 0 |
| Case 8-2 | 50 | 10 | 0 |
| Case 9-1 | 50 | 5 | 5 |
| Case 9-2 | 50 | 5 | 10 |
| Case 9-3 | 50 | 5 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Zhu, H.; Xu, D.; Cai, G. Aerodynamic Thermal Simulation and Heat Flux Distribution Study of Mechanical Expansion Reentry Vehicle. Aerospace 2023, 10, 310. https://doi.org/10.3390/aerospace10030310
Sun J, Zhu H, Xu D, Cai G. Aerodynamic Thermal Simulation and Heat Flux Distribution Study of Mechanical Expansion Reentry Vehicle. Aerospace. 2023; 10(3):310. https://doi.org/10.3390/aerospace10030310
Chicago/Turabian StyleSun, Junjie, Hao Zhu, Dajun Xu, and Guobiao Cai. 2023. "Aerodynamic Thermal Simulation and Heat Flux Distribution Study of Mechanical Expansion Reentry Vehicle" Aerospace 10, no. 3: 310. https://doi.org/10.3390/aerospace10030310
APA StyleSun, J., Zhu, H., Xu, D., & Cai, G. (2023). Aerodynamic Thermal Simulation and Heat Flux Distribution Study of Mechanical Expansion Reentry Vehicle. Aerospace, 10(3), 310. https://doi.org/10.3390/aerospace10030310





