Angle-of-Attack Estimation for General Aviation Aircraft
Abstract
:1. Introduction
2. Methodology
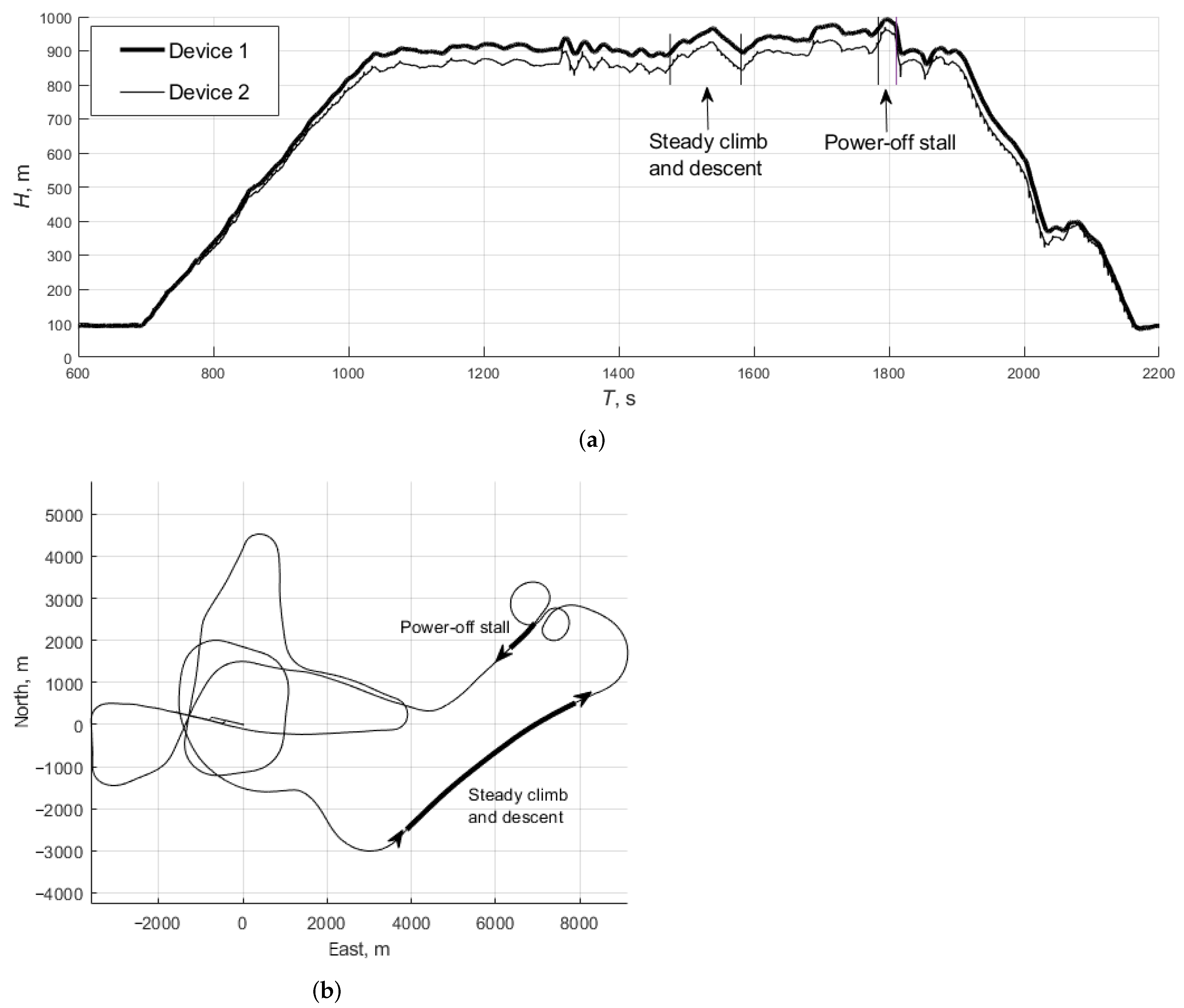
3. Results
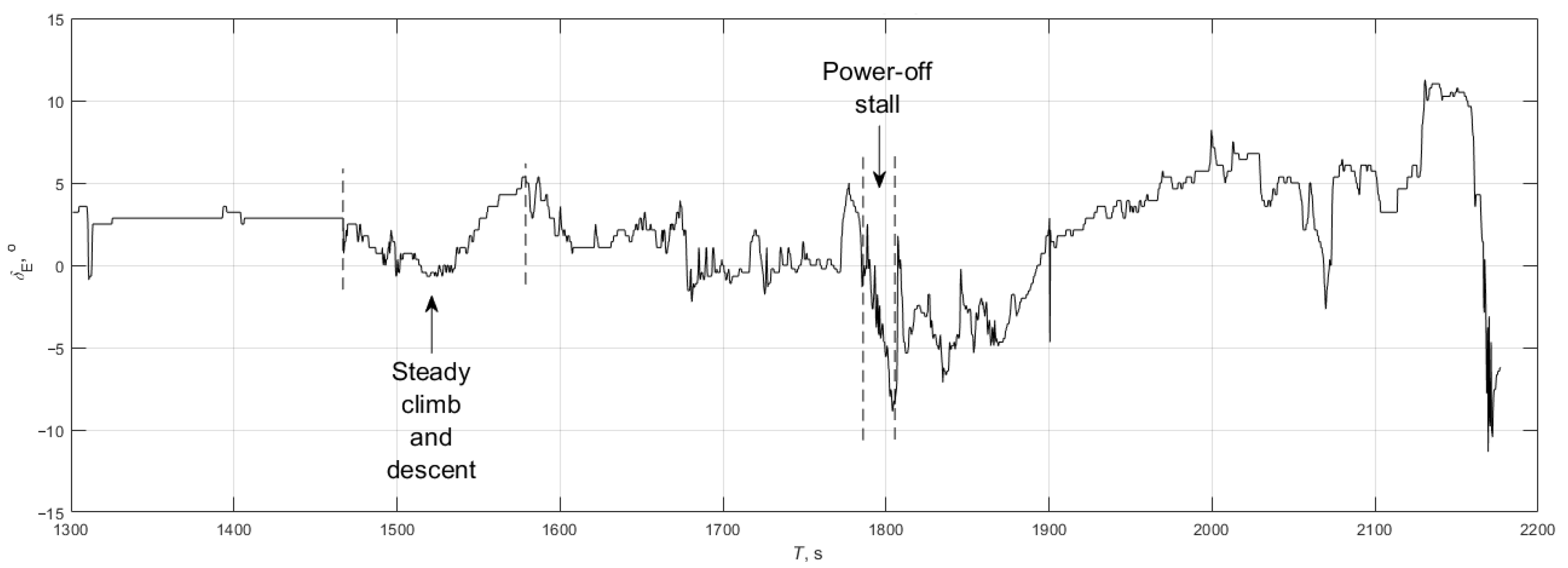
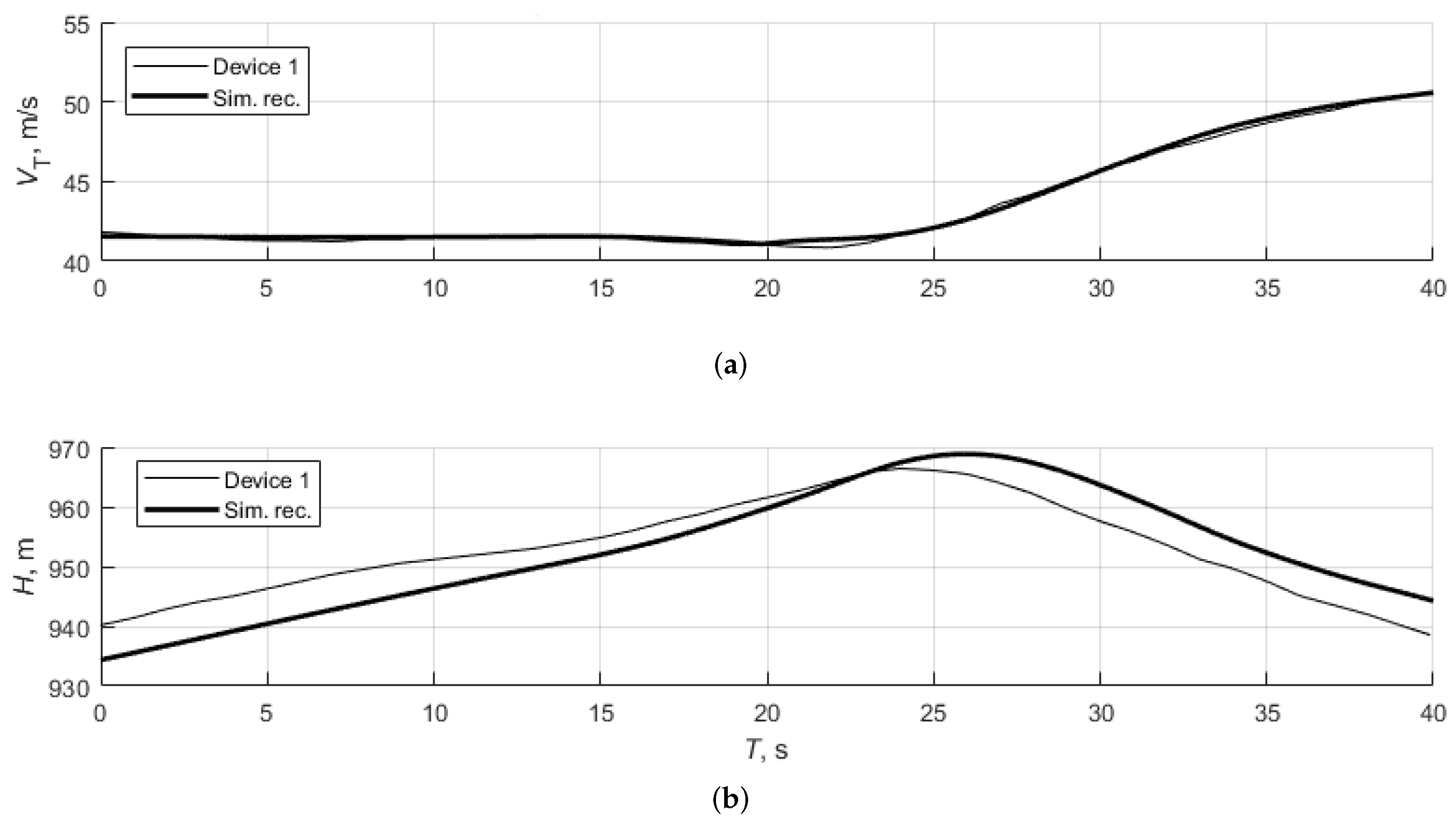
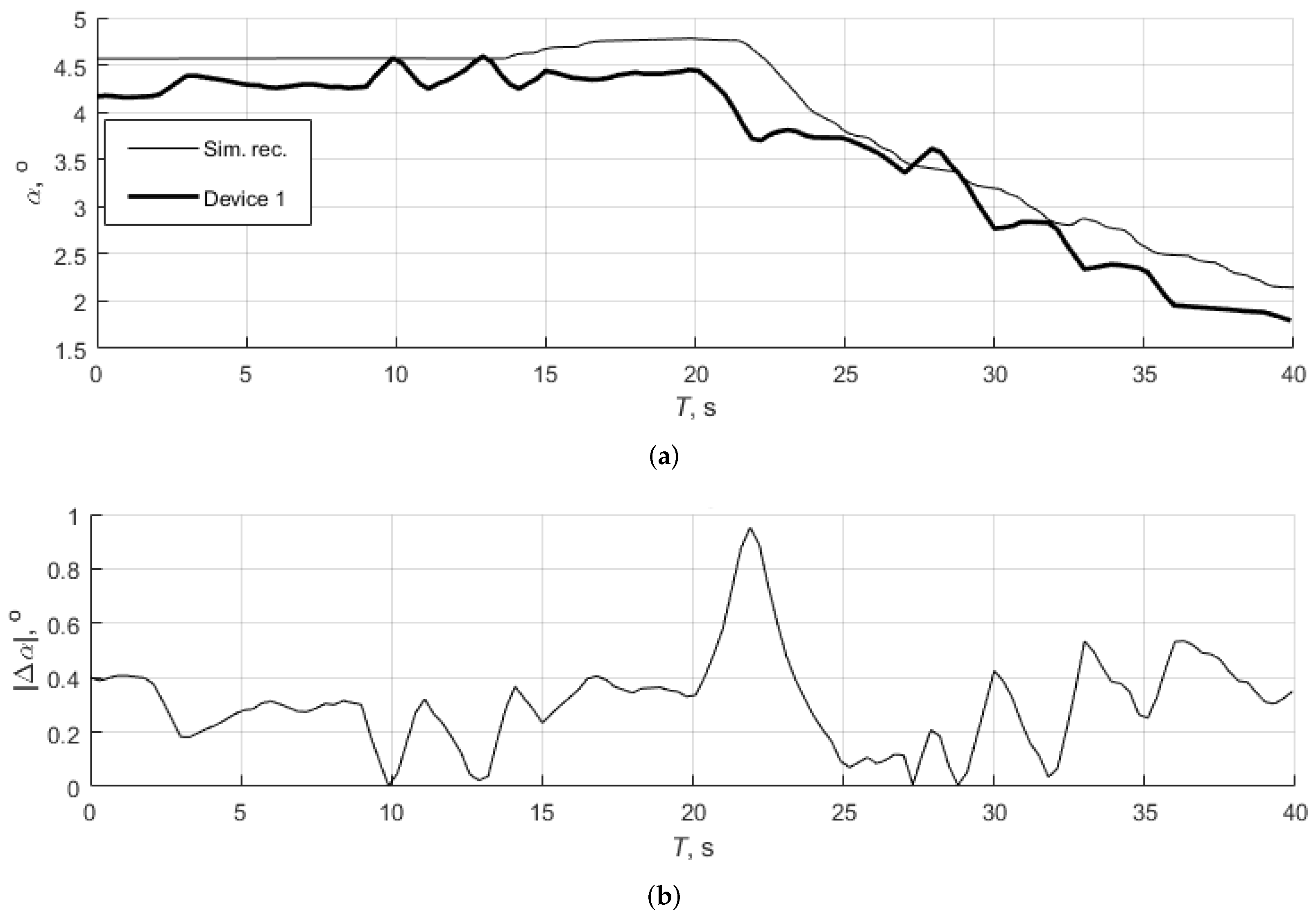
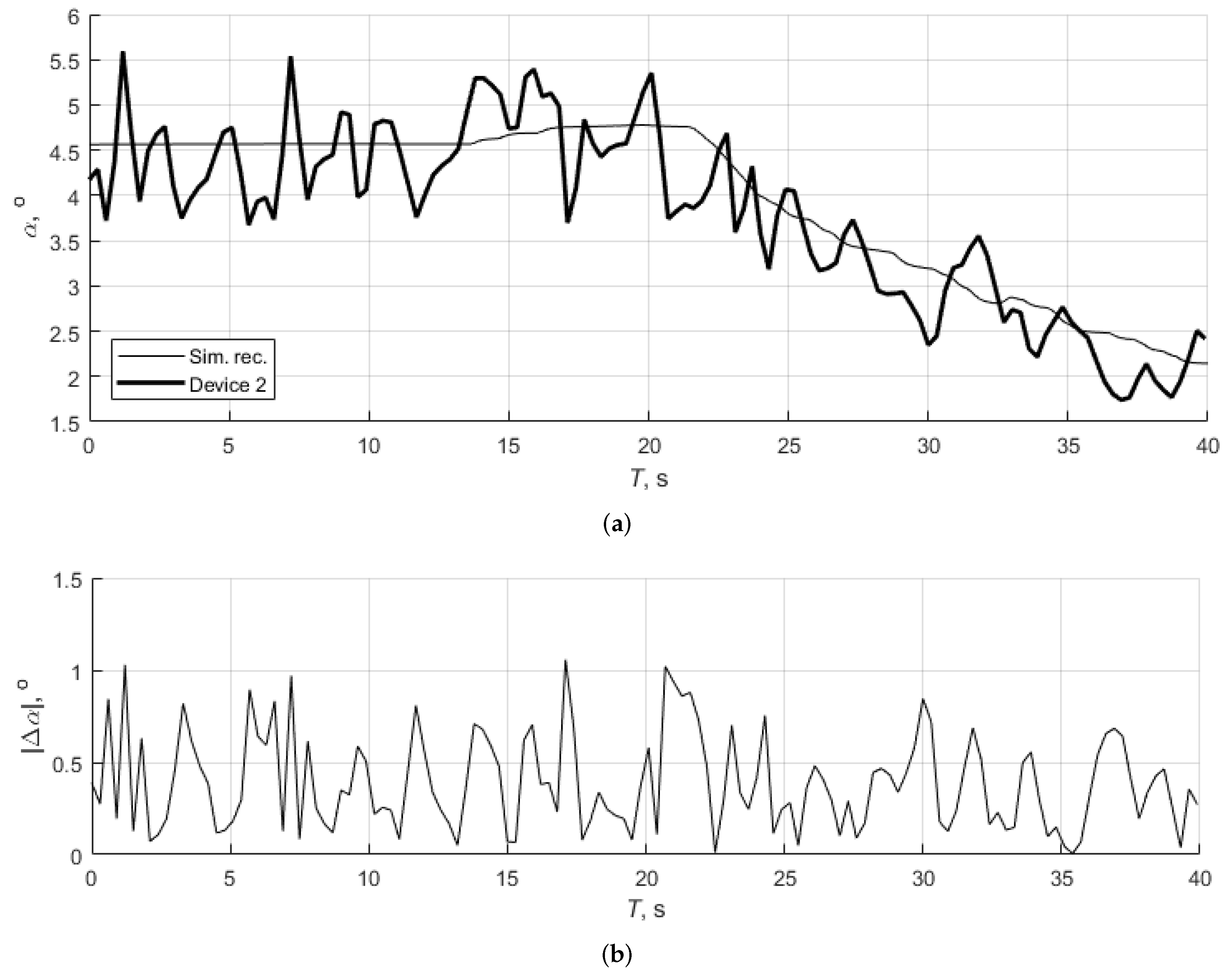
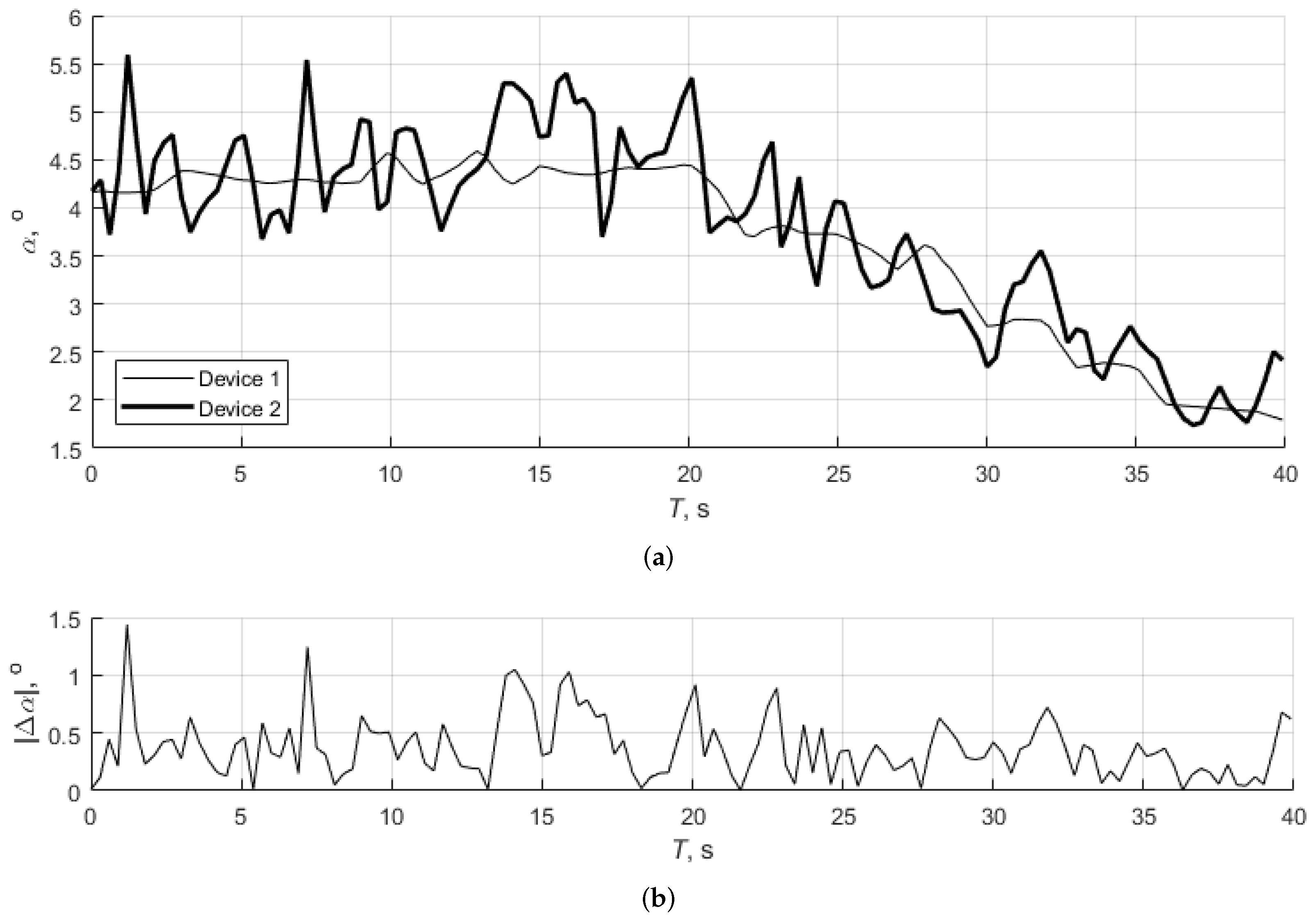
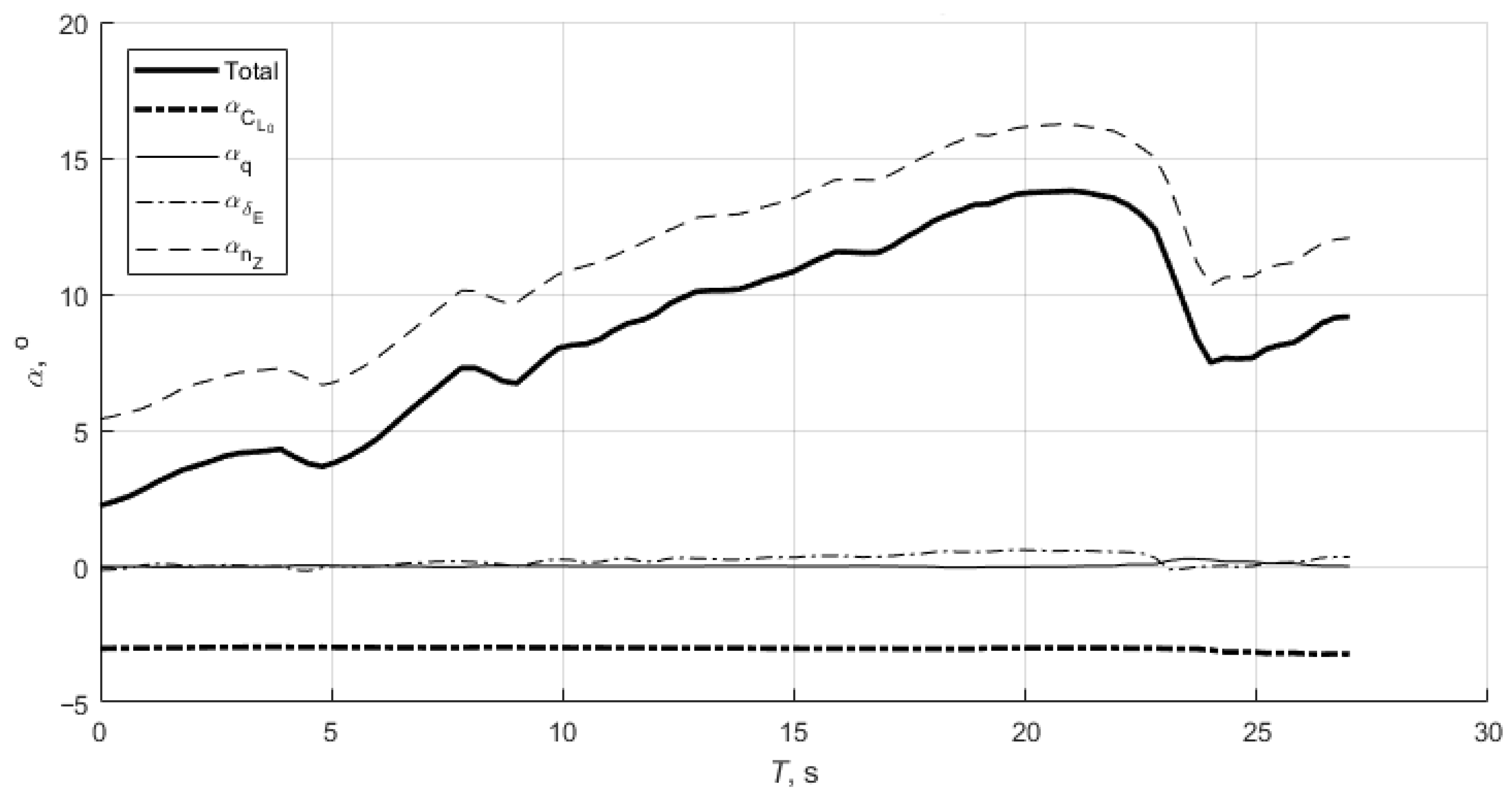
3.1. Test 1: Steady Climb and Descent
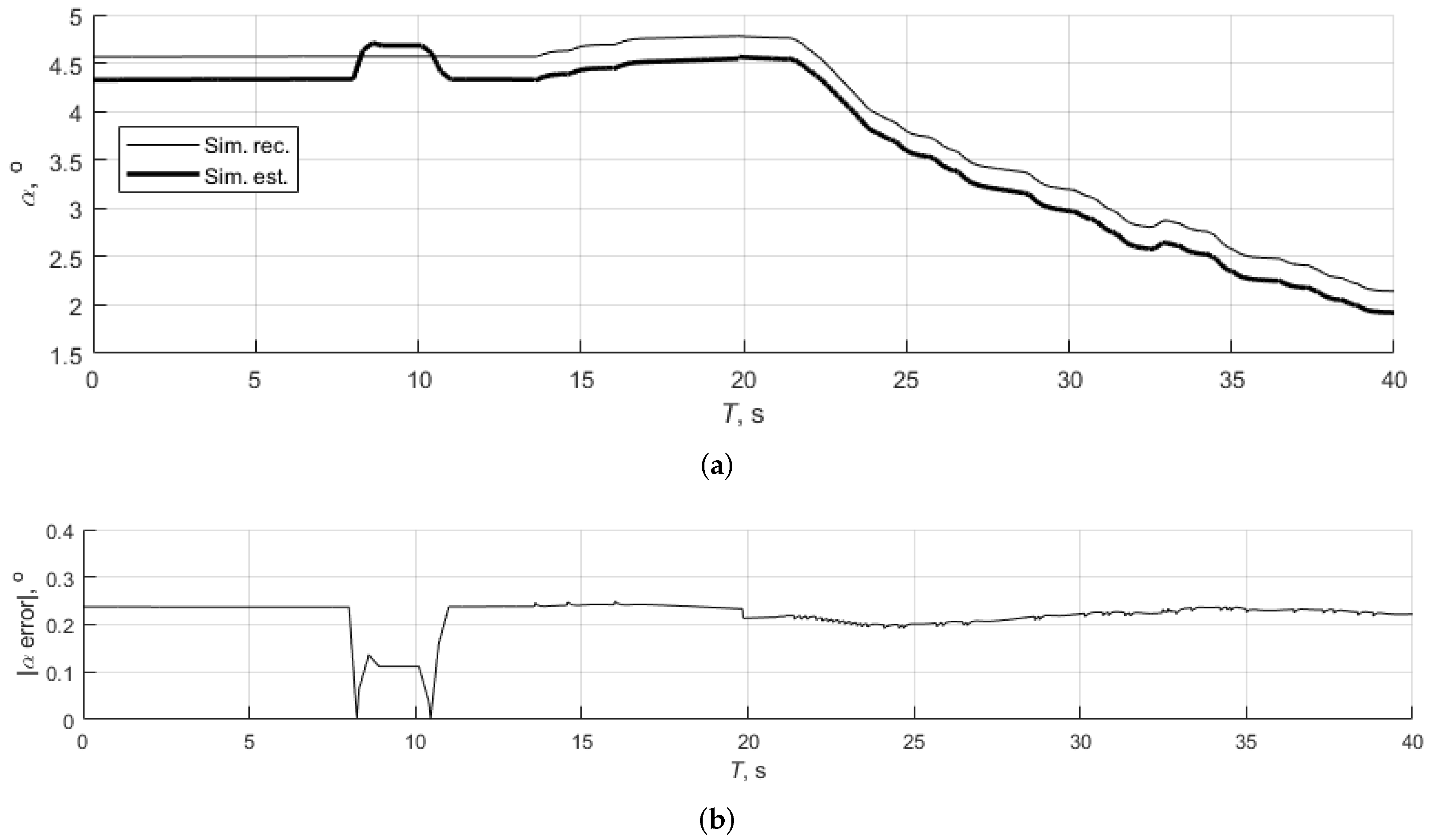
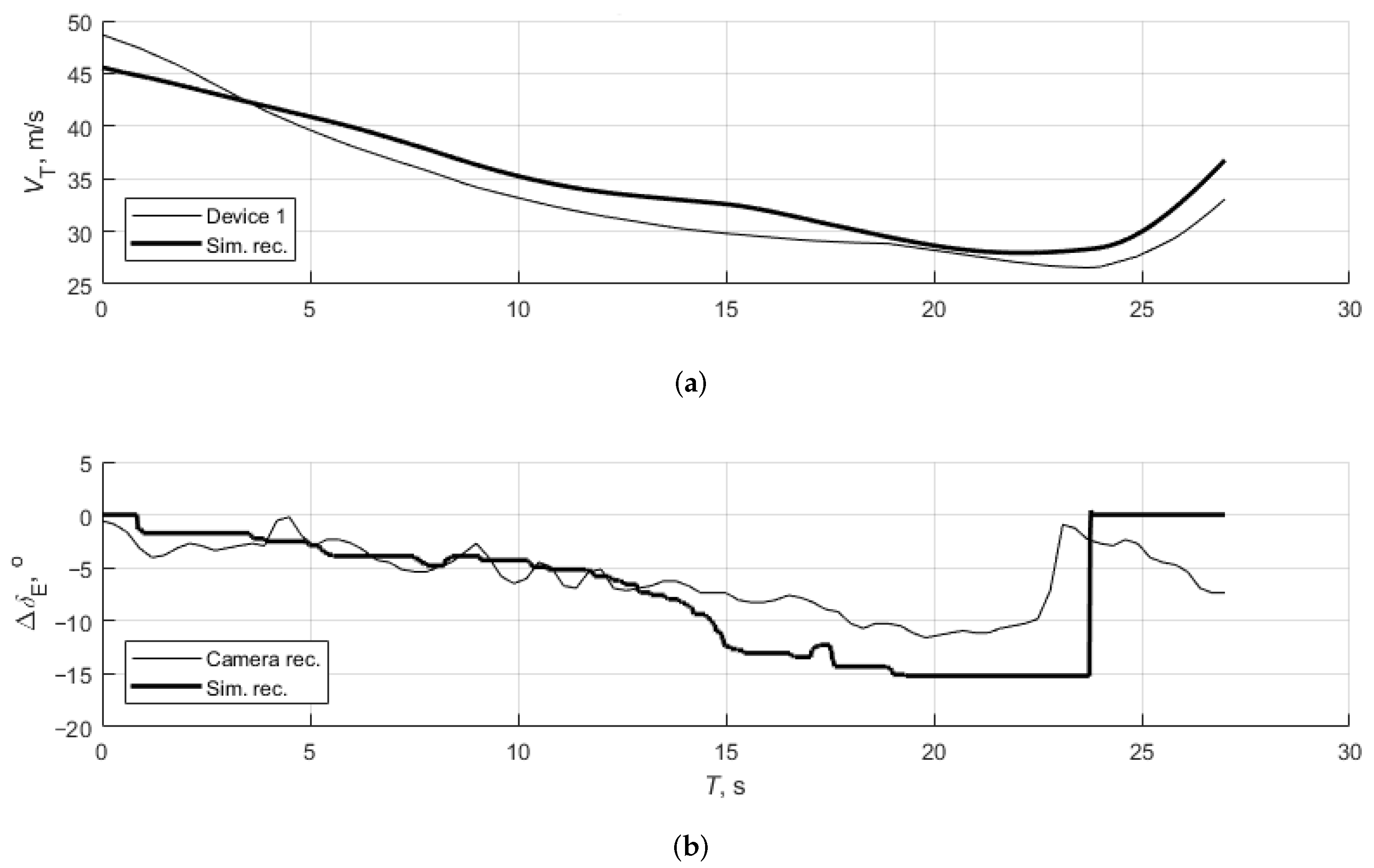
3.2. Test 2: Stall with Idle Power
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Treaster, A.L.; Yocum, A.M. The Calibration and Application of Five-Hole Probes; Technical Report NAVSEA TM 78-10; Pennsylvania State Univ University Park Applied Research Lab: State Collage, PA, USA, 1978. [Google Scholar]
- Lerro, A.; Battipede, M. Safety Analysis of a Certifiable Air Data System Based on Synthetic Sensors for Flow Angle Estimation. Appl. Sci. 2021, 11, 3127. [Google Scholar] [CrossRef]
- Lie, F.A.P. Synthetic Air Data Estimation: A Case Study of Model-Aided Estimation. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2014. [Google Scholar]
- Lerro, A.; Gili, P.; Pisani, M. Verification in Relevant Environment of a Physics-Based Synthetic Sensor for Flow Angle Estimation. Electronics 2022, 11, 165. [Google Scholar] [CrossRef]
- Lerro, A.; Brandl, A.; Battipede, M.; Gili, P. A Data-Driven Approach to Identify Flight Test Data Suitable to Design Angle of Attack Synthetic Sensor for Flight Control Systems. Aerospace 2020, 7, 63. [Google Scholar] [CrossRef]
- Tian, P.; Chao, H.; Rhudy, M.; Gross, J.; Wu, H. Wind Sensing and Estimation Using Small Fixed-Wing Unmanned Aerial Vehicles: A Survey. J. Aerosp. Inf. Syst. 2021, 18, 132–143. [Google Scholar] [CrossRef]
- Lie, F.A.P.; Gebre-Egziabher, D. Synthetic Air Data System. J. Aircr. 2013, 50, 1234–1249. [Google Scholar] [CrossRef]
- Calia, A.; Denti, E.; Galatolo, R.; Schettini, F. Air Data Computation Using Neural Networks. J. Aircr. 2008, 45, 2078–2083. [Google Scholar] [CrossRef]
- Sun, K.; Regan, C.D.; Gebre-Egziabher, D. Observability and Performance Analysis of a Model-Free Synthetic Air Data Estimator. J. Aircr. 2019, 56, 1471–1486. [Google Scholar] [CrossRef]
- Lerro, A.; Brandl, A.; Gili, P. Model-Free Scheme for Angle-of-Attack and Angle-of-Sideslip estimation. J. Guid. Control Dyn. 2021, 44, 595–600. [Google Scholar] [CrossRef]
- Lerro, A.; Gili, P.; Fravolini, M.L.; Napolitano, M. Experimental Analysis of Neural Approaches for Synthetic Angle-of-Attack Estimation. Int. J. Aerosp. Eng. 2021, 2021, 9982722. [Google Scholar] [CrossRef]
- Valasek, J.; Harris, J.; Pruchnicki, S.; McCrink, M.; Gregory, J.; Sizoo, D.G. Derived Angle of Attack and Sideslip Angle Characterization for General Aviation. J. Guid. Control Dyn. 2020, 43, 1039–1055. [Google Scholar] [CrossRef]
- General Aviation Joint Steering Committee (GAJSC). Loss of Control Work Group Approach and Landing. 2012. Available online: https://www.gajsc.org/safety-enhancem,ents/loss-of-control/ (accessed on 30 January 2023).
- Berndt, J.S. JSBSim: An Open Source, Platform-Independent, Flight Dynamics Model in C++: 2011. Available online: https://jsbsim.sourceforge.net/ (accessed on 30 January 2023).
- Basler, M.; Spott, M.; Buchanan, S.; Berndt, J.; Buckel, B.; Ludwicki, R.; Moore, C.; Olson, C.; Perry, D.; Selig, M.; et al. The FlightGear Manual. For FlightGear Version 2020.3.15. 2022. Available online: https://flightgear.sourceforge.net/manual/2020.3/en/getstart-en.html (accessed on 30 January 2023).

| Parameter | Mass, kg |
|---|---|
| Empty aircraft | 693.5 |
| Pilot | 102 |
| Co-pilot | 87 |
| Flight engineer | 87 |
| Equipment | 5 |
| Initial fuel | 104 |
| Total take-off mass | 1079 |
| Wind speed (at 914 m) | 2.57 m/s |
| Wind direction (at 914 m, in ref. to N) | 200° |
| Air temperature (at 914 m) | 0 °C |
| Air pressure (at airfield, 91 m) | 1010 hPa |
| Data Source | Mean Difference and Max. Deviation | Mean Difference and Max. Deviation without and |
|---|---|---|
| Simulation estimation | −0.21° ± 0.35° | −0.23° ± 0.02° |
| Device 1 estimation | −0.30° ± 0.65° | −0.26° ± 0.64° |
| Device 2 estimation | −0.17° ± 1.2° | −0.13° ± 1.12° |
| Data Source | Estimated Stall AoA | Estimated Stall AoA without and |
|---|---|---|
| Simulation estimation | 13.1° | 11.7° |
| Device 1 estimation | 13.8° | 13.2° |
| Device 2 estimation | 15.0° | 14.4° |
| Simulation recording | 14.4° | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanković, M.; Vrdoljak, M.; Andrić, M.; Kozmar, H. Angle-of-Attack Estimation for General Aviation Aircraft. Aerospace 2023, 10, 315. https://doi.org/10.3390/aerospace10030315
Ivanković M, Vrdoljak M, Andrić M, Kozmar H. Angle-of-Attack Estimation for General Aviation Aircraft. Aerospace. 2023; 10(3):315. https://doi.org/10.3390/aerospace10030315
Chicago/Turabian StyleIvanković, Marin, Milan Vrdoljak, Marijan Andrić, and Hrvoje Kozmar. 2023. "Angle-of-Attack Estimation for General Aviation Aircraft" Aerospace 10, no. 3: 315. https://doi.org/10.3390/aerospace10030315
APA StyleIvanković, M., Vrdoljak, M., Andrić, M., & Kozmar, H. (2023). Angle-of-Attack Estimation for General Aviation Aircraft. Aerospace, 10(3), 315. https://doi.org/10.3390/aerospace10030315







