Effect of Wavy Leading Edges on Airfoil Trailing-Edge Bluntness Noise
Abstract
:1. Introduction
2. Numerical Setup
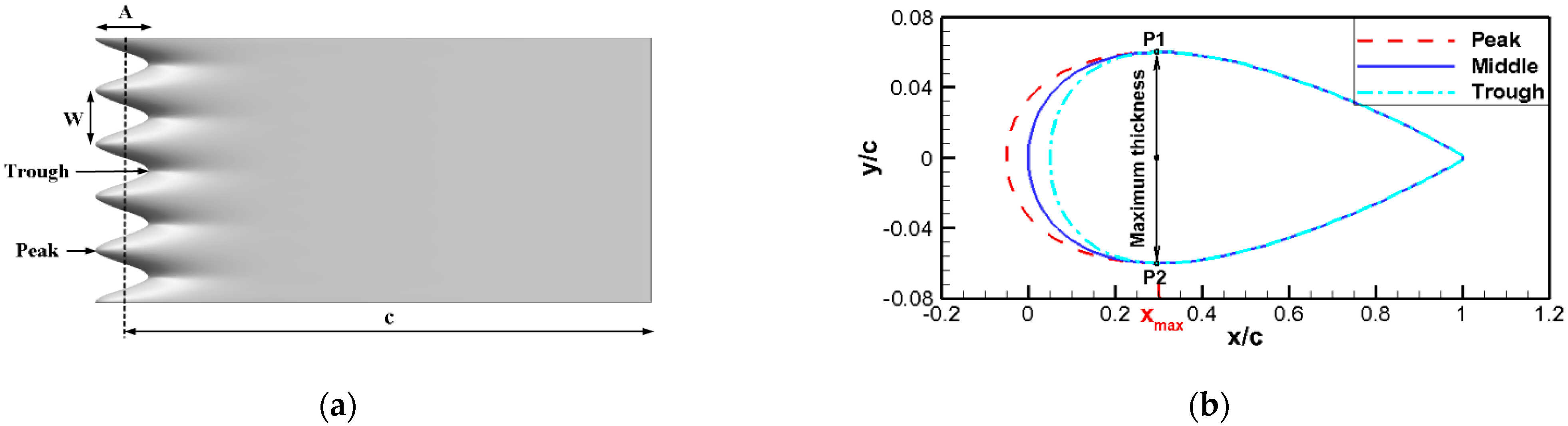
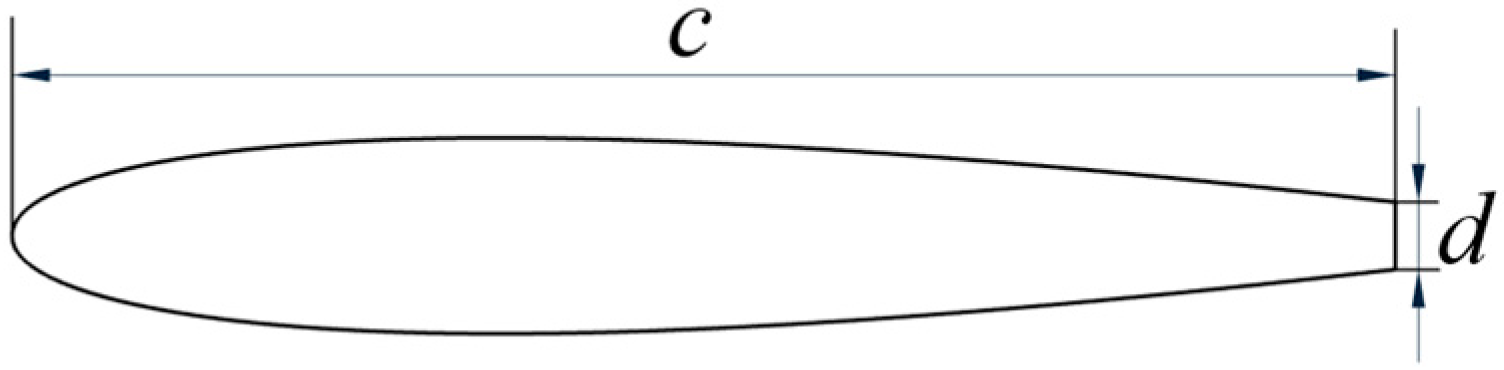
2.1. Design of Wavy Leading Edges and the Blunt Trailing Edge
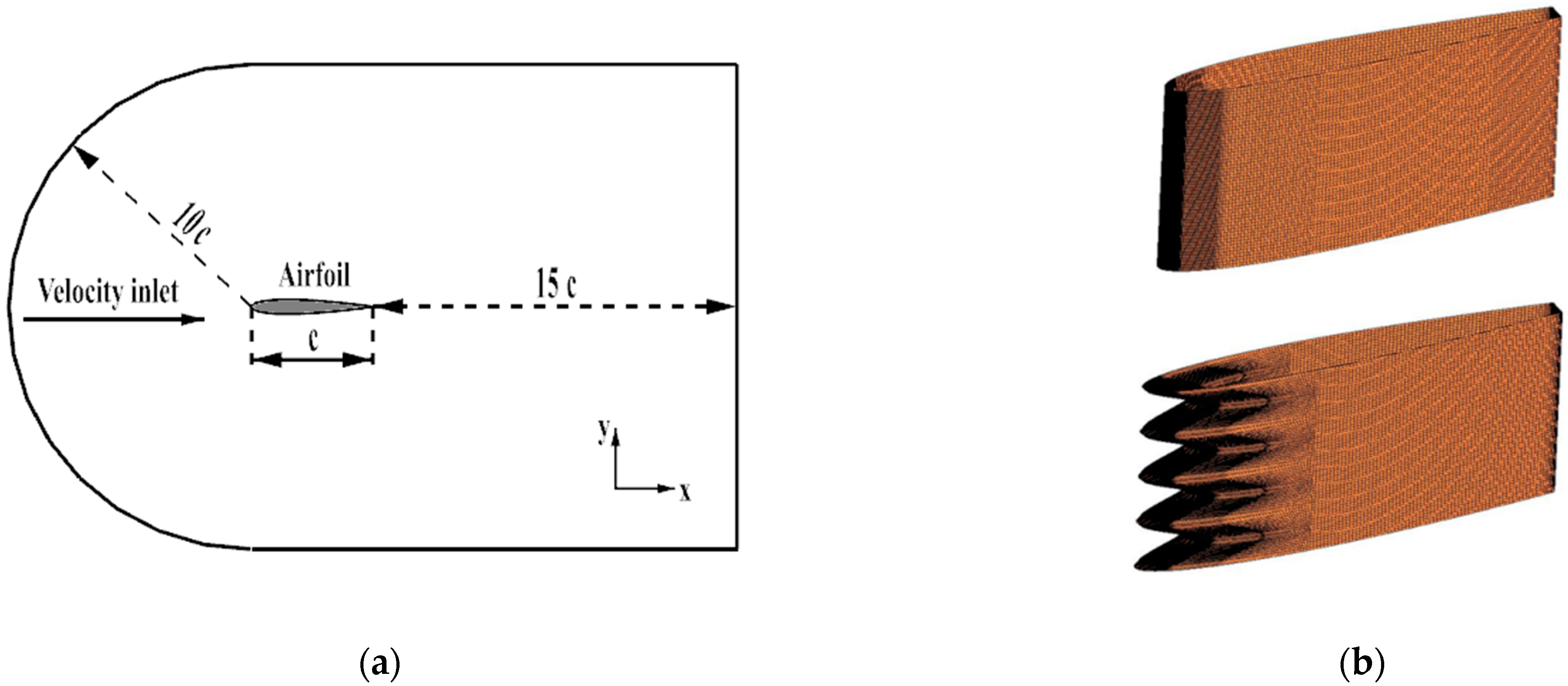
2.2. Aerodynamic Simulation by the IDDES Method
2.3. Noise Prediction by the FW-H Equation
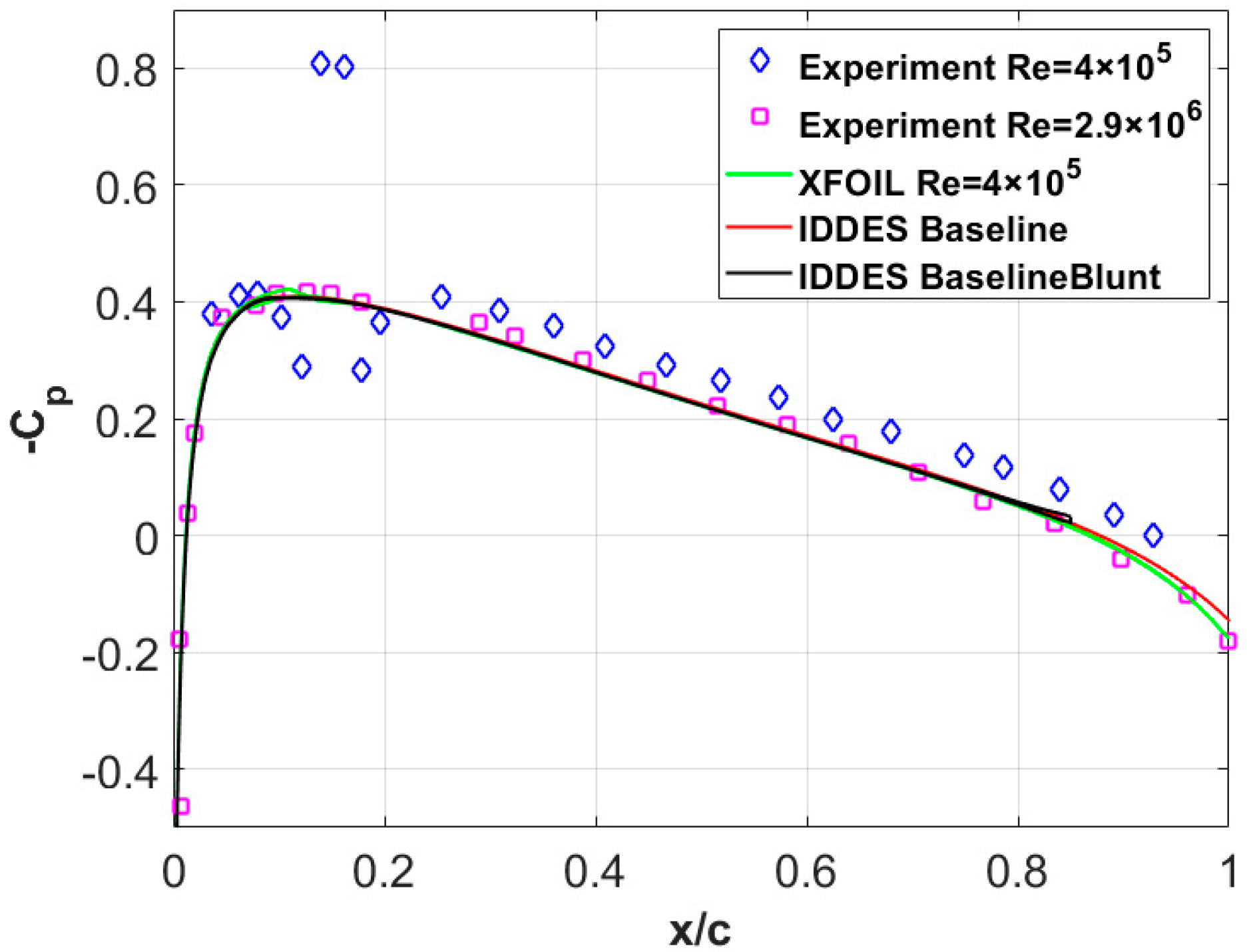
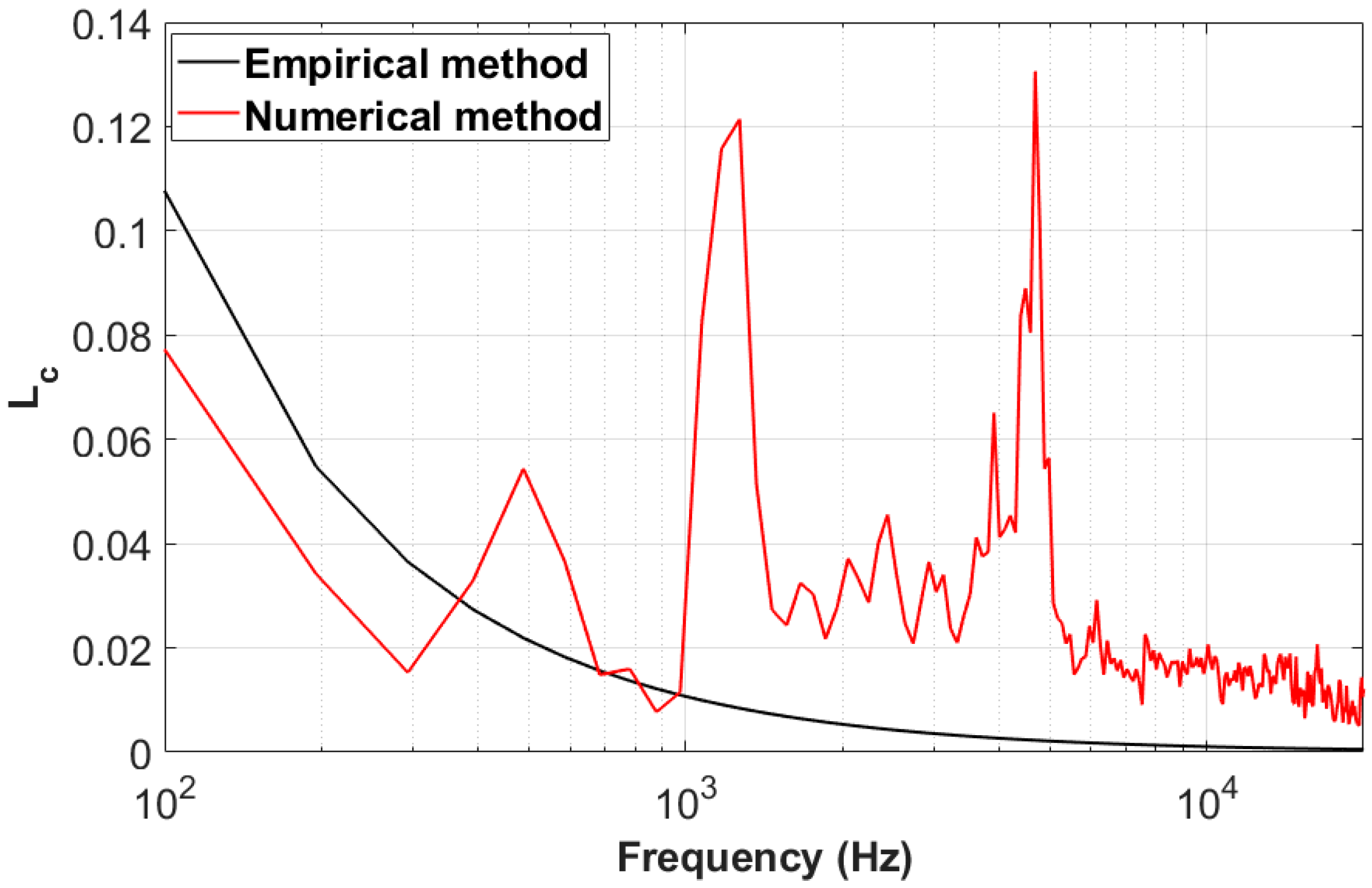
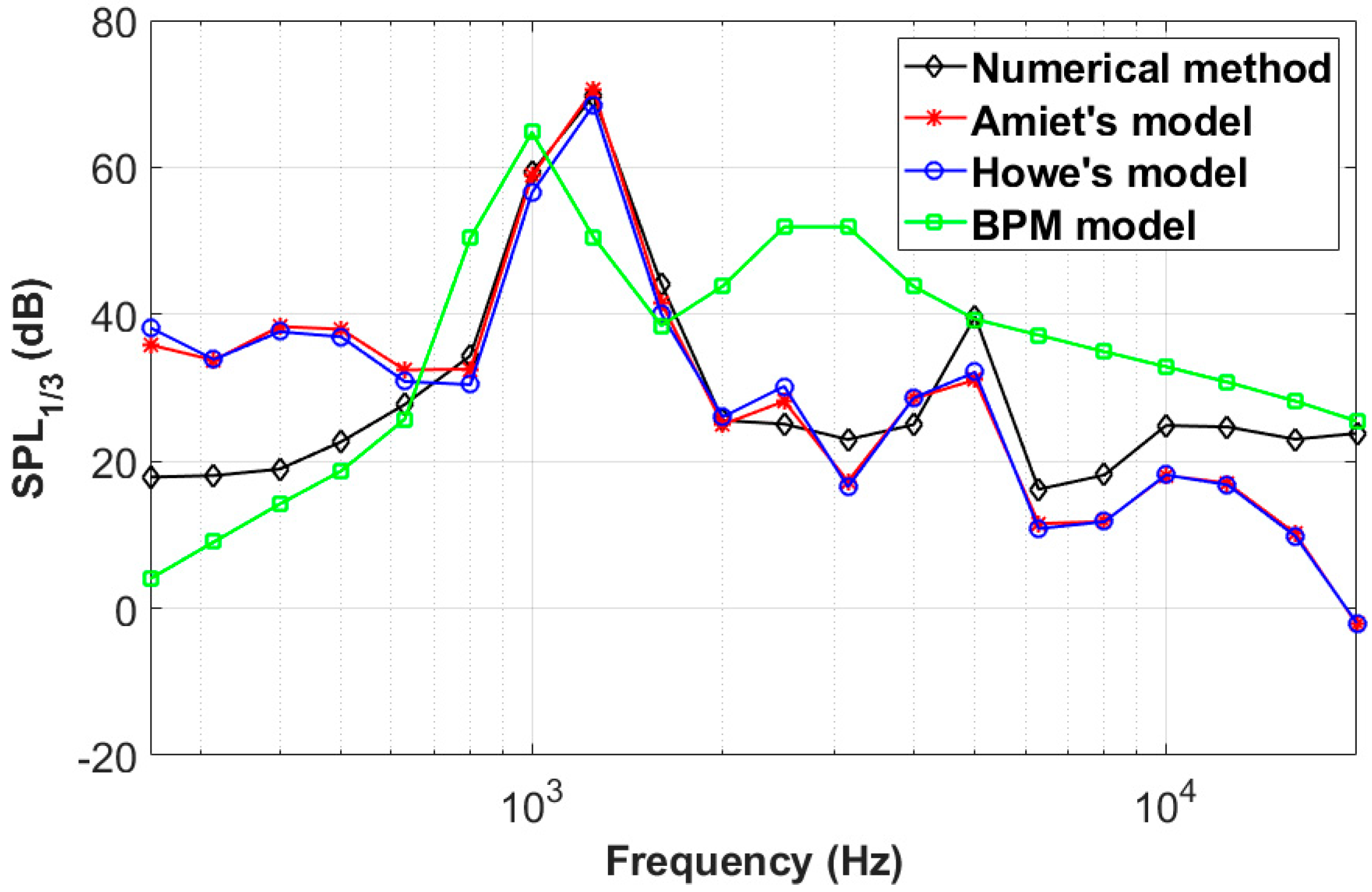
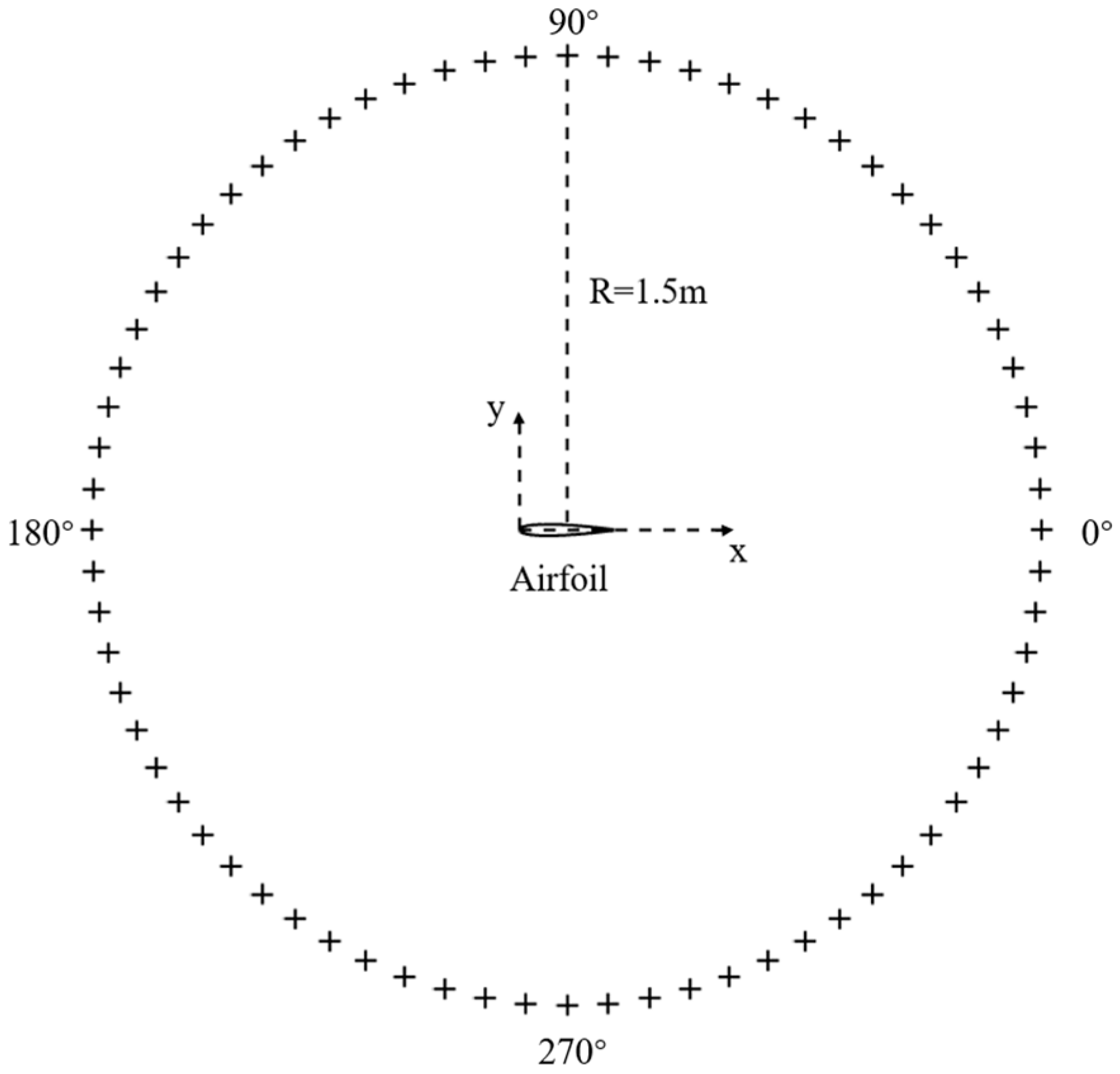
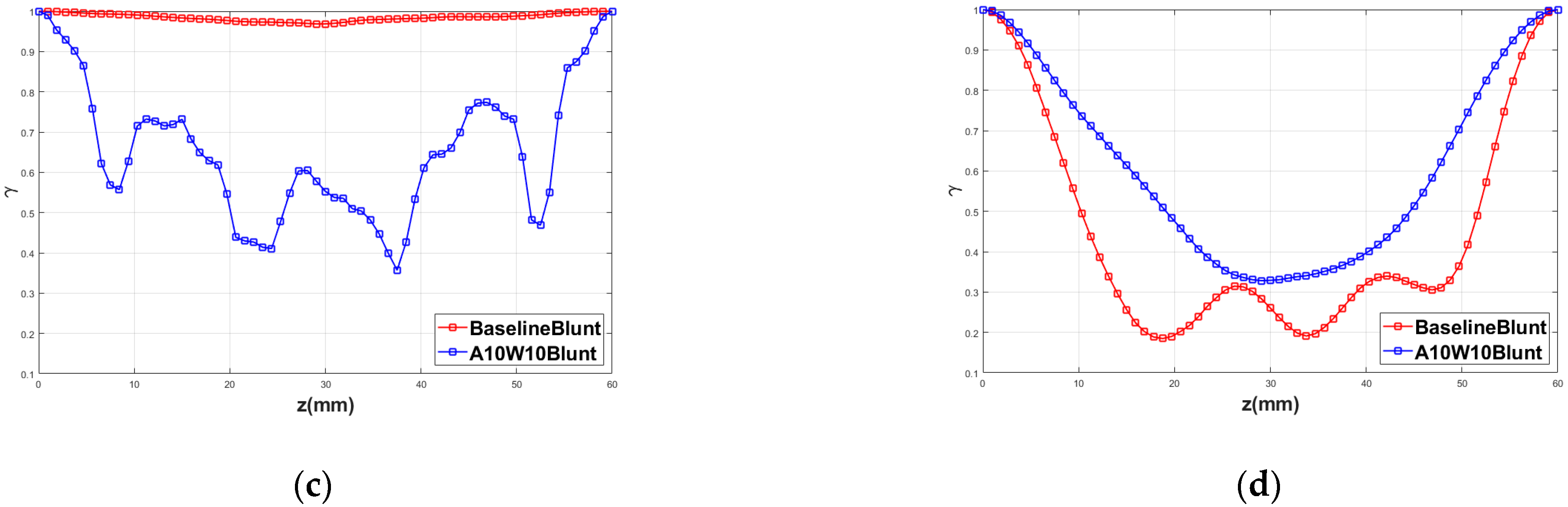
2.4. Validation and Verification of the Numerical Method
3. Results and Discussions
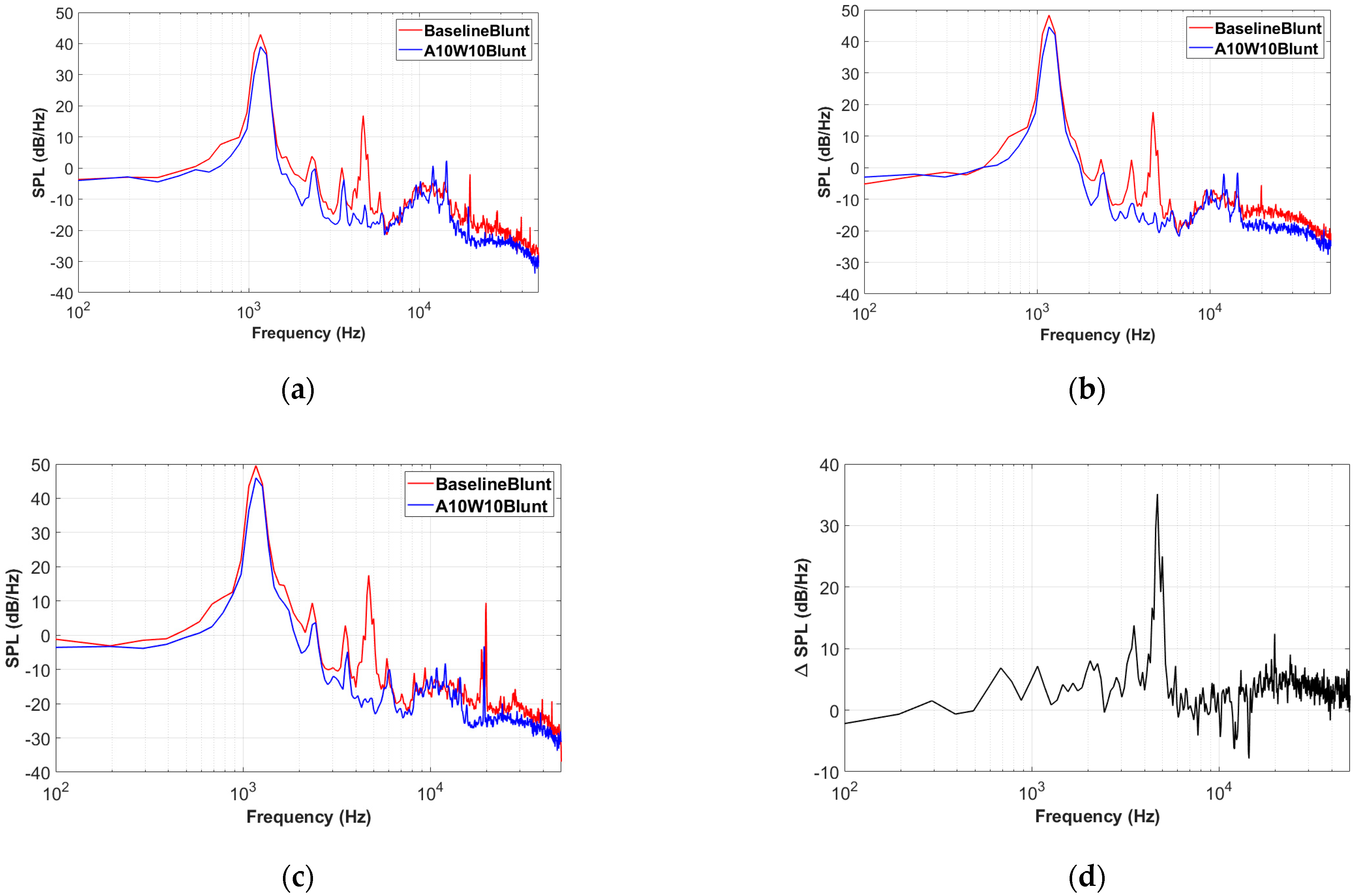
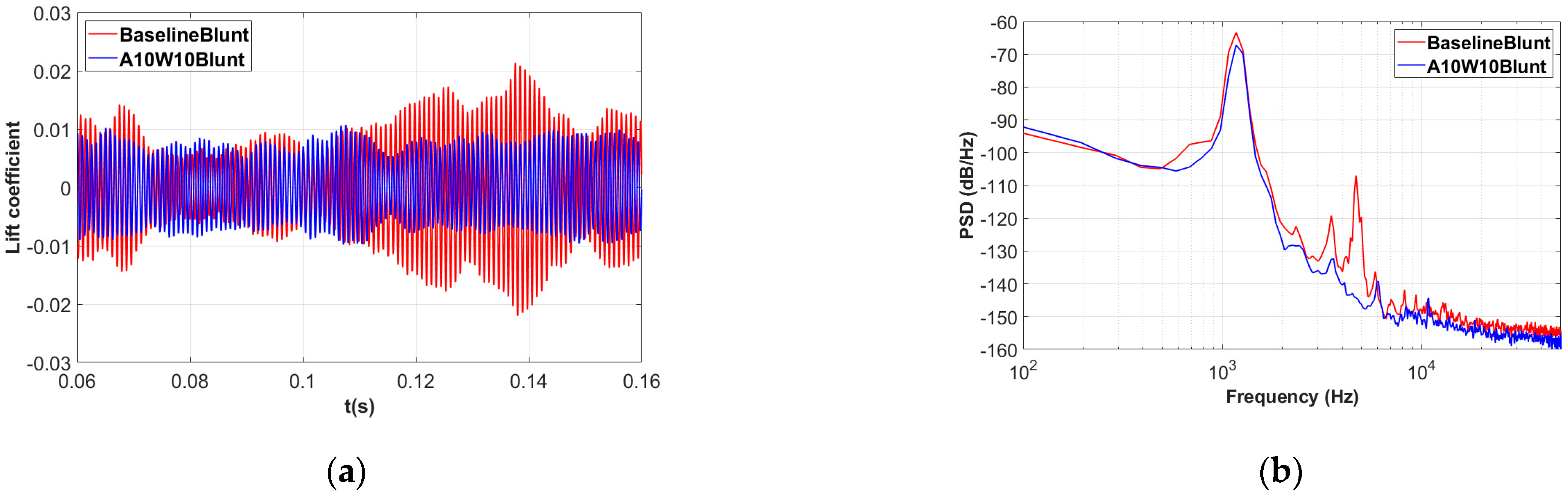
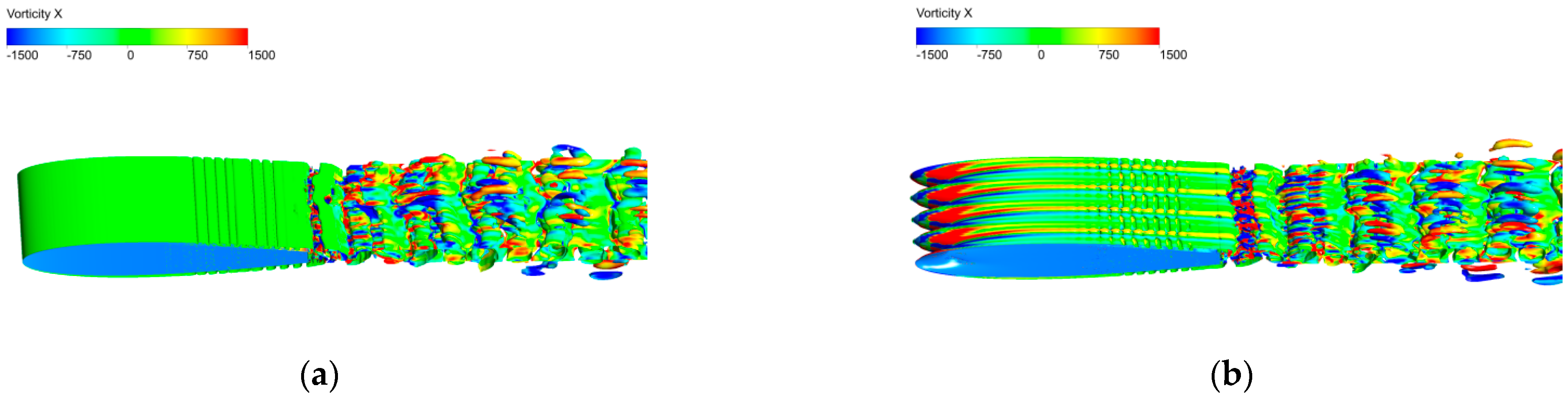
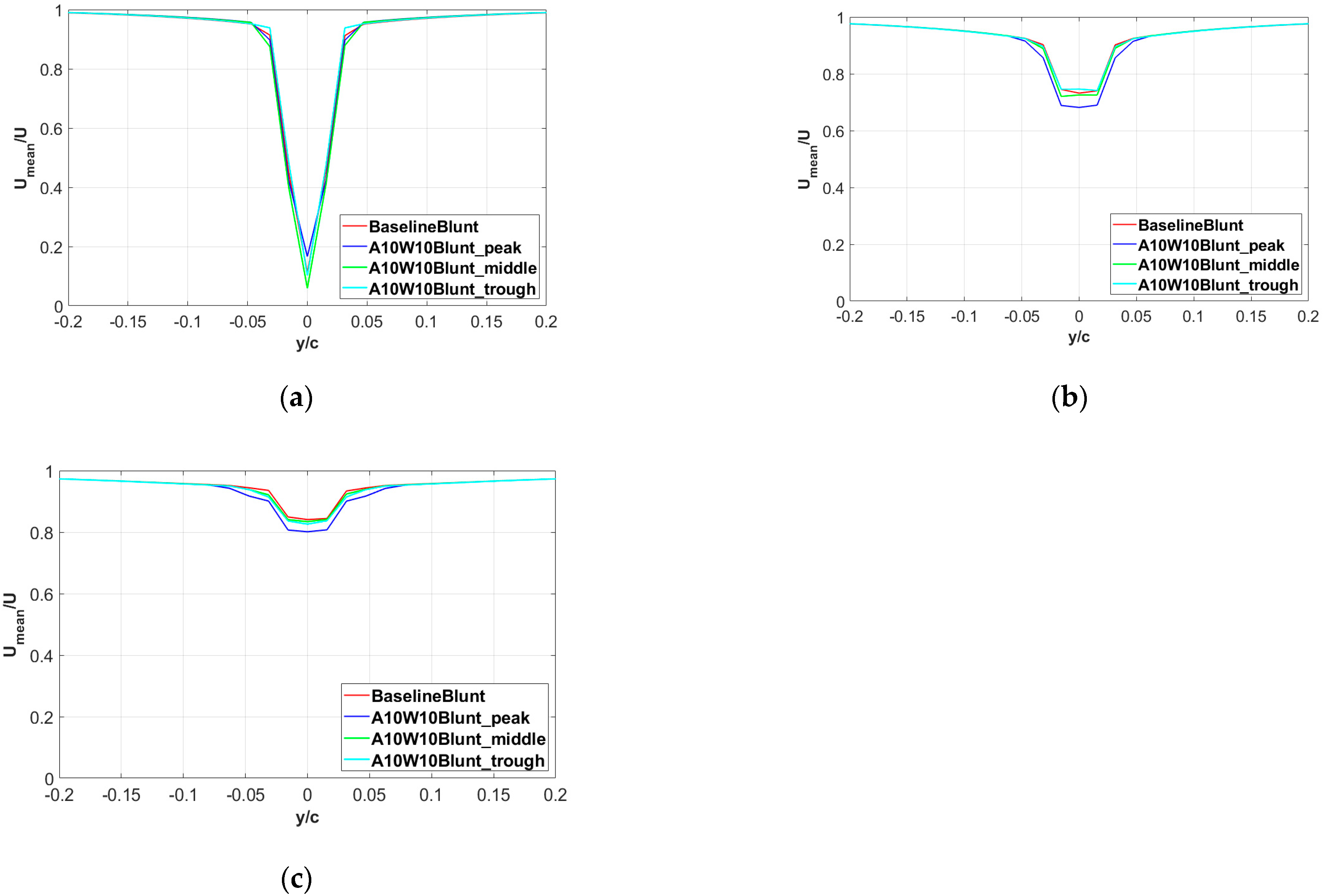
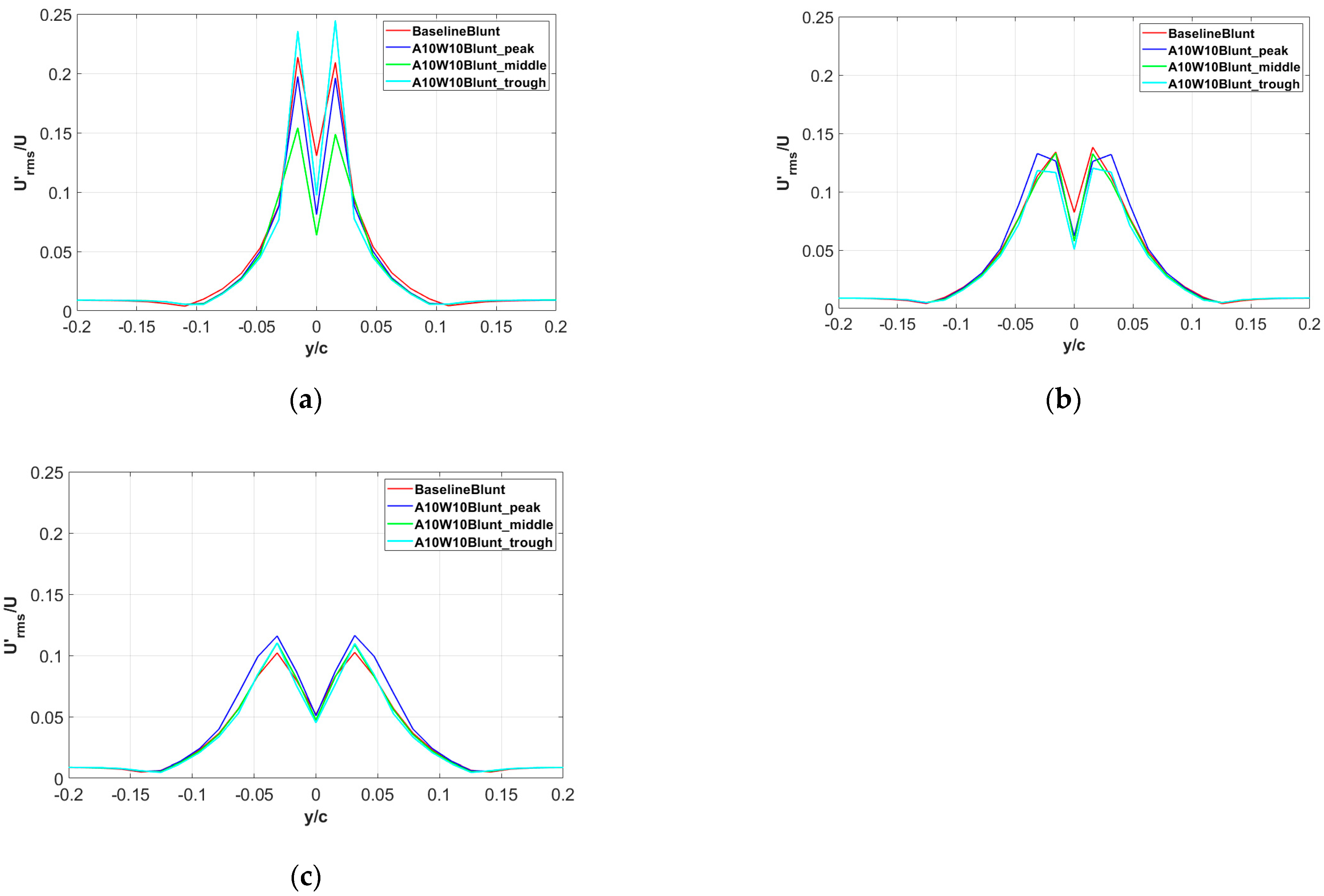
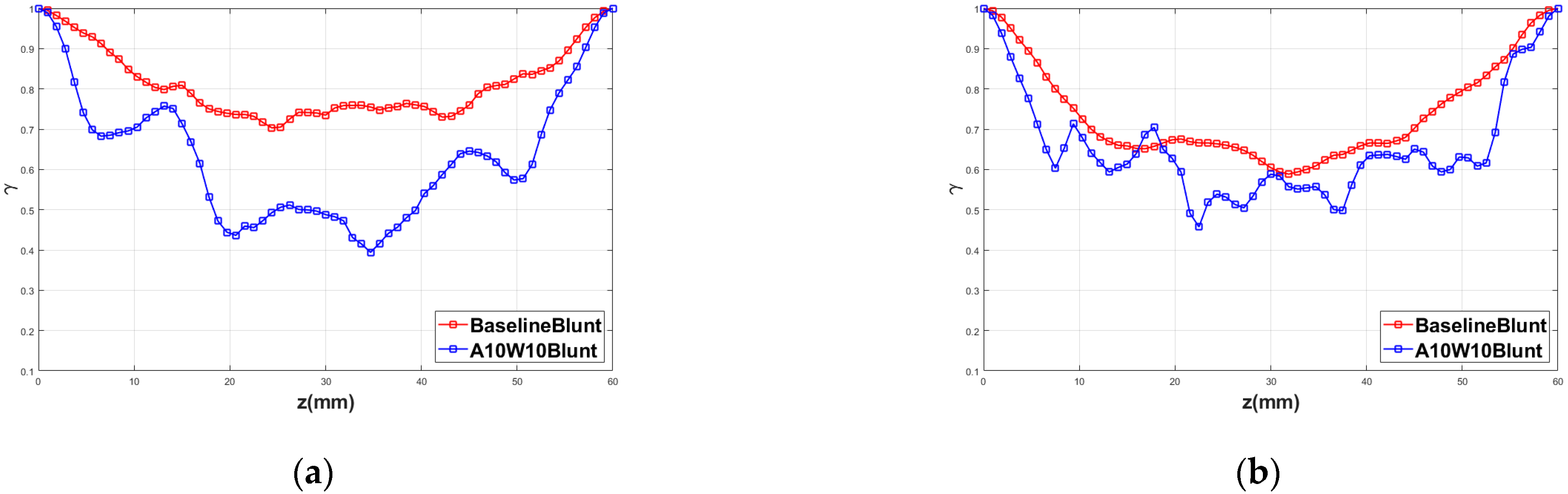
3.1. Noise-Reduction Effects of the Wavy Leading Edges
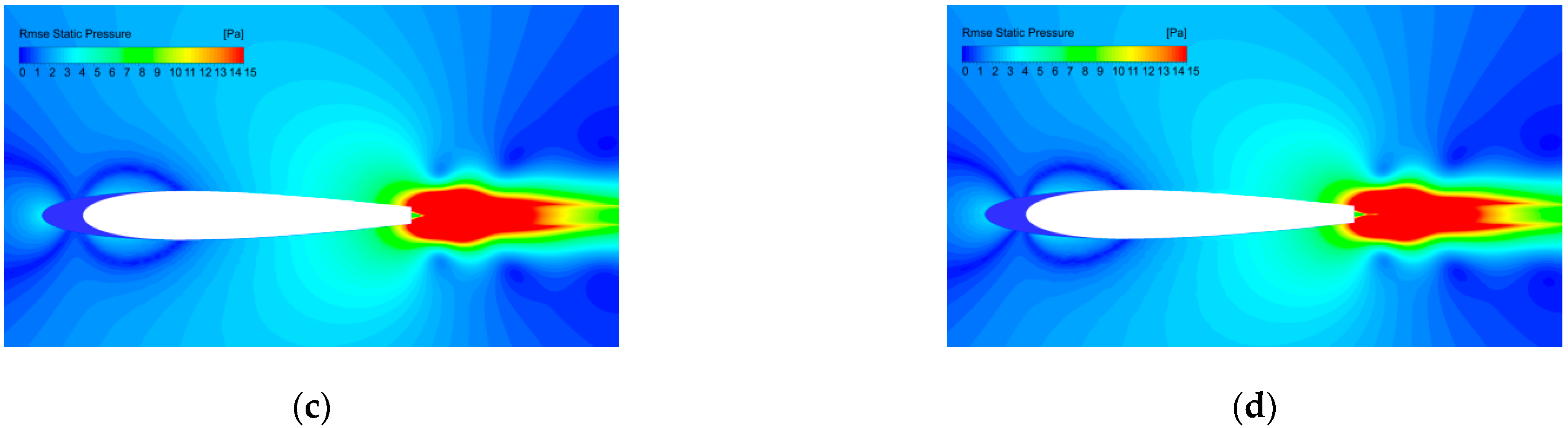
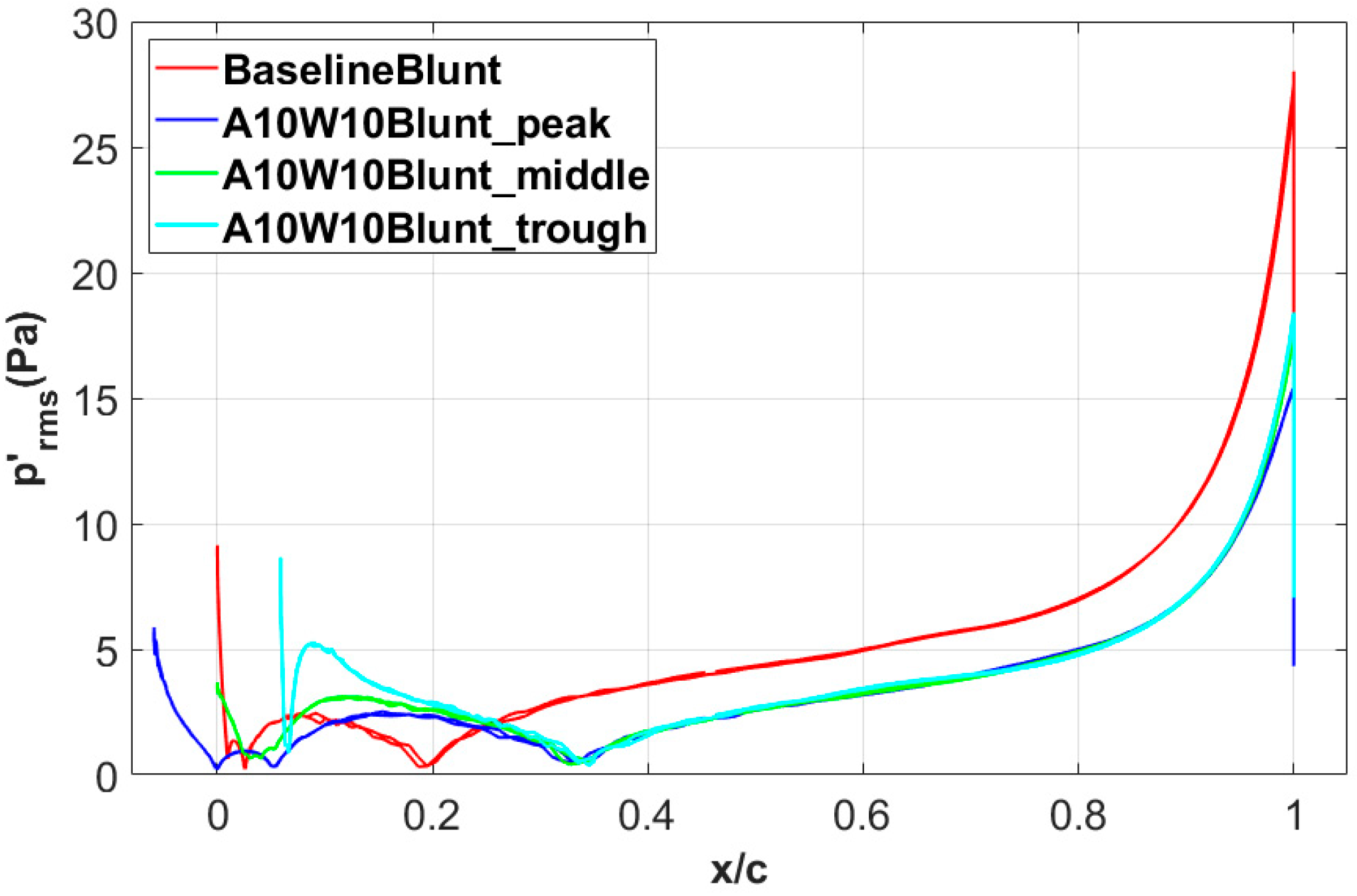
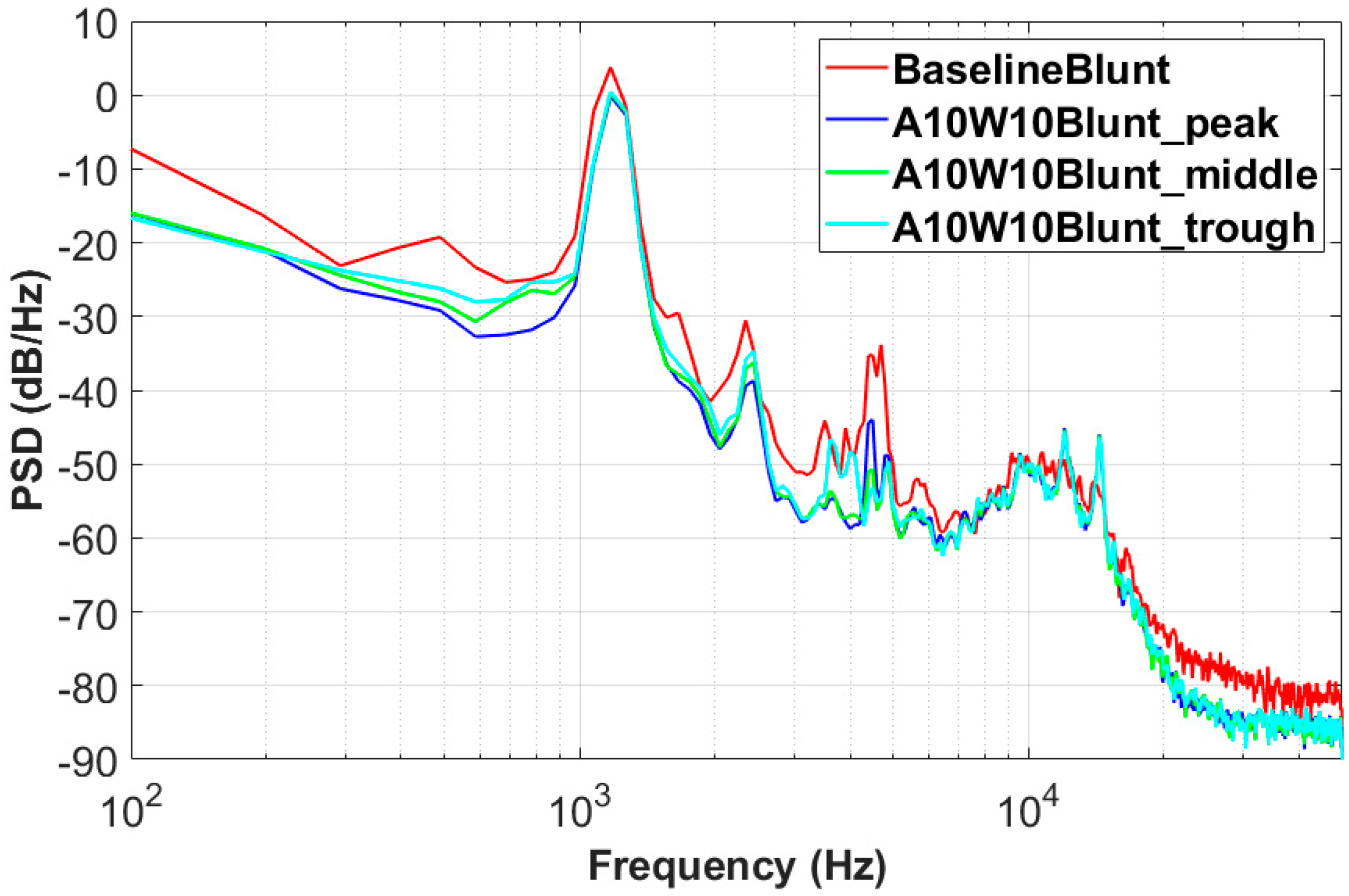
3.2. Noise-Reduction Mechanisms of the Wavy Leading Edges
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brooks, T.F.; Pope, D.S.; Marcolini, M.A. Airfoil Self-Noise and Prediction (NASA Reference Publication); Technical Report 1218; National Aeronautics and Space Administration: Washington, DC, USA, 1989. [Google Scholar]
- Brooks, T.F.; Hodgson, T.H. Trailing edge noise prediction from measured surface pressures. J. Sound Vib. 1981, 78, 69–117. [Google Scholar] [CrossRef]
- Dobrzynski, W. Almost 40 years of airframe noise research: What did we achieve? J. Aircr. 2010, 47, 353–367. [Google Scholar] [CrossRef]
- Christian, A.W.; Cabell, R. Initial investigation into the psychoacoustic properties of small unmanned aerial system noise. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017; Volume 4051. [Google Scholar]
- Xiong, P.; Wu, L.; Chen, X.Y.; Wu, Y.G.; Yang, W.J. Aerodynamic Performance Analysis of a Modified Joukowsky Airfoil: Parametric Control of Trailing Edge Thickness. Appl. Sci. 2021, 11, 8395. [Google Scholar] [CrossRef]
- Avallone, F.; Van Der Velden, W.C.P.; Ragni, D.; Casalino, D. Noise reduction mechanisms of sawtooth and combed-sawtooth trailing-edge serrations. J. Fluid Mech. 2018, 848, 560–591. [Google Scholar] [CrossRef] [Green Version]
- Ali, S.A.S.; Azarpeyvand, M.; Da Silva, C.R.I. Trailing-edge flow and noise control using porous treatments. J. Fluid Mech. 2018, 850, 83–119. [Google Scholar]
- Vathylakis, A.; Chong, T.P.; Joseph, P.F. Poro-serrated trailing-edge devices for airfoil self-noise reduction. AIAA J. 2015, 53, 3379–3394. [Google Scholar] [CrossRef] [Green Version]
- Chong, T.P.; Dubois, E. Optimization of the poro-serrated trailing edges for airfoil broadband noise reduction. J. Acoust. Soc. Am. 2016, 140, 1361–1373. [Google Scholar] [CrossRef] [Green Version]
- Fish, F.E.; Battle, J.M. Hydrodynamic design of the Humpback Whale Flipper. J. Morphol. 1995, 225, 51–60. [Google Scholar] [CrossRef]
- Hansen, K.L.; Kelso, R.M.; Doolan, C.J. Reduction of flow induced tonal noise through leading edge tubercle modifications. In Proceedings of the 16th AIAA/CEAS Aeroacoustics Conference, Stockholm, Sweden, 7–9 June 2010; p. 3700. [Google Scholar]
- Gruber, M.; Joseph, P.F.; Polacsek, C.; Chong, T.P. Noise reduction using combined trailing edge and leading edge serrations in a tandem airfoil experiment. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, CO, USA, 4–6 June 2012; p. 2134. [Google Scholar]
- Wang, L.; Liu, X.M.; Li, D. Noise reduction mechanism of airfoils with leading-edge serrations and surface ridges inspired by owl wings. Phys. Fluids 2021, 33, 015123. [Google Scholar] [CrossRef]
- Chen, W.J.; Qiao, W.Y.; Duan, W.H. Experimental study of airfoil instability noise with wavy leading edges. Appl. Acoust. 2021, 172, 107671. [Google Scholar] [CrossRef]
- Narayanan, S.; Joseph, P.; Haeri, S. Noise reduction studies from the leading edge of serrated flat plates. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 16–20 June 2014; p. 2320. [Google Scholar]
- Chong, T.P.; Vathylakis, A.; McEwen, A. Aeroacoustic and aerodynamic performances of an aerofoil subjected to sinusoidal leading edges. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015; p. 2200. [Google Scholar]
- Chaitanya, P.; Joseph, P.; Narayanan, S. Performance and mechanism of sinusoidal leading edge serrations for the reduction of turbulenc-aerofoil interaction noise. J. Fluid Mech. 2017, 818, 435–464. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.J.; Qiao, W.Y.; Tong, F. Experimental investigation of wavy leading edges on rod-aerofoil interaction noise. J. Sound Vib. 2018, 422, 409–431. [Google Scholar] [CrossRef]
- Clair, V.; Polacsek, C.; Garrec, T. Experimental and numerical investigation of turbulence-airfoil noise reduction using wavy edges. AIAA J. 2013, 51, 2695–2713. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, B.R.; Sharma, A. Numerical analysis of aerodynamic noise mitigation via leading edge serrations for a rod-airfoil configuration. Int. J. Aeroacoustics 2016, 15, 734–756. [Google Scholar] [CrossRef]
- Kim, J.W.; Haeri, S.; Joseph, P.F. On the reduction of aerofoil-turbulence interaction noise associated with wavy leading edges. J. Fluid Mech. 2016, 792, 526–552. [Google Scholar] [CrossRef] [Green Version]
- Aguilera, F.G.; Gill, J.; Angland, D. Wavy leading edge airfoils interacting with anisotropic turbulence. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017; p. 3370. [Google Scholar]
- Chen, W.J.; Qiao, W.Y.; Tong, F.; Wang, L.F.; Wang, X.N. Numerical investigation of wavy leading edges on rod-airfoil interaction noise. AIAA J. 2018, 56, 2553–2567. [Google Scholar] [CrossRef]
- Tong, F.; Qiao, W.Y.; Xu, K.B.; Wang, L.F.; Chen, W.J.; Wang, X.N. On the study of wavy leading-edge vanes to achieve low fan interaction noise. J. Sound Vib. 2018, 419, 200–226. [Google Scholar] [CrossRef]
- Chen, W.J.; Qiao, W.Y.; Wei, Z.J. Aerodynamic performance and wake development of airfoils with wavy leading edges. Aerosp. Sci. Technol. 2020, 106, 106216. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Chong, T.P.; Joseph, P.; Lacagnina, G. Effect of Leading-Edge Serrations on Trailing-Edge-Bluntness Vortex-Shedding Noise Radiation. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019; p. 2437. [Google Scholar]
- Hasheminejad, S.M.; Chong, T.P.; Lacagnina, G. On the manipulation of flow and acoustic fields of a blunt trailing edge aerofoil by serrated leading edges. J. Acoust. Soc. Am. 2020, 147, 3932–3947. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.M.; Wang, G.F.; Xu, J.Z. Aerodynamic control of low-Reynolds-number airfoil with leading-edge protuberances. AIAA J. 2013, 51, 1960–1971. [Google Scholar] [CrossRef]
- Hansen, K.L.; Rostamzadeh, N.; Kelso, R.M.; Dally, B.B. Evolution of the streamwise vortices generated between leading edge tubercles. J. Fluid Mech. 2016, 788, 730–766. [Google Scholar] [CrossRef]
- Skillen, A.; Revell, A.; Pinelli, A.; Piomelli, U.; Favier, J. Flow over a wing with leading-edge undulations. AIAA J. 2015, 53, 464–472. [Google Scholar] [CrossRef]
- Rostamzadeh, N.; Hansen, K.L.; Kelso, R.M.; Dally, B.B. The formation mechanism and impact of streamwise vortices on NACA 0021 airfoil’s performance with undulating leading edge modification. Phys. Fluids 2014, 26, 107101. [Google Scholar] [CrossRef]
- Spalart, P.R.; Jou, W.H.; Strelets, M.; Allmaras, S.R. Comments on the feasibility of LES for wings and on the hybrid RANS/LES approach. In Proceedings of the First AFOSR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997; pp. 137–147. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.; Travin, A. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS Fluent: Theory Guide, Release 2019 R2; ANSYS, Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- Pindi Nataraj, P. Airfoil Self-Noise Predictions Using DDES and the FWH Analogy. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2022. [Google Scholar]
- Drela, M. XFOIL: An analysis and design system for low Reynolds number airfoils. In Low Reynolds Number Aerodynamics: Proceedings of the Conference Notre Dame, Indiana, USA, 5–7 June 1989; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–12. [Google Scholar]
- Garcia-Sagrado, A.; Hynes, T. Wall pressure sources near an airfoil trailing edge under turbulent boundary layers. J. Fluids Struct. 2012, 30, 3–34. [Google Scholar] [CrossRef]
- Gregory, N.; O’reilly, C.L. Low-speed aerodynamic characteristics of NACA 0012 aerofoil section, including the effects of upper-surface roughness simulating hoar frost. Tech. Rep. NASA Rep. Memo. 1970, January, 3726. [Google Scholar]
- Amiet, R.K. Noise due to turbulent flow past a trailing edge. J. Sound Vib. 1976, 47, 387–393. [Google Scholar] [CrossRef]
- Howe, M.S. Trailing edge noise at low Mach numbers. J. Sound Vib. 1999, 225, 211–238. [Google Scholar] [CrossRef]
- Lee, S.; Shum, G. Prediction of airfoil trailing-edge noise using empirical wall-pressure spectrum models. AIAA J. 2019, 57, 888–897. [Google Scholar] [CrossRef]
- Corcos, G.M. The structure of the turbulent pressure field in boundary-layer flows. J. Fluid Mech. 1964, 18, 353–378. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.C.; Wu, Z.Y.; Wharton, J.; Ren, L.Q. Numerical study on reduction of aerodynamic noise around an airfoil with biomimetic structures. J. Sound Vib. 2017, 394, 46–58. [Google Scholar] [CrossRef]
- Welch, P.D. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.J.; Wang, X.N.; Qiao, W.Y.; Wang, L.F.; Tong, F. Rod-airfoil interaction noise reduction using leading edge serrations. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015; p. 3264. [Google Scholar]





| Mesh | Grid Number | CD | ΔCD |
|---|---|---|---|
| Coarser | 2,658,154 | 0.018473 | −0.038% |
| Coarse | 6,410,842 | 0.018461 | −0.103% |
| Medium | 8,912,634 | 0.018480 | --- |
| Fine | 11,414,426 | 0.018469 | −0.060% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Y.; Chen, W.; Wang, X.; Tong, F.; Qiao, W. Effect of Wavy Leading Edges on Airfoil Trailing-Edge Bluntness Noise. Aerospace 2023, 10, 353. https://doi.org/10.3390/aerospace10040353
Xing Y, Chen W, Wang X, Tong F, Qiao W. Effect of Wavy Leading Edges on Airfoil Trailing-Edge Bluntness Noise. Aerospace. 2023; 10(4):353. https://doi.org/10.3390/aerospace10040353
Chicago/Turabian StyleXing, Yudi, Weijie Chen, Xingyu Wang, Fan Tong, and Weiyang Qiao. 2023. "Effect of Wavy Leading Edges on Airfoil Trailing-Edge Bluntness Noise" Aerospace 10, no. 4: 353. https://doi.org/10.3390/aerospace10040353
APA StyleXing, Y., Chen, W., Wang, X., Tong, F., & Qiao, W. (2023). Effect of Wavy Leading Edges on Airfoil Trailing-Edge Bluntness Noise. Aerospace, 10(4), 353. https://doi.org/10.3390/aerospace10040353







