Optimal Design and Analysis of a High-Load Supersonic Compressor Based on a Surrogate Model
Abstract
:1. Introduction
2. Research Object and Numerical Simulation Method
2.1. Research Object
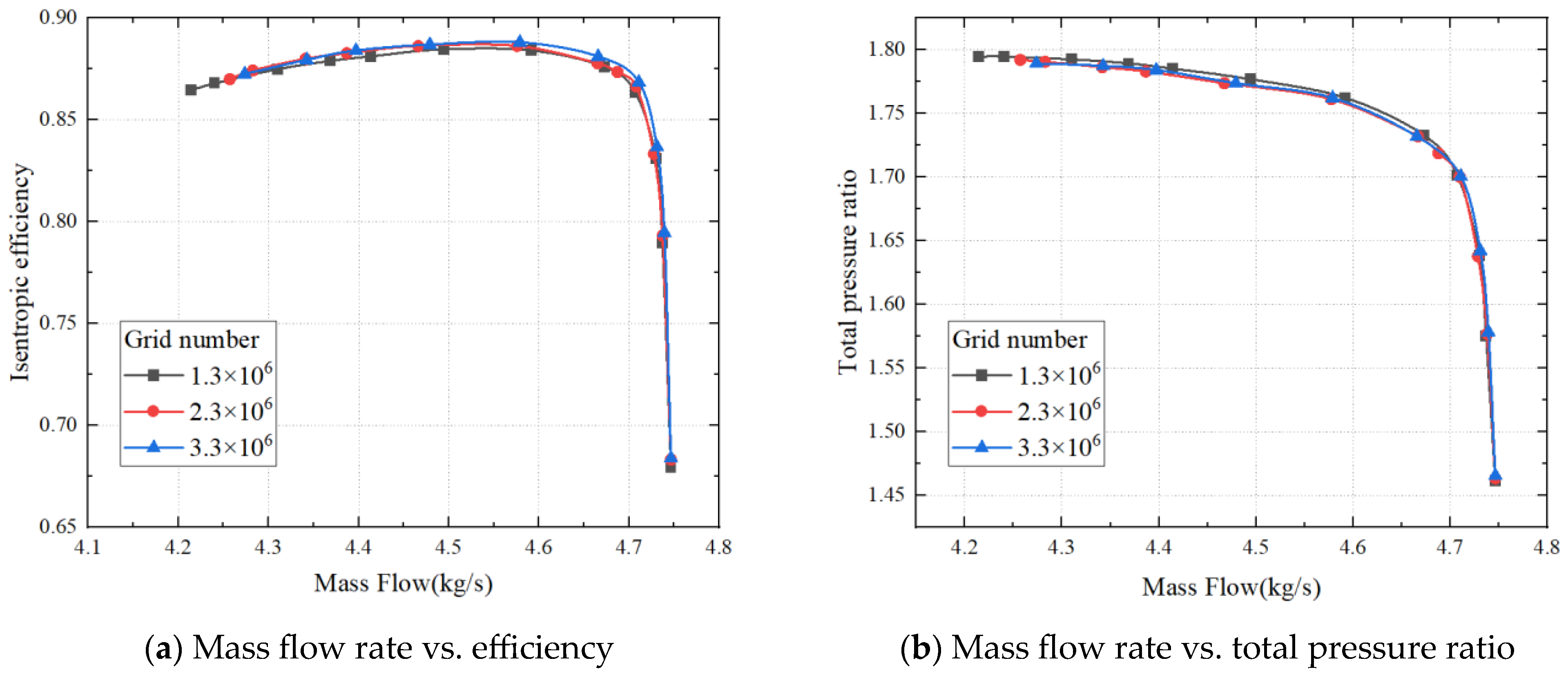
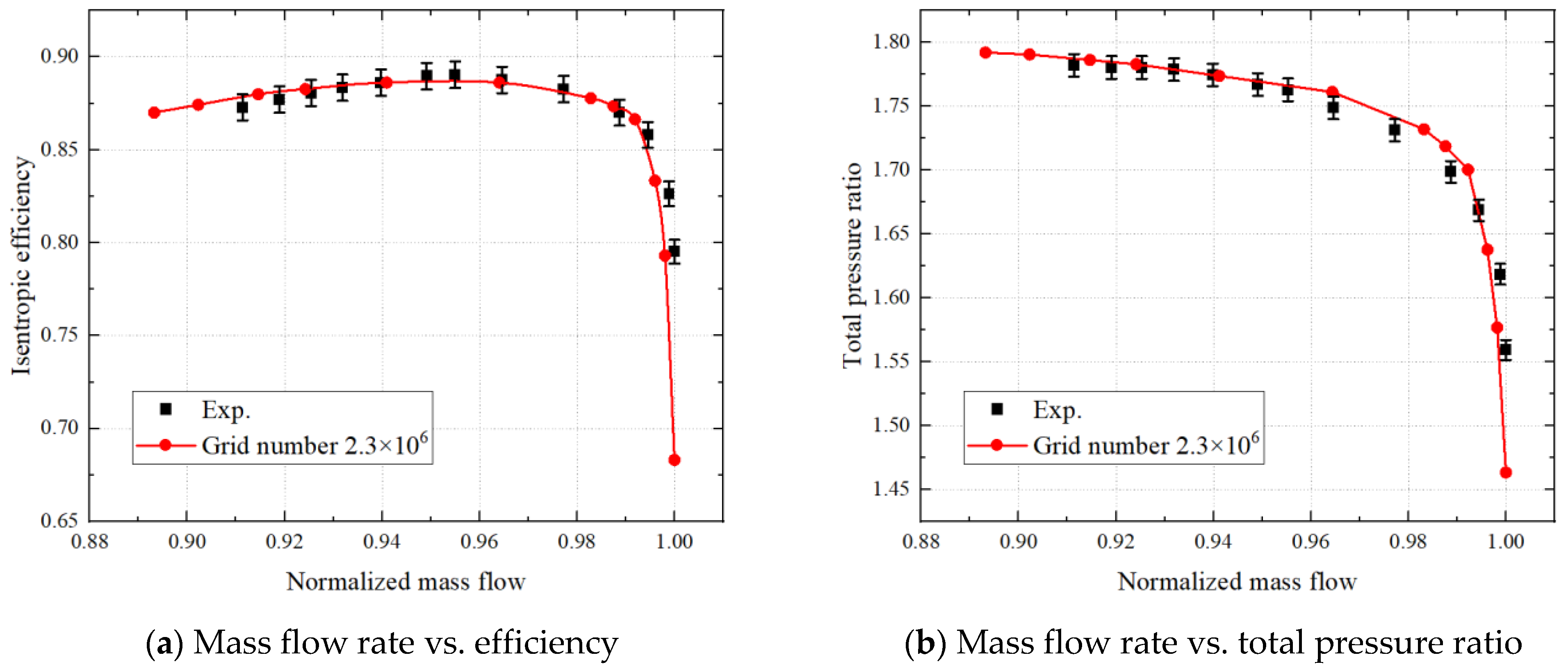
2.2. Numerical Method
3. Optimum Design Method for a High-Load Supersonic Compressor
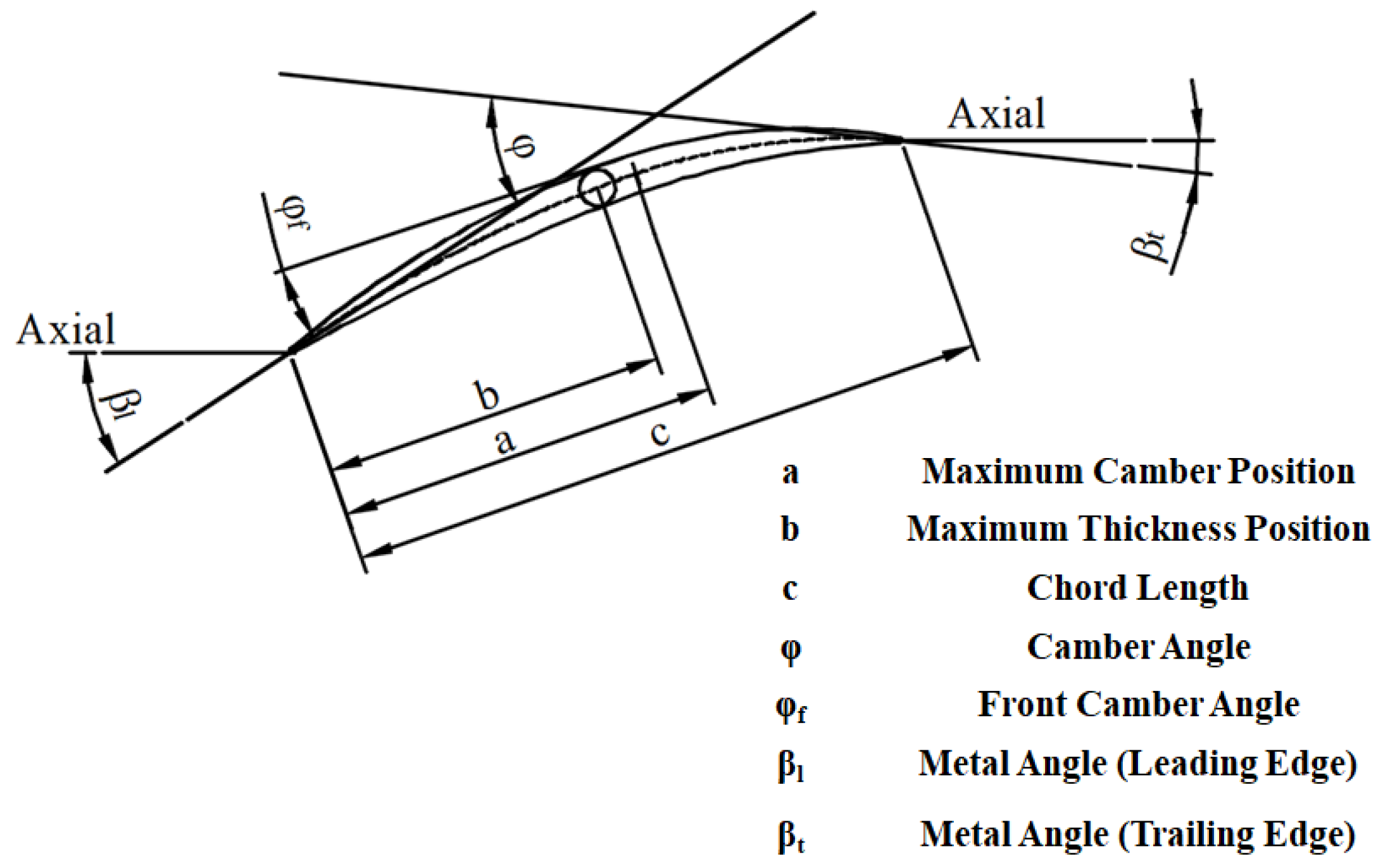
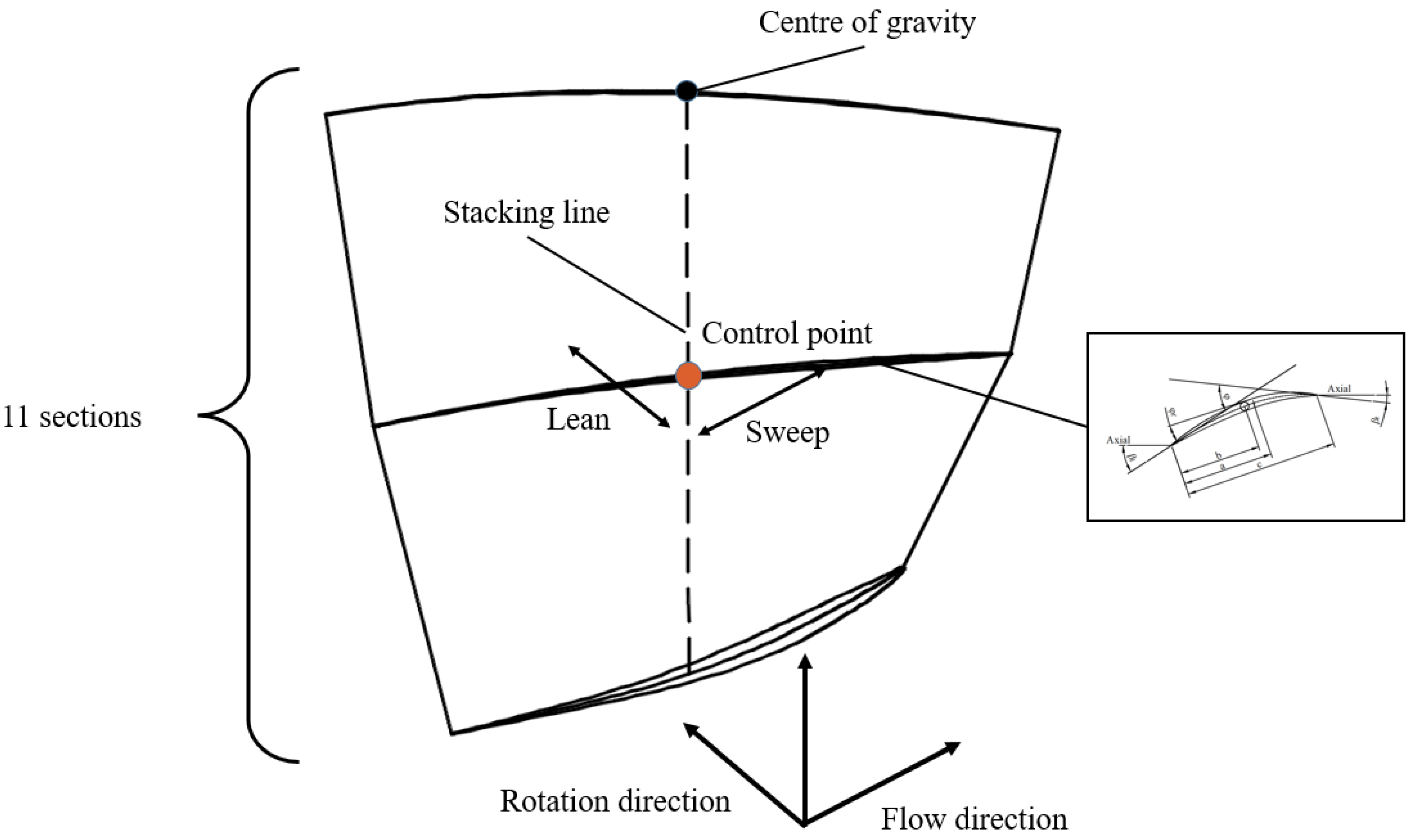
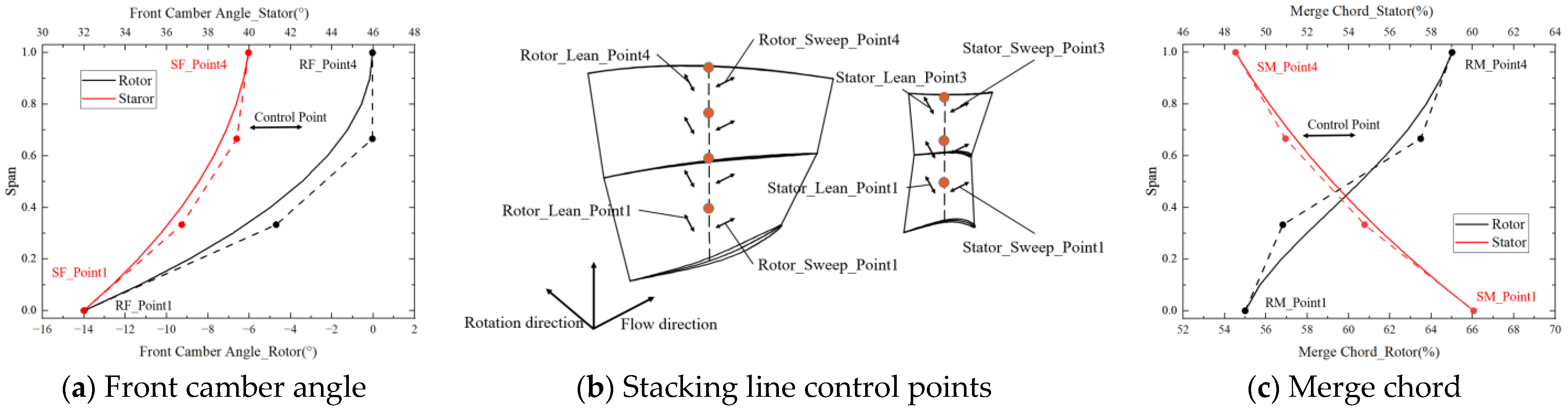
3.1. Parameterization Method
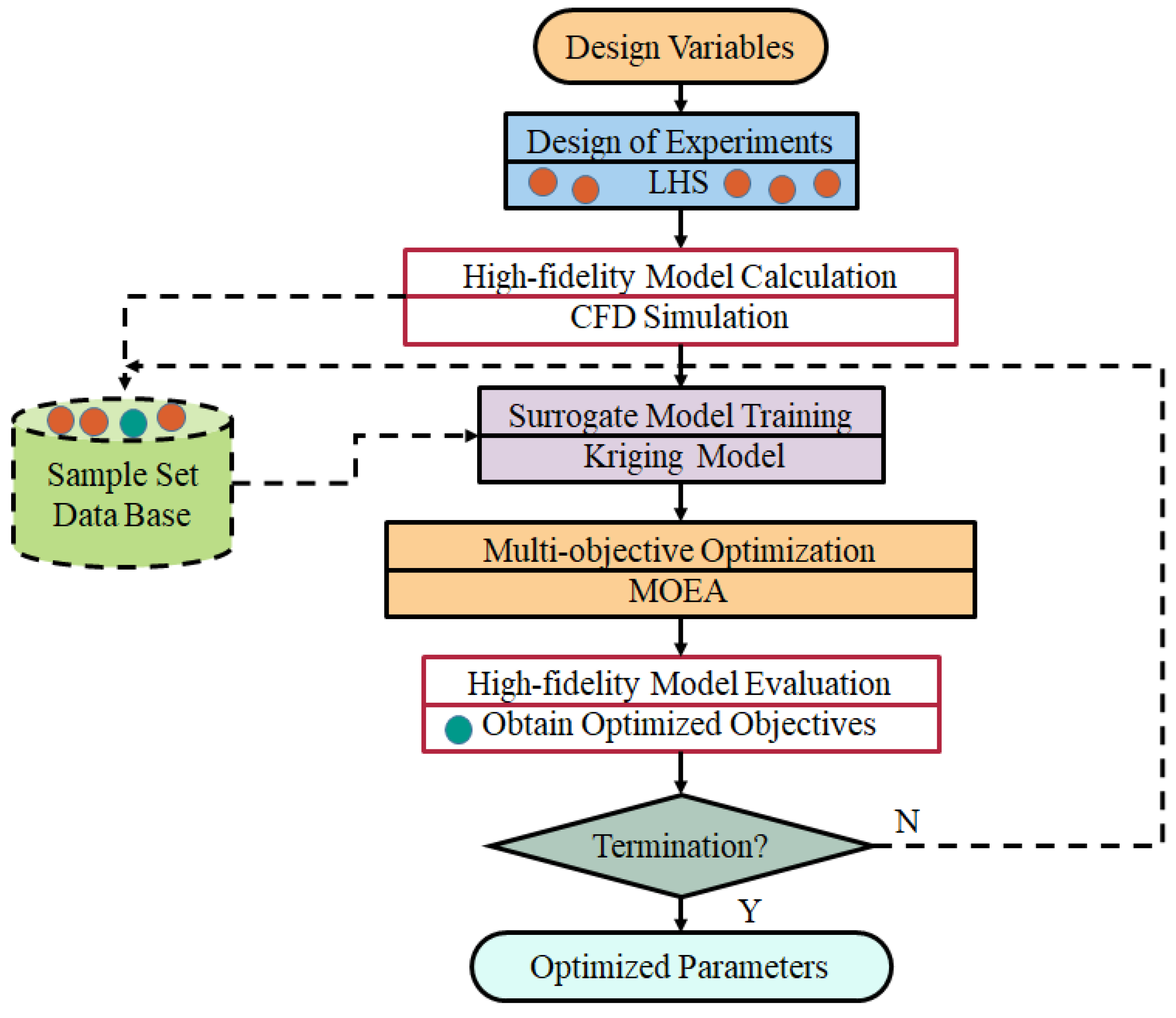
3.2. Numerical Optimization Method
- (1)
- Apply the optimization algorithm to the surrogate model.
- (2)
- After the optimization process, verify whether it is the best solution through accurate model calculation of the optimization results.
- (3)
- Add a new set of samples to the database, including the optimization solutions of the previous generation, to enrich the model and build a better surrogate model. Then, verify the results of the optimization solutions using the high-fidelity numerical method in order to ensure the accuracy of the new surrogate model.
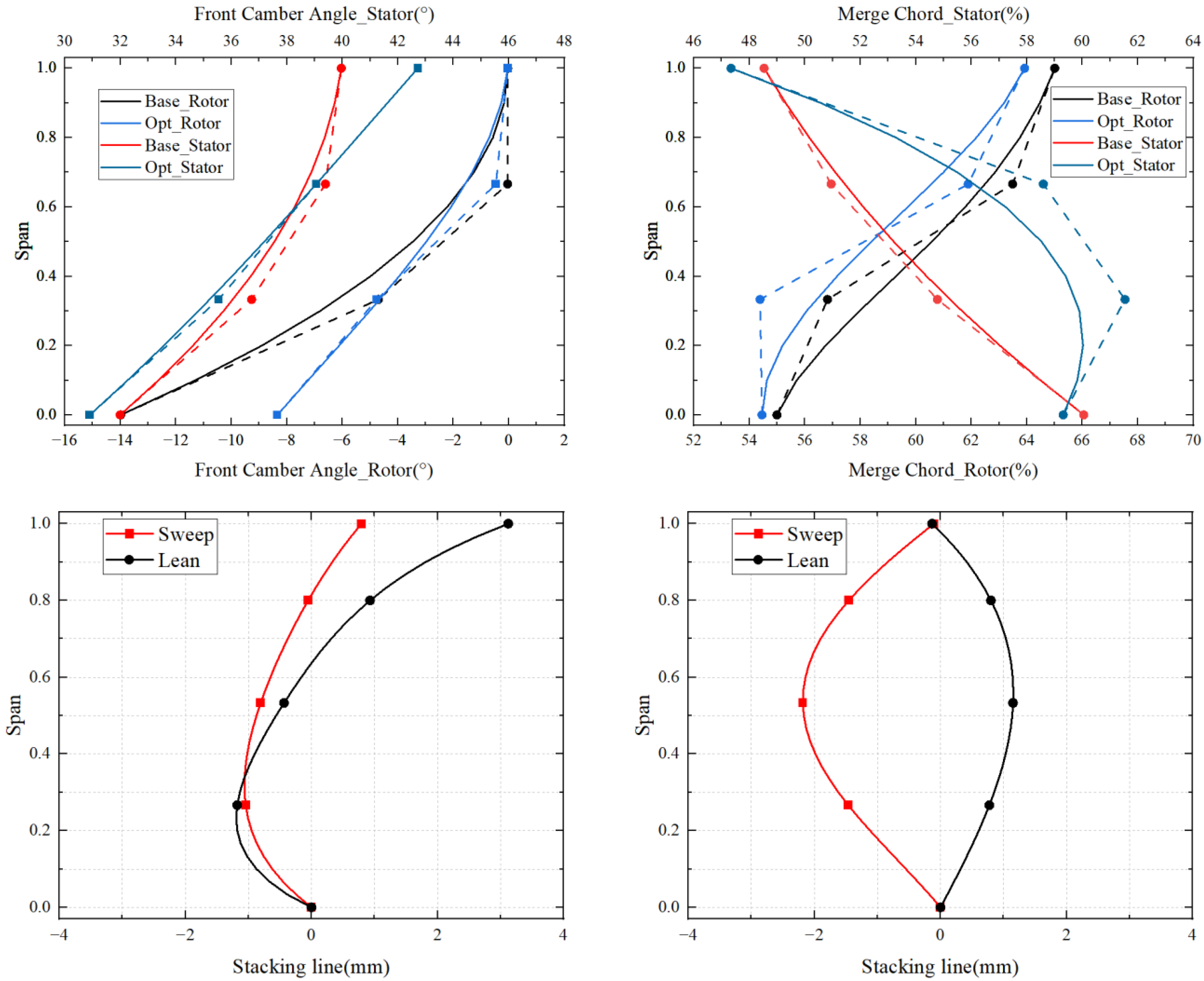
3.3. Optimization Variables
3.4. Optimization Objective Function and Constraints
4. Optimization Results and Analysis
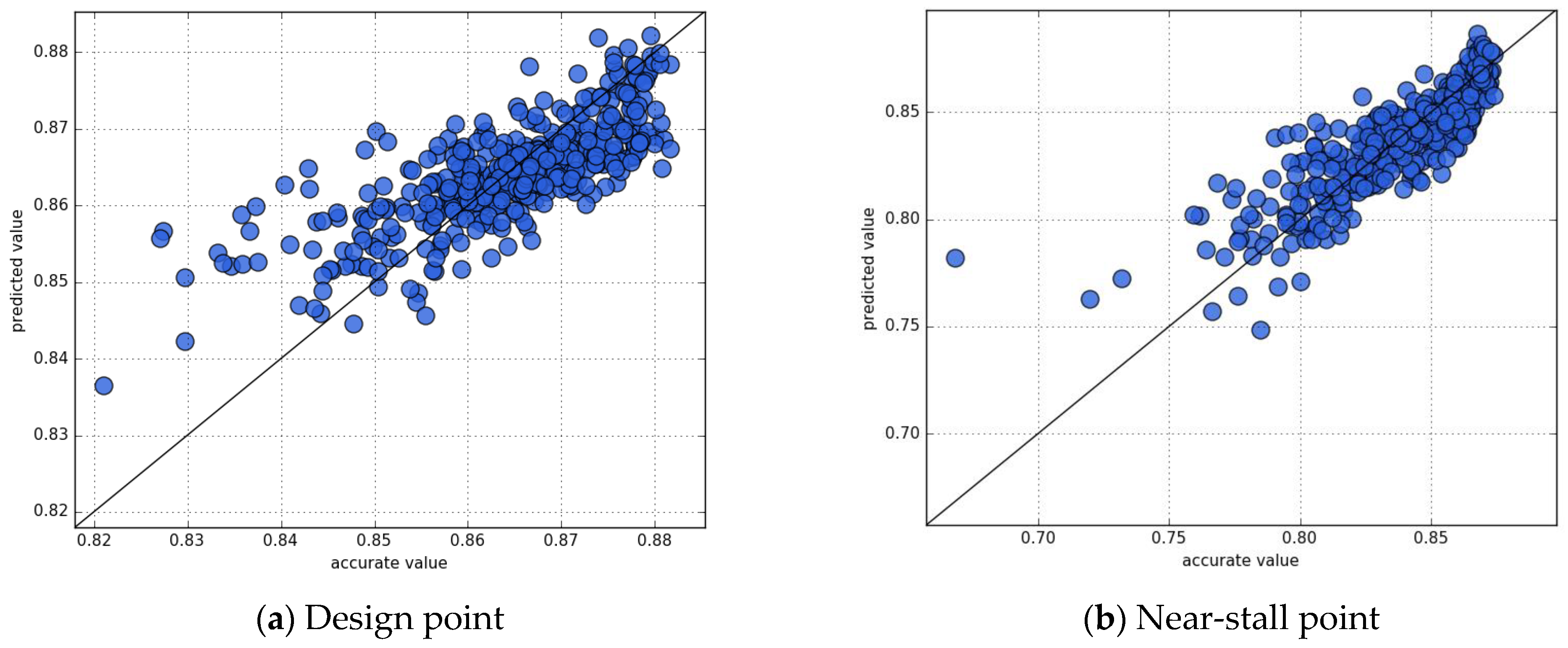
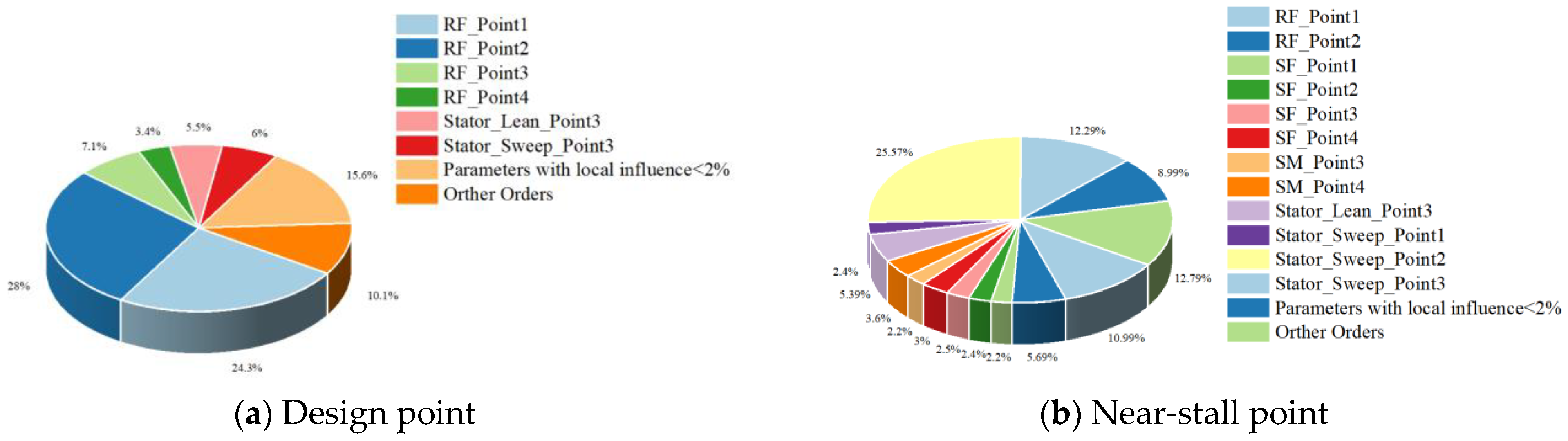
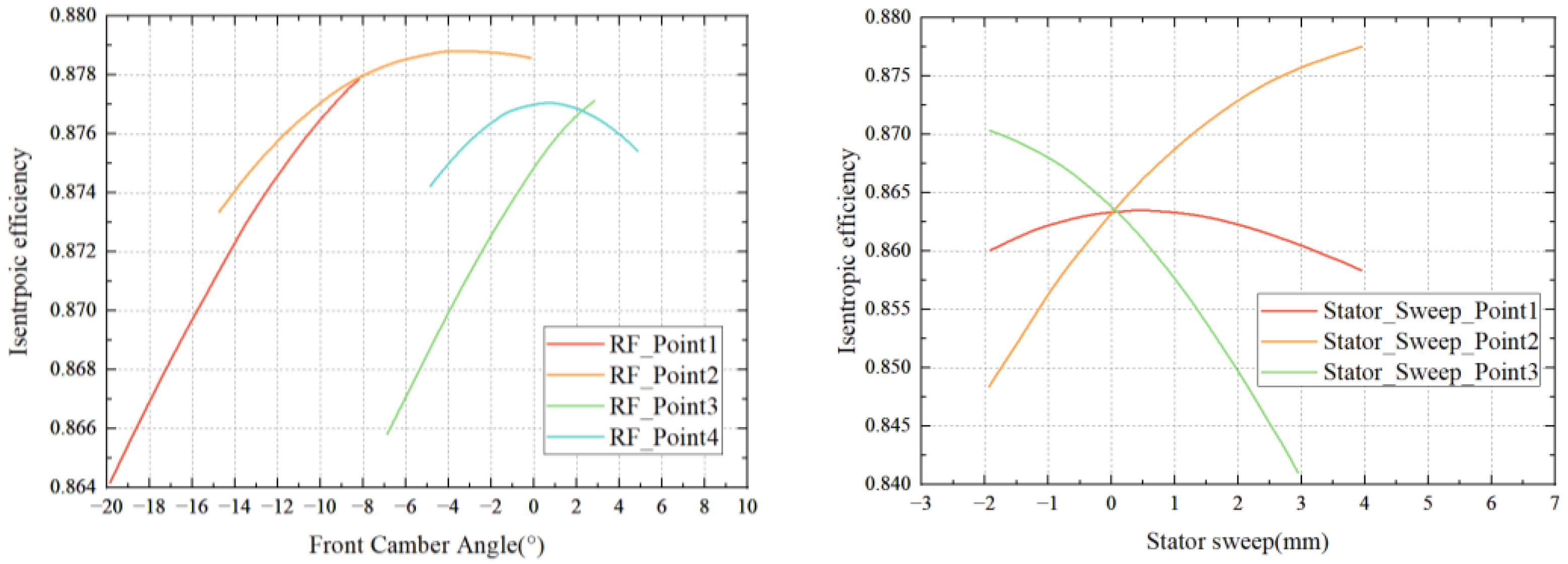
4.1. Analysis of Optimization Algorithm Model Results
4.2. Analysis of Aerodynamic Performance of Compressors
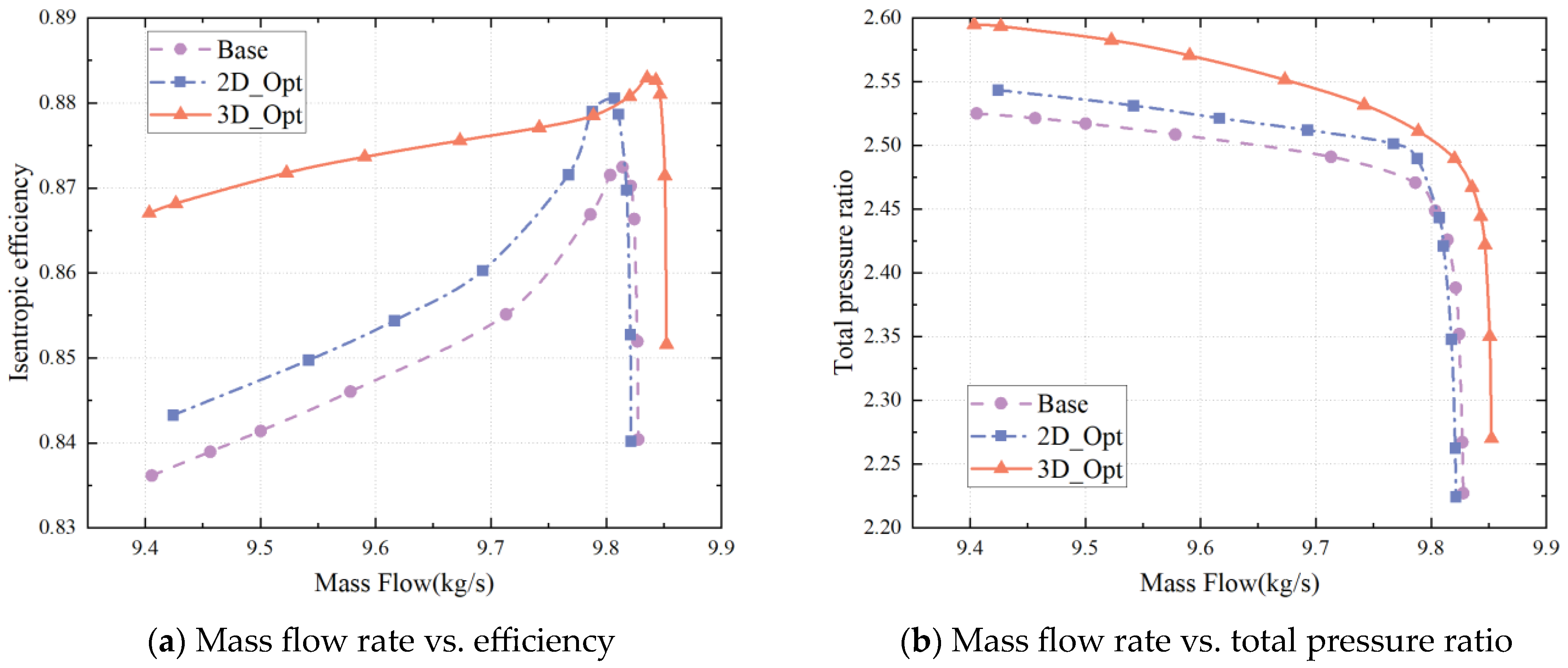
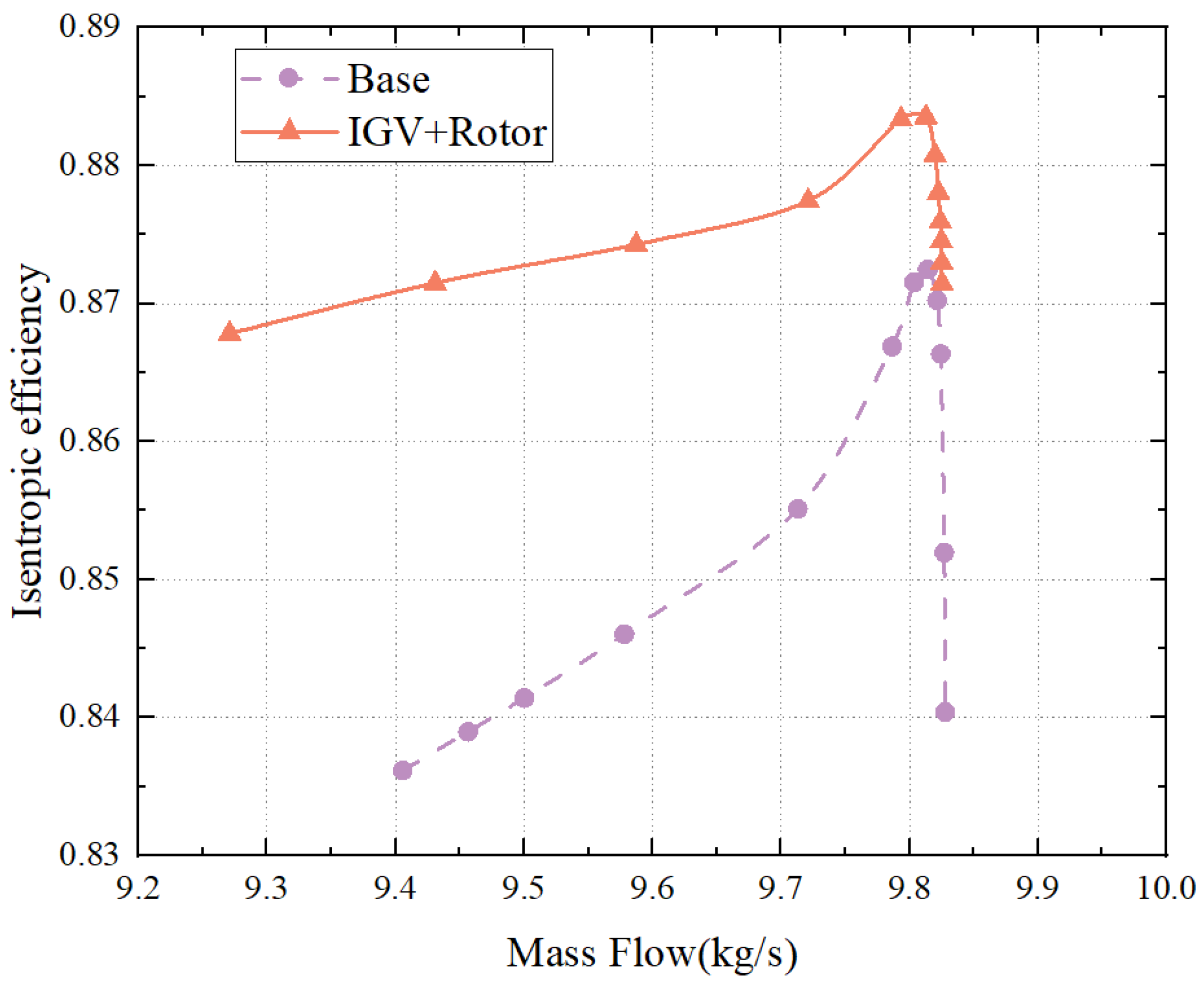
4.2.1. Overall Performance Comparison
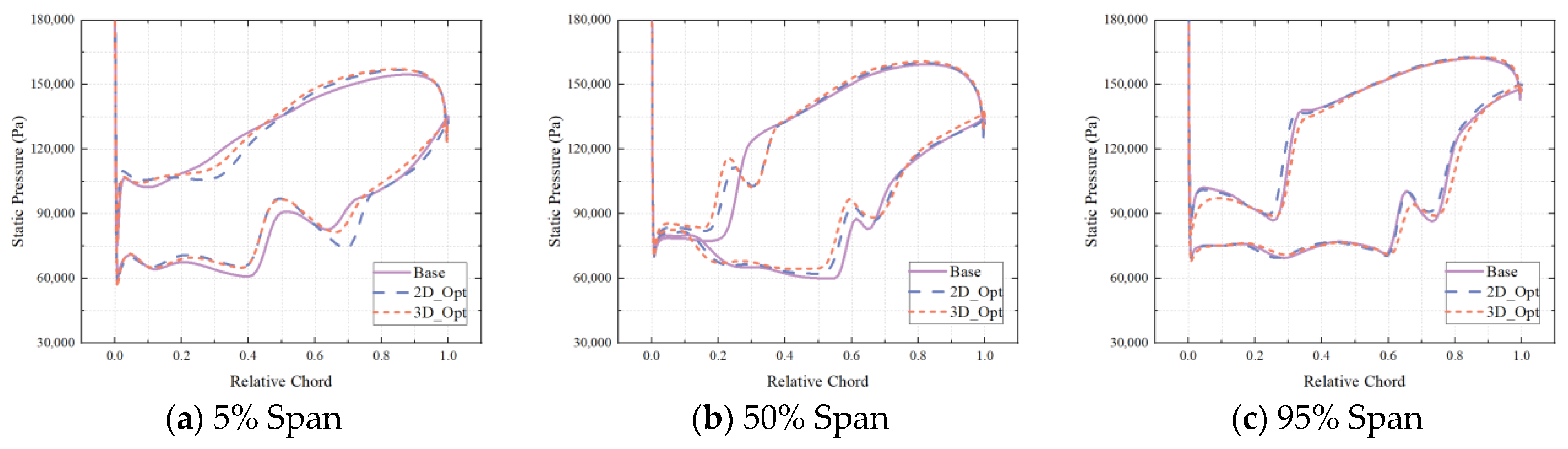
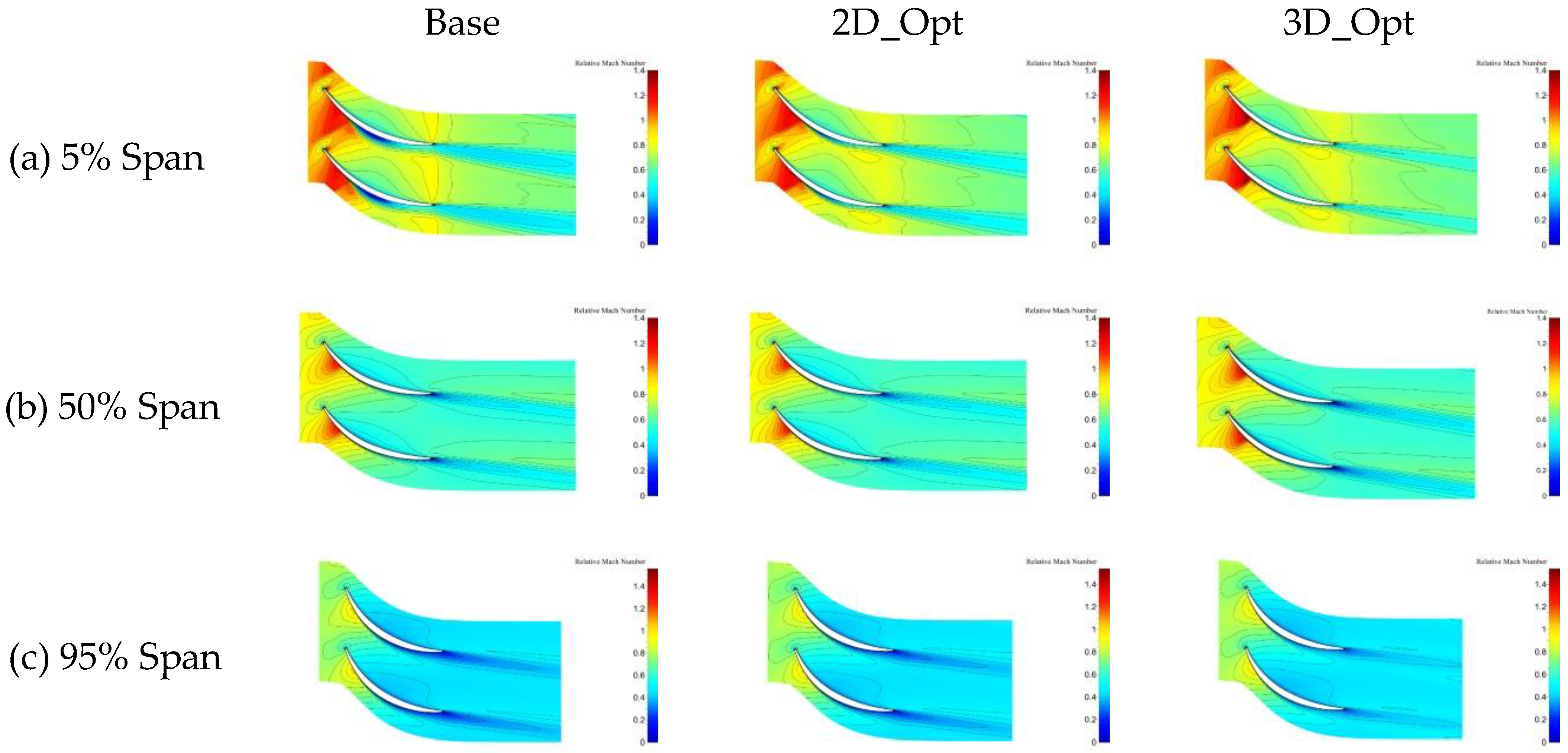
4.2.2. Impact of Optimization on Design Conditions
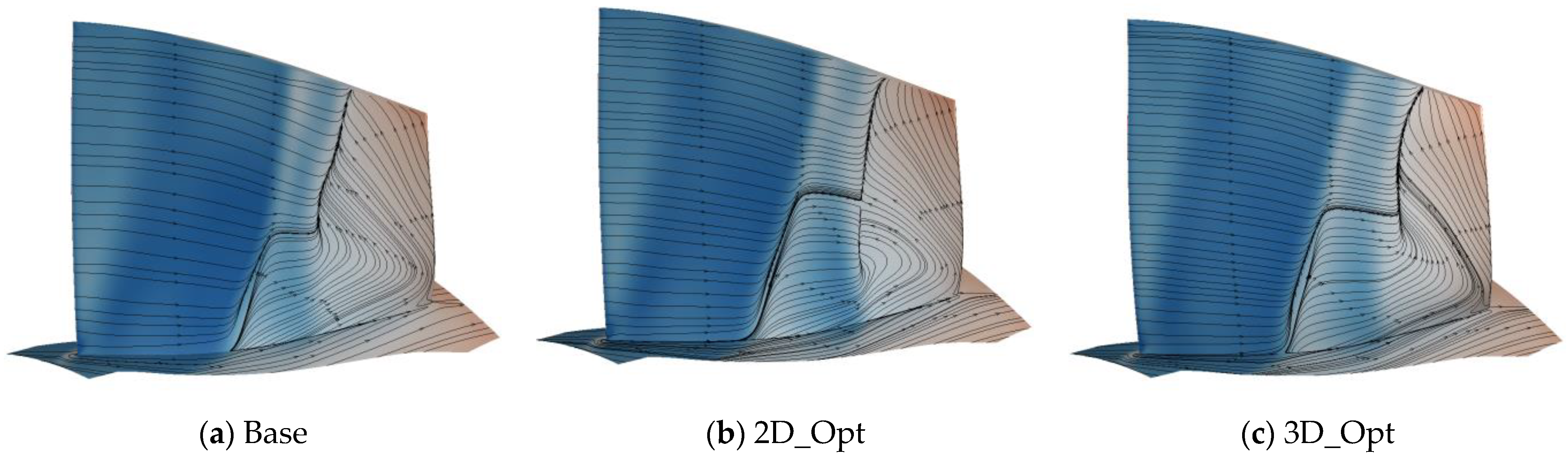
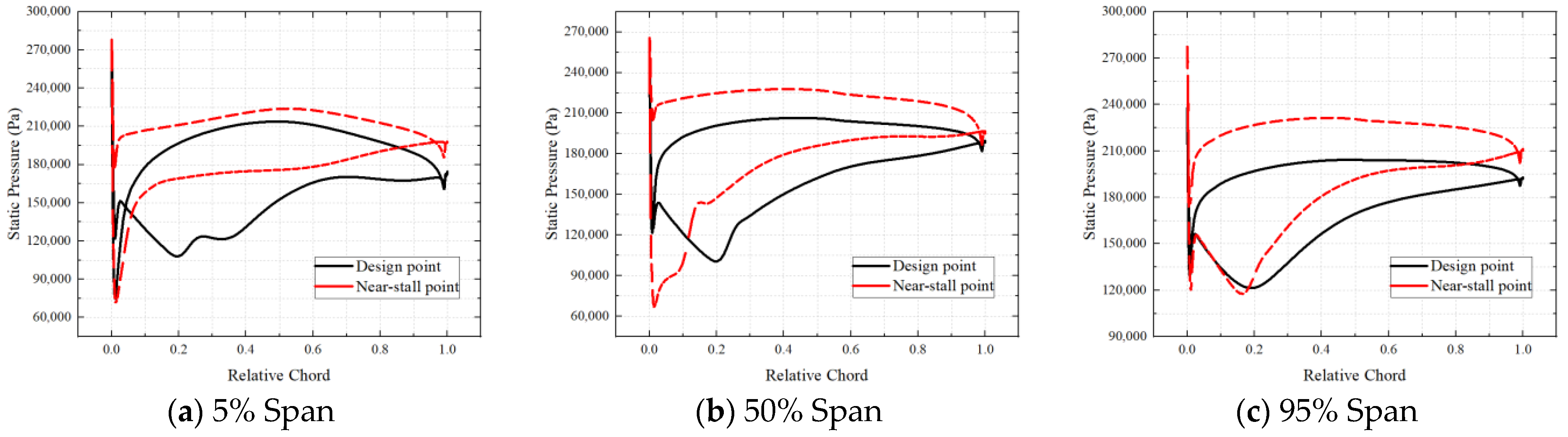
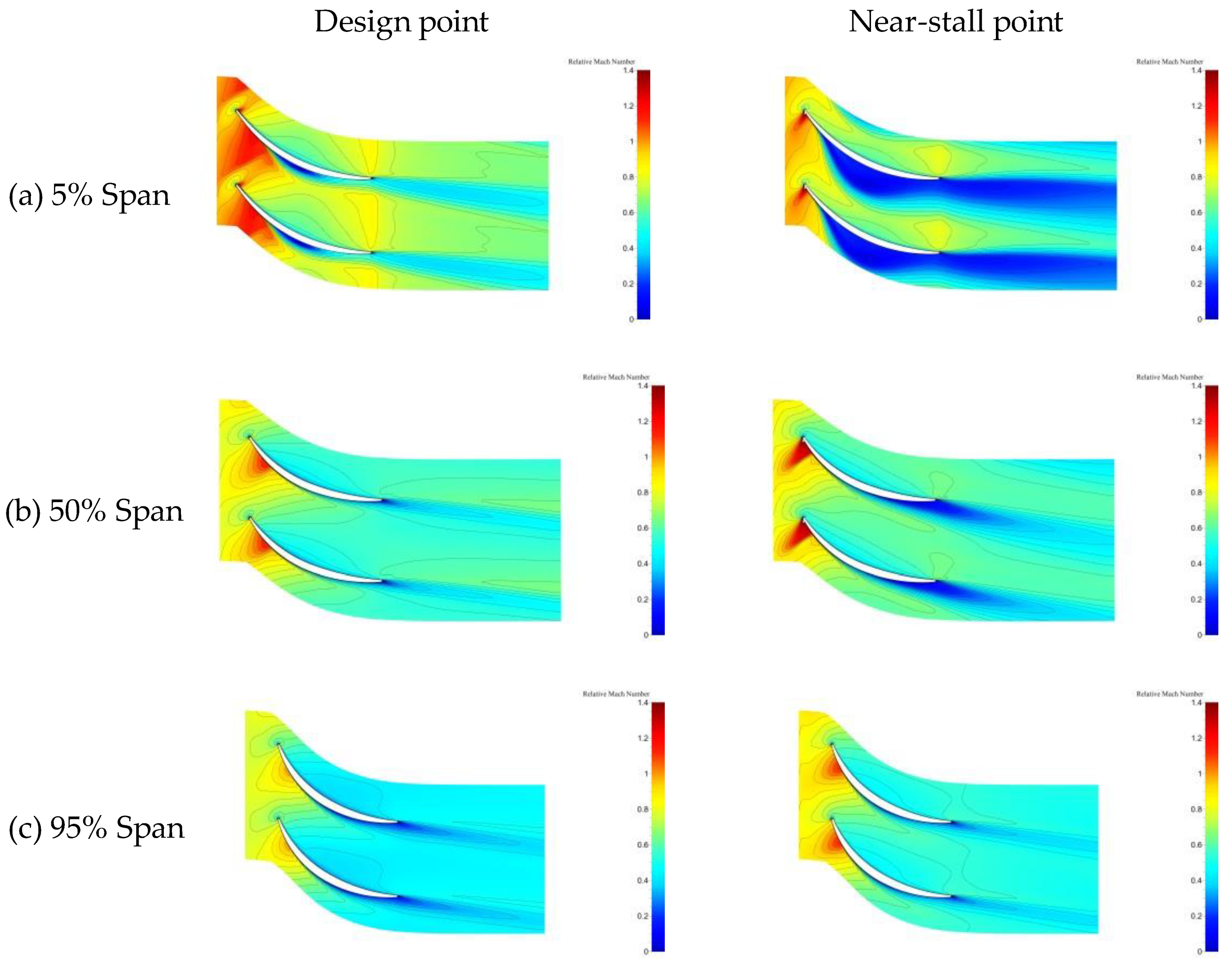
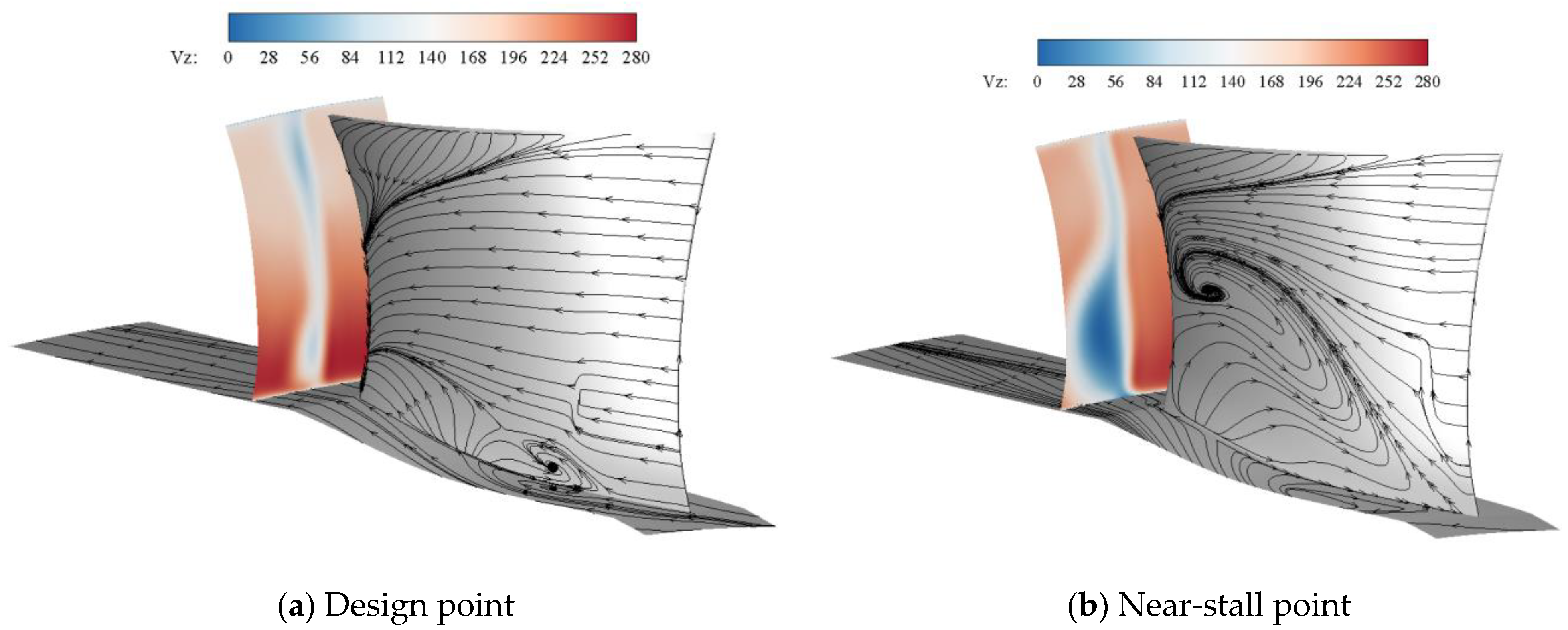
4.2.3. Effect of Optimization on Near-Stall Conditions
5. Conclusions
- The MCA blade was used to identify key design parameters, which were then utilized to create a 2D profile. The blade parameters were regulated throughout the span through the use of a third-order Bessel curve, providing a smooth and continuous shape with minimal optimization variables and the ability to incorporate design knowledge. The optimization process was carried out through a multi-objective approach, using the Kriging model as a surrogate model. As a result, the flow rate at the design point improved by 0.25%, the isentropic efficiency increased by 1.05%, and the stall margin expanded by 3.5%, leading to the significantly improved performance of the compressor.
- The results of the sensitivity analysis, carried out based on the optimized parameters derived from the trained Kriging model, indicate that the compressor stator optimally operates under the design conditions, where the variations in the rotor blade profile have a greater impact on the performance of the compressor in this stage. Under near-stall conditions, significant changes in the compressor stator sweep have a pronounced effect on the compressor’s performance in this stage.
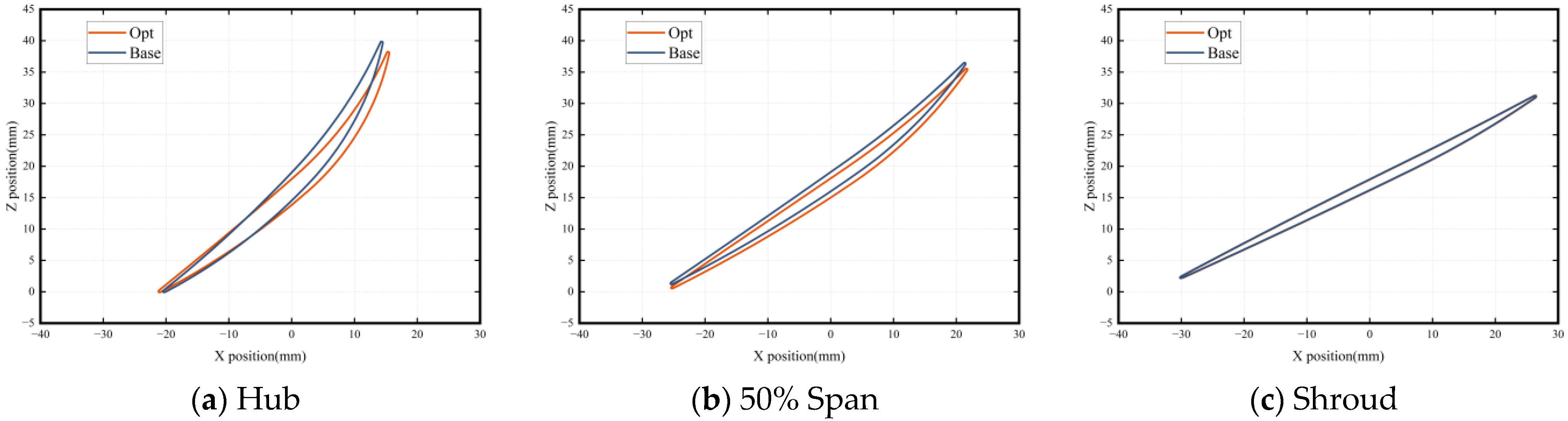
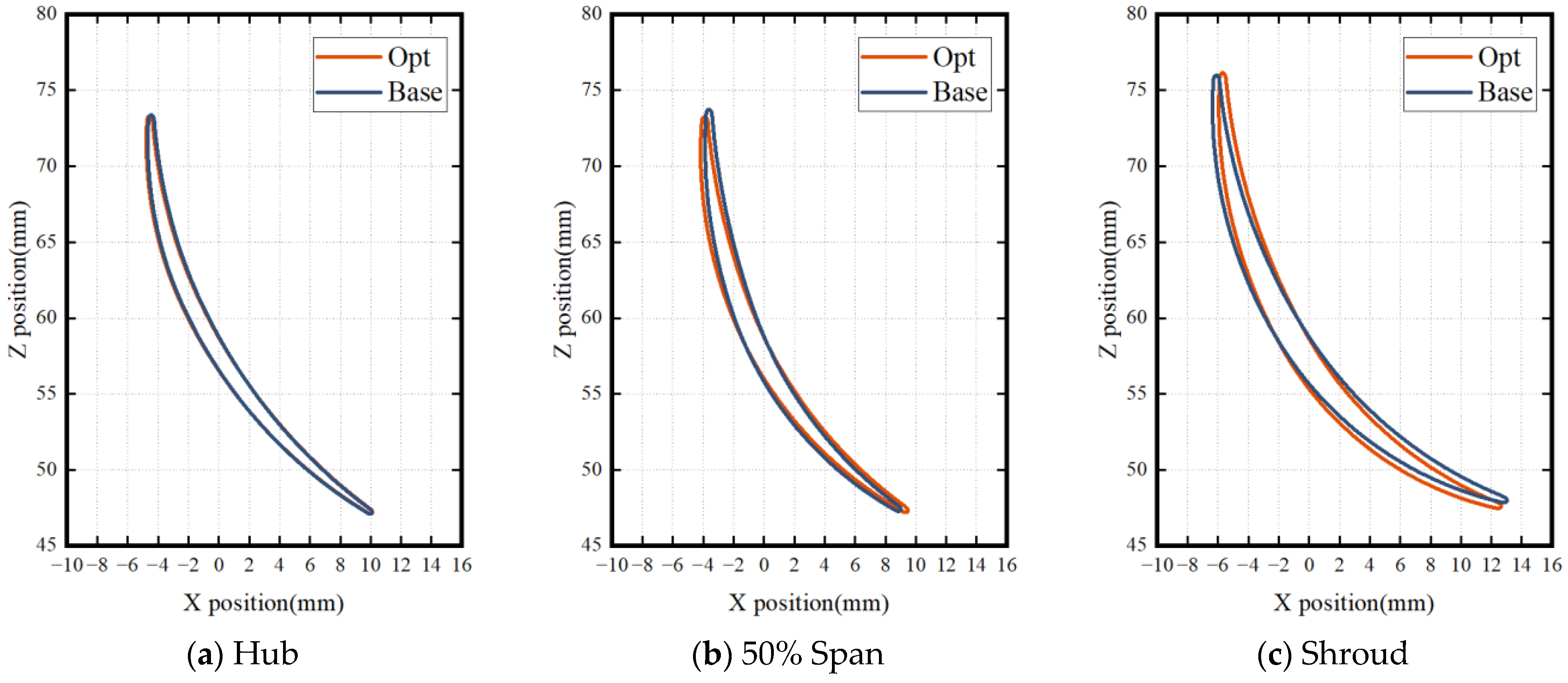
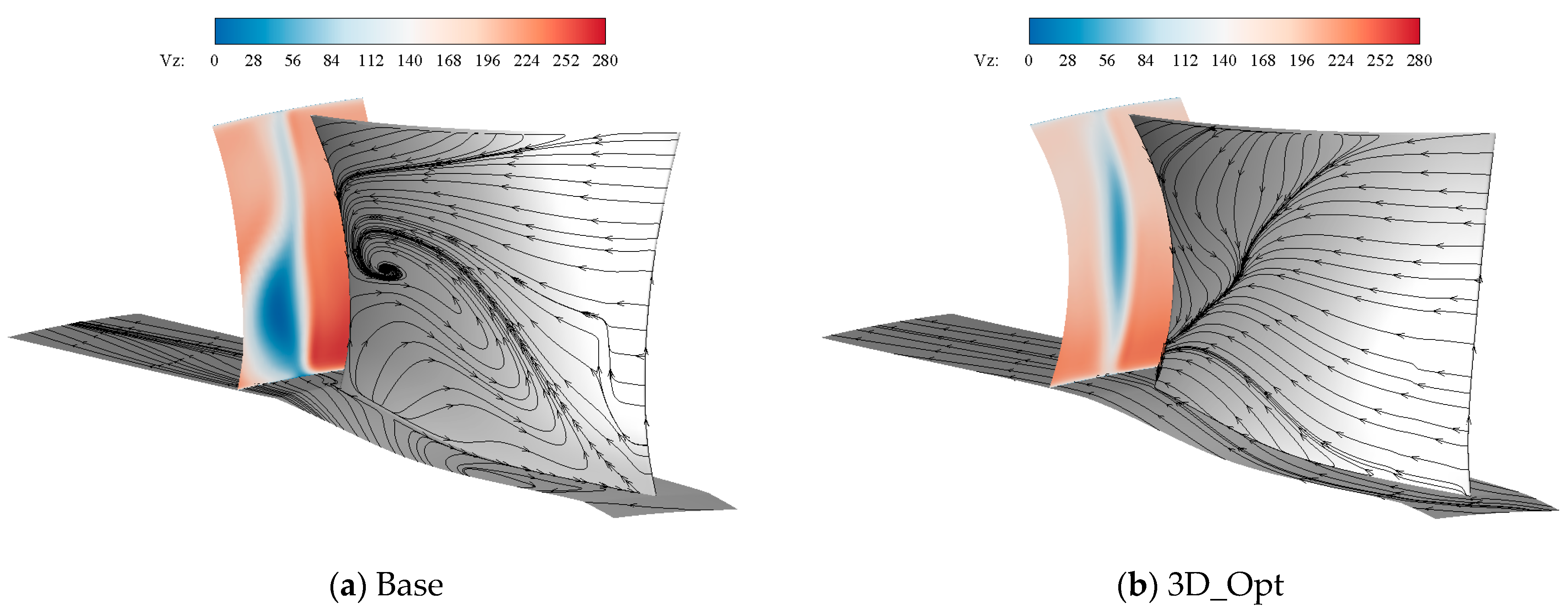
- The optimization of the rotors’ 2D profile changes the shock structure within the supersonic compressor channel, decreases the boundary layer separation on the rotor surface, and reduces the strength of radial flow migration. Therefore, the performance of the supersonic rotor tip is improved. By optimizing the stacking line of the rotors, the flow rate of the rotor is increased, the blocking flow of the compressor is improved, and the position of the shock in the blade channel is shifted backward. However, there is a slight increase in radial flow migration on the rotor surface as a result of the stacking line optimization.
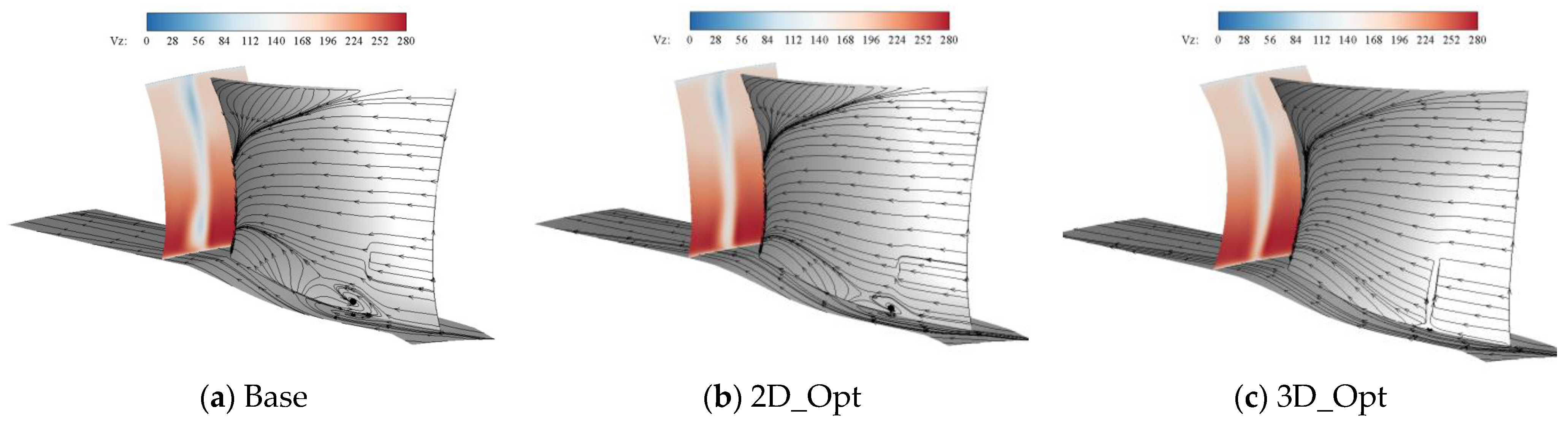
- The concentrated shedding vortex at the blade roots is weakened, but not eliminated, by the optimization of the stators’ 2D profile. With the increase in the outlet static pressure, the concentrated shedding vortex at the prototype stator roots gradually develops to produce an angular stall with a strong three-dimensional spatial flow, which results in the divergence of the calculation results of the prototype supersonic compressor. The stacking line optimization enables low-energy fluid to converge in the middle of the blade, resulting in a more uniform distribution of the low-speed zone along the span of the blade, eliminating the concentrated shedding vortex at the blade root caused by the shock and greatly improving the comprehensive margin of the compressor.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, M.Z. Development of fan/compressor techniques and suggestions on further researches. J. Aeros. Power 2002, 17, 1–15. [Google Scholar]
- Weise, A. A Supersonic Axial Compressor. Report, No. 171; Lilienthal Society, 1937; Available online: https://asmedigitalcollection.asme.org/gasturbinespower/article-abstract/83/3/258/428100/A-Review-of-Supersonic-Compressor-Development?redirectedFrom=fulltext (accessed on 10 January 2023).
- Kantrowitz, A.; Donaldson, C. Preliminary Investigation of Supersonic Diffusers; NACA-ACR-L5D20; NACA: Washington, DC, USA, 1945.
- Kantrowitz, A. The Supersonic Axial-Flow Compressor; NACA-Report 974, NACA-ACR-L6D02; NACA: Washington, DC, USA, 1946.
- Wennerstrom, A.J.; Hearsey, R.M. The Design of an Axial Compressor Stage for a Total Pressure Ratio of 3 to 1; Aerospace Research Labs Wright-Patterson AFB: Fairborn, OH, USA, 1971.
- Wennerstrom, A.J.; Buzzell, W.A.; Derose, R.D. Test of a Supersonic Axial Compressor Stage Incorporating Splitter Vanes in the Rotor; ARL TR 75-0165; Aerospace Research Labs Wright-Patterson AFB: Fairborn, OH, USA, 1975. [CrossRef]
- Simon, H. A Contribution to the Theoretical and Experimental Examination of the Flow through Plane Supersonic Deceleration Cascades and Supersonic Compressor Rotors. ASME J. Eng. Power 1973, 95, 233–243. [Google Scholar] [CrossRef]
- Wennerstrom, A.J. Some Experiments with a Supersonic Axial Compressor Stage. ASME J. Turbomach. 1987, 109, 388–397. [Google Scholar] [CrossRef]
- Küsters, K.; Schreiber, A. Compressor cascade flow with strong shock-wave/boundary-layer interaction. AIAA J. 1998, 36, 2072–2078. [Google Scholar] [CrossRef]
- Kempf, S.G. Numerical Study of The Stability of Embedded Supersonic Compressor Stages. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2003. [Google Scholar]
- Benini, E. Three-Dimensional Multi-Objective Design Optimization of a Transonic Compressor Rotor. J. Propuls. Power 2003, 20, 559–565. [Google Scholar] [CrossRef]
- Lian, Y.; Liou, M.-S. Multi-Objective Optimization of Transonic Compressor Blade Using Evolutionary Algorithm. J. Propuls. Power 2005, 21, 979–987. [Google Scholar] [CrossRef] [Green Version]
- Pan, R.; Song, Z.; Liu, B. Optimization Design and Analysis of Supersonic Tandem Rotor Blades. Energies 2020, 13, 3228. [Google Scholar] [CrossRef]
- Venturelli, G.; Benini, E. Kriging-assisted design optimization of S-shape supersonic compressor cascades. Aerosp. Sci. Technol. 2016, 58, 275–297. [Google Scholar] [CrossRef]
- Cui, C.; Zhou, Z.; Liu, E. Aerodynamic Optimization Design of a Supersonic Compressor Rotor with High Pressure Ratio. Int. J. Aerosp. Eng. 2021, 2021, 1–24. [Google Scholar] [CrossRef]
- Liu, S.; Geng, S.; Li, X.; Jin, Y.; Zhang, H. Optimization Design of Aspect Ratio and Solidity of a Heavy-Duty Gas Turbine Transonic Compressor Rotor. Machines 2023, 11, 82. [Google Scholar] [CrossRef]
- Weilin Yi, Hongliang Cheng, Investigation on the Optimal Design and Flow Mechanism of High Pressure Ratio Impeller with Machine Learning Method. Int. J. Aerosp. Eng. 2020, 2020, 8855314. [CrossRef]
- Ma, C.; Yang, Z.; Jiao, K.; Liu, Z.; Du, Q. Multi-objective optimization of the centrifugal compressor impeller in 130 kW PEMFC through coupling SVM with NSGA -III algorithms. Int. J. Green Energy 2021, 18, 1383–1395. [Google Scholar] [CrossRef]
- Wang, X.; Hirsch, C.; Kang, S.; Lacor, C. Multi-objective optimization of turbomachinery using improved NSGA-II and approximation model. Comput. Methods Appl. Mech. Eng. 2010, 200, 883–895. [Google Scholar] [CrossRef]
- Yang, X. Application of Flow through Model in Combined Compressor Design and Analysis. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2016. [Google Scholar]
- Shao, F.; Yang, J.; Liu, Z.; Hu, J. Improved streamline curvature throughflow method and its application in a bypass compression system design. J. Aerosp. Power 2008, 23, 1072–1076. [Google Scholar]
- Koch, C.C.; Smith, L.H., Jr. Loss Sources and Magnitudes in Axial-Flow Compressors. ASME J. Eng. Power 1976, 98, 411–424. [Google Scholar] [CrossRef]
- Roberts, W.B.; Serovy, G.K.; Sandercock, D.M. Design Point Variation of Three-Dimensional Loss and Deviation for Axial Compressor Middle Stages. ASME J. Turbomach. 1988, 110, 426–433. [Google Scholar] [CrossRef]
- Gallimore, S.J. Spanwise Mixing in Multistage Axial Flow Compressors: Part II—Throughflow Calculations Including Mixing. ASME J. Turbomach. 1986, 108, 10–16. [Google Scholar] [CrossRef]
- Anderson, M.R.; Bonhaus, D.L. A Comprehensive Through-Flow Solver Method for Modern Turbomachinery Design. In Proceedings of the ASME Turbo Expo 2015, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Gu, F.; Anderson, M.R. CFD-Based Throughflow Solver in a Turbomachinery Design System. In Proceedings of the ASME Turbo Expo 2007, Montreal, QC, Canada, 14–17 May 2007. [Google Scholar]
- Huang, S.; Cheng, J.; Yang, C.; Zhou, C.; Zhao, S.; Lu, X. Optimization design of a 2.5 stage highly loaded axial compressor with a Bezier surface modeling method. Appl. Sci. 2020, 10, 3860. [Google Scholar] [CrossRef]
- Lee, C.; Koo, D.; Zingg, D.W. Comparison of B-spline surface and free-form deformation geometry control for aerodynamic optimization. AIAA J. 2017, 55, 228–240. [Google Scholar] [CrossRef] [Green Version]
- Kang, S.; Hirsch, C. Three Dimensional Flow in a Linear Compressor Cascade at Design Conditions. In Proceedings of the ASME 1991 International Gas Turbine and Aeroengine Congress and Exposition, American Society of Mechanical Engineers, Orlando, FL, USA, 3–6 June 1991. [Google Scholar]
- Zhang, H.; Wang, S.; Wang, Z. Variation of Vortex Structure in a Compressor Cascade at Different Incidences. J. Propuls. Power 2012, 23, 221–226. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Loading factor | 0.35 |
| Design speed/(rpm) | 25,000 |
| Design mass flow/(kg/s) | 9.8 |
| Design total pressure ratio | 2.35 |
| Design isentropic efficiency | 0.87 |
| Blade number | 65, 34, 67 |
| Diameter of inlet casing (mm) | 190 |
| Inlet hub tip ratio | 0.74 |
| Rotor tip clearance (mm) | 0.2 |
| Rotor tip speed (m/s) | 497 |
| Rotor average aspect ratio | 0.74 |
| Rotor average solidity | 1.88 |
| Stator average aspect ratio | 0.95 |
| Stator average solidity | 1.86 |
| Rotor average diffusion factor | 0.54 |
| Stator average diffusion factor | 0.48 |
| Parameters | Value |
|---|---|
| RF_Point1(deg) | −13.96 [−20, −8] |
| RF_Point2(deg) | −4.7 [−15, 0] |
| RF_Point3(deg) | −0.05 [−7, 3] |
| RF_Point4(deg) | −0.04 [−5, 5] |
| SF_Point1(deg) | 32 [25, 40] |
| SF_Point2(deg) | 36.74 [30, 40] |
| SF_Point3(deg) | 39.38 [33, 45] |
| SF_Point4(deg) | 39.97 [35, 50] |
| RM_Point1(%) | 55 [50, 60] |
| RM_Point2(%) | 56.83 [50, 63] |
| RM_Point3(%) | 63.5 [58, 70] |
| RM_Point4(%) | 65 [60, 75] |
| SM_Point1(%) | 60.05 [55, 70] |
| SM_Point2(%) | 54.78 [50, 65] |
| SM_Point3(%) | 50.94 [45, 60] |
| SM_Point4(%) | 48.53 [40, 55] |
| Rotor_Lean_Point1(m) | 0 [−0.005, 0.001] |
| Rotor_Lean_Point2(m) | 0 [−0.002, 0.002] |
| Rotor_Lean_Point3(m) | 0 [−0.002, 0.003] |
| Rotor_Lean_Point4(m) | 0 [−0.001, 0.003] |
| Rotor_Sweep_Point1(m) | 0 [−0.002, 0.002] |
| Rotor_Sweep_Point2(m) | 0 [−0.002, 0.002] |
| Rotor_Sweep_Point3(m) | 0 [−0.002, 0.002] |
| Rotor_Sweep_Point4(m) | 0 [−0.002, 0.002] |
| Stator_Lean_Point1(m) | 0 [−0.005, 0.001] |
| Stator_Lean_Point2(m) | 0 [−0.004, 0.001] |
| Stator_Lean_Point3(m) | 0 [−0.002, 0.002] |
| Stator_Sweep_Point1(m) | 0 [−0.002, 0.004] |
| Stator_Sweep_Point2(m) | 0 [−0.002, 0.004] |
| Stator_Sweep_Point3(m) | 0 [−0.002, 0.003] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Zhao, S.; Zhou, C.; Wu, Y.; Yuan, H.; Lu, X. Optimal Design and Analysis of a High-Load Supersonic Compressor Based on a Surrogate Model. Aerospace 2023, 10, 364. https://doi.org/10.3390/aerospace10040364
Zhou S, Zhao S, Zhou C, Wu Y, Yuan H, Lu X. Optimal Design and Analysis of a High-Load Supersonic Compressor Based on a Surrogate Model. Aerospace. 2023; 10(4):364. https://doi.org/10.3390/aerospace10040364
Chicago/Turabian StyleZhou, Shiji, Shengfeng Zhao, Chuangxin Zhou, Yunfeng Wu, Hang Yuan, and Xingen Lu. 2023. "Optimal Design and Analysis of a High-Load Supersonic Compressor Based on a Surrogate Model" Aerospace 10, no. 4: 364. https://doi.org/10.3390/aerospace10040364
APA StyleZhou, S., Zhao, S., Zhou, C., Wu, Y., Yuan, H., & Lu, X. (2023). Optimal Design and Analysis of a High-Load Supersonic Compressor Based on a Surrogate Model. Aerospace, 10(4), 364. https://doi.org/10.3390/aerospace10040364






