Structural Dynamic Characterization of a Modular Morphing Wing Exploiting Finite Elements and Taguchi Methodology

Abstract

Detrimental environmental impacts due to the increasing demands of the aviation industry have gained tremendous global attention. With a potential fuel saving, along with high aerodynamic performance and maneuverability during different phases of a flight, adaptable wing design has become a viable alternative to its fixed-shape counterpart. A morphing wing design embraces, and can respond accordingly to, most of the flight condition variations effectively and efficiently. Despite these prospects, morphing wing design comes with some challenges due to its inherent complexity caused by an increased number of degrees of freedom. With the availability of various morphing parameters, the vibration signature of a morphing wing design plays a vital role in terms of its structural as well as aeroelastic characteristics. In the present paper, the dynamic characteristics of a re-configurable modular morphing wing developed in-house by a research team at Toronto Metropolitan University are investigated. This modular morphing wing, developed based on the idea of a parallel robot, consists of a number of structural elements connected to each other and to the wing ribs through eyebolt joints. Timoshenko bending beam theories, in conjunction with finite element methodology, are exploited. The free vibration of un-morphed (original) and morphed configurations undergoing multiple levels of sweep and spanwise morphing is presented through a design of experiment methodology.

1. Introduction

The ever-increasing demands of the aviation industry have raised serious concerns regarding its adverse CO${}_2$ footprints. Currently, by emanating 628 Mt of CO${}_2$ yearly, the aviation industry contributes approximately $3\%$ to the human-made CO${}_2$ production and around $12\%$ to all transport categories [1]. These enormous emissions of CO${}_2$ and other NOx are deemed to be major contributing factors towards the greenhouse effect as well as climate change [2]. Nonetheless, it is expected that 1300 new airports will be constructed by 2050 to meet the high demand for the aviation industry. Therefore, in order to establish a balance between demand and detrimental environmental impacts, the aviation industry is currently facing a plethora of challenges [1].

As a preemptive measure against the above-stated anticipated environmental threats, the International Air Transport Association (IATA) has outlined a three-step strategy for the aviation industry [3]. Following these guidelines and the technology development roadmap, the aviation industry has turned towards treating the environment as a focal point. According to this technology development roadmap, aircraft airframes and engines are the two main areas that are critical in diminishing fuel consumption as well as emissions [4]. This legal requirement has, therefore, initiated tremendous continuing research towards green and renewable-energy based aircraft design [1,5,6].

Due to its inherent characteristics of reducing fuel consumption, morphing wing technology is regarded as an immensely promising research area in environment-friendly aircraft design. Indeed, with high anticipation of performance, maneuverability, and environmental impact alleviation, tremendous funding has been allocated towards morphing wing technology [7,8,9]. Depending on the mission distance, approximately 3–5% fuel savings can be achieved by employing morphing wing technology [10].

Despite all of the active research and designs, morphing wing technology is still at its rudimentary stages and has not been applied to commercial aircraft globally. Nonetheless, morphing wings offer adaptability in response to the different flight phases and varying gust conditions. In general, morphing wings’ adaptability can be classified into two major categories: in-plane (including sweep, spanwise expansion/contraction, and chord length variation) and out-of-plane (dihedral/gull, twist, and spanwise bending) motions. Hinged devices, including flaps, ailerons, and slats, are generally not considered to be morphing devices. Therefore, the Grumman F14 Tomcat, equipped with variable sweep-wing (colloquially known as a swing wing) and the Bell Boeing V-22 Osprey, with title rotors, do not fall into the strictly defined morphing wing design category.

Morphing wings achieve fuel savings by reducing drag. Spanwise expansion lowers the induced drag (i.e., end vortices), which constitutes approximately $30\%$ of the total drag during cruising of a commercial aircraft. The Boeing 777x is an example of spanwise expansion wing morphing. Sweep morphing is instrumental in decreasing the wave drag. Twist morphing, on the other hand, also contributes to induced drag reduction by tailoring the lift distribution for any flight condition. It is noteworthy that even with a $1\%$ reduction in drag achieved by morphing wings, a substantial yearly savings of USD 140 M can be achieved for the US fleet of wide-body transport aircraft [10].

Besides fuel economy, it has been shown that morphing wings are instrumental in achieving several other advantages, including high lift-to-drag (L/D) ratio, maneuverability, and flight envelope expansion [10,11]. Spanwise expansion/contraction and sweep change the wing aspect ratio, and thereby the corresponding lift distribution and L/D ratio. The enhancement of the L/D ratio, in turn, improves the range and endurance of the aircraft [12]. In addition, the sweep alters the longitudinal and lateral stability of the wing due to the relocation of the aerodynamic and gravity centers [13]. On the other hand, dihedral morphing alters rolling stability. It can provide better agility, reduction in induced drag, and improvement in stall characteristics [10].

Current work does not present a detailed review of various aspects in the application of morphing wings. Interested readers are referred to the extensive review papers by Barbarino et al. [10], Ameduri and Concilio [7], Ajaj et al. [14], and Dhara et al. [15] for the morphing and structural concepts in terms of active systems, challenges, aeroelastic stability, and the evolution of morphing technologies with regards to both fixed and rotary wing aircraft.

Nonetheless, the morphing mechanism imposes a cost on the system with the advantages it brings in. For example, the addition of a mechanism design to incorporate wing morphing causes a weight penalty to the aircraft along with the complexity of the system. Moreover, spanwise morphing can lead to an increase in wing root moment. Sweep morphing, on the other hand, could lower lift coefficient. In spite of improving the wing loading, chord morphing can contribute to increasing the induced drag [16]. Therefore, the morphing wing design needs to be optimized under the conflicting multiple objectives of overall weight, aerodynamic performance, structural properties, and actuation system [11].

Another crucial challenge in the successful application of a morphing wing to the aircraft lies in selecting the best-suited skin adaptable to various morphing configurations. Skin for a morphing wing must have flexibility and load-bearing capabilities. Due to inherent high stiffness and strength, conventional skins made of aluminum or polymer-based materials cannot be deformed with ease during morphing. There has been a tremendous amount of research directed towards finding and designing a suitable skin for the morphing wing. Hajarian et al. [17] have proposed a new flexible sandwich structure composed of elastomer and honeycomb core with glass composites. These authors have experimentally and numerically shown the flexibility and load-bearing abilities of the structure. The flexibility of their structure can be varied during manufacturing as per requirement. Such a structure can be used as skin for the camber morphing of the airfoil. However, authors have not shown the application of this skin to the in-plane and out-of-plane wing morphing. Ahmad et al. [18] have carried out a comparative experimental work on three elastomeric materials, including Latex, Oppo, and Ecoflex. They have characterized these material under the deformation modes of uni-axial, pure shear, bi-axial, and equibiaxial. These are the possible deformation modes of the skin during in-plane or out-of-plane wing morphing. After developing and successfully implementing a four-parameter material model for the numerical studies, these authors conclude that, due to less stiffness, Ecoflex is the best suited skin for in-plane and out-of-plane wing morphing. However, these authors have also mentioned the limitation of their proposed material model to some elastomers.

Most of the existing work on morphing wings is focused on the application and optimization of controllers and smart materials [19,20,21]. However, some aeroelastic analyses have also been performed on a single morphing parameter of the wing [22]. Most of the available published work on morphing wings address morphing under the effect of only a single rather than multiple morphing parameters in combinations, except for the studies by Ramrakhyani et al. [23] and Neal et al. [24].

In their effort to implement multiple morphing parameters simultaneouly Finistauri et al. [25], followed by Moosavian et al. [26], have successfully applied the concept of a parallel robot manipulator to design a morphing wing. Their presented wing design is capable of spanwise, dihedral, and sweep morphing simultaneously in response to the flight condition requirements. Essentially, this designed morphing wing is modular in nature, and the optimum number of modules can be determined on the basis of a mission requirement. This modular characteristic of the wing phases out the cumbersome wing redesign tasks. Nevertheless, their work has remained limited due to the kinematic-based design of the wing, disregarding any structural and/or aerodynamic analysis. In an earlier work by the authors [27], the free vibration analysis of this re-configurable modular morphing wing was presented, and the effects of topology, material properties, and spanwise expansion on the dynamic response of the system were explored. To the best of the authors’ knowledge, the combined effect of spanwise expansion and sweep on the dynamic response of a morphing wing has not been reported in the literature. The changes in modal frequencies caused by these two morphing parameters will lead to alteration in the aeroelastic characteristics of the wing. Therefore, the flutter might be associated with different mode shapes of the system occurring at a different airspeed. This could be beneficial in delaying flutter or devastating by causing flutter inception before the designed flutter speed. Furthermore, the dynamic behavior of individual constituent members defines the overall deformed shape of the wing. Consequently, the overall wing might exhibit a different pressure drag compared to the intended design. This change in drag could offset the possible advantage of fuel savings by the intended morphing wing design. Moreover, information on dynamic behavior of the constituent members will also be helpful in finding any undesired vibration that could lead to nuance to the passenger, and in determining the possible members’ failures. Hence, it is deemed imperative to include the effect of sweep as a logical next step of the authors’ recent work [27].

The objective of the present paper is multifold.

• First, to perform a modal analysis of the re-configurable modular morphing wing by using two modules in un-morphed configuration.
• Then, to investigate the natural frequencies and modes of the morphing wing under the morphing effects of various sweep angles and spanwise expansions.
• Finally, to execute the statistical analysis by using the Taguchi method to determine the most effective morphing factor/parameter governing the natural frequencies of the morphing wing.

2. Theoretical Treatise

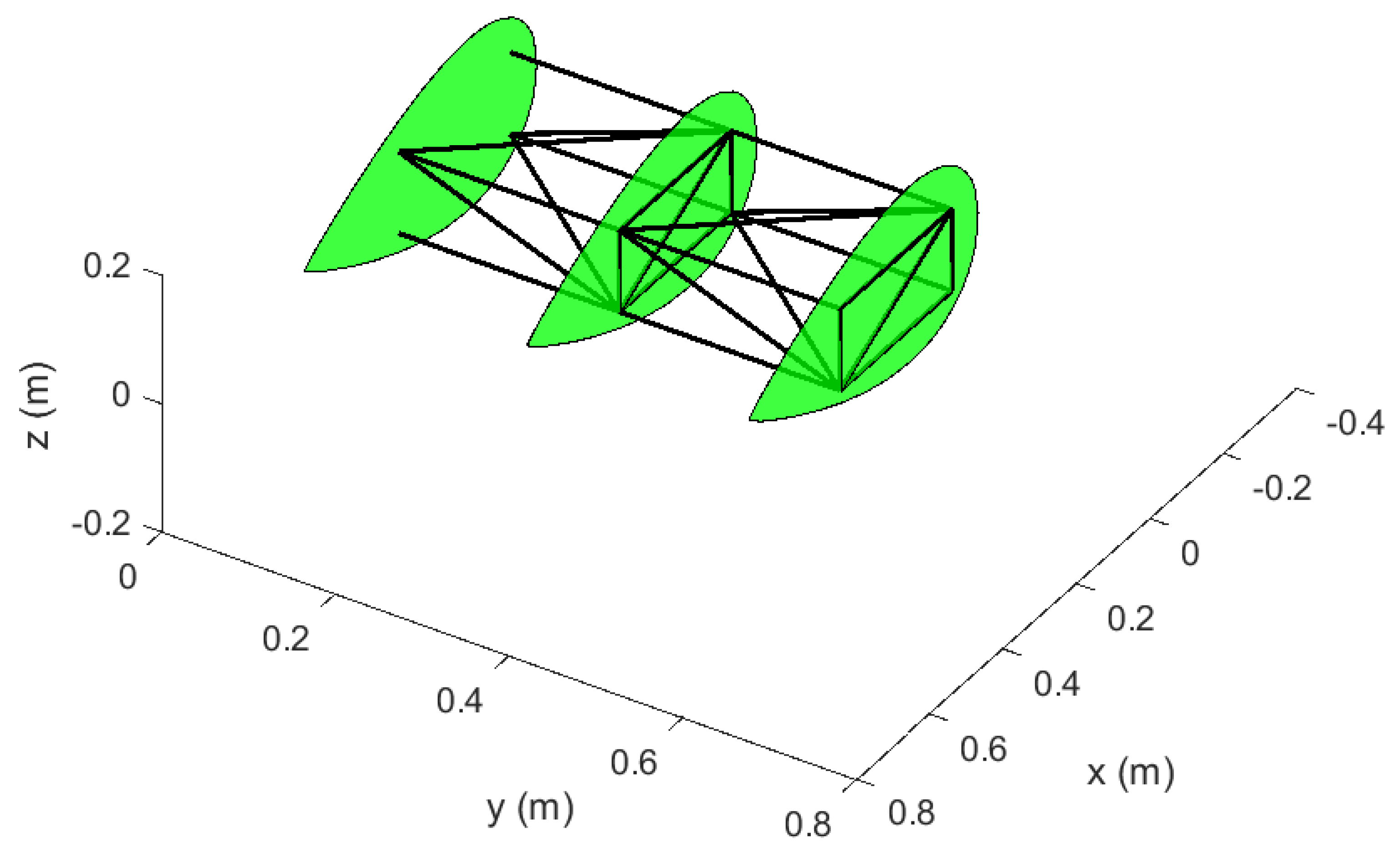
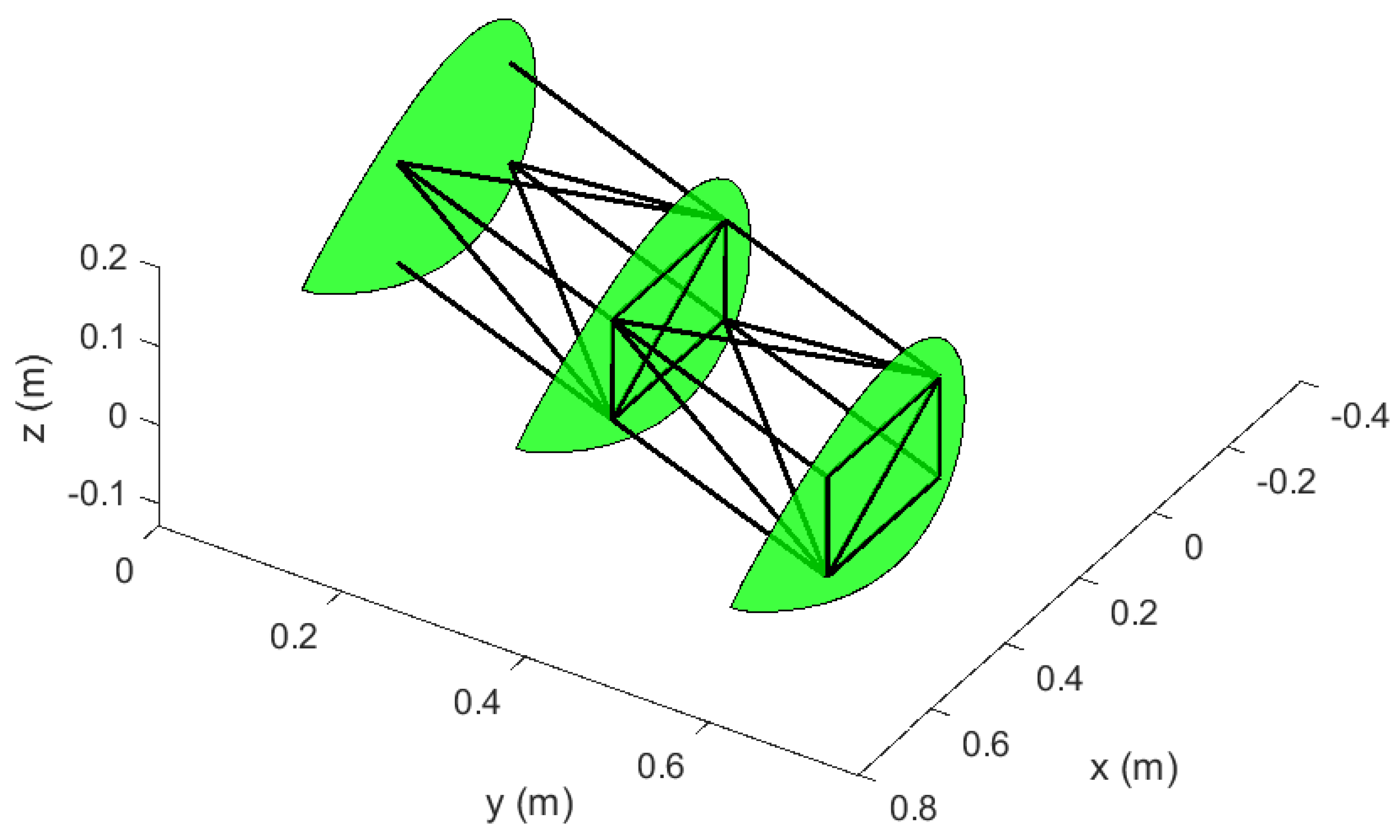
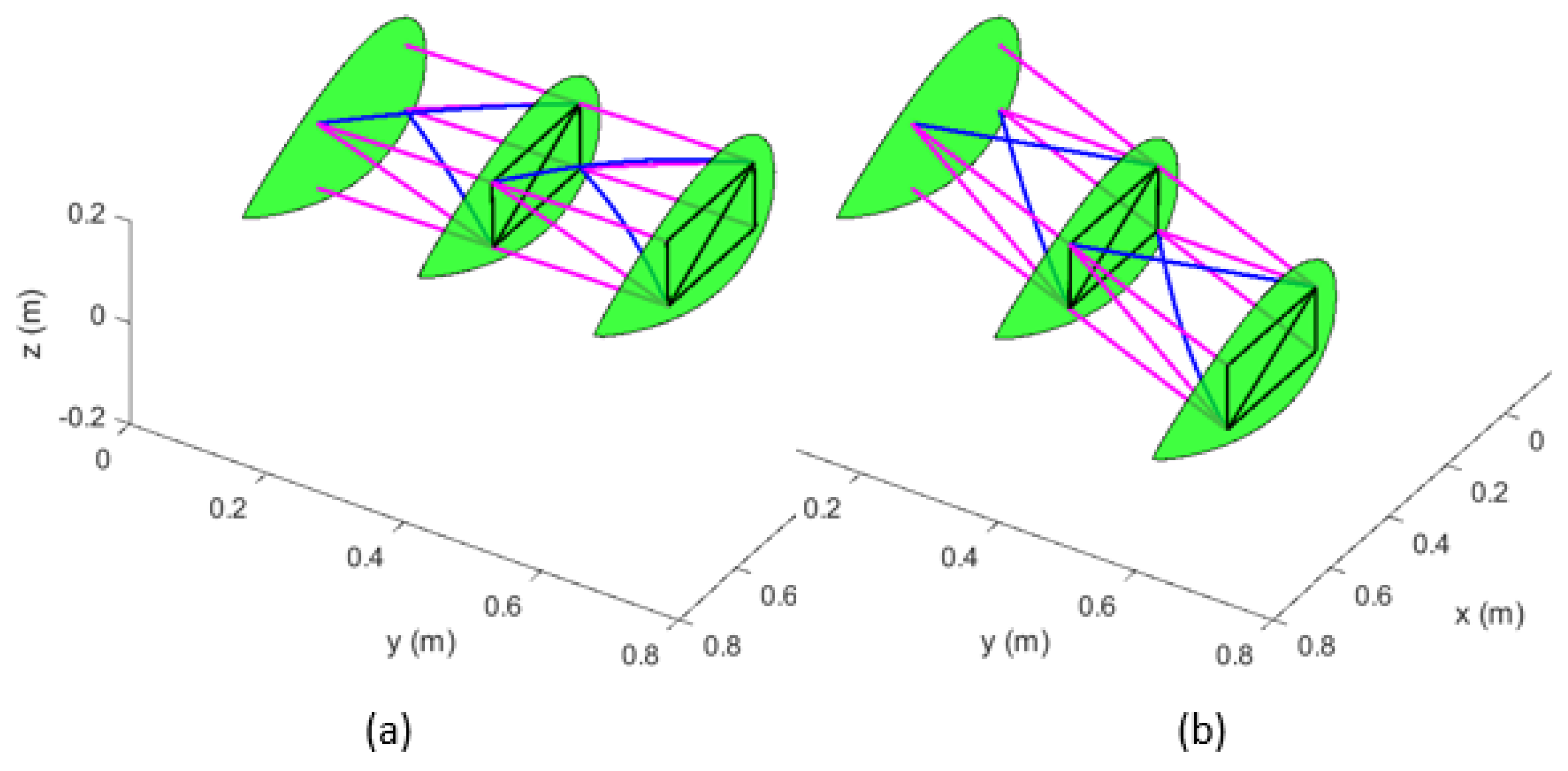
2.1. Mechanism Architecture

As mentioned earlier, a re-configurable modular morphing wing is analyzed here. The architecture of each module consists of 8 load-bearing structural members and two wing ribs. Spherical (eyebolt) joints are used here to connect these structural members to each other and to the wing ribs. Four of these members (active members), arranged in diagonal orientation, are controlled by actuators, and the other four are passive members. This work is carried out on the optimal topological configuration of the morphing wing presented by Finistauri and Moosavian [16,28]. The architecture of the wing is illustrated in Figure 1. The spherical joint is also shown in Figure 1 as an inset. Moreover, the optimal topological configuration is illustrated in a simplified CAD model in Figure 2.

Multiple morphing configurations, i.e., spanwise expansion, sweep, twist and dihedral, can be achieved with this optimal topology. A comprehensive procedure for obtaining these multiple morphing configurations is documented by Moosavian [26].

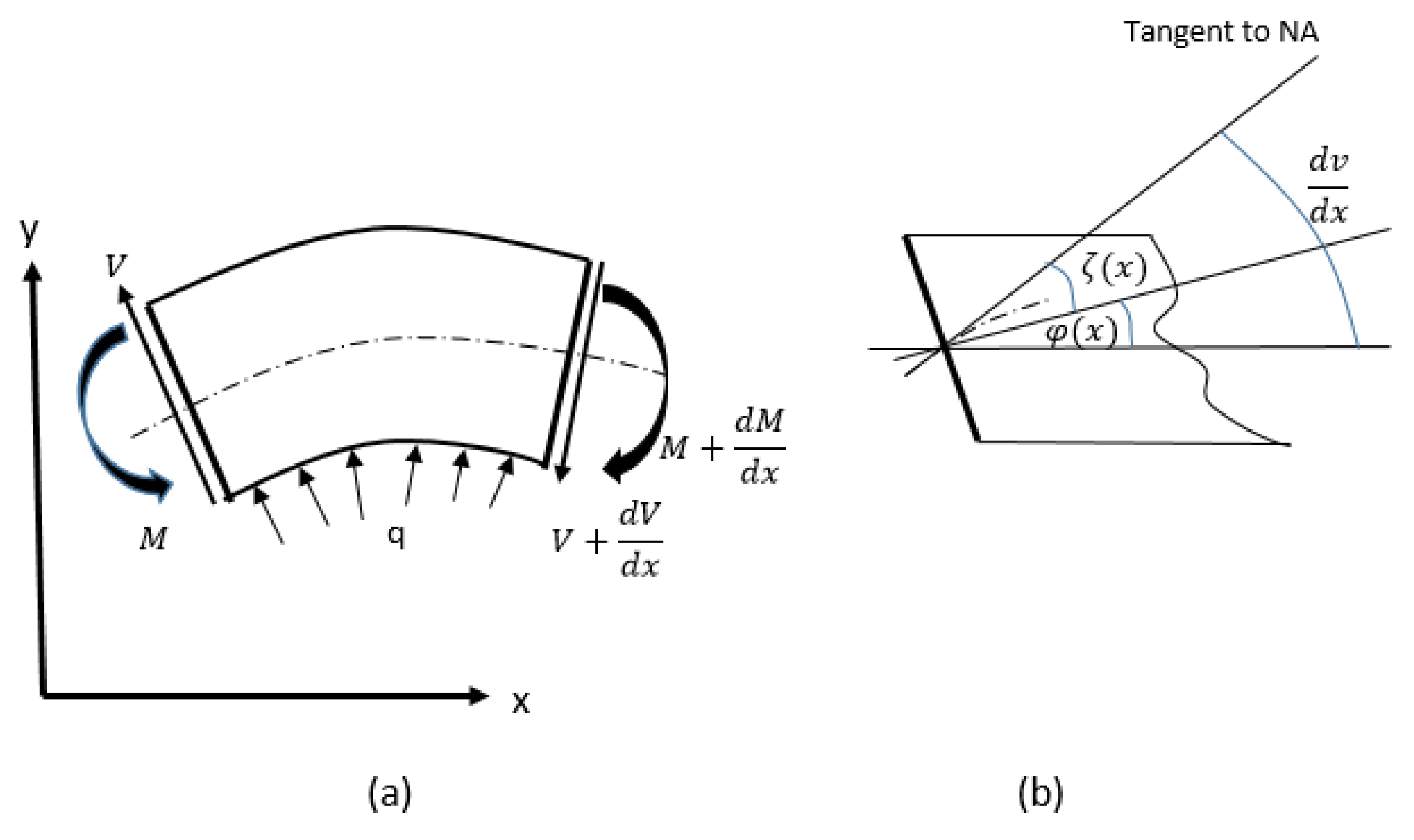
2.2. Governing Equations

The structural elements are modeled here as Timoshenko beams, where the shear deformation and rotary inertial effects are included in the differential equations governing the flexural behavior of the system.

For a deformed Timoshenko beam section in the $xy$ plane, as depicted in Figure 3, the slope can be presented as [29]:

$$\frac{dv}{dx}=\varphi \left(x\right)+\zeta \left(x\right),$$

(1)

where $\zeta \left(x\right)$ and $\varphi \left(x\right)$ represent the shear deformation and flexural bending, respectively. This gives the moment equation the following form:

$$M\left(x\right)=EI\frac{d\varphi \left(x\right)}{dx},$$

(2)

where E and I are the modulus of elasticity and second area moment of inertia, respectively. Shear force is related to the shear deformation as:

$$V\left(x\right)={\kappa }_{s}AG\zeta \left(x\right),$$

(3)

where A, G, and ${\kappa }_s$ are the cross-sectional area, shear modulus, and the shear correction factor, respectively, and ${\kappa }_{s}A=A_s$ is the shear area. The ${\kappa }_s$ for the solid circular cross-section is 0.9.

For a varying cross-section Timoshenko beam under a distributed load, q, the governing equations can be written as:

$$G{\kappa }_s\left[\frac{\partial A}{\partial x}(\varphi \left(x\right)-\frac{\partial v}{\partial x})+A(\frac{\partial \varphi }{\partial x}-\frac{{\partial }^{2}v}{\partial x^2})\right]+\rho A\frac{{\partial }^{2}v}{\partial t^2}=q(x,t),$$

(4)

$$GA{\kappa }_s\left[\frac{\partial v}{\partial x}-\varphi \right]+E\left[\frac{\partial I}{\partial x}\frac{\partial \varphi }{\partial x}+I\frac{{\partial }^2\varphi }{\partial x^2}\right]=\rho I\frac{{\partial }^2\varphi }{\partial t^2}.$$

(5)

For a homogeneous, uniform, and linearly elastic Timoshenko beam, the above-mentioned governing Equations (4) and (5) take the form:

$$GA{\kappa }_s\left[\frac{{\partial }^{2}v}{\partial x^2}-\frac{\partial \varphi }{\partial x}\right]=\rho A\frac{{\partial }^{2}v}{\partial t^2}-q(x,t),$$

(6)

$$EI\left[\frac{{\partial }^2\varphi }{\partial x^2}\right]+GA{\kappa }_s\left[\frac{\partial v}{\partial x}-\varphi \right]=\rho I\frac{{\partial }^2\varphi }{\partial t^2}.$$

(7)

By applying the standard finite element methodology (FEM) [30], the stiffness matrix of the Timoshenko beam element of length L in 3D with 6 degrees of freedom (DOF) at each node, including axial and torsional stiffness, can be presented as follows:

$$\left[k\right]=\left[\begin{array}{cc}{\overline{k}}_{11}& {\overline{k}}_{12}\\ {\overline{k}}_{21}& {\overline{k}}_{22}\end{array}\right],$$

(8)

where ${\overline{k}}_{11}$, ${\overline{k}}_{12}$, ${\overline{k}}_{21}$, and ${\overline{k}}_{22}$ are given below.

$$\left[{\overline{k}}_{11}\right]=\left[\begin{array}{cccccc}\frac{AE}{L}& 0& 0& 0& 0& 0\\ 0& 12C& 0& 0& 0& 6LC\\ 0& 0& 12C& 0& 6LC& 0\\ 0& 0& 0& \frac{GJ}{L}& 0& 0\\ 0& 0& 6LC& 0& (4+\psi )L^{2}C& 0\\ 0& 6LC& 0& 0& 0& (4+\psi )L^{2}C\end{array}\right],$$

(9)

$$\left[{\overline{k}}_{12}\right]=\left[\begin{array}{cccccc}\frac{-AE}{L}& 0& 0& 0& 0& 0\\ 0& -12C& 0& 0& 0& 6LC\\ 0& 0& -12C& 0& 6LC& 0\\ 0& 0& 0& \frac{-GJ}{L}& 0& 0\\ 0& 0& -6LC& 0& (2-\psi )L^{2}C& 0\\ 0& -6LC& 0& 0& 0& (2-\psi )L^{2}C\end{array}\right],$$

(10)

$$\left[{\overline{k}}_{21}\right]={\left[{\overline{k}}_{12}\right]}^T,$$

(11)

and

$$\left[{\overline{k}}_{22}\right]=\left[\begin{array}{cccccc}\frac{AE}{L}& 0& 0& 0& 0& 0\\ 0& 12C& 0& 0& 0& -6LC\\ 0& 0& 12C& 0& -6LC& 0\\ 0& 0& 0& \frac{GJ}{L}& 0& 0\\ 0& 0& -6LC& 0& (4+\psi )L^{2}C& 0\\ 0& -6LC& 0& 0& 0& (4+\psi )L^{2}C\end{array}\right],$$

(12)

where J is the torsion constant, $C=\frac{EI}{L^3(1+\psi )}$, and $\psi =12\frac{EI}{{\kappa }_{s}AG{L}^2}$.

Based on the energy formulation, the consistent mass matrix for the Timoshenko beams can be computed, as also given by Davis et al. [31], as follows:

$$\left[m\right]=\left[\begin{array}{cccccccccccc}\frac{\rho AL}{3}& 0& 0& 0& 0& 0& \frac{\rho AL}{6}& 0& 0& 0& 0& 0\\ 0& m_{2,2}& 0& 0& 0& m_{2,6}& 0& m_{2,8}& 0& 0& 0& m_{2,12}\\ 0& 0& m_{3,3}& 0& m_{3,5}& 0& 0& 0& m_{3,9}& 0& m_{3,11}& 0\\ 0& 0& 0& \frac{\rho L{I}_o}{3}& 0& 0& 0& 0& 0& \frac{\rho L{I}_o}{6}& 0& 0\\ 0& 0& m_{5,3}& 0& m_{5,5}& 0& 0& 0& m_{5,9}& 0& m_{5,11}& 0\\ 0& m_{6,2}& 0& 0& 0& m_{6,6}& 0& m_{6,8}& 0& 0& 0& m_{6,12}\\ \frac{\rho AL}{6}& 0& 0& 0& 0& 0& \frac{\rho AL}{3}& 0& 0& 0& 0& 0\\ 0& m_{8,2}& 0& 0& 0& m_{8,6}& 0& m_{8,8}& 0& 0& 0& m_{8,12}\\ 0& 0& m_{9,3}& 0& m_{9,5}& 0& 0& 0& m_{9,9}& 0& m_{9,11}& 0\\ 0& 0& 0& \frac{\rho L{I}_o}{6}& 0& 0& 0& 0& 0& \frac{\rho L{I}_o}{3}& 0& 0\\ 0& 0& m_{11,3}& 0& m_{11,5}& 0& 0& 0& m_{11,9}& 0& m_{11,11}& 0\\ 0& m_{12,2}& 0& 0& 0& m_{12,6}& 0& m_{12,8}& 0& 0& 0& m_{12,12}\end{array}\right],$$

(13)

where $\rho$ and $I_o$ are the mass density of the material and polar moment of inertia, respectively. The elements $m_{i,j}$ and $m_{r,s}$ can be computed by using the following equation:

$$\begin{array}{cc}{m}_{i,j}=m_{r,s}=\rho A{\left[X\right]}^{-t}\left[H\right]\left[X\right]& i,j\in \{2,6,8,12\}\\ & r,s\in \{3,5,9,11\}\end{array},$$

(14)

where $\left[H\right]$ is given below:

$$\left[H\right]=\left[\begin{array}{cccc}\frac{L^7}{252}+\gamma (\frac{L^5}{20}+\frac{L^3\beta }{3}+\frac{L}{{\beta }^2})& & & \\ \frac{L^6}{72}+\gamma (\frac{L^4}{8}+\frac{L^2\beta }{2})& \frac{L^5}{20}+\frac{\gamma L^3}{3}& & Symmetrical\\ \frac{L^5}{30}+\gamma (\frac{L^3}{6}+L)& \frac{L^4}{8}+\frac{\gamma L^2}{2}& \frac{L^3}{3}+\gamma L& \\ \frac{L^4}{24}& \frac{L^3}{6}& \frac{L^2}{2}& L\end{array}\right],$$

(15)

and $\left[X\right]$ is given as:

$$\left[X\right]=\frac{EI}{L^3(1+\psi )}\left[\begin{array}{cccc}0& 0& 0& 1\\ \beta & 0& 1& 0\\ \frac{L^3}{6}& \frac{L^2}{2}& L& 1\\ \frac{L^2}{2}+\beta & L& 1& 0\end{array}\right],$$

(16)

with $\beta =\frac{EI}{{\kappa }_{s}AG}$ and $\gamma =\frac{I}{A}$.

2.3. Application of Hinged Nodes

Spherical joints implemented here can be considered as 3-dimensional (3D) hinged nodes. Indeed, a beam that with an internal hinge acts as two beams connected at the hinge with a two-valued slope in both transverse directions and a two-valued twist angle at the hinge. The bending slope of each beam at the hinge can be computed from the corresponding beam deflections at the hinged node. By applying the procedure given by Logan [30] and partitioning the original element matrix, considering the hinged node as the second (right) node of a beam element, the condensed stiffness matrix, $\left[K_{c2}\right]$, of that element in the $xy$ and $xz$ planes can be computed as follows:

$$\left[k_{c2}\right]=\left[\begin{array}{cccc}{k}_{11}-\frac{k_{14}^2}{k_{44}}& 0& k_{12}-\frac{k_{14}{k}_{42}}{k_{44}}& k_{13}-\frac{k_{14}{k}_{43}}{k_{44}}\\ 0& 0& 0& 0\\ k_{21}-\frac{k_{24}{k}_{41}}{k_{44}}& 0& k_{22}-\frac{k_{24}^2}{k_{44}}& k_{23}-\frac{k_{24}{k}_{43}}{k_{44}}\\ k_{31}-\frac{k_{34}{k}_{41}}{k_{44}}& 0& k_{32}-\frac{k_{34}{k}_{42}}{k_{44}}& k_{33}-\frac{k_{34}^2}{k_{44}}\end{array}\right],$$

(17)

where $k_{ij}$ are original elements of the stiffness matrix of the Timoshenko beam element in the $xy$ and $xz$ planes bending. Now, for the case of the first (left) node of the beam element to be hinged, the condensed stiffness matrix $\left[K_{c1}\right]$ in the $xy$ and $xz$ planes can then be computed as follows:

$$\left[k_{c1}\right]=\left[\begin{array}{cccc}{k}_{11}-\frac{k_{12}^2}{k_{22}}& k_{13}-\frac{k_{12}{k}_{23}}{k_{22}}& k_{14}-\frac{k_{12}{k}_{24}}{k_{22}}& 0\\ k_{31}-\frac{k_{32}{k}_{21}}{k_{22}}& k_{33}-\frac{k_{23}^2}{k_{22}}& k_{34}-\frac{k_{32}{k}_{24}}{k_{22}}& 0\\ k_{41}-\frac{k_{42}{k}_{21}}{k_{22}}& k_{43}-\frac{k_{42}{k}_{23}}{k_{22}}& k_{44}-\frac{k_{24}^2}{k_{22}}& 0\\ 0& 0& 0& 0\end{array}\right].$$

(18)

These condensed stiffness matrices in the $xy$ and $xz$ planes along with the beam axial displacement matrix along the x axis will constitute the beam condensed stiffness matrix in 3D for 6DOF. No twisting DOF will be applied for the resultant condensed stiffness matrices. The condensed mass matrices can be computed by following a similar procedure as outlined above.

2.4. Conventional Modal Analysis

Modal analysis is performed using the conventional FEM, based on the equations of motion written as:

$$\left[M\right]\ddot{d}+\left[K\right]d=0,$$

(19)

where d is the displacement vector of the whole system, with $d_i$ for a nodal displacement vector with 6DOFs (refer to Figure 4) written as:

$$d_i=\left[\begin{array}{c}{v}_{xi}\\ v_{yi}\\ v_{zi}\\ {\varphi }_{xi}\\ {\varphi }_{yi}\\ {\varphi }_{zi}\end{array}\right],$$

(20)

and $\left[M\right]$ and $\left[K\right]$ are the assembled global mass and stiffness matrices of the system, respectively. The following harmonic solution, (21), is applied for the system’s governing Equations (6) and (7),

$$d=d_o{e}^{-i\omega t}.$$

(21)

By applying this harmonic solution and considering $q=0$, along with stiffness and mass matrices of the Timoshenko beam, the system’s linear eigenvalue problem (22) is written as:

$$[K-{\omega }^{2}M]d_o=0.$$

(22)

Therefore, circular natural frequency $\omega$ (eigenvalue) and the corresponding mode shape (eigenvector) $d_o$ can be computed by solving the linear eigensystem in Equation (22).

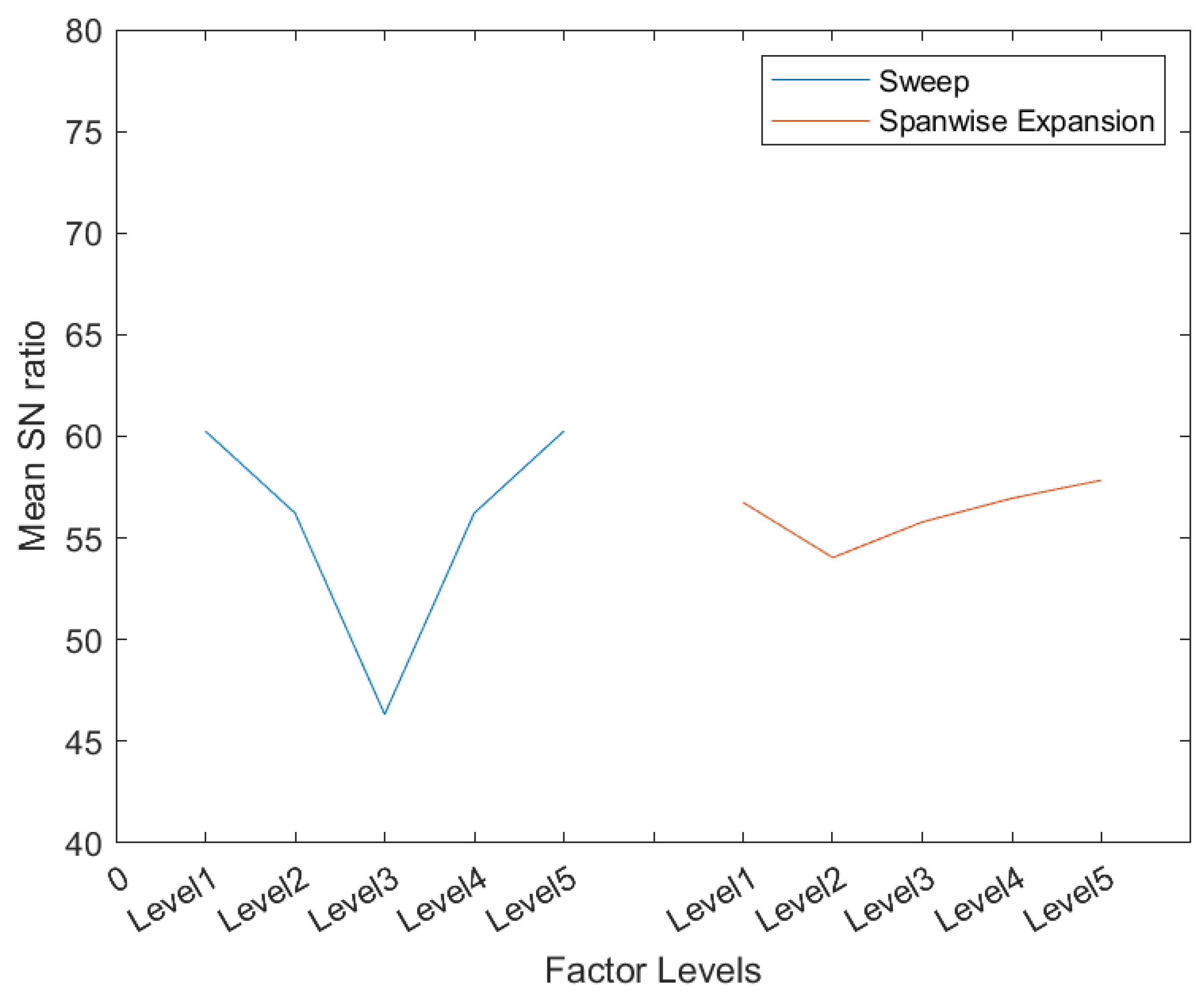
2.5. Taguchi Method

The Taguchi method, developed by a Japanese engineer and statistician, is a statistical tool used in robust design of experiments to diminish the variation in a process [32,33,34]. It is applied to investigate the effect of various parameters (factors) on the mean and variance of a process characteristic. This method utilizes an orthogonal array composed of an arrangement of the governing parameters (factors) and their corresponding various levels (values). Instead of testing all the combinations of parameters and their levels, the Taguchi method needs a certain number of combination pairs defined in orthogonal arrays. Therefore, with a minimum number of experiments or simulations, the factor affecting the performance characteristic of a process the most is determined. First, a target value of the performance characteristic is selected. Then, based on the number of parameters and their level, orthogonal arrays are selected from readily available lookup online tables. The process or simulation characteristic is then performed/computed for each combination in the array to obtain data. In order to measure the effect of each parameter (factor), the signal-to-noise ratio (SN) is computed for each experiment/simulation. SN ratio is a logarithmic form used to find the deviation from a target value of the performance characteristic.

Three approaches can be applied in the Taguchi method to find the optimum combination of parameters. These approaches are as follows:

Larger is better:

$$\mathrm{SN}=-10log\left[\frac{1}{N}\sum _{i=1}^n\frac{1}{Y_i^2}\right]$$

(23)

Nominal is better:

$$\mathrm{SN}=10log\left[\frac{Y_m}{S^2}\right]$$

(24)

Smaller is better:

$$\mathrm{SN}=-10log\left[\frac{1}{N}\sum _{i=1}^N{Y}_i^2\right]$$

(25)

where N, Y, $Y_m$, and $S^2$ are the number of observations (simulations), observed value (difference from the target value), mean observed value, and the variance, respectively.

After computing the SN ratio for each experiment or simulation, the mean SN ratio of each factor and level is calculated. These mean SN ratios of each factor and level are then plotted to visually find the range. The factor with highest range is regarded as the most dominant factor on the performance characteristic of a process.

3. Methodology

In this work, the dynamic characteristics of a morphing wing consisting of two modules are explored based on FEM. As mentioned earlier, the load-bearing structural members in each module are modeled as Timoshenko beams. Therefore, there are 8 beams in each module. Furthermore, each rib is modeled as a planar assembly of 5 rigid beams, i.e., there are in total 26 beams. Each beam is discretized into a number of 2-noded elements with six degrees of freedom (6 DOF) per node (refer to Equations (8) and (13)). The spherical (eyebolt) joints between wing rib and load-bearing structural members (beams), and between load-bearing members, are modeled as 3D hinged joints, allowing only the linear motions along three coordinate axes (refer to Equations (17) and (18)). Based on the Timoshenko beam theory and the 3D hinged joint presented in the previous section, modal analysis of the two-module morphing wing will be performed. However, modules can be added per mission requirements. The following assumptions are made for this analysis:

• Wing ribs can be represented by 5 structural beams;
• Structural members representing wing ribs are of the order of 1000 stiffer than the other structural members of the module;
• Initially all structural beams are considered straight and stress-free;
• Plane sections remain plane during bending, but are no longer perpendicular to the neutral axis;
• All structural elements are perfectly elastic, homogeneous, and isotropic;
• Diameter of each beam is assumed to remain uniform during expansion morphing, but is updated by keeping the mass of the member constant.

Conventional finite element methodology (FEM), based on Timoshenko beam theory, is applied to compute the assembled global stiffness and mass matrices of the modular morphing wing. For the end elements of each beam, condensed stiffness and mass matrices are implemented using the hinged nodal analysis presented previously. Fixed boundary conditions are applied for the left end of the first module, representing attachment to the fuselage. The linear eigensystem, Equation (22), is solved to perform the modal analysis of the assembled mass and stiffness matrices. The first 10 natural frequencies and the corresponding mode shapes are computed. After validation of the computed natural frequencies, various parametric analyses are performed to investigate the effect of two morphing parameters (sweep and spanwise expansion) on the vibration signature of the wing. The Taguchi methodology is applied as the tool for the design of the experiment for this purpose. Signal-to-noise ratios (SN) of each factor’s (parameter’s) levels are computed for the first 10 natural frequencies by applying the maximum is better methodology of the Taguchi technique. This procedure is depicted in the flow chart in Figure 5. For any beam’s extension during morphing, the total mass of the beam remains constant due to the telescopic characteristic of the actuation system applied here. However, the stiffness of each beam and its effective diameter are updated accordingly.

4. FEM-Based Numerical Simulation and Discussion

As mentioned earlier in this paper, the morphing wing studied here consists of two modules. Moreover, there are 26 beams in total. The diameter of each beam in its un-morphed (benchmark) configuration is 0.0254 m (1 in). The distance between two wing ribs, i.e., the un-morphed module length, is 0.254 m (10 in) (refer to Figure 2). Mechanical properties of structural beams (active and passive) are given in

Table 1. Mechanical properties of steel.

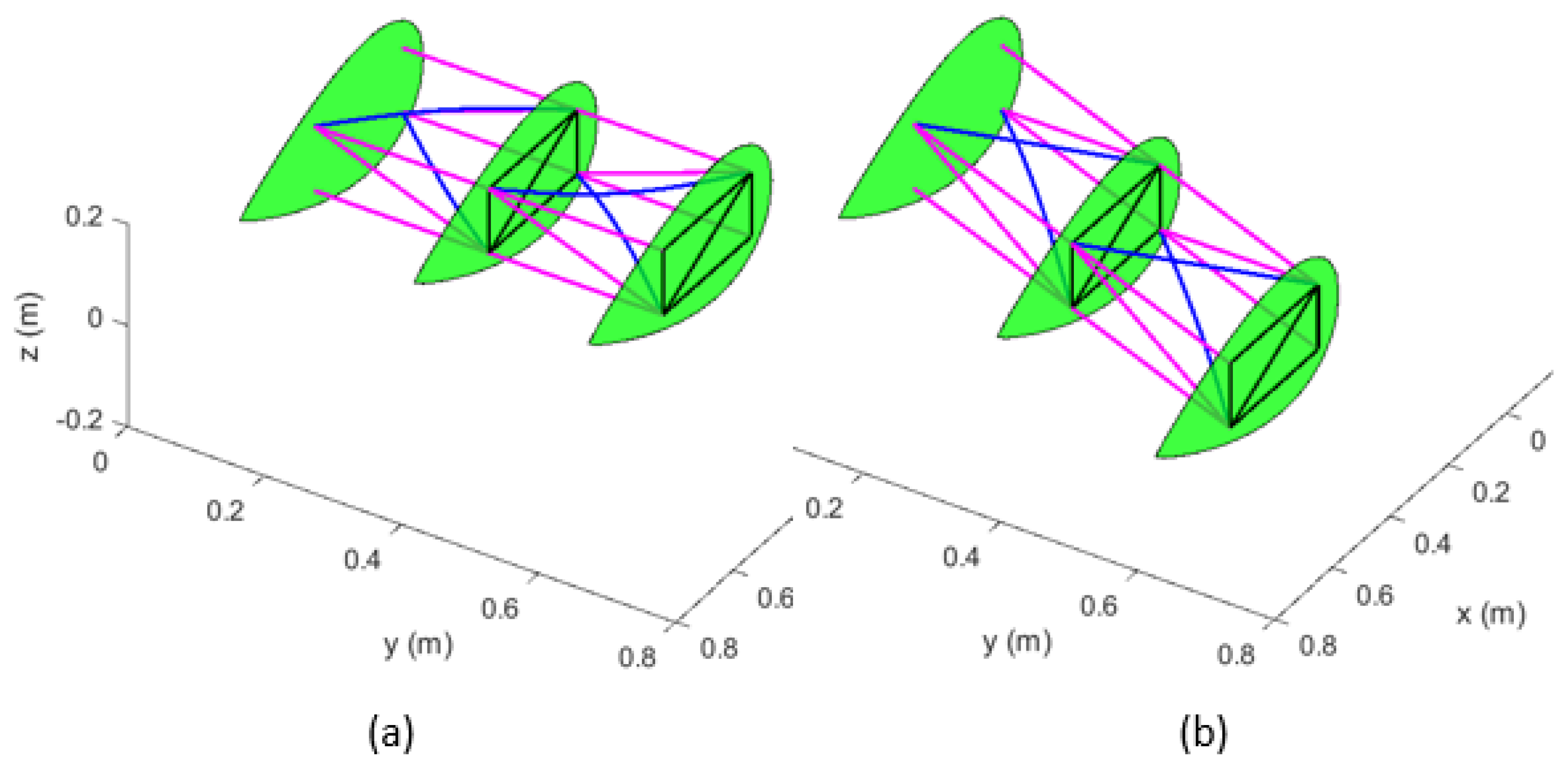
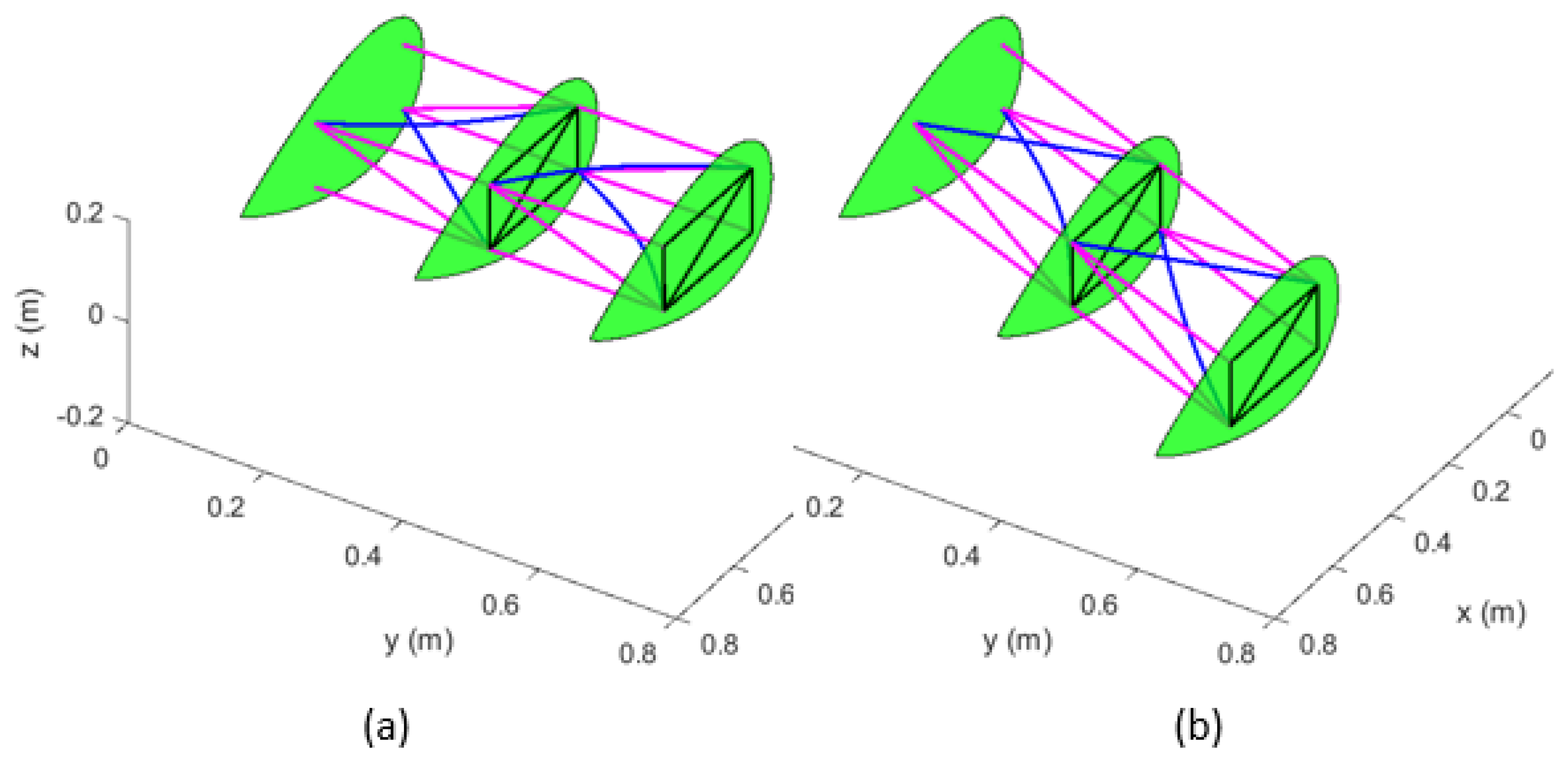
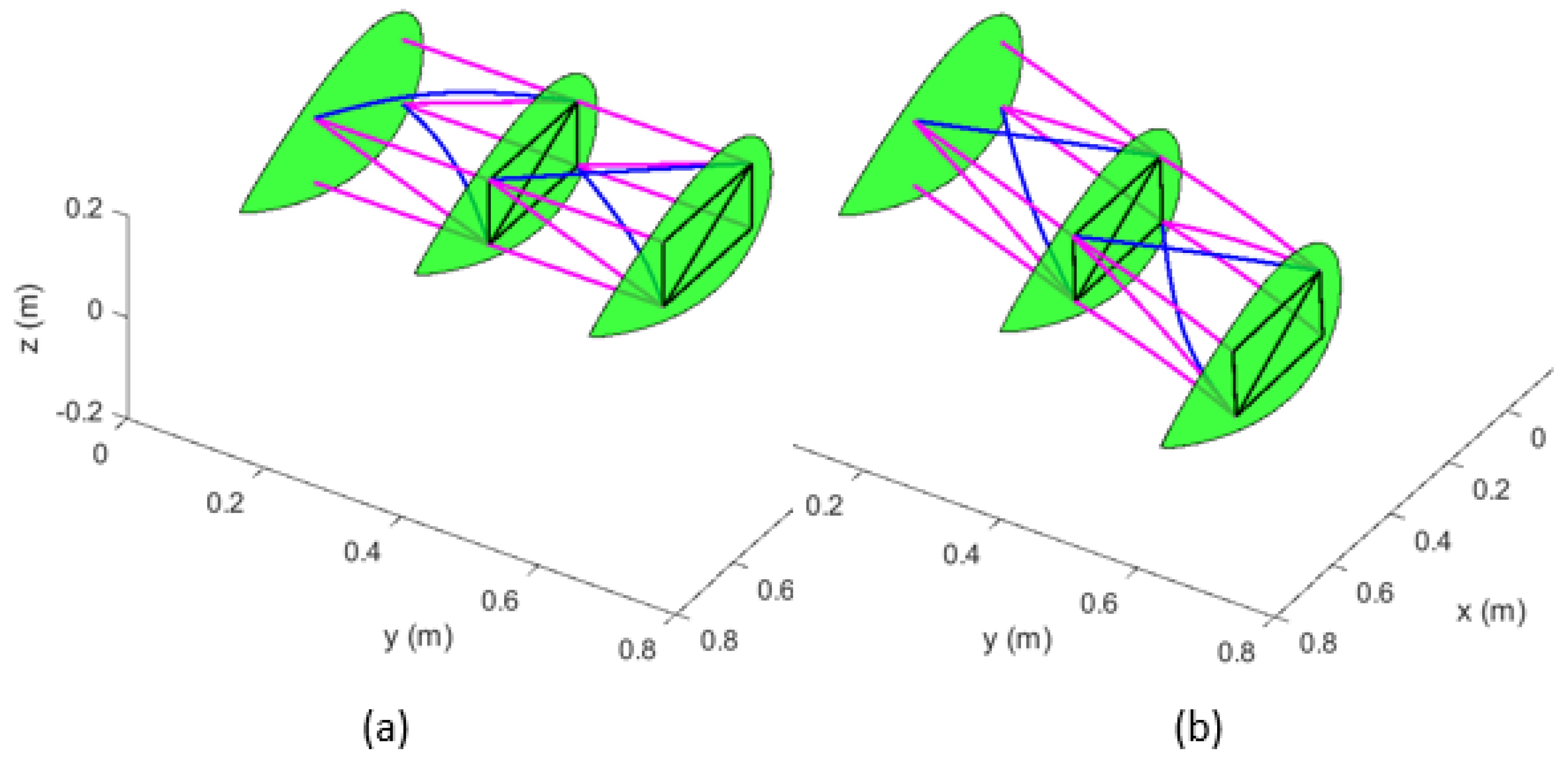
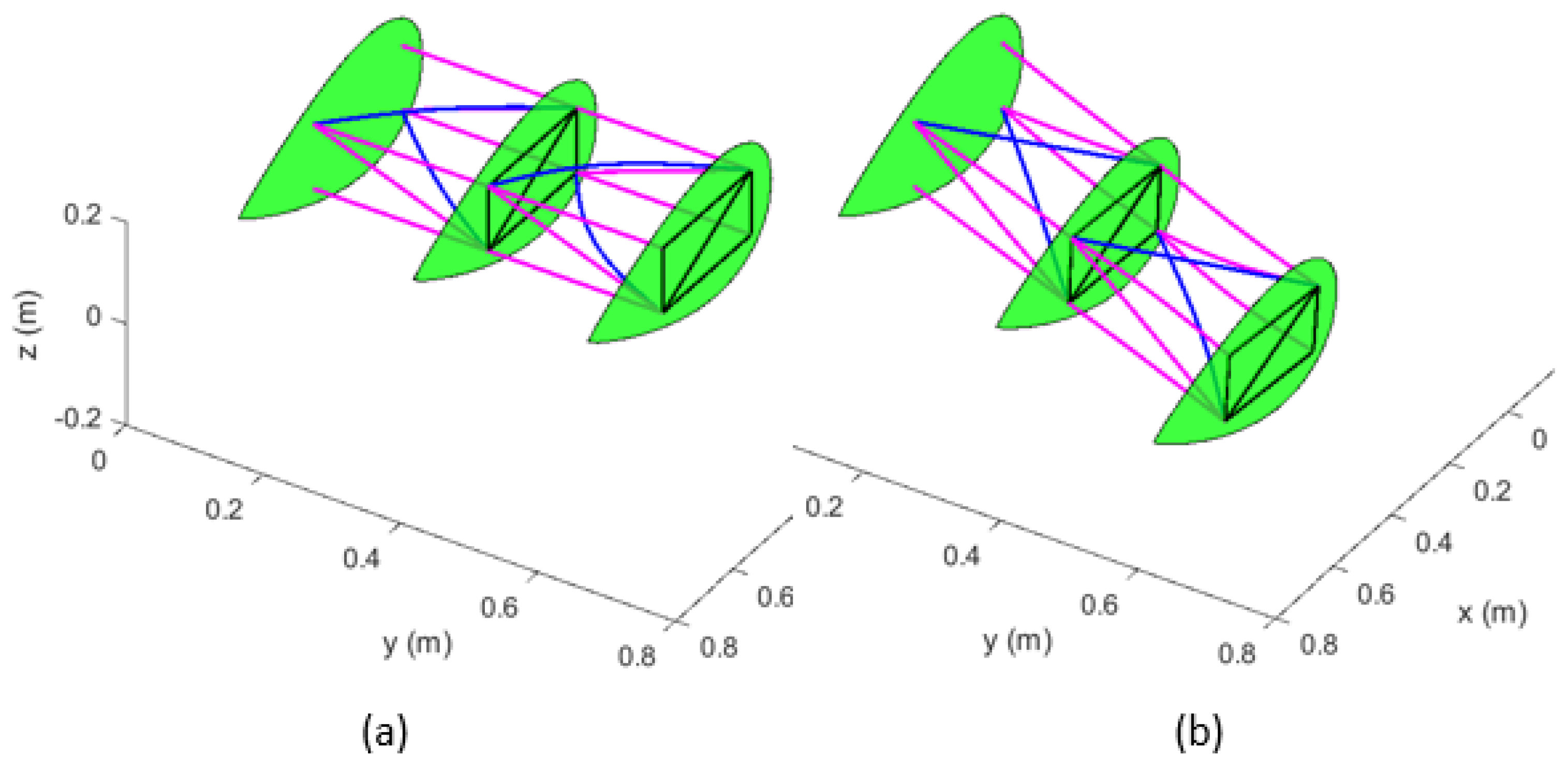
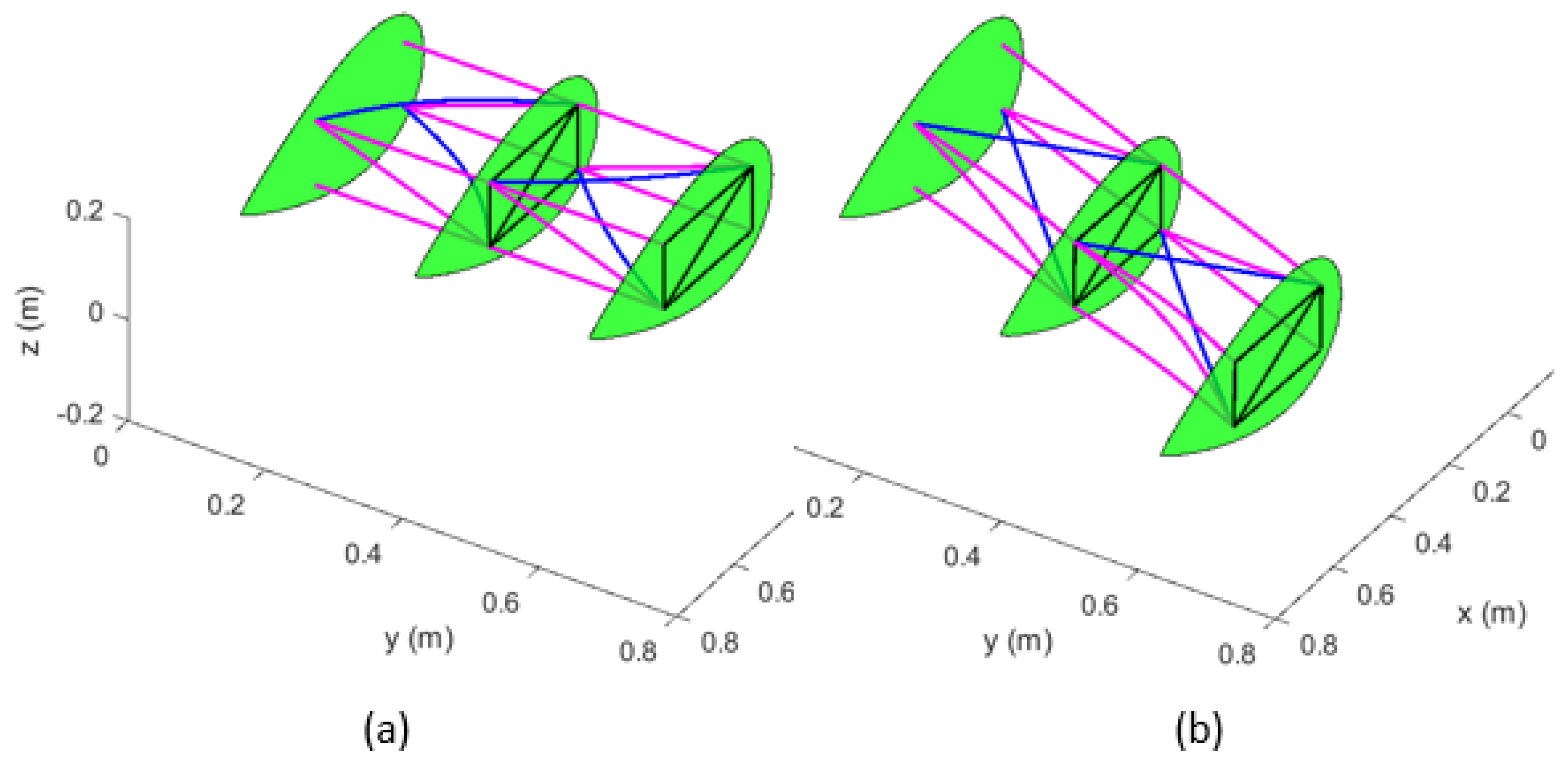
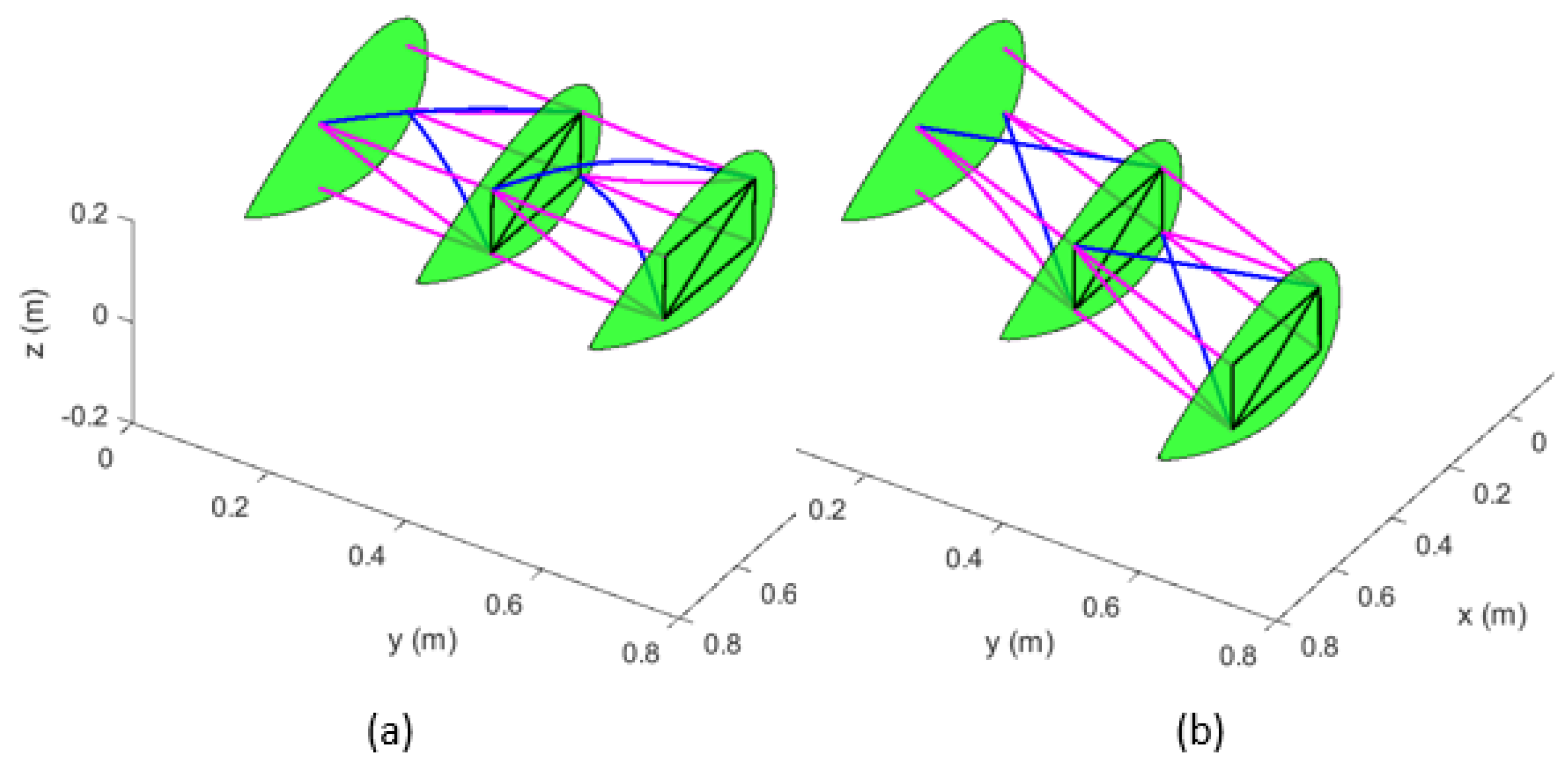
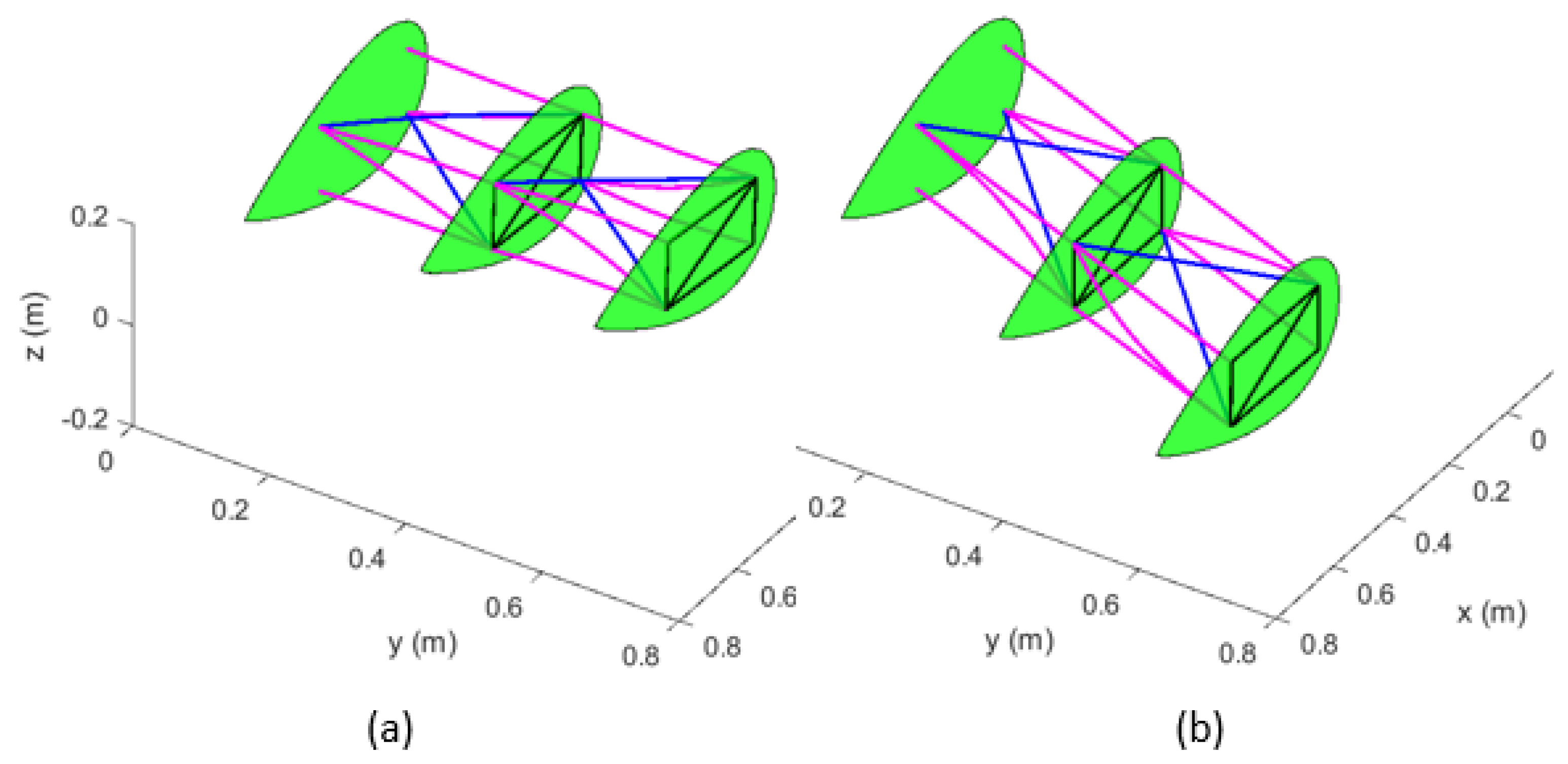
Material	Density	Modulus of Elasticity	Poisson Ratio	Shear Modulus
	kg/m${}^3$	Pa		Pa
Low Carbon Steel	7750.4	1.8616 $\times {10}^{11}$	0.3	7.16 $\times {10}^{10}$

.

Based on a comprehensive convergence test, it is noted that 30 elements per beam are sufficient for the converged solution (see Figure 6). Therefore, in the subsequent simulations, all 8 load-bearing beams in each module are discretized into 30 Timoshenko elements with 6 DOF per node. However, for the 5 beams, representing each wing rib, 4 Timoshenko elements are deemed sufficient.

Modal analysis, based on the conventional finite element methodology (FEM), is performed and the frequency results are compared with those obtained from the dynamic stiffness method (DSM). Details of the validation results are given in the authors’ earlier publication and are omitted here for the sake of brevity [27].

First, the un-morphed wing is simulated as the benchmark case for the modal analysis. With the x axis along the aircraft longitudinal direction and the y axis along the wing span direction, the un-morphed wing configuration is shown in Figure 7. Airfoils have been added here for visual ease. The computed first 10 natural frequencies of the benchmark case are presented in

Table 2. Benchmark case (un–morphed) natural frequencies, $f=\frac{\omega }{2\pi }$(Hz), of the wing.

Mode	1	2	3	4	5	6	7	8	9	10
	243.33	304.88	306.71	307.54	308.39	313.15	314.24	314.38	391.93	455.56

.

In the ensuing paragraphs, modal analyses of the wing in morphed configurations are presented. Various combinations of sweep and spanwise expansion have been applied, and their effects on the free vibration of the wing are investigated. As mentioned earlier in this paper, for every expansion case of the morphing wing, the diameter (therefore, area and moment of inertia) of each structural beam was calculated by keeping its corresponding mass constant.

The two morphing parameters/factors, i.e., sweep and spanwise expansion, along with their respective 5 levels applied in this work, are given in

Table 3. Governing factors and their levels.

Factor	Levels
	1	2	3	4	5
Sweep (${}^{\circ }$)	−30	−15	0	15	30
Spanwise Expansion (%)	0.0	0.05	0.1	0.15	0.2

.

For a complete design of experiments (DOE), a total of $5^2=25$ simulations are needed to investigate the effects of various combinations of the two factors’ levels. The Taguchi orthogonal array (L25), for this DOE, is presented in

Table 4. Taguchi orthogonal array for simulations.

Numerical Simulation	Factor Levels
	Sweep	Spanwise Expansion
1	1	1
2	1	2
3	1	3
4	1	4
5	1	5
6	2	1
7	2	2
8	2	3
9	2	4
10	2	5
11	3	1
12	3	2
13	3	3
14	3	4
15	3	5
16	4	1
17	4	2
18	4	3
19	4	4
20	4	5
21	5	1
22	5	2
23	5	3
24	5	4
25	5	5

[32,33,34].

The resulting first 10 natural frequencies, corresponding to the 25 simultionss, are presented in

Table 5. Taguchi-based natural frequencies of the morphed wing.

Numerical Simulation	Natural Frequencies $\mathit{f}=\frac{\mathit{\omega }}{2\mathit{\pi }}\left(\mathbf{Hz}\right)$
	1	2	3	4	5	6	7	8	9	10
1	150.78	157.83	158.98	160.34	232.45	320.59	414.51	443.34	446.58	456.17
2	141.15	148.48	149.66	150.87	212.76	295.31	375.81	400.22	403.09	410.97
3	132.23	139.83	141.02	142.10	195.44	272.46	341.48	362.47	365.03	371.51
4	123.98	131.81	133.01	133.98	180.15	251.78	311.00	329.32	331.61	336.95
5	116.33	124.38	125.57	126.44	166.59	233.02	283.93	300.09	302.15	306.57
6	206.52	223.30	224.66	227.19	288.80	403.47	427.33	434.92	440.33	458.29
7	193.33	211.25	212.54	214.90	267.22	375.35	403.88	410.59	418.18	431.41
8	180.96	199.92	201.16	203.37	247.97	348.65	380.72	388.10	396.64	405.95
9	169.38	189.27	190.49	192.54	230.77	323.77	357.80	366.92	375.80	381.81
10	158.58	179.27	180.49	182.37	215.34	300.78	335.10	346.81	355.75	358.87
11	243.33	304.88	306.71	307.54	308.39	313.15	314.24	314.38	391.93	455.56
12	225.62	289.46	291.37	291.82	292.79	297.26	298.30	298.44	364.72	421.30
13	209.32	274.72	276.71	276.74	277.96	282.10	283.09	283.22	340.23	390.01
14	194.37	260.67	262.38	262.73	263.85	267.66	268.59	268.73	318.04	361.42
15	180.70	247.31	248.73	249.44	250.45	253.95	254.82	254.95	297.80	335.28
16	206.52	223.30	224.66	227.19	288.80	403.47	427.33	434.92	440.33	458.29
17	193.34	211.25	212.54	214.90	267.21	375.36	403.88	410.59	418.18	431.41
18	180.96	199.92	201.16	203.37	247.97	348.66	380.72	388.11	396.64	405.95
19	169.38	189.27	190.49	192.54	230.77	323.78	357.80	366.92	375.80	381.81
20	158.58	179.27	180.49	182.37	215.34	300.78	335.10	346.81	355.75	358.87
21	150.78	157.83	158.98	160.34	232.45	320.60	414.51	443.34	446.58	456.17
22	141.15	148.48	149.66	150.87	212.75	295.32	375.81	400.22	403.09	410.97
23	132.23	139.83	141.02	142.10	195.44	272.47	341.48	362.47	365.03	371.51
24	123.98	131.81	133.01	133.98	180.15	251.79	311.00	329.32	331.61	336.95
25	116.33	124.38	125.57	126.44	166.59	233.02	283.93	300.10	302.15	306.57

, and their corresponding mode shapes have been extracted. Simulation 11, in essence, represents the benchmark case. By comparison with the natural frequencies of the original/un-morphed configuration (see Table 2), it is found that the first 5 natural frequencies diminish in their values. However, the next 5 frequencies increase compared to their benchmark case’s counterparts.

By changing the sweep, while keeping the span length the same, the configuration of the wing is altered in terms of mass and stiffness distribution. The increase in the sixth and higher natural frequencies could be attributed to the above-stated fact that the morphed wing is in fact a different configuration. This change in configuration, indeed, leads to different mode shapes as compared to their corresponding benchmark case for modes higher than 5.

The undeformed wing in morphed configuration for simulation 25 is shown in Figure 8. For illustration purposes, only the first 10 mode shapes for simulation 25, involving sweep of ${30}^{\circ }$ and a spanwise expansion of $20\%$, are extracted and presented in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18. For the sake of comparison, the un-morphed wing’s mode shapes are also presented in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18. The purpose of these plots is to showcase how the various internal constituent members respond to morphing in terms of their flexural or axial motion, if any. This information is necessary in order to tailor the overall stiffness of the wing required for aircraft performance against drag reduction and hazard assessment of the wing. It is clear from these plots that the constituent structural beams undergo local flexural motion, individually or in combination, without producing considerable in-plane or out-of-plane motion of the entire wing. This can be attributed to the inclusion of the spherical joints at the beam end connections. These joints do not transfer the bending of the beams and resist only the axial displacement to the ribs. It is clear from these plots that different beams exhibit flexural motion for the morphed case as compared to the un-morphed case. For example, in mode 1, the upper diagonal beam of module 1 exhibits distinct flexural motion in the un-morphed configuration. However, in the morphed configuration, the flexural motion of the lower diagonal beam of module 2 is clearly visible. Also, in mode 6, it is found that all upper and lower diagonal beams in the un-morphed configuration exhibit noticeable flexural motion. On the contrary, the corresponding morphed configuration presents no flexural motion of diagonal beams. Similar observations can be made in other modes as well. Moreover, it is observed from these figures that in both un-morphed and morphed configurations, the first 5 mode shapes exhibit flexural motion of the top and bottom diagonal (active) members in each module. However, unlike the un-morphed configurations, flexural motion of the upstream and downstream diagonal (active) members become evident for modes 6 and higher. Therefore, it can be deduced that new modes become visible after mode 5 during sweep morphing. The increase in natural frequencies of mode 5 and higher in sweep morphing, as noticed above, can be attributed to this observation.

Signal-to-noise ratios (SN), as per the Taguchi methodology, are computed for all 25 simulations to investigate the effect of factors and their levels on changing the natural frequencies of the system. This change in frequencies is based on their difference from the corresponding un-morphed wing’s natural frequencies. The maximum is better methodology is adopted to compute the SN ratio [32,33,34]. By following the Taguchi technique, the mean SN ratios of the two factors’ levels for the second mode, shifted along abscissa for visual discernability, are given in Figure 19. This figure clearly reveals that sweep is the most effective morphing factor in controlling the natural frequencies of the wing, followed by the spanwise expansion. This indicates that the sweep morphing, which essentially changes the aspect ratio of the wing, also contributes to changing the stiffness of the system more as compared to spanwise expansion. It is also observed that expanding the wing in the spanwise direction at any non-zero sweep angle results in a high rate of decrease in frequencies as compared to sweep morphing for modes 6 and up. Consequently, it is found that spanwise expansion is the most effective parameter for modes 6 and higher (see Figure 20 for mode 8). Therefore, it is concluded that sweep morphing leads to new stiffer modes in terms of flexural motion of the upstream and downstream diagonal (active) beams for mode 6 and higher. However, spanwise expansion decreases these newly generated modes with a higher rate as compared to mode 5 and lower, which are related to the vibration of upper and lower diagonal (active) beams of each module.

5. Conclusions

By offering a high lift-to-drag ratio, improved aerodynamic performance, and enhancement in maneuverability and flight envelope, the morphing wing aircraft can lead to considerable fuel efficiency. Therefore, the green aircraft concept is logically linked to the future development of a morphing wing. Contrary to these leverages, a cost is associated with a variable-shape wing in terms of increased weight, complexities of the system, control system, and aeroelastic characteristics. Therefore, an optimum solution is always imperative for these conflicting parameters to offset the associated penalties. Dynamic characterization of a morphing wing is the preliminary step required for this optimization. Therefore, a detailed investigation of the dynamic characteristics of the morphing wing must be performed and comprehended. In this paper, the free vibration of a special re-configurable modular morphing wing design, developed in-house at Toronto Metropolitan University, has been studied. Despite a truss-type configuration, it is shown here that structural members exhibit bending; therefore, truss element analysis is evidently a non-conservative approach. By designing an experimental procedure, under the combined effect of varying sweep and spanwise expansion, it is also shown that the studied topology leads to non-symmetrical bending; vertical bending (flapping) is more than $90\%$ higher in amplitude compared to in-plane bending (lead-lag) of the wing. This is in line with the common behavior of typical aircraft wings. No bending–twist coupling is obvious in this configuration for the studied first 10 modes. It is evident that sweep, due to its underlying effect of changing the wing’s aspect ratio, governs the natural frequencies of the morphing wing for modes 5 and lower. However, spanwise expansion remains dominant in terms of its effect on the natural frequencies for modes 6 and higher. It is also found that during the spanwise expansion morphing, the upper and lower diagonal constituent beam members exhibit distinct flexural motion as compared to the upstream and downstream members for modes 5 and lower. However, during the sweep morphing, upstream and downstream diagonal members’ flexural motion is dominant for modes 6 and higher. Therefore, it can be concluded that sweep morphing, due to its lesser contribution to the flapping motion of the wing, will offers higher stiffness against aeroelastic instability. In conclusion, more than 10 modes must be considered in order to obtain any subsequent reliable aeroelastic characteristics. Moreover, it can be concluded that the representation of a wing by one single beam or plate structural member does not provide a comprehensive picture of dynamic characteristics of athe morphing wing studied here.