Experimental Aeroelastic Investigation of an All-Movable Horizontal Tail Model with Bending and Torsion Free-Plays
Abstract
1. Introduction
2. Experimental Model
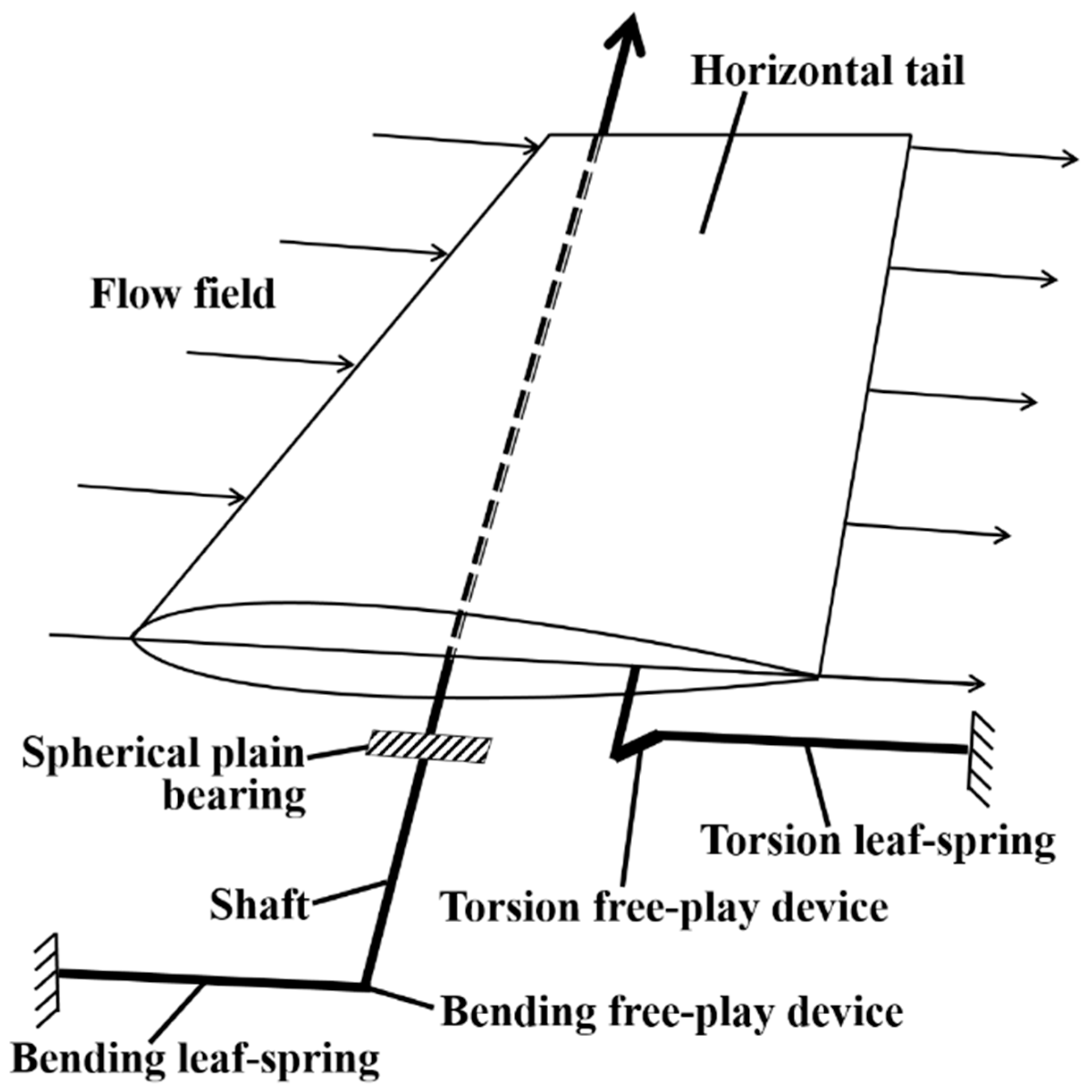
2.1. The Principle of the Model
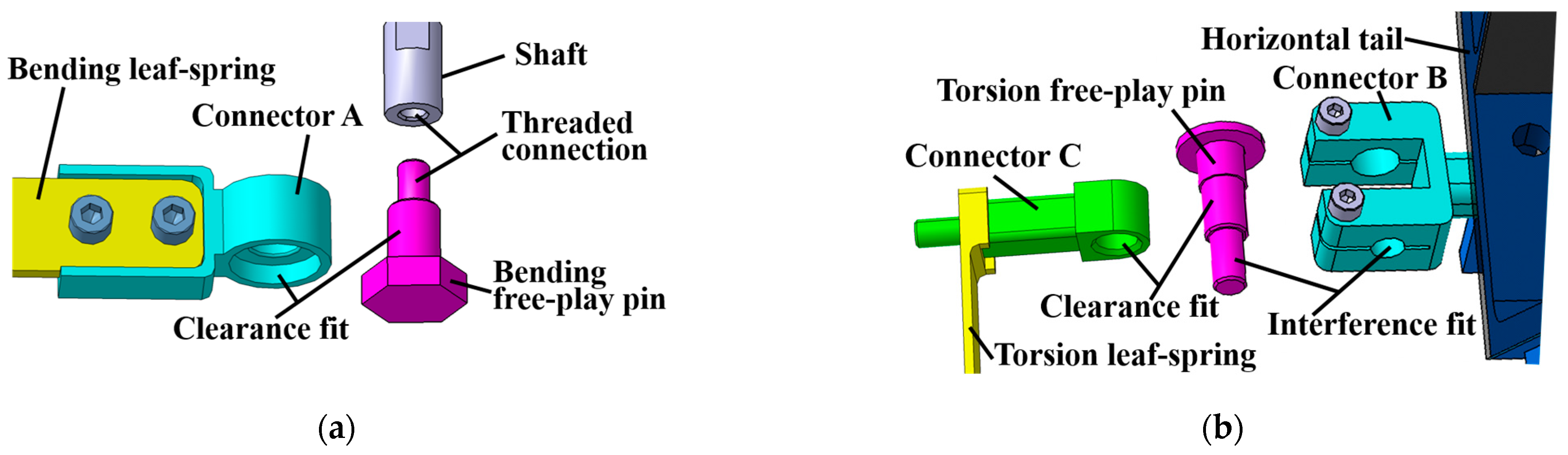
2.2. Model Design and Manufacture
3. Experimental Setup and Methodology
3.1. Free-Plays and Angle of Attack Measurements
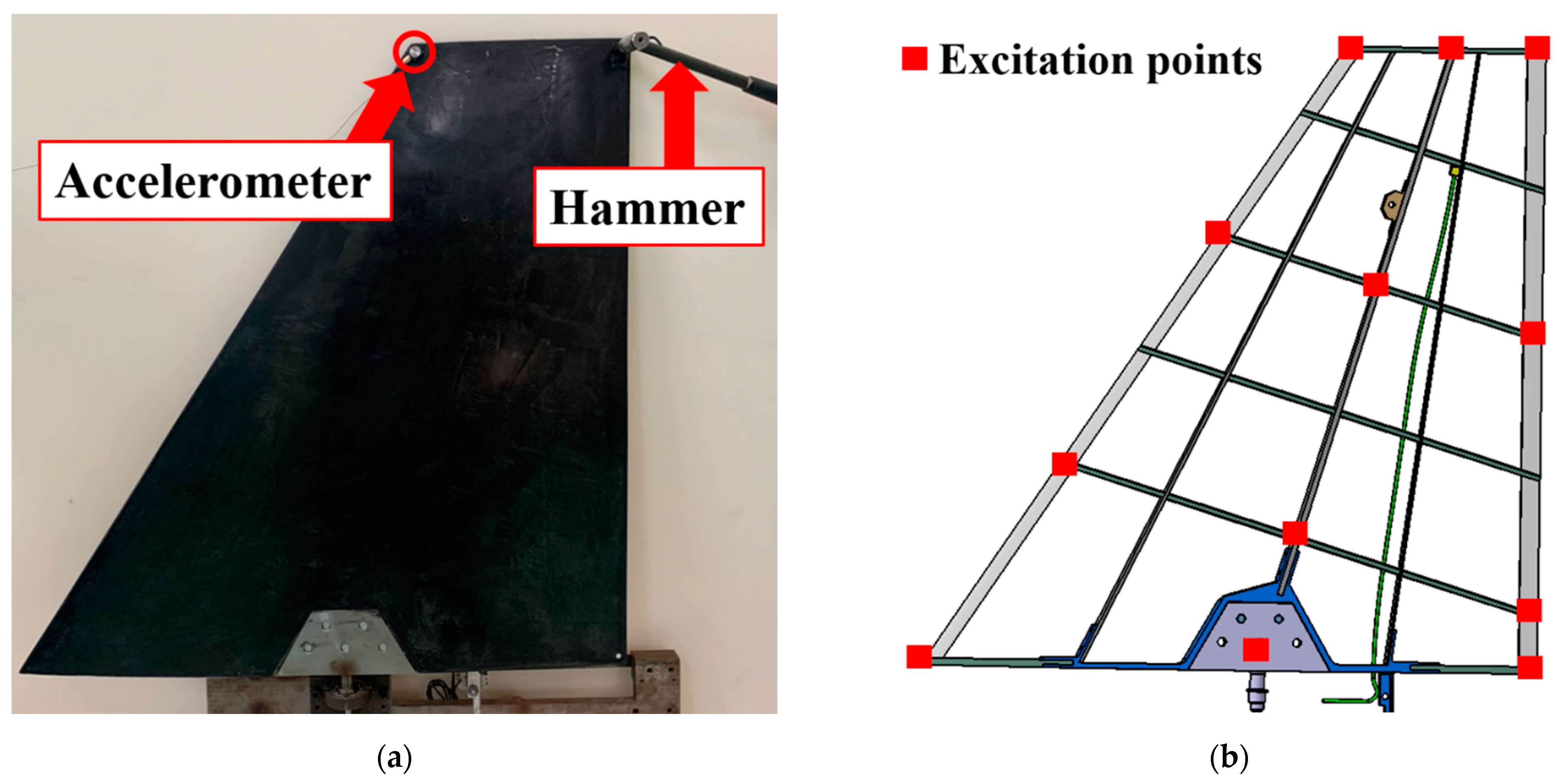
3.2. Ground Vibration Test
3.3. Data Acquisition in Wind Tunnel Tests
- Two strain gauges were glued to near the fixed end of the leaf-springs and were used to measure the bending angle and torsion angle. The experimental sampling rate was 128 points per second, and the sampling length was 3840 points;
- A built-in shear piezoelectric accelerometer manufactured by PCB piezotronics incorporated was placed inside the skin of the model (i.e., as shown in Figure 3a: the position of the accelerometer was 534.1 mm from the root and 96.4 mm from the trailing edge). The sensitivity of the accelerometer was 100.0 mV/g (10.20 mV/m/s2). The experimental sampling rate was set to 128 Hz;
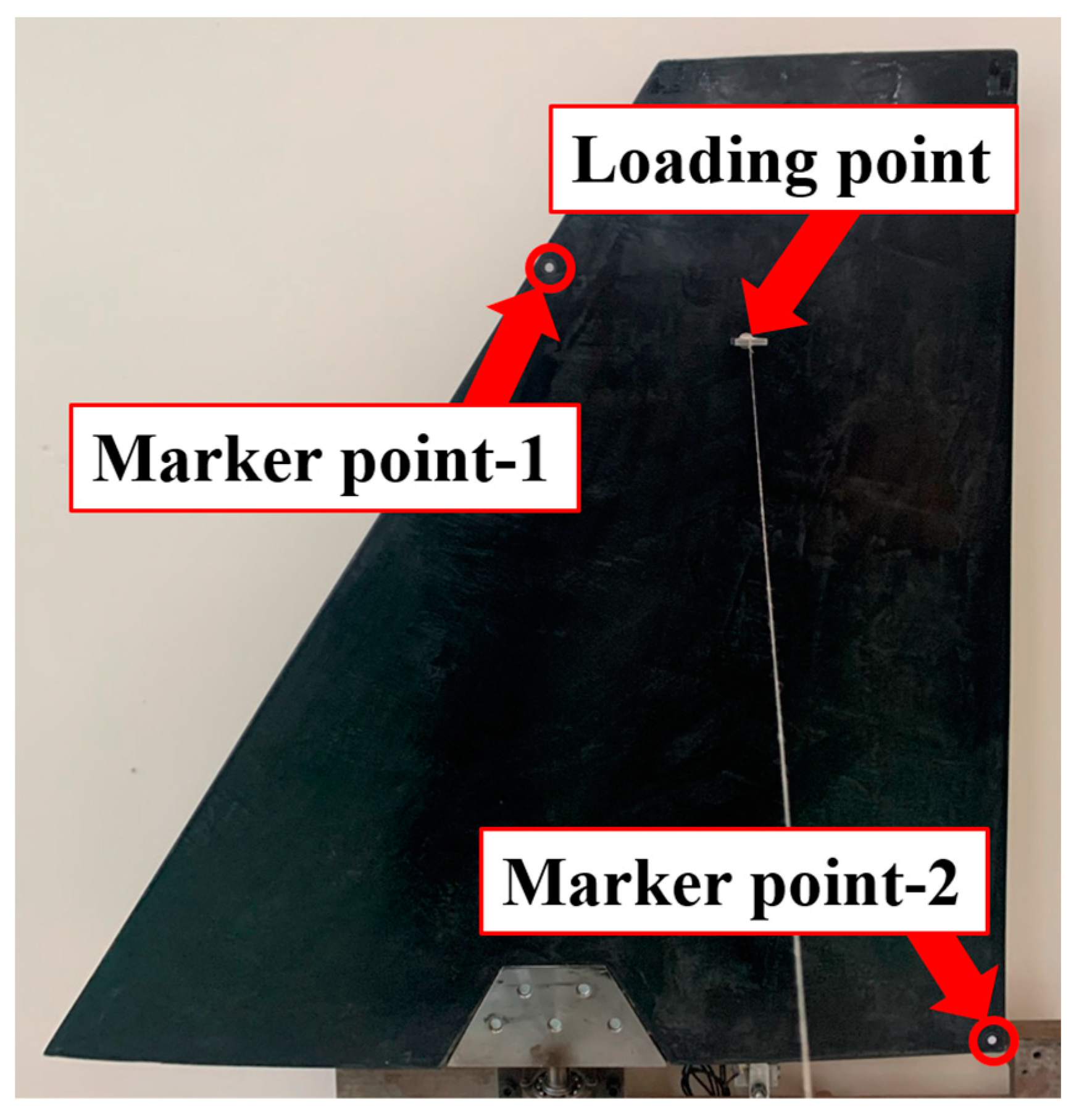
- A set of marker points was pasted on one side of the model to obtain the transient states during the vibration process (i.e., the instantaneous displacement of each marker point could be measured by the binocular vision measurement system with a sampling frequency of 43 Hz, as shown in Figure 8b).
4. Results and Discussions
4.1. Aeroelastic Response of the Single Free-Play System
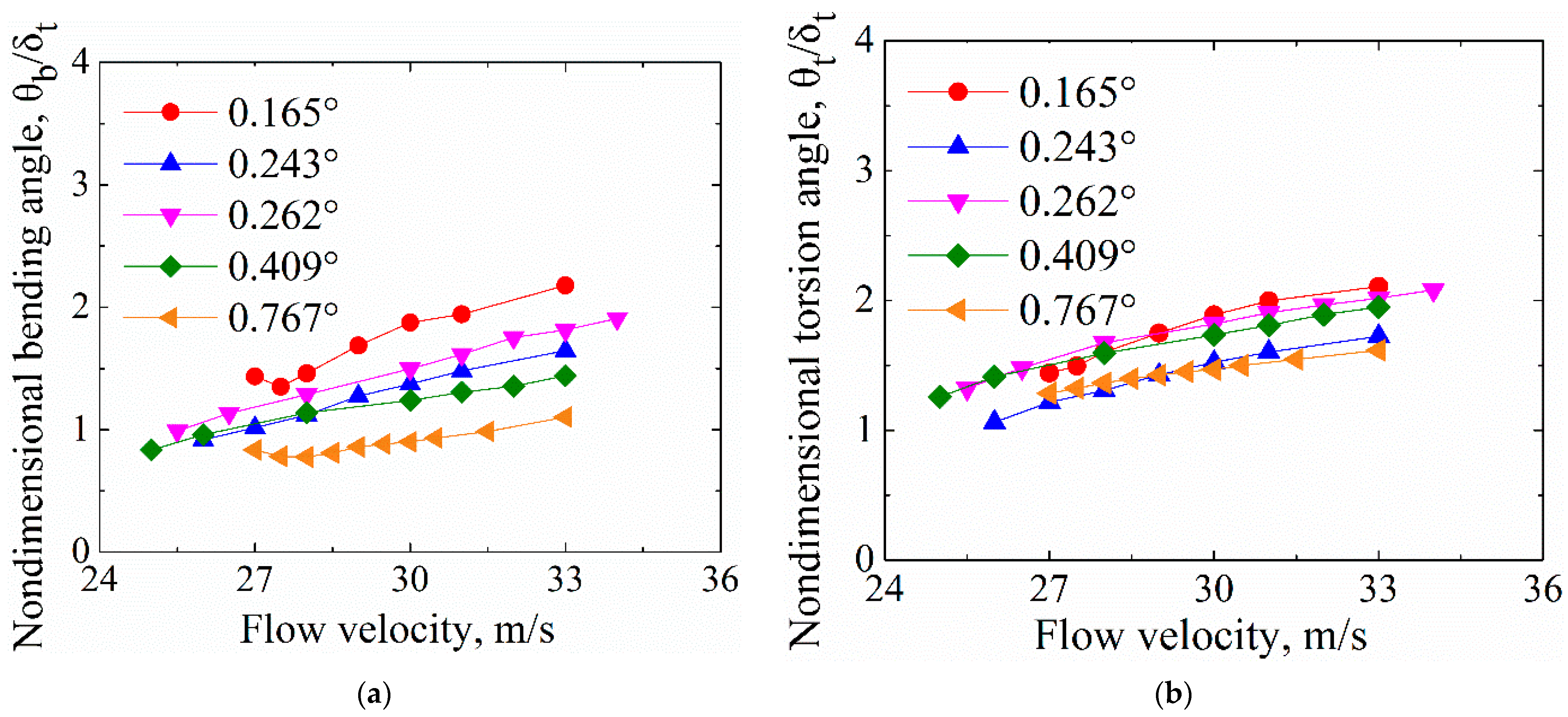
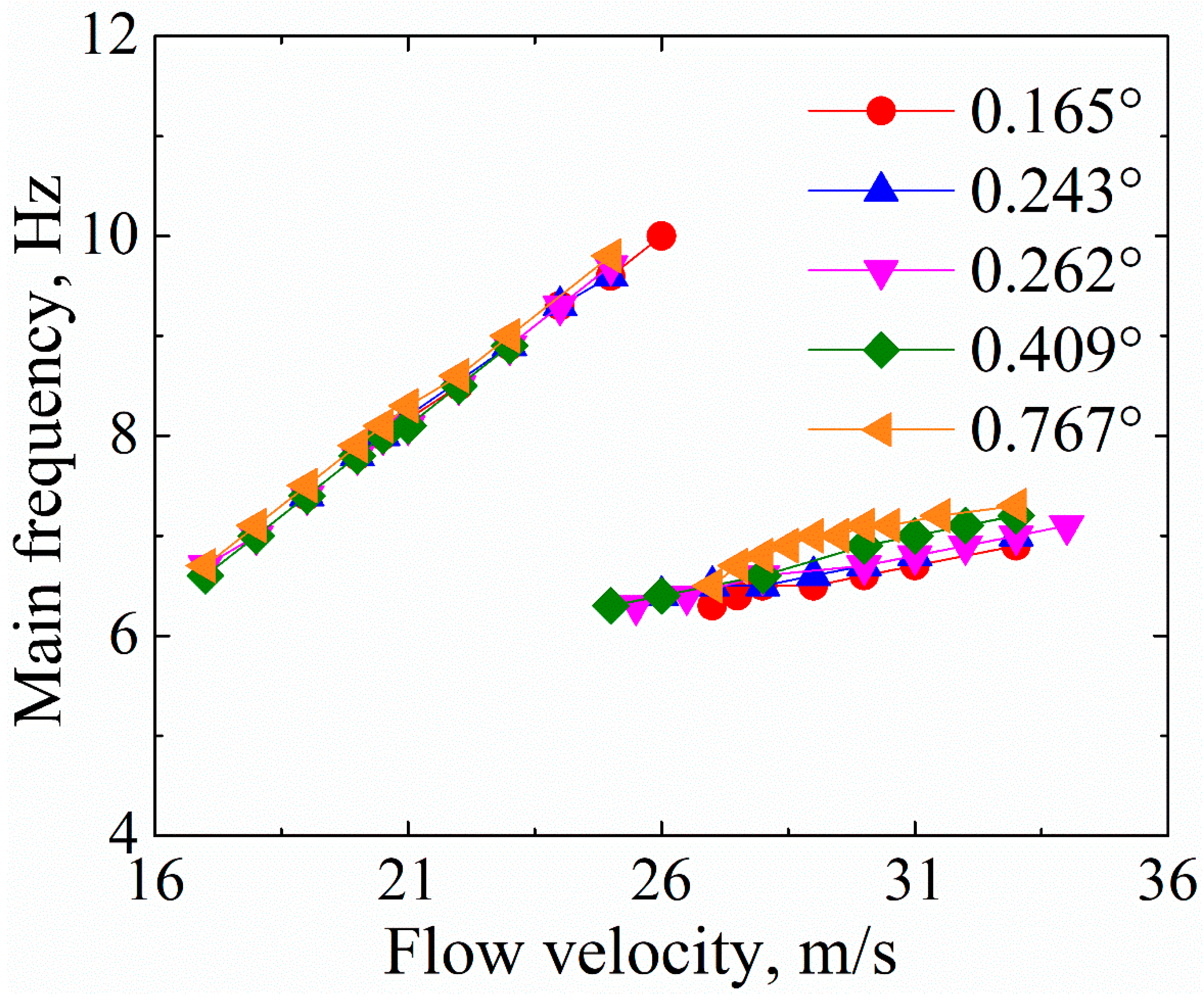
4.2. Aeroelastic Response of Multiple Free-Plays System
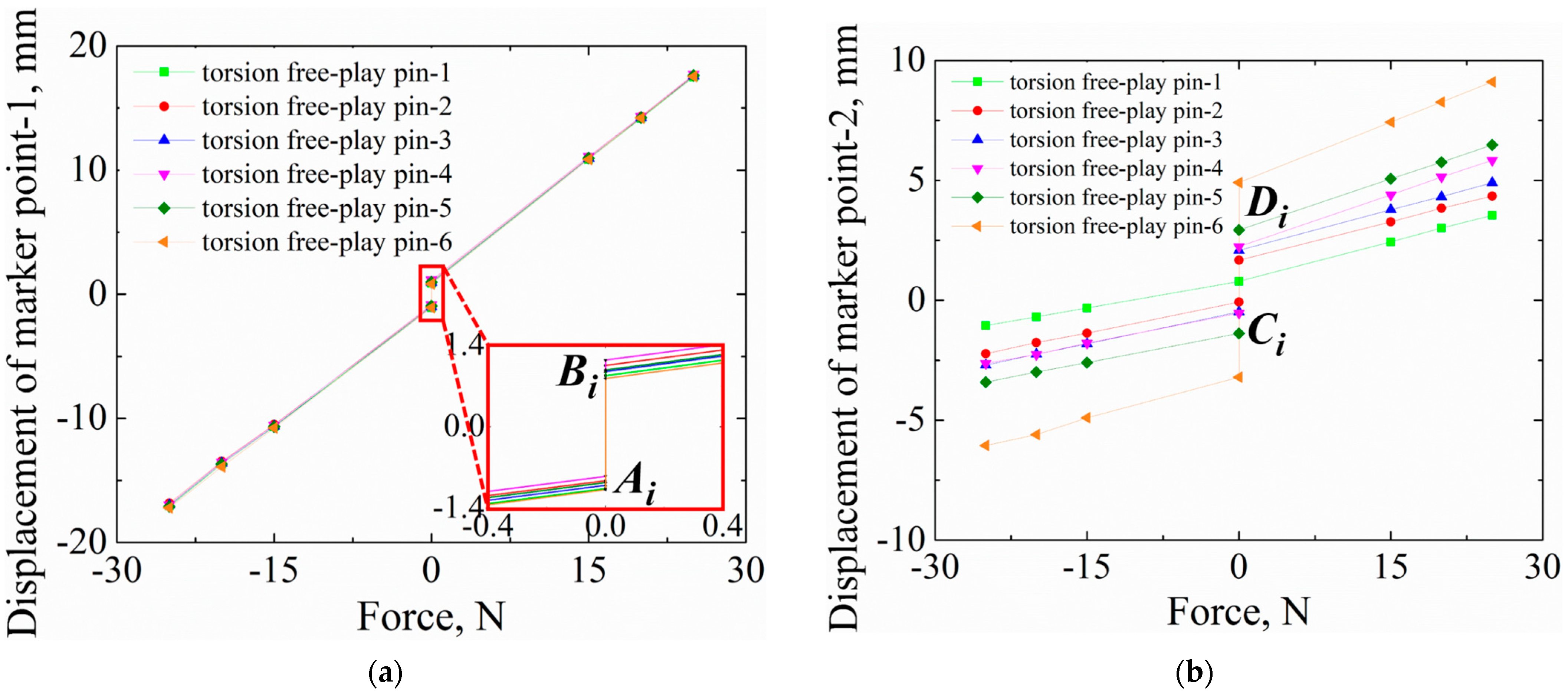
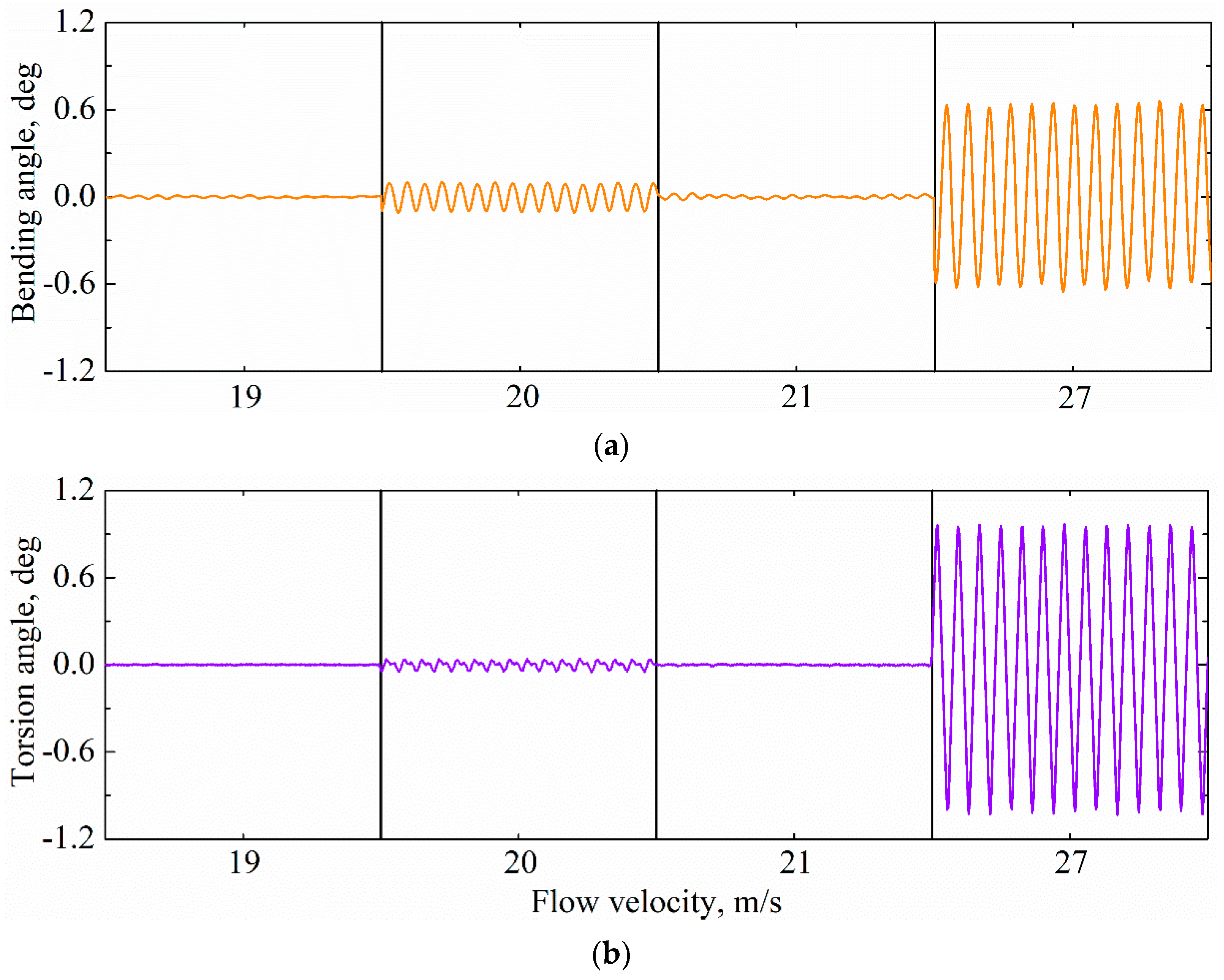
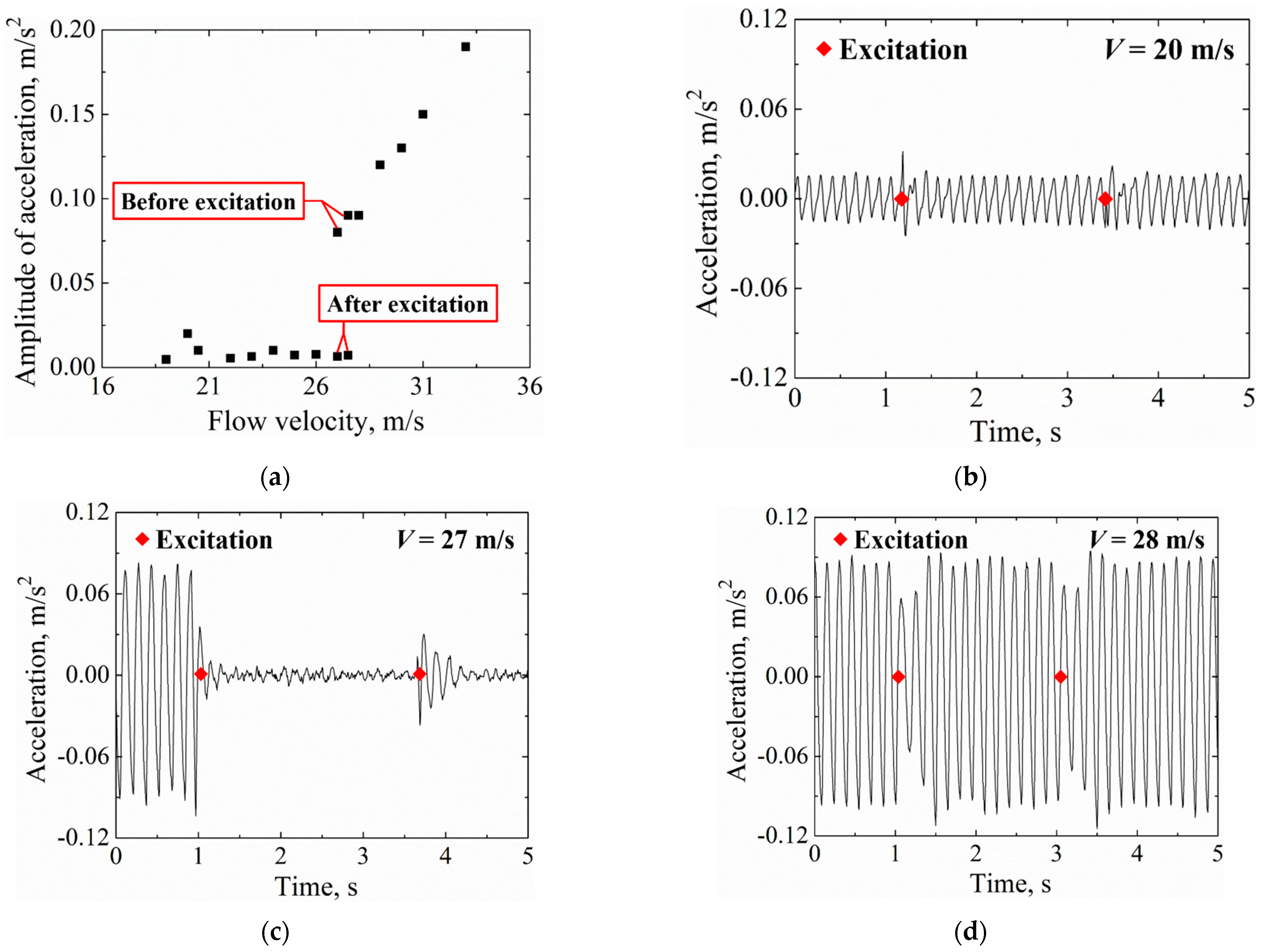
- The S-LCO appeared at V = 20 m/s and disappeared at V = 21 m/s, which is the same as the result in Section 4.1. Moreover, the L-LCO occurred when the flow velocity increased to 27 m/s. Therefore, it can be inferred that the L-LCO was caused by the torsion free-play. In addition, for simplicity, the critical flow velocities that led to the occurrences of S-LCO and L-LCO are called VS-LCO and VL-LCO, respectively;
- For S-LCO, the amplitude of bending angle was greater than that of torsion angle. However, the opposite was true for the L-LCO;
- For the L-LCO induced by torsion free-play, the vibration characteristics were very different in the free-play region and the stiffness region (see Figure 11b, V = 27 m/s). The torsion velocity was relatively stable in the free-play region, but it was more variable in the stiffness region.
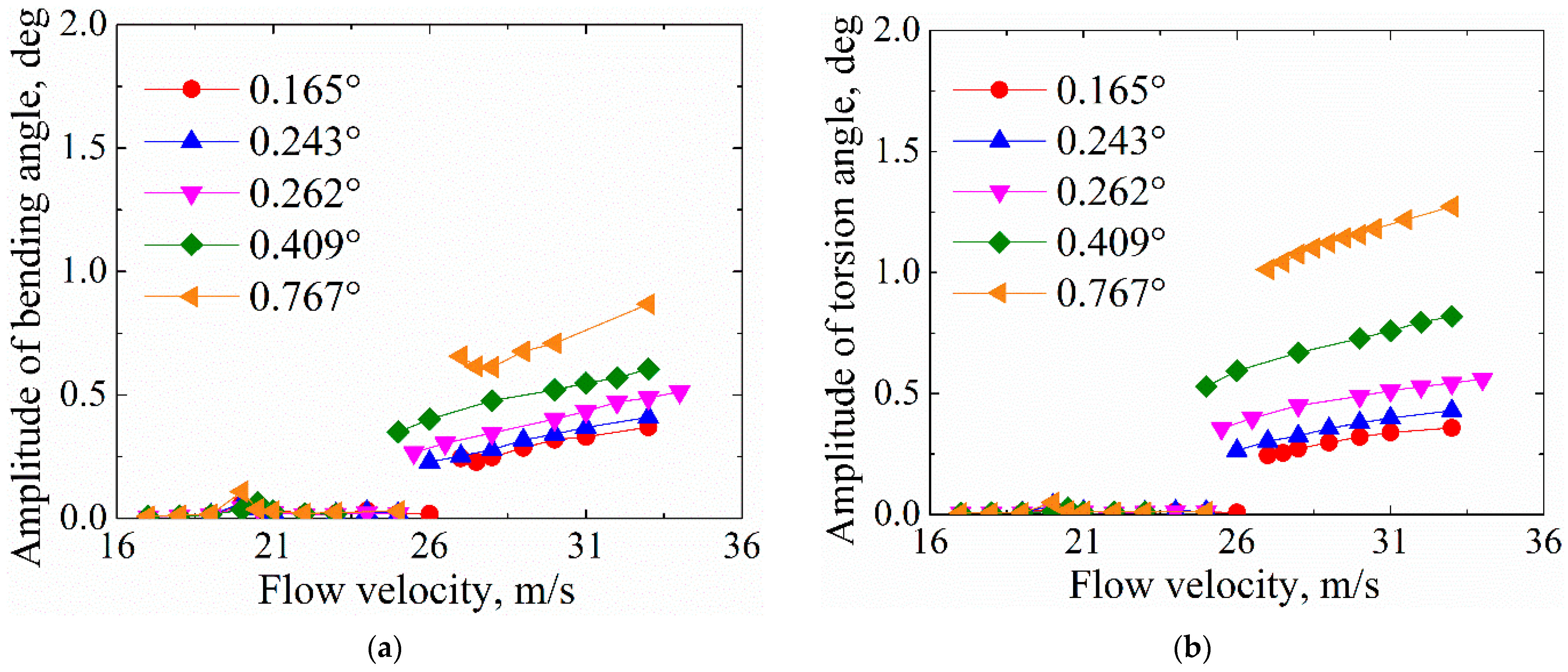
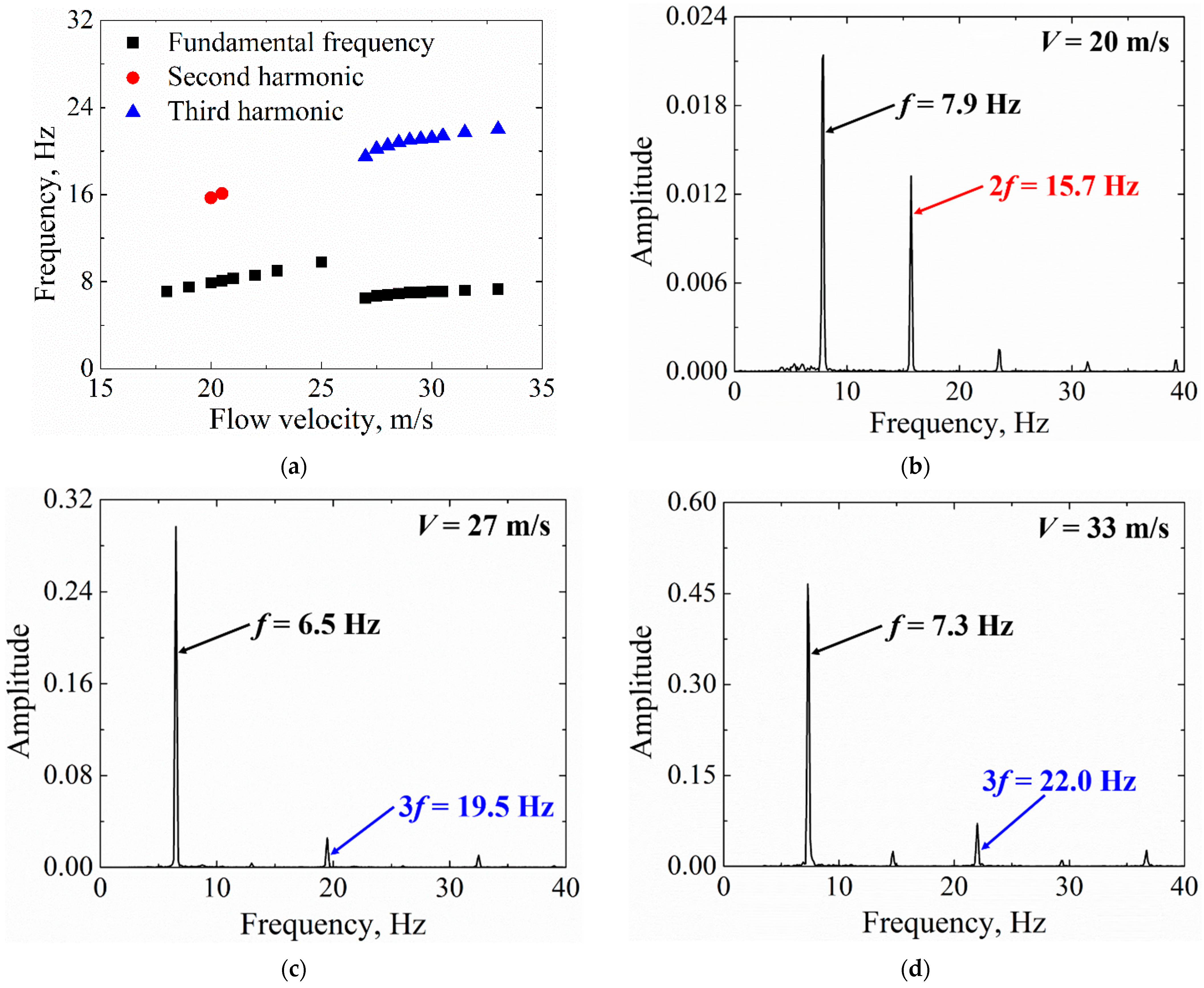
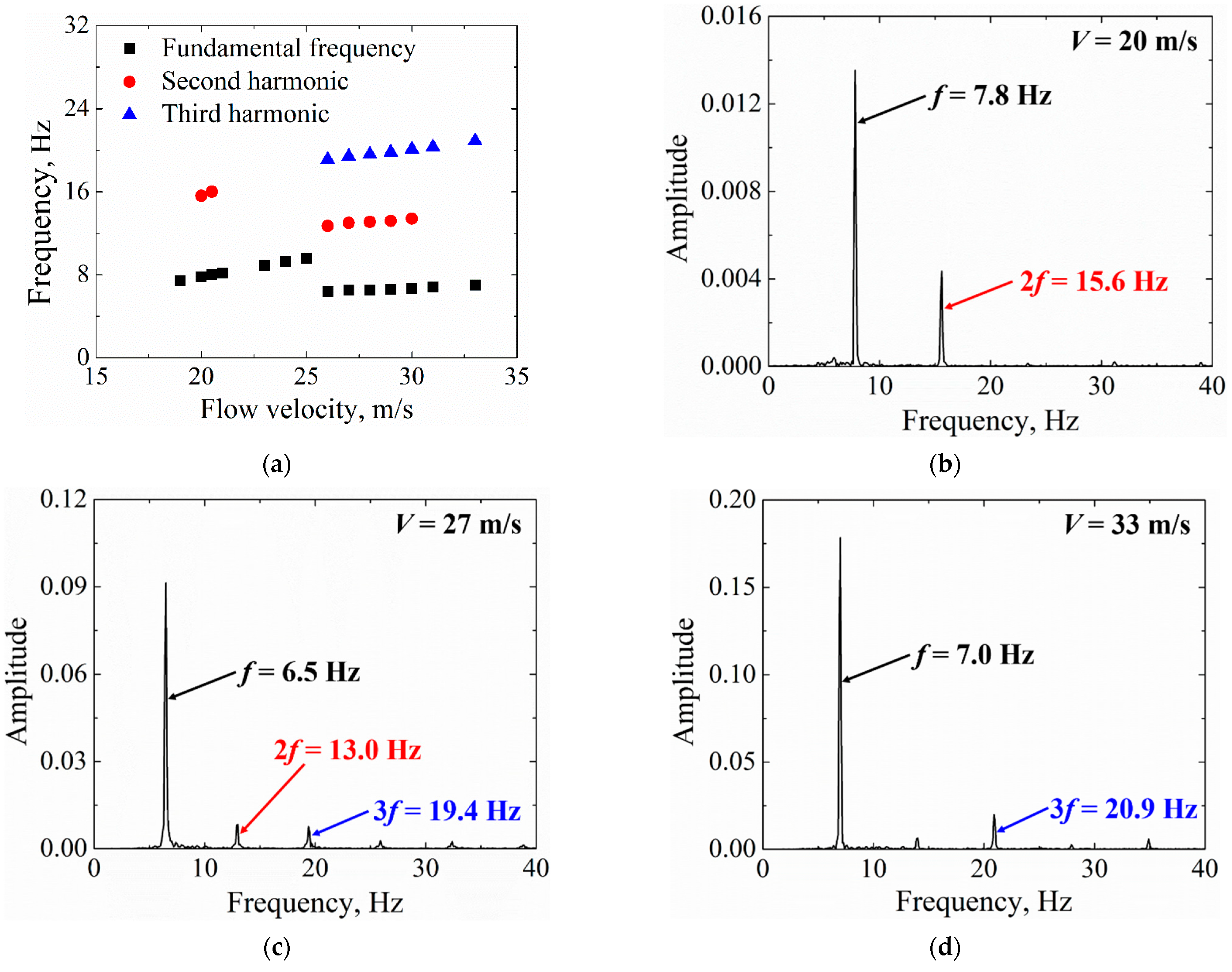
- Significant second order harmonics can sometimes be found in L-LCOs, and their appearance is related to the torsion free-play angle (see Figure 17c and Figure 18c). Additionally, a further increase in the flow velocity seems to result in a disappearance of second order harmonics in L-LCO (see Figure 16c,d).
4.3. Stability of Limit Cycles
5. Conclusions
- The all-movable horizontal tail with multiple free-plays experienced two independent LCOs, which were induced by bending free-play (S-LCO) and torsion free-play (L-LCO), respectively. Further analyses of the LCOs indicated that the S-LCO mainly contained bending vibration, while the L-LCO contained both bending vibration and torsion vibration.
- The torsion free-play angle only affected the characteristics of the L-LCO it triggered, not those of the S-LCO. The amplitude and frequency of the L-LCO increased continuously with the increase in torsion free-play angle and flow velocity.
- High-order harmonics always appeared along with LCOs. It was also found that the characteristics of high-order harmonics were related to the free-play angle and flow velocity.
- The L-LCO was unstable only when the flow velocity was slightly greater than VL-LCO. Otherwise, the L-LCO was stable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hilger, J.; Ritter, M.R. Nonlinear Aeroelastic Simulations and Stability Analysis of the Pazy Wing Aeroelastic Benchmark. Aerospace 2021, 8, 308. [Google Scholar] [CrossRef]
- Kheiri, M. Nonlinear Dynamics of Imperfectly-supported Pipes Conveying Fluid. J. Fluids Struct. 2020, 93, 102850. [Google Scholar] [CrossRef]
- Yuan, W.; Poirel, D.; Wang, B. Simulations of Pitch–Heave Limit-Cycle Oscillations at a Transitional Reynolds Number. AIAA J. 2013, 51, 1716–1732. [Google Scholar] [CrossRef]
- Eaton, A.J.; Howcroft, C.; Coetzee, E.B.; Neild, S.A.; Lowenberg, M.H.; Cooper, J.E. Numerical Continuation of Limit Cycle Oscillations and Bifurcations in High-Aspect-Ratio Wings. Aerospace 2018, 5, 78. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, D.; Zhu, X. Generation and Mitigation Mechanism Studies of Nonlinear Thermoacoustic Instability in a Modelled Swirling Combustor with a Heat Exchanger. Aerospace 2021, 8, 60. [Google Scholar] [CrossRef]
- Breitbach, E. Effects of Structural Nonlinearities on Aircraft Vibration and Flutter. In Proceedings of the 45th Structures and Materials AGARD Panel Meeting, AGARD Report 665, Voss, Norway, 26 September 1977. [Google Scholar]
- Lee, B.H.K.; Price, S.J.; Wong, Y.S. Nonlinear Aeroelastic Analysis of Airfoils: Bifurcation and Chaos. Prog. Aerosp. Sci. 1999, 35, 205–334. [Google Scholar] [CrossRef]
- Zhang, X.; Kheiri, M.; Xie, W.F. Nonlinear Dynamics and Gust Response of a Two-dimensional Wing. Int. J. Non-Linear Mech. 2020, 123, 103478. [Google Scholar] [CrossRef]
- Huang, C.; Huang, J.; Song, X.; Zheng, G.; Yang, G. Three Dimensional Aeroelastic Analyses Considering Free-play Nonlinearity Using Computational Fluid Dynamics/Computational Structural Dynamics Coupling. J. Sound Vib. 2021, 494, 115896. [Google Scholar] [CrossRef]
- Candon, M.; Levinski, O.; Ogawa, H.; Carrese, R.; Marzocca, P. A Nonlinear Signal Processing Framework for Rapid Identification and Diagnosis of Structural Freeplay. Mech. Syst. Signal Process. 2022, 163, 107999. [Google Scholar] [CrossRef]
- He, H.; Tang, H.; Yu, K.; Li, J.; Yang, N.; Zhang, X. Nonlinear Aeroelastic Analysis of the Folding Fin with Freeplay Under Thermal Environment. Chin. J. Aeronaut. 2020, 33, 2357–2371. [Google Scholar] [CrossRef]
- Candon, M.; Carrese, R.; Ogawa, H.; Marzocca, P.; Mouser, C.; Levinski, O.; Silva, W.A. Characterization of a 3DOF Aeroelastic System with Freeplay and Aerodynamic Nonlinearities-Part I: Higher-order Spectra. Mech. Syst. Signal Process. 2019, 118, 781–807. [Google Scholar] [CrossRef]
- Ma, Z.S.; Wang, B.; Zhang, X.; Ding, Q. Nonlinear System Identification of Folding Fins with Freeplay Using Direct Parameter Estimation. Int. J. Aerosp. Eng. 2019, 2019, 3978260. [Google Scholar] [CrossRef]
- Kholodar, D.B. Nature of Freeplay-induced Aeroelastic Oscillations. J. Aircr. 2014, 51, 571–583. [Google Scholar] [CrossRef]
- Tian, W.; Gu, Y.; Liu, H.; Wang, X.; Yang, Z.; Li, Y.; Li, P. Nonlinear Aeroservoelastic Analysis of a Supersonic Aircraft with Control Fin Free-play by Component Mode Synthesis Technique. J. Sound Vib. 2021, 493, 115835. [Google Scholar] [CrossRef]
- Tang, D.; Dowell, E.H. Aeroelastic Response Induced by Free Play, part 2: Theoretical/Experimental Correlation Analysis. AIAA J. 2011, 49, 2543–2554. [Google Scholar] [CrossRef]
- Wu, Z.; Yang, N.; Yang, C. Identification of Nonlinear Structures by the Conditioned Reverse Path Method. J. Aircr. 2015, 52, 373–386. [Google Scholar] [CrossRef]
- Hu, P.; Zhao, H.; Xue, L.; Ni, K.; Liu, H. High-fidelity Modeling and Simulation of Flutter/LCO for All-movable Horizontal Tail with Free-play. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Portland, OR, USA, 8–11 August 2011. [Google Scholar] [CrossRef]
- Kim, J.Y.; Kim, K.S.; Lee, I.; Park, Y.K. Transonic Aeroelastic Analysis of All-Movable Wing with Free Play and Viscous Effects. J. Aircr. 2008, 45, 1820–1824. [Google Scholar] [CrossRef]
- Tang, D.; Dowell, E.H. Computational/Experimental Aeroelastic Study for a Horizontal-Tail Model with Free Play. AIAA J. 2013, 51, 341–352. [Google Scholar] [CrossRef]
- Ni, K.; Hu, P.; Zhao, H.; Dowell, E.H. Flutter and LCO of an All-movable Horizontal Tail with Freeplay. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar] [CrossRef]
- Arévalo, F.; García-Fogeda, P. Aeroelastic Characteristics of Slender Wing/Bodies with Freeplay Non-Linearities. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2010, 225, 347–359. [Google Scholar] [CrossRef]
- Kim, S.H.; Lee, I. Aeroelastic Analysis of a Flexible Airfoil with a Free-play Nonlinearity. J. Sound Vib. 1996, 193, 823–846. [Google Scholar] [CrossRef]
- Chen, P.C.; Ritz, E.; Lindsley, N. Nonlinear Flutter Analysis for the Scaled F-35 with Horizontal-Tail Free Play. J. Aircr. 2014, 51, 883–889. [Google Scholar] [CrossRef]
- Chen, P.C.; Lee, D.H. Flight-loads Effects on Horizontal Tail Free-play-induced Limit Cycle Oscillation. J. Aircr. 2008, 45, 478–485. [Google Scholar] [CrossRef]
- Zhang, X.; Kheiri, M.; Xie, W.F. Aeroservoelasticity of an Airfoil with Parametric Uncertainty and Subjected to Atmospheric Gusts. AIAA J. 2021, 59, 4326–4341. [Google Scholar] [CrossRef]
- Tian, W.; Yang, Z.; Zhao, T. Nonlinear Aeroelastic Characteristics of an All-movable Fin with Freeplay and Aerodynamic Nonlinearities in Hypersonic Flow. Int. J. Non-Linear Mech. 2019, 116, 123–139. [Google Scholar] [CrossRef]
- Yuan, W.; Zhang, X.; Poirel, D. Numerical Modelling of Aerodynamic Response to Gust. In Proceedings of the AIAA SciTech Forum, Virtual Event, 11–15 and 19–21 January 2021. [Google Scholar] [CrossRef]
- Yuan, W.; Sandhu, R.; Poirel, D. Fully Coupled Aeroelastic Analyses of Wing Flutter towards Application to Complex Aircraft Configurations. J. Aerosp. Eng. 2021, 34, 04020117. [Google Scholar] [CrossRef]
- Di Leone, D.; Lo Balbo, F.; De Gaspari, A.; Ricci, S. Model Updating and Aeroelastic Correlation of a Scaled Wind Tunnel Model for Active Flutter Suppression Test. Aerospace 2021, 8, 334. [Google Scholar] [CrossRef]
- Afonso, F.; Coelho, M.; Vale, J.; Lau, F.; Suleman, A. On the Design of Aeroelastically Scaled Models of High Aspect-Ratio Wings. Aerospace 2020, 7, 166. [Google Scholar] [CrossRef]
- Banazadeh, A.; Hajipouzadeh, P. Using Approximate Similitude to Design Dynamic Similar Models. Aerosp. Sci. Technol. 2019, 94, 105375. [Google Scholar] [CrossRef]
- Zuo, C.; Wei, C.; Ma, J.; Yue, T.; Liu, L.; Shi, Z. Full-Field Displacement Measurements of Helicopter Rotor Blades Using Stereophotogrammetry. Int. J. Aerosp. Eng. 2021, 2021, 8811601. [Google Scholar] [CrossRef]
- Baqersad, J.; Poozesh, P.; Niezrecki, C.; Avitabile, P. Photogrammetry and Optical Methods in Structural Dynamics-A Review. Mech. Syst. Signal Process. 2017, 86, 17–34. [Google Scholar] [CrossRef]
- Tavallaeinejad, M.; Salinas, M.F.; Paidoussis, M.P.; Legrand, M.; Kheiri, M.; Botez, R.M. Dynamics of Inverted Flags: Experiments and Comparison with Theory. J. Fluids Struct. 2021, 101, 103199. [Google Scholar] [CrossRef]






| Description | Value |
|---|---|
| The length of root chord, mm | 659.1 |
| The length of tip chord, mm | 220.3 |
| The length of span, mm | 650.6 |
| Swept angle of the leading edge, deg. | 34 |
| Airfoil | NACA 0012 |
| The thickness of skin, mm | 1.0 |
| The thickness of ribs, mm | 1.0 |
| The thickness of beams (from leading edge to trailing edge), mm | 3.5, 6.0, and 2.0 |
| The length and diameter of the shaft, mm | 111.0 and 8.0 |
| The length, height, and thickness of the bending leaf-spring, mm | 141.0, 20.0, and 3.5 |
| The length, height, and thickness of the torsion leaf-spring, mm | 237.0, 16.0, and 3.2 |
| Components | Materials |
|---|---|
| Beam-rib–skin structure | GFRP (Glass fiber reinforced plastics) |
| Fairing | Pine and GFRP |
| The joint of the tail root and the shaft | Aluminum alloy |
| Leaf-springs and shaft | Steel |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, X.; Bai, Y.; Qian, W.; Li, Y.; Chen, X. Experimental Aeroelastic Investigation of an All-Movable Horizontal Tail Model with Bending and Torsion Free-Plays. Aerospace 2023, 10, 434. https://doi.org/10.3390/aerospace10050434
Ai X, Bai Y, Qian W, Li Y, Chen X. Experimental Aeroelastic Investigation of an All-Movable Horizontal Tail Model with Bending and Torsion Free-Plays. Aerospace. 2023; 10(5):434. https://doi.org/10.3390/aerospace10050434
Chicago/Turabian StyleAi, Xinyu, Yuguang Bai, Wei Qian, Yuhai Li, and Xiangyan Chen. 2023. "Experimental Aeroelastic Investigation of an All-Movable Horizontal Tail Model with Bending and Torsion Free-Plays" Aerospace 10, no. 5: 434. https://doi.org/10.3390/aerospace10050434
APA StyleAi, X., Bai, Y., Qian, W., Li, Y., & Chen, X. (2023). Experimental Aeroelastic Investigation of an All-Movable Horizontal Tail Model with Bending and Torsion Free-Plays. Aerospace, 10(5), 434. https://doi.org/10.3390/aerospace10050434






