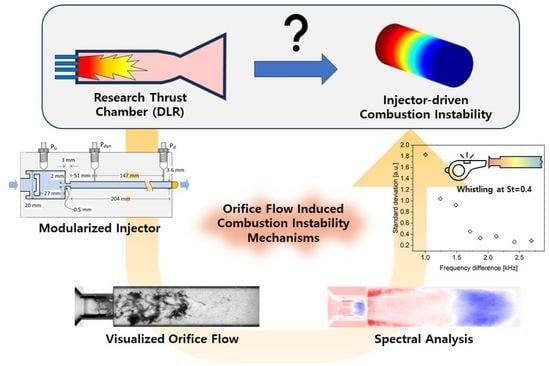
Orifice Flow Dynamics in a Rocket Injector as an Excitation Source of Injector-Driven Combustion Instabilities
Abstract
:1. Introduction
2. Experimental Setup and Methods
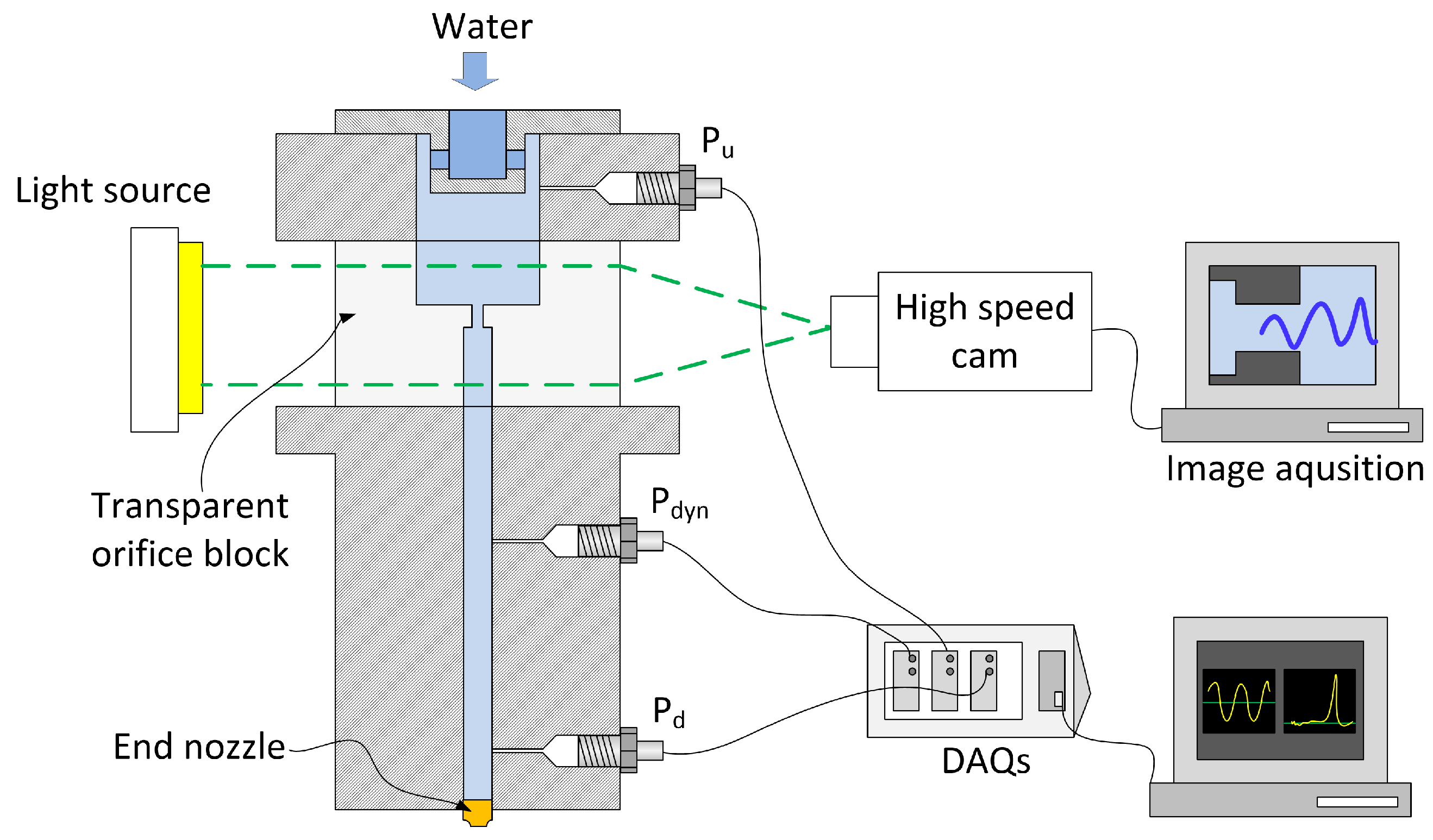
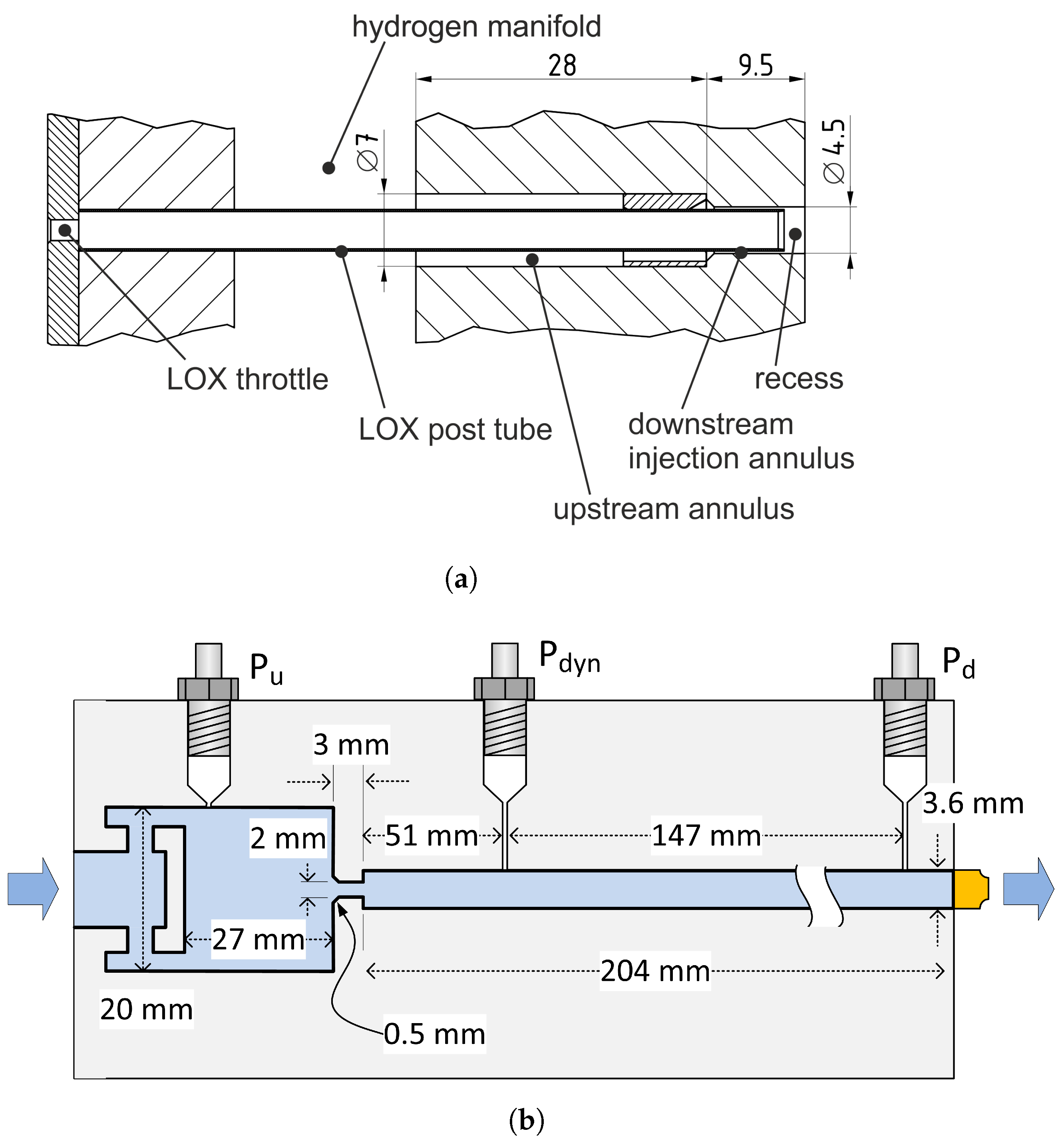
2.1. Experimental Setup and Modular Injector Tube
2.2. Experimental Conditions
3. Results and Discussion
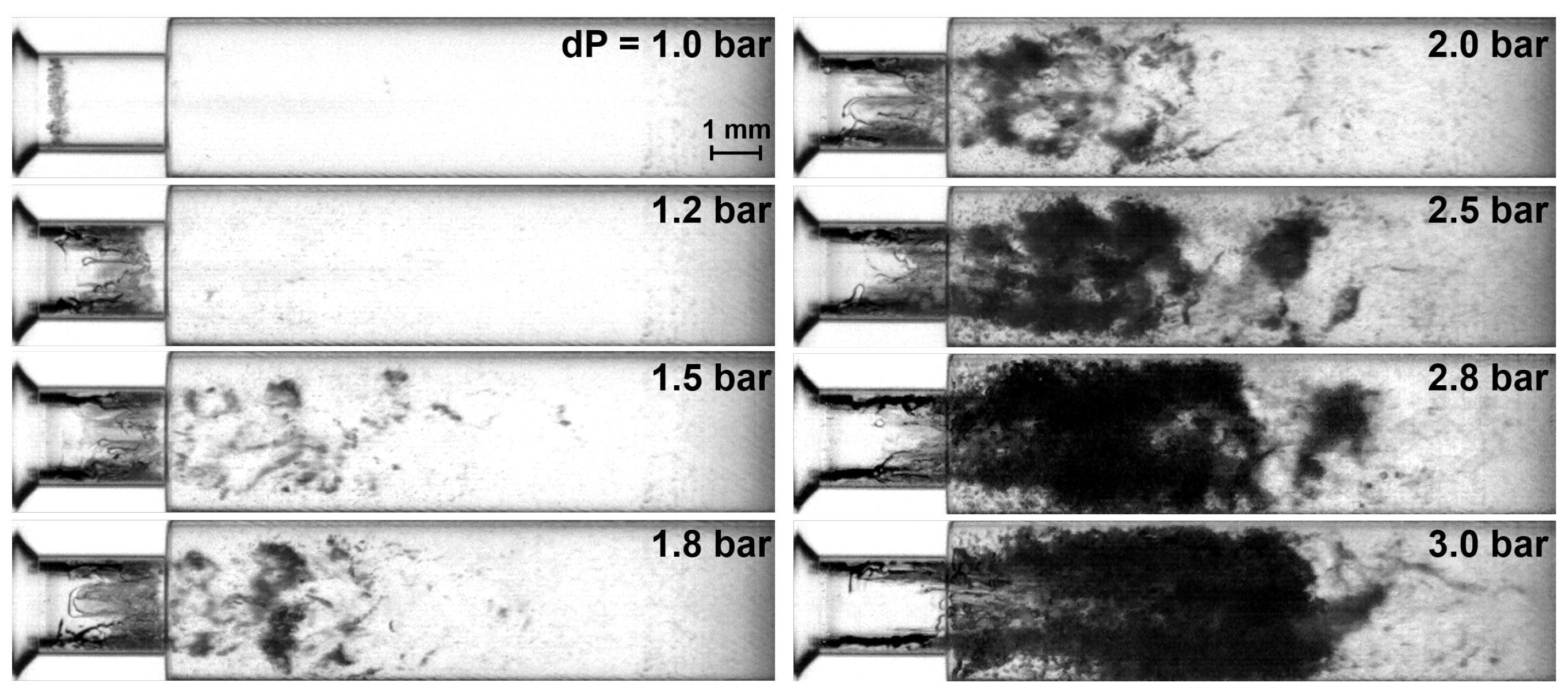
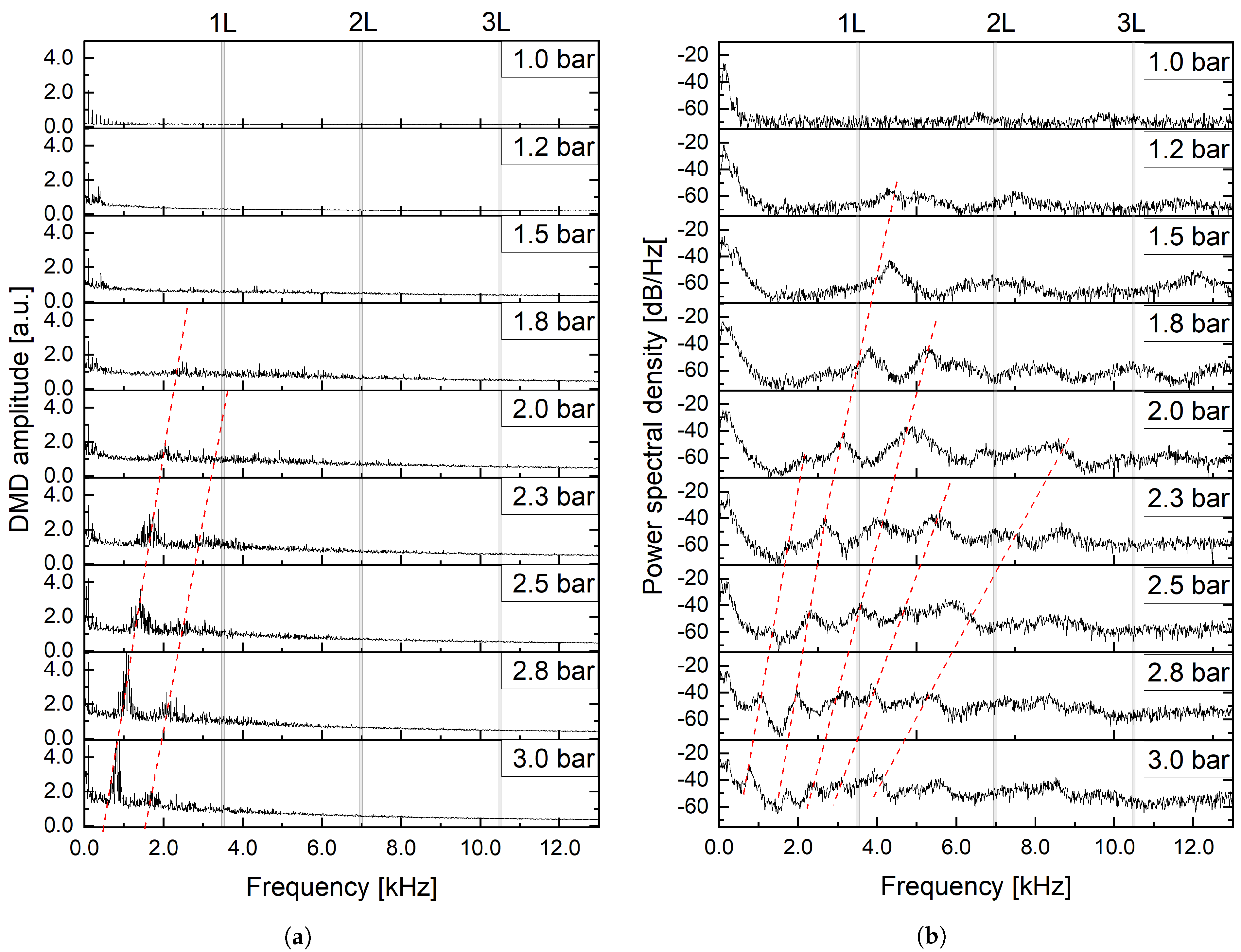
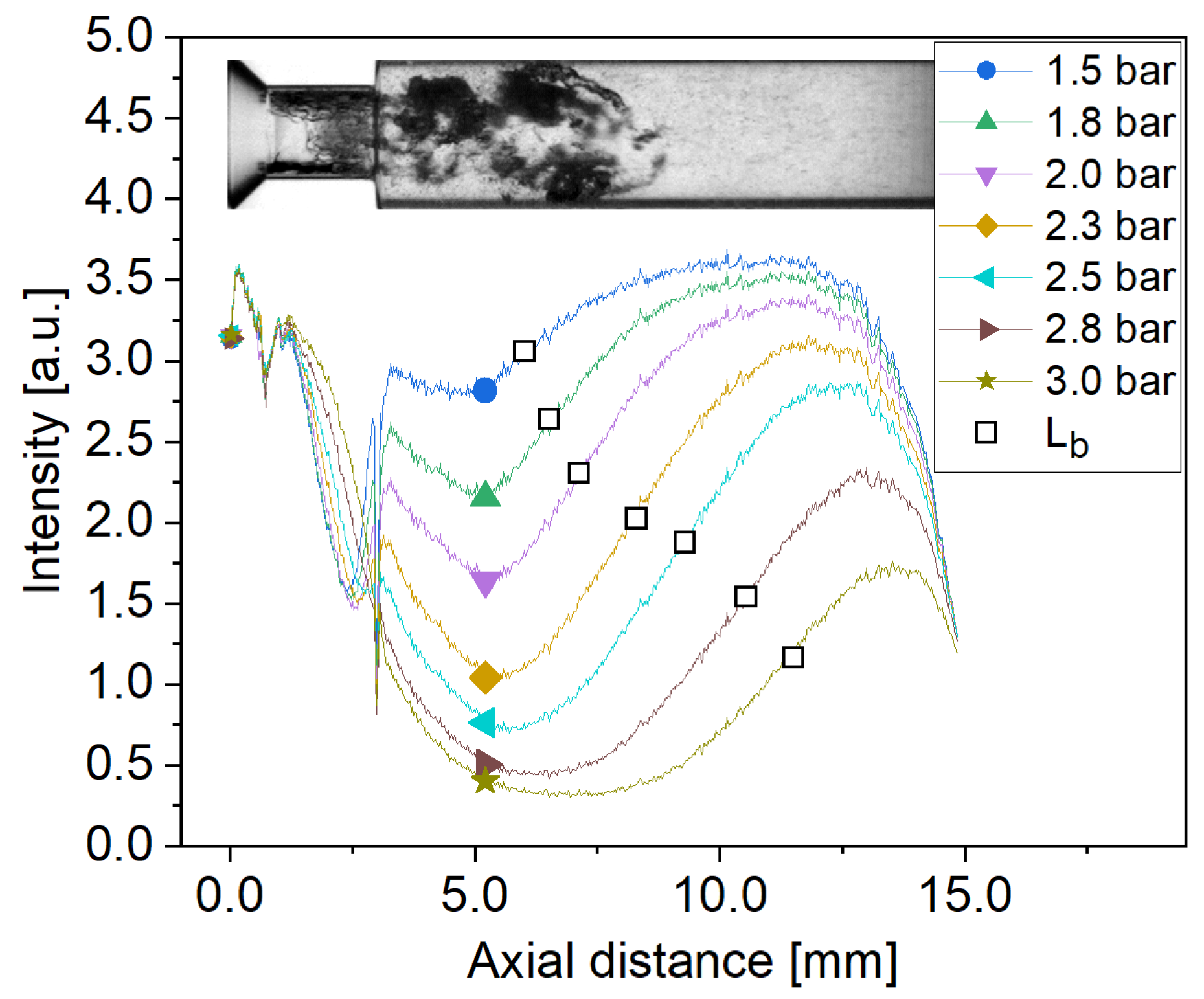
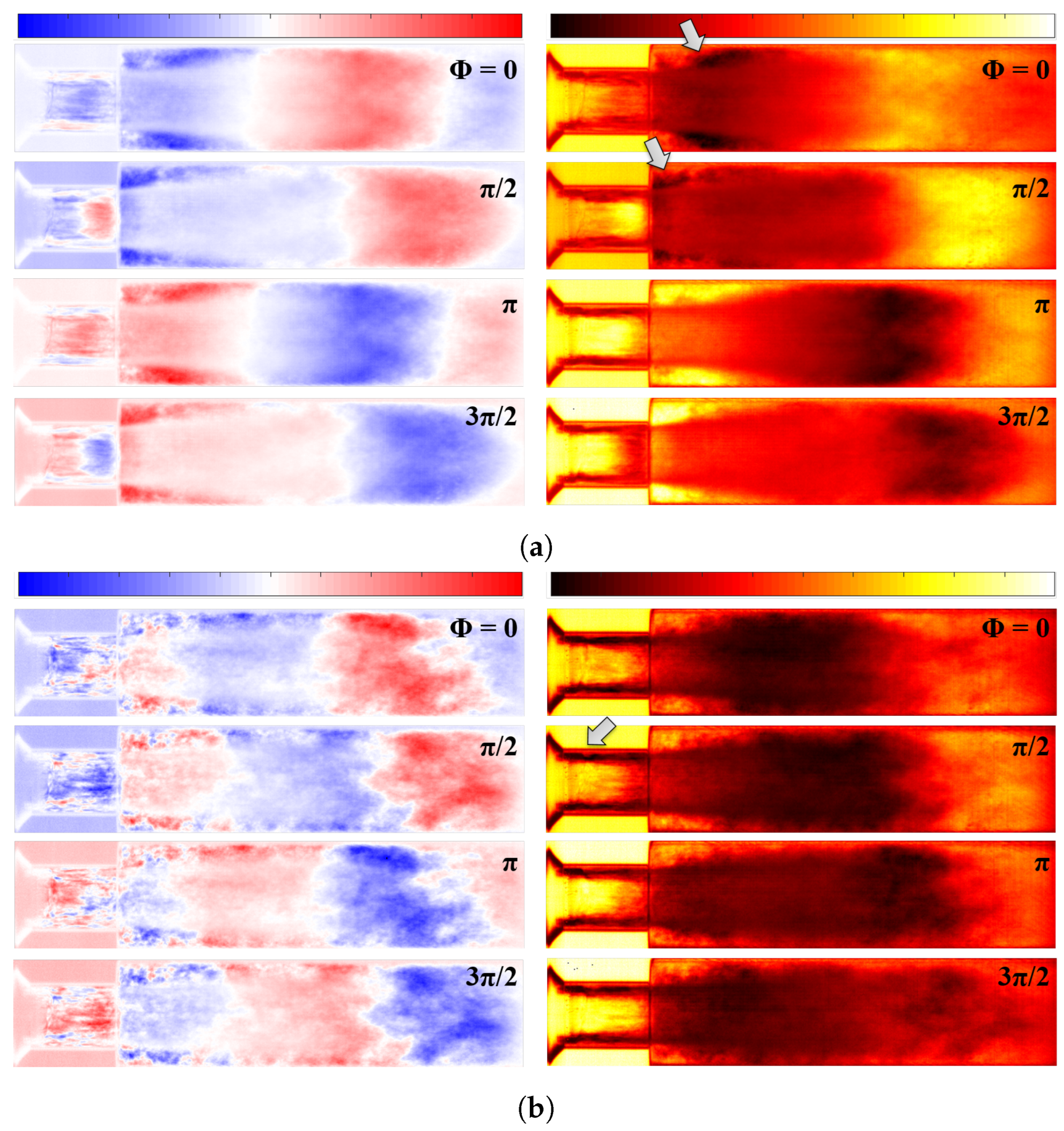
3.1. Periodic Fluctuation of Cavitating Flow
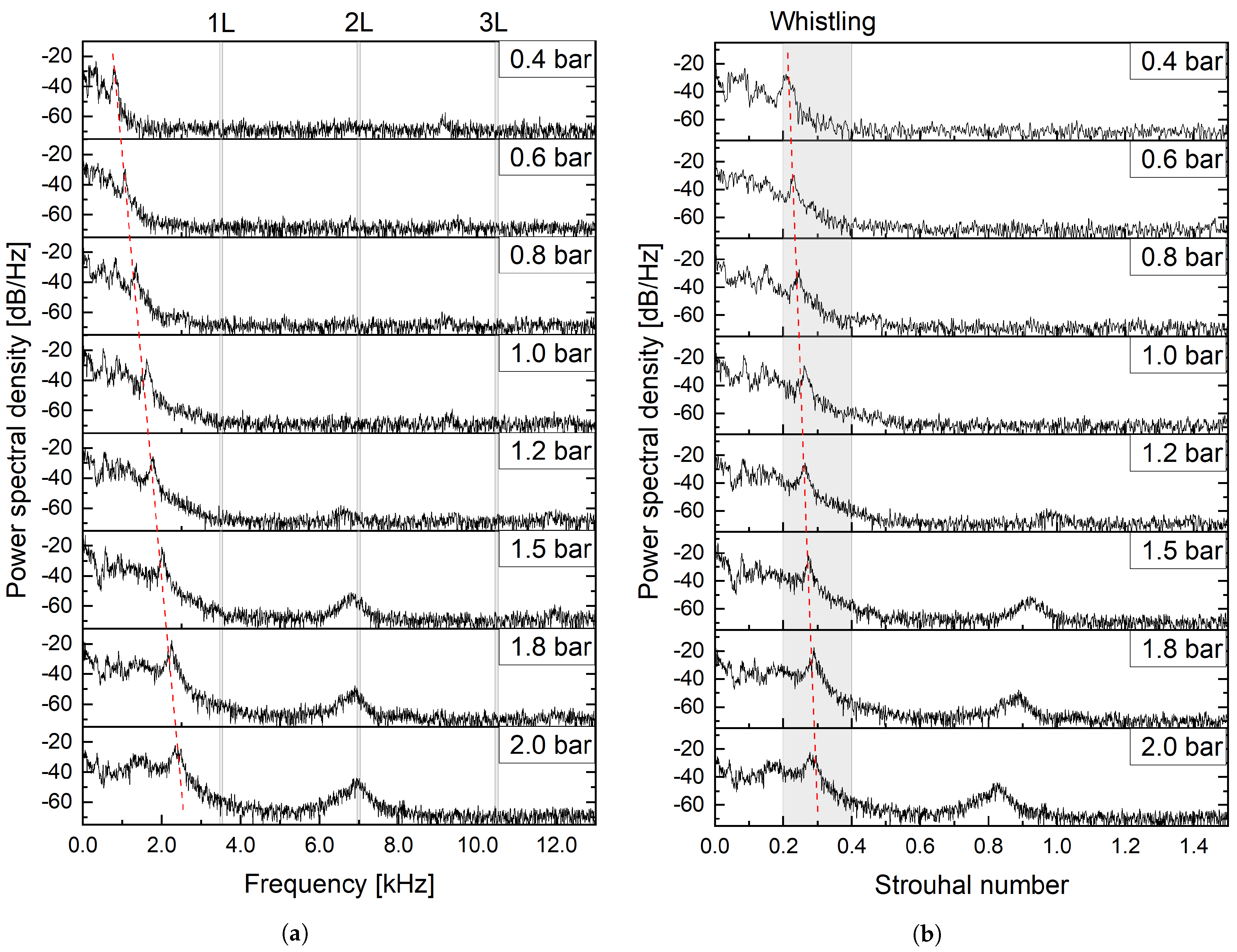
3.2. Periodic Fluctuation of Non-Cavitating Flow
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sutton, G.P.; Biblarz, O. Rocket Propulsion Elements; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Gröning, S.; Hardi, J.S.; Suslov, D.; Oschwald, M. Injector-driven combustion instabilities in a hydrogen/oxygen rocket combustor. J. Propuls. Power 2016, 32, 560–573. [Google Scholar] [CrossRef]
- Armbruster, W.; Hardi, J.S.; Suslov, D.; Oschwald, M. Injector-Driven Flame Dynamics in a High-Pressure Multi-Element Oxygen–Hydrogen Rocket Thrust Chamber. J. Propuls. Power 2019, 35, 632–644. [Google Scholar] [CrossRef]
- Armbruster, W.; Hardi, J.; Oschwald, M. Impact of shear-coaxial injector hydrodynamics on high-frequency combustion instabilities in a representative cryogenic rocket engine. Int. J. Spray Combust. Dyn. 2022, 14, 118–130. [Google Scholar] [CrossRef]
- Tsohas, J.; Heister, S. Cfd simulations of liquid rocket coaxial injector hydrodynamics. In Proceedings of the 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Denver, CO, USA, 2–5 August 2009; p. 5387. [Google Scholar]
- Hardi, J.; Martin, J.; Son, M.; Armbruster, W.; Deeken, J.C.; Suslov, D.; Oschwald, M. Combustion Stability Characteristics of a sub-scale LOX/LNG Rocket Thrust Chamber. In Proceedings of the Aerospace Europe Conference 2020, Bordeaux, France, 25–28 February 2020. [Google Scholar]
- Klein, S.; Börner, M.; Hardi, J.S.; Suslov, D.; Oschwald, M. Injector-coupled thermoacoustic instabilities in an experimental LOX-methane rocket combustor during start-up. Ceas Space J. 2020, 12, 267–279. [Google Scholar] [CrossRef]
- Hitt, M.; Lineberry, D.; Ahuja, V.; Frederick, R. Experimental investigation of cavitation induced feedline instability from an orifice. In Proceedings of the 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Atlanta, GA, USA, 30 July–1 August 2012; p. 4029. [Google Scholar]
- Sato, K.; Saito, Y. Unstable cavitation behavior in a circular-cylindrical orifice flow. JSME Int. J. Ser. Fluids Therm. Eng. 2002, 45, 638–645. [Google Scholar] [CrossRef]
- Sugimoto, Y.; Sato, K. Visualization of unsteady behavior of cavitation in circular cylindrical orifice with abruptly expanding part. In Proceedings of the 13th International Topical Meeting on Nuclear Reactor Thermal Hydraulics, Kanazawa, Japan, 27 September–2 October 2009; Volume 13. [Google Scholar]
- Esposito, C.; Mendez, M.; Steelant, J.; Vetrano, M.R. Spectral and modal analysis of a cavitating flow through an orifice. Exp. Therm. Fluid Sci. 2021, 121, 110251. [Google Scholar] [CrossRef]
- Ge, M.; Petkovšek, M.; Zhang, G.; Jacobs, D.; Coutier-Delgosha, O. Cavitation dynamics and thermodynamic effects at elevated temperatures in a small Venturi channel. Int. J. Heat Mass Transf. 2021, 170, 120970. [Google Scholar] [CrossRef]
- Ge, M.; Manikkam, P.; Ghossein, J.; Subramanian, R.K.; Coutier-Delgosha, O.; Zhang, G. Dynamic mode decomposition to classify cavitating flow regimes induced by thermodynamic effects. Energy 2022, 254, 124426. [Google Scholar] [CrossRef]
- Egerer, C.P.; Hickel, S.; Schmidt, S.J.; Adams, N.A. Large-eddy simulation of turbulent cavitating flow in a micro channel. Phys. Fluids 2014, 26, 085102. [Google Scholar] [CrossRef]
- Brandao, F.L.; Bhatt, M.; Mahesh, K. Numerical study of cavitation regimes in flow over a circular cylinder. J. Fluid Mech. 2020, 885, A19. [Google Scholar] [CrossRef]
- Sadri, M.; Kadivar, E. Numerical investigation of the cavitating flow and the cavitation-induced noise around one and two circular cylinders. Ocean. Eng. 2023, 277, 114178. [Google Scholar] [CrossRef]
- Anderson, A. Dependence of Pfeifenton (pipe tone) frequency on pipe length, orifice diameter, and gas discharge pressure. J. Acoust. Soc. Am. 1952, 24, 675–681. [Google Scholar] [CrossRef]
- Testud, P.; Moussou, P.; Hirschberg, A.; Aurégan, Y. Noise generated by cavitating single-hole and multi-hole orifices in a water pipe. J. Fluids Struct. 2007, 23, 163–189. [Google Scholar] [CrossRef]
- Alenius, E.; Åbom, M.; Fuchs, L. Large eddy simulations of acoustic-flow interaction at an orifice plate. J. Sound Vib. 2015, 345, 162–177. [Google Scholar] [CrossRef]
- Lacombe, R.; Föller, S.; Jasor, G.; Polifke, W.; Aurégan, Y.; Moussou, P. Identification of aero-acoustic scattering matrices from large eddy simulation: Application to whistling orifices in duct. J. Sound Vib. 2013, 332, 5059–5067. [Google Scholar] [CrossRef]
- Son, M.; Armbruster, W.; Tonti, F.; Hardi, J. Numerical study of acoustic resonance in a LOX injector post induced by orifice flow. In Proceedings of the AIAA Propulsion and Energy 2021 Forum, Virtual Event, 9–11 August 2021; p. 3568. [Google Scholar]
- Brokof, P.; Guzmán-Iñigo, J.; Yang, D.; Morgans, A.S. The acoustics of short circular holes with reattached bias flow. J. Sound Vib. 2023, 546, 117435. [Google Scholar] [CrossRef]
- Abom, M.; Allam, S.; Boij, S. Aero-acoustics of flow duct singularities at low mach numbers. In Proceedings of the 12th AIAA/CEAS Aeroacoustics Conference (27th AIAA Aeroacoustics Conference), Cambridge, MA, USA, 8–10 May 2006; p. 2687. [Google Scholar]
- Moussou, P.; Testud, P.; Aure´gan, Y.; Hirschberg, A. An acoustic criterion for the whistling of orifices in pipes. In Proceedings of the ASME Pressure Vessels and Piping Conference, San Antonio, TX, USA, 22–26 July 2007; Volume 42827, pp. 345–353. [Google Scholar]
- Testud, P.; Aurégan, Y.; Moussou, P.; Hirschberg, A. The whistling potentiality of an orifice in a confined flow using an energetic criterion. J. Sound Vib. 2009, 325, 769–780. [Google Scholar] [CrossRef]
- Lacombe, R.; Moussou, P.; Aurégan, Y. Whistling of an orifice in a reverberating duct at low Mach number. J. Acoust. Soc. Am. 2011, 130, 2662–2672. [Google Scholar] [CrossRef] [PubMed]
- Kiesbauer, J. Control valves for critical applications. Hydrocarb. Process. 2001, 80, 89–100. [Google Scholar]
- Yan, Y.; Thorpe, R. Flow regime transitions due to cavitation in the flow through an orifice. Int. J. Multiph. Flow 1990, 16, 1023–1045. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Kutz, J.N.; Brunton, S.L.; Brunton, B.W.; Proctor, J.L. Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems; Society for Industrial & Applied Mathematics: New York, NY, USA, 2016. [Google Scholar]
- Demmel, J. Singular value decomposition. In Templates for the Solution of Algebraic Eigenvalue Problems: A Practical Guide; Society for Industrial & Applied Mathematics: New York, NY, USA, 2000; pp. 135–147. [Google Scholar]
- Franc, J.P. The Rayleigh-Plesset equation: A simple and powerful tool to understand various aspects of cavitation. In Fluid Dynamics of Cavitation and Cavitating Turbopumps; Springer: Berlin/Heidelberg, Germany, 2007; pp. 1–41. [Google Scholar]





| Campaign | BKD [3] | Present |
|---|---|---|
| Medium | LOX | Water |
| Temperature () | 112 | Room temperature |
| First longitudinal mode, 1 L () | 5.2 | 3.5 |
| Second longitudinal mode, 2 L () | 10.4 | 7.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, M.; Börner, M.; Armbruster, W.; Hardi, J.S. Orifice Flow Dynamics in a Rocket Injector as an Excitation Source of Injector-Driven Combustion Instabilities. Aerospace 2023, 10, 452. https://doi.org/10.3390/aerospace10050452
Son M, Börner M, Armbruster W, Hardi JS. Orifice Flow Dynamics in a Rocket Injector as an Excitation Source of Injector-Driven Combustion Instabilities. Aerospace. 2023; 10(5):452. https://doi.org/10.3390/aerospace10050452
Chicago/Turabian StyleSon, Min, Michael Börner, Wolfgang Armbruster, and Justin S. Hardi. 2023. "Orifice Flow Dynamics in a Rocket Injector as an Excitation Source of Injector-Driven Combustion Instabilities" Aerospace 10, no. 5: 452. https://doi.org/10.3390/aerospace10050452
APA StyleSon, M., Börner, M., Armbruster, W., & Hardi, J. S. (2023). Orifice Flow Dynamics in a Rocket Injector as an Excitation Source of Injector-Driven Combustion Instabilities. Aerospace, 10(5), 452. https://doi.org/10.3390/aerospace10050452