Combined Experimental and Numerical Investigation of a Hypersonic Turbulent Boundary Layer by Means of FLDI and Large-Eddy Simulations
Abstract
:1. Introduction
2. Materials and Methods
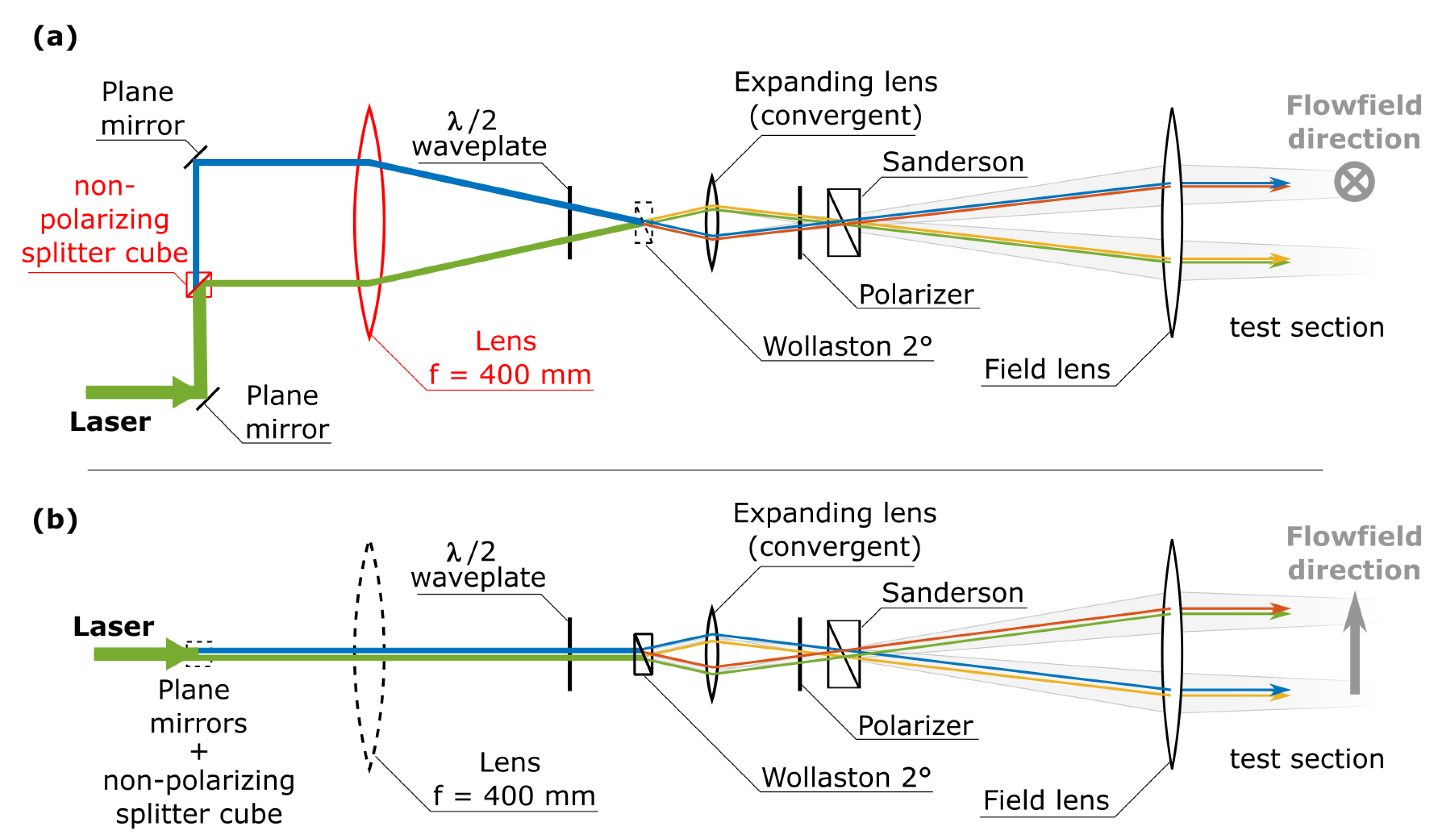
2.1. Experimental Setup
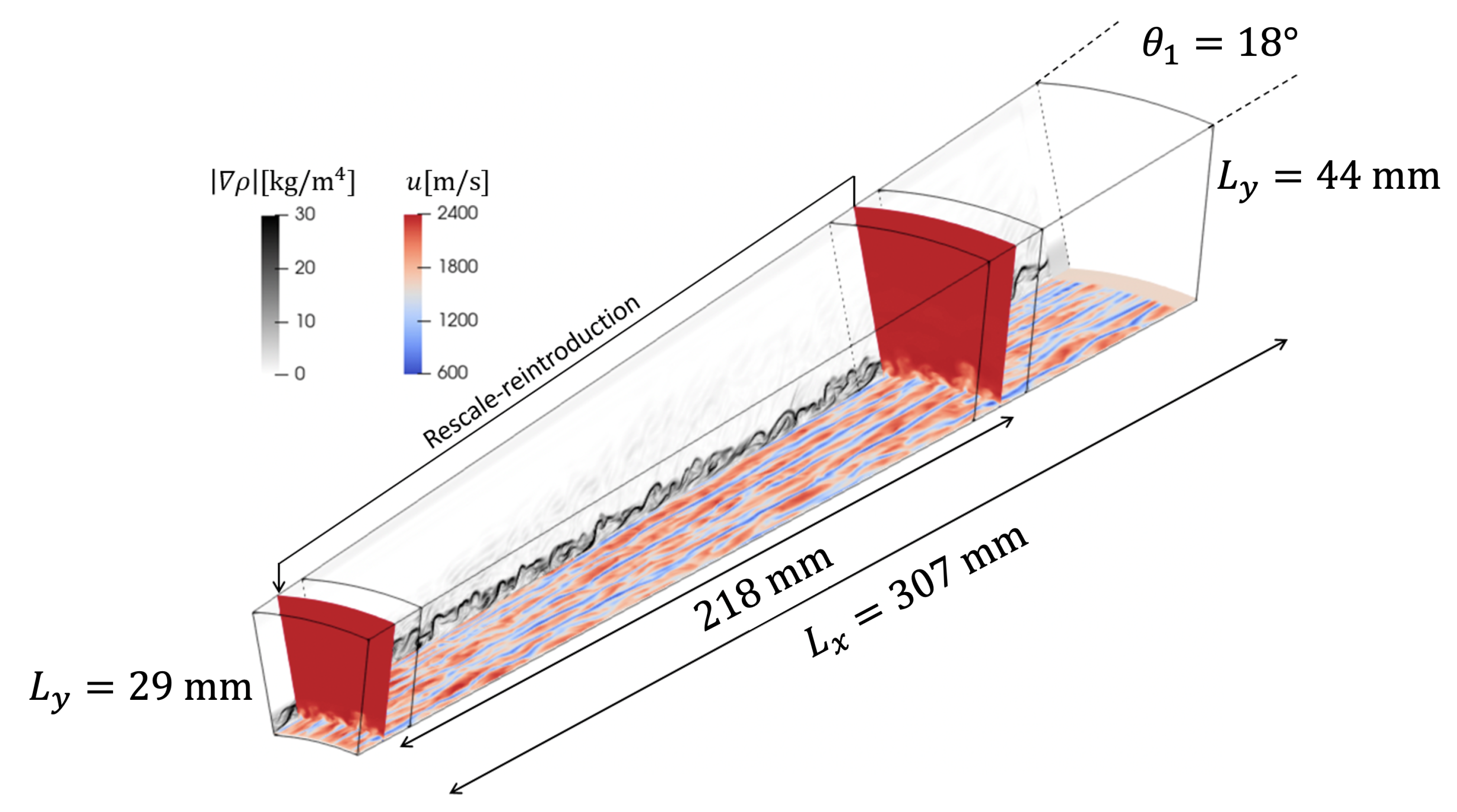
2.2. Computational Tools
2.2.1. LES Solver
2.2.2. Computational FLDI
3. Results
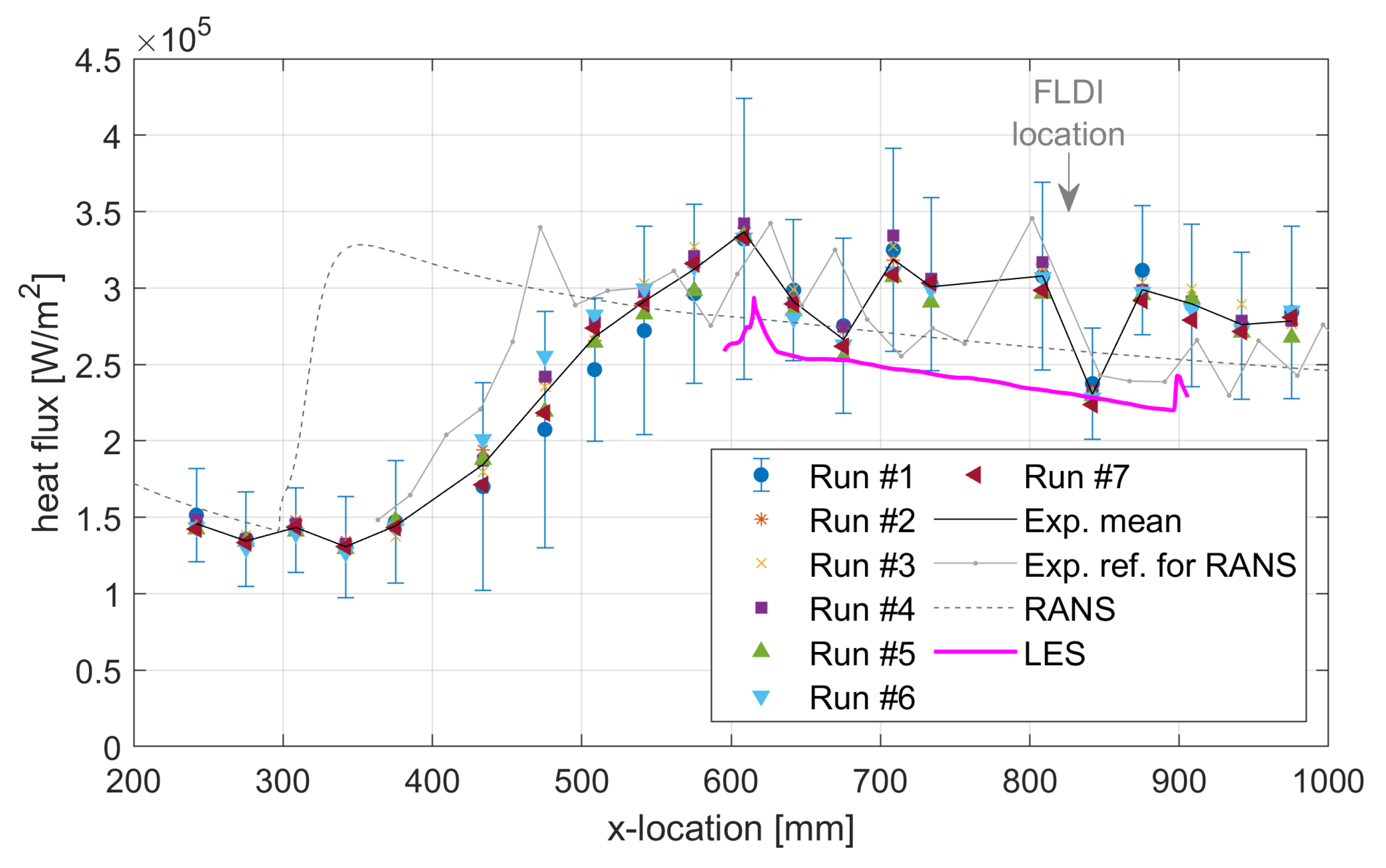
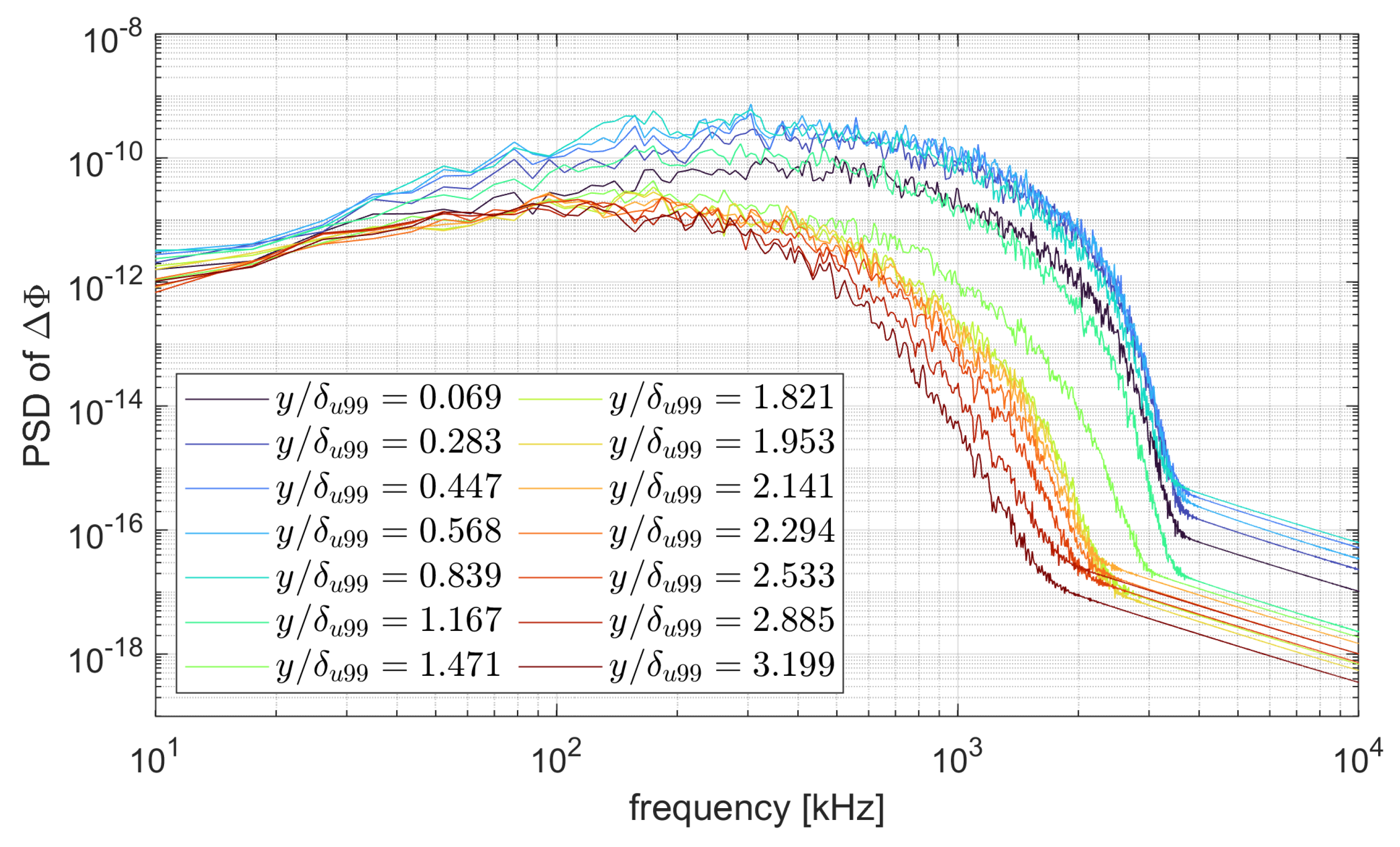
3.1. Experimental Data
3.2. LES Data
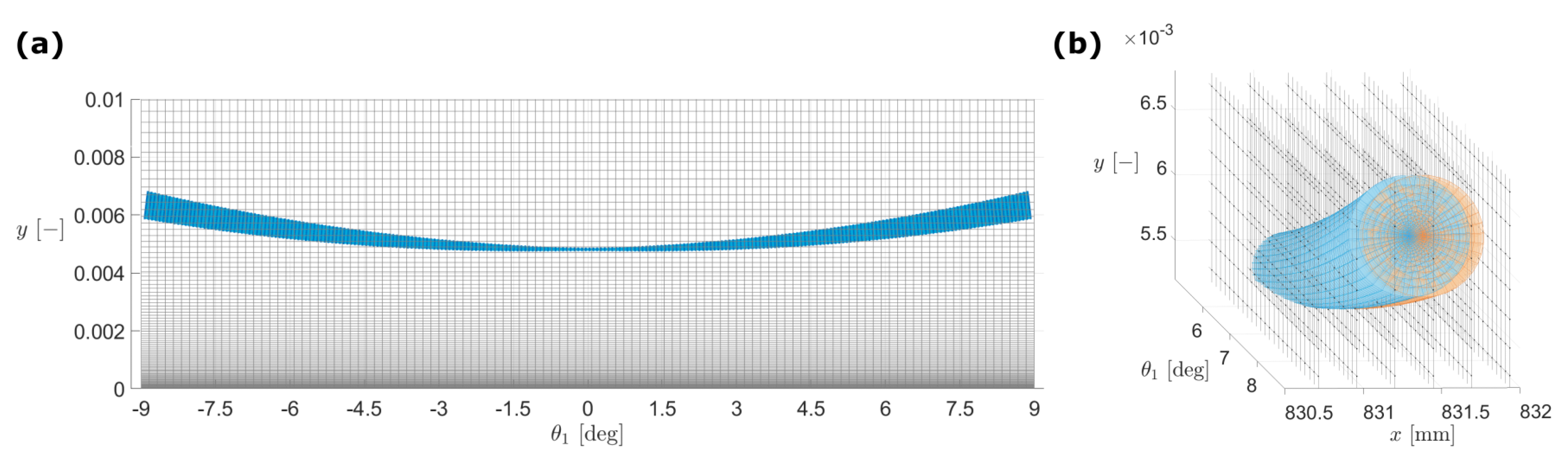
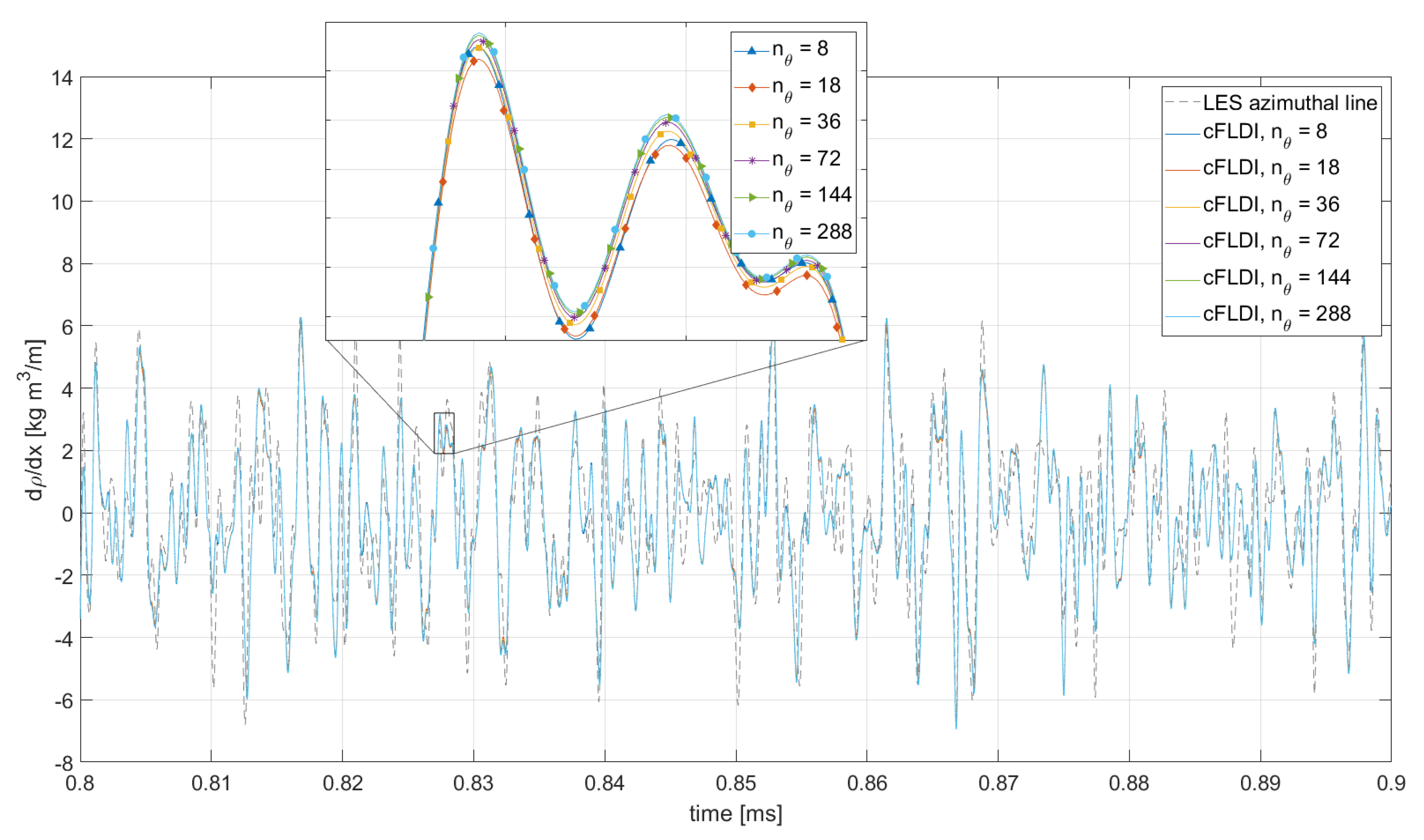
3.3. Computational FLDI
4. Discussion
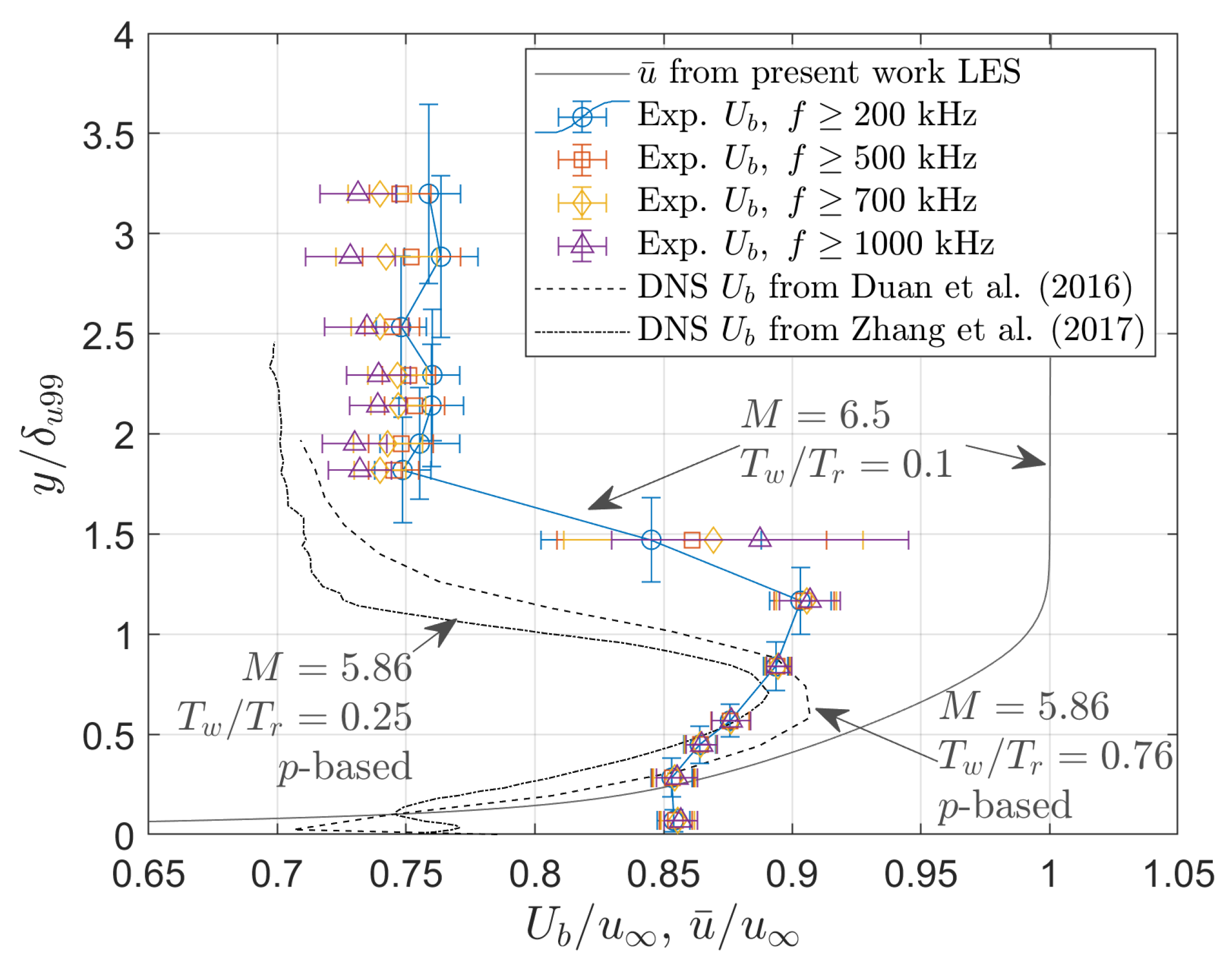
4.1. Velocity Measurements
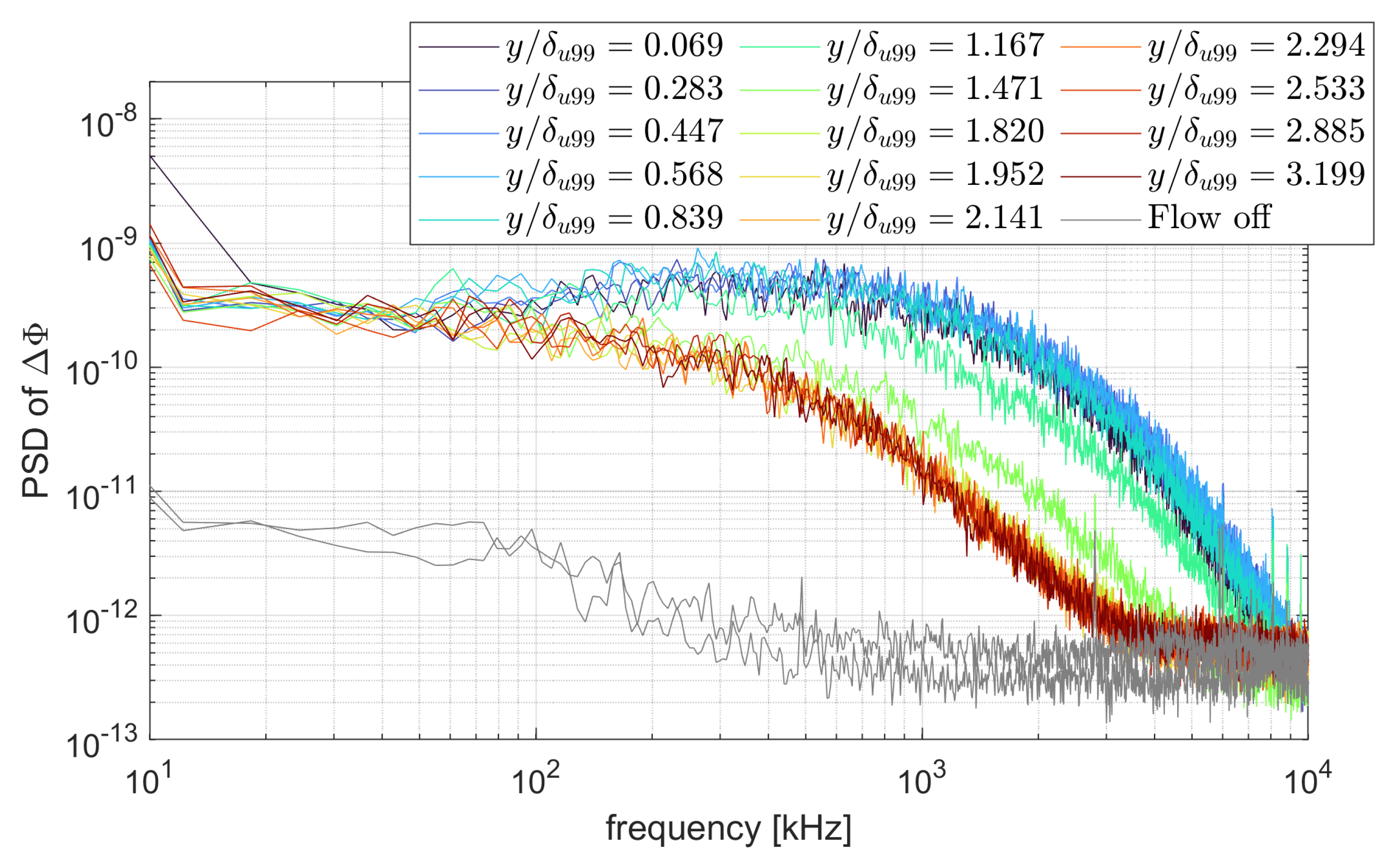
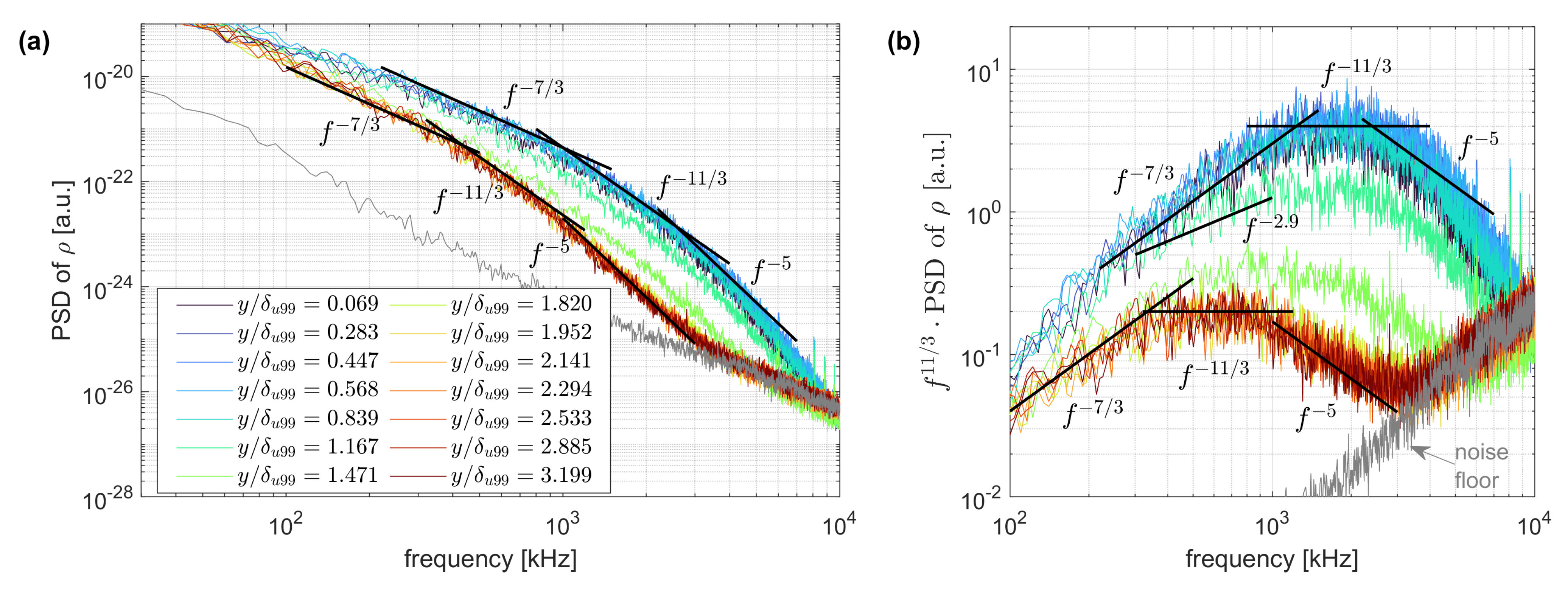
4.2. Spectra of Density Fluctuations
4.3. Constraints for Experimental and Numerical Direct Spectral Comparison
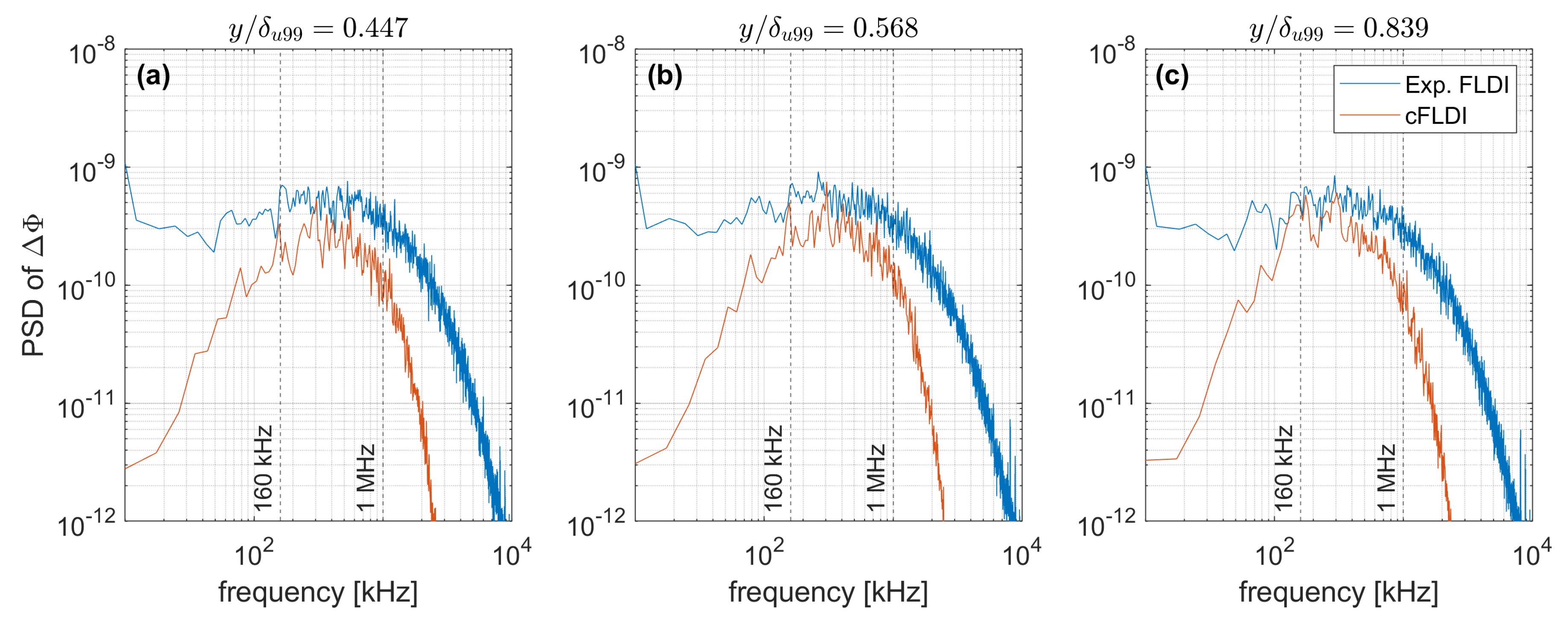
4.4. Direct Comparison between Experimental and Numerical Spectra
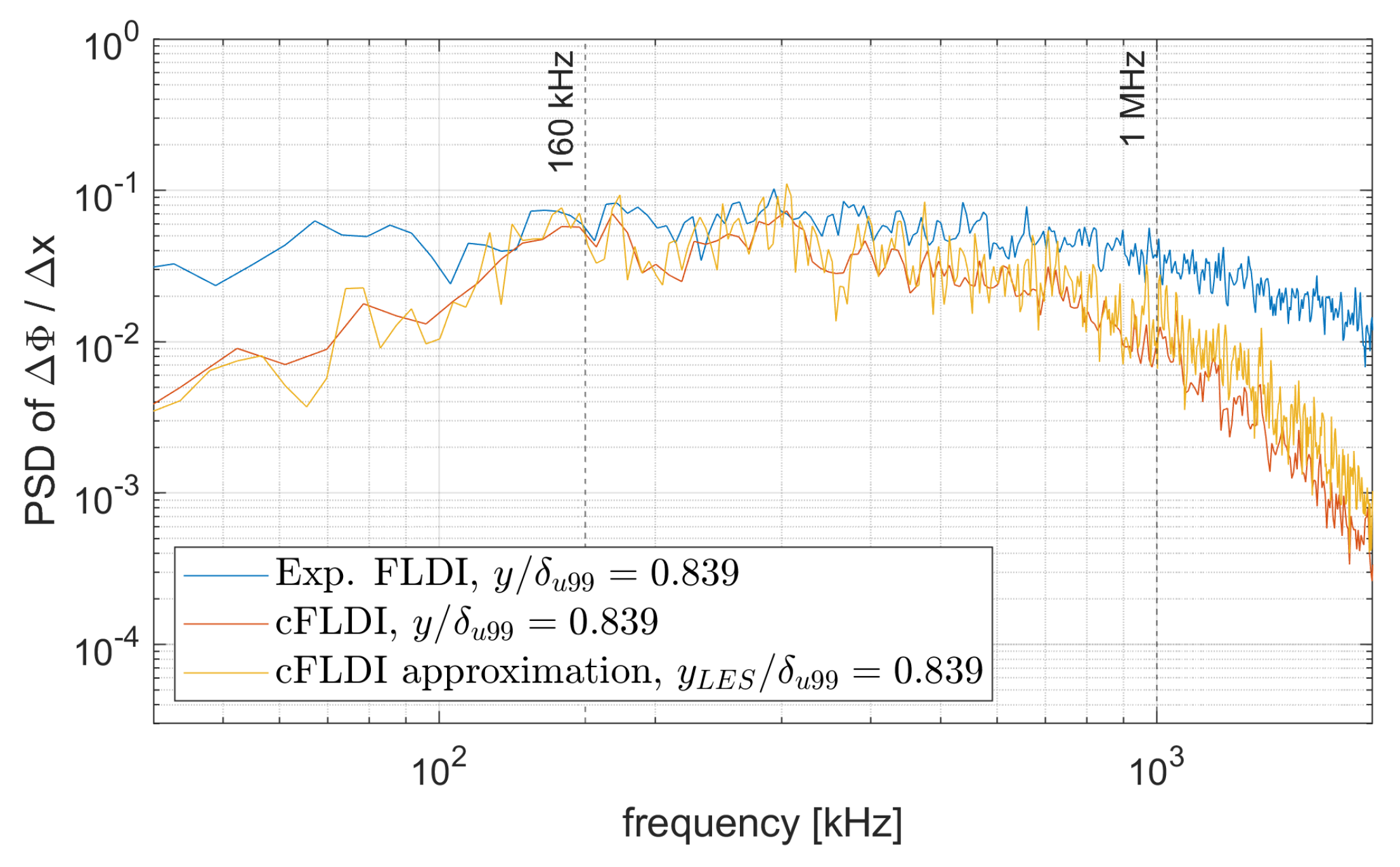
4.5. On the Simplified Comparison between Experimental FLDI and Numerical Solutions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| cFLDI | Computational Focused Laser Differential Interferometer |
| DNS | Direct Numerical Simulation |
| FLDI | Focused Laser Differential Interferometer |
| HEG | High-Enthalpy Shock Tunnel Göttingen |
| LES | Large-Eddy Simulation |
| RANS | Reynolds-Averaged Navier–Stokes |
| SA | Spalart–Allmaras |
| QSV | Quasi-Spectral Viscosity |
Appendix A

| [MPa] | [-] | [-] | [-] | [-] | [-] | R [J/(kg·K)] |
|---|---|---|---|---|---|---|
| x [m] | y [m] | u [m/s] | v [m/s] | p [Pa] | T [K] | M [-] | [kg/(m·s)] | [kg/m] |
|---|---|---|---|---|---|---|---|---|
References
- Ingenito, A.; Bruno, C. Physics and Regimes of Supersonic Combustion. AIAA J. 2010, 48, 515–525. [Google Scholar] [CrossRef]
- Roy, C.J.; Blottner, F.G. Review and assessment of turbulence models for hypersonic flows. Prog. Aerosp. Sci. 2006, 42, 469–530. [Google Scholar] [CrossRef]
- Pirozzoli, S.; Bernardini, M. Turbulence in supersonic boundary layers at moderate Reynolds number. J. Fluid Mech. 2011, 688, 120. [Google Scholar] [CrossRef]
- Duan, L.; Choudhari, M.M.; Zhang, C. Pressure fluctuations induced by a hypersonic turbulent boundary layer. J. Fluid Mech. 2016, 804, 578–607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, C.; Duan, L.; Choudhari, M.M. Direct Numerical Simulation Database for Supersonic and Hypersonic Turbulent Boundary Layers. AIAA J. 2018, 56, 4297–4311. [Google Scholar] [CrossRef] [PubMed]
- Harvey, J.; Bergman, R.; Holden, M. An experimental study of hypersonic turbulence on a sharp cone. In Proceedings of the 20th Fluid Dynamics, Plasma Dynamics and Lasers Conference, Buffalo, NY, USA, 12–14 June 1989. [Google Scholar] [CrossRef]
- Yoder, D.; DeBonis, J.; Georgiadis, N. Modeling of turbulent free shear flows. Comput. Fluids 2015, 117, 212–232. [Google Scholar] [CrossRef] [Green Version]
- Papamoschou, D.; Robey, H.F. Optical technique for direct measurement of power spectra in compressible turbulence. Exp. Fluids 1994, 17, 10–15. [Google Scholar] [CrossRef]
- Duan, L.; Choudhari, M.M.; Wu, M. Numerical study of acoustic radiation due to a supersonic turbulent boundary layer. J. Fluid Mech. 2014, 746, 165–192. [Google Scholar] [CrossRef]
- Lawson, J.M.; Neet, M.C.; Hofferth, J.W.; Austin, J.M. Supersonic Freestream Density Fluctuations from Focused Laser Differential Interferometry and Pitot-Probe Measurements. AIAA J. 2022, 60, 5173–5186. [Google Scholar] [CrossRef]
- Gillespie, G.I.; Ceruzzi, A.P.; Laurence, S.J. A multi-point focused laser differential interferometer for characterizing freestream disturbances in hypersonic wind tunnels. Exp. Fluids 2022, 63, 180. [Google Scholar] [CrossRef]
- Laufer, J. Some Statistical Properties of the Pressure Field Radiated by a Turbulent Boundary Layer. Phys. Fluids 1964, 7, 1191. [Google Scholar] [CrossRef]
- Martin, M.P. Direct numerical simulation of hypersonic turbulent boundary layers. Part 1. Initialization and comparison with experiments. J. Fluid Mech. 2007, 570, 347–364. [Google Scholar] [CrossRef] [Green Version]
- Bernardini, M.; Pirozzoli, S. Wall pressure fluctuations beneath supersonic turbulent boundary layers. Phys. Fluids 2011, 23, 085102. [Google Scholar] [CrossRef]
- Lagha, M.; Kim, J.; Eldredge, J.D.; Zhong, X. Near-wall dynamics of compressible boundary layers. Phys. Fluids 2011, 23, 065109. [Google Scholar] [CrossRef] [Green Version]
- Duan, L.; Beekman, I.; Martin, M.P. Direct numerical simulation of hypersonic turbulent boundary layers. Part 3. Effect of Mach number. J. Fluid Mech. 2011, 672, 245–267. [Google Scholar] [CrossRef] [Green Version]
- Duan, L.; Martin, M.P. Direct numerical simulation of hypersonic turbulent boundary layers. Part 4. Effect of high enthalpy. J. Fluid Mech. 2011, 684, 25–59. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Duan, L.; Choudhary, M.M. Acoustic Radiation from a Mach 14 Turbulent Boundary layer. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Duan, L.; Choudhari, M.M. Effect of wall cooling on boundary-layer-induced pressure fluctuations at Mach 6. J. Fluid Mech. 2017, 822, 5–30. [Google Scholar] [CrossRef] [Green Version]
- Wenzel, C.; Selent, B.; Kloker, M.; Rist, U. DNS of compressible turbulent boundary layers and assessment of data/scaling-law quality. J. Fluid Mech. 2018, 842, 428–468. [Google Scholar] [CrossRef]
- Duan, L.; Choudhari, M.M.; Chou, A.; Munoz, F.; Radespiel, R.; Schilden, T.; Schröder, W.; Marineau, E.C.; Casper, K.M.; Chaudhry, R.S.; et al. Characterization of Freestream Disturbances in Conventional Hypersonic Wind Tunnels. J. Spacecr. Rocket. 2019, 56, 357–368. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Scalo, C. Trapped waves in supersonic and hypersonic turbulent channel flow over porous walls. J. Fluid Mech. 2021, 920, A24. [Google Scholar] [CrossRef]
- Xu, D.; Wang, J.; Wan, M.; Yu, C.; Li, X.; Chen, S. Compressibility effect in hypersonic boundary layer with isothermal wall condition. Phys. Rev. Fluids 2021, 6, 054609. [Google Scholar] [CrossRef]
- Xu, D.; Wang, J.; Wan, M.; Yu, C.; Li, X.; Chen, S. Effect of wall temperature on the kinetic energy transfer in a hypersonic turbulent boundary layer. J. Fluid Mech. 2021, 929, A33. [Google Scholar] [CrossRef]
- Huang, J.; Duan, L.; Choudhari, M.M. Direct numerical simulation of hypersonic turbulent boundary layers: Effect of spatial evolution and Reynolds number. J. Fluid Mech. 2022, 937, A3. [Google Scholar] [CrossRef]
- Trettel, A.; Larsson, J. Mean velocity scaling for compressible wall turbulence with heat transfer. Phys. Fluids 2016, 28, 026102. [Google Scholar] [CrossRef]
- Pecnik, R.; Patel, A. Scaling and modelling of turbulence in variable property channel flows. J. Fluid Mech. 2017, 823, R1. [Google Scholar] [CrossRef] [Green Version]
- Owen, F.K.; Horstman, C.C. On the structure of hypersonic turbulent boundary layers. J. Fluid Mech. 1972, 53, 611–636. [Google Scholar] [CrossRef]
- Williams, O.J.; Sahoo, D.; Baumgartner, M.L.; Smits, A.J. Experiments on the structure and scaling of hypersonic turbulent boundary layers. J. Fluid Mech. 2018, 834, 237–270. [Google Scholar] [CrossRef] [Green Version]
- Tsuji, Y.; Fransson, J.H.M.; Alfredsson, P.H.; Johansson, A.V. Pressure statistics and their scaling in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 2007, 585, 1–40. [Google Scholar] [CrossRef]
- Choi, H.; Moin, P. On the space-time characteristics of wall-pressure fluctuations. Phys. Fluids A Fluid Dyn. 1990, 2, 1450–1460. [Google Scholar] [CrossRef]
- Parziale, N. Slender-Body Hypervelocity Boundary-Layer Instability. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2013. [Google Scholar]
- Fulghum, M.R. Turbulence Measurements in High-Speed Wind Tunnels Using Focusing Laser Differential Interferometry. Ph.D. Thesis, The Pennsylvania State University, University Park, PA, USA, 2014. [Google Scholar]
- Chou, A.; Leidy, A.; King, R.A.; Bathel, B.F.; Herring, G. Measurements of Freestream Fluctuations in the NASA Langley 20-Inch Mach 6 Tunnel. In Proceedings of the 2018 Fluid Dynamics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef] [Green Version]
- Birch, B.; Buttsworth, D.; Zander, F. Measurements of freestream density fluctuations in a hypersonic wind tunnel. Exp. Fluids 2020, 61, 158. [Google Scholar] [CrossRef]
- Ceruzzi, A.; McManamen, B.; Cadou, C.P. Demonstration of Two-Point Focused Laser Differential Interferometry (2pFLDI) in a Mach 18 flow. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15 and 19–21 January 2021. [Google Scholar] [CrossRef]
- Bathel, B.F.; Weisberger, J.M.; Herring, G.C.; King, R.A.; Jones, S.B.; Kennedy, R.E.; Laurence, S.J. Two-point, parallel-beam focused laser differential interferometry with a Nomarski prism. Appl. Opt. 2020, 59, 244. [Google Scholar] [CrossRef] [PubMed]
- Weisberger, J.M.; Bathel, B.F.; Herring, G.C.; Buck, G.M.; Jones, S.B.; Cavone, A.A. Multi-point line focused laser differential interferometer for high-speed flow fluctuation measurements. Appl. Opt. 2020, 59, 11180. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Yu, T.; Lin, L.; Zhao, J.; Wu, J. Nonlinear Instability Characterization of Hypersonic Laminar Boundary Layer. AIAA J. 2020, 58, 5254–5263. [Google Scholar] [CrossRef]
- Benitez, E.K.; Jewell, J.S.; Schneider, S.P. Focused Laser Differential Interferometry with Contoured Tunnel Windows. AIAA J. 2021, 59, 419–429. [Google Scholar] [CrossRef]
- Gragston, M.; Siddiqui, F.; Schmisseur, J.D. Detection of second-mode instabilities on a flared cone in Mach 6 quiet flow with linear array focused laser differential interferometry. Exp. Fluids 2021, 62, 81. [Google Scholar] [CrossRef]
- Siddiqui, F.; Gragston, M.; Saric, W.S.; Bowersox, R.D.W. Mack-mode instabilities on a cooled flared cone with discrete roughness elements at Mach 6. Exp. Fluids 2021, 62, 213. [Google Scholar] [CrossRef]
- Siddiqui, F.; Gragston, M.; Bowersox, R.D.W. Measurement of Wall-Cooling Effects on Hypersonic Boundary-Layer Transition Using Focused Laser Differential Interferometry. AIAA J. 2022, 60, 6214–6224. [Google Scholar] [CrossRef]
- Schmidt, B.E.; Shepherd, J.E. Analysis of focused laser differential interferometry. Appl. Opt. 2015, 54, 8459. [Google Scholar] [CrossRef] [Green Version]
- Lawson, J.M.; Neet, M.C.; Grossman, I.J.; Austin, J.M. Static and dynamic characterization of a focused laser differential interferometer. Exp. Fluids 2020, 61, 187. [Google Scholar] [CrossRef]
- Hameed, A.; Parziale, N.J. Focused Laser Differential Interferometric Investigation of Turbulent Jet Spectra. J. Spacecr. Rocket. 2022, 59, 1565–1573. [Google Scholar] [CrossRef]
- Ceruzzi, A.P.; Cadou, C.P. Interpreting single-point and two-point focused laser differential interferometry in a turbulent jet. Exp. Fluids 2022, 63, 112. [Google Scholar] [CrossRef]
- Lawson, J.M.; Austin, J.M. Focused laser differential interferometer response to shock waves. Meas. Sci. Technol. 2021, 32, 055203. [Google Scholar] [CrossRef]
- Camillo, G.P.; Wagner, A. Focused laser differential interferometry post-processing methodology for flowfields with circular symmetry. Rev. Sci. Instrum. 2023, 94, 045102. [Google Scholar] [CrossRef]
- Benitez, E.K.; Borg, M.P.; Rhodes, C.; Jewell, J.S. Optical-Axis Spatial Sensitivity of a Simulated Focused Laser Differential Interferometer. AIAA J. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Benitez, E.K.; Jewell, J.S. Simulated Focused Laser Differential Interferometry of Time-Varying Signals. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA & Virtual, 3–7 January 2022. [Google Scholar] [CrossRef]
- Benitez, E.K.; Borg, M.P.; Hill, J.L.; Aultman, M.T.; Duan, L.; Running, C.L.; Jewell, J.S. Quantitative focused laser differential interferometry with hypersonic turbulent boundary layers. Appl. Opt. 2022, 61, 9203. [Google Scholar] [CrossRef] [PubMed]
- Deutsches Zentrum für Luft-und Raumfahrt (DLR). The High Enthalpy Shock Tunnel Göttingen of the German Aerospace Center (DLR). J. Large-Scale Res. Facil. 2018, 4, A133. [Google Scholar] [CrossRef]
- Wagner, A. Passive Hypersonic Transition Control by Means of Ultrasonically Absorptive Thermal Protection Materials (UAT); Report AFRL-AFOSR-UK-TR-2020-0025; Deutsches Zentrum für Luft-und Raumfahrt: Cologne, Germany, 2020. [Google Scholar]
- Wartemann, V.; Camillo, G.P.; Reiter, P.; Neumann, J.; Wagner, A. Influence of transpiration cooling on second-mode instabilities investigated on hypersonic, conical flows. CEAS Space J. 2019, 11, 341–350. [Google Scholar] [CrossRef]
- Wartemann, V.; Camillo, G.P.; Neumann, J.; Weber, A.; Wagner, A. Stability Analyses of Hypersonic, Conical Flows with Transpiration Cooling. In IUTAM Laminar-Turbulent Transition; Springer International Publishing: Cham, Switzerland, 2021; pp. 671–689. [Google Scholar] [CrossRef]
- Ceruzzi, A.; Cadou, C.P. Simultaneous Velocity and Density Gradient Measurements using Two-Point Focused Laser Differential Interferometry. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Camillo, G.P.; Wagner, A. A low-effort and inexpensive methodology to determine beam separation distance of multi-foci FLDI. Exp. Fluids 2022, 63, 53. [Google Scholar] [CrossRef]
- Sanderson, S.R. Simple, adjustable beam splitting element for differential interferometers based on photoelastic birefringence of a prismatic bar. Rev. Sci. Instrum. 2005, 76, 113703. [Google Scholar] [CrossRef] [Green Version]
- Lawson, J.M.; Neet, M.C.; Grossman, I.J.; Austin, J.M. Characterization of a Focused Laser Differential Interferometer. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Nagarajan, S.; Lele, S.; Ferziger, J. A robust high-order compact method for large eddy simulation. J. Comput. Phys. 2003, 191, 392–419. [Google Scholar] [CrossRef]
- Sousa, V.C.B.; Scalo, C. A Unified Quasi-Spectral Viscosity (QSV) Approach to Shock Capturing and Large-Eddy Simulation. J. Comput. Phys. 2022, 459, 111139. [Google Scholar] [CrossRef]
- Gottlieb, S. On high order strong stability preserving Runge-Kutta and multi step time discretizations. J. Sci. Comput. 2005, 25, 105–128. [Google Scholar] [CrossRef]
- Lele, S.K. Compact finite difference scheme with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Spalart, P.R.; Allmaras, S.R. A One-Equation Turbulence Moel for Aerodynamics Flow. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar] [CrossRef]
- Taylor, G.I.; Maccoll, J.W. The Air Pressure on a Cone Moving at High Speeds.—I. Proc. R. Soc. Lond. Series A 1933, 139, 278–297. [Google Scholar] [CrossRef] [Green Version]
- Urbin, G.; Knight, D. Large-eddy simulation of a supersonic boundary layer using an unstructured grid. AIAA J. 2001, 39, 1288–1295. [Google Scholar] [CrossRef]
- Toki, T.; Sousa, V.C.B.; Chen, Y.; Camillo, G.P.; Wagner, A.; Scalo, C. Large-eddy simulation of a hypersonic turbulent boundary layer over a cone in support of focused laser differential interferometry (FLDI) measurements. In Proceedings of the 12th International Symposium on Turbulence and Shear Flow Phenomena, Osaka, Japan, 19–22 July 2022. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; The MIT Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Phillips, O.M. On the generation of sound by supersonic turbulent shear layers. J. Fluid Mech. 1960, 9, 1–28. [Google Scholar] [CrossRef]
- George, W.J.; Beuther, P.; Arndt, R. Pressure spectra in turbulent free shear flows. In Proceedings of the 6th Aeroacoustics Conference, Hartford, CT, USA, 6–8 June 1980. [Google Scholar] [CrossRef]
- Biagioni, L.; d’Agostino, L. Measurement of energy spectra in weakly compressible turbulence. In Proceedings of the 30th Fluid Dynamics Conference, Norfolk, VA, USA, 28 June–1 July 1999. [Google Scholar] [CrossRef]
- Bernardini, M.; Pirozzoli, S.; Grasso, F. The wall pressure signature of transonic shock/boundary layer interaction. J. Fluid Mech. 2011, 671, 288–312. [Google Scholar] [CrossRef]
- Masutti, D.; Spinosa, E.; Chazot, O.; Carbonaro, M. Disturbance Level Characterization of a Hypersonic Blowdown Facility. Phys. Fluids 2012, 50, 2720–2730. [Google Scholar] [CrossRef]
- Ceruzzi, A.P. Development of Two-Point Focused Laser Differential Interferometry for Applications in High-Speed Wind Tunnels. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2022. [Google Scholar]

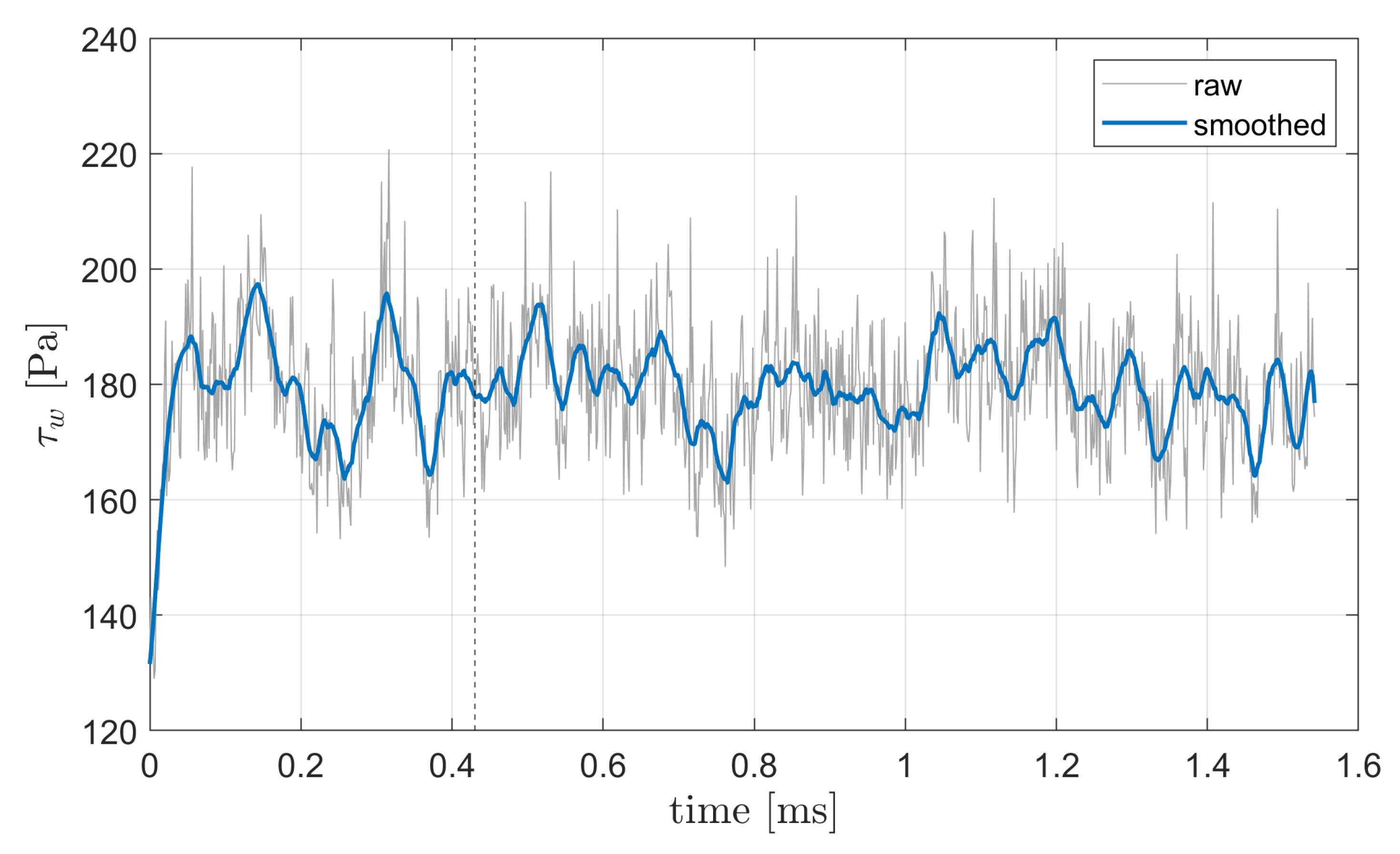


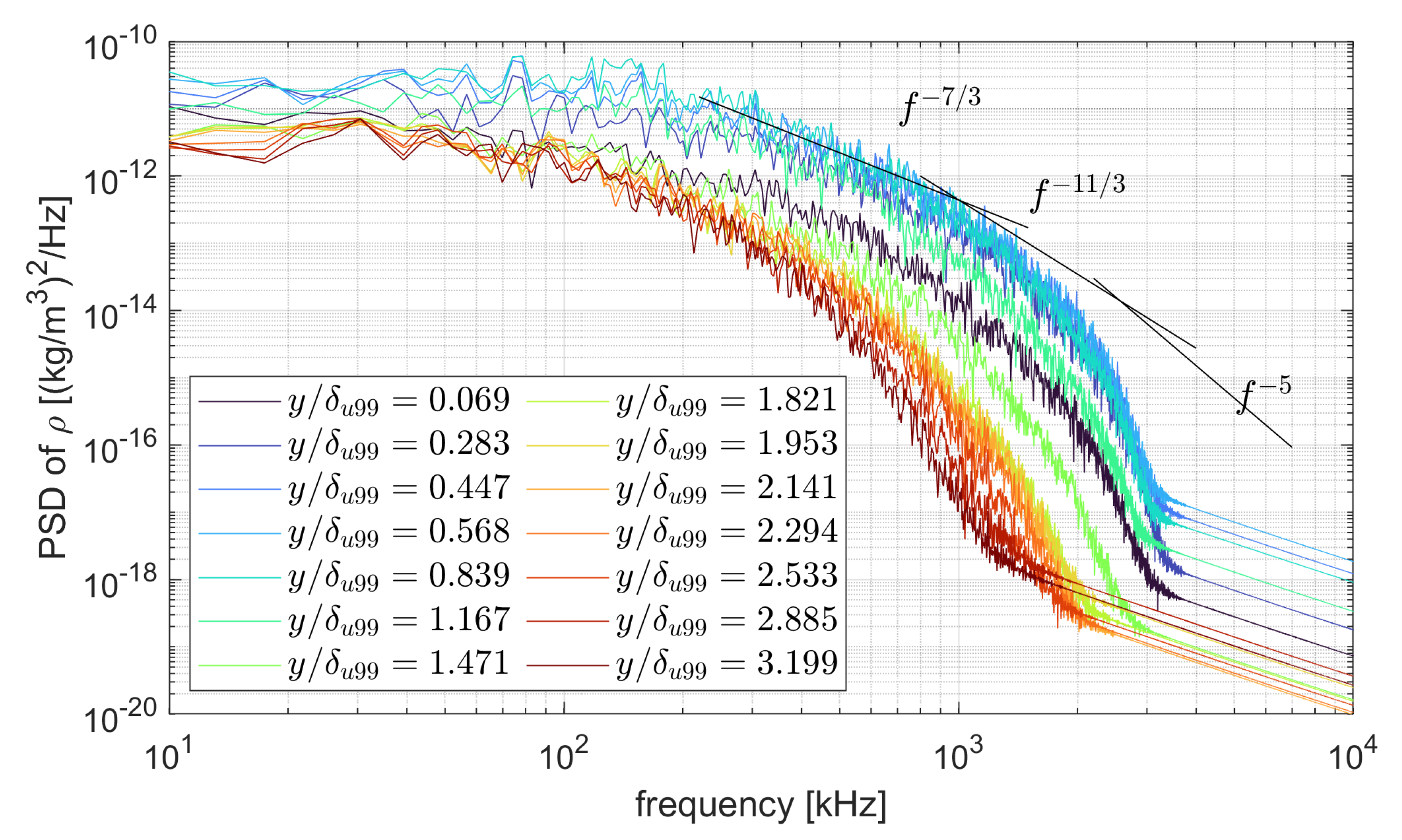
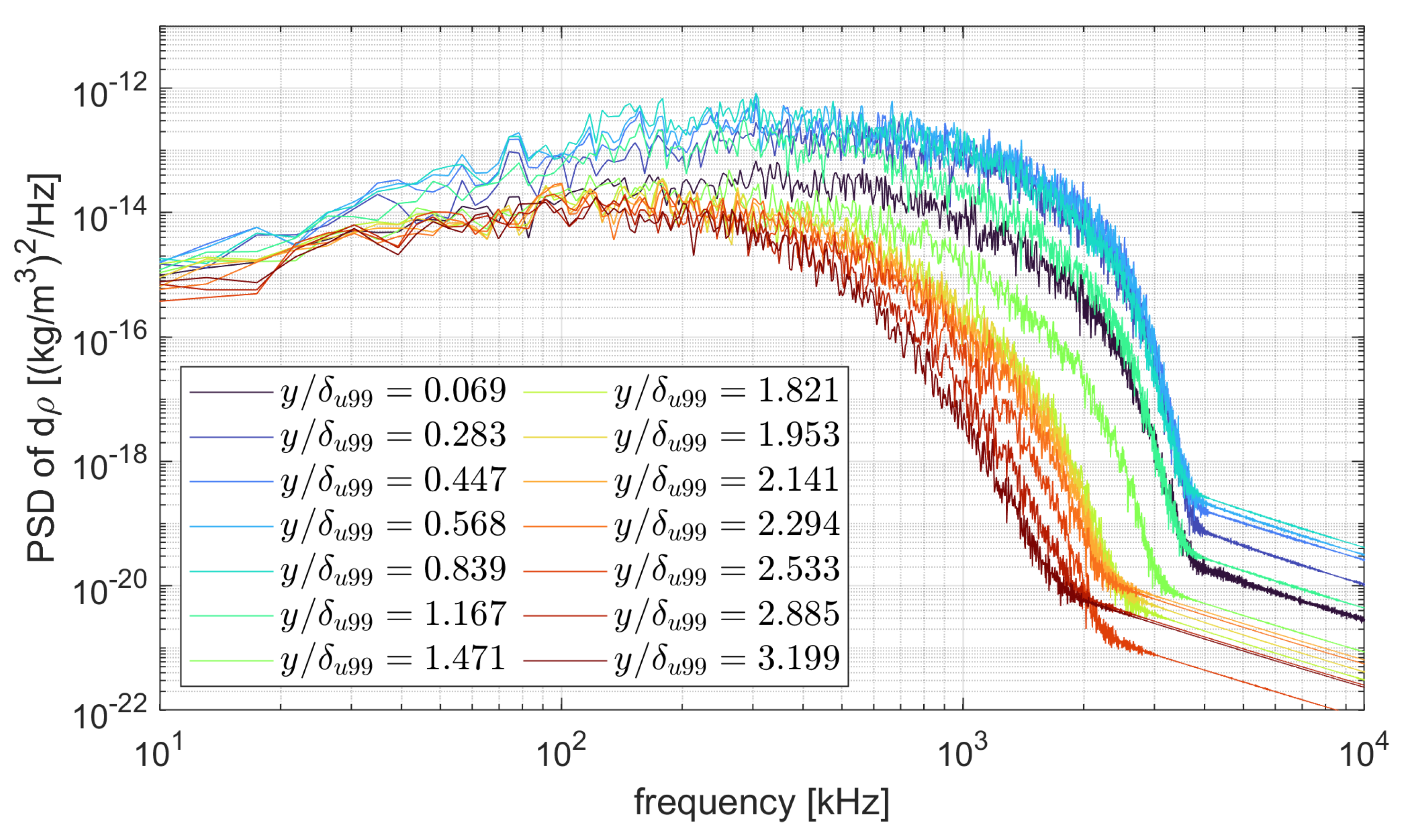
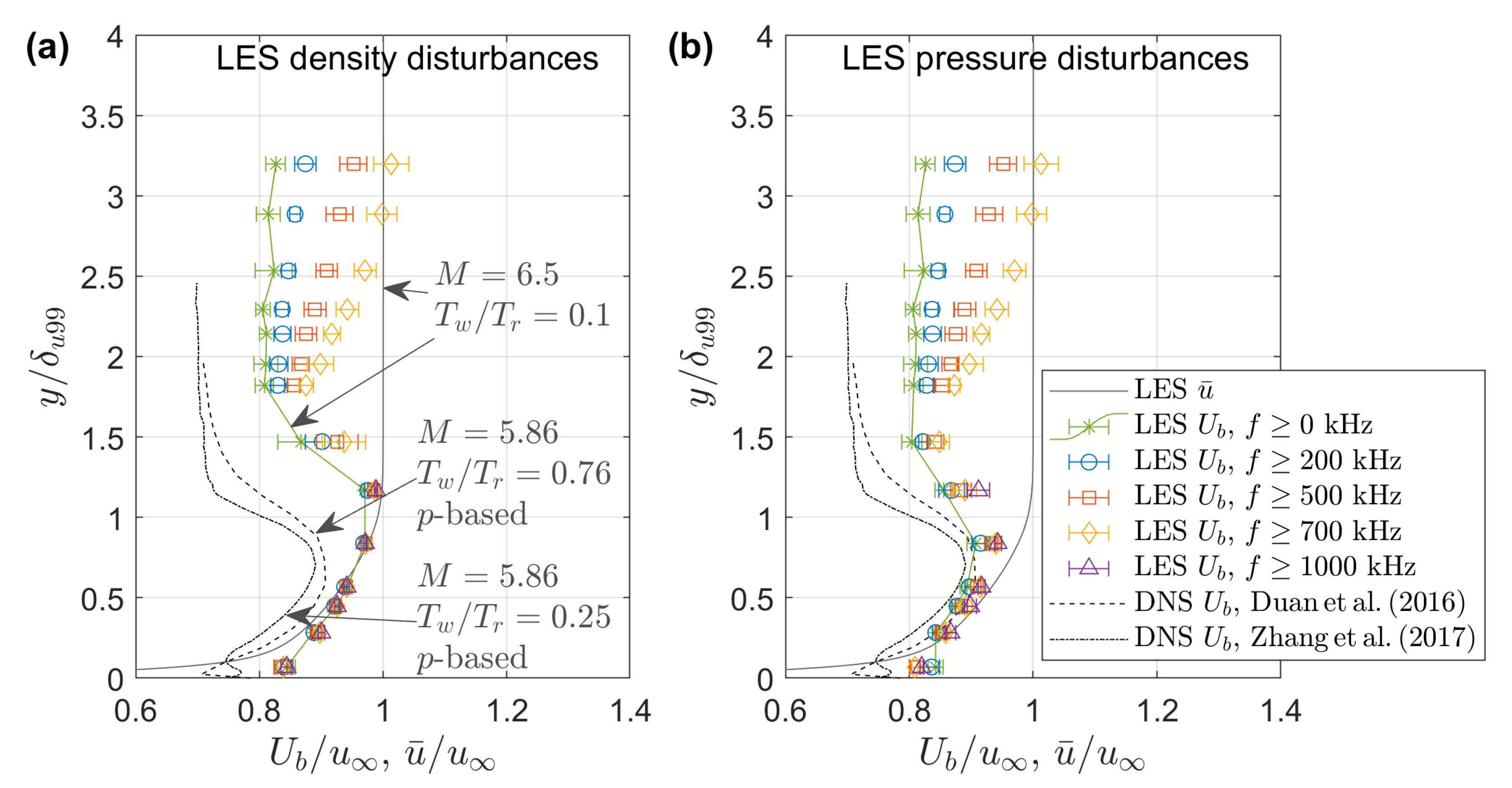

| [MPa] | [K] | [MJ/kg] | [-] | [ m] | [Pa] | [K] | [g/m] | [m/s] | [-] |
|---|---|---|---|---|---|---|---|---|---|
| Run # | [mm] | ||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | 1 | ||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 |
| [nm] | [mm] | d [m] | [m] | [mm] | [mm] |
|---|---|---|---|---|---|
| 45 | ≈ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camillo, G.P.; Wagner, A.; Toki, T.; Scalo, C. Combined Experimental and Numerical Investigation of a Hypersonic Turbulent Boundary Layer by Means of FLDI and Large-Eddy Simulations. Aerospace 2023, 10, 570. https://doi.org/10.3390/aerospace10060570
Camillo GP, Wagner A, Toki T, Scalo C. Combined Experimental and Numerical Investigation of a Hypersonic Turbulent Boundary Layer by Means of FLDI and Large-Eddy Simulations. Aerospace. 2023; 10(6):570. https://doi.org/10.3390/aerospace10060570
Chicago/Turabian StyleCamillo, Giannino Ponchio, Alexander Wagner, Takahiko Toki, and Carlo Scalo. 2023. "Combined Experimental and Numerical Investigation of a Hypersonic Turbulent Boundary Layer by Means of FLDI and Large-Eddy Simulations" Aerospace 10, no. 6: 570. https://doi.org/10.3390/aerospace10060570
APA StyleCamillo, G. P., Wagner, A., Toki, T., & Scalo, C. (2023). Combined Experimental and Numerical Investigation of a Hypersonic Turbulent Boundary Layer by Means of FLDI and Large-Eddy Simulations. Aerospace, 10(6), 570. https://doi.org/10.3390/aerospace10060570







