Flight Load Calculation Using Neural Network Residual Kriging
Abstract
1. Introduction
2. Methodology
2.1. Static Aeroelastic Response Equation
2.2. Neural Network
2.3. Kriging
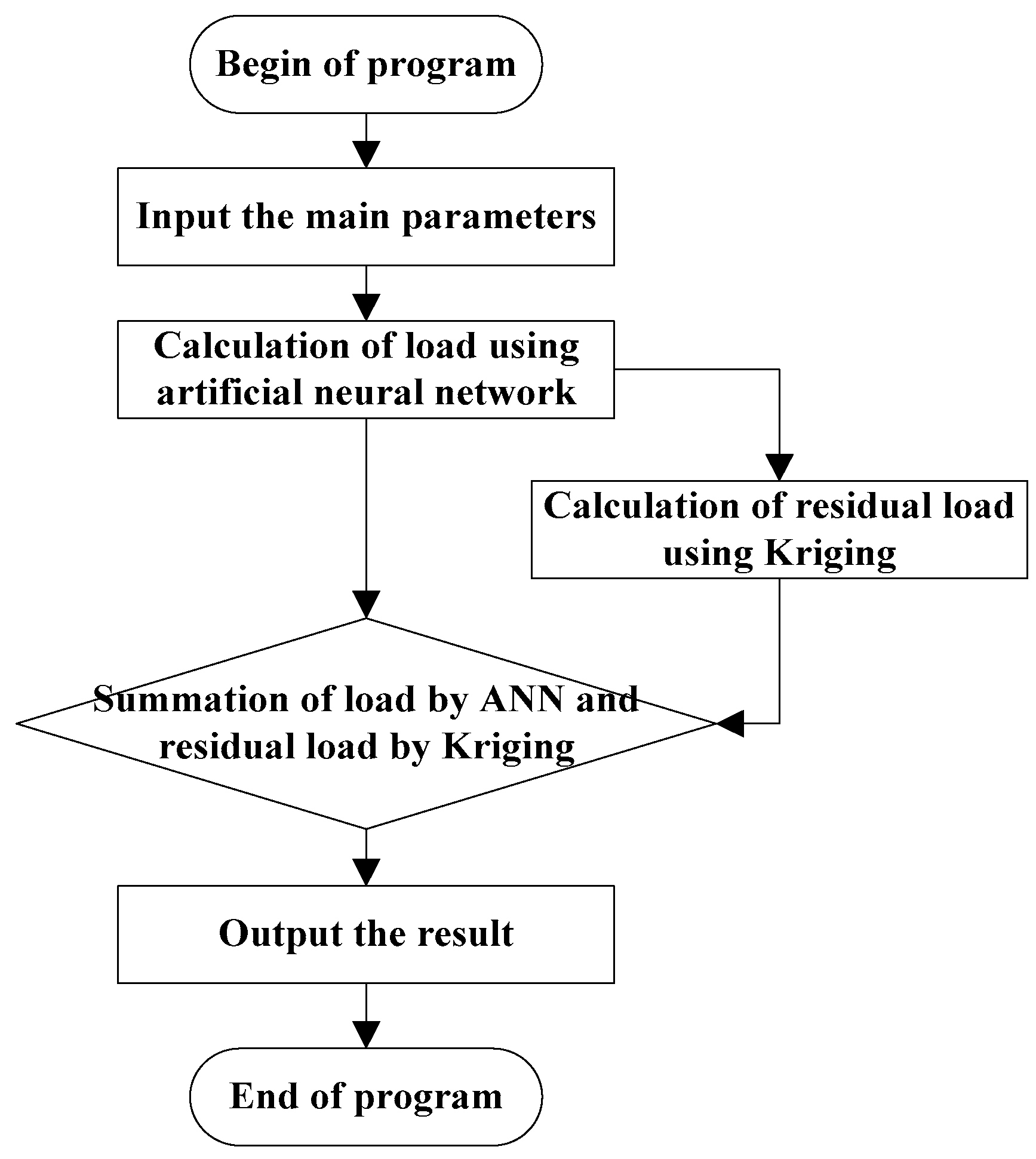
2.4. Neural Network Residual Kriging
2.5. Mean Absolute Error (MAE), Mean Squared Error (MSE), and Root Mean Squared Error (RMSE)
2.6. Correlation Coefficient R and Coefficient of Determination R-Square
3. Flight Load Calculation Modeling
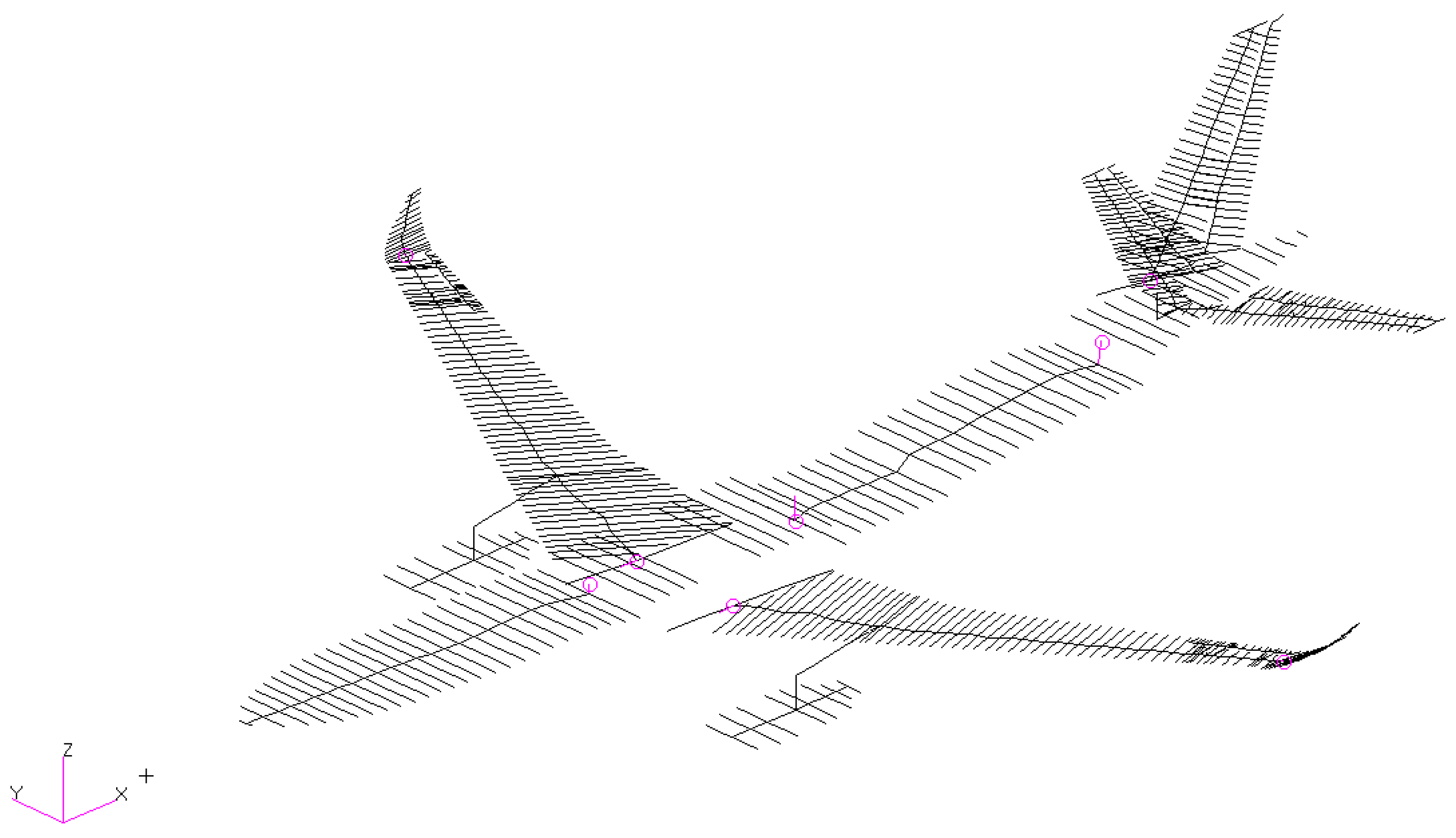
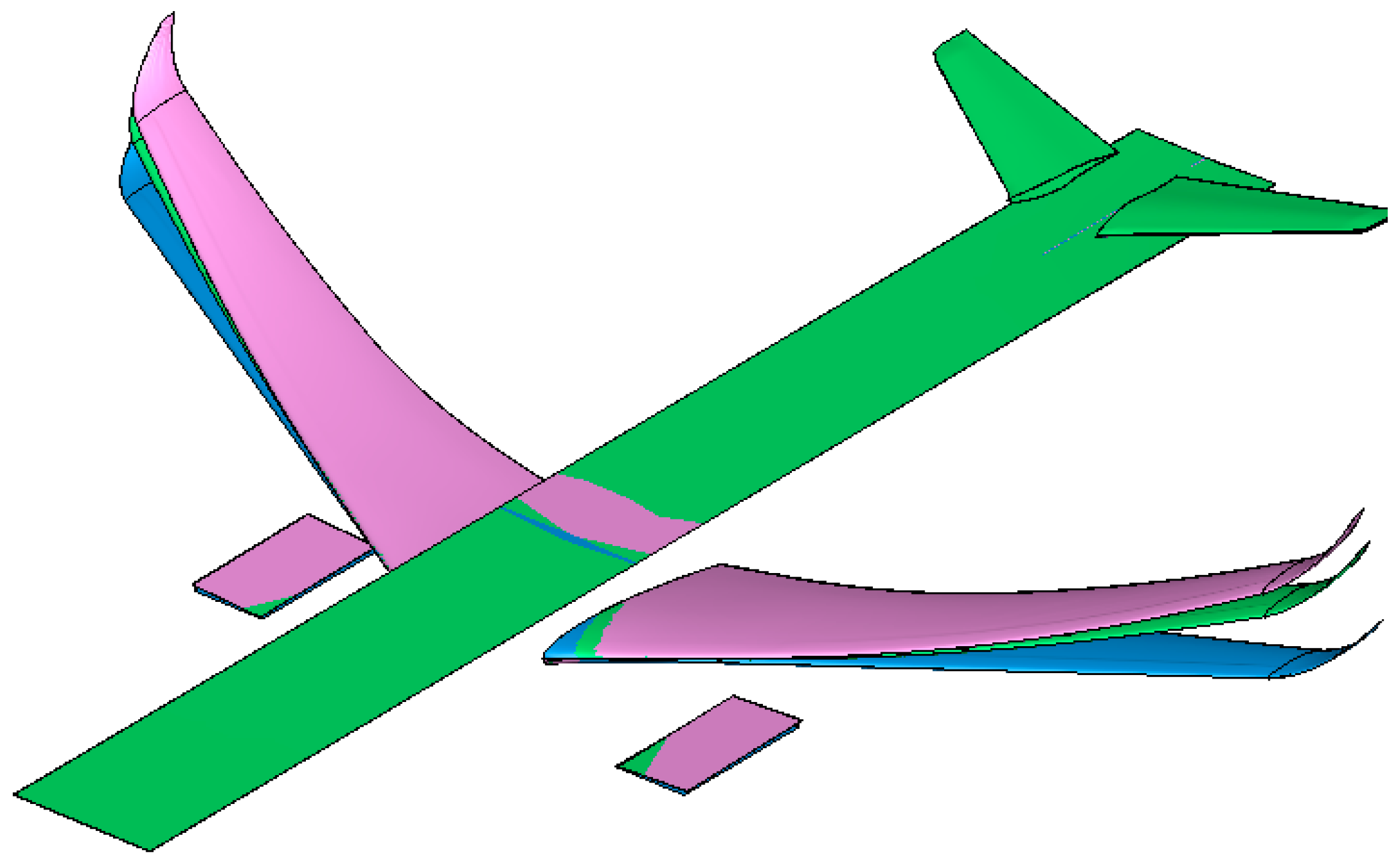
3.1. Aircraft Model
3.2. Input and Output Data
3.3. Training and Test Data
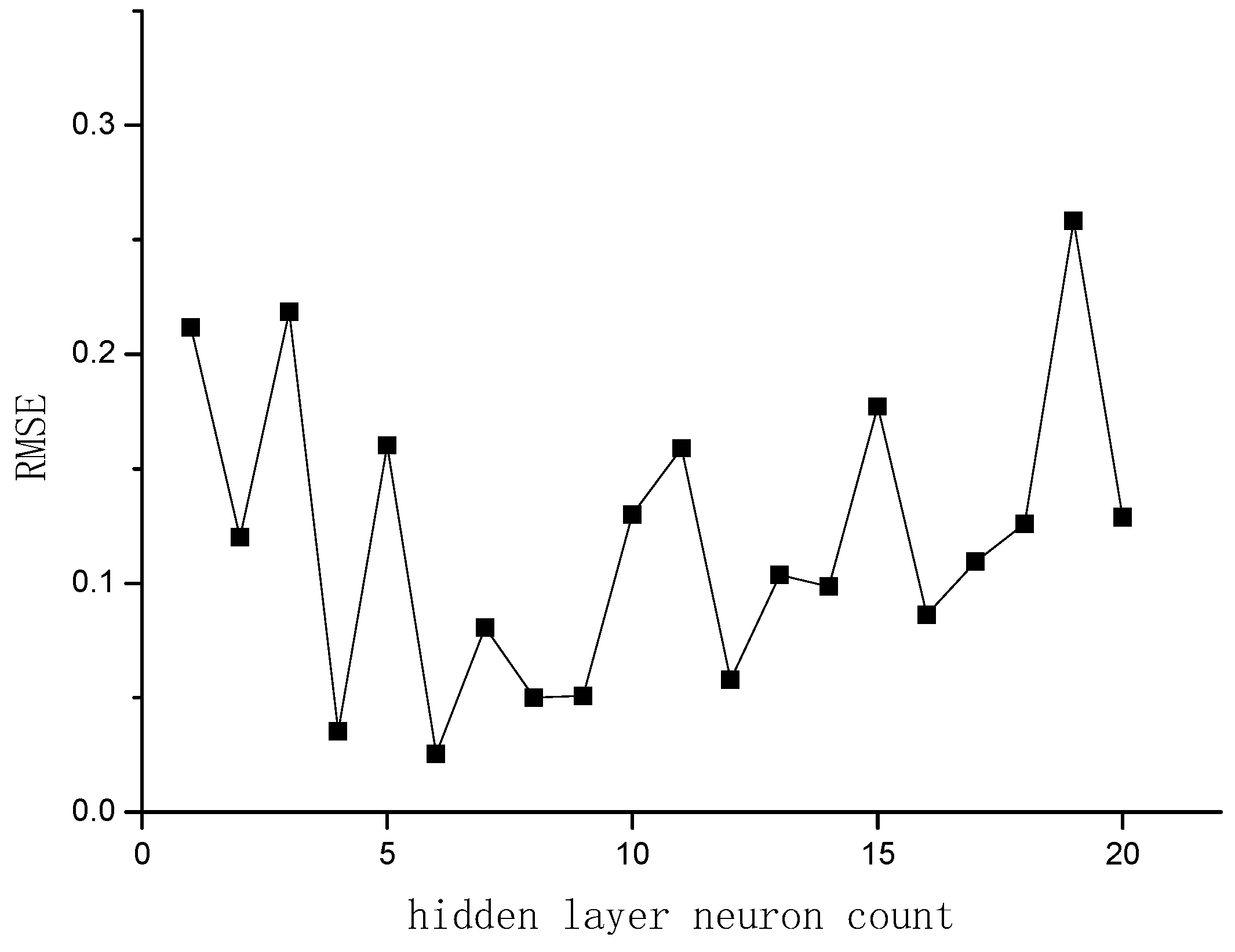
3.4. BP Modelling
3.5. Kriging and NNRK Modelling
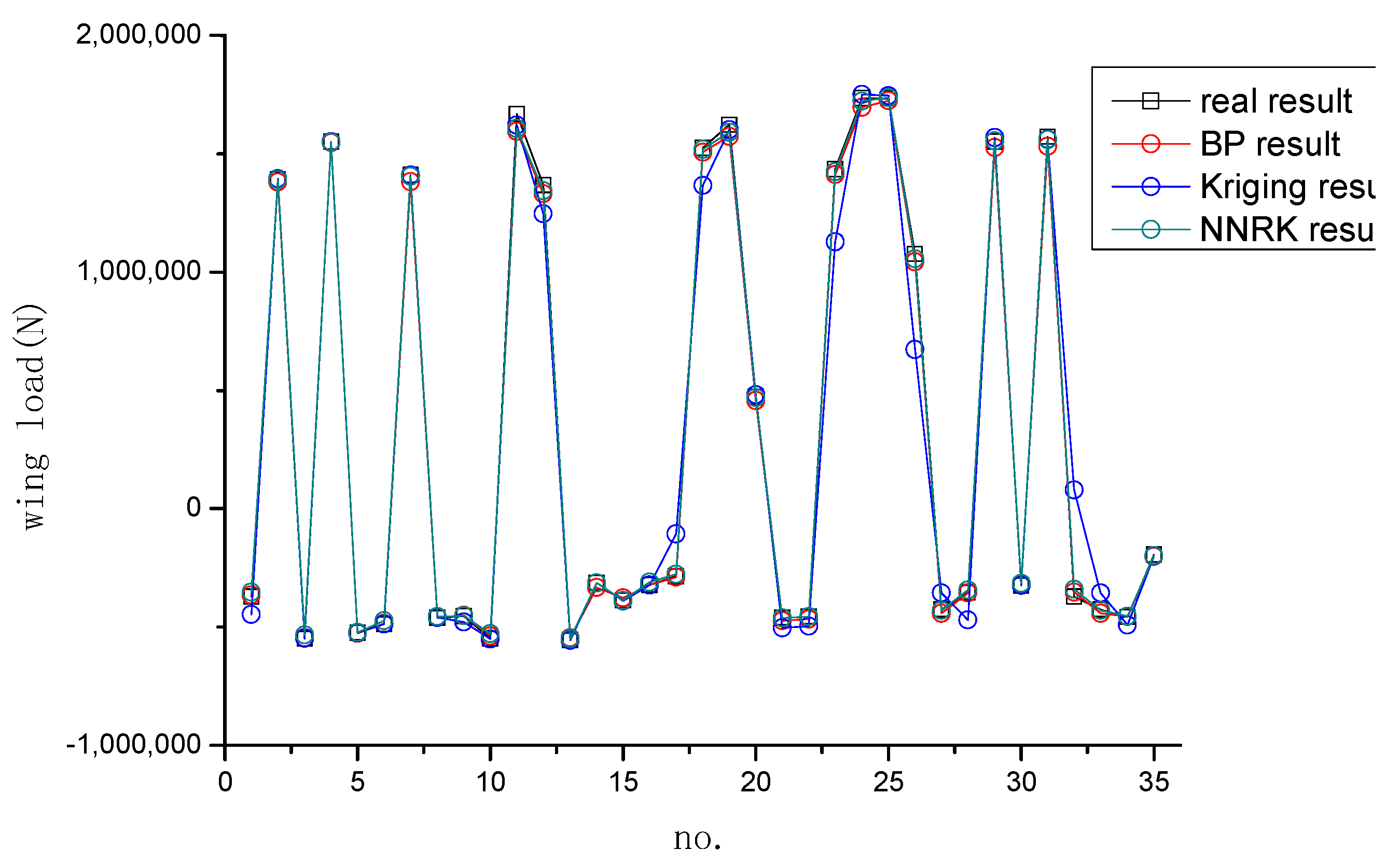
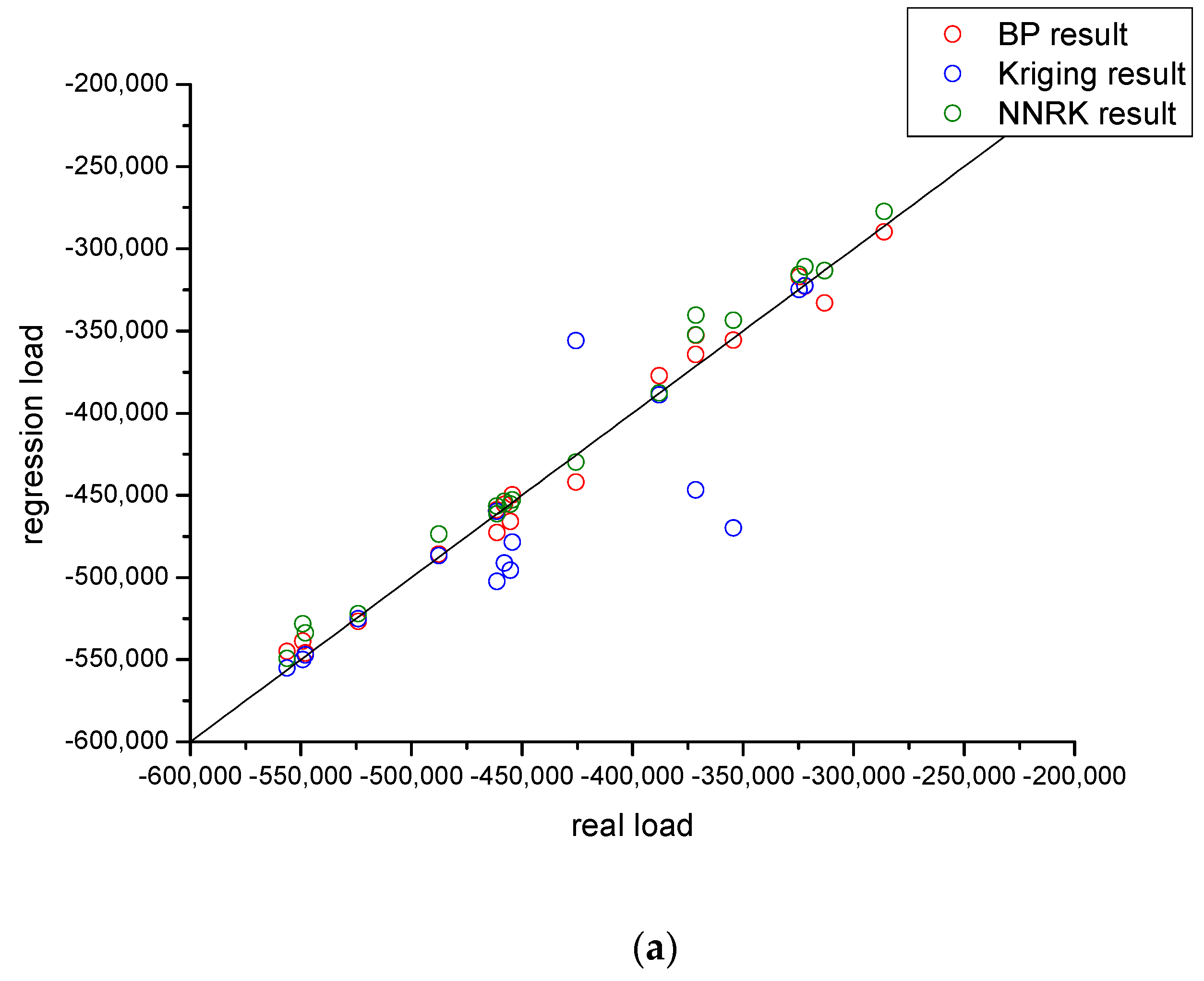
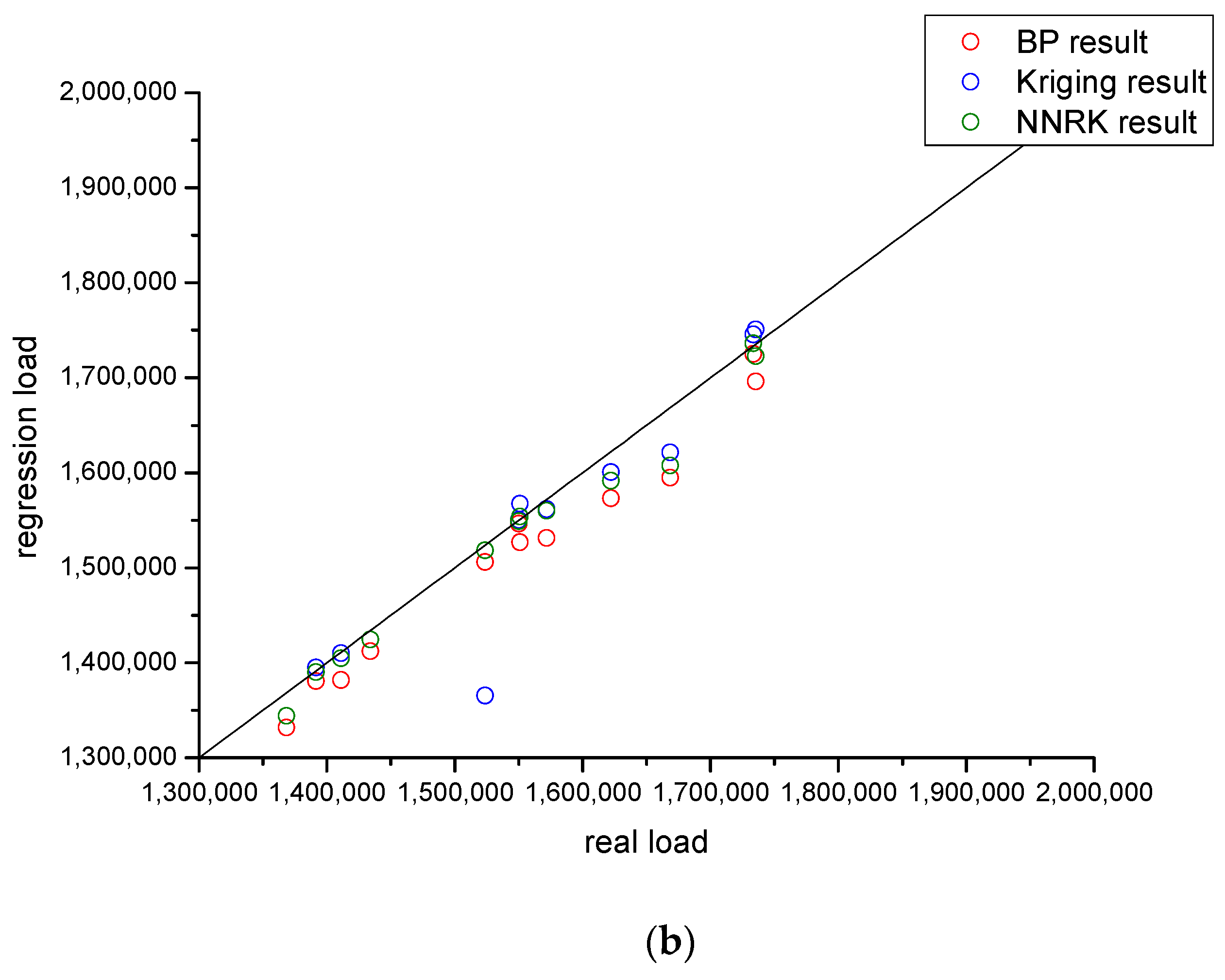
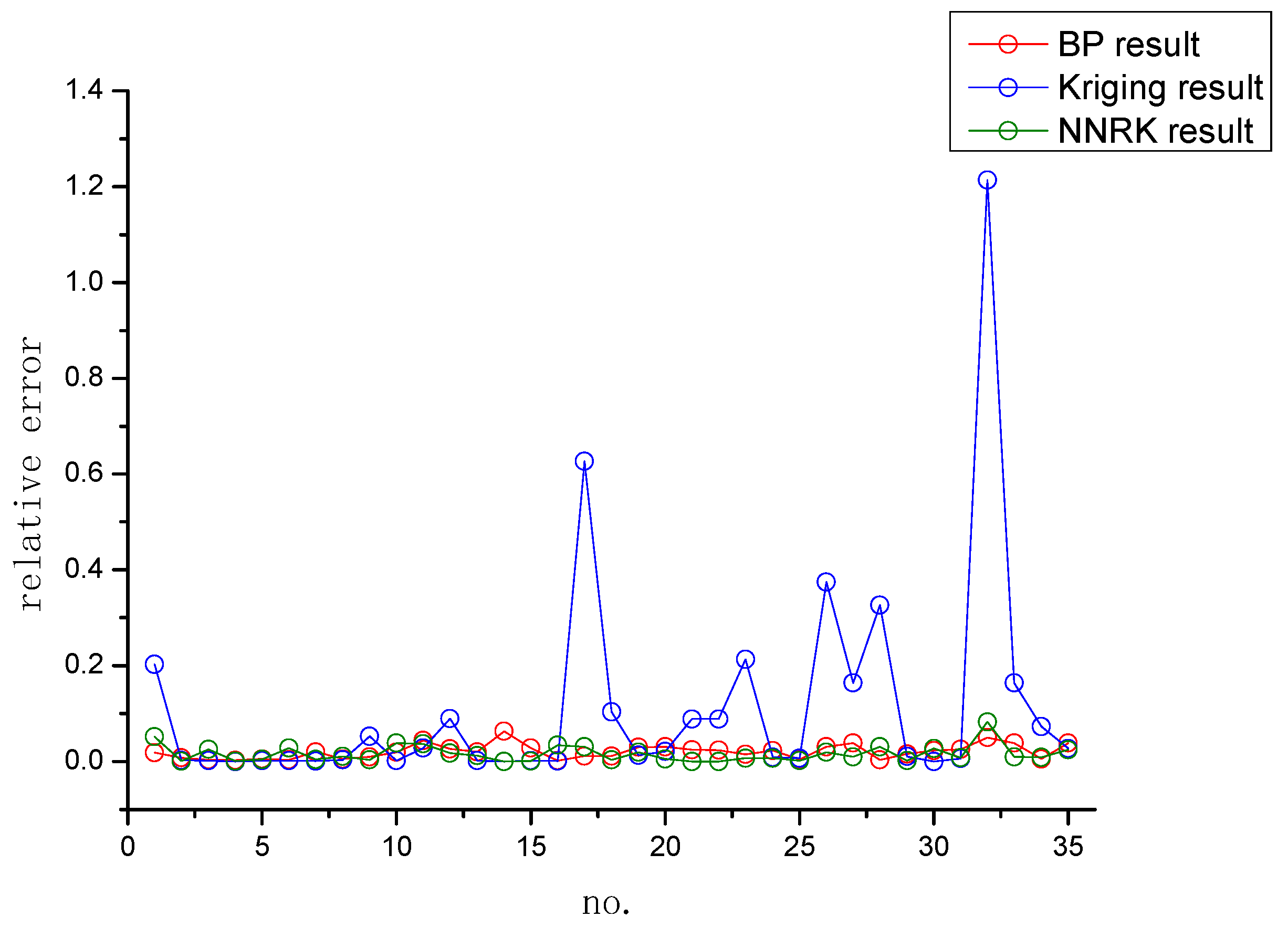
4. Result and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Livne, E.; Weisshaar, T.A. Aeroelasticity of nonconventional airplane configurations—Past and future. J. Aircr. 2003, 40, 1047–1065. [Google Scholar] [CrossRef]
- Lee, S.J.; Im, D.K.; Kang, M.K.; Lee, I.; Kwon, J.H. Efficient Aeroelastic Analysis Method Including Inverse Design for Body Effects. J. Aircr. 2009, 46, 2164–2169. [Google Scholar] [CrossRef]
- Castellani, M.; Cooper, J.E.; Lemmens, Y. Nonlinear static aeroelasticity of high-aspect-ratio-wing aircraft by finite element and multibody methods. J. Aircr. 2017, 54, 548–560. [Google Scholar] [CrossRef]
- Zink, P.S.; Raveh, D.E.; Mavris, D.N. Robust structural design of an active aeroelastic wing with maneuver load inaccuracies. J. Aircr. 2004, 41, 585–593. [Google Scholar] [CrossRef]
- Rodden, W.P.; Johnson, E.H. MSC Nastran v68 Aeroelastic Analysis User’s Guide; MSC Software Corporation: Los Angeles, NY, USA, 1994; pp. 73–76. [Google Scholar]
- Venkayya, V.; Tischler, V. Force and displacement transformation for aero-structure interaction analysis. In Proceedings of the 10th AIAA/IAAMO Multidisciplinary Analysis and Optimization Conference, AIAA, Albany, NY, USA, 30 August–1 September 2004. [Google Scholar]
- Dehart, J.; Cramer, K.; Miller, S. Application of the PANAIR production code to a complex canard/wing configuration. In Proceedings of the 21st Aerospace Sciences Meeting, AIAA, Reno, NV, USA, 10–13 January 1983. [Google Scholar]
- Liu, Y.Z.; Zhu, S.Y.; Wan, Z.Q.; Yang, C. A High Efficiency Aeroelastic Analysis Method based on Rigid External Aerodynamic Force and Elastic Correction by High-Order Panel Method. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, AIAA, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Raveh, D.; Karpel, M. Structural optimization of flight vehicles with non-linear aerodynamic loads. In Proceedings of the 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, AIAA, St. Louis, MO, USA, 2–4 September 1998. [Google Scholar]
- Yu, D.O.; Kwon, O.J. Predicting wind turbine blade loads and aeroelastic response using a coupled CFD-CSD method. Renew. Energy 2014, 70, 184–196. [Google Scholar] [CrossRef]
- Tang, D.; Dowell, E.H. Experimental and theoretical study on aeroelastic response of high-aspect-ratio wings. AIAA J. 2001, 39, 1430–1441. [Google Scholar] [CrossRef]
- Wan, Z.Q.; Zhang, B.C.; Yang, C.; Xu, Y. Static aeroelastic analysis of a high-aspect-ratio wing based on wind-tunnel experimental aerodynamic forces. Sci. China Technol. Sci. 2011, 54, 2716–2722. [Google Scholar] [CrossRef]
- Kutz, J.N. Deep Learning in Fluid Dynamics. J. Fluid Mech. 2017, 814, 1–4. [Google Scholar] [CrossRef]
- Lye, K.O.; Mishra, S.; Ray, D. Deep Learning Observables in Computational Fluid Dynamics. J. Comput. Phys. 2020, 410, 109339. [Google Scholar] [CrossRef]
- Halder, R.; Damodaran, M.; Khoo, B.C. Deep Learning Based Reduced Order Model for Airfoil-Gust and Aeroelastic Interaction. AIAA J. 2020, 58, 4304–4321. [Google Scholar] [CrossRef]
- Wang, X.; Kou, J.Q.; Zhang, W.W. Multi-Fidelity Surrogate Reduced-Order Modeling of Steady Flow Estimation. Int. J. Numer. Methods Fluids 2020, 92, 1826–1844. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, C.; Zheng, Y.; Bai, J.; Li, Z.; Xia, Q.; Fu, Q. Non-Intrusive Reduced-Order Model for Predicting Transonic Flow with Varying Geometries. Chin. J. Aeronaut. 2020, 33, 508–519. [Google Scholar] [CrossRef]
- Ignatyev, D.; Khrabrov, A. Experimental Study and Neural Network Modeling of Aerodynamic Characteristics of Canard Aircraft at High Angles of Attack. Aerospace 2018, 5, 26. [Google Scholar] [CrossRef]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds Averaged Turbulence Modelling Using Deep Neural Networks with Embedded Invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Dong, Y.Q. An Application of Deep Neural Networks to the in-Flight Parameter Identification for Detection and Characterization of Aircraft Icing. Aerosp. Sci. Technol. 2018, 77, 34–49. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, X.; Liu, S.; Deng, X. Recurrent Neural Network-Based Model Predictive Control for Multiple Unmanned Quadrotor Formation Flight. Int. J. Aerosp. Eng. 2019, 2019, 7272387. [Google Scholar] [CrossRef]
- Mersha, B.W.; Jansen, D.N.; Ma, H. Angle of Attack Prediction Using Recurrent Neural Networks in Flight Conditions with Faulty Sensors in the Case of F-16 Fighter Jet. Complex Intell. Syst. 2021, 9, 2599–2611. [Google Scholar] [CrossRef]
- Lee, H.; Puranik, T.G.; Fischer, O.P.; Mavris, D.N. Flight Data Driven System Identification Using Neural Networks for Landing Safety Assessment. In Proceedings of the 2021 IEEE/AIAA 40th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 3–7 October 2021. [Google Scholar]
- Simpson, T.W.; Mistree, F. Kriging Models for Global Approximation in Simulation-Based Multidisciplinary Design Optimization. AIAA J. 2001, 39, 2233–2241. [Google Scholar] [CrossRef]
- Yang, L.H.; Liu, S.A.; Zhang, G.Y.; Wang, C.X. Global Optimization for Ducted Coaxial-Rotors Aircraft Based on Kriging Model and Improved Particle Swarm Optimization Algorithm. J. Cent. South Univ. 2015, 22, 1315–1323. [Google Scholar] [CrossRef]
- Gong, Q.; Zhang, J.G.; Su, D. Reliability Simulation Combining Kriging and Monte Carlo Radius-Outside Importance Sampling in Space Structure Latch. Appl. Mech. Mater. 2012, 166–169, 1872–1878. [Google Scholar] [CrossRef]
- Kanazaki, M.; Jeong, S.; Yamamoto, K. High-Lift System Optimization Based on the Kriging Model Using a High-Fidelity Flow Solver. Trans. Jpn. Soc. Aeronaut. Space Sci. 2006, 49, 169–174. [Google Scholar] [CrossRef]
- Ollar, J.; Mortished, C.; Jones, R.; Sienz, J.; Toropov, V. Gradient Based Hyper-Parameter Optimisation for Well Conditioned Kriging Metamodels. Struct. Multidiscip. Optim. 2016, 55, 2029–2044. [Google Scholar] [CrossRef]
- Lee, S.; Kang, S.; Lee, K. Development of a Gaussian Process Modeling Application for the Prediction of Missile Aerodynamic Coefficients. AIAA J. 2019, 57, 2280–2296. [Google Scholar] [CrossRef]
- Weinmeister, J.; Gao, X.; Roy, S. Analysis of a Polynomial Chaos-Kriging Metamodel for Uncertainty Quantification in Aerodynamics. AIAA J. 2019, 57, 2280–2296. [Google Scholar] [CrossRef]
- Zhou, C.C.; Ji, M.Y.; Zhao, H.D.; Fei, C. Uncertainty Analysis of Motion Error for Mechanisms and Kriging-Based Solutions. Proc. Inst. Mech. Eng. Part O-J. Risk Reliab. 2021, 235, 731–743. [Google Scholar]
- Jeong, S.; Murayama, M.; Yamamoto, K. Efficient Optimization Design Method Using Kriging Model. J. Aircr. 2005, 42, 413–420. [Google Scholar] [CrossRef]
- Bae, H.G.; Kwon, J.H. A Study on Constrained Efficient Global Optimization Method for Noisy Computational Fluid Dynamics Data. Proc. Inst. Mech. Eng. Part G-J. Aerosp. Eng. 2014, 228, 908–919. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Singh, V.P. Estimating Spatial Precipitation Using Regression Kriging and Artificial Neural Network Residual Kriging (Rknnrk) Hybrid Approach. Water Resour. Manag. 2015, 29, 2189–2204. [Google Scholar] [CrossRef]
- Tarasov, D.; Buevich, A.; Shichkin, A.; Subbotina, I.; Tyagunov, A.; Baglaeva, E. Chromium Distribution Forecasting Using Multilayer Perceptron Neural Network and Multilayer Perceptron Residual Kriging. In Proceedings of the International Conference of Numerical Analysis and Applied Mathematics (ICNAAM 2017) 1978, Thessaloniki, Greece, 25–30 September 2017. [Google Scholar]
- Tarasov, D.A.; Buevich, A.G.; Sergeev, A.P.; Shichkin, A.V. High Variation Topsoil Pollution Forecasting in the Russian Subarctic: Using Artificial Neural Networks Combined with Residual Kriging. Appl. Geochem. 2018, 88, 188–197. [Google Scholar] [CrossRef]
- Sergeev, A.P.; Tarasov, D.A.; Buevich, A.G.; Subbotina, I.E.; Shichkin, A.V.; Sergeeva, M.V.; Lvova, O.A. High Variation Subarctic Topsoil Pollutant Concentration Prediction Using Neural Network Residual Kriging. Appl. Math. Comput. Sci. 2017, 1836, 020023. [Google Scholar]
- Shen, Z.Q.; Shi, J.B.; Wang, K.; Kong, F.S.; Bailey, J.S. Neural Network Ensemble Residual Kriging Application for Spatial Variability of Soil Properties. Pedosphere 2004, 14, 289–296. [Google Scholar]
- Demyanov, V.; Soltani, S.; Kanevski, M.; Canu, S.; Maignan, M.; Savelieva, E.; Timonin, V.; Pisarenko, V. Wavelet Analysis Residual Kriging Vs. Neural Network Residual Kriging. Stoch. Environ. Res. Risk Assess. 2001, 15, 18–32. [Google Scholar] [CrossRef]
- Sato, K.; Inage, K.; Fujii, T. On the Performance of Neural Network Residual Kriging in Radio Environment Mapping. IEEE Access 2019, 7, 94557–94568. [Google Scholar] [CrossRef]
- Angiulli, G.; De Carlo, D.; Sgró, A.; Versaci, M.; Morabito, F.C. Accurate Modelling of Lossy Siw Resonators Using a Neural Network Residual Kriging Approach. IEICE Electron. Express 2017, 14, 20170073. [Google Scholar] [CrossRef]

| Meaning | Unit |
|---|---|
| Total weight | kg |
| Center of gravity | % |
| Pitch moment of inertia | kg × m2 |
| Altitude | m |
| Mach number | Non-dimensional |
| Airspeed | m/s |
| Velocity pressure | pa |
| Pitch rate | |
| Load factor | Non-dimensional |
| Angle of attack |
| Meaning | Unit |
|---|---|
| Wing load | N |
| BP | Kriging | NNRK | |
|---|---|---|---|
| MAE | 0.020730 | 0.112119 | 0.016246 |
| MSE | 0.000648 | 0.065690 | 0.000575 |
| RMSE | 0.025456 | 0.256301 | 0.023981 |
| R-square | 0.999790 | 0.982193 | 0.999820 |
| BP | Kriging | NNRK | |
|---|---|---|---|
| Random dataset 1 | 0.050018 | 0.746040 | 0.027682 |
| Random dataset 2 | 0.028923 | 0.935631 | 0.024446 |
| Random dataset 3 | 0.160216 | 1.041563 | 0.040264 |
| Random dataset 4 | 0.036385 | 0.101322 | 0.025585 |
| Random dataset 5 | 0.044994 | 0.071680 | 0.030333 |
| Random dataset 6 | 0.034482 | 0.081201 | 0.019517 |
| Random dataset 7 | 0.078744 | 0.844058 | 0.018788 |
| Random dataset 8 | 0.067317 | 1.399952 | 0.060299 |
| Random dataset 9 | 0.057461 | 0.054945 | 0.053900 |
| BP | Kriging | NNRK | |
|---|---|---|---|
| Time (s) | 1.31 | 0.078 | 1.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Q.; Wan, Z.; Yang, C. Flight Load Calculation Using Neural Network Residual Kriging. Aerospace 2023, 10, 599. https://doi.org/10.3390/aerospace10070599
Yan Q, Wan Z, Yang C. Flight Load Calculation Using Neural Network Residual Kriging. Aerospace. 2023; 10(7):599. https://doi.org/10.3390/aerospace10070599
Chicago/Turabian StyleYan, Qi, Zhiqiang Wan, and Chao Yang. 2023. "Flight Load Calculation Using Neural Network Residual Kriging" Aerospace 10, no. 7: 599. https://doi.org/10.3390/aerospace10070599
APA StyleYan, Q., Wan, Z., & Yang, C. (2023). Flight Load Calculation Using Neural Network Residual Kriging. Aerospace, 10(7), 599. https://doi.org/10.3390/aerospace10070599





