Influence of a Deflectable Leading-Edge on a Flapping Airfoil

Abstract

Flapping wing dynamics are of great interest in many research areas, such as bioinspired systems and aircraft aeroelasticity. The findings of the present study provide significant insight into the importance of the leading-edge dynamic incidence on the propulsive performance of flapping airfoils. The main objective is to improve the propulsive characteristics by adding a pitching leading-edge to a conventional NACA0012 airfoil at the lower spectrum of the Reynolds number. The problem is solved numerically at a Reynolds number of ${10}^4$ under various flapping conditions. The results show that the leading-edge pitching amplitude has a great impact on the propulsive power and efficiency, providing meaningful improvements. The required power coefficient is reduced overall, although not as significantly as the propulsive power. The influence of the movable leading-edge on the pressure distribution is analyzed, showing that the enlargement of the frontal area is the root cause of propulsive augmentation. The proposed geometry provides an innovative way of flapping an airfoil with propulsive purposes, offering remarkable improvements that can defy conventional flapping.

1. Introduction

Flapping airfoils offer the possibility of understanding how both thrust and lift can be generated using solely one surface. Applications of unsteady airfoils span from aircraft elasticity [1] to marine engineering [2], but when looking at the lower Reynolds number range, a connection is seen with natural flight.

The first explanation of how flapping airfoils produce thrust and lift came from Knoller [3] and Betz [4], who saw that, when an airfoil oscillates, it presents an effective angle of attack that generates an aerodynamic force that has the thrust and lift components. The main limitation of the pioneering theory was that it was only based on the airfoil kinematics, neglecting any real-fluid effects. The work of von Kármán and Burgers [5] offers a complete explanation based on the vortices of the airfoil’s wake and their orientation. One of the first mathematical theories regarding unsteady airfoils was made by Theodorsen [6], who predicted the unsteady aerodynamics of pitching and plunging airfoils. Garrick [7] extended the study to the propulsion capabilities of a movable wing with three degrees of freedom. Nowadays, with the available computational power, numerical methods have evolved to offer flow solutions based on Navier–Stokes equations.

The study of unsteady airfoils encircles flow structures, propulsive performance, energy harvesting, and bionics. Within these topics, flapping is the most studied, followed by pure pitching, and lastly, pure plunging [8]. Pure plunging studies are generally shadowed by more complex kinematics, but the combined motion of plunging and pitching is not always a guarantee of higher thrust production. However, it often leads to a better propulsive efficiency [9].

An alternative way to improve the performance of unsteady airfoils is by modifying the leading-edge geometry. This may be accomplished using concepts such as DDLE (Dynamically Deformed Leading-Edge) or VDLE (Variable Droop Leading-Edge), which are commonly used for dynamic stall mitigation [10]. Innovative concepts, such as rotating cylinders at the leading-edge, have been used as active flow control techniques to prevent flow separation [11]. Others use bioinspired solutions, for instance, alula deployment at pre-stall conditions to significantly improve lift [12] or adding an active elastic leading-edge deformation that can improve airfoils with energy extraction purposes [13]. While these are examples of active systems that deliver aerodynamic and/or propulsive improvements, other investigations have employed passive solutions, which generally offer lower energy consumption and a lower system complexity. Liu et al. [14] attached a rigid flat plate to the trailing edge of a foil that exhibited passive motion determined by the fluid–structure interaction. The results showed that with an adequate level of flexibility, this modification was responsible for at least half of the thrust production. A similar concept was used by Tian et al. [15], who studied the power-extracting capabilities of an oscillating airfoil. However, the authors concluded that the passive deformation could not reach the efficacy hoped without some level of active control.

Geissler and van der Wall [16] identified that flow separation limits the flapping-wing efficiency and proposed a time-dependent deflectable leading-edge that reduces the LEV (Leading-Edge Vortex) size. The authors tested a plunging airfoil at a Mach of $0.3$, $Re={10}^6$, and a reduced frequency equal to $0.5$ and searched for improvements in the propulsive coefficients. The results showed that the propulsive efficiency of the deformable leading-edge with a droop amplitude of $10°$ was roughly doubled compared to the rigid airfoil. Niu et al. [17] made changes to the leading-edge by using a VDLE to improve the aerodynamic characteristics of a pitching NACA0012 airfoil. By deflecting the leading-edge, adverse pressure gradients were lowered due to the lower local angle of attack near the leading-edge. This effect increased the lift and reduced the drag and pitching moment at higher pitch angles.

The VDLE concept was also used by Chandrasekhara et al. [18] to control dynamic stall in the compressible regime. They used a VR-12 airfoil with a movable leading-edge as it underwent a sinusoidal pitch oscillation. By drooping the leading-edge, the frontal part of the airfoil presented a lower incidence and the tendency of the airfoil to enter dynamic stall was reduced. The results showed that reductions of up to 75% were achieved, making the concept desirable for rotor dynamics, as it can eliminate torsional instabilities. Similarly, Xing et al. [19] looked into the role of the leading-edge, proposing an inflatable frontal structure as a way to reduce dynamic stall phenomena.

With a micro air vehicle design in mind, Drost et al. [20] studied the use of a dynamic leading-edge in a thin, flat, rigid plunging airfoil. By actively moving the leading-edge, the LEV at high angles of attack has its strength reduced. By moving the leading-edge dynamically, the results showed that the boundary layer and flow separation were altered significantly, increasing the lift-to-drag ratio. The authors indicated that this is an adequate alternative when it comes to eliminating the complexity of adding systems, such as blowing or suction.

In their work, Geissler and van der Wall [16] mentioned that the influence of a dynamic leading-edge deformation in the domain of incompressible flows, where birds and insects live, is of high interest. To our knowledge, no published work has explored such a regime with an innovative geometry. Although dynamically changing the leading-edge has been widely studied in the field of flow separation control and dynamic stall, these works have generally focused on the higher Reynolds spectrum and rotor dynamics. Contrary to those, this study focused on improving the known propulsive characteristics of flapping airfoils, rather than looking at stall or flow separation prevention. Our preliminary studies [21,22] explored the low Reynolds regime by proposing a modified version of the NACA0012 airfoil with a movable leading-edge.

The present work focuses on studying the influence of a pitching leading-edge added to the traditional NACA0012 at a lower Reynolds state. The leading-edge pitching amplitude is changed parametrically under different oscillating conditions. The propulsive characteristics are evaluated using propulsive indicators, and associations between force generation, pressure distribution, and flow features are given. The real cause of propulsive augmentation is also exposed.

2. Methodology

2.1. Geometry & Kinematics

The present study used a modified version of the NACA0012 airfoil, the so-called NACA0012-IK30, that was specifically designed to investigate the influence of a pitching leading-edge on the propulsive performance of unsteady airfoils. Figure 1 shows the proposed geometry, which is an NACA0012 airfoil split into two parts at 30% of the chord, which is also the leading-edge pivot point. Between these two parts, there is a circular arc that creates a gap of 1 $\mathrm{m}$$\mathrm{m}$.

Choosing a circular section to divide the two parts was a design choice based on a compromise between improving the propulsive capabilities while keeping the leading-edge pitching mechanism simple. Selecting a different section would require a more complex pitching mechanism involving an intricate rotational system.

The airfoil follows a sinusoidal waveform for both plunging and pitching of the leading-edge. The back part has no pitching prescribed to it. The vertical translation is given by

$$y=Acos\left(2\pi ft\right),$$

(1)

where A and f are the plunging amplitude and frequency, respectively. The angle of attack of the leading-edge is written as

$${\alpha }_1=A_{\alpha }cos(2\pi ft+\varphi ),$$

(2)

where $A_{\alpha }$ is the leading-edge pitching amplitude and $\varphi$ is the phase angle, which was set to 90$°$ throughout out the study. This means that when the airfoil is halfway up or down, with its maximum plunging velocity, the leading-edge is at its maximum deflection.

Considering the plunging and pitching velocities, one can define the effective angle of attack as

$${\alpha }_{\mathrm{eff}}=arctan\left(-\frac{\dot{y}}{U}\right)+\alpha ,$$

(3)

where U is the freestream velocity, and $\alpha$ is the airfoil angle of attack, which is calculated by

$$\alpha =arctan\left(\frac{c_{1}sin{\alpha }_1+c_{2}sin{\alpha }_2}{c_{1}cos{\alpha }_1+c_{2}cos{\alpha }_2}\right).$$

(4)

In the present study, the back part had no pitching, and its mean angle of attack was set at 0$°$, reducing Equation (4) to

$$\alpha =arctan\left(\frac{c_{1}sin{\alpha }_1}{c_{1}cos{\alpha }_1+c_2}\right).$$

(5)

2.2. Experimental Apparatus

The proposed geometry was firstly subjected to an experimental study, which consisted of a brief investigation that focused on flow visualization. Experiments were conducted at the facilities of the AEROG-UBI anemometry laboratory, using an open circuit, open section, and blower wind tunnel with an $0.3\times 0.2$ $\mathrm{m}$ outlet section. The flow velocity was measured at the outlet section center with a two-component Laser Doppler velocimeter (Dantec Flowlite 2D), which had been used previously in the anemometry laboratory and is explained in detail in [23,24,25]. The horizontal and vertical mean velocities were determined by a two-velocity channel Dantec BSA F60 processor. Adjustments to the mean velocity were made by opening a guillotine located upstream. The wing was put at 2 $\mathrm{c}$$\mathrm{m}$ from the exit section, with a 20 $\mathrm{c}$$\mathrm{m}$ chord and a 40 $\mathrm{c}$$\mathrm{m}$ span. A wing span larger than the outlet section was selected to mitigate the wing tip effects (wing tip vortices) and remove the possibility of capturing it by the image acquisition system. The wing model was supported by a structure linked to the plunging motor, which itself was fixed to the ground. The general assembly is shown in Figure 2a,b.

The plunging motor was a stepper motor connected to a linear slide, with these being the ARM46AC and EASM4XD020ARAC, respectively, both produced by Oriental Motor Co., Ltd., Tokyo, Japan. The linear actuator had a stroke rate of $0.2$ $\mathrm{m}$ with a lead of $0.0012$ $\mathrm{m}$ and a maximum operating speed of $0.8$ $\mathrm{m}$/${\mathrm{s}}^{-1}$. This apparatus has been used and validated previously while studying the effects of unequal ascending and descending velocities in a plunging airfoil [26]. The pitching motion of the leading-edge was accomplished by the PKE543AC-PS50 stepper motor, also produced by Oriental Motor Co., Ltd. It was fixed at one of the wing tips, having a basic step angle of $0.0144$$°$ with a gear ratio of 50:1. The desired kinematics were prescribed using the ARD-CD and RKSD503-CD controllers for plunging and pitching, respectively. These two controllers were connected to a laptop equipped with MEXE02 support software using the CC05IF-USB data setting software communication cable.

The wing was designed with CATIA V5 R20 software, and its production was accomplished using additive manufacturing. The wing was produced using the Original Prusa i3 MK3S+ 3D printer with a PLA filament. On the other wing tip, a camera was fixed to capture the flow field. The camera was a GoPro HERO10, which offers a wide view of phenomena close to the airfoil with a Lagrangian perspective. Video recordings were shot at a 2704 × 1520 pixel resolution at 240 frames per second. To enhance the flow features, videos were lightly processed on MATLAB. Image processing was used to gather some instructions, such as resizing, grayscale conversion, pixel value adjustment, and sharpening. The flow was marked with smoke by using a machine that thermally vaporized a water–glycerol mixture, which condensed into small particles. The smoke was inserted into the wing tunnel through a tube. Downstream of this tube, a flow straightener was placed to remove any vertical velocity components created from the smoke insertion. At the outlet section, the smoke particles were illuminated using an array of LEDs, as shown in Figure 2c.

2.3. Numerical Methodology

Following the experimental study, the NACA0012-IK30 airfoil was studied numerically using Ansys^® Fluent 2022 R1. Similar numerical methodologies have been used and validated in previous investigations while studying oscillating airfoils [27,28]. The flow surrounding the flapping airfoil was assumed to be turbulent with a laminar-to-turbulent transition. The Reynolds stress tensor was modeled according to Boussinesq’s hypothesis, relating the turbulent stresses to the mean velocity gradients in a similar way that viscous stresses are dependent on velocity gradients. The turbulence model used was the $\gamma$ (intermittency) transition model, which is an extension of the $\gamma -R{e}_{\theta }$ transition model [29]. The latter could not be used as it is the Galilean variant, which means that it cannot be applied to surfaces moving relative to the coordinate system for which the velocity field is computed. The Fluent solver implementation of the $\gamma$ transition model is only available in combination with other turbulence models, from which the SST $k-\omega$ model was chosen for the present study.

The governing equations were solved using the pressure-based coupled algorithm that links the momentum- and pressure-based continuity equations. Gradients were evaluated with the Least Squares Cell-Based method, and the pressure interpolation scheme was second-order accurate. The convective terms for the momentum, turbulent kinetic energy, specific dissipation rate, and intermittency were discretized with the second-order upwind scheme, while diffusive terms were central-differenced and second-order accurate. Transient discretization was accomplished with the first-order implicit.

The computational domain consisted of four parts: the NACA0012-IK30 airfoil, the inlet, the outlet, and the interior. Solving the -IK30 numerically presented several challenges regarding the design process of the mesh due to the relative motion between the front and back parts. This was tackled by using an overset mesh configuration, where two component meshes and a background mesh were designed. In Figure 3, the component meshes of both the frontal and back parts and the background mesh are shown.

The background mesh (cf. Figure 3c) comprised an unstructured outer zone with triangular elements and an inner zone, where a structured mesh with rectangular elements was used. The inlet and outlet were placed far away from the airfoil, at about twenty airfoil chords. The motion of the component meshes was accomplished using User-Defined Functions (UDFs). The motion parameters, for instance, the frequency and plunging and pitching amplitudes were determined based on the dimensionless parameters that govern the problem. These are the Reynolds number, $Re=\rho Uc/\mu$, reduced frequency, $k=2\pi fc/U$, nondimensional amplitude, $h=A/c$, and nondimensional velocity, $kh$, where $\rho$ is the fluid density, $\mu$ is the dynamic viscosity, c is the aerodynamic chord when the leading-edge has no deflection, and A is the plunging amplitude.

The parameters used to evaluate the propulsive performance of the proposed airfoil were the mean propulsive power, mean required power, and propulsive efficiency. In its coefficient form, the propulsive power is given by

$$C_{P_P}=\frac{(T_1+T_2)U}{0.5\rho U^{3}S}={\left(C_t\right)}_1+{\left(C_t\right)}_2,$$

(6)

which has the same value as the thrust coefficient. $T_1$ and $T_2$ are the thrust forces of the frontal and back parts, respectively. The required power coefficient is

$$C_{P_R}=\frac{-\dot{y}(L_1+L_2)-\dot{{\alpha }_1}{M}_1}{0.5\rho U^{3}S}=-\left(\left({\left(C_l\right)}_1+{\left(C_l\right)}_2\right)\frac{\dot{y}}{U}+{\left(C_m\right)}_1\frac{\dot{{\alpha }_1}c}{U}\right),$$

(7)

where $L_1$ and $L_2$ are the lift forces of the frontal and back parts, respectively, and $M_1$ is the pitching moment of the leading-edge calculated at the pivot. The term ${\left(C_m\right)}_2$ does not exist in Equation (7), since no pitching is prescribed to the back part. The Fluent solver provides all these coefficients based on the air density, $\rho$, wind speed, U, and wing area, S, which for the 2D case equals the chord length. The propulsive efficiency is then calculated by

$$\eta =\frac{\overline{C_{P_P}}}{\overline{C_{P_R}}},$$

(8)

where $\overline{C_{P_P}}$ and $\overline{C_{P_R}}$ are the mean propulsive power and required power coefficients, respectively. These two values were obtained in the last simulated period, where transients were found to be negligible.

The numerical methodology was put through a grid and time step independence study, in which the number of elements was increased by a factor of 2, and the time step was reduced by a factor of $1/2$ for three meshes. All mesh elements close to the walls were designed to have a $y^{+}$ of approximately 1. The conditions used for the study were $Re=1.0\times {10}^4$, $k=1.0$, $h=0.50$, and $A_{\alpha }=5°$. The propulsive coefficients are plotted against the dimensionless time $t/T$ in Figure 4, where T is the motion period. N represents the number of mesh elements, with the final mesh ($2N$) having approximately two hundred thousand elements.

As seen in Figure 4, no considerable differences were seen, indicating that mesh and time step independence were achieved. Additionally, the present methodology was compared against numerical data of a plunging NACA0012 [30] and with experimental data from Heathcote et al. [31], as shown in Figure 5. The mean propulsive and required power coefficients were used to verify the reliability of the CFD results at this low Reynolds state. Computations were conducted at $Re=2.0\times {10}^4$, $h=0.175$, and with a Strouhal number, $St$, of between $0.1$ and $0.4$. The Strouhal number is related to the nondimensional velocity, $kh$, as $kh=\pi St$.

3. Results and Discussion

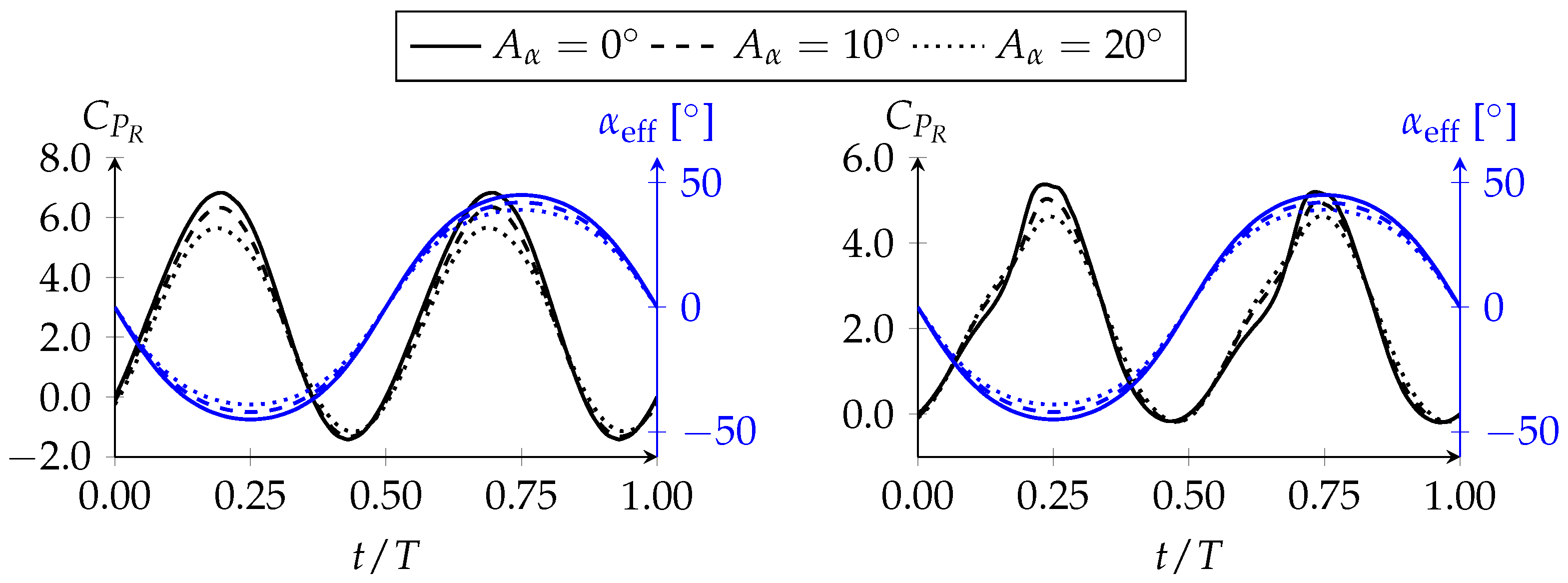
The propulsive capabilities of the NACA0012-IK30 were tested numerically at a Reynolds number of ${10}^4$ with two nondimensional plunging amplitudes, $h=0.25$ and $0.50$, and three nondimensional velocities, $kh=0.25$, $0.50$ and $1.00$. For each of these conditions, five leading-edge pitching amplitudes were considered ( 0$°$, 5$°$, 10$°$, 15$°$, and 20$°$).

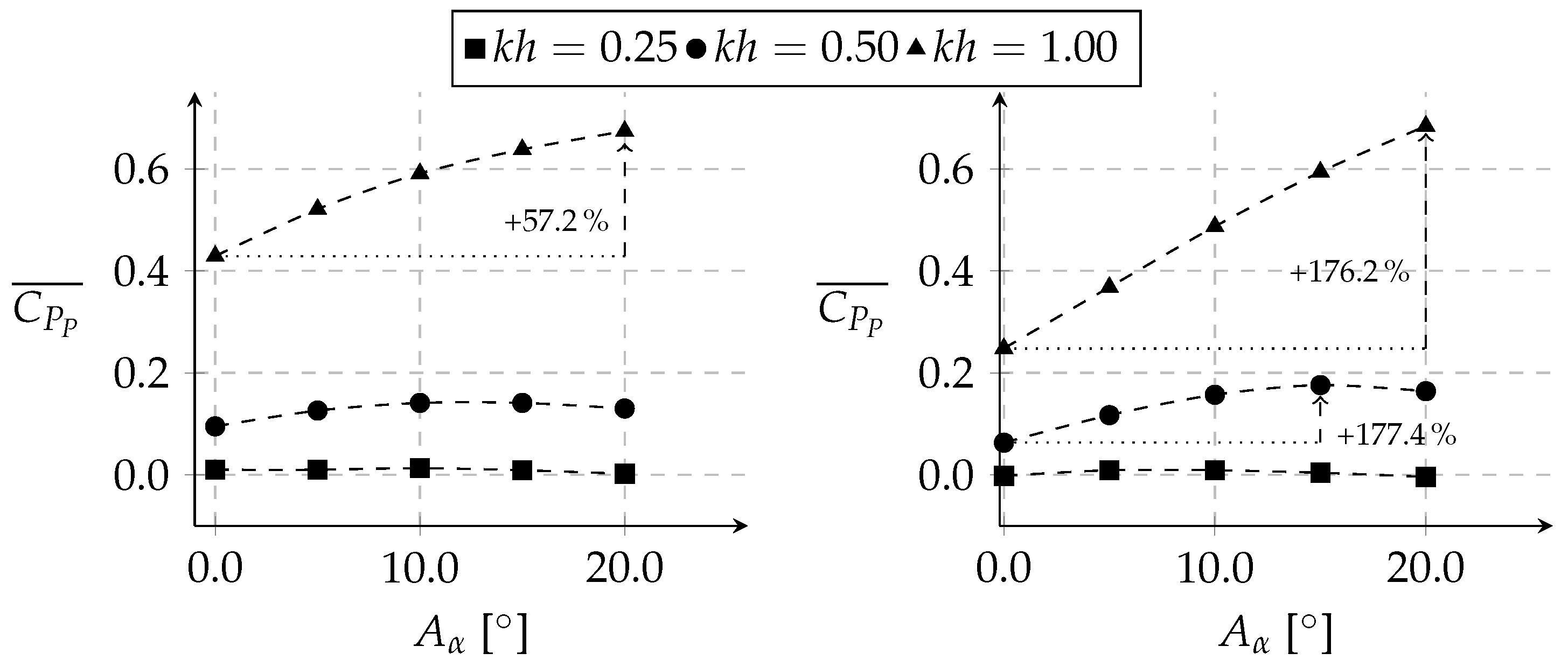
At first, the propulsive performance was evaluated using the three fundamental parameters commonly used for flapping airfoils: the mean propulsive power, the mean required power, and the propulsive efficiency. In Figure 6, the mean propulsive power coefficient is plotted against the leading-edge pitching amplitude for the three nondimensional velocities considered. Overall, increasing the pitching amplitude was shown to be beneficial up to a certain amplitude, where $\overline{C_{P_P}}$ then started decreasing, except when $kh=1.00$, where the maximum was not reached. The results also show that the slower flapping condition did not benefit from the dynamic leading-edge or presented good propulsive capabilities, being very close to a drag-producing regime. While both nondimensional amplitudes had fairly similar behaviors, with $h=0.50$, improvements in terms of magnitude were much more significant. When it came to the mean propulsive power, improvements of up to $177.4\%$ relative to the plunging-only leading-edge were achieved. Additionally, the results indicate that the higher the nondimensional velocity is, the higher the leading-edge pitching amplitude needs to be to achieve the optimal propulsive power.

When it comes to the mean required power coefficient, as shown in Figure 7, the influence of the dynamically activated leading-edge is beneficial overall but is rather small, except for the case with the lower nondimensional amplitude and highest nondimensional velocity. In this specific case, the required power decreases linearly as $A_{\alpha }$ increases, with a $13.0\%$ reduction compared to the plunging-only leading-edge.

Combining the two propulsive coefficients results in the propulsive efficiency shown in Figure 8. The graphs indicate that when the leading-edge is deflected, great improvements are achieved for both nondimensional amplitudes with increases of up to $229.8\%$. Overall, a higher propulsive efficiency is seen for the middle nondimensional velocity, although it is not clear whether $kh=1.00$ could offer better efficiency at larger pitching amplitudes, since no larger values were considered.

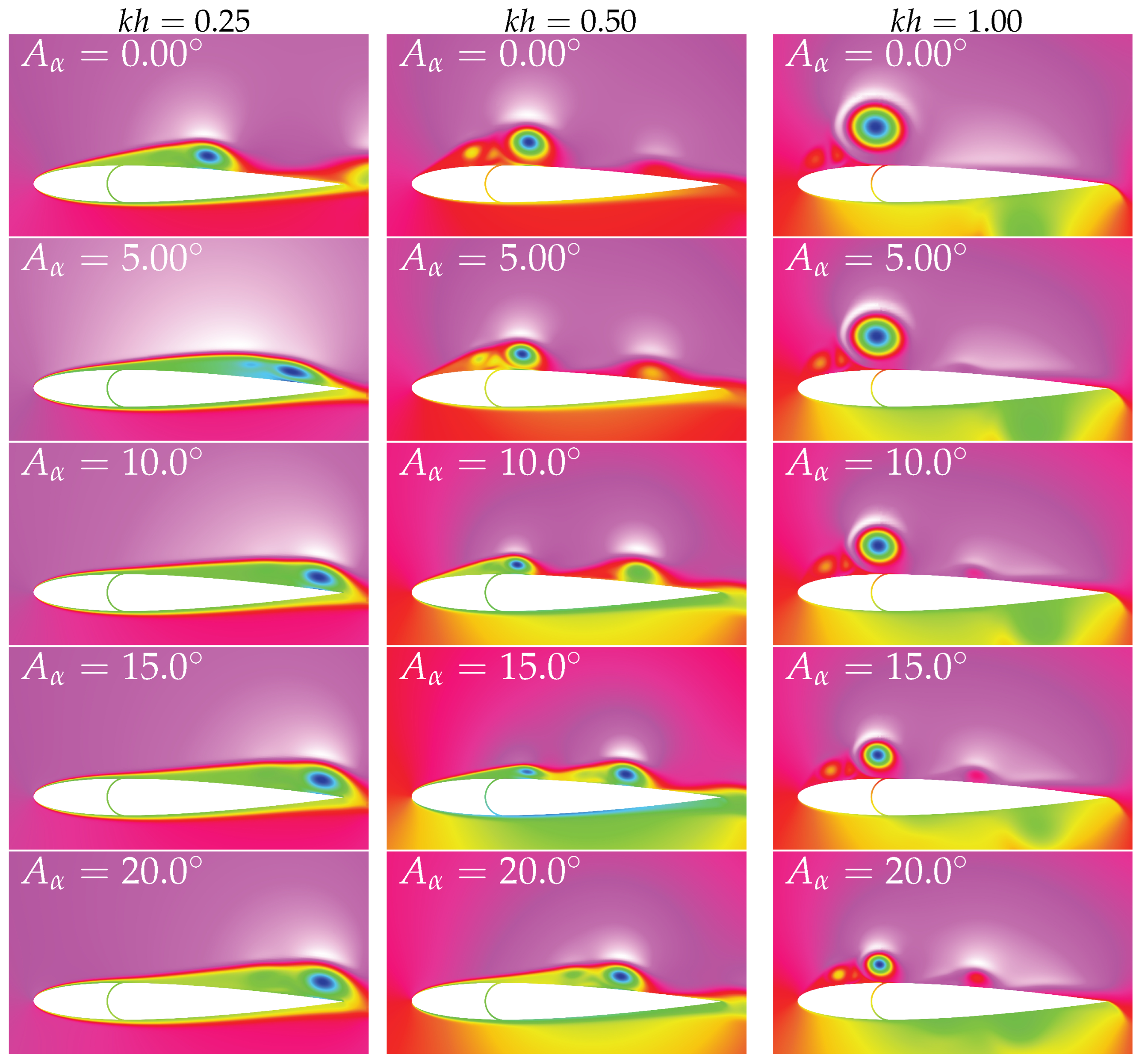
Based on these results, it is clear that adding a pitching leading-edge provides great advantages to the propulsive characteristics of the conventional NACA0012 plunging airfoil. These improvements are inevitably related to changes induced in the flow field by the dynamic leading-edge. In Figure 9 and Figure 10, the influence of the leading-edge pitching amplitude on the flow features is analyzed for all conditions presented before. The representation of the numerical field uses the total pressure contour to observe flow separation, since separated flow regions show lower values due to associated losses. Snapshots are given at the end of the oscillation period ($t/T=1.0$), as they provide a representation of what occurred during the entire period.

As expected, all conditions show some flow separation, as the airfoil is oscillating at nondimensional velocities that surpass its static stall angle (≈ 12$°$). The cases with a plunging-only leading-edge experience a maximum effective angle of attack at between 14$°$ and 45$°$ ($max{\alpha }_{\mathrm{eff}}=arctan\left(kh\right)$), which can be reduced by ≈ 6$°$ when the leading-edge pitches at 20$°$.

Still, even though both nondimensional amplitudes have the same effective angle of attack profile, the phenomena seen around the airfoil are different. When the airfoil oscillates with a larger nondimensional amplitude, flow features are scaled up with the leading-edge vortex occupying the whole upper surface of the airfoil when there is no deflection of the leading-edge.

For both amplitudes, as the nondimensional velocity increases, the presence of the leading-edge vortex becomes more evident and moves upstream. This is expected as the effective angle of attack that triggers separation is reached quicker, and thus, the LEV (leading-edge vortex) formation starts earlier. In a plunging airfoil, the leading-edge vortex only works as a thrust enhancement feature when located upstream of the maximum thickness position, described by Gao et al. [32] as a thrust booster for plunging airfoils. The NACA0012-IK30 airfoil follows the same principle, even though it should not be considered to be a traditional plunging airfoil.

Focusing on the influence of the leading-edge pitching amplitude, we see that it has a crucial role in dictating the LEV size. The size and growing process of the leading-edge vortex are explained. Images show that the LEV presents its maximum size when there is no leading-edge deflection. With an increase in the pitching amplitude to 20$°$, the vortex reduces its size to approximately 50 percent for both nondimensional amplitudes. This decrease is caused by the reduction in the adverse pressure gradient as a consequence of lowering the effective angle of attack of the leading-edge part.

As seen for the mean propulsive coefficients, the pitching amplitude has a small influence at the lowest nondimensional velocity, which is also seen in the flow fields obtained numerically. However, for the other two, the influence is much more evident. We verify that, when increasing the pitching amplitude, the leading-edge vortex present in $A_{\alpha }=0.00°$ becomes smaller and feeds another vortex that appears beyond the maximum thickness position. This feeding process alone is not beneficial for propulsive improvement, since it increases the suction force after the maximum thickness position, which inevitably increases drag.

At the same time, looking back at Figure 6, we see that its concave-shaped function means that there is an optimal pitching amplitude value that maximizes the mean propulsive power. For instance, at $kh=0.50$, that value is somewhere between 10$°$ and 15$°$, which causes flow separation in the flow field. This result is central to the analysis of the proposed mechanism, because it clearly indicates that we are not pursuing the total elimination of the LEV. Instead, we are looking for a way to exploit its presence. This is contrary to flow separation occurring at a higher Reynolds numbers, which is not desirable at all, meaning that understanding the LEV dynamics (its position, intensity, and residence time on the airfoil) is crucial to optimally use the NACA0012-IK30 as a thrust enhancement mechanism.

Additionally, determining the evolution of the propulsive coefficients over time is crucial to understanding where propulsive improvements come from and, more specifically, the time frames in which they occur. The following graphs are focused on the conditions that show good propulsive characteristics and a clear dependence on the leading-edge pitching amplitude, $kh=0.50$ and $1.00$.

In Figure 11, the propulsive power is shown as a function of $t/T$ for a nondimensional velocity of $0.50$. To simplify the analysis, only three leading-edge pitching amplitudes are presented, together with the changes in the effective angle of attack over time. Deflecting the leading-edge improves the propulsive power for the vast majority of the oscillating period with the greatest improvements seen when the airfoil has its maximum effective angle of attack ($t/T=0.25$ and $t/T=0.75$). However, the results also show that a continuous increase in $A_{\alpha }$ may not be beneficial when the pitching amplitude can lead to the degradation of the propulsive power, as observed in $t/T=0.50$.

At the highest nondimensional velocity, shown in Figure 12, propulsive power is highly favored by the leading-edge pitching amplitude. Once again, bigger improvements are seen when the airfoil is at its maximum plunging velocity. This coincides with the instant where the leading-edge has its maximum angle of attack, enlarging the frontal area of the airfoil, which leads to an increase in thrust. This is presented in the following text using the pressure distribution around the airfoil. For the range studied, higher pitching amplitudes lead to higher propulsive power values, although a pitching amplitude ceiling similar to the $kh=0.50$ case is expected, since excessive deflection presents no real benefit. This ceiling was not observed, solely due to the relative importance between the plunging and pitching terms of the effective angle of attack. The reduction in ${\alpha }_{\mathrm{eff}}$ that the leading-edge can provide is limited to 6$°$ when the pitching amplitude is set at 20$°$. Thus, increasing the $kh$ makes the effective angle of attack induced by the plunging motion more dominant. This is the reason why we need higher pitching amplitudes at higher nondimensional velocities to achieve higher propulsive power values, as seen in Figure 6.

Concerning the required power, it was seen that its mean value decreases with the leading-edge pitching amplitude but, overall, shows a small dependence on it, except in some cases at the lowest nondimensional amplitude. This is reinforced in Figure 13, which shows that the deflection of the leading-edge indeed causes a reduction in power consumption during the acceleration phases of the period.

In Figure 14, the power consumption for the highest nondimensional velocity is shown. Overall, the required power coefficient is similar to the previous case, having its biggest reduction at $t/T=0.25$ and $t/T=0.75$, where the airfoil experiences a smaller effective angle of attack compared to the baseline case. Although this was also verified for $h=0.50$, for the rest of the period, the leading-edge deflection slightly increases the power consumption, counteracting those gains. This is why some of the cases analyzed in terms of the mean power consumption are almost independent of the pitching amplitude.

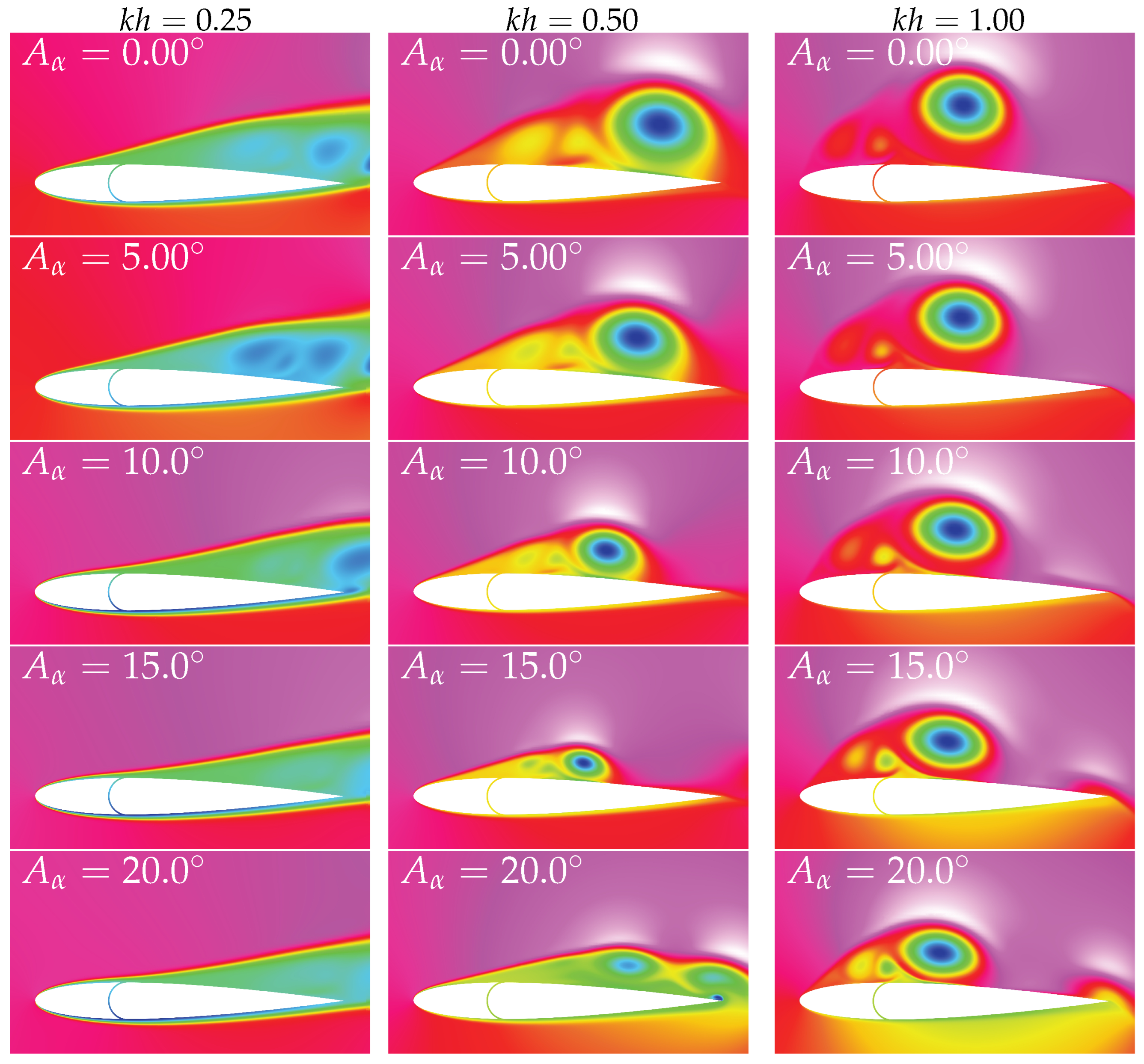
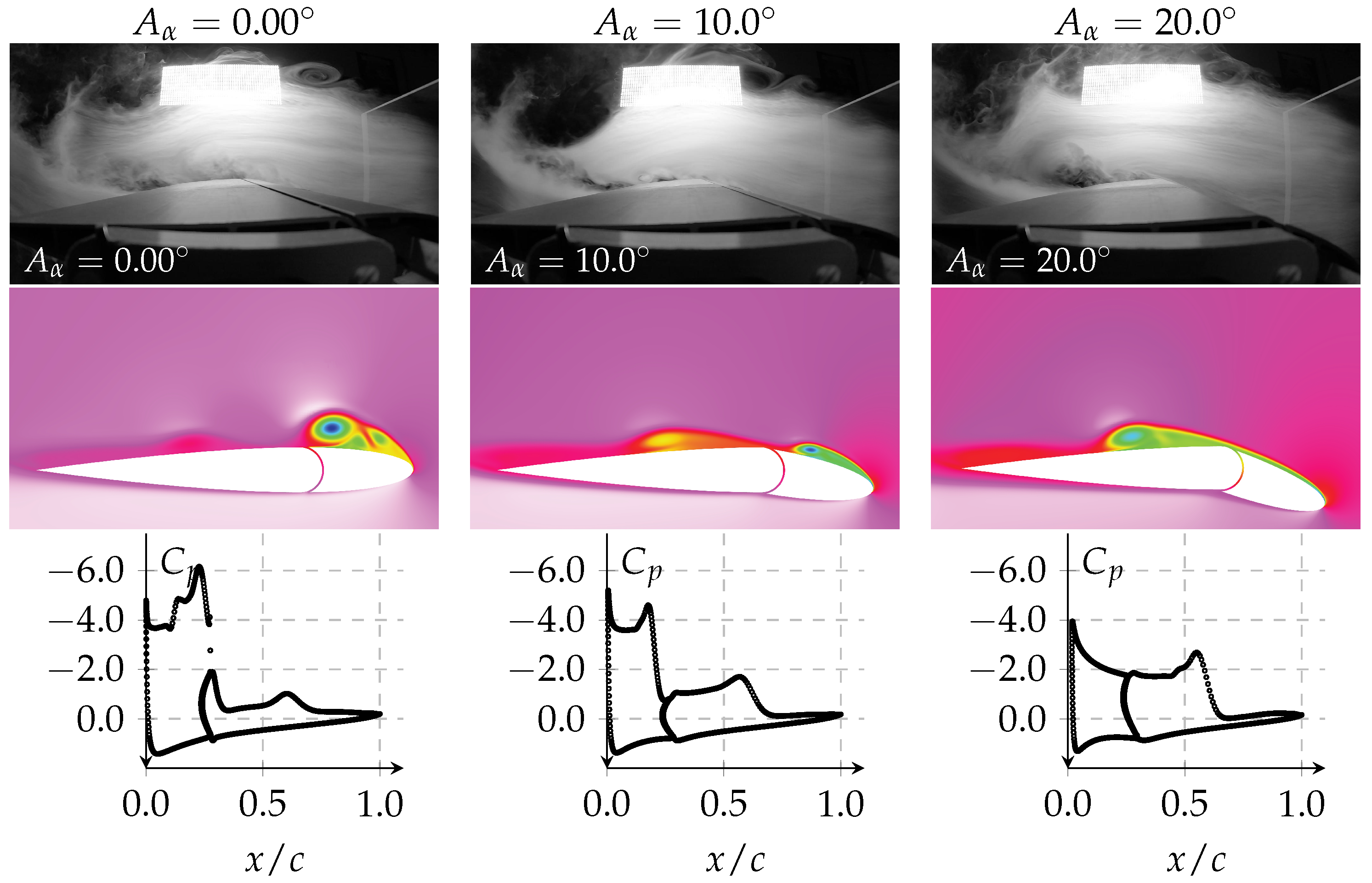
To better understand the impact of the dynamically activated leading-edge, some snapshots of the numerical flow field are presented, together with the airfoil pressure distribution. The flow fields are shown only for $h=0.50$ at $t/T=0.75$ where satisfactory propulsive improvements are seen for $kh=0.50$ and $1.00$. Flow visualization data are also provided for supplemental comparisons.

In Figure 15, the conditions $h=0.50$ and $kh=0.50$ are presented. The influence of the movable leading-edge on the flow field features is clear, especially regarding the dynamics of the leading-edge vortex and the pressure distribution around the airfoil. By increasing the leading-edge pitching amplitude, the suction peak located at the front decreases. Not only that, a low-pressure zone located beyond the maximum thickness position grows in intensity. For $A_{\alpha }=20°$, the intensity approaches the suction level present at the leading-edge, but interestingly, it does not reduce the propulsion considerably, as seen in Figure 11 (right).

This is an effect that is worth taking some time to analyze. When looking at $C_p$ and $C_{P_P}$, we verified that a lower suction peak at the leading-edge does not influence the suction force considerably when going from a pitching amplitude of 0$°$ to 10$°$ or even 20$°$. How could this happen if the suction force located at the frontal part of the airfoil is a major contributor to thrust enhancement? This could only be justified by the enlarged frontal area created by the leading-edge deflection. Even if the suction peak becomes smaller, integrating it into a larger frontal area results in a larger or similar suction force, as seen by the propulsive power increase that was verified. This is also verified in the following text for $kh=1.00$.

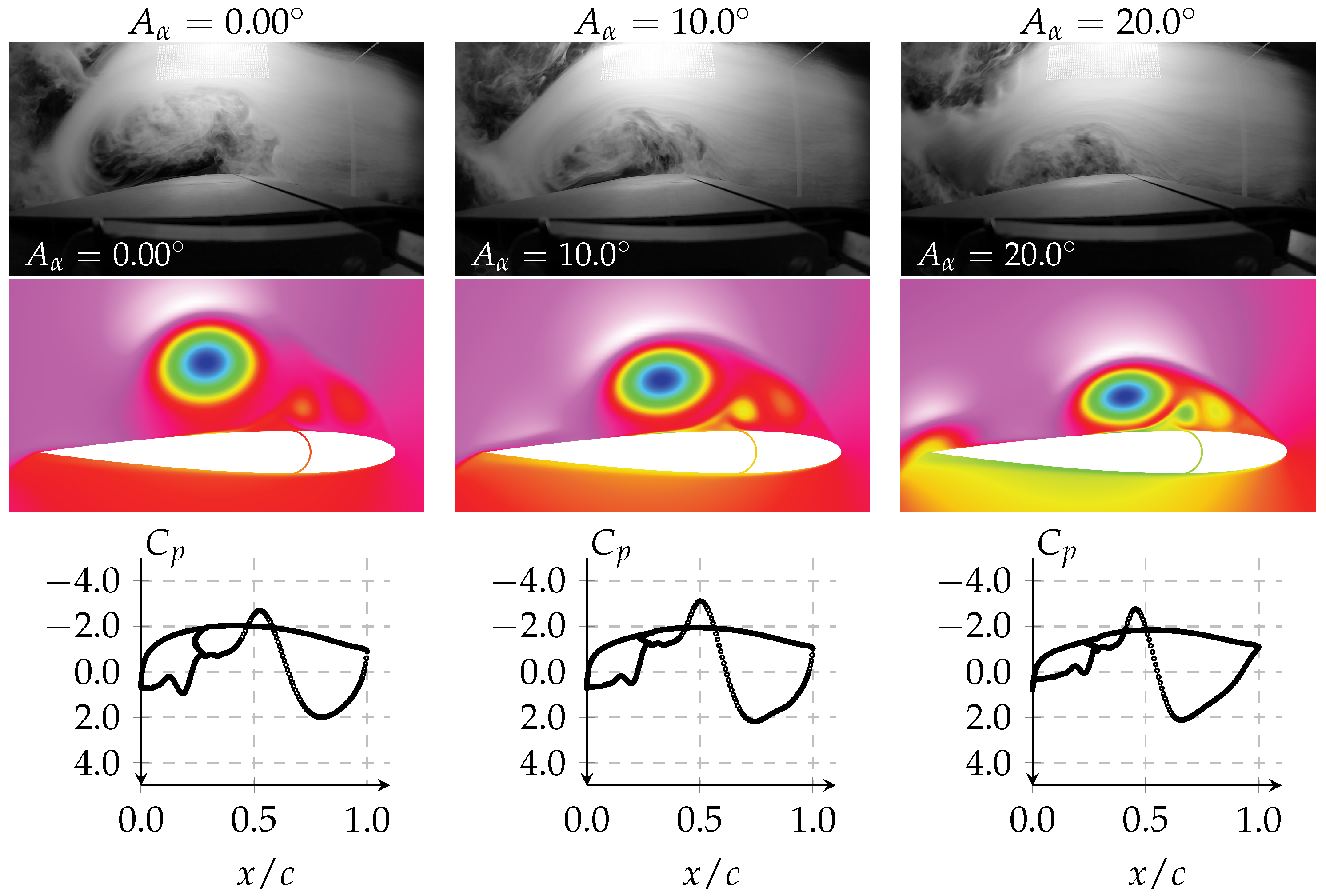
In Figure 16, the same plunging amplitude is considered, but the nondimensional velocity is increased to $1.00$. The results are similar to those for $kh=0.50$, but the effects are magnified, as expected by the higher effective angle of attack imposed by the larger nondimensional velocity. However, contrary to the previous case, the suction peak is not greatly influenced by the leading-edge deflection, reinforcing the fact that propulsive augmentation comes mainly from the increase in the frontal area created by the pitching of the frontal part. Unlike the previous case, the leading-edge pitching amplitudes considered cannot mitigate LEV formation. For that, a higher $A_{\alpha }$ must be considered. As mentioned before, this is a condition where the plunging component of the motion dominates the effective angle of attack.

The presence of the leading-edge vortex is justified by a strong adverse pressure gradient located right at the leading-edge, which is seen in the pressure distribution graphs close to $x/c=0.00$ where there is a rapid increase in pressure. This pressure gradient at the leading-edge can be alleviated using leading-edge deflection, as verified in Figure 15 when $A_{\alpha }=20°$. However, it comes at the expense of enlarging the suction at the back part of the airfoil. Meanwhile, the size of the vortex its not controlled by the existing pressure gradient. Instead, it is governed by the angular deviation between the shear layer that appears following separation and the leading-edge chord direction, as illustrated in Figure 17.

Figure 18 summarizes the influence of the pitching amplitude on the leading-edge vortex’s size and its intensity at the highest nondimensional amplitude and velocity. The frames shown were taken at the end of the oscillation period ($t/T=1.0$) when the LEV was fully developed, being a cumulative representation of what occurred during the full period.

Although the size of the leading-edge vortex is reduced considerably, by about 50%, as mentioned before, its intensity stays fairly unchanged, judging by the similar pressure distributions. This is also observed during the descending phase, as shown in Figure 16. However, it is worth mentioning that this is a plunging-dominated condition and the suction does remain somewhat unaffected until a certain pitching amplitude, and from there on, the suction present at the leading-edge starts shrinking, as seen in Figure 15.

4. Conclusions

A modified NACA0012 airfoil was proposed and successfully tested. A numerical study was conducted at a Reynolds number of ${10}^4$ using the turbulence $\gamma$ (intermittency) transition model under different flapping conditions with experimental flow visualization data complementing the numerical computations.

The proposed movable leading-edge was investigated parametrically, with special focus placed on its augmentation potential regarding its propulsive capabilities. The mean propulsive power is highly favored by the pitching leading-edge, mainly for $kh\ge 0.5$. At the lowest nondimensional velocity, where the airfoil is near the drag-production regime, the dynamic leading-edge holds no real benefit. Additionally, higher flapping velocities require larger pitching amplitudes to maximize the propulsive power. The mechanism also reduces the power consumption, but improvements are not as significant as for propulsive power.

Flow fields obtained numerically were used to correlate the propulsive power with the flow features. The results show that propulsive improvements can be obtained by exploiting the presence of the leading-edge vortex rather than eliminating it. A deeper analysis of the propulsive coefficients over time showed that the overall improvements in terms of either propulsive or required power occur roughly where the airfoil has its leading-edge maximum deflected. This is reinforced by the pressure coefficient distribution, which indicates that the propulsive power mainly increases due to the enlargement of the frontal area, rather than the modification of the pressure distribution.

Future research is in progress to compare the proposed mechanism with standard flapping commonly seen in the literature. The comparison will be made by using gradient-based numerical optimization focusing on the maximization of thrust for both methods of flapping. Additionally, there is also interest in looking for alternative shapes for the leading-edge of the second part that could provide better flow reattachment. This will be important for conditions where flow separation does not start at the frontal part and could be achieved by designing new pitching mechanisms and using newer concepts, such as morphing structures.