Survey of Semi-Empirical Jet Noise Models for Preliminary Aircraft Engine Design

Abstract

Scientific research studies on jet noise generation have been ongoing since the early 1950s, when turbojets were first used in commercial aircraft. Several numerical methods have been developed with the aim of reducing the environmental issues related to the impact of jet noise on community annoyance. Among them, the development of fast and comprehensive tools for jet noise prediction captured the attention of researchers and engineers, being very useful in the preliminary design phase of aircraft engines. This work deals with an extensive survey of James R. Stone’s models, initially formulated for the National Aeronautics and Space Administration (NASA) by Modern Technologies Corporation (MTC), and their implementation in a contemporary numerical framework. The models and their implementation are validated by simulating different engine settings and nozzle configurations taken from the literature with the main scope of highlighting the strengths and weaknesses of the different semi-empirical formulations and setting guidelines for their effective use during the design phases of the next generation of supersonic aircraft.

1. Introduction

The general concerns related to the environmental and community issues caused by rapidly growing air and urban traffic have prompted governments, scientists and manufacturers to invest heavily in deeply lessening the effect of aircraft and propulsion systems [1,2]. Among the multiple components of aircraft noise, jet noise [3] has been long recognized as a crucial source during the aircraft take-off phase. With the advent of ultra-high by-pass ratio (UHBR) engines [4], the overall EPNdB values at the ICAO certification points did not become more dominated by the jet noise. Fan noise mostly drives the noise reduction target of 65% (−15 EPNdB) [5], set as 2050 goal by the European Commission. However, the recent renewed interest in commercial supersonic aircraft, due to increased globalization, poses new problems for public acceptance and emission regulations, and jet noise would become once again a dominant noise source for the next generation of supersonic long-range aircraft.

Jet noise is the acoustic disturbance produced by the propulsive flow ejected from the engine exhaust. The complex interactions occurring among the high-speed combusted flow and the external air field generate some phenomena, such as nonlinear velocity fields, highly turbulent flows, intermittent phenomena, and shock waves for non-perfectly expanded jets. Although a comprehensive unsteady CFD approach might capture the jet noise mechanisms [6,7,8,9], it would be unlikely to be practical, given the difficulties related to high Reynolds number jet flows and complex nozzle configurations, especially in order to handle the need to have relatively fast predictions during the design phase of an aircraft. In this scenario, semi-empirical approaches still represent a viable approach to fast jet noise estimations.

James R. Stone showed that the semi-analytical jet noise model initially created by Modern Technologies Corporation (MTC) for the National Aeronautics and Space Administration (NASA) could be further improved. Stone published their model for the first time in 1983 [10] and continued with advances in their subsequent publications released in 1999 [11] and 2009 [12].

This paper deals with an extensive survey of Stone’s models and their implementation in a contemporary numerical framework developed by the authors. The models and their implementation are validated by simulating different engine settings and nozzle configurations taken from the literature with the main scope of highlighting the strengths and weaknesses of the different semi-analytical formulations. The paper defines guidelines for the effective use of the models during the design phases of the next generation of supersonic aircraft. Moreover, this work paves the way for subsequent comprehensive validation and tuning for specific nozzle configurations of interest for the SENECA European project, an H2020 funded initiative [13] focusing on noise and emissions in the vicinity of airports and the global climate impact of supersonic aircraft.

More specifically, after an introduction to the jet noise mechanisms in Section 2, the survey on the jet noise models is illustrated in Section 3, whereas the implementation and the validation against relevant test cases are provided in Section 4. Finally, the outcomes of the work are shown in Section 5.

2. Mechanisms behind Jet Noise Generation

Jet noise refers to a branch of aeroacoustics concerned with the production of noise caused by the flow jets and turbulent vortexes resulting from the aerodynamic shear layer [14].

More specifically, the term jet noise encompasses all the instances of noisy emissions that arise when a stream of air is discharged from the engine nozzle at a velocity significantly higher than that of the surrounding environment. However, the exact mechanisms responsible for noise generation have not been yet fully understood due to the complex three-dimensional effects occurring in the flow (e.g., non-linear velocity field, intermittent occurrences) [3].

The conventional statistical approach formulated by Reynolds to approximate turbulence in aerodynamic flows, involving the decomposition of every physical quantity of the turbulent field into mean and fluctuating components, serves the purpose of modeling the macroscopic properties of turbulent flow and making predictions regarding noise generation. Nonetheless, this approach falls short in accurately describing the fluctuating quantities, while many of the mechanisms governing noise generation are associated with these fluctuations [15].

The classical method of analyzing jet noise involves isolating its different contributions [16]: jet mixing noise, which arises from the shear flow between the jet exiting the nozzle and the surrounding free air; and shock-associated noise, which results from the supersonic flow at the exit, as depicted in Figure 1. Other acoustic sources within the jet flow also contribute to noise generation, particularly at lower speeds, including combustion noise and sounds produced by the interactions between turbulent flow and fans, compressors, and turbine systems. However, these other sources are not considered in the present study.

2.1. Turbulent Mixing Noise

Jet mixing noise arises from the turbulent mixing among the flow ejected from the engine with the surrounding ambient flow, typically air. Initially, this mixing occurs within an annular shear layer that expands as the nozzle lengthens. The mixing region generally encompasses the entire jet, up to approximately four or five diameters from the nozzle [17]. Higher-frequency components tend to concentrate near the nozzle, where turbulence vortexes are smaller. In contrast, the lower-frequency zone emerges further downstream, where the vortex size matches that of the jet diameter.

From a physical point of view, the flow of a jet induces pressure fluctuations, originating from both organized vortical structures and less regular random structures [18]. However, only a small fraction of the energy associated with these fluctuations manifests as pressure disturbances that propagate with typical sound characteristics. An analysis of the acoustic emission field of a turbulent jet reveals that the acoustic energy spans a broad range of frequencies, indicating the involvement of turbulent structures at various scales in sound generation.

One of the focuses of research in this field aims at a deep understanding of the noise generation mechanisms exhibited by each turbulent structure within the fluid domain [19]. Acquiring comprehensive knowledge of these causes would enable engineering solutions that directly address the reduction of the noise sources by modifying the flow, with the final result of reducing aircraft noise pollution near airports and enhancing cabin comfort [20].

Numerous studies target to develop novel methodological approaches for analyzing turbulent jet data, proposing several correlations between acoustic pressure fluctuations and phenomena originating within the fluid field [16]. The definition of jet refers to a flow introduced into a stationary environment, resulting in an interaction that induces intense mixing and the formation of an expanding flow layer along the jet axis. The conical region between the outlet section and the point where the flow layer intersects the jet axis is referred to as the potential core.

However, when considering the actual design of turbofan engines commonly employed in commercial aircraft, the flow configuration that closely resembles reality is the coaxial jet arrangement. In this configuration, two flows, typically with varying velocities, are introduced into the environment through separate coaxial outlet sections. This adds complexity to the flow’s topology, resulting in both an inner potential core and an outer potential core. These cores interact with each other, as depicted in Figure 2. The extension of the main jet’s potential core is heavily influenced by the velocity ratio between the main and secondary jets [21], a parameter that also governs the decay of velocity along the jet axis.

2.2. Shock Associated Noise

In supersonic jet flows, there exist regions known as shock cells that undergo continuous expansion and contraction [22]. These shock cells can extend up to approximately ten jet diameters from the nozzle and contribute to two additional components of jet noise: screech tones [23] and broadband shock-associated noises [24]. Screech tones in supersonic jets arise from a feedback mechanism wherein a convective disturbance in the shear layer produces sound as it interacts with the permanent shock wave structure within the jet. This feedback loop comprises three primary elements: the downstream propagation of wave instability, the shock cell arrangement in the jet plume, and the interaction of acoustic waves immediately outside the jet. Screech tones are dependent on jet temperature, and influence the peak position of the broadband shock noise. Their effect could be mitigated through appropriate nozzle design, and it is reduced when jet temperatures reach high values.

Broadband shock-associated noises (BBSAN), as illustrated in Figure 3, manifest in supersonic jets when the jet operates under off-design conditions [24]. This occurs when the static pressure at the nozzle exit does not match the external pressure. Nozzles operating at their designated pressure ratios can also exhibit a periodic shock cell structure in the spray plume if the characteristic waves are not effectively canceled by the spray walls. BBSAN is observed in convergent or convergent-divergent nozzles when the flow is either over-expanded or under-expanded. In the far field, BBSAN produces a large spectral peak, exceeding the mixing noise levels of the jet at large angles to the jet axis.

The peak frequency of BBSAN depends on the spacing between shock cells in the jet, the convection velocity of turbulence within the jet’s shear layer, as well as the observer’s position. The amplitude of BBSAN is influenced by factors such as the distance between the observer and the jet diameter, the polar and azimuthal observation angles, the geometry of the nozzle, the degree of off-design operation, and, to a lesser extent, the stagnation temperature. The Stone’s model was designed to fit a discrete number of experimental test cases, where the effect of screech tones was secondary compared with BBSAN, thus screech tones are not included in the discussion.

3. Description of Stone’s Model

For many years, the National Aeronautics and Space Administration (NASA) has been actively involved in aircraft noise research, technological advancements, and occasional engine system testing and flight tests. Since 1995, the Modern Technologies Corporation (MTC) has been developing practical and user-friendly semi-empirical models to predict jet noise, collaborating with NASA and the aviation propulsion industry. The outcome of MTC’s project is currently incorporated into General Electric’s (GE) design and data reduction software, as well as included into the ANOPP code developed in the framework of the Aircraft NOise Prediction Program [25] at NASA Langley Research Center (LaRC) and into the Footprint/Radius (FOOTPR) [26] code at NASA Glenn Research Center (GRC).

The dedicated model for predicting jet noise primarily originated from the work of J. R. Stone [27]. Following the approach illustrated in Figure 1 and Figure 4, Stone decomposes the noise generated by turbulent mixing into several components. The lowest frequency component, known as “large-scale mixing noise” denoted by “L”, originates downstream of the nozzle exit and results from the mixing of coherent, large-scale turbulent structures of the jet with the surrounding environment. The relatively higher frequency mixing noise near the nozzle exit, called “small-scale mixing noise” denoted by “S”, is likely caused by small-scale turbulent mixing in the initial shear layer. The most challenging component to characterize is the “transitional/intermediate scale mixing noise” denoted by “T”, which occurs predominantly at middle-to-high frequencies and is crucial for fully correlating dual-stream mixing noise. Consequently, this component is specifically applied to coannular nozzle configurations. In terms of broadband shock noise, there are two components: inner stream shock noise (denoted by “I,sh”), applicable to single-stream cases, and outer-stream shock noise (denoted by “O,sh”), used exclusively for dual-stream configurations.

The source noise models employed in the Stone study are semi-empirical and based on real physical scaling laws calibrated with measured test data. The data utilized encompassed jet mixing and shock noise from single-stream and dual-stream nozzles, covering a wide range of geometries and test conditions, including modifications to suppress noise in one or both streams.

The evolution of this prediction, analysis, and correlation approach has followed a reverse direction, from complexity to simplicity. However, this approach has yielded a robust capability.

In this work, we will solely focus on highlighting the differences between the 1983 and 2009 models developed by Stone, while detailed descriptions of the models can be found in the corresponding papers available online.

In the 1983 model, Stone presented an equation for calculating the uncorrected noise level $SPL$, considering parameters such as area ratio, velocity ratio, and temperature ratio between the inner and outer streams:

$$SPL-UO{L}_I=5·log\left(\frac{T_1}{T_2}\right)+10·log\left[{\left(1-\frac{V_2}{V_1}\right)}^m+1.2·\frac{{[1+(\left(A_2{V}_2^2\right)/\left(A_1{V}_1^2\right))]}^4}{{[1+(A_2/A_1)]}^3}\right]$$

(1)

where subscript 1 is relative to the fully expanded primary (inner) jet, while subscript 2 is to the fully expanded secondary (outer) jet. The exponent m depends on area ratio following the relations:

$$\begin{array}{cc}\hfill m=1.1\sqrt{A_2/A_1}& for{A}_2/A_1<29.7\hfill \\ \hfill m=6.0& for{A}_2/A_1\ge 29.7\hfill \end{array}$$

(2)

The relative sound pressure level $UO{L}_I$ for the inner or single stream is correlated as a function of the effective directivity angle ${\theta }^{\prime }=\theta {(V_1/c_a)}^{0.1}$ and the logarithmic Strouhal number $logS$:

$$\begin{array}{c}\hfill UO{L}_I=141+10·log\left[{\left(\frac{{\rho }_a}{{\rho }_{ISA}}\right)}^2{\left(\frac{c_a}{c_{ISA}}\right)}^4\right]+10·log\left(\frac{A_1}{R^2}\right)+10·log{\left(\frac{{\rho }_1}{{\rho }_a}\right)}^{\omega }+10·log{\left(\frac{V_e}{c_a}\right)}^{7.5}\\ \hfill -15·log[{(1+M_{c}cos\theta )}^2+0.04M_c^2]-10·log\left[1-M_{0}cos(\theta -\alpha )\right]+3·log\left(\frac{2A_1}{\pi D_1^2}+\frac{1}{2}\right)\end{array}$$

(3)

$$\begin{array}{c}\hfill V_e=V_1{[1-(V_0/V_1)cos\alpha ]}^{2/3}\\ \hfill M_c=0.62(V_1-V_{0}cos\alpha )/c_a\\ \hfill \omega =\frac{3{(V_e/c_a)}^{3.5}}{0.6+{(V_e/c_a)}^{3.5}}-1\end{array}$$

(4)

where the subscript a refers to an ambient condition, 0 refers to the aircraft, $V_e$$\omega$ and $M_c$ are modified velocities to take into account the relative speed between the aircraft and the engine. The variable $\theta$ is the directivity angle from the observer position to the engine inlet axis, R is the distance between the observer and the engine outlet. Stone identified in this model only a single component for the mixing noise contribution, called merged noise.

Similarly, Stone also included the contribution of noise resulting from the presence of shocks. The expression for the uncorrected $UO{L}_{S,j}$, without considering refraction and assuming no interaction for dual streams, is as follows:

$$\begin{array}{c}\hfill UO{L}_{S,j}=162+10·log\left[{\left(\frac{{\rho }_a}{{\rho }_{ISA}}\right)}^2{\left(\frac{c_a}{c_{ISA}}\right)}^4\right]+10·log\left(\frac{A_j}{R^2}\right)+10·log\left[\frac{{(M_j^2-1)}^2}{1+{(M_j^2-1)}^2}\right]\\ \hfill -10·log\left[1-M_{0}cos(\theta -\alpha )\right]+F(\theta -{\theta }_M)\end{array}$$

(5)

where the subscript j refers to 1 for the inner stream and 2 for the outer stream that is supersonic, ${\theta }_M$ is the Mach angle equal to 180 (deg) $-{sin}^{-1}(1/M_j)$, while the function F is given by

$$\begin{array}{cc}\hfill F=0& for\theta \le {\theta }_M\hfill \\ \hfill F=-0.75& for\theta >{\theta }_M\hfill \end{array}$$

(6)

Stone compiled a table correlating $SPL-UO{L}_I$ with the logarithm of the Strouhal number and directivity angle, based on extensive experimental data from various nozzle configurations for both mixing and supersonic noise. By determining the directivity angle $\theta$ and the Strouhal number and inputting the jet parameters (geometric inputs, operating conditions, ambient conditions), it is possible to extract the corresponding $SPL-UO{L}_I$ value from the tables. By solving Equations (3) and (5), the $SPL$ of the specific jet configuration can be obtained. In the case of a dual-stream jet, Equation (1) can be used to apply a correction. This process is summarized in Figure 5.

Exploiting the definition of the Strouhal number, which establishes a correlation between the jet’s frequency and characteristics with this dimensionless number, the results can be converted into $1/3$ octave bands, as reported in the cited paper.

In the 2009 model’s update, Stone examined additional experiments, specifically focusing on engines with high bypass ratios and external plugs. Specifically, Stone divided the mixing noise contribution into three parts: large scale (named merged in the earlier version), small scale, and transitional scale (named pre-merged in the earlier version). The shock noise contribution varies depending on the location of the shock, distinguishing between inner stream (or single) shock noise and outer stream shock noise. The presence of an engine plug introduces additional noise components, such as inner stream plug separation noise and plug (or downstream) shock noise in the case of supersonic flow beyond the plug. When comparing the 2009 model to the 1983 model, Stone provided seven tables containing spectral directivity relations for each possible noise component, instead of two tables as in the earlier version. Additionally, the equations for the overall noise level uncorrected for refraction $UOL$ in each component exhibit some differences from the previously presented formulations. Regarding the mixing noise contribution, the formulations for large, small, and transitional scales are as follows:

$$\begin{array}{c}\hfill UO{L}_L=C_L+10·log\left[{\left(\frac{{\rho }_a}{{\rho }_{ISA}}\right)}^2{\left(\frac{c_a}{c_{ISA}}\right)}^4\right]+10·log\left(\frac{A_L}{R_{cor,L}^2}\right)+10·log{\left(\frac{{\rho }_L}{{\rho }_a}\right)}^{{\omega }_L}\\ \hfill -20·log[{(1+M_{c,L}cos{\theta }_{cor,L})}^2+0.09M_{c,L}^2]\end{array}$$

(7)

$$\begin{array}{c}\hfill UO{L}_S=C_S+10·log\left[{\left(\frac{{\rho }_a}{{\rho }_{ISA}}\right)}^2{\left(\frac{c_a}{c_{ISA}}\right)}^4\right]+10·log\left(\frac{A_S}{R_{cor,S}^2}\right)+10·log{\left(\frac{{\rho }_S}{{\rho }_a}\right)}^{{\omega }_S}\\ \hfill +75·log\left(\frac{V_{e,S}}{c_a}\right)-20·log[{(1+M_{c,S}cos{\theta }_{cor,S})}^2+0.09M_{c,S}^2]\end{array}$$

(8)

$$\begin{array}{c}\hfill UO{L}_T=C_T+10·log\left[{\left(\frac{{\rho }_a}{{\rho }_{ISA}}\right)}^2{\left(\frac{c_a}{c_{ISA}}\right)}^4\right]+10·log\left(\frac{A_T}{R_{cor,T}^2}\right)+10·log{\left(\frac{{\rho }_T}{{\rho }_a}\right)}^{{\omega }_T}\\ \hfill +75·log\left(\frac{V_{e,T}}{c_a}\right)-20·log[{(1+M_{c,T}cos{\theta }_{cor,T})}^2+0.09M_{c,T}^2]\end{array}$$

(9)

$$\begin{array}{c}\hfill {(R_{cor}/R)}^2=1+{(X_s/R)}^2+2(X_s/R)cos\theta \\ \hfill {\theta }_{cor}=co{s}^{-1}[(R/R_{cor})cos\theta +X_s/R_{cor}]\end{array}$$

(10)

The variable $R_{cor}$ represents the distance between the observer and the noise source, which varies for each component, and depends also on the axial source location relative to outer stream nozzle exit $X_s$. This is because experimental measurements of jet noise are typically conducted at a distance from the nozzle that is in the far field of individual noise sources but not far enough to treat the entire exhaust plume as a point source at the center of the nozzle exit plane, see Figure 6, as assumed in the previous Stone model.

The convective Mach number $M_c$, effective velocity $V_e$, and density effect on noise, represented by the variable exponent $\omega$, also differ for each component and depend on the jet nozzle configuration and operating conditions.

The coefficients $C_L$, $C_S$, and $C_T$ are calculated using specific formulations derived from data obtained from experiments. This represents a significant difference compared to the 1983 model, where the coefficient was fixed at the value of 141 as shown in Equation (3):

$$\begin{array}{c}\hfill C_L=140.0+10log[{(V_{e,L}/c_{amb})}^8/\{1+0.02{(V_{e,L}/c_{amb})}^5\}]\\ \hfill C_S=130.0+[6/\{1+1.5{(V_O/V_I)}^{3.5}\}]\\ \hfill C_T=127.0+8.0/[1+0.25{\left\{(V_O/V_I)(A_O/A_I)\right\}}^5]\end{array}$$

(11)

For the calculation of inner or outer stream shock noise when the flow is fully expanded supersonic, the 2009 model employs the following formulation:

$$\begin{array}{c}\hfill UO{L}_{Sh,j}=C_{Sh,j}+10·log\left[{\left(\frac{{\rho }_a}{{\rho }_{ISA}}\right)}^2{\left(\frac{c_a}{c_{ISA}}\right)}^4\right]+10·log\left(\frac{A_j}{R_{cor,j}^2}\right)+10·log\left[{\beta }_j^4/(1+{\beta }_j^4)\right]\\ \hfill -40·log\left[1-M_{0}cos{\theta }_{cor,j}\right]+F({\theta }_{cor,j}-{\theta }_{M,j})\end{array}$$

(12)

where the subscript j refers to 1 for the inner stream and 2 for the outer stream that is supersonic, ${\theta }_M$ is the Mach angle equal to 180 (deg) $-{sin}^{-1}(1/M_j)$, while the function F is given by

$$\begin{array}{cc}\hfill F=0& for{\theta }_{cor,j}<{\theta }_{M,j}\hfill \\ \hfill F=-0.75({\theta }_{cor,j}-{\theta }_{M,j})& for{\theta }_{cor,j}\ge {\theta }_{M,j}\hfill \end{array}$$

(13)

and the shock strength parameter ${\beta }_j$ is calculated as

$${\beta }_j={\left[{(M_j^2-M_{d,j}^2)}^2+0.01M_{d,j}/(1-D_{1,j}/D_{2,j})\right]}^{1/4}$$

(14)

$M_d$ is the design Mach number of the nozzle, $D_1$ is the inner stream nozzle exit inner diameter and $D_2$ is the inner stream nozzle exit outer diameter.

By comparing Equation (12) to the previous Equation (5), we can observe that the shock strength term is more prominently highlighted, and the function F is defined to incorporate the values of directivity angles. Additionally, in this case, the coefficient $C_{sh}$ is determined using various formulations derived from experimental data, in contrast to the fixed value of 162 in Equation (5):

$$\begin{array}{c}\hfill C_{sh}=158.0-50log[1+{(D_1/D_2)}^2]\end{array}$$

(15)

Test Cases

The comparison between the Stone’s model published in 1983 and the one published in 2009 was made using different test cases across the published works of Stone, varying nozzles and flow conditions. The first test case is a conventional profile jet mixing case, from a 1983 paper, with a dual-stream nozzle and subsonic flow. The second test case is a coaxial coplanar nozzle, from the same paper, with dual-stream flow with the supersonic inner flow. The third test case is an inverted-velocity-profile coanular jet, which corresponds to a dual-stream nozzle where the outer-stream velocity is higher than the inner stream, presented in the article published in 1999, containing a preliminary version of the 2009 model. The fourth test case is an external plug nozzle, from the more recent paper published in 2009, which also introduced the newest version of the model. In this last case, the distance of the primary exit plane from the plug tip is 1.12 m, while the plug tip radius is 0.05 m. All the conditions are summarized in

Table 1. Test cases selected from Stone’s reference works.

		TC1	TC2	TC3	TC4
${\rho }_{amb}$	Ambient density [kg/m3]	1.225	1.225	1.225	1.239
$c_{amb}$	Ambient speed of sound [m/s]	340.3	340.3	337.9	336.3
R	Source to observer distance [m]	7.1–5.0–6.1–8.7	7.1	12.2	12.2
${\rho }_I$	Inner stream density [kg/m3]	0.369	0.740–0.801–0.419	0.716	0.483
${\rho }_O$	Outer stream density [kg/m3]	1.377	1.377	0.675	1.240
$V_I$	Inner stream velocity [m/s]	593	490–571–790	367	481.56
$V_O$	Outer stream velocity [m/s]	216	216	548	326.42
$M_I$	Inner stream Mach number	0.951	1.13–1.37–1.38	0.828	0.895
$M_O$	Outer stream Mach number	0.678	0.678	1.200	0.971
$D_{I,in}$	Inner stream diameter [m]	0.1010	0.1010	0.11788	0.70965
$D_{I,out}$	Outer stream inner diameter [m]	0.1090	0.1090	0.12195	1.5077
$D_{O,out}$	Outer stream outer diameter [m]	0.2096	0.2096	0.15488	1.9566
$T_I$	Inner stream total temperature [K]	1129	592–594–1124	553	833.71
$T_O$	Outer stream total temperature [K]	280	280	664	333.71
$M_f$	Flight velocity [m/s]	0	0	0	67.25
$\alpha$	Angle of attack [deg]	0	0	0	0
$\theta$	Theta Polar angle of emission [deg]	45–90–125–145	45	60–90–120–140	55–90–130–165

.

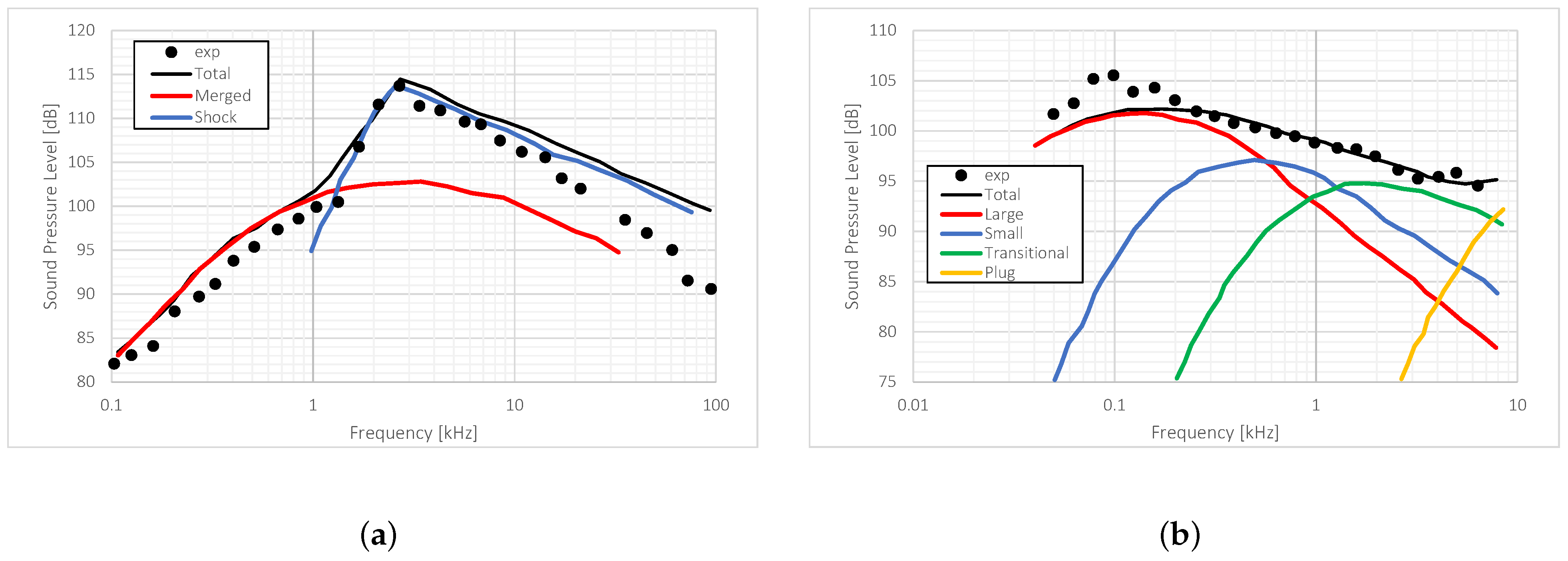
In Figure 7, a sample of the numerical outcomes derived using Stone’s model, is shown. The supersonic nozzle sound pressure levels as they change with noise frequencies are shown in Figure 7a, relative to the early model in 1983 paper. The Stone model’s output, the solid curve, is the sum of the contributions from shock presence and turbulence (shown in the image as mixing noise with the label jet). The semi-empirical model has a fair low-frequency agreement with the data, but it overestimates the high-frequency portion. The sound pressure level of a circular nozzle with an exterior plug is illustrated in Figure 7b, which compares numerical and experimental data, relative to the 2009 paper. The contribution of each turbulence scale to the mixing noise is shown in the figure, with the plug noise contribution emerging in the high-frequency range. In the medium and high-frequency zones, Stone’s model and the data are very well matched, whereas the low-frequency results are notably underestimated. Stone remarks, in their publications, on the challenge of accurately matching the experimental results, due to the complexity of the geometries, the several noise sources present (valves, elbows, obstructions, combustor), and the uncertainty of instrumentation.

4. Implementation and Validation

Concerning some of the coefficients specified to match the experimental curves, the two Stone models taken into consideration in this study maintain a comparable mathematical structure for all the noise components. The most recent model is more complex than the previous one because it uses a large amount of experimental data to account for various nozzle configurations, including single-stream and dual-stream, with and without shock waves, and plugs in the inner nozzle. Both models have been implemented within the same numerical framework, according to the structure shown in Figure 8. As in the case of the mathematical equation to determine the acoustic coefficients, all of the spectrum directivity tables from Stone’s published papers were included in the numerical code. Input values include the nozzle’s geometric properties, and the operating and ambient conditions. The software outputs the jet noise prediction curves together with the values of each mixing, shock, and plug component in terms of frequencies.

Figure 9 shows the test case 1 results, reported in Table 1. Stone’s model published in 2009 is represented by the blue curve with the label “CIRA_v09”, whereas Stone’s model published in 1983 is represented by the red curve with the label “CIRA_v83”. CIRA’s numerical implementation of the 1983 model is in perfect agreement with the Stone curve. The most recent model exhibits strong agreement with the experiment in the high-frequency area but poor adherence in the low and medium-frequency regions. The older model was built using the data from Stone’s first studies, but the more recent model is based on more modern engines with higher by-pass ratios and jet velocities and, as a result, it performs better in higher levels of frequency noise.

Figure 10 shows the second set of tests reported in Table 1. CIRA’s 1983 model implementation, which also had the possibility to analyze a supersonic nozzle, is exactly in line with Stone’s original implementation. According to the findings of the literature, this model tends to overstate the noise in the high-frequency zone. In the high-frequency region, where, as anticipated, the most recent model performs better, the 2009 model exhibits greater agreement than the 1983 model compared with the experiments.

The third and fourth test case results, related to Table 1 and shown in Figure 11 and Figure 12, are made with the only model from 2009, because the model from 1983 is unable to simulate those nozzle configurations. Even though there is a general overestimation of the experimental data, the model 2009 curve for the inverted-velocity-profile nozzle of test case 3 has a comparable shape to the measurements. According to Stone, it was challenging to assess the operating conditions and geometric factors in this specific test scenario, which made it challenging to choose the appropriate values for the numerical model. Regarding the last test case, the numerical results are in very good agreement with Stone’s implementation of the model.

5. Conclusions

This paper illustrated a comprehensive survey and the implementation of semi-empirical models enabling the prediction of jet noise generated by propulsion systems employing various nozzle configurations. These configurations include single or dual streams with subsonic or supersonic ejected flows. The first model was introduced by Stone in 1983, with subsequent extensions and improvements published in 1999 and 2009. In particular, the paper described the formulation and implementation of the 1983 and 2009 models within a modern numerical framework. The differences between the two models were shown, referring to a huge set of benchmark cases and encompassing several complex geometries and conditions. It was highlighted that the main drawback of Stone’s empirical approach is the model dependency on the experimental data from which the fitting originated. More specifically, the first model of 1983 resulted in the most suitable single-stream jet compared to the 2009 model. In fact, despite the 2009 model being conceived for both single and dual stream jets with a more complex nozzle (e.g., secondary stream shock jet, nozzle plug), the 1983 model still remains more accurate for single stream and specifically at low frequencies, whereas the 2009 one exhibits more accuracy at high frequencies. Despite these inconsistencies, Stone’s models offer a straightforward and efficient approach to provide reasonably accurate estimations of jet noise. This work paved the way for the design of the next generation of supersonic aircraft in the framework of the SENECA project, serving as a valuable guideline for the effective use of the semi-empirical jet noise models during the aircraft preliminary design phase.