A Rapid Surrogate Model for Estimating Aviation Noise Impact across Various Departure Profiles and Operating Conditions
Abstract
1. Introduction
2. Background and Literature Review
2.1. Aviation Noise—Influencing Factors
2.2. Current Noise Modeling Paradigms
2.3. Attempts at Rapid Noise Estimation
2.4. Model Order Reduction Techniques
3. Methodology
3.1. Data Collection
3.2. Model Order Reduction
3.3. Surrogate Model Development
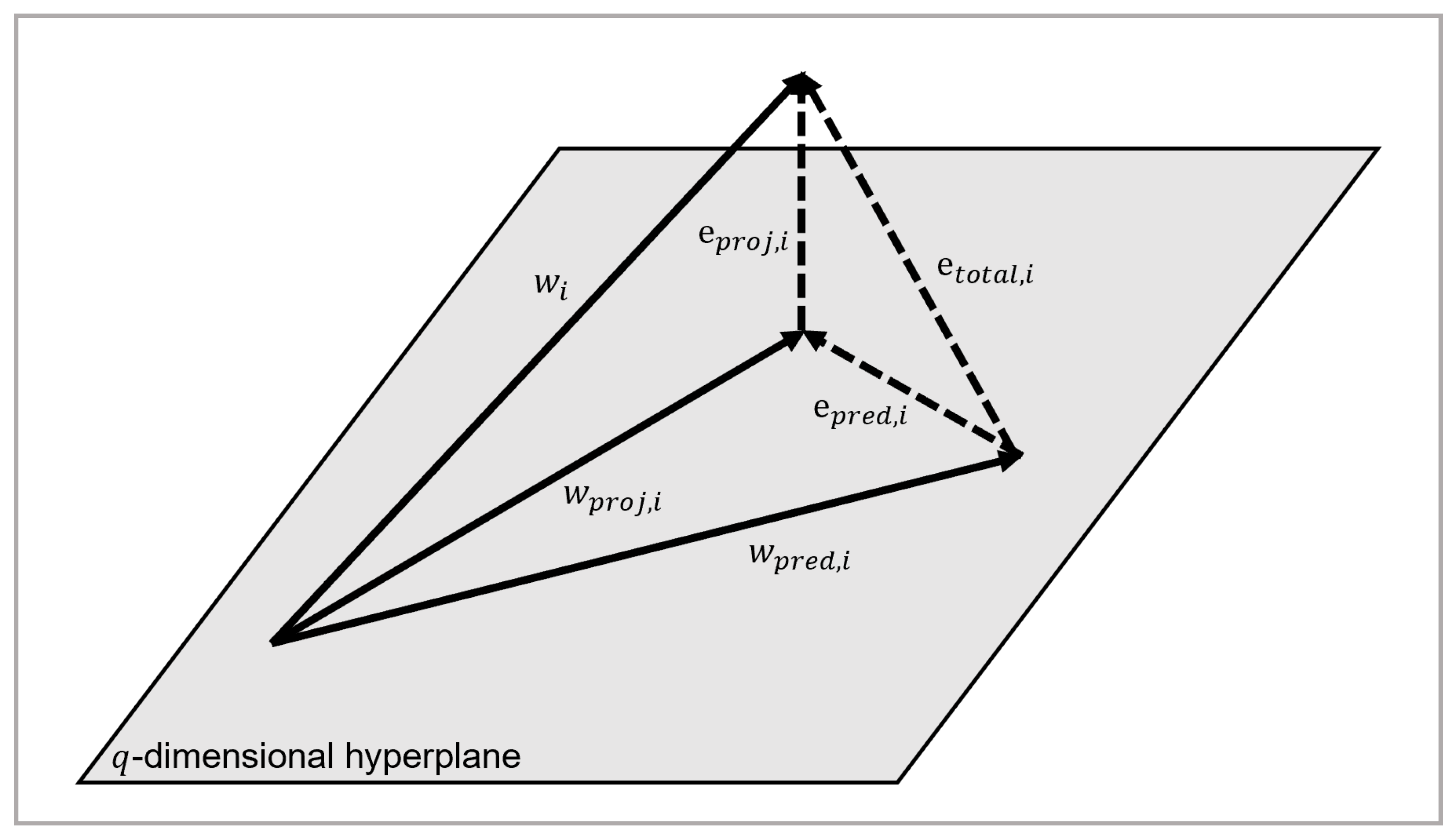
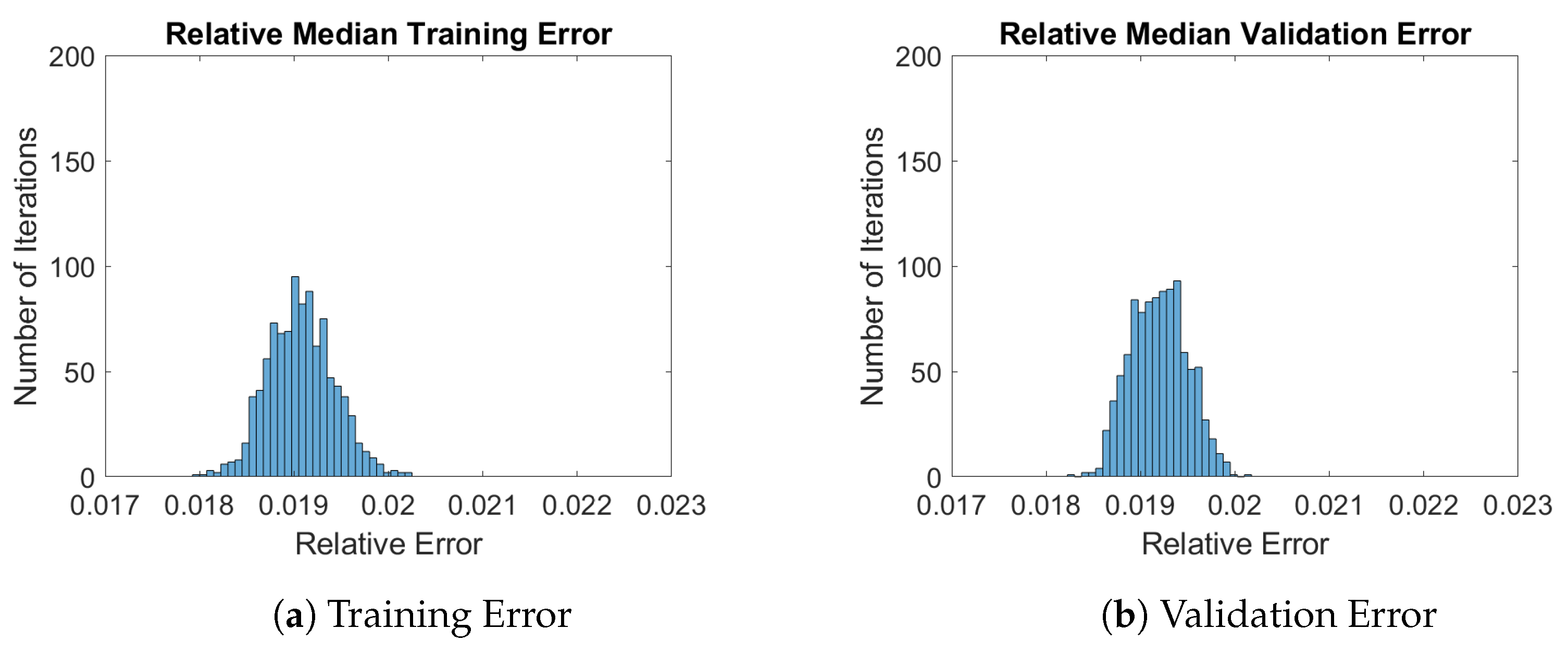
3.4. Error Quantification
4. Implementation and Results
4.1. Obtaining AEDT Snapshots
4.2. Implementing Model Order Reduction
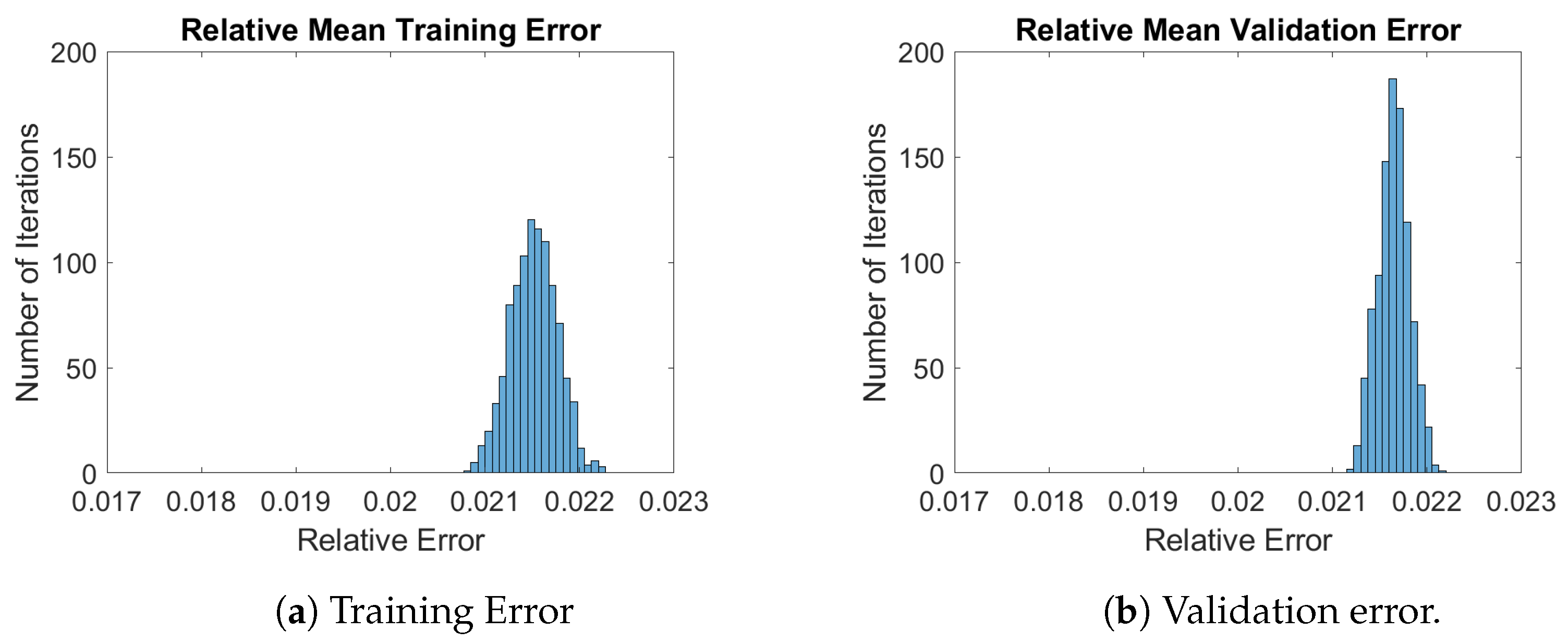
4.3. Implementing the Surrogate Model
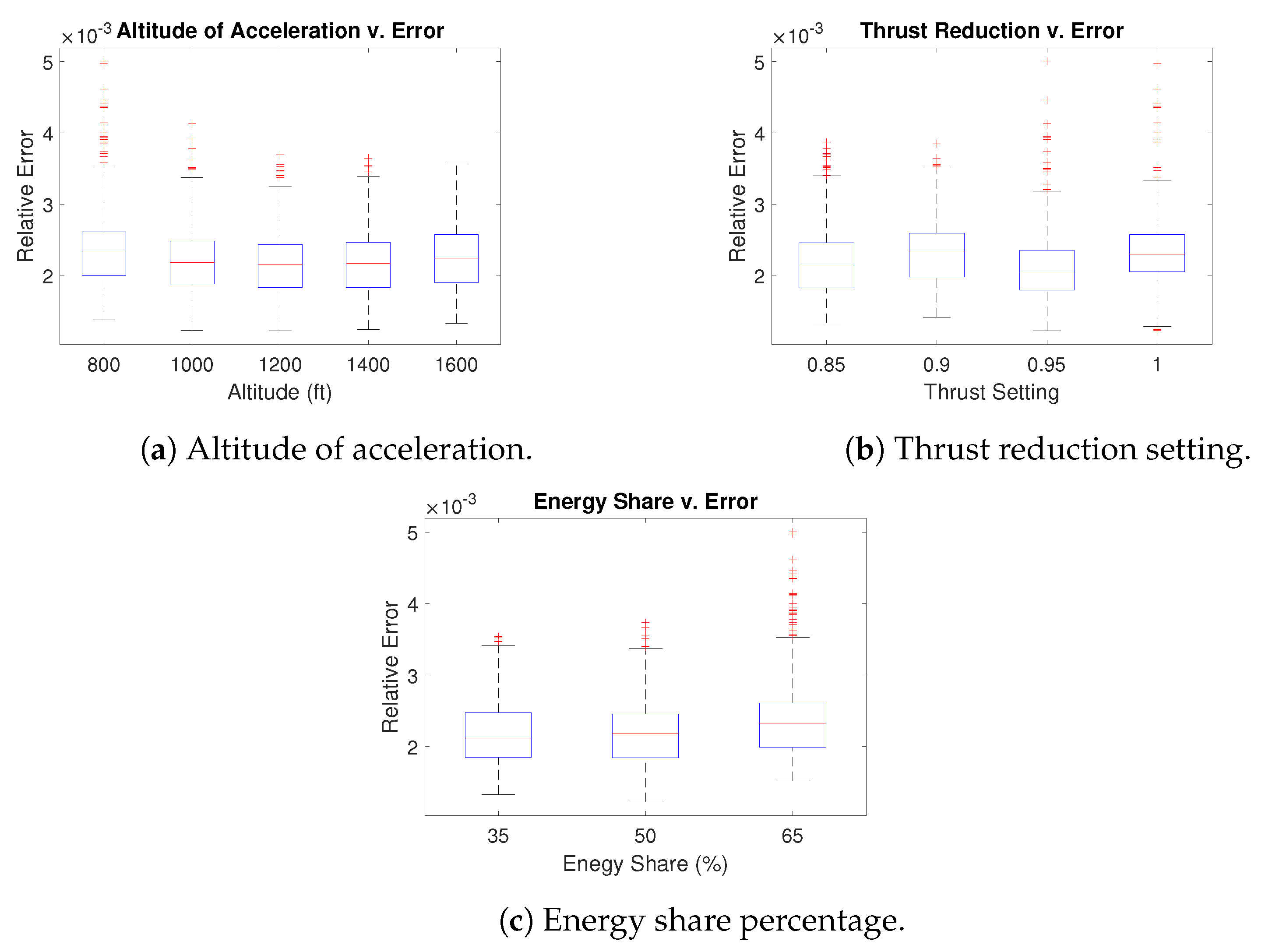
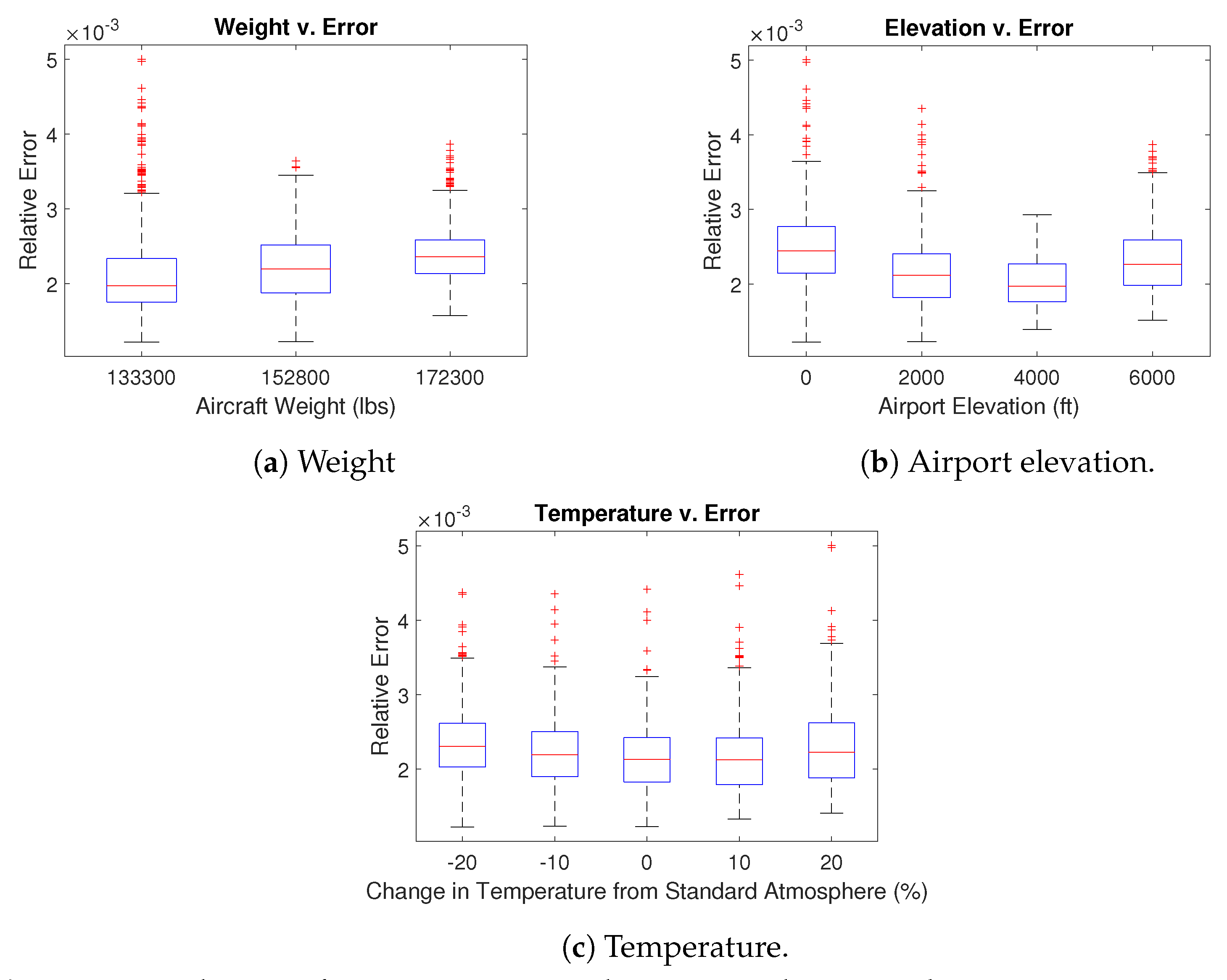
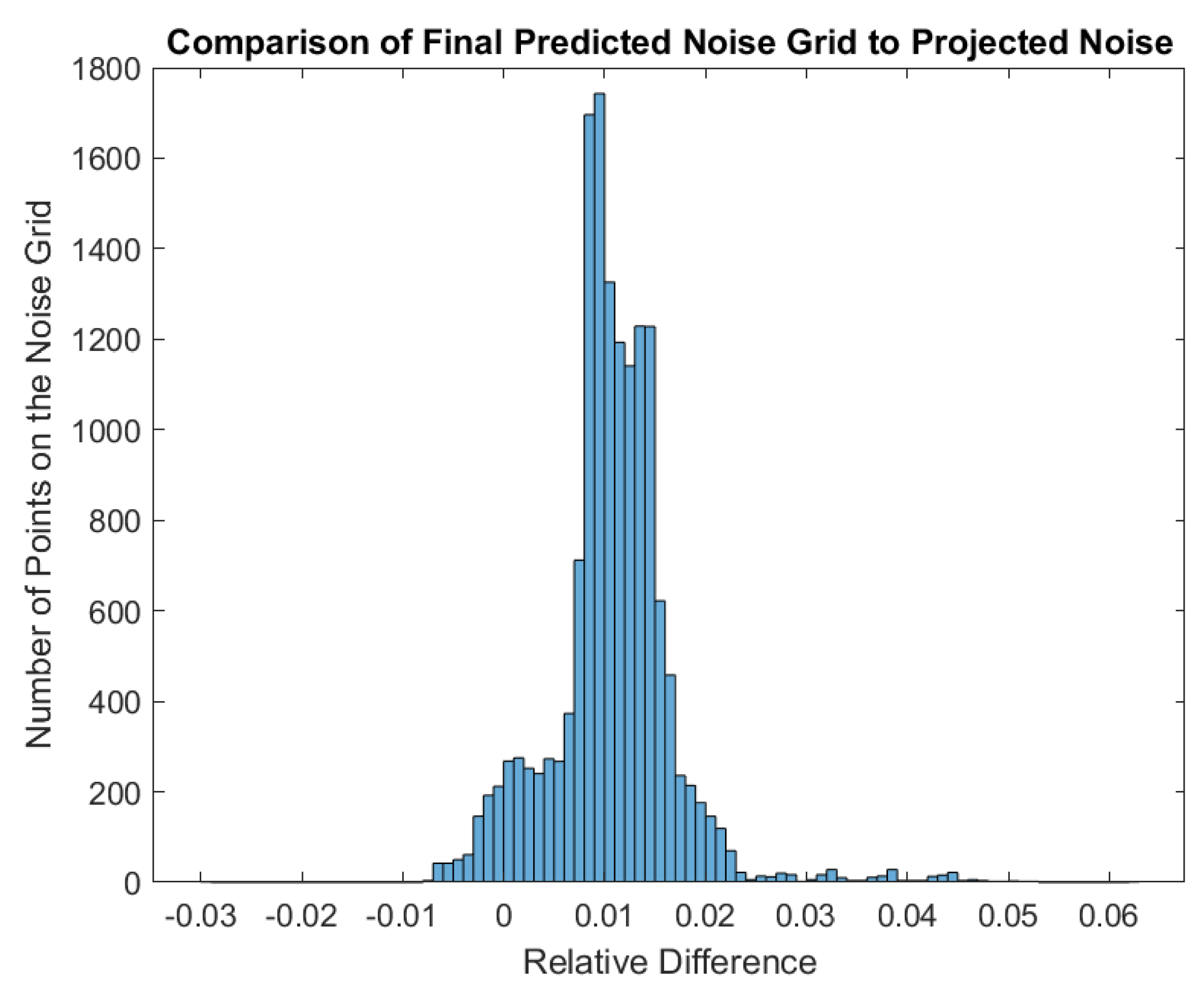
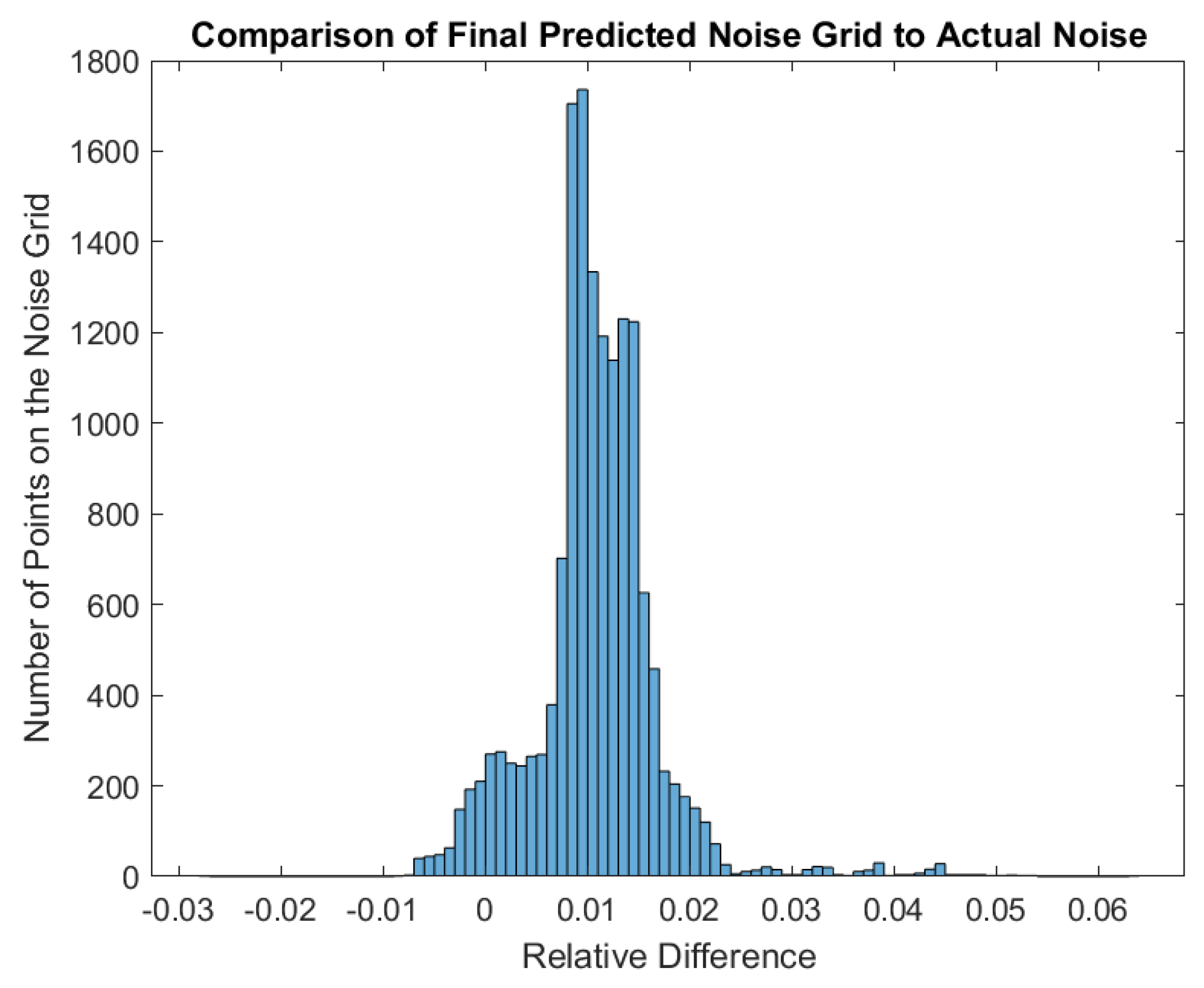
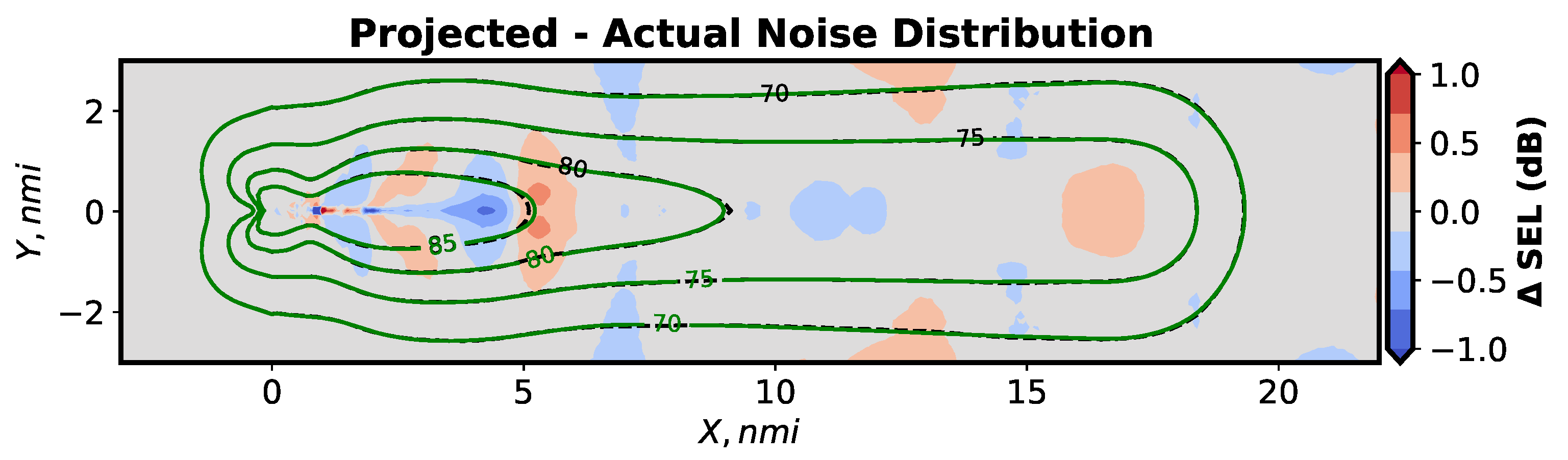
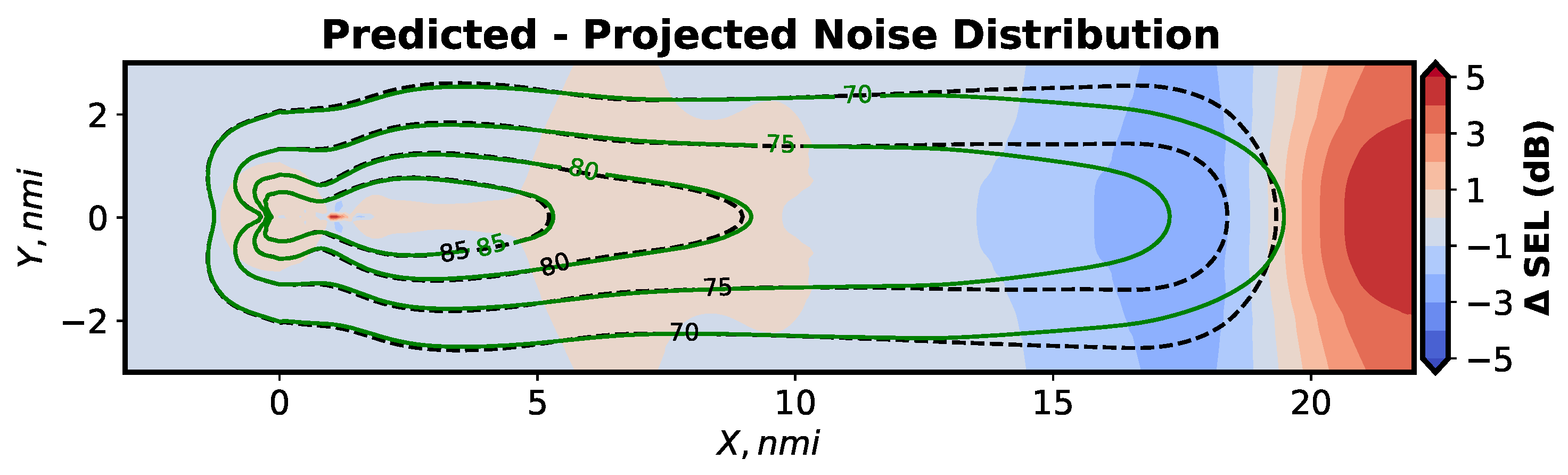
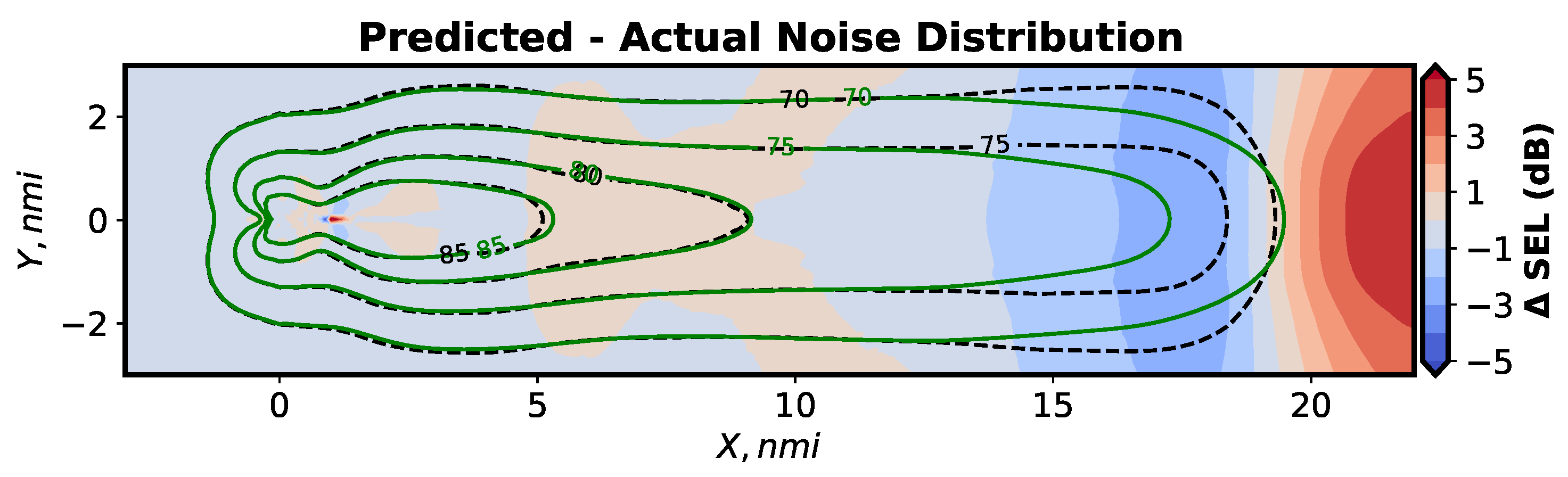
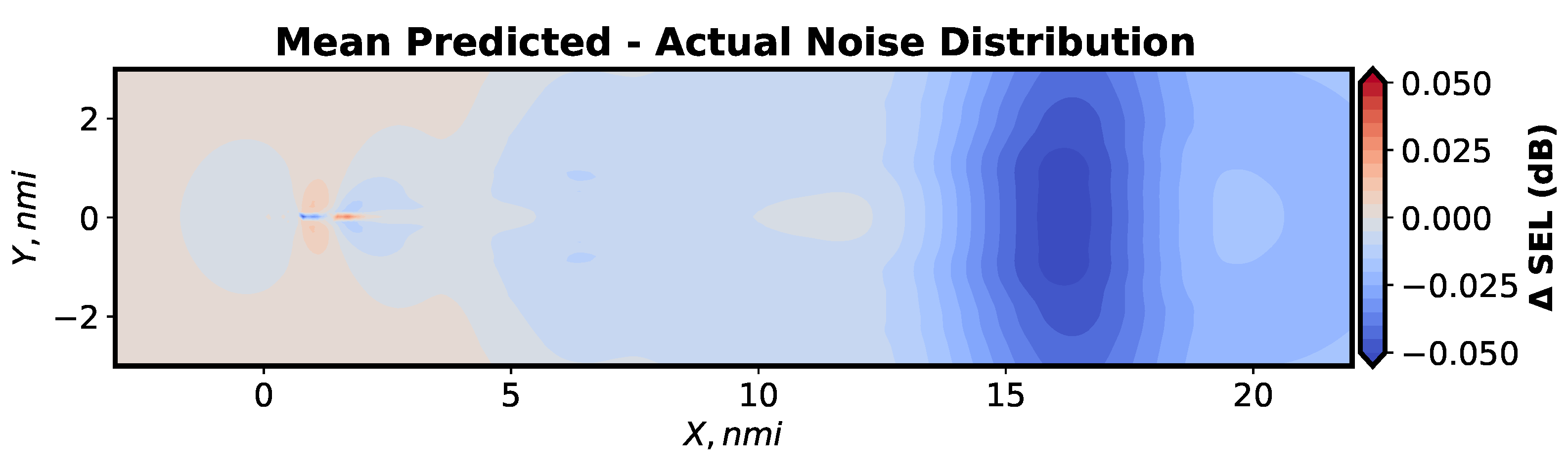
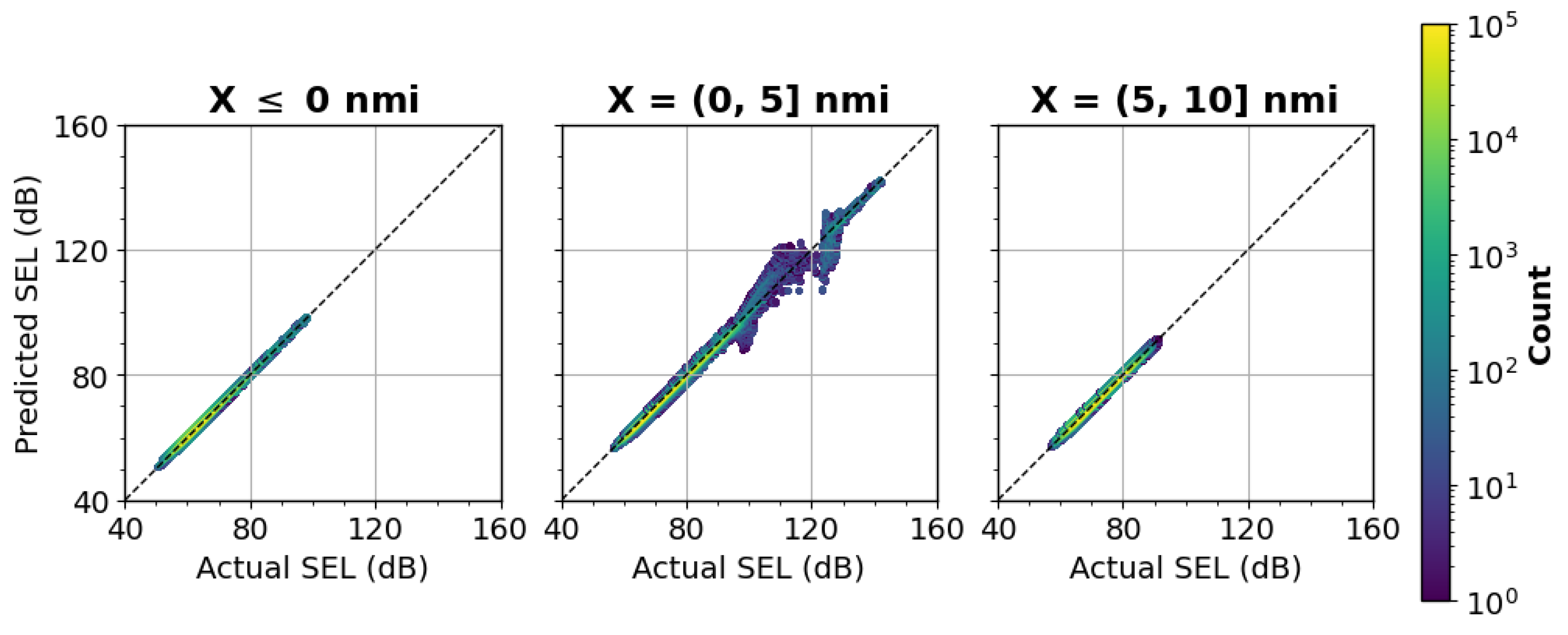
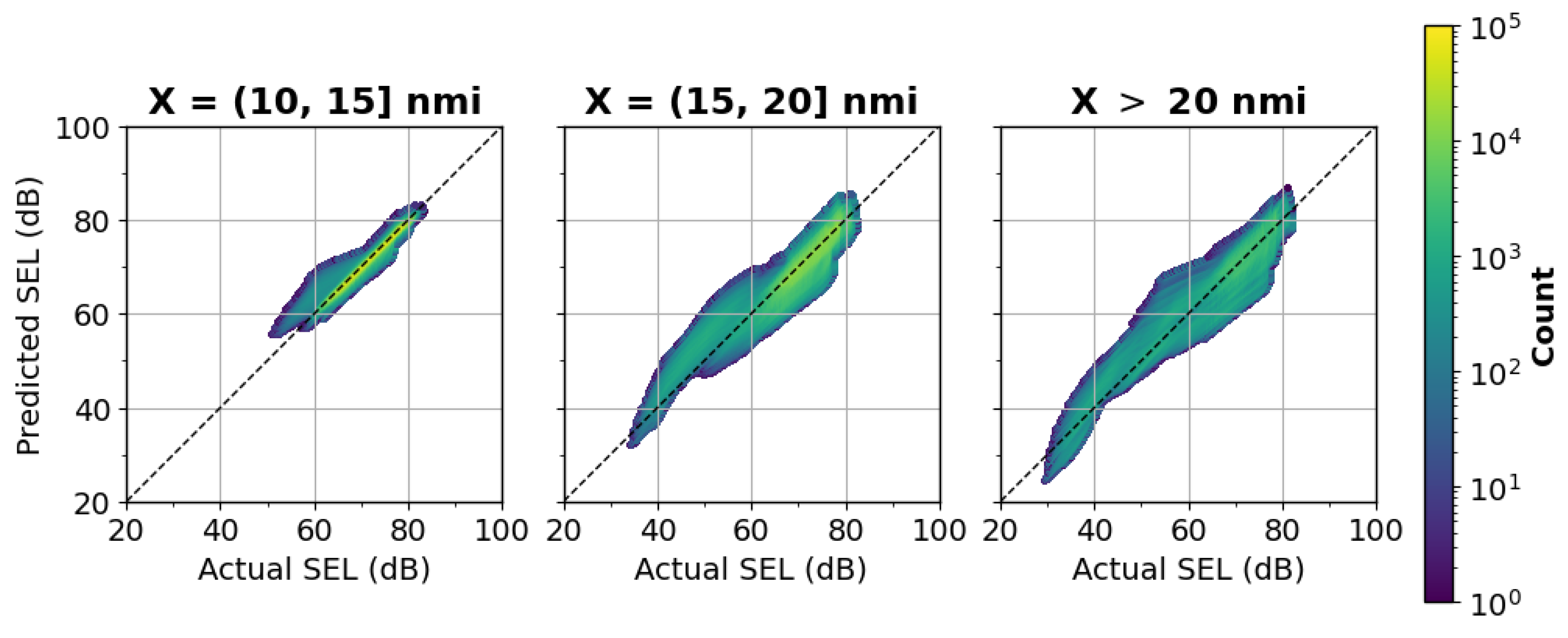
4.4. Total Error and Noise Grid Comparisons
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AEDT | Aviation Environmental Design Tool |
| AGL | above ground level |
| ANGIM | airport noise grid interpolation method |
| DoE | design of experiments |
| FAA | Federal Aviation Administration |
| MOR | model order reduction |
| MSL | mean sea level |
| NPD | noise–power–distance |
| PCA | principal component analysis |
| RIC | relative information content |
| ROM | reduced-order modeling |
| SEL | sound exposure level |
| SVD | singular value decomposition |
Appendix A. Surrogate Model Files
References
- Federal Aviation Administration. FAA Aerospace Forecast: 2022–2042. 2022. Available online: https://www.faa.gov/sites/faa.gov/files/2022-06/FY2022_42_FAA_Aerospace_Forecast.pdf (accessed on 14 May 2023).
- Boeing. Commercial Market Outlook: 2022–2041. 2022. Available online: https://www.boeing.com/commercial/market/commercial-market-outlook/index.page (accessed on 14 May 2023).
- Airbus. Global Market Forecast: 2022–2041. 2022. Available online: https://www.airbus.com/en/products-services/commercial-aircraft/market/global-market-forecast (accessed on 14 May 2023).
- Zellmann, C.; Schäffer, B.; Wunderli, J.M.; Isermann, U.; Paschereit, C.O. Aircraft Noise Emission Model Accounting for Aircraft Flight Parameters. J. Aircr. 2018, 55, 682–695. [Google Scholar] [CrossRef]
- Putnam, T.W. Review of Aircraft Noise Propagation; Technical Memorandum NASA TM X-56033; NASA Flight Research Center: Edwards, CA, USA, 1975. Available online: https://www.nasa.gov/centers/dryden/pdf/87865main_H-895.pdf (accessed on 14 May 2023).
- Morrell, S.; Taylor, R.; Lyle, D. A review of health effects of aircraft noise. Aust. N. Z. J. Public Health 1997, 21, 221–236. [Google Scholar] [CrossRef] [PubMed]
- Federal Aviation Administration. The FAA Airport Noise Program. 2015. Available online: https://www.faa.gov/newsroom/faa-airport-noise-program (accessed on 14 May 2023).
- Federal Aviation Administration. FAA History of Noise. 2022. Available online: https://www.faa.gov/regulations_policies/policy_guidance/noise/history (accessed on 14 May 2023).
- Erkelens, L. Research into new noise abatement procedures for the 21st century. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Dever, CO, USA, 4–17 August 2000. [Google Scholar] [CrossRef]
- Lim, D.; Behere, A.; Jin, Y.C.D.; Li, Y.; Kirby, M.; Gao, Z.; Mavris, D.N. Improved Noise Abatement Departure Procedure Modeling for Aviation Environmental Impact Assessment. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Behere, A.; Lim, D.; Li, Y.; Jin, Y.C.D.; Gao, Z.; Kirby, M.; Mavris, D.N. Sensitivity Analysis of Airport level Environmental Impacts to Aircraft thrust, weight, and departure procedures. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Oruc, R.; Baklacioglu, T. Modeling of aircraft performance parameters with metaheuristic methods to achieve specific excess power contours using energy maneuverability method. Energy 2022, 259, 125069. [Google Scholar] [CrossRef]
- McRae, M.; Lee, R.A.; Steinschneider, S.; Galgano, F. Assessing Aircraft Performance in a Warming Climate. Weather Clim. Soc. 2021, 13, 39–55. [Google Scholar] [CrossRef]
- Huber, J.; Barringto, J.P. Three dimensional atmospheric propagation module for noise prediction. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar] [CrossRef]
- Behere, A.; Mavris, D.N. Optimization of Takeoff Departure Procedures for Airport Noise Mitigation. Transp. Res. Rec. 2021, 2675, 81–92. [Google Scholar] [CrossRef]
- Behere, A.R. A Reduced Order Modeling Methodology for the Parametric Estimation and Optimization of Aviation Noise. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2022. [Google Scholar]
- Behere, A.; Kirby, M.; Mavris, D.N. Relative Importance of Parameters in Departure Procedure Design for LTO Noise, Emission, and Fuel Burn Minimization. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022. [Google Scholar] [CrossRef]
- Aviation Environmental Design Tool (AEDT) Version 3e User Manual; User Manual; U.S. Department of Transportation Federal Aviation Administration: Washington, DC, USA, 2022.
- Aviation Environmental Design Tool (AEDT) Version 3e Technical Manual; Technical Manual; U.S. Department of Transportation Federal Aviation Administration: Washington, DC, USA, 2022.
- Behere, A.; Bhanpato, J.; Puranik, T.G.; Kirby, M.; Mavris, D.N. Data-driven Approach to Environmental Impact Assessment of Real-World Operations. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 January 2021. [Google Scholar] [CrossRef]
- Bernardo, J.E. Formulation and Implementation of a Generic Fleet-Level Noise Methodology. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2013. [Google Scholar]
- LeVine, M.J.; Bernardo, J.E.; Kirby, M.; Mavris, D.N. Average Generic Vehicle Method for Fleet-Level Analysis of Noise and Emission Tradeoffs. J. Aircr. 2018, 55, 929–946. [Google Scholar] [CrossRef]
- Zanella, P. Sensitivity Analysis for Noise and Emissions Based on Parametric Tracks. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- LeVine, M.J.; Kaul, A.; Bernardo, J.E.; Kirby, M.; Mavris, D.N. Methodology for Calibration of ANGIM Subjected to Atmospheric Uncertainties. In Proceedings of the 2013 Aviation Technology, Integration, and Operations Conference, Los Angeles, CA, USA, 12–14 August 2013. [Google Scholar] [CrossRef]
- Bertram, A.; Othmer, C.; Zimmermann, R. Towards Real-time Vehicle Aerodynamic Design via Multi-fidelity Data-driven Reduced Order Modeling. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Gogu, C. Improving the efficiency of large scale topology optimization through on-the-fly reduced order model construction. Int. J. Numer. Methods Eng. 2015, 101, 281–304. [Google Scholar] [CrossRef]
- Fossati, M. Evaluation of Aerodynamic Loads via Reduced-Order Methodology. AIAA J. 2015, 53, 2389–2405. [Google Scholar] [CrossRef]
- Mainini, L.; Willcox, K. Surrogate Modeling Approach to Support Real-Time Structural Assessment and Decision Making. AIAA J. 2015, 53, 1612–1626. [Google Scholar] [CrossRef]
- Amsallem, D.; Cortial, J.; Farhat, C. Towards Real-Time Computational-Fluid-Dynamics-Based Aeroelastic Computations Using a Database of Reduced-Order Information. AIAA J. 2010, 48, 2029–2037. [Google Scholar] [CrossRef]
- Behere, A.; Rajaram, D.; Puranik, T.G.; Kirby, M.; Mavris, D.N. Reduced Order Modeling Methods for Aviation Noise Estimation. Sustainability 2021, 13, 1120. [Google Scholar] [CrossRef]
- Behere, A.; Mavris, D.N. Principal Component Analysis of Aviation Noise Grids for Dimensionality Reduction. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar] [CrossRef]
- Benner, P.; Ohlberger, M.; Cohen, A.; Willcox, K. Model Reduction and Approximation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2017. [Google Scholar] [CrossRef]



| DoE Variables | Levels | Number of Levels |
|---|---|---|
| Altitude of Acceleration (ft AGL) | 800, 1000, 1200, 1400, 1600 | 5 |
| Thrust Reduction | 0%, 5%, 10%, 15% | 4 |
| Energy Share Percentage | 35%, 50%, 65% | 3 |
| Aircraft Weight (lbs) | 133,000, 152,800, 172,300 | 3 |
| Airport Elevation (ft MSL) | 0, 2000, 4000, 6000 | 4 |
| Temperature Difference from Standard Atmosphere | 0, , | 5 |
| Total Number of Cases | 3600 |
| Matrix | Size | Number of Floats |
|---|---|---|
| 15,311 × 3600 | 55,119,600 | |
| 15,311 × 13 | 199,053 | |
| 13 × 3600 | 46,800 | |
| 15,311 × 1 | 15,311 | |
| 261,154 |
| Count | |
| Mean Difference | SEL dB |
| Standard Deviation | SEL dB |
| Minimum Difference | SEL dB |
| 5% | SEL dB |
| 25% | SEL dB |
| 50% | SEL dB |
| 75% | SEL dB |
| 95% | SEL dB |
| Maximum Difference | SEL dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, H.; Bhanpato, J.; Behere, A.; Mavris, D.N. A Rapid Surrogate Model for Estimating Aviation Noise Impact across Various Departure Profiles and Operating Conditions. Aerospace 2023, 10, 627. https://doi.org/10.3390/aerospace10070627
Peng H, Bhanpato J, Behere A, Mavris DN. A Rapid Surrogate Model for Estimating Aviation Noise Impact across Various Departure Profiles and Operating Conditions. Aerospace. 2023; 10(7):627. https://doi.org/10.3390/aerospace10070627
Chicago/Turabian StylePeng, Howard, Jirat Bhanpato, Ameya Behere, and Dimitri N. Mavris. 2023. "A Rapid Surrogate Model for Estimating Aviation Noise Impact across Various Departure Profiles and Operating Conditions" Aerospace 10, no. 7: 627. https://doi.org/10.3390/aerospace10070627
APA StylePeng, H., Bhanpato, J., Behere, A., & Mavris, D. N. (2023). A Rapid Surrogate Model for Estimating Aviation Noise Impact across Various Departure Profiles and Operating Conditions. Aerospace, 10(7), 627. https://doi.org/10.3390/aerospace10070627







