Study on Low-Velocity Impact Performance of Coal-Based Carbon Foam Sandwich Structures in Thermal Protection Systems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Structures and Materials
2.2. Tests
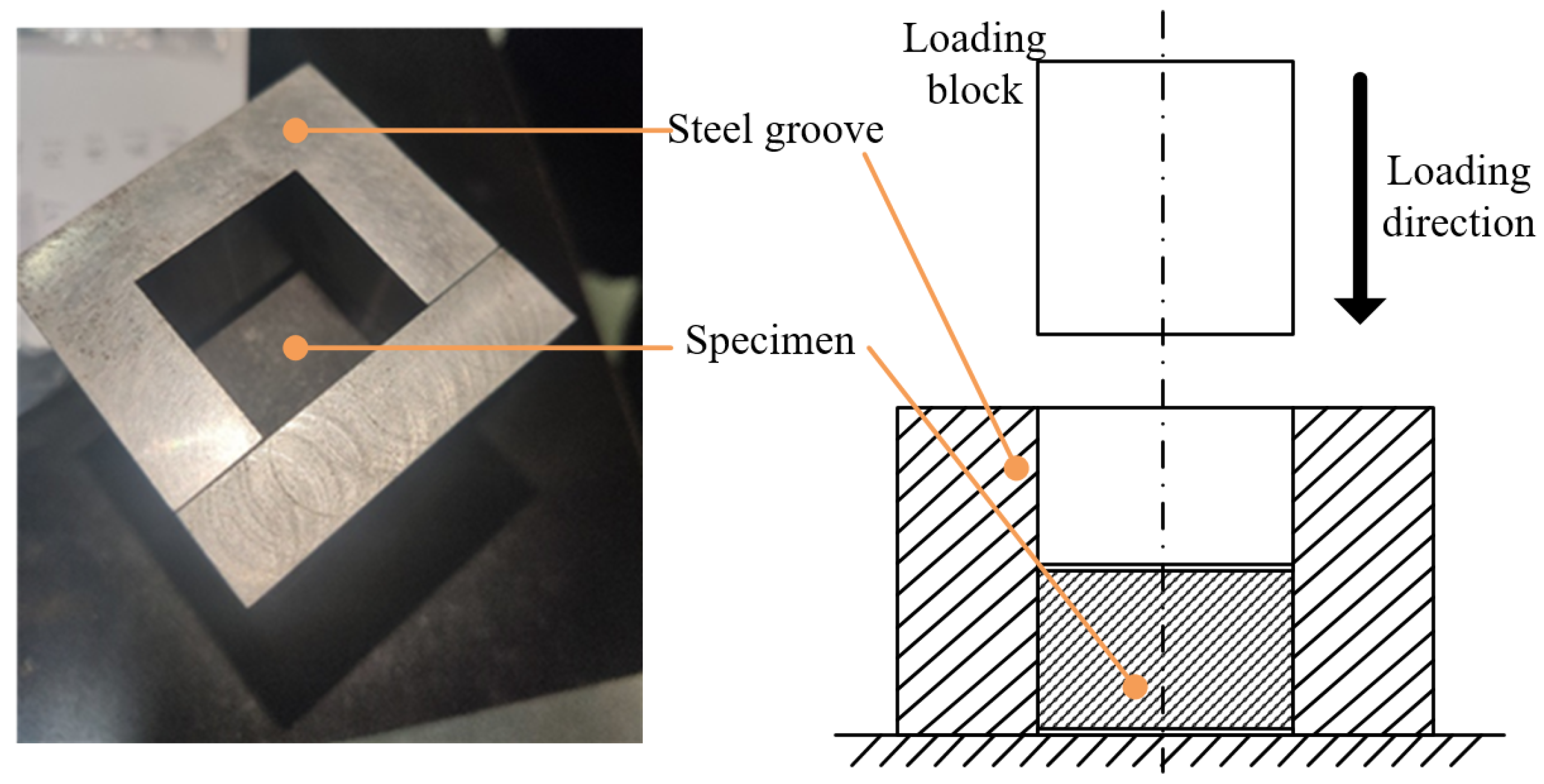
2.2.1. Tests for CCF
2.2.2. Tests for RPS and CPS
2.3. Simulations
2.3.1. Mechanical Constitutive Model of CCF
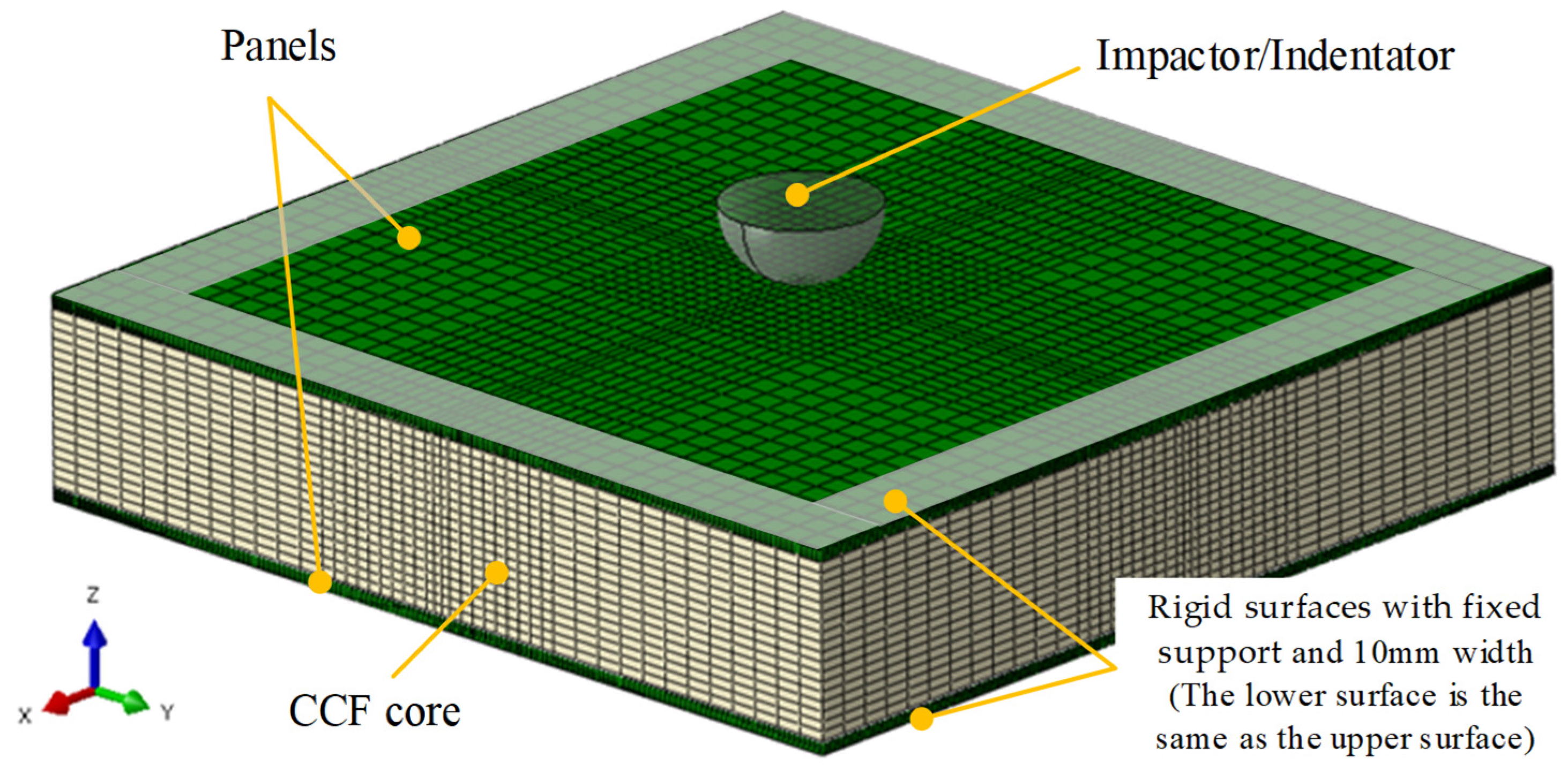
2.3.2. Finite Element Models of RPS and CPS
3. Results and Discussions
3.1. Results and Discussion of Tests for CCF
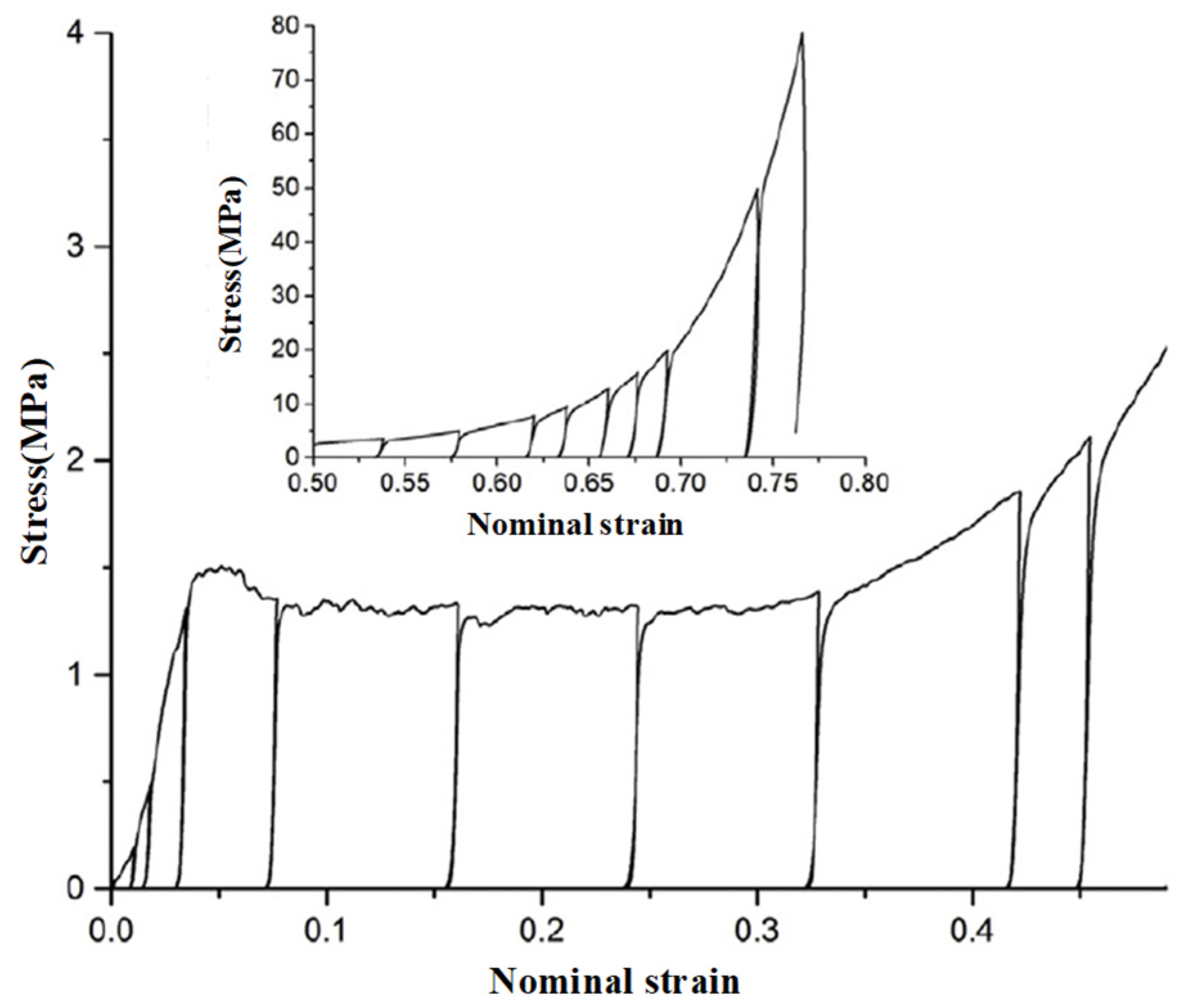
3.1.1. Basic Mechanical Properties
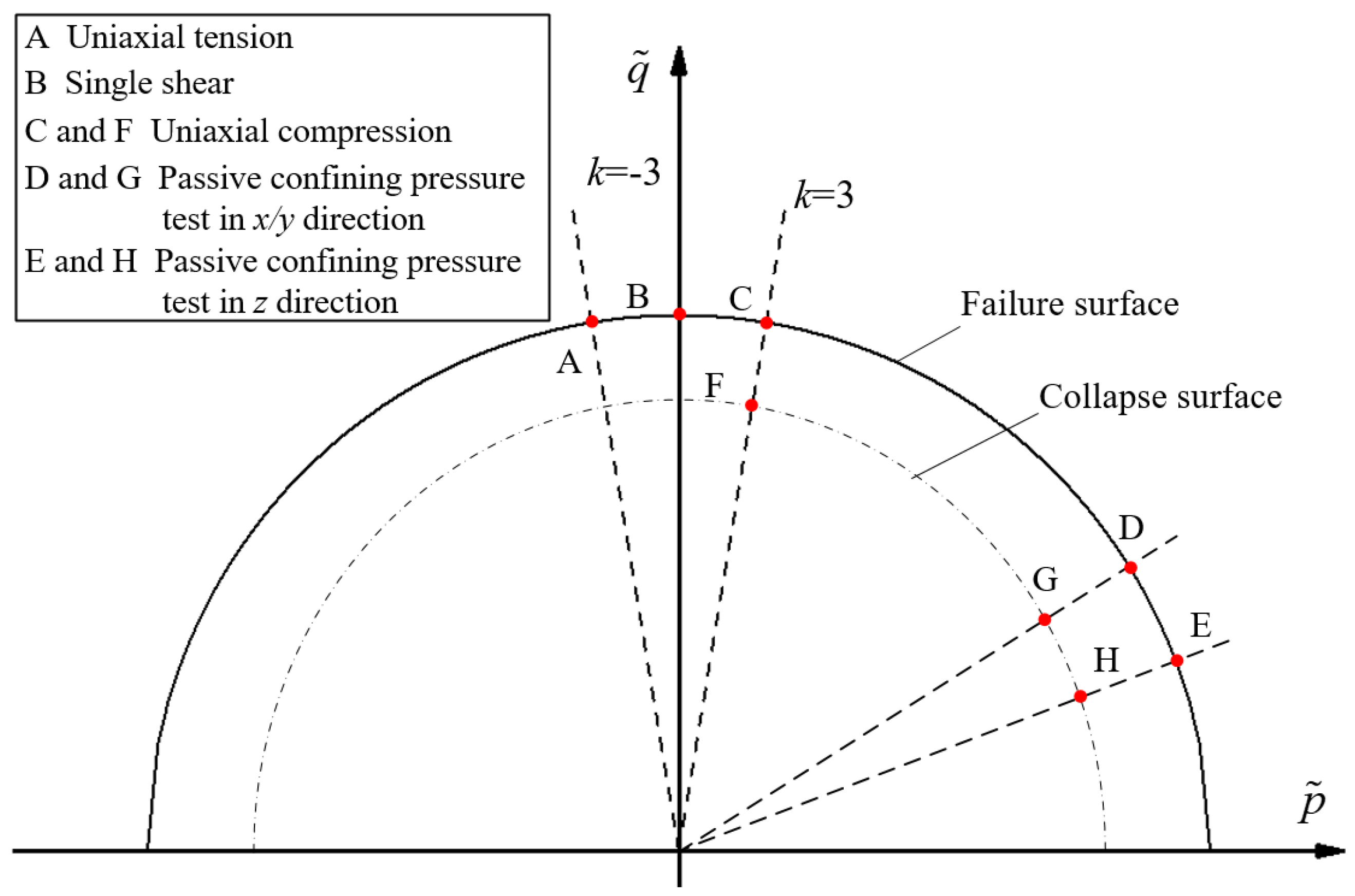
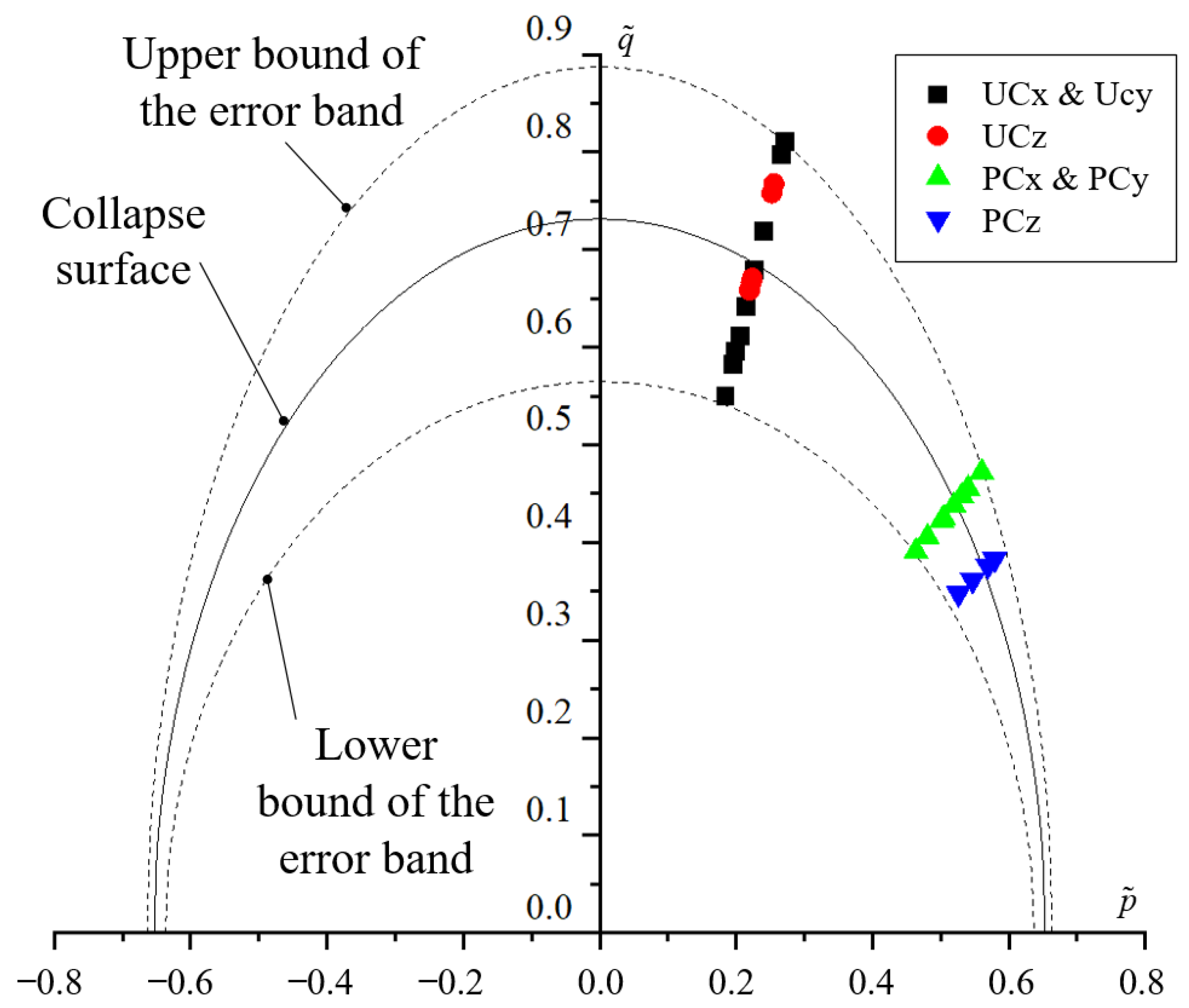
3.1.2. Multiaxial Loading Failure Criteria
3.1.3. Hardening Rules
3.2. Results and Discussion of Tests and Simulations of RPS and CPS
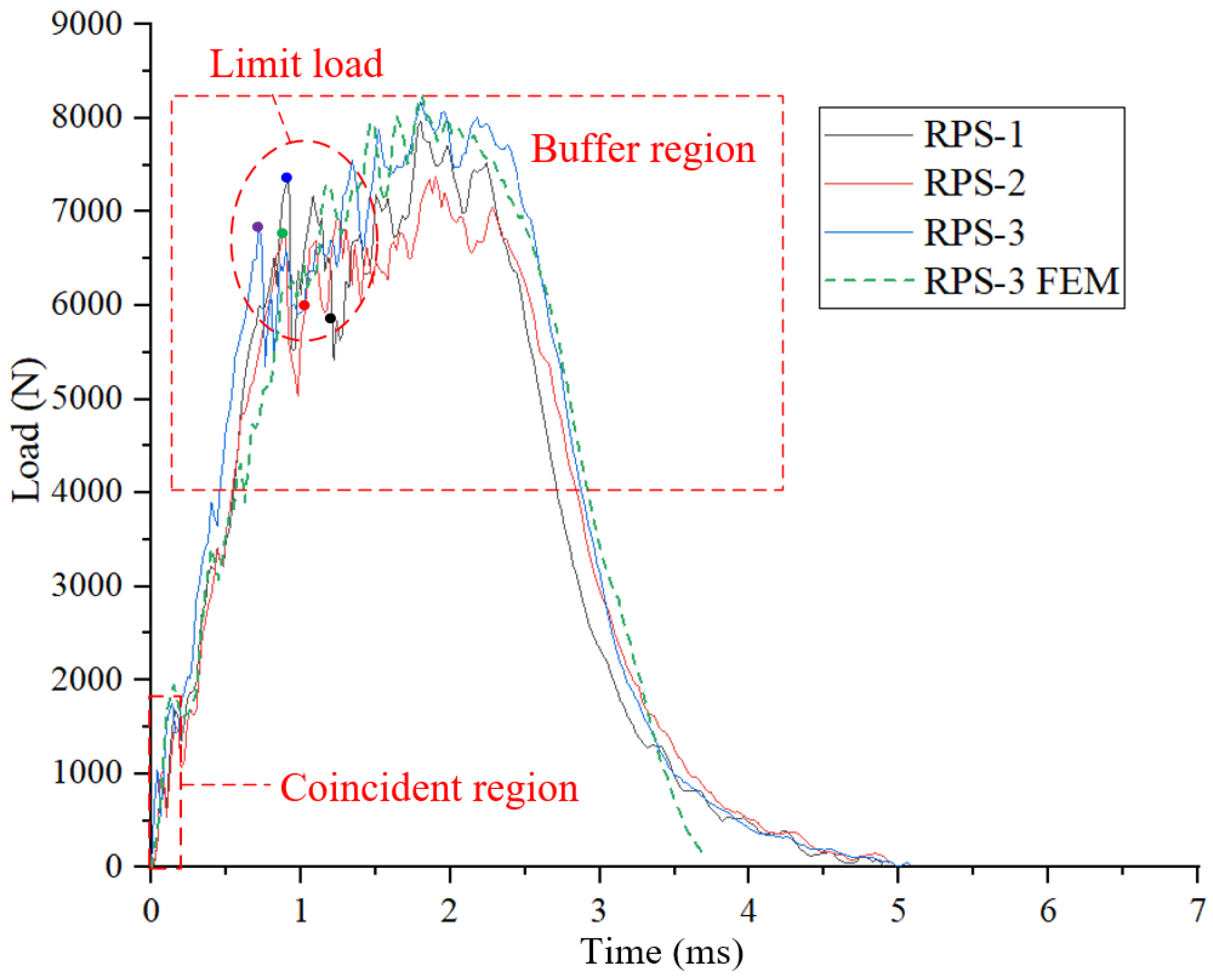
3.2.1. Low-Velocity Impact Tests and Simulations of RPS
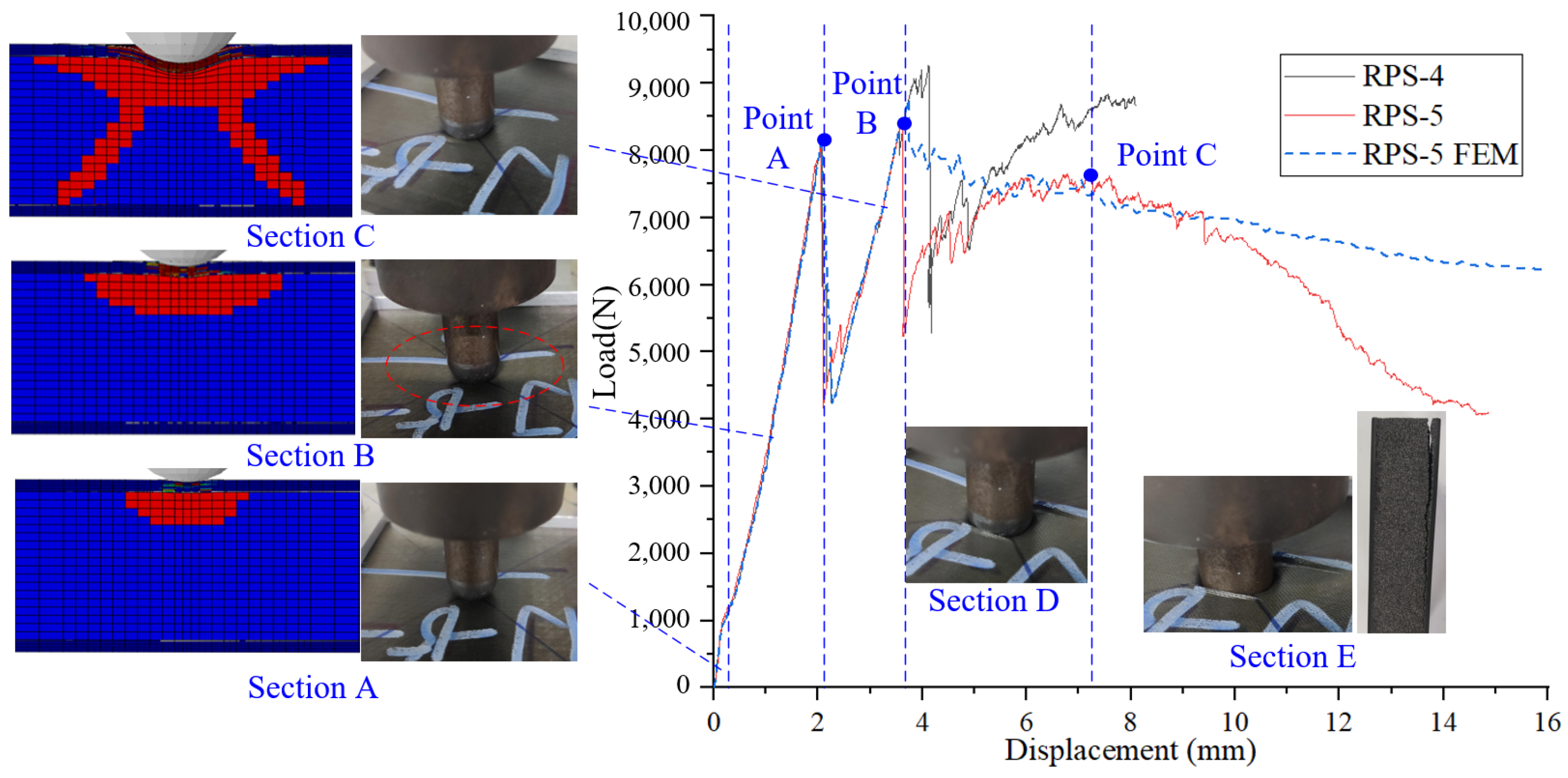
3.2.2. Quasi-Static Indentation Tests and Simulations of RPS
3.2.3. Low-Velocity Impact Tests and Simulations of CPS
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Glass, D. Ceramic Matrix Composite (CMC) Thermal Protection Systems (TPS) and Hot Structures for Hypersonic Vehicles. In Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008. [Google Scholar]
- Pichon, T.; Barreteau, R.; Soyris, P.; Foucault, A.; Parenteau, J.; Prel, Y.; Guedron, S. CMC thermal protection system for future reusable launch vehicles: Generic shingle technological maturation and tests. Acta Astronaut. 2009, 65, 165–176. [Google Scholar] [CrossRef]
- Jayaseelan, D.D.; Xin, Y.; Vandeperre, L.; Brown, P.; Lee, W. Development of multi-layered thermal protection system (TPS) for aerospace applications. Compos. Part B Eng. 2015, 79, 392–405. [Google Scholar] [CrossRef]
- Uyanna, O.; Najafi, H. Thermal protection systems for space vehicles: A review on technology development, current challenges and future prospects. Acta Astronaut. 2020, 176, 341–356. [Google Scholar] [CrossRef]
- Le, V.T.; San, H.N.; Goo, N.S. Advanced sandwich structures for thermal protection systems in hypersonic vehicles: A review. Compos. Part B Eng. 2021, 226, 109301. [Google Scholar] [CrossRef]
- Melis, M.E.; Pereira, M.; Revilock, D.; Carney, K.S. A summary of the NASA glenn ballistic impact lab contributions to the Columbia accident investigation. In Proceedings of the Annual Reliability and Maintainability Symposium, Alexandria, VA, USA, 24–27 July 2005. [Google Scholar]
- Grosch, D.; Bertrand, F. Thermal Protection System (TPS) Impact Experiments. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 14th AIAA/ASME/AHS Adaptive Structures Conference 7th, Newport, RL, USA, 1–4 May 2006. [Google Scholar]
- Singh, M. In-Space Repair and Refurbishment of Thermal Protection System Structures for Reusable Launch Vehicles. In Proceedings of the International Conference and Exposition of the European Ceramic Society, Berlin, Germany, 17–21 June 2007. E-16249. [Google Scholar]
- Melis, M.E.; Brand, J.H.; Pereira, J.M.; Revilock, D.M. Reinforced Carbon-Carbon Subcomponent Flat Plate Impact Testing for Space Shuttle Orbiter Return to Flight. In Proceedings of the 2006 National Space and Missile Materials Symposium (NSMMS), Orlando, FL, USA, 26–30 June 2006; NASA/TM-2007-214384. NASA: Washington, DC, USA, 2007. [Google Scholar]
- Melis, M.E.; Revilock, D.M.; Pereira, M.J.; Lyle, K.H. Impact Testing on Reinforced Carbon-Carbon Flat Panels with Ice Projectiles for the Space Shuttle Return to Flight Program; NASA: Washington, DC, USA, 2009. [Google Scholar]
- Snapp, C.; Rodriguez, A. Orbiter Thermal Protection System Lessons Learned. In Proceedings of the AIAA SPACE 2011 Conference & Exposition, Long Beach, CA, USA, 27–29 September 2011. [Google Scholar]
- Grujicic, M.; Pandurangan, B.; Zhao, C.; Biggers, S.; Morgan, D. Hypervelocity impact resistance of reinforced carbon-carbon/carbon-foam thermal protection systems. Appl. Surf. Sci. 2006, 252, 5035–5050. [Google Scholar] [CrossRef]
- Chen, C.; Kennel, E.B.; Stiller, A.H.; Stansberry, P.G.; Zondlo, J.W. Carbon foam derived from various precursors. Carbon 2006, 44, 1535–1543. [Google Scholar] [CrossRef]
- Yu, M.; Ao, X.; Chen, Q. Fabrication of ultralight reticulated carbon foams for thermal insulation from raffinate pitch of low-temperature coal tar. J. Anal. Appl. Pyrolysis 2022, 163, 105494. [Google Scholar] [CrossRef]
- Hu, L.; He, R.; Lei, H.; Fang, D. Carbon aerogel for insulation applications: A review. Int. J. Thermophys. 2019, 40, 39. [Google Scholar] [CrossRef]
- Su, R.; Wang, X.; Wang, D.; Li, L.; Liang, G.; Zheng, Z.; Li, K. Preparation of carbon foam-reinforced carbon aerogels and their copyrolysis mechanism. Microporous Mesoporous Mater. 2021, 319, 111059. [Google Scholar] [CrossRef]
- Wu, S.; Chen, D.; Zhao, G.; Cheng, Y.; Sun, B.; Yan, X.; Han, W.; Chen, G.; Zhang, X. Controllable synthesis of a robust sucrose-derived bio-carbon foam with 3D hierarchical porous structure for thermal insulation, flame retardancy and oil absorption. Chem. Eng. J. 2022, 434, 134514. [Google Scholar] [CrossRef]
- Xu, G.; Yang, T.; Fang, Z.; Wang, Q.; Yang, C.; Zhao, X. Preparation and characterization of coal-based carbon foams by microwave heating process under ambient pressure. Diam. Relat. Mater. 2018, 86, 63–70. [Google Scholar] [CrossRef]
- CFOAM® Carbon Foam Typical Properties (Metric). Available online: https://www.cfoam.com/spec-sheets/ (accessed on 1 July 2023).
- Wang, D.; Zhuang, Q.; Li, K.; Wang, Y. Study on Correlation of Mechanical and Thermal Properties of Coal-Based Carbon Foam with the Weight Loss Rate after Oxidation. Materials 2022, 15, 4887. [Google Scholar] [CrossRef]
- Calvo, M.; García, R.; Moinelo, S.R. Carbon Foams from Different Coals. Energy Fuels 2008, 22, 3376–3383. [Google Scholar] [CrossRef]
- Yang, N.; Gao, X.; Shen, Y.; Wang, M.; Chang, L.; Lv, Y. Effects of coal characteristics on the structure and performance of coal-based carbon foam prepared by self-foaming technique under atmospheric pressure. J. Anal. Appl. Pyrolysis 2022, 164, 105516. [Google Scholar] [CrossRef]
- Bruneton, E.; Tallaron, C.; Gras-Naulin, N.; Cosculluela, A. Evolution of the structure and mechanical behaviour of a carbon foam at very high temperatures. Carbon 2002, 40, 1919–1927. [Google Scholar] [CrossRef]
- Ravishankar, B.; Haftka, R.; Sankar, B. Uncertainty analysis of integrated thermal protection system with rigid insulation bars. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 19th AIAA/ASME/AHS Adaptive Structures Conference 13th, Denver, CO, USA, 4–7 April 2011. [Google Scholar]
- Grujicic, M.; Zhao, C.; Biggers, S.; Kennedy, J.; Morgan, D. Suitability of a Coal-Derived Carbon-Based Foam for use in Thermal Protection Systems of Common Aero Vehicles. Multidiscip. Model. Mater. Struct. 2007, 3, 1–26. [Google Scholar] [CrossRef]
- Suzuki, T.; Aoki, T.; Ogasawara, T.; Fujita, K. Nonablative lightweight thermal protection system for Mars Aeroflyby Sample collection mission. Acta Astronaut. 2017, 136, 407–420. [Google Scholar] [CrossRef]
- Ogasawara, T.; Ayabe, S.; Ishida, Y.; Aoki, T.; Kubota, Y. Heat-resistant sandwich structure with carbon fiber-polyimide composite faces and a carbon foam core. Compos. Part A Appl. Sci. Manuf. 2018, 114, 352–359. [Google Scholar] [CrossRef]
- Kubota, Y.; Miyamoto, O.; Aoki, T.; Ishida, Y.; Ogasawara, T.; Umezu, S. New thermal protection system using high-temperature carbon fibre-reinforced plastic sandwich panel. Acta Astronaut. 2019, 160, 519–526. [Google Scholar] [CrossRef]
- Bale, S.D.; Goetz, K.; Harvey, P.R.; Turin, P.; Bonnell, J.W.; Dudok de Wit, T.; Ergun, R.E.; MacDowall, R.J.; Pulupa, M.; André, M.; et al. The FIELDS instrument suite for Solar Probe Plus: Measuring the coronal plasma and magnetic field, plasma waves and turbulence, and radio signatures of solar transients. Space Sci. Rev. 2016, 204, 49–82. [Google Scholar] [CrossRef]
- Congdon, E.; Mehoke, D.; Buchta, M.; Nagle, D.; Zhang, D. Development of high-temperature optical coating for thermal management on solar probe plus. In Proceedings of the 10th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, Chicago, IL, USA, 28 June–1 July 2010. [Google Scholar]
- Heisler, E.; Abel, E.; Congdon, E.; Eby, D. Full-scale thermal simulator development for the solar probe plus thermal protection system. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017. [Google Scholar]
- Smith, R.; Bucior, S.; Hahn, J. Integration and Test Challenges of Parker Solar Probe. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020. [Google Scholar]
- Korreck, K.E.; Szabo, A.; Chinchilla, T.N.; Lavraud, B.; Luhmann, J.; Niembro, T.; Higginson, A.; Alzate, N.; Wallace, S.; Paulson, K.; et al. Source and Propagation of a Streamer Blowout Coronal Mass Ejection Observed by the Parker Solar Probe. Astrophys. J. Suppl. Ser. 2020, 246, 69. [Google Scholar] [CrossRef]
- Da Silva, L.F.M.; Adams, R.D. Effect of temperature on the mechanical and bonding properties of a carbon-reinforced bismaleimide. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2008, 222, 45–52. [Google Scholar] [CrossRef]
- Yang, B.; Yue, Z.; Geng, X.; Wang, P.; Gan, J.; Liao, B. Effects of space environment temperature on the mechanical properties of carbon fiber/bismaleimide composites laminates. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 3–16. [Google Scholar] [CrossRef]
- Cai, Y.; Cheng, L.; Zhang, H.; Yin, X.; Yin, H.; Yan, G. Effects of graphite filler on the thermophysical properties of 3D C/SiC composites. J. Alloys Compd. 2019, 770, 989–994. [Google Scholar] [CrossRef]
- Patel, M.; Saurabh, K.; Prasad, V.V.B.; Subrahmanyam, J. High temperature C/C-SiC composite by liquid silicon infiltration: A literature review. Bull. Mater. Sci. 2012, 35, 63–73. [Google Scholar] [CrossRef]
- Li, K.; Gao, X.; Roy, A. Micromechanical modeling of three-dimensional open-cell foams using the matrix method for spatial frames. Compos. Part B Eng. 2005, 36, 249–262. [Google Scholar] [CrossRef]
- Sihn, S.; Roy, A.K. Modeling and prediction of bulk properties of open-cell carbon foam. J. Mech. Phys. Solids 2004, 52, 167–191. [Google Scholar] [CrossRef]
- Druma, C.; Alam, M.K.; Druma, A.M. Finite Element Model of Thermal Transport in Carbon Foams. J. Sandw. Struct. Mater. 2004, 6, 527–540. [Google Scholar] [CrossRef]
- Yu, Q.; Thompson, B.E.; Straatman, A.G. A Unit Cube-Based Model for Heat Transfer and Fluid Flow in Porous Carbon Foam. J. Heat Transf. 2006, 128, 352–360. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Gibson, L.J. Multiaxial failure criteria for brittle foams. Int. J. Mech. Sci. 1990, 32, 479–496. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A. Multi-axial yield behaviour of polymer foams. Acta Mater. 2001, 49, 1859–1866. [Google Scholar] [CrossRef]
- Sun, Y.; Amirrasouli, B.; Razavi, S.; Li, Q.; Lowe, T.; Withers, P. The variation in elastic modulus throughout the compression of foam materials. Acta Mater. 2016, 110, 161–174. [Google Scholar] [CrossRef]
- ASTM C297/C297M—16; Standard Test Method for Flatwise Tensile Strength of Sandwich Constructions. ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM-C365/C365M—16; Standard Test Method for Flatwise Compressive Properties of Sandwich Cores. ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM-E132/E132M—17; Standard Test Method for Poisson’s Ratio at Room Temperature. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM C273/C273M—11; Standard Test Method for Shear Properties of Sandwich Core Materials. ASTM International: West Conshohocken, PA, USA, 2011.
- ASTM D7766/D7766M—16; Standard Practice for Damage Resistance Testing of Sandwich Constructions. ASTM International: West Conshohocken, PA, USA, 2016.
- Cheng, X.; Zhang, J.; Bao, J.; Zeng, B.; Cheng, Y.; Hu, R. Low-velocity impact performance and effect factor analysis of scarf-repaired composite laminates. Int. J. Impact Eng. 2018, 111, 85–93. [Google Scholar] [CrossRef]
- Abaqus, G. Abaqus 6.11; Dassault Systemes Simulia Corporation: Providence, RI, USA, 2011. [Google Scholar]










| Symbol | Property | CFRC | C/SiC |
|---|---|---|---|
| (GPa) | Modulus along 1 direction | 167 | 57.27 |
| (GPa) | Modulus along 2 direction | 9.13 | 57.27 |
| (GPa) | Modulus along 3 direction | 9.13 | 4.56 |
| Poisson’s ratio in 12 plane | 0.35 | 0.36 | |
| Poisson’s ratio in 13 plane | 0.35 | 0.32 | |
| Poisson’s ratio in 23 plane | 0.30 | 0.32 | |
| (GPa) | Shear modulus in 12 plane | 4.93 | 3.01 |
| (GPa) | Shear modulus in 13 plane | 4.93 | 3.01 |
| (GPa) | Shear modulus in 23 plane | 0.86 | 1.02 |
| (MPa) | Tensile strength along 1 direction | 2761 | 204 |
| (MPa) | Tensile strength along 2 direction | 38.4 | 204 |
| (MPa) | Tensile strength along 3 direction | 38.4 | 23.7 |
| (MPa) | Compressive strength along 1 direction | 1420 | 360 |
| (MPa) | Compressive strength along 2 direction | 179 | 360 |
| (MPa) | Compressive strength along 3 direction | 179 | 87 |
| (MPa) | Shear strength in 12 plane | 75 | 104 |
| (MPa) | Shear strength in 13 plane | 75 | 104 |
| (MPa) | Shear strength in 23 plane | 30 | 56 |
| (N·mm) | Fiber tensile energy release rate | 180 | 35 |
| (N·mm) | Fiber compressive energy release rate | 100 | 15 |
| (N·mm) | Matix tensile energy release rate | 4 | 35 |
| (N·mm) | Matrix compressive energy release rate | 10 | 15 |
| (g·cm−3) | Density | 1.65 | 2.03 |
| (W·m−1·K−1) | Thermal conductivity in fiber direction | 0.72 | 28.8 |
| (W·m−1·K−1) | Thermal conductivity out of plane | 0.34 | 11.0 |
| C (J·g−1·K−1) | Specific heat capacity | 1.08 | 0.69 |
| Test | Referenced ASTM | Number of Specimens | Properties (i = x, y, z; j = xy, xz) |
|---|---|---|---|
| UT test | C297 [45] | UTx-1~3 | Tension strength ; Young‘s modulus |
| UTy-1~3 | |||
| UTz-1~3 | |||
| UC test | C365 [46] E132 [47] | UCx-1~5 | Compressive strength ; Young‘s modulus ; Poisson’s ratio Platform stress |
| UCy-1~5 | |||
| UCz-1~5 | |||
| SS test | C273 [48] | SSxy-1~3 | Shear strength ; Shear modulus |
| SSxz-1~3 | |||
| PC test | C365 [46] | PCx-1~4 | Failure stresses and platform stresses in all three directions |
| PCy-1~4 | |||
| PCz-1~4 |
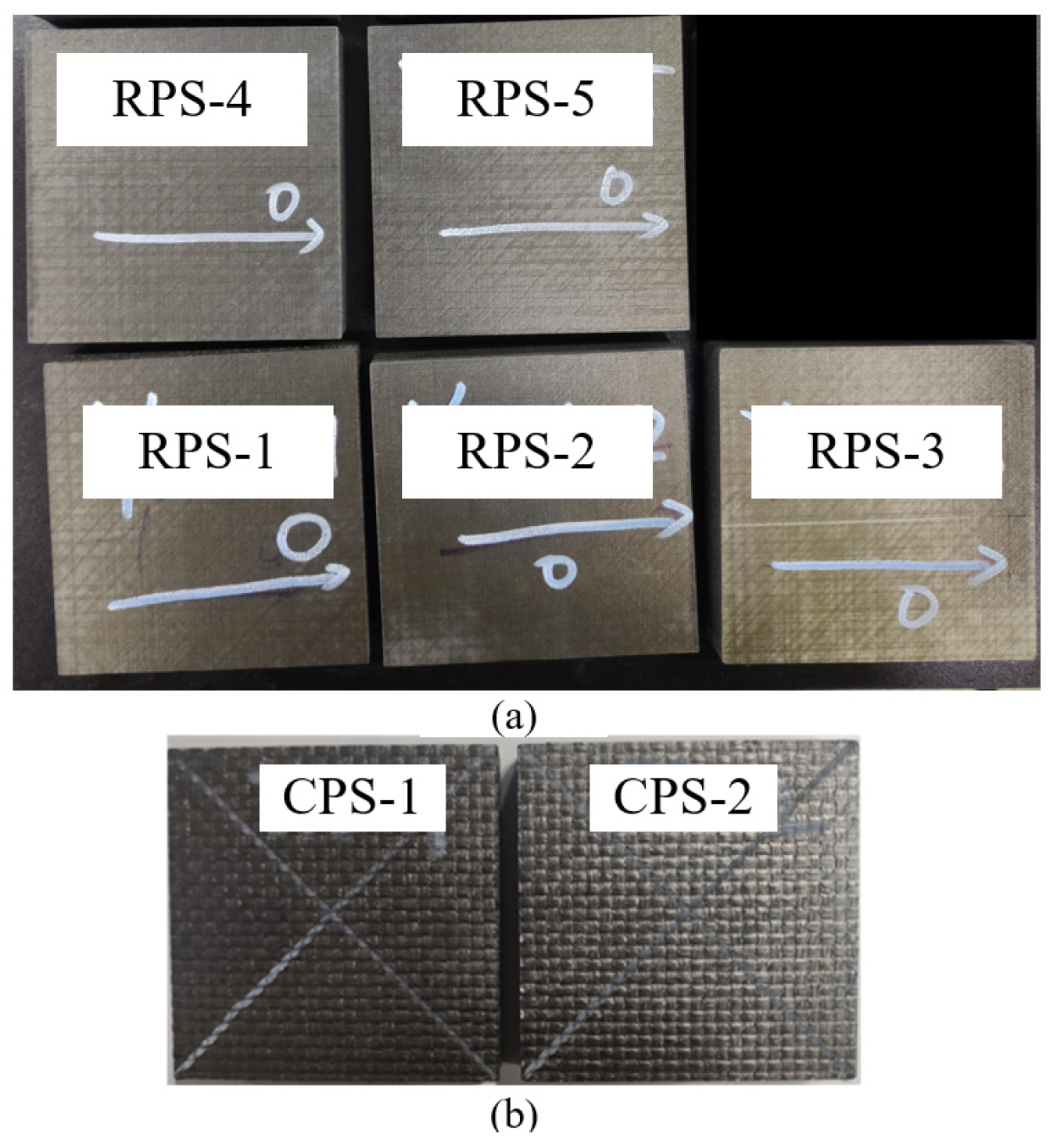
| Test | Number of Specimens | Load |
|---|---|---|
| Low-velocity impact test of RPS | RPS-1 | Impact energy 20 J |
| RPS-2 | Impact energy 20 J | |
| RPS-3 | Impact energy 25 J | |
| Low-velocity impact test of CPS | CPS-1 | Impact energy 10 J |
| CPS-2 | Impact energy 20 J | |
| Quasi-static indentation test of RPS | RPS-4 | Indentation depth 8 mm |
| RPS-5 | Indentation depth 15 mm |
| Property | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Results | 751 | 943 | 1283 | 953 | 1120 | 3.51 | 3.48 | 4.01 | 9.72 | 8.55 | 16.7 | 2.03 | 2.89 |
| 798 | 856 | 1170 | 899 | 1201 | 3.03 | 3.42 | 4.17 | 8.11 | 10.1 | 14.0 | 2.20 | 2.64 | |
| 912 | 742 | 1256 | 925 | 1098 | 3.07 | 3.46 | 4.52 | 10.34 | 8.31 | 12.8 | 2.21 | 2.29 | |
| 950 | 746 | 1232 | 9.22 | 8.22 | 13.1 | ||||||||
| 792 | 913 | 1287 | 9.74 | 10.9 | 16.8 | ||||||||
| 855 | 887 | 1245 | |||||||||||
| 977 | 831 | 1260 | |||||||||||
| 934 | 910 | 1264 | |||||||||||
| Average value | 871 | 854 | 1250 | 926 | 1140 | 3.20 | 3.45 | 4.23 | 9.43 | 9.22 | 14.7 | 2.15 | 2.61 |
| Standard deviation | 79 | 71 | 35 | 22 | 44 | 0.22 | 0.02 | 0.21 | 0.75 | 1.08 | 1.7 | 0.08 | 0.25 |
| Property | ||
|---|---|---|
| Results | 0.21 | 0.57 |
| 0.24 | 0.55 | |
| 0.23 | 0.56 | |
| 0.22 | 0.55 | |
| 0.24 | 0.56 | |
| Average value | 0.23 | 0.56 |
| Standard deviation | 0.011 | 0.007 |
| X Direction (MPa) | Y Direction (MPa) | Z Direction (MPa) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −10.2 | −9.05 | −9.98 | −10.6 | −5.41 | −5.91 | −5.90 | −6.58 | −5.67 | −5.29 | −5.95 | −5.02 | |
| −5.82 | −5.14 | −5.67 | −5.99 | −9.53 | −10.4 | −10.4 | −11.6 | −5.67 | −5.29 | −5.95 | −5.02 | |
| −6.18 | −5.46 | −6.03 | −6.37 | −5.75 | −6.28 | −6.27 | −7.00 | −16.5 | −15.4 | −17.3 | −14.6 | |
| UT test (MPa) | (−0.35, 1.05) | UC test (MPa) | (0.35, 1.04) | PC test (MPa) | (0.71, 0.60) | SS test (MPa) | (0, 1.02) |
| (−0.30, 0.91) | (0.29, 0.87) | (0.63, 0.53) | (0, 1.11) | ||||
| (−0.31, 0.92) | (0.37, 1.11) | (0.70, 0.59) | (0, 1.11) | ||||
| (−0.35, 1.05) | (0.33, 0.99) | (0.74, 0.62) | (0, 1.20) | ||||
| (−0.34, 1.03) | (0.35, 1.04) | (0.67, 0.56) | (0, 1.09) | ||||
| (−0.35, 1.04) | (0.31, 0.92) | (0.73, 0.61) | (0, 0.95) | ||||
| (−0.32, 0.95) | (0.36, 1.08) | (0.72, 0.61) | |||||
| (−0.33, 0.99) | (0.30, 0.89) | (0.81, 0.68) | |||||
| (−0.36, 1.07) | (0.29, 0.88) | (0.78, 0.52) | |||||
| (0.39, 1.17) | (0.73, 0.48) | ||||||
| (0.38, 1.14) | (0.82, 0.54) | ||||||
| (0.32, 0.95) | (0.69, 0.46) | ||||||
| (0.29, 0.87) | |||||||
| (0.30, 0.89) | |||||||
| (0.38, 1.14) |
| Directions | (MPa) | ||||
|---|---|---|---|---|---|
| X | −6.33 | −5.13 | −7.44 | −5.99 | −5.43 |
| Y | −6.71 | −7.56 | −5.71 | −5.51 | −7.58 |
| Z | −11.12 | −9.78 | −9.66 | −9.84 | −11.26 |
| X Direction (MPa) | Y Direction (MPa) | Z Direction (MPa) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −10.2 | −9.05 | −9.98 | −10.6 | −5.41 | −5.91 | −5.90 | −6.58 | −5.67 | −5.29 | −5.95 | −5.02 | |
| −5.82 | −5.14 | −5.67 | −5.99 | −9.53 | −10.4 | −10.4 | −11.6 | −5.67 | −5.29 | −5.95 | −5.02 | |
| −6.18 | −5.46 | −6.03 | −6.37 | −5.75 | −6.28 | −6.27 | −7.00 | −16.5 | −15.4 | −17.3 | −14.6 | |
| UC test (MPa) | (0.23, 0.68) | PC test (MPa) | (0.50, 0.42) | |
| (0.18, 0.55) | (0.48, 0.41) | |||
| (0.27, 0.80) | (0.46, 0.39) | |||
| (0.21, 0.64) | (0.54, 0.46) | |||
| (0.19, 0.58) | (0.50, 0.43) | |||
| (0.24, 0.72) | (0.52, 0.44) | |||
| (0.27, 0.81) | (0.53, 0.45) | |||
| (0.20, 0.61) | (0.56, 0.47) | |||
| (0.20, 0.60) | (0.57, 0.38) | |||
| (0.27, 0.81) | (0.55, 0.36) | |||
| (0.25, 0.76) | (0.58, 0.38) | |||
| (0.22, 0.67) | (0.53, 0.35) | |||
| (0.22, 0.66) | ||||
| (0.22, 0.67) | ||||
| (0.26, 0.77) | ||||
| Number of Specimen | Slope (MPa) | Fluctuation | |||||
|---|---|---|---|---|---|---|---|
| Elastic Section | 1st | 2nd | 3rd | 4th | 5th | ||
| PCx-1 | 883 | 879 | 875 | 874 | 867 | 858 | 2.83% |
| PCy-1 | 832 | 824 | 821 | 824 | 819 | 798 | 4.09% |
| PCz-1 | 1355 | 1351 | 1352 | 1346 | 1338 | 1326 | 2.14% |
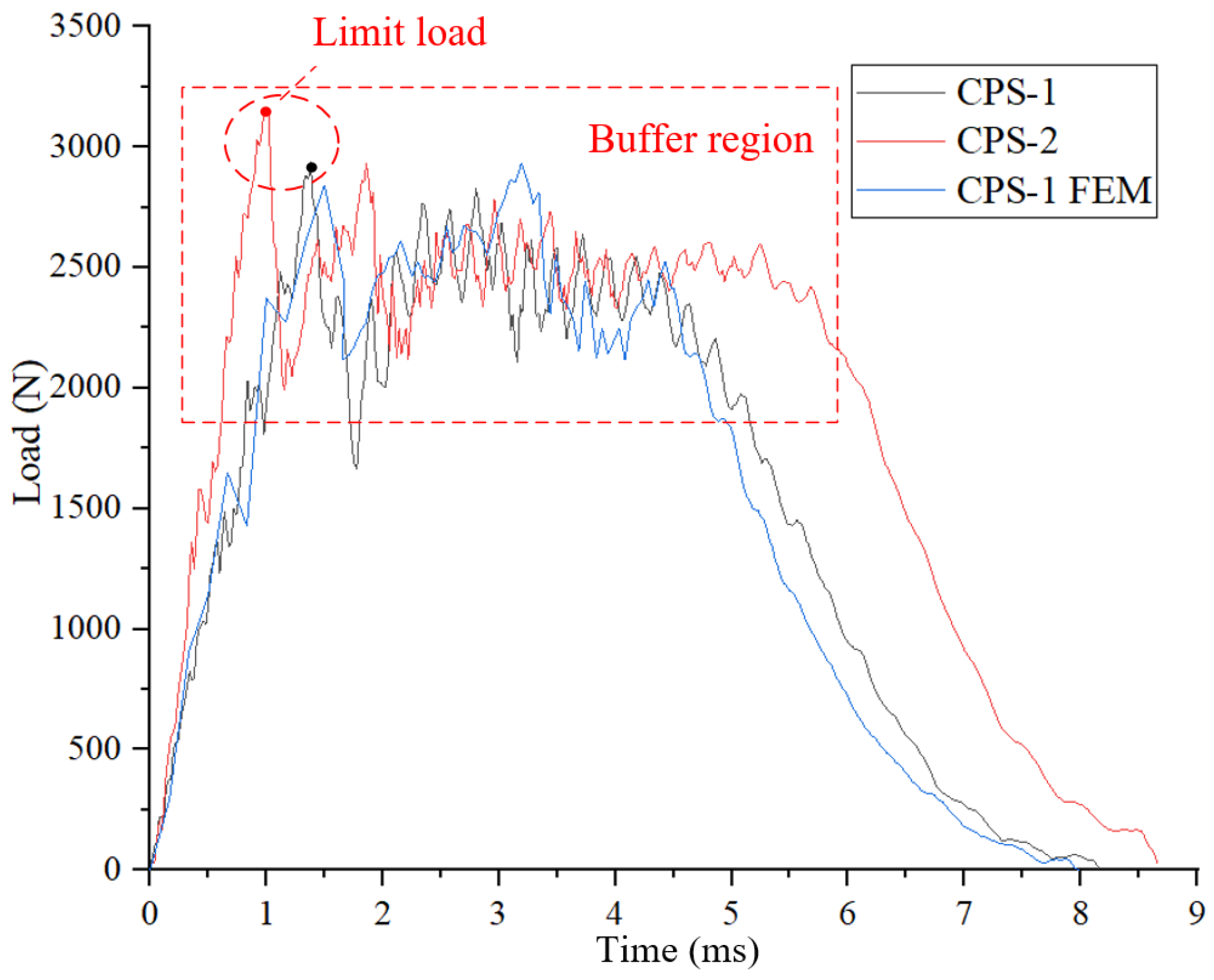
| Number of Specimen | Impact Energy (J) | Limit Load (N) | Maximum Load (N) | Indentation Diameter (mm) | Indentation Diameter (mm) |
|---|---|---|---|---|---|
| RPS-1 | 20 | 7409 | 7978 | 22.41 | 3.14 |
| RPS-2 | 20 | 6815 | 7372 | 23.18 | 2.59 |
| RPS-3 | 25 | 6895 | 8185 | 24.52 | 4.14 |
| Number of Specimen | Impact Energy (J) | Limit Load (N) | Maximum Load (N) | Indentation Diameter (mm) | Indentation Diameter (mm) |
|---|---|---|---|---|---|
| CPS-1 | 10 | 2937 | 2937 | 11.95 | 4.48 |
| CPS-2 | 20 | 3153 | 3153 | 30.28 | 5.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, Q.; Yue, P.; Li, K.; Guo, X.; Cheng, X. Study on Low-Velocity Impact Performance of Coal-Based Carbon Foam Sandwich Structures in Thermal Protection Systems. Aerospace 2023, 10, 630. https://doi.org/10.3390/aerospace10070630
Zhuang Q, Yue P, Li K, Guo X, Cheng X. Study on Low-Velocity Impact Performance of Coal-Based Carbon Foam Sandwich Structures in Thermal Protection Systems. Aerospace. 2023; 10(7):630. https://doi.org/10.3390/aerospace10070630
Chicago/Turabian StyleZhuang, Qikai, Peijie Yue, Kai Li, Xin Guo, and Xiaoquan Cheng. 2023. "Study on Low-Velocity Impact Performance of Coal-Based Carbon Foam Sandwich Structures in Thermal Protection Systems" Aerospace 10, no. 7: 630. https://doi.org/10.3390/aerospace10070630
APA StyleZhuang, Q., Yue, P., Li, K., Guo, X., & Cheng, X. (2023). Study on Low-Velocity Impact Performance of Coal-Based Carbon Foam Sandwich Structures in Thermal Protection Systems. Aerospace, 10(7), 630. https://doi.org/10.3390/aerospace10070630







