A Method for Constructing Health Indicators of the Engine Bleed Air System Using Multi-Level Feature Extraction
Abstract
:1. Introduction
- 1.
- To address the challenge of assessing the operational status of engine bleed air systems, we propose a multi-level feature extraction approach for constructing HIs (Health Indicators) that quantify the health status of the engine bleed air system based on data collected from each flight cycle.
- 2.
- In the process of constructing health indicators for the engine bleed air system, we solve the issue of varying cycle lengths in the flight data. We introduce a data-level feature extraction method that transforms the original QAR data, which has unequal cycle lengths, into samples of equal length with consistent feature spaces. Additionally, we apply significant compensation to certain elements within the samples to highlight their numerical features.
- 3.
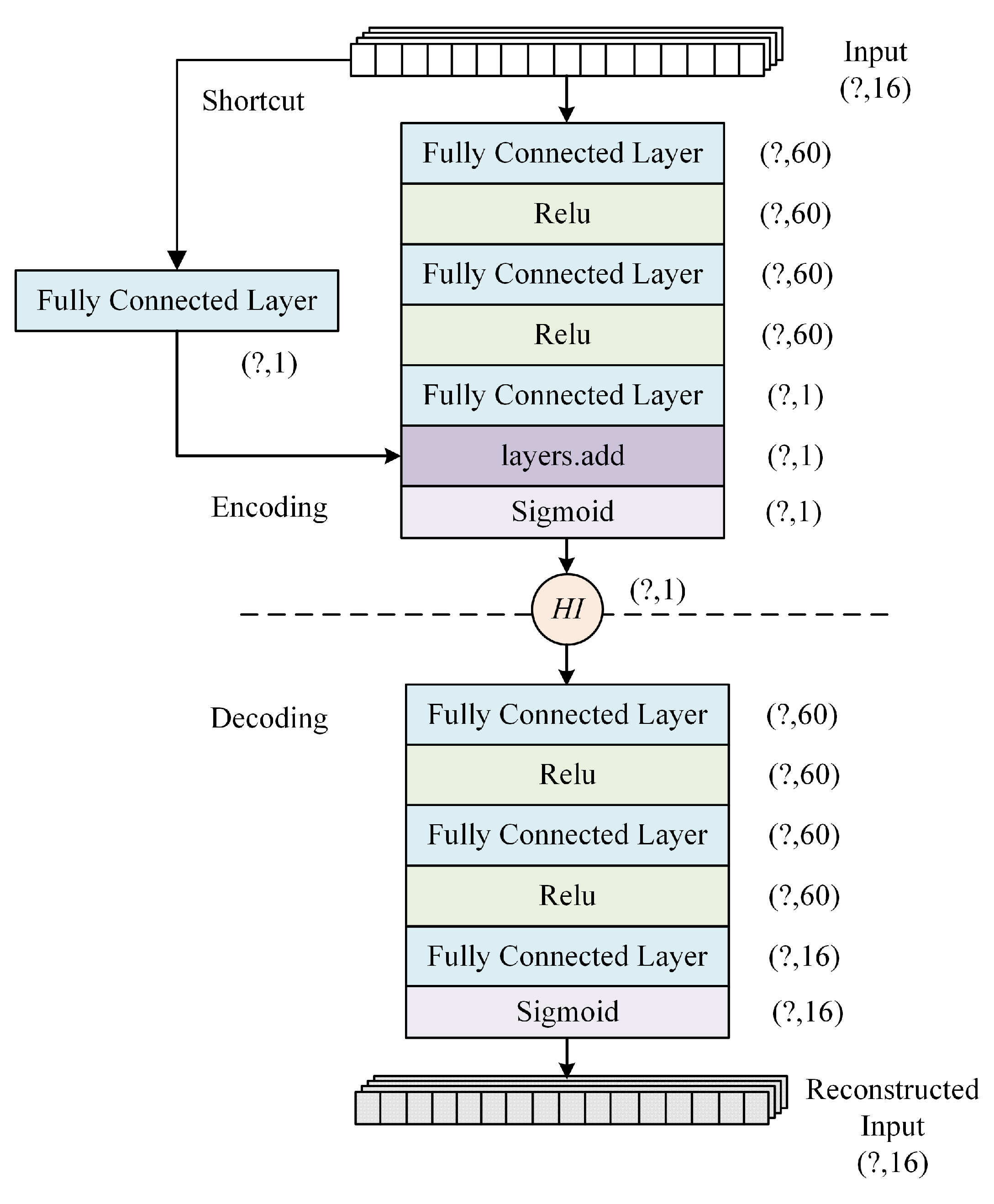
- Considering the unannotated nature of actual flight data, we propose an enhanced approach named RDAE (ResNet Deep Autoencoder). RDAE is based on the autoencoder algorithm and aims to extract features from preprocessed data using unsupervised learning. The effectiveness of the proposed methods was validated through experiments conducted on one year of QAR data from a specific airline company.
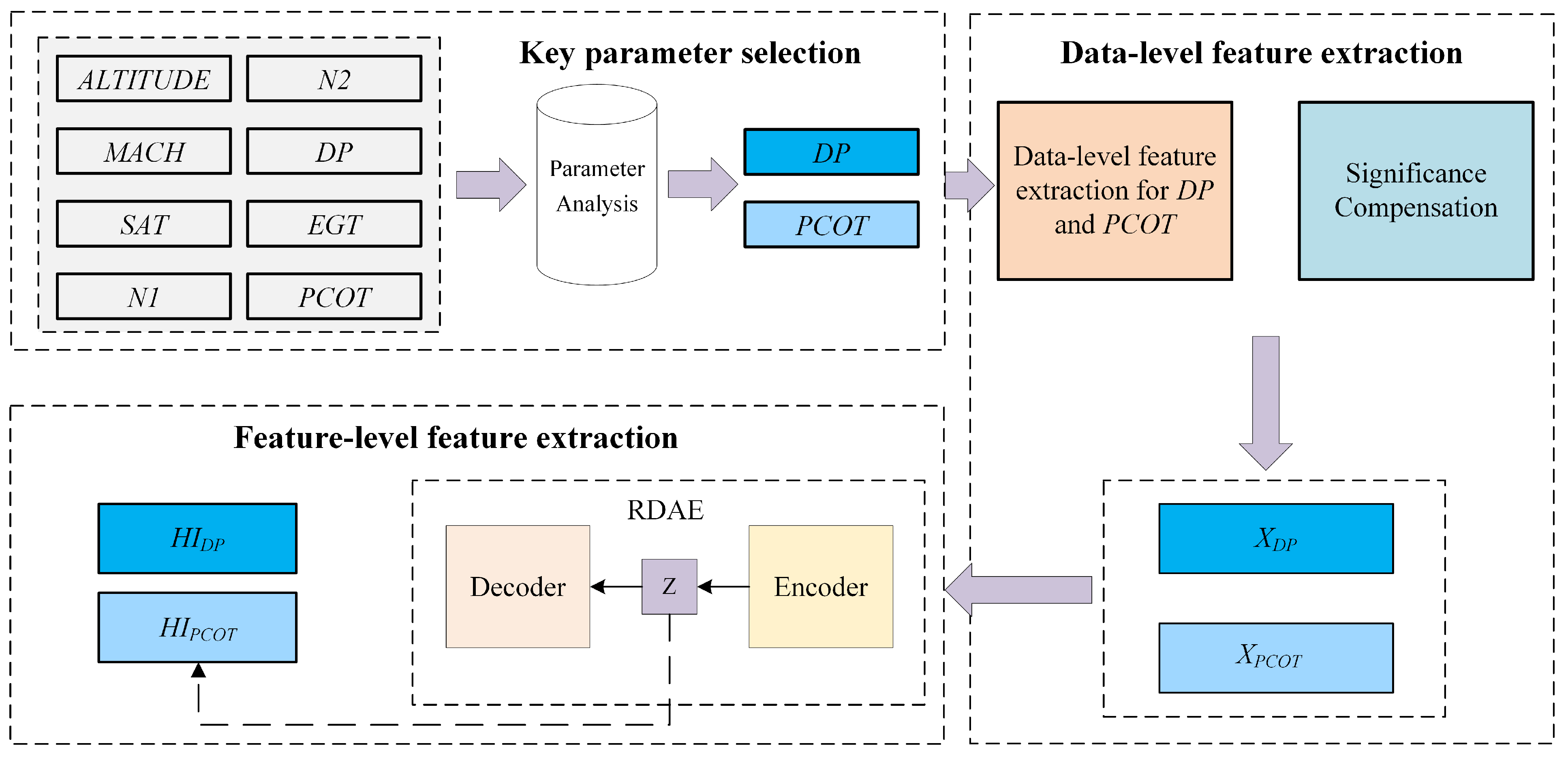
2. Methodology
2.1. Key Parameter Selection
2.2. Data-Level Feature Extraction
| Algorithm 1 Data-level feature extraction from and |
|
- 1.
- Determine whether each row of data in each flight cycle satisfies the basic conditions. The basic conditions include both engine start valves closed, APU bleed valve closed, engine anti-ice valves and wing anti-ice valves closed, and left and right isolation valves open.
- 2.
- If each row of data in the flight cycle satisfies the basic conditions, determine the stage of the bleed air and check if it satisfies the criteria for the . If it satisfies the criteria, add the current to Queue 2. Because involves multi-level bleed air pressures (such as 5th stage, 9th stage, etc.), the same pressure value represents different meanings at different stages. Therefore, it requires judgment. However, is a temperature value generated by a single sensor, so it does not require any judgment and can be directly placed into Queue 2.
- 3.
- After scanning each row of data in the flight cycle, Queue 2 contains the collection of or values for that flight cycle.
- 4.
- If Queue 2 is not empty, perform feature calculations on Queue 2. The calculations can include finding the maximum, minimum, and average values of queue 2, as well as determining the number of elements in different pressure ranges for detecting abnormal or values. The number of elements in each range represents the frequency of occurrence within the range, and since the QAR data has a sampling frequency of 1 Hz, the occurrence value is equal to the time duration.
| Algorithm 2 The method for |
|
| Algorithm 3 The method for |
|
2.3. Feature-Level Feature Extraction
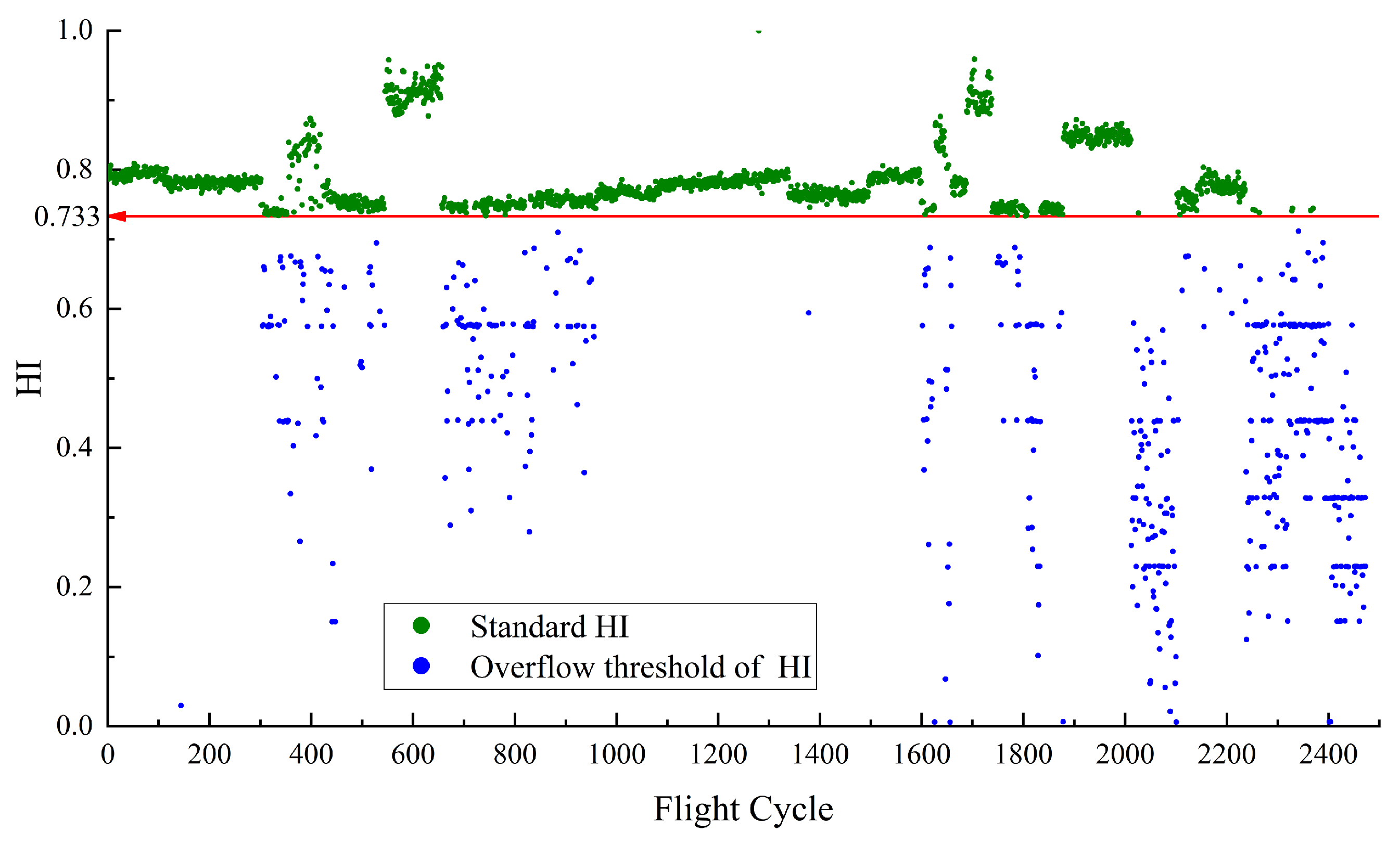
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shang, L.; Liu, G. Sensor and actuator fault detection and isolation for a high performance aircraft engine bleed air temperature control system. IEEE Trans. Control Syst. Technol. 2011, 19, 1260–1268. [Google Scholar] [CrossRef]
- Jianzhong, S.; Fangyuan, W.; Shungang, N. Aircraft air conditioning system health state estimation and prediction for predictive maintenance. Chin. J. Aeronaut. 2020, 33, 947–955. [Google Scholar]
- Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage Propagation Modeling for Aircraft Engine Run-to-Failure Simulation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; IEEE: Piscataway, NJ, USA, 2008. [Google Scholar]
- Wu, Y.; Yuan, M.; Dong, S.; Lin, L.; Liu, Y. Remaining useful life estimation of engineered systems using vanilla LSTM neural networks. Neurocomputing 2018, 275, 167–179. [Google Scholar] [CrossRef]
- Guo, Y.; Sun, Y.; He, Y.; Du, F.; Su, S.; Peng, C. A Data-Driven Integrated Safety Risk Warning Model Based on Deep Learning for Civil Aircraft. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 1707–1719. [Google Scholar] [CrossRef]
- Lan, C.E.; Kaiyuan, W.; Jiang, Y. Flight Characteristics Analysis Based on QAR Data of a Jet Transport during Landing at a High-altitude Airport. Chin. J. Aeronaut. 2012, 25, 13–24. [Google Scholar] [CrossRef] [Green Version]
- Zou, F. Review of aero-engine defect detection technology. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; Volume 1, pp. 1524–1527. [Google Scholar]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Gui, G.; Liu, F.; Sun, J.; Yang, J.; Zhou, Z.; Zhao, D. Flight delay prediction based on aviation big data and machine learning. IEEE Trans. Veh. Technol. 2019, 69, 140–150. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Li, B.; Zhao, Y.P.; Chen, Y.B. Unilateral alignment transfer neural network for fault diagnosis of aircraft engine. Aerosp. Sci. Technol. 2021, 118, 107031. [Google Scholar] [CrossRef]
- Qin, H.; Yang, R.; Guo, C.; Wang, W. Fault diagnosis of electric rudder system using PSOFOA-BP neural network. Measurement 2021, 186, 110058. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, D.; Duan, Z.; Chen, Y. Application of IDE-ELM in fault diagnosis of civil aircraft steering system. Electron. Opt. Control 2020, 27, 97–101. [Google Scholar]
- Liang, K.; Zuo, H.; Sun, J.; Wang, R. Application of multiple linear regression to fault diagnosis of bleed air system. J. Beijing Univ. Aeronaut. Astronaut. 2015, 41, 1651. [Google Scholar]
- Su, S.; Sun, Y.; Li, L.; Peng, C.; Zhang, H.; Zhang, T. Risk Warning for Aircraft Bleed Air System with Multivariate State Estimation Technique. J. Aerosp. Inf. Syst. 2022, 19, 550–564. [Google Scholar] [CrossRef]
- Al-Wadiee, W. Failure Forecast of Boeing 737 Bleed Air System Using Artificial Neural Networks. Ph.D. Thesis, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia, 2011. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Yue, C.; Zhao, Y. An improved aeroservoelastic modeling approach for state-space gust analysis. J. Fluids Struct. 2020, 99, 103148. [Google Scholar] [CrossRef]
- Lim, H.J.; Kim, M.K.; Sohn, H.; Park, C.Y. Impedance based damage detection under varying temperature and loading conditions. NDT E Int. 2011, 44, 740–750. [Google Scholar] [CrossRef]
- Li, R.; Verhagen, W.J.C.; Curran, R. A systematic methodology for Prognostic and Health Management system architecture definition. Reliab. Eng. Syst. Saf. 2020, 193, 106598. [Google Scholar] [CrossRef]
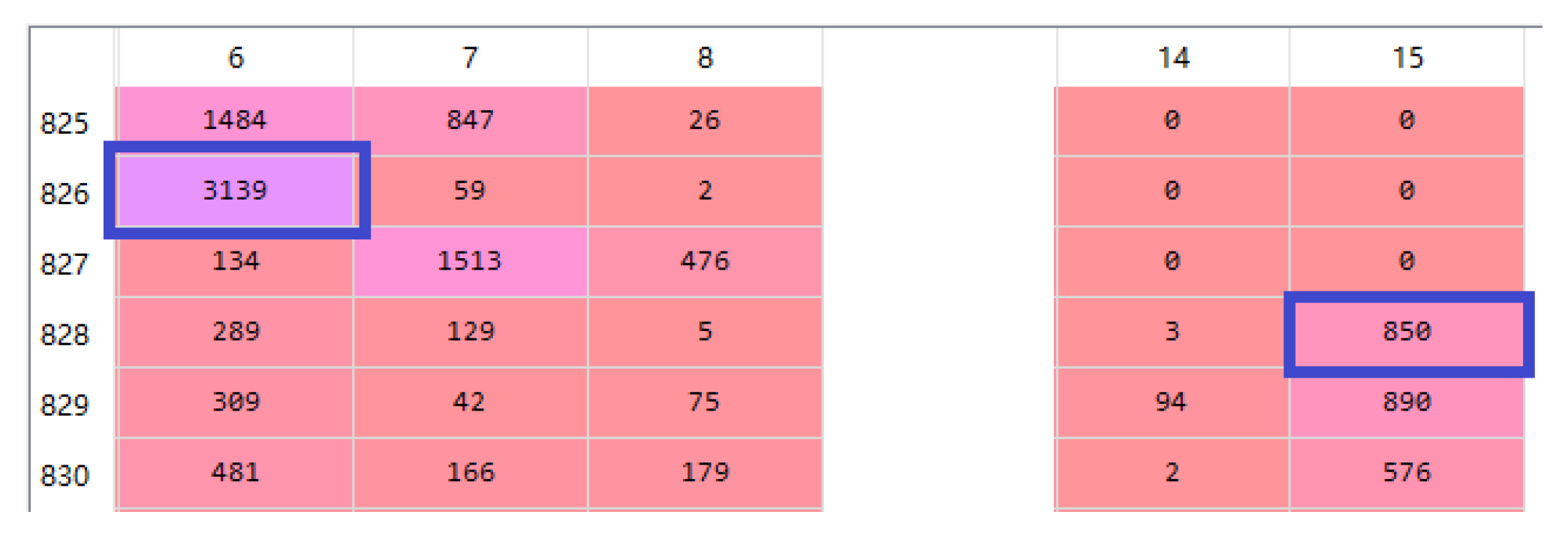

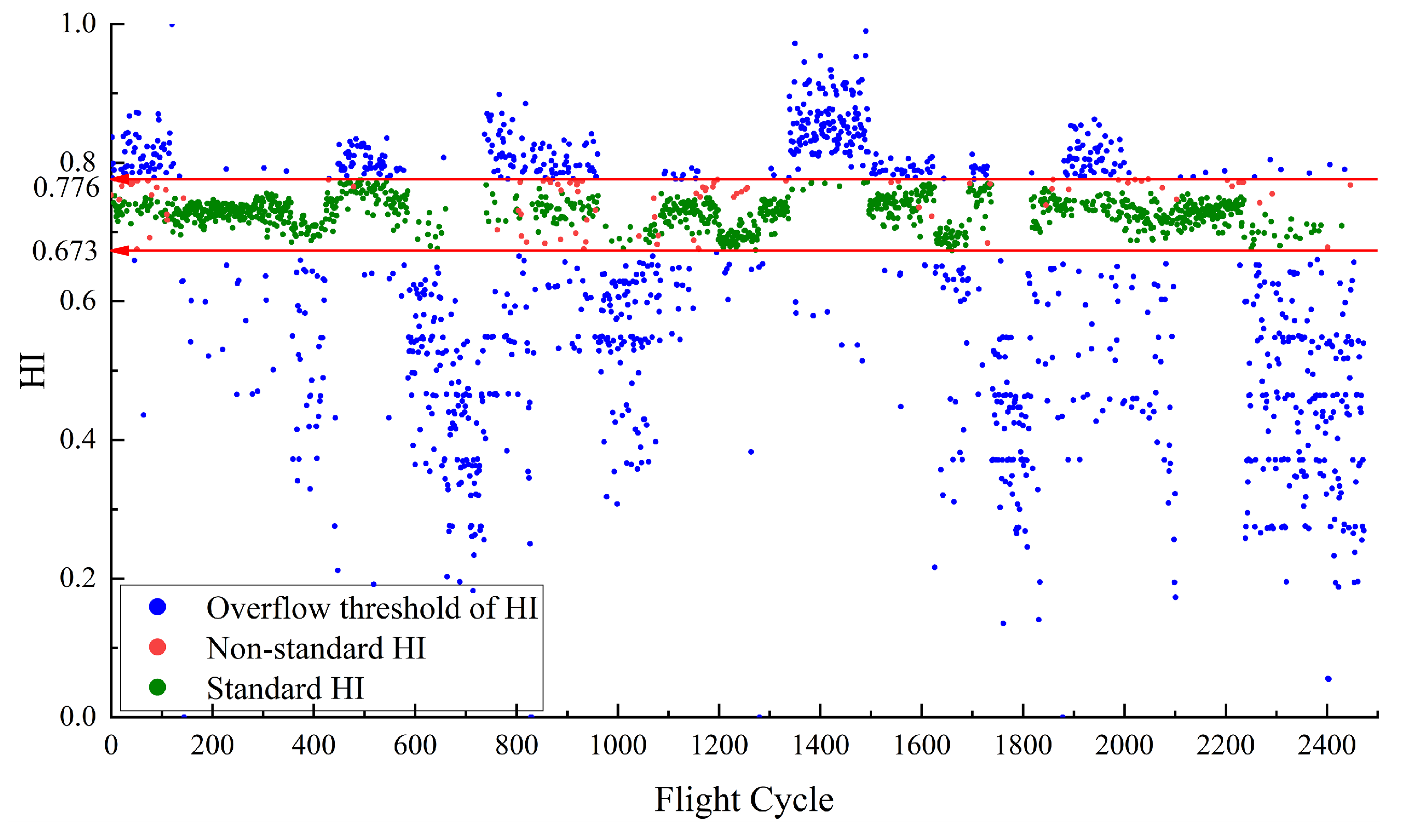

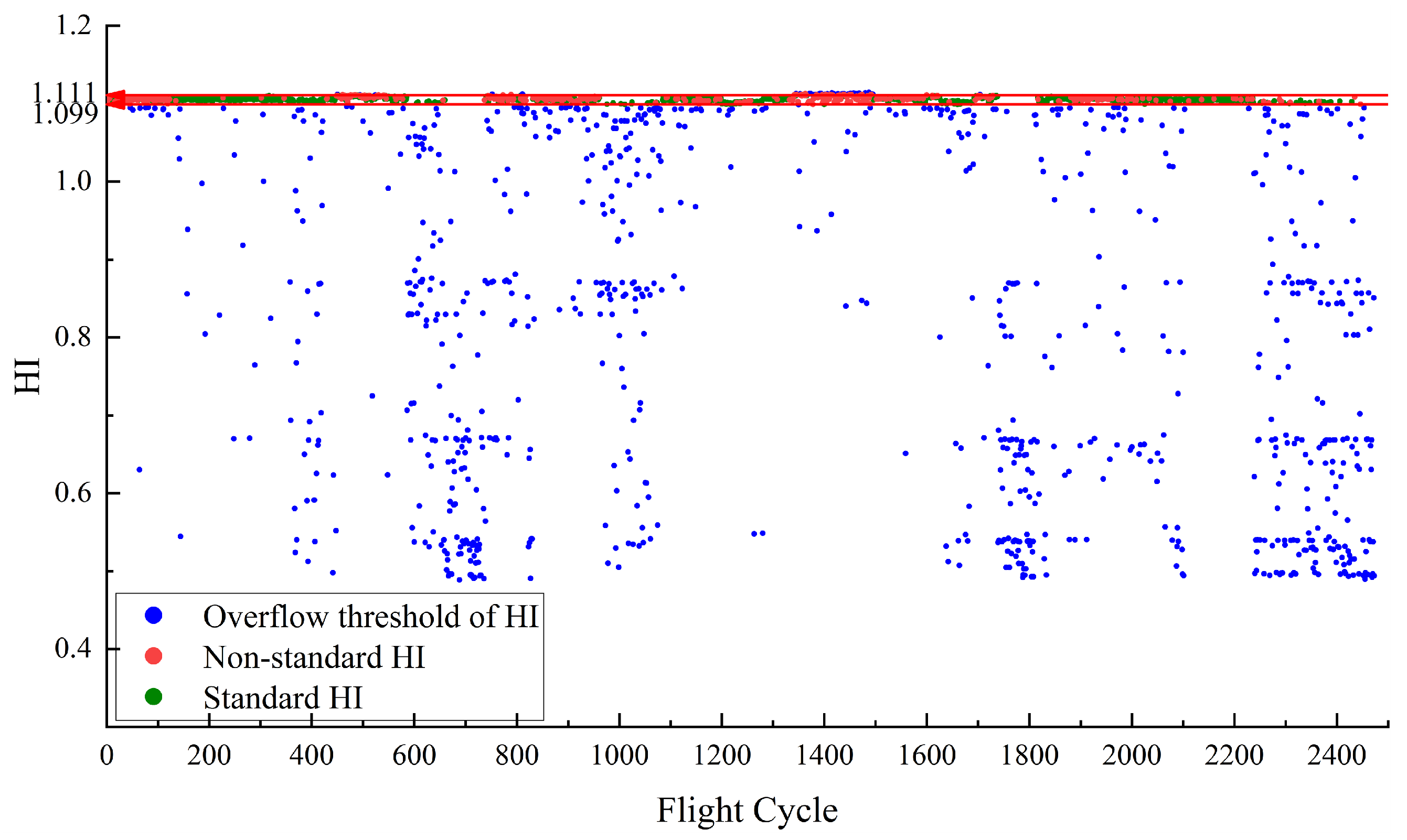

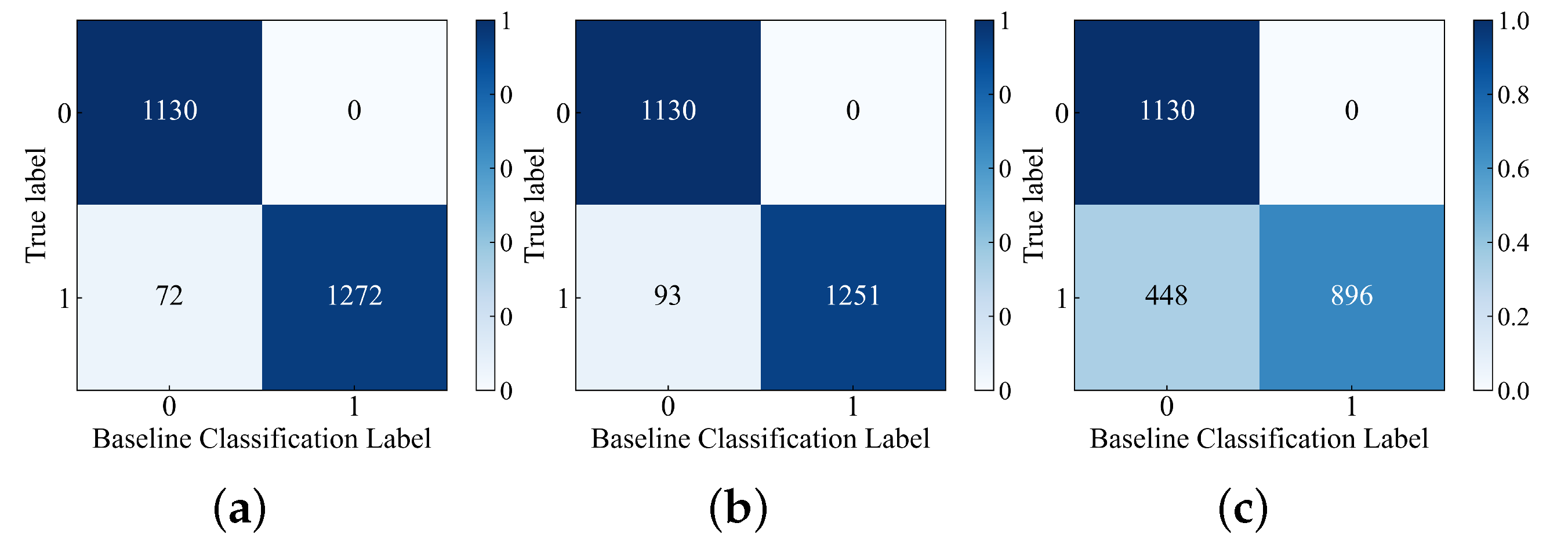

| Name | Column Indices | The Meanings | Units |
|---|---|---|---|
| 0 | The maximum value of . | psi | |
| 1 | The minimum value of . | psi | |
| 2 | The mean value of . | psi | |
| 3 | The number of occurrences when 70 > . | - | |
| 4 | The number of occurrences when 60 > . | - | |
| 5 | The number of occurrences when 55 > . | - | |
| 6 | The number of occurrences when 34 > . | - | |
| ⋯ | ⋯ | ⋯ | ⋯ |
| 14 | The number of occurrences when 14 > . | - | |
| 15 | The number of occurrences when 10 > . | - |
| Name | Column Indices | The Meanings | Units |
|---|---|---|---|
| 0 | The maximum value of . | °F | |
| 1 | The mean value of . | °F | |
| 2 | The number of occurrences when 460 > . | - | |
| 3 | The number of occurrences when 465 > . | - | |
| 4 | The number of occurrences when 470 > . | - | |
| 4 | The number of occurrences when 475 > . | - | |
| 5 | The number of occurrences when 480 > . | - | |
| 6 | The number of occurrences when 485 > . | - | |
| 7 | The number of occurrences when 490 > . | - |
| Model | ||
|---|---|---|
| RDAE | 0.0523 | 0.0000 |
| DAE | 0.0692 | 0.0035 |
| KPCA | 0.3333 | 0.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, Z.; Cao, X.; Hu, F.; Wang, P.; Chen, X.; Dong, L. A Method for Constructing Health Indicators of the Engine Bleed Air System Using Multi-Level Feature Extraction. Aerospace 2023, 10, 645. https://doi.org/10.3390/aerospace10070645
Duan Z, Cao X, Hu F, Wang P, Chen X, Dong L. A Method for Constructing Health Indicators of the Engine Bleed Air System Using Multi-Level Feature Extraction. Aerospace. 2023; 10(7):645. https://doi.org/10.3390/aerospace10070645
Chicago/Turabian StyleDuan, Zhaobin, Xidan Cao, Fangyu Hu, Peng Wang, Xi Chen, and Lei Dong. 2023. "A Method for Constructing Health Indicators of the Engine Bleed Air System Using Multi-Level Feature Extraction" Aerospace 10, no. 7: 645. https://doi.org/10.3390/aerospace10070645
APA StyleDuan, Z., Cao, X., Hu, F., Wang, P., Chen, X., & Dong, L. (2023). A Method for Constructing Health Indicators of the Engine Bleed Air System Using Multi-Level Feature Extraction. Aerospace, 10(7), 645. https://doi.org/10.3390/aerospace10070645





