Aeroelastic Response of Spinning Projectiles with Large Slenderness Ratio at Supersonic Speed
Abstract
:1. Introduction
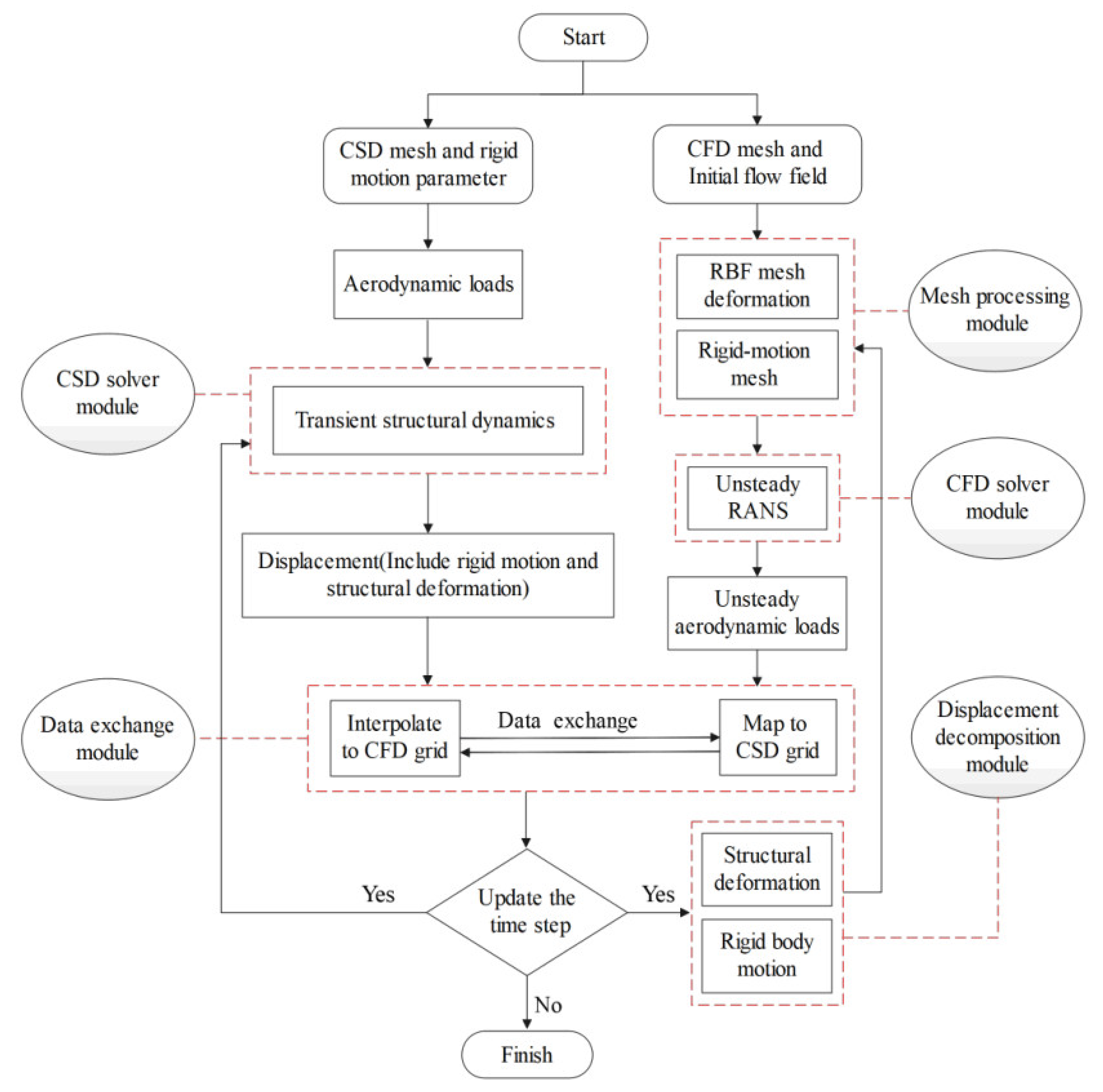
2. Numerical Method for Aeroelasticity of Spinning Projectiles
- The mesh processing module consists of the rigid-motion mesh sub-module and the radial basis function (RBF) mesh deformation sub-module, which are respectively used to adapt to the rigid motion and aeroelastic deformation;
- The CFD solver module is exploited to simulate the flow over deformed spinning projectiles. The Unsteady Reynolds-averaged Navier–Stokes (URANS) equations and the shear-stress transport (SST) turbulence model are employed to obtain the unsteady flow. And then the unsteady aerodynamic force is derived by integrating the pressure and friction force on the surface of projectiles;
- The CSD solver module focuses on the exploration of the structural dynamic response. The Newmark integral form is adopted to solve the structural dynamics equations;
- The displacement decomposition module is employed to deal with the displacement obtained by the CSD solver module. The displacement is decomposed into two parts, that is, the displacement caused by rigid motion and by aeroelastic deformation. Then, the corresponding algorithm can be used to solve the mesh deformation problem in the fluid domain;
- The data exchange module aims to exchange crucial data for solving the flow and structural fields. In this module, the aerodynamic load and displacement obtained by the CFD/CSD solver module are exchanged to realize the fluid-solid coupling calculation.
2.1. CFD Solver Module
2.2. CSD Solver Module
2.3. Mesh Processing Module
2.3.1. Rigid-Motion Mesh Method
2.3.2. RBF Mesh Deformation Method
2.4. Displacement Decomposition Module
2.5. Data Exchange Module
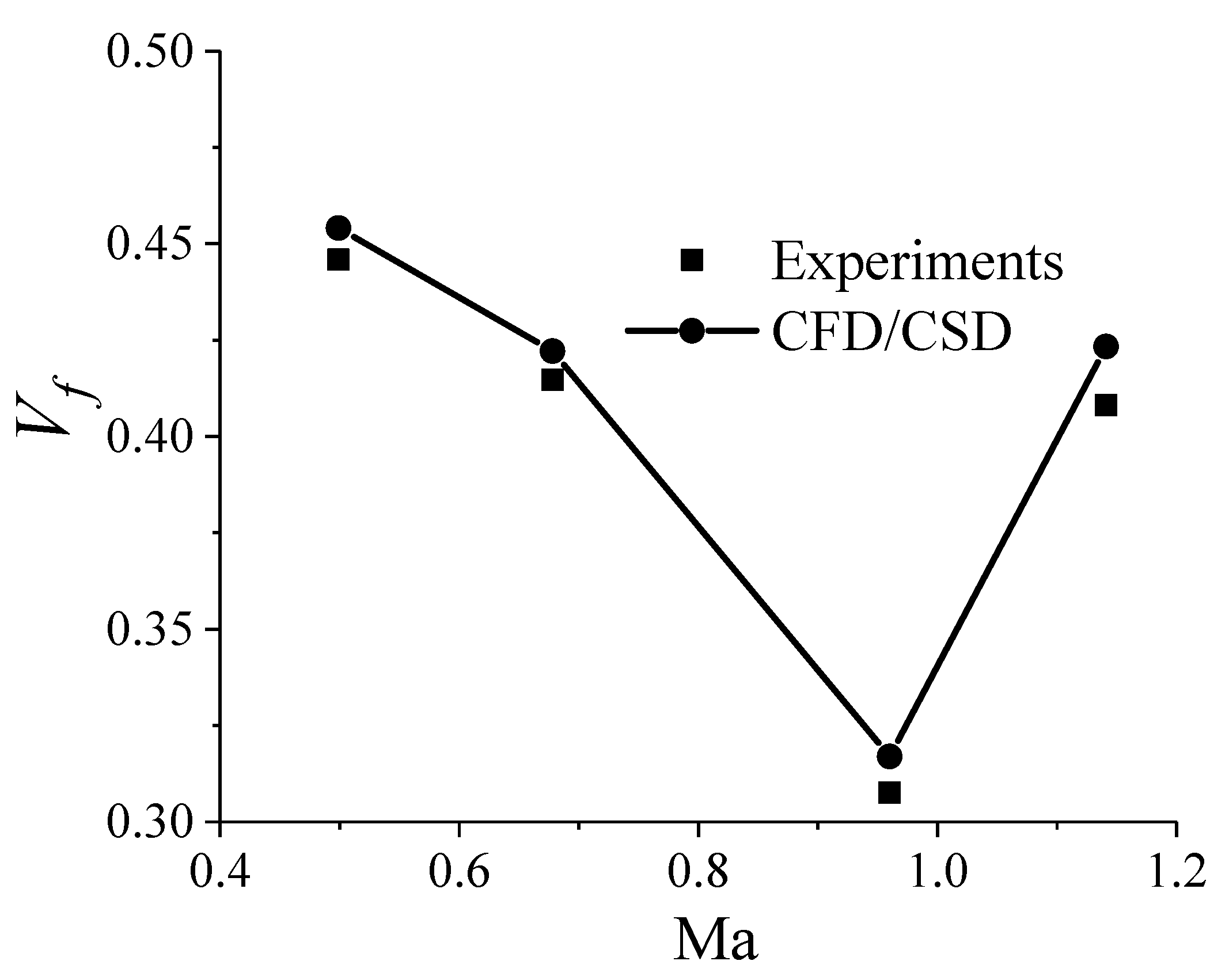
3. Validation of Numerical Method
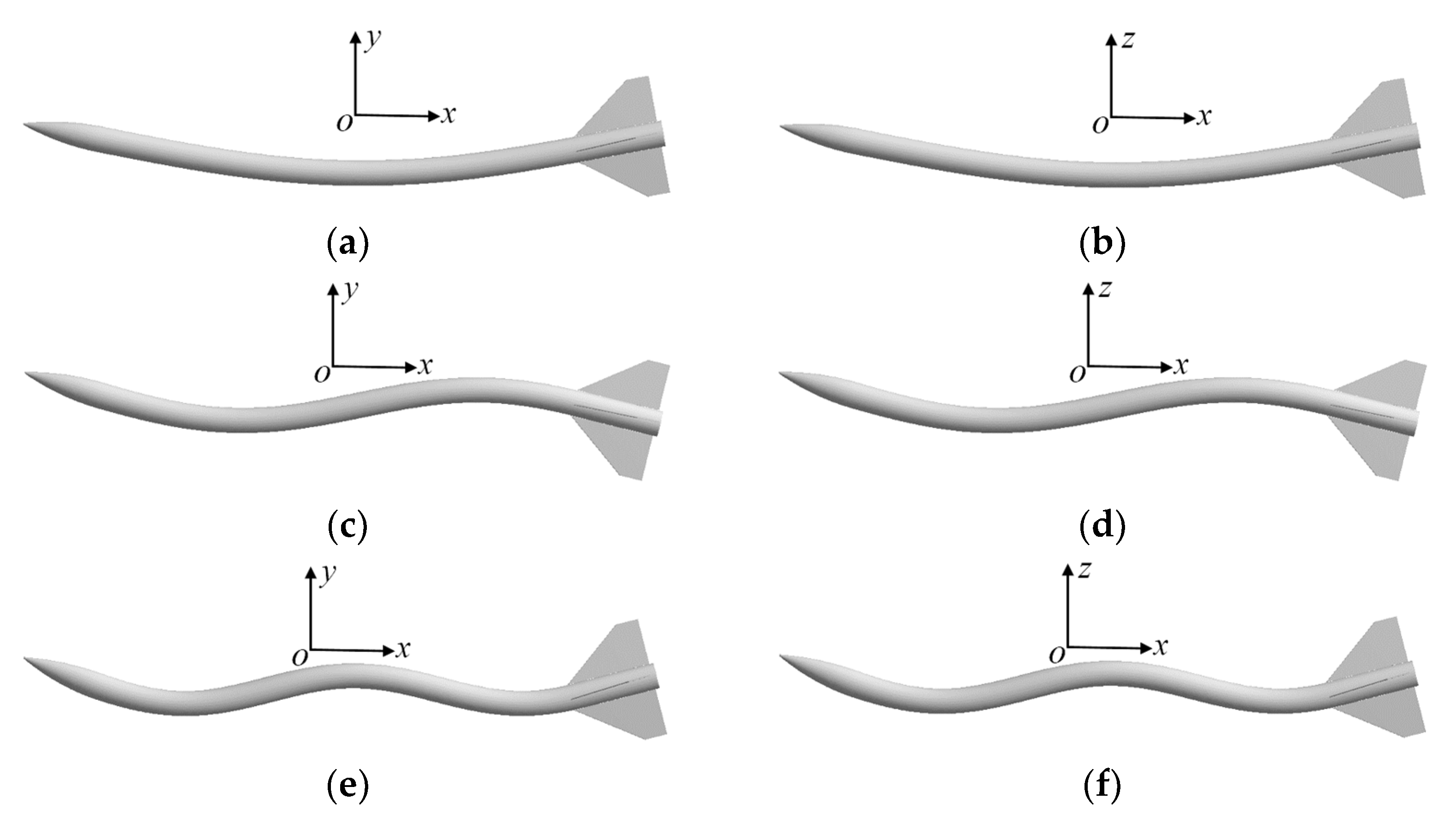
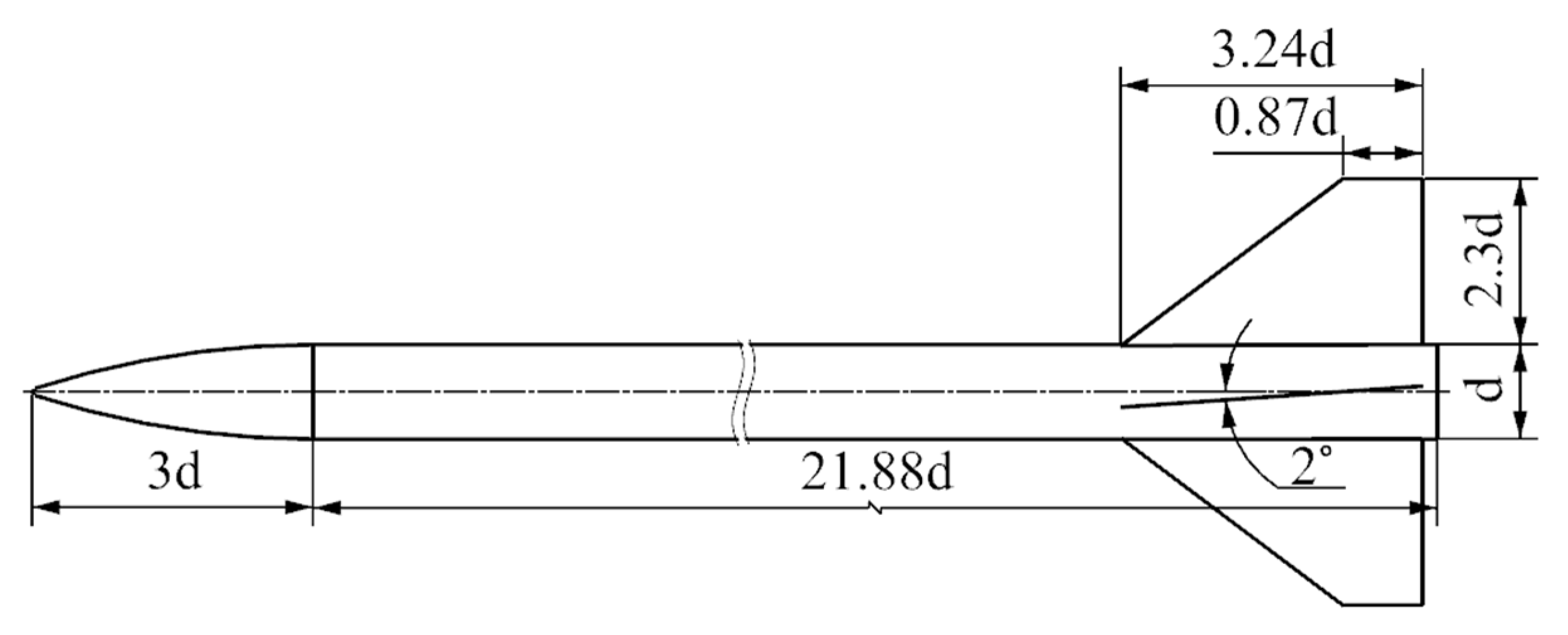
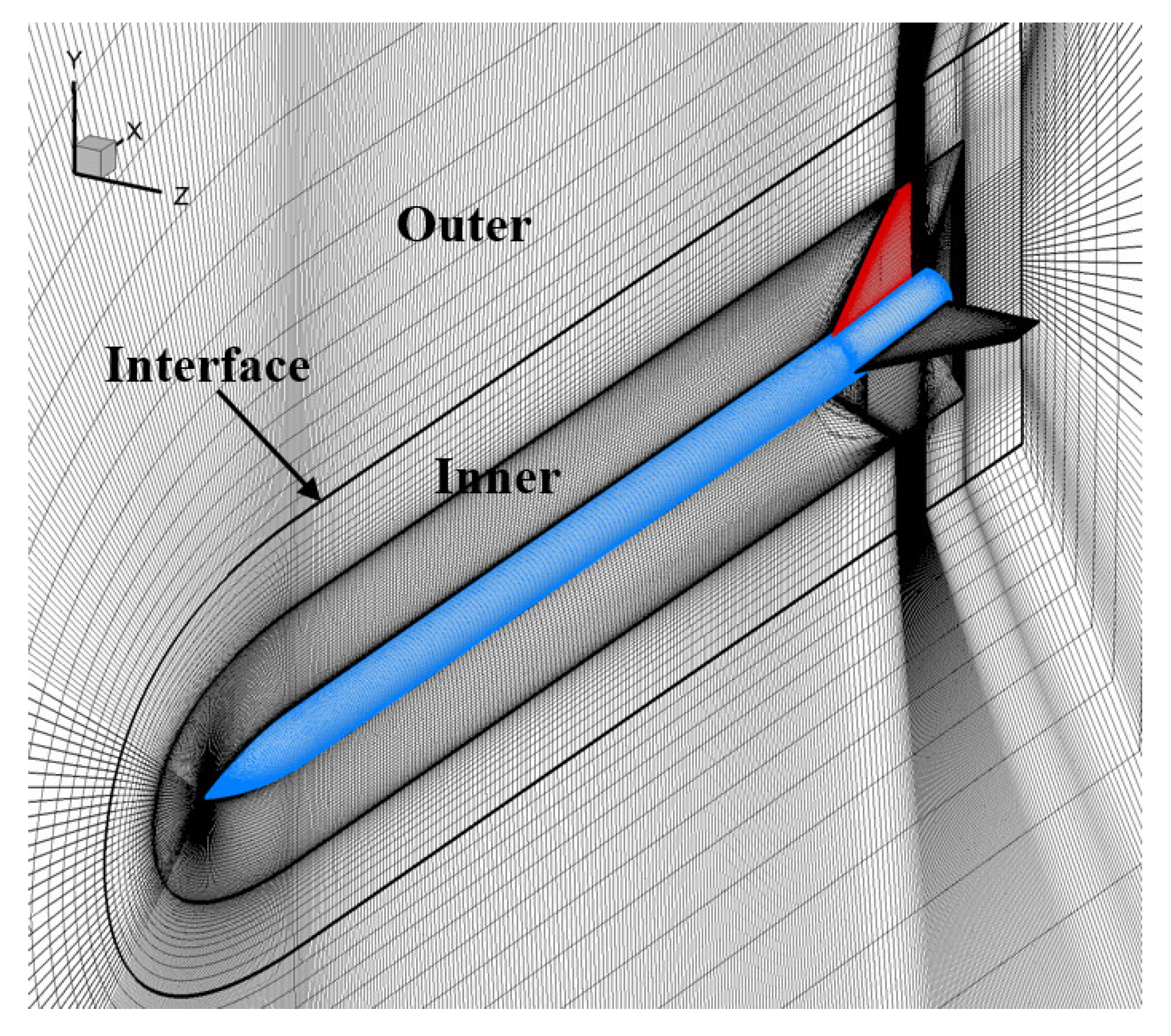
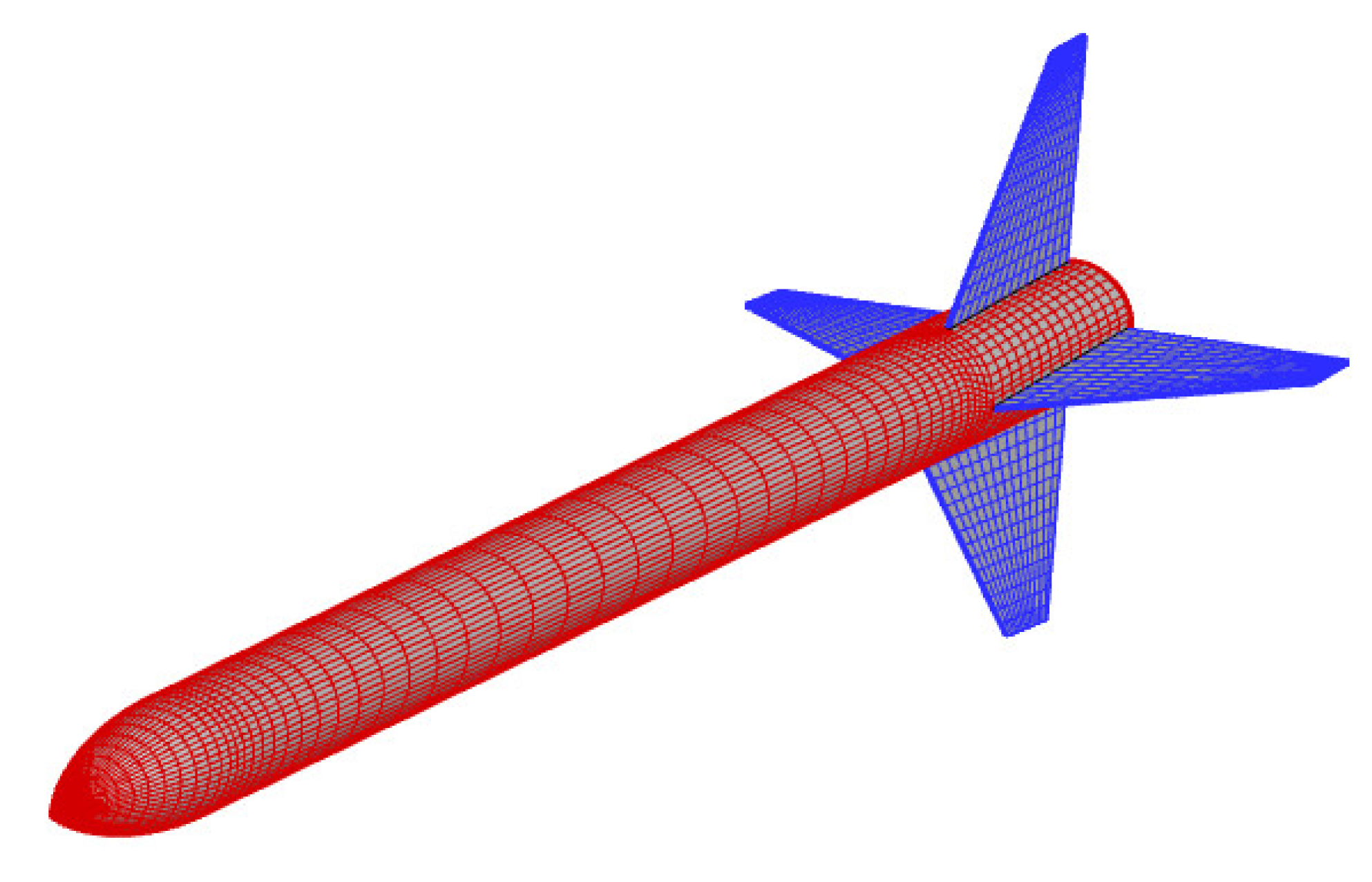
4. Computational Model and Grid
5. Results and Discussion
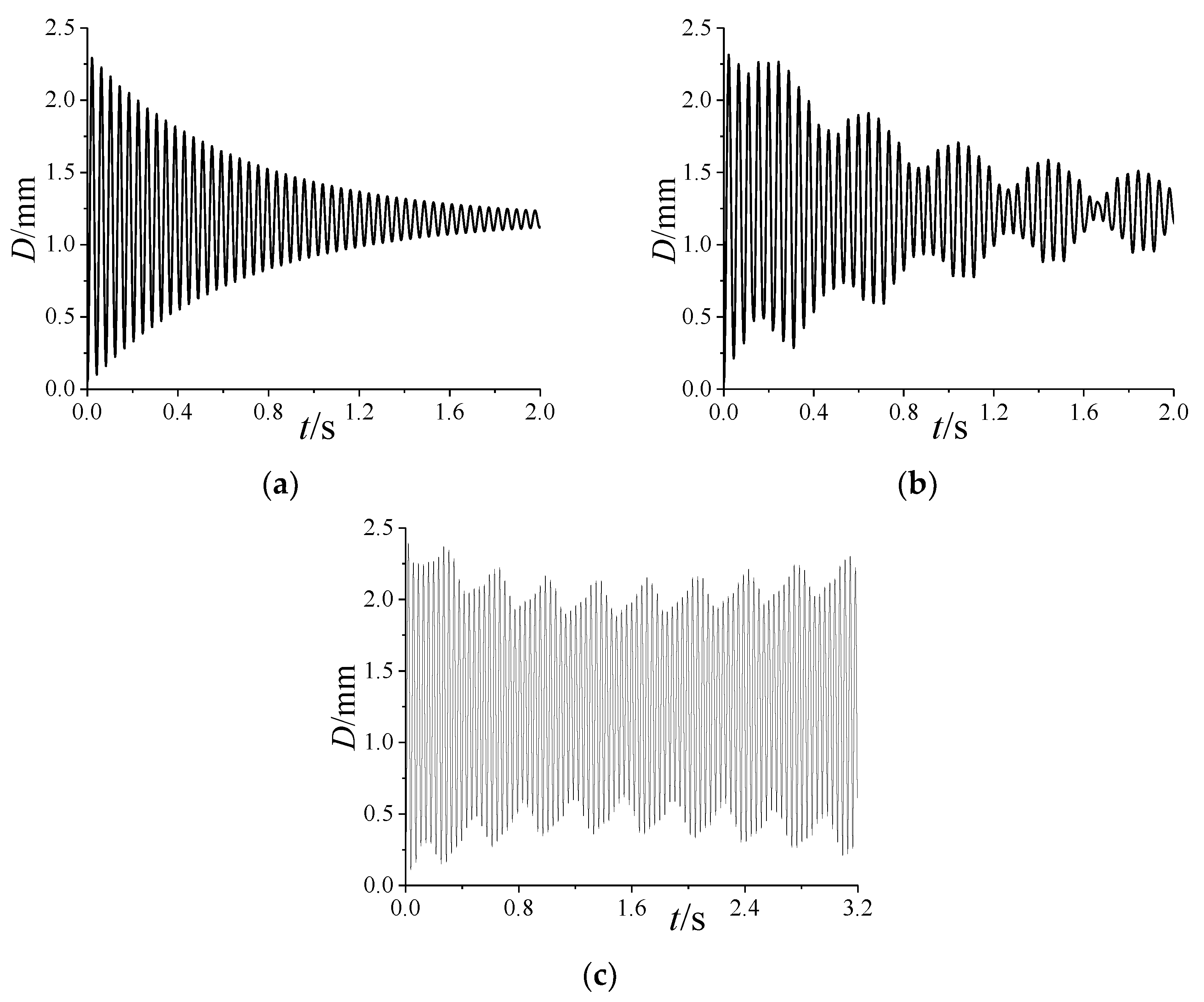
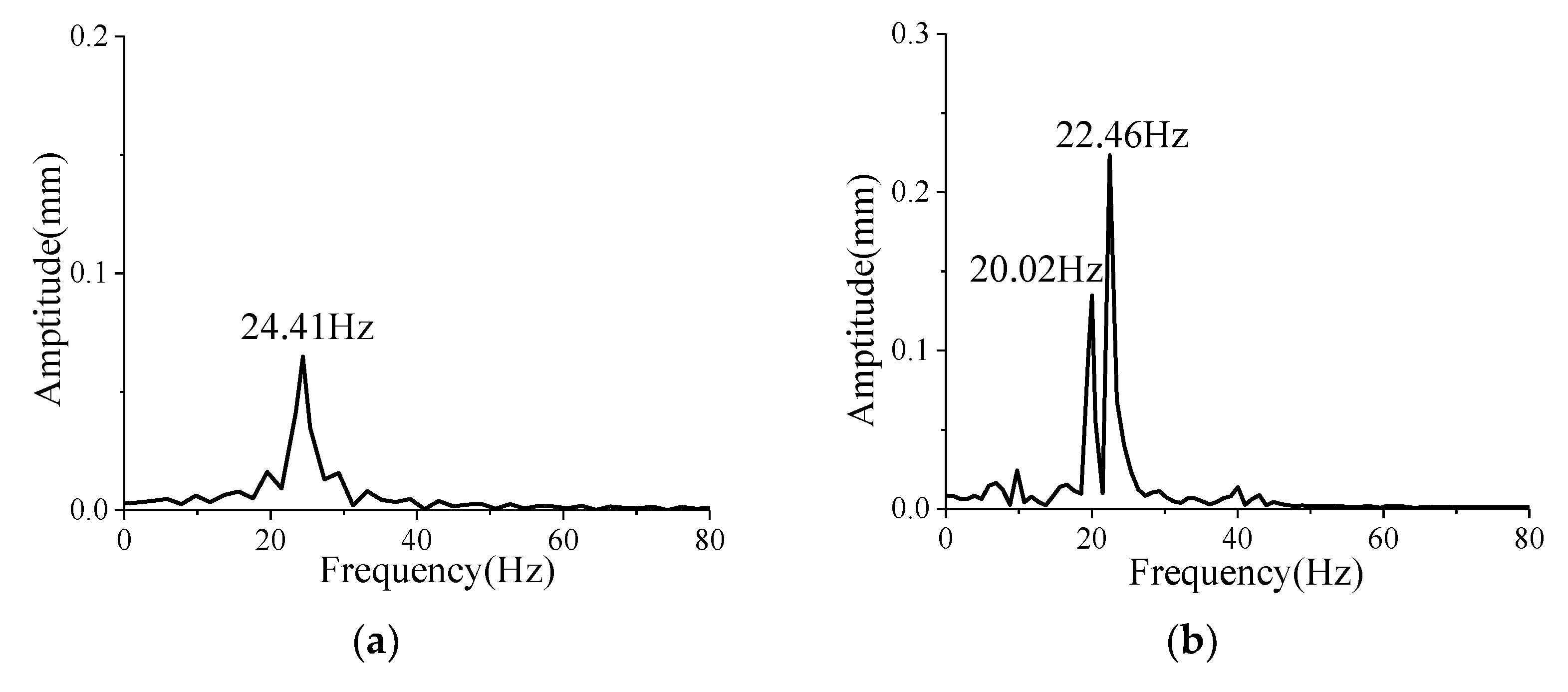
5.1. Effects of Spinning Motion
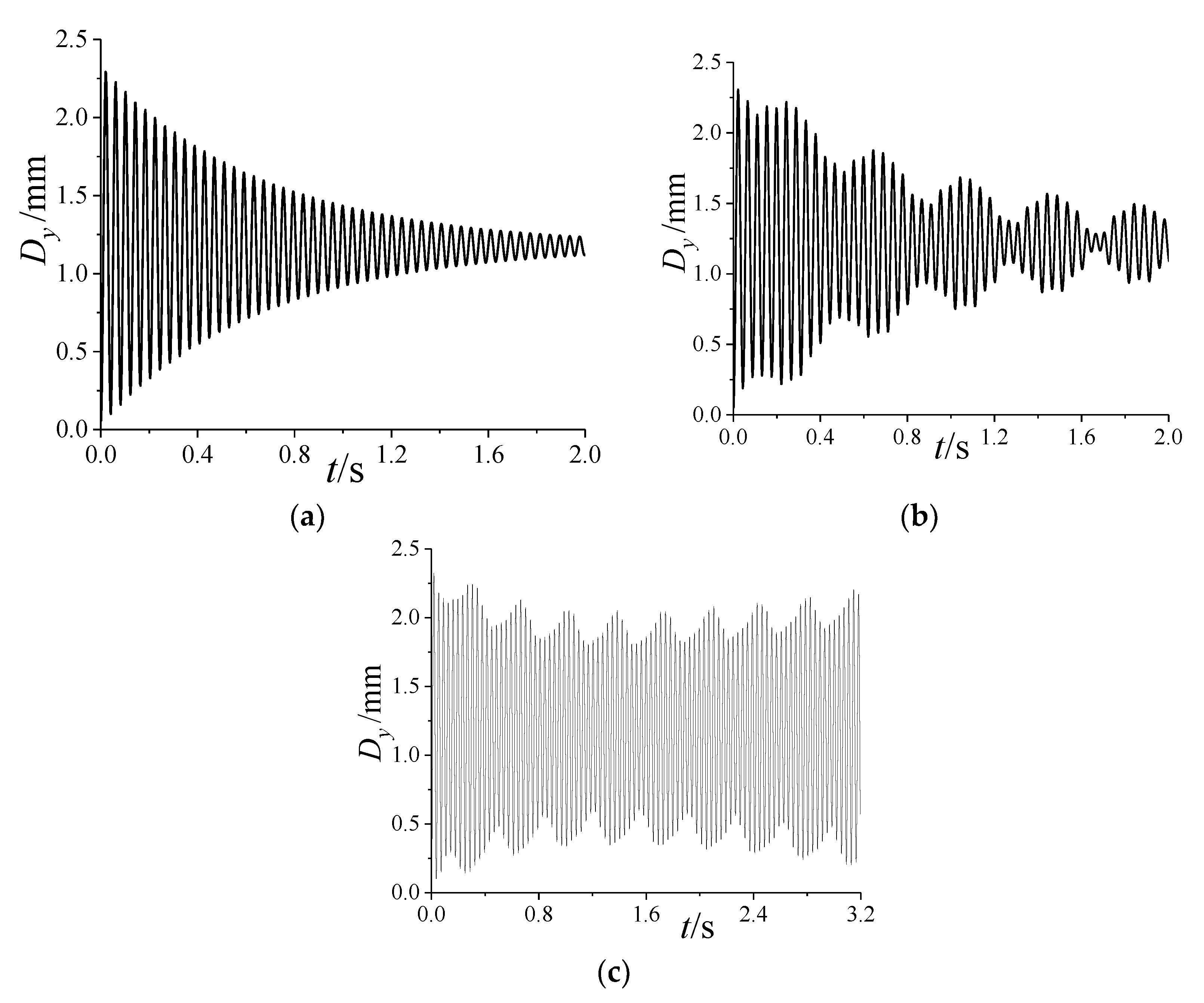
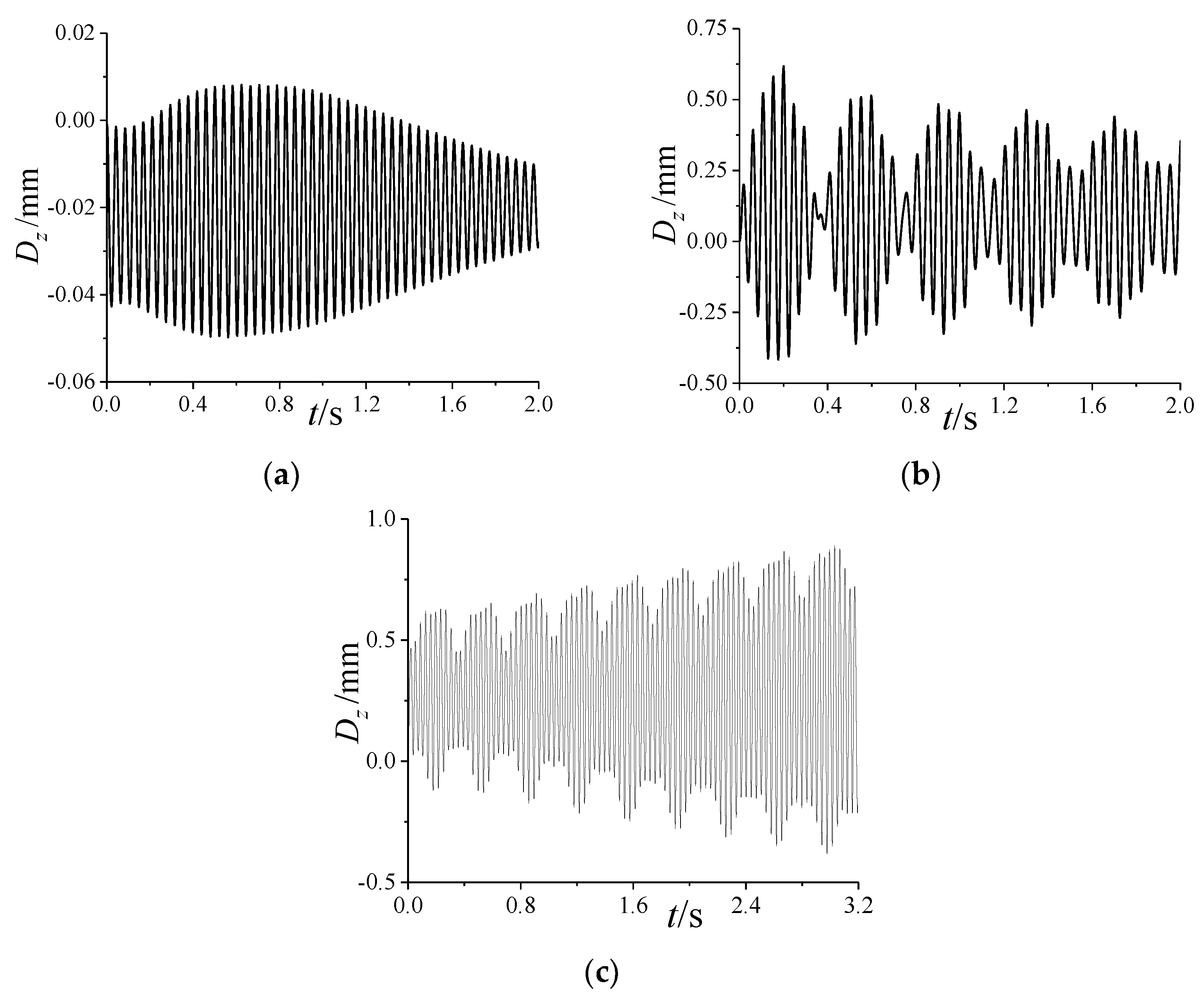
5.1.1. Dynamic Aeroelastic Response
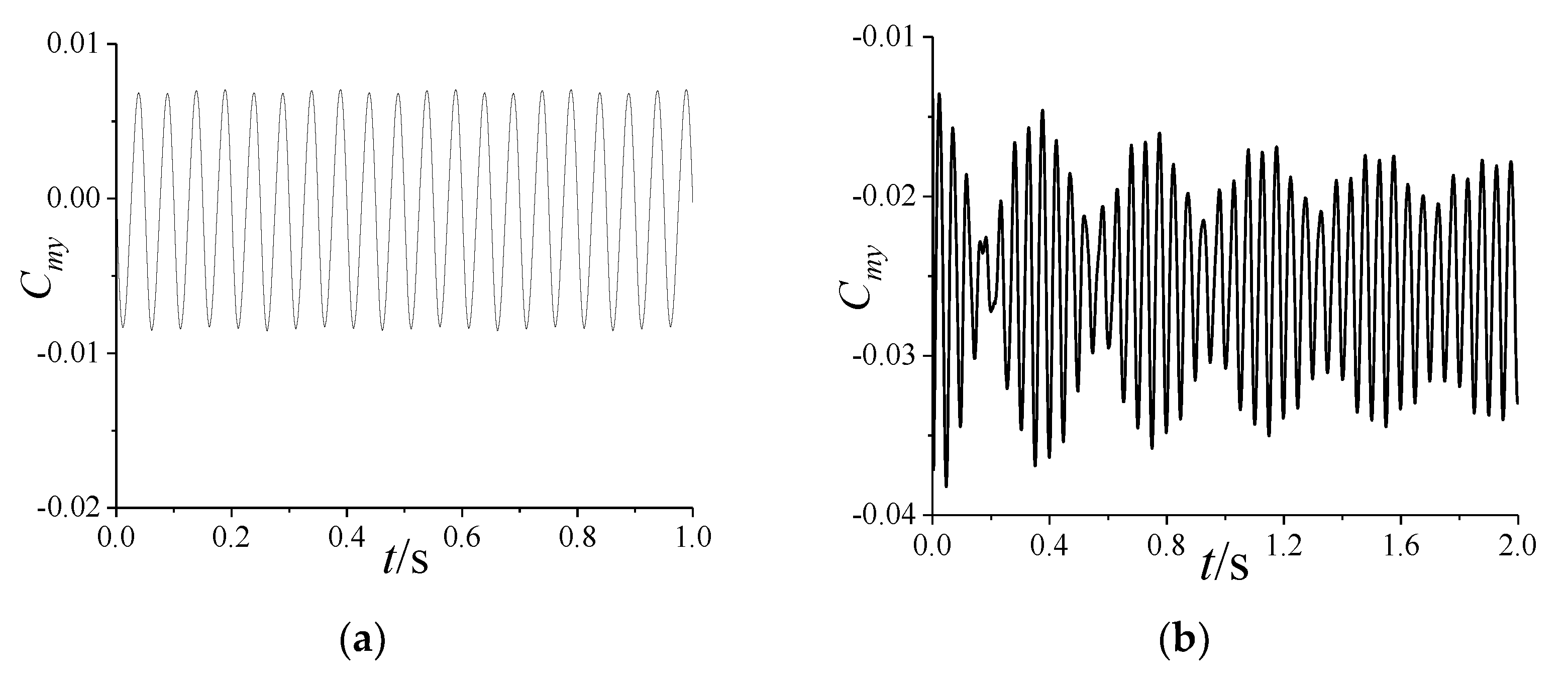
5.1.2. Variation in Aerodynamic Characteristics
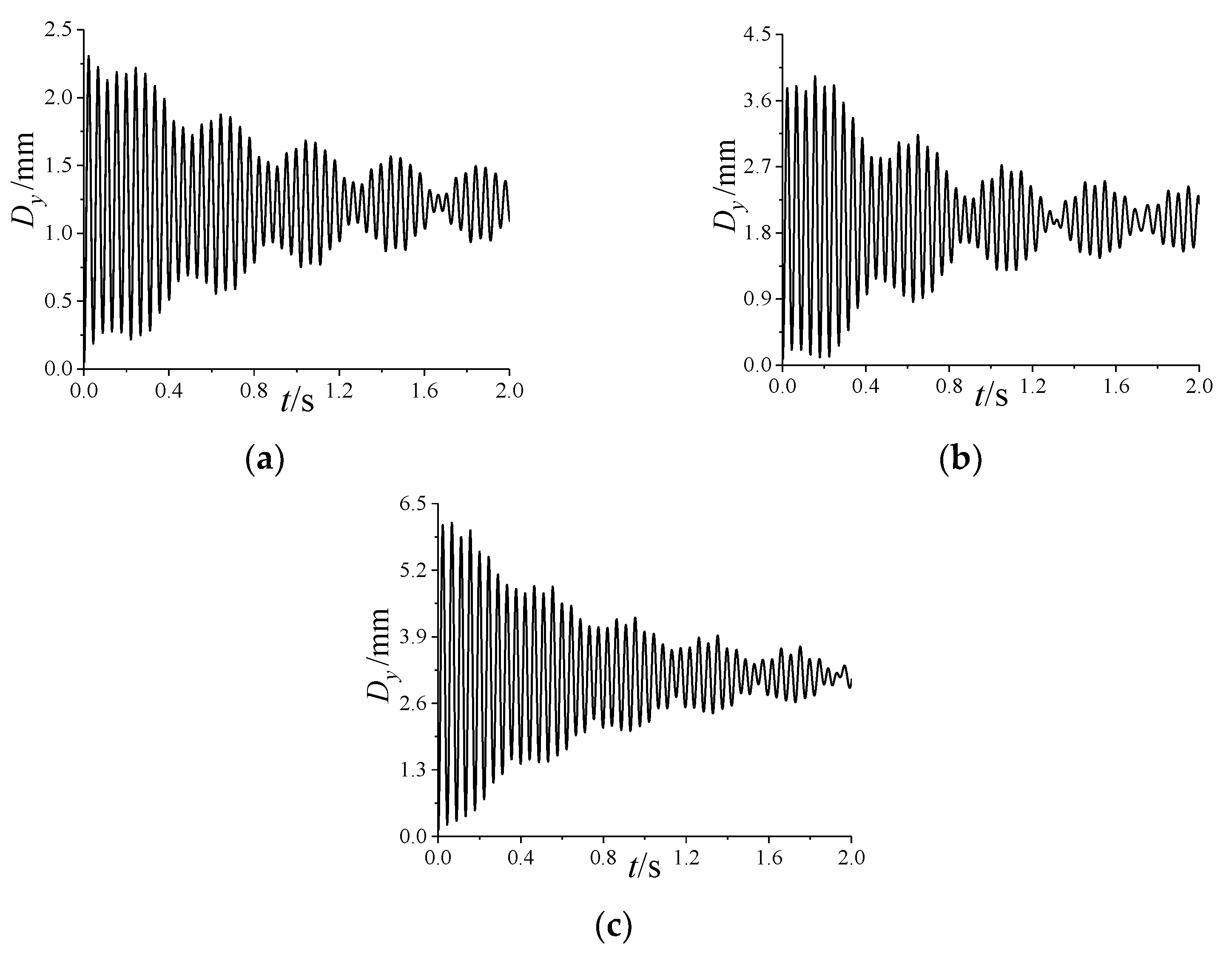
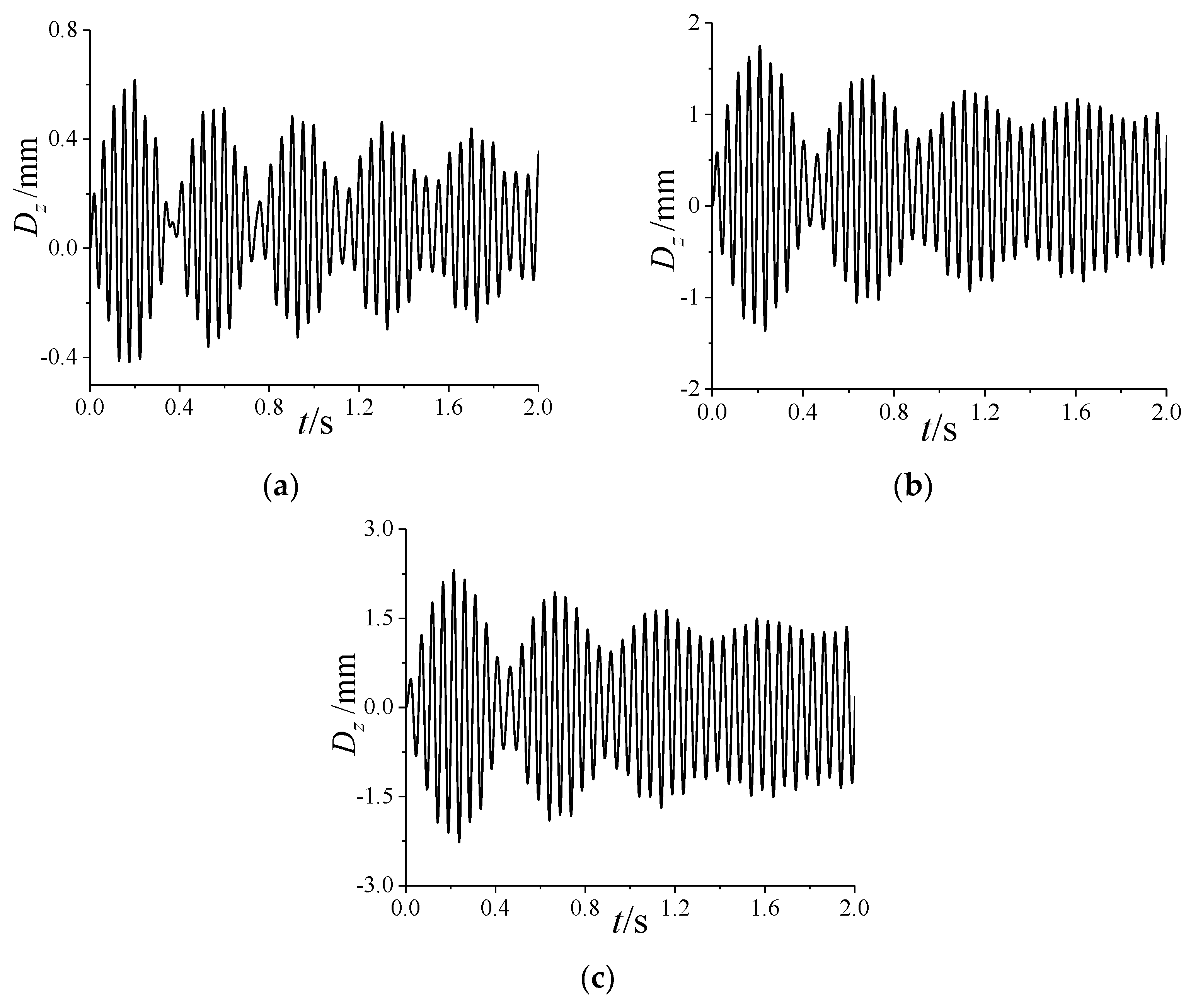
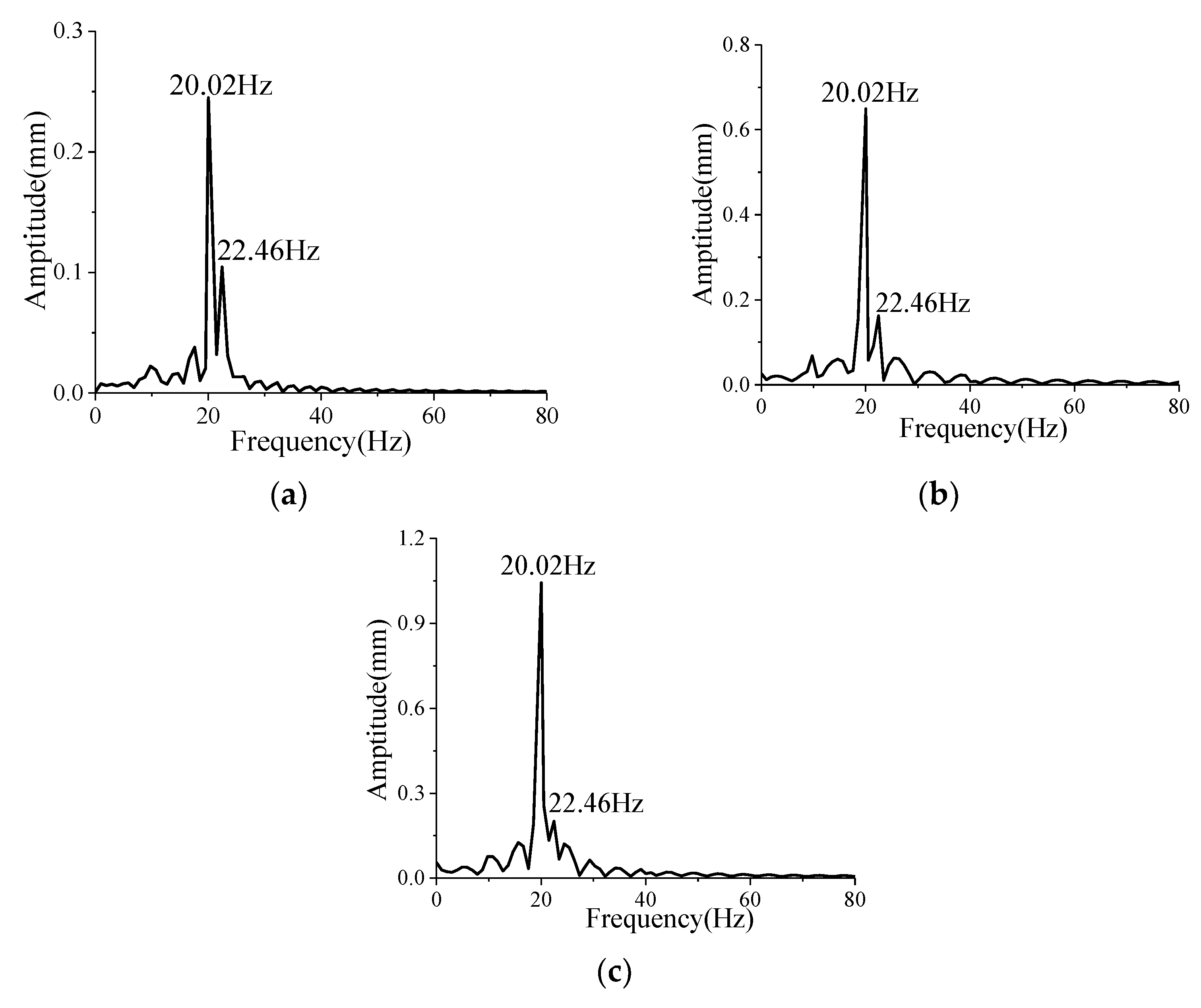
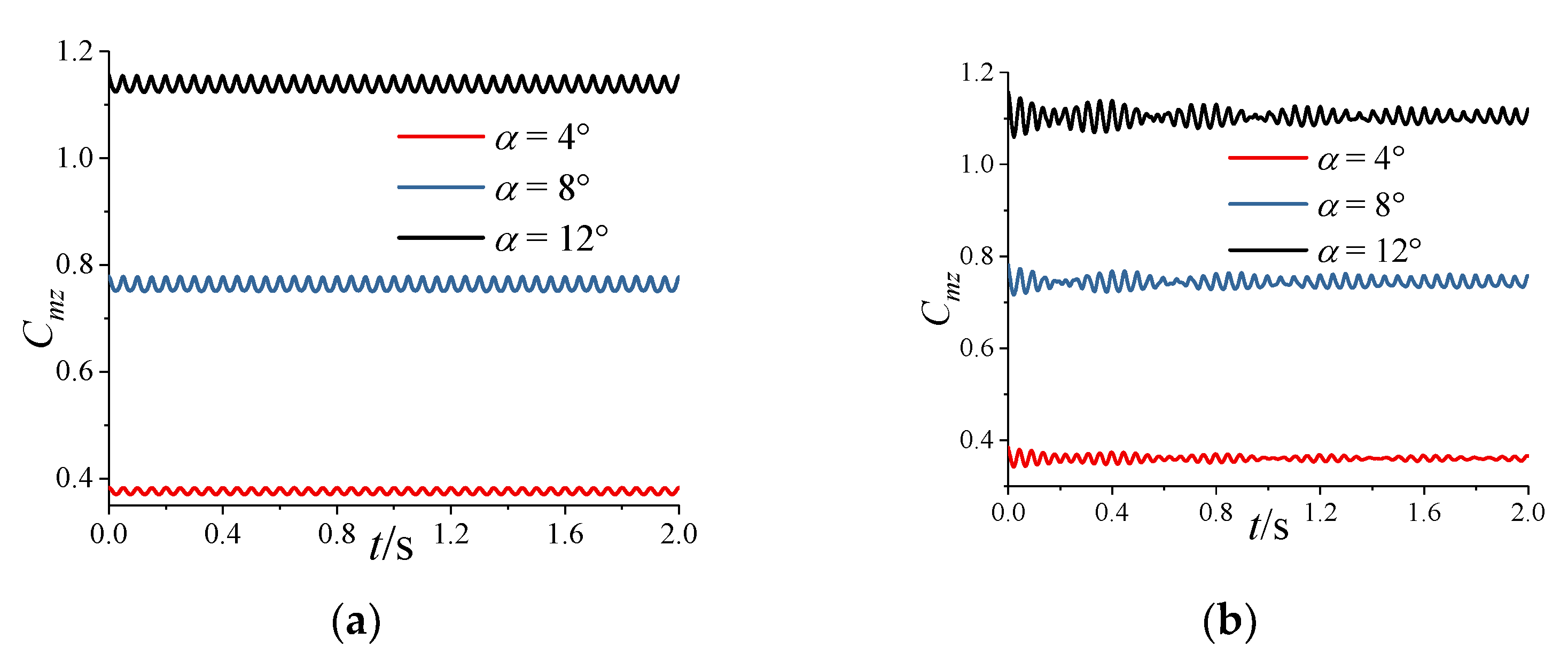
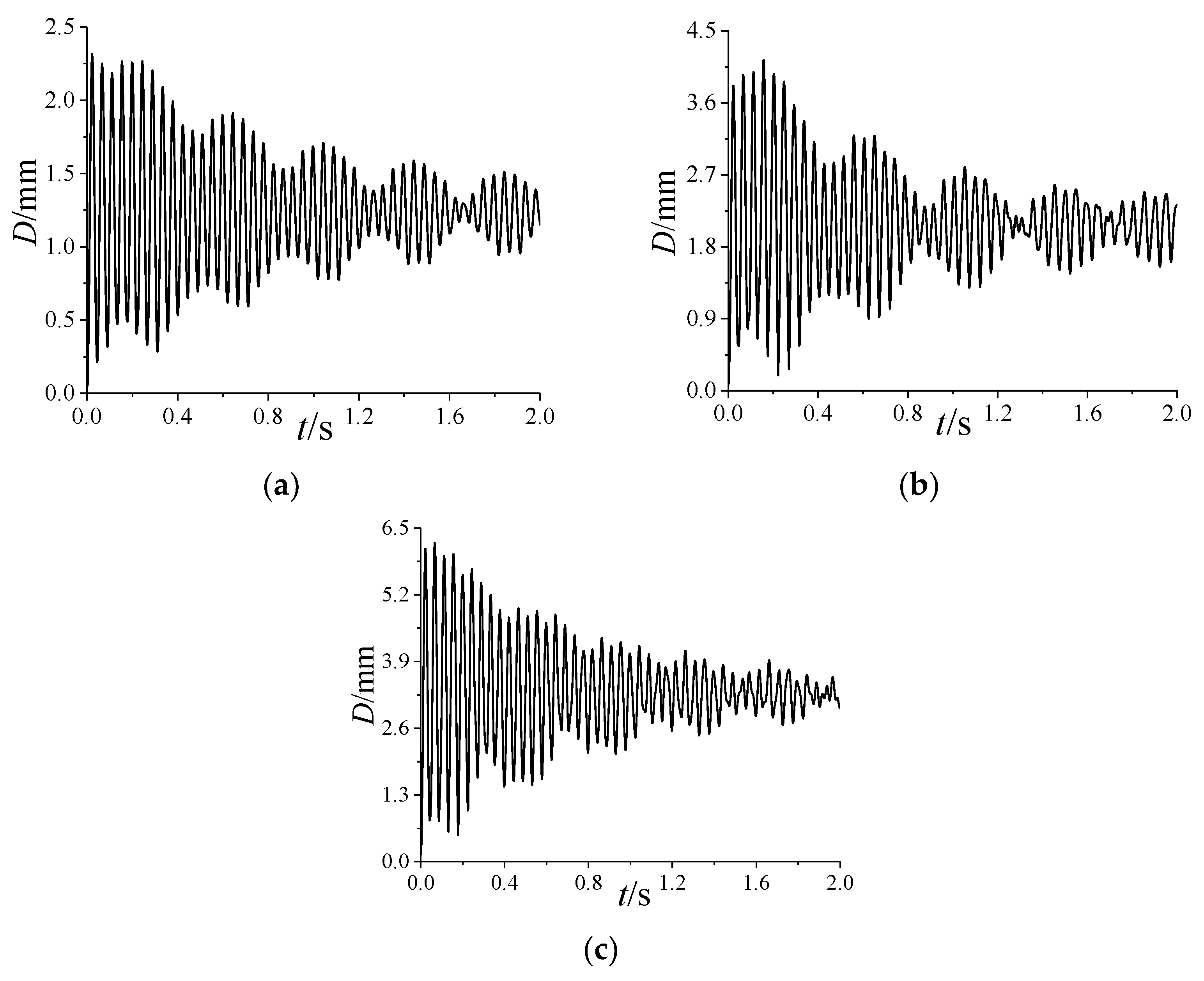
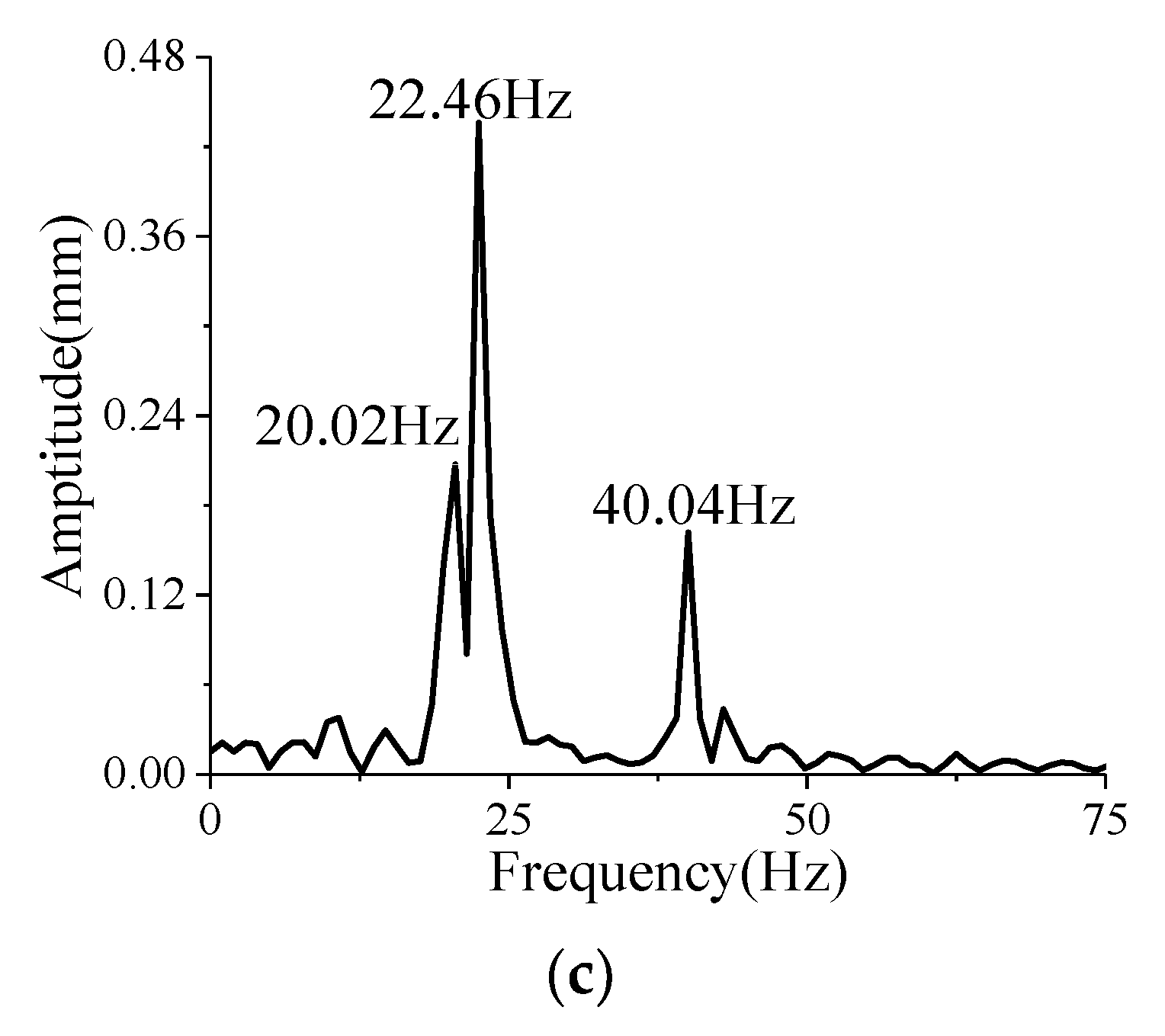
5.2. Effects of Attack Angle
5.2.1. Dynamic Aeroelastic Response
5.2.2. Variation in Aerodynamic Characteristics
6. Conclusions
- The coupling of the first two modes of projectiles induced by the spinning motion can lead to the occurrence of beat vibration, which causes the amplitude of the vibration to fluctuate periodically;
- The increase in the angle of attack reduces the coupling degree of the first two modes, which weakens the beat vibration; the increase in spinning speed causes the difference between the first two natural frequencies to increase, which induces a more obvious beat vibration phenomenon;
- The time-averaged aeroelastic deformation caused by time-averaged aerodynamic loads is beneficial to the convergence of the vibration of the spinning projectile, but the rotation-induced Magnus effect makes the vibration more easily divergent.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A


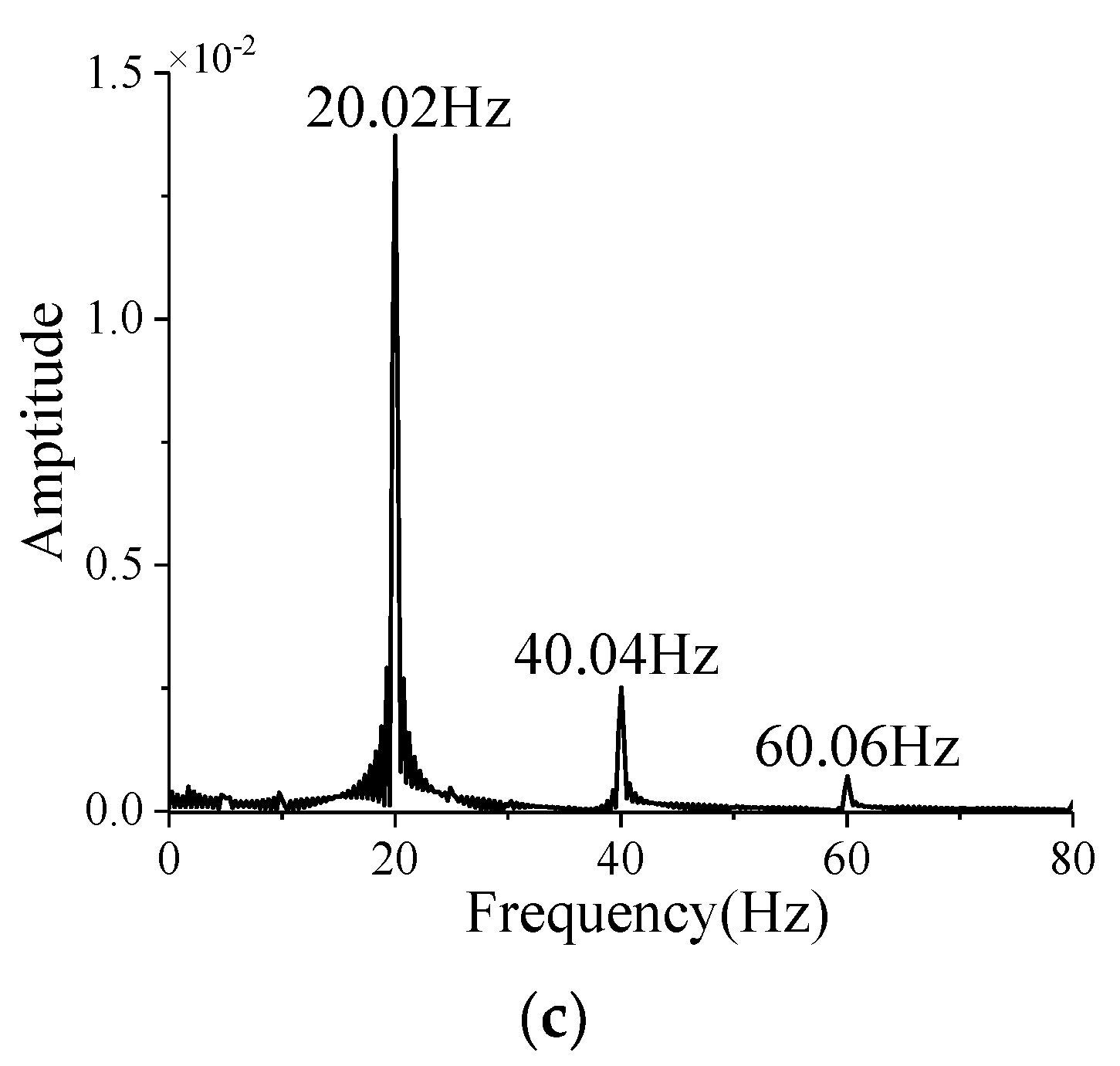
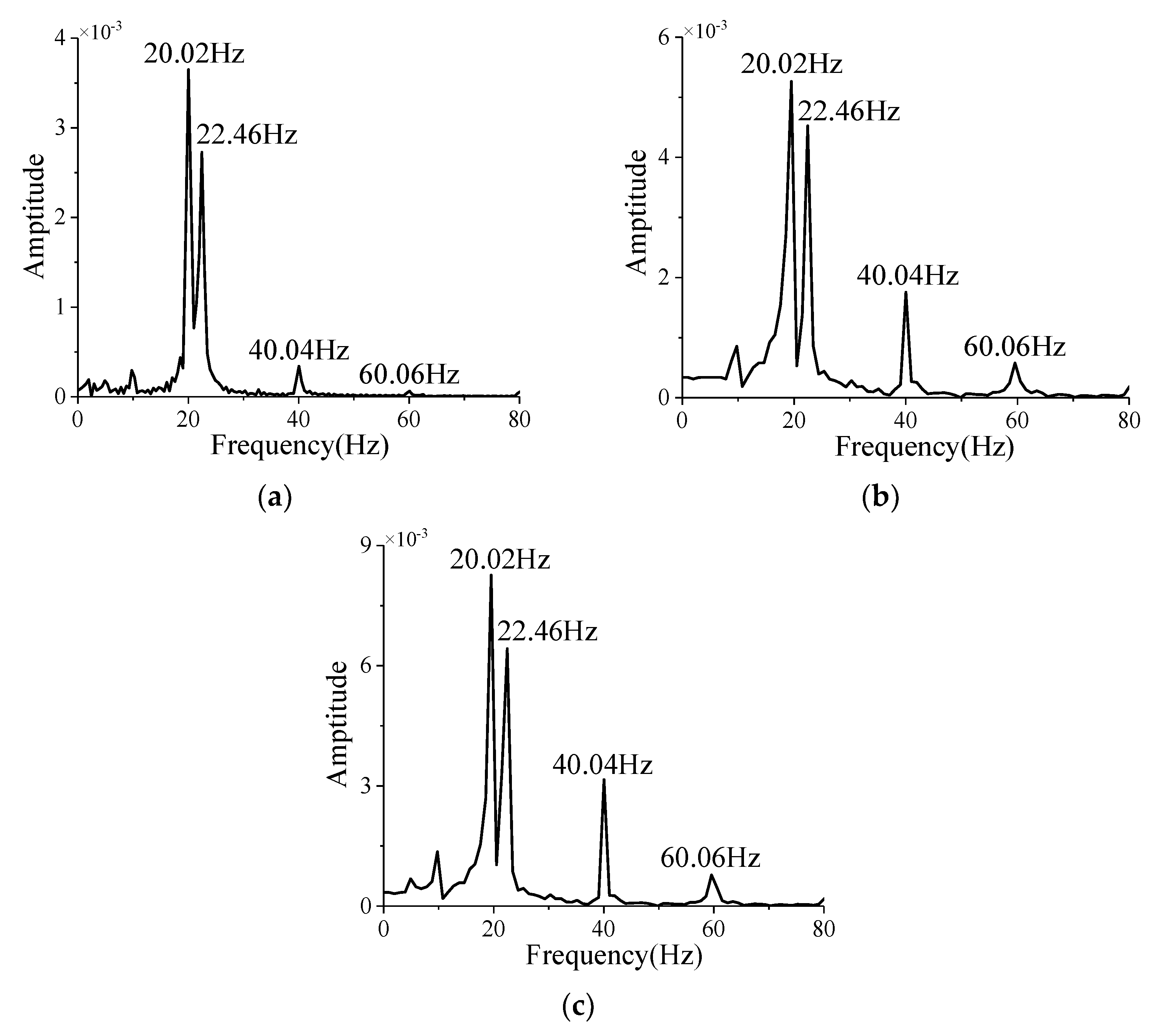
References
- Curry, W.H.; Uselton, J.C. Some comments on the aerodynamic characteristics of the Tomahawk sounding rocket. In Proceedings of the Sounding Rocket Vehicle Technology Specialist Conference, Williamsburg, VA, USA, 27 February–1 March 1967; p. 1312. [Google Scholar]
- Reis, G.E.; Sundberg, W.D. Calculated aeroelastic bending of a sounding rocket based on flight data. J. Spacecr. Rockets 1971, 4, 1489–1494. [Google Scholar] [CrossRef]
- Cochran, J.E., Jr.; Christensen, D.E. Free−flight rocket attitude motion due to transverse vibration. J. Spacecr. Rockets 1980, 17, 425–431. [Google Scholar] [CrossRef]
- Flatus, D.H. Aeroelastic stability of slender, spinning missiles. J. Guid. Control Dyn. 1992, 15, 144–151. [Google Scholar] [CrossRef]
- Waszak, M.R.; Schmidt, D.K. Flight dynamics of aeroelastic vehicles. J. Aircr. 1988, 25, 563–571. [Google Scholar] [CrossRef]
- Buttrill, C.; Arbuckle, P.; Zeiler, T. Nonlinear simulation of a flexible aircraft in maneuvering flight. In Proceedings of the Flight Simulation Technologies Conference, Monterey, CA, USA, 17–19 August 1987; p. 2501. [Google Scholar]
- Waszak, M.R.; Buttrill, C.S.; Schmidt, D.K. Modeling and Model Simplification of Aeroelastic Vehicles: An Overview; NASA TM: Moffett Field, CA, USA, 1992; p. 107691.
- Oliveira, E.J.; Gasbarri, P.; Milagre da Fonseca, I. Flight dynamics numerical computation of a sounding rocket including elastic deformation model. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Dallas, TX, USA, 22–26 June 2015; p. 2710. [Google Scholar]
- Schmidt, D.K.; Raney, D.L. Modeling and simulation of flexible flight vehicles. J. Guid. 2001, 24, 539–546. [Google Scholar] [CrossRef]
- Murphy, C.H.; Mermagen, W.H., Sr. Flight motion of a continuously elastic finned missile. J. Guid. 2003, 26, 89–98. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.W.; Nahon, M.; Sharf, I. Dynamics modeling and simulation of flexible airships. AIAA J. 2009, 47, 592–605. [Google Scholar] [CrossRef] [Green Version]
- Saltari, F.; Riso, C.; Matteis, G.D.; Mastroddi, F. Finite−element−based modeling for flight dynamics and aeroelasticity of flexible aircraft. J. Aircr. 2017, 54, 2350–2366. [Google Scholar] [CrossRef]
- Verhaegen, A.; Żbikowski, R. Aeroservoelastic modelling and control of a slender anti−air missile for active damping of longitudinal bending vibrations. Aerosp. Sci. Technol. 2017, 66, 20–27. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Xu, Y.; Xie, C.C. Review of studies on aeroelasticty of hypersonic vehicles. Astronaut. Sin. 2010, 31, 1–11. [Google Scholar]
- Blades, E.; Newman, J. Aeroelastic effects of spinning missiles. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; p. 2243. [Google Scholar]
- Schütte, A.; Einarsson, G.; Raichle, A.; Schöning, B.; Mönnich, W.; Orlt, M.; Neumann, J.; Arnold, J.; Forkert, T. Numerical simulation of maneuvering aircraft by aerodynamic, flight mechanics and structural mechanics coupling. J. Aircr. 2009, 46, 53–64. [Google Scholar] [CrossRef]
- Kim, J.Y.; Cho, S.I.; Lee, I.; Paek, S.K. Flutter Characteristics of a Rolling Wraparound Fin Projectile Considering Aeroelastic Deflections. J. Spacecr. Rockets 2012, 49, 709–719. [Google Scholar] [CrossRef]
- Li, H.; Ye, Z.Y. Effects of rotational motion on dynamic aeroelasticity of flexible spinning missile with large slenderness ratio. Aerosp. Sci. Technol. 2019, 94, 105384. [Google Scholar] [CrossRef]
- Abbas, L.K.; Chen, D.Y.; Rui, X.T. Numerical calculation of effect of elastic deformation on aerodynamic characteristics of a rocket. Int. J. Aerosp. Eng. 2014, 2014, 478534. [Google Scholar] [CrossRef] [Green Version]
- Li, M.J.; Rui, X.T.; Abbas, L.K. Elastic dynamic effects on the trajectory of a flexible launch vehicle. J. Spacecr. Rockets 2015, 52, 1586–1602. [Google Scholar] [CrossRef]
- Hua, R.H.; Ye, Z.Y.; Wu, J. Effect of elastic deformation on flight dynamics of projectiles with large slenderness ratio. Aerosp. Sci. Technol. 2017, 71, 347–359. [Google Scholar] [CrossRef]
- Yang, L.; Ye, Z.Y.; Wu, J. The influence of the elastic vibration of the carrier to the aerodynamics of the external store in air−launch−to−orbit process. Acta Astronaut. 2016, 128, 440–454. [Google Scholar] [CrossRef] [Green Version]
- Lu, T.Y.; Wu, X.S.; Lei, J.M.; Yin, J.T. Numerical study on the aerodynamic coupling effects of spinning and coning motions for a finned vehicle. Aerosp. Sci. Technol. 2018, 77, 399–408. [Google Scholar] [CrossRef]
- Hua, R.; Yuan, X.; Tang, Z.; Ye, Z. Study on flight dynamics of flexible projectiles based on closed−loop feedback control. Aerosp. Sci. Technol. 2019, 90, 327–341. [Google Scholar] [CrossRef]
- Yin, J.T.; Lei, J.M.; Wu, X.S.; Lu, T.Y. Effect of elastic deformation on the aerodynamic characteristics of a high−speed spinning projectile. Aerosp. Sci. Technol. 2015, 45, 254–264. [Google Scholar] [CrossRef]
- Yin, J.; Lei, J.; Wu, X.; Lu, T. Aerodynamic characteristics of a spinning projectile with elastic deformation. Aerosp. Sci. Technol. 2016, 51, 181–191. [Google Scholar] [CrossRef]
- Kamakoti, R.; Shyy, W. Fluid–structure interaction for aeroelastic applications. Prog. Aerosp. Sci. 2004, 40, 535–558. [Google Scholar] [CrossRef]
- Pandya, S.A.; Venkateswaran, S.; Pulliam, T.H. Implementation of preconditioned dual−Time procedures in overflow. In Proceedings of the 41st AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003; p. 72. [Google Scholar]
- Vatsa, V.; Turkel, E. Choice of variables and preconditioning for time dependent problems. In Proceedings of the 16th AIAA Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003; p. 3692. [Google Scholar]
- Menter, F.R. Two−equation eddy−viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Nelson, H.D.; McVaugh, J.M. The dynamics of rotor−bearing systems using finite elements. J. Eng. Ind. 1976, 98, 593–600. [Google Scholar] [CrossRef]
- Geradin, M.; Kill, N. A new approach to finite element modelling of flexible rotors. Eng. Comput. 1984, 1, 52–64. [Google Scholar] [CrossRef]
- Hall, J.F. Problems encountered from the use (or misuse) of Rayleigh damping. Earthq. Eng. Struct. Dyn. 2006, 35, 525–545. [Google Scholar] [CrossRef]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- De Boer, A.; Van der Schoot, M.S.; Bijl, H. Mesh deformation based on radial basis function interpolation. Comput. Struct. 2007, 85, 784–795. [Google Scholar] [CrossRef]
- Niu, J.P.; Lei, J.M.; He, J.D. Radial basis function mesh deformation based on dynamic control points. Aerosp. Sci. Technol. 2017, 64, 122–132. [Google Scholar] [CrossRef]
- Löhner, R. Robust, vectorized search algorithms for interpolation on unstructured grids. J. Comput. Phys. 1995, 118, 380–387. [Google Scholar] [CrossRef]
- Smith, M.J.; Hodges, D.H.; Cesnik, C.E.S. Evaluation of computational algorithms suitable for fluid−structure interactions. J. Aircr. 2000, 37, 282–294. [Google Scholar] [CrossRef]
- Yates, E.C., Jr. AGARD standard aeroelastic configurations for dynamic response. Candidate configuration I.−wing 445.6; NASA TM: Moffett Field, CA, USA, 1987; p. 100492.
- Li, H.K.; Zhong, Y.W.; Wei, B.W.; Du, L.; Wang, G. Beat vibration mechanism of a sluice pier under high−speed flood discharge excitation. J. Low Freq. Noise Vib. Act. Control 2020, 39, 28–43. [Google Scholar] [CrossRef]
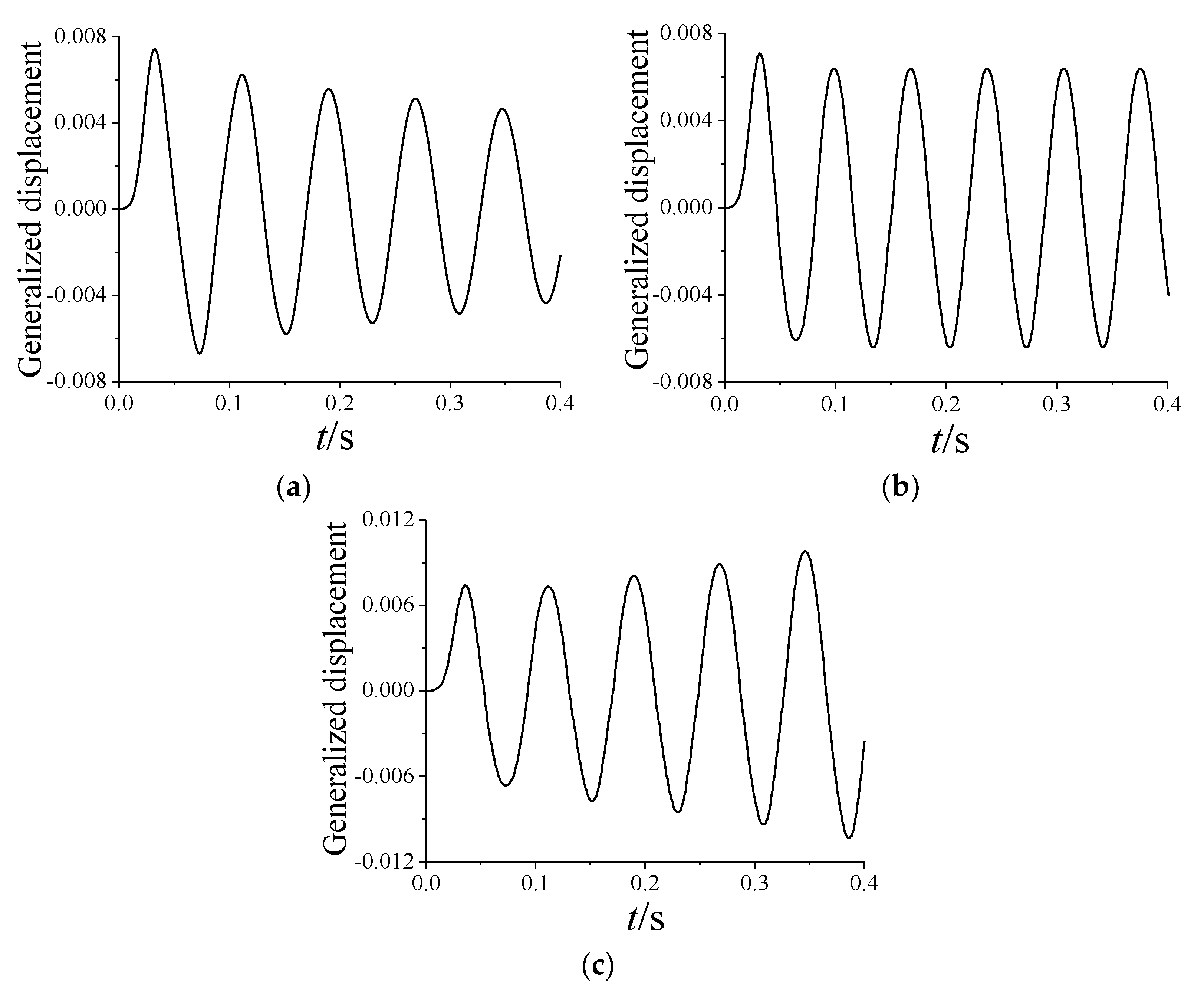


| Mode | First | Second | Third | Fourth | Fifth | Sixth |
|---|---|---|---|---|---|---|
| Frequency (Hz) | 21.81 | 22.22 | 122.59 | 122.77 | 314.06 | 314.10 |
| Damping Ratio | 0.011 | 0.012 | 0.062 | 0.062 | 0.141 | 0.141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Lei, J.; Yu, Y.; Yin, J. Aeroelastic Response of Spinning Projectiles with Large Slenderness Ratio at Supersonic Speed. Aerospace 2023, 10, 646. https://doi.org/10.3390/aerospace10070646
Liu Q, Lei J, Yu Y, Yin J. Aeroelastic Response of Spinning Projectiles with Large Slenderness Ratio at Supersonic Speed. Aerospace. 2023; 10(7):646. https://doi.org/10.3390/aerospace10070646
Chicago/Turabian StyleLiu, Qi, Juanmian Lei, Yong Yu, and Jintao Yin. 2023. "Aeroelastic Response of Spinning Projectiles with Large Slenderness Ratio at Supersonic Speed" Aerospace 10, no. 7: 646. https://doi.org/10.3390/aerospace10070646
APA StyleLiu, Q., Lei, J., Yu, Y., & Yin, J. (2023). Aeroelastic Response of Spinning Projectiles with Large Slenderness Ratio at Supersonic Speed. Aerospace, 10(7), 646. https://doi.org/10.3390/aerospace10070646





