Cooperation of Thin-Airfoil Theory and Deep Learning for a Compact Airfoil Shape Parameterization
Abstract
:1. Introduction
2. Methodology
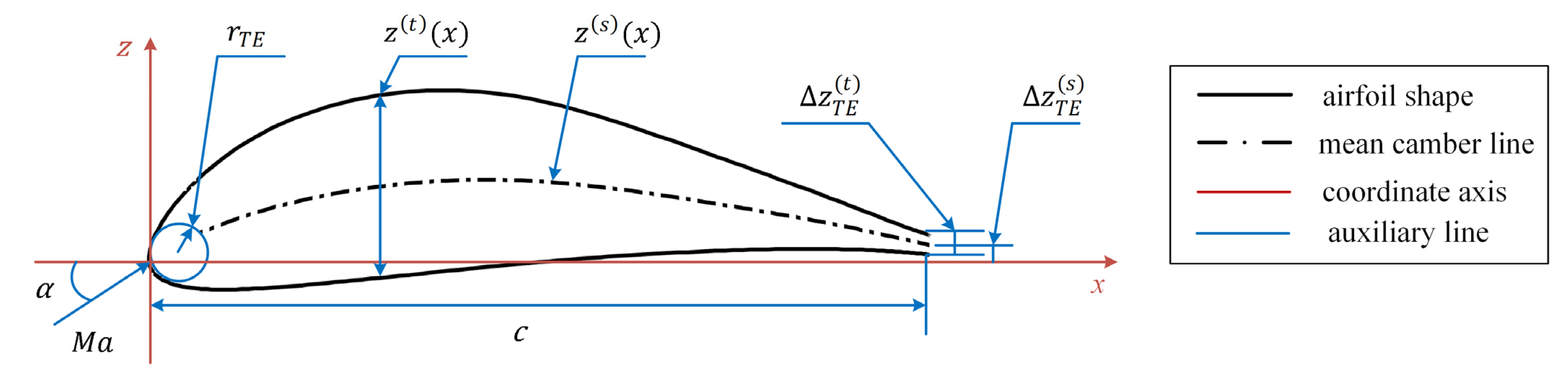
2.1. Problem Definition
2.2. Representation of Mean Camber Line
2.3. Representation of Airfoil Thickness Distribution
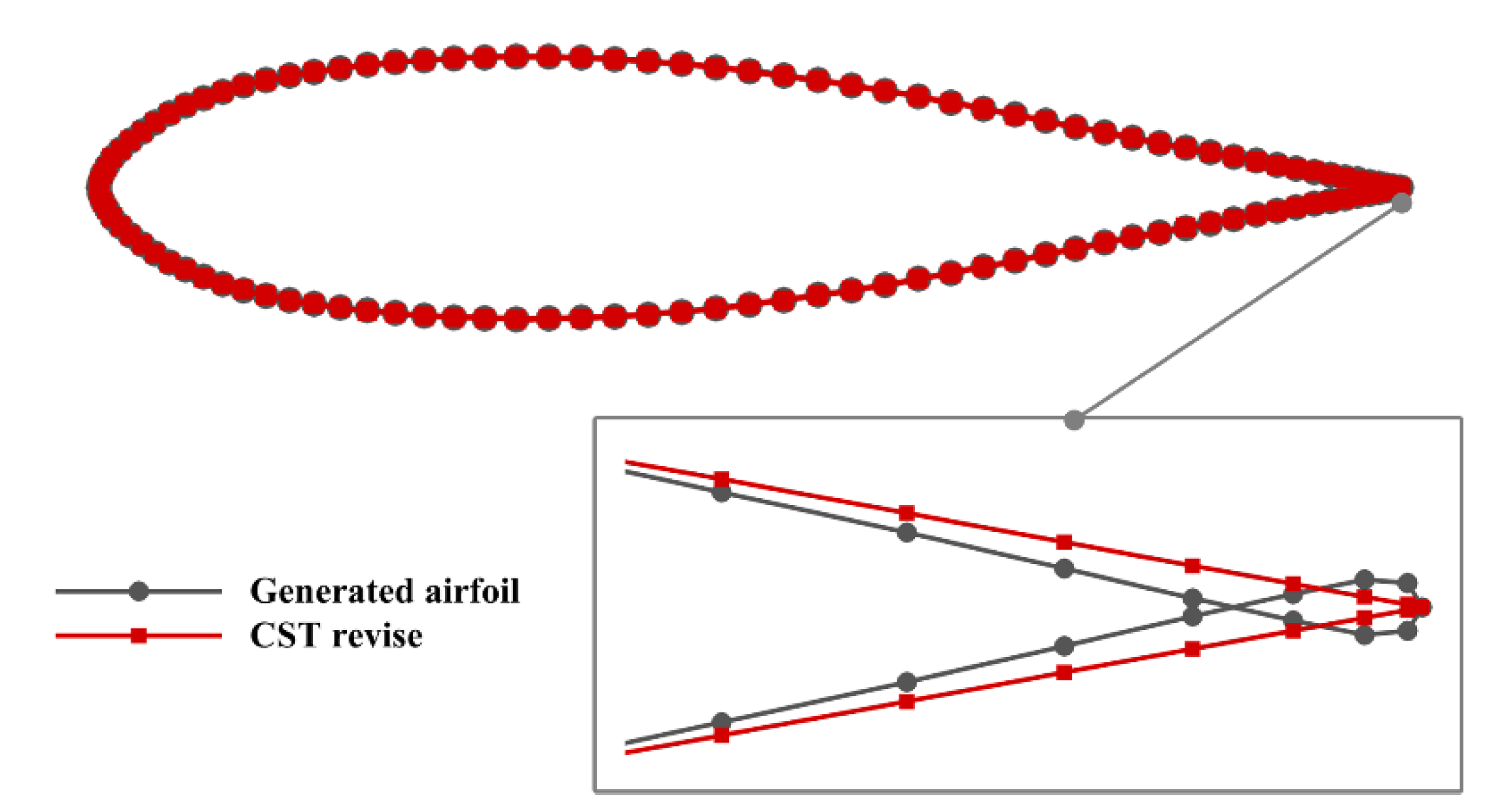
2.3.1. CST Method
2.3.2. SVD Method
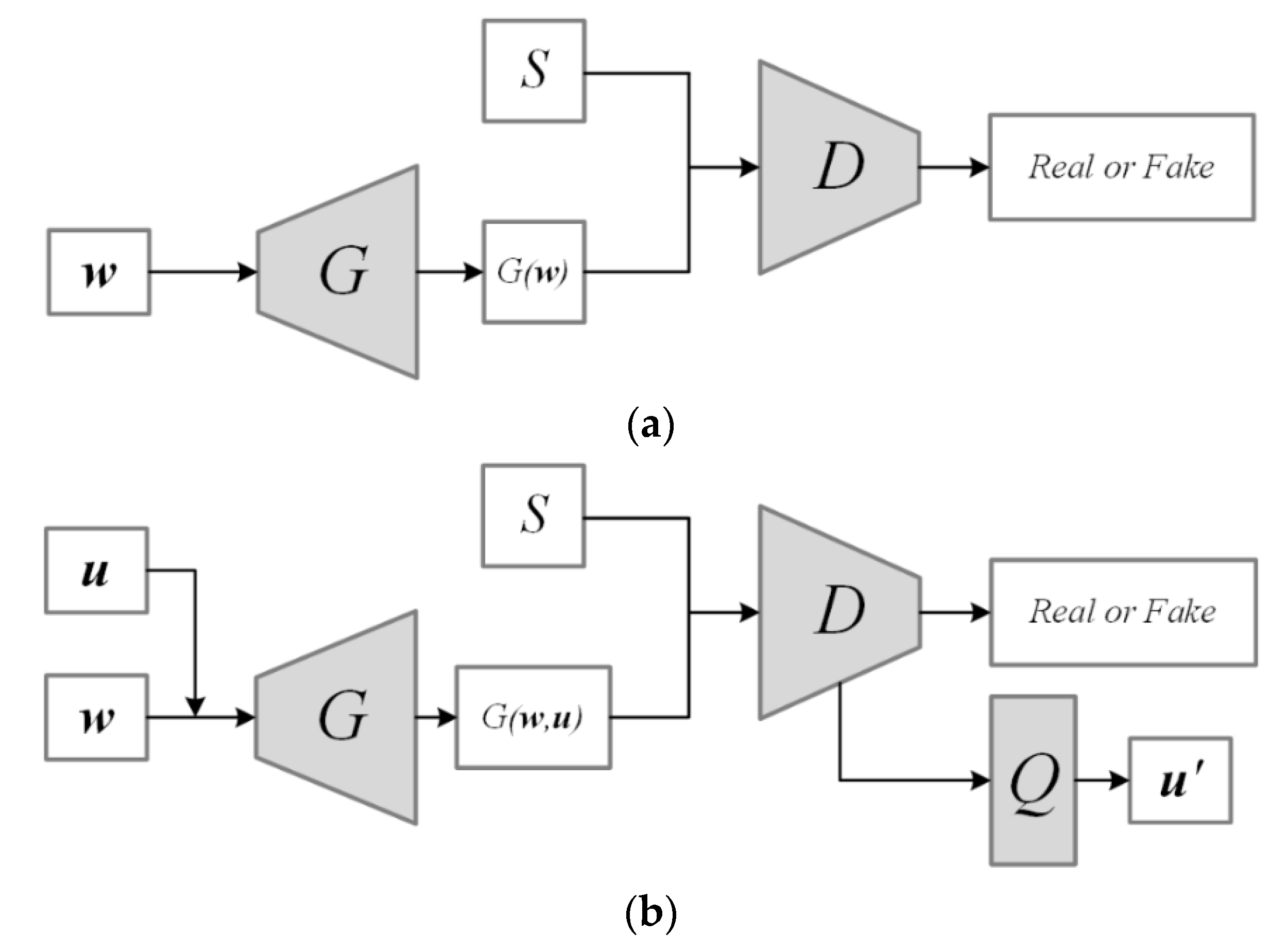
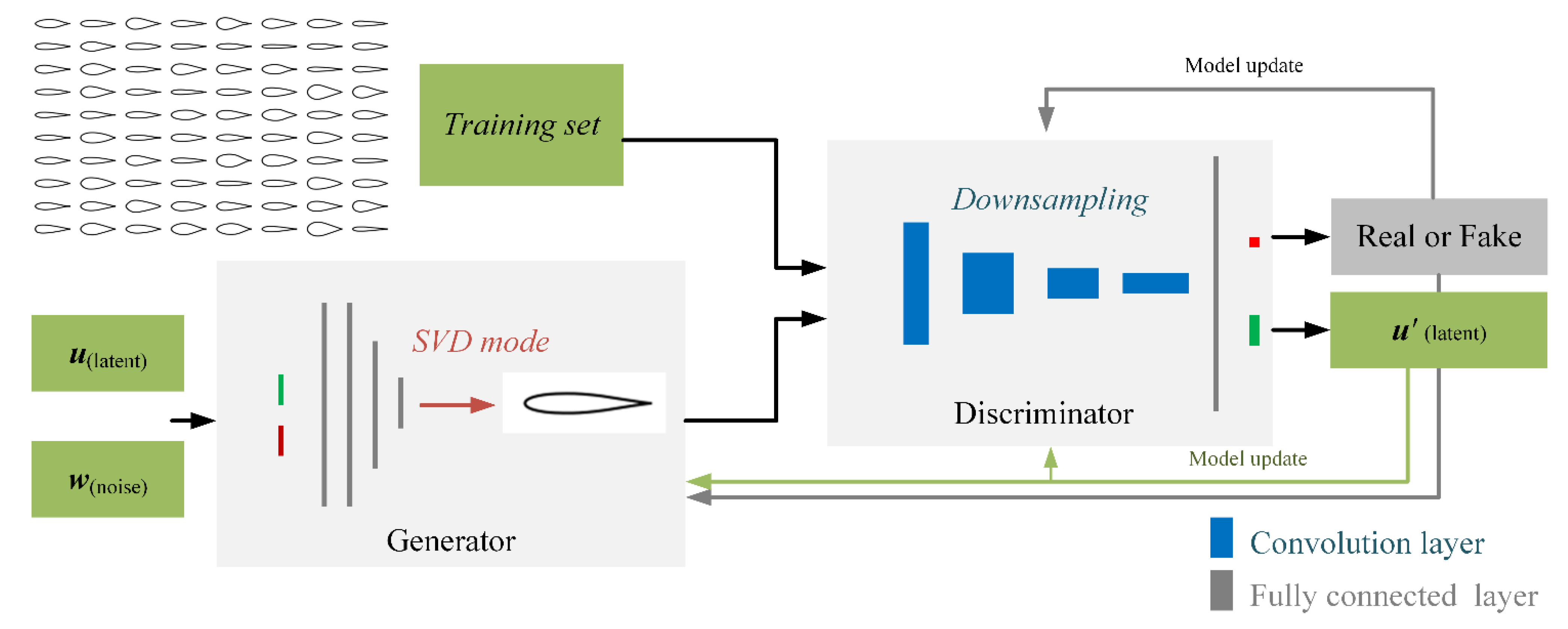
2.3.3. Deep Learning Method
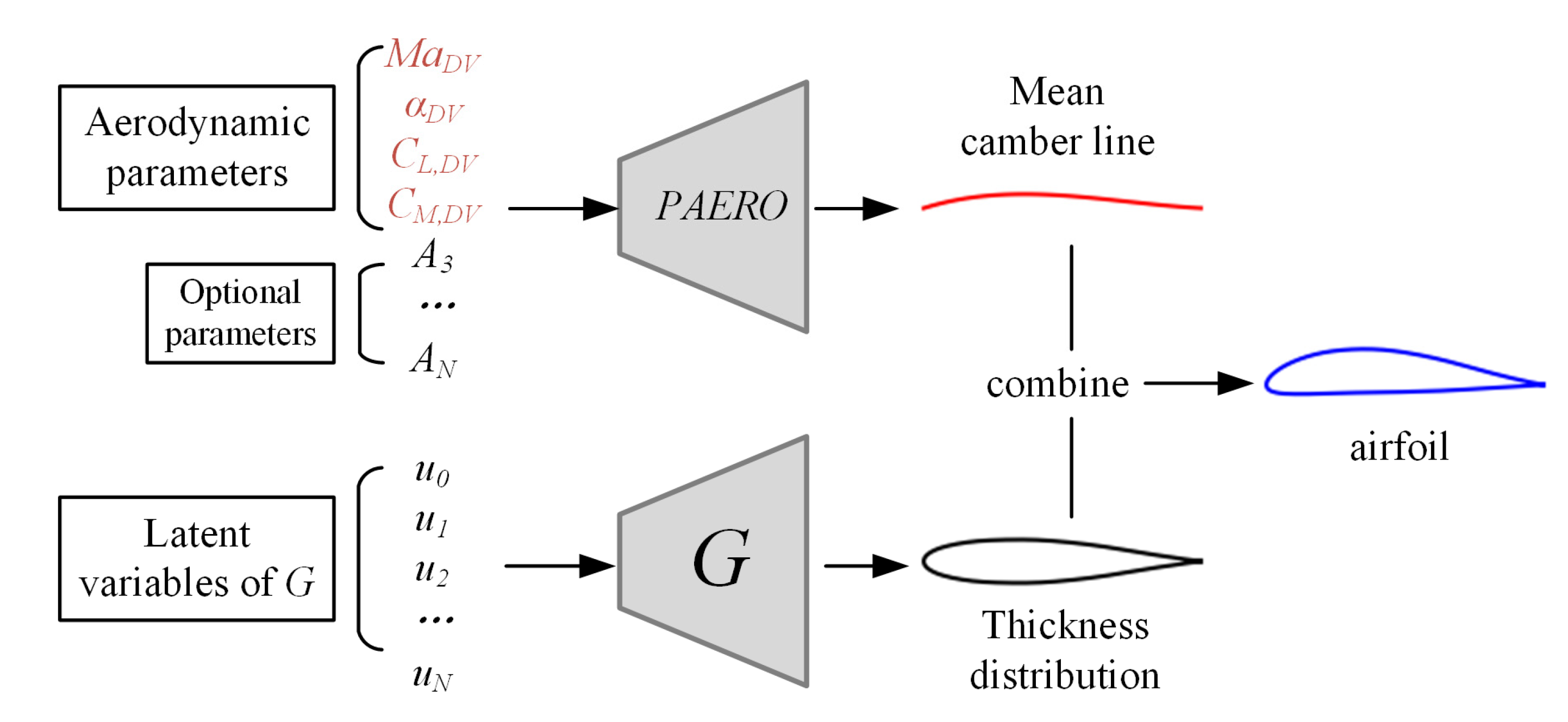
2.4. Summary
3. Results and Discussion
3.1. Model Training and Airfoil Thickness Synthesis
3.1.1. Data Preparation
- (1)
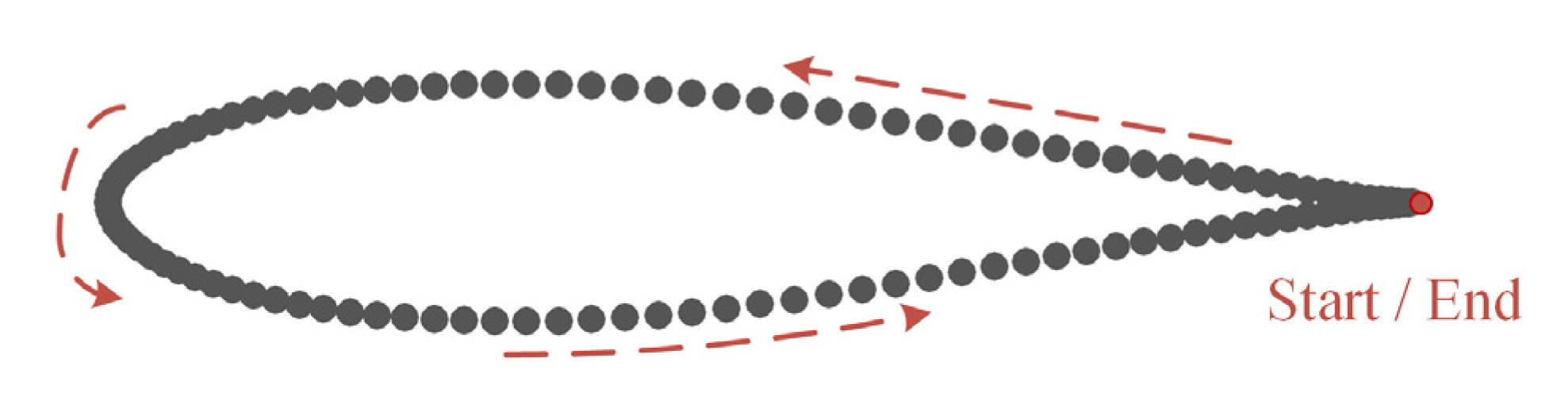
- Remove the airfoils with incomplete data, and order the airfoil coordinates in a counterclockwise direction starting from the trailing edge, as shown in Figure 5.
- (2)
- Convert a blunt trailing edge into a sharp trailing edge, adjust the angle of attack to 0 degree, and synchronize the x coordinates.
- (3)
- Remove the airfoils with more than one local maximum thickness.
- (4)
- Remove the airfoil mean cambers.
3.1.2. Model Training
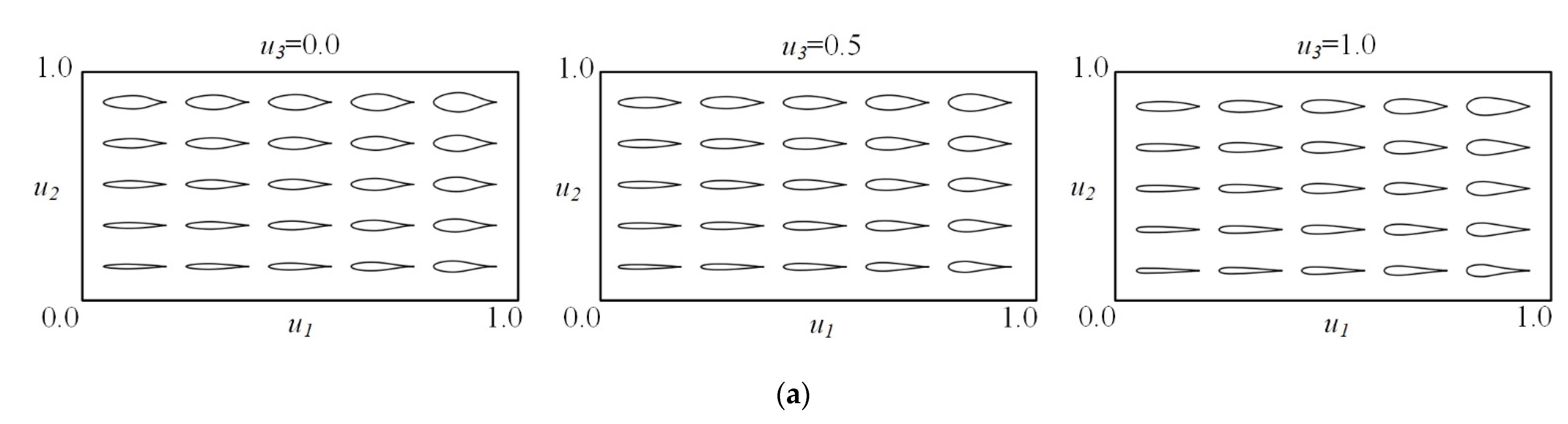
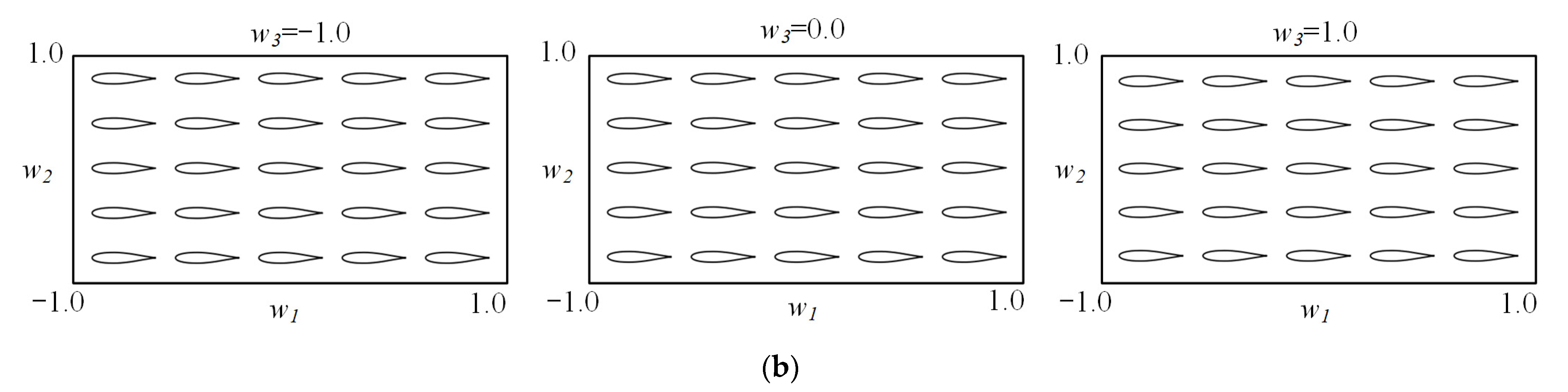
3.1.3. Symmetrical Airfoil Synthesis
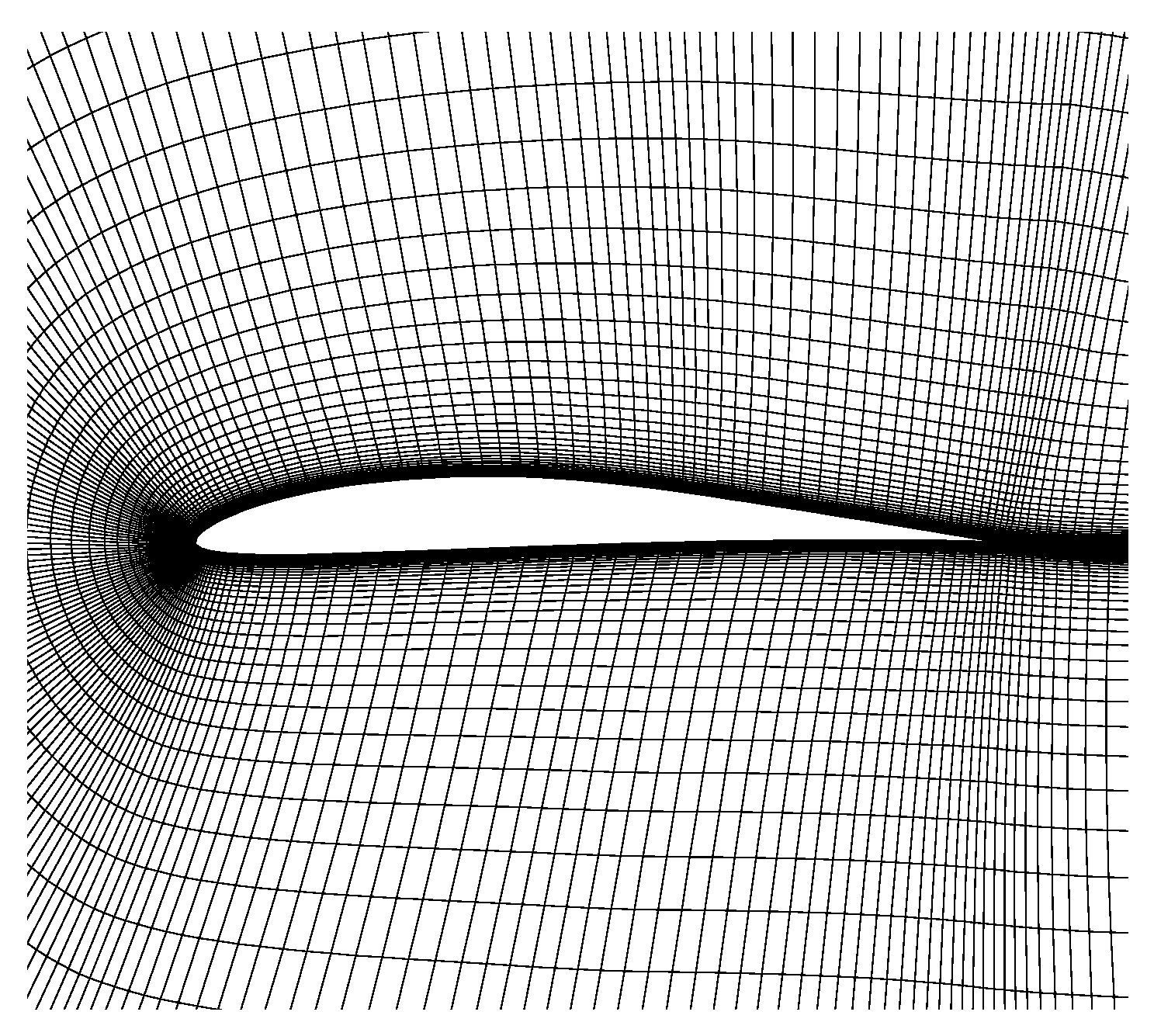
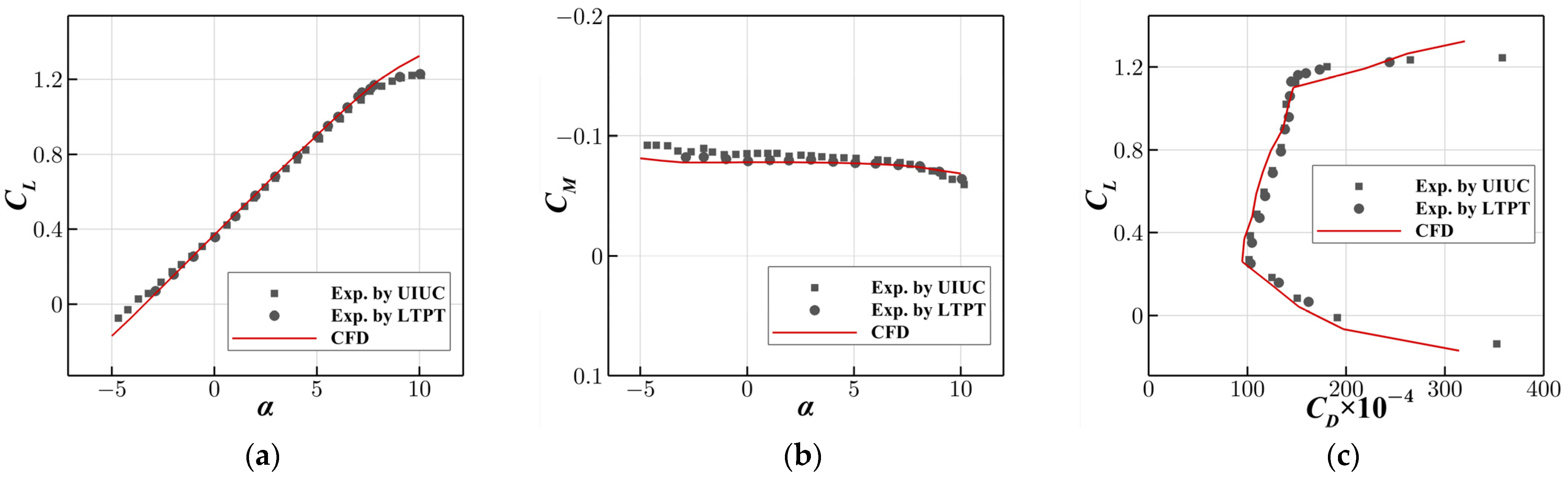
3.2. Verification of Aerodynamic Performance Parameters
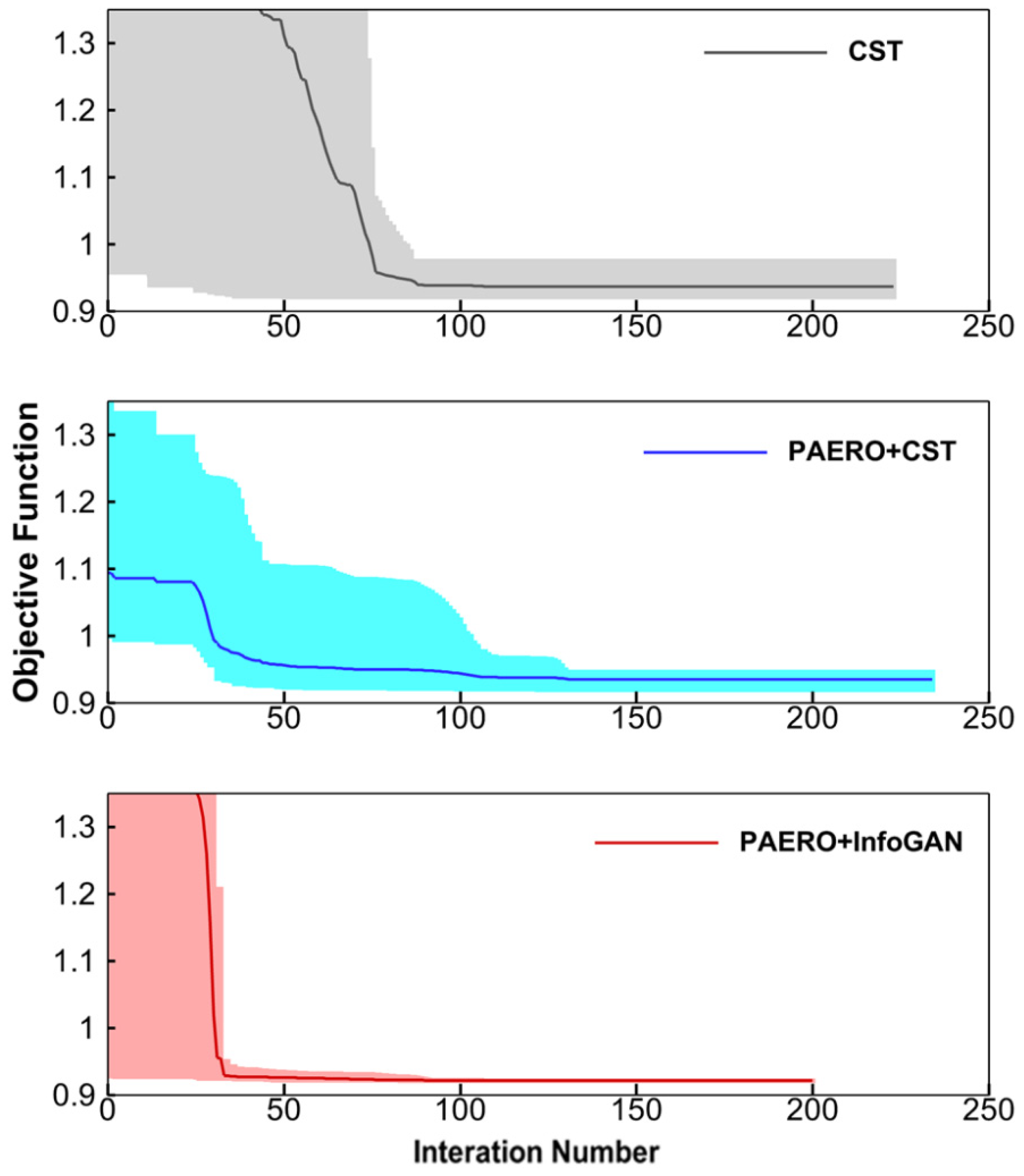
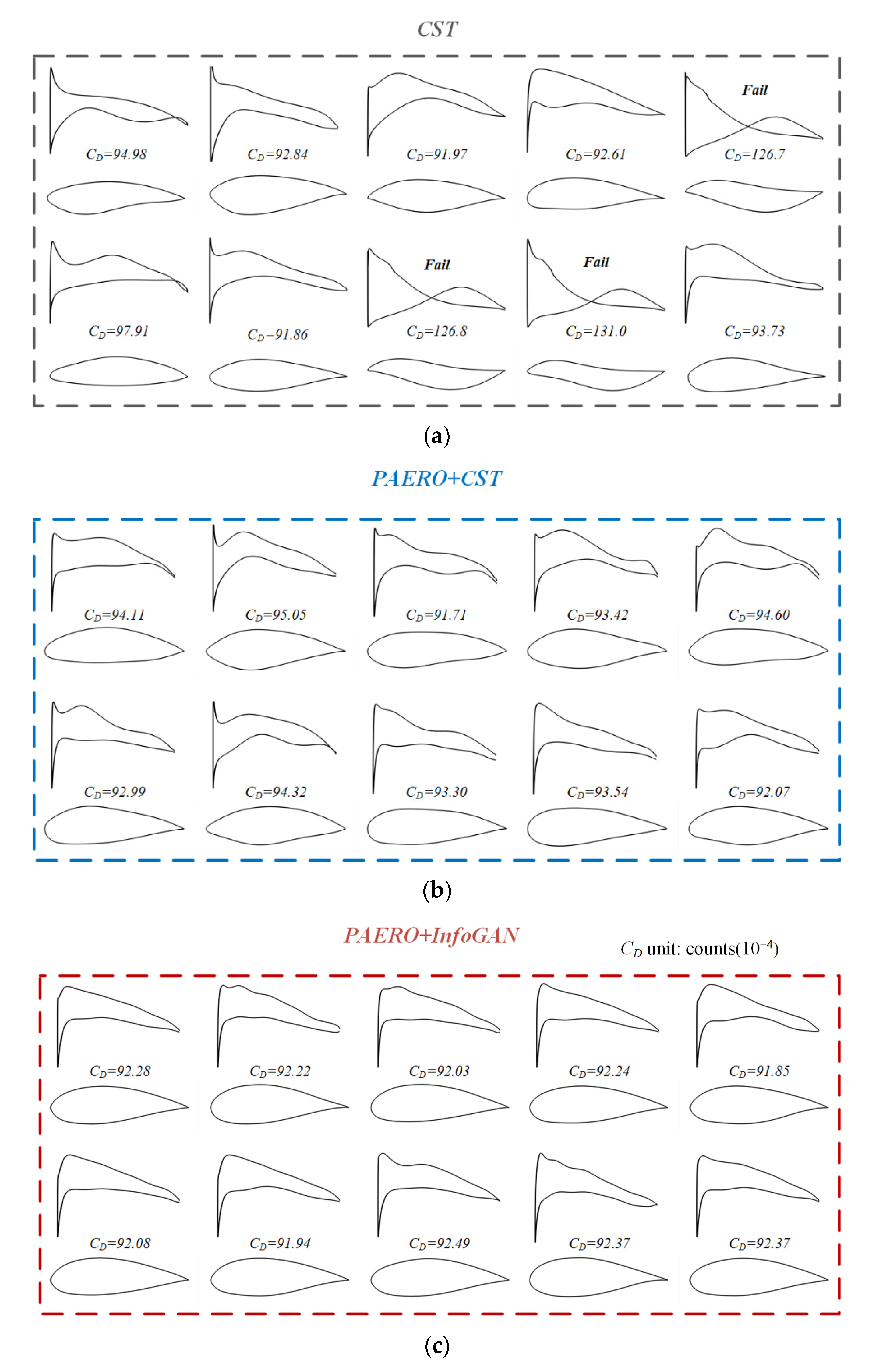
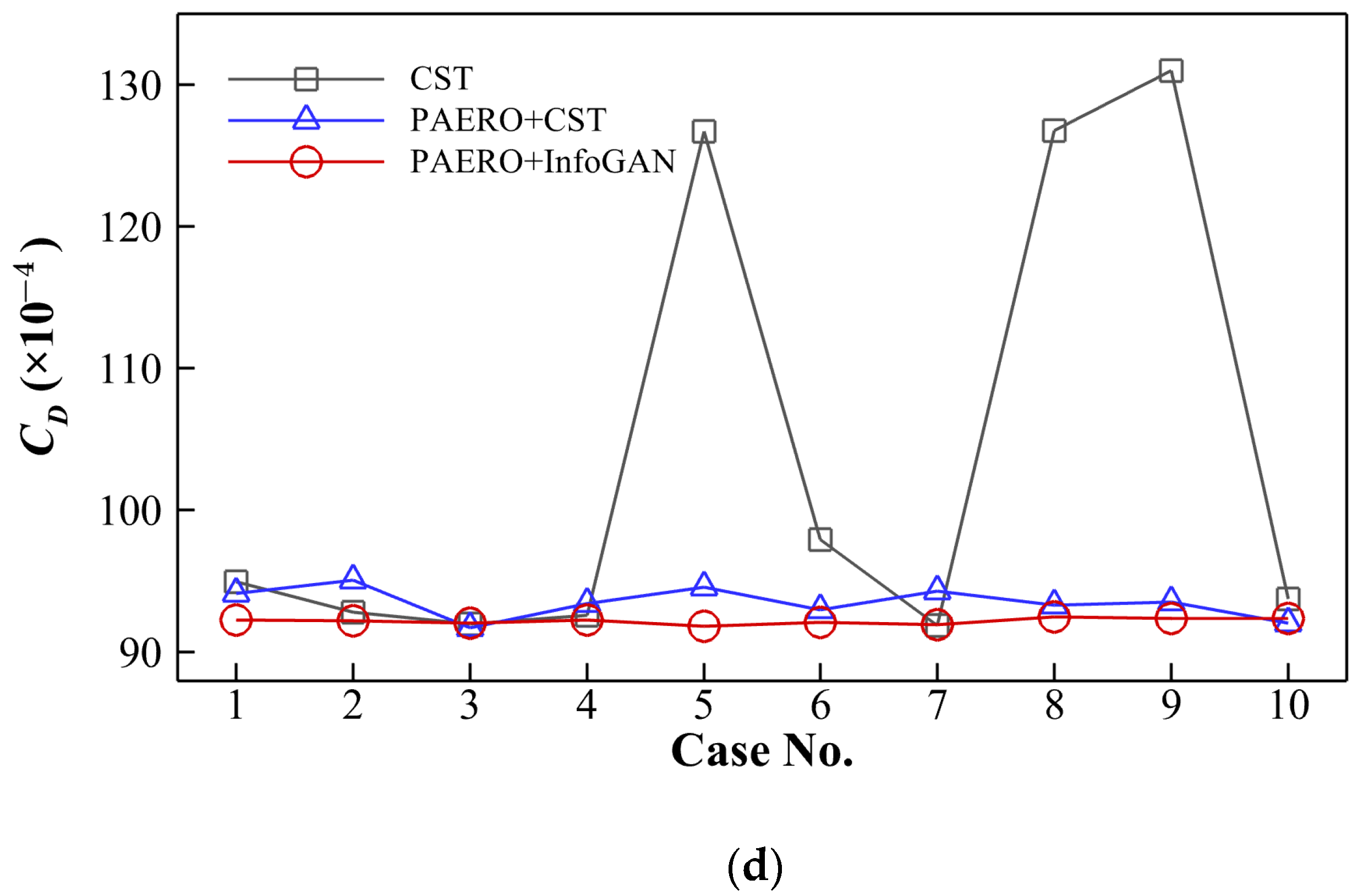
3.3. Airfoil Shape Optimization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ith Fourier coefficient | |
| CD | drag coefficient |
| CL | lift coefficient |
| CL,DV | design variable corresponding to lift coefficient |
| CM | pitching moment coefficient around the quarter-chord point |
| CM,DV | design variable corresponding to pitching moment coefficient |
| D | discriminator |
| DV | design vector |
| dlatent | latent dimension |
| dnoise | noise dimension |
| G | generator |
| Ma | freestream Mach number |
| MaDV | design variable corresponding to freestream Mach number |
| prior distribution of latent variables | |
| Pdata | data distribution |
| PG | generative distribution |
| prior distribution of noise variables | |
| Q | auxiliary distribution |
| Re | Reynolds number |
| latent variable for generative model | |
| noise variable for generative model | |
| normalized mean camber curve | |
| normalized thickness distribution | |
| α | angle of attack |
| αDV | design variable corresponding to angle of attack |
| λi | ith Lagrange multiplier |
| ordinate of the mean camber curve on the trailing edge | |
| trailing-edge thickness |
References
- Shan, S.; Wang, G.G. Survey of Modeling and Optimization Strategies to Solve High-Dimensional Design Problems with Computationally-Expensive Black-Box Functions. Struct. Multidiscip. Optim. 2010, 41, 219–241. [Google Scholar]
- Forrester, A.; Keane, A.J. Recent Advances in Surrogate-Based Optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Kenway, G.; Mader, C.A.; He, P.; Martins, J.R.R.A. Effective Adjoint Approaches for Computational Fluid Dynamics. Prog. Aerosp. Sci. 2019, 110, 100524. [Google Scholar] [CrossRef]
- Jameson, A. Aerodynamic Design via Control Theory. J. Sci. Comput. 1988, 3, 233–260. [Google Scholar] [CrossRef] [Green Version]
- Han, Z.H.; Xu, C.Z.; Qiao, J.L.; Liu, P. Recent Propress of Efficient Global Aerodynamic Shape Optimization Using Surrogate-Based Approach. Acta Aeronaut. Astronaut. Sin. 2020, 41, 623344. [Google Scholar]
- Powell, M.J.D. The BOBYQA Algorithm for Bound Constrained Optimization without Derivatives; Department of Applied Mathematics and Theoretical Physics, University of Cambridge: Cambridge, UK, 2009. [Google Scholar]
- Li, J.; Du, X.; Martins, J. Machine Learning in Aerodynamic Shape Optimization. Prog. Aerosp. Sci. 2022, 134, 100849. [Google Scholar] [CrossRef]
- Sobieczky, H. Parametric Airfoils and Wings. In Recent Development of Aerodynamic Design Methodologies. Notes on Numerical Fluid Mechanics (NNFM); Fujii, K., Dulikravich, G.S., Eds.; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1999; pp. 71–87. ISBN 978-3-322-89954-5. [Google Scholar]
- Kulfan, B.M. Universal Parametric Geometry Representation Method. J. Aircr. 2008, 45, 142–158. [Google Scholar] [CrossRef]
- Rajnarayan, D.; Ning, A.; Mehr, J.A. Universal Airfoil Parametrization Using B-Splines. In AIAA Paper 2018–3949, Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Atlanta, GA, USA, 2018. [Google Scholar]
- Hicks, R.M.; Henne, P.A. Wing Design by Numerical Optimization. J. Aircr. 1978, 15, 407–412. [Google Scholar] [CrossRef]
- Sederberg, T.W.; Parry, S.R. Free-Form Deformation of Solid Geometric Models. ACM SIGGRAPH Comput. Graph. 1986, 20, 151–160. [Google Scholar] [CrossRef]
- Masters, D.A.; Taylor, N.J.; Rendall, T.C.S.; Allen, C.B.; Poole, D.J. Geometric Comparison of Aerofoil Shape Parameterization Methods. AIAA J. 2017, 55, 1575–1589. [Google Scholar] [CrossRef]
- Li, J.; Bouhlel, M.A.; Martins, J. Data-Based Approach for Fast Airfoil Analysis and Optimization. AIAA J. 2019, 57, 581–596. [Google Scholar] [CrossRef]
- Chen, W.; Chiu, K.; Fuge, M.D. Airfoil Design Parameterization and Optimization Using Bézier Generative Adversarial Networks. AIAA J. 2020, 58, 4723–4735. [Google Scholar] [CrossRef]
- Selig, M.S. UIUC Airfoil Coordinates Database. Available online: https://m-selig.ae.illinois.edu/ads/coord_database.html (accessed on 17 July 2023).
- Du, X.; He, P.; Martins, J. A B-Spline-Based Generative Adversarial Network Model for Fast Interactive Airfoil Aerodynamic Optimization. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6 January 2020. [Google Scholar]
- Du, X.; He, P.; Martins, J.R.R.A. Rapid Airfoil Design Optimization via Neural Networks-Based Parameterization and Surrogate Modeling. Aerosp. Sci. Technol. 2021, 113, 106701. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Martins, J.; Shu, C. Efficient Aerodynamic Shape Optimization with Deep-Learning-Based Geometric Filtering. AIAA J. 2020, 58, 4243–4259. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M. On Deep-Learning-Based Geometric Filtering in Aerodynamic Shape Optimization. Aerosp. Sci. Technol. 2021, 112, 106603. [Google Scholar] [CrossRef]
- Achour, G.; Sung, W.J.; Pinon-Fischer, O.J.; Mavris, D.N. Development of a Conditional Generative Adversarial Network for Airfoil Shape Optimization. In AIAA Paper 2020–2261, Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6 January 2020; American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2020. [Google Scholar]
- Yilmaz, E.; German, B. Conditional Generative Adversarial Network Framework for Airfoil Inverse Design. In AIAA Paper 2020–3185, Proceedings of the AIAA Aviation 2020 Forum, Virtual Event, 15–19 June 2020; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2020. [Google Scholar]
- Sekar, V.; Zhang, M.; Shu, C.; Khoo, B.C. Inverse Design of Airfoil Using a Deep Convolutional Neural Network. AIAA J. 2019, 57, 993–1003. [Google Scholar] [CrossRef]
- Wang, J.; Li, R.; He, C.; Chen, H.; Cheng, R.; Zhai, C.; Zhang, M. An Inverse Design Method for Supercritical Airfoil Based on Conditional Generative Models. Chin. J. Aeronaut. 2022, 35, 62–74. [Google Scholar] [CrossRef]
- Lei, R.; Bai, J.; Wang, H.; Zhou, B.; Zhang, M. Deep Learning Based Multistage Method for Inverse Design of Supercritical Airfoil. Aerosp. Sci. Technol. 2021, 119, 107101. [Google Scholar] [CrossRef]
- Abbott, I.H.; Doenhoff, A.E. Theory of Wing Sections; Dover Publications Inc.: New York, NY, USA, 1959; p. x + 693. [Google Scholar]
- Deng, F.; Xue, C.; Qin, N. Parameterizing Airfoil Shape Using Aerodynamic Performance Parameters. AIAA J. 2022. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein Generative Adversarial Networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 214–223. [Google Scholar]
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets. Adv. Neural Inf. Process. Syst. 2016. [Google Scholar]
- Li, J.; He, S.; Martins, J. Data-Driven Constraint Approach to Ensure Low-Speed Performance in Transonic Aerodynamic Shape Optimization. Aerosp. Sci. Technol. 2019, 92, 536–550. [Google Scholar] [CrossRef]
- Deng, F.; Yi, J. Fast Inverse Design of Transonic Airfoils by Combining Deep Learning and Efficient Global Optimization. Aerospace 2023, 10, 125. [Google Scholar] [CrossRef]
- PyTorch. Available online: https://Github.Com/Pytorch/Pytorch (accessed on 17 July 2023).
- Kulfan, B.; Bussoletti, J. “Fundamental” Parameteric Geometry Representations for Aircraft Component Shapes. In AIAA Paper 2006–6948, Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006; American Institute of Aeronautics and Astronautics: Portsmouth, VA, USA, 2006. [Google Scholar]
- NASA CFL3D. Available online: https://cfl3d.larc.nasa.gov/ (accessed on 17 July 2023).
- Selig, M.S.; McGranahan, B.D. Wind Tunnel Aerodynamic Tests of Six Airfoils for Use on Small Wind Turbines. J. Sol. Energy Eng. 2004, 126, 986–1001. [Google Scholar] [CrossRef]





| Generator | Discriminator | ||||
|---|---|---|---|---|---|
| Layer | Neurons | AF | Layer | Filters | AF |
| FC layer | 128 | ReLU | C layer | 10 | LeakyReLU |
| FC layer | 128 | ReLU | C layer | 20 | LeakyReLU |
| FC layer | 64 | ReLU | C layer | 40 | LeakyReLU |
| FC layer | 20 | ReLU | C layer | 80 | LeakyReLU |
| SVD mode layer | FC layer | 1 | |||
| FC layer(Q) | 3 | Sigmoid | |||
| dlatent | |
|---|---|
| 2 | 33.11 |
| 3 | 12.01 |
| 4 | 7.253 |
| 6 | 6.234 |
| 8 10 | 5.067 3.367 |
| No. | Grid | CL | CD | CM |
|---|---|---|---|---|
| 1 | 0.3773 | 0.01012 | −0.07740 | |
| 2 | 0.3817 | 0.009681 | −0.07792 | |
| 3 | 0.3876 | 0.009594 | −0.07860 |
| Functions | Description | Quantity | |
|---|---|---|---|
| Minimize | CD | Drag coefficient | 1 |
| With respect to | DV α | Design variables Angle of attack | 12 1 |
| Subject to | CL = 0.5 CM ≥ −0.07 area ≥ 0.07 | Lift coefficient Quarter-chord pitching moment Area constraint | 1 1 1 |
| Variable Type | Symbol | Value Range |
|---|---|---|
| Camber representation | 0.6 0.5 [1.8, 2.2] [−0.06, −0.08] [−0.02, 0.02] | |
| Thickness representation (InfoGAN) | [0, 1] | |
| Thickness representation (CST) | [0.01, 0.4] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, J.; Deng, F. Cooperation of Thin-Airfoil Theory and Deep Learning for a Compact Airfoil Shape Parameterization. Aerospace 2023, 10, 650. https://doi.org/10.3390/aerospace10070650
Yi J, Deng F. Cooperation of Thin-Airfoil Theory and Deep Learning for a Compact Airfoil Shape Parameterization. Aerospace. 2023; 10(7):650. https://doi.org/10.3390/aerospace10070650
Chicago/Turabian StyleYi, Jianmiao, and Feng Deng. 2023. "Cooperation of Thin-Airfoil Theory and Deep Learning for a Compact Airfoil Shape Parameterization" Aerospace 10, no. 7: 650. https://doi.org/10.3390/aerospace10070650
APA StyleYi, J., & Deng, F. (2023). Cooperation of Thin-Airfoil Theory and Deep Learning for a Compact Airfoil Shape Parameterization. Aerospace, 10(7), 650. https://doi.org/10.3390/aerospace10070650






