Efficient Uncertainty Analysis of External Heat Flux of Solar Radiation with External Heat Flux Expansion for Spacecraft Thermal Design
Abstract
1. Introduction
2. External Heat Flux of Solar Radiation
2.1. External Heat Flux of Direct Solar Radiation
2.2. External Heat Flux of Indirect Solar Radiation
- (1)
- Reference coordinate systems, such as body, orbit, and geocentric inertial coordinate systems, are established and orbit parameters are provided;
- (2)
- A thermal–physical model of the spacecraft structure is constructed, a grid of thermal analysis surface elements is partitioned, and the surface equation and radiation characteristics for each thermal analysis surface element are determined;
- (3)
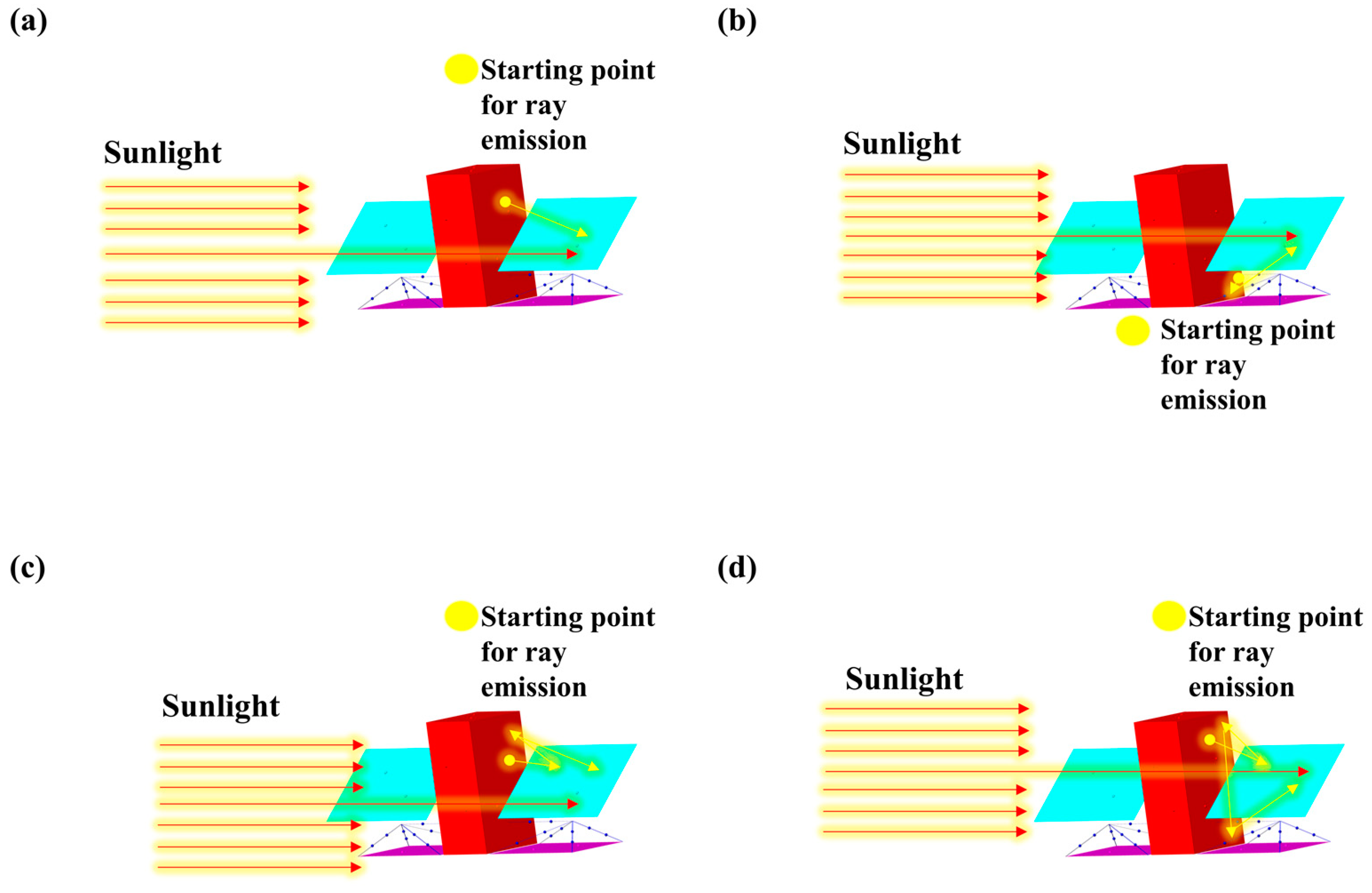
- A target surface element of the spacecraft emits a random ray;
- (4)
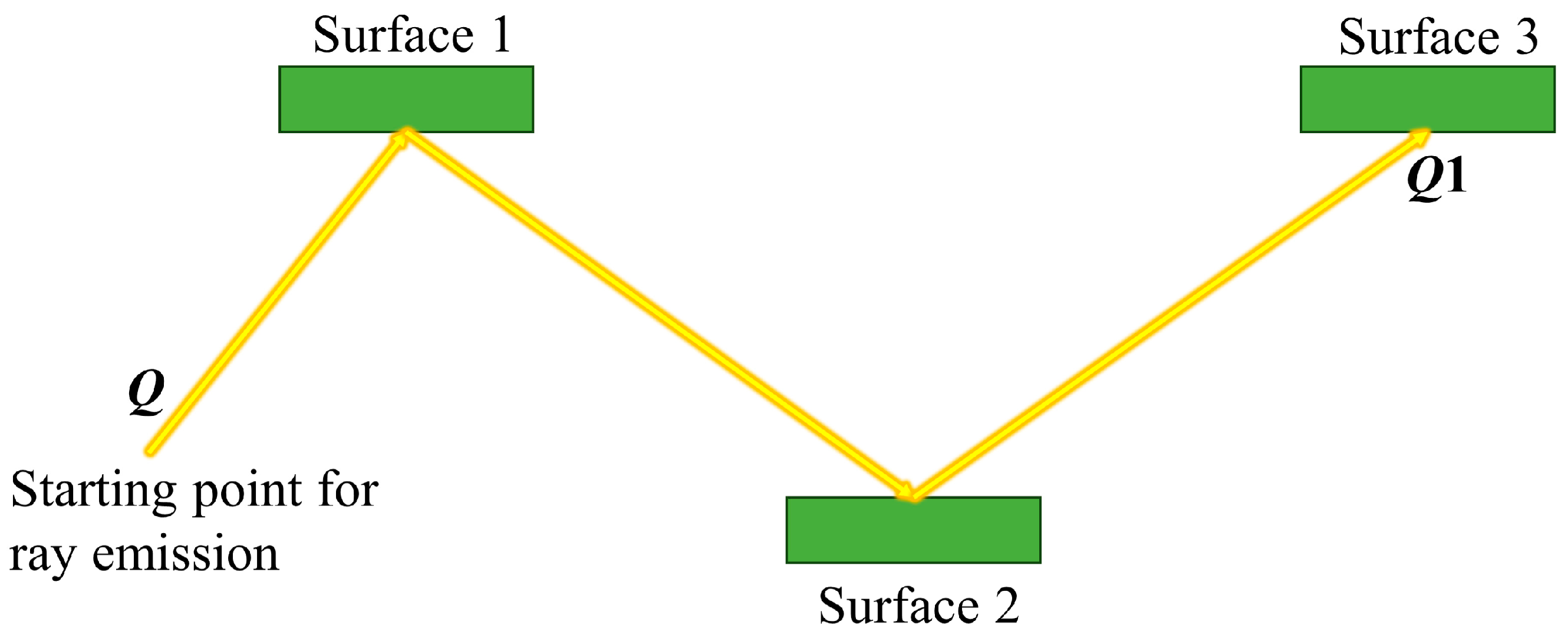
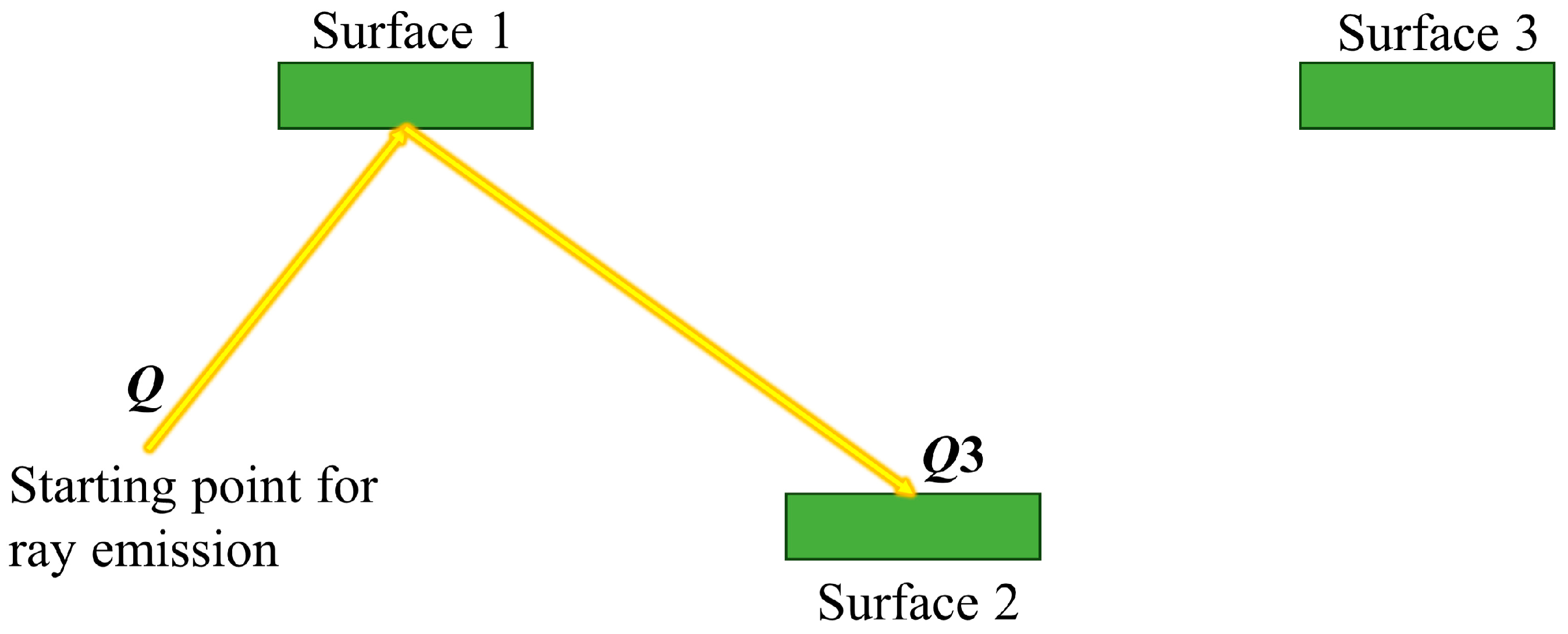
- The intersection of the ray with the surface element of the system (spacecraft and radiation source) is calculated and the method for further tracking the ray is determined according to the ray-tracing technique;
- (5)
- If the ray is absorbed by the radiation source’s surface, the external heat flux absorbed by the ray on the target surface element’s surface is accounted for using the reverse process.
3. External Heat Flux of Solar Radiation Uncertainty Calculation
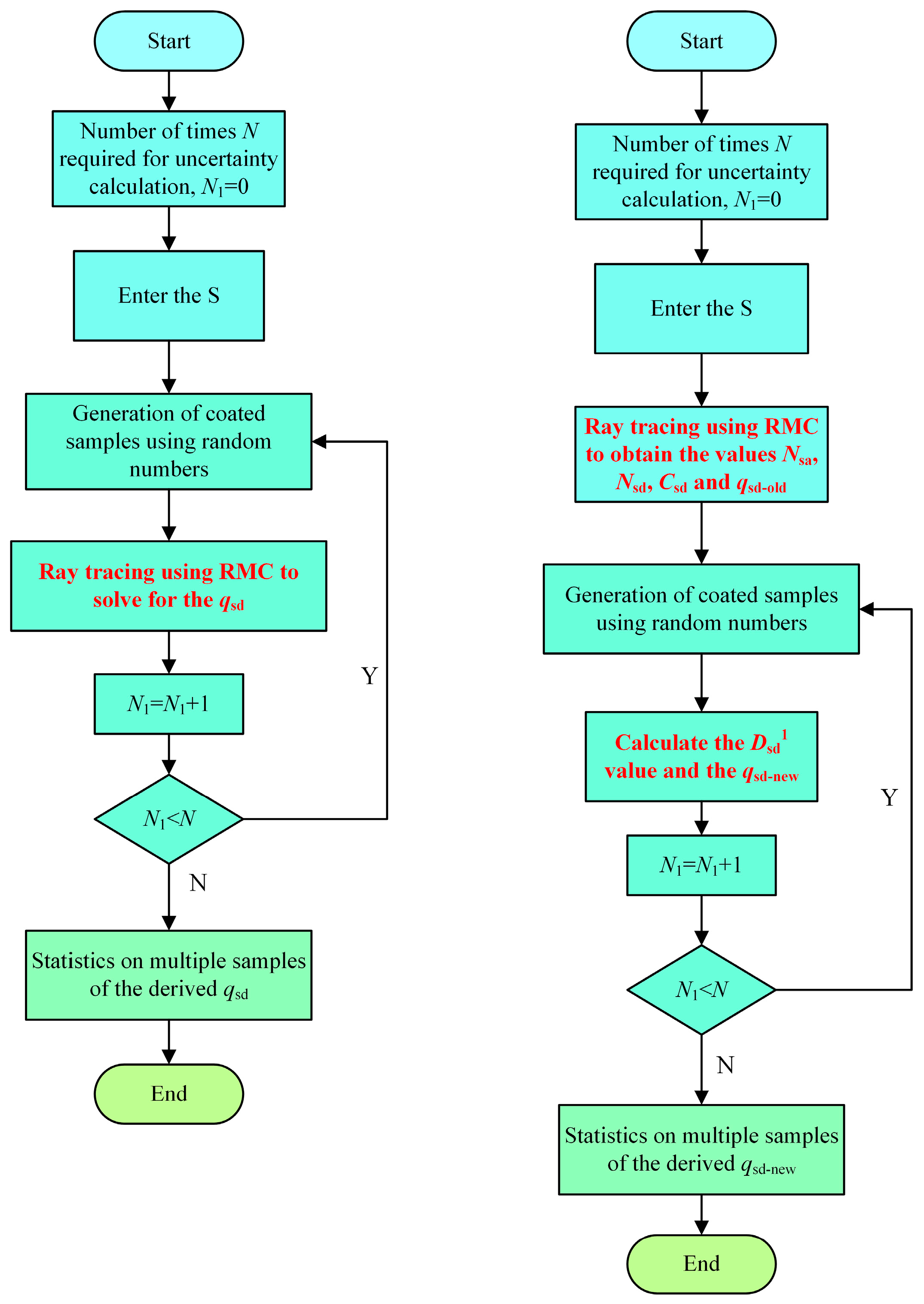
3.1. Direct Solar Radiation Uncertainty Analysis with EHFE
3.1.1. Direct Solar Radiation EHFE Equation
3.1.2. External Heat Flux of Direct Solar Radiation Uncertainty Analysis
- (1)
- Generation of samples of solar absorbance of all face elements of the spacecraft using random numbers;
- (2)
- RMC for ray-tracing, ray-shading, and obscuring judgments, and solving for external heat flux of direct solar radiation;
- (3)
- Repeating (1) and (2) to generate multiple samples for statistics.
- (1)
- Ray tracing using RMC to solve for the initial working conditions of the external heat flux of direct solar radiation and recording the values of Nsa and Nsd;
- (2)
- Generation of samples of solar absorbance of all face elements of the spacecraft using random numbers;
- (3)
- Updating of element Dsd to generate element based on samples of solar absorbance corresponding to the new working condition;
- (4)
- Using Equation (5) to solve for ;
- (5)
- Repeating (2)–(4) to generate multiple samples for statistics.
3.2. Indirect Solar Radiation Uncertainty Analysis with EHFE
3.2.1. Indirect Solar Radiation EHFE Equation
3.2.2. External Heat Flux of Indirect Solar Radiation Uncertainty Analysis
- (1)
- Samples of solar absorbance and reflectance for all face elements of the spacecraft are generated using random numbers;
- (2)
- RMC ray tracing is performed to calculate the external heat flux of indirect solar radiation;
- (3)
- Steps (1) and (2) are repeated to generate multiple samples for statistics.
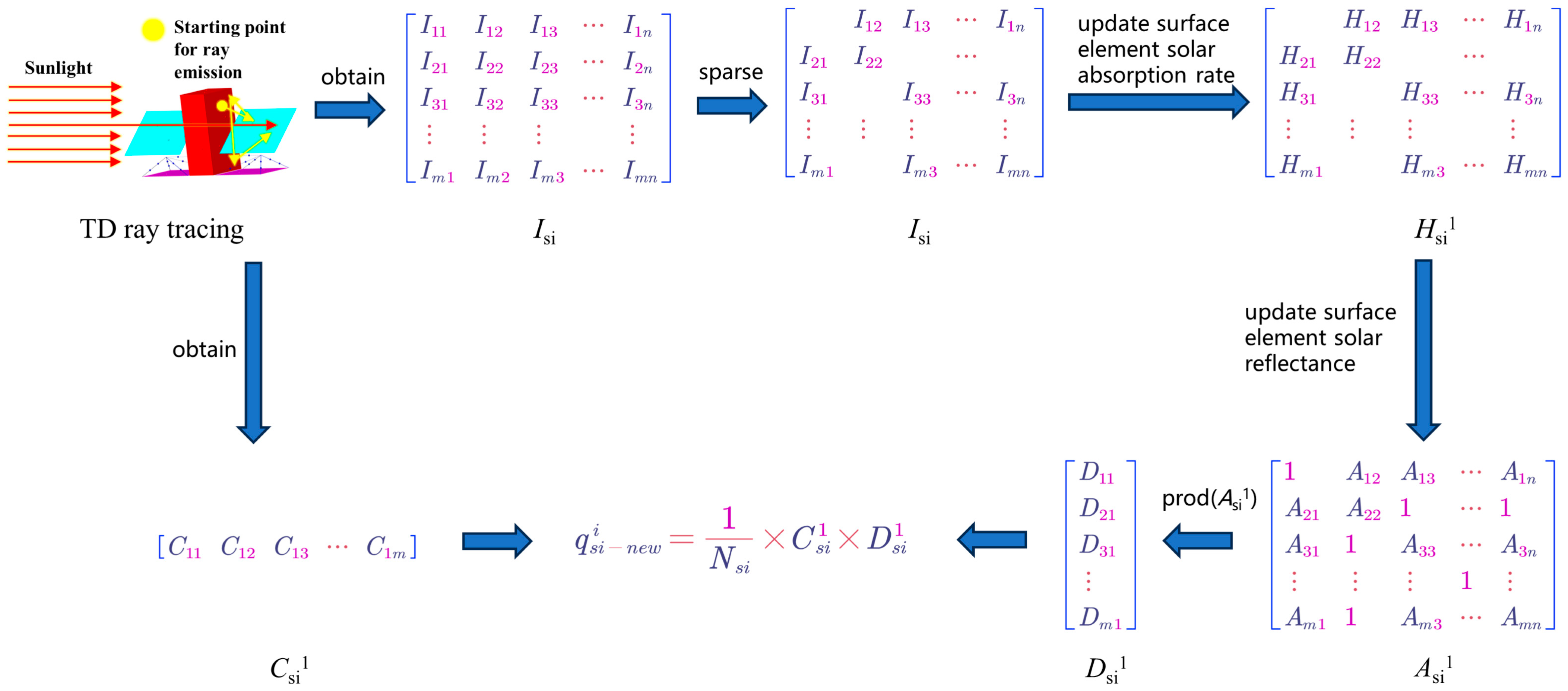
- (1)
- RMC ray tracing is performed to solve for the external heat flux of indirect solar radiation. In addition, the Isi, Hsi, and Csi matrices are obtained;
- (2)
- Samples of solar absorbance and reflectance for all face elements of the spacecraft are generated using random numbers;
- (3)
- Based on the new solar absorbance sample and the intersecting surface element-numbering matrix Isi, the corresponding elements of matrices Asi, Hsi, and Csi are updated. Matrices Asi1, Hsi1, and Csi1 are generated considering the uncertainty parameters. Matrix Asi1 is used to obtain matrix Dsi1;
- (4)
- Equation (13) is used to solve for ;
- (5)
- Steps (2)–(4) are repeated to generate multiple samples for statistics.
4. Validation Model
5. Results and Discussion
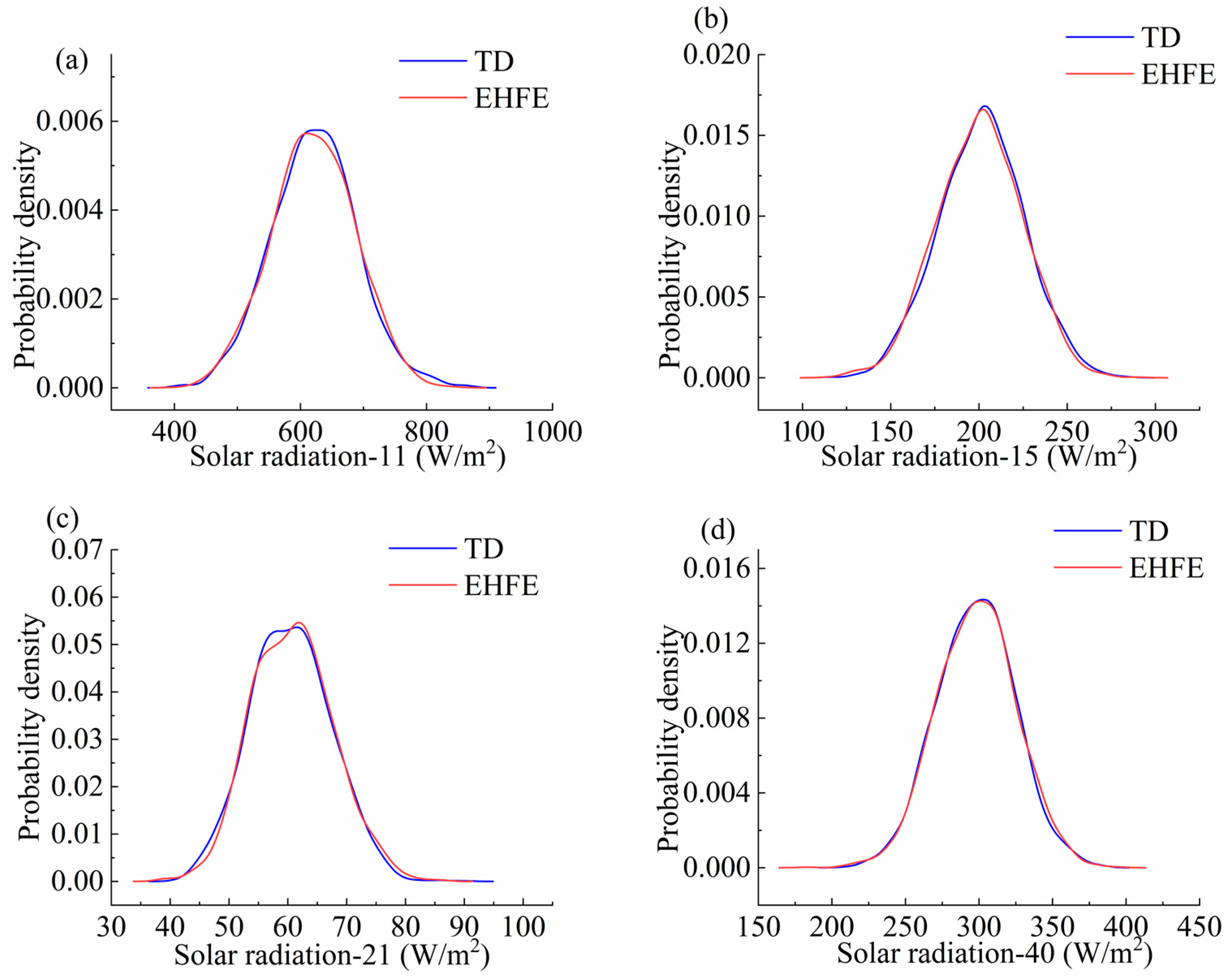
5.1. External Heat Flux of Solar Radiation Uncertainty Analysis
5.2. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| S | the solar constant (W/m2) |
| Ei | node i surface element |
| external heat flux of direct solar radiation absorbed by the face element Ei (W/m2) | |
| external heat flux of indirect solar radiation absorbed by the face element Ei (W/m2) | |
| external heat flux of solar radiation absorbed by the face element Ei (W/m2) | |
| Dsi | the combined solar spectral reflectance matrix of the spacecraft face element coating |
| Isi | the intersecting face number matrix |
| Hsi | solar absorbance matrix of intersecting surface elements from Isi |
| Asi | solar spectral reflectance matrix of intersecting surface elements from Isi |
| Csi | the multiplication of each common factor of the EHFE formula by qsd,j/αs,j |
| Nmin | the minimum number of model runs |
| Nσ | number of standard deviations |
| P | percentile |
| ΔP | deviation from percentile |
| Greek symbols | |
| the solar absorption rate of surface element i | |
| the reflectance of the solar spectrum for the face element of the τth intersection of the jnth ray | |
| α | the surface solar absorption rate |
| ρ | the surface solar reflectance |
| θ | the angle between the normal vector of the face element Ei and the solar ray vector (deg) |
| Subscripts/Superscripts | |
| i | current node |
| j | node other that current |
| Acronyms | |
| MC | Monte Carlo |
| RMC | Reverse Monte Carlo |
| EHFE | external heat flux expansion |
| TD | Thermal Desktop |
| CI | confidence interval |
References
- Kuzenov, V.V.; Ryzhkov, S.V.; Varaksin, A.Y. Calculation of heat transfer and drag coefficients for aircraft geometric models. Appl. Sci. 2022, 12, 11011. [Google Scholar] [CrossRef]
- Fagherazzi, M.; Santi, M.; Barato, F.; Pizzarelli, M. A Simplified Thermal Analysis Model for Regeneratively Cooled Rocket Engine Thrust Chambers and Its Calibration with Experimental Data. Aerospace 2023, 10, 403. [Google Scholar] [CrossRef]
- Ishimoto, T.; Bevans, J.T. Temperature variance in spacecraft thermal analysis. J. Spacecr. Rockets 1968, 5, 1372–1376. [Google Scholar] [CrossRef]
- Howell, J.R. Monte Carlo treatment of data uncertainties in thermal analysis. J. Spacecr. Rockets 1973, 10, 411–414. [Google Scholar] [CrossRef]
- Thunnissen, D.P.; Tsuyuki, G.T. Margin determination in the design and development of a thermal control system. SAE Trans. 2004, 113, 899–916. [Google Scholar]
- Thunnissen, D.P.; Au, S.K.; Tsuyuki, G.T. Uncertainty quantification in estimating critical spacecraft component temperatures. J. Thermophys. Heat Transf. 2007, 21, 422–430. [Google Scholar] [CrossRef]
- Gómez-San-Juan, A.; Pérez-Grande, I.; Sanz-Andrés, A. Uncertainty calculation for spacecraft thermal models using a generalized SEA method. Acta Astronaut. 2018, 151, 691–702. [Google Scholar] [CrossRef]
- Xiong, Y.; Guo, L.; Yang, Y.; Wang, H. Intelligent sensitivity analysis framework based on machine learning for spacecraft thermal design. Aerosp. Sci. Technol. 2021, 118, 106927. [Google Scholar] [CrossRef]
- Kato, H.; Ando, M.; Fukuzoe, M. Toward Uncertainty Quantification in Satellite Thermal Design. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2019, 17, 134–141. [Google Scholar] [CrossRef]
- Regis, R.G. Evolutionary programming for high-dimensional constrained expensive black-box optimization using radial basis functions. IEEE Trans. Evol. Comput. 2013, 18, 326–347. [Google Scholar] [CrossRef]
- Kleijnen, J.P. Kriging metamodeling in simulation: A review. Eur. J. Oper. Res. 2009, 192, 707–716. [Google Scholar] [CrossRef]
- Han, Z.-H.; Zhang, Y.; Song, C.-X.; Zhang, K.-S. Weighted gradient-enhanced kriging for high-dimensional surrogate modeling and design optimization. AIAA J. 2017, 55, 4330–4346. [Google Scholar] [CrossRef]
- Qian, J.; Yi, J.; Cheng, Y.; Liu, J.; Zhou, Q. A sequential constraints updating approach for Kriging surrogate model-assisted engineering optimization design problem. Eng. Comput. 2020, 36, 993–1009. [Google Scholar] [CrossRef]
- Datta, R.; Regis, R.G. A surrogate-assisted evolution strategy for constrained multi-objective optimization. Expert Syst. Appl. 2016, 57, 270–284. [Google Scholar] [CrossRef]
- Song, Z.; Murray, B.T.; Sammakia, B.; Lu, S. Multi-Objective Optimization of Temperature Distributions Using Artificial Neural Networks. In Proceedings of the 13th InterSociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, San Diego, CA, USA, 30 May–1 June 2012; pp. 1209–1218. [Google Scholar]
- Altan, A.; Aslan, Ö.; Hacıoğlu, R. Real-Time Control Based on NARX Neural Network of Hexarotor UAV with Load Transporting System for Path Tracking. In Proceedings of the 2018 6th International Conference on Control Engineering & Information Technology (CEIT), Istanbul, Turkey, 25–27 October 2018; pp. 1–6. [Google Scholar]
- Kromanis, R.; Kripakaran, P. Support vector regression for anomaly detection from measurement histories. Adv. Eng. Inform. 2013, 27, 486–495. [Google Scholar] [CrossRef]
- Rahmani, S.; Ebrahimi, M.; Honaramooz, A. A surrogate-based optimization using polynomial response surface in collaboration with population-based evolutionary algorithm. In Advances in Structural and Multidisciplinary Optimization, Proceedings of the 12th World Congress of Structural and Multidisciplinary Optimization (WCSMO12) 12, Braunschweig, Germany, 5–9 June 2017; Springer: Cham, Switzerland, 2018; pp. 269–280. [Google Scholar]
- Kersch, A.; Morokoff, W.; Schuster, A. Radiative heat transfer with quasi-Monte Carlo methods. Transp. Theor. Stat. Phys. 1994, 23, 1001–1021. [Google Scholar] [CrossRef]
- Liu, Y.; Li, G.-H.; Jiang, L.-X. A new improved solution to thermal network problem in heat-transfer analysis of spacecraft. Aerosp. Sci. Technol. 2010, 14, 225–234. [Google Scholar] [CrossRef]
- Yuan, M.; Li, Y.-Z.; Sun, Y.; Ye, B. The space quadrant and intelligent occlusion calculation methods for the external heat flux of China space Station. Appl. Therm. Eng. 2022, 212, 118572. [Google Scholar] [CrossRef]
- Yang, W.; Cheng, H.; Cai, A. Thermal analysis for folded solar array of spacecraft in orbit. Appl. Therm. Eng. 2004, 24, 595–607. [Google Scholar] [CrossRef]
- Farrahi, A.; Pérez-Grande, I. Simplified analysis of the thermal behavior of a spinning satellite flying over Sun-synchronous orbits. Appl. Therm. Eng. 2017, 125, 1146–1156. [Google Scholar] [CrossRef]
- Krainova, I.; Nenarokomov, A.; Nikolichev, I.; Titov, D.; Chumakov, V. Radiative Heat Fluxes in Orbital Space Flight. J. Eng. Thermophys. 2022, 31, 441–457. [Google Scholar] [CrossRef]
- Li, P.; Cheng, H.-E.; Qin, W.-B. Numerical simulation of temperature field in solar arrays of spacecraft in low earth orbit. Numer. Heat Transf. A Appl. 2006, 49, 803–820. [Google Scholar] [CrossRef]
- Selvadurai, S.; Chandran, A.; Valentini, D.; Lamprecht, B. Passive Thermal Control Design Methods, Analysis, Comparison, and Evaluation for Micro and Nanosatellites Carrying Infrared Imager. Appl. Sci. 2022, 12, 2858. [Google Scholar] [CrossRef]
- Yang, F.; Li, J.; Xu, C.; Li, D.; Qiu, H.; Xu, A. MPI Parallelization of Numerical Simulations for Pulsed Vacuum Arc Plasma Plumes Based on a Hybrid DSMC/PIC Algorithm. Aerospace 2022, 9, 538. [Google Scholar] [CrossRef]
- Fu, X.; Hua, Y.; Ma, W.; Cui, H.; Zhao, Y. An Innovative External Heat Flow Expansion Formula for Efficient Uncertainty Analysis in Spacecraft Earth Radiation Heat Flow Calculations. Aerospace 2023, 10, 605. [Google Scholar] [CrossRef]






| Parameters | Numerical Value |
|---|---|
| Semimajor axis/(km) | 6878 |
| Eccentricity | 0 |
| Orbit inclination/(°) | 0 |
| Attitude | Z-axis to ground orientation |
| Input Parameters | Average Value |
|---|---|
| Satellite body solar absorption rate | 0.46 |
| Antennae solar absorption rate | 0.65 |
| Solar panel solar absorption rate | 0.41 |
| Truss solar absorption rate | 0.56 |
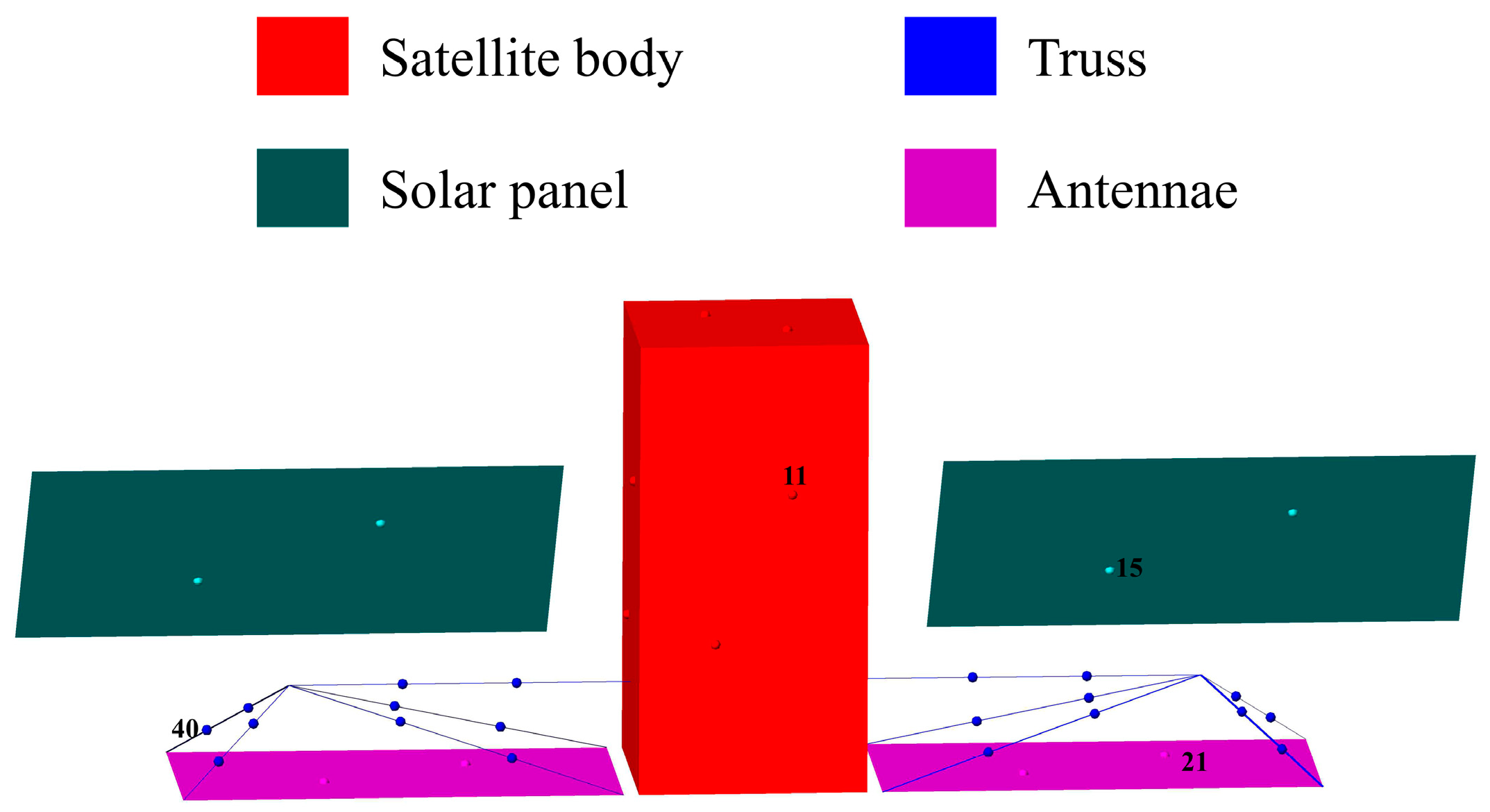
| Number of Surface Elements | Spacecraft Components Belonging to Surface Elements |
|---|---|
| 11 | Satellite body |
| 15 | Solar panel |
| 21 | Antennae |
| 40 | Truss |
| TD Model (W/m2) | EHFE Equation (W/m2) | Relative Error (%) | Absolute Error (W/m2) | |
|---|---|---|---|---|
| Surface element 11 mean | 622.52 | 620.71 | 0.292 | 1.817 |
| Surface element 11 standard deviation | 67.59 | 66.28 | 1.937 | 1.309 |
| Surface element 15 mean | 201.64 | 200.44 | 0.597 | 1.205 |
| Surface element 15 standard deviation | 24.10 | 24.12 | 0.076 | 0.018 |
| Surface element 21 mean | 60.51 | 60.82 | 0.515 | 0.312 |
| Surface element 21 standard deviation | 6.86 | 6.94 | 1.228 | 0.084 |
| Surface element 40 mean | 298.11 | 298.38 | 0.092 | 0.273 |
| Surface element 40 standard deviation | 26.47 | 27.05 | 2.209 | 0.585 |
| TD Model (W/m2) | EHFE Equation (W/m2) | Relative Error (%) | Absolute Error (W/m2) | ||
|---|---|---|---|---|---|
| 95.40% | Lower CI for surface element 11 | 486.90 | 485.53 | 0.28 | 1.37 |
| Upper CI for surface element 11 | 761.07 | 749.66 | 1.50 | 11.41 | |
| Lower CI for surface element 15 | 153.11 | 152.85 | 0.17 | 0.26 | |
| Upper CI for surface element 15 | 249.57 | 247.04 | 1.01 | 2.53 | |
| Lower CI for surface element 21 | 47.24 | 47.86 | 1.30 | 0.62 | |
| Upper CI for surface element 21 | 74.27 | 75.25 | 1.32 | 0.98 | |
| Lower CI for surface element 40 | 244.71 | 245.02 | 0.13 | 0.31 | |
| Upper CI for surface element 40 | 352.54 | 352.23 | 0.09 | 0.30 | |
| 99.70% | Lower CI for surface element 11 | 414.55 | 435.39 | 5.03 | 20.85 |
| Upper CI for surface element 11 | 852.90 | 811.77 | 4.82 | 41.13 | |
| Lower CI for surface element 15 | 131.81 | 127.23 | 3.47 | 4.57 | |
| Upper CI for surface element 15 | 271.61 | 271.02 | 0.22 | 0.59 | |
| Lower CI for surface element 21 | 43.03 | 40.38 | 6.16 | 2.65 | |
| Upper CI for surface element 21 | 82.66 | 82.79 | 0.16 | 0.13 | |
| Lower CI for surface element 40 | 222.89 | 209.10 | 6.19 | 13.79 | |
| Upper CI for surface element 40 | 377.96 | 378.81 | 0.23 | 0.86 |
| Uncertainty in External Heat Flux of Solar Radiation | |
|---|---|
| TD(s) | 13,020 |
| EHFE equation (s) | 753 |
| Speed multiplier (multiple) | 17 |
| TD Model (W/m2) | EHFE Equation (W/m2) | Relative Error (%) | Absolute Error (W/m2) | |
|---|---|---|---|---|
| Cutoff factor 0.1 Lower CI for Surface Element 40 | 222.89 | 209.10 | 6.19 | 13.79 |
| Cutoff factor 0.01 Lower CI for Surface Element 40 | 222.83 | 227.24 | 1.98 | 4.41 |
| Cutoff factor 0.001 Lower CI for Surface Element 40 | 222.82 | 219.08 | 1.68 | 3.74 |
| Cutoff Factor 0.01 Uncertainty in External Heat Flux of Solar Radiation | Cutoff Factor 0.001 Uncertainty in External Heat Flux of Solar Radiation | |
|---|---|---|
| TD (s) | 13,190 | 13,380 |
| EHFE equation (s) | 943 | 1102 |
| Speed multiplier (multiple) | 14 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, X.; Liang, L.; Ma, W.; Cui, H.; Zhao, Y. Efficient Uncertainty Analysis of External Heat Flux of Solar Radiation with External Heat Flux Expansion for Spacecraft Thermal Design. Aerospace 2023, 10, 672. https://doi.org/10.3390/aerospace10080672
Fu X, Liang L, Ma W, Cui H, Zhao Y. Efficient Uncertainty Analysis of External Heat Flux of Solar Radiation with External Heat Flux Expansion for Spacecraft Thermal Design. Aerospace. 2023; 10(8):672. https://doi.org/10.3390/aerospace10080672
Chicago/Turabian StyleFu, Xiaoyi, Lei Liang, Wenlai Ma, Hutao Cui, and Yang Zhao. 2023. "Efficient Uncertainty Analysis of External Heat Flux of Solar Radiation with External Heat Flux Expansion for Spacecraft Thermal Design" Aerospace 10, no. 8: 672. https://doi.org/10.3390/aerospace10080672
APA StyleFu, X., Liang, L., Ma, W., Cui, H., & Zhao, Y. (2023). Efficient Uncertainty Analysis of External Heat Flux of Solar Radiation with External Heat Flux Expansion for Spacecraft Thermal Design. Aerospace, 10(8), 672. https://doi.org/10.3390/aerospace10080672









