Nonlinear Time Series Analysis and Prediction of General Aviation Accidents Based on Multi-Timescales
Abstract
:1. Introduction
- (1)
- With a focus on understanding the time series features of accidents and constructing time series on multiple scales, the periodic variation factors of three scale subseries (EF-, ET-, and HM-) are eliminated using seasonal decomposition. The 0–1 test, phase space reconstruction, and Lyapunov exponent are used to investigate the intrinsic dynamical and chaotic features of the multi-timescale series.
- (2)
- Based on the results of the multi-timescale series chaotic characteristics analysis of general aviation accidents, the chaotic sparrow search algorithm is used to optimize the parameters of the LSSVM model, and an improved prediction model for the CSSA-LSSVM model is presented.
- (3)
- Using simulation experiments to prove the rationality of the above methodologies and predict the development trend of general aviation safety, potential risks can be identified in an immediate response by analyzing general aviation accident time series predictions, which is crucial to enhancing general aviation safety.
2. Data Processing
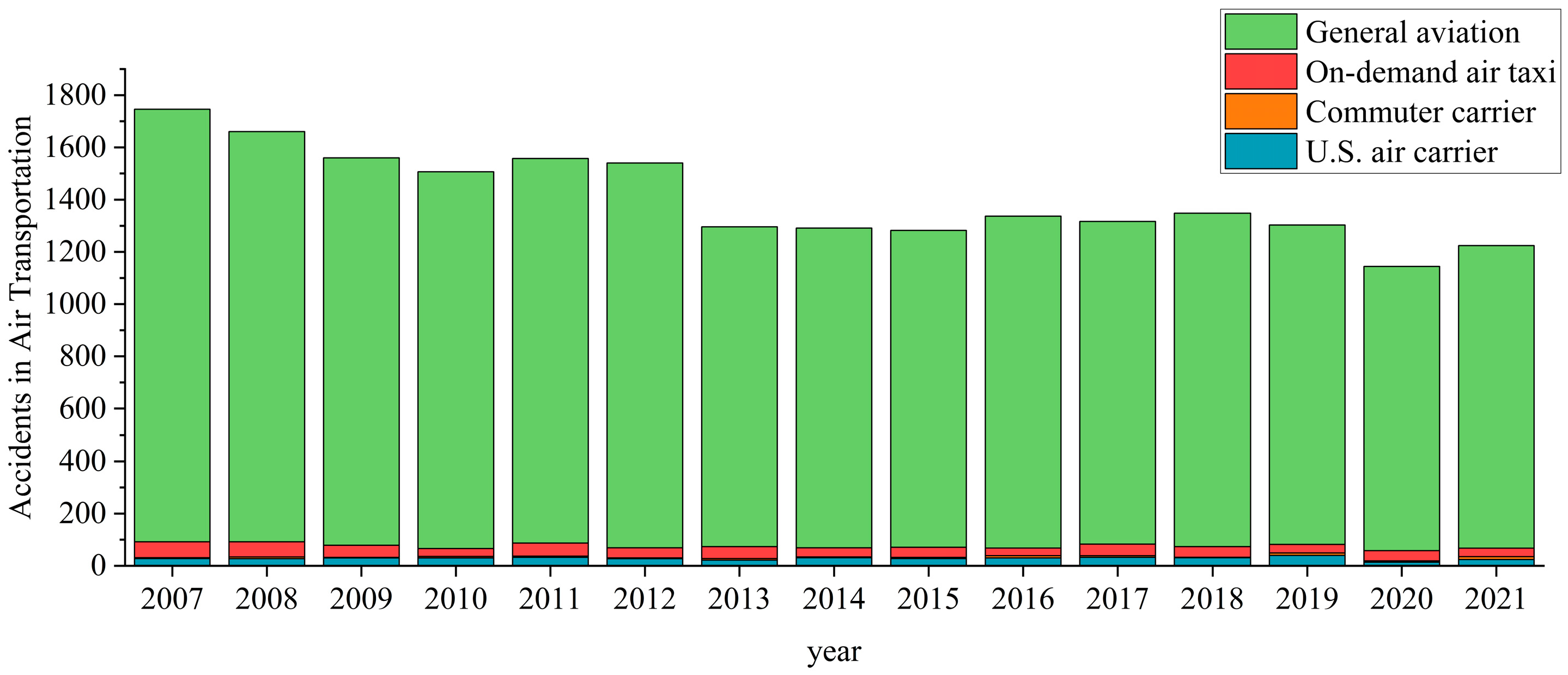
2.1. Data Sources
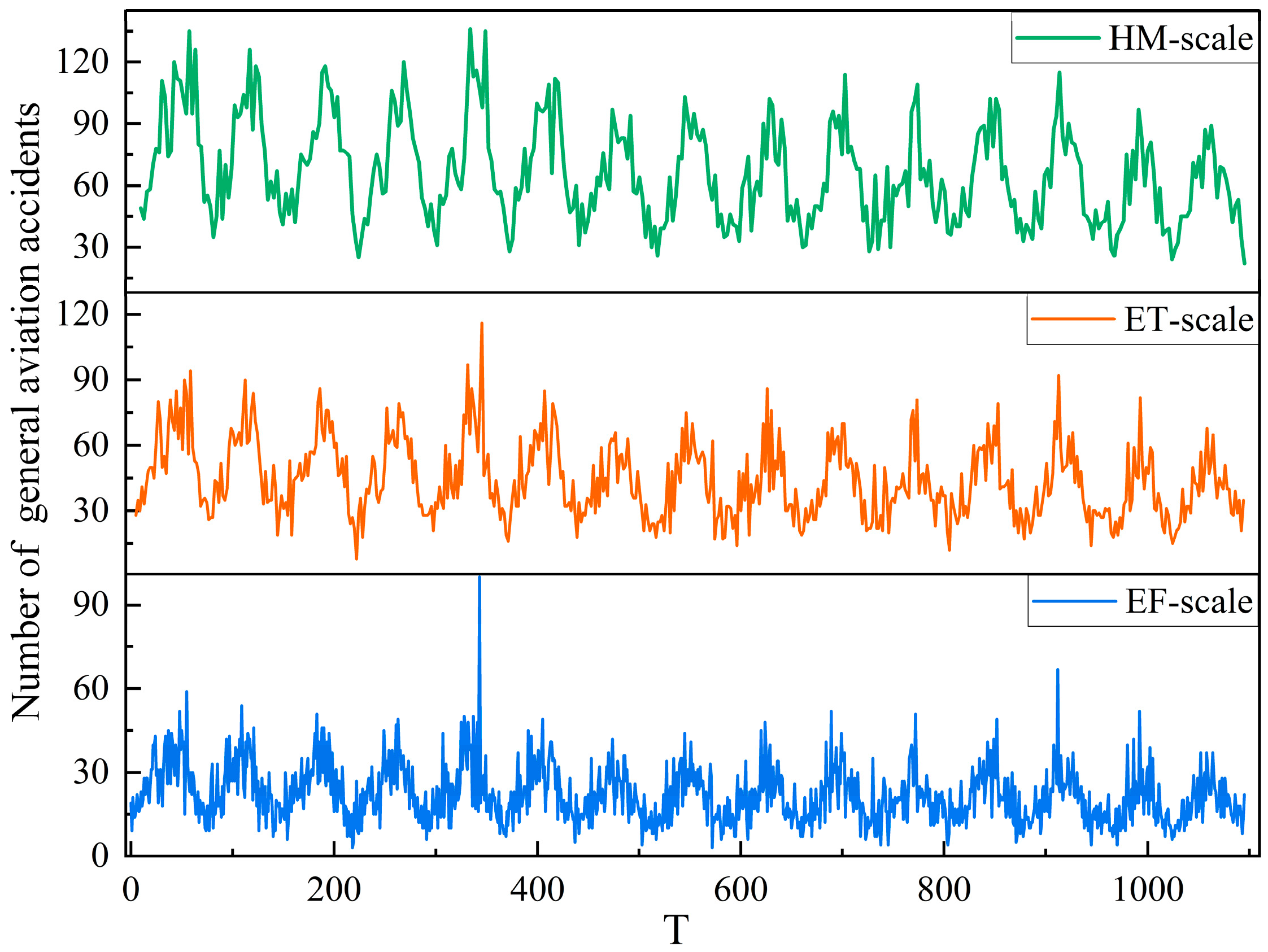
2.2. Time Series Construction
3. Methodology
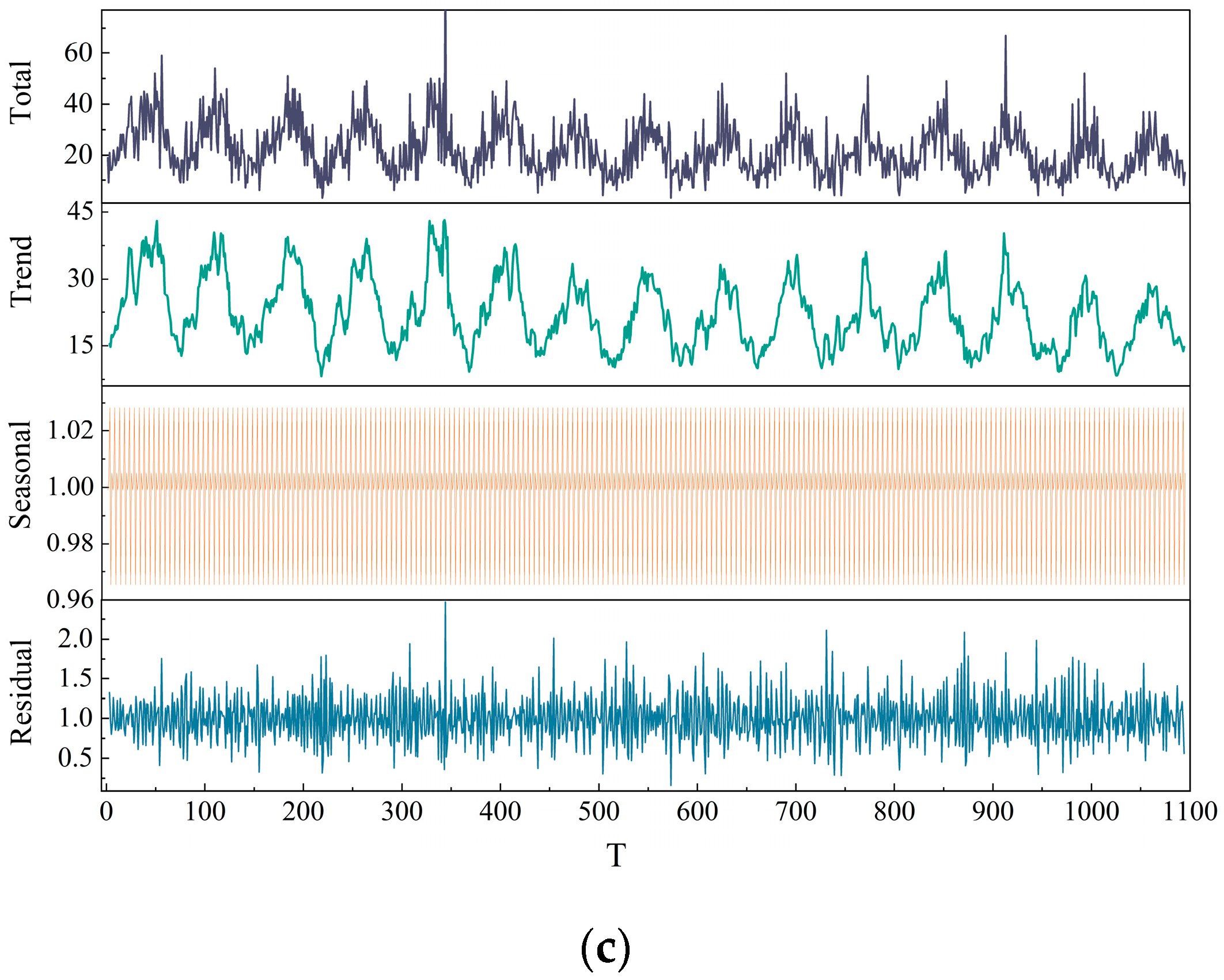
3.1. Time Series Seasonality Decomposition
3.2. Multi-Timescale Series Nonlinear Analysis
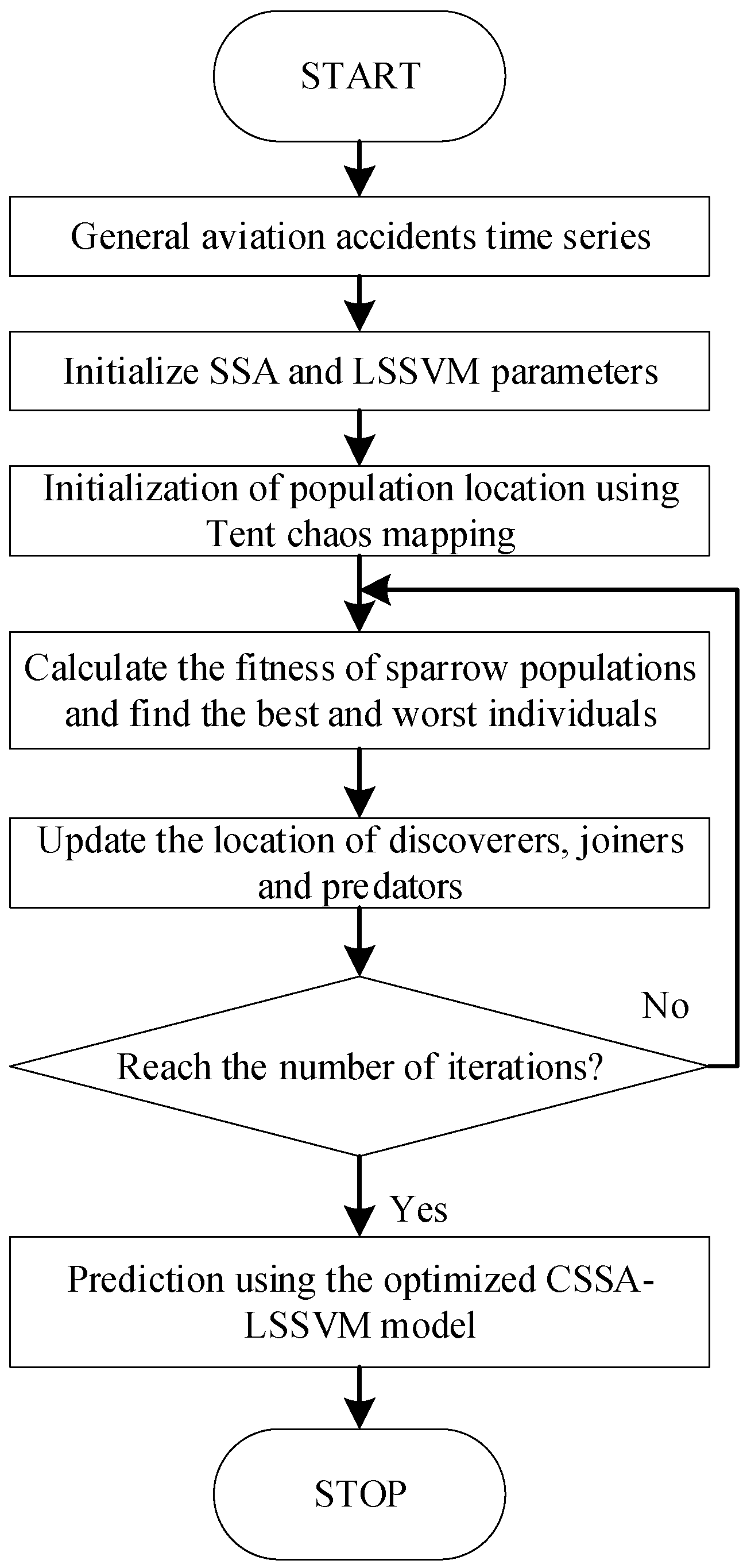
3.3. Multi-Timescale Series Prediction Model
- Initialize population:
- 2.
- Discoverer explores new solutions:
- 3.
- Joiner updates position:
- 4.
- Predator updates position
4. Simulation Analysis
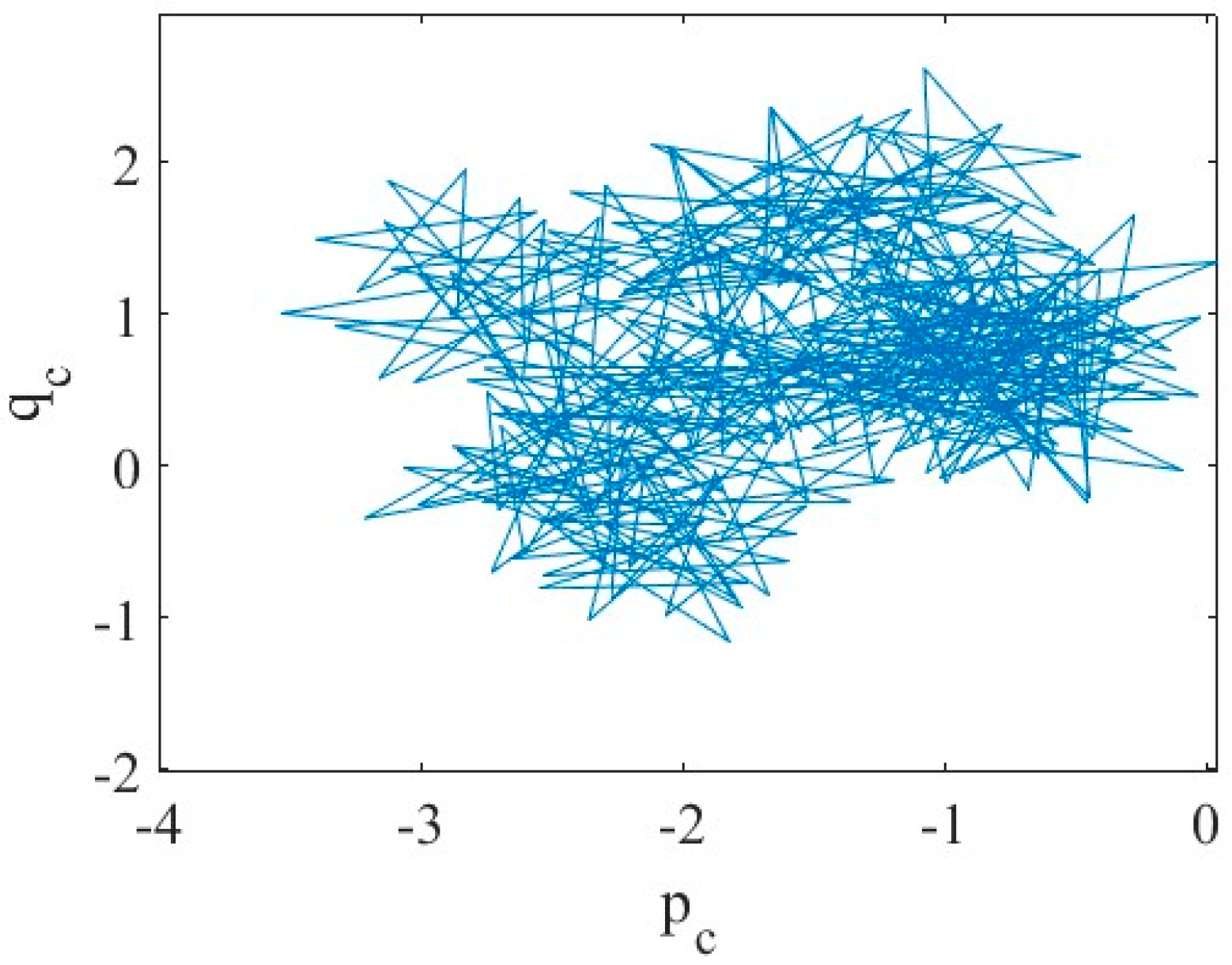
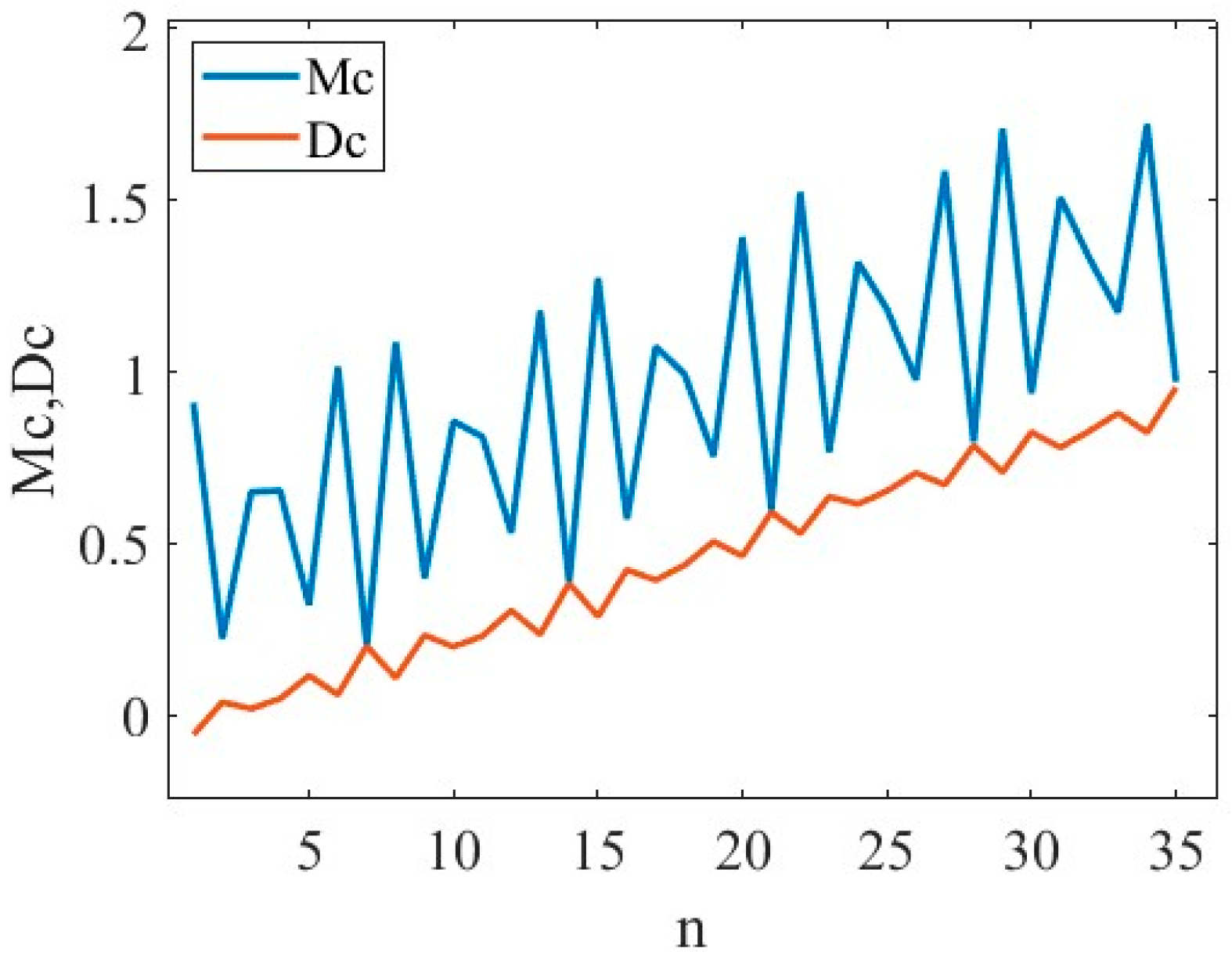
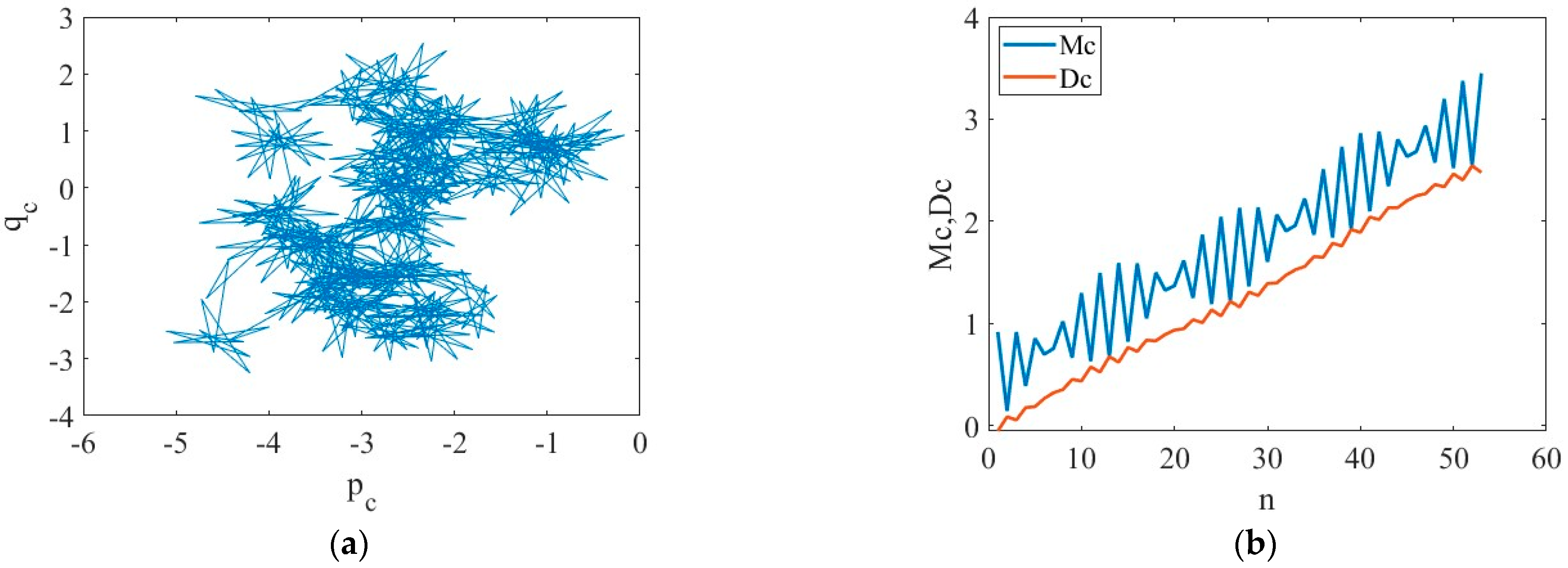
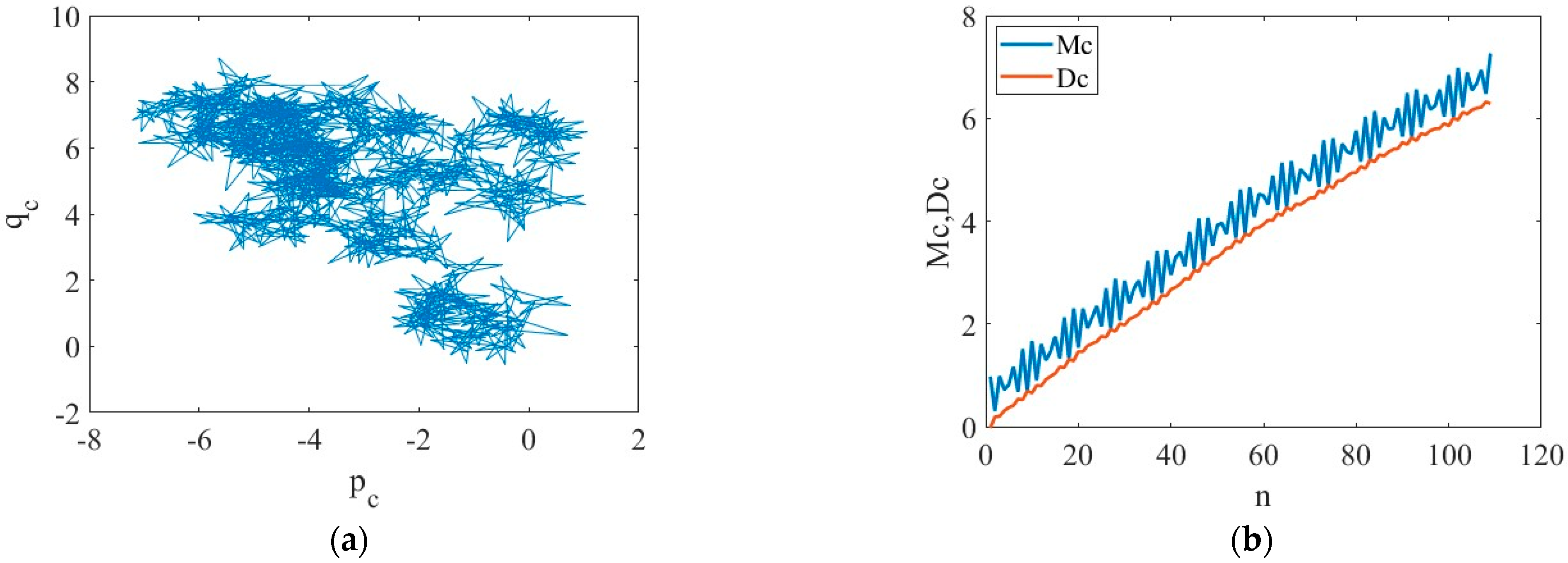
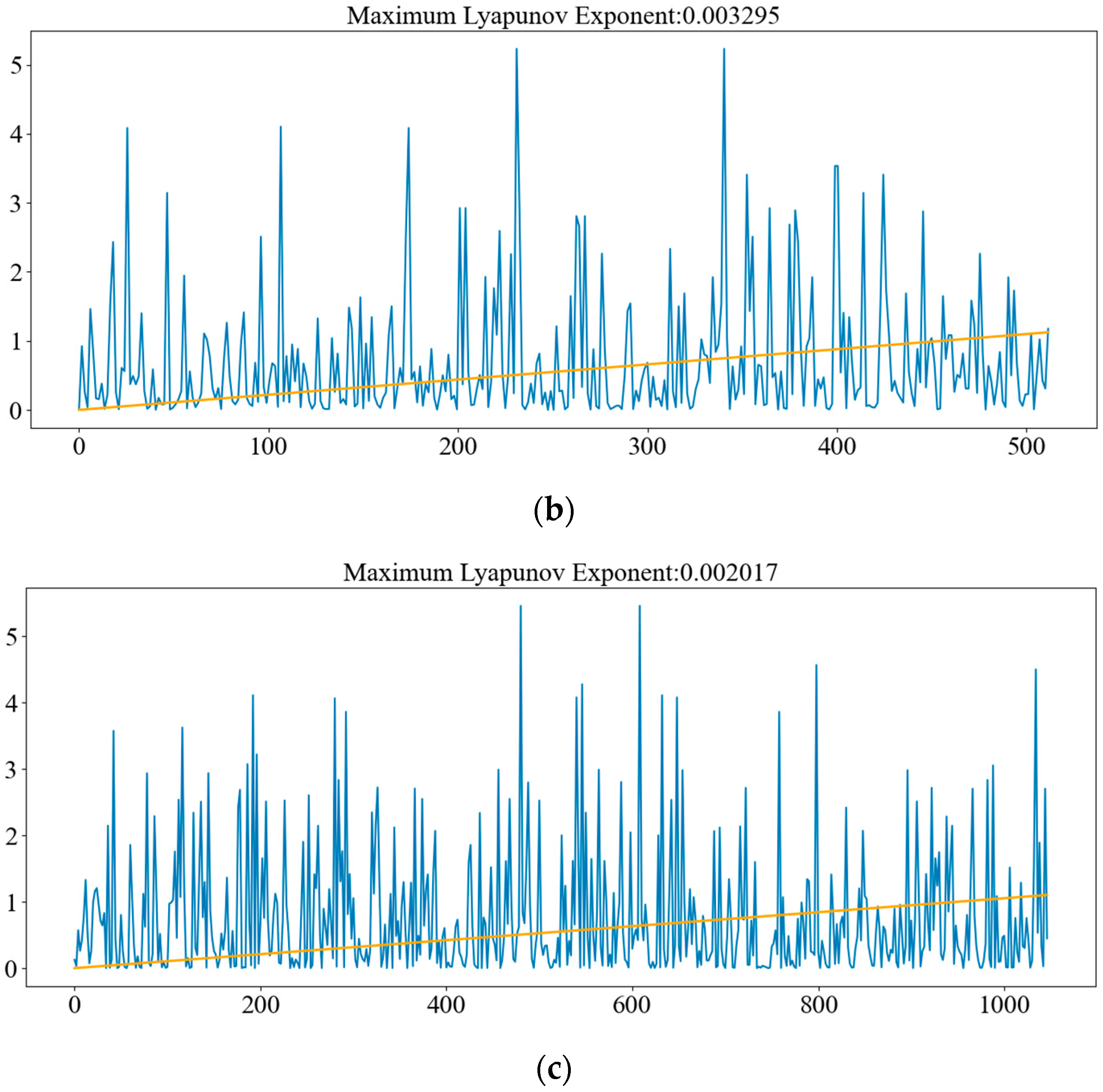
4.1. Multi-Timescale Series Nonlinearity Validation
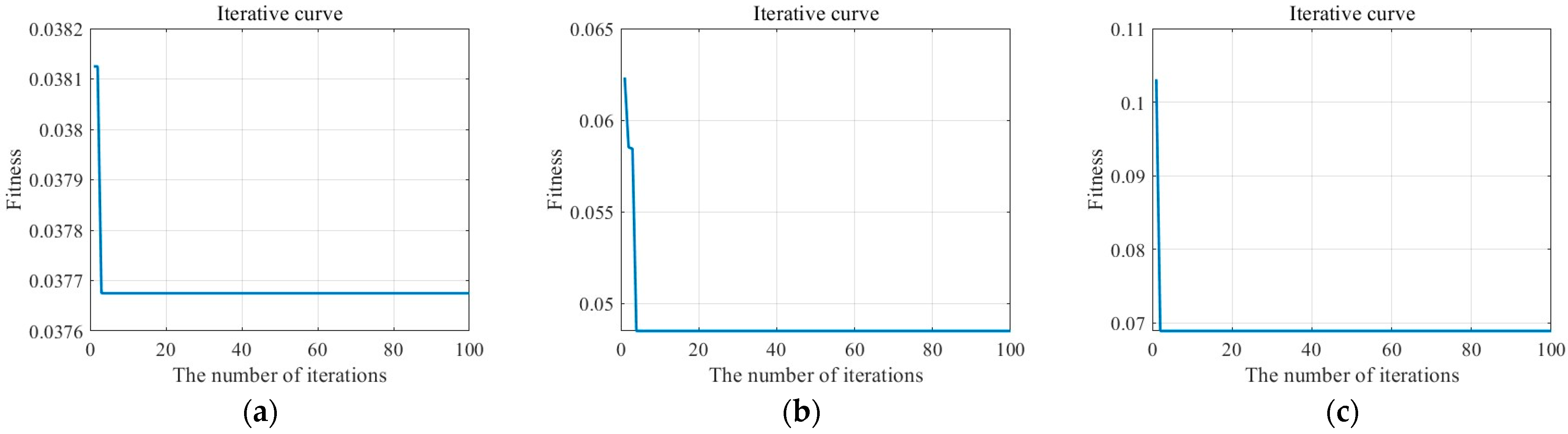
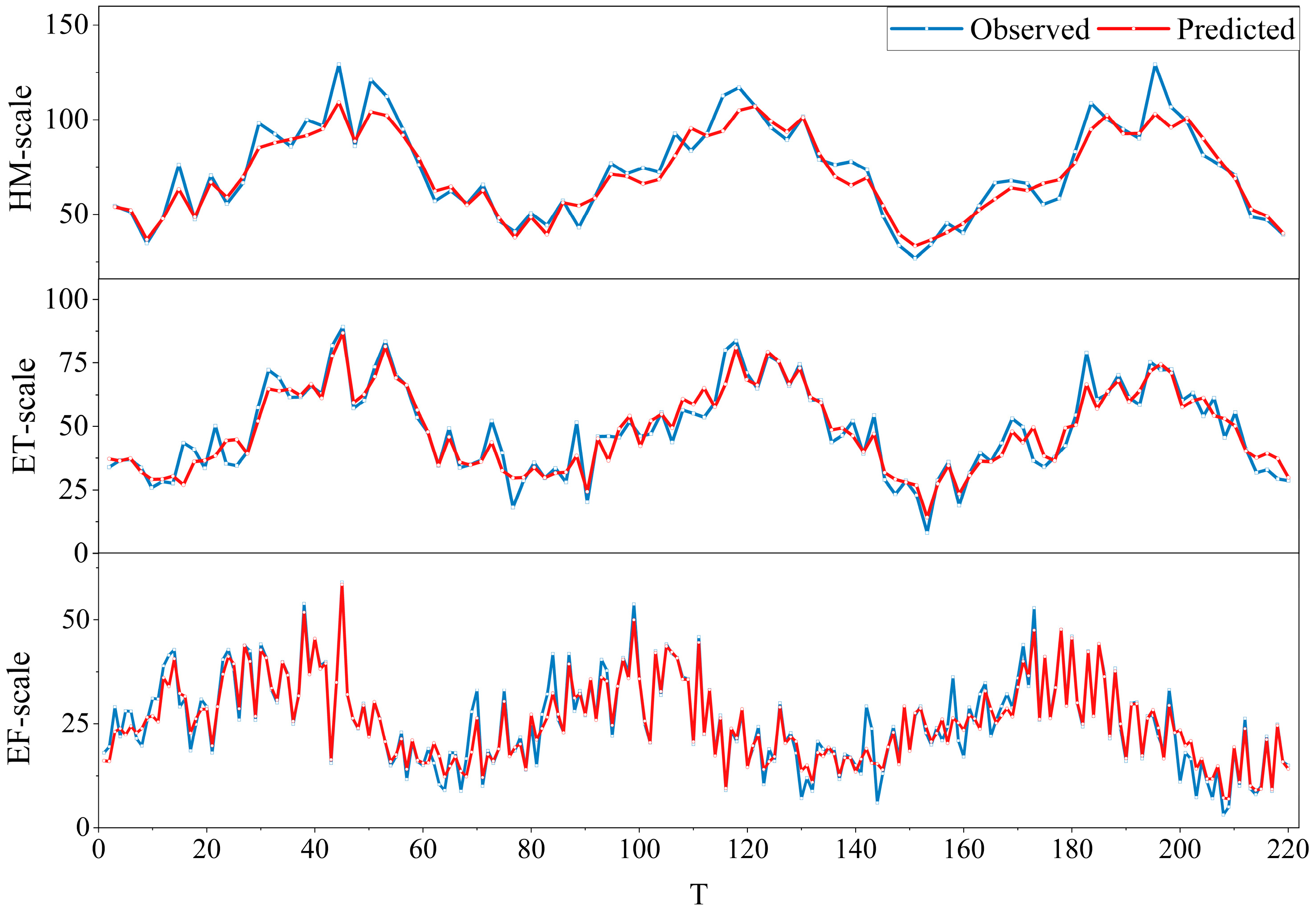
4.2. Multi-Timescale Series Predicting Simulation Analysis
5. Conclusions
- (1)
- The residual parts of the decomposition show the apparent randomness and irregular oscillations of the general aviation accident time series. As a consequence, the nonlinear characteristics of the time series have been investigated in this study. The 0–1 test shows that the phase diagram possesses Brownian motion features, and the Lyapunov exponent is positive at all three timescales. Both prove that the multi-timescale series of general aviation accidents show a chaotic pattern. With a decreasing timescale, there is no substantial change in time delay, embedding size, or maximum Lyapunov exponent.
- (2)
- The parameters of the LSSVM model are optimized by the chaotic sparrow search algorithm, and the prediction method of the CSSA-LSSVM model is proposed. The experimental simulation prediction effect is quantified and analyzed with the root mean square error (RMSE), mean absolute error (MAE), and correlation coefficient (R2). Compared with the original LSSVM model, the proposed CSSA-LSSVM model has obvious advantages and shows higher prediction results in simulation experiments. The accuracy of RMSE, MAE, and R2 is significantly improved in these three performance evaluations.
- (3)
- By comparing with other conventional time series prediction algorithms, the CSSA-LSSVM model is superior to them in terms of lesser errors, faster iterative convergence, and better fit. In addition, by comparing the prediction effect over different timescales, the prediction error is shown to be lower at a smaller timescale (EF-scale), showing that dividing the general aviation accident time series into fine-grained subseries benefits accurate prediction. While the timescale with the most accurate fit is ET-scale, indicating that the smallest granularity is not the best, the performance of multiple granularities must be examined to discover the optimal value.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- ICAO. ICAO Annex 13 to the Convention on International Civil Aviation: Aircraft Accident and Incident Investigation; ICAO: Montreal, QC, Canada, 2010. [Google Scholar]
- He, P.; Sun, R. Research on Cross-Correlation, Co-Integration, and Causality Relationship between Civil Aviation Incident and Airline Capacity in China. Sustainability 2022, 14, 4999. [Google Scholar] [CrossRef]
- Bao, J.; Chen, Y.; Yin, J.; Chen, X.; Zhu, D. Exploring Topics and Trends in Chinese ATC Incident Reports Using a Domain-Knowledge Driven Topic Model. J. Air Transp. Manag. 2023, 108, 102374. [Google Scholar] [CrossRef]
- Kuhn, K.D. Using Structural Topic Modeling to Identify Latent Topics and Trends in Aviation Incident Reports. Transp. Res. Part C Emerg. Technol. 2018, 87, 105–122. [Google Scholar] [CrossRef]
- Arnaldo Valdés, R.M.; Gómez Comendador, V.F.; Perez Sanz, L.; Rodriguez Sanz, A. Prediction of Aircraft Safety Incidents Using Bayesian Inference and Hierarchical Structures. Saf. Sci. 2018, 104, 216–230. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, J.; Sun, Y.; Li, C.; Dong, Z. Adaptive Flight Accident Prediction Method Based on Volterra Series. Fire Control Command Control 2020, 45, 115–119. [Google Scholar] [CrossRef]
- Yu, H.; Li, X. On the Chaos Analysis and Prediction of Aircraft Accidents Based on Multi-Timescales. Phys. Stat. Mech. Its Appl. 2019, 534, 120828. [Google Scholar] [CrossRef]
- Ni, X.; Wang, H.; Che, C.; Hong, J.; Sun, Z. Civil Aviation Safety Evaluation Based on Deep Belief Network and Principal Component Analysis. Saf. Sci. 2019, 112, 90–95. [Google Scholar] [CrossRef]
- Zeng, J.; Li, X. Prediction of Mine Subsidence Area Based on Chaotic Time Series Analysis. Gold Sci. Technol. 2019, 27, 249. [Google Scholar]
- Meng, Y.; Xu, L.; Yang, J. Application of Multi-Scale Chaotic Time Series Prediction in Early Warning of Electric Equipment Current-Carrying Fault. Dianji Yu Kongzhi Xuebao Electric Mach. Control 2015, 19, 1–7. [Google Scholar] [CrossRef]
- Ales, S.; Nico, P.; Paolo, P. Chaos based portfolio selection: A nonlinear dynamics approach. Expert Syst. Appl. 2022, 188, 116055. [Google Scholar] [CrossRef]
- Yuan, P.; Lin, X. How Long Will the Traffic Flow Time Series Keep Efficacious to Forecast the Future? Phys. Stat. Mech. Its Appl. 2017, 467, 419–431. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Y. A Method for Predicting Air Traffic Flow Based on a Combined GA, RBF, and Improved Cao Method. J. Transp. Inf. Saf. 2023, 41, 115–123. [Google Scholar] [CrossRef]
- Li, G.; Guo, M.; Zhang, H.; Luo, Y. Traffic Status Prediction Method of Regional Air Route Network Based on Chaos Theory. Aeronaut. Comput. Tech. 2020, 50, 61–66. [Google Scholar]
- Cheng, A.; Jiang, X.; Li, Y.; Zhang, C.; Zhu, H. Multiple Sources and Multiple Measures Based Traffic Flow Prediction Using the Chaos Theory and Support Vector Regression Method. Phys. Stat. Mech. Its Appl. 2017, 466, 422–434. [Google Scholar] [CrossRef]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar] [CrossRef]
- Bergel-Hayat, R.; Zukowska, J. Road Safety Trends at National Level in Europe: A Review of Time-Series Analysis Performed during the Period 2000–2012. Transp. Rev. 2015, 35, 650–671. [Google Scholar] [CrossRef]
- Gaspard, P. Dynamical systems and their linear stability. In Chaos, Scattering and Statistical Mechanics; Cambridge Nonlinear Science Series; Cambridge University Press: Cambridge, UK, 1998; pp. 12–42. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. The 0-1 Test for Chaos: A Review. In Chaos Detection and Predictability; Skokos, C., Gottwald, G.A., Laskar, J., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2016; Volume 915, pp. 221–247. ISBN 978-3-662-48408-1. [Google Scholar]
- Wen, F.; Wan, Q. Time Delay Estimation Based on Mutual Information Estimation. In Proceedings of the 2009 2nd International Congress on Image and Signal Processing, Tianjin, China, 17–19 October 2009; pp. 1–5. [Google Scholar]
- Xu, X.; Liu, X.; Chen, X. The Cao Method for Determining the Minimum Embedding Dimension of Sea Clutter. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar]
- Hong, W.C. Phase Space Reconstruction and Recurrence Plot Theory. In Hybrid Intelligent Technologies in Energy Demand Forecasting; Springer: Cham, Switzerland, 2020; pp. 153–179. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Rand, D., Young, L.-S., Eds.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1981; Volume 898, pp. 366–381. ISBN 978-3-540-11171-9. [Google Scholar]
- Ji, T.; Wang, J.; Li, M.; Wu, Q. Short-Term Wind Power Forecast Based on Chaotic Analysis and Multivariate Phase Space Reconstruction. Energy Convers. Manag. 2022, 254, 115196. [Google Scholar] [CrossRef]
- Cencini, M.; Ginelli, F. Lyapunov Analysis: From Dynamical Systems Theory to Applications. J. Phys. Math. Theor. 2013, 46, 250301. [Google Scholar] [CrossRef]
- Deng, C.; Zhang, X.; Huang, Y.; Bao, Y. Equipping Seasonal Exponential Smoothing Models with Particle Swarm Optimization Algorithm for Electricity Consumption Forecasting. Energies 2021, 14, 4036. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, Q.; Ding, Y.; Zhang, D. Application of a Hybrid ARIMA-LSTM Model Based on the SPEI for Drought Forecasting. Environ. Sci. Pollut. Res. 2022, 29, 4128–4144. [Google Scholar] [CrossRef]
- Amshi, A.H.; Prasad, R.; Sharma, B.K. Forecasting Cholera Disease Using SARIMA and LSTM Models with Discrete Wavelet Transform as Feature Selection. IFS 2023, 1–13. [Google Scholar] [CrossRef]
- Qian, G.; Tordesillas, A.; Zheng, H. Landslide Forecast by Time Series Modeling and Analysis of High-Dimensional and Non-Stationary Ground Motion Data. Forecasting 2021, 3, 850–867. [Google Scholar] [CrossRef]
- Madeira, T.; Melício, R.; Valério, D.; Santos, L. Machine Learning and Natural Language Processing for Prediction of Human Factors in Aviation Incident Reports. Aerospace 2021, 8, 47. [Google Scholar] [CrossRef]
- Aryal, S.; Nadarajah, D.; Kasthurirathna, D.; Rupasinghe, L.; Jayawardena, C. Comparative Analysis of the Application of Deep Learning Techniques for Forex Rate Prediction. In Proceedings of the 2019 International Conference on Advancements in Computing (ICAC), Malabe, Sri Lanka, 5–7 December 2019; pp. 329–333. [Google Scholar]
- Rafsanjani, M.K.; Samareh, M. Chaotic Time Series Prediction by Artificial Neural Networks. JCM 2016, 16, 599–615. [Google Scholar] [CrossRef]
- Lin, L.; Li, M.; Ma, L.; Nazari, M.; Mahdavi, S.; Yunianta, A. Using Fuzzy Uncertainty Quantization and Hybrid RNN-LSTM Deep Learning Model for Wind Turbine Power. IEEE Trans. Ind. Appl. 2020, 1. [Google Scholar] [CrossRef]
- Liu, Y.; Du, R.; Niu, D. Forecast of Coal Demand in Shanxi Province Based on GA—LSSVM under Multiple Scenarios. Energies 2022, 15, 6475. [Google Scholar] [CrossRef]
- Guo, Z.; Hu, L.; Wang, J.; Hou, M. Short-Term Load Forecasting Based on SSA-LSSVM Model. In Proceedings of the 2021 4th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China, 23–25 April 2021; pp. 1215–1219. [Google Scholar]
- Tan, G.; Yan, J.; Gao, C.; Yang, S. Prediction of Water Quality Time Series Data Based on Least Squares Support Vector Machine. Procedia Eng. 2012, 31, 1194–1199. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J. Residuals-Based Deep Least Square Support Vector Machine with Redundancy Test Based Model Selection to Predict Time Series. Tsinghua Sci. Technol. 2019, 24, 706–715. [Google Scholar] [CrossRef]
- Sun, W.; Gao, Q. Short-Term Wind Speed Prediction Based on Variational Mode Decomposition and Linear–Nonlinear Combination Optimization Model. Energies 2019, 12, 2322. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, S. A Stochastic Configuration Network Based on Chaotic Sparrow Search Algorithm. Knowl.-Based Syst. 2021, 220, 106924. [Google Scholar] [CrossRef]
- Bao, Y.; Wang, T.; Qiu, G. Research on Applicability of SVM Kernel Functions Used in Binary Classification. In Proceedings of the International Conference on Computer Science and Information Technology, Kunming, China, 21–23 September 2013; Patnaik, S., Li, X., Eds.; Advances in Intelligent Systems and Computing. Springer: New Delhi, India, 2014; Volume 255, pp. 833–844. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Li, Z.; Luo, X.; Liu, M.; Cao, X.; Du, S.; Sun, H. Wind Power Prediction Based on EEMD-Tent-SSA-LS-SVM. Energy Rep. 2022, 8, 3234–3243. [Google Scholar] [CrossRef]
- Xie, Z.; Enyuan, X.; Hongzhi, L.; Yifei, Z.; Mengqi, W. Fluctuation Characteristics of Arrival Flight Flow Based on Limited Penetrable Visibility Graph. J. Transp. Syst. Eng. Inf. Technol. 2022, 6, 244–257. [Google Scholar] [CrossRef]


| NTSB-No. | Event Date | City | State | N# | Highest Injury Level |
|---|---|---|---|---|---|
| DEN07CA046 | 1 January 2007 17:30 | Walden | Colo. | N821GS | None |
| DFW07LA052 | 2 January 2007 13:40 | Tulsa | Okla. | YV-2045 | None |
| CHI07FA052 | 2 January 2007 16:00 | Washington | Ind. | N678DC | Fatal |
| DFW07FA049 | 2 January 2007 22:35 | Armstrong | Texas | N3940R | Fatal |
| CHI07CA054 | 3 January 2007 14:51 | Alton | Ill. | N364MA | None |
| DEN07LA044 | 3 January 2007 17:05 | Baldwin City | Kan. | N113JD | Serious |
| DFW07FA051 | 4 January 2007 14:35 | Batesville | Ark. | N2658 | Fatal |
| SEA07CA042 | 4 January 2007 18:00 | Buckley | Wash. | N186AC | None |
| NYC07CA054 | 4 January 2007 18:45 | Hackettstown | N.J. | N695X | None |
| ATL07FA031 | 5 January 2007 1:37 | Columbia | S.C. | N55YS | Fatal |
| DEN07FA045 | 5 January 2007 8:56 | Manzanilla | Colo. | N8231D | Fatal |
| CHI07CA055 | 5 January 2007 16:45 | Bristol | Wis. | N63332 | None |
| Prediction Model | RMSE | MAE | R2 |
|---|---|---|---|
| CSSA-LSSVM | 8.10 | 6.12 | 0.88 |
| SSA-LSSVM | 8.62 | 6.24 | 0.88 |
| GA-LSSVM | 8.79 | 6.42 | 0.87 |
| PSO-LSSVM | 8.96 | 6.28 | 0.88 |
| LSSVM | 9.10 | 5.03 | 0.86 |
| CNN | 10.31 | 7.30 | 0.80 |
| ANN | 11.68 | 9.67 | 0.73 |
| LSTM | 14.26 | 11.71 | 0.49 |
| ARIMA | 20.62 | 17.67 | 0.01 |
| Holt-Winters | 27.23 | 21.61 | −0.80 |
| Timescale | RMSE | MAE | R2 |
|---|---|---|---|
| EF-scale | 3.43 | 2.34 | 0.88 |
| ET-scale | 5.22 | 3.72 | 0.91 |
| HM-scale | 8.10 | 6.12 | 0.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, H.; Shi, Z.; Zhou, J.; Liu, W. Nonlinear Time Series Analysis and Prediction of General Aviation Accidents Based on Multi-Timescales. Aerospace 2023, 10, 714. https://doi.org/10.3390/aerospace10080714
Wang Y, Zhang H, Shi Z, Zhou J, Liu W. Nonlinear Time Series Analysis and Prediction of General Aviation Accidents Based on Multi-Timescales. Aerospace. 2023; 10(8):714. https://doi.org/10.3390/aerospace10080714
Chicago/Turabian StyleWang, Yufei, Honghai Zhang, Zongbei Shi, Jinlun Zhou, and Wenquan Liu. 2023. "Nonlinear Time Series Analysis and Prediction of General Aviation Accidents Based on Multi-Timescales" Aerospace 10, no. 8: 714. https://doi.org/10.3390/aerospace10080714






