Star-Identification System Based on Polygon Recognition
Abstract
:1. Introduction
2. Description of Algorithm
2.1. Creation of Star Catalog
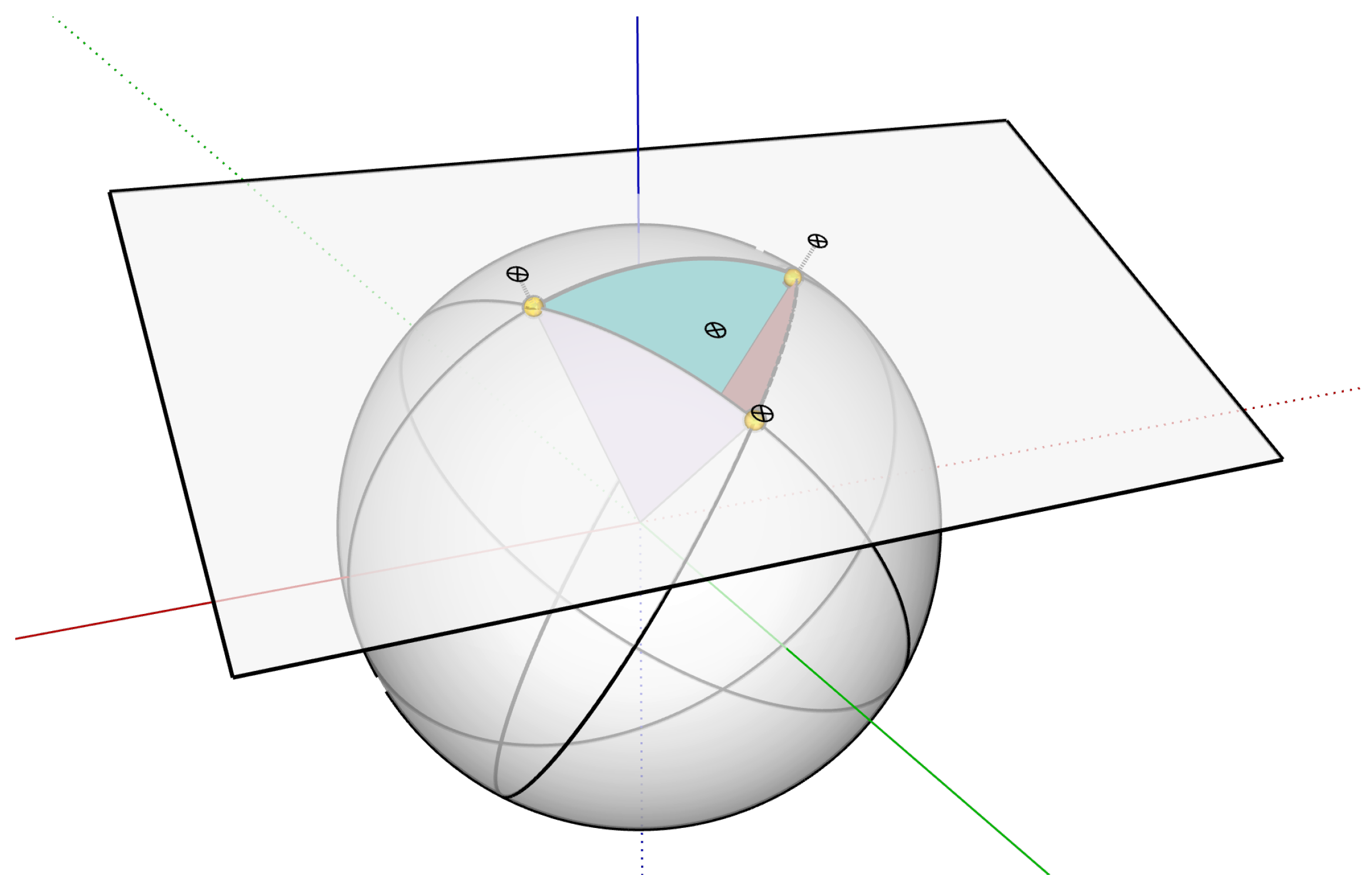
2.2. Invariant Algorithm
- Choice of central star A;
- Search for the nearest neighbor star to A, which is B.
- Creation of a straight line between A and B, named AB.
- Sorted from the smallest to the largest angle between the line AB and each of the other stars, measured counterclockwise.
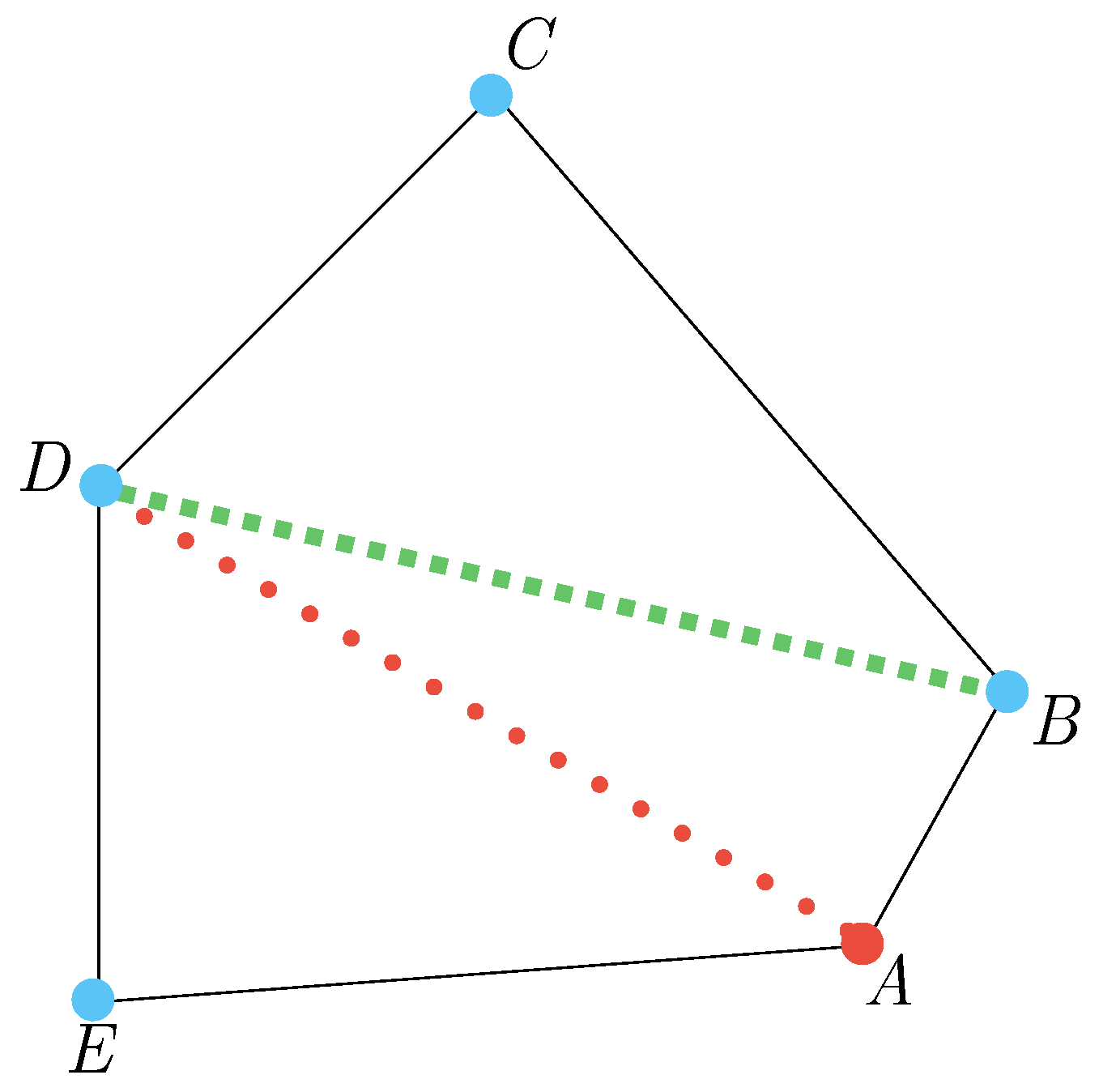
2.3. Technique for Vertices Removal and Replacement
2.4. Binary Search Method
2.5. Verification Algorithm
2.5.1. Verification by Internal Polygons
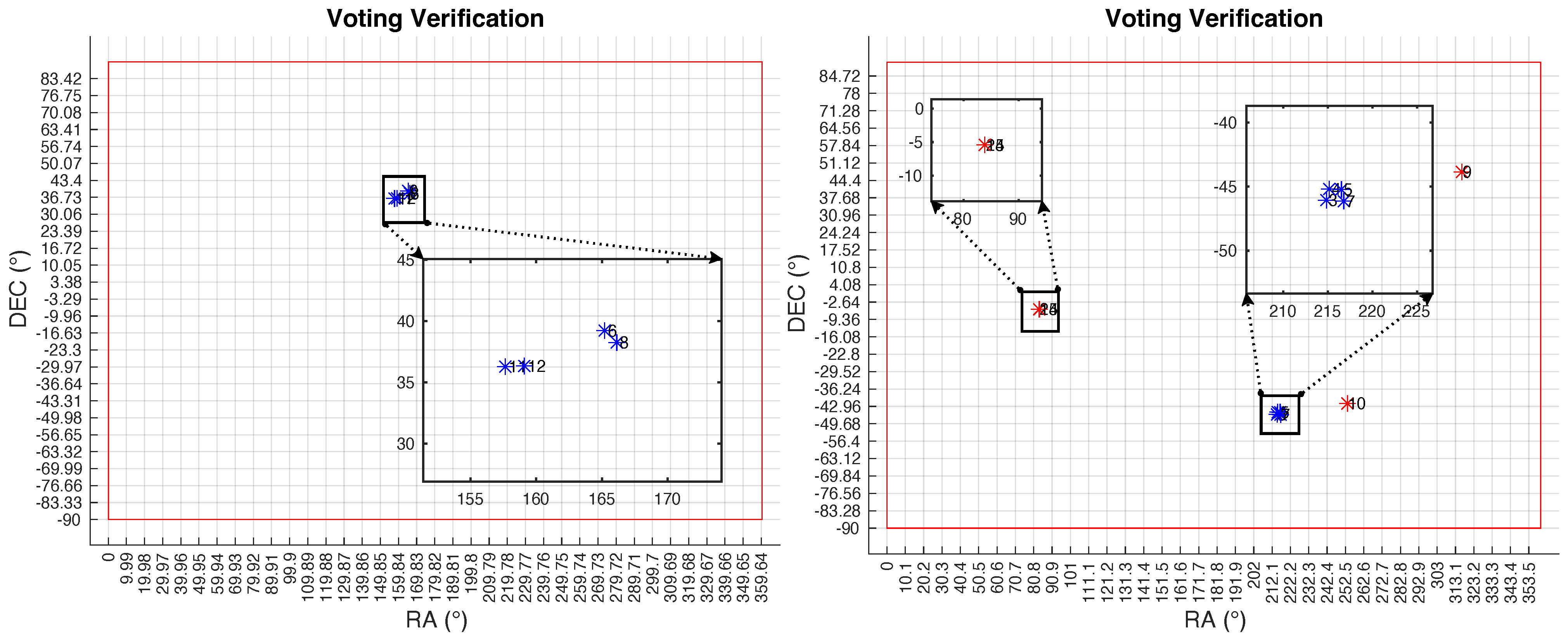
2.5.2. Voting Verification
- For all stars found in the global search, the distance between their coordinates is obtained in a great circle.
- They are grouped into regions with distances smaller than the FOV of the real image.
- The method cannot decide, if it has found only one star.
- If two stars are in the same region, the method verifies their identification; otherwise, it cancels both.
- In groups with several stars in each, the group with the largest number is verified.
3. Implementation
3.1. Hardware and Test Bench Setup
3.2. Image Acquisition Process
3.3. Experimental Procedure
- Each image pixel is analyzed from left to right and then from top to bottom.
- For each pixel considered as an object (other than 0), the mask of Figure 7 is applied, and the labels already assigned are analyzed. The current pixel in work is represented by .
- If a label already exists within the mask, it is replaced in the pixel, and if several labels are assigned, the smallest one is taken.
- A second scanning assigns the labels to the neighbors.
| Algorithm 1 Match invariants with the kd-tree search algorithm |
| for each in do if (RangeSearchkd-tree() in point ) ≠ 0 then match = matched invariants if (RangeSearchkd-tree(match(,)) in point (,)) ≠ 0 then match = update matches print verified stars end if end if end for |
4. Experimental Results
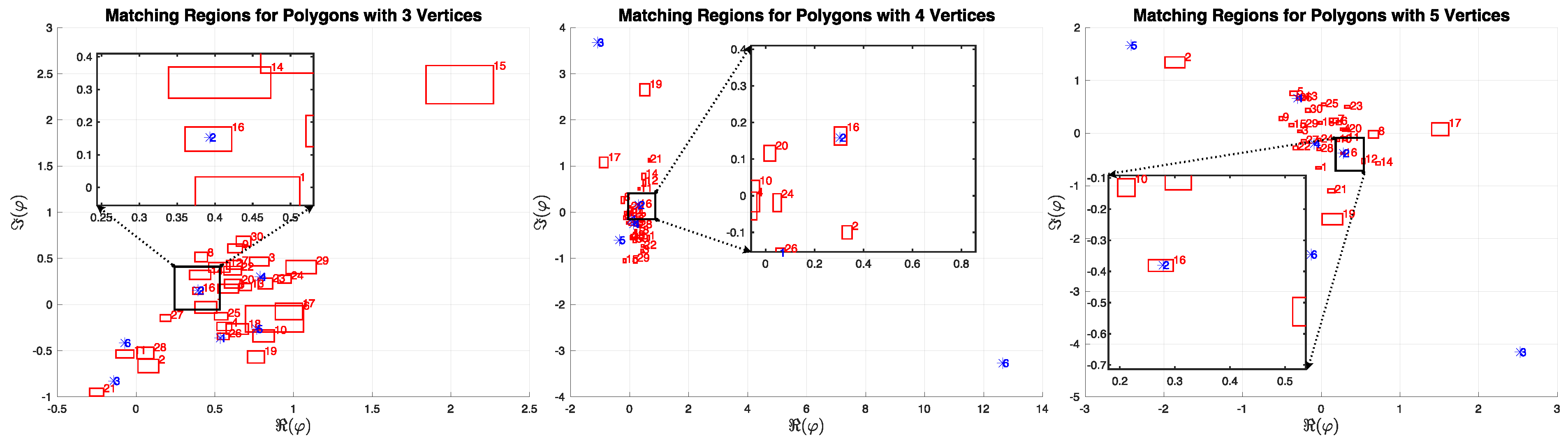
4.1. Matching Regions for Polygons with Three, Four, and Five Vertices
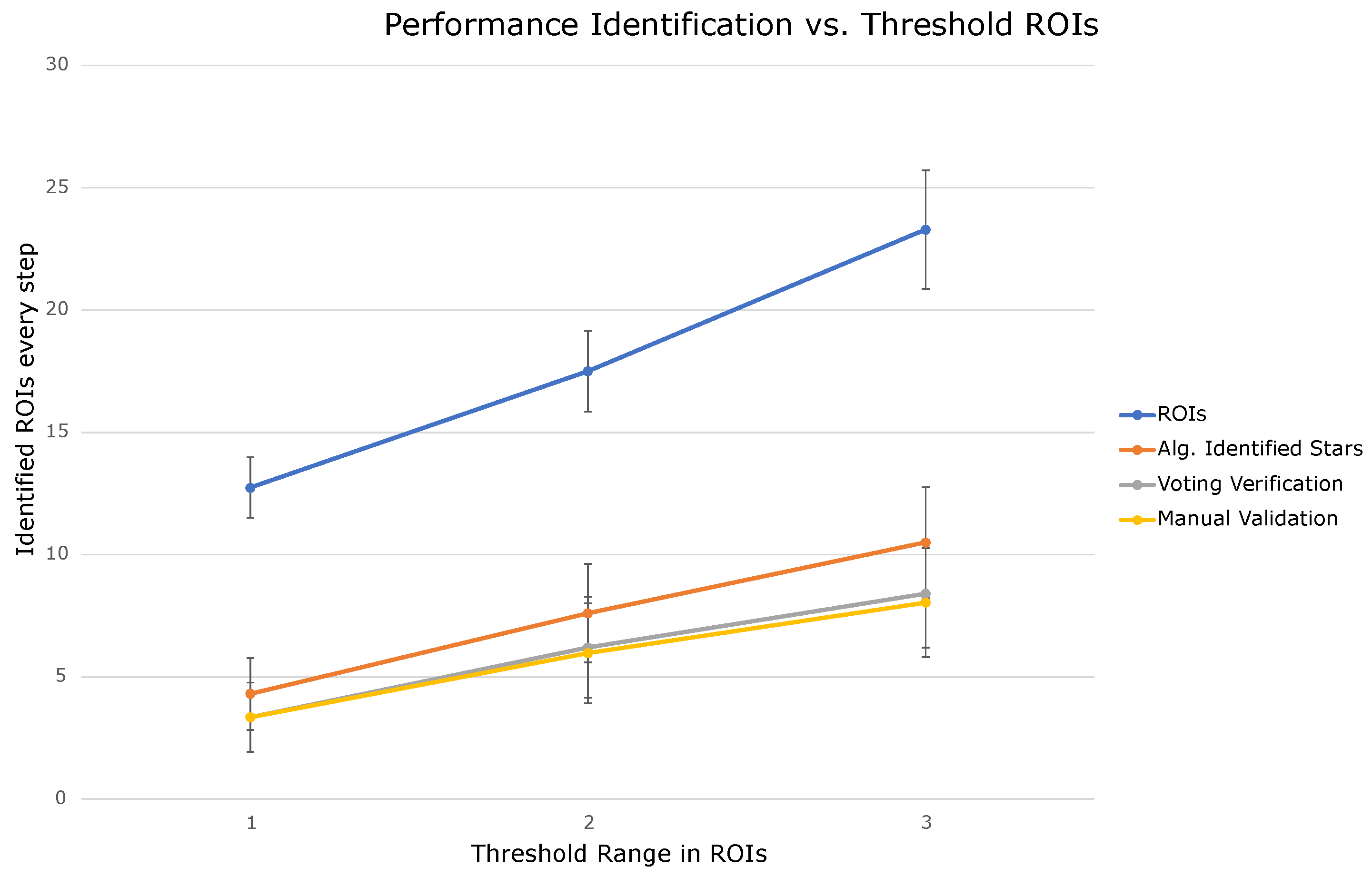
4.2. Voting Verification Results
4.3. Results of Identification in Our Catalogs
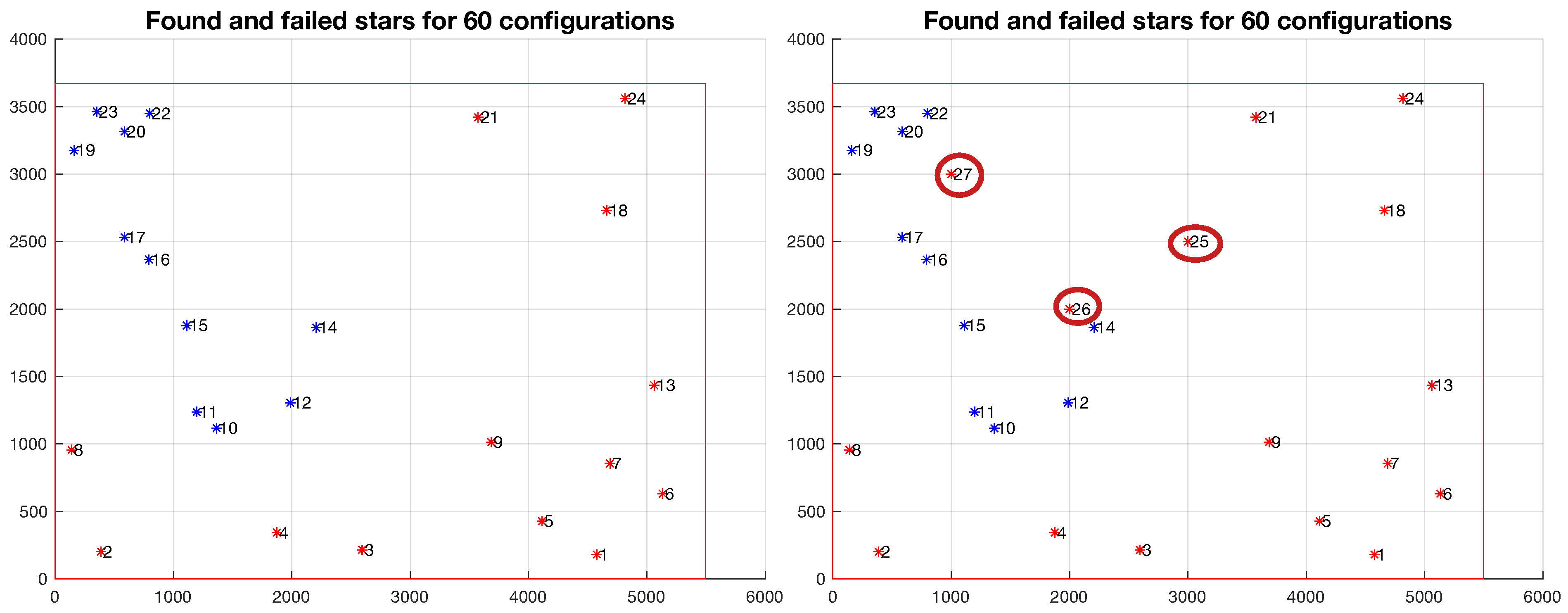
4.4. Performance and Results with Addition of False Stars
4.5. Relationship to Earlier Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FOV | Field of view for each optical setup |
| ROI | Region of interest |
| GAIA DR2 | Data Release version 2 of the space mission Gaia |
| RA, barycentric right ascension in ICRS system | |
| DEC, barycentric declination in ICRS system | |
| The invariant complex number associated with every polygon | |
| Catalog of invariant complex numbers from GAIA Database polygons | |
| Catalog of invariant complex numbers from our real-images polygons | |
| Polygons created with five, four, and three stars in the vertices | |
| The maximum value of the histogram | |
| Threshold fixed value for considering a region of pixels to be relevant | |
| Threshold dynamic value that adjusts with bisection algorithm | |
| Noise catalog with 100 invariants for each polygon | |
| and | Region or box with minimum and maximum of the |
Appendix A
Appendix A.1. Tables of Results of the 100 Images Acquired
| 15–20 ROIs | 21–30 ROIs | 31–40 ROIs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. Image | ROIs | A.-Id. Stars | V1 | V2 | ROIs | A.-Id. Stars | V1 | V2 | ROIs | A.-Id. Stars | V1 | V2 | Id. (Yes/No) |
| 1 | 12 | 1 | 1 | 0 | 16 | 2 | 2 | 1 | 21 | 14 | 10 | 10 | 001 |
| 2 | 13 | 7 | 2 | 2 | 14 | 5 | 3 | 3 | 27 | 13 | 12 | 12 | 111 |
| 3 | 15 | 7 | 4 | 4 | 20 | 11 | 11 | 11 | 24 | 14 | 12 | 12 | 111 |
| 4 | 14 | 8 | 8 | 8 | 15 | 8 | 8 | 8 | 24 | 14 | 13 | 13 | 111 |
| 5 | 13 | 11 | 10 | 10 | 17 | 14 | 13 | 13 | 22 | 12 | 9 | 8 | 111 |
| 6 | 6 | 0 | 0 | 0 | 11 | 3 | 2 | 2 | 13 | 2 | 2 | 0 | 010 |
| 7 | 9 | 5 | 3 | 3 | 13 | 5 | 2 | 2 | 13 | 5 | 2 | 2 | 111 |
| 8 | 10 | 6 | 4 | 4 | 10 | 6 | 4 | 4 | 10 | 6 | 4 | 4 | 111 |
| 9 | 13 | 0 | 0 | 0 | 17 | 1 | 1 | 1 | 31 | 13 | 11 | 11 | 001 |
| 10 | 11 | 3 | 3 | 3 | 21 | 4 | 3 | 3 | 21 | 4 | 3 | 3 | 111 |
| 11 | 16 | 3 | 2 | 2 | 20 | 4 | 3 | 3 | 26 | 10 | 7 | 7 | 111 |
| 12 | 10 | 7 | 5 | 5 | 19 | 11 | 10 | 10 | 23 | 14 | 11 | 11 | 111 |
| 13 | 10 | 1 | 1 | 0 | 21 | 4 | 0 | 0 | 40 | 8 | 3 | 3 | 001 |
| 14 | 15 | 8 | 7 | 7 | 19 | 7 | 6 | 6 | 25 | 16 | 14 | 14 | 111 |
| 15 | 14 | 4 | 4 | 4 | 19 | 12 | 12 | 12 | 23 | 12 | 12 | 12 | 111 |
| 16 | 10 | 4 | 2 | 2 | 22 | 15 | 14 | 14 | 28 | 15 | 13 | 13 | 111 |
| 17 | 14 | 6 | 5 | 5 | 19 | 12 | 8 | 8 | 31 | 17 | 16 | 16 | 111 |
| 18 | 17 | 4 | 3 | 3 | 18 | 6 | 6 | 6 | 23 | 8 | 7 | 7 | 111 |
| 19 | 14 | 2 | 2 | 1 | 22 | 8 | 4 | 4 | 22 | 8 | 4 | 4 | 011 |
| 20 | 16 | 1 | 1 | 1 | 20 | 3 | 2 | 2 | 27 | 7 | 7 | 7 | 011 |
| 21 | 13 | 3 | 2 | 2 | 23 | 9 | 7 | 7 | 23 | 9 | 7 | 7 | 111 |
| 22 | 17 | 8 | 7 | 7 | 24 | 18 | 15 | 12 | 29 | 16 | 12 | 12 | 111 |
| 23 | 13 | 11 | 10 | 10 | 19 | 14 | 13 | 8 | 27 | 16 | 15 | 9 | 111 |
| 24 | 18 | 5 | 2 | 2 | 18 | 5 | 2 | 2 | 31 | 11 | 8 | 7 | 101 |
| 25 | 11 | 3 | 2 | 2 | 18 | 9 | 7 | 6 | 22 | 8 | 7 | 7 | 111 |
| 26 | 13 | 6 | 5 | 5 | 18 | 4 | 3 | 3 | 18 | 4 | 3 | 3 | 111 |
| 27 | 9 | 1 | 1 | 1 | 24 | 4 | 0 | 1 | 24 | 4 | 2 | 1 | 001 |
| 28 | 13 | 7 | 6 | 6 | 17 | 10 | 9 | 9 | 23 | 16 | 11 | 11 | 111 |
| 29 | 11 | 8 | 7 | 7 | 15 | 9 | 8 | 8 | 15 | 9 | 8 | 8 | 111 |
| 30 | 14 | 10 | 10 | 10 | 30 | 17 | 15 | 15 | 31 | 18 | 16 | 16 | 111 |
| 31 | 15 | 9 | 9 | 9 | 23 | 12 | 11 | 11 | 27 | 12 | 10 | 10 | 111 |
| 32 | 14 | 6 | 6 | 6 | 21 | 11 | 11 | 11 | 31 | 20 | 16 | 16 | 111 |
| 33 | 11 | 4 | 4 | 4 | 15 | 5 | 4 | 4 | 25 | 9 | 2 | 2 | 111 |
| 34 | 14 | 8 | 8 | 8 | 17 | 12 | 11 | 11 | 23 | 15 | 15 | 15 | 111 |
| 35 | 14 | 8 | 8 | 8 | 16 | 10 | 10 | 10 | 24 | 18 | 16 | 16 | 111 |
| 36 | 13 | 8 | 6 | 6 | 17 | 4 | 3 | 3 | 24 | 18 | 13 | 13 | 111 |
| 37 | 11 | 2 | 2 | 1 | 16 | 14 | 13 | 13 | 23 | 18 | 16 | 16 | 011 |
| 38 | 13 | 9 | 9 | 9 | 18 | 11 | 11 | 11 | 24 | 17 | 15 | 15 | 111 |
| 39 | 7 | 0 | 0 | 0 | 13 | 4 | 3 | 3 | 24 | 9 | 8 | 8 | 011 |
| 40 | 12 | 4 | 4 | 4 | 20 | 12 | 11 | 11 | 20 | 12 | 11 | 11 | 111 |
| 41 | 11 | 0 | 0 | 0 | 17 | 9 | 4 | 4 | 20 | 10 | 6 | 6 | 011 |
| 42 | 12 | 7 | 5 | 5 | 22 | 12 | 12 | 12 | 22 | 12 | 12 | 12 | 111 |
| 43 | 11 | 4 | 4 | 4 | 19 | 12 | 11 | 11 | 29 | 13 | 7 | 7 | 111 |
| 44 | 12 | 2 | 2 | 2 | 15 | 5 | 3 | 3 | 19 | 10 | 10 | 10 | 111 |
| 45 | 11 | 0 | 0 | 0 | 14 | 8 | 6 | 6 | 17 | 9 | 6 | 6 | 011 |
| 46 | 10 | 0 | 0 | 0 | 15 | 10 | 7 | 7 | 19 | 8 | 6 | 6 | 011 |
| 47 | 12 | 4 | 3 | 3 | 15 | 4 | 4 | 4 | 20 | 8 | 5 | 5 | 111 |
| 48 | 11 | 4 | 4 | 4 | 18 | 7 | 6 | 5 | 29 | 14 | 10 | 10 | 111 |
| 49 | 12 | 6 | 6 | 5 | 16 | 8 | 7 | 7 | 23 | 11 | 10 | 9 | 111 |
| 50 | 12 | 5 | 5 | 5 | 15 | 4 | 4 | 4 | 18 | 3 | 3 | 3 | 111 |
| 51 | 11 | 3 | 2 | 1 | 15 | 6 | 6 | 2 | 15 | 9 | 9 | 3 | 111 |
| 52 | 10 | 4 | 4 | 4 | 13 | 7 | 7 | 7 | 15 | 7 | 7 | 7 | 111 |
| 15–20 ROIs | 21–30 ROIs | 31–40 ROIs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. Image | ROIs | A.-Id. Stars | V1 | V2 | ROIs | A.-Id. Stars | V1 | V2 | ROIs | A.-Id. Stars | V1 | V2 | Id. (Yes/No) |
| 53 | 11 | 4 | 2 | 1 | 16 | 13 | 10 | 9 | 17 | 12 | 11 | 9 | 111 |
| 54 | 11 | 7 | 6 | 3 | 14 | 8 | 7 | 2 | 21 | 13 | 13 | 5 | 111 |
| 55 | 14 | 3 | 2 | 2 | 14 | 3 | 2 | 2 | 21 | 6 | 3 | 2 | 111 |
| 56 | 12 | 0 | 0 | 0 | 15 | 5 | 3 | 3 | 23 | 11 | 8 | 8 | 011 |
| 57 | 12 | 1 | 1 | 0 | 17 | 3 | 0 | 0 | 26 | 11 | 9 | 9 | 001 |
| 58 | 15 | 9 | 7 | 7 | 20 | 12 | 11 | 11 | 27 | 14 | 11 | 11 | 111 |
| 59 | 11 | 4 | 3 | 3 | 14 | 5 | 3 | 3 | 24 | 4 | 4 | 4 | 111 |
| 60 | 12 | 5 | 4 | 2 | 22 | 9 | 5 | 5 | 22 | 9 | 9 | 5 | 111 |
| 61 | 15 | 6 | 5 | 5 | 18 | 11 | 8 | 8 | 24 | 11 | 11 | 11 | 111 |
| 62 | 12 | 4 | 2 | 2 | 15 | 7 | 5 | 5 | 23 | 7 | 2 | 2 | 010 |
| 63 | 12 | 3 | 2 | 2 | 13 | 5 | 3 | 3 | 16 | 5 | 3 | 3 | 111 |
| 64 | 8 | 1 | 1 | 1 | 13 | 4 | 4 | 4 | 21 | 9 | 8 | 7 | 011 |
| 65 | 14 | 4 | 4 | 4 | 16 | 4 | 4 | 4 | 23 | 10 | 8 | 8 | 111 |
| 66 | 14 | 5 | 3 | 3 | 17 | 4 | 2 | 1 | 24 | 12 | 11 | 11 | 111 |
| 67 | 14 | 3 | 3 | 3 | 21 | 13 | 11 | 11 | 24 | 12 | 12 | 12 | 111 |
| 68 | 16 | 8 | 6 | 6 | 19 | 13 | 11 | 11 | 27 | 13 | 9 | 9 | 111 |
| 69 | 13 | 4 | 3 | 3 | 18 | 7 | 7 | 7 | 24 | 12 | 9 | 9 | 111 |
| 70 | 14 | 1 | 1 | 0 | 16 | 2 | 2 | 2 | 29 | 13 | 8 | 8 | 011 |
| 71 | 9 | 2 | 1 | 1 | 14 | 0 | 0 | 0 | 20 | 3 | 2 | 2 | 001 |
| 72 | 19 | 5 | 2 | 1 | 19 | 5 | 2 | 2 | 19 | 5 | 2 | 1 | 111 |
| 73 | 22 | 4 | 2 | 2 | 22 | 4 | 2 | 2 | 22 | 4 | 2 | 2 | 111 |
| 74 | 10 | 0 | 0 | 0 | 15 | 3 | 1 | 1 | 23 | 14 | 9 | 9 | 001 |
| 75 | 12 | 0 | 0 | 0 | 23 | 5 | 4 | 4 | 23 | 5 | 4 | 4 | 011 |
| 76 | 15 | 4 | 2 | 2 | 17 | 4 | 3 | 3 | 24 | 9 | 9 | 9 | 111 |
| 77 | 13 | 7 | 6 | 6 | 16 | 10 | 8 | 8 | 24 | 17 | 13 | 13 | 111 |
| 78 | 12 | 5 | 3 | 3 | 22 | 20 | 20 | 20 | 22 | 20 | 20 | 20 | 111 |
| 79 | 14 | 1 | 1 | 0 | 17 | 10 | 8 | 8 | 30 | 12 | 7 | 7 | 011 |
| 80 | 13 | 9 | 8 | 8 | 17 | 9 | 8 | 8 | 21 | 9 | 8 | 8 | 111 |
| 81 | 12 | 2 | 2 | 2 | 15 | 7 | 6 | 6 | 25 | 8 | 6 | 6 | 111 |
| 82 | 12 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 18 | 3 | 2 | 1 | 000 |
| 83 | 18 | 8 | 7 | 7 | 18 | 8 | 7 | 7 | 31 | 7 | 3 | 3 | 111 |
| 84 | 14 | 6 | 5 | 5 | 14 | 6 | 5 | 5 | 25 | 8 | 5 | 5 | 111 |
| 85 | 13 | 9 | 9 | 9 | 17 | 10 | 9 | 9 | 17 | 10 | 10 | 9 | 111 |
| 86 | 11 | 0 | 0 | 0 | 17 | 2 | 1 | 1 | 28 | 5 | 5 | 5 | 001 |
| 87 | 15 | 5 | 5 | 5 | 18 | 8 | 7 | 7 | 27 | 11 | 8 | 8 | 111 |
| 88 | 11 | 2 | 2 | 1 | 15 | 6 | 2 | 2 | 21 | 7 | 5 | 5 | 001 |
| 89 | 16 | 3 | 2 | 2 | 24 | 8 | 4 | 4 | 34 | 17 | 13 | 13 | 111 |
| 90 | 13 | 1 | 0 | 0 | 20 | 6 | 4 | 1 | 25 | 5 | 4 | 4 | 001 |
| 91 | 12 | 3 | 0 | 1 | 20 | 12 | 12 | 12 | 29 | 20 | 18 | 18 | 011 |
| 92 | 11 | 1 | 0 | 0 | 16 | 6 | 6 | 6 | 26 | 16 | 15 | 15 | 011 |
| 93 | 13 | 2 | 2 | 2 | 17 | 7 | 6 | 6 | 17 | 7 | 6 | 6 | 111 |
| 94 | 11 | 8 | 7 | 7 | 14 | 8 | 6 | 6 | 20 | 3 | 2 | 2 | 111 |
| 95 | 11 | 1 | 0 | 1 | 17 | 7 | 5 | 5 | 17 | 7 | 5 | 5 | 011 |
| 96 | 15 | 4 | 3 | 3 | 15 | 4 | 3 | 3 | 15 | 4 | 3 | 3 | 111 |
| 97 | 10 | 1 | 0 | 0 | 19 | 5 | 2 | 2 | 28 | 6 | 3 | 3 | 011 |
| 98 | 17 | 9 | 8 | 8 | 22 | 15 | 14 | 14 | 26 | 18 | 15 | 15 | 111 |
| 99 | 13 | 4 | 3 | 3 | 17 | 5 | 5 | 5 | 24 | 12 | 9 | 9 | 111 |
| 100 | 14 | 6 | 5 | 5 | 14 | 6 | 5 | 5 | 24 | 9 | 5 | 5 | 111 |
References
- Lavender, A. Satellites Orbiting the Earth in 2022. 2022. Available online: https://www.pixalytics.com/satellites-in-2022/ (accessed on 28 June 2023).
- UNOOSA. United Nations Office for Outer Space Affairs, Online Index of Objects Launched into Outer Space. 2023. Available online: https://www.unoosa.org/oosa/osoindex/search-ng.jspx?lf_id= (accessed on 28 June 2023).
- Kulu, E. World’s Largest Database of Nanosatellites, over 3600 Nanosats and CubeSats. 2023. Available online: https://www.nanosats.eu (accessed on 28 June 2023).
- Grøtte, M.E.; Gravdahl, J.T.; Johansen, T.A.; Larsen, J.A.; Vidal, E.M.; Surma, E. Spacecraft Attitude and Angular Rate Tracking using Reaction Wheels and Magnetorquers. IFAC-PapersOnLine 2020, 53, 14819–14826. [Google Scholar] [CrossRef]
- Liebe, C. Pattern recognition of star constellations for spacecraft applications. IEEE Aerosp. Electron. Syst. Mag. 1992, 7, 34–41. [Google Scholar] [CrossRef]
- Terma-Company. Star Trackers for Various Missions. 2022. Available online: https://www.terma.com/products/space/star-trackers/ (accessed on 28 June 2023).
- SODERN-Ariane-Group. World Leader in Star Trackers. 2023. Available online: https://sodern.com/en/viseurs-etoiles/ (accessed on 28 June 2023).
- VECTRONIC-Aerospace-GmbH. Star Trackers VST-68M, VST-41M. 2023. Available online: https://www.vectronic-aerospace.com/star-trackers/ (accessed on 28 June 2023).
- Fialho, M.A.A.; Mortari, D. Theoretical Limits of Star Sensor Accuracy. Sensors 2019, 19, 5355. [Google Scholar] [CrossRef]
- Spratling, B.; Mortari, D. A Survey on Star Identification Algorithms. Algorithms 2009, 2, 93–107. [Google Scholar] [CrossRef]
- Padgett, C.; Kreutz-Delgado, K. A grid algorithm for autonomous star identification. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 202–213. [Google Scholar] [CrossRef]
- Rijlaarsdam, D.; Yous, H.; Byrne, J.; Oddenino, D.; Furano, G.; Moloney, D. A Survey of Lost-in-Space Star Identification Algorithms Since 2009. Sensors 2020, 20, 2579. [Google Scholar] [CrossRef] [PubMed]
- Mortari, D.; Samaan, M.A.; Bruccoleri, C.; Junkins, J.L. The Pyramid Star Identification Technique. Navigation 2004, 51, 171–183. [Google Scholar] [CrossRef]
- Li, J.; Wei, X.; Zhang, G. Iterative algorithm for autonomous star identification. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 536–547. [Google Scholar] [CrossRef]
- Wei, X.; Wen, D.; Song, Z.; Xi, J.; Zhang, W.; Liu, G.; Li, Z. A star identification algorithm based on radial and dynamic cyclic features of star pattern. Adv. Space Res. 2019, 63, 2245–2259. [Google Scholar] [CrossRef]
- Hernández, E.A.; Alonso, M.A.; Chávez, E.; Covarrubias, D.H.; Conte, R. Robust polygon recognition method with similarity invariants applied to star identification. Adv. Space Res. 2017, 59, 1095–1111. [Google Scholar] [CrossRef]
- Chávez, E.; Chávez Cáliz, A.C.; López-López, J.L. Affine invariants of generalized polygons and matching under affine transformations. Comput. Geom. 2016, 58, 60–69. [Google Scholar] [CrossRef]
- ESA. European Space Agency. Gaia Data Release 2 (GAIA DR2). 2018. Available online: https://www.cosmos.esa.int/web/gaia/dr2 (accessed on 28 June 2023).
- Perryman, M.A.C.; Lindegren, L.; Kovalevsky, J.; Hoeg, E.; Bastian, U.; Bernacca, P.L.; Crézé, M.; Donati, F.; Grenon, M.; Grewing, M.; et al. The Hipparcos Catalogue. Astron. Astrophys. 1997, 323, L49–L52. [Google Scholar]
- Høg, E.; Fabricius, C.; Makarov, V.V.; Urban, S.; Corbin, T.; Wycoff, G.; Bastian, U.; Schwekendiek, P.; Wicenec, A. The Tycho-2 catalogue of the 2.5 million brightest stars. Astron. Astrophys. 2000, 355, L27–L30. [Google Scholar]
- Monet, D.G.; Levine, S.E.; Canzian, B.; Ables, H.D.; Bird, A.R.; Dahn, C.C.; Guetter, H.H.; Harris, H.C.; Henden, A.A.; Leggett, S.K.; et al. The USNO-B Catalog. Astron. J. 2003, 125, 984–993. [Google Scholar] [CrossRef]
- ESA. European Space Agency, Gaia Archive. 2023. Available online: https://gea.esac.esa.int/archive/ (accessed on 28 June 2023).
- Astropy Collaboration; Price-Whelan, A.M.; Lim, P.L.; Earl, N.; Starkman, N.; Bradley, L.; Shupe, D.L.; Patil, A.A.; Corrales, L.; Brasseur, C.E.; et al. The Astropy Project: Sustaining and Growing a Community-oriented Open-source Project and the Latest Major Release (v5.0) of the Core Package. Astrophys. J. 2022, 935, 167. [Google Scholar] [CrossRef]
- Luque-Suarez, F.; López-López, J.L.; Chavez, E. Indexed Polygon Matching Under Similarities. In Similarity Search and Applications; Reyes, N., Connor, R., Kriege, N., Kazempour, D., Bartolini, I., Schubert, E., Chen, J.J., Eds.; Series Title: Lecture Notes in Computer Science; Springer International Publishing: Cham, Swtizerland, 2021; Volume 13058, pp. 295–306. [Google Scholar] [CrossRef]
- Brualdi, R.A. Introductory Combinatorics, 5th ed.; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Celestron-LLC. Classification Using Nearest Neighbors. 2023. Available online: https://www.mathworks.com/help/stats/classification-using-nearest-neighbors.html (accessed on 28 June 2023).
- Leake, C.; Arnas, D.; Mortari, D. Non-Dimensional Star-Identification. Sensors 2020, 20, 2697. [Google Scholar] [CrossRef]
- Berry, R.; Burnell, J. The Handbook of Astronomical Image Processing, 2nd ed.; Willmann-Bell: Richmond, VA, USA, 2005. [Google Scholar]
- ZWO-Company. ASI178MM (Mono). 2023. Available online: https://astronomy-imaging-camera.com/product/asi178mm-mono/ (accessed on 28 June 2023).
- ZWO-Company. ASI183MM (Mono). 2023. Available online: https://astronomy-imaging-camera.com/product/asi183mm-mono/ (accessed on 28 June 2023).
- Celestron-LLC. Advanced VX 6″ Schmidt-Cassegrain Telescope. 2023. Available online: https://www.celestron.com/products/advanced-vx-6-schmidt-cassegrain-telescope (accessed on 28 June 2023).
- Kowa-Optimed-Deutschland-GmbH. LM75HC 1″ 75 mm 5MP C-Mount Lens. 2023. Available online: https://www.kowa-lenses.com/en/lm75hc–5mp-industrial-lens-c-mount (accessed on 28 June 2023).
- ESA. European Space Agency, Gaia Data Release Documentation. 14.1.1 Gaia Source. 2021. Available online: https://gea.esac.esa.int/archive/documentation/GDR2/Gaia_archive/chap_datamodel/sec_dm_main_tables/ssec_dm_gaia_source.html (accessed on 28 June 2023).
- Joye, W.A.; Mandel, E. New Features of SAOImage DS9. In Proceedings of the Astronomical Data Analysis Software and Systems XII, Strasbourg, France, 12–15 October 2003; Volume 295, p. 489. [Google Scholar]
- Liebe, C. Accuracy performance of star trackers—A tutorial. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 587–599. [Google Scholar] [CrossRef]
- He, L.; Chao, Y.; Suzuki, K.; Wu, K. Fast connected-component labeling. Pattern Recognit. 2009, 42, 1977–1987. [Google Scholar] [CrossRef]
- Osuna, M.H. Image Processing Algorithms for Star Centroid Calculation: Small Satellite Application. Master’s Thesis, CICESE, Ensenada, México, 2017. [Google Scholar]
- AbuBaker, A.; Qahwaji, R.; Ipson, S.; Saleh, M. One Scan Connected Component Labeling Technique. In Proceedings of the 2007 IEEE International Conference on Signal Processing and Communications, Dubai, United Arab Emirates, 24–27 November 2007; IEEE: Dubai, United Arab Emirates, 2007; pp. 1283–1286. [Google Scholar] [CrossRef]
- Weisstein, E.W.; Bisection. From MathWorld–A Wolfram Web Resource. 2023. Available online: https://mathworld.wolfram.com/Bisection.html (accessed on 28 June 2023).
- Delabie, T.; Schutter, J.D.; Vandenbussche, B. An Accurate and Efficient Gaussian Fit Centroiding Algorithm for Star Trackers. J. Astronaut. Sci. 2014, 61, 60–84. [Google Scholar] [CrossRef]
- Samaan, M.A. Toward Faster and More Accurate Star Sensors Using Recursive Centroiding and Star Identification. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2003. [Google Scholar]
- Nightingale, A.M.; Gordeyev, S. Shack-Hartmann wavefront sensor image analysis: A comparison of centroiding methods and image-processing techniques. Opt. Eng. 2013, 52, 071413. [Google Scholar] [CrossRef]
- Stone, R.C. A Comparison of Digital Centering Algorithms. Astron. J. 1989, 97, 1227. [Google Scholar] [CrossRef]
- Lang, D.; Hogg, D.W.; Mierle, K.; Blanton, M.; Roweis, S. Astrometry.net: Blind Astrometric Calibration of Arbitrary Astronomical Images. Astron. J. 2010, 139, 1782–1800. [Google Scholar] [CrossRef]
- Astrometry.net. Album of Images: GustavoRamosStarIDInvariant. 2023. Available online: https://nova.astrometry.net/albums/4273 (accessed on 28 June 2023).








| Settings | ASI178 & 6 SCT | ASI178 & L75 | ASI183 & 6 SCT | ASI183 & L75 |
|---|---|---|---|---|
| Sensor size (inches) | 1/1.8 | 1/1.8 | 1 | 1 |
| Pixel size (m) | 2.4 | 2.4 | 2.4 | 2.4 |
| Resolution (pixels) | 3096 × 2080 | 3096 × 2080 | 5496 × 3672 | 5496 × 3672 |
| ADC (bits) | 14 | 14 | 12 | 12 |
| QE (%) | 81% at = 500 nm | 81% at = 500 nm | 84% at = 550 nm | 84% at = 550 nm |
| Focal length (mm) | 1500 | 75 | 1500 | 75 |
| Pixel scale (arcsec/pix) | 0.33 | 6.6 | 0.33 | 6.6 |
| Radial FOV (degrees) | 0.191 | 3.813 | 0.337 | 6.732 |
| ROIs | Alg.-Identified Stars | Voting Verification | Manual Validation | Identified | |||||
|---|---|---|---|---|---|---|---|---|---|
| Threshold in ROIs | Mean | Mean | Mean | Mean | Images | ||||
| 15–20 | 12.74 | 2.48 | 4.31 | 2.95 | 3.35 | 2.83 | 3.35 | 2.83 | 71 |
| 21–30 | 17.5 | 3.31 | 7.61 | 4.03 | 6.21 | 4.14 | 5.97 | 4.10 | 88 |
| 31–40 | 23.29 | 4.85 | 10.5 | 4.51 | 8.41 | 4.41 | 8.04 | 4.47 | 97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos-Alcaraz, G.E.; Alonso-Arévalo, M.A.; Nuñez-Alfonso, J.M. Star-Identification System Based on Polygon Recognition. Aerospace 2023, 10, 748. https://doi.org/10.3390/aerospace10090748
Ramos-Alcaraz GE, Alonso-Arévalo MA, Nuñez-Alfonso JM. Star-Identification System Based on Polygon Recognition. Aerospace. 2023; 10(9):748. https://doi.org/10.3390/aerospace10090748
Chicago/Turabian StyleRamos-Alcaraz, Gustavo E., Miguel A. Alonso-Arévalo, and Juan M. Nuñez-Alfonso. 2023. "Star-Identification System Based on Polygon Recognition" Aerospace 10, no. 9: 748. https://doi.org/10.3390/aerospace10090748
APA StyleRamos-Alcaraz, G. E., Alonso-Arévalo, M. A., & Nuñez-Alfonso, J. M. (2023). Star-Identification System Based on Polygon Recognition. Aerospace, 10(9), 748. https://doi.org/10.3390/aerospace10090748







