Distributed Adaptive Path-Following Control for Distance-Based Formation of Fixed-Wing UAVs under Input Saturation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Rigid Graph Theory
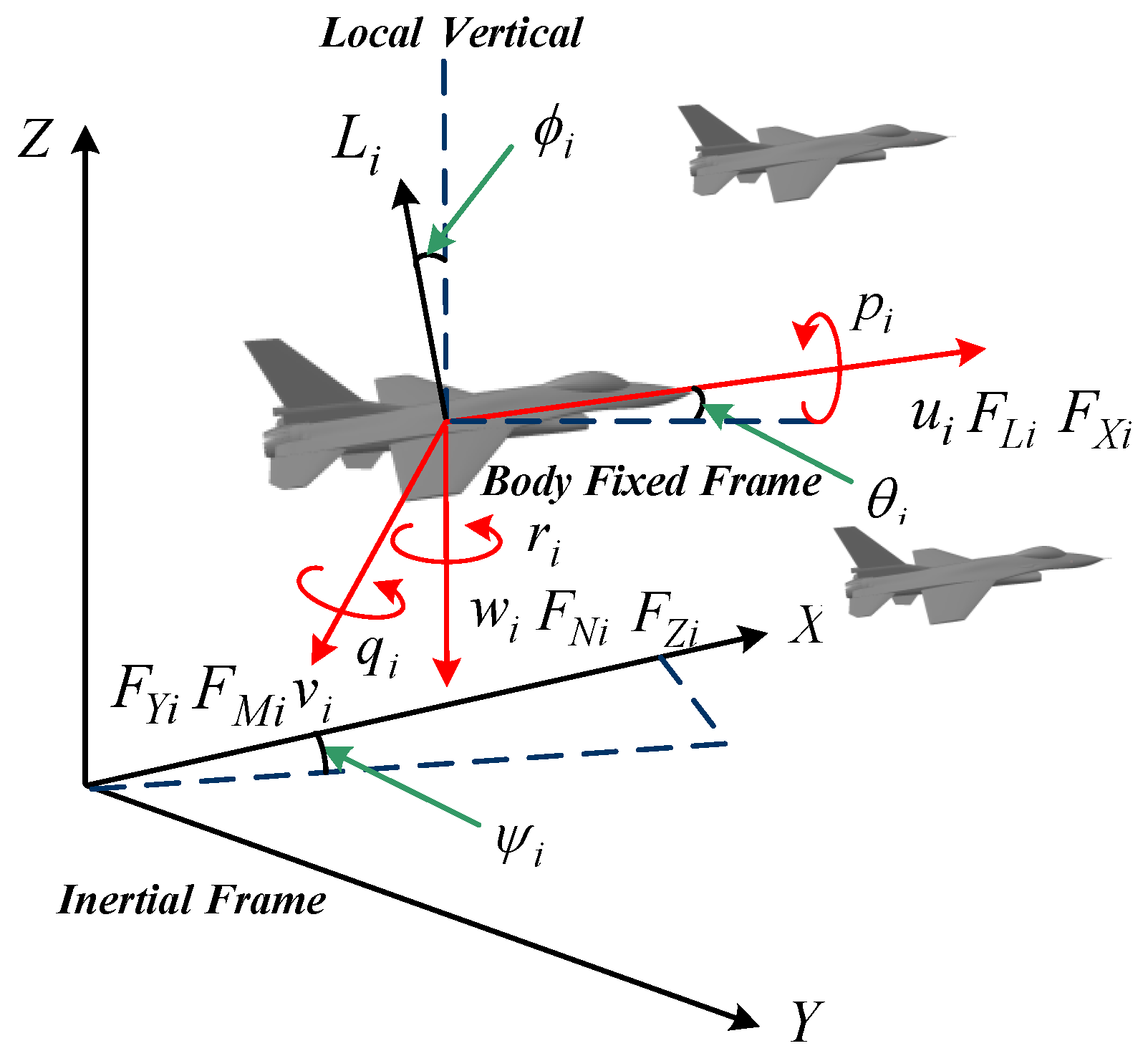
2.2. Model of the Fixed-Wing UAV
2.3. Input Saturation Model
2.4. Fault Model
2.5. Control Objective
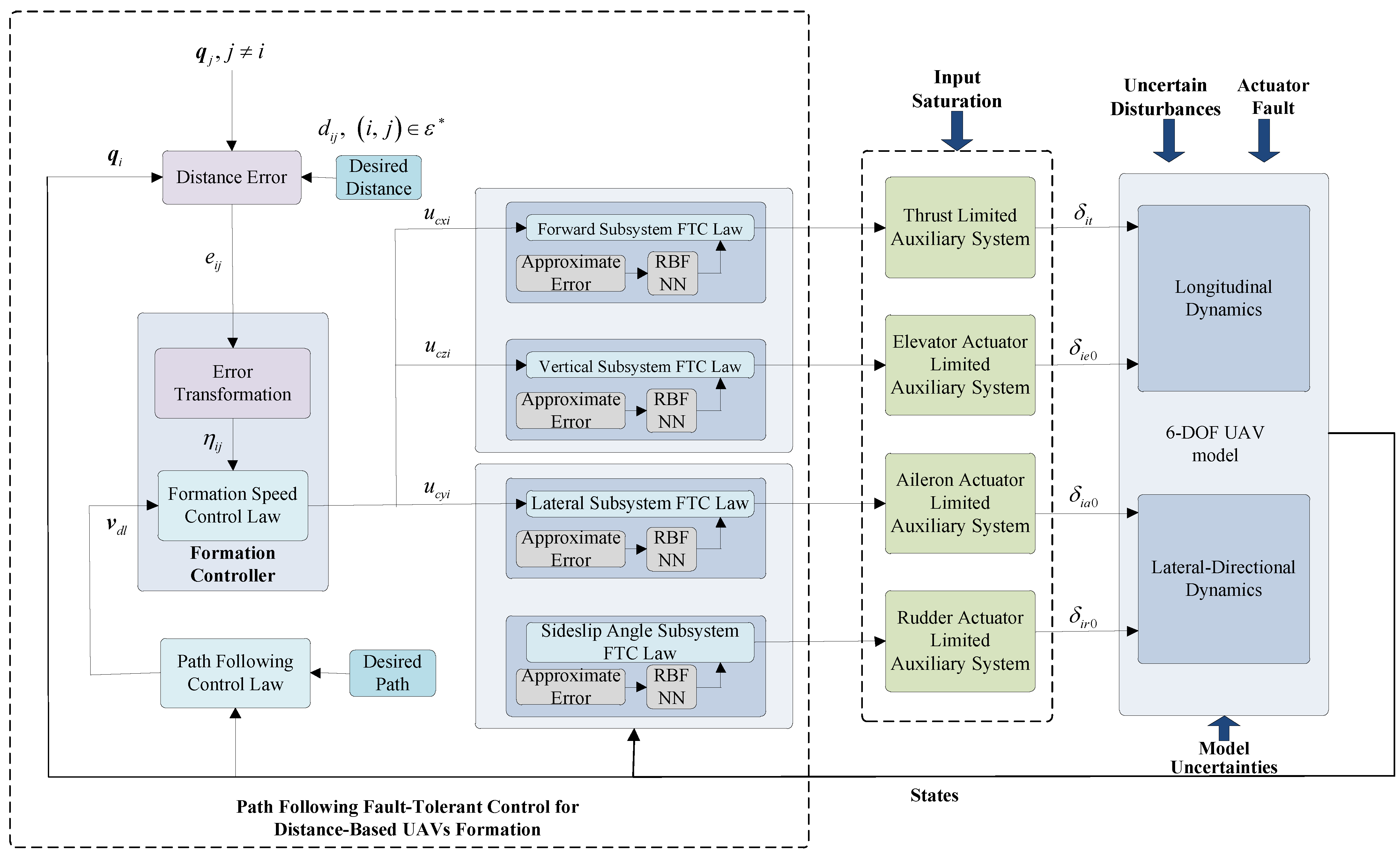
3. Distributed Adaptive Fault-Tolerant Controller Design and Analysis
3.1. Path-Following Controller of Leader UAV
3.2. Distance-Based Formation Controller Design of UAVs
3.2.1. Tracking Speed Control Law for UAVs
3.2.2. PPC Design for Longitudinal Dynamics
3.2.3. The Transverse Lateral Controller Design of the Drone under Restricted Conditions
3.3. Stability Analysis
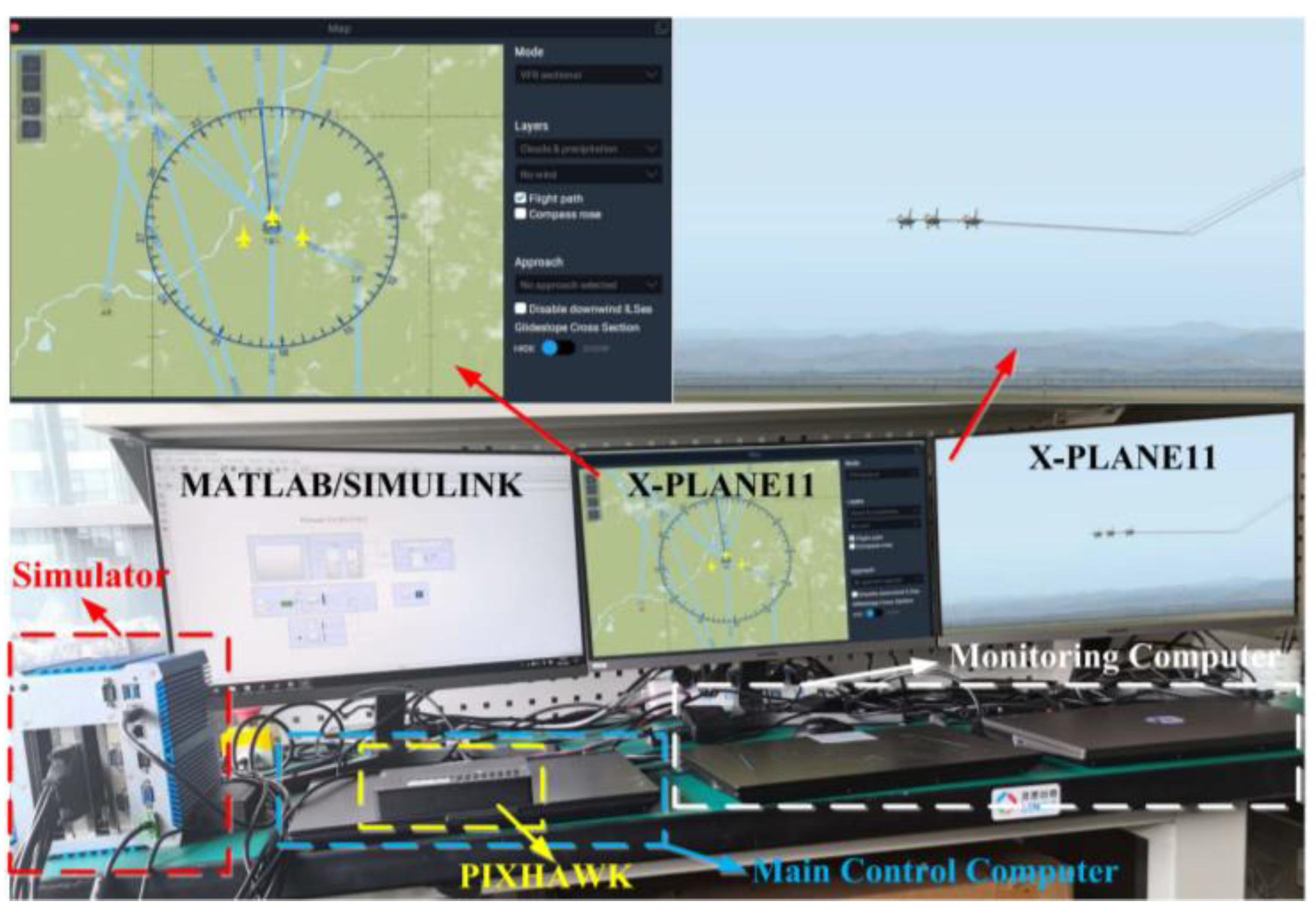
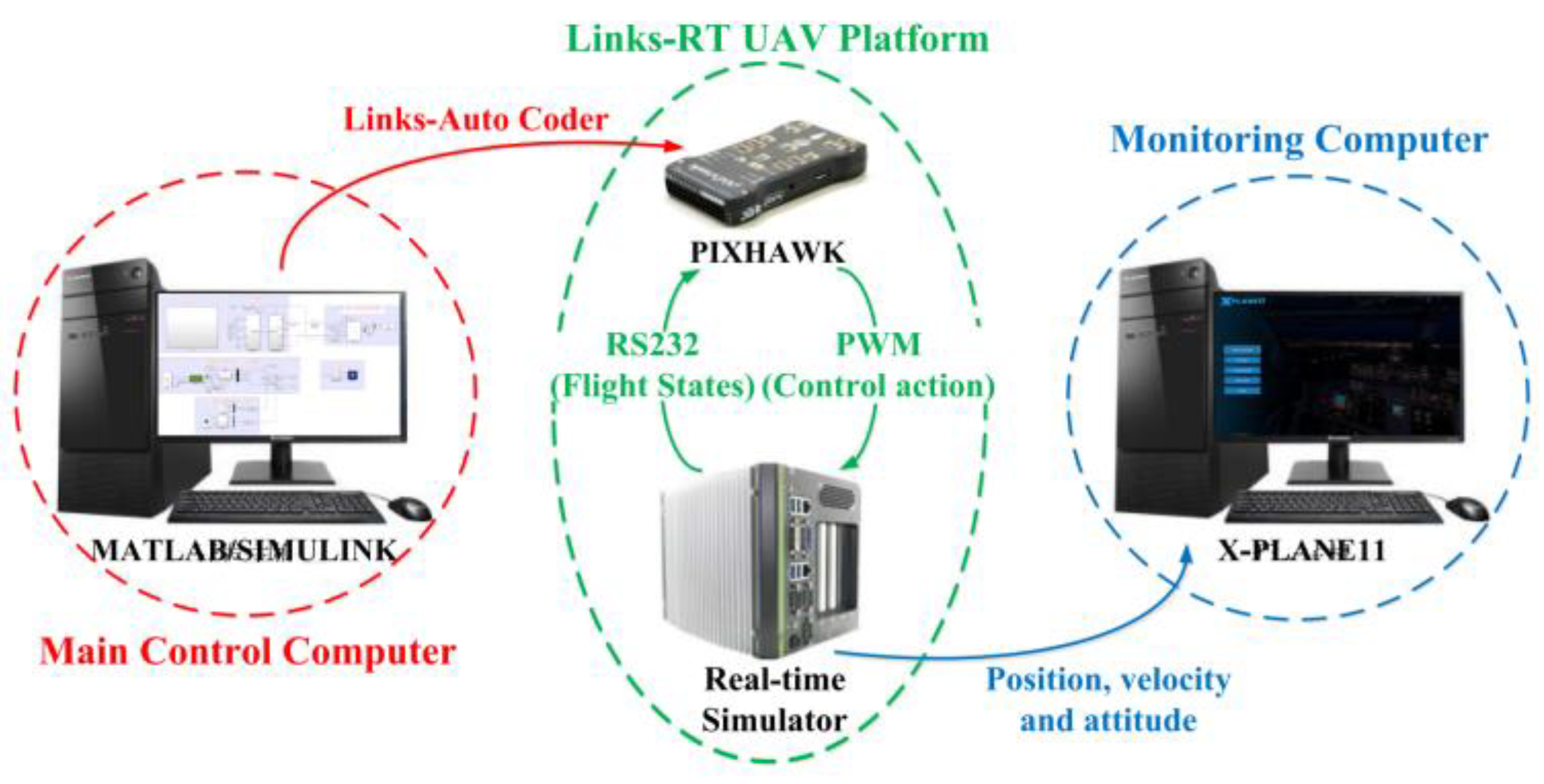
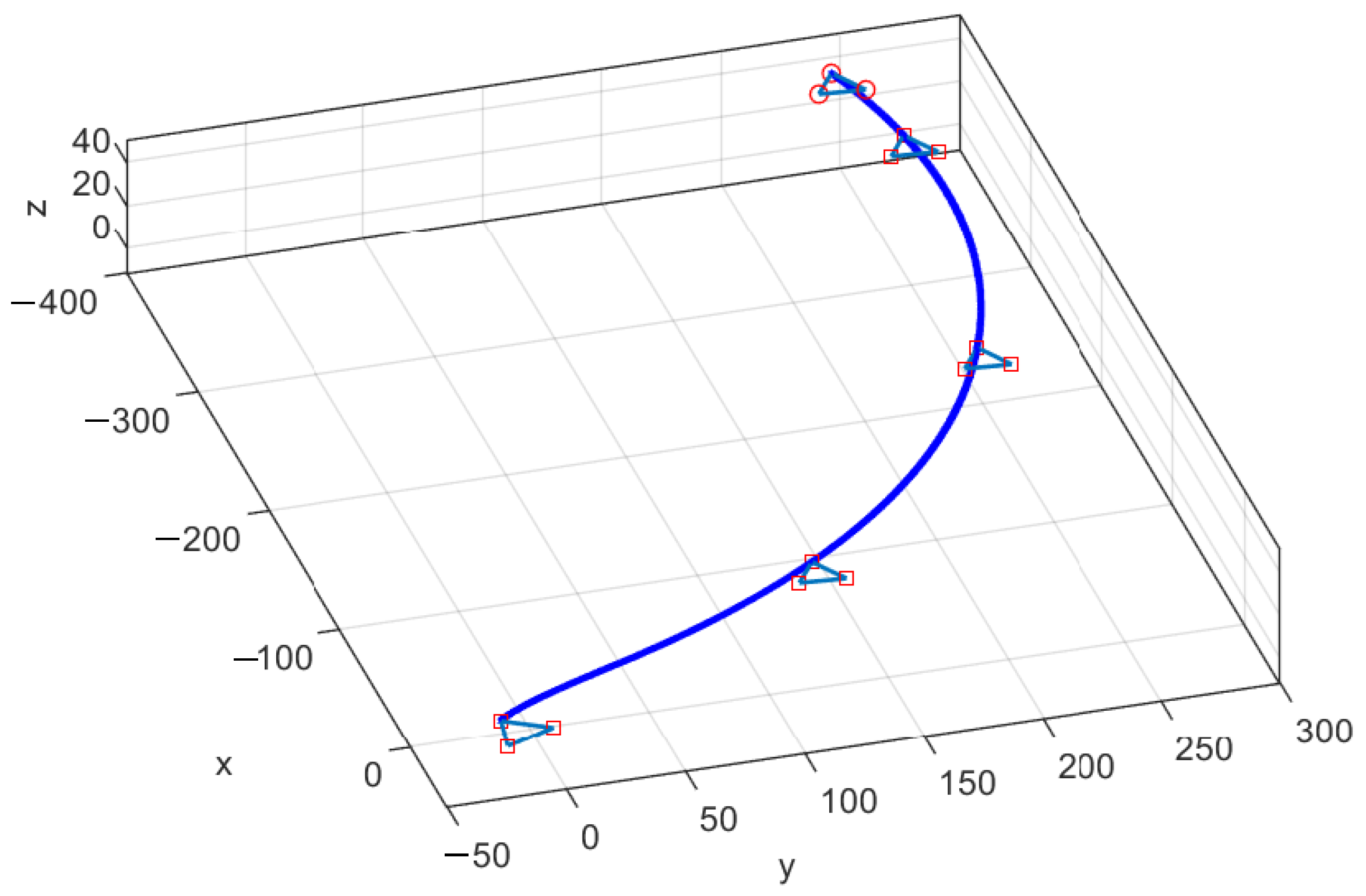
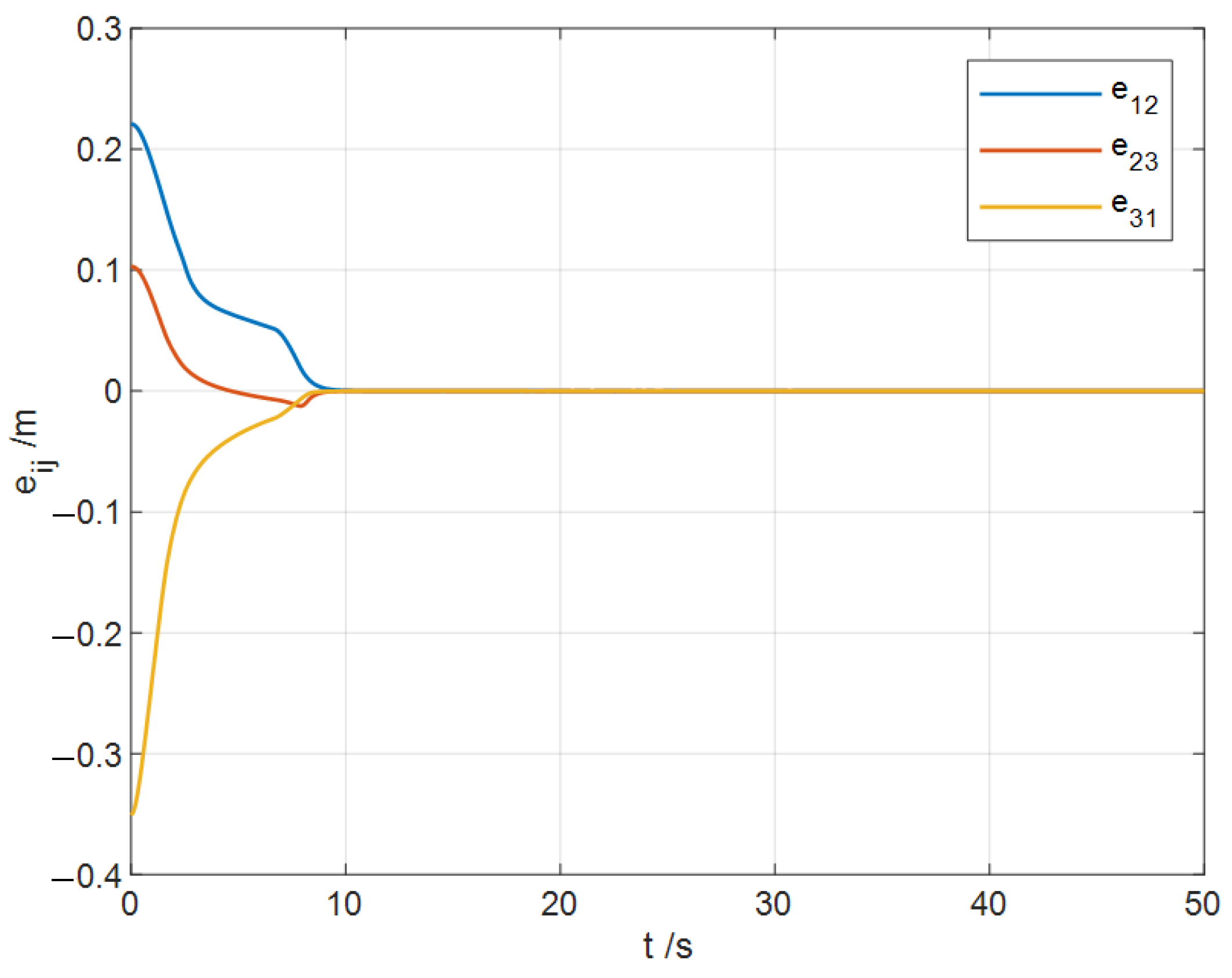
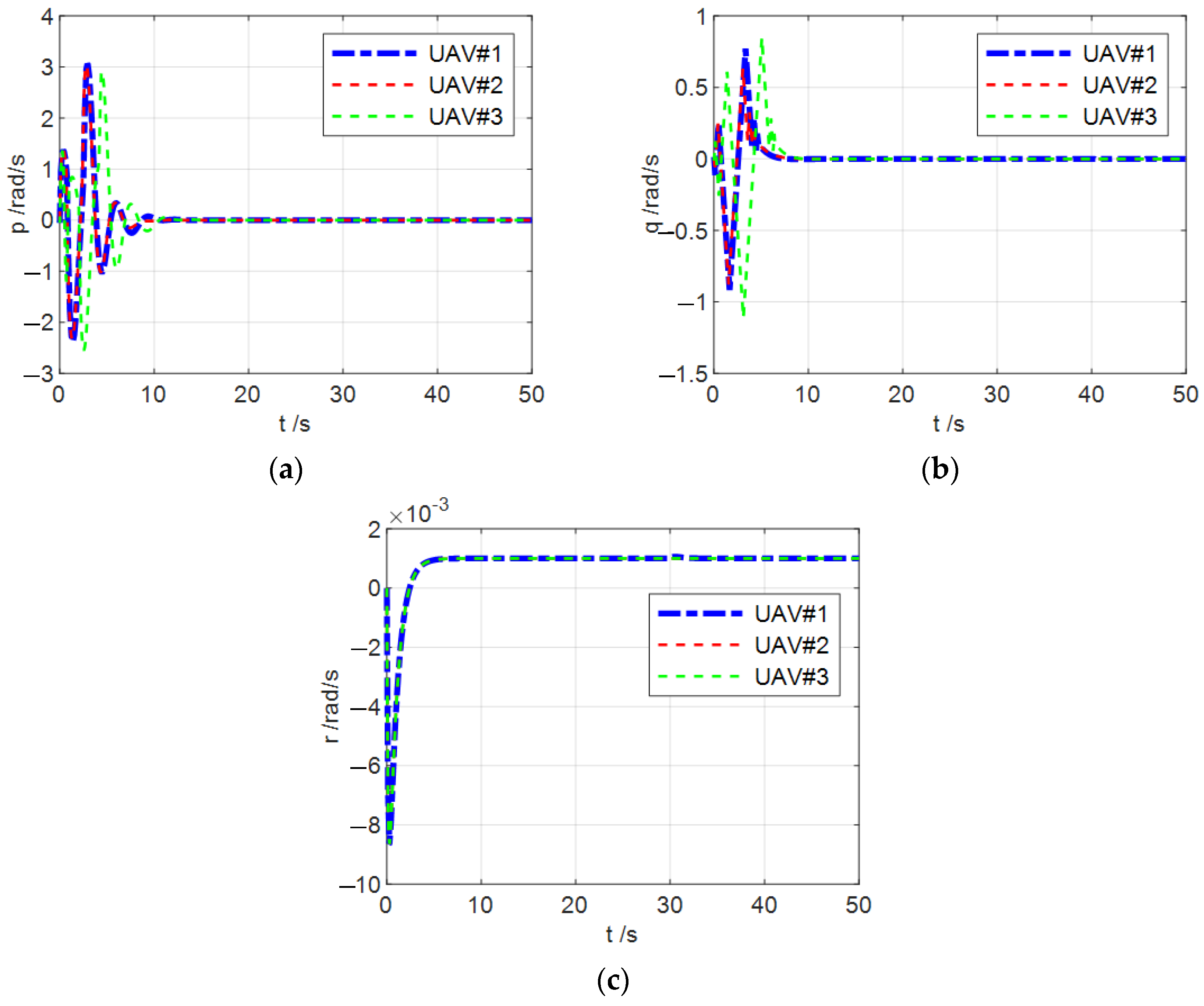
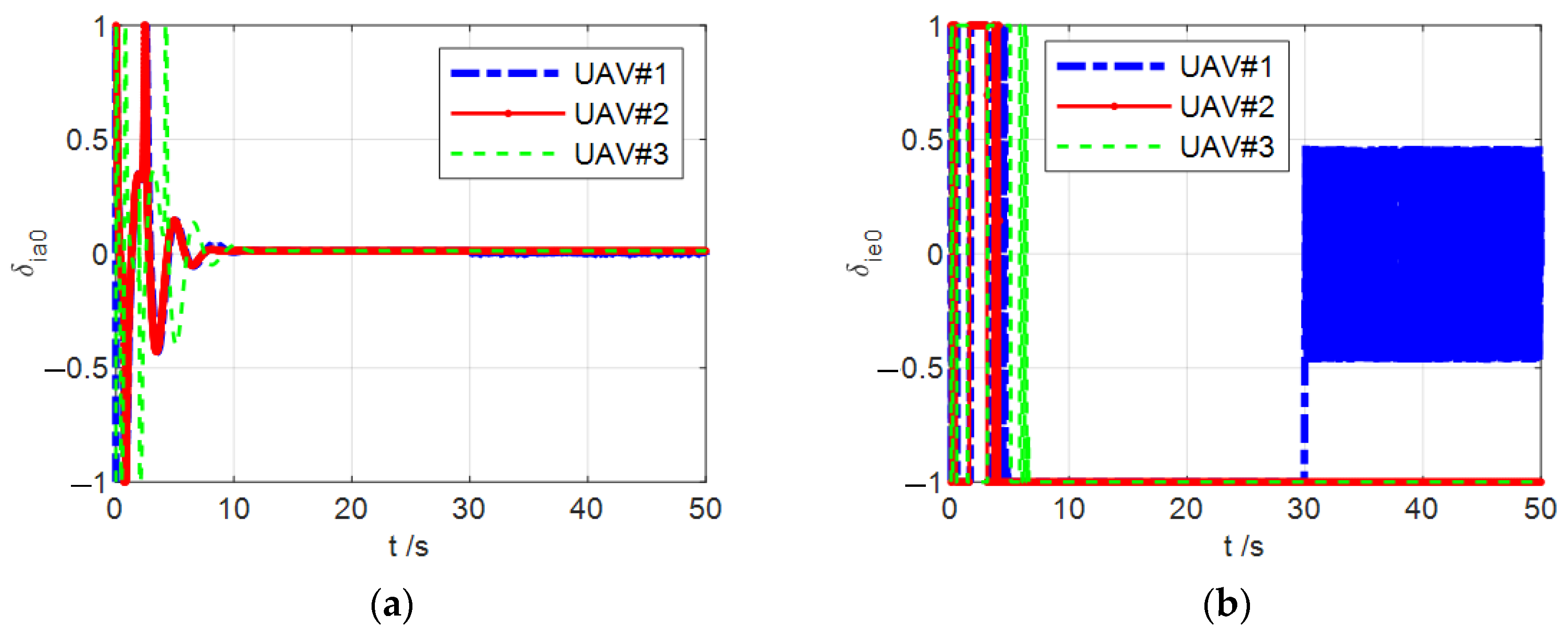
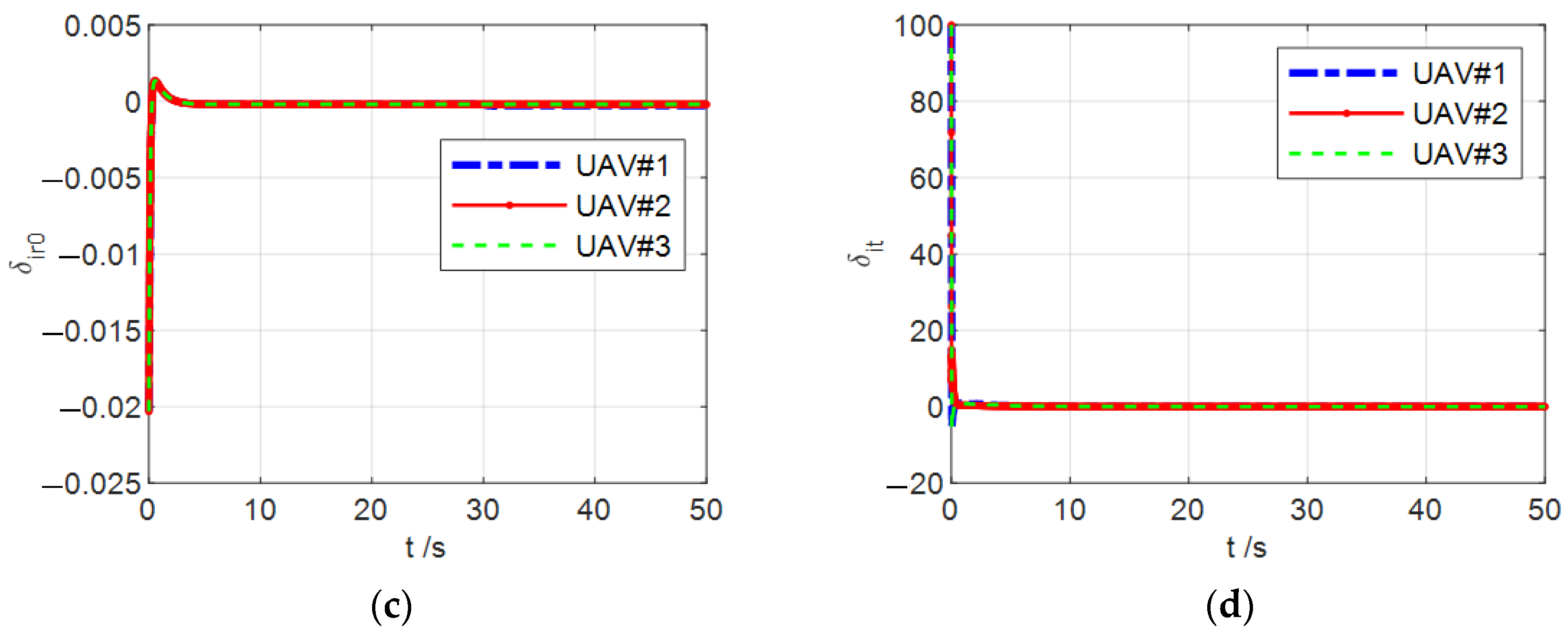
4. Simulation Results
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Subscript i | the ith UAV |
| , g | the positions of the UAV in the inertia frame |
| velocity, sideslip angle, angle of attack | |
| velocity, sideslip angle, angle of attack | |
| roll, pitch, yaw angles | |
| thrust, drag, side forces | |
| roll, pitch, yaw rates | |
| roll, pitch, and yaw moments | |
| aileron, elevator, rudder deflections, instantaneous thrust throttle setting | |
| maximum thrust force, aerodynamic coefficient | |
| external disturbances |
References
- Ouyang, Q.; Wu, Z.; Cong, Y.; Wang, Z. Formation control of unmanned aerial vehicle swarms: A comprehensive review. Asian J. Control 2023, 25, 570–593. [Google Scholar] [CrossRef]
- Chen, L.; Xiao, J.; Lin, R.C.H.; Feroskhan, M. Angle-Constrained Formation Maneuvering of Unmanned Aerial Vehicles. IEEE Trans. Control Syst. Technol. 2023, 31, 1733–1746. [Google Scholar] [CrossRef]
- Shao, X.L.; Liu, H.C.; Zhang, W.D.; Zhao, J.; Zhang, Q.Z. Path driven formation-containment control of multiple UAVs: A path-following framework. Aerosp. Sci. Technol. 2023, 135, 108168. [Google Scholar] [CrossRef]
- Nian, X.H.; Zhou, W.X.; Li, S.L.; Wu, H.Y. 2-D path following for fixed wing UAV using global fast terminal sliding mode control. ISA Trans. 2023, 136, 162–172. [Google Scholar] [CrossRef] [PubMed]
- Chung, S.-J.; Paranjape, A.A.; Dames, P.; Shen, S.; Kumar, V. A Survey on Aerial Swarm Robotics. IEEE Trans. Robot. 2018, 34, 837–855. [Google Scholar] [CrossRef]
- Cabecinhas, D.; Cunha, R.; Silvestre, C. Rotorcraft path following control for extended flight envelope coverage. In Proceedings of the 48th IEEE Conference on Decision and Control, CDC 2009, Combined with the 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 16–18. [Google Scholar]
- Cabecinhas, D.; Cunha, R.; Silvestre, C. A Globally Stabilizing Path Following Controller for Rotorcraft with Wind Disturbance Rejection. IEEE Trans. Control Syst. Technol. 2015, 23, 708–714. [Google Scholar] [CrossRef]
- Klausen, K.; Fossen, T.I.; Johansen, T.A.; Aguiar, A.P. Cooperative path-following for multirotor UAVs with a suspended payload. In Proceedings of the IEEE Conference on Control Applications (CCA), Sydney, Australia, 21–23 September 2015; pp. 1354–1360. [Google Scholar]
- Akkinapalli, V.S.; Niermeyer, P.; Lohmann, B.; Holzapfel, F. Adaptive nonlinear design plant uncertainty cancellation for a multirotor. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 1102–1110. [Google Scholar]
- Rucco, A.; Aguiar, A.P.; Hauser, J. Trajectory optimization for constrained UAVs: A Virtual Target Vehicle approach. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 236–245. [Google Scholar]
- Rucco, A.; Aguiar, A.P.; Pereira, F.L.; de Sousa, J.B. A Predictive Path-Following Approach for Fixed-Wing Unmanned Aerial Vehicles in Presence of Wind Disturbances. In Proceedings of the Second Iberian Robotics Conference, Lisbon, Portugal, 19–21 November 2015. [Google Scholar]
- Desai, J.P.; Ostrowski, J.P.; Kumar, V. Controlling formations of multiple mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), Leuven, Belgium, 20–20 May 1998; pp. 2864–2869. [Google Scholar]
- Byrnes, C.I.; Isidori, A. Asymptotic stabilization of minimum phase nonlinear systems. IEEE Trans. Autom. Control 1991, 36, 1122–1137. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S. Sliding Mode Control: Theory And Applications; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Shah, M.Z.; Samar, R.; Bhatti, A.I. Lateral track control of UAVs using the sliding mode approach: From design to flight testing. Trans. Inst. Meas. Control 2014, 37, 457–474. [Google Scholar] [CrossRef]
- Thanh, H.L.N.N.; Vu, M.T.; Mung, N.X.; Nguyen, N.P.; Phuong, N.T. Perturbation observer-based robust control using a multiple sliding surfaces for nonlinear systems with influences of matched and unmatched uncertainties. Mathematics 2020, 8, 1371. [Google Scholar] [CrossRef]
- Alattas, K.A.; Mobayen, S.; Din, S.U.; Asad, J.H.; Fekih, A.; Assawinchaichote, W.; Vu, M.T. Design of a non-singular adaptive integral-type finite time tracking control for nonlinear systems with external disturbances. IEEE Access 2021, 9, 102091–102103. [Google Scholar] [CrossRef]
- Mofid, O.; Amirkhani, S.; Din, S.U.; Mobayen, S.; Vu, M.T.; Assawinchaichote, W. Finite-time convergence of perturbed nonlinear systems using adaptive barrier-function nonsingular sliding mode control with experimental validation. J. Vib. Control 2023, 29, 3326–3339. [Google Scholar] [CrossRef]
- Rojsiraphisal, T.; Mobayen, S.; Asad, J.H.; Vu, M.T.; Chang, A.; Puangmalai, J. Fast terminal sliding control of underactuated robotic systems based on disturbance observer with experimental validation. Mathematics 2021, 9, 1935. [Google Scholar] [CrossRef]
- Alattas, K.A.; Vu, M.T.; Mofid, O.; El-Sousy, F.F.M.; Alanazi, A.K.; Awrejcewicz, J.; Mobayen, S. Adaptive nonsingular terminal sliding mode control for performance improvement of perturbed nonlinear systems. Mathematics 2022, 10, 1064. [Google Scholar] [CrossRef]
- Mobayen, S.; Bayat, F.; Din, S.U.; Vu, M.T. Barrier function-based adaptive nonsingular terminal sliding mode control technique for a class of disturbed nonlinear systems. ISA Trans. 2023, 134, 481–496. [Google Scholar] [CrossRef]
- Ghaffari, V.; Mobayen, S.; Din, S.U.; Rojsiraphisal, T.; Vu, M.T. Robust tracking composite nonlinear feedback controller design for time-delay uncertain systems in the presence of input saturation. ISA Trans. 2022, 129, 88–99. [Google Scholar] [CrossRef]
- Roza, A.; Maggiore, M. Path following controller for a quadrotor helicopter. In Proceedings of the American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 4655–4660. [Google Scholar]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. Backstepping/nonlinear H∞ control for path tracking of a quadrotor unmanned aerial vehicle. In Proceedings of the American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 3356–3361. [Google Scholar]
- Kaminer, I.; Yakimenko, O.; Pascoal, A.; Ghabcheloo, R. Path Generation, Path Following and Coordinated Control for TimeCritical Missions of Multiple UAVs. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 4906–4913. [Google Scholar]
- Xargay, E.; Kaminer, I.; Pascoal, A.; Hovakimyan, N.; Dobrokhodov, V.; Cichella, V.; Aguiar, A.P.; Ghabcheloo, R. Time-Critical Cooperative Path Following of Multiple Unmanned Aerial Vehicles over Time-Varying Networks. J. Guid. Control Dyn. 2013, 36, 499–516. [Google Scholar] [CrossRef]
- Chen, H.; Cong, Y.; Wang, X.; Xu, X.; Shen, L. Coordinated Path Following Control of Fixed-wing Unmanned Aerial Vehicles. IEEE Trans. Cybern. 2019, 52, 2540–2554. [Google Scholar]
- Ren, W.; Atkins, E. Distributed multi-vehicle coordinated control via local information exchange. Int. J. Robust Nonlinear Control 2007, 17, 1002–1033. [Google Scholar] [CrossRef]
- Meng, Z.; Anderson, B.D.; Hirche, S. Formation control with mismatched compasses. Automatica 2016, 69, 232–241. [Google Scholar] [CrossRef]
- Ramazani, S.; Selmic, R.; de Queiroz, M. Rigidity-based multiagent layered formation control. IEEE Trans. Cybern. 2017, 47, 1902–1913. [Google Scholar] [CrossRef]
- Cai, X.; de Queiroz, M. Rigidity-based stabilization of multi-agent formations. J. Dyn. Syst. Meas. Control 2014, 136, 014502. [Google Scholar] [CrossRef]
- Dorfler, F.; Francis, B. Geometric analysis of the formation problem for autonomous robots. IEEE Trans. Autom. Control 2010, 5, 2379–2384. [Google Scholar] [CrossRef]
- Krick, L.; Broucke, M.E.; Francis, B.A. Stabilisation of infinitesimally rigid formations of multi-robot networks. Int. J. Control 2009, 82, 423–439. [Google Scholar] [CrossRef]
- Oh, K.K.; Ahn, H.-S. Formation control of mobile agents based on inter-agent distance dynamics. Automatica 2011, 47, 2306–2312. [Google Scholar] [CrossRef]
- Babazadeh, R.; Selmic, R. Distance-based multi-agent formation control with energy constraints using SDRE. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 41–56. [Google Scholar] [CrossRef]
- Cai, X.; Queiroz, M. Formation maneuvering and target interception for multi-agent systems via rigid graphs. Asian J. Control 2015, 17, 1174–1186. [Google Scholar] [CrossRef]
- Aryankia, K.; Selmic, R.R. Neuro-Adaptive Formation Control and Target Tracking for Nonlinear Multi-Agent Systems with Time-Delay. IEEE Control Syst. Lett. 2021, 5, 791–796. [Google Scholar] [CrossRef]
- Vu, D.V.; Trinh, M.H.; Ahn, H.S. Distance--Based Formation Tracking with Unknown Bounded Reference Velocities. In Proceedings of the 20th International Conference on Control, Automation and Systems (ICCAS), Busan, Republic of Korea, 13–16 October 2020; pp. 524–529. [Google Scholar]
- Yu, Z.; Qu, Y.; Zhang, Y. Distributed Fault-Tolerant Cooperative Control for Multi-UAVs Under Actuator Fault and Input Saturation. IEEE Trans. Control Syst. Technol. 2018, 27, 2417–2429. [Google Scholar] [CrossRef]
- Chang, S.J.; Lee, J.Y.; Park, J.B.; Choi, Y.H. An online fault tolerant actor-critic neuro-control for a class of nonlinear systems using neural network HJB approach. Int. J. Control Autom. Syst. 2015, 13, 311–318. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, Z.; Zhang, Y.; Qu, Y.; Su, C.Y. Distributed Finite-Time Fault-Tolerant Containment Control for Multiple Unmanned Aerial Vehicles. IEEE Trans. Neural Netw. Learn. Syst. 2019, 99, 2077–2091. [Google Scholar] [CrossRef]
- Hou, Z.; Fantoni, I. Leader-follower formation saturatedcontrol for multiple quadrotors with switching topology. In Proceedings of the Workshop on Research, Education and Development of Unmanned Aerial Systems (RED-UAS), Cancun, Mexico, 23–25 November 2015; pp. 8–14. [Google Scholar]
- Xiang, X.; Liu, C.; Su, H.; Zhang, Q. On decentralized adaptive full-order slidingmode control of multiple UAVs. ISA Trans. 2017, 71, 196–205. [Google Scholar] [CrossRef] [PubMed]
- Asimow, L.; Roth, B. The rigidity of graphs, II. J. Math. Anal. Appl. 1979, 68, 171–190. [Google Scholar] [CrossRef]
- Dogan, A.; Venkataramanan, S. Nonlinear Control for Reconfiguration of Unmanned-Aerial-Vehicle Formation. J. Guid. Control Dyn. 2005, 28, 667–678. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, Y.; Jiang, B.; Yu, X.; Fu, J.; Jin, Y.; Chai, T. Distributed adaptive fault-tolerant close formation flight control of multiple trailing fixed-wing UAVs. ISA Trans. 2020, 106, 181–199. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Qu, Y.; Zhang, Y. Safe Control of Trailing UAV in Close Formation Flight against Actuator Fault and Wake Vortex Effect. Aerosp. EnceTechnol. 2018, 77, 189–205. [Google Scholar] [CrossRef]
- Payne, A.N. Adaptive one-step-ahead control subject to an input-amplitude constraint. Int. J. Control 1986, 43, 1257–1269. [Google Scholar] [CrossRef]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 1.2 | 0.8 | ||
| 0.6 | 1 | ||
| [1.5,0,0;0,2,0;0,0,2] | 0.8 | ||
| 0.01 | 1.2 | ||
| 0.01 | 1.2 | ||
| 0.01 | 1.3 | ||
| 0.02 | 0.8 | ||
| 0.01 | 0.5 | ||
| 0.01 | 5 | ||
| 1.2 | 3 | ||
| 3 | 3 | ||
| 1.8 | 2 | ||
| 2 | 0.05 | ||
| 1 | 0.05 | ||
| 1 | 0.02 | ||
| 1.5 | 0.05 | ||
| 2 | 0.05 | ||
| 2.5 | 0.05 | ||
| 2 | 100 | ||
| 1.2 | 150 | ||
| 0.9 | 150 | ||
| 2.5 | 150 | ||
| 4.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Wang, H.; Li, S.; Liu, S. Distributed Adaptive Path-Following Control for Distance-Based Formation of Fixed-Wing UAVs under Input Saturation. Aerospace 2023, 10, 768. https://doi.org/10.3390/aerospace10090768
Wu J, Wang H, Li S, Liu S. Distributed Adaptive Path-Following Control for Distance-Based Formation of Fixed-Wing UAVs under Input Saturation. Aerospace. 2023; 10(9):768. https://doi.org/10.3390/aerospace10090768
Chicago/Turabian StyleWu, Junfeng, Huan Wang, Shanshan Li, and Shuguang Liu. 2023. "Distributed Adaptive Path-Following Control for Distance-Based Formation of Fixed-Wing UAVs under Input Saturation" Aerospace 10, no. 9: 768. https://doi.org/10.3390/aerospace10090768
APA StyleWu, J., Wang, H., Li, S., & Liu, S. (2023). Distributed Adaptive Path-Following Control for Distance-Based Formation of Fixed-Wing UAVs under Input Saturation. Aerospace, 10(9), 768. https://doi.org/10.3390/aerospace10090768






