Numerical Simulation of Transonic Compressors with Different Turbulence Models
Abstract
:1. Introduction
2. Computational Models
3. Control Equations and Numerical Methods
3.1. Control Equations and Turbulence Models
3.2. Numerical Scheme
3.3. Computational Grids and Boundary Conditions
4. Analysis of Calculation Results
4.1. Compressor Performance Curve
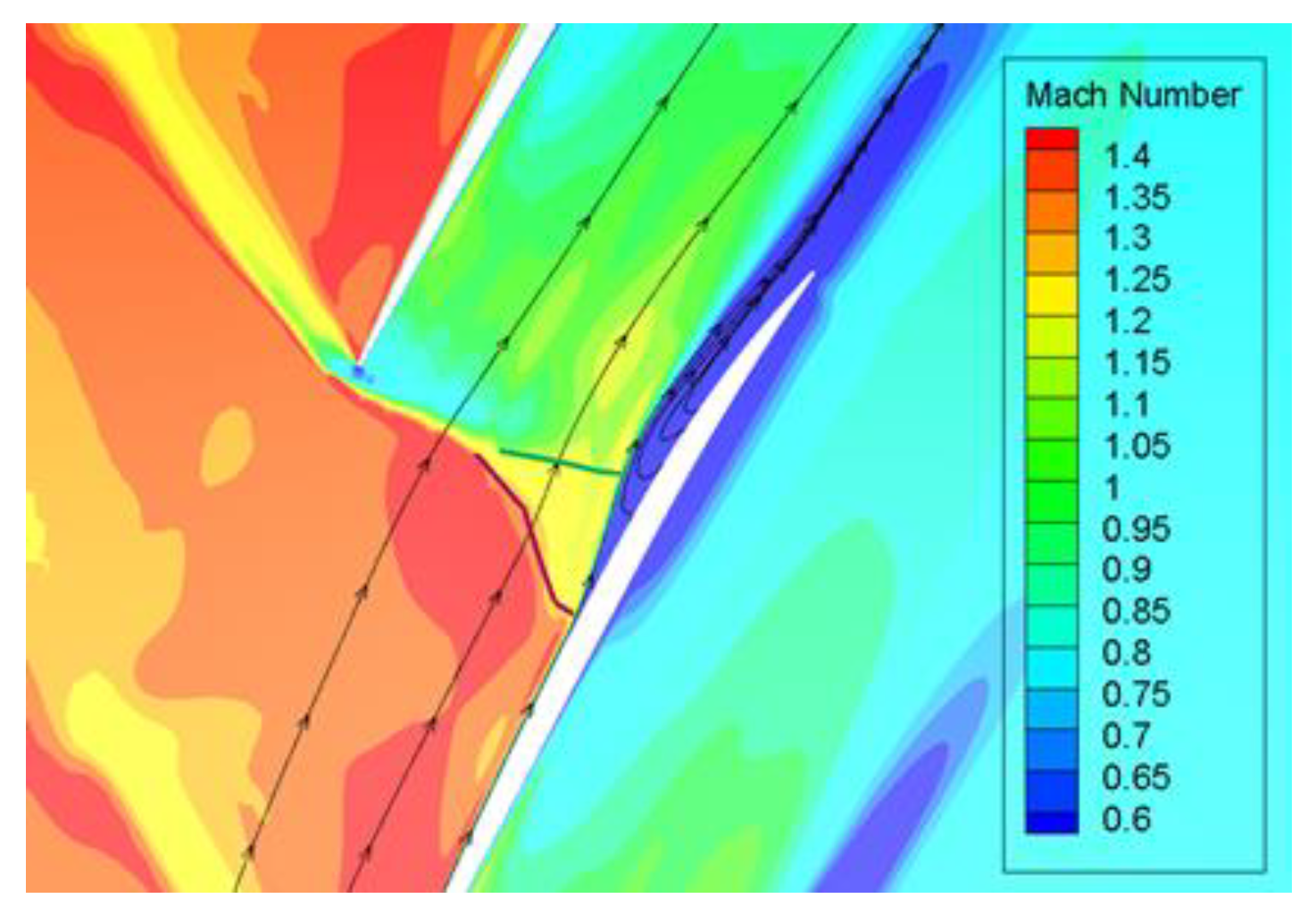
4.2. Computational Flow Field Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- Inlet Boundary Conditions
- 2.
- Outlet Boundary Conditions
- 3.
- Wall Boundary Conditions
References
- Sandberg, R.D.; Michelassi, V. Fluid dynamics of axial turbomachinery: Blade-and stage-level simulations and models. Ann. Rev. Fluid Mech. 2022, 54, 255–285. [Google Scholar] [CrossRef]
- Mani, M.; Dorgan, A.J. A perspective on the state of aerospace computational fluid dynamics technology. Ann. Rev. Fluid Mech. 2023, 55, 431–457. [Google Scholar] [CrossRef]
- Spotts, N.; Gao, X. Comparative Study of Turbulence Models for RANS Simulations of Rotor 67. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Klausmann, F.; Franke, D.; Foret, J.; Schiffer, H.P. Transonic compressor Darmstadt-Open test case Introduction of the TUDa open test case. J. Glob. Power Propuls. Soc. 2022, 6, 318–329. [Google Scholar] [CrossRef]
- He, X.; Zhao, F.; Vahdati, M. Uncertainty Quantification of Spalart-Allmaras Turbulence Model Coefficients for Simplified Compressor Flow Features. J. Fluids Eng. 2019, 142, 9. [Google Scholar] [CrossRef]
- He, X.; Zhao, F.; Vahdati, M. Evaluation of Spalart-Allmaras Turbulence Model Forms for a Transonic Axial Compressor. In Proceedings of the GPPS Chania20, Chania, Greece, 7–9 September 2020. [Google Scholar]
- Brandstetter, C.; Juengst, M.; Schiffer, H.P. Measurements of Radial Vortices, Spill Forward, and Vortex Breakdown in a Transonic Compressor. J. Turbomach. 2018, 17, 12–18. [Google Scholar] [CrossRef]
- Foret, J.; Franke, D.; Klausmann, F.; Klausmann, F.; Schneider, A.; Schiffer, H.P.; Becker, B.; Muller, H. Experimental Aerodynamic and Aeroelastic Investigation of a Highly-Loaded 1.5-Stage Transonic Compressor with Tandem Stator. Int. J. Tubomach. Propuls. Power 2021, 6, 21. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Li, Q.; Jing, F.; Chu, W. Mechanism Underlying the Effect of Self-Circulating Casings with Different Circumferential Coverage Ratios on the Aerodynamic Performance of a Transonic Centrifugal Compressor. Aerospace 2023, 10, 312. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, P.; Zhao, B.; Yang, C. Assessment of a novel k–ω turbulence model for transonic centrifugal impeller simulations. Trans. Can. Soc. Mech. Eng. 2022, 46, 3. [Google Scholar] [CrossRef]
- Ali, S.; Elliott, K.J.; Savory, E.; Zhang, C.; Martinuzzi, R.J.; Lin, W. Investigation of the Performance of Turbulence Models with Respect to High Flow Curvature in Centrifugal Compressors. J. Fluids Eng. 2016, 138, 5. [Google Scholar] [CrossRef]
- Moreno, J.; Dodds, J.; Vahdati, M.; Stapelfeldt, S. Deficiencies in Turbulence Modelling for the Prediction of the Stability Boundary in Highly Loaded Compressors. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Simoes, M.R.; Montojos, B.G.; Moura, N.R.; Su, J. Validation of turbulence models for simulation of axial flow compressor. In Proceedings of the 20th International Congress of Mechanical Engineering, Gramado, Brazil, 15–20 November 2009. [Google Scholar]
- Liu, Y.; Yan, H.; Liu, Y.; Lu, L.; Li, Q. Numerical study of corner separation in a linear compressor cascade using various turbulence models. Chin. J. Aeronaut. 2016, 29, 639–652. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, X.; Wang, D. Evaluation of Different Spalart–Allmaras Turbulence Models for Turbomachinery Flow Field Analysis. J. Propuls. Tech. 2022, 43, 4. (In Chinese) [Google Scholar]
- Chen, X.; Koppe, B.; Lange, M.; Chu, W.; Mailach, R. Comparison of turbulence modeling for a compressor rotor at different tip clearances. AIAA J. 2022, 60, 1186–1198. [Google Scholar] [CrossRef]
- Urasek, D.C.; Gorrel, W.T.; Cunnan, W.S. Performance of Two-Stage Fan Having Low-Aspect-Ratio, First-Stage Rotor Blading; Technical Paper 1493; NASA: Cleveland, OH, USA, 1979.
- Cunnan, W.S.; Stevans, W.; Urasek, D.C. Design and Performance of a 427-Meter-per-Second-Tip-Speed Two-Stage Fan Having a 2.40 Pressure Ratio; Technical Paper 1314; NASA: Cleveland, OH, USA, 1978.
- Suder, K.L.; Hathaway, M.D.; Okiishi, T.H.; Strazisar, A.J.; Adamczyk, J.J. Measurements of the Unsteady Flow Field within the Stator Row of a Transonic Axial-Flow Fan: I—Measurement and Analysis Technique; Technical Memorandum 88945; NASA: Cleveland, OH, USA, 1987.
- Gao, G.; Yong, Y. On incompressible turbulent flow: Partial average based theory and applications. J. Hydraul. Res. 2005, 43, 399–407. [Google Scholar] [CrossRef]
- Spalart, P.R.; Allmaras, S.R. A one-equation turbulence model for aerodynamic flows. In Proceedings of the AIAA 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar]
- Menter, F.; Rumsey, C. Assessment of two-equation turbulence models for transonic flows. In Proceedings of the Fluid Dynamics Conference, Colorado Springs, CO, USA, 20–23 June 1994. [Google Scholar]
- Launder, D.B.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 2. [Google Scholar] [CrossRef]
- Wolfshtein, M. The Velocity and Temperature Distribution in one-Dimensional Flow with Turbulence Augmentation and Pressure Gradient. Int. J. Heat Mass Transfer 1969, 12, 301–308. [Google Scholar] [CrossRef]
- Jongen, T. Simulation and Modeling of Turbulent Incompressible Flows. Ph.D. Thesis, EPF Lausanne, Lausanne, Switzerland, 1992. [Google Scholar]
- Strazisar, A.J.; Wood, J.R.; Hathaway, M.D.; Suder, K.L. Laser Anemometer Measurements in a Transonic Axial-Flow Fan Rotor; Technical Paper 2879; NASA: Cleveland, OH, USA, 1989. [Google Scholar]


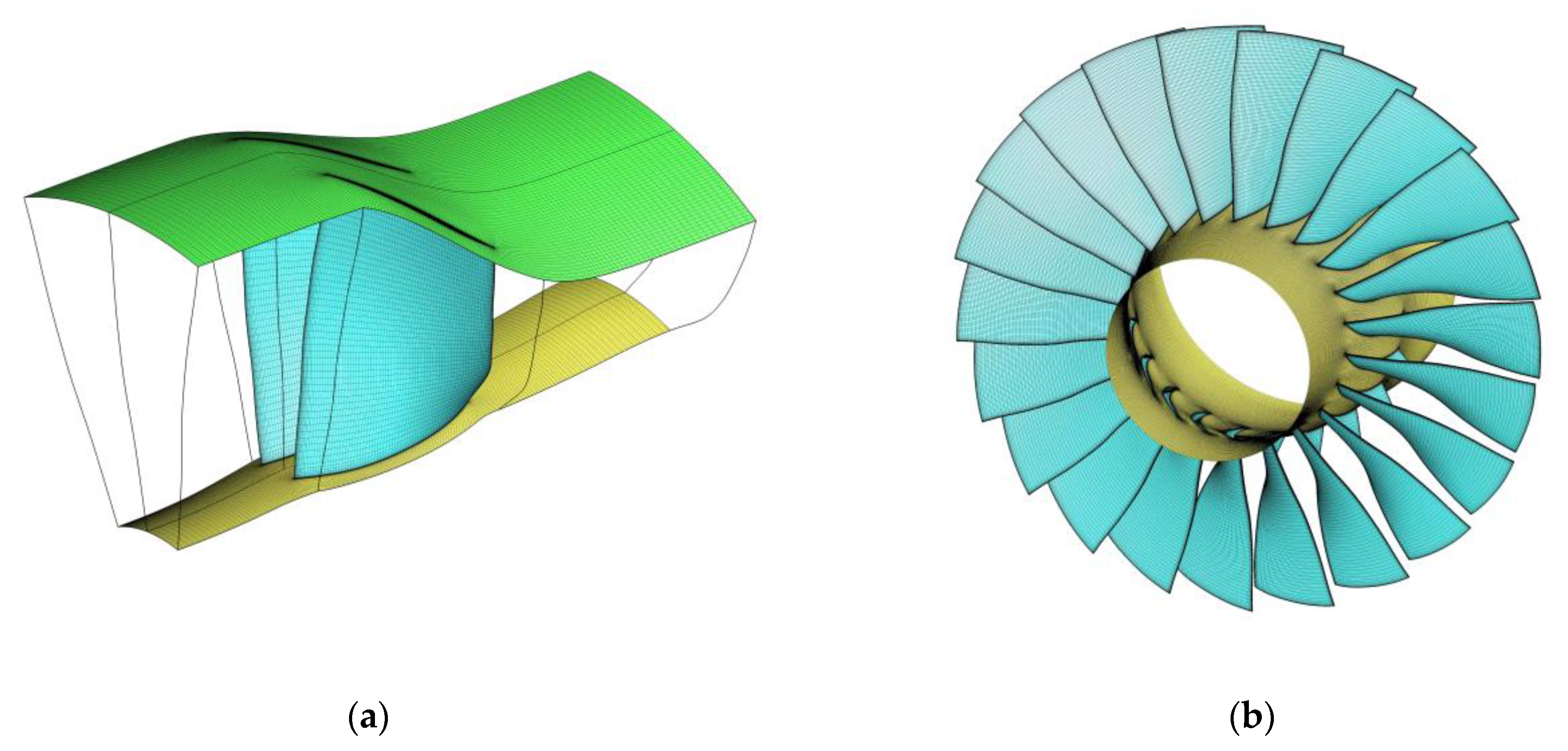
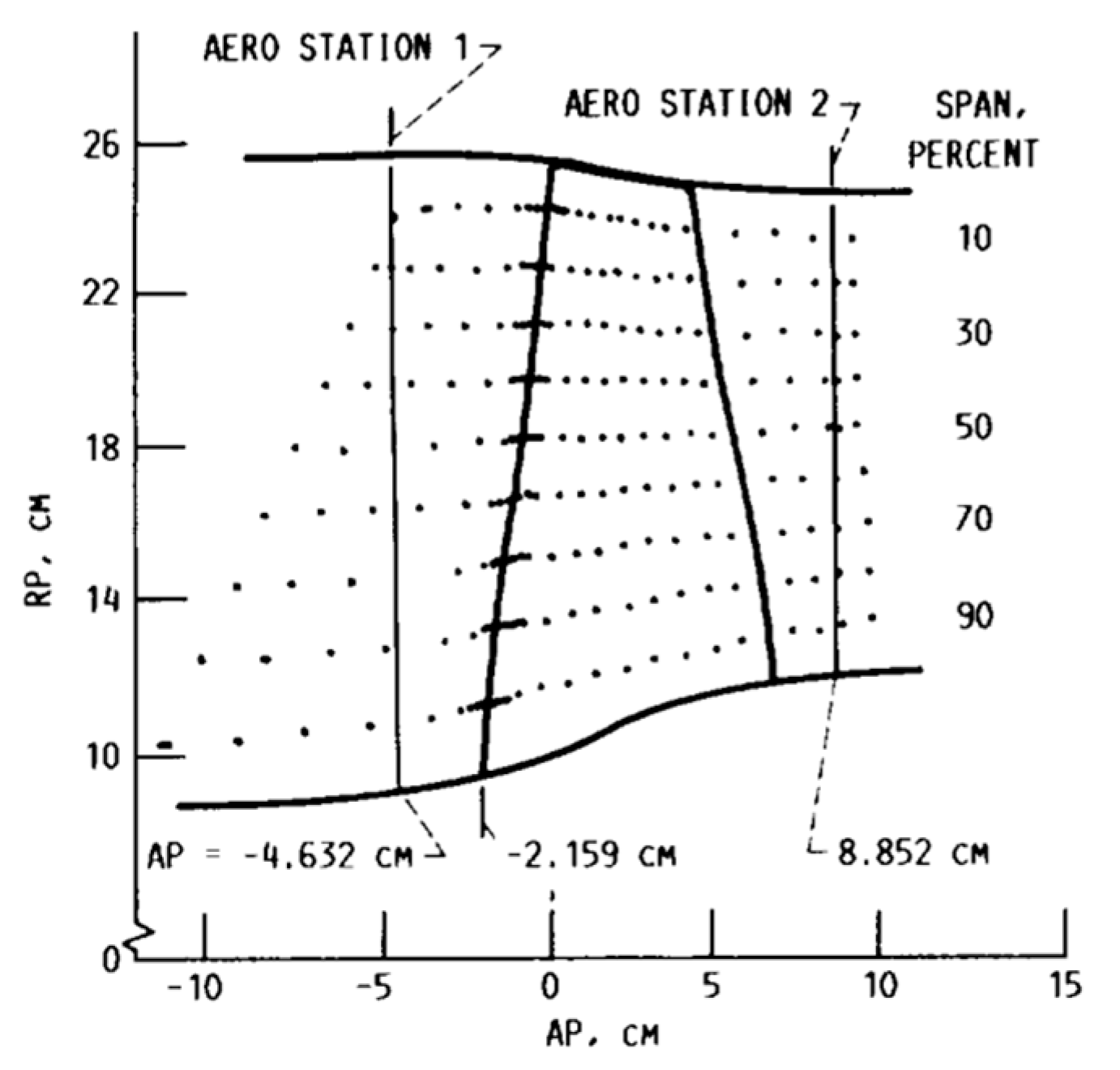
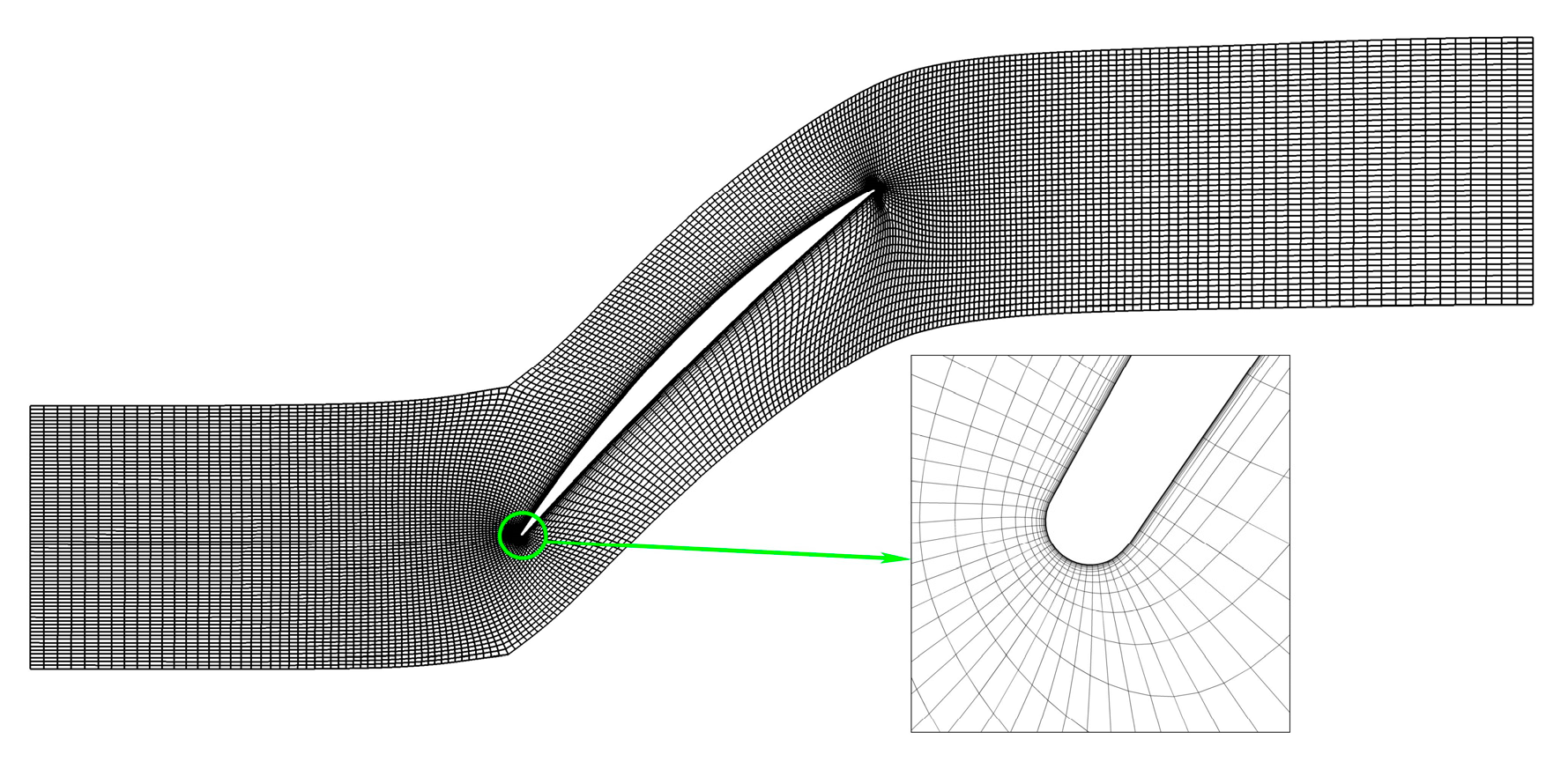

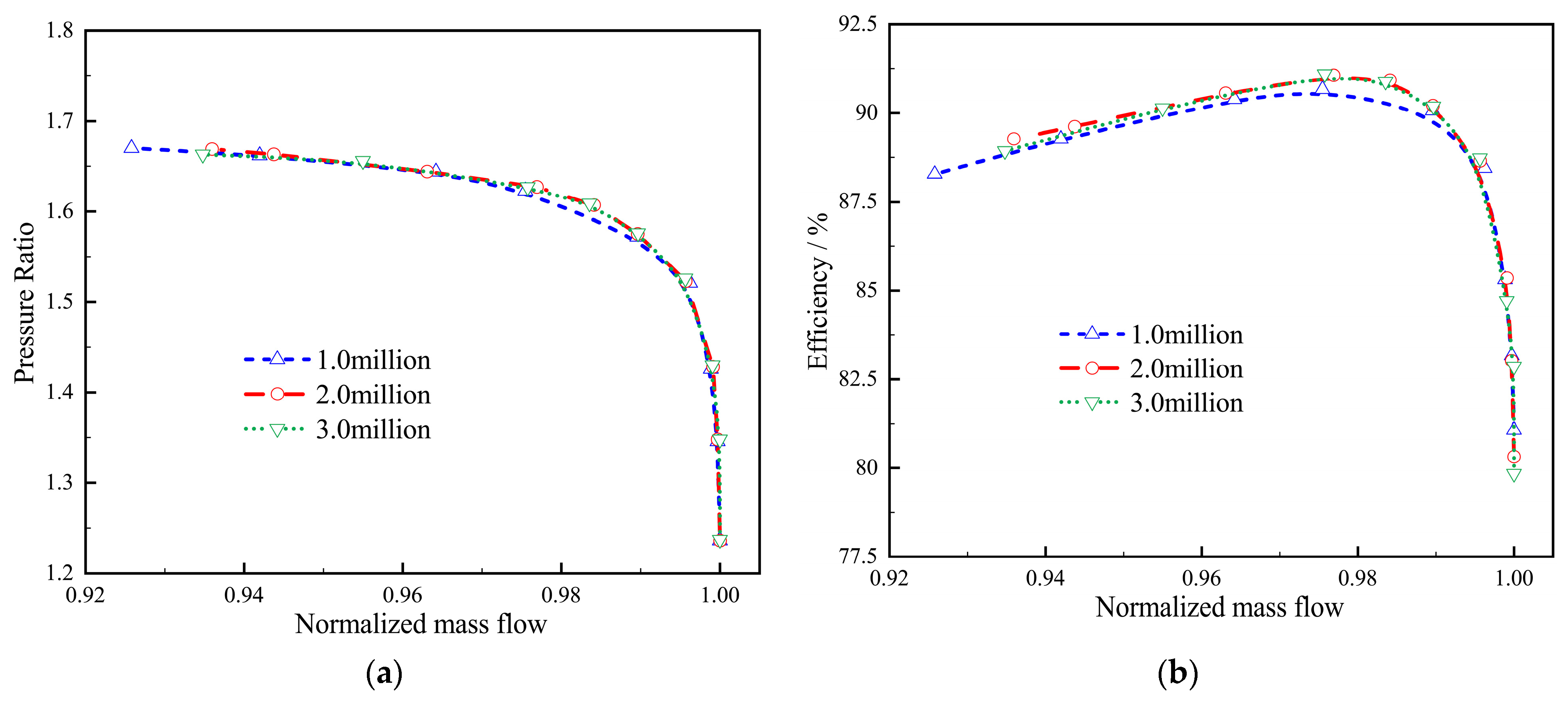
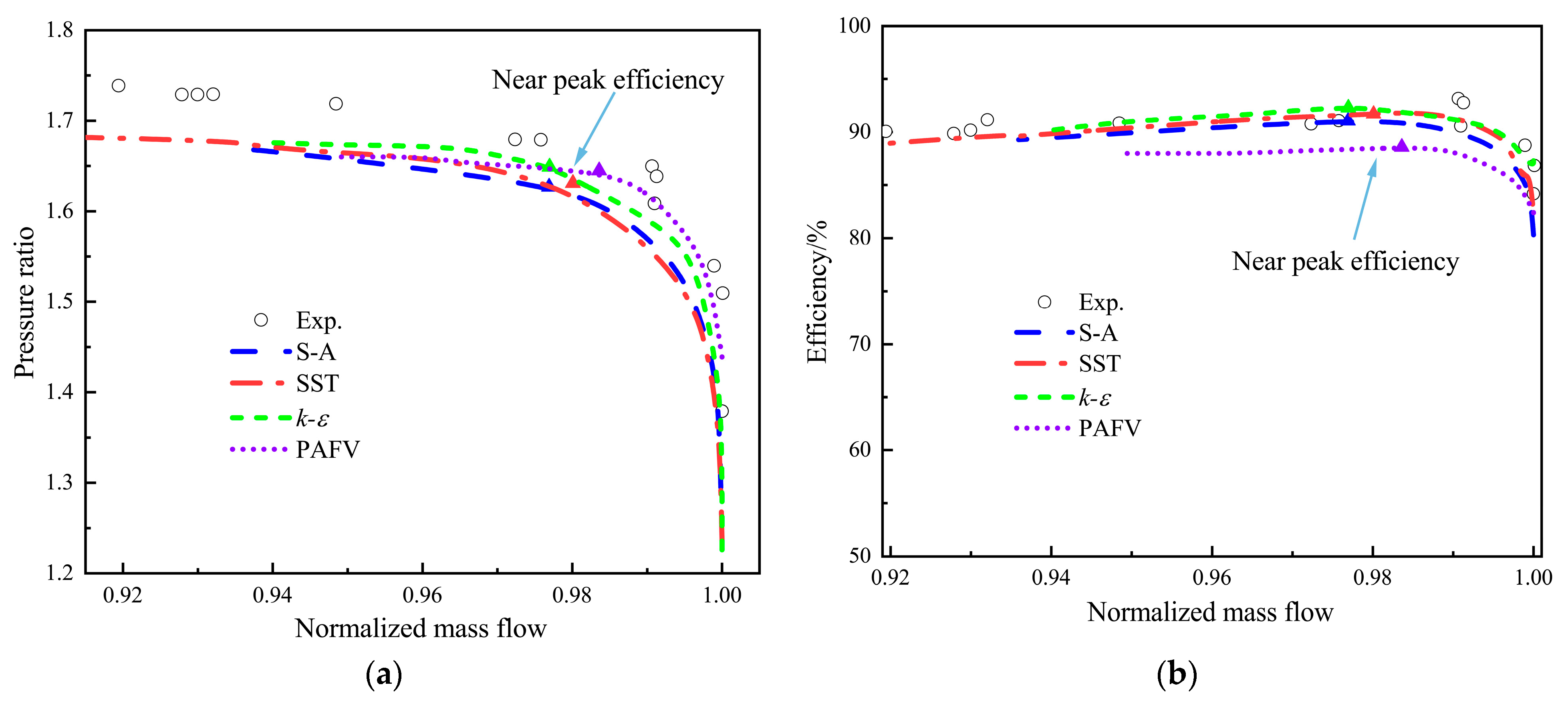
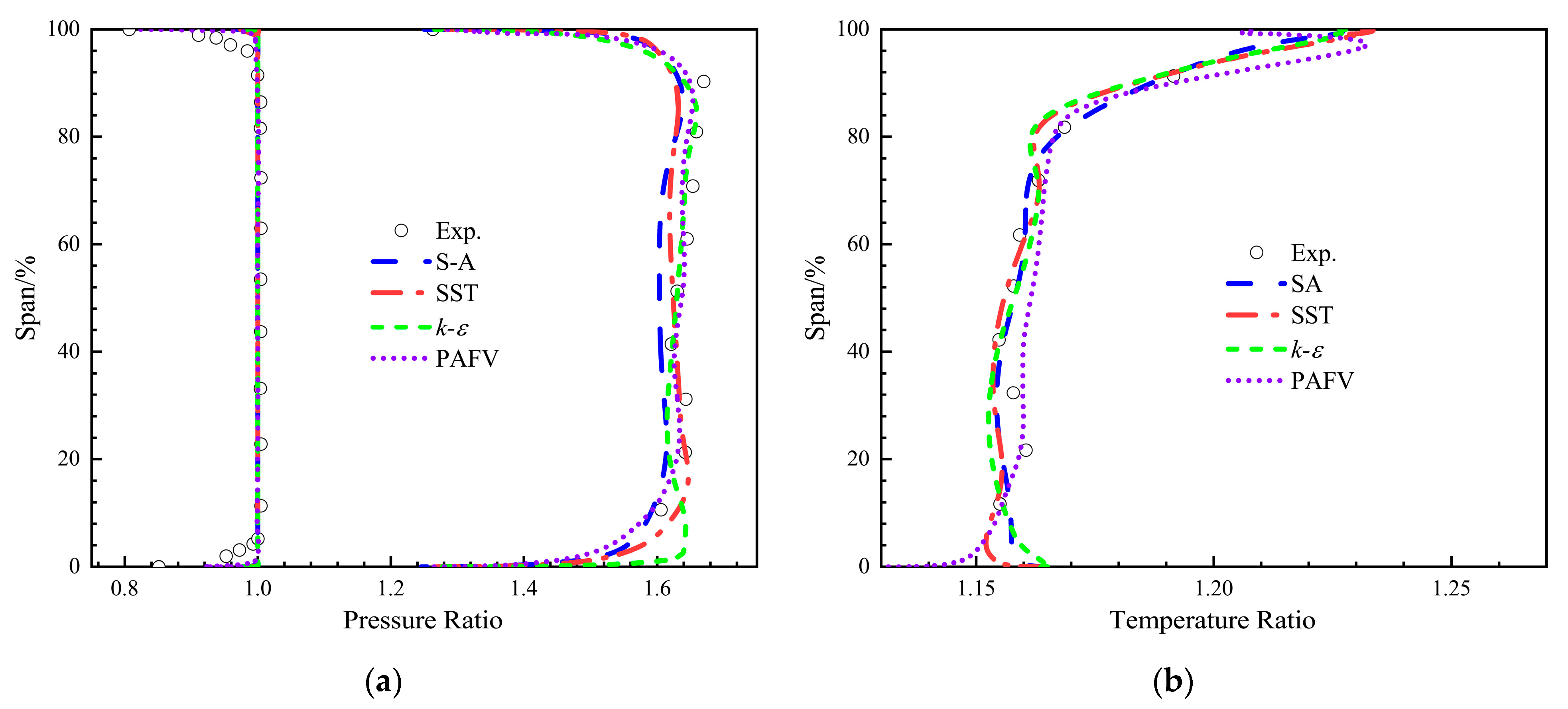
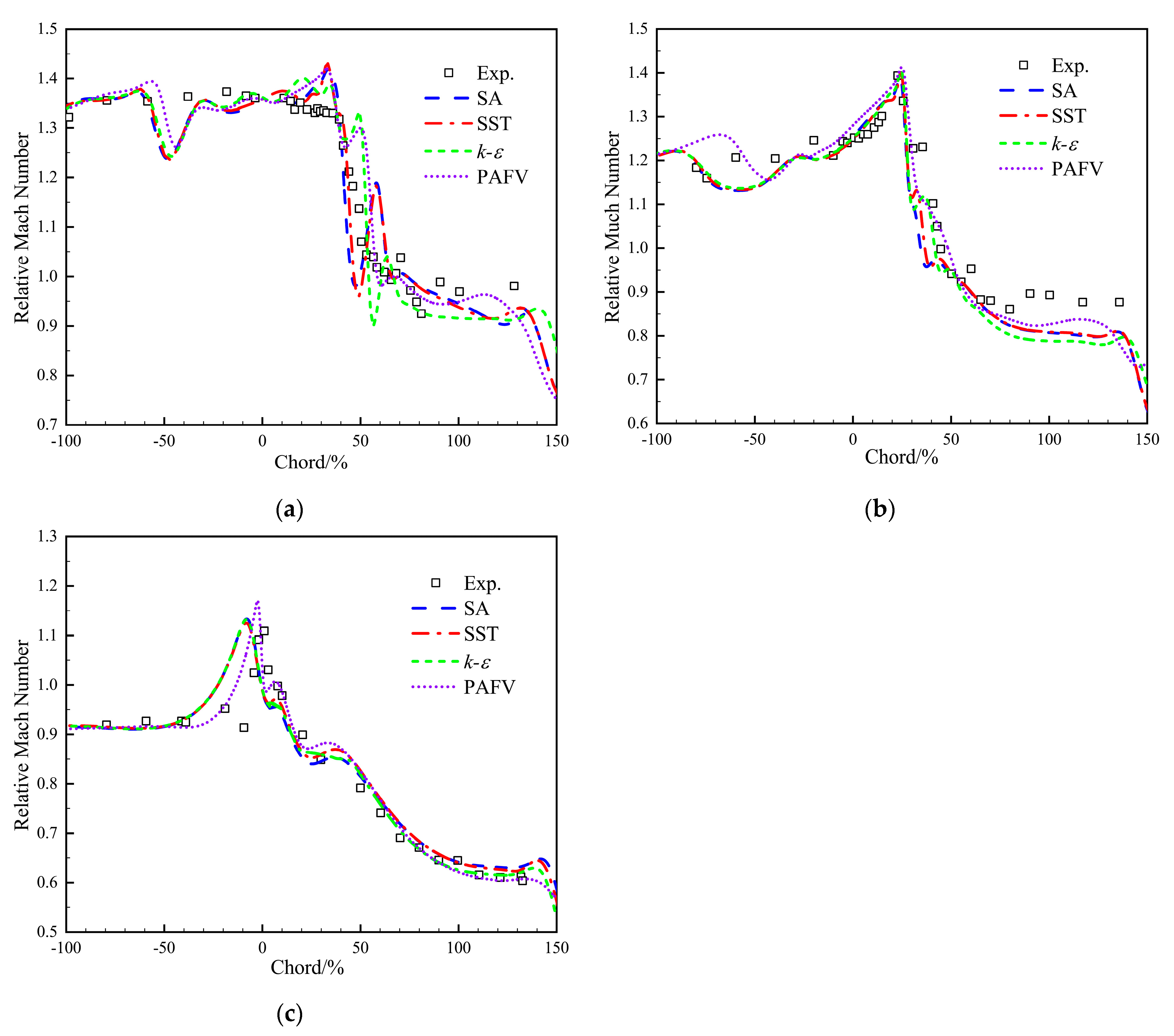

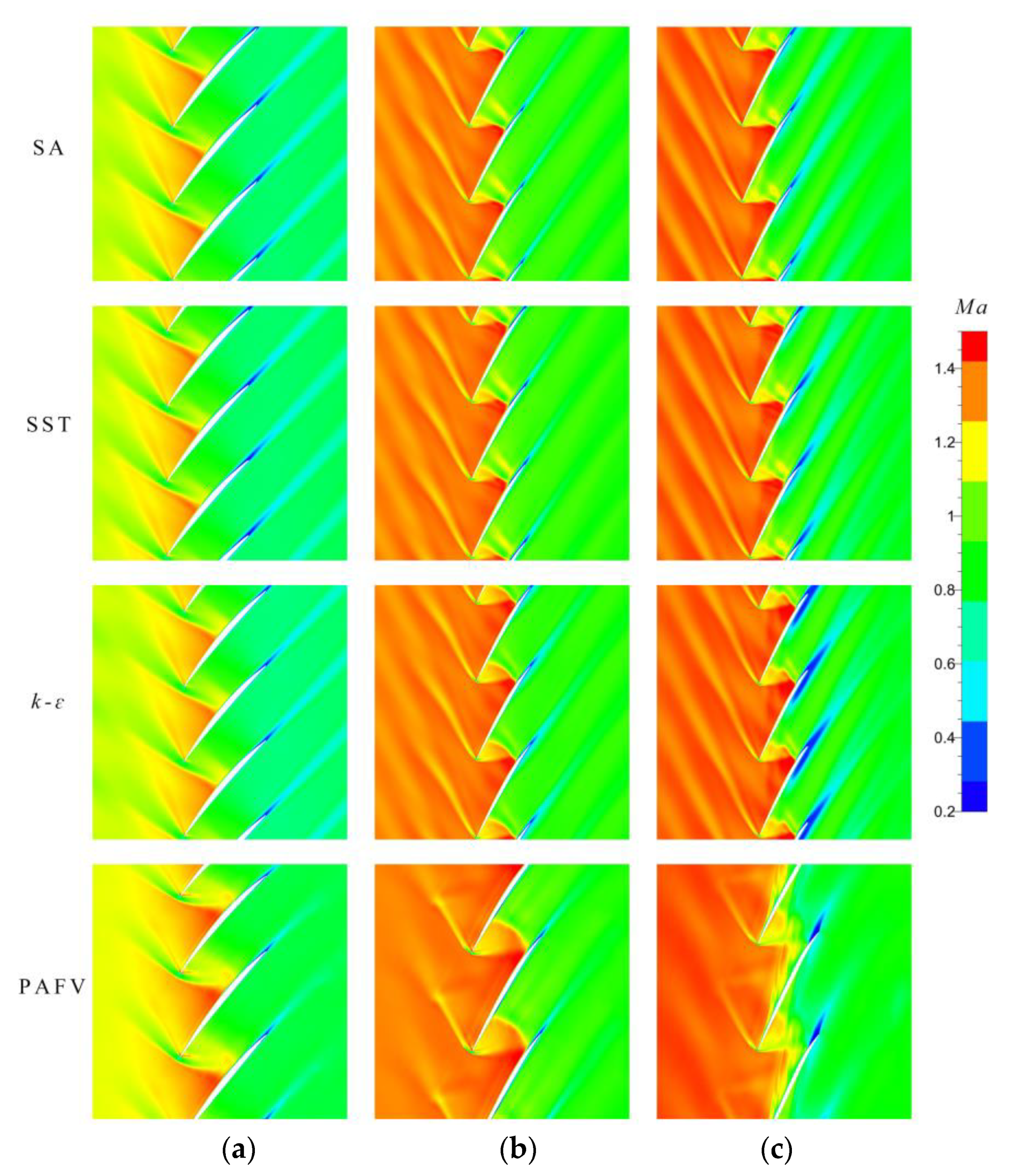

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Inlet diameter | 0.514 m | Rotational speed | 16,043 RPM |
| Outlet diameter | 0.485 m | Design pressure ratio | 1.63 |
| Imported wheel ratio | 0.375 | Blade tip tangent velocity | 429 m/s |
| Export wheel ratio | 0.478 | Design of blade tip Ma | 1.38 |
| Spread–sine ratio | 1.56 | Total inlet temperature | 15 °C [288 K] |
| Surface fineness | 0.8 μm | Total inlet pressure | 101,325 Pa |
| Radius of blade root guide circle | 1.78 mm | Design flow | 33.25 kg/s |
| Blade tip clearance | 1 mm | Blockage flow | 34.96 kg/s |
| Number of blades | 22 |
| Blockage Flow (kg/s) | Near Stall Point Pressure Ratio | Maximum Efficiency | Design Point Efficiency | |
|---|---|---|---|---|
| S-A | 34.65 | 1.669 | 91.06% | 90.21% |
| SST | 34.66 | 1.683 | 91.70% | 90.40% |
| k-ɛ | 34.72 | 1.676 | 92.30% | 91.00% |
| PAFV | 34.76 | 1.661 | 88.60% | 87.30% |
| Exp. | 34.96 | 1.728 | 93.18% | 90.58% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, W.; Sun, Z.; Zhou, J.; Zhang, K.; Wang, J.; Tian, X.; Tian, J. Numerical Simulation of Transonic Compressors with Different Turbulence Models. Aerospace 2023, 10, 784. https://doi.org/10.3390/aerospace10090784
Yan W, Sun Z, Zhou J, Zhang K, Wang J, Tian X, Tian J. Numerical Simulation of Transonic Compressors with Different Turbulence Models. Aerospace. 2023; 10(9):784. https://doi.org/10.3390/aerospace10090784
Chicago/Turabian StyleYan, Wenhui, Zhaozheng Sun, Junwei Zhou, Kun Zhang, Jiahui Wang, Xiao Tian, and Junqian Tian. 2023. "Numerical Simulation of Transonic Compressors with Different Turbulence Models" Aerospace 10, no. 9: 784. https://doi.org/10.3390/aerospace10090784
APA StyleYan, W., Sun, Z., Zhou, J., Zhang, K., Wang, J., Tian, X., & Tian, J. (2023). Numerical Simulation of Transonic Compressors with Different Turbulence Models. Aerospace, 10(9), 784. https://doi.org/10.3390/aerospace10090784






