Fatigue Reliability Analysis of Composite Material Considering the Growth of Effective Stress and Critical Stiffness
Abstract
:1. Introduction
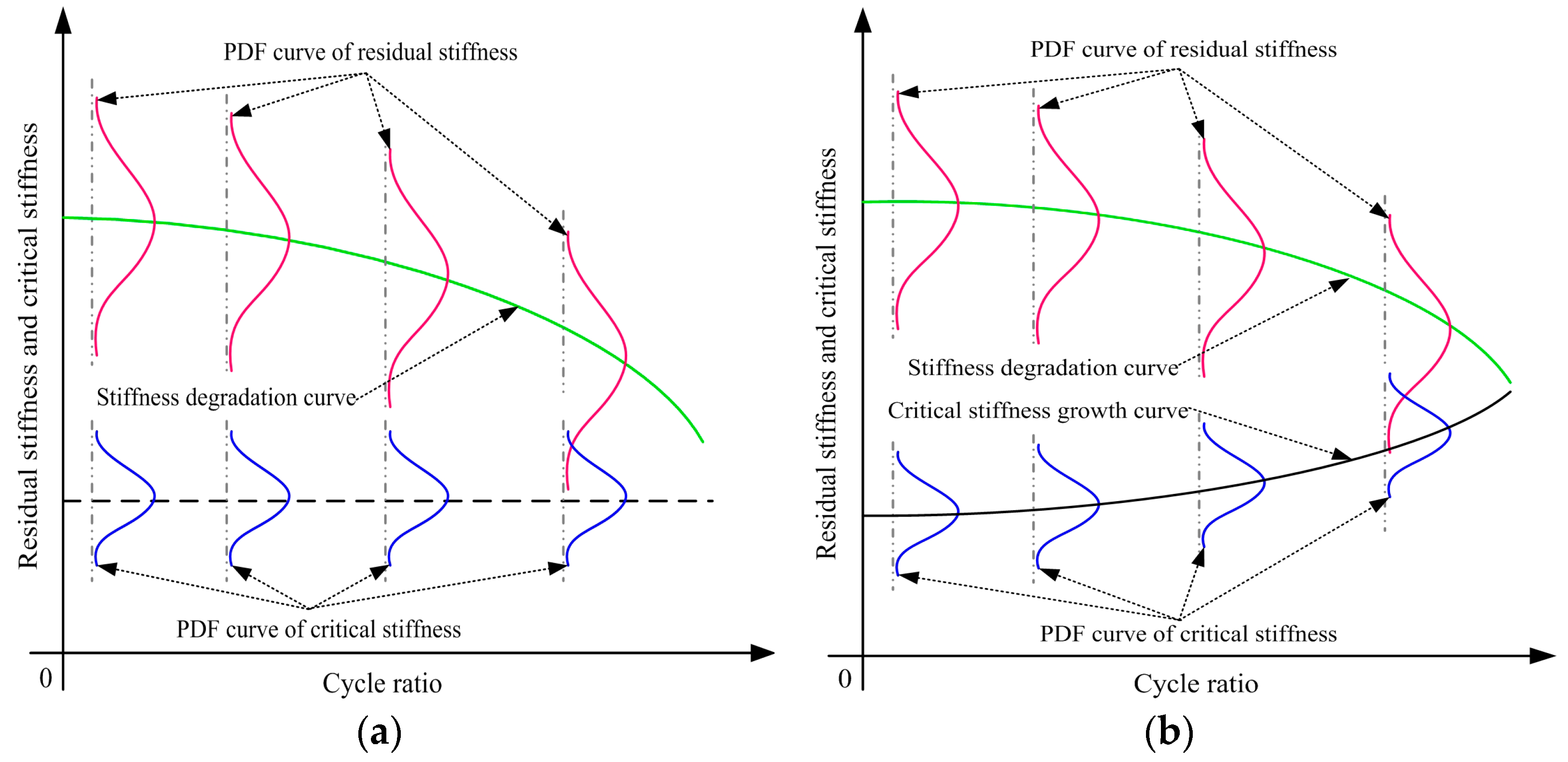
2. Fatigue Damage Characterized by Performance Degradation
2.1. Fatigue Damage Characterized by Strength Degradation
2.2. Fatigue Damage Characterized by Stiffness Degradation
3. Performance Degradation of Composite Material
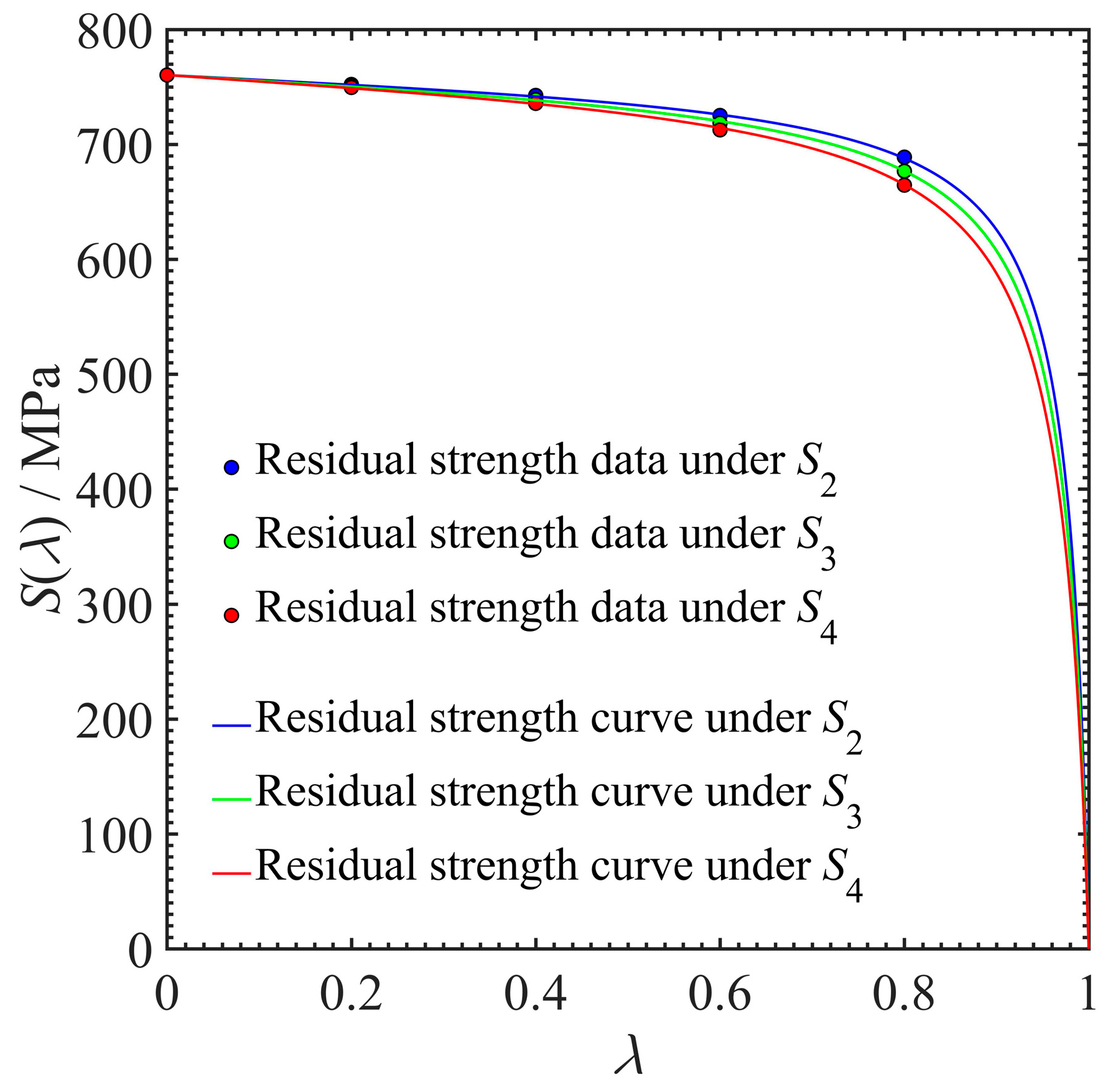
3.1. Probabilistic Model of Residual Strength
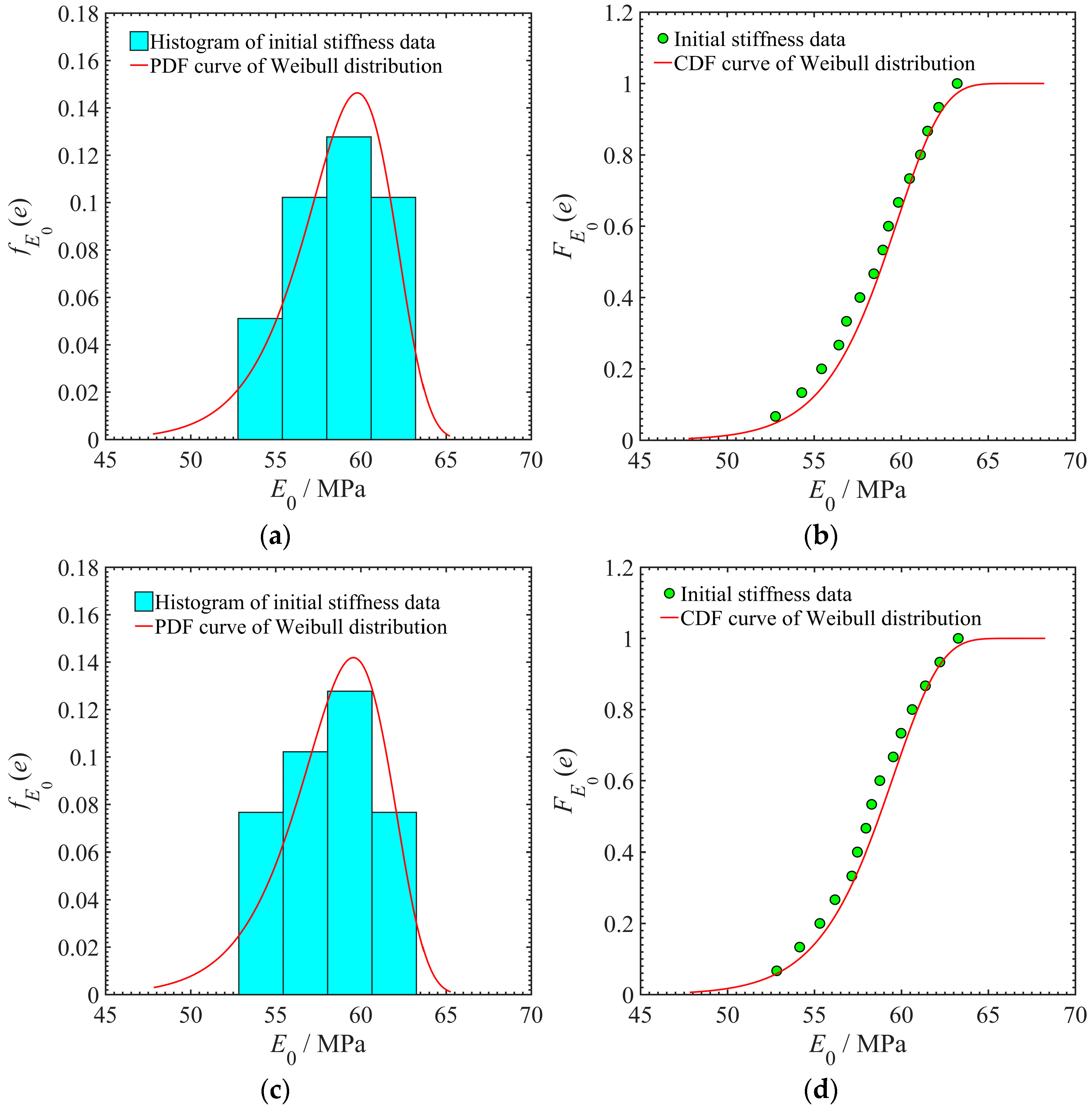
3.2. Probabilistic Model of Residual Stiffness
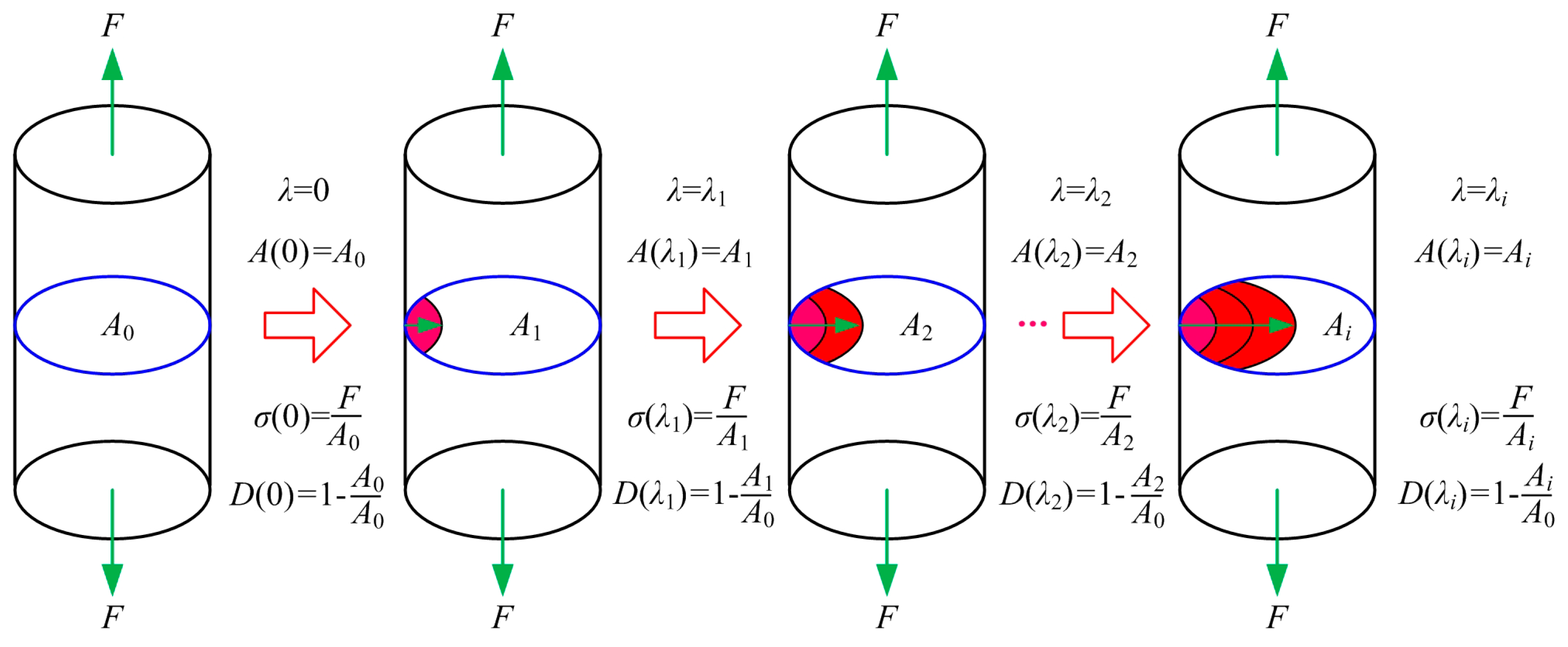
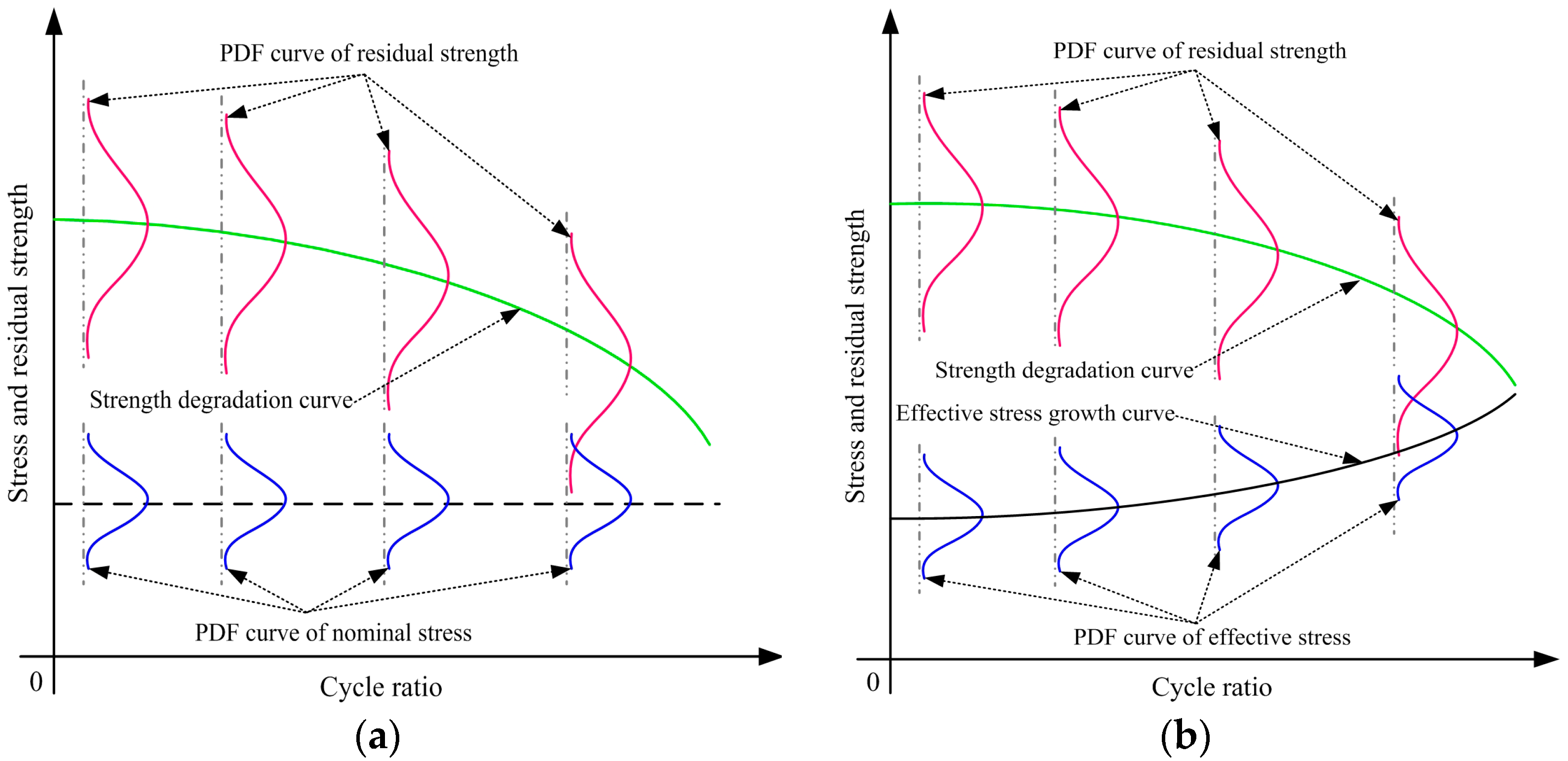
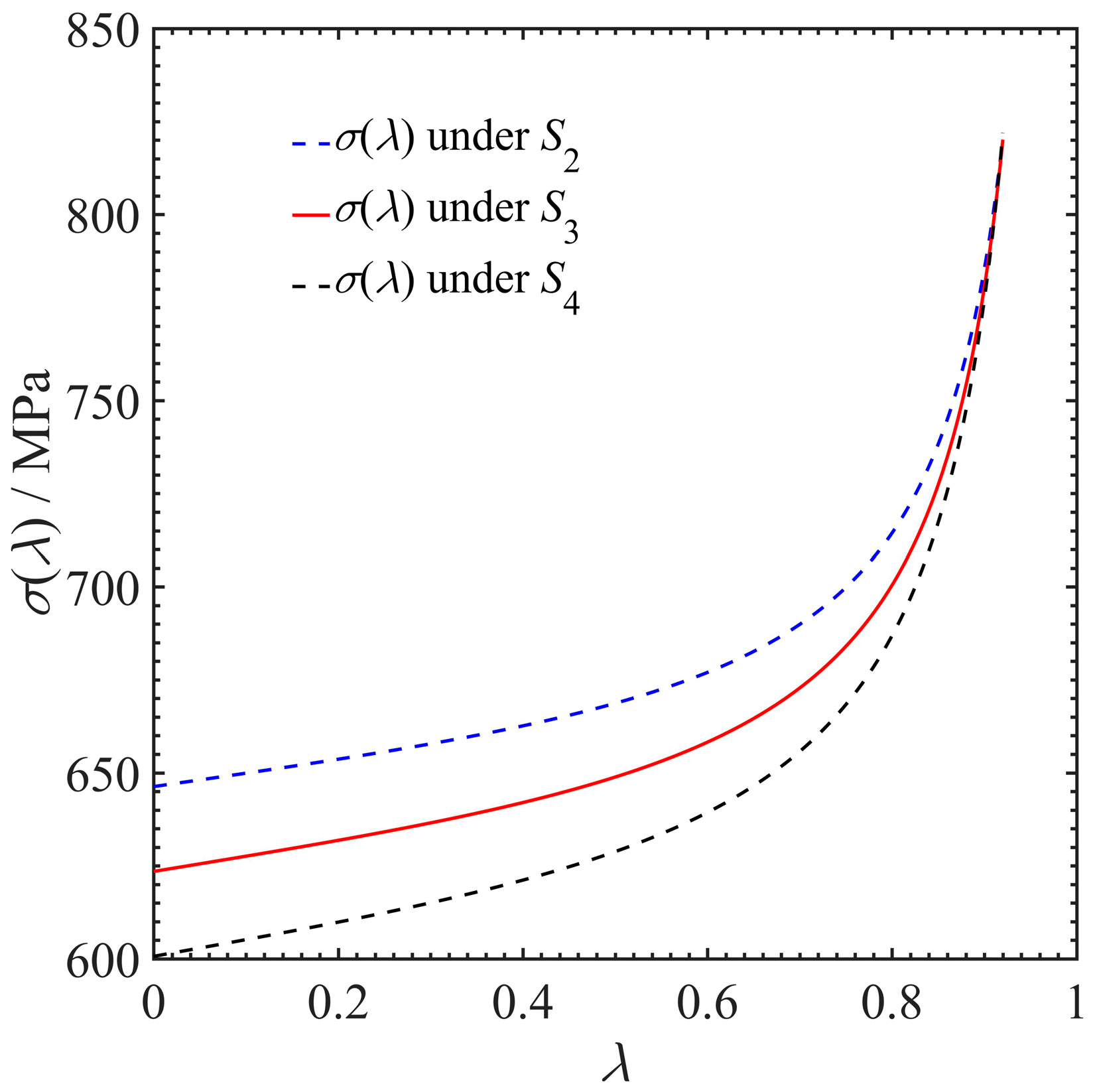
4. Effective Stress Growth and Critical Stiffness Increase
4.1. Effective Stress Growth Caused by Fatigue Damage
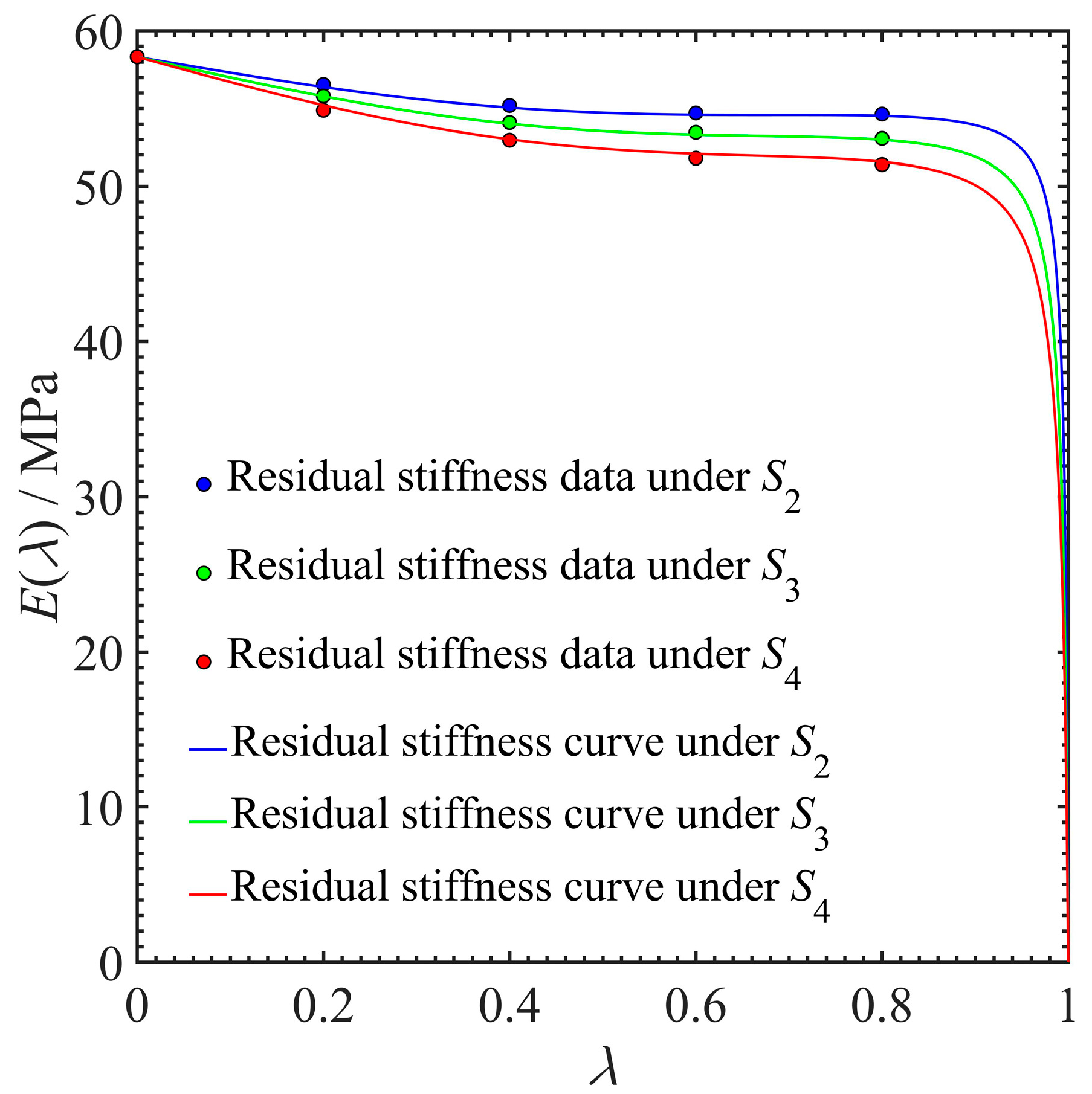
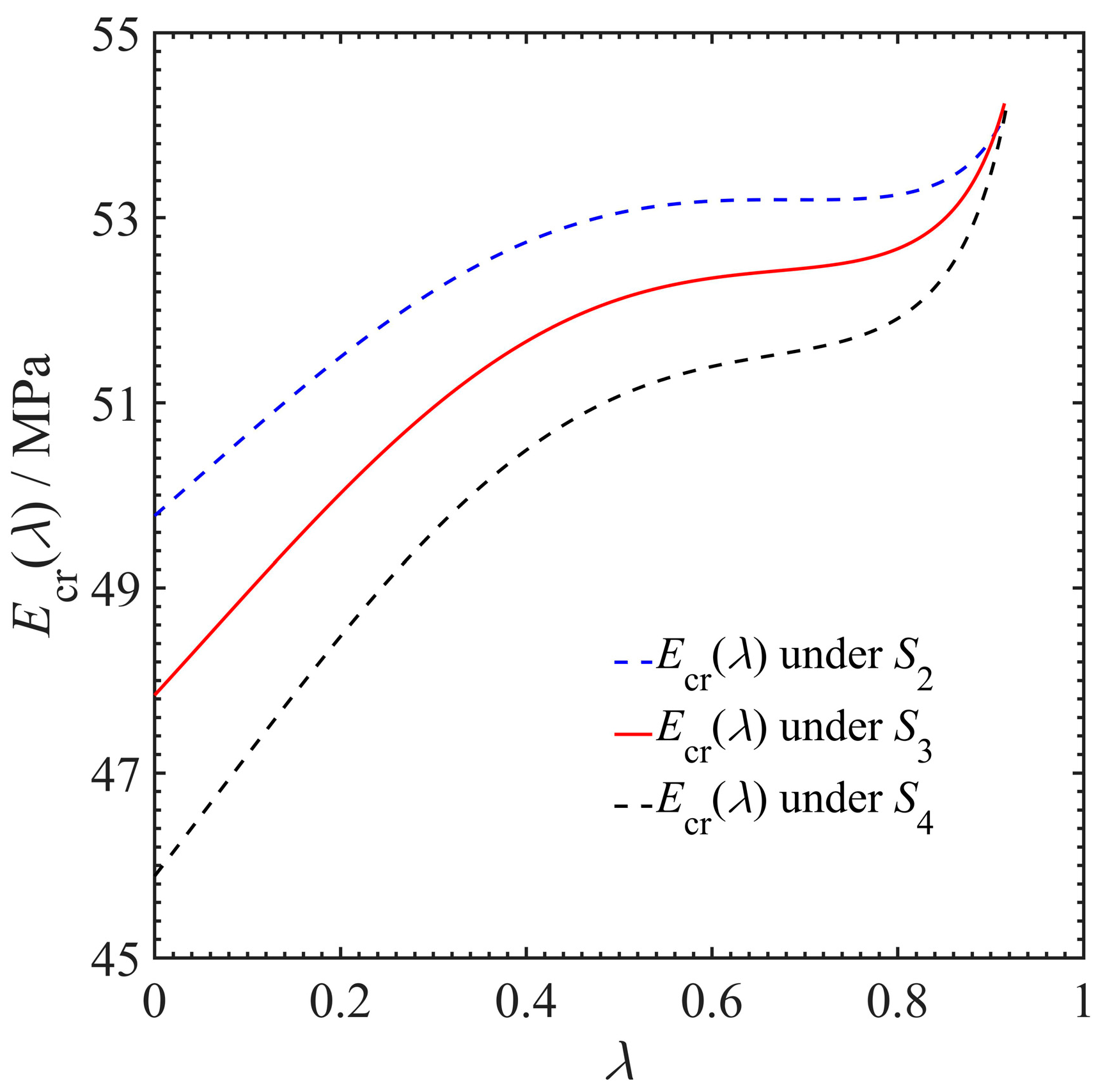
4.2. Critical Stiffness Increase Caused by Fatigue Damage
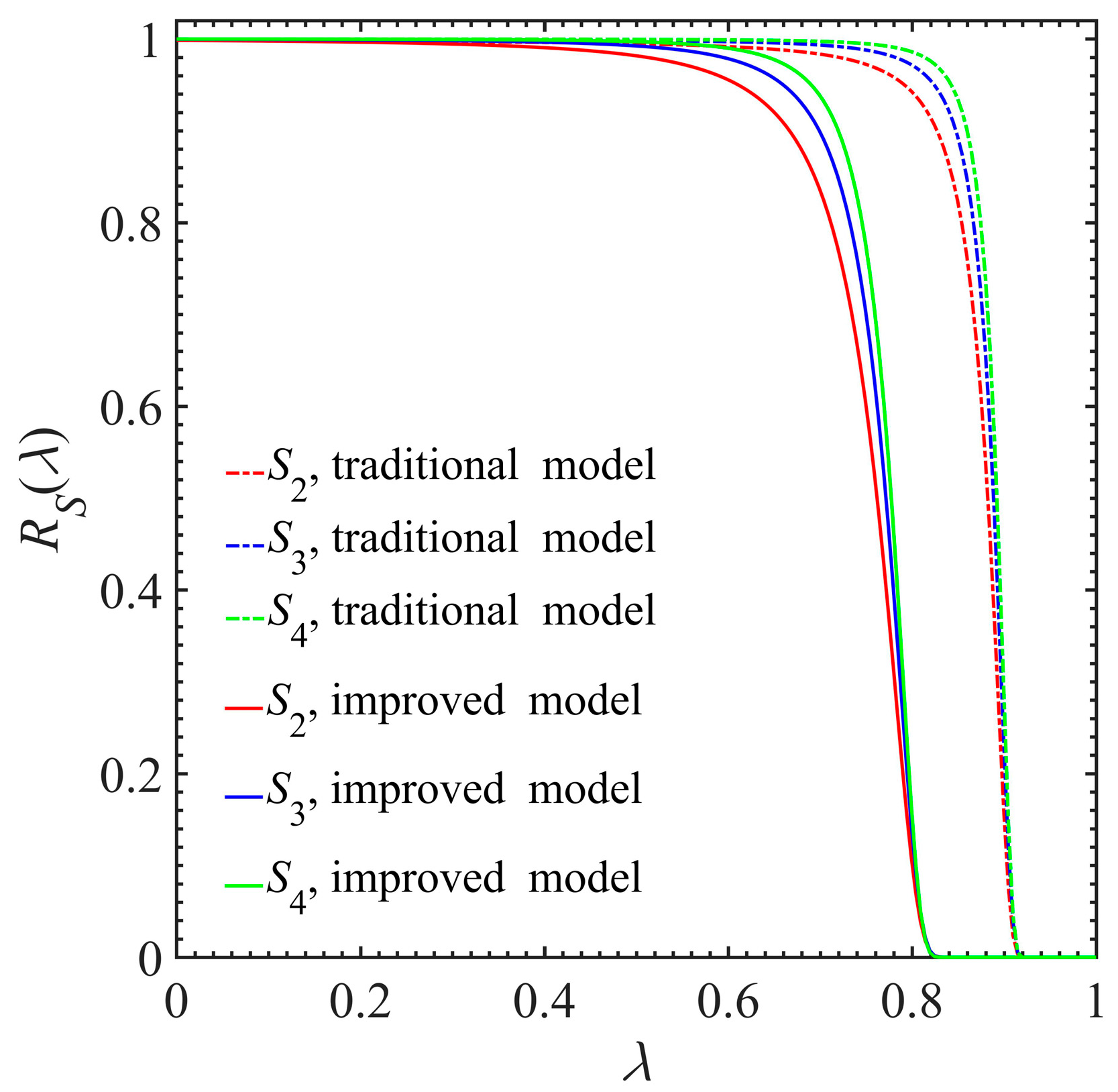
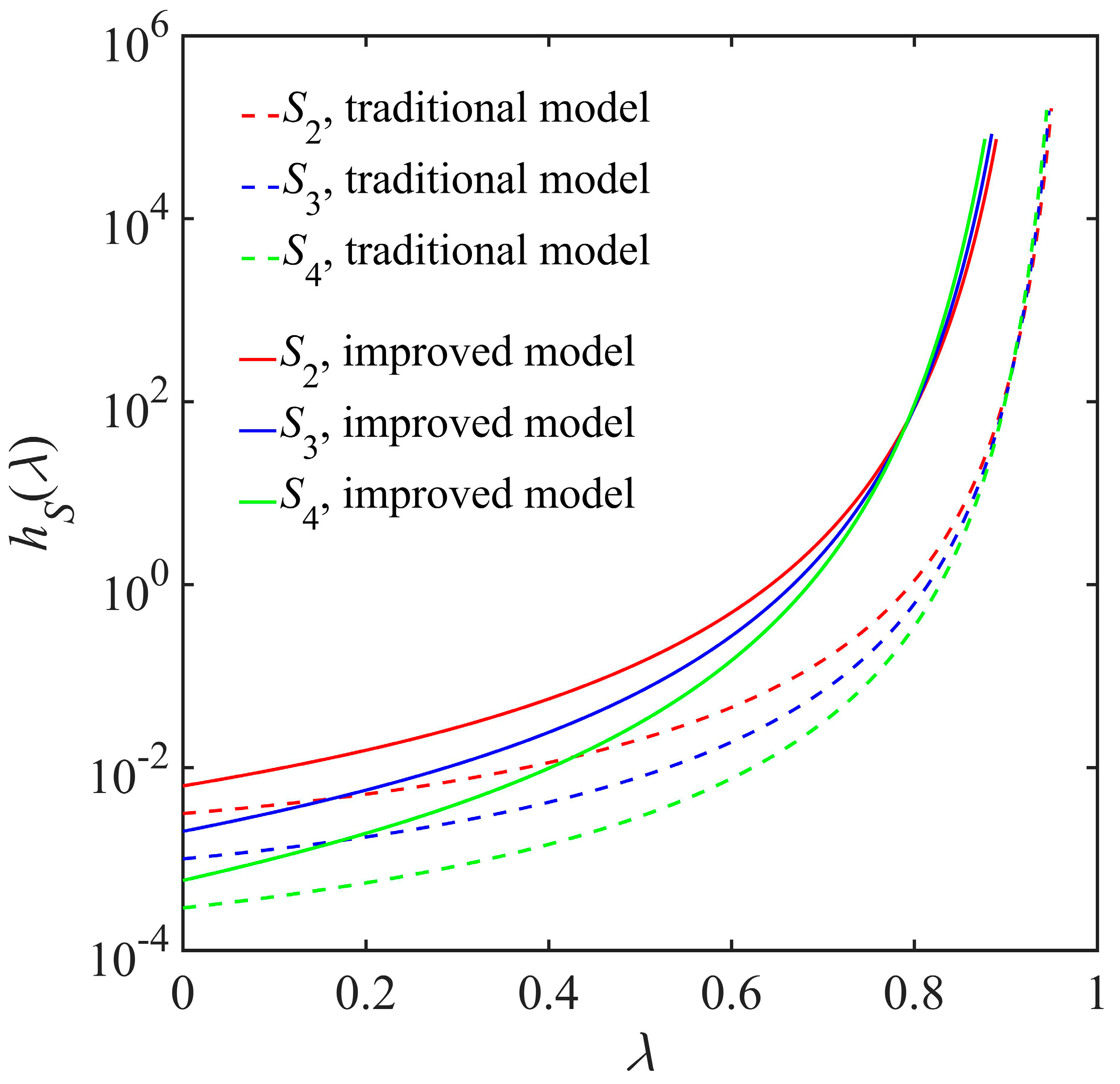
5. Fatigue Reliability Analysis Considering Effective Stress Growth
5.1. Improved Strength-Based Fatigue Reliability Model
5.2. Improved Stiffness-Based Fatigue Reliability Model
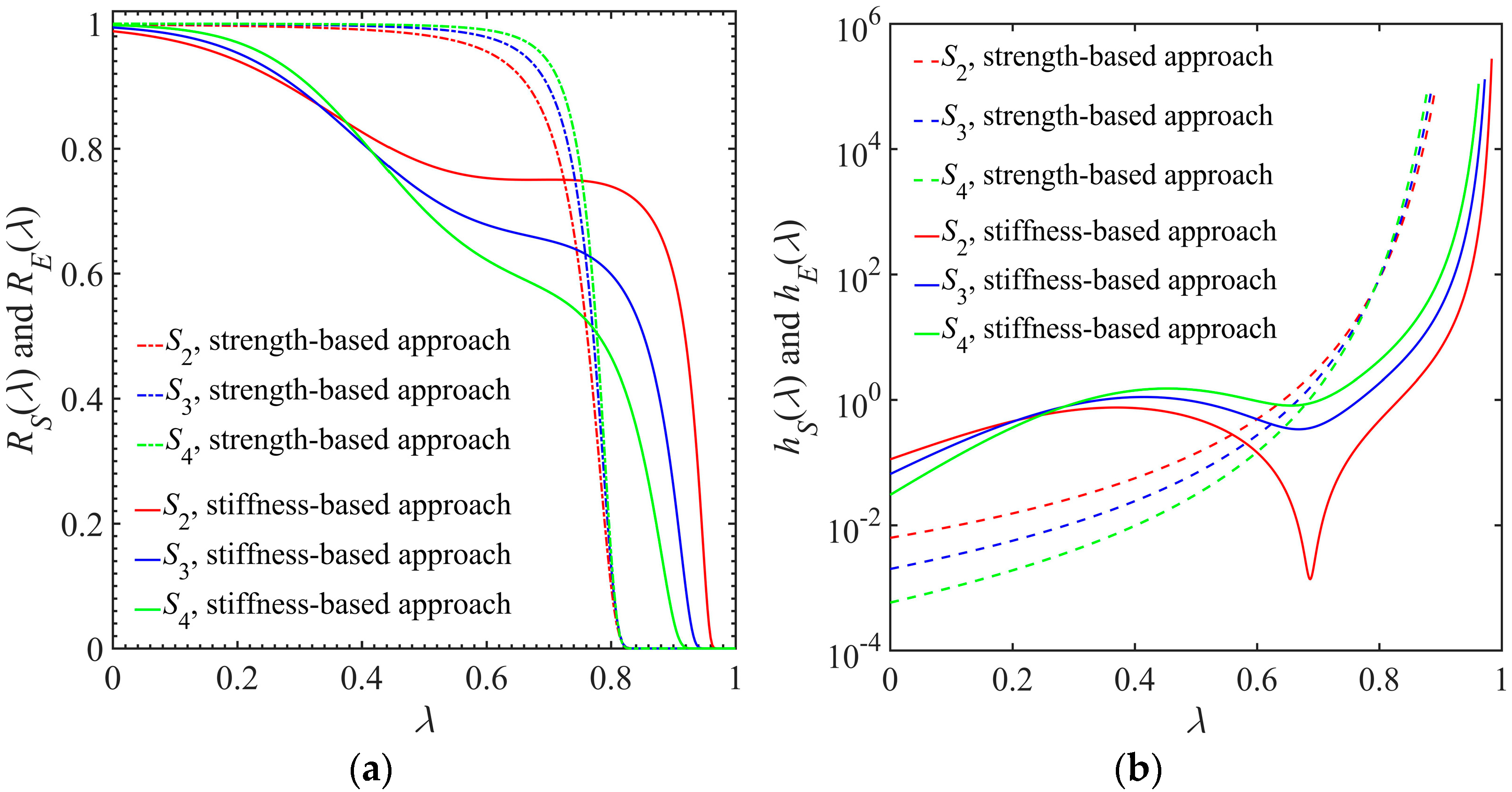
5.3. Comparison between Different Reliability Analysis Approaches
6. Conclusions
- (1)
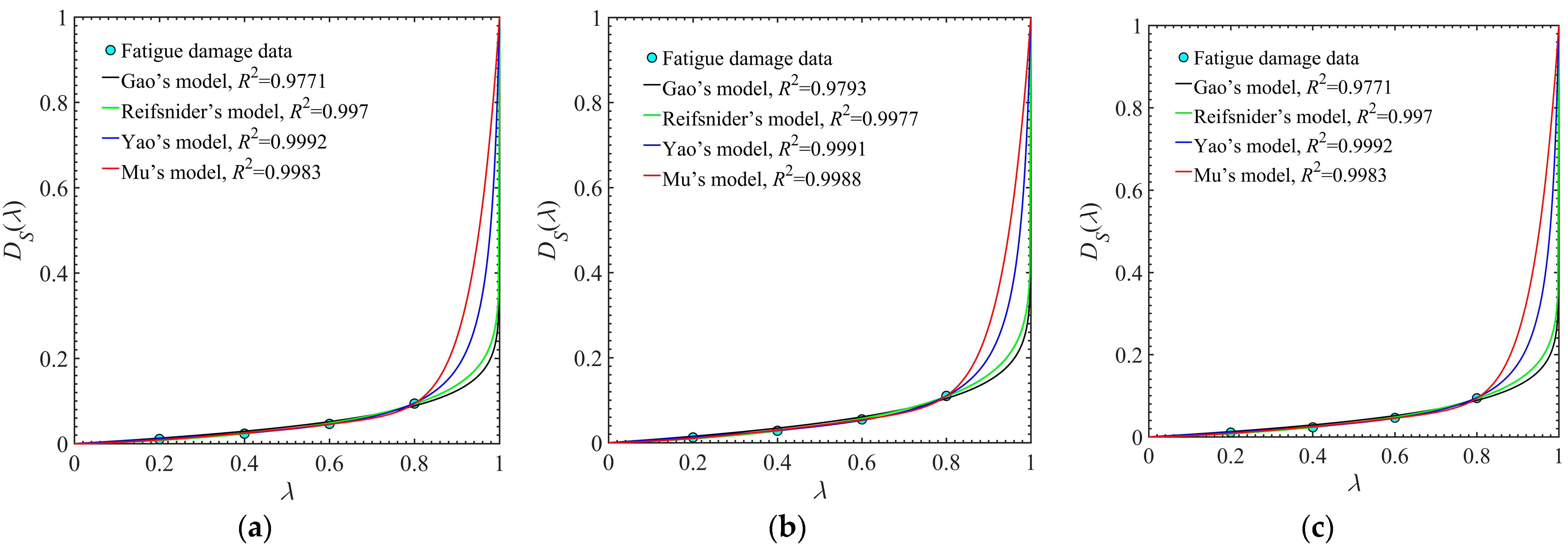
- The fatigue damage accumulation of a composite material is quantified from the perspective of performance degradation. The fitting accuracy of some representative fatigue damage models is compared based on the fatigue damage data of Gr/PEEK [0/45/90/−45]2S laminates. Yao’s model and Gao’s model are adopted to characterize the strength-based and stiffness-based fatigue damage, respectively.
- (2)
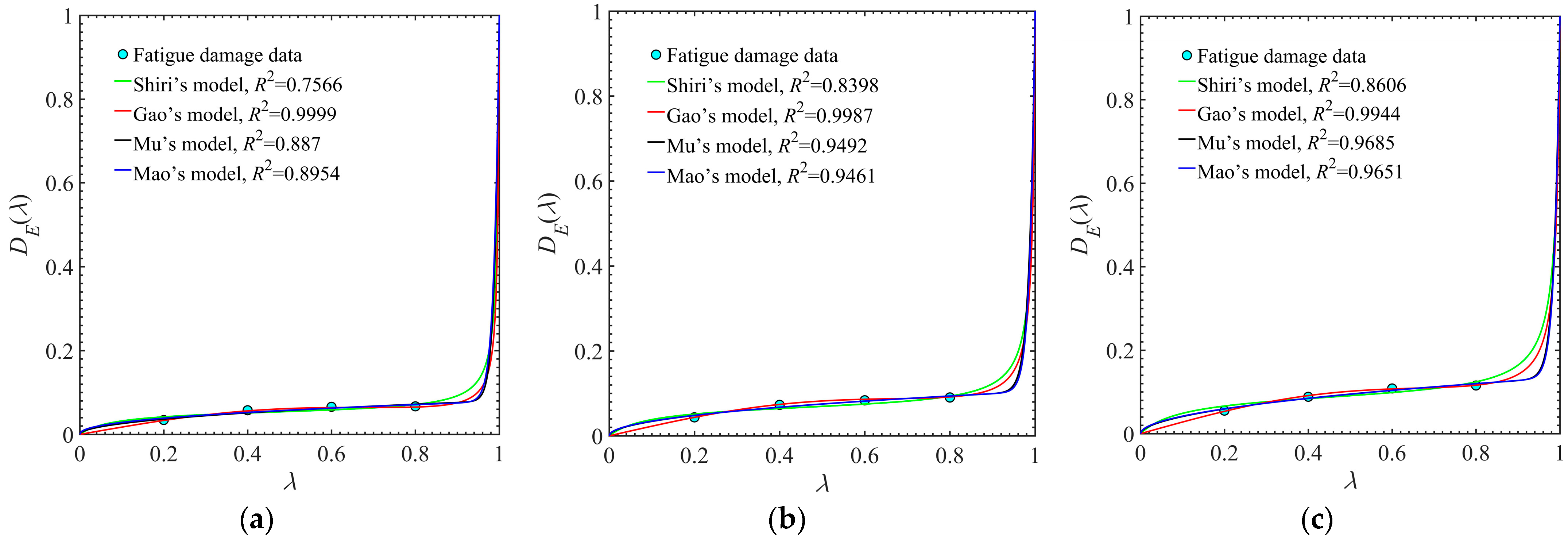
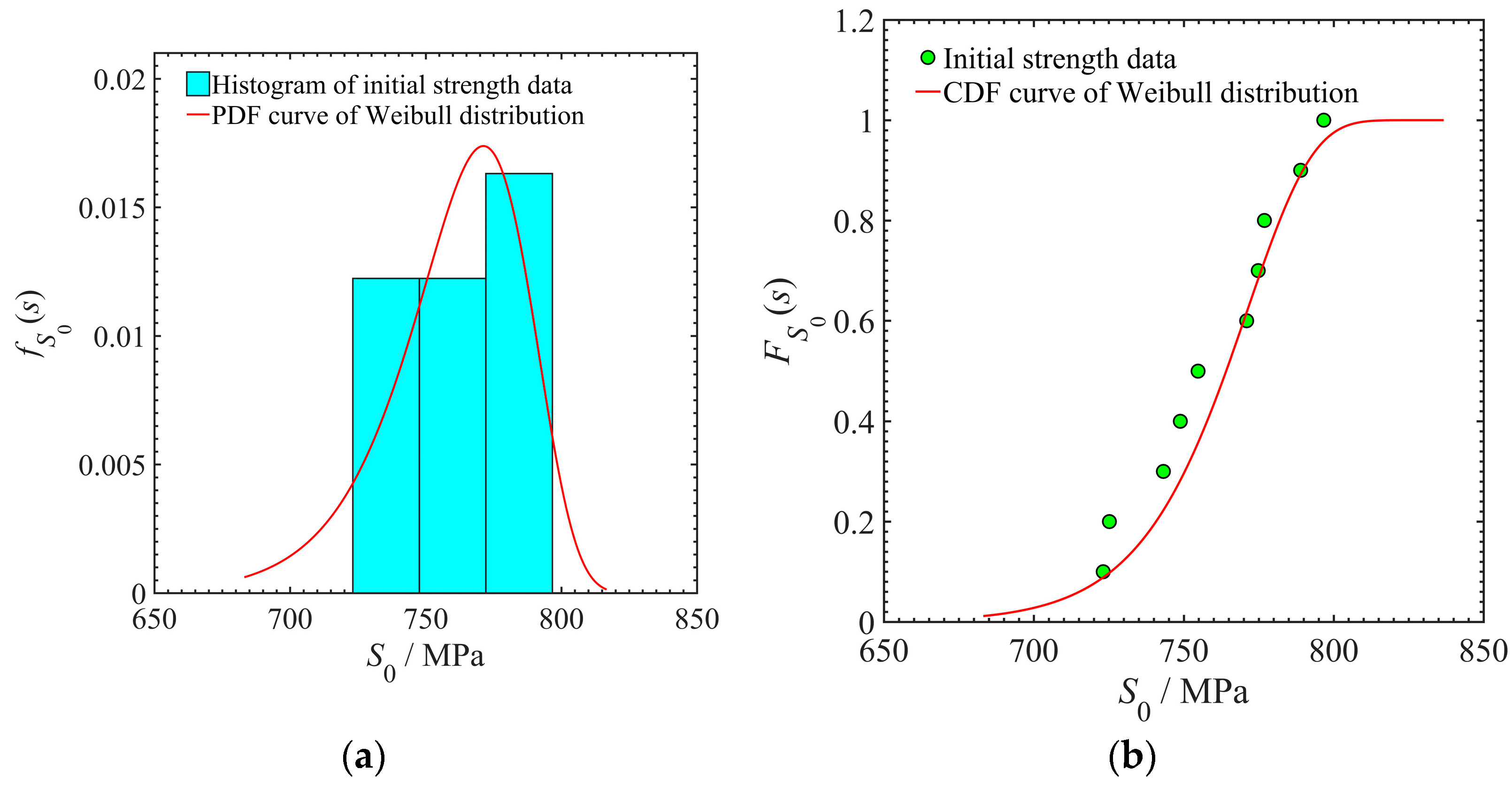
- The Weibull distribution is applied to depict the probability distributions of initial strength and initial stiffness. A pair of probabilistic models of residual strength and residual stiffness are developed to characterize the performance degradation of a composite material. The strength and stiffness degradation data of Gr/PEEK [0/45/90/−45]2S laminates are used to verify the developed probabilistic models.
- (3)
- The effective bearing area of a composite material is treated as damage metric, and the growth mechanisms of effective stress and critical stiffness caused by fatigue damage accumulation are elaborated. A pair of strength-based and stiffness-based fatigue reliability models are proposed. The fatigue reliability and failure rate of Gr/PEEK [0/45/90/−45]2S laminates under different conditions are compared and discussed.
- (4)
- The strength degradation and stiffness degradation are dominated by the same damage state of composite materials. There is a certain correlation between these two degradation behaviors. In the future, the induced mechanisms and coupling effects between strength degradation behavior and stiffness degradation behavior will be further studied and discussed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saracyakupoglu, T. Usage of additive manufacturing and topology optimization process for weight reduction studies in the aviation industry. Adv. Sci. Technol. Eng. Syst. J. 2021, 6, 815–820. [Google Scholar] [CrossRef]
- Parveez, B.; Kittur, M.I.; Badruddin, I.A.; Kamangar, S.; Hussien, M.; Umarfarooq, M.A. Scientific advancements in composite materials for aircraft applications: A review. Polymers 2022, 14, 5007. [Google Scholar] [CrossRef]
- Towsyfyan, H.; Biguri, A.; Boardman, R.; Blumensath, T. Successes and challenges in non-destructive testing of aircraft composite structures. Chin. J. Aeronaut. 2020, 33, 771–791. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.P.; Keshtegar, B.; Qian, G.; Wang, Q.Y. Probabilistic framework for fatigue life assessment of notched components under size effects. Int. J. Mech. Sci. 2020, 181, 105685. [Google Scholar] [CrossRef]
- Li, H.; Soares, C.G. Assessment of failure rates and reliability of floating offshore wind turbines. Reliab. Eng. Syst. Saf. 2022, 228, 108777. [Google Scholar] [CrossRef]
- Li, X.Q.; Song, L.K.; Bai, G.C. Recent advances in reliability analysis of aeroengine rotor system: A review. Int. J. Struct. Integr. 2022, 13, 1–29. [Google Scholar] [CrossRef]
- Larsson, T.S.; Rönnbäck, A.; Vanhatalo, E. Integrating mixture experiments and six sigma methodology to improve fibre-reinforced polymer composites. Qual. Reliab. Eng. Int. 2022, 38, 2233–2254. [Google Scholar] [CrossRef]
- Zhu, S.P.; Liu, Q.; Peng, W.; Zhang, X.C. Computational-experimental approaches for fatigue reliability assessment of turbine bladed disks. Int. J. Mech. Sci. 2018, 142–143, 502–517. [Google Scholar] [CrossRef]
- Teng, D.; Feng, Y.W.; Chen, J.Y.; Lu, C. Structural dynamic reliability analysis: Review and prospects. Int. J. Struct. Integr. 2022, 13, 753–783. [Google Scholar] [CrossRef]
- Li, X.K.; Zhu, S.P.; Liao, D.; Correia, J.A.F.O.; Berto, F.; Wang, Q.Y. Probabilistic fatigue modelling of metallic materials under notch and size effect using the weakest link theory. Int. J. Fatigue 2022, 159, 106788. [Google Scholar] [CrossRef]
- Crane, R.; Dillingham, G.; Oakley, B. Progress in the reliability of bonded composite structures. Appl. Compos. Mater. 2017, 24, 221–233. [Google Scholar] [CrossRef]
- Solazzi, L.; Vaccari, M. Reliability design of a pressure vessel made of composite materials. Compos. Struct. 2022, 279, 114726. [Google Scholar] [CrossRef]
- Fei, C.W.; Li, H.; Lu, C.; Han, L.; Keshtegar, B.; Taylan, O. Vectorial surrogate modeling method for multi-objective reliability design. Appl. Math. Model. 2022, 109, 1–20. [Google Scholar] [CrossRef]
- Zaharia, S.M.; Pop, M.A.; Udroiu, R. Reliability and lifetime assessment of glider wing’s composite spar through accelerated fatigue life testing. Materials 2020, 13, 2310. [Google Scholar] [CrossRef]
- Zhang, C.Z.; Chen, H.P.; Tee, K.F.; Liang, D.F. Reliability-based lifetime fatigue damage assessment of offshore composite wind turbine blades. J. Aerosp. Eng. 2021, 34, 4021019.1–4021019.11. [Google Scholar] [CrossRef]
- Talreja, R. A mechanisms-based reliability model for fatigue of composite laminates. Z. Angew. Math. Mech.-J. Appl. Math. Mech. 2015, 95, 1058–1066. [Google Scholar] [CrossRef]
- Cheng, H.C.; Hwu, F.S. Fatigue reliability analysis of composites based on residual strength. Adv. Compos. Mater. 2008, 15, 385–402. [Google Scholar] [CrossRef]
- Chen, C.L.; Tsai, Y.T.; Wang, K.S. Characteristics of reliability-dependent hazard rate for composites under fatigue loading. J. Mech. Eng. 2009, 25, 195–203. [Google Scholar] [CrossRef]
- Gao, J.X.; Zhu, P.N.; Yuan, Y.P.; Wu, Z.F.; Xu, R.X. Strength and stiffness degradation modeling and fatigue life prediction of composite materials based on a unified fatigue damage model. Eng. Fail. Anal. 2022, 137, 106290. [Google Scholar] [CrossRef]
- Ma, H.D.; Ma, Q.; Bai, X.Z.; Xu, J.L.; An, Z.W. A material property degradation model of composite laminates considering stress level. Mech. Adv. Mater. Struct. 2023, 30, 272–283. [Google Scholar] [CrossRef]
- Feng, Y.; He, Y.T.; Gao, C. TT fatigue behaviors of composite T800/MTM46 cross-ply laminate and reliability analysis on fatigue life. Adv. Mech. Eng. 2017, 9, 1–14. [Google Scholar] [CrossRef]
- Häusler, S.; Fink, R.; Benz, C.; Sander, M. An investigation of the residual stiffness of a glass fibre reinforced composite in high cycle fatigue experiments. Procedia Struct. 2022, 38, 230–237. [Google Scholar] [CrossRef]
- Wang, X.J.; Ma, Y.J.; Wang, L.; Geng, X.Y.; Wu, D. Composite laminate oriented reliability analysis for fatigue life under non-probabilistic time-dependent method. Comput. Methods Appl. Mech. Eng. 2017, 326, 1–19. [Google Scholar] [CrossRef]
- Wu, Z.W.; Fang, G.D.; Fu, M.Q.; Chen, X.J.; Liang, J.; Lv, D.K. Random fatigue damage accumulation analysis of composite thin-wall structures based on residual stiffness method. Compos. Struct. 2019, 211, 546–556. [Google Scholar] [CrossRef]
- Van Paepegem, W.; Degrieck, J. A new coupled approach of residual stiffness and strength for fatigue of fibre-reinforced composites. Int. J. Fatigue 2002, 24, 747–762. [Google Scholar] [CrossRef]
- Gao, J.X.; Yuan, Y.P. Probabilistic modeling of stiffness degradation for fiber reinforced polymer under fatigue loading. Eng. Fail. Anal. 2020, 116, 104733. [Google Scholar] [CrossRef]
- Shiri, S.; Yazdani, M.; Pourgol-Mohammad, M. A fatigue damage accumulation model based on stiffness degradation of composite materials. Mater. Des. 2015, 88, 1290–1295. [Google Scholar] [CrossRef]
- Hu, Y.N.; Wu, S.C.; Xie, C.; Wu, W.W.; Zhang, J. Fatigue life evaluation of Ti–6Al–4V welded joints manufactured by electron beam melting. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 2210–2221. [Google Scholar] [CrossRef]
- Li, X.Q.; Song, L.K.; Bai, G.C. Physics-informed distributed modeling for CCF reliability evaluation of aeroengine rotor systems. Int. J. Fatigue 2023, 167, 107342. [Google Scholar] [CrossRef]
- Li, H.; Diaz, H.; Soares, C.G. A developed failure mode and effect analysis for floating offshore wind turbine support structures. Renew. Energ. 2021, 164, 133–145. [Google Scholar] [CrossRef]
- Shi, B.K.; Deng, Z.M.; Tan, L.S.; Zhao, Y.L.; Zhang, X.J. Micromechanics-based reliability analysis method for laminated composite structures. Mech. Adv. Mater. Struct. 2020, 28, 2096–2113. [Google Scholar] [CrossRef]
- Niu, X.P.; Zhu, S.P.; He, J.C.; Liao, D.; Correia, J.A.F.O.; Berto, F.; Wang, Q.Y. Defect tolerant fatigue assessment of AM materials: Size effect and probabilistic prospects. Int. J. Fatigue 2022, 160, 106884. [Google Scholar] [CrossRef]
- Liu, X.T.; Liu, J.Z.; Wang, H.J.; Yang, X.B. Prediction and evaluation of fatigue life considering material parameters distribution characteristic. Int. J. Struct. Integr. 2022, 13, 309–326. [Google Scholar] [CrossRef]
- Gao, P.; Xie, L.Y. Reliability evaluation based on different distributions of random load. Sci. World J. 2013, 2013, 415327. [Google Scholar] [CrossRef] [PubMed]
- Reifsnider, K.L.; Henneke, E.G.; Stinchcomb, W.W. Damage mechanics and NDE of composite laminates. In Mechanics of Composite Materials; Hashin, Z., Herakovich, C.T., Eds.; Elsevier Press Inc.: Oxford, UK, 1983; pp. 399–420. [Google Scholar]
- Yao, W.; Himmel, N. A new cumulative fatigue damage model for fibre-reinforced plastics. Compos. Sci. Technol. 2000, 60, 59–64. [Google Scholar] [CrossRef]
- Mu, P.G.; Wan, X.P.; Zhao, M.Y. A new pair of cumulative fatigue damage models for composite materials. Adv. Mater. Res. 2011, 160–162, 226–230. [Google Scholar] [CrossRef]
- Hwu, F.S. Study on Fatigue Reliability of Quasi-homogeneous Gr/PEEK Composite Laminate under Variable Load. Ph.D. Thesis, National Taiwan University, Taipei, Taiwan, 2000. (In Chinese). [Google Scholar]
- Mao, H.; Mahadevan, S. Fatigue damage modelling of composite materials. Compos. Struct. 2002, 58, 405–410. [Google Scholar] [CrossRef]
- Guo, J.Y.; Li, Y.F.; Peng, W.W.; Huang, H.Z. Bayesian information fusion method for reliability analysis with failure-time data and degradation data. Qual. Reliab. 2022, 38, 1944–1956. [Google Scholar] [CrossRef]
- Li, H.; Huang, C.G.; Soares, C.G. A real-time inspection and opportunistic maintenance strategies for floating offshore wind turbines. Ocean Eng. 2022, 256, 111433. [Google Scholar] [CrossRef]
- Li, H.; Soares, C.G.; Huang, H.Z. Reliability analysis of a floating offshore wind turbine using Bayesian Networks. Ocean Eng. 2020, 217, 107827. [Google Scholar] [CrossRef]
- Chou, P.C.; Croman, R. Residual strength in fatigue based on strength-life equal rank assumption. J. Compos. Mater. 1978, 12, 177–194. [Google Scholar] [CrossRef]
- He, J.C.; Zhu, S.P.; Luo, C.; Niu, X.; Wang, Q.Y. Size effect in fatigue modelling of defective materials: Application of the calibrated weakest-link theory. Int. J. Fatigue 2022, 165, 107213. [Google Scholar] [CrossRef]
- Lemaitre, J. Evaluation of dissipation and damage in metals, submitted to dynamic loading. In Proceedings of the Conference lnternationale sur Ie Comportement Mecanique des Materiaux, Kyoto, Japan, 15–20 August 1971. [Google Scholar]
- Shi, B.K.; Deng, Z.M. Multiscale reliability analysis of composite structures based on computer vision. Compos. Struct. 2022, 292, 115587. [Google Scholar] [CrossRef]
- Maurizio Gobbato, J.P.; Conte, J.B.; Kosmatka, C.R.F. A reliability-based framework for fatigue damage prognosis of composite aircraft structures. Probabilistic Eng. Mech. 2012, 29, 176–188. [Google Scholar] [CrossRef]
- Li, X.Q.; Song, L.K.; Choy, Y.S.; Bai, G.C. Multivariate ensembles-based hierarchical linkage strategy for system reliability evaluation of aeroengine cooling blades. Aerosp. Sci. Technol. 2023, 138, 108325. [Google Scholar] [CrossRef]
- Yang, L.; Shuang, L.Z. The preliminary analysis of reliability for a composite structure with damage. Eng. Fract. Mech. 1990, 37, 1157–1163. [Google Scholar] [CrossRef]
- Li, H.; Teixeira, A.P.; Soares, C.G. A two-stage failure mode and effect analysis of an offshore wind turbine. Renew. Energ. 2020, 162, 1438–1461. [Google Scholar] [CrossRef]
- Zhang, H.; Song, L.K.; Bai, G.C. Active extremum Kriging-based multi-level linkage reliability analysis and its application in aeroengine mechanism systems. Aerosp. Sci. Technol. 2022, 131, 107968. [Google Scholar] [CrossRef]
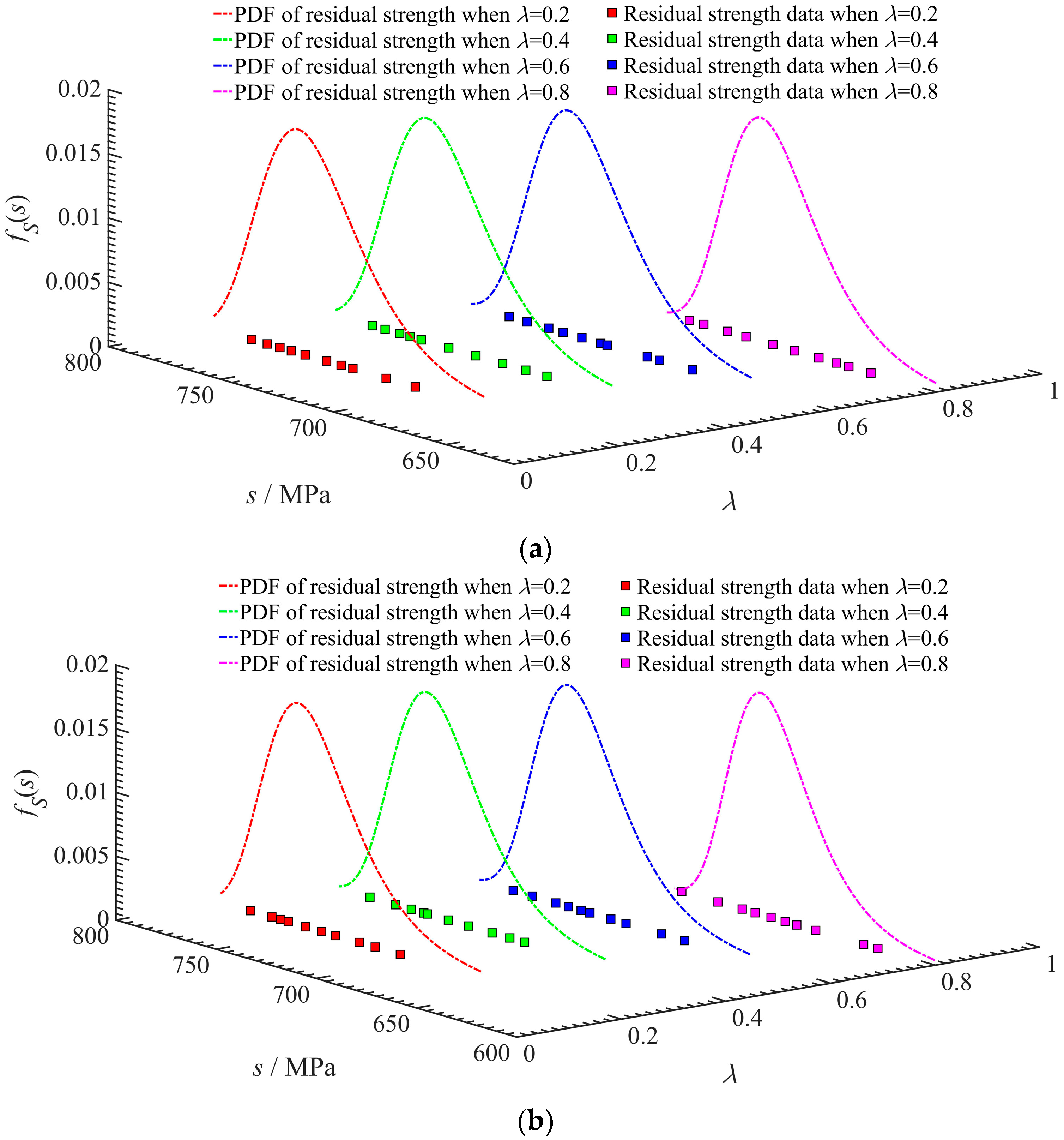
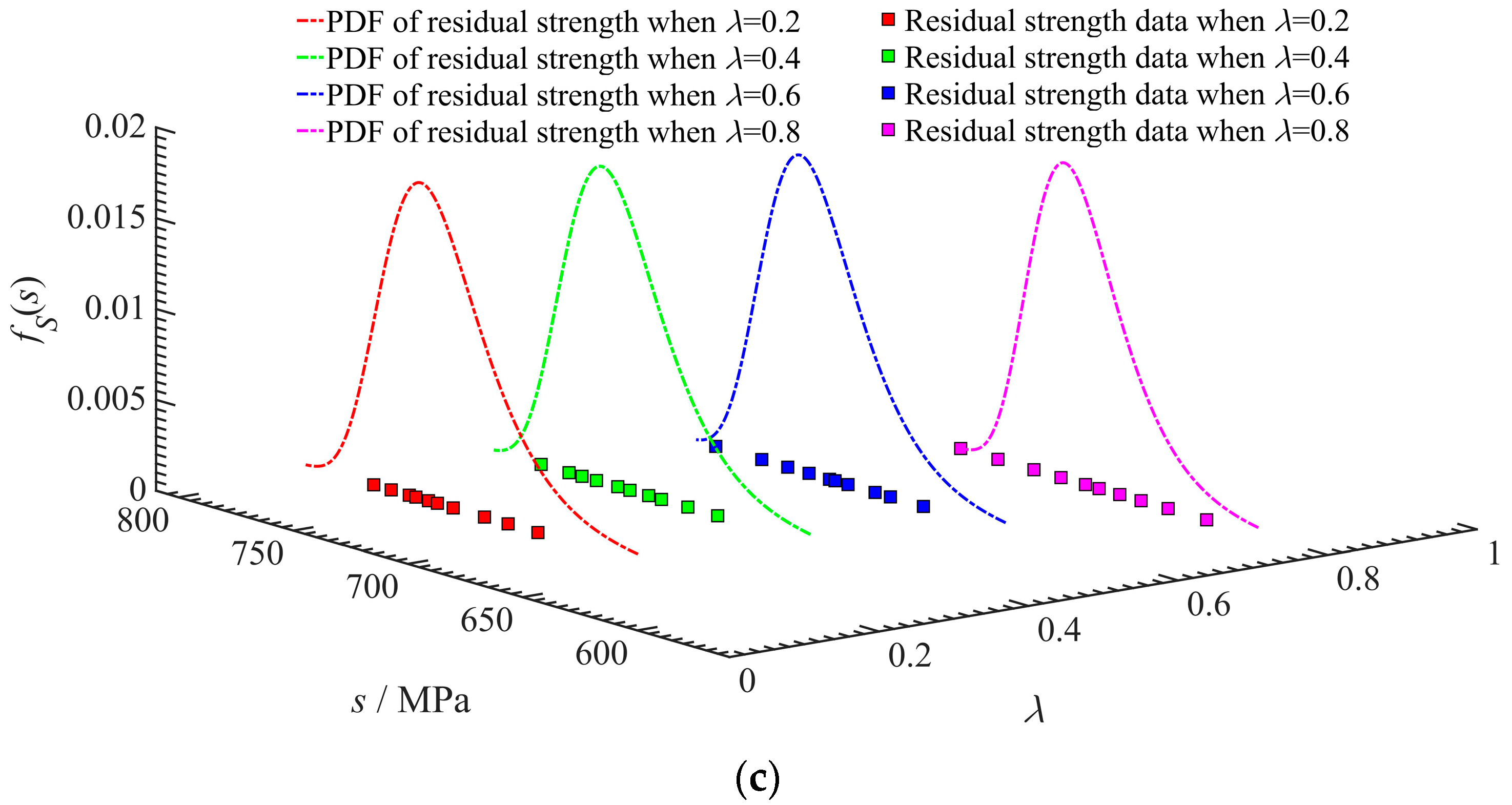
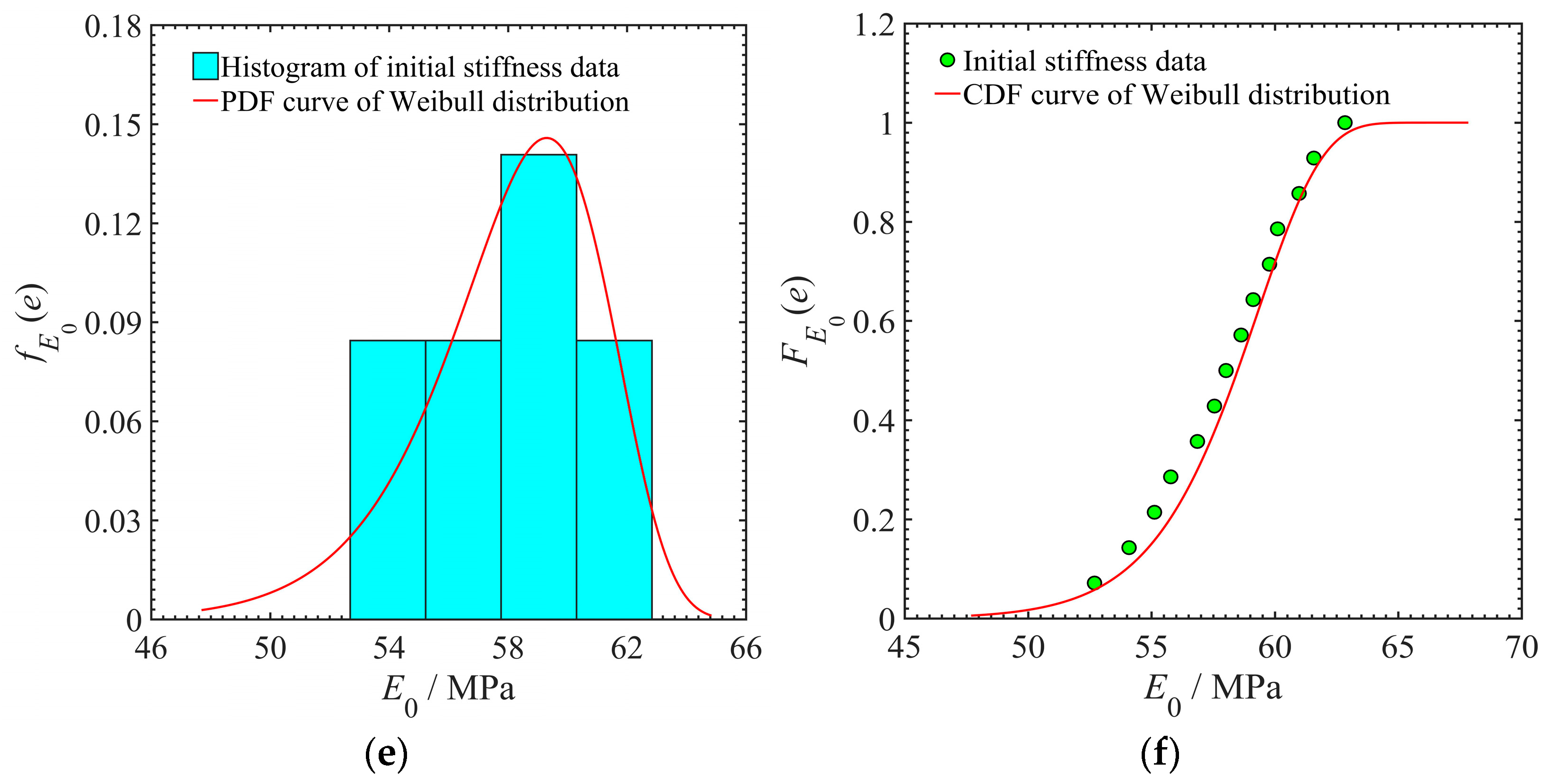
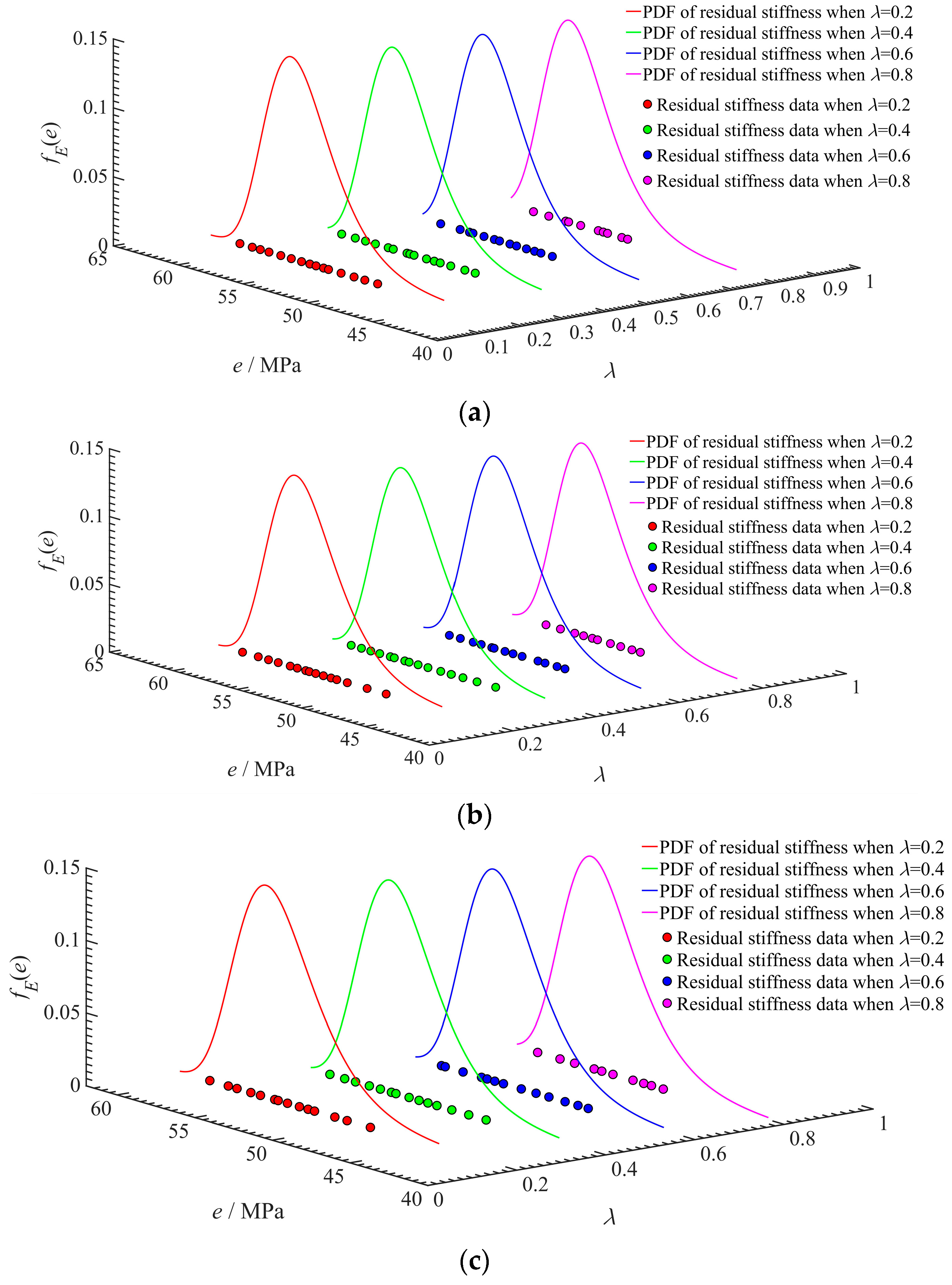


| Researchers | Models | Parameters |
|---|---|---|
| Gao [34] | ||
| Reifsnider [35] | , | |
| Yao [36] | , | |
| Mu [37] | , , |
| Stress Levels/MPa | Models | Parameters | Goodness of Fit | ||
|---|---|---|---|---|---|
| a | b | c | R2 | ||
| S2 = 646.31 | Gao’s model | 0.0577 | — | — | 0.9771 |
| Reifsnider’s model | 0.0755 | 1.433 | — | 0.997 | |
| Yao’s model | 1.603 | −9.358 | — | 0.9992 | |
| Mu’s model | 16.1 | 1.51 | 0.1027 | 0.9983 | |
| S3 = 623.50 | Gao’s model | 0.0683 | — | — | 0.9793 |
| Reifsnider’s model | 0.0883 | 1.411 | — | 0.9977 | |
| Yao’s model | 1.611 | -9.344 | — | 0.9991 | |
| Mu’s model | 15.48 | 1.518 | 0.1237 | 0.9988 | |
| S4 = 600.68 | Gao’s model | 0.0787 | — | — | 0.9784 |
| Reifsnider’s model | 0.1025 | 1.422 | — | 0.9975 | |
| Yao’s model | 1.584 | 0.06 | — | 0.9993 | |
| Mu’s model | 14.7 | 1.51 | 0.1417 | 0.9989 | |
| Researchers | Models | Parameters |
|---|---|---|
| Shiri [27] | , | |
| Gao [19] | , | |
| Mu [37] | , , | |
| Mao [39] | , , |
| Stress Levels/MPa | Models | Parameters | Goodness of Fit | ||
|---|---|---|---|---|---|
| α | β | γ | R2 | ||
| S2 = 646.31 | Shiri’s model | 2.906 | 1.348 | — | 0.7566 |
| Gao’s model | 2.896 | 1.556 | — | 0.9999 | |
| Mu’s model | 94.56 | 0.5177 | 0.087 | 0.887 | |
| Mao’s model | 0.0783 | 0.437 | 82.8 | 0.8954 | |
| S3 = 623.50 | Shiri’s model | 2.868 | 1.316 | — | 0.8398 |
| Gao’s model | 2.831 | 1.546 | — | 0.9987 | |
| Mu’s model | 75.46 | 0.5184 | 0.1161 | 0.9492 | |
| Mao’s model | 0.1044 | 0.4804 | 83.67 | 0.9461 | |
| S4 = 600.68 | Shiri’s model | 2.844 | 1.3 | — | 0.8606 |
| Gao’s model | 2.799 | 1.537 | — | 0.9944 | |
| Mu’s model | 75.09 | 0.5569 | 0.1541 | 0.9685 | |
| Mao’s model | 0.8658 | 80.78 | 0.5055 | 0.9651 | |
| Initial Strength Data/MPa | Mean Value/MPa | Standard Deviation/MPa |
|---|---|---|
| 723.13, 725.19, 743.20, 748.85, 754.77, 770.98, 774.84, 776.90, 788.99, 796.70 | 760.36 | 25.42 |
| Stress Level/MPa | Initial Stiffness Data/MPa | Mean value/MPa | Standard Deviation/MPa |
|---|---|---|---|
| S2 = 646.31 | 52.78, 54.29, 55.43, 56.42, 56.86, 57.63, 58.43, 58.95, 59.27, 59.84, 60.48, 61.11, 61.52, 62.16, 63.22 | 58.56 | 3.00 |
| S3 = 623.50 | 52.83, 54.15, 55.31, 56.18, 57.15, 57.47, 57.96, 58.29, 58.76, 59.53, 59.98, 60.62, 61.38, 62.21, 63.27 | 58.34 | 2.95 |
| S4 = 600.68 | 52.69, 54.09, 55.12, 55.78, 56.86, 57.55, 58.02, 58.63, 59.12, 59.78, 60.11, 60.98, 61.58, 62.84 | 58.08 | 2.94 |
| Stress Level/MPa | Shape Parameter C | Scale Parameter D |
|---|---|---|
| S2 = 646.31 | 23.8008 | 59.9005 |
| S3 = 623.50 | 22.9969 | 59.6813 |
| S4 = 600.68 | 23.5257 | 59.4076 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.-X.; Heng, F.; Yuan, Y.-P.; Liu, Y.-Y. Fatigue Reliability Analysis of Composite Material Considering the Growth of Effective Stress and Critical Stiffness. Aerospace 2023, 10, 785. https://doi.org/10.3390/aerospace10090785
Gao J-X, Heng F, Yuan Y-P, Liu Y-Y. Fatigue Reliability Analysis of Composite Material Considering the Growth of Effective Stress and Critical Stiffness. Aerospace. 2023; 10(9):785. https://doi.org/10.3390/aerospace10090785
Chicago/Turabian StyleGao, Jian-Xiong, Fei Heng, Yi-Ping Yuan, and Yuan-Yuan Liu. 2023. "Fatigue Reliability Analysis of Composite Material Considering the Growth of Effective Stress and Critical Stiffness" Aerospace 10, no. 9: 785. https://doi.org/10.3390/aerospace10090785
APA StyleGao, J.-X., Heng, F., Yuan, Y.-P., & Liu, Y.-Y. (2023). Fatigue Reliability Analysis of Composite Material Considering the Growth of Effective Stress and Critical Stiffness. Aerospace, 10(9), 785. https://doi.org/10.3390/aerospace10090785







