4.1. Experimental Setup
In HIL guidance, the pilot controls the inner loop of seeker, and its dynamic characteristics slightly change. In the parameter identification experiment of the pilot model, the pilot tracks and compensates for the error angle of the target in the field of view. In order to make the excitation signal have a wide frequency range and high signal-to-noise ratio, and show a certain randomness, the excitation signal was designed as the superposition of some sinusoidal signals [
47]:
In order to fully excite the pilot’s response, the spectrum of the excitation signal should be distributed halfway between high frequency and low frequency. Therefore, the frequency of the sinusoidal signal was designed to be evenly distributed in , according to the logarithmic scale. The amplitude distribution was similar to a first-order low-pass filter.
The variance of the excitation signal was defined as the integral of the square of the sinusoidal signal amplitude. The relationship is shown in Equation (19), and the derivation process is provided in
Appendix B.
In addition, Damveld [
40] mentioned that the phase has a small effect on the experimental results and was randomly selected. The excitation signal with a number of sinusoidal signals is shown in
Figure 8. It can be seen that the maximum field angle is less than 15 degrees.
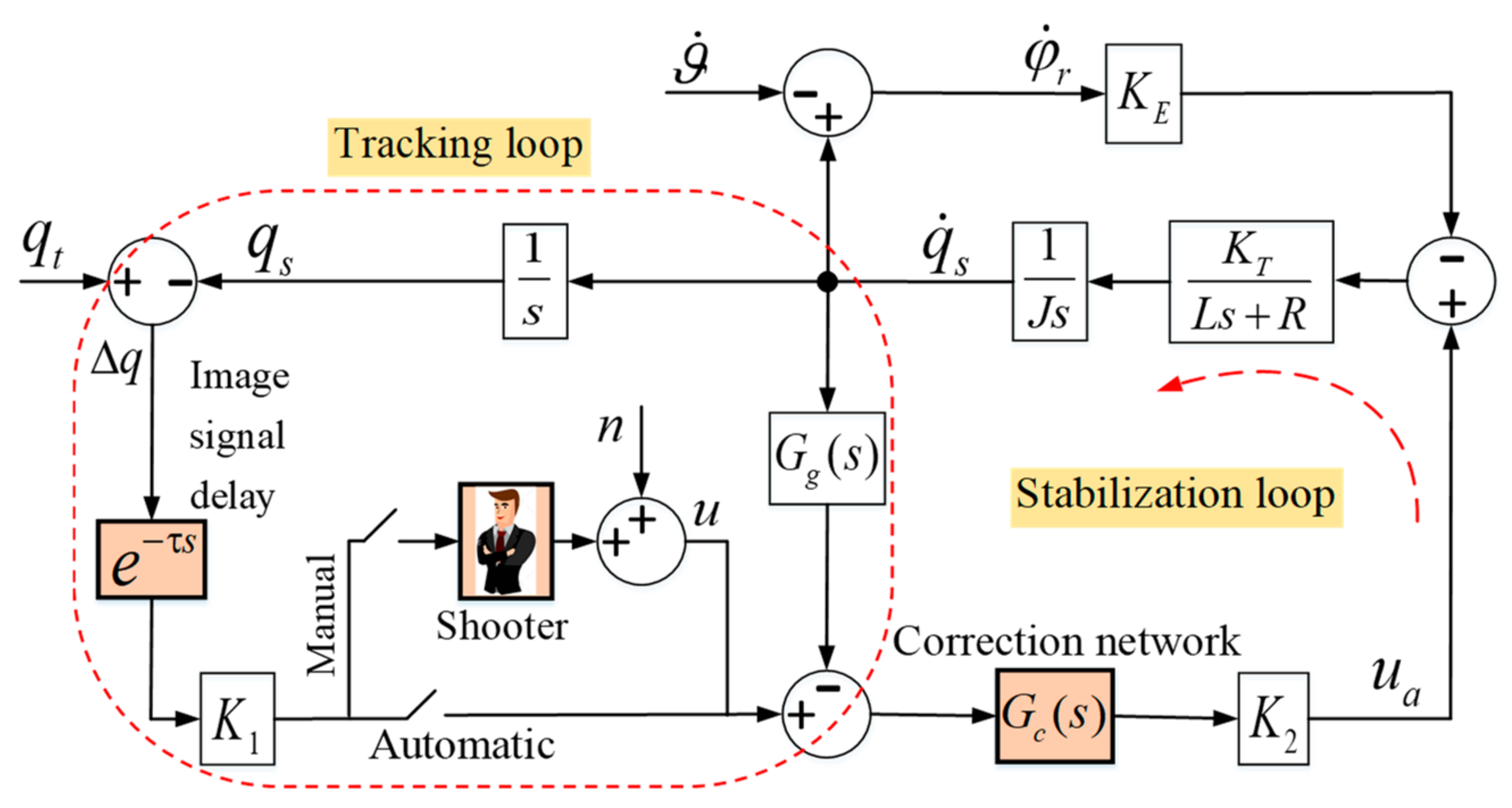
Figure 9 shows the hardware-in-the-loop simulation system and HIL experimental flow. The dynamic simulation module was developed on the basis of embedded system RTX, which collects the output of the handle and simulates the dynamic of the seeker system in real-time (cf.
Figure 1), with a calculation frequency of 1000 Hz. The display module was developed using vista2D+MFC to present the LOS error angle through the UDP communication protocol. According to the error signal, the participants manipulate the handle to point the optical axis of the seeker to the target in order to reduce tracking error. It can be seen from the test time axis of
Figure 9 that a preparation time of 10 s was set as the initial transient response time before the test in order to ensure that the participants could stably track the error signal. The test was divided into two stages:
Training stage: the participants were trained for five rounds. The duration of each test round was 90 s. A fade-in time of 6 s and a fade-out time of 4 s was introduced to make the participants adapt to the task and turn into a linear control behavior.
Test stage: it was performed under three conditions; no delay condition (phase I), small delay condition (phase II) and large delay condition (phase III). Phase II and phase III displayed the field error angle with an image signal delay of and , respectively. As in the training stage, the participants also conducted five rounds of tests.
Six participants were selected to perform the HIL experiment. Participant A as a “new-hand”, did not carry out the preliminary training stage, but only carried out the test stage of five rounds. As an “old-hand”, participants B~F had five rounds of early training, and then five rounds of testing. During the test phase, a short rest period was provided to prevent the participants from becoming fatigued. After each test round, the participants were informed of their tracking score, so as to motivate them to improve their tracking performance during the initial familiarity period and maintain a stable performance after reaching a certain proficiency level. Mcruer [
22] believes that participants need a transition process in order to adapt to changes in the dynamics of the controlled object. During the transition process, participants still maintain the original control mode, and then gradually adapt to the dynamic characteristics of the controlled object, and finally complete the compensation operation. In this experiment, the fade-in time provided sufficient time for the participants to make their control strategy adapt to the dynamics of the changed controlled object. That is, a delay link was added to the control loop.
4.2. Dynamic Parameter Selection
The signals of all the participants were recorded in the experiment. In order to reduce the signal noise influence and improve the accuracy of the pilot model parameter estimation, repeated experimental signals of all the participants were averaged. Taking “old-hand” participant B as an example,
Figure 10 shows the LOS error angle signal, output signal, excitation signal (LOS angle) and tracking signal (optical axis space angle) for 25 s before the test. It can be seen from
Figure 10c that participant B successfully aligned the optical axis with the target.
Figure 11 presents the amplitude spectrum of all the signals of
Figure 10, where the frequency of the excitation signal shown in
Figure 8a is indicated by a circle. It can be seen that, in the whole control loop, all the signals had a high signal-to-noise ratio at the excitation frequency, which met the requirements of the identification experiment.
The LOS error angle signal
and pilot output signal
in
Figure 10 were used to identify the pilot model parameter vector
in Equation (3). The HGOA (cf.
Figure 6) was used. The GA was iterated 100 times before the GN optimization algorithm was used. The upper and lower bounds of the GA parameter field were set as shown in
Table 3. The lower bound of the parameter field was set to 0, while the upper bound was set large enough to make the initial parameter field include all the possible solutions. In the process of GA optimization, the crossover probability and mutation probability of genes were set to 0.7 and 0.1, respectively. In order to simplify the calculation, the initial residual variance identification value
was set to 1. After the GA iteration, the result was used as the initial value for the GN optimization. If the iteration step of the parameter vector, objective function and residual variance identification value were smaller than the convergence index, the GN iterations were stopped.
GA is a search algorithm based on a probabilistic heuristic. The results of each iteration are not exactly the same under a certain iteration step constraint. The GA identification operation was repeated several times for the experimental results of each participant, and the eight solutions with the smallest iteration results were substituted into the GN algorithm for further optimization.
Figure 12 shows all the iterative processes of these eight solutions for “old-hand” participant B. It can be seen that the final values given by the GA are different after eight repetitions. After performing the optimization using the GN algorithm, the same results were obtained. In other words, the value of the global minimum logarithmic likelihood function was obtained, and the corresponding model parameters were the identification results. Because the initial identification values of the residual variance in the two optimization algorithms were both set to 1, the obtained objective function values were large. Finally, the identification value of each algorithm was obtained through the previously mentioned alternate iteration process.
One hundred initial parameter vectors were randomly selected from the parameter domain in
Table 3. The HGOA was used for optimization. The obtained results are presented in
Figure 13, in ascending order. It can be seen that the HGOA can highly reduce the initial value selection, and accurately converge to the global minimum.
The test data of all the participants were collected for 80 s in the middle of the five rounds of the test stage. The parameter estimation value was first obtained using the MLE method. The global optimal solution was then determined using the HGOA, so as to obtain the dynamic parameter vector
.
Figure 14 shows the difference in the mean value of the frequency response obtained by participant B, after five rounds of test stage. Under the same excitation signal and control object conditions, participant B had a very similar frequency response in the training stage and phase I stage. This shows that participant B had a good training effect and reached the control level of the “old-hand”. In addition, the frequency response of participant B had clear adaptive changes to the time delay. Its amplitude at low frequency decreased to ensure the stability margin of the seeker loop, and it provided the lead phase to compensate for the impact of the time delay. The identification results of all the participants are shown in
Table 4. Due to the individual differences of the participants and different control strategies, the experimental results were slightly different.
Figure 15 shows the Bode diagram of the identification model for all the participants. It can be seen that the amplitude frequency characteristics of participant A are significantly lower than those of other participants, which resulted in a lower tracking performance. In order to more truly and generally reflect the dynamic characteristics of the pilots, the identification results of participants B~F were selected for further analysis.
The correlation coefficient
is generally used to evaluate the accuracy of an identification model. It can be used to represent the ability of the identification model output to reproduce the measured output. If
is close to 1, the output of the identification model can well fit the measurement output, and the identification model can truly reflect the dynamic characteristics of the actual object. On the other hand, if
is close to 0, the identification result is poor and the dynamic characteristics of the actual object are not captured.
is expressed as follows [
48]:
Figure 16 shows a comparison between the measured output of participant B and the PEC model output. It can be seen that the output of the PEC model can better fit the measured output.
Table 5 shows the
values of all the participants. It can be seen that the
values of the PEC model for participants B~F are greater than 70%. Therefore, the PEC identification model can better fit and reflect the dynamic characteristics of the pilots.
It can be seen from
Figure 14 that trained pilots will adjust their control behavior in order to adapt to the dynamic changes of the controlled object caused by time delay. Simultaneously, it can be observed from
Table 4 that differences in the identification results of trained pilots exist. The difference of pilot dynamics in [
33] is mainly reflected in the visual perception lead time constant
and visual perception response delay
. Moreover, the
of trained pilots is usually stable at almost 0.15 s. Thus, based on the identification results of participants B~F (cf.
Table 4), the average value of
was considered and the value range of
was given, so as to represent the different control strategies and tracking compensation behaviors used by different pilots when facing the dynamic changes of the controlled object caused by delay. The values of the dynamic parameter vector
are presented in
Table 6.
It can be seen from the Bode diagram shown in
Figure 14 and
Figure 15 that the dynamic response of the new-hand and old-hand are quite different. The dynamic response of the new-hand trained by the simulator can be expressed by the PEC model shown in Equation (3). When the dynamic parameters of the new-hand meet
Table 6, they can be judged to have a good operation performance and meet the conditions for becoming a professional pilot, so as to improve the efficiency of the pilot training and screening.
Figure 17 shows the open-loop frequency response (Bode diagram) of the seeker tracking loop, including the image signal delay, pilot link and stabilization loop.
Figure 17 validates the crossing theorem proposed by McRuer. That is, in the amplitude frequency characteristic curve, the slope at the amplitude crossover frequency is almost
, while the slope at the high-frequency input area is less than
, because the participants have an adaptive advance adjustment behavior when dealing with image signal delay.