Measurement of the Convection Velocities in a Hypersonic Turbulent Boundary Layer Using Two-Point Cylindrical-Focused Laser Differential Interferometer
Abstract
1. Introduction
2. Experimental Description
2.1. Facility and Test Condition
2.2. The Flat Plate Model
2.3. Measurement Methods
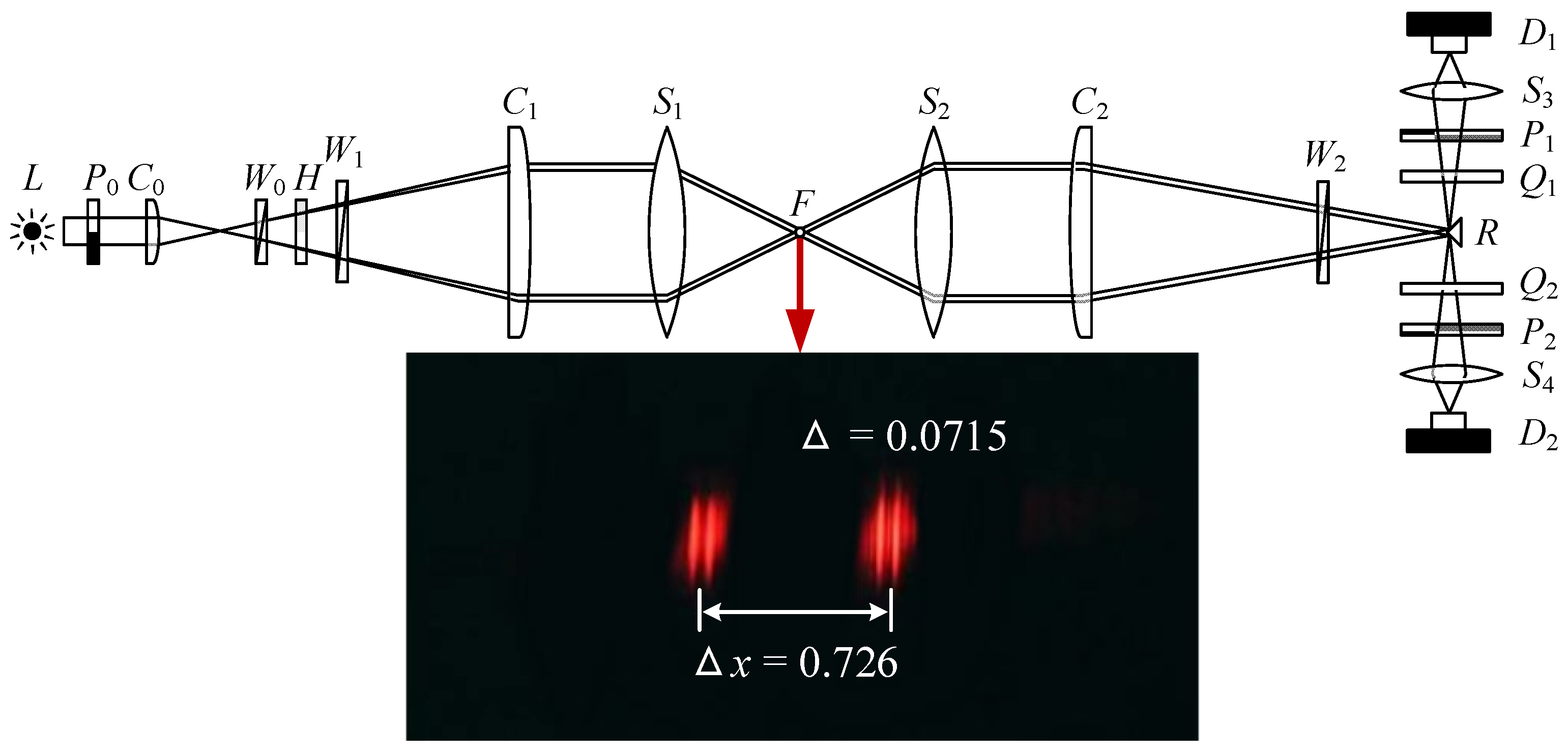
2.3.1. 2P-CFLDI System
2.3.2. Schlieren System
2.3.3. Piezoelectric Pressure Sensors
3. 2P-CFLDI Dataset Validation
3.1. Density Gradient Fluctuations Intensity
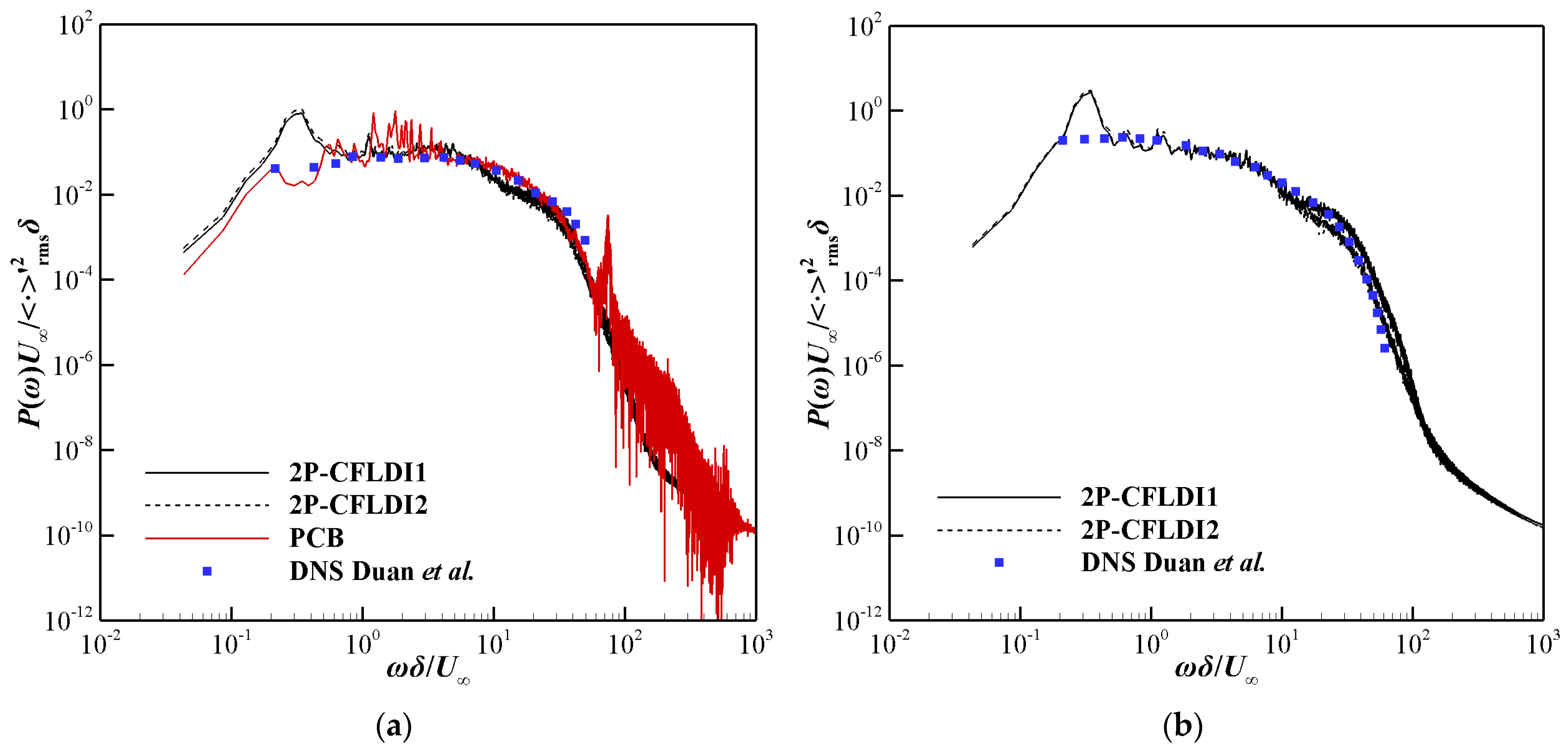
3.2. Power Spectral Density (PSD)
4. Results
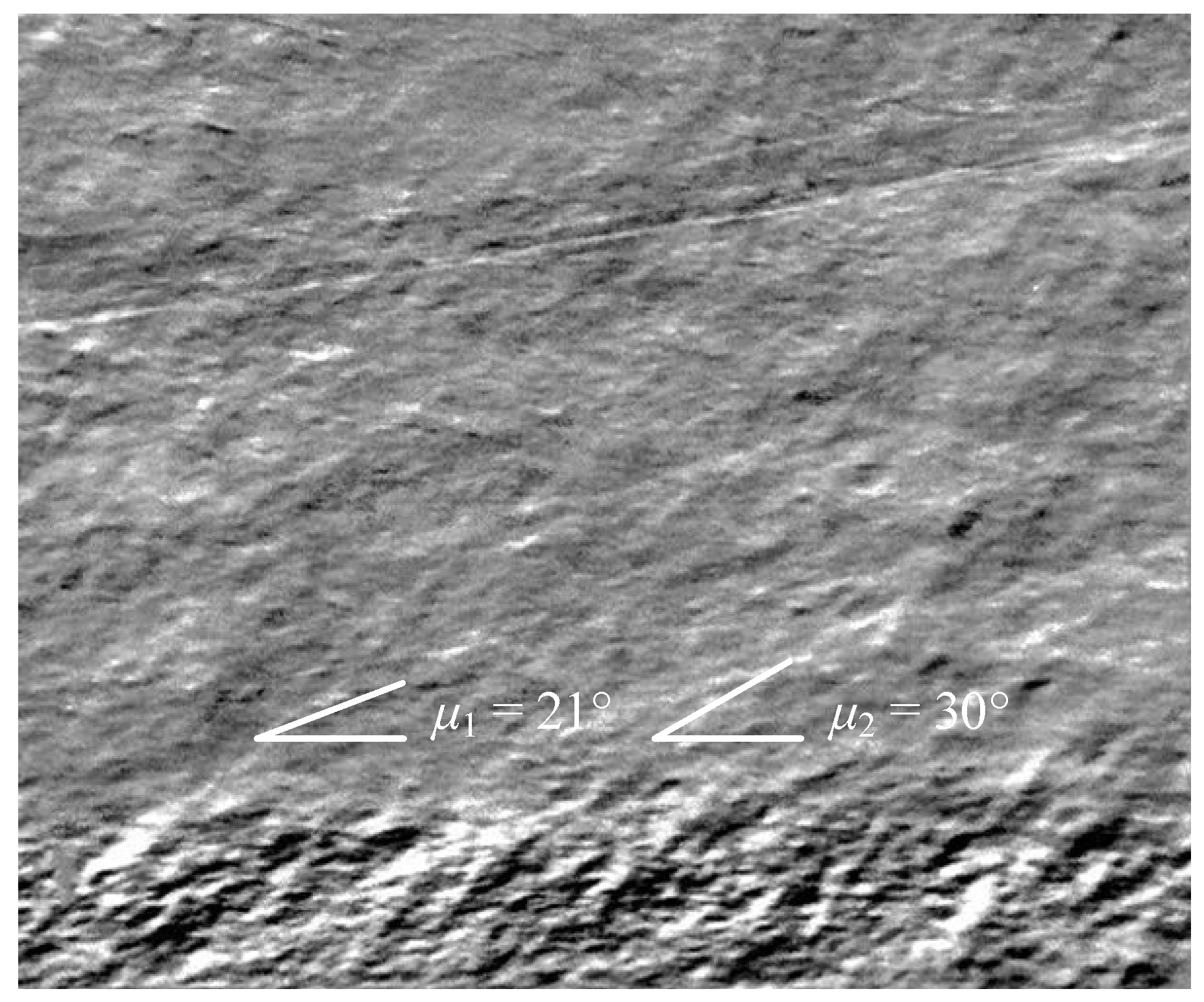
4.1. Schlieren
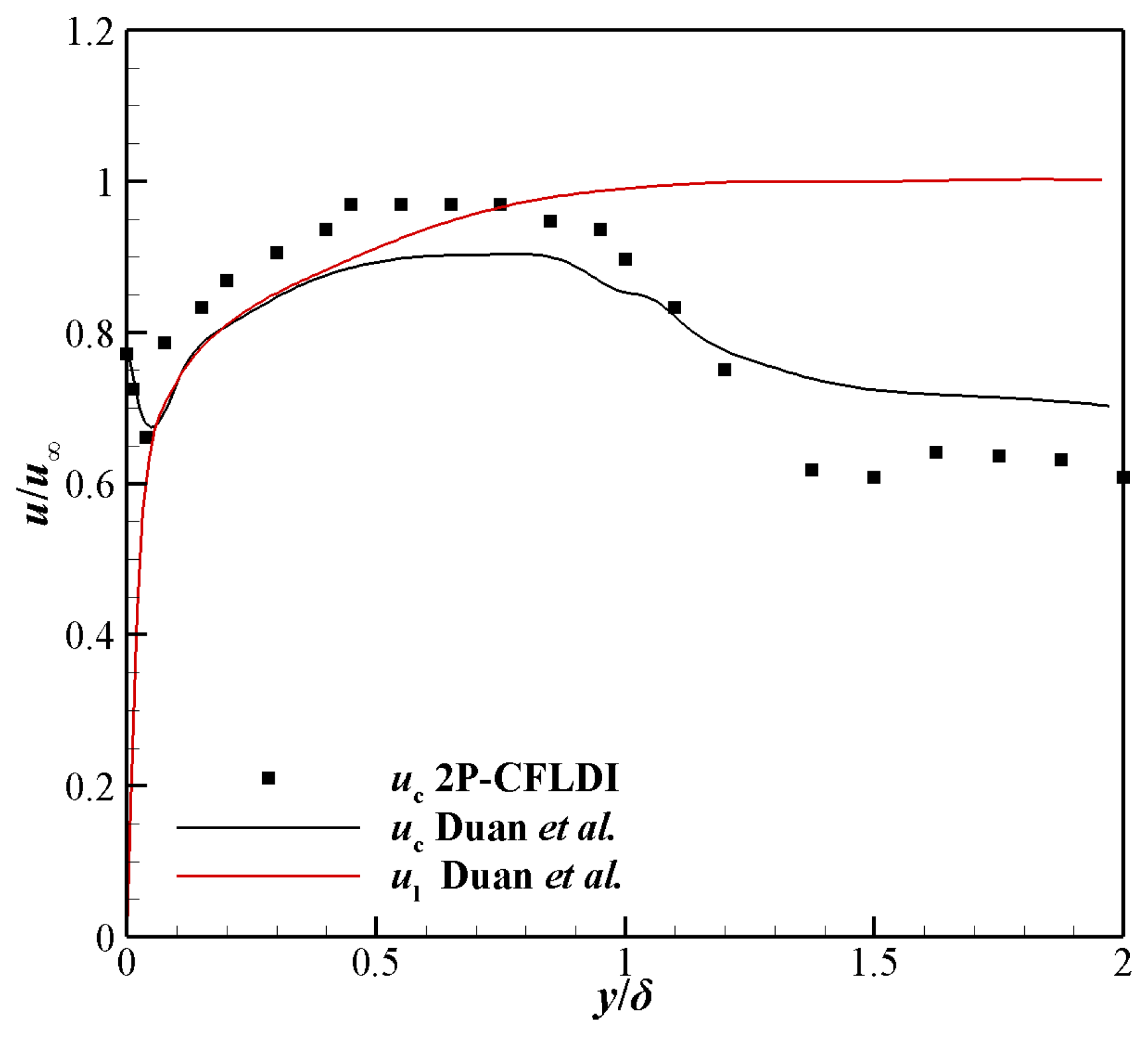
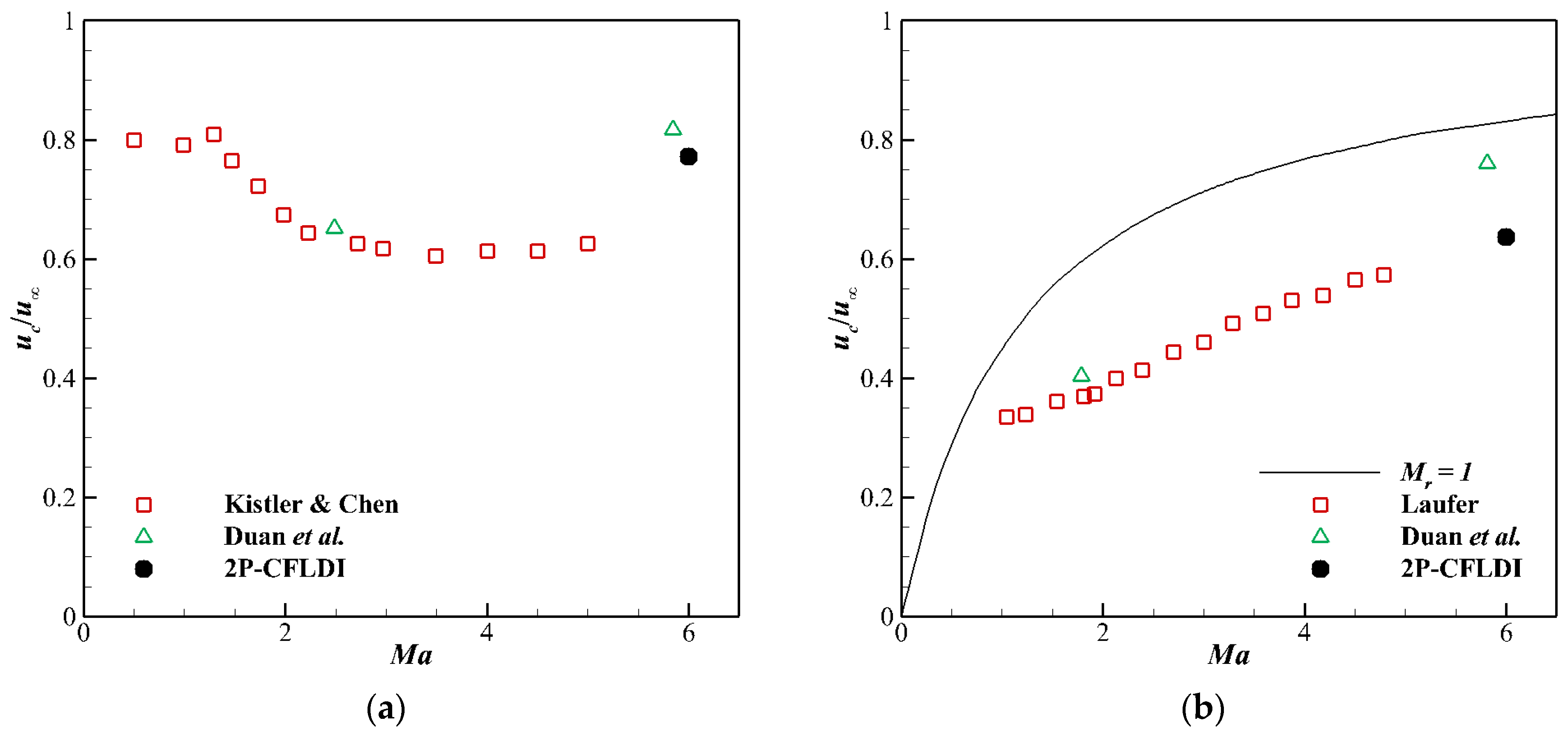
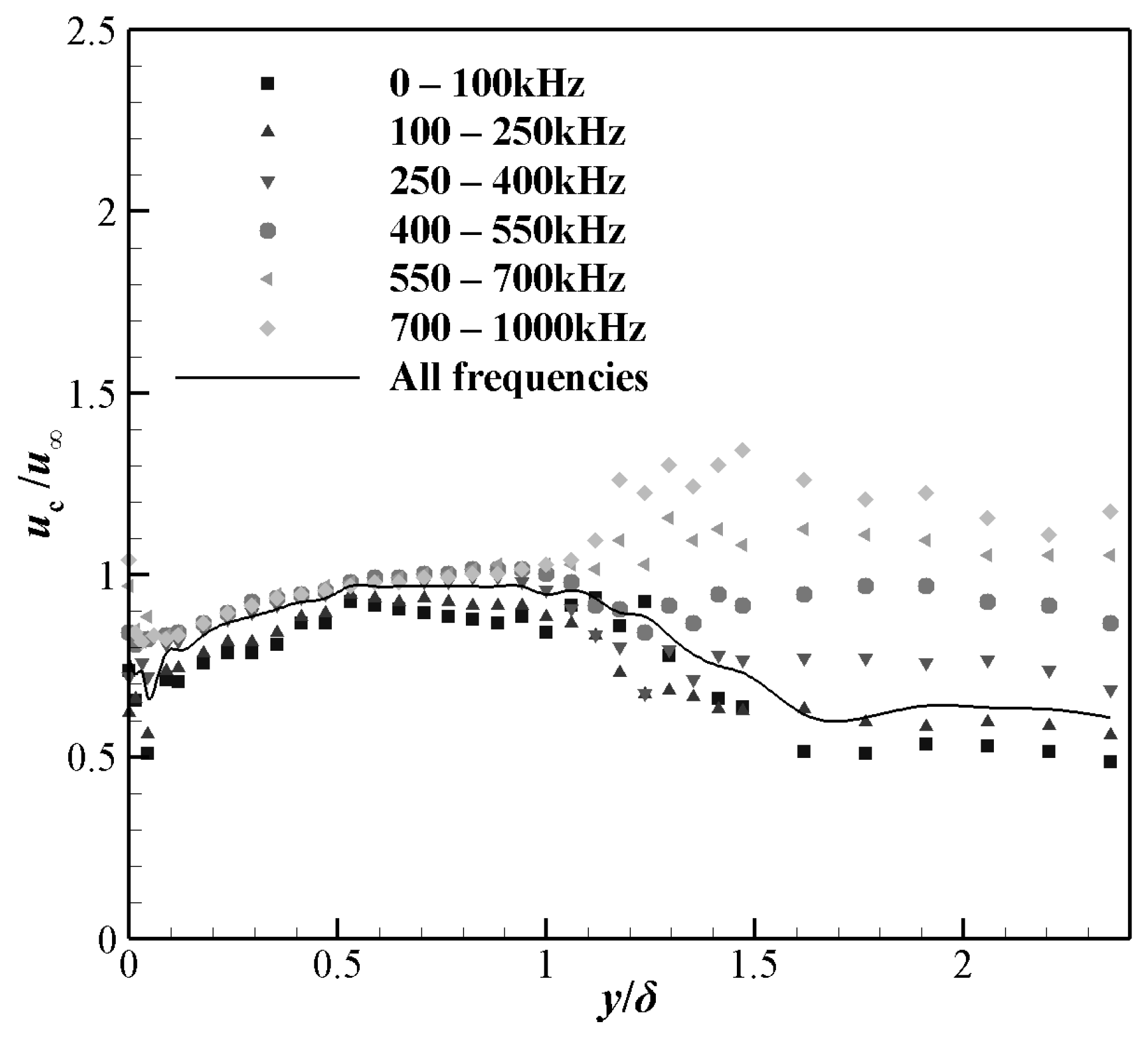
4.2. 2P-CFLDI
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bertin, J.J. Hypersonic Aerothermodynamics; AIAA Education Series; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1994; ISBN 978-1-56347-036-3. [Google Scholar]
- Beckwith, I.E. Development of a High Reynolds Number Quiet Tunnel for Transition Research. AIAA J. 1975, 13, 300–306. [Google Scholar] [CrossRef]
- Laufer, J. Some Statistical Properties of the Pressure Field Radiated by a Turbulent Boundary Layer. Phys. Fluids 1964, 7, 1191. [Google Scholar] [CrossRef]
- Schneider, S.P. Development of Hypersonic Quiet Tunnels. J. Spacecr. Rocket. 2008, 45, 641–664. [Google Scholar] [CrossRef]
- Phillips, O.M. On the Generation of Sound by Supersonic Turbulent Shear Layers. J. Fluid. Mech. 1960, 9, 1–28. [Google Scholar] [CrossRef]
- Ffowcs Williams, J.E. The Noise from Turbulence Convected at High Speed. Philos. Trans. R. Soc. London Ser. A Math. Phys. Sci. 1963, 255, 469–503. [Google Scholar] [CrossRef]
- Laufer, J. Aerodynamic Noise in Supersonic Wind Tunnels. J. Aerosp. Sci. 1961, 28, 685–692. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Wyngaard, J.C.; Izumi, Y.; Coté, O.R. Spectral Characteristics of Surface-layer Turbulence. Q. J. R. Meteorol. Soc. 1972, 98, 563–589. [Google Scholar] [CrossRef]
- Willmarth, W.W.; Wooldridge, C.E. Measurements of the Fluctuating Pressure at the Wall beneath a Thick Turbulent Boundary Layer. J. Fluid. Mech. 1962, 14, 187–210. [Google Scholar] [CrossRef]
- Schewe, G. On the Structure and Resolution of Wall-Pressure Fluctuations Associated with Turbulent Boundary-Layer Flow. J. Fluid. Mech. 1983, 134, 311–328. [Google Scholar] [CrossRef]
- Bull, M.K. Wall-Pressure Fluctuations beneath Turbulent Boundary Layers: Some Reflections on Forty Years of Research. J. Sound. Vib. 1996, 190, 299–315. [Google Scholar] [CrossRef]
- Klinner, J.; Hergt, A.; Willert, C. Experimental Investigation of the Transonic Flow around the Leading Edge of an Eroded Fan Airfoil. Exp. Fluids 2014, 55, 1800. [Google Scholar] [CrossRef]
- Owen, F.K.; Horstman, C.C. On the Structure of Hypersonic Turbulent Boundary Layers. J. Fluid. Mech. 1972, 53, 611–636. [Google Scholar] [CrossRef]
- Spina, E.F.; Donovan, J.F.; Smits, A.J. Convection Velocity in Supersonic Turbulent Boundary Layers. Phys. Fluids A Fluid. Dyn. 1991, 3, 3124–3126. [Google Scholar] [CrossRef]
- Krogstad, P.A.; Kaspersen, J.H.; Rimestad, S. Convection Velocities in a Turbulent Boundary Layer. Phys. Fluids 1998, 10, 949–957. [Google Scholar] [CrossRef]
- Russo, G.P. Hot Wire Anemometer. In Aerodynamic Measurements; Elsevier: Amsterdam, The Netherlands, 2011; pp. 67–98. ISBN 978-1-84569-992-5. [Google Scholar]
- Finke, C.P. Temperature-Compensated Calibration and Measurements with Cross-Style Hotwire Anemometers. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2021. [Google Scholar]
- Siddiqui, F.; Gragston, M.; Bowersox, R.D.W. Measurement of Wall-Cooling Effects on Hypersonic Boundary-Layer Transition Using Focused Laser Differential Interferometry. AIAA J. 2022, 60, 6214–6224. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Chen, L.; Yao, X. Tunable Spatial Resolution Focused Laser Differential Interferometer for Density Fluctuation Measurement. Appl. Sci. 2023, 13, 3253. [Google Scholar] [CrossRef]
- Camillo, G.P.; Wagner, A.; Toki, T.; Scalo, C. Combined Experimental and Numerical Investigation of a Hypersonic Turbulent Boundary Layer by Means of FLDI and Large-Eddy Simulations. Aerospace 2023, 10, 570. [Google Scholar] [CrossRef]
- Houpt, A.; Leonov, S. Cylindrical Focused Laser Differential Interferometer. AIAA J. 2021, 59, 1142–1150. [Google Scholar] [CrossRef]
- Hopkins, K.J.; Porat, H.; McIntyre, T.J.; Wheatley, V.; Veeraragavan, A. Measurements and Analysis of Hypersonic Tripped Boundary Layer Turbulence. Exp. Fluids 2021, 62, 164. [Google Scholar] [CrossRef]
- Jewell, J.S.; Parziale, N.J.; Lam, K.-L.; Hagen, B.J.; Kimmel, R.L. Disturbance and Phase Speed Measurements for Shock Tubes and Hypersonic Boundary-Layer Instability. In Proceedings of the 32nd AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Washington, DC, USA, 13–17 June 2016; AIAA AVIATION Forum. American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2016. [Google Scholar]
- Gillespie, G.I.; Ceruzzi, A.P.; Laurence, S.J. A Multi-Point Focused Laser Differential Interferometer for Characterizing Freestream Disturbances in Hypersonic Wind Tunnels. Exp. Fluids 2022, 63, 180. [Google Scholar] [CrossRef]
- Hildebrand, N.; Choudhari, M.M.; Deegan, C.P.; Huang, J.; Duan, L. Direct Numerical Simulation of Acoustic Disturbances in a Hypersonic Two-Dimensional Nozzle Configuration. AIAA J. 2022, 60, 3452–3463. [Google Scholar] [CrossRef]
- Auvity, B.; Etz, M.R.; Smits, A.J. Effects of Transverse Helium Injection on Hypersonic Boundary Layers. Phys. Fluids 2001, 13, 3025–3032. [Google Scholar] [CrossRef]
- Williams, O.J.H.; Smits, A.J. Effect of Tripping on Hypersonic Turbulent Boundary-Layer Statistics. AIAA J. 2017, 55, 3051–3058. [Google Scholar] [CrossRef]
- Weisberger, J.M.; Bathel, B.F.; Herring, G.C.; Buck, G.M.; Jones, S.B.; Cavone, A.A. Multi-Point Line Focused Laser Differential Interferometer for High-Speed Flow Fluctuation Measurements. Appl. Opt. 2020, 59, 11180. [Google Scholar] [CrossRef]
- Ceruzzi, A.; Callis, B.; Weber, D.; Cadou, C.P. Application of Focused Laser Differential Interferometry (FLDI) in a Supersonic Boundary Layer. In AIAA Scitech 2020 Forum; AIAA SciTech Forum; American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2020. [Google Scholar]
- Ceruzzi, A.; McManamen, B.; Cadou, C.P. Demonstration of Two-Point Focused Laser Differential Interferometry (2pFLDI) in a Mach 18 Flow. In AIAA Scitech 2021 Forum; AIAA SciTech Forum; American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2021; 2p. [Google Scholar]
- Huang, R.; Liu, W.; Cheng, J.; Wu, J. Measurement of Hypersonic Turbulent Boundary Layer on a Flat Plate Using Cylindrical Focused Laser Differential Interferometer. Phys. Fluids 2023, 35, 035121. [Google Scholar] [CrossRef]
- Parziale, N. Slender-Body Hypervelocity Boundary-Layer Instability. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2013. [Google Scholar]
- Benitez, E.K.; Borg, M.P.; Luke Hill, J.; Aultman, M.T.; Duan, L.; Running, C.L.; Jewell, J.S. Quantitative Focused Laser Differential InterferomXetry with Hypersonic Turbulent Boundary Layers. Appl. Opt. 2022, 61, 9203–9216. [Google Scholar] [CrossRef]
- Benitez, E.K.; Borg, M.P.; Rhodes, C.; Jewell, J.S. Optical-Axis Spatial Sensitivity of a Simulated Focused Laser Differential Interferometer. AIAA J. 2023, 61, 1925–1938. [Google Scholar] [CrossRef]
- Parziale, N.J.; Shepherd, J.E.; Hornung, H.G. Free-Stream Density Perturbations in a Reflected-Shock Tunnel. Exp. Fluids 2014, 55, 1665. [Google Scholar] [CrossRef]
- Welch, P. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging over Short, Modified Periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Duan, L.; Choudhari, M.M.; Zhang, C. Pressure Fluctuations Induced by a Hypersonic Turbulent Boundary Layer. J. Fluid Mech. 2016, 804, 578–607. [Google Scholar] [CrossRef] [PubMed]
- Liepmann, H.W.; Roshko, A. Elements of Gasdynamics; Courier Dover Publications: Westford, MA, USA, 1957; ISBN 0-486-41963-0. [Google Scholar]
- Sasoh, A. Compressible Fluid Dynamics and Shock Waves; Springer: Singapore, 2020; ISBN 9789811505034. [Google Scholar]
- Laufer, J. Sound Radiation from a Turbulent Boundary Layer; Jet Propulsion Lab: Pasadena, CA, USA, 1964; JPL-TR-32-119. [Google Scholar]
- Kim, J.; Hussain, F. Propagation Velocity of Perturbations in Turbulent Channel Flow. Phys. Fluids A Fluid Dyn. 1993, 5, 695–706. [Google Scholar] [CrossRef]
- Kistler, A.L.; Chen, W.S. The Fluctuating Pressure Field in a Supersonic Turbulent Boundary Layer. J. Fluid Mech. 1963, 16, 41–64. [Google Scholar] [CrossRef]






| Ma | Reunit [m−1] | p0 [MPa] | T0 [K] | Tw [K] |
|---|---|---|---|---|
| 6 | 1.08 × 107 | 1 | 430 | 300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, R.; Xue, T.; Wu, J. Measurement of the Convection Velocities in a Hypersonic Turbulent Boundary Layer Using Two-Point Cylindrical-Focused Laser Differential Interferometer. Aerospace 2024, 11, 100. https://doi.org/10.3390/aerospace11010100
Huang R, Xue T, Wu J. Measurement of the Convection Velocities in a Hypersonic Turbulent Boundary Layer Using Two-Point Cylindrical-Focused Laser Differential Interferometer. Aerospace. 2024; 11(1):100. https://doi.org/10.3390/aerospace11010100
Chicago/Turabian StyleHuang, Ranran, Tao Xue, and Jie Wu. 2024. "Measurement of the Convection Velocities in a Hypersonic Turbulent Boundary Layer Using Two-Point Cylindrical-Focused Laser Differential Interferometer" Aerospace 11, no. 1: 100. https://doi.org/10.3390/aerospace11010100
APA StyleHuang, R., Xue, T., & Wu, J. (2024). Measurement of the Convection Velocities in a Hypersonic Turbulent Boundary Layer Using Two-Point Cylindrical-Focused Laser Differential Interferometer. Aerospace, 11(1), 100. https://doi.org/10.3390/aerospace11010100






