Research of Unsteady Aerodynamic Characteristics of Electrically Controlled Rotor Airfoils with Trailing-Edge Flaps
Abstract
:1. Introduction
2. ECR with TEF
2.1. Airfoil Geometry
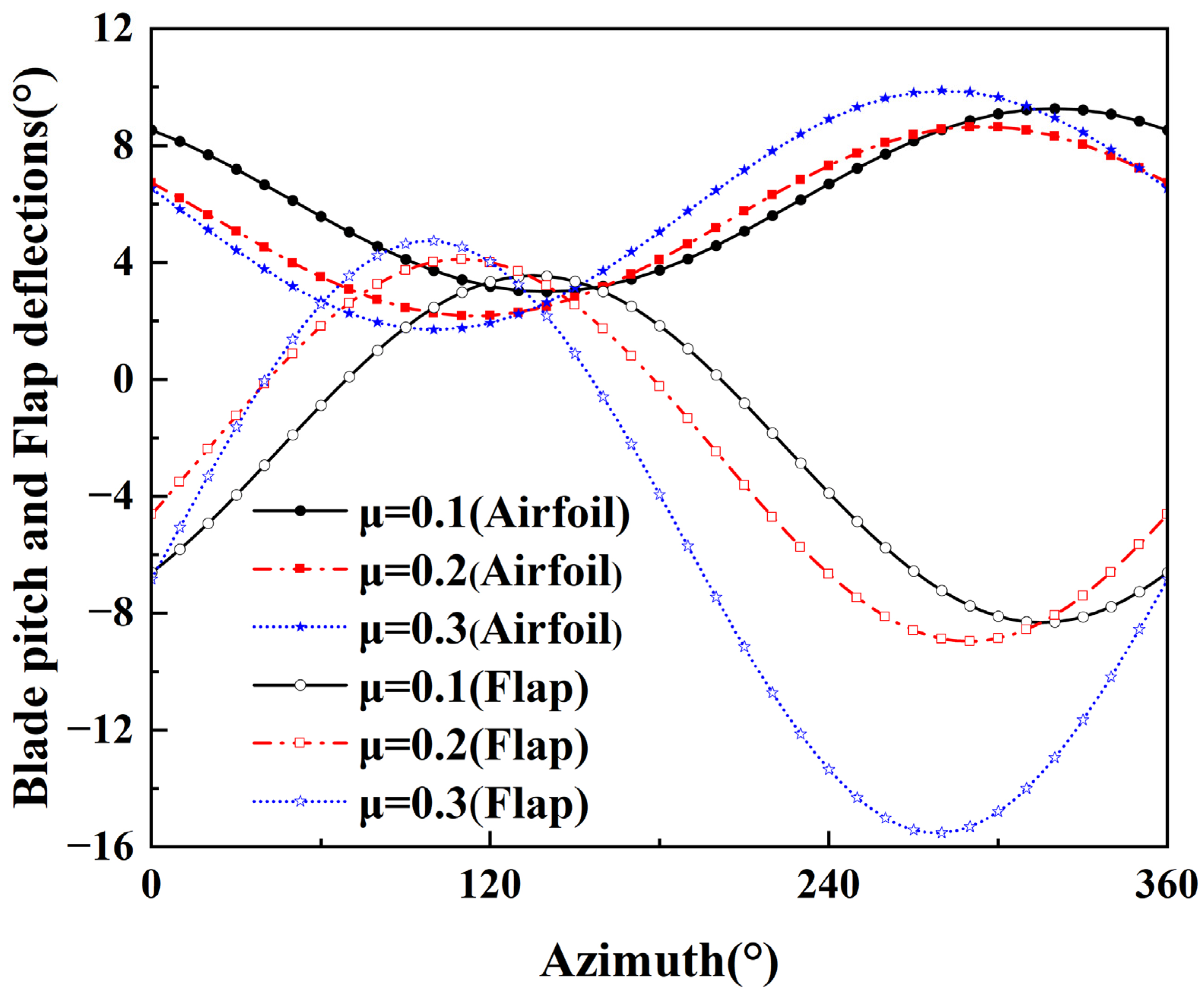
2.2. Control Laws for ECR
3. The CFD Solver and Grid Geometries
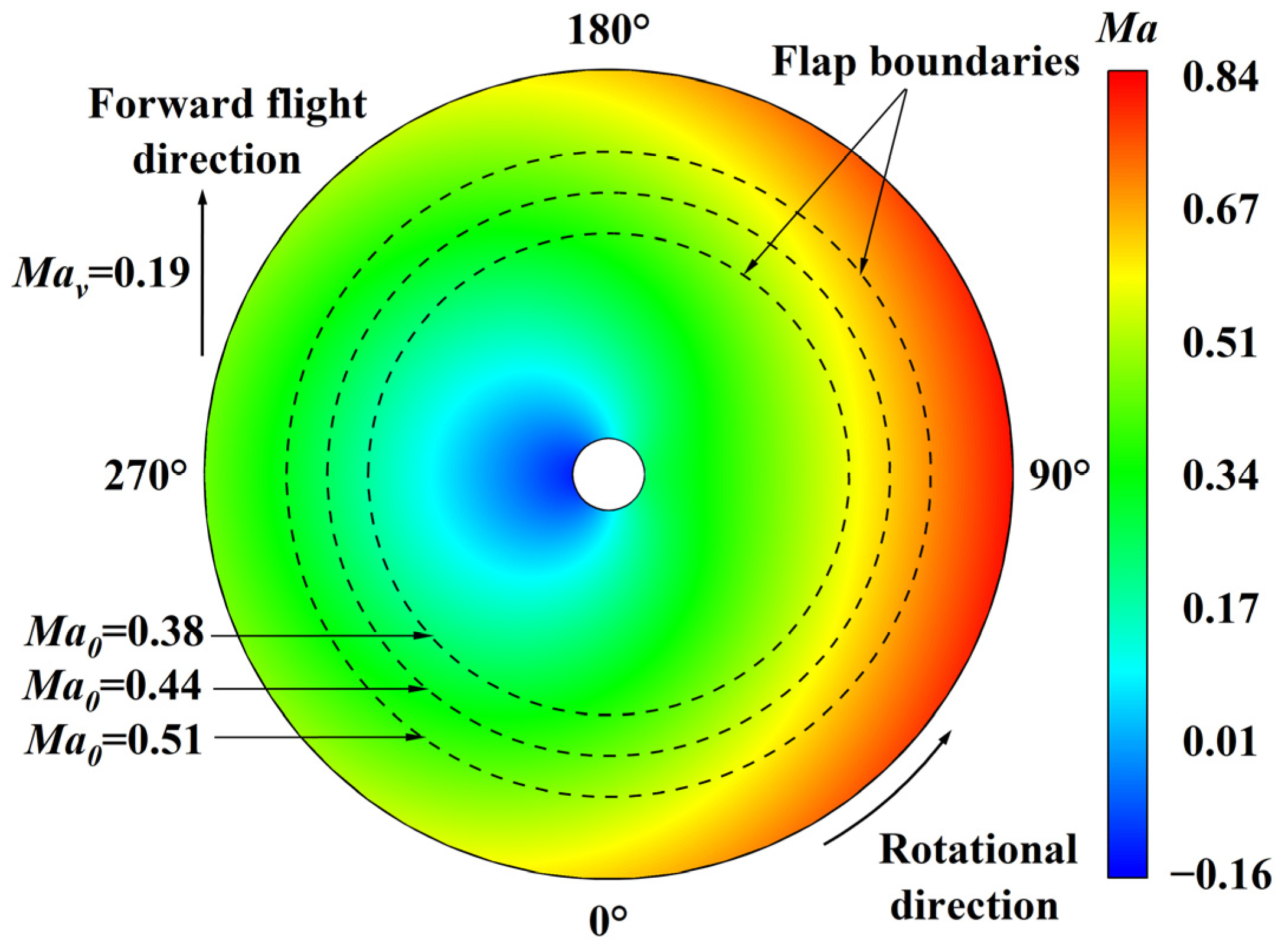
4. Analysis of the Aerodynamic Environment of a Helicopter Rotor
5. Simulation Result and Analysis
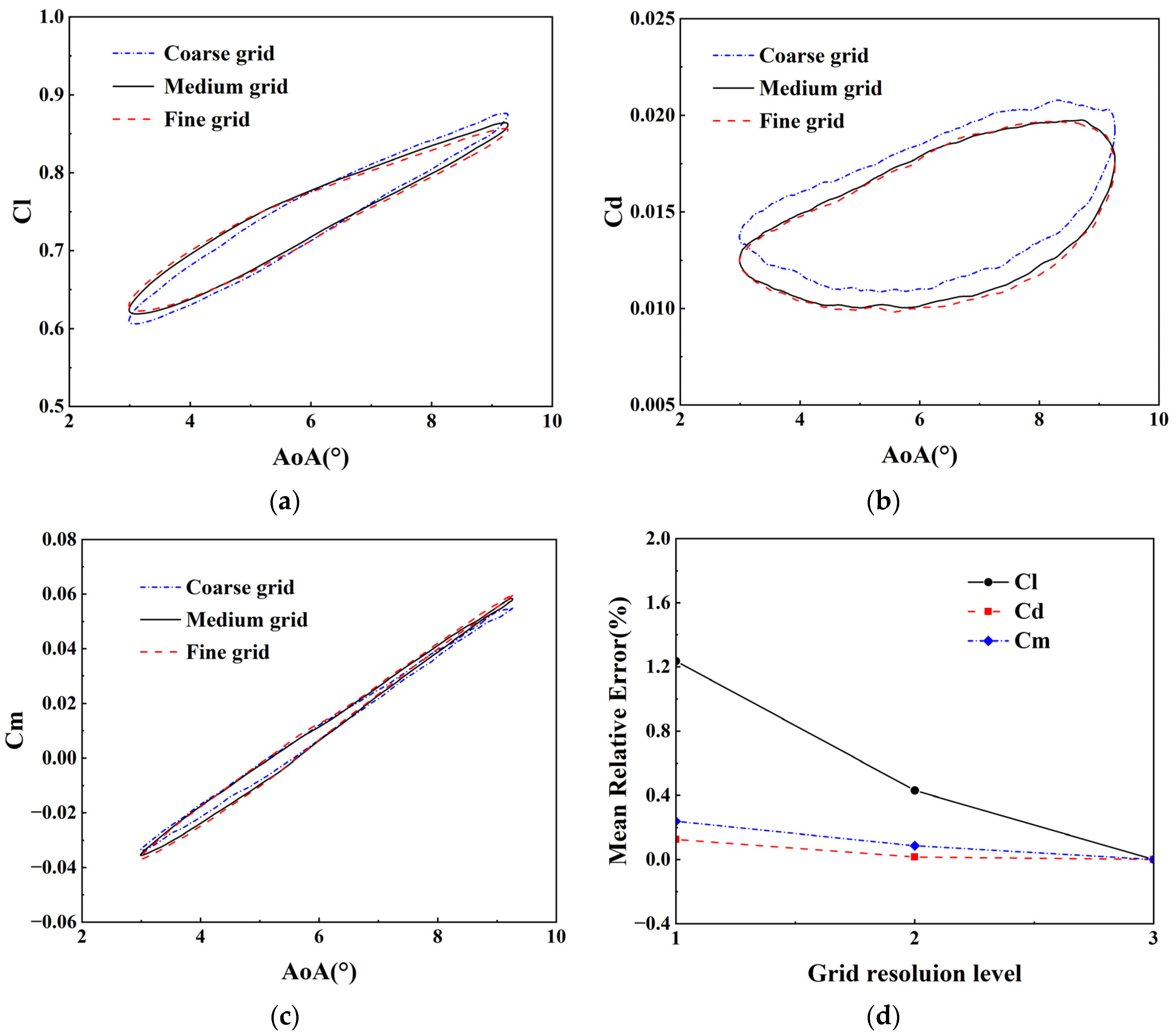
5.1. Effect of Grid Resolution
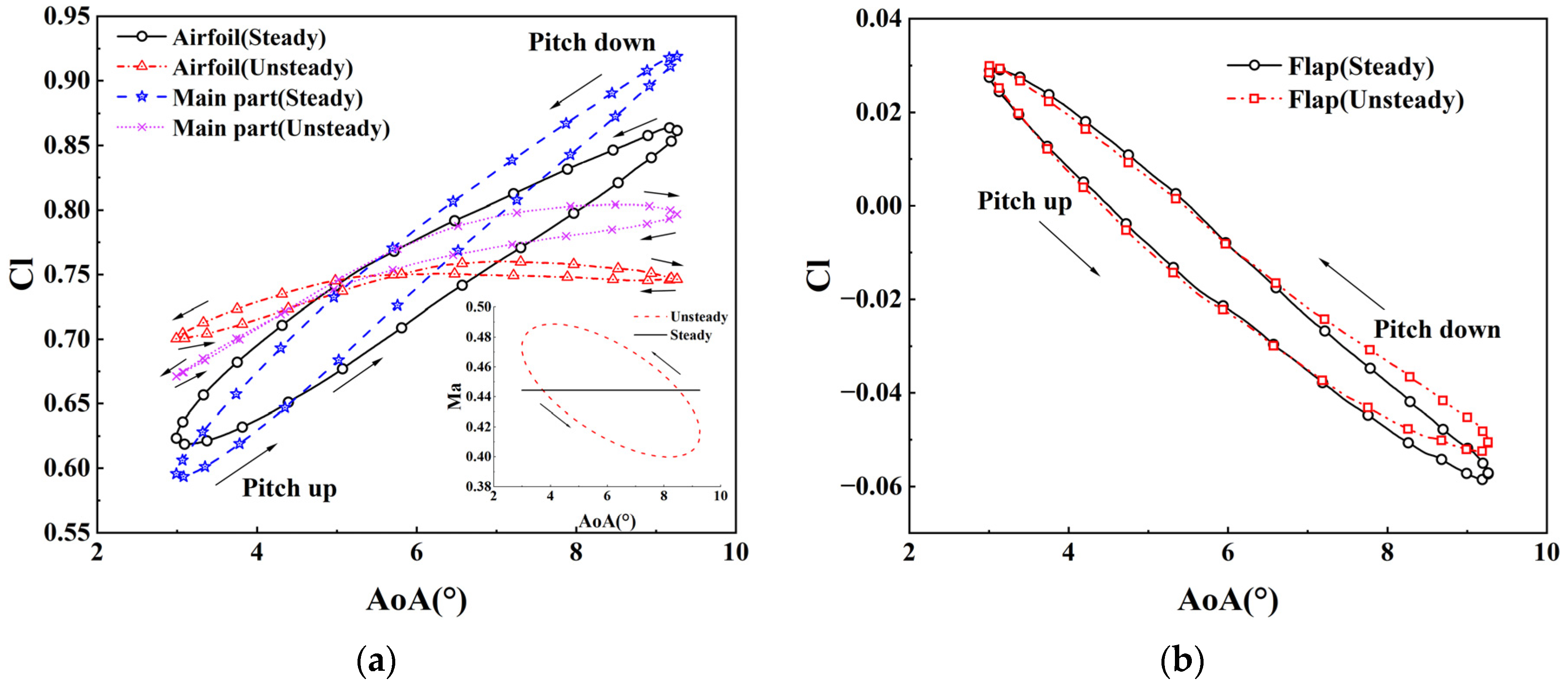
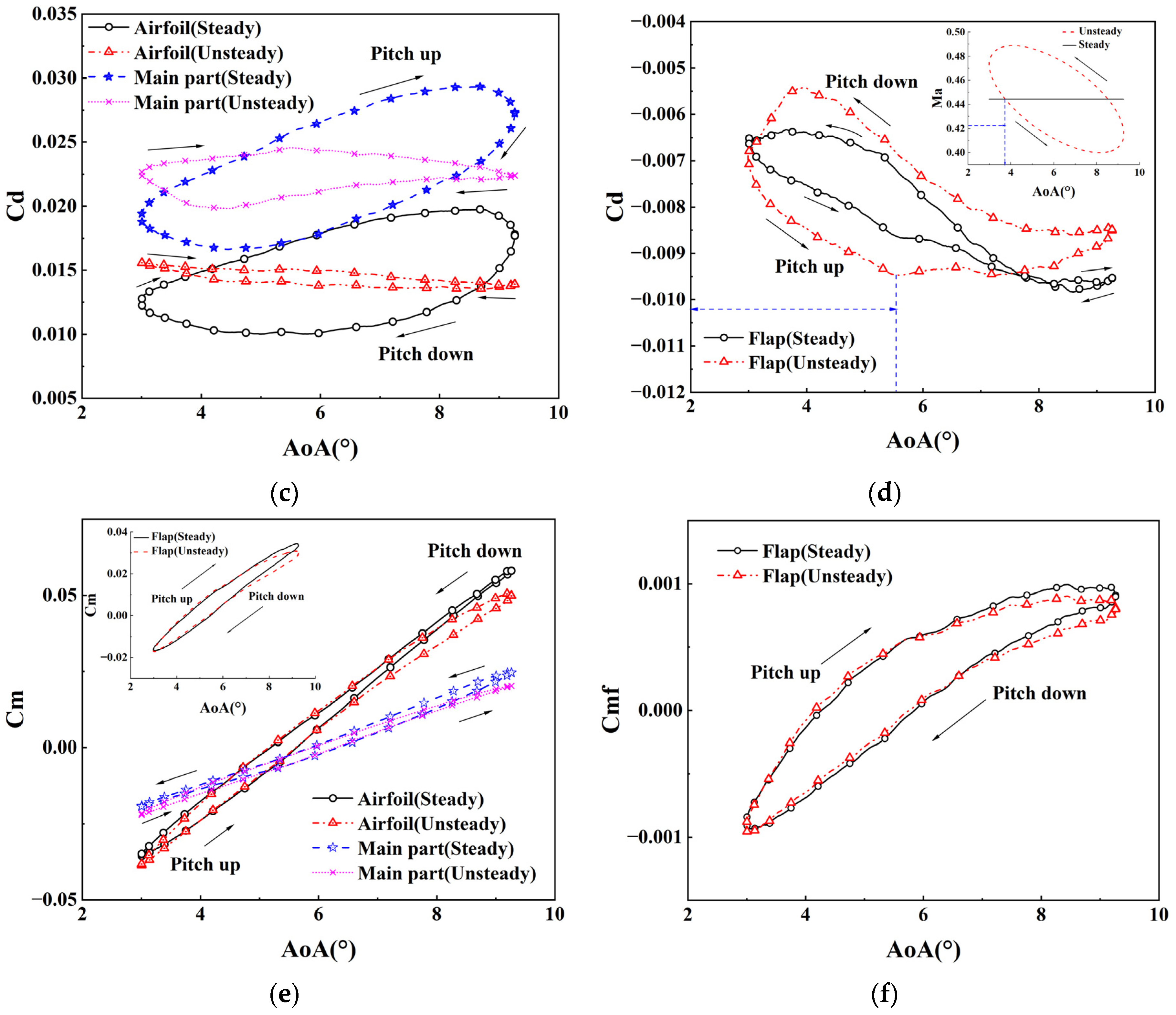
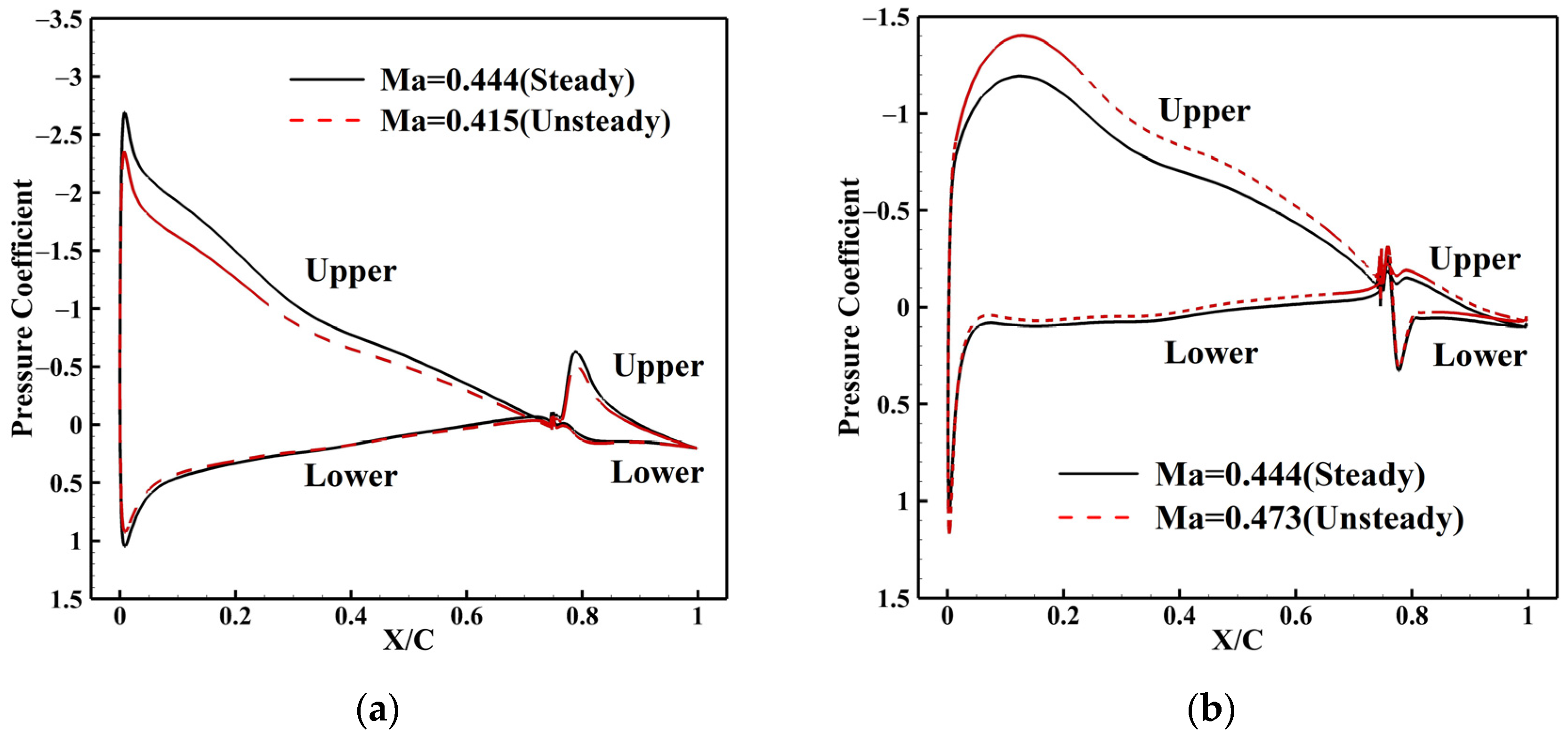
5.2. Aerodynamic Characteristics at μ of 0.1
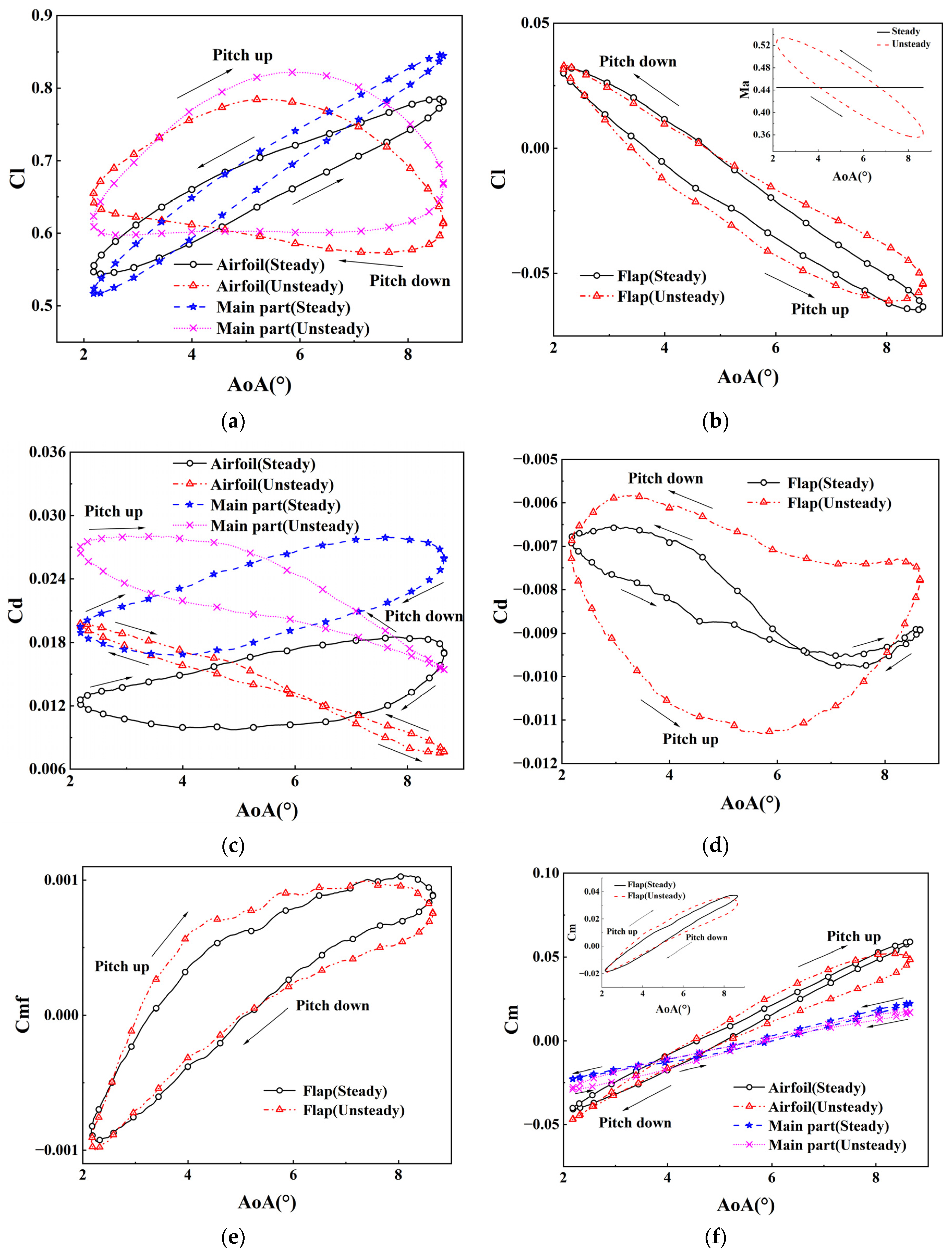
5.3. Aerodynamic Characteristics at μ of 0.2
5.4. Aerodynamic Characteristics at μ of 0.3
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shen, J.W.; Chopra, I. Swashplateless helicopter rotor with trailing-edge flaps. J. Aircr. 2004, 41, 208–214. [Google Scholar] [CrossRef]
- Mccloud, J.L., III. An analytical study of a multicycle controllable twist rotor. In Proceedings of the Annual National Forum, Washington, DC, USA, 13–15 May 1975. [Google Scholar]
- Lemnios, A.Z.; Dunn, F.K. Theoretical Study of Multicyclic Control of a Controllable Twist Rotor; No. NASA-CR-151959; NASA: Washington, DC, USA, 1976. [Google Scholar]
- Mccloud, J.L., III; Weisbrich, A.L. Wind-tunnel test results of a full-scale multicyclic controllable twist rotor. In Proceedings of the American Helicopter Society, Annual National Forum, Washington, DC, USA, 15–17 May 1978. No. AHS 78-60. [Google Scholar]
- Wei, F.S.; Weisbrich, A.L. Multicyclic Controllable Twist Rotor Data Analysis; No. NASA-CR-152251; NASA: Washington, DC, USA, 1979. [Google Scholar]
- Chopra, I. Status of Application of Smart Structures Technology to Rotorcraft Systems. J. Am. Helicopter Soc. 2000, 45, 228–252. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Review of Smart-Materials Actuation Solutions for Aeroelastic and Vibration Control. J. Intell. Mater. Syst. Struct. 2000, 11, 525–544. [Google Scholar] [CrossRef]
- Derham, R. The Aeromechanics of Smart/Active Rotors. In Proceedings of the AHS Aeromechanics Specialists’ Meeting, Atlanta, Georgia, 13–15 November 2000. [Google Scholar]
- Hassan, A.A.; Straub, F.K.; Noonan, K.W. Experimental/numerical evaluation of integral trailing edge flaps for helicopter rotor applications. J. Am. Helicopter Soc. 2005, 50, 3–17. [Google Scholar] [CrossRef]
- Dieterich, O.; Enenkl, B.; Roth, D. Trailing edge flaps for active rotor control aeroelastic characteristics of the ADASYS rotor system. In Proceedings of the American Helicopter Society 62nd Annual Forum Proceedings, Alexandria, VA, USA, 9–11 May 2006; The AHS International, Inc.: Rocklin, CA, USA, 2006. [Google Scholar]
- Roth, D.; Enenkl, B.; Dieterich, O. Active rotor control by flaps for vibration reduction-full scale demonstrator and first flight test results. In Proceedings of the 32nd European Rotor Craft Forum, Maastricht, The Netherlands, 12–14 September 2006. [Google Scholar]
- Rabourdin, A.; Maurich, J.; Dieterich, O. Blue Pulse: Active Rotor Control at Airbus Helicopters—New EC145 Demonstrator and Flight Test Results. In Proceedings of the American Helicopter Society 70th Annual Forum Proceedings, Alex-Alexandria, VA, USA, 27–29 May 2009; The AHS International, Inc.: Rocklin, CA, USA, 2009. [Google Scholar]
- Leishman, J.G. Principles of Helicopter Aerodynamics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Conlisk, A.T. Modern helicopter aerodynamics. Annu. Rev. Fluid Mech. 1997, 29, 515–567. [Google Scholar] [CrossRef]
- Krzysiak, A.; Narkiewicz, J. Aerodynamic Loads on Airfoil with Trailing-Edge Flap Pitching with Different Frequencies. J. Aircr. 2006, 43, 407–418. [Google Scholar] [CrossRef]
- Lee, T.; Su, Y.Y. Unsteady airfoil with a harmonically deflected trailing-edge flap. J. Fluids Struct. 2011, 27, 1411–1424. [Google Scholar] [CrossRef]
- He, G.S.; Deparday, J. Stall Delay and Leading-Edge Suction for a Pitching Airfoil with Trailing-Edge Flap. AIAA J. 2020, 58, 5146–5155. [Google Scholar] [CrossRef]
- Pohl, J.; Semaan, R.; Jones, A.R. Dynamic Lift Measurements on an Airfoil with Periodic Flap Motion at High Reynolds Number. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. AIAA Paper 2019-1396. [Google Scholar]
- Shen, J.; Chopra, I. Aeroelastic Stability of Trailing-Edge Flap Helicopter Rotors. J. Am. Helicopter Soc. 2003, 48, 236–243. [Google Scholar] [CrossRef]
- Straub, F.K.; Charles, B.D. Aeroelastic analysis of rotors with trailing edge flaps using comprehensive codes. J. Am. Helicopter Soc. 2001, 46, 192–199. [Google Scholar] [CrossRef]
- Mishra, A.; Sitaraman, J.; Baeder, J. Computational investigation of trailing edge flap for control of vibration. In Proceedings of the 25th AIAA Applied Aerodynamics Conference, Miami, FL, USA, 25–28 June 2007; p. 4290. [Google Scholar]
- Gerontakos, P.; Lee, T. Dynamic stall flow control via a trailing-edge flap. AIAA J. 2006, 44, 469–480. [Google Scholar] [CrossRef]
- Gharali, K.; Johnson, D.A. Dynamic stall simulation of a pitching airfoil under unsteady freestream velocity. J. Fluids Struct. 2013, 42, 228–244. [Google Scholar] [CrossRef]
- Xing, S.L.; Xu, H.Y. Trailing Edge Flap Effects on Dynamic Stall Vortex and Unsteady Aerodynamic Forces on a Pitching Airfoil, International Journal of Aerospace Engineering. Int. J. Aerosp. Eng. 2022, 2022, 20. [Google Scholar]
- Su, T.Y. A Fuzzy Logic/CFD Combined Approach for Modeling the Unsteady Aerodynamics of an Airfoil with Trailing Edge Flap. J. Nanchang Hangkong Univ. 2022, 36, 14–21. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, Q.J. Unsteady aerodynamic characteristic analysis of rotor airfoil under variational free stream velocity condition. Hangkong Dongli Xuebao/J. Aerosp. Power 2017, 32, 364–372. [Google Scholar] [CrossRef]
- Pierce, G.A.; Kunz, D.L. The effect of varying freestream velocity on dynamic stall characteristics. In Proceedings of the 32nd Annual National Forum of the American Helicopter Society, Washington, DC, USA, 21 May 1976; NASA: Washington, DC, USA, 1976. [Google Scholar]
- Visbal, M.R.; Shang, J.S. Investigation of the flow structure around a rapidly pitching airfoil. AIAA J. 1989, 27, 1044–1051. [Google Scholar] [CrossRef]
- Leishman, J.G.; Beddoes, T.S. A semi-empirical model for dynamic stall. J. Am. Helicopter Soc. 1989, 34, 3–17. [Google Scholar]
- Su, T.Y.; Lu, Y. Aerodynamic characteristics analysis of electrically controlled rotor based on viscous vortex particle method. Aerosp. Sci. Technol. 2019, 97, 105645. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, H.W. Paramenter Study of the Airfoil with Flap Used for Electrical Controlled Rotor. Helicopter Tech. 2004, 3, 18–22. [Google Scholar] [CrossRef]
- Wang, J.; Yang, M. CFD Simulation of Unsteady Aerodynamics of Airfoil with Trailing-Edge Flap. Comput. Simul. 2011, 28, 88–92. [Google Scholar] [CrossRef]
- Liu, L.; Padthe, A.; Friedmann, P.; Quon, E.; Smith, M.J. Unsteady aerodynamics of an airfoil/flap combination on a helicopter rotor using computational fluid dynamics and approximate methods. J. Am. Helicopter Soc. 2011, 56, 1–13. [Google Scholar] [CrossRef]
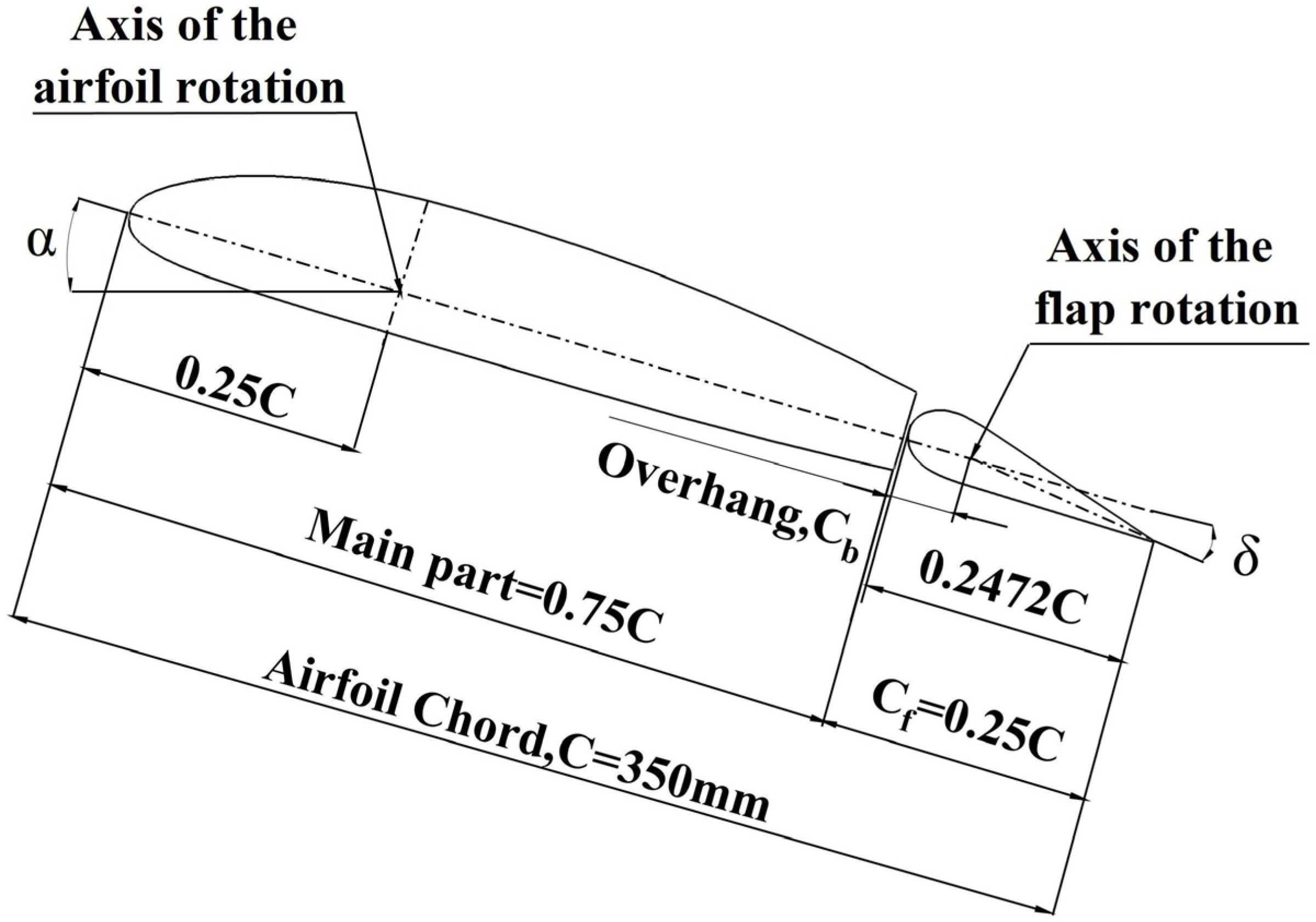



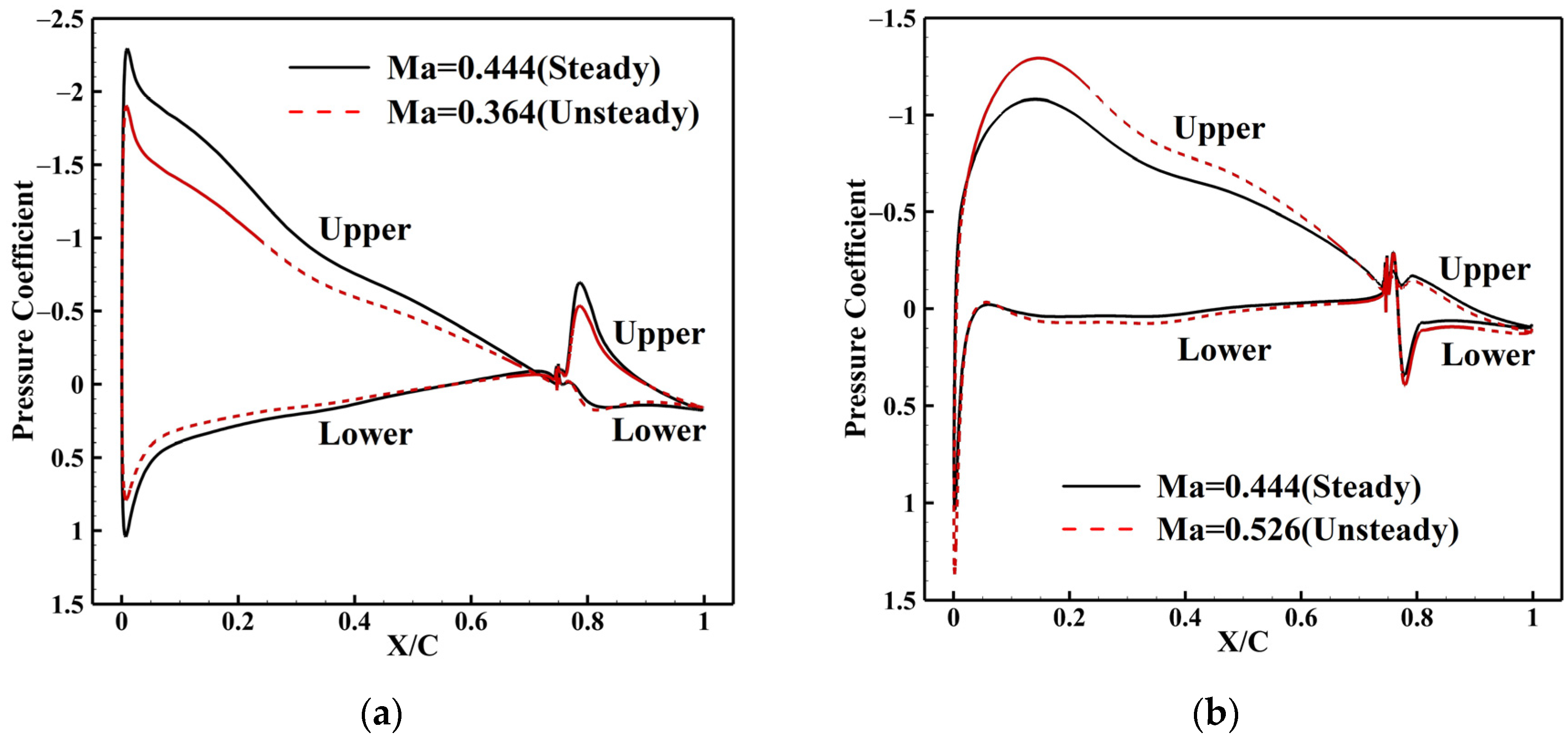
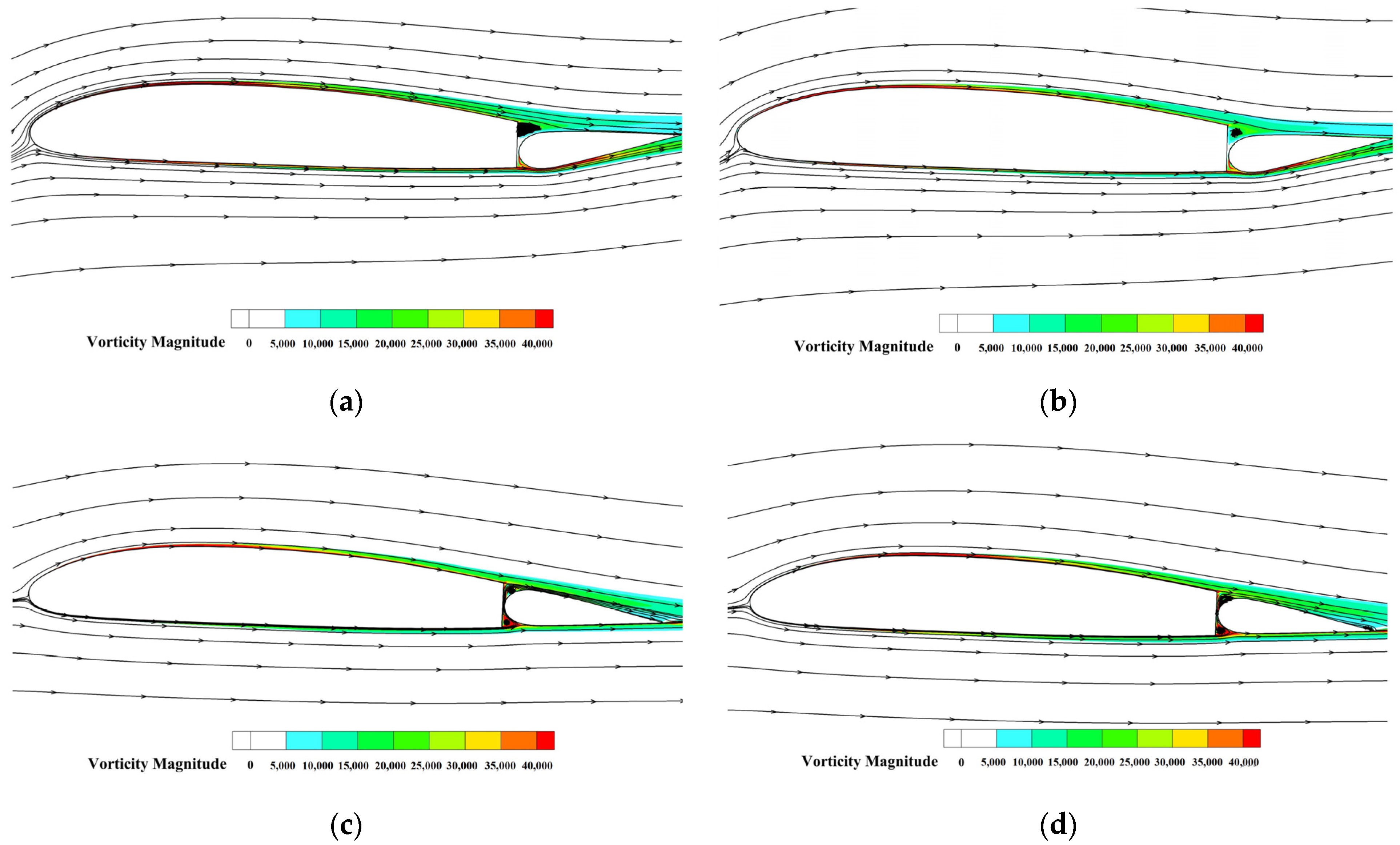



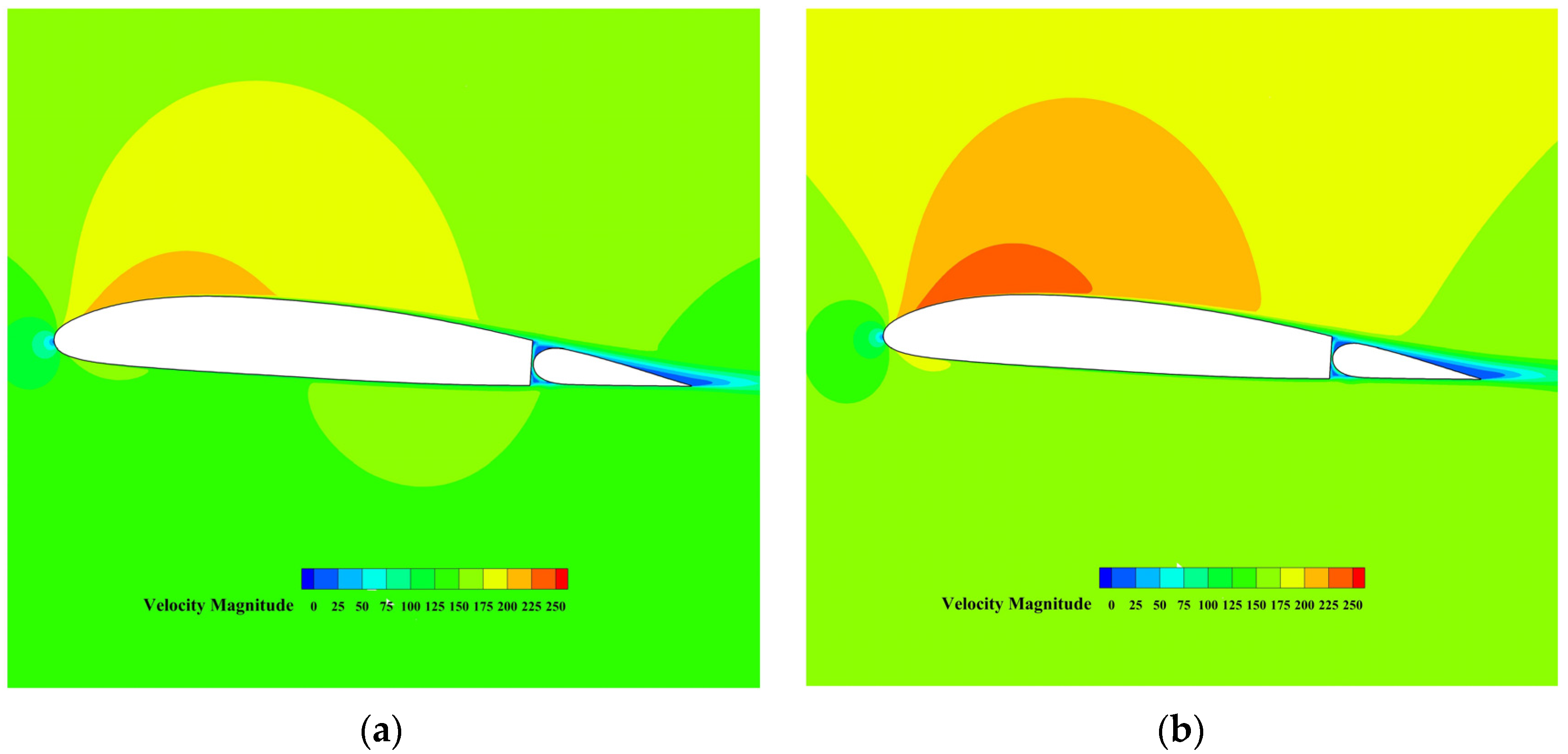

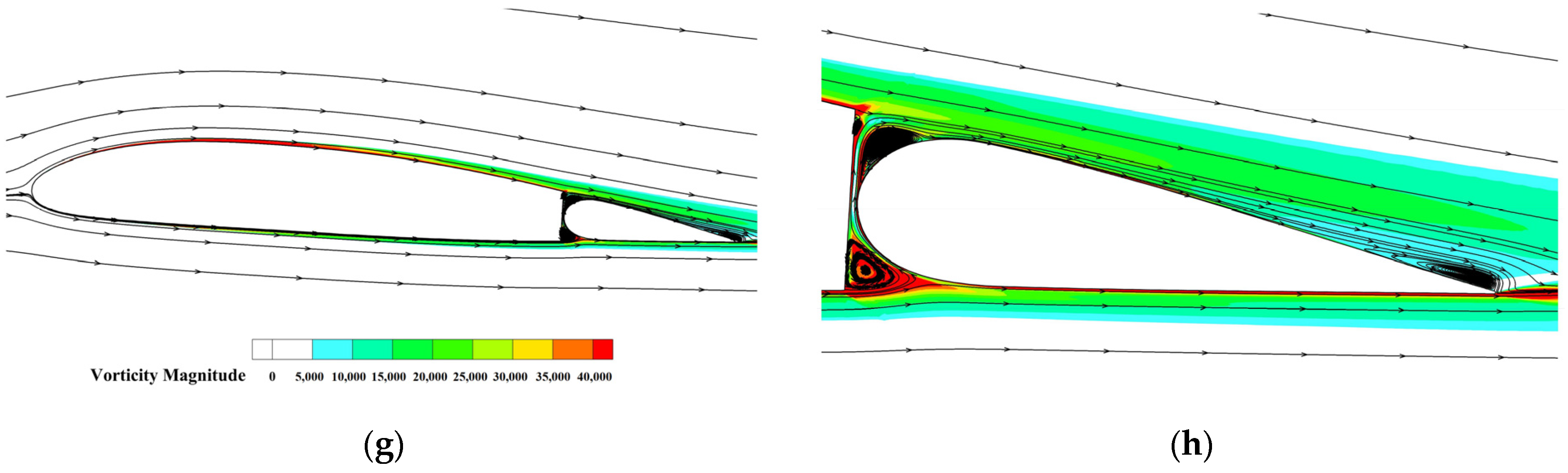
| Properties | Design Value |
|---|---|
| Airfoil | OA 212 |
| Rotor radius | 5.345 m |
| Rotor speed | 40.42 rad/s |
| Flap midspan location | 0.7 R |
| Flap spanwise length | 1.069 m (0.2 R) |
| Airfoil chord (with flap), C | 0.35 m |
| Flap chord ratio, Rf | 0.25 |
| Nose overhang, Cb | 0.0625 C |
| Distance of airfoil axis of rotation from airfoil leading edge | 0.25 C |
| Grid | Dimensions | Total Cells (Three Planes) |
|---|---|---|
| Coarse | 200 × 80; 200 × 60 | 32,000 |
| Medium | 310 × 120; 300 × 80 | 68,950 |
| Fine | 400 × 140; 400 × 100 | 117,200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, C.; Li, H.; Su, T.; Frank, C.A.; Li, K. Research of Unsteady Aerodynamic Characteristics of Electrically Controlled Rotor Airfoils with Trailing-Edge Flaps. Aerospace 2024, 11, 18. https://doi.org/10.3390/aerospace11010018
Liang C, Li H, Su T, Frank CA, Li K. Research of Unsteady Aerodynamic Characteristics of Electrically Controlled Rotor Airfoils with Trailing-Edge Flaps. Aerospace. 2024; 11(1):18. https://doi.org/10.3390/aerospace11010018
Chicago/Turabian StyleLiang, Changwu, Hong Li, Taoyong Su, Caleb Alistair Frank, and Kewei Li. 2024. "Research of Unsteady Aerodynamic Characteristics of Electrically Controlled Rotor Airfoils with Trailing-Edge Flaps" Aerospace 11, no. 1: 18. https://doi.org/10.3390/aerospace11010018
APA StyleLiang, C., Li, H., Su, T., Frank, C. A., & Li, K. (2024). Research of Unsteady Aerodynamic Characteristics of Electrically Controlled Rotor Airfoils with Trailing-Edge Flaps. Aerospace, 11(1), 18. https://doi.org/10.3390/aerospace11010018






