Deciding Technosignature Search Strategies: Multi-Criteria Fuzzy Logic to Find Extraterrestrial Intelligence
Abstract
:1. Introduction
2. Methodology
2.1. Fuzzy Sets
2.2. The Fuzzy Analytic Hierarchy Process (AHP)
- .
- .
- If , then .
- If is more important than , then .
2.3. Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)
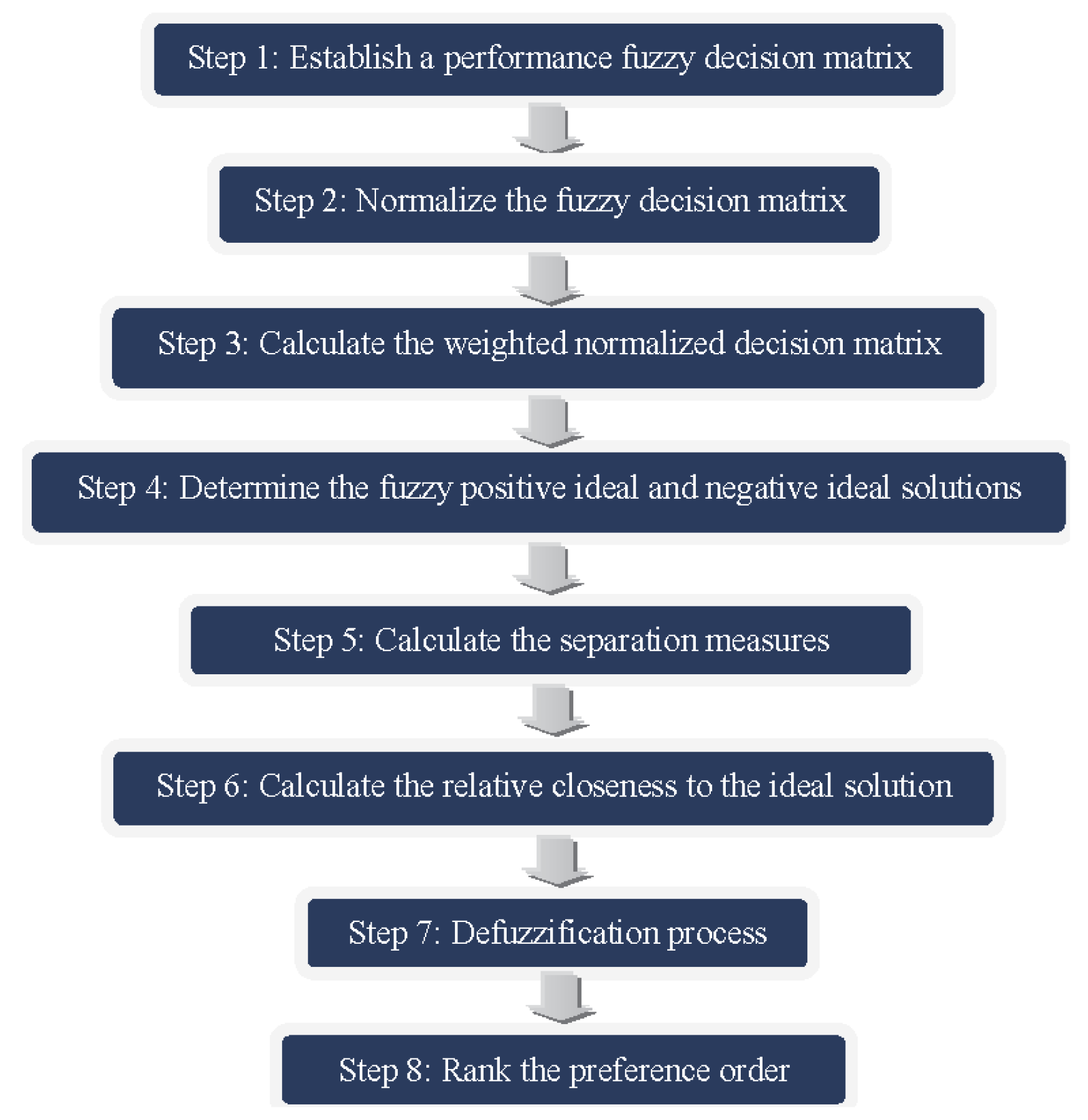
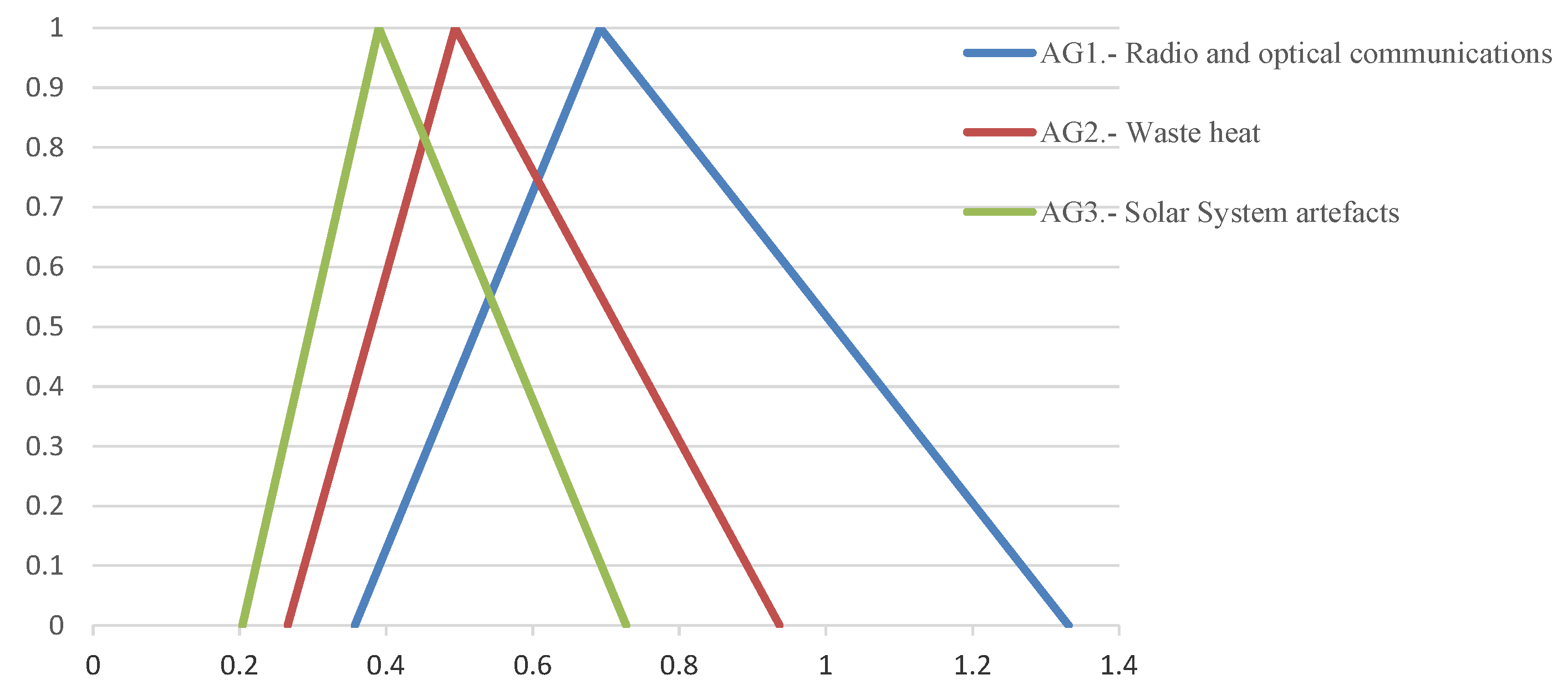
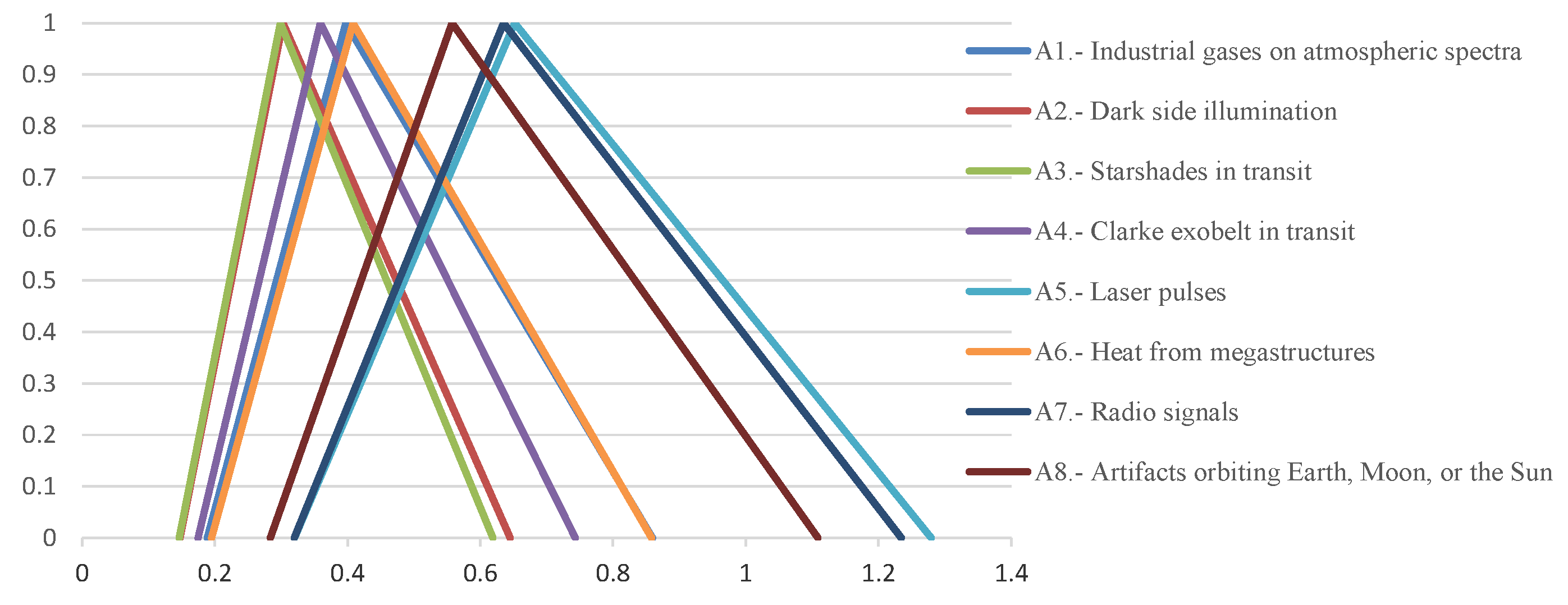
- Step 1. Establish a performance fuzzy decision matrix (Table 2). It is composed of rows and columns so that the rows constitute the alternatives to be evaluated and the columns show the valuations of each of the criteria that influence the assessment process for each one of the alternatives. In this study, such valuations are obtained via linguistic labels through triangular fuzzy numbers (see Figure 1). For simplicity of representation, the stages of the TOPSIS algorithm are shown with real values or crisp numbers. The only difference concerning the fuzzy version lies in applying the arithmetic operations of triangular fuzzy numbers, detailed in [36,37].
- Step 2. Normalize the fuzzy decision matrix. The decision matrix defined in the previous step is normalized through the following expression:where corresponds to an element of the normalized decision matrix N.
- Step 3. Calculate the weighted normalized decision matrix. Once the global weight vector of the criteria is obtained (via the fuzzy version of the AHP methodology in our decision problem), the normalized decision matrix is multiplied by such a vector as follows:where satisfy
- Step 4. Determine the fuzzy positive ideal and negative ideal solutions. The characteristics of the criteria determine both solutions since, in the case of a benefit criterion, the solution will correspond to the maximum valuation of the alternatives for such a criterion. Likewise, if the criterion is cost-based, the value will be obtained through the minimum valuation. An analogous but inverse case occurs to determine the solution. Mathematically, such concepts ( and ) are defined through the following:where the parameter is associated with cost criteria, while the parameter J corresponds to benefit criteria.
- Step 5. Calculate the separation measures of each alternative. The separation distances of each alternative from (namely, ) and (namely, ) are determined by the n-dimensional Euclidean distance method:
- Step 6. Calculate the relative closeness to the ideal solution. Hence, a closeness coefficient for each alternative can be calculated as follows:
- Step 7. Defuzzification process. Since each closeness coefficient is a triangular fuzzy number in the fuzzy version of the TOPSIS methodology, that coefficient must be transformed into a crisp one. To deal with such a defuzzification process, we shall apply the following expression:
- Step 8. Rank the preference order. It becomes clear that a given alternative stands closer to the and farther from the (and hence, its ranking is higher) as becomes closer to 1. Therefore, a ranking of alternatives in descending order is generated according to values.
3. Prioritization Problem: Selecting TS Search Strategies
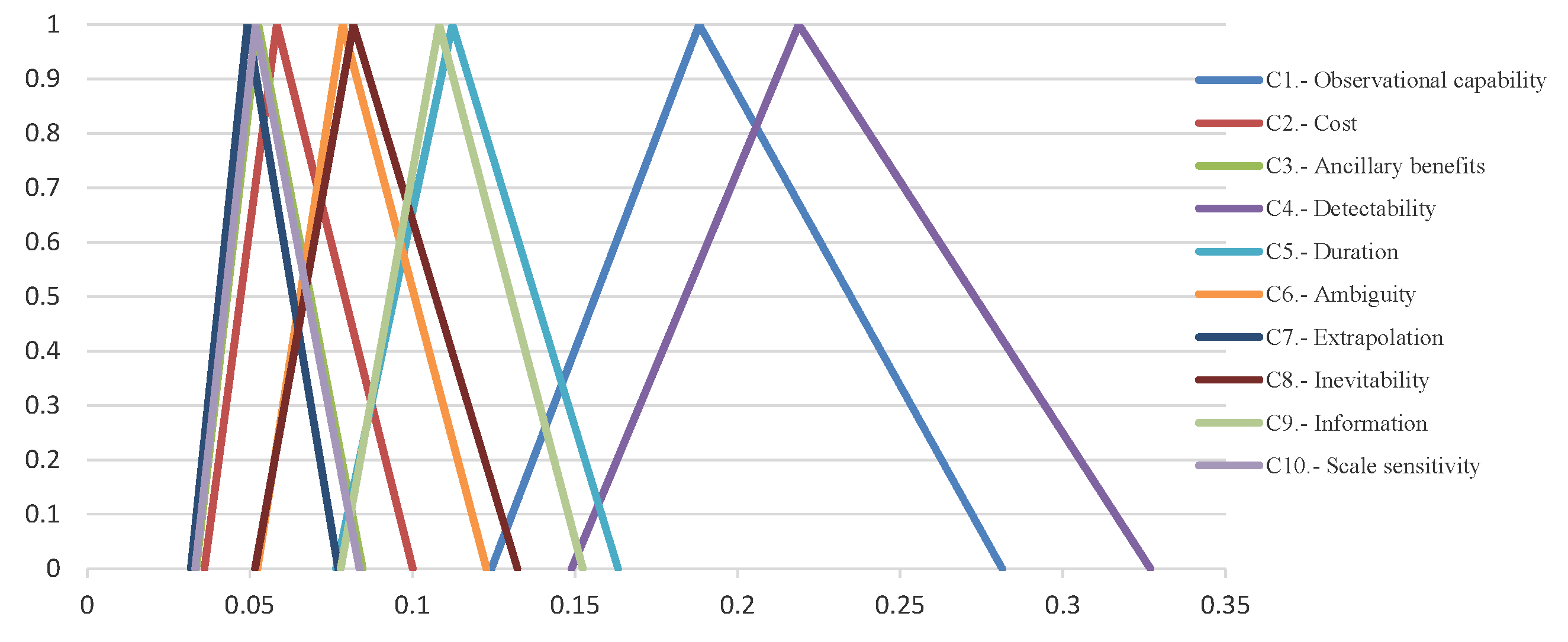
3.1. Definition of the Criteria
- —Observing Capability: This criterion evaluates the current technological capabilities of astronomy in detecting specific TSs. It encompasses the sophistication of observational equipment, the extent of astronomical knowledge, and the ability to distinguish between natural cosmic phenomena and potential TSs.
- —Cost: A multifaceted criterion that encompasses the financial investment required, the allocation of telescope time, computational resources, and other opportunity costs associated with the search.
- —Ancillary Benefits: Every search for alien civilizations should be structured in a manner that yields valuable scientific data, regardless of the success in discovering extraterrestrial life. This criterion appraises the capacity of a TS search strategy to contribute to broader scientific knowledge.
- —Detectability: This involves assessing the strength of the TS signal relative to background cosmic noise. A key factor here is the signal’s clarity and distinctness, which significantly impacts the likelihood of accurate detection.
- —Duration: The temporal aspect of a TS’s detectability is evaluated here. This criterion measures the length of time for which a TS remains observable.
- —Ambiguity: This criterion assesses the likelihood of a TS being erroneously interpreted as a natural phenomenon unrelated to extraterrestrial life. Minimizing ambiguity is crucial for the validity of any potential discovery.
- —Extrapolation: Here, the focus is on our capability to comprehend, interpret, and potentially utilize the underlying technology of a detected TS, should it be within the realms of our current or near-future technological understanding.
- —Inevitability: This criterion evaluates the likelihood that a given technology, used by an advanced civilization, would naturally produce a detectable TS. It reflects the probability that certain technologies are universal and would manifest detectable signatures.
- —Information: This axis gauges the richness of the information carried by a detected TS, including the quantity and diversity of data. It reflects the potential scientific value embedded within the signal.
- —Scale Sensitivity: Introduced as an additional axis, this criterion quantifies the variability in the assessment of the other merit axes as a function of the TS’s size or intensity, within a plausible expected range.
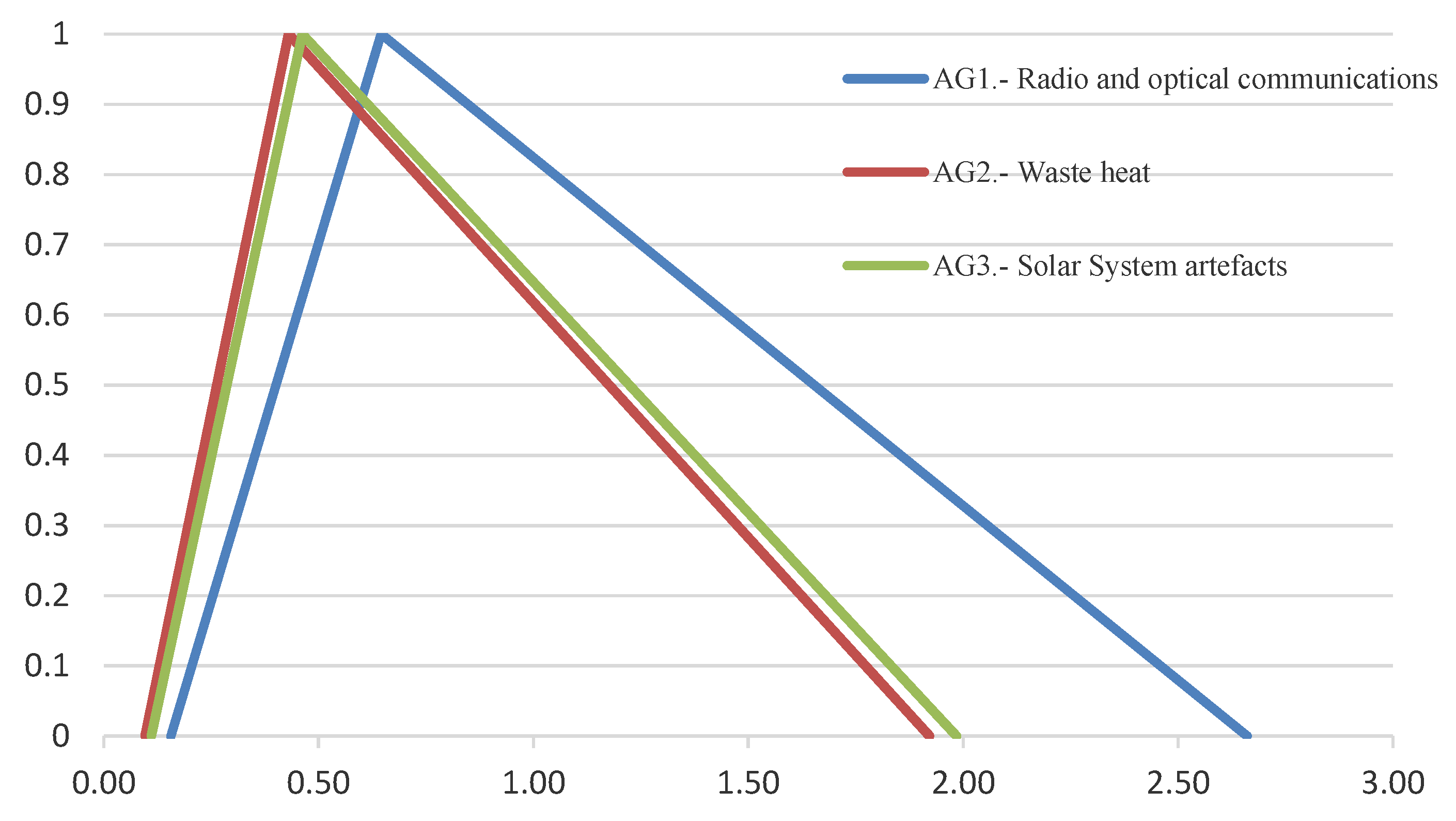
3.2. Description of the Alternatives
- —Radio and Optical Communications: This category encompasses the search for technologically generated electromagnetic signals. The focus is on identifying emissions that exhibit temporal or frequency characteristics atypical of natural astrophysical sources. The approach capitalizes on the premise that advanced civilizations may utilize specific electromagnetic wavelengths for communication, which would manifest as anomalies when contrasted against the cosmic electromagnetic background.
- —Waste Heat: This segment explores the detection of alien megastructures and technological artifacts located beyond the confines of our solar system. The primary indicator for such structures is the thermal emission, or ’waste heat,’ that they generate, potentially discernible in the infrared spectrum. These emissions would stand out from the background galactic noise, offering tangible evidence of technologically advanced civilizations.
- —Solar System Artefacts: This category is focused on the discovery of non-human, technologically crafted objects, substances, patterns, or processes that exist within the solar system. The premise here is that traces or remnants of extraterrestrial visitations or activities might be found closer to home, embedded within the fabric of our solar system. The search in this domain involves scrutinizing celestial bodies, including moons, asteroids, and planets, for anomalies that do not align with known natural processes or formations.
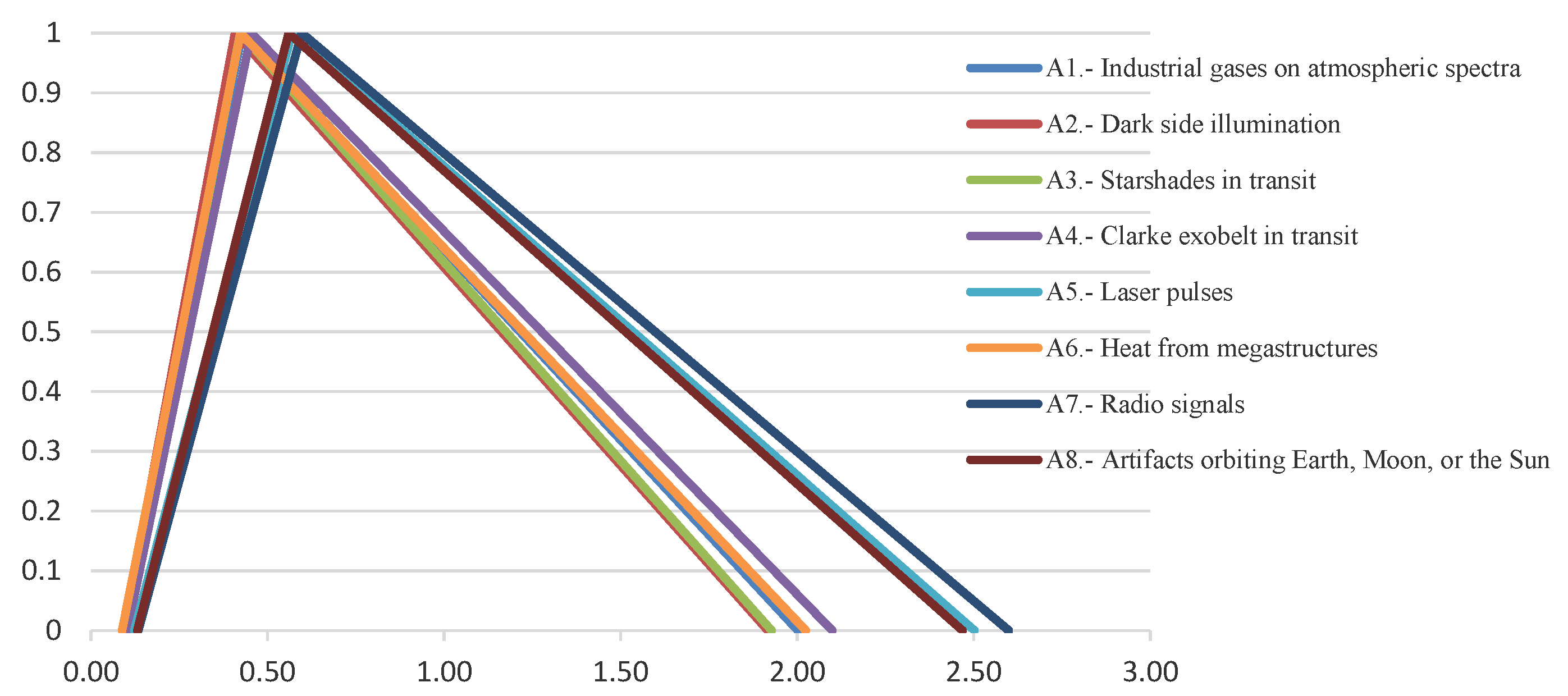
- —Industrial Gases in Atmospheric Spectra: This TS involves the detection of non-natural gases, such as chlorofluorocarbons, in the atmospheric spectra of exoplanets. The presence of these gases could indicate industrial activities, suggesting a technologically advanced civilization.
- —Dark Side Illumination: This category refers to the observation of artificial light sources on the dark side of an exoplanet or celestial body. Such illumination could be indicative of city lights or other forms of artificial lighting, pointing to the existence of intelligent life.
- —Starshades in Transit: The focus here is on identifying artificial structures that transit a star, leading to dimming patterns inconsistent with natural celestial bodies. Such anomalies could hint at large-scale space constructions, possibly for energy collection or habitation.
- —Clarke Exobelt in Transit: This TS involves the detection of a dense belt of satellites or debris around an exoplanet, akin to the concept of a ’Clarke Belt’ in Earth orbit. Such a belt could signify a high level of technological development in satellite deployment and space activities.
- —Laser Pulses: The capture of high-intensity, narrow-bandwidth light signals, potentially indicative of directed energy systems or interstellar communication efforts.
- —Heat from Megastructures: The observation of an infrared excess emanating from a star or galaxy, suggesting widespread energy utilization. Such a scenario could point to megastructures like a Dyson sphere, indicating an advanced civilization harnessing a star’s energy.
- —Radio Signals: This involves the reception of narrow-bandwidth radio signals exhibiting patterns or characteristics unlikely to be of natural origin. These signals could be indicative of communication or other technological activities.
- —Artifacts Orbiting Earth, Moon, or the Sun: The discovery of artificial objects in stable orbits around Earth, the Moon, or traversing interstellar space. This category also includes the identification of non-natural structures or objects on the Moon or other celestial bodies, potentially left behind by advanced civilizations.
3.3. Obtaining the Weights of the Criteria
- Q1: Mark the relevance order that you consider appropriate for each Axis of Merit () plus the criterion Scale Sensitivity to prioritize TSs. Note that multiple criteria may be chosen to be equally important.
- Q2: Compare the criterion () you have ranked in the first position with those you have designated for the second position and subsequent orders. For this comparison, utilize the following specified linguistic labels, (EqI), (Sl + I), (+I), (St + I), (Ex + I), which correspond to the scale of the valuation in the pair-wise comparison process (Table 1).
3.4. Prioritization of the Alternatives
4. Results and Discussion
5. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TS | Technosignature |
| SETI | Search for Extraterrestrial Intelligence |
| MCDM | Multi-Criteria Decision Making |
| AHP | Analytic Hierarchy Process |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
Appendix A
| Criteria | Expert 1 () | Expert 2 () | Expert 3 () | Expert 4 () | Expert 5 () |
|---|---|---|---|---|---|
| (0.193, 0.337, 0.547) | (0.258, 0.395, 0.583) | (0.040, 0.063, 0.097) | (0.136, 0.188, 0.248) | (0.042, 0.062 0.090) | |
| (0.052, 0.112, 0.255) | (0.033, 0.056, 0.094) | (0.040, 0.063, 0.097) | (0.036, 0.063, 0.116) | (0.036, 0.048 0.069) | |
| (0.025, 0.048, 0.089) | (0.033, 0.056, 0.094) | (0.040, 0.063, 0.097) | (0.036, 0.063, 0.116) | (0.036, 0.048 0.069) | |
| (0.052, 0.112, 0.255) | (0.069, 0.132, 0.272) | (0.314, 0.438, 0.600) | (0.136, 0.188, 0.248) | (0.056, 0.087 0.134) | |
| (0.034, 0.067, 0.131) | (0.033, 0.056, 0.094) | (0.040, 0.063, 0.097) | (0.136, 0.188, 0.248) | (0.324, 0.435 0.557) | |
| (0.052, 0.112, 0.255) | (0.033, 0.056, 0.094) | (0.040, 0.063, 0.097) | (0.015, 0.021, 0.031) | (0.056, 0.087 0.134) | |
| (0.022, 0.037, 0.068) | (0.033, 0.056, 0.094) | (0.040, 0.063, 0.097) | (0.015, 0.021, 0.031) | (0.036, 0.048 0.069) | |
| (0.034, 0.067, 0.131) | (0.045, 0.079, 0.140) | (0.040, 0.063, 0.097) | (0.136, 0.188, 0.248) | (0.056, 0.087 0.134) | |
| (0.022, 0.037, 0.068) | (0.033, 0.056, 0.094) | (0.040, 0.063, 0.097) | (0.036, 0.063, 0.116) | (0.036, 0.048 0.069) | |
| (0.034, 0.067, 0.131) | (0.033, 0.056, 0.094) | (0.040, 0.063, 0.097) | (0.015, 0.021, 0.031) | (0.036, 0.048 0.069) | |
| Criteria | Expert 6 () | Expert 7 () | Expert 8 () | Expert 9 () | Expert 10 () |
| (0.248, 0.386, 0.579) | (0.040, 0.063, 0.097) | (0.178, 0.209, 0.242) | (0.070, 0.131, 0.258) | (0.037, 0.049, 0.071) | |
| (0.032, 0.055, 0.094) | (0.040, 0.063, 0.097) | (0.023, 0.030, 0.039) | (0.029, 0.044, 0.068) | (0.037, 0.049, 0.071) | |
| (0.032, 0.055, 0.094) | (0.040, 0.063, 0.097) | (0.020, 0.023, 0.030) | (0.029, 0.044, 0.068) | (0.043, 0.064, 0.094) | |
| (0.066, 0.129, 0.270) | (0.314, 0.438, 0.600) | (0.178, 0.209, 0.242) | (0.262, 0.394, 0.554) | (0.043, 0.064, 0.094) | |
| (0.043, 0.077, 0.139) | (0.040, 0.063, 0.097) | (0.023, 0.030, 0.039) | (0.034, 0.056, 0.090) | (0.058, 0.089, 0.139) | |
| (0.032, 0.055, 0.094) | (0.040, 0.063, 0.097) | (0.178, 0.209, 0.242) | (0.034, 0.056, 0.090) | (0.043, 0.064, 0.094) | |
| (0.032, 0.055, 0.094) | (0.040, 0.063, 0.097) | (0.023, 0.030, 0.039) | (0.034, 0.056, 0.090) | (0.043, 0.064, 0.094) | |
| (0.032, 0.055, 0.094) | (0.040, 0.063, 0.097) | (0.020, 0.023, 0.030) | (0.070, 0.131, 0.258) | (0.043, 0.064, 0.094) | |
| (0.032, 0.055, 0.094) | (0.040, 0.063, 0.097) | (0.178, 0.209, 0.242) | (0.029, 0.044, 0.068) | (0.332, 0.445, 0.578) | |
| (0.043, 0.077, 0.139) | (0.040, 0.063, 0.097) | (0.023, 0.030, 0.039) | (0.029, 0.044, 0.068) | (0.037, 0.049, 0.071) |
| Experts | Alternatives | Criteria | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| —Radio and Optical | VH | L | H | VH | B | L | VL | M | H | H | |
| VH | M | H | VL | VB | VL | VL | VH | VH | M | ||
| M | M | L | L | B | VL | H | L | VH | VH | ||
| VH | VL | VL | M | VB | VL | L | VL | VH | L | ||
| VH | M | M | VH | M | H | VH | VH | H | M | ||
| VH | L | H | M | M | M | M | M | H | M | ||
| M | M | L | M | M | M | M | M | L | M | ||
| VH | VL | VH | VH | VH | VL | VL | VH | VH | VL | ||
| M | L | M | M | VB | H | L | L | M | H | ||
| VH | VL | H | M | M | M | VL | M | H | VH | ||
| —Waste Heat | H | H | H | H | VH | M | VH | H | H | M | |
| VH | M | M | L | H | VH | H | H | L | VH | ||
| H | H | H | H | H | VH | VH | VH | VL | H | ||
| M | L | M | M | VH | L | VL | VH | L | H | ||
| VH | M | L | M | VH | L | L | H | M | H | ||
| M | M | M | H | H | H | L | M | M | H | ||
| H | M | H | VH | VH | H | VL | VH | VH | M | ||
| L | H | VH | L | M | VH | M | M | VL | VH | ||
| H | M | M | H | H | H | H | VH | L | VH | ||
| H | L | H | M | VH | M | H | M | H | VH | ||
| —Solar System Artifacts | M | M | H | VL | VH | VL | H | L | VH | H | |
| M | VH | L | H | VH | VL | VH | M | VH | M | ||
| H | H | H | M | H | L | H | L | VH | VH | ||
| H | H | H | L | H | H | M | M | H | M | ||
| M | M | VH | L | M | M | H | L | VH | M | ||
| M | H | M | VH | B | VH | VH | L | VH | VH | ||
| M | M | H | M | M | H | VH | M | H | M | ||
| VL | VH | VH | VL | M | M | VH | VL | L | VH | ||
| VH | H | VH | H | M | VL | H | VL | VH | VL | ||
| M | M | VH | L | VH | VL | M | VL | VH | L | ||
| Experts | Alternatives | Criteria | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| —Industrial gases on atmospheric spectra | VL | H | H | L | M | VH | VL | H | L | L | |
| H | M | M | M | VH | M | M | H | M | H | ||
| L | VH | VH | H | M | M | L | M | L | H | ||
| L | VL | H | M | VB | H | H | H | VL | M | ||
| VH | H | M | M | H | L | H | M | L | L | ||
| H | H | M | H | H | L | M | M | M | M | ||
| M | M | M | M | M | M | M | M | M | M | ||
| VL | VH | M | VL | M | VH | VH | M | VL | M | ||
| H | M | VH | H | H | H | VH | H | VH | M | ||
| H | M | H | M | VH | M | VL | M | L | H | ||
| —Dark side illumination | VL | H | H | VL | M | VH | VL | H | L | L | |
| L | M | VL | L | VH | H | H | M | H | VH | ||
| VL | VH | H | M | M | L | M | M | L | H | ||
| L | VL | M | L | VB | M | H | L | L | M | ||
| H | M | L | M | M | L | H | M | L | L | ||
| L | VH | H | L | M | H | L | L | H | L | ||
| M | M | M | M | M | M | M | M | M | M | ||
| VL | VH | M | VL | M | VH | VH | M | VL | M | ||
| VL | VH | VL | M | H | H | VH | M | H | L | ||
| L | H | L | L | VH | VH | VL | M | L | VH | ||
| —Starshades in transit | M | M | H | L | M | H | L | M | L | M | |
| H | M | L | H | VH | H | M | M | VH | M | ||
| M | M | H | H | M | L | H | VL | L | H | ||
| L | VL | M | L | B | M | M | M | L | M | ||
| M | H | VL | L | M | M | M | VL | L | L | ||
| L | VH | H | L | M | H | H | L | H | L | ||
| M | M | M | M | M | M | M | M | M | M | ||
| VL | VH | M | VL | M | VH | VH | M | VL | M | ||
| M | VH | M | M | M | H | M | M | M | H | ||
| M | VL | L | M | VH | M | VH | VL | L | VH | ||
| —Clarke exobelt in transit | M | M | H | M | M | H | L | H | L | L | |
| VL | M | M | VL | H | H | VH | L | VH | VH | ||
| L | H | H | M | M | M | H | L | L | H | ||
| L | VL | M | L | B | M | M | M | L | M | ||
| H | M | VL | L | M | L | M | L | L | L | ||
| L | VH | H | L | H | H | M | L | H | L | ||
| M | M | M | M | M | M | M | M | M | M | ||
| VL | VH | M | VL | M | VH | VH | M | VL | M | ||
| M | H | M | M | VH | VH | H | H | H | VH | ||
| M | VL | L | M | VH | VL | VL | M | L | H | ||
| —Laser pulses | VH | VL | H | VH | B | L | H | M | H | H | |
| M | M | M | H | B | VL | L | L | H | L | ||
| M | L | L | M | B | VL | H | L | VH | H | ||
| H | L | M | VL | VB | VL | L | H | VH | M | ||
| VH | L | M | H | VB | VL | L | L | H | M | ||
| M | M | M | H | H | VL | M | H | H | H | ||
| M | M | M | M | M | M | M | M | M | M | ||
| VH | VL | M | VH | VH | VL | VL | M | VH | VL | ||
| M | H | M | H | VB | L | H | L | H | M | ||
| VH | VL | L | H | VB | L | L | L | L | L | ||
| —Heat from megastructures | H | H | H | H | H | M | L | H | VL | M | |
| H | M | L | VH | H | H | VL | H | L | L | ||
| H | H | H | H | H | VH | VH | VH | VL | H | ||
| H | L | M | VH | VH | H | VL | VH | L | H | ||
| L | M | L | L | H | H | VL | L | M | L | ||
| M | M | M | M | VH | L | L | M | H | M | ||
| M | M | M | M | M | M | M | M | M | M | ||
| VL | VH | M | VL | M | VH | VH | M | VL | M | ||
| VH | M | H | H | VH | L | M | VH | H | L | ||
| M | M | L | M | VH | M | H | L | L | VH | ||
| —Radio signals | VH | L | H | VH | B | L | H | M | H | H | |
| VH | L | H | VH | VB | VL | VL | M | VH | VL | ||
| VH | L | L | M | B | VL | M | L | VH | H | ||
| H | M | L | L | B | VL | H | L | VH | M | ||
| M | H | VL | M | VB | M | M | M | H | L | ||
| M | M | M | H | H | L | L | M | H | H | ||
| M | M | M | M | M | M | M | M | M | M | ||
| VH | VL | M | VH | VH | VL | VL | M | VH | VL | ||
| M | L | M | L | VB | M | H | VL | H | M | ||
| VH | VL | L | H | B | VL | VL | L | H | L | ||
| —Artifacts orbiting Earth, Moon, or the Sun | M | M | H | M | VH | VL | VH | VL | VH | M | |
| H | H | H | M | VH | L | H | VH | VH | H | ||
| H | M | H | M | H | L | H | L | VH | H | ||
| M | M | H | H | VH | VL | H | M | VH | H | ||
| VL | H | VH | L | M | M | VL | L | H | H | ||
| H | H | H | M | H | L | VH | L | VH | H | ||
| M | M | M | M | M | M | M | M | M | M | ||
| VL | VH | M | VL | M | VH | VH | M | VL | M | ||
| VH | VH | VH | VH | VH | VL | VH | H | VH | VL | ||
| L | M | L | L | VH | VL | VL | L | VH | H | ||
References
- Wright, J.T.; Sheikh, S.; Almár, I.; Denning, K.; Dick, S.; Tarter, J. Recommendations from the Ad Hoc Committee on SETI Nomenclature. arXiv 2018, arXiv:1809.06857. [Google Scholar]
- Cocconi, G.; Morrison, P. Searching for Interstellar Communications. Nature 1959, 184, 844–846. [Google Scholar] [CrossRef]
- Sheikh, S.; Berea, A.; Davis, R.; De la Torre, G.G.; DeMarines, J.; Fisher, T.; Foote, S.; Gelino, D.; Grinspoon, D.; Profitiliotis, G.; et al. Technosignatures as a Priority in Planetary Science: A White Paper for the Planetary Science Decadal Survey 2020. Bull. AAS 2021, 53, 7. [Google Scholar] [CrossRef]
- NASA Science Mission Directorate. Science 2020–2024: A Vision for Scientific Excellence. 2020. Available online: https://science.nasa.gov/about-us/science-strategy (accessed on 1 November 2023).
- Socas-Navarro, H.; Haqq-Misra, J.; Wright, J.T.; Kopparapu, R.; Benford, J.; Davis, R. Concepts for future missions to search for technosignatures. Acta Astronaut. 2021, 182, 446–453. [Google Scholar] [CrossRef]
- Wright, J.T. Searches for Technosignatures in Astronomy and Astrophysics. arXiv 2019, arXiv:1907.07831. [Google Scholar]
- Sheikh, S.Z. The Nine Axes of Merit for Technosignature Searches. Int. J. Astrobiol. 2020, 19, 237–243. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K. Fuzzy multiple criteria decision-making techniques and applications—Two decades review from 1994 to 2014. Expert Syst. Appl. 2015, 42, 4126–4148. [Google Scholar] [CrossRef]
- Tavana, M.; Khalili-Damghani, K.; Abtahi, A.R. A hybrid fuzzy group decision support framework for advanced-technology prioritization at NASA. Expert Syst. Appl. 2013, 40, 480–491. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; Fernández-Martínez, M.; Saucedo-Fernández, A.A.; Trigo-Rodriguez, J.M. Evaluation of NEA deflection techniques. A fuzzy Multi-Criteria Decision Making analysis for planetary defense. Acta Astronaut. 2020, 176, 383–397. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; Moya, A.; Rodríguez-Mozos, J.M. A fuzzy Multi-Criteria Decision Making approach for Exo-Planetary Habitability. Astron. Comput. 2021, 36, 100471. [Google Scholar] [CrossRef]
- Bazzocchi, M.C.F.; Sánchez-Lozano, J.M.; Hakima, H. Fuzzy multi-criteria decision-making approach to prioritization of space debris for removal. Adv. Space Res. 2021, 67, 1155–1173. [Google Scholar] [CrossRef]
- Tavana, M.; Heidary, M.S.; Mina, H. A fuzzy preference programming and weighted influence non-linear gauge system for mission architecture assessment at NASA. Appl. Soft Comput. 2023, 145, 110572. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw Hill International: New York, NY, USA, 1980. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Kaya, İ.; Çolak, M.; Terzi, F. Use of MCDM techniques for energy policy and decision-making problems: A review. Int. J. Energy Res. 2018, 42, 2344–2372. [Google Scholar] [CrossRef]
- Sotoudeh-Anvari, A. The applications of MCDM methods in COVID-19 pandemic: A state of the art review. Appl. Soft Comput. 2022, 126, 109238. [Google Scholar] [CrossRef] [PubMed]
- Chejarla, K.C.; Vaidya, O.S.; Kumar, S. MCDM applications in logistics performance evaluation: A literature review. J. Multi-Criteria Decis. Anal. 2022, 29, 274–297. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; Fernández-Martínez, M. Near-Earth object hazardous impact: A Multi-Criteria Decision Making approach. Sci. Rep. 2016, 6, 37055. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; Fernández-Martínez, M.; Lamata, M.T. Near-Earth Asteroid impact dates: A Reference Ideal Method (RIM) approach. Eng. Appl. Artif. Intell. 2019, 81, 157–168. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Pal, S.; Shiu, S. Foundations of Soft Case-Based Reasoning; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Gündogdu, F.K.; Kahraman, G. Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 2019, 36, 337–352. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean Membership Grades in Multicriteria Decision Making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Cuong, B.C. Picture fuzzy sets. J. Comput. Sci. Cybern. 2014, 30, 409. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Logic. Neutrosophy, Neutrosophic Set, Neutrosophic Probability and Statistics; InfoLearnQuest: Philadelphia, PA, USA, 2007. [Google Scholar]
- Zhuolin, L.; Zhen, Z.; Wenyu, Y. Consensus reaching with consistency control in group decision making with incomplete hesitant fuzzy linguistic preference relations. Comput. Ind. Eng. 2022, 170, 108311. [Google Scholar] [CrossRef]
- Wenyu, Y.; Zhen, Z.; Zhong, Q. Consensus reaching for MAGDM with multi-granular hesitant fuzzy linguistic term sets: A minimum adjustment-based approach. Ann. Oper. Res. 2021, 300, 443–466. [Google Scholar] [CrossRef]
- Zhen, Z.; Xinyue, K.; Wenyu, Y.; Yuan, G. Consistency improvement for fuzzy preference relations with self-confidence: An application in two-sided matching decision making. J. Oper. Res. Soc. 2021, 72, 1914–1927. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; Fernández-Martínez, M. Assessment of Near-Earth Asteroid Deflection Techniques via Spherical Fuzzy Sets. Adv. Astron. 2021, 2021, 6678056. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; García-Cascales, M.S.; Lamata, M.T. GIS-based onshore wind farm site selection using Fuzzy Multi-Criteria Decision Making methods. Evaluating the case of Southeastern Spain. Appl. Energy 2016, 171, 86–102. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; Correa-Rubio, J.C.; Fernández-Martínez, M. A double fuzzy multi-criteria analysis to evaluate international high-performance aircrafts for defense purposes. Eng. Appl. Artif. Intell. 2022, 115, 105339. [Google Scholar] [CrossRef]
- Saaty, T.L. Fundamentals of Decision Making and Priority Theory with the AHP; RWS Publisher: Pittsburgh, PA, USA, 1994. [Google Scholar]
- García Cascales, M.S.; Lamata, M.T.; Sánchez-Lozano, J.M. Evaluation of photovoltaic cells in a multi-criteria decision making process. Ann. Oper. Res. 2012, 199, 373–391. [Google Scholar] [CrossRef]
- Triantaphyllou, E. Multi-Criteria Decision Making: A Comparative Study; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- García Cascales, M.S.; Lamata, M.T. A modification to the index of Liou and Wang for ranking fuzzy number. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2007, 4, 411–424. [Google Scholar] [CrossRef]
- Zadeh, L.; Kacprzyt, J. Computing with Words in Information/Intelligent Systems. Part 1; Physica-Verlag (Springer): Berlin/Heidelberg, Germany; New York, NY, USA, 1999. [Google Scholar]

| Labels | Verbal Judgments of Preferences | Triangular Fuzzy Scale |
|---|---|---|
| EqI | and are Equally Important | (1, 1, 1) |
| Sl + I | is Slightly More Important than | (2, 3, 4) |
| +I | is More Important than | (4, 5, 6) |
| St + I | is Strongly More Important than | (6, 7, 8) |
| Ex + I | is Extremely More Important than | (8, 9, 9) |
| MCDM | ||||
|---|---|---|---|---|
| … | ||||
| … | ||||
| … | … | … | … | |
| … |
| Expert | Reported Order of Importance |
|---|---|
| Criteria | Paired Comparisons | Triangular Fuzzy Numbers |
|---|---|---|
| (1, 1, 1) | (0.193, 0.337, 0.547) | |
| (1/4, 1/3, 1/2) | (0.052, 0.112, 0.255) | |
| (1/4, 1/3, 1/2) | (0.052, 0.112, 0.255) | |
| (1/4, 1/3, 1/2) | (0.052, 0.112, 0.255) | |
| (1/6, 1/5, 1/4) | (0.034, 0.067, 0.131) | |
| (1/6, 1/5, 1/4) | (0.034, 0.067, 0.131) | |
| (1/6, 1/5, 1/4) | (0.034, 0.067, 0.131) | |
| (1/8, 1/7, 1/6) | (0.025, 0.048, 0.089) | |
| (1/9, 1/9, 1/8) | (0.022, 0.037, 0.068) | |
| (1/9, 1/9, 1/8) | (0.022, 0.037, 0.068) |
| Criteria | Weights (Fuzzy Numbers) | Weights (%) |
|---|---|---|
| —Observing Capability | (0.124, 0.188, 0.281) | 18.82 |
| —Cost | (0.036, 0.058, 0.100) | 5.83 |
| —Ancillary Benefits | (0.034, 0.053, 0.085) | 5.26 |
| —Detectability | (0.149, 0.219, 0.327) | 21.88 |
| —Duration | (0.077, 0.112, 0.163) | 11.24 |
| —Ambiguity | (0.052, 0.079, 0.123) | 7.85 |
| —Extrapolation | (0.032, 0.049, 0.077) | 4.93 |
| —Inevitability | (0.052, 0.082, 0.132) | 8.19 |
| —Information | (0.078, 0.108, 0.152) | 10.82 |
| —Scale Sensitivity | (0.033, 0.052, 0.084) | 5.18 |
| Linguistic Label | Linguistic Label | Fuzzy Numbers |
|---|---|---|
| Very low (VL) | Very brief (VB) | (0, 1, 3) |
| Low (L) | Brief (B) | (1, 3, 5) |
| Medium (M) | Medium (M) | (3, 5, 7) |
| High (H) | High (H) | (5, 7, 9) |
| Very high (VH) | Very high (VH) | (7, 9, 10) |
| Alternatives | Criteria | ||||
|---|---|---|---|---|---|
| —Radio and optical communications | (5.8, 7.8, 9.1) 1st | (1.5, 3.2, 5.2) 1st | (3.5, 5.4, 7.3) 3rd | (3.7, 5.6, 7.3) 2nd | (5.4, 7.4, 8.8) 2nd |
| —Waste heat | (4.6, 6.6, 8.4) 2nd | (3.2, 5.2, 7.2) 2nd | (4.0, 6.0, 7.9) 2nd | (3.8, 5.8, 7.7) 3rd | (5.8, 7.8, 9.3) 1st |
| —Solar System artefacts | (3.5, 5.4, 7.3) 3rd | (4.6, 6.6, 8.4) 3rd | (5.2, 7.2, 8.8) 1st | (2.6, 4.4, 6.3) 1st | (5.0, 7.0, 8.6) 3rd |
| —Radio and optical communications | (2.0, 3.6, 5.6) 1st | (2.0, 3.6, 5.5) 1st | (3.5, 5.4, 7.1) 2nd | (5.2, 7.2, 8.8) 2nd | (3.7, 5.6, 7.4) 3rd |
| —Waste heat | (4.4, 6.4, 8.1) 3rd | (3.4, 5.2, 7.0) 2nd | (5.2, 7.2, 8.8) 1st | (2.6, 4.4, 6.3) 3rd | (5.4, 7.4, 9.0) 1st |
| —Solar System artefacts | (2.4, 4.0, 5.9) 2nd | (5.4, 7.4, 9.0) 3rd | (1.3, 3.0, 5.0) 3rd | (6.0, 8.0, 9.3) 1st | (3.9, 5.8, 7.5) 2nd |
| Alternatives | Criteria | ||||
|---|---|---|---|---|---|
| —Industrial gases on atmospheric spectra | (3.2, 5.0, 6.9) 4th | (4.1, 6.0, 7.8) 6th | (4.4, 6.4, 8.2) 2nd | (3.1, 5.0, 7.0) 5th | (4.8, 6.8, 8.5) 5th |
| —Dark side illumination | (1.2, 2.8, 4.8) 8th | (4.7, 6.6, 8.2) 8th | (2.6, 4.4, 6.4) 7th | (1.6, 3.4, 5.4) 1st | (4.4, 6.4, 8.1) 7th |
| —Starshades in transit | (2.5, 4.4, 6.4) 6th | (3.8, 5.6, 7.3) 4th | (2.9, 4.8, 6.8) 5th | (2.3, 4.2, 6.2) 3rd | (4.2, 6.2, 7.9) 8th |
| —Clarke exobelt in transit | (2.0, 3.8, 5.8) 7th | (3.6, 5.4, 7.2) 3rd | (3.1, 5.0, 7.0) 3rd | (1.8, 3.6, 5.6) 2nd | (4.6, 6.6, 8.3) 6th |
| .-Laser pulses | (4.8, 6.8, 8.4) 2nd | (1.7, 3.4, 5.4) 1st | (2.8, 4.8, 6.8) 6th | (4.5, 6.4, 8.2) 8th | (6.4, 8.4, 9.6) 1st |
| —Heat from megastructures | (3.7, 5.6, 7.5) 3rd | (3.6, 5.6, 7.5) 4th | (3.0, 5.0, 7.0) 4th | (3.9, 5.8, 7.6) 6th | (5.4, 7.4, 9.0) 3rd |
| —Radio signals | (5.2, 7.2, 8.7) 1st | (1.8, 3.6, 5.6) 2nd | (2.5, 4.4, 6.4) 8th | (4.2, 6.2, 7.9) 7th | (6.4, 8.4, 9.6) 1st |
| —Artifacts orbiting Earth, Moon, or the Sun | (3.2, 5.0, 6.9) 4th | (4.4, 6.4, 8.2) 7th | (4.6, 6.6, 8.4) 1st | (2.9, 4.8, 6.7) 4th | (5.4, 7.4, 8.9) 4th |
| —Industrial gases on atmospheric spectra | (3.8, 5.8, 7.6) 4th | (3.4, 5.2, 7.0) 4th | (3.8, 5.8, 7.8) 2nd | (2.0, 3.8, 5.7) 7th | (3.2, 5.2, 7.2) 4th |
| —Dark side illumination | (4.4, 6.4, 8.1) 8th | (3.6, 5.4, 7.2) 5th | (2.8, 4.8, 6.8) 3rd | (2.3, 4.2, 6.2) 5th | (3.2, 5.2, 7.0) 6th |
| —Starshades in transit | (4.0, 6.0, 7.9) 7th | (4.0, 6.0, 7.8) 7th | (1.9, 3.6, 5.6) 8th | (2.3, 4.2, 6.1) 6th | (3.4, 5.4, 7.3) 3rd |
| —Clarke exobelt in transit | (3.9, 5.8, 7.6) 5th | (3.7, 5.6, 7.4) 6th | (2.6, 4.6, 6.6) 4th | (2.5, 4.4, 6.3) 4th | (3.6, 5.6, 7.4) 2nd |
| —Laser pulses | (0.6, 2.0, 4.0) 1st | (2.5, 4.4, 6.4) 2nd | (2.4, 4.4, 6.4) 6th | (5.0, 7.0, 8.7) 3rd | (2.9, 4.8, 6.8) 7th |
| —Heat from megastructures | (4.0, 6.0, 7.8) 6th | (2.7, 4.4, 6.2) 2nd | (4.2, 6.2, 7.9) 1st | (1.9, 3.6, 5.6) 8th | (3.2, 5.2, 7.1) 5th |
| —Radio signals | (1.1, 2.6, 4.6) 2nd | (2.5, 4.2, 6.2) 1st | (2.1, 4.0, 6.0) 7th | (5.6, 7.6, 9.2) 1st | (2.6, 4.4, 6.4) 8th |
| —Artifacts orbiting Earth, Moon, or the Sun | (1.6, 3.2, 5.1) 3rd | (4.6, 6.4, 8.0) 8th | (2.5, 4.4, 6.3) 5th | (5.7, 7.6, 8.9) 2nd | (3.9, 5.8, 7.8) 1st |
| Alternatives | Fuzzy Numbers | Defuzzification Process | Ranking |
|---|---|---|---|
| —Radio and optical communications | (0.156, 0.645, 2.660) | 0.900 | 1st |
| —Waste heat | (0.097, 0.430, 1.921) | 0.623 | 3rd |
| —Solar System artefacts | (0.110, 0.462, 1.984) | 0.657 | 2nd |
| Alternatives | Fuzzy Numbers | Defuzz. Process | Ranking |
|---|---|---|---|
| —Industrial gases on atmospheric spectra | (0.093, 0.428, 2.003) | 0.635 | 5th |
| —Dark side illumination | (0.093, 0.408, 1.917) | 0.607 | 8th |
| —Starshades in transit | (0.096, 0.423, 1.928) | 0.619 | 7th |
| —Clarke exobelt in transit | (0.103, 0.454, 2.100) | 0.670 | 4th |
| —Laser pulses | (0.123, 0.569, 2.503) | 0.817 | 2nd |
| —Heat from megastructures | (0.088, 0.424, 2.025) | 0.635 | 6th |
| —Radio signals | (0.134, 0.597, 2.600) | 0.854 | 1st |
| —Artifacts orbiting Earth, Moon, or the Sun | (0.131, 0.560, 2.468) | 0.806 | 3rd |
| Alternatives | Weights by Experts Group | Criteria with Same Weights | ||
|---|---|---|---|---|
| Defuzz. Process | Ranking | Defuzz. Process | Ranking | |
| —Radio and optical communications | 0.8995 | 1st | 0.7429 | 1st |
| —Waste heat | 0.6229 | 3rd | 0.5300 | 2nd |
| —Solar System artefacts | 0.6573 | 2nd | 0.4152 | 3rd |
| Alternatives | Weights by Experts Group | Criteria with Same Weights | ||
|---|---|---|---|---|
| Defuzz. Process | Ranking | Defuzz. Process | Ranking | |
| —Industrial gases on atmospheric spectra | 0.6347 | 5th | 0.4396 | 5th |
| —Dark side illumination | 0.6068 | 8th | 0.3339 | 7th |
| —Starshades in transit | 0.6192 | 7th | 0.3268 | 8th |
| —Clarke exobelt in transit | 0.6698 | 4th | 0.3923 | 6th |
| —Laser pulses | 0.8169 | 2nd | 0.7012 | 1st |
| —Heat from megastructures | 0.6347 | 6th | 0.4478 | 4th |
| —Radio signals | 0.8535 | 1st | 0.6825 | 2nd |
| —Artifacts orbiting Earth, Moon, or the Sun | 0.8064 | 3rd | 0.6039 | 3rd |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Lozano, J.M.; Peña-Asensio, E.; Socas-Navarro, H. Deciding Technosignature Search Strategies: Multi-Criteria Fuzzy Logic to Find Extraterrestrial Intelligence. Aerospace 2024, 11, 88. https://doi.org/10.3390/aerospace11010088
Sánchez-Lozano JM, Peña-Asensio E, Socas-Navarro H. Deciding Technosignature Search Strategies: Multi-Criteria Fuzzy Logic to Find Extraterrestrial Intelligence. Aerospace. 2024; 11(1):88. https://doi.org/10.3390/aerospace11010088
Chicago/Turabian StyleSánchez-Lozano, Juan Miguel, Eloy Peña-Asensio, and Hector Socas-Navarro. 2024. "Deciding Technosignature Search Strategies: Multi-Criteria Fuzzy Logic to Find Extraterrestrial Intelligence" Aerospace 11, no. 1: 88. https://doi.org/10.3390/aerospace11010088
APA StyleSánchez-Lozano, J. M., Peña-Asensio, E., & Socas-Navarro, H. (2024). Deciding Technosignature Search Strategies: Multi-Criteria Fuzzy Logic to Find Extraterrestrial Intelligence. Aerospace, 11(1), 88. https://doi.org/10.3390/aerospace11010088






