Clustering and Cooperative Guidance of Multiple Decoys for Defending a Naval Platform against Salvo Threats
Abstract
1. Introduction
2. Problem Definition and Systems Modeling
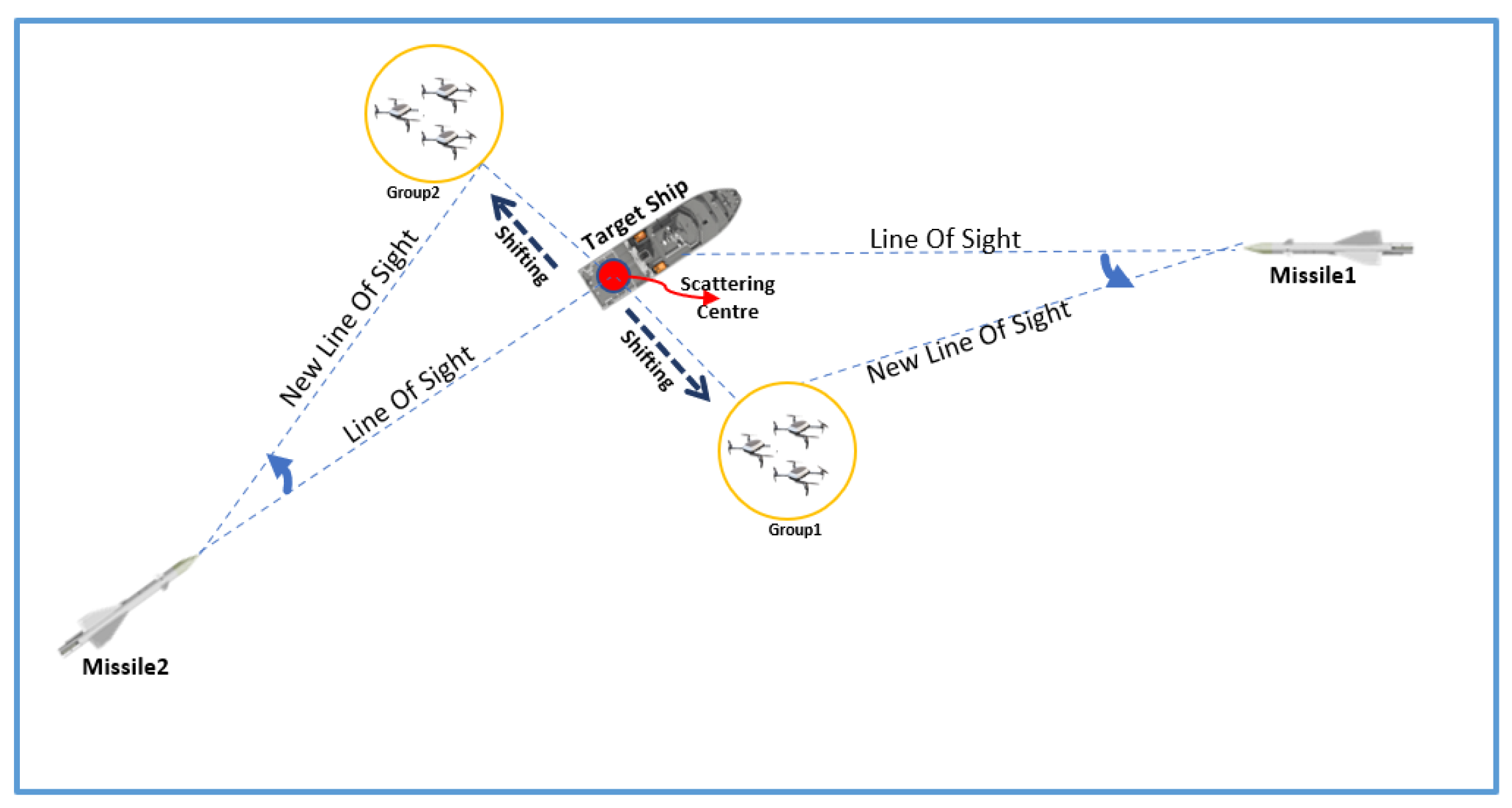
2.1. Problem Definition
2.2. Systems Modeling
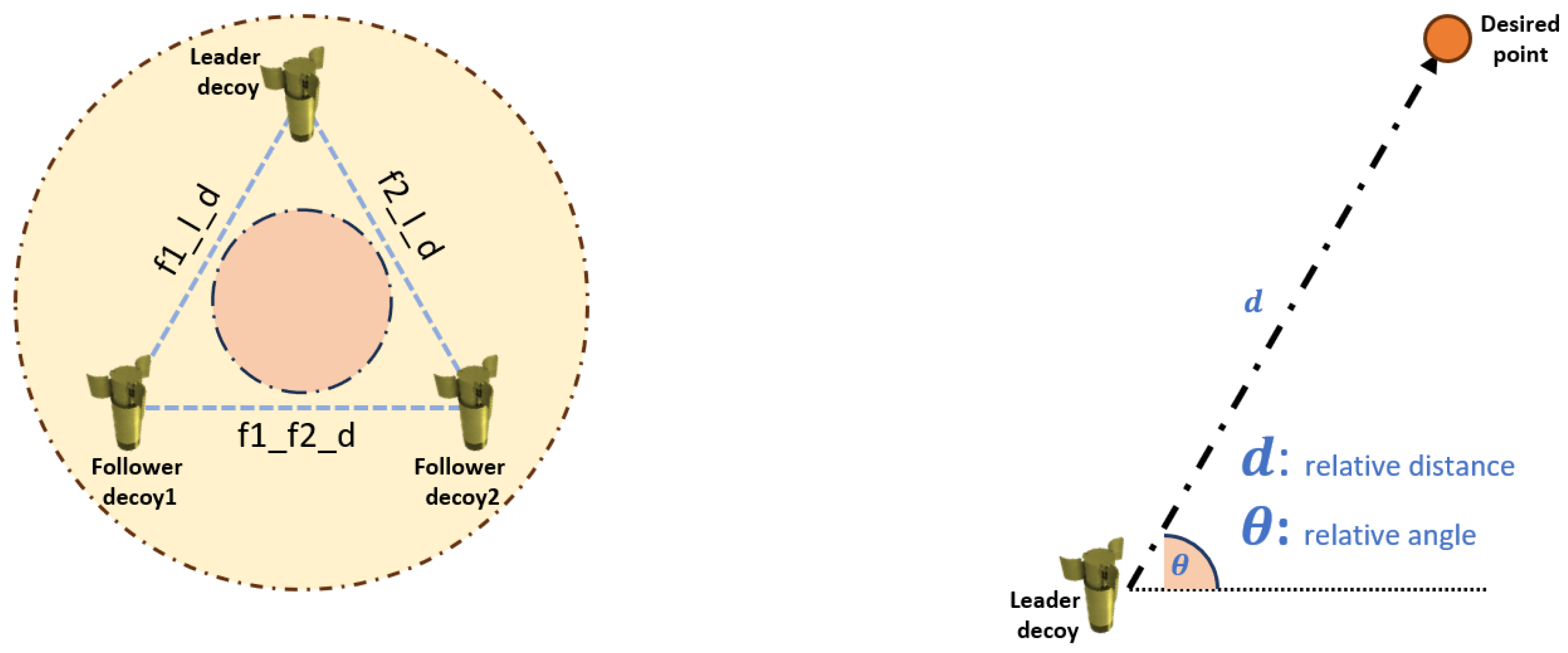
2.2.1. Decoy Modeling
2.2.2. Target Model
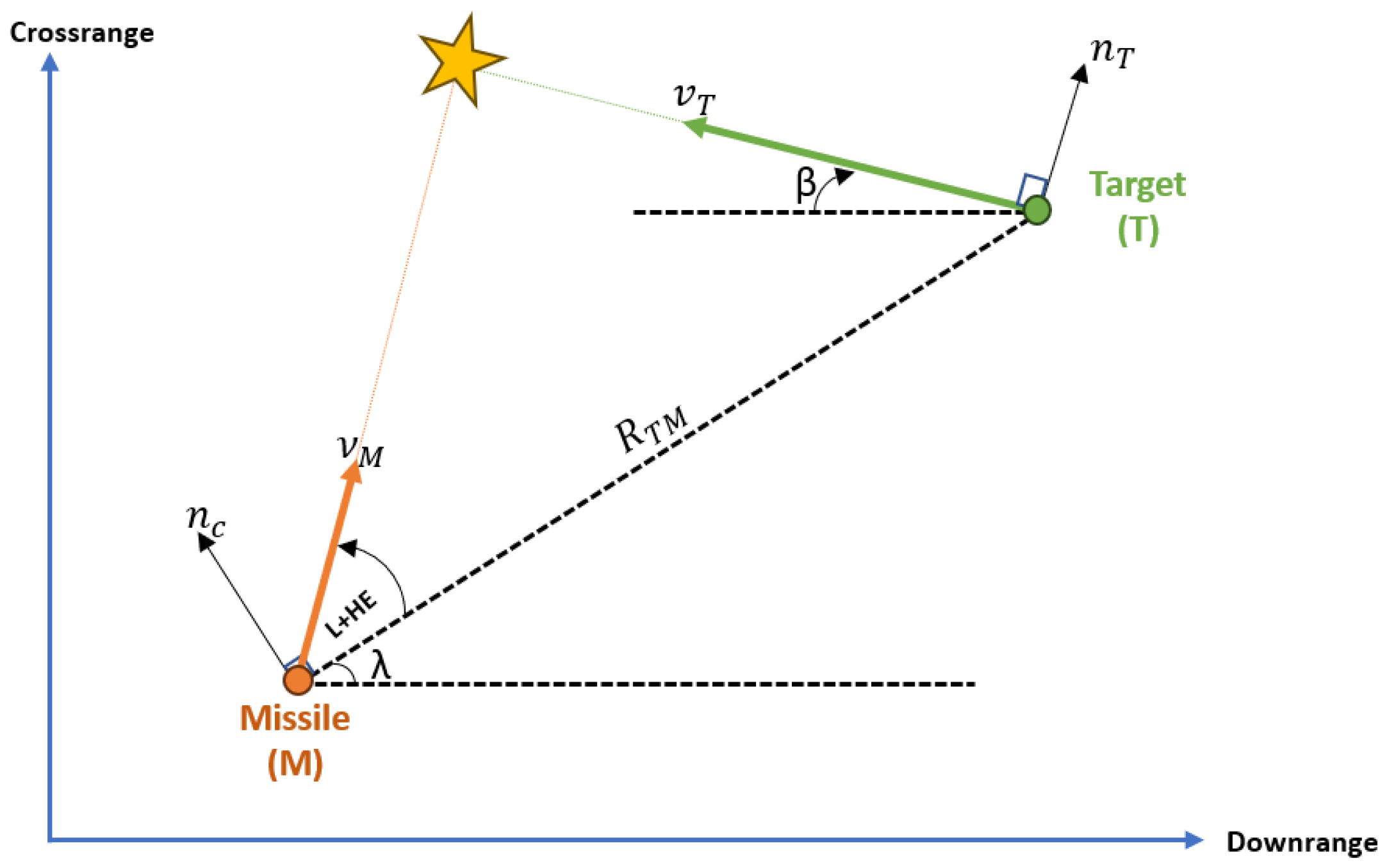
2.2.3. Missile Model
3. Multi-Agent Reinforcement Learning (MARL)
3.1. Multi-Agent Deep Deterministic Policy Gradient (MADDPG)
3.2. Multi-Agent Twin-Delayed Deep Deterministic Policy Gradient (MATD3)
| Algorithm 1 MATD3 |
| Initialize replay buffer D and network parameters for t = 1 to Tmax do Select actions Execute actions and observe Store transition in D x ← x′ for agent i to N do Sample a random minibatch of S samples from D Minimize Q-function loss for both critics if t mod d = 0 then Update policy with gradient Update target networks |
| end for end for |
4. Environmental Setup
4.1. Observation Space and Action Space
4.2. Reward Formulation
5. Discussion and Analysis
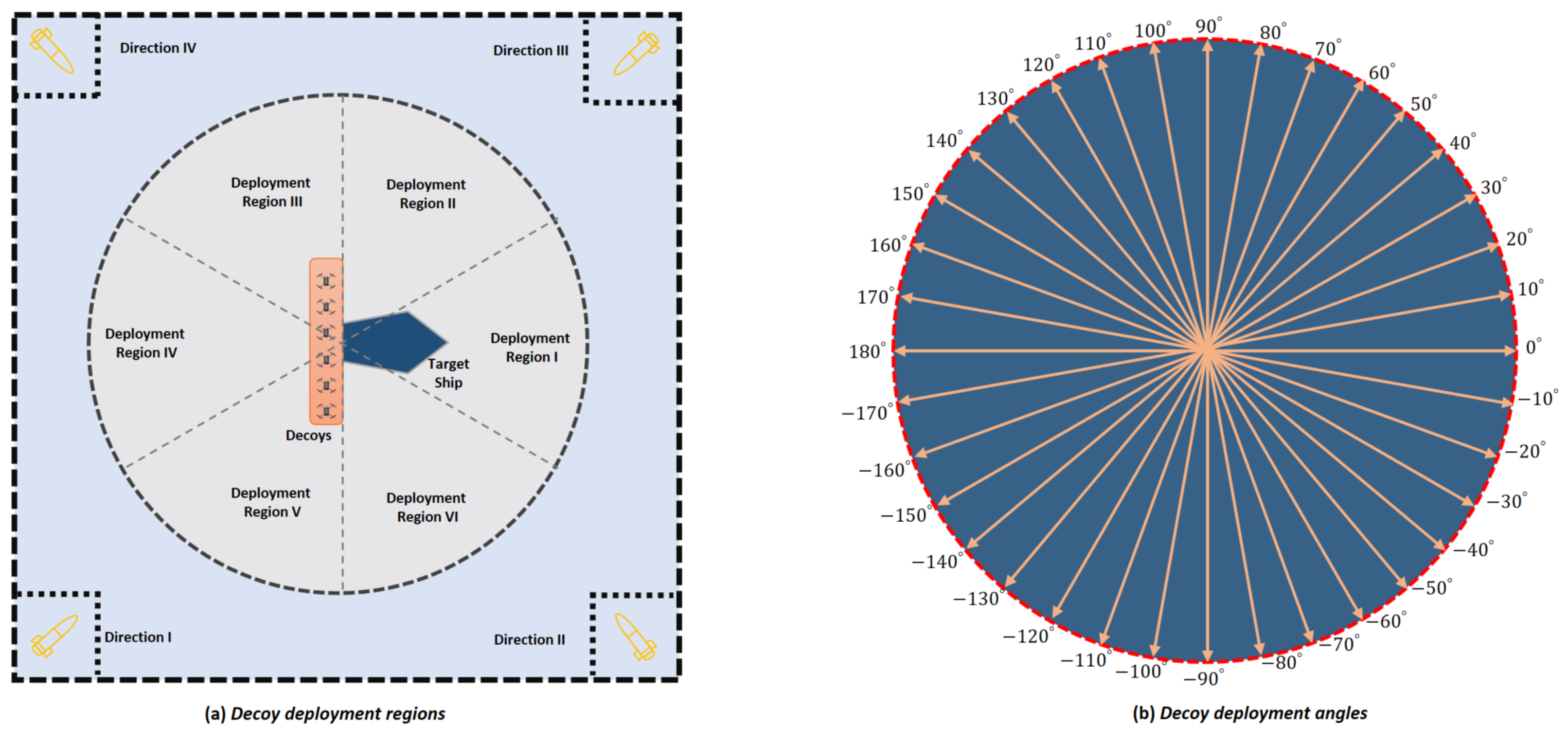
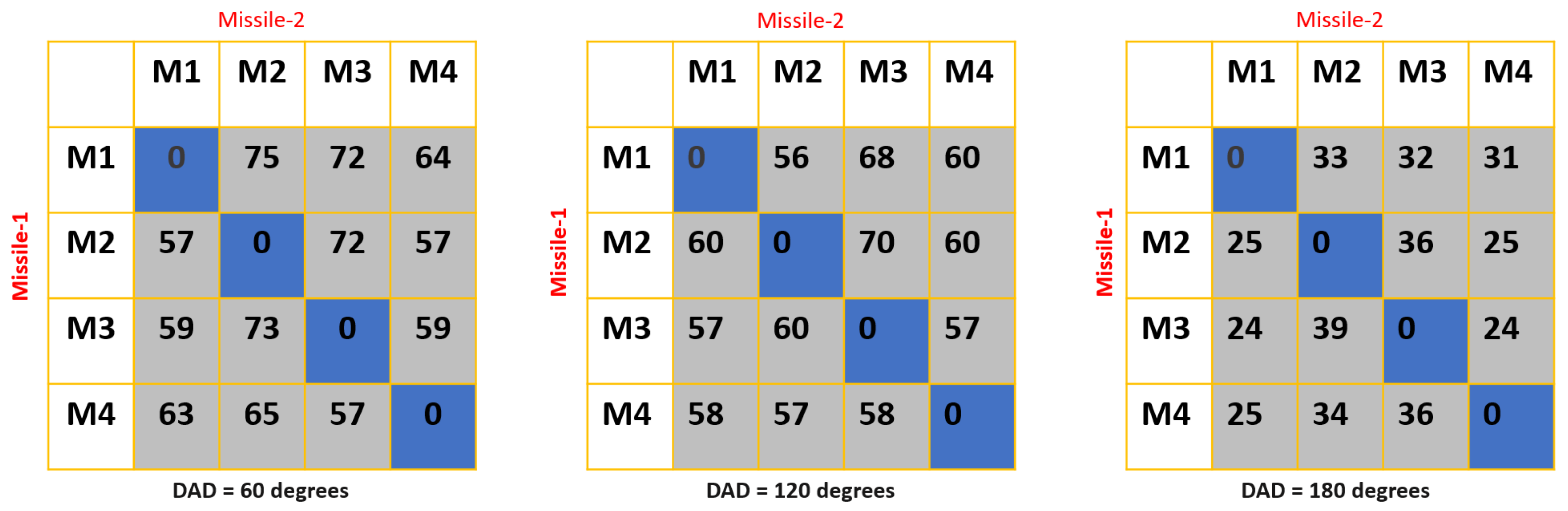
5.1. An Assessment Based on Missile Launch Directions and Varied Decoy Deployment Regions
5.2. An Evaluation of the Effectiveness of the Decoy Deployment Strategy with Respect to the Maximum Speed of the Decoys and the Missile Speed
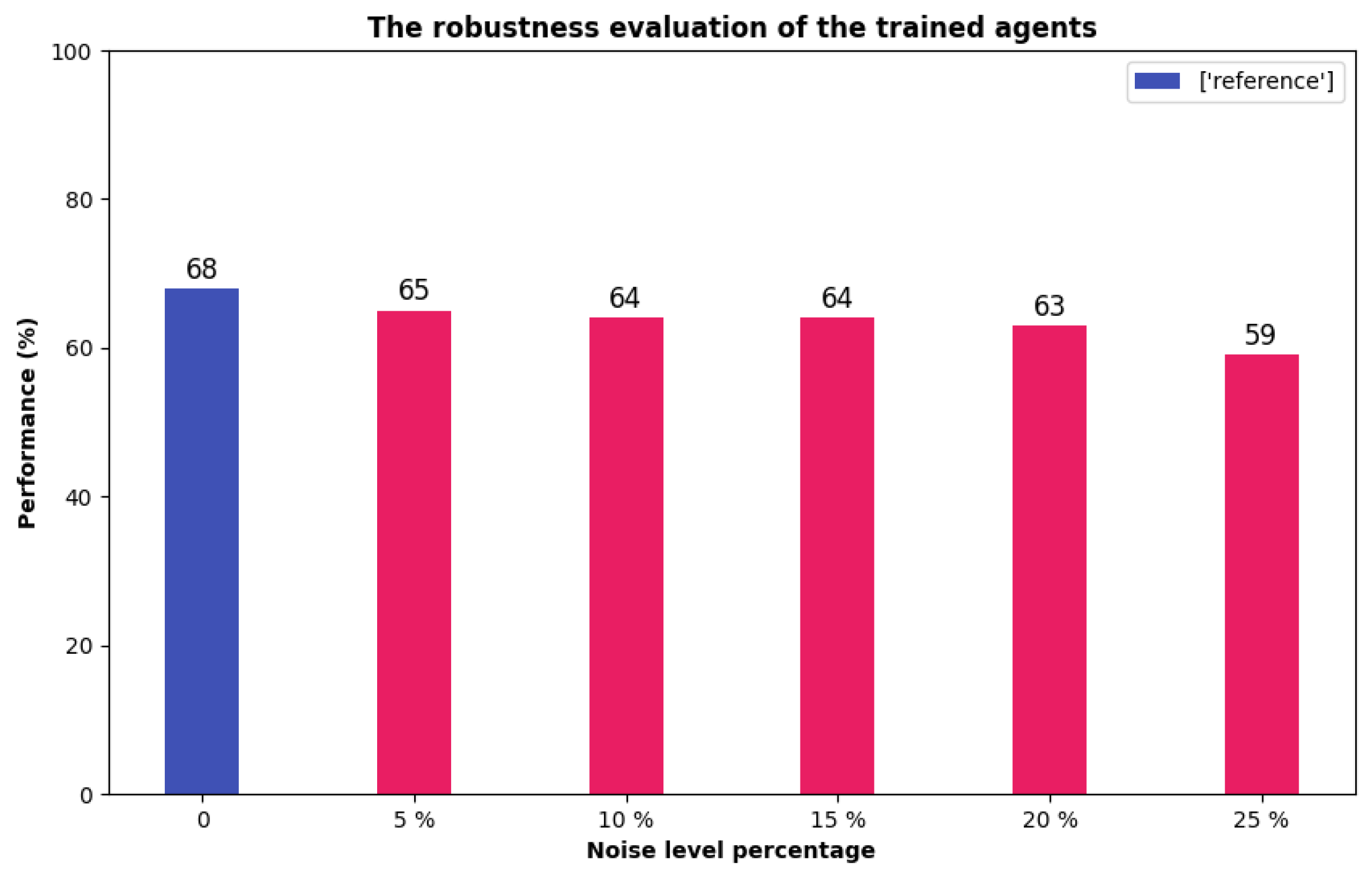
5.3. Robustness Evaluation of Trained Decoys under Noisy Conditions
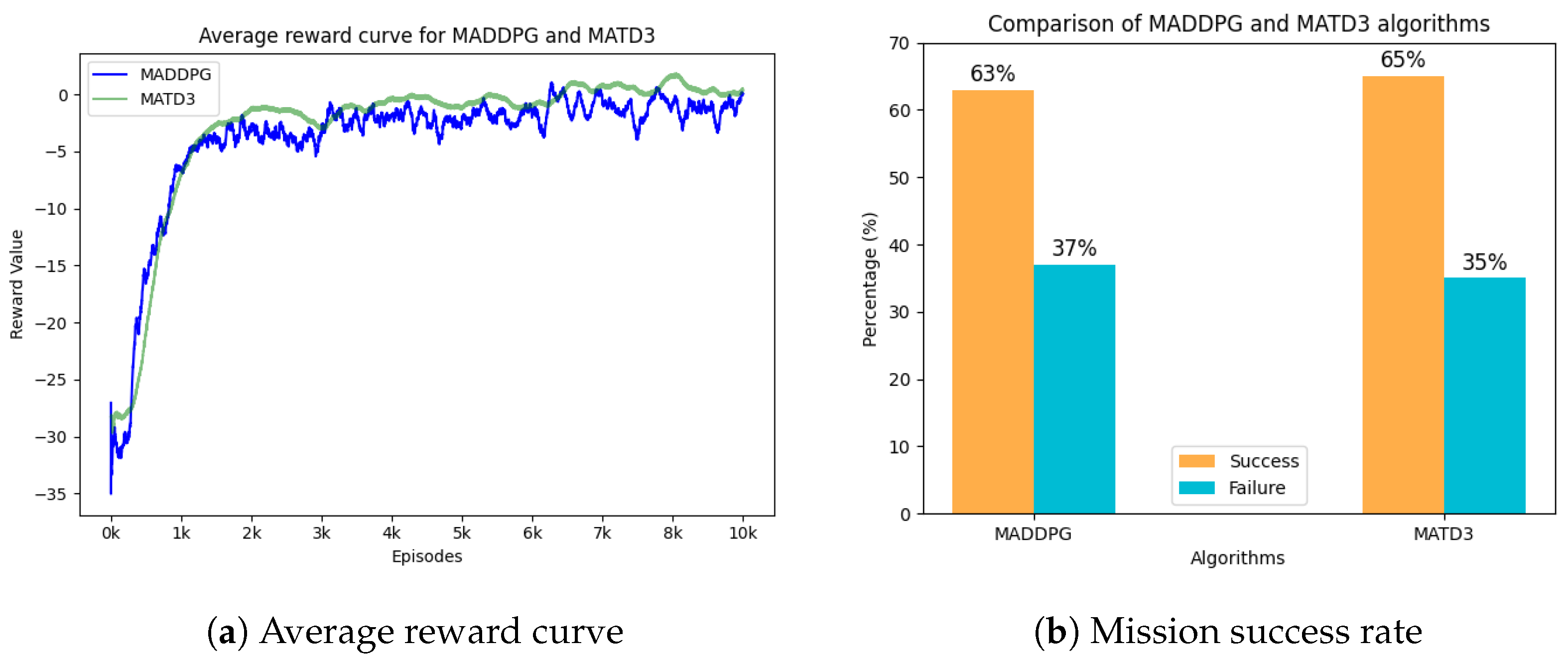
5.4. Comparisons of MADDPG and MATD3 Algorithms
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roome, S. Digital radio frequency memory. Electron. Commun. Eng. J. 1990, 2, 147–153. [Google Scholar] [CrossRef]
- Kwak, C. Application of DRFM in ECM for pulse type radar. In Proceedings of the 2009 34th International Conference on Infrared, Millimeter, and Terahertz Waves, Busan, Republic of Korea, 21–25 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–2. [Google Scholar]
- Davidson, K.; Bray, J. Understanding digital radio frequency memory performance in countermeasure design. Appl. Sci. 2020, 10, 4123. [Google Scholar] [CrossRef]
- Javed, H.; Khalid, M.R. A novel strategy to compensate the effects of platform motion on a moving DRFM jammer. In Proceedings of the 2021 International Bhurban Conference on Applied Sciences and Technologies (IBCAST), Islamabad, Pakistan, 12–16 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 956–960. [Google Scholar]
- Mears, M.J. Cooperative electronic attack using unmanned air vehicles. In Proceedings of the 2005, American Control Conference, Portland, OR, USA, 8–10 June 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 3339–3347. [Google Scholar]
- Mears, M.J.; Akella, M.R. Deception of radar systems using cooperatively controlled unmanned air vehicles. In Proceedings of the 2005 IEEE Networking, Sensing and Control, Tucson, AZ, USA, 19–22 March 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 332–335. [Google Scholar]
- Ilaya, O.; Bil, C.; Evans, M. Distributed and cooperative decision making for multi-UAV systems with applications to collaborative electronic warfare. In Proceedings of the 7th AIAA ATIO Conf, 2nd CEIAT Int’l Conf on Innov and Integr in Aero Sciences, 17th LTA Systems Tech Conf, Belfast, Northern Ireland, 18–20 September 2007; Followed by 2nd TEOS Forum. p. 7885. [Google Scholar]
- Akhil, K.; Ghose, D.; Rao, S.K. Optimizing deployment of multiple decoys to enhance ship survivability. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1812–1817. [Google Scholar]
- Vermeulen, A.; Maes, G. Missile avoidance maneuvres with simultaneous decoy deployment. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; p. 6277. [Google Scholar]
- Chen, Y.M.; Wu, W.Y. Cooperative electronic attack for groups of unmanned air vehicles based on multi-agent simulation and evaluation. Int. J. Comput. Sci. Issues 2012, 9, 1. [Google Scholar]
- Kwon, S.J.; Seo, K.M.; Kim, B.s.; Kim, T.G. Effectiveness analysis of anti-torpedo warfare simulation for evaluating mix strategies of decoys and jammers. In Proceedings of the Advanced Methods, Techniques, and Applications in Modeling and Simulation: Asia Simulation Conference 2011, Seoul, Republic of Korea, 16–18 November 2011; Proceedings. Springer: Berlin/Heidelberg, Germany, 2012; pp. 385–393. [Google Scholar]
- Jeong, J.; Yu, B.; Kim, T.; Kim, S.; Suk, J.; Oh, H. Maritime application of ducted-fan flight array system: Decoy for anti-ship missile. In Proceedings of the 2017 Workshop on Research, Education and Development of Unmanned Aerial Systems (RED-UAS), Linköping, Sweden, 3–5 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 72–77. [Google Scholar]
- Shames, I.; Dostovalova, A.; Kim, J.; Hmam, H. Task allocation and motion control for threat-seduction decoys. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, Australia, 12–15 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 4509–4514. [Google Scholar]
- Dileep, M.; Yu, B.; Kim, S.; Oh, H. Task assignment for deploying unmanned aircraft as decoys. Int. J. Control. Autom. Syst. 2020, 18, 3204–3217. [Google Scholar] [CrossRef]
- Jiang, D.; Zhang, Y.; Xie, D. Research on cooperative radar jamming effectiveness based on drone cluster. In Proceedings of the International Conference on Electronic Information Technology (EIT 2022), Chengdu, China, 18–20 March 2022; SPIE: Bellingham, DC, USA, 2022; Volume 12254, pp. 339–344. [Google Scholar]
- Conte, C.; Verini Supplizi, S.; de Alteriis, G.; Mele, A.; Rufino, G.; Accardo, D. Using drone swarms as a countermeasure of radar detection. J. Aerosp. Inf. Syst. 2023, 20, 70–80. [Google Scholar] [CrossRef]
- Bildik, E.; Yuksek, B.; Tsourdos, A.; Inalhan, G. Development of Active Decoy Guidance Policy by Utilising Multi-Agent Reinforcement Learning. In Proceedings of the AIAA SCITECH 2023 Forum, Online, 23–27 January 2023; p. 2668. [Google Scholar]
- Kim, K. Engagement-Scenario-Based Decoy-Effect Simulation Against an Anti-ship Missile Considering Radar Cross Section and Evasive Maneuvers of Naval Ships. J. Ocean. Eng. Technol. 2021, 35, 238–246. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Ackermann, J.; Gabler, V.; Osa, T.; Sugiyama, M. Reducing overestimation bias in multi-agent domains using double centralized critics. arXiv 2019, arXiv:1910.01465. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; PMLR. pp. 1587–1596. [Google Scholar]



| Reward Coefficients | ||||||
|---|---|---|---|---|---|---|
| c1 | c2 | c3 | c4 | c5 | c6 | c7 |
| 0.1 | 10 | 1000 | 1 | 20 | 20 | 0.8 |
| Missile Speed (in Mach) | |||||
|---|---|---|---|---|---|
| Decoy Max Speed | 0.7 | 0.8 | 0.9 | 1 | 1.1 |
| 20 | 65 | 62 | 63 | 64 | 62 |
| 25 | 65 | 67 | 66 | 68 | 65 |
| 30 | 64 | 67 | 64 | 66 | 64 |
| 35 | 63 | 60 | 63 | 66 | 63 |
| 40 | 60 | 60 | 58 | 60 | 58 |
| Missile Speed (in Mach) | |||||
|---|---|---|---|---|---|
| Decoy Max Speed | 0.7 | 0.8 | 0.9 | 1 | 1.1 |
| 20 | 67 | 63 | 64 | 66 | 66 |
| 25 | 65 | 64 | 65 | 68 | 67 |
| 30 | 66 | 68 | 68 | 71 | 68 |
| 35 | 63 | 64 | 62 | 69 | 64 |
| 40 | 61 | 58 | 59 | 64 | 61 |
| Decoy Maximum Speed (m/s) | |||||
|---|---|---|---|---|---|
| 20 | 25 | 30 | 35 | 40 | |
| simulation sample time (st = 0.1 s) | 245 | 249 | 252 | 257 | 260 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bildik, E.; Tsourdos, A. Clustering and Cooperative Guidance of Multiple Decoys for Defending a Naval Platform against Salvo Threats. Aerospace 2024, 11, 799. https://doi.org/10.3390/aerospace11100799
Bildik E, Tsourdos A. Clustering and Cooperative Guidance of Multiple Decoys for Defending a Naval Platform against Salvo Threats. Aerospace. 2024; 11(10):799. https://doi.org/10.3390/aerospace11100799
Chicago/Turabian StyleBildik, Enver, and Antonios Tsourdos. 2024. "Clustering and Cooperative Guidance of Multiple Decoys for Defending a Naval Platform against Salvo Threats" Aerospace 11, no. 10: 799. https://doi.org/10.3390/aerospace11100799
APA StyleBildik, E., & Tsourdos, A. (2024). Clustering and Cooperative Guidance of Multiple Decoys for Defending a Naval Platform against Salvo Threats. Aerospace, 11(10), 799. https://doi.org/10.3390/aerospace11100799







