Study on Rain Absorption Performance and Flow Field of Transonic Compressor under Different Working Conditions
Abstract
:1. Introduction
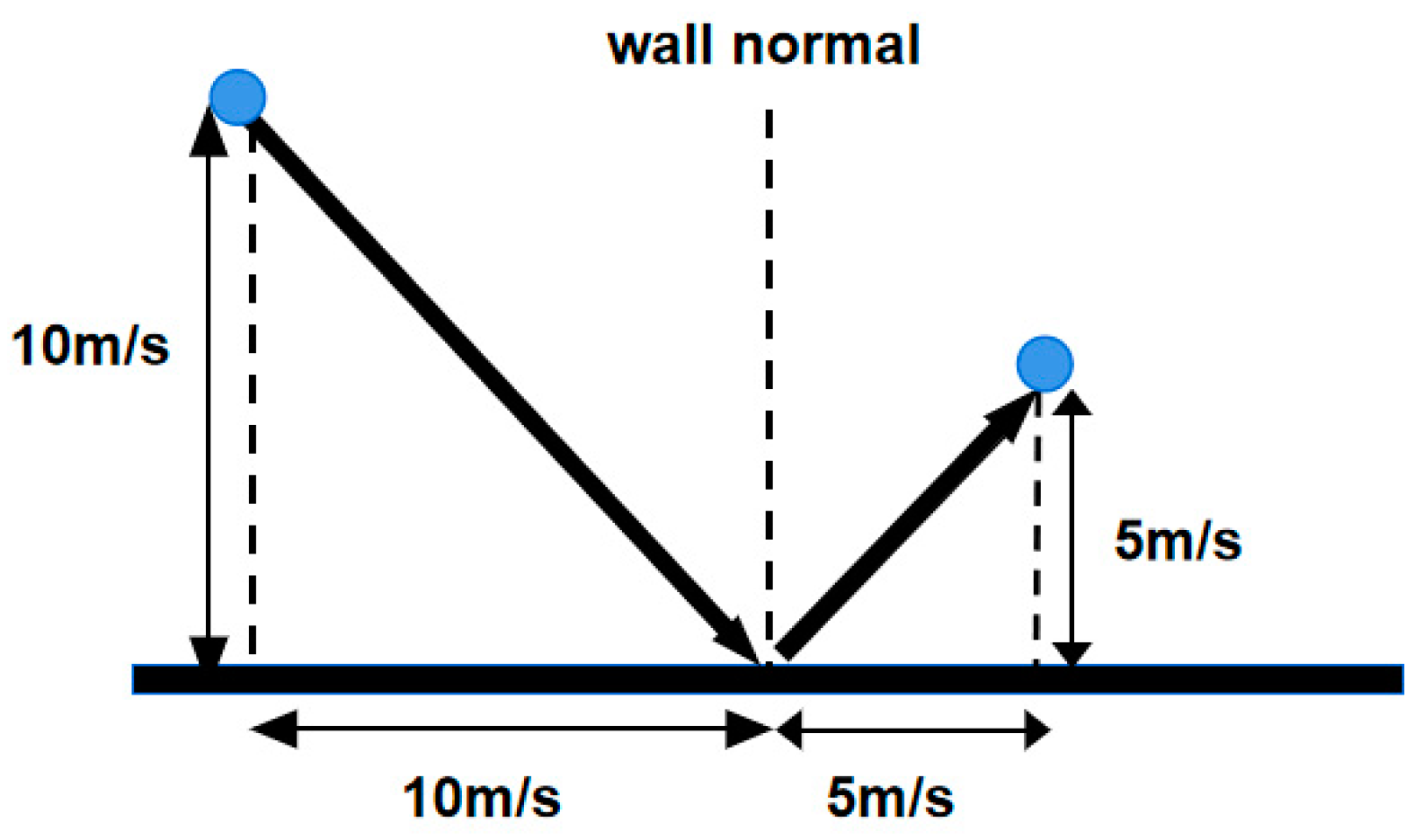
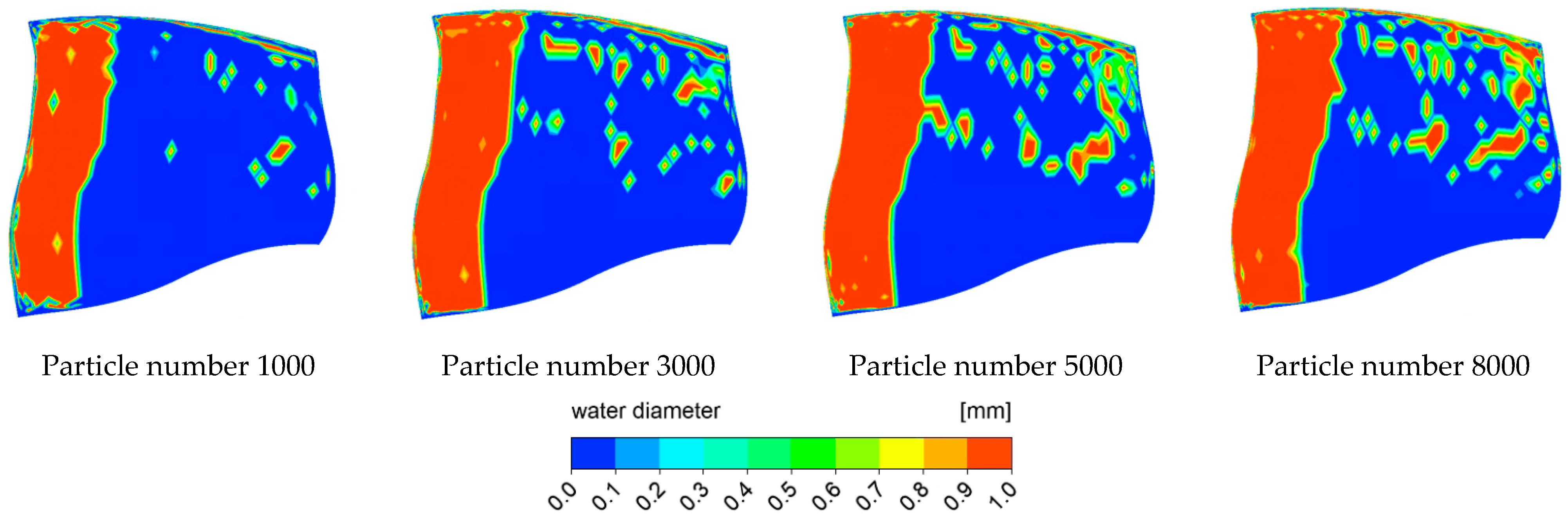
2. Physical Models and Grids
3. Results and Analysis
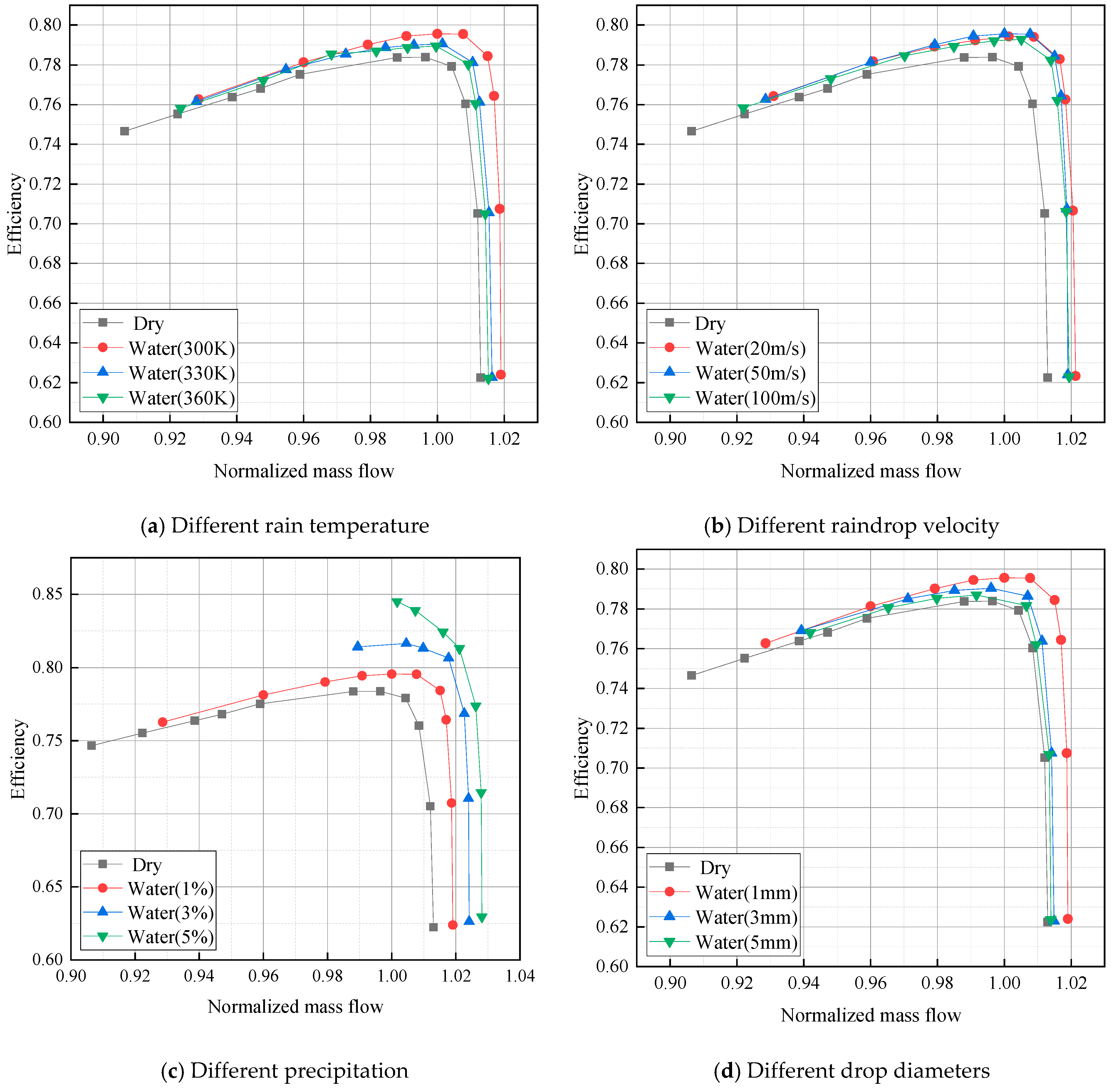
3.1. Overall Performance Analysis
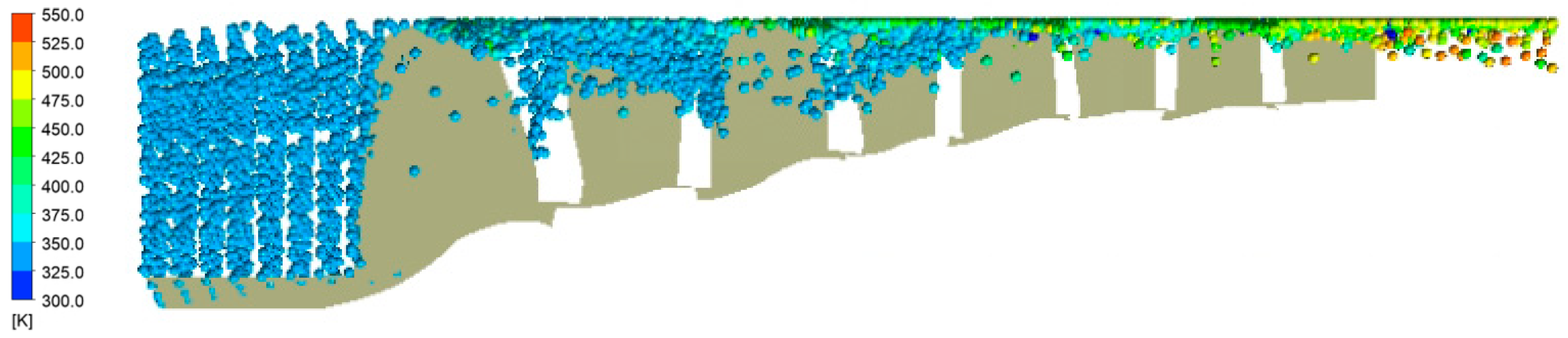
3.2. Flow Field Characteristic Analysis
4. Conclusions
- (1)
- After the compressor absorbs rain, it will increase the flow rate near the stall point and near the blocking point, reduce the stable working range, increase the total pressure ratio and efficiency of the compressor, and reduce the total temperature ratio of the compressor, which has the greatest impact on the performance of the factor of rainfall absorption when the design flow point is 1%, 3% and 5%. The overall pressure ratio of the compressor increased by 7.5%, 15% and 19.7%; the efficiency increased by 1.38%, 3.4% and 6.33%; the total temperature ratio decreased by 1.04%, 3.77% and 7.18%; and the stable working range decreased by 15%, 67.4% and 75.2%, respectively.
- (2)
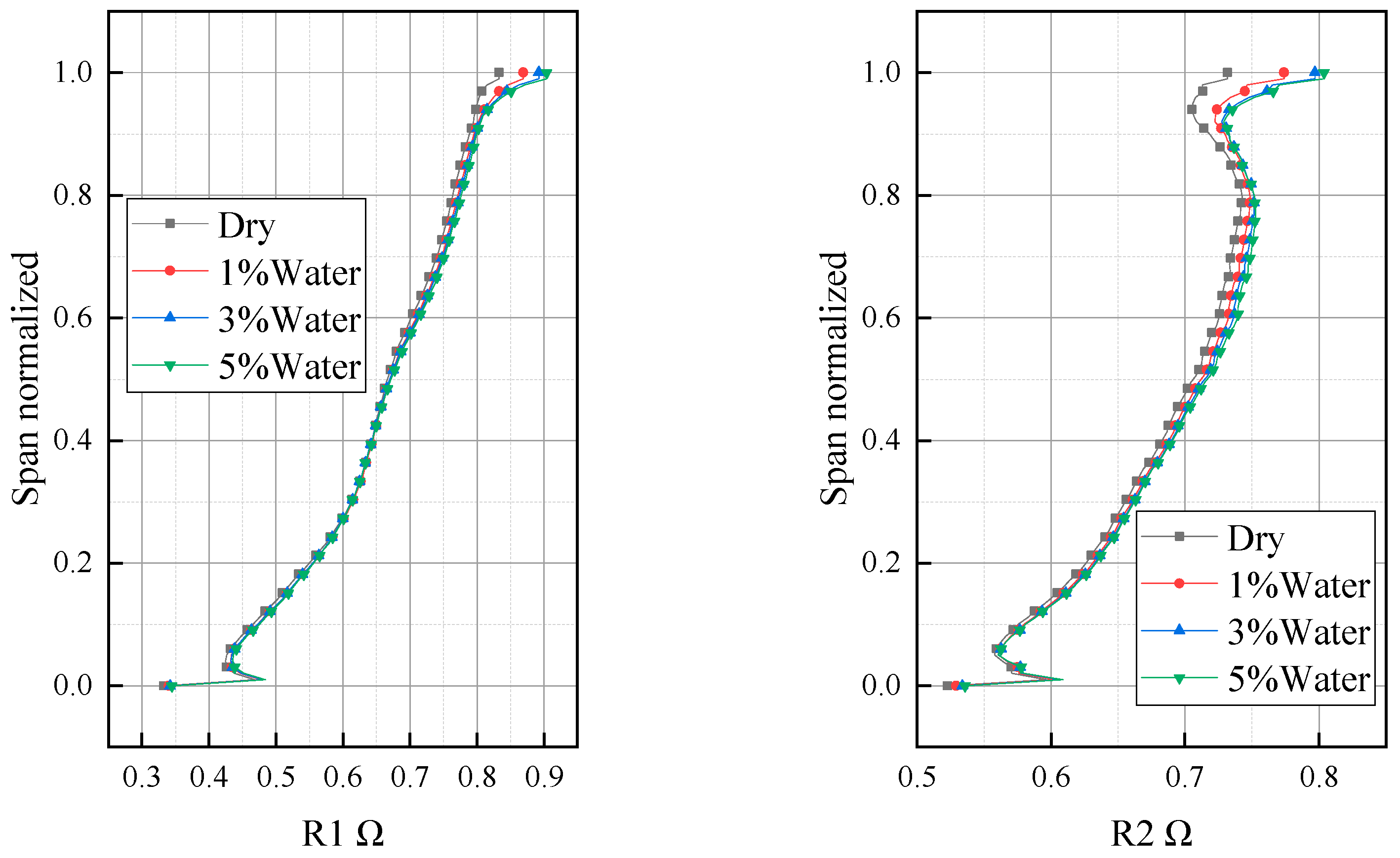
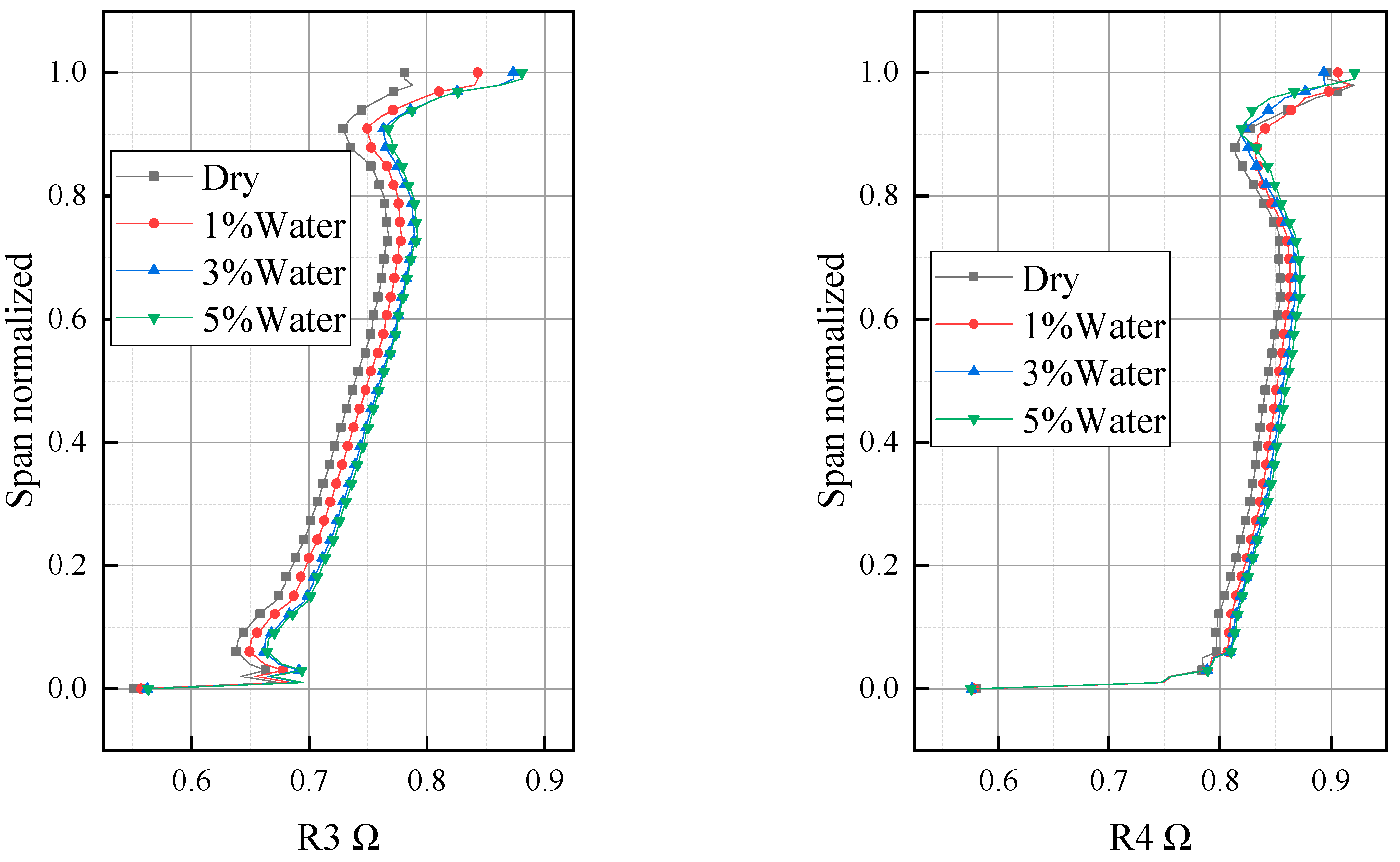
- Rain absorption increases the compressor’s reaction force and increases the load on the moving blade, and the reaction force increases with the increase in rain absorption. The influence range of rain absorption on the reaction force gradually expands from the tip area of the blade to the whole blade height direction with the flow direction.
- (3)
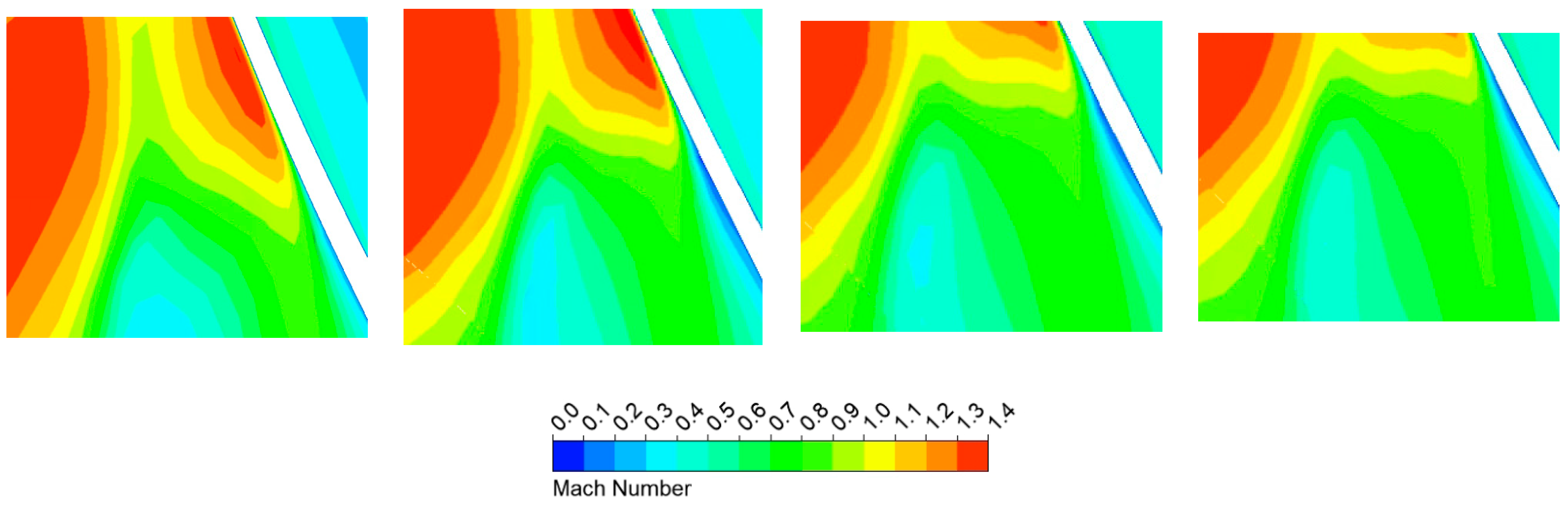
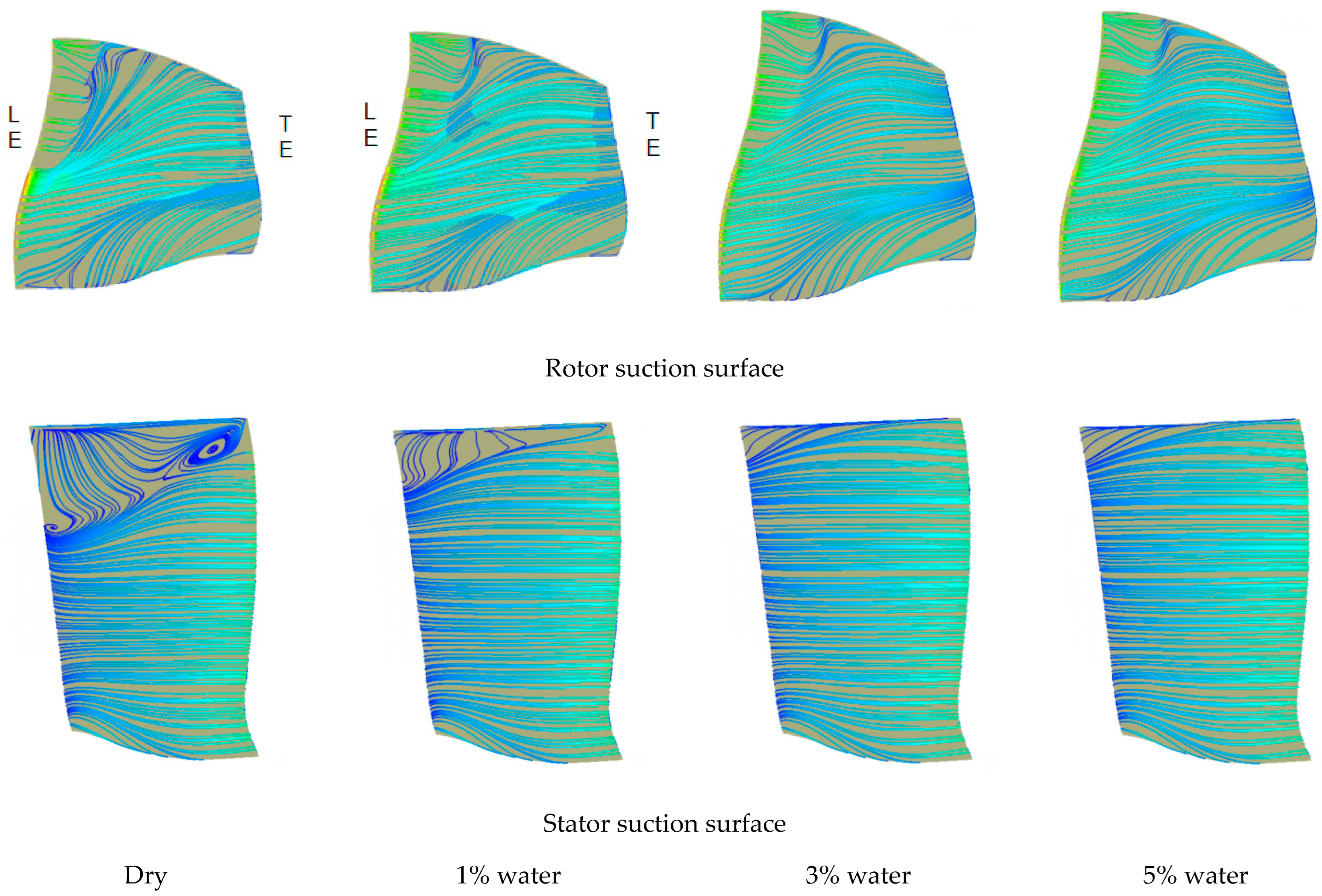
- After the compressor absorbs rain, the shock wave position moves to the downstream of the compressor, and under the same back pressure, the compressor absorbs rain, which can change the working point from stall state to stable state. The influence of rain absorption on the compressor flow field is mainly in the tip area but has little effect on the velocity field and temperature field in the middle and root area. After the compressor absorbs rain, the static entropy of the blade tip region will decrease, and the loss will also decrease. Rain absorption can weaken the separation flow on the blade, thereby improving the flow field.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- National Transportation Safety Board. Aircraft Accident Report; NTSB-AAR-76-8; National Transportation Safety Board: Washington, DC, USA, 1994; p. 47. [Google Scholar]
- Power Loss in Inclement Weather. In Proceedings of the Flight Safety Foundation 45th Annual International Air Safety Seminar, Long Beach CA, USA, 29–31 October 2013; pp. 238–248.
- Civil Aviation Administration of China. Part 33 of the Civil Aviation Regulations of China—Aircraft Engine airworthiness Regulations: CCAR33[S]; Civil Aviation Administration of China: Beijing, China, 2012; pp. 42–52. [Google Scholar]
- Kleinschmidt, R.V. Value of wet compression in gas-turbine cycles. Mech. Eng. 1947, 69, 115–116. [Google Scholar]
- Smith, E. Wet Compression: Gas Turbine Power Output Enhancement for Peak-Load Demand. Power J. Int. 2000, 29–32. [Google Scholar]
- Cataldi, G.; Gu¨ntner, H.; Matz, C.; McKay, T.; Hoffmann, J.; Nemet, A.; Lecheler, S.; Braun, J. Influence of high fogging systems on gas turbine engine operation and performance. In Turbo Expo: Power for Land, Sea, and Air; ASME: New York, NY, USA, 2004; Volume 41693, pp. 653–663. [Google Scholar]
- Khan, A.; Bradshaw, C.R. Quantitative comparison of the performance of vapor compression cycles with compressor vapor or liquid injection. Int. J. Refrig. 2023, 154, 386–394. [Google Scholar] [CrossRef]
- Yusha, V.L.; Chernov, G.I.; Sadvakasov, D.H. The efficiency theoretical analysis of the ammonia refrigeration cycle based on the compression in the wet vapor region. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2020; Volume 2285. [Google Scholar]
- Ustaoglu, A. Parametric study of absorption refrigeration with vapor compression refrigeration cycle using wet, isentropic and azeotropic working fluids: Conventional and advanced exergy approach. Energy 2020, 201, 117491. [Google Scholar] [CrossRef]
- Tsuchiya, T.; Murthy, S. Water ingestion into jet engine axial compressors. In Proceedings of the 20th Aerospace Sciences Meeting, Orlando, FL, USA, 11–14 January 1982; p. 196. [Google Scholar]
- Murthy, S.N.B. Dynamic Performance of High Bypass Ratio Turbine Engines with Water Ingestion. 1996. Available online: https://ntrs.nasa.gov/citations/19960018580 (accessed on 18 September 2024).
- Mathioudakis, K. Analysis of the Effects of Water Injection on the Performance of a Gas Turbine. J. Eng. Gas Turbines Power 2002, 124, 489–495. [Google Scholar] [CrossRef]
- Murthy, S. Transient performance of fan engine with water ingestion. In Proceedings of the 27th Joint Propulsion Conference, Sacramento, CA, USA, 24–26 June 1993; p. 1897. [Google Scholar]
- Ludorf, R.K.; Elder, R.L.; Tronbøl, T.H.; Øverli, J. Stage Re-Matching as a Result of Droplet Evaporation in a Compressor; American Society of Mechanical Engineers: New York, NY, USA, 1995. [Google Scholar]
- Loebig, J.; Vittal, B.; Booher, M. Numerical simulation of water/methanol evaporation in an axial flow gas turbine compressor. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH, USA, 13–15 July 1998; p. 3559. [Google Scholar]
- Khan, J.R.; Wang, T. Simulation of inlet fogging and wet-compression in a single stage compressor including erosion analysis. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; Volume 43178, pp. 193–206. [Google Scholar]
- Sequeira, A.; Salunkhe, P.; Varpe, M. Numerical investigations on the effect of humidity and water ingestion on the performance of a subsonic axial flow compressor. UPB Sci. Bull. Ser. D Mech. Eng. 2021, 83, 95–106. [Google Scholar]
- Roumeliotis, I.; Alexiou, A.; Aretakis, N.; Sieros, G.; Mathioudakis, K. Development and integration of rain ingestion effects in engine performance simulations. J. Eng. Gas Turbines Power 2015, 137, 041202. [Google Scholar] [CrossRef]
- Khan, A.; Irfan, M.; Niazi, U.M.; Shah, I.; Legutko, S.; Rahman, S.; Alwadie, A.S.; Jalalah, M.; Glowacz, A.; Khan, M.K.A. Centrifugal compressor stall control by the application of engineered surface roughness on diffuser shroud using numerical simulations. Materials 2021, 14, 2033. [Google Scholar] [CrossRef] [PubMed]
- Strub, R.A.; Bonciani, L.; Borer, C.J.; Casey, M.V.; Cole, S.L.; Cook, B.B.; Kotzur, J.; Simon, H.; Strite, M.A. Influence of the Reynolds number on the performance of centrifugal compressors. J. Turbomach. 1987, 109, 541–544. [Google Scholar] [CrossRef]
- Tanner, F.X. Development and validation of a cascade atomization and drop breakup model for high-velocity dense sprays. At. Sprays 2004, 14, 32. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’connell, J.P. The Properties of Gases and Liquids; Mcgraw-hill: New York, NY, USA, 2001. [Google Scholar]
- Sun, L.; Zheng, Q.; Li, Y.; Bhargava, R. Understanding effects of wet compression on separated flow behavior in an axial compressor stage using CFD analysis. J. Turbomach. 2011, 133, 031026. [Google Scholar] [CrossRef]
- Ranz, W.E. Evaporation from Drops-I and-II. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]
- Wang, Z.; Luo, M.; Wang, J. Numerical study on variation of rain absorption performance of multistage axial Compressor (Chinese). Therm. Energy Power Eng. 2021, 36, 8. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, S.; Li, S.; Song, X. Study on Rain Absorption Performance and Flow Field of Transonic Compressor under Different Working Conditions. Aerospace 2024, 11, 829. https://doi.org/10.3390/aerospace11100829
Luo S, Li S, Song X. Study on Rain Absorption Performance and Flow Field of Transonic Compressor under Different Working Conditions. Aerospace. 2024; 11(10):829. https://doi.org/10.3390/aerospace11100829
Chicago/Turabian StyleLuo, Shamiao, Shaobin Li, and Xizhen Song. 2024. "Study on Rain Absorption Performance and Flow Field of Transonic Compressor under Different Working Conditions" Aerospace 11, no. 10: 829. https://doi.org/10.3390/aerospace11100829
APA StyleLuo, S., Li, S., & Song, X. (2024). Study on Rain Absorption Performance and Flow Field of Transonic Compressor under Different Working Conditions. Aerospace, 11(10), 829. https://doi.org/10.3390/aerospace11100829



