Three-Dimensional Event-Triggered Predefined-Time Cooperative Guidance Law
Abstract
:1. Introduction
- To address the drawback that the fixed-time guidance laws designed in [14,15,16,17,18,19,20,21,22] cannot explicitly obtain the upper bounds of the system states’ settling time, a new predefined-time cooperative guidance law is designed by referring to the predefined-time cooperative guidance law proposed in [24], and it is extended to 3D space.
- In response to the problem of missile energy depletion that may be caused by the event-triggered mechanism not considered in [24,25,26,27,28], this study introduces the event-triggered mechanism into the predefined-time consistency theory for the first time, which reduces the energy consumption in the guidance process.
- For [14,15,16,17,18,19,20,21,26,27], communication failure and time-delay are not considered, for [25] only communication failure is considered, and for [28] only communication time-delay is considered. Given this, the robustness of the proposed predefined-time guidance law under the above scenarios is studied.
2. Preliminaries
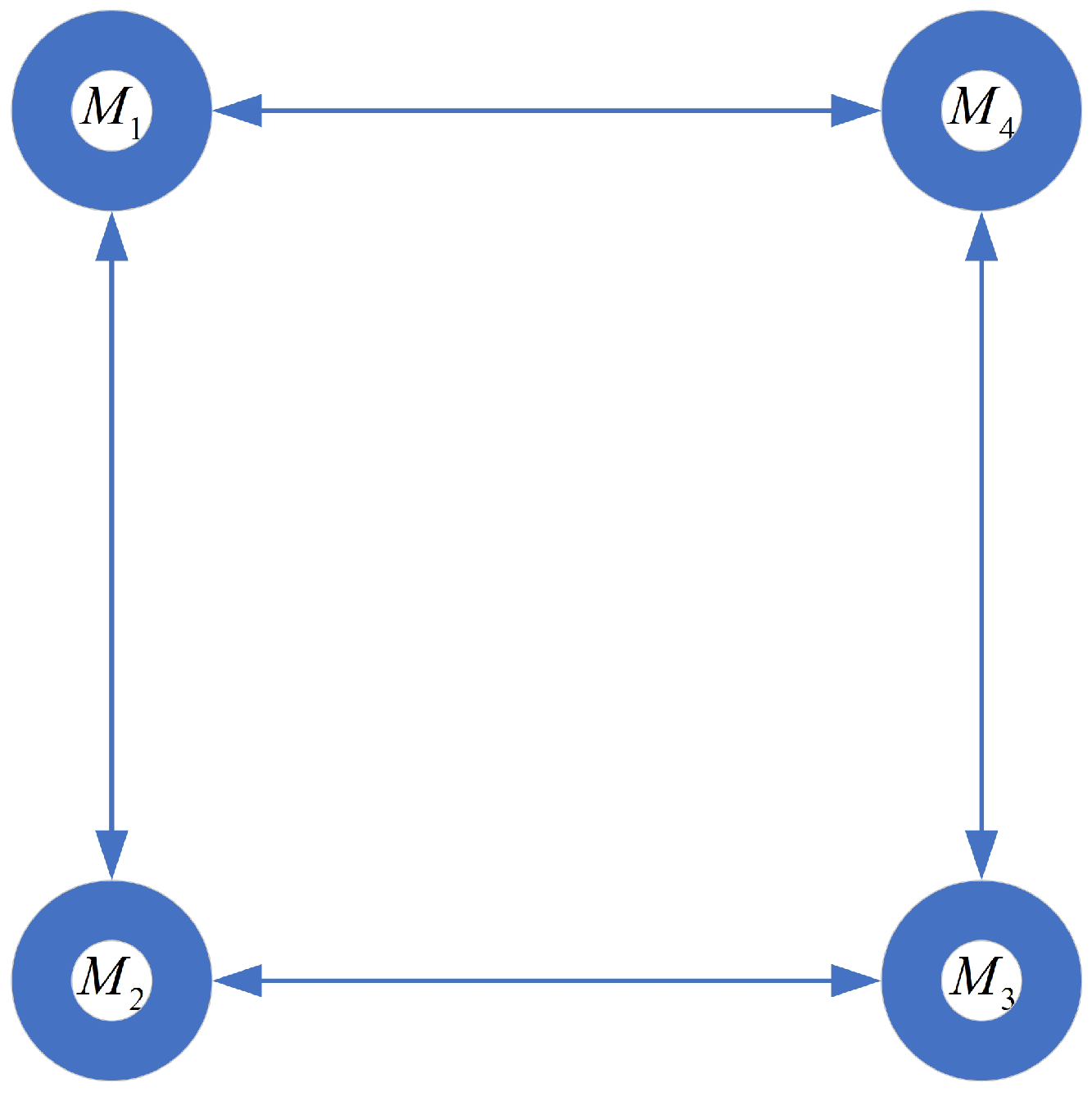
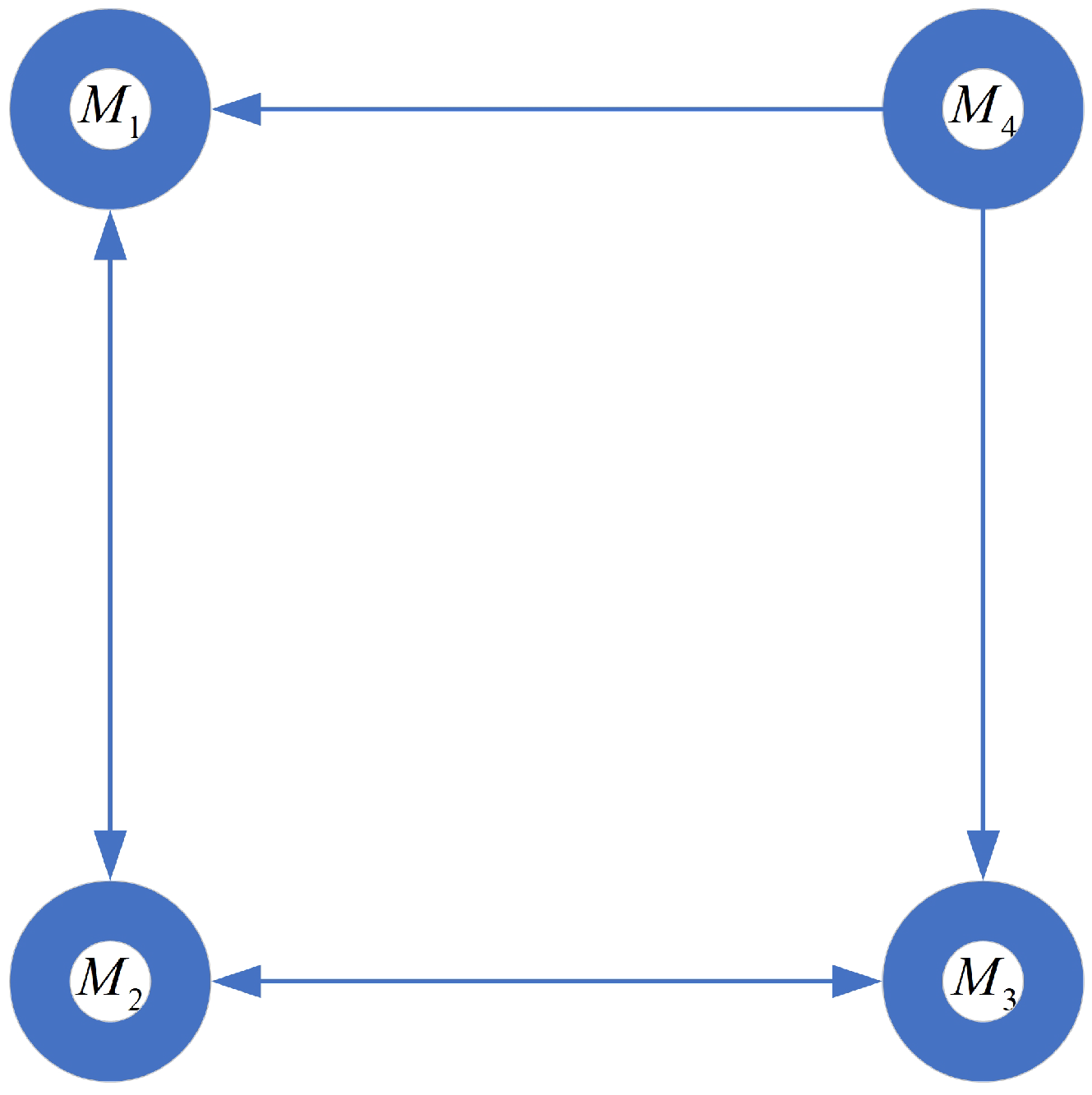
2.1. Graph Theory
2.2. Predefined-Time Stability
2.3. Other Definitions and Citations
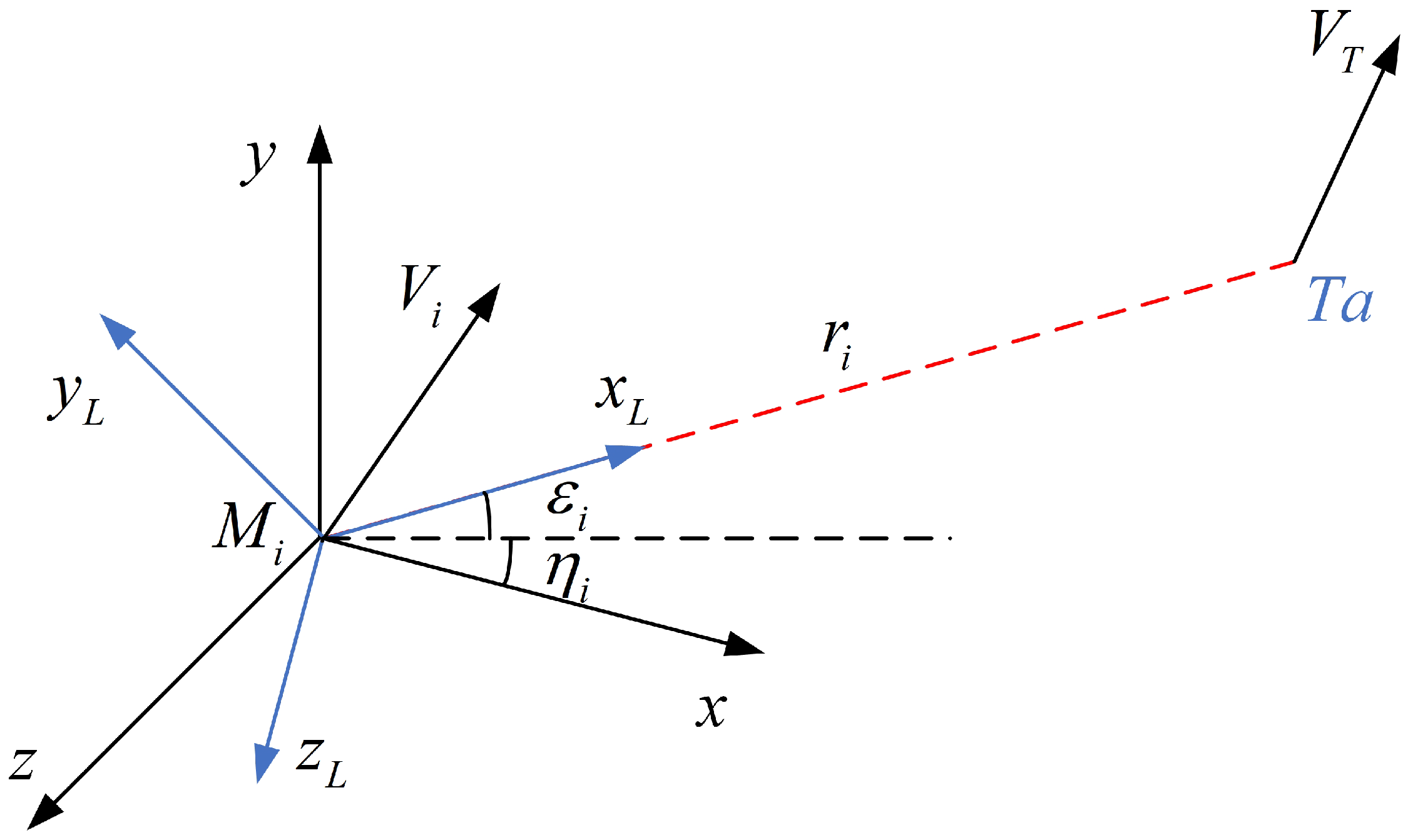
3. Engagement Kinematic Model
4. Main Result
4.1. Predefined-Time Cooperative Guidance Law Along the LOS Direction
4.2. LOS Longitudinal Predefined-Time Cooperative Guidance Law
- Case 1: If , then . Consider the Lyapunov function , and its time derivative is
- Case 2: If , , from (25) we have that the system state has converged to the region . Now, the system dynamics satisfy , which means that the system state has converged to the region . Consider the Lyapunov function , and its time derivative is
4.3. LOS Lateral Predefined-Time Cooperative Guidance Law
4.4. Event-Triggered Scheduling of the Guidance Command Along the LOS Direction
5. Failures Analysis
5.1. Predefined-Time Cooperative Guidance Law with Communication Failure
5.2. Predefined-Time Cooperative Guidance Law with Input Time-Delay
6. Simulation Results and Analysis
6.1. Simulation of Guidance Law with Impact Time and Angle Constraints
6.2. Simulation of Guidance Law Based on the Event-Triggered Mechanism
6.3. Simulation of Disturbance Observation
6.4. Simulation of Guidance Law with Communication Failure and Input Time-Delay
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, J.; Song, S.; Xu, S. Three-dimensional cooperative guidance law for multiple missiles with finite-time convergence. Aerosp. Sci. Technol. 2017, 67, 193–205. [Google Scholar] [CrossRef]
- Teng, L.; Li, C.; Guo, Y.; Ma, G. Three-dimensional finite-time cooperative guidance for multiple missiles without radial velocity measurements. Chin. J. Aeronaut. 2019, 32, 1294–1304. [Google Scholar]
- Yang, B.; Jing, W.; Gao, C. Three-dimensional cooperative guidance law for multiple missiles with impact angle constraint. J. Syst. Eng. Electron. 2020, 31, 1286–1296. [Google Scholar]
- Li, W.; Wen, Q.; He, L.; Xia, Q. Three-dimensional impact angle constrained distributed cooperative guidance law for anti-ship missiles. J. Syst. Eng. Electron. 2021, 32, 447–459. [Google Scholar]
- Yang, X.; Song, S. Three-dimensional consensus algorithm for nonsingular distributed cooperative guidance strategy. Aerosp. Sci. Technol. 2021, 118, 106958. [Google Scholar] [CrossRef]
- Li, H.; Deng, Y.; Cai, Y. Three-dimensional cooperative interception guidance law with impact time constraint. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 191–201. [Google Scholar]
- Zhang, W.; Du, X.; Xia, Q. A three-dimensional cooperative guidance law based on consensus theory for maneuvering targets. Math. Probl. Eng. 2019, 2019, 2120745. [Google Scholar] [CrossRef]
- Xu, X.; Chen, C.; Ren, Z.; Li, S. Multiple tactical missiles cooperative attack with formation-containment tracking requirement along the planned trajectory. IEEE Access 2020, 8, 87929–87946. [Google Scholar] [CrossRef]
- Wang, X.H.; Tan, C.P. 3-d impact angle constrained distributed cooperative guidance for maneuvering targets without angular-rate measurements. Control Eng. Pract. 2018, 78, 142–159. [Google Scholar] [CrossRef]
- Liu, S.; Yan, B.; Zhang, T.; Dai, P.; Liu, R.; Yan, J. Three-dimensional cooperative guidance law for intercepting hypersonic targets. Aerosp. Sci. Technol. 2022, 129, 107815. [Google Scholar] [CrossRef]
- Wang, X.; Lu, H.; Huang, X.; Yang, Y.; Zuo, Z. Three-dimensional time-varying sliding mode guidance law against maneuvering targets with terminal angle constraint. Chin. J. Aeronaut. 2022, 35, 303–319. [Google Scholar] [CrossRef]
- Liu, Z.; Lv, Y.; Zhou, J.; Hu, L. On 3d simultaneous attack against manoeuvring target with communication delays. Int. J. Adv. Robot. Syst. 2020, 17, 1729881419894808. [Google Scholar] [CrossRef]
- Yu, C.; Zhu, B.; Zheng, J.; Wang, W. Three dimensional cooperative guidance for intercepting a manoeuvering target. IET Control Theory Appl. 2024, 18, 530–540. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, W.; Liu, X.; Cheng, J. Three-dimensional fixed-time robust cooperative guidance law for simultaneous attack with impact angle constraint. Aerosp. Sci. Technol. 2021, 110, 106523. [Google Scholar] [CrossRef]
- Yu, H.; Dai, K.; Li, H.; Zou, Y.; Ma, X.; Ma, S.; Zhang, H. Cooperative guidance law for multiple missiles simultaneous attacks with fixed-time convergence. Int. J. Control 2023, 96, 2167–2180. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, X.; Chen, W. Three-dimensional event-triggered fixed-time cooperative guidance law against maneuvering target with the constraint of relative impact angles. J. Frankl. Inst. 2023, 360, 3914–3966. [Google Scholar] [CrossRef]
- Sinha, A.; Kumar, S.R.; Mukherjee, D. Three-dimensional nonlinear cooperative salvo using event-triggered strategy. J. Guid. Control Dyn. 2021, 44, 328–342. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, X. Multiple missiles fixed-time cooperative guidance without measuring radial velocity for maneuvering targets interception. ISA Trans. 2022, 126, 388–397. [Google Scholar] [CrossRef]
- Dong, W.; Wang, C.; Wang, J.; Zuo, Z.; Shan, J. Fixed-time terminal angle-constrained cooperative guidance law against maneuvering target. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1352–1366. [Google Scholar] [CrossRef]
- You, H.; Chang, X.; Zhao, J.; Wang, S.; Zhang, Y. Three-dimensional impact-angle-constrained fixed-time cooperative guidance algorithm with adjustable impact time. Aerosp. Sci. Technol. 2023, 141, 108574. [Google Scholar] [CrossRef]
- Ma, M.-C.; Song, S.-M. Three-dimensional prescribed performance cooperative guidance law with spatial constraint for intercepting manoeuvring targets. Int. J. Control 2023, 96, 1424–1435. [Google Scholar] [CrossRef]
- Yu, H.; Dai, K.; Li, H.; Zou, Y.; Ma, X.; Ma, S.; Zhang, H. Three-dimensional adaptive fixed-time cooperative guidance law with impact time and angle constraints. Aerosp. Sci. Technol. 2022, 123, 107450. [Google Scholar] [CrossRef]
- Sánchez-Torres, J.D.; Sanchez, E.N.; Loukianov, A.G. Predefined-time stability of dynamical systems with sliding modes. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 5842–5846. [Google Scholar]
- Sinha, A.; Kumar, S.R. Cooperative target capture using predefined-time consensus over fixed and switching networks. Aerosp. Sci. Technol. 2022, 127, 107686. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, S.; Guo, J. Two-stage cooperative guidance strategy using a prescribed-time optimal consensus method. Aerosp. Sci. Technol. 2020, 100, 105641. [Google Scholar] [CrossRef]
- Cui, L.; Jin, N.; Chang, S.; Zuo, Z. Prescribed-time guidance scheme design for missile salvo attack. J. Frankl. Inst. 2022, 359, 6759–6782. [Google Scholar] [CrossRef]
- Wang, Z.; Fu, W.; Fang, Y.; Zhu, S.; Wu, Z.; Wang, M. Prescribed-time cooperative guidance law against maneuvering target based on leader-following strategy. ISA Trans. 2022, 129, 257–270. [Google Scholar] [CrossRef]
- Wang, Z.; Fu, Z.; Wu, Z.; Zhu, C.; Li, J. Three-dimensional cooperative guidance law against maneuvering target with time-varying communication delays. Int. J. Aeronaut. Space Sci. 2023, 25, 605–621. [Google Scholar] [CrossRef]
- Zhang, D.; Yu, H.; Dai, K.; Yi, W.; Zhang, H.; Lei, Z. Multiple-missile fixed-time integrated guidance and control design with multi-stage interconnected observers under impact angle and input saturation constraints. IET Control Theory Appl. 2024. [Google Scholar] [CrossRef]
- Aldana-López, R.; Gómez-Gutiérrez, D.; Jiménez-Rodríguez, E.; Sánchez-Torres, J.D.; Loukianov, A.G. On predefined-time consensus protocols for dynamic networks. J. Frankl. Inst. 2020, 357, 11880–11899. [Google Scholar] [CrossRef]
- Defoort, M.; Polyakov, A.; Demesure, G.; Djemai, M.; Veluvolu, K. Leader-follower fixed-time consensus for multi-agent systems with unknown nonlinear inherent dynamics. IET Control Theory Appl. 2015, 9, 2165–2170. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2011, 57, 2106–2110. [Google Scholar] [CrossRef]
- Sánchez-Torres, J.D.; Gómez-Gutiérrez, D.; López, E.; Loukianov, A.G. A class of predefined-time stable dynamical systems. IMA J. Math. Control. Inf. 2018, 35 (Suppl. 1), i1–i29. [Google Scholar] [CrossRef]
- Jiménez-Rodríguez, E.; Sánchez-Torres, J.D.; Gómez-Gutiérrez, D.; Loukianov, A.G. Predefined-time stabilization of high order systems. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 5836–5841. [Google Scholar]
- Jiménez-Rodríguez, E.; Sánchez-Torres, J.D.; Loukianov, A.G. On optimal predefined-time stabilization. Int. J. Robust Nonlinear Control 2017, 27, 3620–3642. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Tang, Y.; Liu, C. Predefined-time consensus tracking of second-order multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 2550–2560. [Google Scholar] [CrossRef]
- Olver, F.W. NIST Handbook of Mathematical Functions Hardback and CD-ROM; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Zhou, J.; Yang, J. Distributed guidance law design for cooperative simultaneous attacks with multiple missiles. J. Guid. Control. Dyn. 2016, 39, 2439–2447. [Google Scholar] [CrossRef]
- Aragues, R.; Shi, G.; Dimarogonas, D.V.; Sagüés, C.; Johansson, K.H.; Mezouar, Y. Distributed algebraic connectivity estimation for undirected graphs with upper and lower bounds. Automatica 2014, 50, 3253–3259. [Google Scholar] [CrossRef]
- Zhou, J.; Lü, Y.; Li, Z.; Yang, J. Cooperative guidance law design for simultaneous attack with multiple missiles against a maneuvering target. J. Syst. Sci. Complex. 2018, 31, 287–301. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, H.H.; Li, X.; Yao, Y. Fault tolerance of cooperative interception using multiple flight vehicles. J. Frankl. Inst. 2013, 350, 2373–2395. [Google Scholar] [CrossRef]
- Cucuzzella, M.; Incremona, G.P.; Ferrara, A. Event-triggered variable structure control. Int. J. Control 2020, 93, 252–260. [Google Scholar] [CrossRef]
- Sinha, A.; Mishra, R.K. Consensus in first order nonlinear heterogeneous multi-agent systems with event-based sliding mode control. Int. J. Control 2020, 93, 858–871. [Google Scholar] [CrossRef]
- Balhance, N.; Weiss, M.; Shima, T. Cooperative guidance law for intrasalvo tracking. J. Guid. Control Dyn. 2017, 40, 1441–1456. [Google Scholar] [CrossRef]
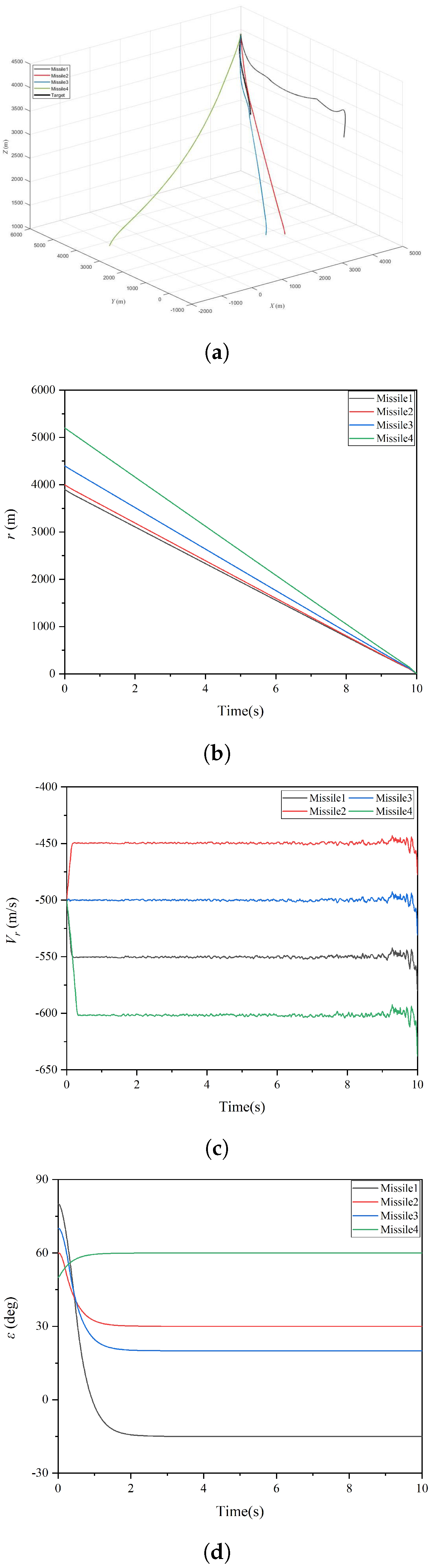
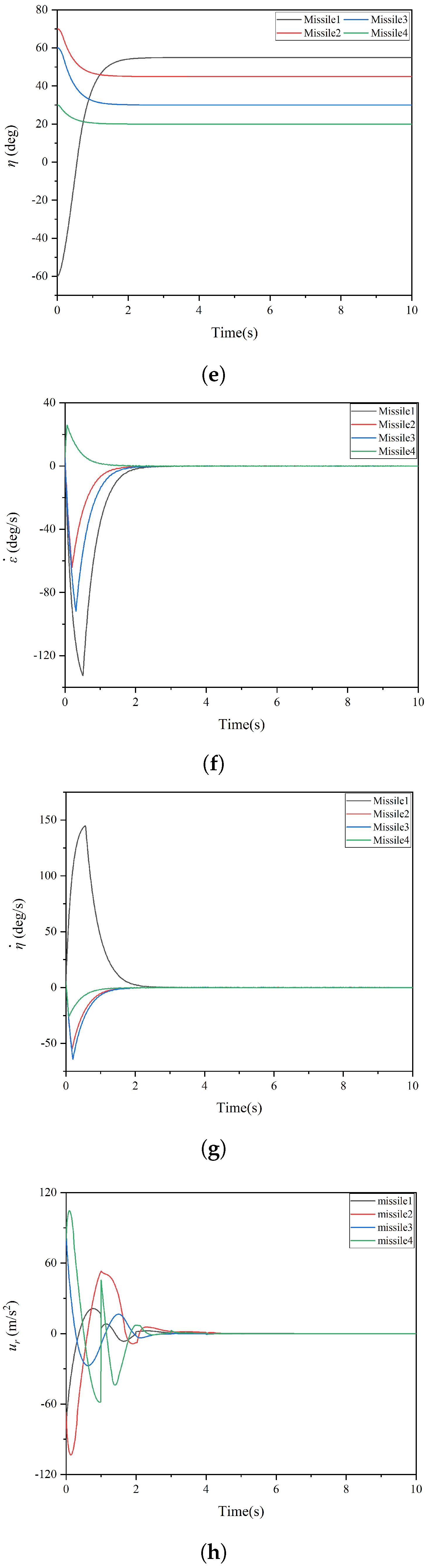


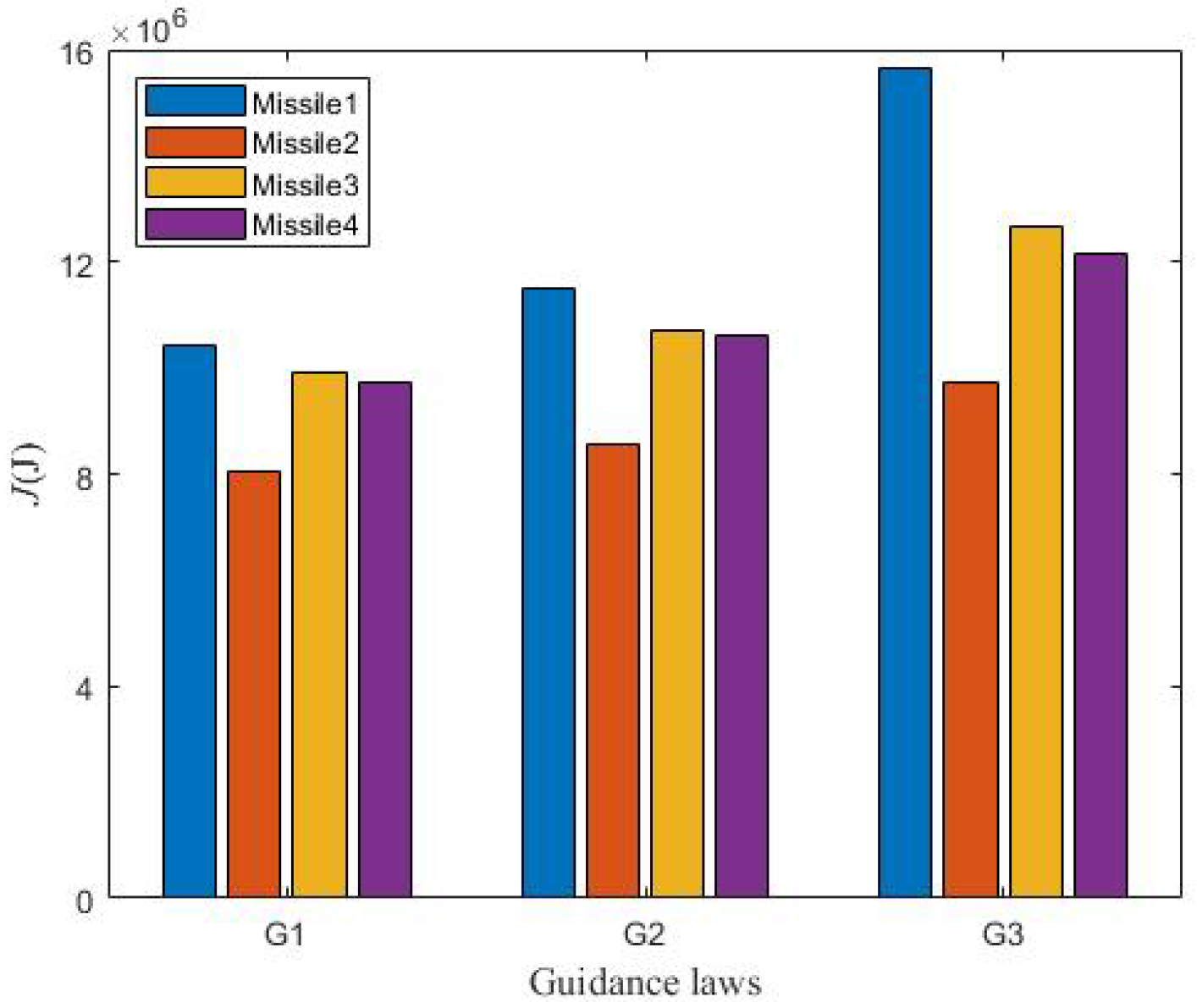
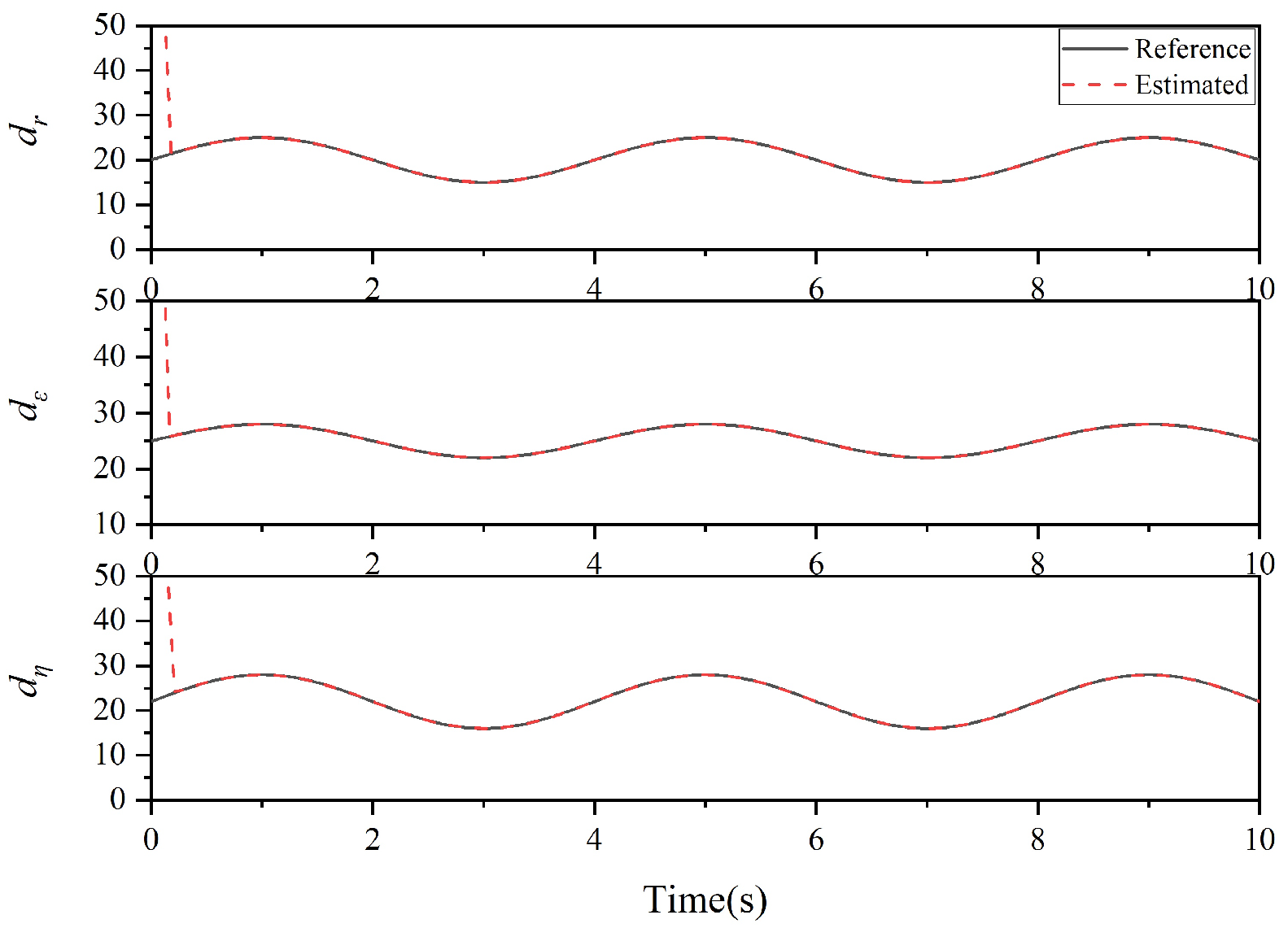
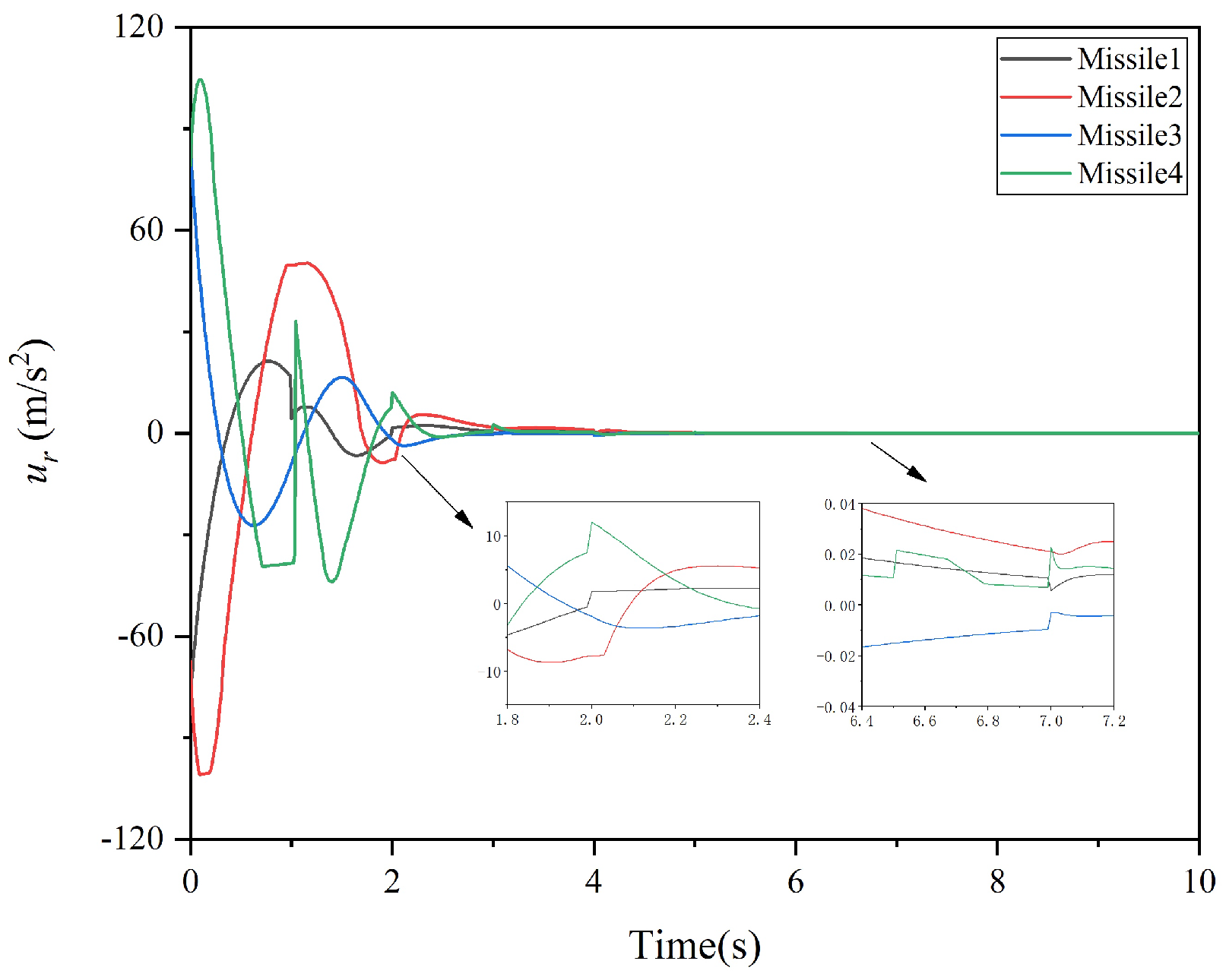
| Missile | Position (m,m,m) | (m/s) | (deg) | (deg) | (deg) | (deg) |
|---|---|---|---|---|---|---|
| (3300, −680, 3500) | −500 | 80 | −60 | −15 | 55 | |
| (1680, −240, 1660) | −500 | 60 | 70 | 30 | 45 | |
| (940, −370, 1800) | −500 | 70 | 60 | 20 | 30 | |
| (−1660, 3000, 1260) | −500 | 50 | 30 | 60 | 20 |
| Missiles in G1 and G3 | Impact Time (s) | Miss Distance (m) |
|---|---|---|
| Missile1-G1 | 10.12 | 0.300 |
| Missile1-G3 | 10.98 | 1.692 |
| Missile2-G1 | 10.12 | 0.245 |
| Missile2-G3 | 10.95 | 1.579 |
| Missile3-G1 | 10.12 | 0.273 |
| Missile3-G3 | 11.06 | 2.016 |
| Missile4-G1 | 10.12 | 0.328 |
| Missile4-G3 | 10.99 | 1.035 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Yu, H.; Dai, K.; Yi, W.; Zhang, H.; Guan, J.; Yuan, S. Three-Dimensional Event-Triggered Predefined-Time Cooperative Guidance Law. Aerospace 2024, 11, 999. https://doi.org/10.3390/aerospace11120999
Zhang D, Yu H, Dai K, Yi W, Zhang H, Guan J, Yuan S. Three-Dimensional Event-Triggered Predefined-Time Cooperative Guidance Law. Aerospace. 2024; 11(12):999. https://doi.org/10.3390/aerospace11120999
Chicago/Turabian StyleZhang, Dingye, Hang Yu, Keren Dai, Wenjun Yi, He Zhang, Jun Guan, and Shusen Yuan. 2024. "Three-Dimensional Event-Triggered Predefined-Time Cooperative Guidance Law" Aerospace 11, no. 12: 999. https://doi.org/10.3390/aerospace11120999
APA StyleZhang, D., Yu, H., Dai, K., Yi, W., Zhang, H., Guan, J., & Yuan, S. (2024). Three-Dimensional Event-Triggered Predefined-Time Cooperative Guidance Law. Aerospace, 11(12), 999. https://doi.org/10.3390/aerospace11120999







