Hybrid Rocket Engine Burnback Simulations Using Implicit Geometry Descriptions
Abstract
:1. Introduction
1.1. Level Set Method
1.2. Fast Marching Method
1.3. Signed Distance Function
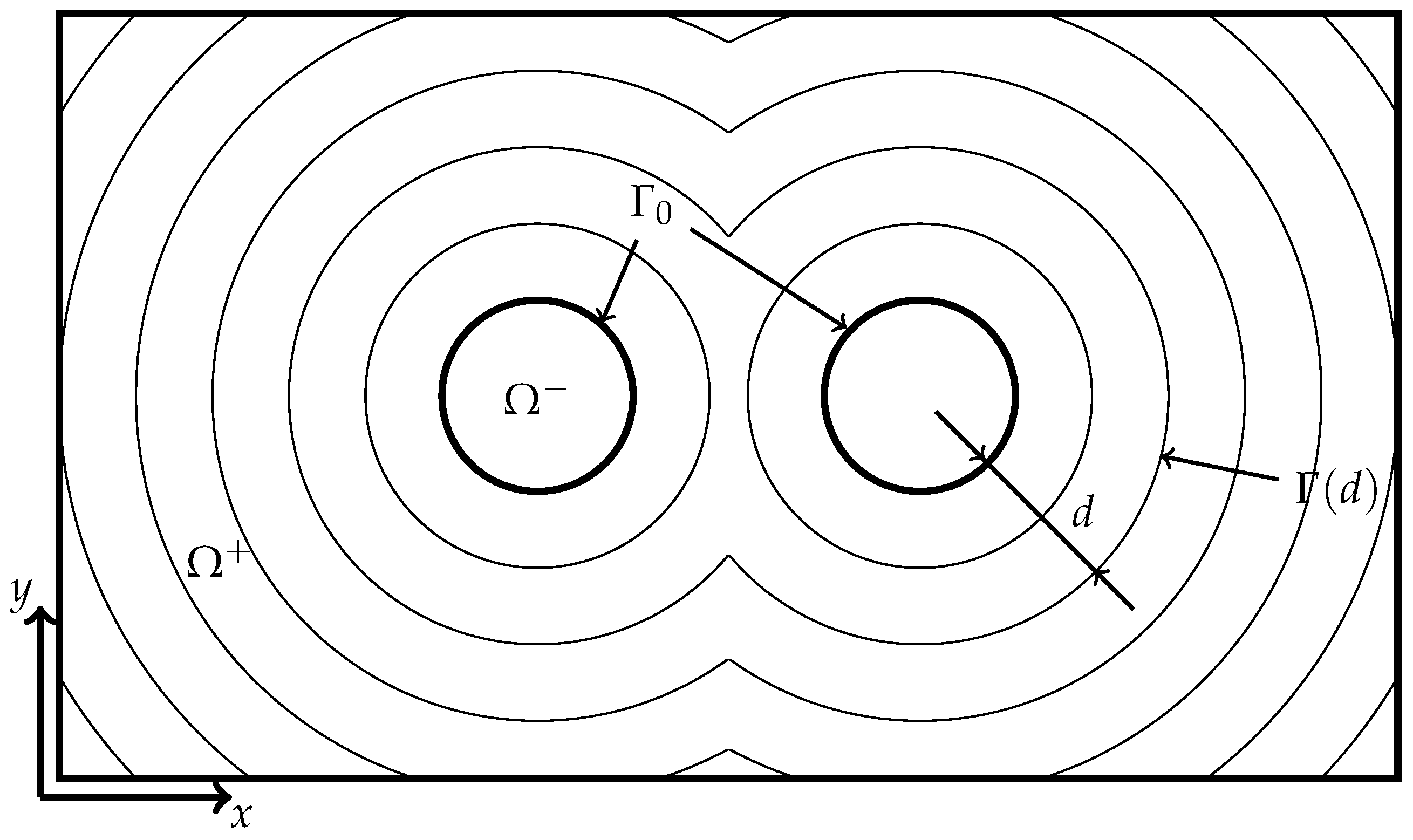
2. Methods
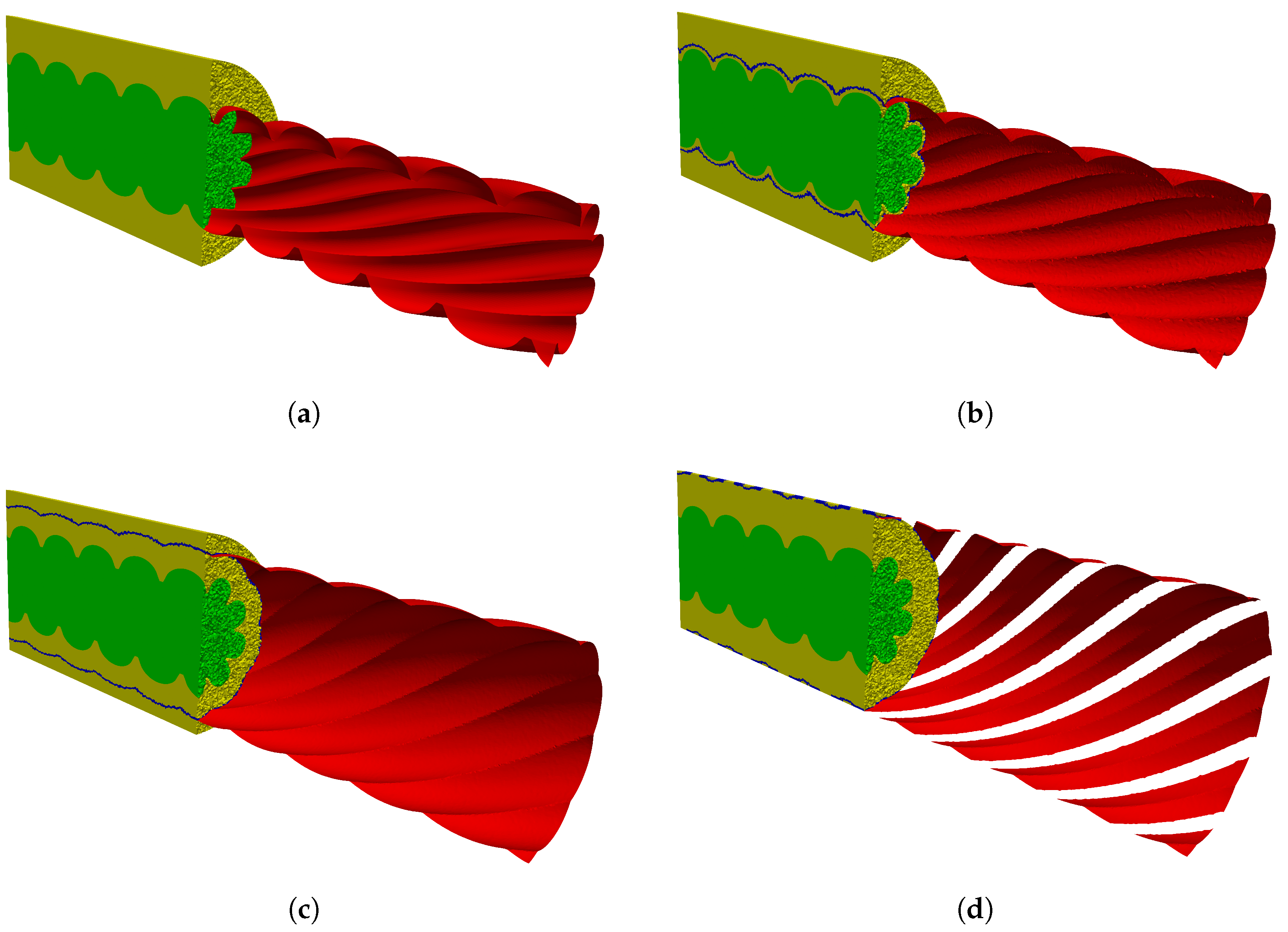
2.1. Implicit Surface Tracking
2.2. Meshing
2.3. Calculation of Output Values
2.3.1. Direct Method
2.3.2. Interpolation Method
3. Validation and Results
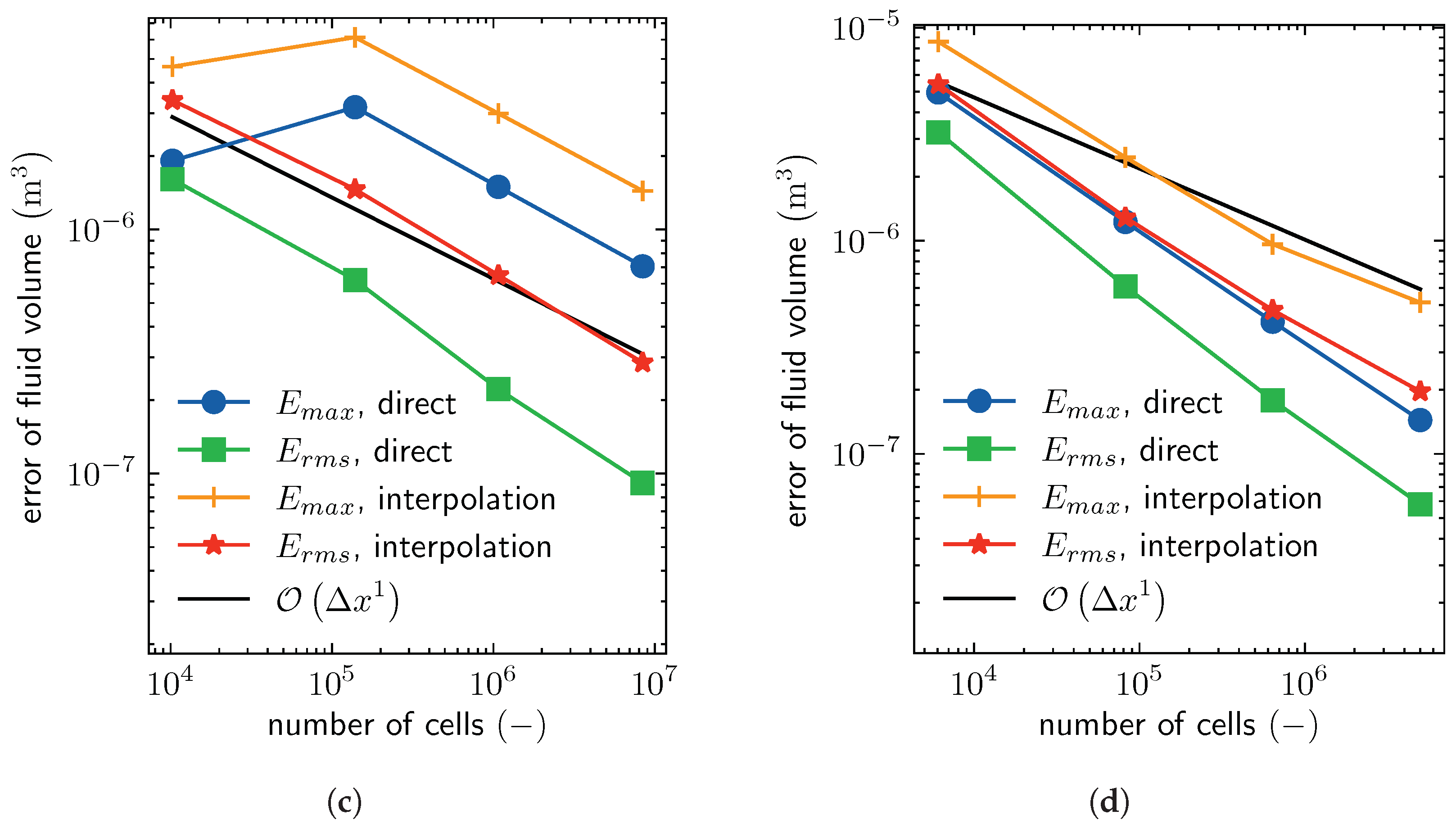
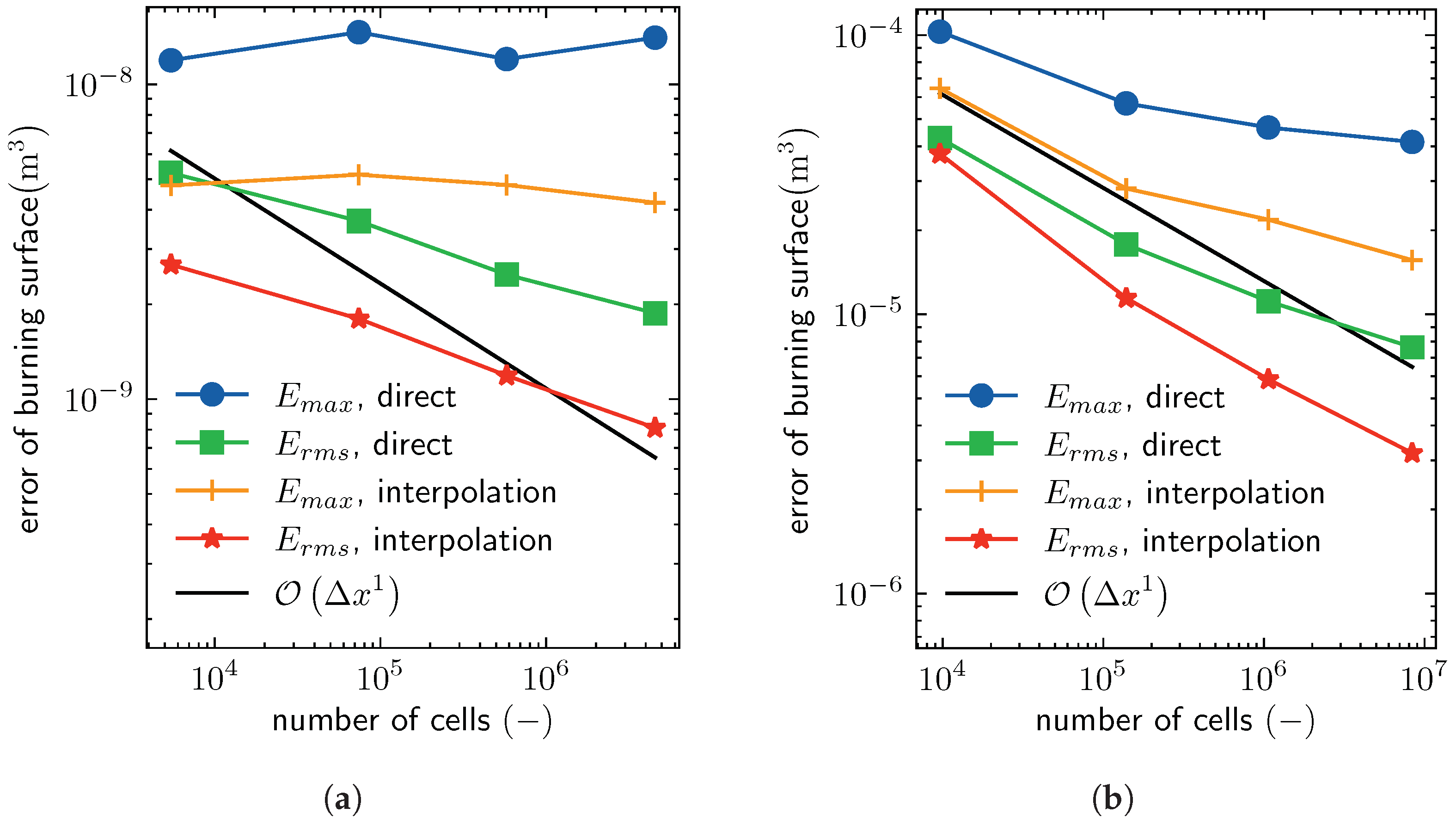
3.1. Convergence
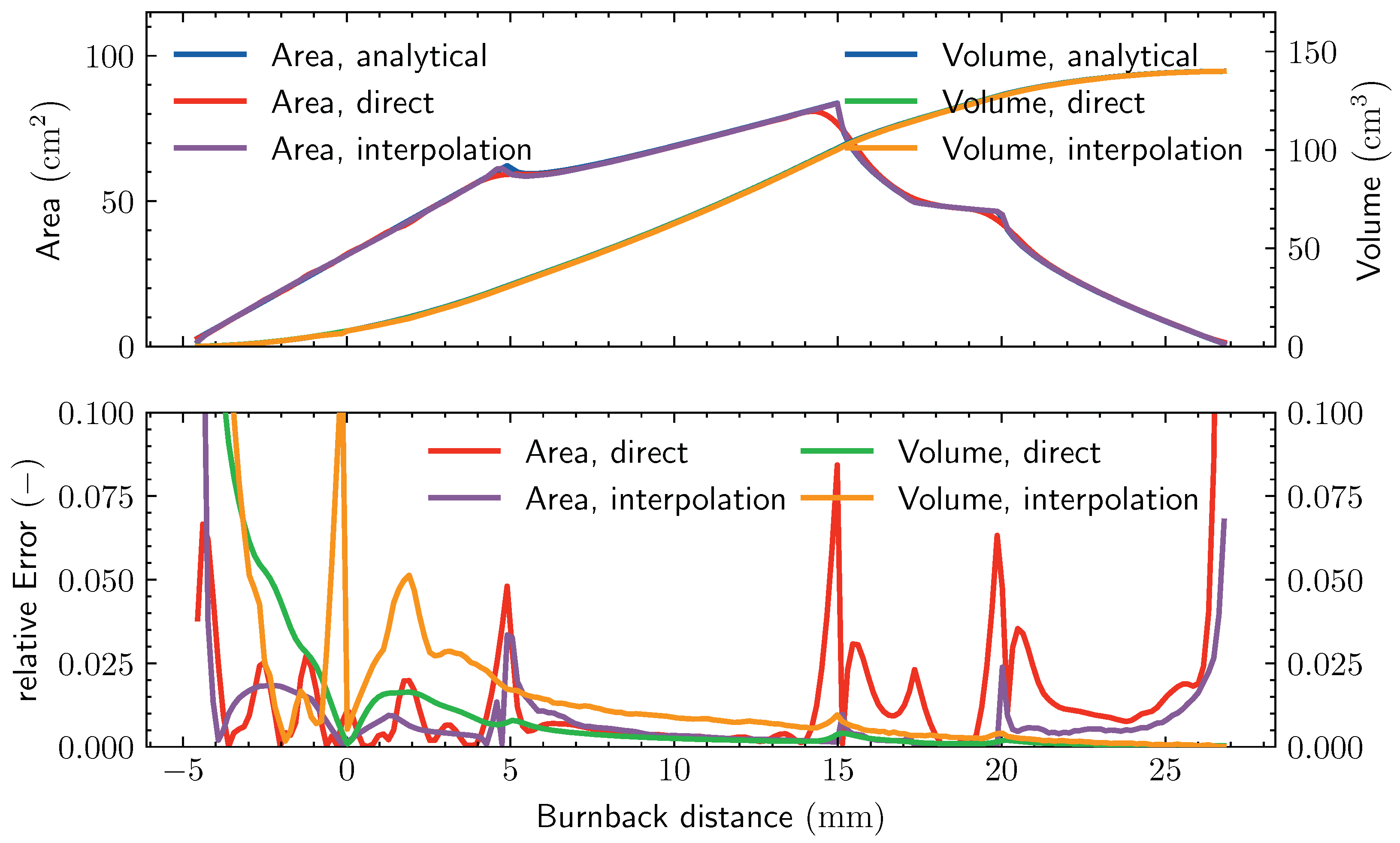
3.2. Accuracy
3.3. Application to the VISERION Engine
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AHRES | Advanced Hybrid Rocket Engine Simulation |
| ALDUINA | Advanced Lithergol Demonstrator Unit for Increased Altitudes |
| ARIEL | ATEK Hybrid Rocket Engine Laboratory device |
| DLR | German Aerospace Center |
| FMM | Fast Marching Method |
| HTPB | Hydroxyl-terminated Polybutadiene |
| LSM | Level Set Method |
| MDF | Minimum Distance Function |
| SDF | Signed Distance Function |
| SPP | Solid Propellant Rocket Motor Performance Computer Program |
| TAU | Triangular Adaptive Upwind |
References
- Božić, O.; Porrmann, D.; Lancelle, D.; Hartwig, A. Program AHRES and its Contribution to Assess Features and Current Limitations of Hybrid Rocket Propulsion. In Proceedings of the 63rd International Astronautical Congress, Naples, Italy, 1–5 October 2012. [Google Scholar]
- Schwamborn, D.; Gerhold, T.; Heinrich, R. The DLR TAU-code: Recent applications in research and industry. In Proceedings of the European Conference on Computational Fluid Dynamics, Egmond aan Zee, The Netherlands, 5–8 September 2006. [Google Scholar]
- May, S.; Božić, O. CFD Simulation of Chemical Non-Equilibrium Reacting Flow within the AHRES Hybrid Rocket Engine. In Proceedings of the 6th European Conference for Aeronautics and Space Sciences, Kraków, Poland, 29 June–3 July 2015. [Google Scholar]
- May, S.; Božić, O. Numerical Simulation of the Flow and Combustion Inside the Reaction Chamber of the AHRES Hybrid Rocket Engine. In Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Springer International Publishing: Cham, Switzerland, 2016; pp. 801–809. [Google Scholar] [CrossRef]
- May, S.; Karl, S.; Božić, O. Development of an Eddy Dissipation Model for the use in Numerical Hybrid Rocket Engine Combustion Simulation. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences, Milano, Italy, 3–6 July 2017. [Google Scholar] [CrossRef]
- Poppe, G.; May, S.; Bierwagen, N.M.; Eggers, T. The Site Trauen of the German Aerospace Center - Past, Present and Future of the Largest Test Site for Rocket Engines in Germany. In Proceedings of the 3rd Ground-Based Space Facilities Symposium, Marseille, France, 6–8 December 2022. [Google Scholar]
- Viserion Press Release. Available online: https://www.dlr.de/en/latest/news/2021/03/20210719_hybrid-rocket-engine-viserion-successfully-tested (accessed on 1 October 2023).
- Dabanović, A.; Martin, J.; May, S.; Eggers, T. Design of a sounding rocket upper stage based on the hybrid rocket engine VISERION. CEAS Space J. 2022, 15, 467–476. [Google Scholar] [CrossRef]
- Poppe, G.; Bozic, O.; May, S.; Bierwagen, N.M. Characterization of Regression Rate and Combustion Process in a High-Pressure 2D Hybrid Rocket Engine with Optical Access. In Proceedings of the International Astronautical Congress, IAC, Bremen, Germany, 1–5 October 2018. [Google Scholar]
- Glaser, C.; Hijlkema, J.; Anthoine, J. Evaluation of Regression Rate Enhancing Concepts and Techniques for Hybrid Rocket Engines. Aerotec. Missili Spaz. 2022, 101, 267–292. [Google Scholar] [CrossRef]
- Miller, W.H.; Douglass, H.W.; Collins, J.H.; Keller, R.B., Jr. Solid Rocket Motor Performance Analysis and Prediction; Techreport NASA-SP-8039; National Aeronautics and Space Administration, Lewis Research Center: Cleveland, OH, USA, 1971. [Google Scholar]
- Brooks, W.T.; Douglass, H.W.; Collins, J.H.; Keller, R.B., Jr. Solid Propellant Grain Design and Internal Ballistics; Techreport NASA-SP-8076; National Aeronautics and Space Administration, Lewis Research Center: Cleveland, OH, USA, 1972. [Google Scholar]
- Ricciardi, A. Generalized geometric analysis of right circular cylindrical star perforated and tapered grains. J. Propuls. Power 1992, 8, 51–58. [Google Scholar] [CrossRef]
- Hartfield, R.; Jenkins, R.; Burkhalter, J.; Foster, W. A Review of Analytical Methods for Solid Rocket Motor Grain Analysis. In Proceedings of the 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Huntsville, AL, USA, 20–23 July 2003; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2003. [Google Scholar] [CrossRef]
- Hartfield, R.; Jenkins, R.; Burkhalter, J.; Foster, W. Analytical Methods for Predicting Grain Regression in Tactical Solid-Rocket Motors. J. Spacecr. Rocket. 2004, 41, 689–693. [Google Scholar] [CrossRef]
- Tola, C.; Nikbay, M. Internal Ballistic Modeling of a Solid Rocket Motor by Analytical Burnback Analysis. J. Spacecr. Rocket. 2019, 56, 498–516. [Google Scholar] [CrossRef]
- Peterson, E.C.; Nielsen, C.C.; Johnson, W.C.; Cook, K.; Barron, J.G. Generalized coordinate grain design and internal ballistics evaluation program. In Proceedings of the 3rd Solid Propulsion Conference, Atlantic City, NJ, USA, 4–6 June 1968; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1968. [Google Scholar] [CrossRef]
- Coats, D.E.; Levine, J.N.; Cohen, N.S.; Nickerson, G.R.; Tyson, T.J. A Computer Program for the Prediction of Solid Propellant Rocket Motor Performance; Techreport ADA015140; Air Force Rocket Propulsion Laboratory, Airforce Systems Command: Edwards, CA, USA, 1975; Volume 1. [Google Scholar]
- Coats, D.E.; Levine, J.N.; Cohen, N.S.; Nickerson, G.R.; Tyson, T.J. A Computer Program for the Prediction of Solid Propellant Rocket Motor Performance; Techreport ADA015141; Air Force Rocket Propulsion Laboratory, Airforce Systems Command: Edwards, CA, USA, 1975; Volume 2. [Google Scholar]
- Coats, D.E.; Levine, J.N.; Cohen, N.S.; Nickerson, G.R.; Tyson, T.J. A Computer Program for the Prediction of Solid Propellant Rocket Motor Performance; Techreport ADA022880; Air Force Rocket Propulsion Laboratory, Airforce Systems Command: Edwards, CA, USA, 1975; Volume 3. [Google Scholar]
- Dervieux, A.; Thomasset, F. A finite element method for the simulation of a Rayleigh-Taylor instability. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1980; pp. 145–158. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Yildirim, C.; Aksel, H. Numerical Simulation of the Grain Burnback in Solid Propellant Rocket Motor. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Tuscon, AZ, USA, 10–13 July 2005. [Google Scholar] [CrossRef]
- Cavallini, E. Modeling and Numerical Simulation of Solid Rocket Motors Internal Ballistics. Ph.D. Thesis, Sapienza Università di Roma, Rome, Italy, 2010. [Google Scholar]
- Gontijo, M.; Filho, R. Two-Phase Tank Emptying and Burnback Coupled Internal Ballistics Prediction on Hybrid Rocket Motors. In Engenharias: Metodologias e Práticas de Caráter Multidisciplinar 3; Atena Editora: Ponta Grossa, PR, Brasil, 2021; pp. 46–56. [Google Scholar] [CrossRef]
- Funami, Y.; Takano, A. Regression-Rate Evaluation of Hybrid-Rocket Fuel Grain with a Star-Fractal Swirl Port. Trans. Jpn. Soc. Aeronaut. Space Sci. 2023, 66, 61–69. [Google Scholar] [CrossRef]
- Liu, S.; Lu, H.; Zhang, B.; Yang, Y.; Sang, D. Study on Burning Surface Regression Algorithm under Erosive Burning Based on CT Images of Solid Rocket Motor Grain. Aerospace 2023, 10, 21. [Google Scholar] [CrossRef]
- Han, C.-H.; Xu, J.-S.; Wang, S.-H. Solid Rocket Motor Propellant Grain Burnback Simulation Based on Level Set Method. J. Phys. Conf. Ser. 2023, 2478, 112010. [Google Scholar] [CrossRef]
- Sethian, J.A. Level Set Methods and Fast Marching Methods—Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Toker, K.A.; Aksel, H.; Tinaztepe, T. 3-dimensional propellant grain burnback calculations on tetrahedron mesh by fast marching method. In Proceedings of the 22nd Applied Aerodynamics Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; p. 4960. [Google Scholar] [CrossRef]
- Reilley, A. openMotor. 2023. Available online: https://github.com/reilleya/openMotor (accessed on 1 October 2023).
- Jupiter, P. SolidPy. 2023. Available online: https://github.com/Projeto-Jupiter/SolidPy (accessed on 1 October 2023).
- Furtney, J. scikit-fmm: The Fast Marching Method for Python. 2023. Available online: https://github.com/scikit-fmm/scikit-fmm (accessed on 1 October 2023).
- Willcox, M.A.; Brewster, M.Q.; Tang, K.C.; Stewart, D.S. Solid Propellant Grain Design and Burnback Simulation Using a Minimum Distance Function. J. Propuls. Power 2007, 23, 465–475. [Google Scholar] [CrossRef]
- Ren, P.; Wang, H.; Zhou, G.; Li, J.; Cai, Q.; Yu, J.; Yuan, Y. Solid rocket motor propellant grain burnback simulation based on fast minimum distance function calculation and improved marching tetrahedron method. Chin. J. Aeronaut. 2021, 34, 208–224. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Huismann, I.; Reimer, L.; Strobl, S.; Eichstädt, J.R.; Tschüter, R.; Rempke, A.; Einarsson, G. Accelerating the FlowSimulator: Profiling and scalability analysis of an industrial-grade CFD-CSM toolchain. In Proceedings of the 9th Edition of the International Conference on Computational Methods for Coupled Problems in Science and Engineering (COUPLED PROBLEMS 2021), Sardinia, Italy, 13–16 June 2021. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.K.; Chan, T.; Merriman, B.; Osher, S. A Variational Level Set Approach to Multiphase Motion. J. Comput. Phys. 1996, 127, 179–195. [Google Scholar] [CrossRef]
- Doi, A.; Koide, A. An Efficient Method of Triangulating Equi-Valued Surfaces by Using Tetrahedral Cells. IEICE Trans. Inf. Syst. 1991, 74, 214–224. [Google Scholar]
- Max, N.L.; Williams, P.L.; Silva, C.T. Approximate Volume Rendering for Curvilinear and Unstructured Grids by Hardware-Assisted Polyhedron Projection. Int. J. Imaging Syst. Technol. 2000, 11, 53–61. [Google Scholar] [CrossRef]
- Tornberg, A.K.; Engquist, B. Numerical approximations of singular source terms in differential equations. J. Comput. Phys. 2004, 200, 462–488. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeriadtke, J.E.; Martin, J.; Wartemann, V. Hybrid Rocket Engine Burnback Simulations Using Implicit Geometry Descriptions. Aerospace 2024, 11, 103. https://doi.org/10.3390/aerospace11020103
Zeriadtke JE, Martin J, Wartemann V. Hybrid Rocket Engine Burnback Simulations Using Implicit Geometry Descriptions. Aerospace. 2024; 11(2):103. https://doi.org/10.3390/aerospace11020103
Chicago/Turabian StyleZeriadtke, Jan Erik, Joël Martin, and Viola Wartemann. 2024. "Hybrid Rocket Engine Burnback Simulations Using Implicit Geometry Descriptions" Aerospace 11, no. 2: 103. https://doi.org/10.3390/aerospace11020103
APA StyleZeriadtke, J. E., Martin, J., & Wartemann, V. (2024). Hybrid Rocket Engine Burnback Simulations Using Implicit Geometry Descriptions. Aerospace, 11(2), 103. https://doi.org/10.3390/aerospace11020103





