Comparison of Two Aerodynamic Models for Projectile Trajectory Simulation
Abstract
1. Introduction
2. Test Bed Vehicle
3. Flight Simulation Model
3.1. Environment
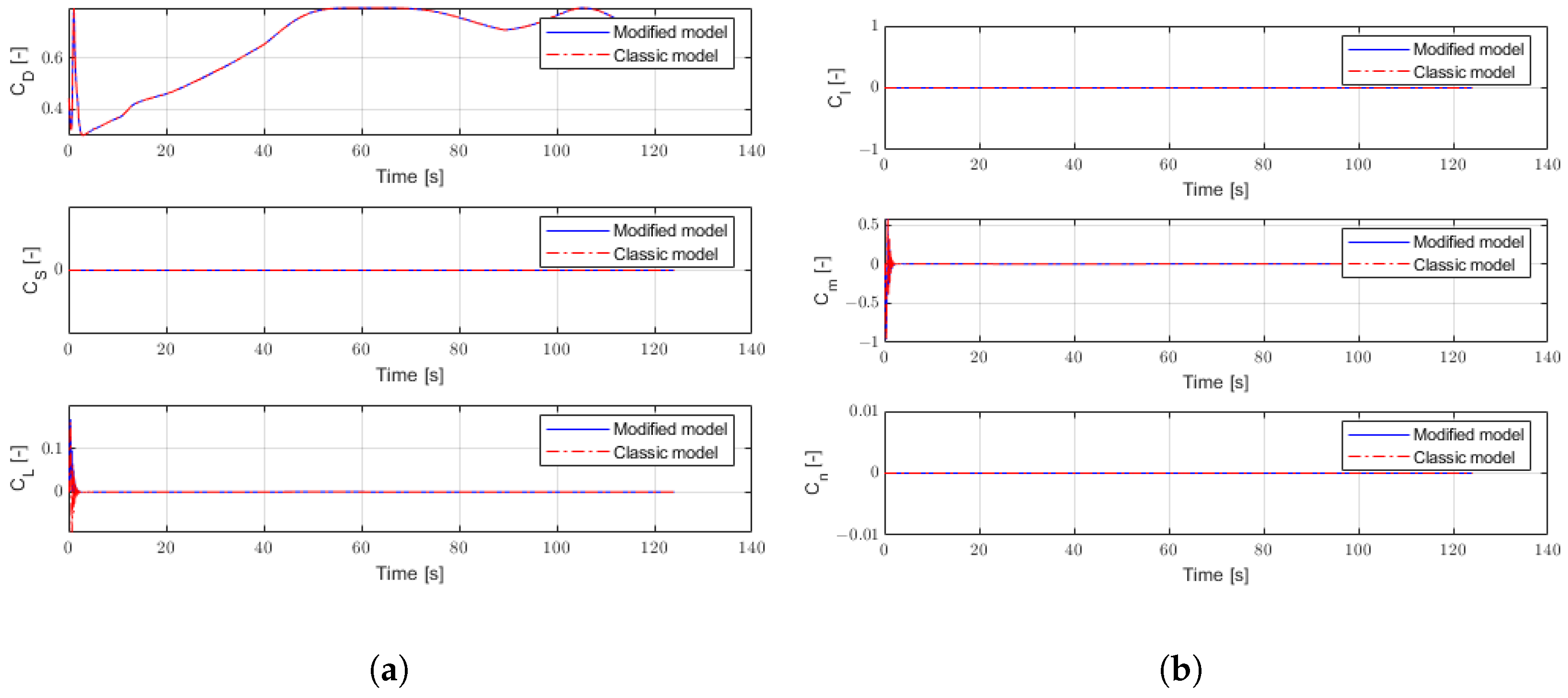
3.2. Aerodynamics
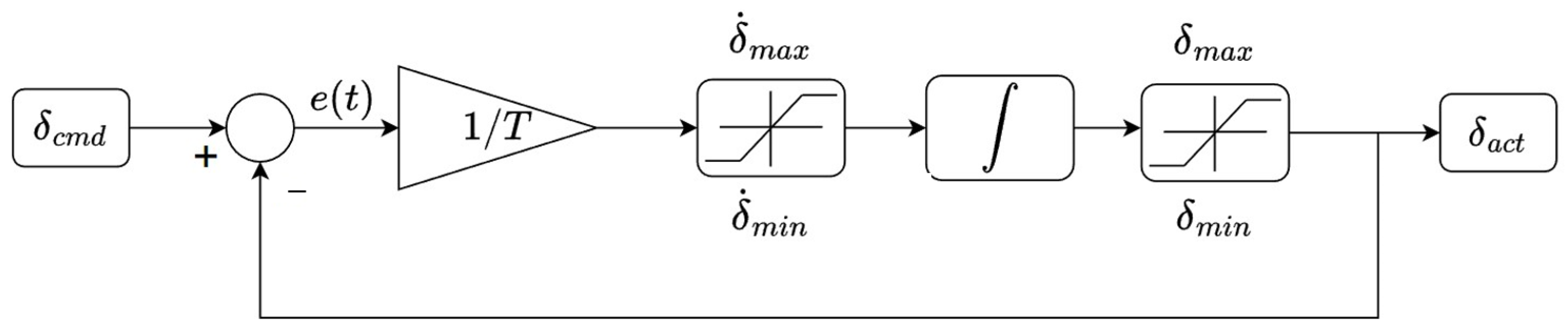
4. Guidance and Control
5. Investigated Research Scenarios
6. Results
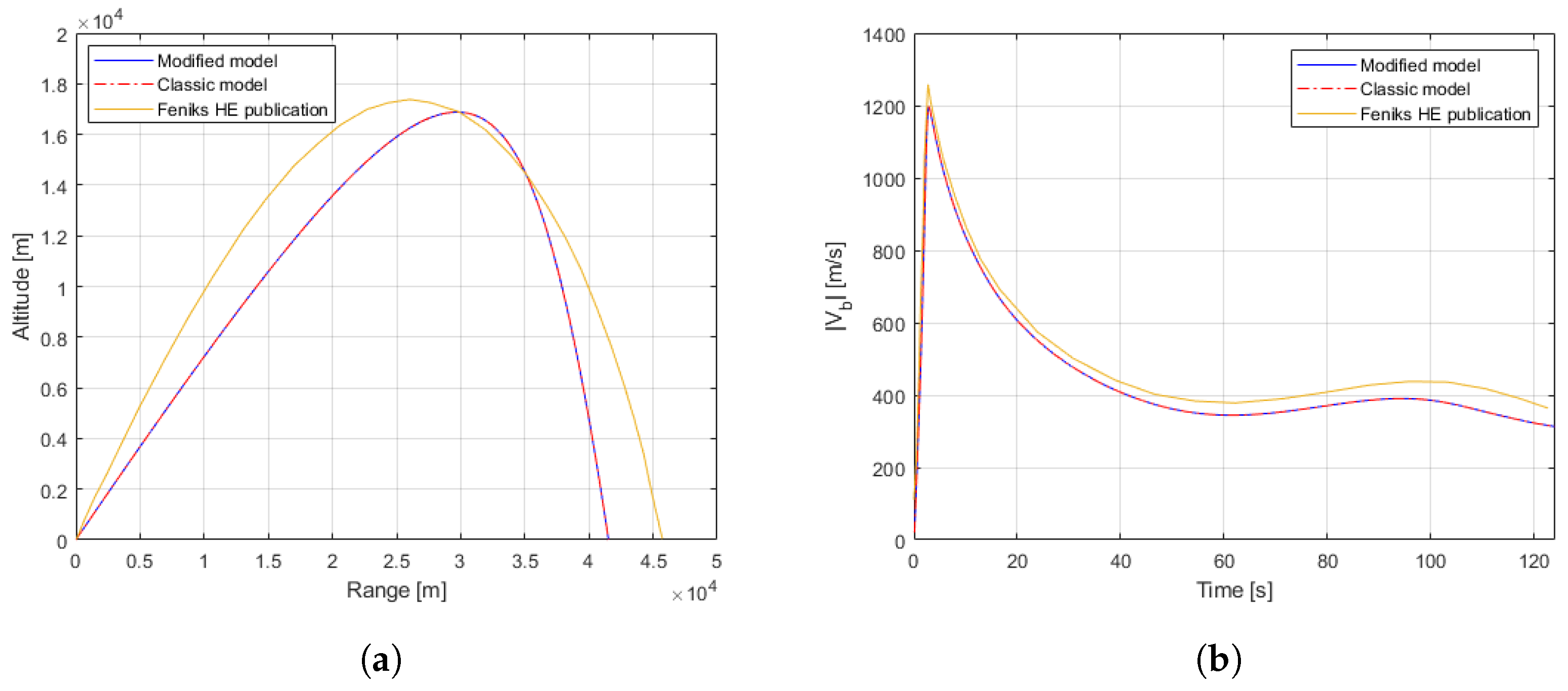
6.1. Ballistic Flight Results
6.2. Altitude Hold and Descent Results
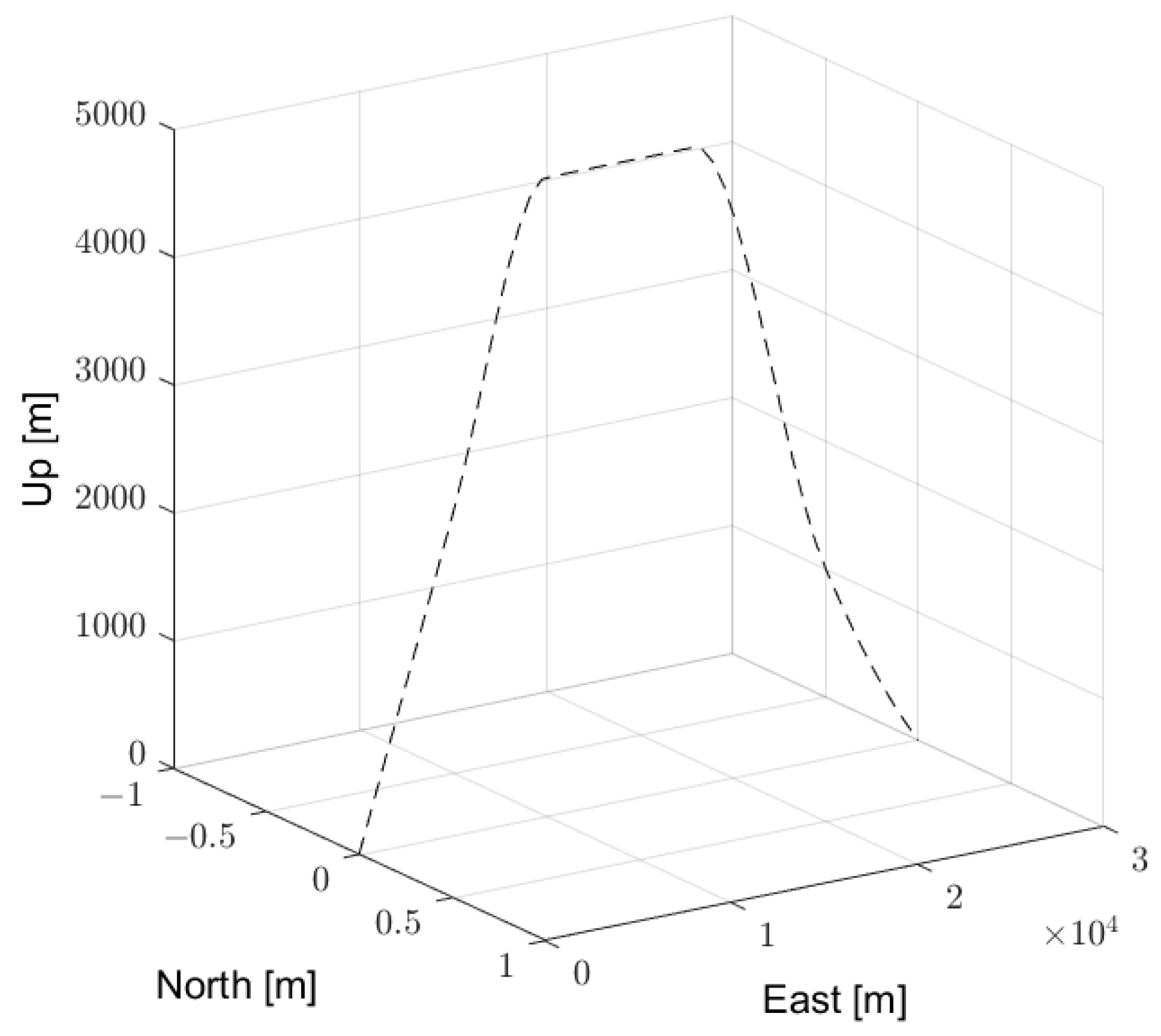
6.3. Obstacle Avoidance Results
6.4. Evasive Manoeuvre Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | Aerodynamic Coordinate System |
| act | current actual signal at the respective timestep |
| B | Body Coordinate System |
| CFD | Computational Fluid Dynamics |
| commanded signal at the respective timestep | |
| LLA | Latitude, Longitude, Altitude |
| North East Down Coordinate System | |
| PID | Proportional-Integral-Derivative controller |
| Latin symbols: | |
| speed of sound at H, [] | |
| centre of mass change in the x direction, [] | |
| transformation matrix from aerodynamic to body frame | |
| transformation matrix from the Body Coordinate System (B) to North East Down Coordinate System () | |
| transformation matrix from the i-th canard reference frame () to the projectile’s Body reference frame (B) | |
| transformation matrix from the i-th canard aerodynamic reference frame () to the i-th canard reference frame () | |
| coefficients of drag, side force, lift and rolling, pitching and yawing moments for , respectively | |
| object reference diameter, [] | |
| e | Oswald efficiency number |
| aerodynamic force vector, [] | |
| gravitational force vector, [] | |
| thrust force vector, [] | |
| gravitational acceleration, [] | |
| H | geopotential altitude, [] |
| reference altitude, [] | |
| I | mass moment of inertia tensor with respect to body coordinate system |
| full mass moments of inertia with respect to body coordinate system , [] | |
| full mass moments of inertia with respect to body coordinate system , [] | |
| k | specific heat ratio |
| L | object length, [] |
| temperature gradient above | |
| m | object mass, [] |
| initial full mass with propellant, [] | |
| mass after propellant exhaustion, [] | |
| M | Mach number, [−] |
| aerodynamic moment vector, [] | |
| control surface index | |
| p | roll rate, [] |
| commanded roll rate, [] | |
| pressure at , [] | |
| air pressure at H, [] | |
| quaternion rotation | |
| , | components of the quaternion rotation vector |
| quaternion rate of change | |
| q | pitch rate, [] |
| commanded pitch rate, [] | |
| r | yaw rate, [] |
| commanded yaw rate, [] | |
| object velocity vector in the frame, [] | |
| object position vector in the frame, [] | |
| R | gas constant of air, [] |
| object reference area, [] | |
| T | Section 3 temperature H, [] |
| T | Section 4 canard servo time constant, [] |
| ambient temperature at the altitude H, [] | |
| ambient temperature at the altitude , [] | |
| object’s velocity magnitude relative to the airflow, [] | |
| linear acceleration vector in the body coordinate system, [] | |
| velocity vector in the body coordinate system, [] | |
| Greek symbols: | |
| angle of attack, [] | |
| angle of attack derivative, [] | |
| total angle of attack, [] | |
| angle of attack in the plane, [] | |
| derivative of angle of attack in the plane, [] | |
| total angle of attack in the plane, [] | |
| derivative of angle of attack in the plane, [] | |
| angle of sideslip derivative, [] | |
| canard deflection angle, [] | |
| commanded canard deflections in the roll, pitch and yaw channels respectively, [] | |
| canard deflection speed, [] | |
| Euler pitch angle, [] | |
| commanded pitch angle, [] | |
| aspect ratio, | |
| air density at H, [] | |
| Euler roll angle, [] | |
| commanded roll angle, [] | |
| aeroballistic incidence roll angle, [] | |
| Euler yaw angle, [] | |
| commanded yaw angle, [] | |
| angular acceleration vector in the body coordinate system, [] | |
| angular velocity vector in the body coordinate system, [] |
References
- Dilley, A.; Mc Bride, R.; Yuki, V.; Brasher, M.; Marquart, E. Dynamic wind tunnel test of an innovative rolling missile model. In Proceedings of the 26th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Seattle, WA, USA, 23–26 June 2008; p. 4032. [Google Scholar]
- Massey, K.; McMichael, J.; Warnock, T.; Hay, F. Design and wind tunnel testing of guidance pins for supersonic projectiles. In Transformational Science And Technology for the Current and Future Force: (With CD-ROM); World Scientific: Singapore, 2006; pp. 121–128. [Google Scholar]
- Thomson, K. Wind Tunnel Tests on a Tube-Launched Missile Configuration with a Deflectable Nose Control and a Novel Wrap—Around Fin Stabiliser; Weapons Systems Research Laboratory: Salisbury, Australia, 1983. [Google Scholar]
- Ożóg, R.; Jacewicz, M.; Głębocki, R. Use of wind tunnel measurements data in cold launched missile flight simulations. Pomiary Autom. Robot. 2020, 24, 49–60. [Google Scholar] [CrossRef][Green Version]
- Chen, G.; Tang, Z.; Wang, W.; Xu, M. A novel aerodynamic modeling method for an axisymmetric missile with tiny units. Adv. Mech. Eng. 2019, 11, 1687814019839511. [Google Scholar] [CrossRef]
- Sahbon, N.; Murpani, S.; Michałów, M.; Miedziński, D.; Sochacki, M. A CFD study of the aerodynamic characteristics of Twardowsky and FOK rockets. Trans. Aerosp. Res. 2022, 2022, 35–58. [Google Scholar] [CrossRef]
- Sahu, J.; Edge, H.L.; Heavey, K.R.; Ferry, E.N. Computational Fluid Dynamics Modeling of Multi-Body Missile Aerodynamic Interference; US Army Research Laboratory, ARL-TR-1765: Aberdeen Proving Ground, MD, USA, 1998. [Google Scholar]
- Mieloszyk, J.; Tarnowski, A.; Tomaszewski, A.; Goetzendorf-Grabowski, T. Validation of flight dynamic stability optimization constraints with flight tests. Aerosp. Sci. Technol. 2020, 106, 106193. [Google Scholar] [CrossRef]
- Ozger, E. Aerodynamic model validation of Eurofighter aircraft. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007; p. 6718. [Google Scholar]
- Fischenberg, D. A method to validate wake vortex encounter models from flight test data. In Proceedings of the 27th International Congress of the Aeronautical Sciences, Nice, France, 19–24 September 2010; International Council of the Aeronautical Sciences: Edinburgh, UK, 2010; pp. 2010–2016. [Google Scholar]
- McClinton, C.; Voland, R.; Holland, S.; Engelund, W.; White, J.; Pahle, J. Wind tunnel testing, flight scaling and flight validation with Hyper-X. In Proceedings of the 20th AIAA Advanced Measurement and Ground Testing Technology Conference, Albuquerque, NM, USA, 15–18 June 1998; p. 2866. [Google Scholar]
- Sethunathan, P.; Anupriya, A.; Prabha, K.H.; Vaishnavi, T. Aerodynamic Characterisitics of a Missile Components. Int. J. Res. Eng. Technol. 2015, 4, 100–104. [Google Scholar]
- Al-Garni, A.Z.; Abdallah, A.M. Aerodynamic-Shape Optimization of Supersonic-Missiles Using Monte-Carlo. Int. Rev. Aerosp. Eng. (I.RE.AS.E) 2008, 20, 10. [Google Scholar]
- Aksu, A. Aerodynamic Parameter Estimation of a Missile. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2013. [Google Scholar]
- Abney, E.; McDaniel, M. High angle of attack aerodynamic predictions using missile datcom. In Proceedings of the 23rd AIAA Applied Aerodynamics Conference, Toronto, ON, Canada, 6–9 June 2005; p. 5086. [Google Scholar]
- Vasile, J.D.; Bryson, J.; Fresconi, F. Aerodynamic design optimization of long range projectiles using missile DATCOM. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1762. [Google Scholar]
- Khanolkar, N.P.; Bhushan, B.; Siddharth, M.; Borrison, E.; Sinha, J. Analysis of aerodynamic characteristics of a missile configuration. In Proceedings of the 2017 International Conference on Infocom Technologies and Unmanned Systems (Trends and Future Directions) (ICTUS), Dubai, United Arab Emirates, 18–20 December 2017; pp. 877–882. [Google Scholar]
- Zhang, W.D.; Wang, Y.B.; Liu, Y. Aerodynamic study of theater ballistic missile target. Aerosp. Sci. Technol. 2013, 24, 221–225. [Google Scholar] [CrossRef]
- Maurice, A.F. Aerodynamic Performance Predictions of a SA-2 Missile Using Missile Datcom. Ph.D. Thesis, Naval Postgraduate School, Monterey, CA, USA, 2009. [Google Scholar]
- Sooy, T.J.; Schmidt, R.Z. Aerodynamic predictions, comparisons, and validations using missile datcom (97) and aeroprediction 98 (ap98). J. Spacecr. Rockets 2005, 42, 257–265. [Google Scholar] [CrossRef]
- Motyl, K.; Musiałek, F. A computer software application for the design and simulation of unguided rockets. Probl. Mechatroniki Uzbroj. Lotnictwo Inżynieria Bezpieczeństwa 2020, 11, 67–80. [Google Scholar] [CrossRef]
- Sahbon, N.; Jacewicz, M.; Lichota, P.; Strzelecka, K. Path-Following Control for Thrust-Vectored Hypersonic Aircraft. Energies 2023, 16, 2501. [Google Scholar] [CrossRef]
- Głębocki, R.; Jacewicz, M. Simulation study of a missile cold launch system. J. Theor. Appl. Mech. 2018, 56, 901–913. [Google Scholar] [CrossRef]
- Głębocki, R.; Jacewicz, M. Parametric study of guidance of a 160-mm projectile steered with lateral thrusters. Aerospace 2020, 7, 61. [Google Scholar] [CrossRef]
- Aly, K.; El-Sheikh, G. An Algorithm for Calculating the Aerodynamic Derivatives of A Super-Sonic Missile. In Proceedings of the International Conference on Electrical Engineering. Military Technical College, 1999, Number 2nd International Conference on Electrical Engineering ICEENG, Cairo, Egypt, 23–25 November 1999; pp. 621–635. [Google Scholar]
- Motyl, K.; Zygmunt, B.K. Computer simulation of the ballistics of a 122 mm missile with a modernized propulsion unit. Mechatron. Probl. Armament Aviat. Secur. Eng. 2016. [Google Scholar] [CrossRef]
- Mathworks. Mathworks. 2023. Available online: https://www.mathworks.com/help/aeroblks/6dofquaternion.html (accessed on 10 October 2023.).
- Zipfel, P.H. Modeling and Simulation of Aerospace Vehicle Dynamics; AIAA: Reston, VA, USA, 2000. [Google Scholar]
- Cook, M.V. Flight Dynamics Principles: A Linear Systems Approach to Aircraft Stability and Control; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
- Tewari, A. Atmospheric and Space Flight Dynamics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Allerton, D. Principles of Flight Simulation; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 27. [Google Scholar]
- National Oceanic and Atmospheric Administration. U.S. Standard Atmosphere; Technical Report; Government Printing Office: Washington, DC, USA, 1976.
- Defense Mapping Agency, Washington, D.C. Department of Defense World Geodetic System 1984: Its Definition and Relationships with Local Geodetic Systems; Defense Technical Information Center: Fort Belvoir, VA, USA, 1991.
- Drob, D.P.; Emmert, J.T.; Meriwether, J.W.; Makela, J.J.; Doornbos, E.; Conde, M.; Hernandez, G.; Noto, J.; Zawdie, K.A.; McDonald, S.E.; et al. An update to the Horizontal Wind Model (HWM): The quiet time thermosphere. Earth Space Sci. 2015, 2, 301–319. [Google Scholar] [CrossRef]
- Blake, W.B. Missile Datcom User’s Manual: 997 FORTRAN 90 Revision; Air Vehicles Directorte, Air Force Research Laboratory, Air Force Materiel: Dayton, OH, USA, 1998. [Google Scholar]
- Rosema, C.; Doyle, J.; Blake, W.B. Missile Data Compendium (DATCOM) User Manual 2014 Revision; Air Force Research Laboratory Headquarters: Greene County, OH, USA, 2014.
- Charnes, A.; Frome, E.L.; Yu, P.L. The equivalence of generalized least squares and maximum likelihood estimates in the exponential family. J. Am. Stat. Assoc. 1976, 71, 169–171. [Google Scholar] [CrossRef]
- Houghton, E.L.; Carpenter, P.W. Aerodynamics for Engineering Students; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Anderson, J. EBOOK: Fundamentals of Aerodynamics (SI Units); McGraw Hill: New York, NY, USA, 2011. [Google Scholar]
- Fleeman, E.L. Tactical Missile Design; American Institute of Aeronautics and Astronautics Reston: Reston, VA, USA, 2006; Volume 468. [Google Scholar]
- Morelli, E.A. Flight test maneuvers for efficient aerodynamic modeling. J. Aircr. 2012, 49, 1857–1867. [Google Scholar] [CrossRef]
- Park, S.; Deyst, J.; How, J. A New Nonlinear Guidance Logic for Trajectory Tracking. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; pp. 2004–4090. [Google Scholar] [CrossRef]
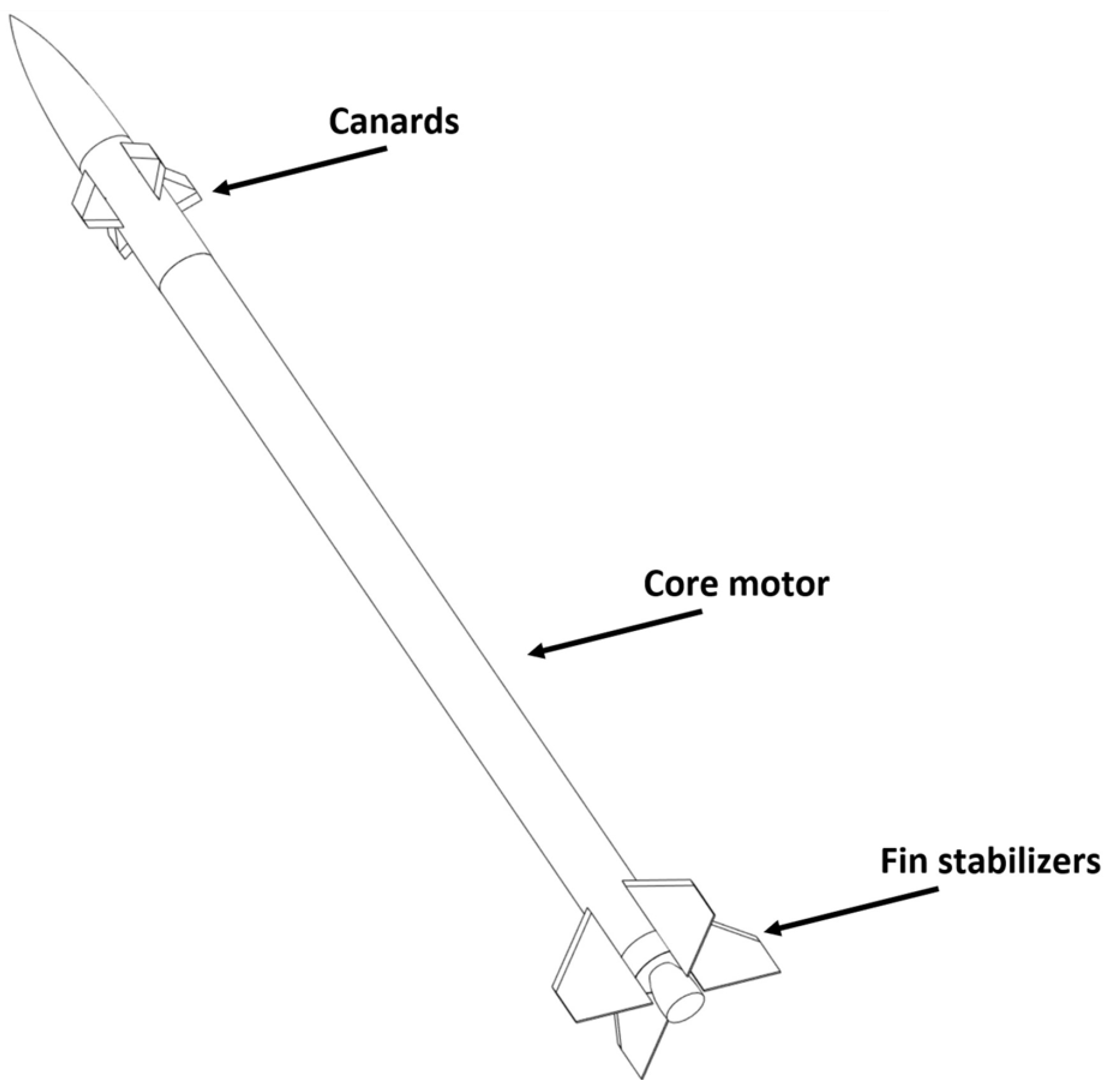

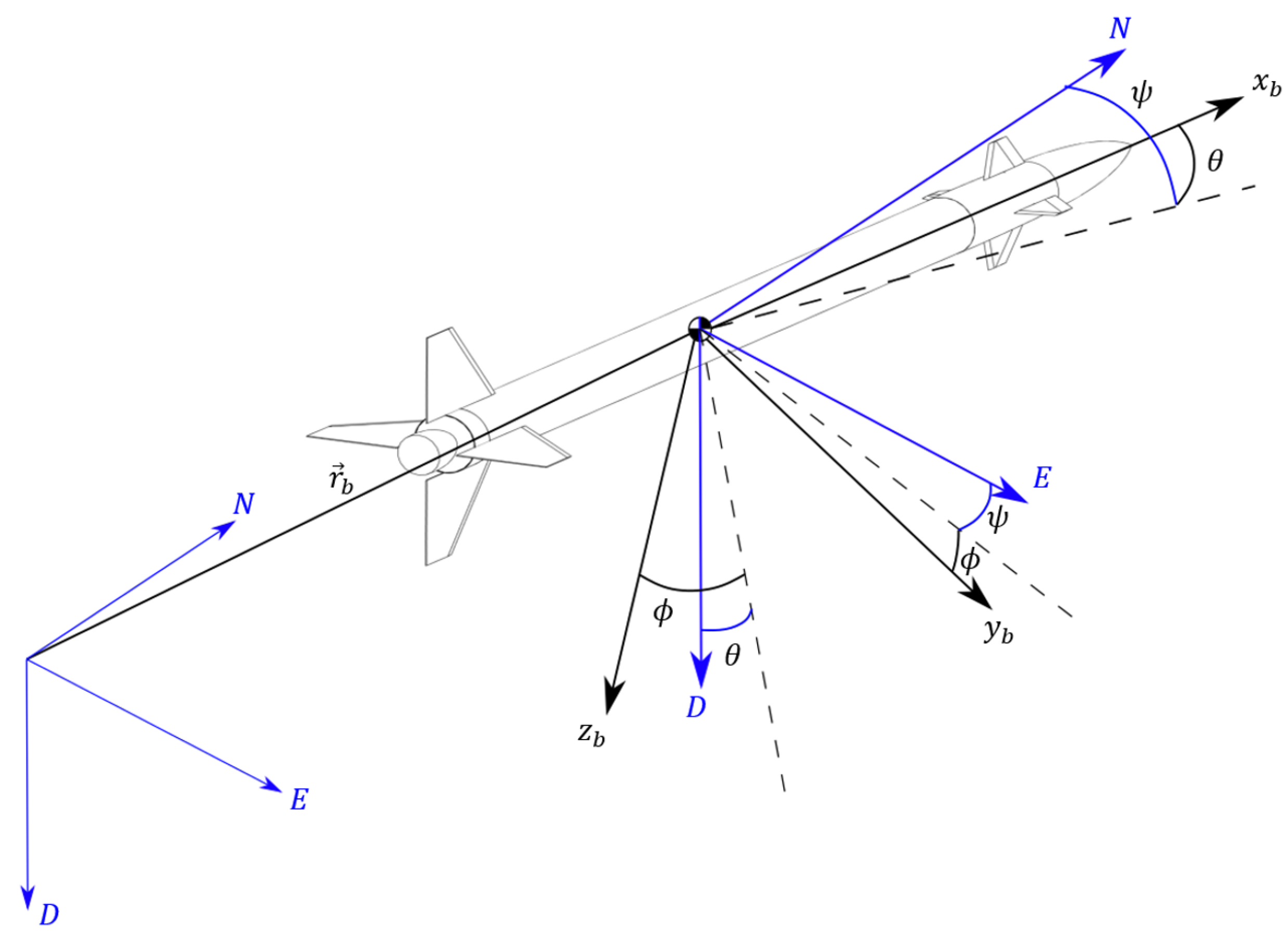
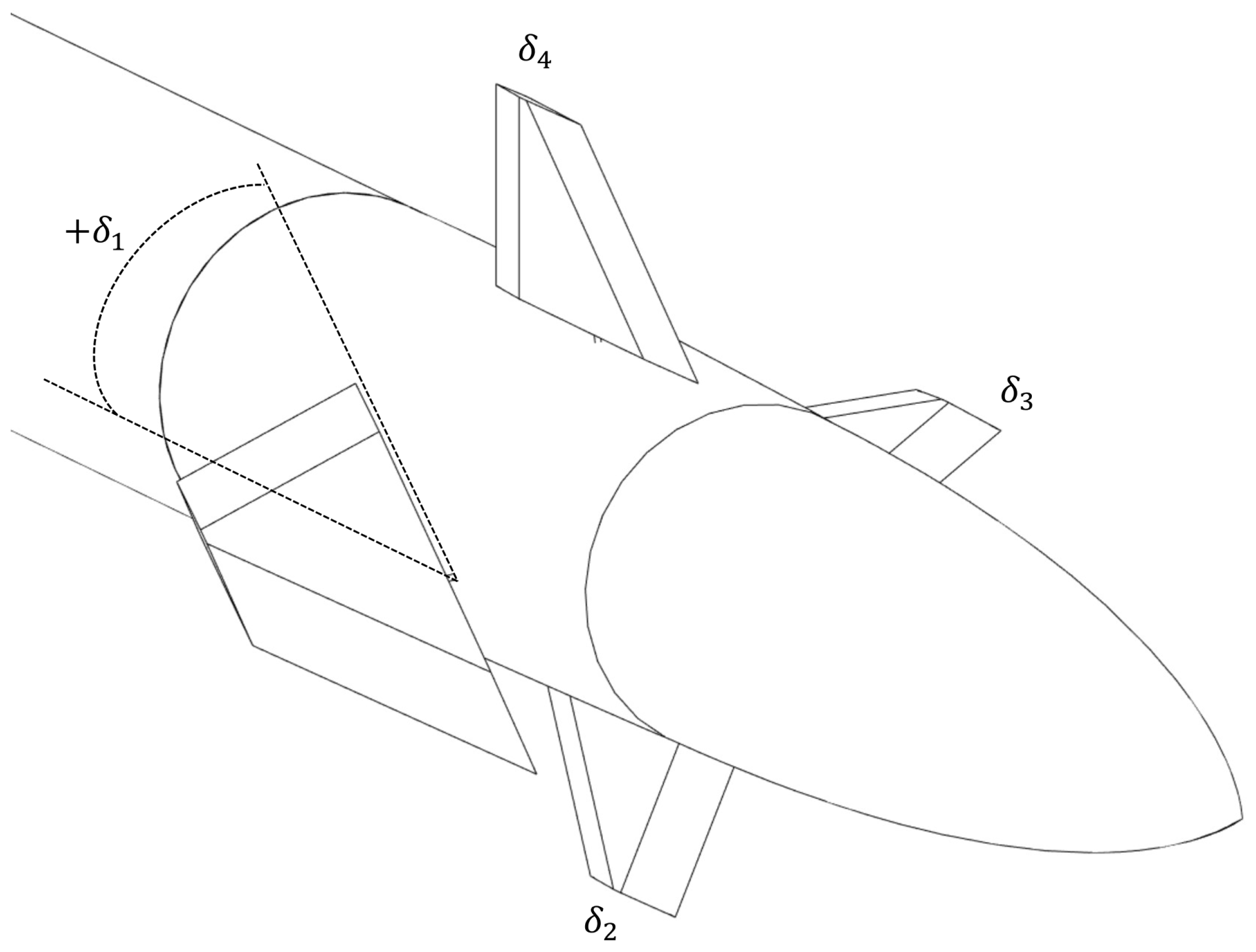
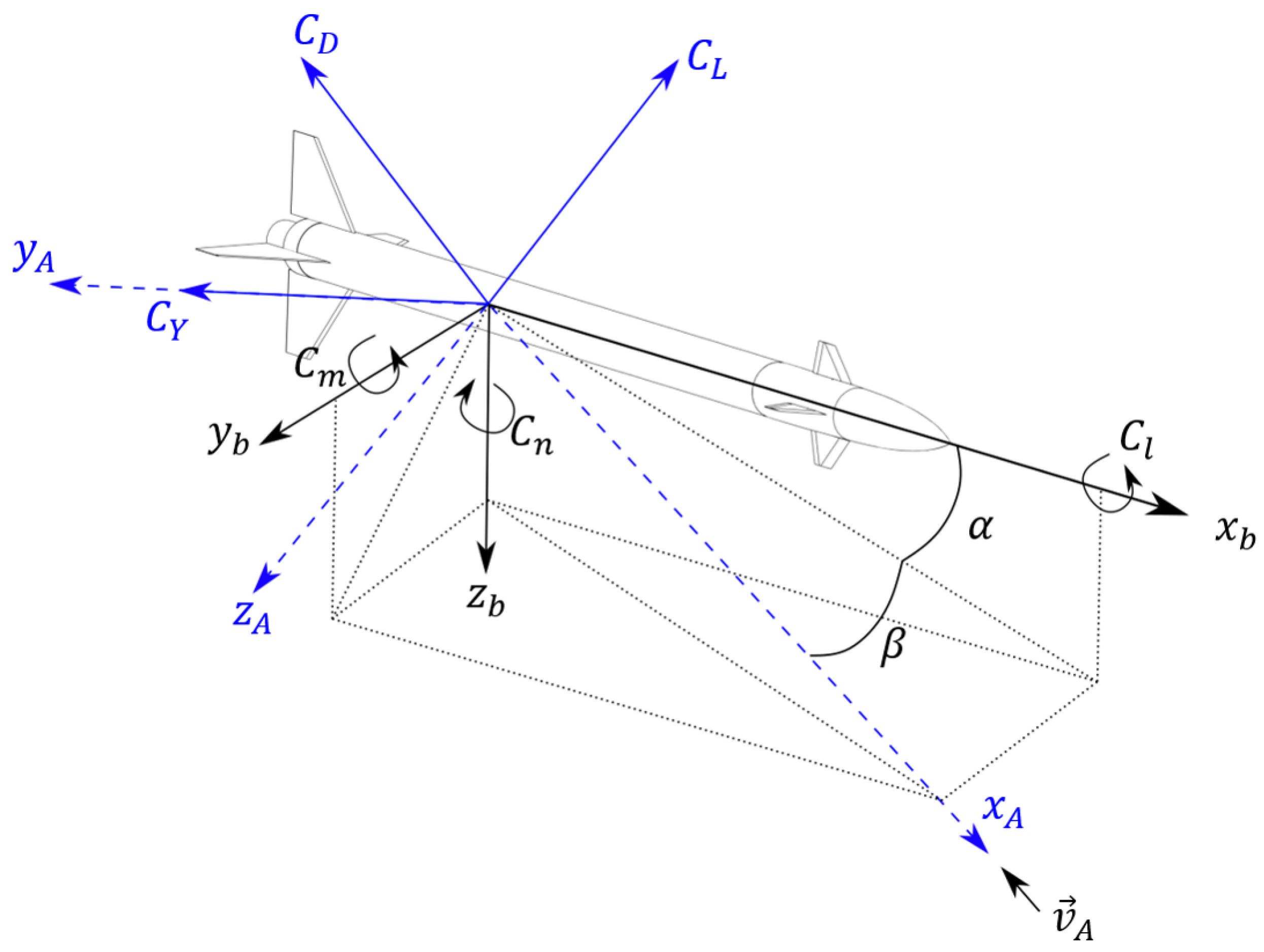






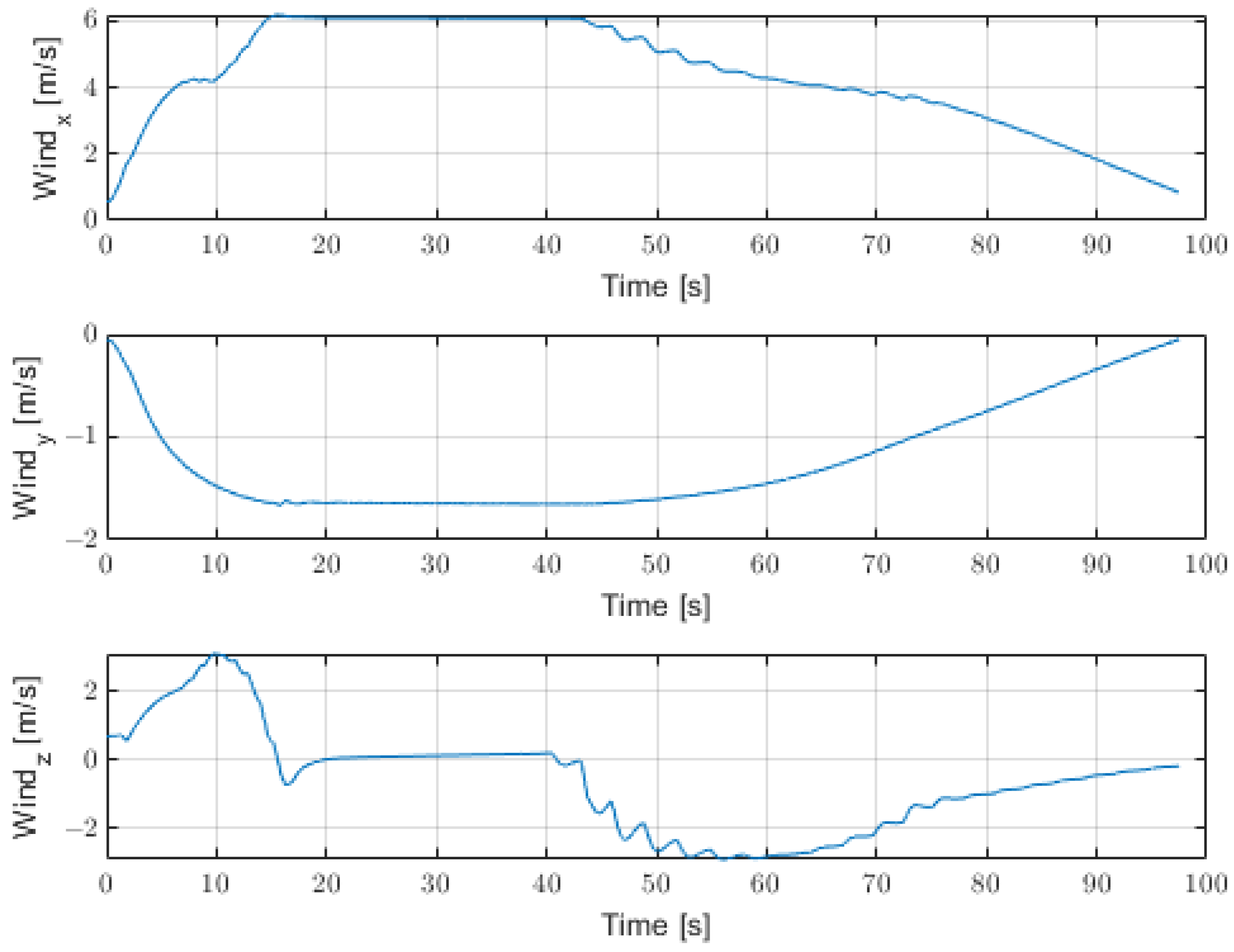

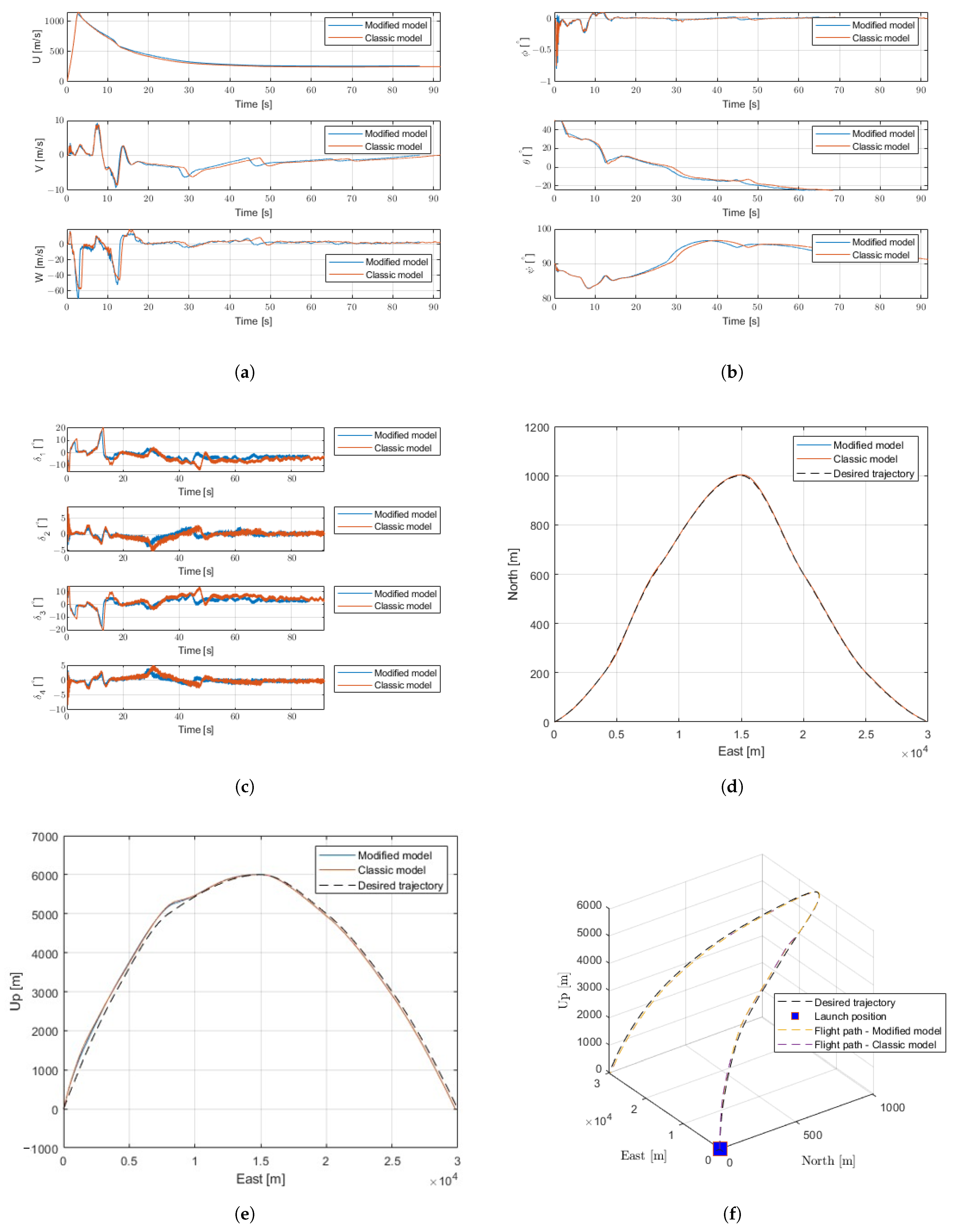
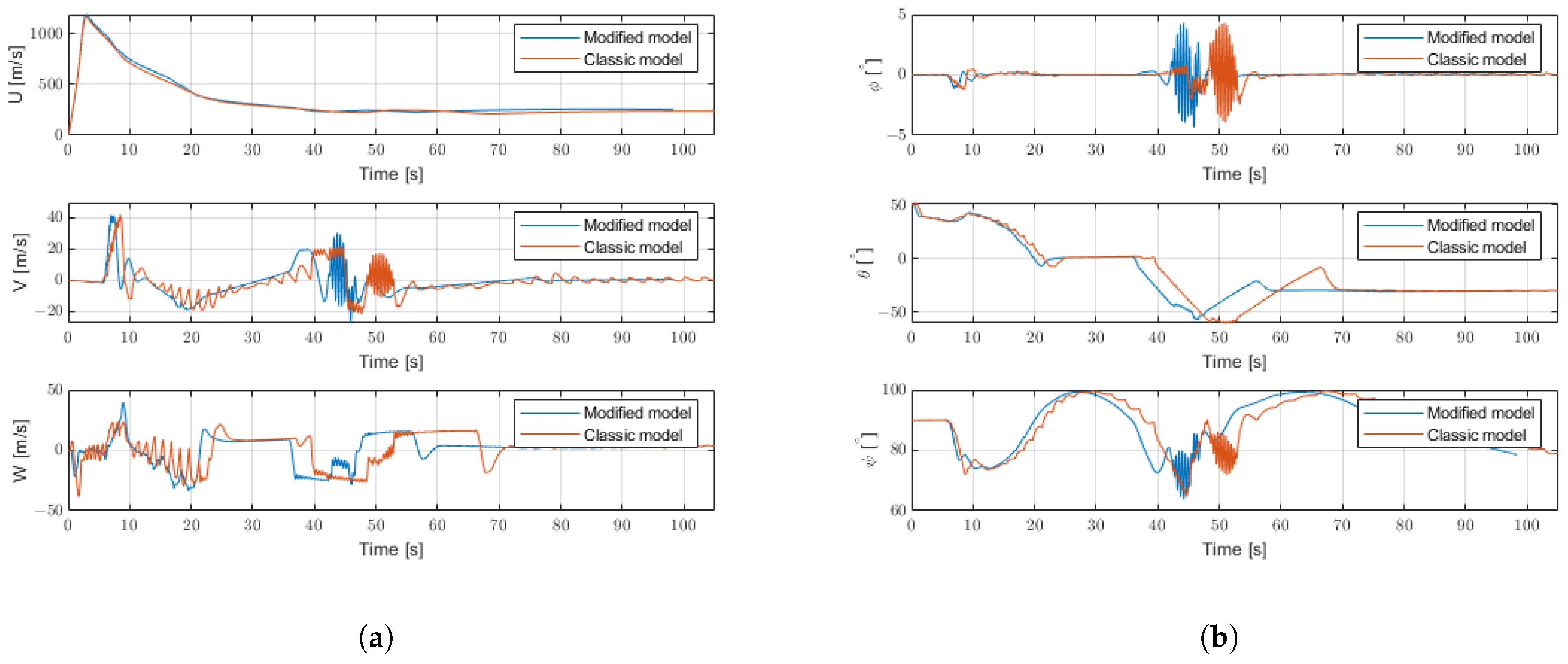
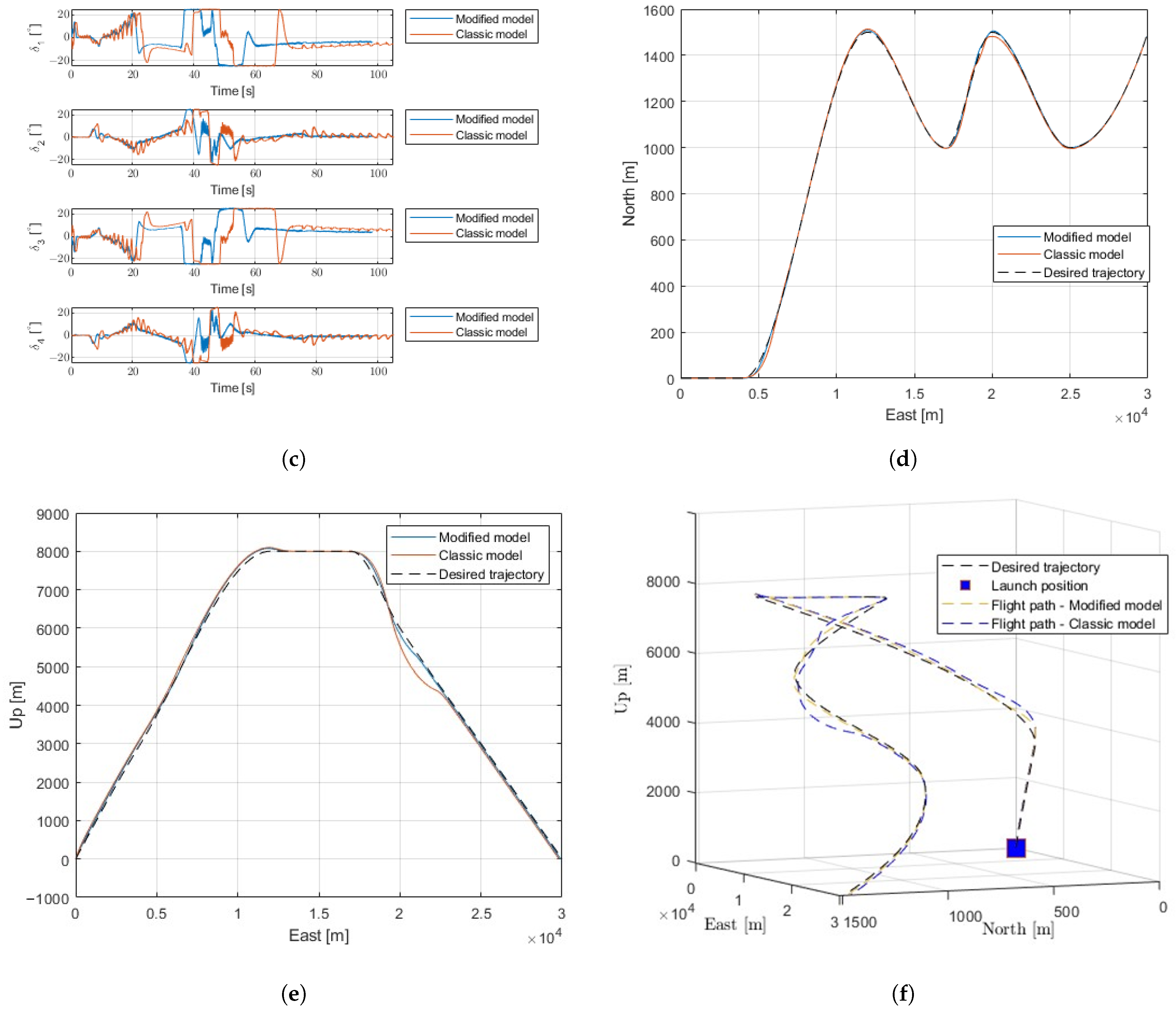
| Parameter | Value | Units |
|---|---|---|
| 60.51 | kg | |
| 35.71 | kg | |
| L | 2.7 | m |
| 0.122 | m | |
| 0.144 | ||
| 34.037 | ||
| 0.098 | ||
| 23.355 |
| M | ||
|---|---|---|
| 0.2 | 0.388 | −789.640 |
| 0.4 | 0.334 | −775.414 |
| 0.6 | 0.320 | −760.700 |
| 0.8 | 0.443 | −744.123 |
| 1 | 0.696 | −767.924 |
| 1.2 | 0.789 | −692.697 |
| 1.4 | 0.641 | −578.439 |
| 1.6 | 0.558 | −498.128 |
| 1.8 | 0.504 | −445.794 |
| 2 | 0.465 | −416.681 |
| 2.2 | 0.442 | −383.414 |
| 2.4 | 0.419 | −365.026 |
| 2.6 | 0.370 | −335.349 |
| 2.8 | 0.351 | −317.579 |
| 3 | 0.333 | −300.399 |
| 3.2 | 0.321 | −285.587 |
| 3.4 | 0.307 | −279.702 |
| 3.6 | 0.294 | −272.634 |
| 3.8 | 0.286 | −262.003 |
| 4 | 0.276 | −254.941 |
| M | ||||||
|---|---|---|---|---|---|---|
| 0.2 | 21.181 | −124.737 | 0.321 | 1.814 | 0.932 | 14.365 |
| 0.4 | 21.475 | −125.694 | 0.330 | 1.839 | 0.945 | 14.565 |
| 0.6 | 22.129 | −128.947 | 0.347 | 1.880 | 0.966 | 14.888 |
| 0.8 | 23.061 | −137.943 | 0.371 | 1.936 | 0.995 | 15.333 |
| 1 | 25.588 | −155.583 | 0.621 | 2.162 | 1.112 | 17.128 |
| 1.2 | 25.798 | −164.733 | 0.808 | 2.189 | 1.126 | 17.343 |
| 1.4 | 22.036 | −129.364 | 0.915 | 1.942 | 0.998 | 15.382 |
| 1.6 | 19.286 | −100.611 | 0.919 | 1.740 | 0.894 | 13.773 |
| 1.8 | 17.451 | −84.123 | 0.880 | 1.555 | 0.798 | 12.302 |
| 2 | 16.421 | −72.245 | 0.856 | 1.417 | 0.728 | 11.214 |
| 2.2 | 15.213 | −63.688 | 0.789 | 1.272 | 0.653 | 10.066 |
| 2.4 | 14.547 | −56.996 | 0.772 | 1.187 | 0.609 | 9.392 |
| 2.6 | 13.470 | −49.429 | 0.733 | 1.106 | 0.568 | 8.749 |
| 2.8 | 12.811 | −44.469 | 0.702 | 1.035 | 0.531 | 8.182 |
| 3 | 12.168 | −40.372 | 0.655 | 0.955 | 0.490 | 7.554 |
| 3.2 | 11.607 | −37.287 | 0.645 | 0.917 | 0.470 | 7.248 |
| 3.4 | 11.391 | −32.316 | 0.612 | 0.853 | 0.438 | 6.743 |
| 3.6 | 11.127 | −30.966 | 0.630 | 0.841 | 0.432 | 6.652 |
| 3.8 | 10.720 | −27.443 | 0.585 | 0.781 | 0.401 | 6.177 |
| 4 | 10.451 | −24.934 | 0.588 | 0.762 | 0.391 | 6.025 |
| M | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 41.455 | 22.289 | −124.697 | −22.241 | 1.175 | 6.438 | −1.914 | 0.983 | −15.152 | 50.830 |
| 0.4 | 42.553 | 22.599 | −125.654 | −22.411 | 1.209 | 6.528 | −1.940 | 0.997 | −15.363 | 51.537 |
| 0.6 | 45.041 | 23.288 | −128.906 | −22.991 | 1.269 | 6.673 | −1.983 | 1.019 | −15.703 | 52.679 |
| 0.8 | 48.696 | 24.270 | −137.899 | −24.595 | 1.357 | 6.872 | −2.042 | 1.050 | −16.173 | 54.255 |
| 1 | 48.696 | 26.934 | −155.533 | −27.741 | 1.357 | 7.677 | −2.280 | 1.172 | −18.066 | 60.606 |
| 1.2 | 102.382 | 27.155 | −164.680 | −29.372 | 2.957 | 7.773 | −2.309 | 1.187 | −18.293 | 61.368 |
| 1.4 | 112.302 | 23.190 | −129.322 | −23.066 | 3.350 | 6.894 | −2.049 | 1.053 | −16.224 | 54.428 |
| 1.6 | 111.166 | 20.293 | −100.579 | −17.939 | 3.369 | 6.173 | −1.835 | 0.943 | −14.527 | 48.734 |
| 1.8 | 110.101 | 18.360 | −84.095 | −14.999 | 3.225 | 5.514 | −1.640 | 0.842 | −12.976 | 43.530 |
| 2 | 113.433 | 17.275 | −72.222 | −12.881 | 3.136 | 5.026 | −1.495 | 0.768 | −11.828 | 39.681 |
| 2.2 | 110.860 | 16.003 | −63.667 | −11.356 | 2.889 | 4.511 | −1.342 | 0.689 | −10.617 | 39.681 |
| 2.4 | 113.266 | 15.301 | −56.978 | −10.162 | 2.826 | 4.209 | −1.252 | 0.643 | −9.906 | 33.231 |
| 2.6 | 107.479 | 14.168 | −49.413 | −8.813 | 2.683 | 3.921 | −1.167 | 0.599 | −9.228 | 30.956 |
| 2.8 | 106.327 | 13.473 | −44.455 | −7.929 | 2.572 | 3.667 | −1.091 | 0.560 | −8.630 | 28.951 |
| 3 | 104.125 | 12.797 | −40.359 | −7.198 | 2.397 | 3.386 | −1.008 | 0.517 | −7.968 | 26.730 |
| 3.2 | 102.148 | 12.206 | −37.275 | −6.648 | 2.362 | 3.249 | −0.967 | 0.496 | −7.645 | 25.647 |
| 3.4 | 105.309 | 11.979 | −32.306 | −5.762 | 2.237 | 3.022 | −0.900 | 0.462 | −7.112 | 23.860 |
| 3.6 | 107.108 | 11.701 | −30.956 | −5.521 | 2.305 | 2.981 | −0.888 | 0.455 | −7.016 | 23.536 |
| 3.8 | 105.628 | 11.272 | −27.434 | −4.893 | 2.140 | 2.769 | −0.824 | 0.423 | −6.516 | 21.858 |
| 4 | 106.246 | 10.990 | −24.926 | −4.446 | 2.149 | 2.700 | −0.804 | 0.412 | −6.355 | 21.318 |
| PID Coefficients | PID | p PID | Altitude PID | PID | q PID | PID | r PID |
|---|---|---|---|---|---|---|---|
| P | 5 | 2.5 | 0.6 | 4 | 4.2 | 5.5 | 2.8 |
| I | 0.1 | 0.05 | 0.001 | 0 | 0 | 0.3 | 0.02 |
| D | 0.3 | 0.1 | 5 | 0.05 | 4 | 0.8 | 0.04 |
| PID Coefficients | PID | p PID | Altitude PID | PID | q PID | PID | r PID |
|---|---|---|---|---|---|---|---|
| P | 5 | 2.5 | 0.5 | 2 | 0.5 | 5.3 | 3 |
| I | 0.1 | 0.05 | 0 | 0 | 0 | 0.3 | 0.01 |
| D | 0.3 | 0.1 | 0.5 | 0.05 | 0.3 | 0.5 | 0.05 |
| Parameter | Value | Unit |
|---|---|---|
| Latitude | 52.178 | |
| Longitude | 20.956 | |
| Altitude | 0 | m |
| 20 | m/s | |
| 0 | ||
| 50 | ||
| 90 | ||
| 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahbon, N.; Welcer, M. Comparison of Two Aerodynamic Models for Projectile Trajectory Simulation. Aerospace 2024, 11, 189. https://doi.org/10.3390/aerospace11030189
Sahbon N, Welcer M. Comparison of Two Aerodynamic Models for Projectile Trajectory Simulation. Aerospace. 2024; 11(3):189. https://doi.org/10.3390/aerospace11030189
Chicago/Turabian StyleSahbon, Nezar, and Michał Welcer. 2024. "Comparison of Two Aerodynamic Models for Projectile Trajectory Simulation" Aerospace 11, no. 3: 189. https://doi.org/10.3390/aerospace11030189
APA StyleSahbon, N., & Welcer, M. (2024). Comparison of Two Aerodynamic Models for Projectile Trajectory Simulation. Aerospace, 11(3), 189. https://doi.org/10.3390/aerospace11030189









