Approach and Landing Energy Prediction Based on a Long Short-Term Memory Model
Abstract
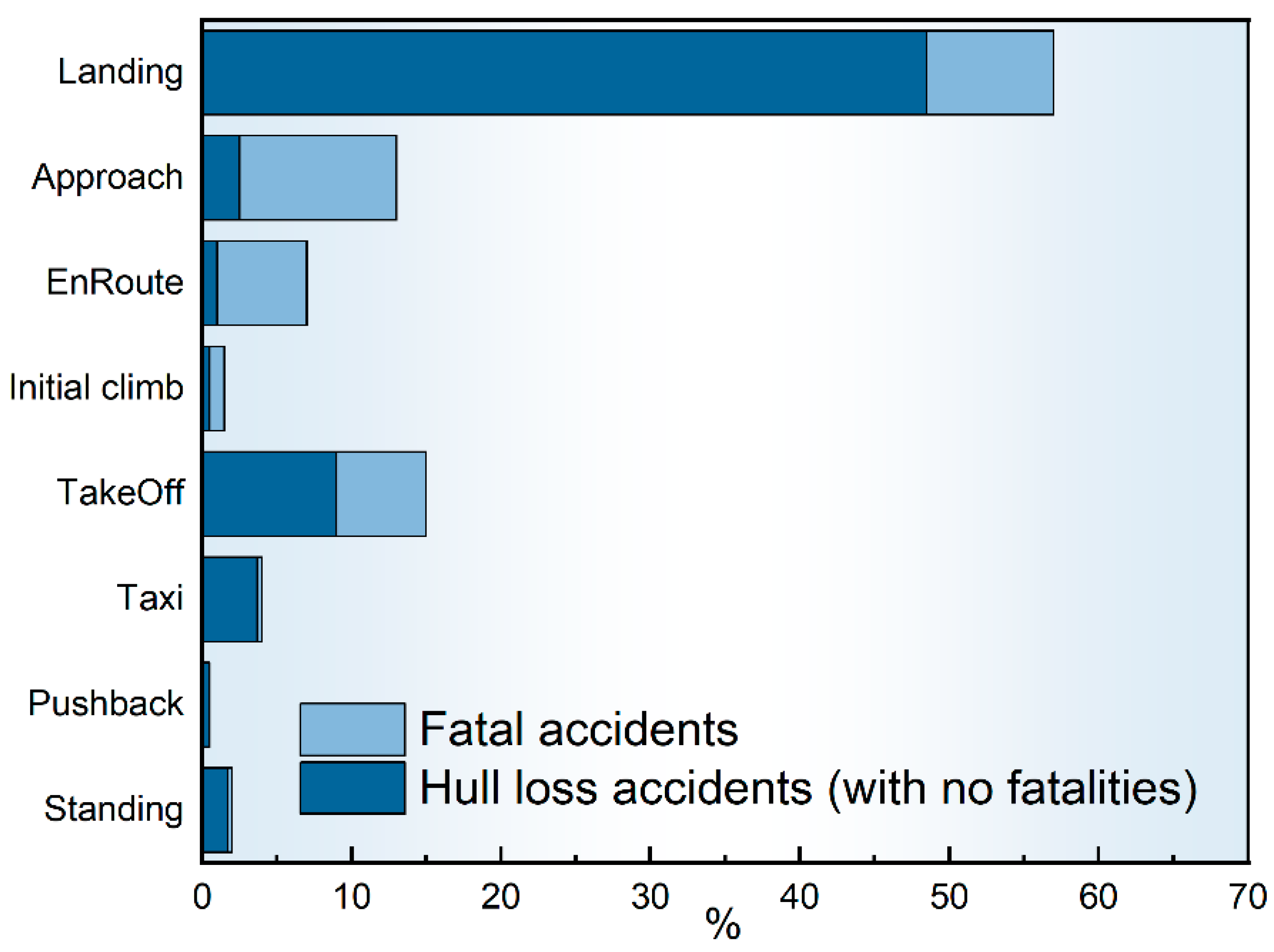
:1. Introduction
2. Theoretical Basis for the Prediction of the Low Energy State of Approach
2.1. Basis of Aircraft System Reliability Modeling
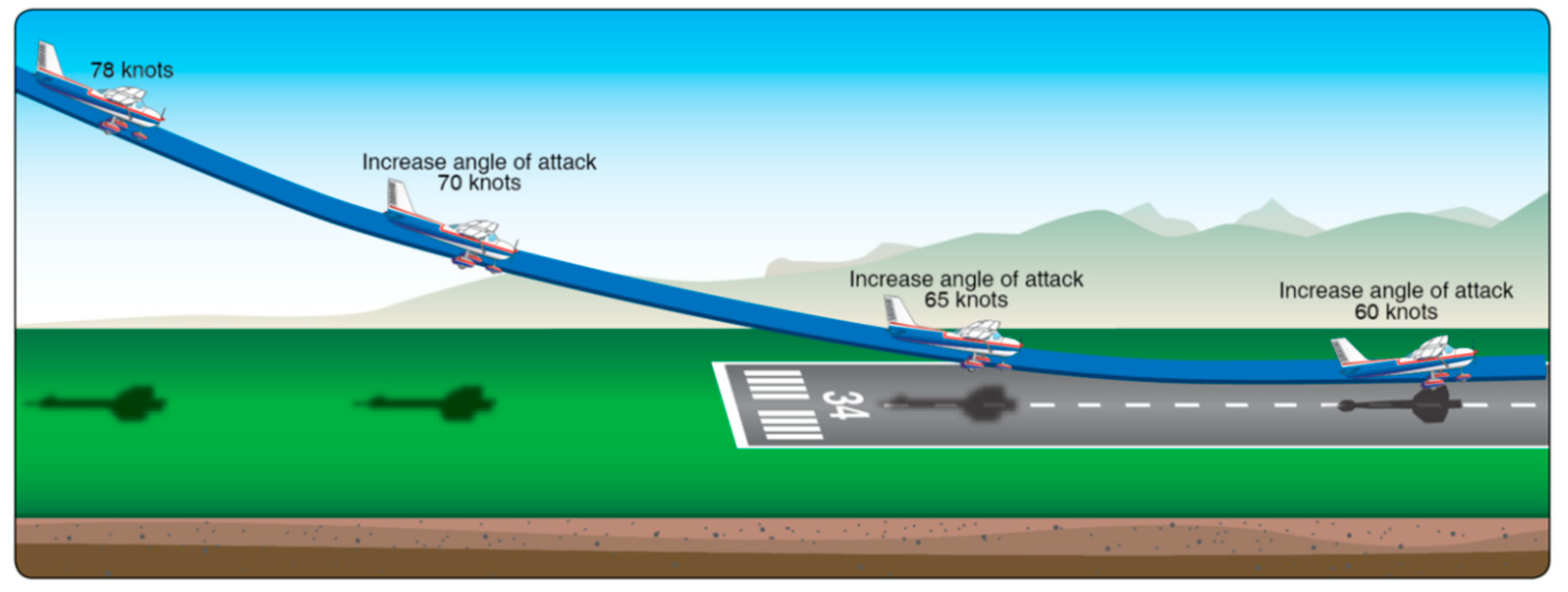
- Indicated airspeed: The indicated airspeed should fall within the range of Vref − 5 kt to Vref + 20 kt. The velocity outside this range might indicate abnormal kinetic energy, making the aircraft difficult to control during the approach and landing phases.
- Descent rate: A descent rate exceeding 1000 ft/min implies that the aircraft is descending too rapidly. Without proper longitudinal control, this could lead to accidents such as heavy landings, runway overruns, or a loss of control. The descent rate can be calculated using the speed index and glide path index.
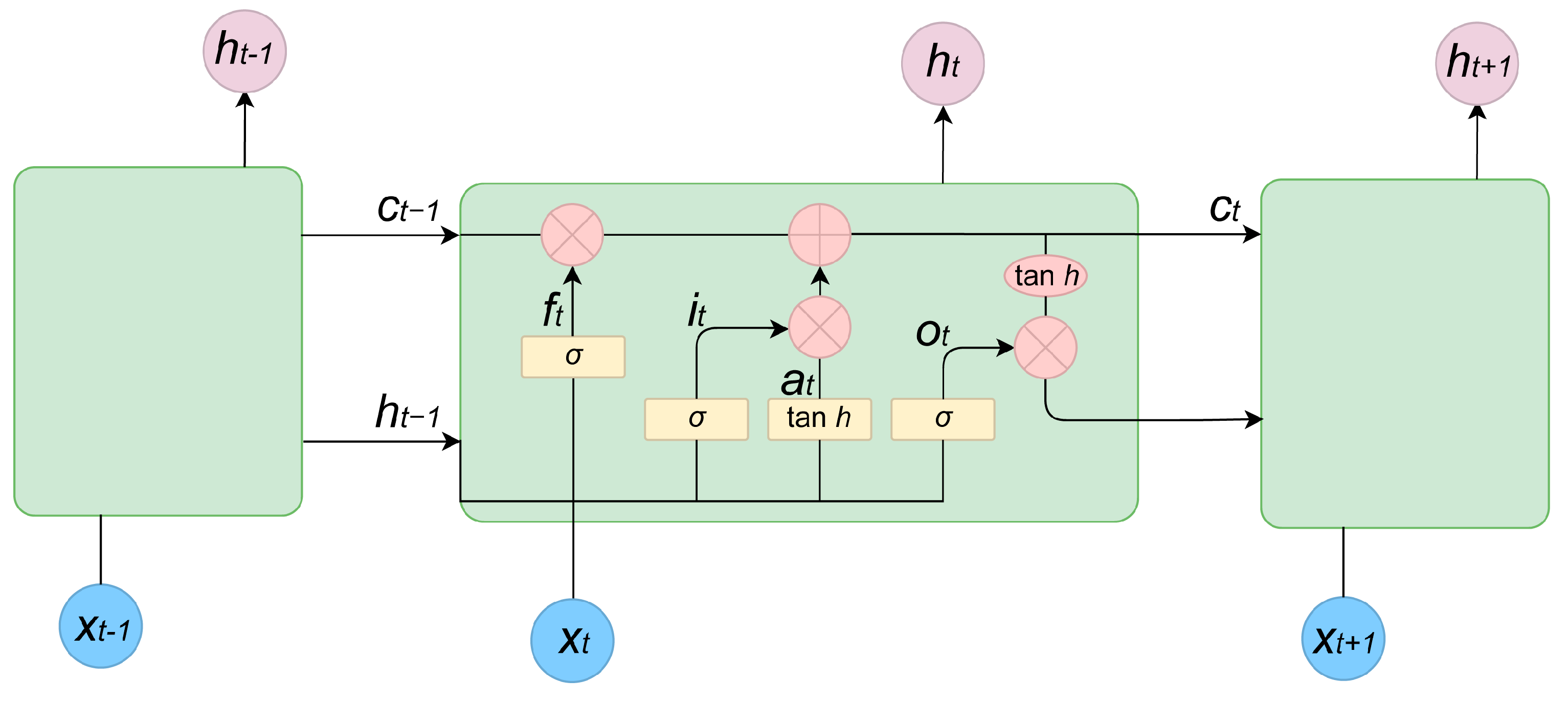
2.2. Overview of LSTM
- (1)
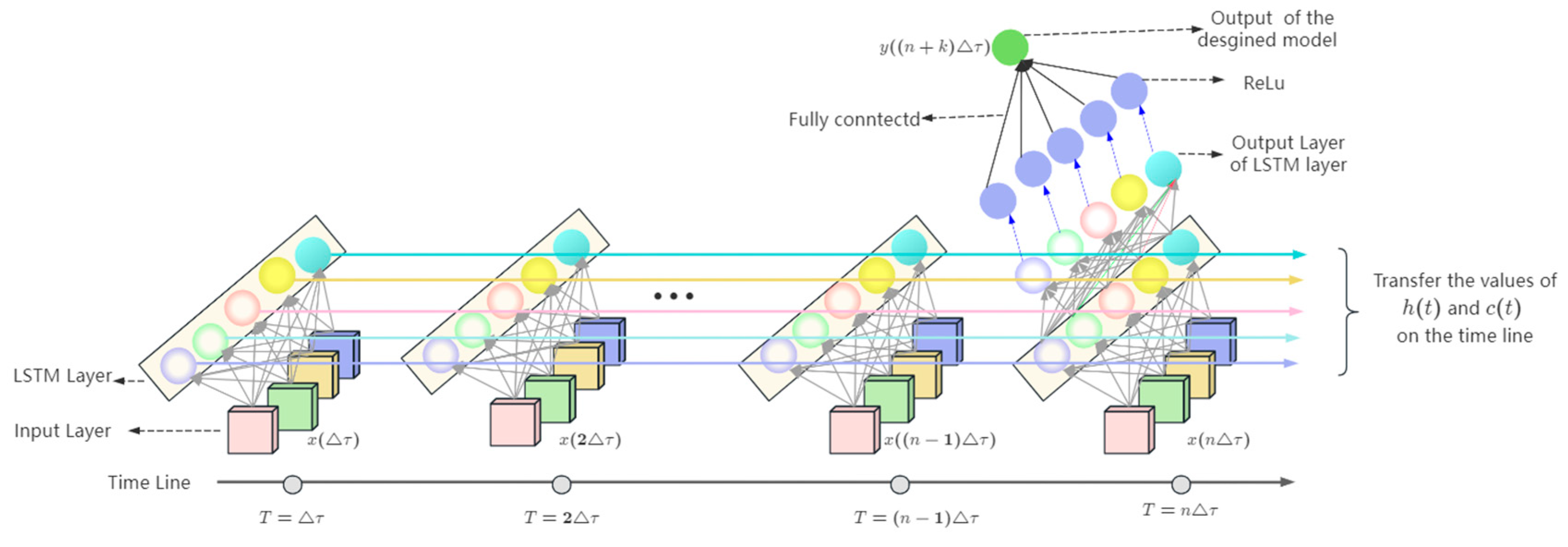
- Forward propagation: Input the flight parameters collected in the aircraft simulator into the LSTM model. The parameters are transmitted forward through the LSTM network by calculating the value of gate , and . The method of computing these values is shown in Equations (1)–(6). The calculation in this step is from inputs to hidden layers and inner gates and then finally to outputs, so it is called the forward propagation.
- (2)
- Loss function calculation: Calculate the loss function, as shown in Equation (7). The symbol M is the number of approach and landing experiments. The symbol Nj means the sample number in the jth experiment. The symbol means the output value of the velocity/altitude/glide angle at the time i, which is calculated through the forward propagation.
- (3)
- Backpropagation: Backpropagation means calculating the correction values of weight and bias given the function loss. It is a process from the outputs to the hidden layers and inner gates of LSTM, so it is called the backpropagation. Specifically, according to the calculated loss function and the gradient value in the current iteration, calculate the gradient value in the next iteration of the loss function for each parameter, as shown in Equation (8). In the equation, means the weight correction value of layer i and layer j in the LSTM model. The symbol means the bias correction value of bj, and means the learning rate.
- (4)
- Parameter updating: the Adam gradient descent method is used to update the gradient values of each parameter of the LSTM model. Repeat the above steps until either the set number of training iterations or the convergence condition is reached.
3. Aircraft Approach and Landing Simulation and Prediction Model
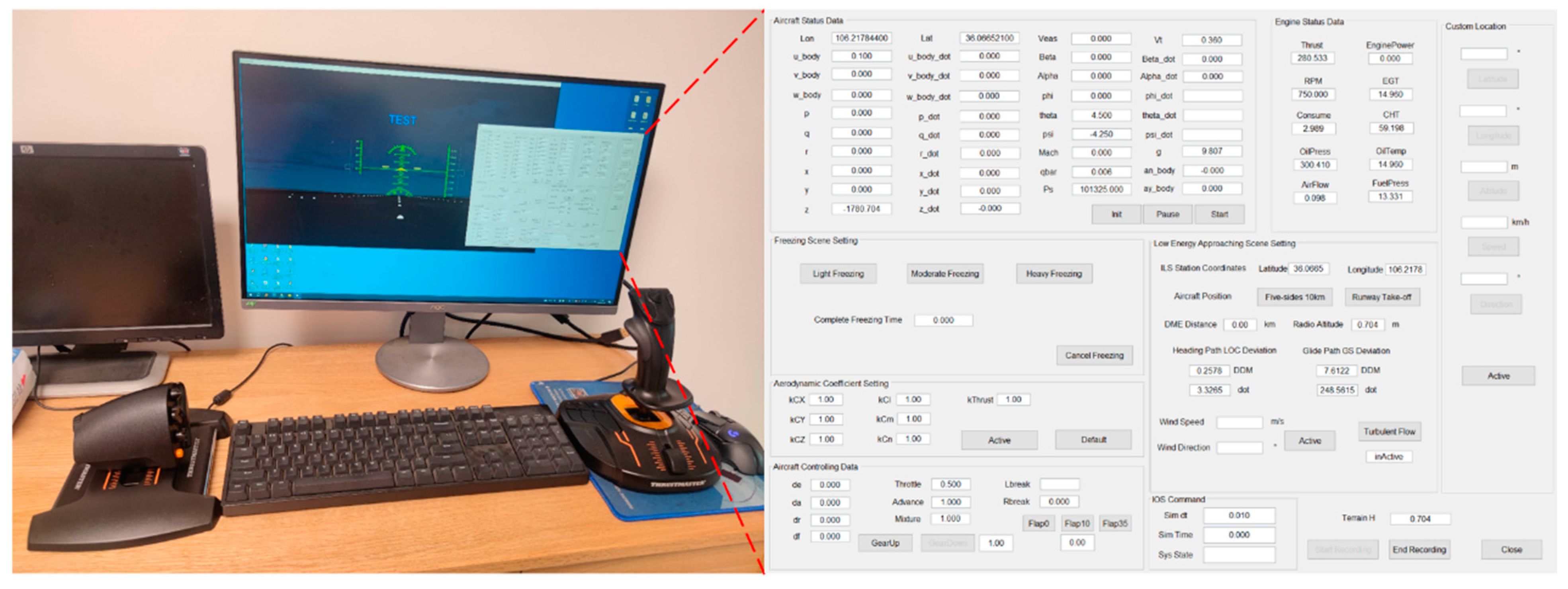
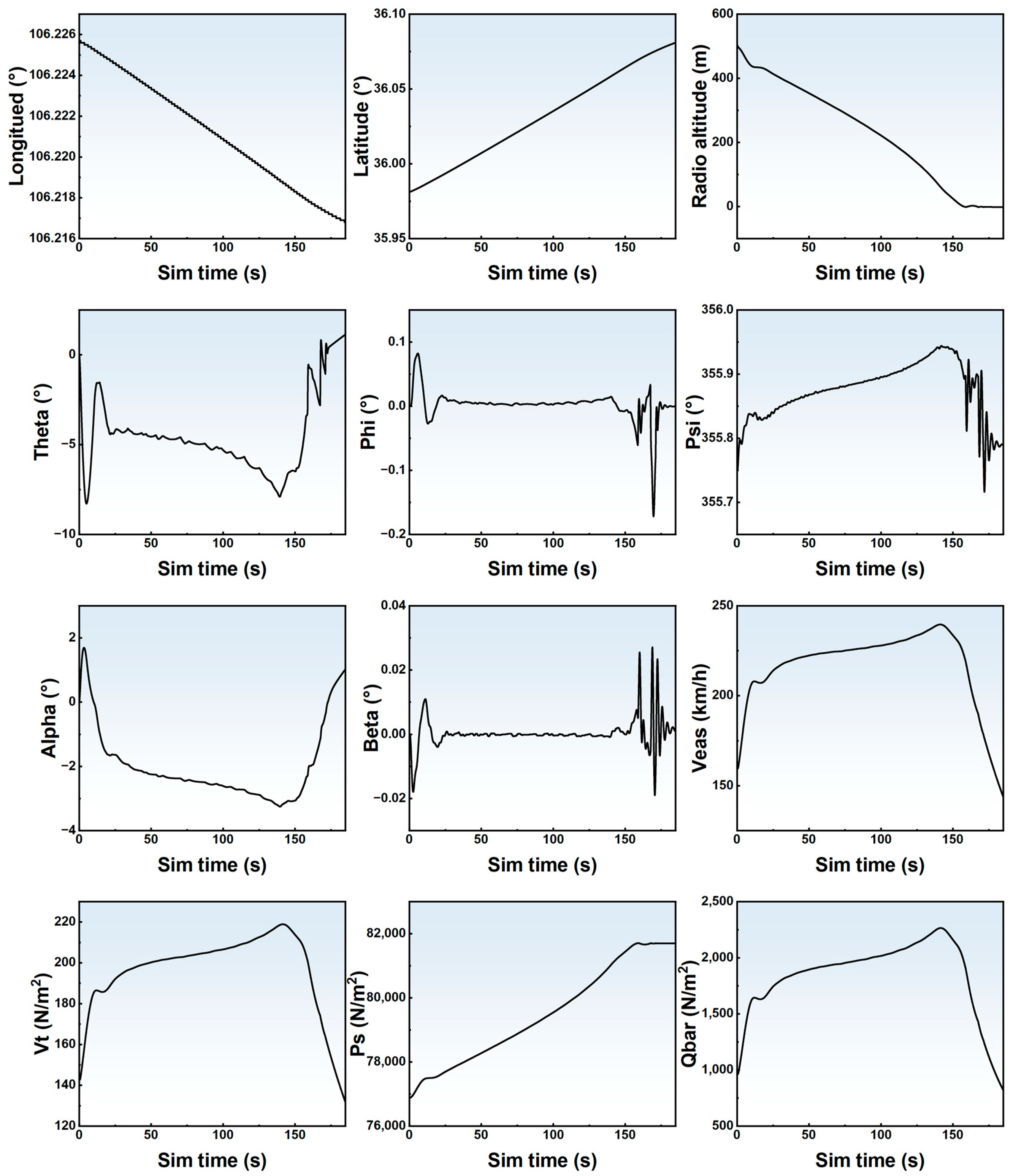
3.1. Semi-Physical Simulation Experiment Based on a Flight Simulator
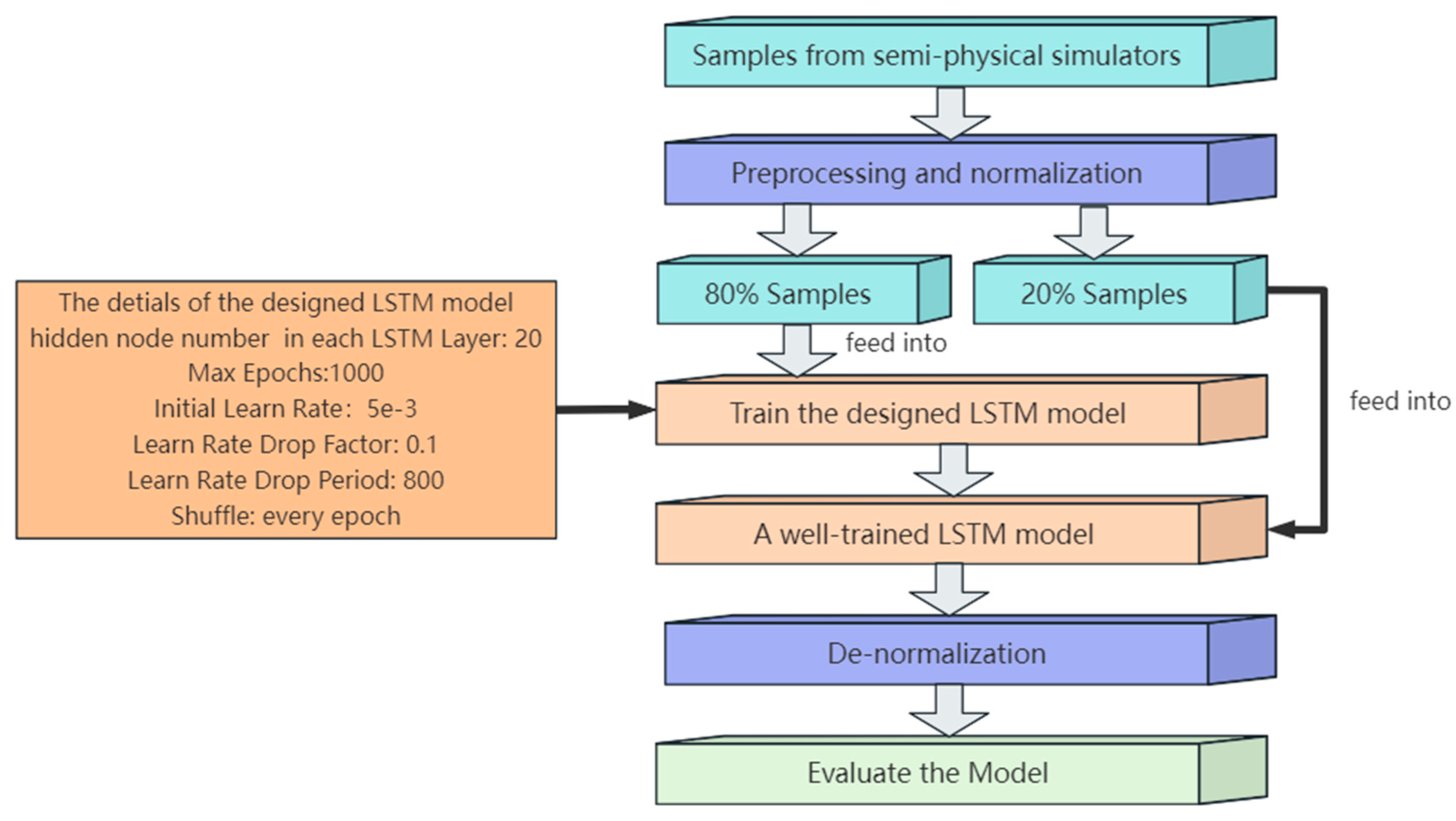
3.2. The Prediction Model Based on LSTM
4. Experiments of LSTM on the Flight Data
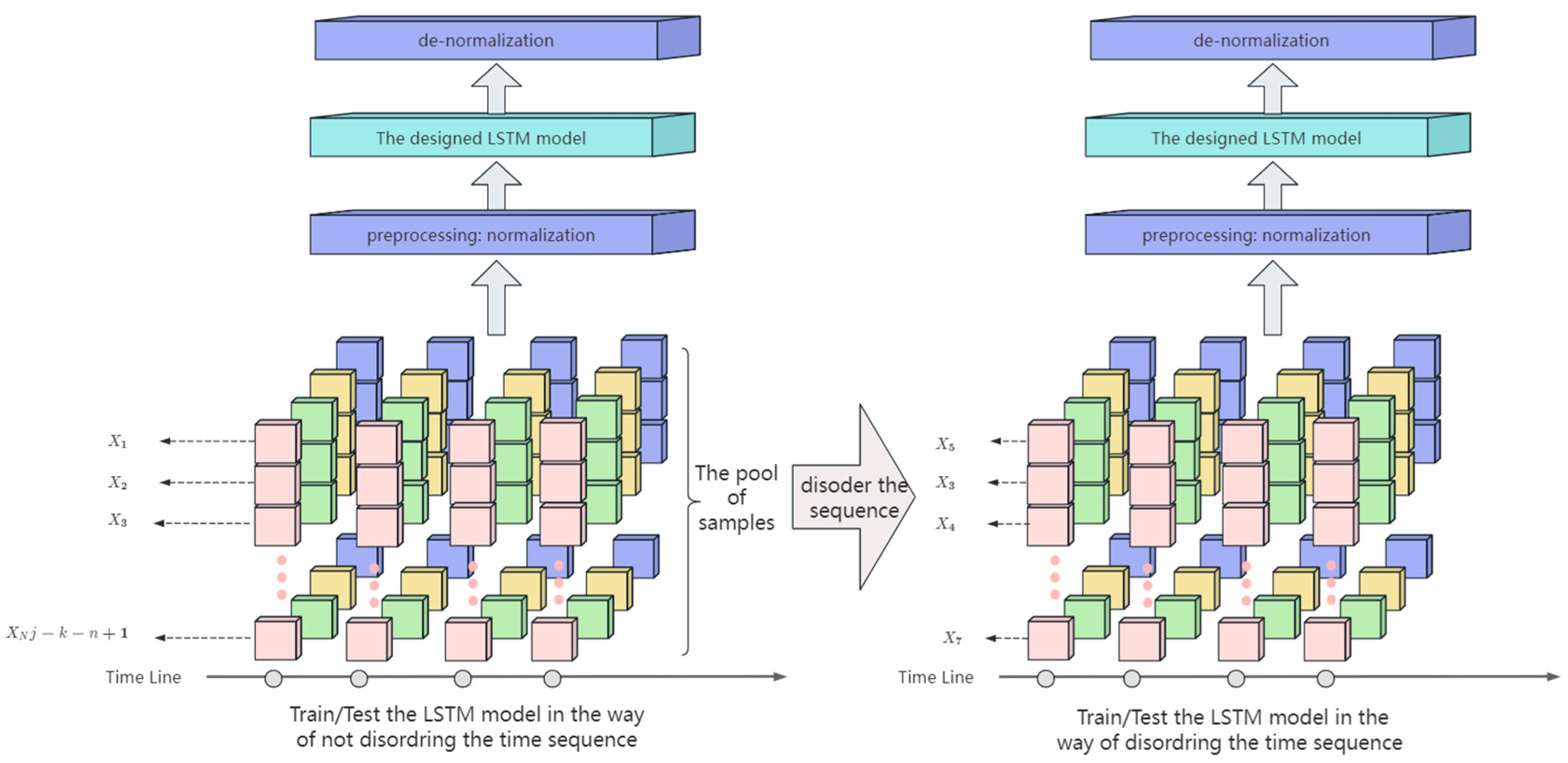
4.1. Strategies for Training and Testing LSTM
- (1)
- Randomly select a single wind-free file without perturbing the time sequence of data in the file; divide the data in the file into 8:2 as a training set and test set, respectively.
- (2)
- Randomly select a single wind-free file; randomly mix up the time sequence of data in the file; divide the data in the file into 8:2 as a training set and test set, respectively.
- (3)
- Randomly select a single wind-free file; sparse the data in the file as follows: 1 in every 10 raw data is kept as a sample; randomly disorder the time sequence of these samples; divide the samples into 8:2 as a training set and test set, respectively.
- (4)
- Select all the wind-free files; sparse the data in each file as follows: 1 in every 100 raw data is kept as a sample; randomly shuffle the time sequence of all the samples in the files; divide the samples into 8:2 as a training set and test set, respectively.
- (5)
- Randomly select eight files including the wind and wind-free conditions for training and select one wind file and one wind-free file for testing; sparse the data in each file as follows: 1 in every 100 raw data is kept as a sample; randomly disarrange the time sequence of the samples in the training set, and do not disarrange the time sequence of samples in the test set.
- (6)
- Randomly select 56 files including the wind, wind-free, and turbulent conditions for training, and select 14 files including the wind, wind-free, and turbulent conditions for testing; sparse the data in each file as follows: one in every 100 raw data is kept as a sample; randomly disorder the time sequence of the samples in the training set, and do not disorder the time sequence of samples in the test set.
- (1)
- In the simulator used for this study, energy state indicators are recorded at specific time intervals as follows: t = 0.01, 0.02, 0.03, and so on. Given the parameters k = 2 and n = 5, the samples extracted from each approach and landing flight experiment for LSTM training and testing are structured as follows:Sample 1: X1 = {x(t = Δt), x(t = 2Δt), x(t = 3Δt), x(t = 4Δt), x(t = 5Δt), y(t = 7Δt)}Sample 2: X2 = {x(t = 2Δt), x(t = 3Δt), x(t = 4Δt), x(t = 5Δt), x(t = 6Δt), y(t = 8Δt)}
- (2)
- Given the value of the altitude/velocity/glide angle at time t −nΔt, t − nΔt + Δt…t − Δt, the LSTM designed in this study can predict the energy state in the approach and landing stages by computing the value of the altitude/velocity/glide angle at time t + (k − 1)Δt. The units of altitude, velocity, and the glide angle are m, km/h, and °, respectively. The value of n, k, and Δt under different strategies is provided in Table 3. Under the premise of satisfying the prediction accuracy, the generalization ability of the prediction model gradually increases with the increase in the values of k and Δt.
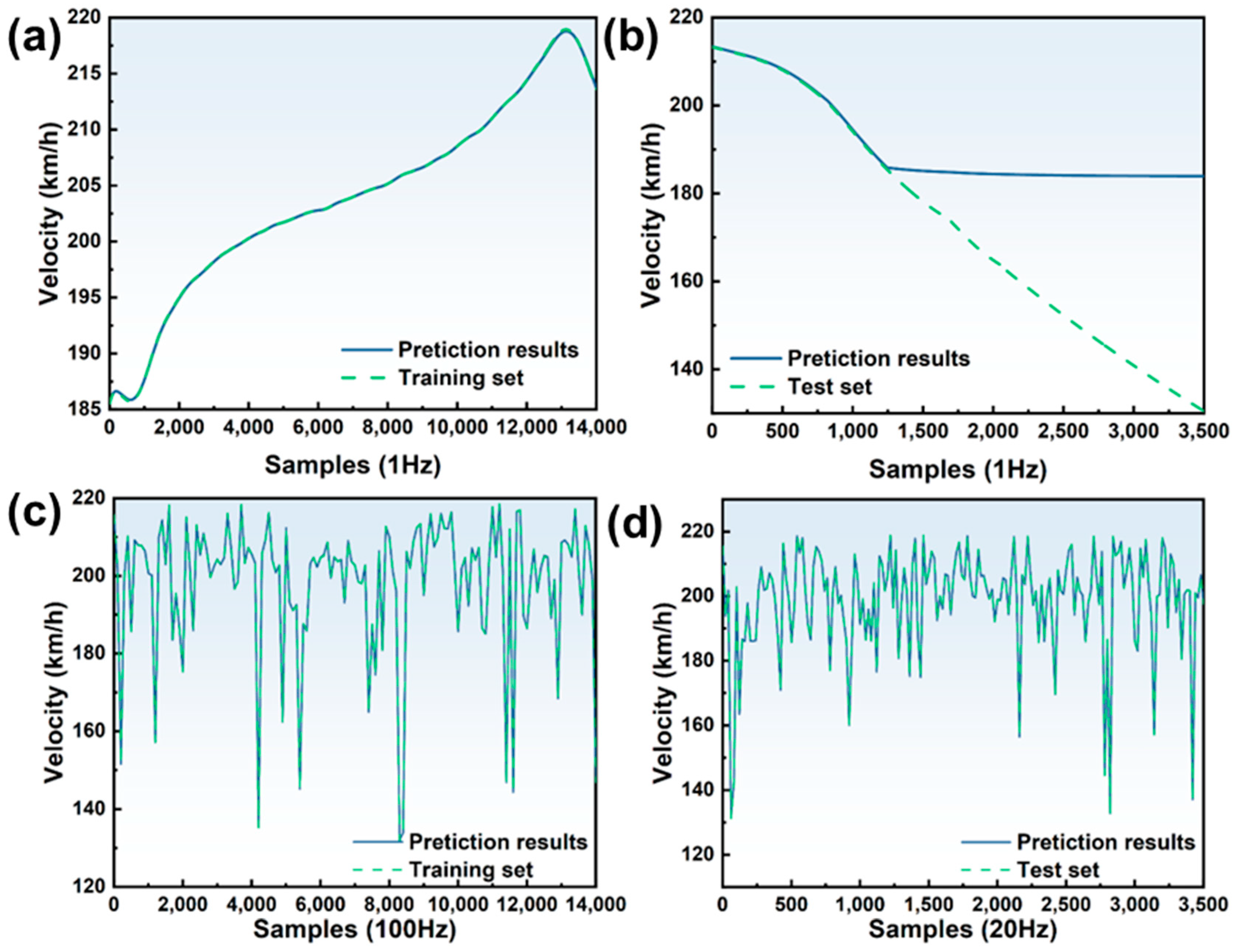
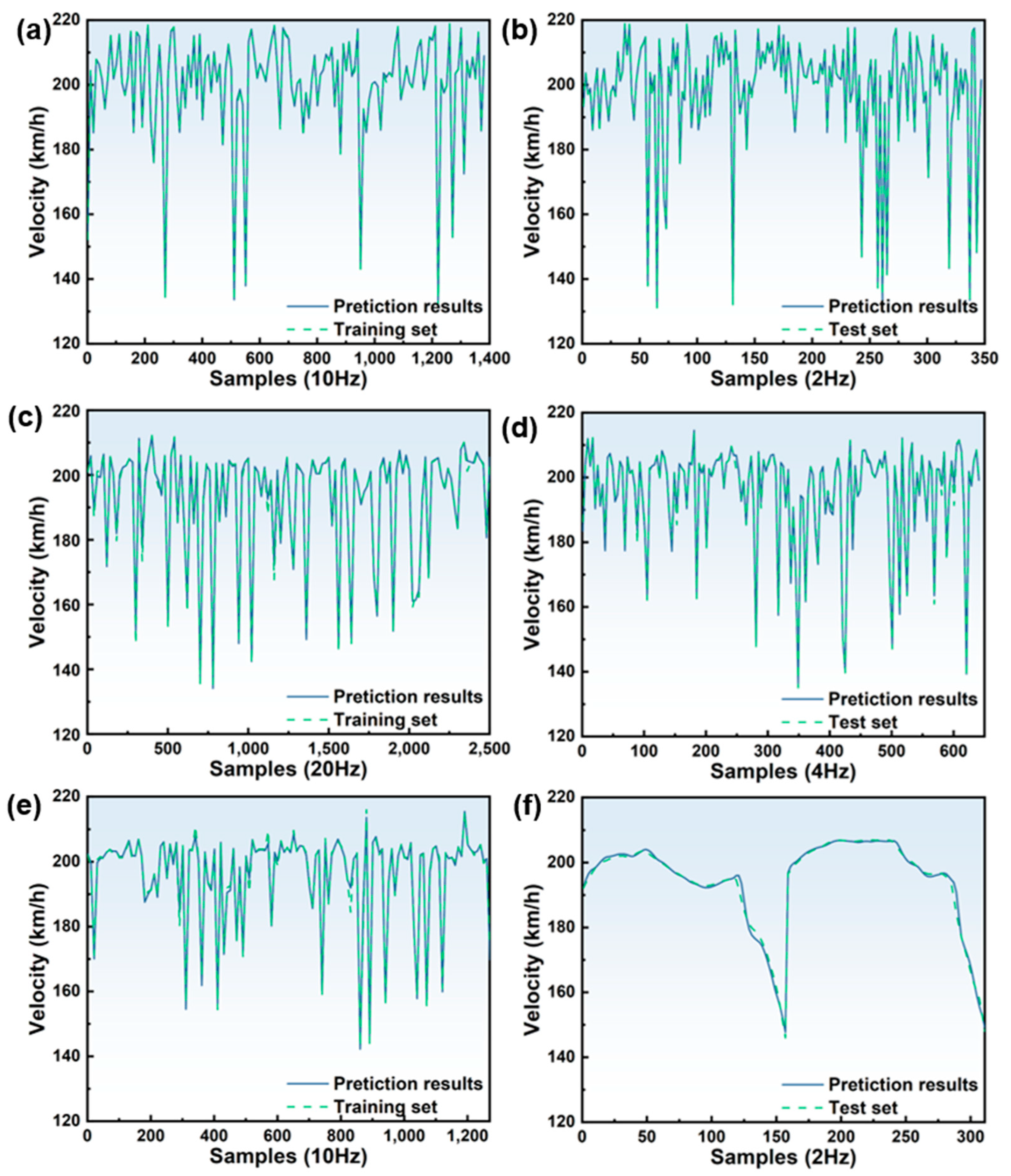
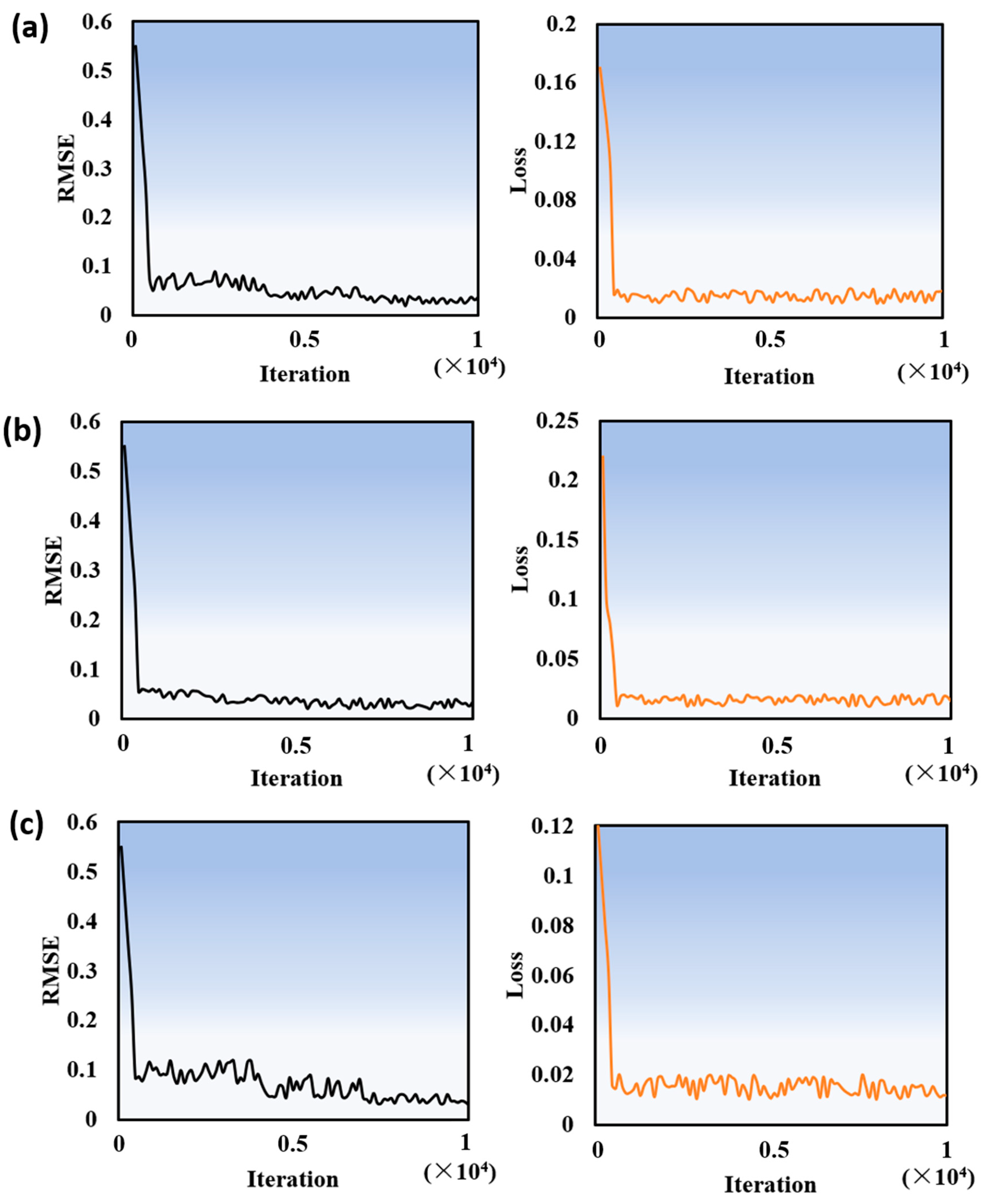
4.2. Result Analysis
- (1)
- To prevent an “overfitting phenomenon”, the time sequence data used for model training must be disordered.
- (2)
- LSTM has high accuracy and a good generalization ability in energy state indicator prediction.
- (3)
- Although the prediction accuracy is different for the three energy state indicators, its potential application value is not affected.
5. Conclusions and Future Work
- (1)
- Through an extensive review of the existing literature, three key flight parameters have been extracted as indicators to characterize the energy state during the approach and landing phases as follows: velocity, altitude, and glide angle.
- (2)
- A semi-physical simulation platform integrating a human–computer interaction for a specific aircraft model has been developed, which overcomes the disadvantage that the traditional pure digital simulation method has in making it difficult to consider the impact of pilots on flight quality. Moreover, the platform can conduct approach and landing simulation experiments under three environmental conditions as follows: calm, windy, and turbulent flow, which are close to the real flight environment. Comprehensive and sufficient flight parameters can be obtained in a short time to train deep learning models with a strong generalization ability.
- (3)
- The established deep learning model, based on LSTM, demonstrated high accuracy in predicting energy state indicators. The R2 value of the altitude prediction model is higher than 0.99, the R2 value of the velocity prediction model is higher than 0.98, and the R2 value of the glide angle prediction model is higher than 0.98. The generalization ability of the model is strong, and the established LSTM model can better predict the aircraft velocity, altitude, and glide angle value in the future 3 s under different wind and turbulent conditions. This predictive strength is invaluable for the early detection of abnormal energy states and for devising control laws tailored to manage and correct such states.
- (4)
- The training strategy of disordering the time sequence of the samples has been proposed to improve the predictive accuracy of LSTM. The training results showed that if a deep learning network for flight parameter prediction is to be established in the aircraft approach and landing stages, the time sequence of training samples should be disordered. A failure to carry this out may result in an “overfitting phenomenon”, which is characterized by high accuracy in the training set but poor performance in the test set. This finding is not only pivotal in optimizing LSTM models but also holds significant implications for developing other types of deep neural networks.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Noort, M.C.; Reader, T.W.; Gillespie, A. Safety voice and safety listening during aviation accidents: Cockpit voice recordings reveal that speaking-up to power is not enough. Saf. Sci. 2021, 139, 105260. [Google Scholar] [CrossRef]
- Kalagher, H.; de Voogt, A.; Boulter, C.J.A.P.; Factors, A.H. Situational Awareness and General Aviation Accidents. Aviat. Psychol. Appl. Hum. Factors 2021, 11, 112–117. [Google Scholar] [CrossRef]
- Perboli, G.; Gajetti, M.; Fedorov, S.; Lo Giudice, S. Natural Language Processing for the identification of Human factors in aviation accidents causes: An application to the SHEL methodology. Expert Syst. Appl. 2021, 186, 7. [Google Scholar]
- Chang, M.; Huang, L.; You, X.Q.; Wang, P.; Francis, G.; Proctor, R.W. The black hole illusion: A neglected source of aviation accidents. Int. J. Ind. Erg. 2022, 87, 7. [Google Scholar] [CrossRef]
- Zajdel, A.; Krawczyk, M.; Szczepanski, C. Pre-Flight Test Verification of Automatic Stabilization System Using Aircraft Trimming Surfaces. Aerospace 2022, 9, 11. [Google Scholar] [CrossRef]
- Dehais, F.; Behrend, J.; Peysakhovich, V.; Causse, M.; Wickens, C.D. Pilot flying and pilot monitoring’s aircraft state awareness during go-around execution in aviation: A behavioral and eye tracking study. Int. J. Aerosp. Psychol. 2017, 27, 15–28. [Google Scholar] [CrossRef]
- Kaszycki, M. Special Conditions: Bombardier Aerospace, Models BD-500-1A10 and BD-500-1A11. In Electronic Flight Control System: Lateral-Directional and Longitudinal Stability and Low-Energy Awareness; FAA: Renton, WA, USA, 2015. [Google Scholar]
- Flight Safety Foundation. Flight safety foundation approach-and-landing accident reduction briefing note 4.2-energy management. Flight Saf. Dig. 2000, 19, 75–80. [Google Scholar]
- Puranik, T.; Jimenez, H.; Mavris, D. Energy-based metrics for safety analysis of general aviation operations. J. Aircr. 2017, 54, 2285–2297. [Google Scholar] [CrossRef]
- Chen, J.P.; Wang, L.X. Hazards of low energy state to flight safety and recovery methods. Acta Aeronaut. Astronat. Sin. 2017, 38, 121077. [Google Scholar]
- Shish, K.; Kaneshige, J.; Acosta, D.; Schuet, S.; Lombaerts, T.; Martin, L.; Madavan, A.N. Aircraft mode and energy-state prediction, assessment, and alerting. J. Guid. Control Dyn. 2017, 40, 804–816. [Google Scholar] [CrossRef]
- Wang, X.; Sembiring, J.; Koppitz, P.; Höhndorf, L.; Wang, C.; Holzapfel, F. Modeling of the aircraft’s low energy state during the final approach phase using operational flight data. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Lu, Z.; Zhang, S.; Dai, R.; Huang, M. Abnormal energy risk criteria of large civil airplanes in approach and landing. Acta Aeronaut. Astronaut. Sin. 2021, 42, 102–115. [Google Scholar]
- Shish, K.H.; Kaneshige, J.; Acosta, D.M.; Schuet, S.; Lombaerts, T.; Martin, L.; Madavan, A.N. Trajectory Prediction and Alerting for Aircraft Mode and Energy State Awareness. In Proceedings of the AIAA Infotech@Aerospace, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Li, L.; Das, S.; John Hansman, R.; Palacios, R.; Srivastava, A.N. Analysis of flight data using clustering techniques for detecting abnormal operations. J. Aerosp. Inf. Syst. 2015, 12, 587–598. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly Detection: A Survey. ACM Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Puranik, T.G.; Mavris, D.N. Identification of instantaneous anomalies in general aviation operations using energy metrics. J. Aerosp. Inf. Syst. 2020, 17, 51–65. [Google Scholar] [CrossRef]
- Matthews, B.; Das, S.; Bhaduri, K.; Das, K.; Martin, R.; Oza, N. Discovering anomalous aviation safety events using scalable data mining algorithms. J. Aerosp. Inf. Syst. 2013, 10, 467–475. [Google Scholar] [CrossRef]
- Gavrilovski, A.; Jimenez, H.; Mavris, D.N.; Rao, A.H.; Shin, S.; Hwang, I.; Marais, K. Challenges and opportunities in flight data mining: A review of the state of the art. In Proceedings of the AIAA Infotech@ Aerospace, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Bay, S.D.; Schwabacher, M. Mining distance-based outliers in near linear time with randomization and a simple pruning rule. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 29–38. [Google Scholar]
- Amidan, B.G.; Ferryman, T.A. APMS SVD Methodology and Implementation (No. PNWD-3026); Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 2000.
- Mugtussids, I.B. Flight Data Processing Techniques to Identify Unusual Events. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2000. [Google Scholar]
- Melnyk, I.; Matthews, B.; Valizadegan, H.; Banerjee, A.; Oza, N. Vector autoregressive model-based anomaly detection in aviation systems. J. Aerosp. Inf. Syst. 2016, 13, 161–173. [Google Scholar] [CrossRef]
- Li, L.; Hansman, R.J.; Palacios, R.; Welsch, R. Anomaly detection via a Gaussian Mixture Model for flight operation and safety monitoring. Transp. Res. Part C Emerg. Technol. 2016, 64, 45–57. [Google Scholar] [CrossRef]
- Basora, L.; Olive, X.; Dubot, T. Recent advances in anomaly detection methods applied to aviation. Aerospace 2019, 6, 117. [Google Scholar] [CrossRef]
- Puranik, T.G.; Harrison, E.; Min, S.; Jimenez, H.; Mavris, D.N. Energy-Based Metrics for General Aviation Flight Data Record Analysis. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016; Volume 3915. [Google Scholar]
- Puranik, T.G.; Mavris, D.N. Anomaly detection in general-aviation operations using energy metrics and flight-data records. J. Aerosp. Inf. Syst. 2018, 15, 22–36. [Google Scholar] [CrossRef]
- Li, G.; Cao, E.; Jia, B.; Zhang, X.; Wang, W.; Huang, H. Mechanical properties and failure behaviors of T1100/5405 composite T-joint under in-plane shear load coupled with initial defect and high-temperature. Compos. Struct. 2023, 324, 117722. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H.; Harford, S. Multivariate LSTM-FCNs for time series classification. Neural. Netw. 2019, 116, 237–245. [Google Scholar] [CrossRef]
- Lazzara, M.; Chevalier, M.; Colombo, M.; Garcia, J.G.; Lapeyre, C.; Teste, O. Surrogate modelling for an aircraft dynamic landing loads simulation using an LSTM AutoEncoder-based dimensionality reduction approach. Aerosp. Sci. Technol. 2022, 126, 16. [Google Scholar] [CrossRef]
- Zhou, D.; Zhuang, X.; Zuo, H.F. A hybrid deep neural network based on multi-time window convolutional bidirectional LSTM for civil aircraft APU hazard identification. Chin. J. Aeronaut. 2022, 35, 344–361. [Google Scholar] [CrossRef]
- Engelmann, J.; Mourning, C.; De Haag, M.U. Feasibility of machine learning methods for predictive alerting of the energy state for aircraft. In Proceedings of the 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; pp. 1–10. [Google Scholar]
- Mi, B.; Huang, H. Intake grille design for an embedded ventilation-and-cooling system in an aircraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 2352–2365. [Google Scholar] [CrossRef]
- De Jong, P.M.; De Gelder, N.; Verhoeven, R.P.M.; Bussink, F.J.L.; Kohrs, R.; Van Paassen, M.M.; Mulder, M. Time and energy management during descent and approach: Batch simulation study. J. Aircr. 2015, 52, 190–203. [Google Scholar] [CrossRef]
- Al-Bakri, F.F.; Al-Bakri, A.F.; Kluever, C.A. Approach and landing guidance for an unpowered gliding vehicle. J. Guid. Control Dyn. 2020, 43, 2366–2371. [Google Scholar] [CrossRef]
- Civil Aviation Administration of China. Requirements for the Certification of the Operation of Large Aircraft Public Air Transport Carriers: CCAR-121-R5; Civil Aviation Administration of China: Beijing, China, 2017.
- Civil Aviation Administration of China. General Operation and Flight Rules: CCAR-01-R3; Civil Aviation Administration of China: Beijing, China, 2018.
- Chiu, T.Y.; Lai, Y.C. Unstable Approach Detection and Analysis Based on Energy Management and a Deep Neural Network. Aerospace 2023, 10, 565. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Windshear Training Aid; Federal Aviation Administration: Washington, DC, USA, 1987.
- Memory, L.S.T. Long short-term memory. Neural Comput. 2010, 9, 1735–1780. [Google Scholar]
- Vepa, R. Flight Dynamics, Simulation, and Control: For Rigid and Flexible Aircraft; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Civil Aviation Administration of China. Visual and Instrument Flight Specifications: MH/T 4023-2007; Civil Aviation Administration of China: Beijing, China, 2007.
- Airbus, S.A.S. A320 Flight Crew Operating Manual; Airbus SAS: Toulouse, France, 2009. [Google Scholar]
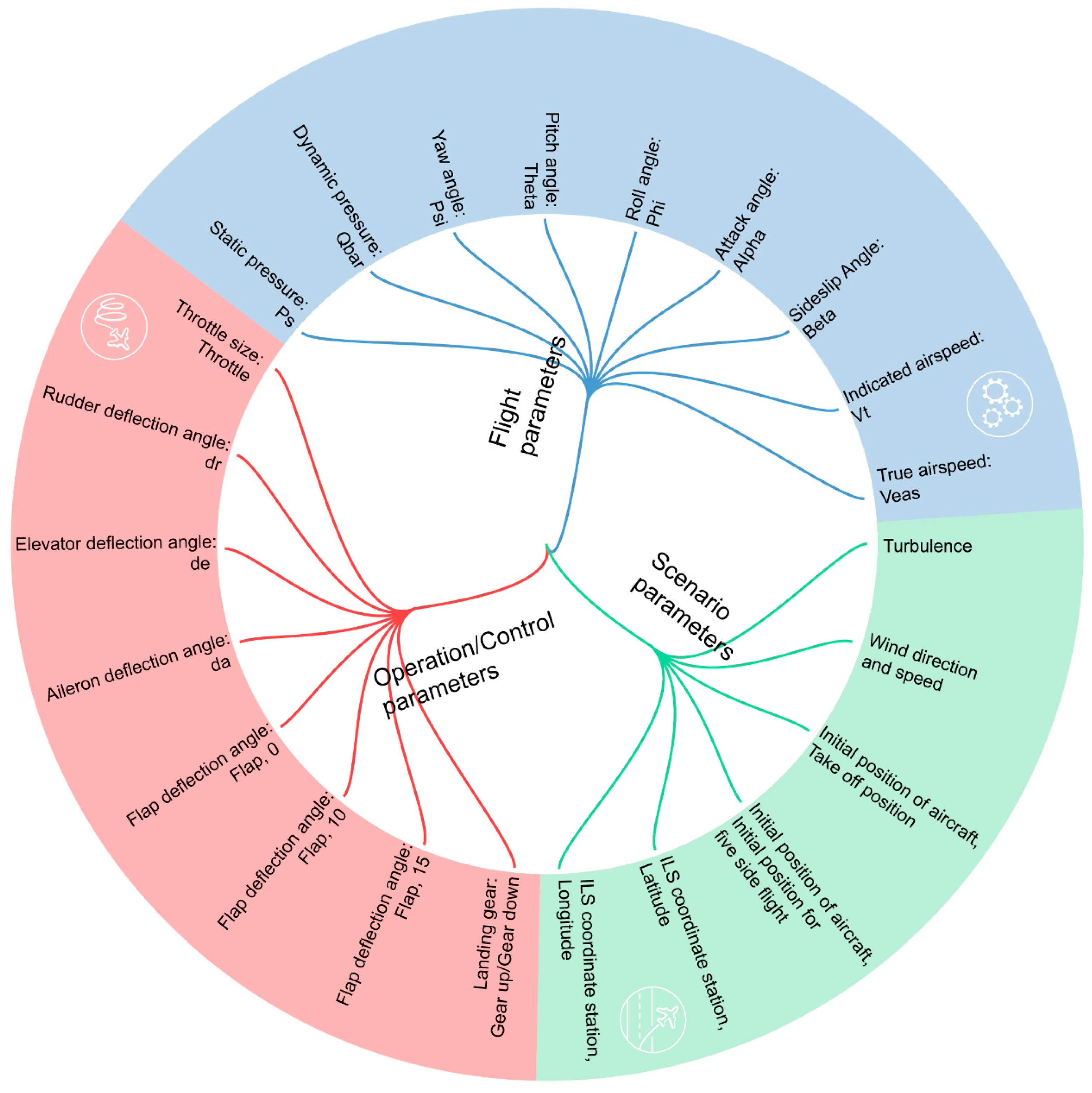

| Energy State Indicators in the Approach and Landing Phase | Sources of the Literature |
|---|---|
| Velocity deviation, glide path deviation, descent rate | Flight Safety Foundation (FSF) [8] |
| Velocity criterion for identifying low kinetic energy and slip deviation criterion for identifying low potential energy | From the airworthiness regulatory requirements [10] |
| Velocity and altitude | Aircraft mode and energy state prediction, assessment as well as alerting [11] |
| Velocity deviation and glide path deviation | Robust autopilot design for landing a large civil aircraft in crosswind [12] |
| Nominal profile deviation and data analysis; data comes from the high-fidelity simulation model and aircraft operation data | CCAR approach and landing procedure of large transport civil aircraft [36,37] |
| Kinetic energy, potential energy, total energy, and their rate of change | Energy-based metrics for safety analysis of general aviation operations [9] |
| Crosswind | 25 knots (13 m/s, 46 km/h, indicated airspeed) |
| Upwind | 40 knots (20 m/s, 74 km/h, indicated airspeed) |
| Downwind | 20 knots (10 m/s, 37 km/h, indicated airspeed) |
| Strategy | Strategy Parameter | Indices of Model Quality | LSTM Method | VAR Method | ||
|---|---|---|---|---|---|---|
| Training Set | Test Set | Training Set | Test Set | |||
| 1 | n = 20, k = 1, Δt = 0.01 | R2 | 0.999960 | 0.038281 | 0.919961 | 0.025812 |
| MAE | 0.033427 | 18.30630 | 0.145758 | 20.67242 | ||
| MBE | −0.011397 | 18.30630 | −0.282941 | 21.28936 | ||
| 2 | n = 20, k = 1, Δt = 0.01 | R2 | 0.999950 | 0.999950 | 0.899952 | 0.889947 |
| MAE | 0.091720 | 0.092625 | 0.275299 | 0.296551 | ||
| MBE | 0.018886 | 0.015178 | 0.129375 | 0.121329 | ||
| 3 | n = 20, k = 1, Δt = 0.1 | R2 | 0.999400 | 0.999290 | 0.909424 | 0.899261 |
| MAE | 0.288590 | 0.291230 | 0.702818 | 0.728703 | ||
| MBE | −0.006848 | 0.003985 | 0.306001 | 0.405864 | ||
| 4 | n = 20, k = 3, Δt = 1 | R2 | 0.994890 | 0.994030 | 0.894941 | 0.883791 |
| MAE | 0.763620 | 0.771280 | 4.723623 | 4.326705 | ||
| MBE | 0.128520 | 0.109820 | 0.810808 | 0.824212 | ||
| 5 | n = 20, k = 3, Δt = 1 | R2 | 0.993760 | 0.992720 | 0.914259 | 0.912721 |
| MAE | 0.840780 | 0.737380 | 1.958741 | 1.984753 | ||
| MBE | 0.141060 | 0.134040 | 0.329649 | 0.362082 | ||
| 6 | n = 20, k = 3, Δt = 1 | R2 | 0.986040 | 0.989760 | 0.956179 | 0.939248 |
| MAE | 1.373400 | 1.803200 | 1.904735 | 2.611392 | ||
| MBE | 0.126260 | −0.083124 | 0.318684 | 0.264489 | ||
| Indices for Predicting Energy State | Prediction Strategy Parameter | Indices of Model Quality | LSTM Method | VAR Method | ||
|---|---|---|---|---|---|---|
| Training Set | Test Set | Training Set | Test Set | |||
| Altitude | n = 20, k = 3, Δt = 1 | R2 | 0.998840 | 0.999220 | 0.938909 | 0.939149 |
| MAE | 3.261000 | 2.659300 | 4.065346 | 3.939079 | ||
| MBE | 1.348400 | 0.815020 | 2.294469 | 1.363921 | ||
| Glide angle | n = 20, k = 3, Δt = 1 | R2 | 0.8476 | 0.85117 | 0.695124 | 0.712240 |
| MAE | 1.178 | 1.3524 | 2.178762 | 2.379448 | ||
| MBE | 0.35965 | 0.23721 | 0.499659 | 0.521442 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Yan, J.; Cao, E.; Yu, Y.; Tian, H.; Huang, H. Approach and Landing Energy Prediction Based on a Long Short-Term Memory Model. Aerospace 2024, 11, 226. https://doi.org/10.3390/aerospace11030226
Hu Y, Yan J, Cao E, Yu Y, Tian H, Huang H. Approach and Landing Energy Prediction Based on a Long Short-Term Memory Model. Aerospace. 2024; 11(3):226. https://doi.org/10.3390/aerospace11030226
Chicago/Turabian StyleHu, Yahui, Jiaqi Yan, Ertai Cao, Yimeng Yu, Haiming Tian, and Heyuan Huang. 2024. "Approach and Landing Energy Prediction Based on a Long Short-Term Memory Model" Aerospace 11, no. 3: 226. https://doi.org/10.3390/aerospace11030226
APA StyleHu, Y., Yan, J., Cao, E., Yu, Y., Tian, H., & Huang, H. (2024). Approach and Landing Energy Prediction Based on a Long Short-Term Memory Model. Aerospace, 11(3), 226. https://doi.org/10.3390/aerospace11030226





