Rotor Performance Predictions for Urban Air Mobility: Single vs. Coaxial Rigid Rotors
Abstract
:1. Introduction
- Summarize major developments of a hybrid BEMT-URANS CFD methodology enabling fast multirotor performance predictions.
- Validate this methodology by comparing single and coaxial CFD rotor performance predictions to experimental data acquired in the NASA Langley 14- by 22-ft. Subsonic Tunnel Facility. Document the effects of fully turbulent versus free-transition airfoil tables on CFD rotor performance predictions using this approach.
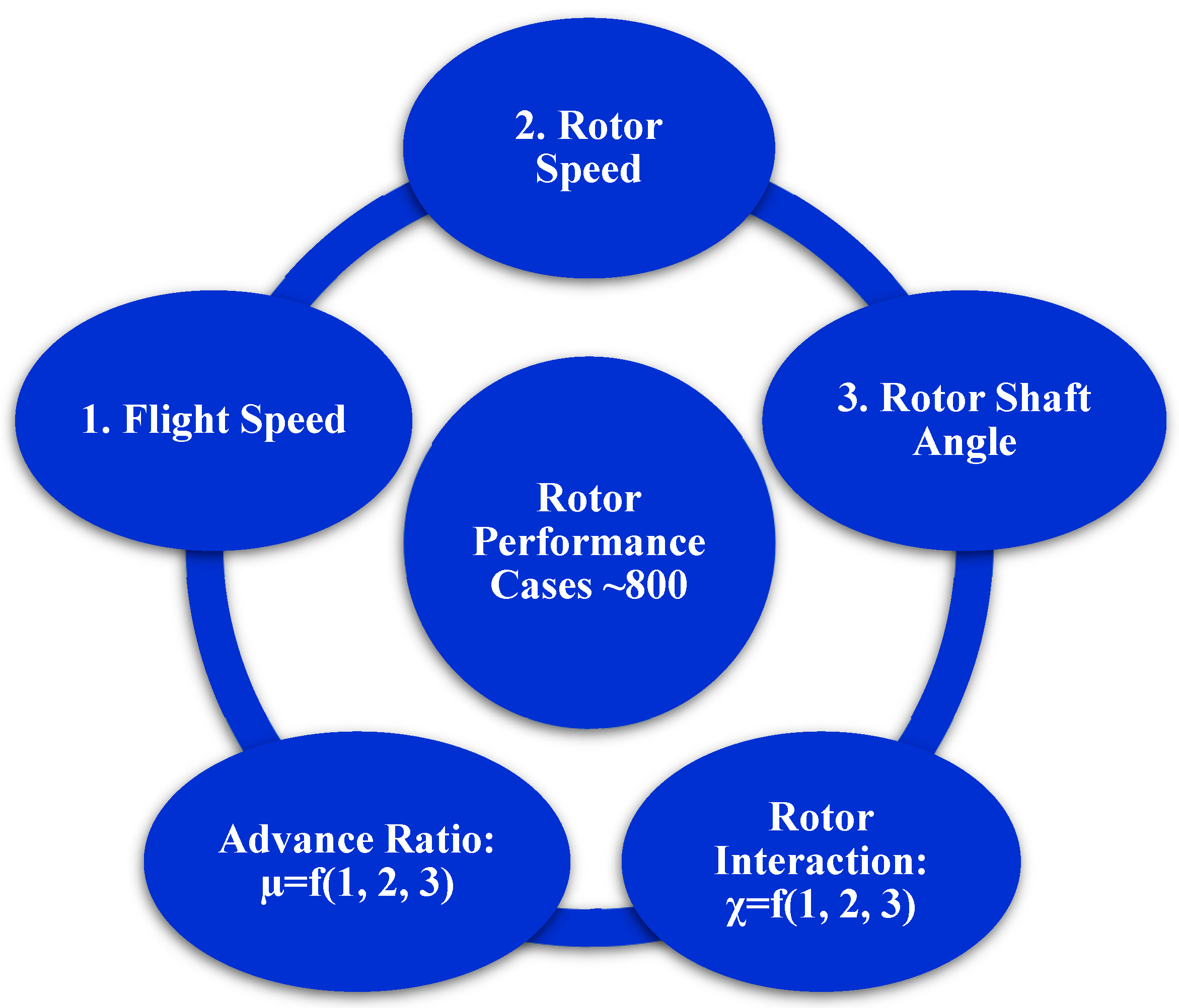
- Provide physical insight into the coaxial rotor flow physics as a function of the rotor shaft angle (SA) from −90 degrees to +90 degrees, which is reported in increments of 15 degrees or less. Compare single versus coaxial rotor performance across a wide range of flight conditions unique to stiff, variable-speed rotor operation.
2. Computational Methods
2.1. Rotorcraft Analysis Methods
2.2. Hybrid BEMT-URANS CFD Methodology for Multirotor Systems
2.3. GPU Acceleration and Computational Resources
2.4. Validation and Uncertainty Quantification
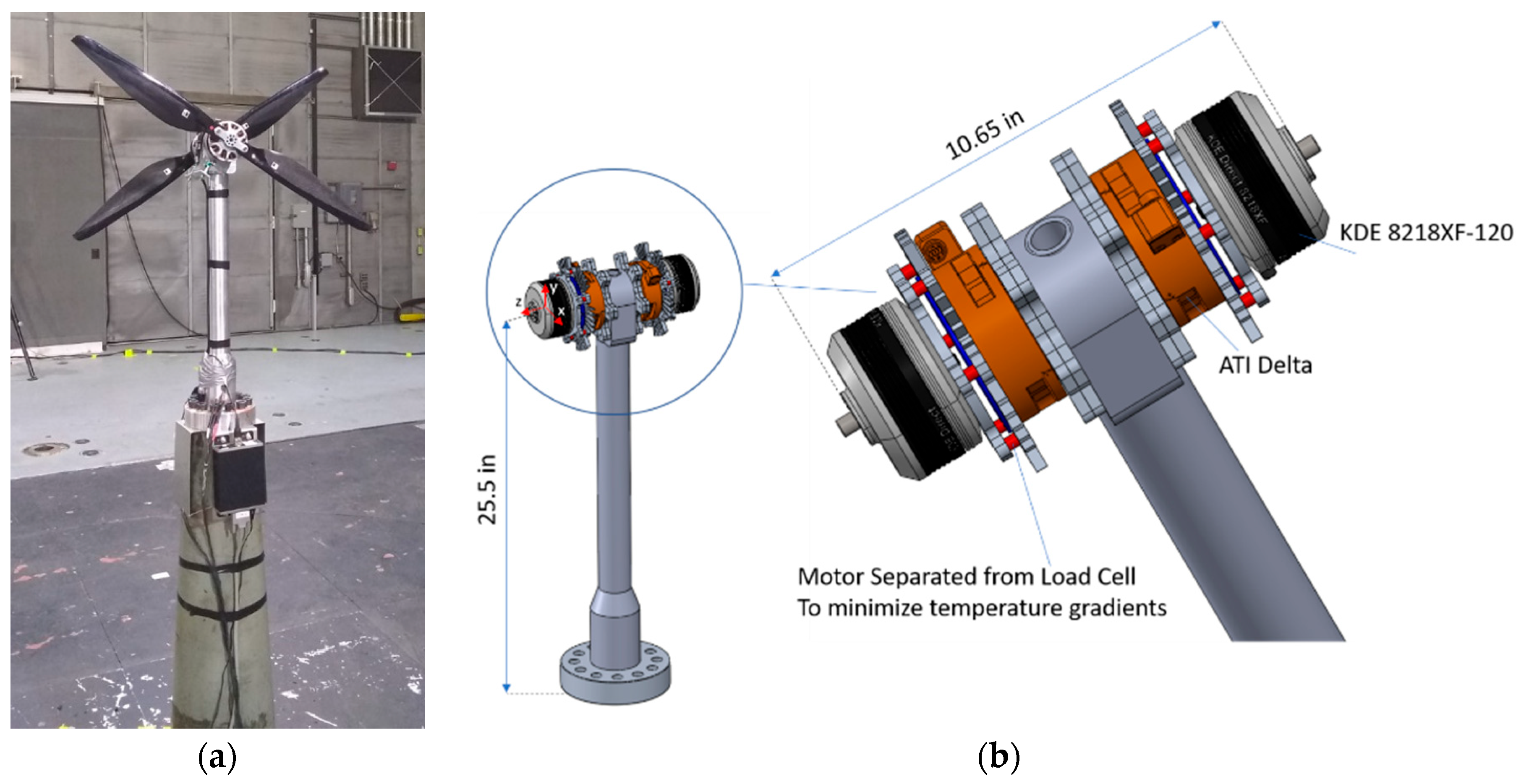
3. Experimental Test Setup
4. CFD Model Setup
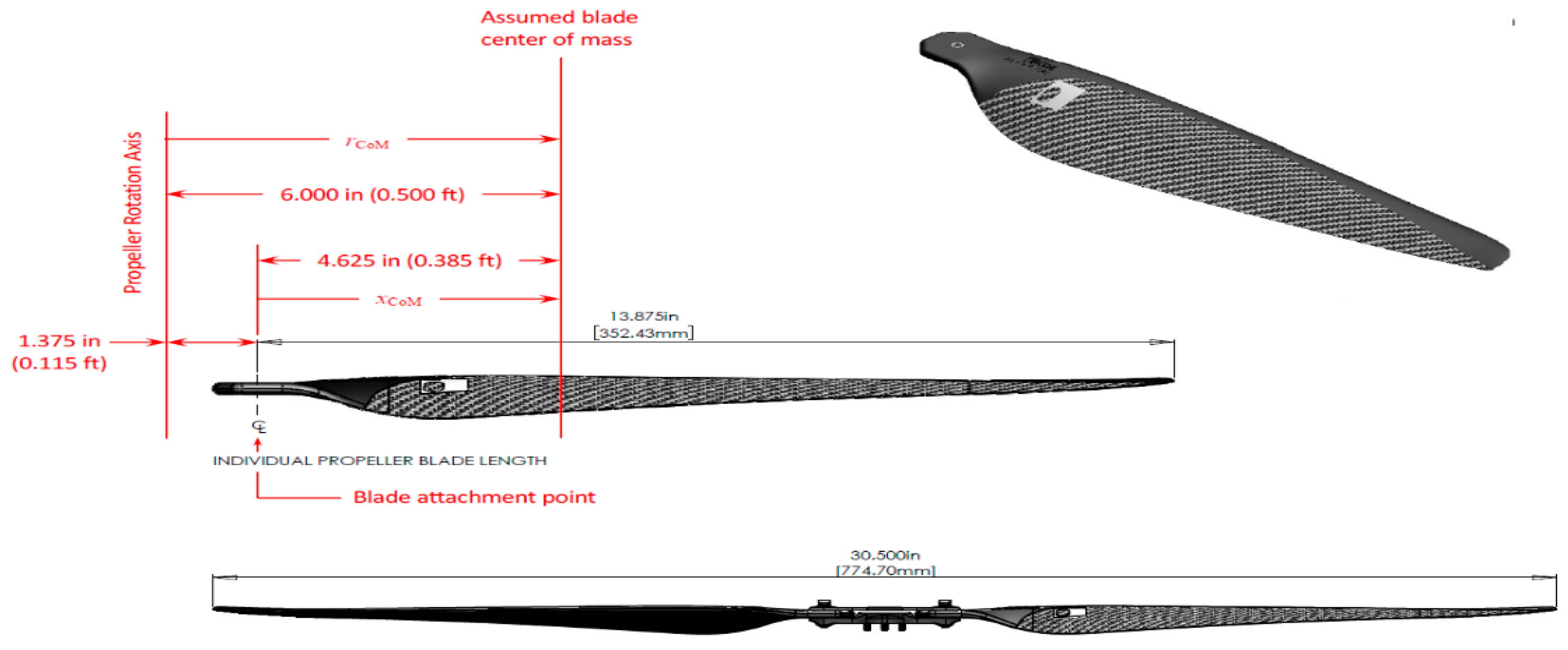
4.1. Rotor Geometry Verification
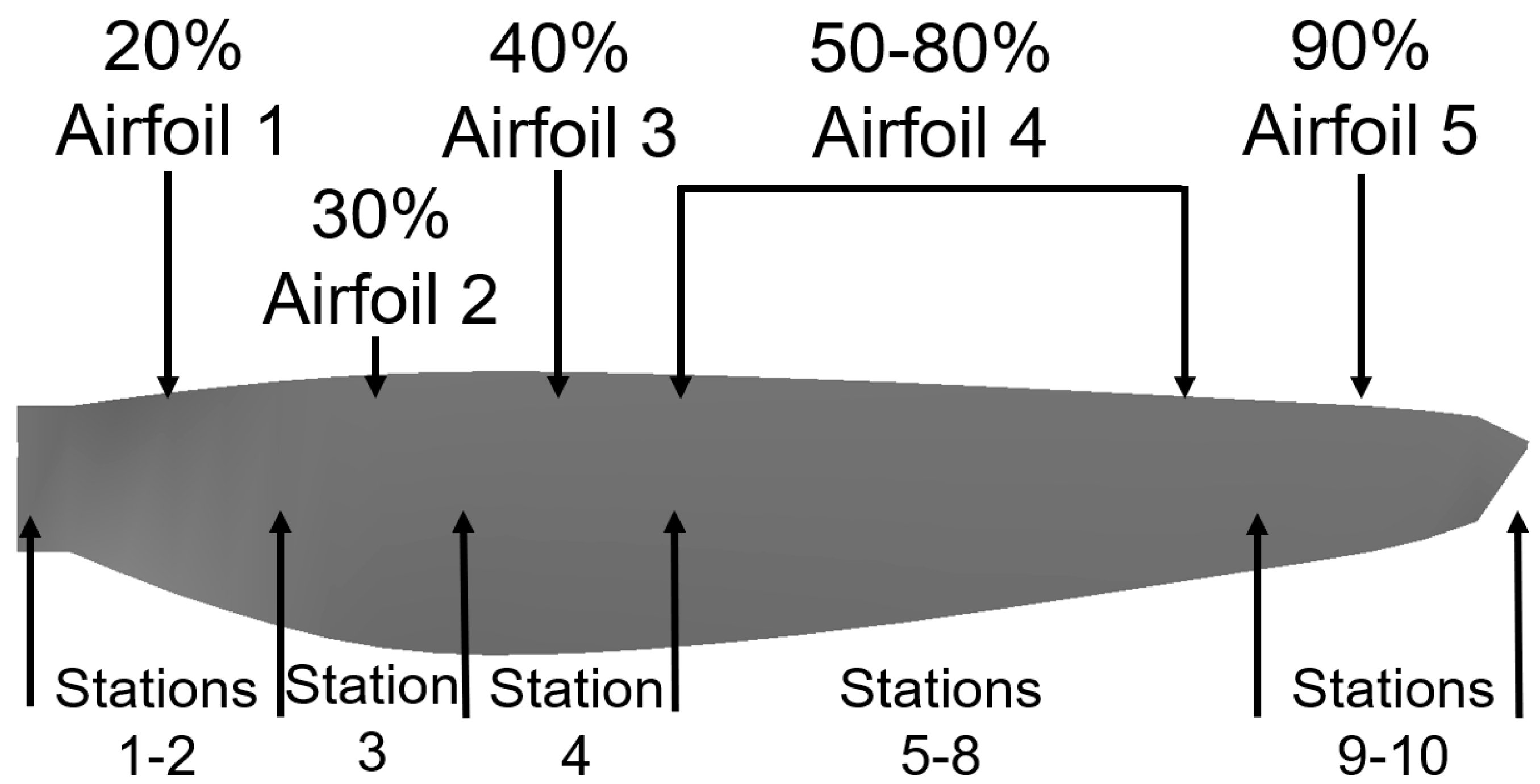
4.2. Blade Discretization into Radial Stations for the Airfoil Look-Up Tables
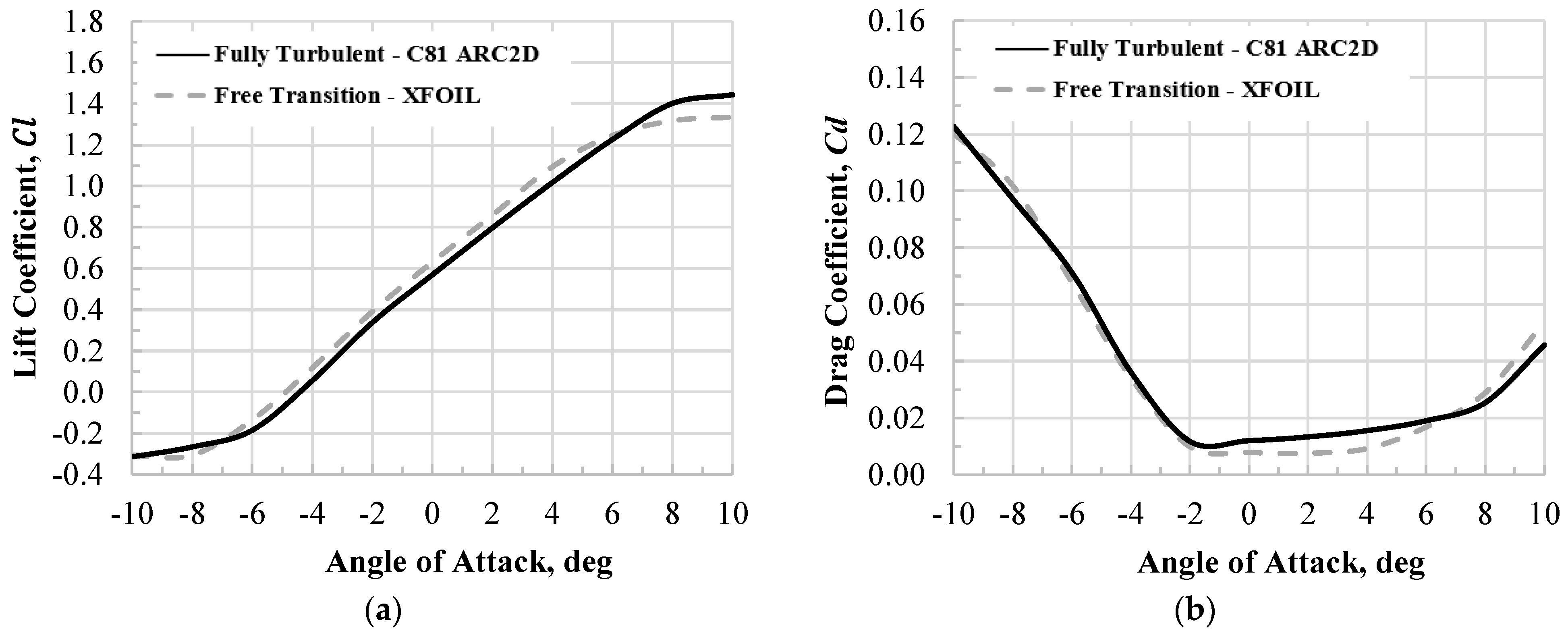
4.3. C81 Airfoil Table Generation
4.4. RotCFD Model Creation
5. Results
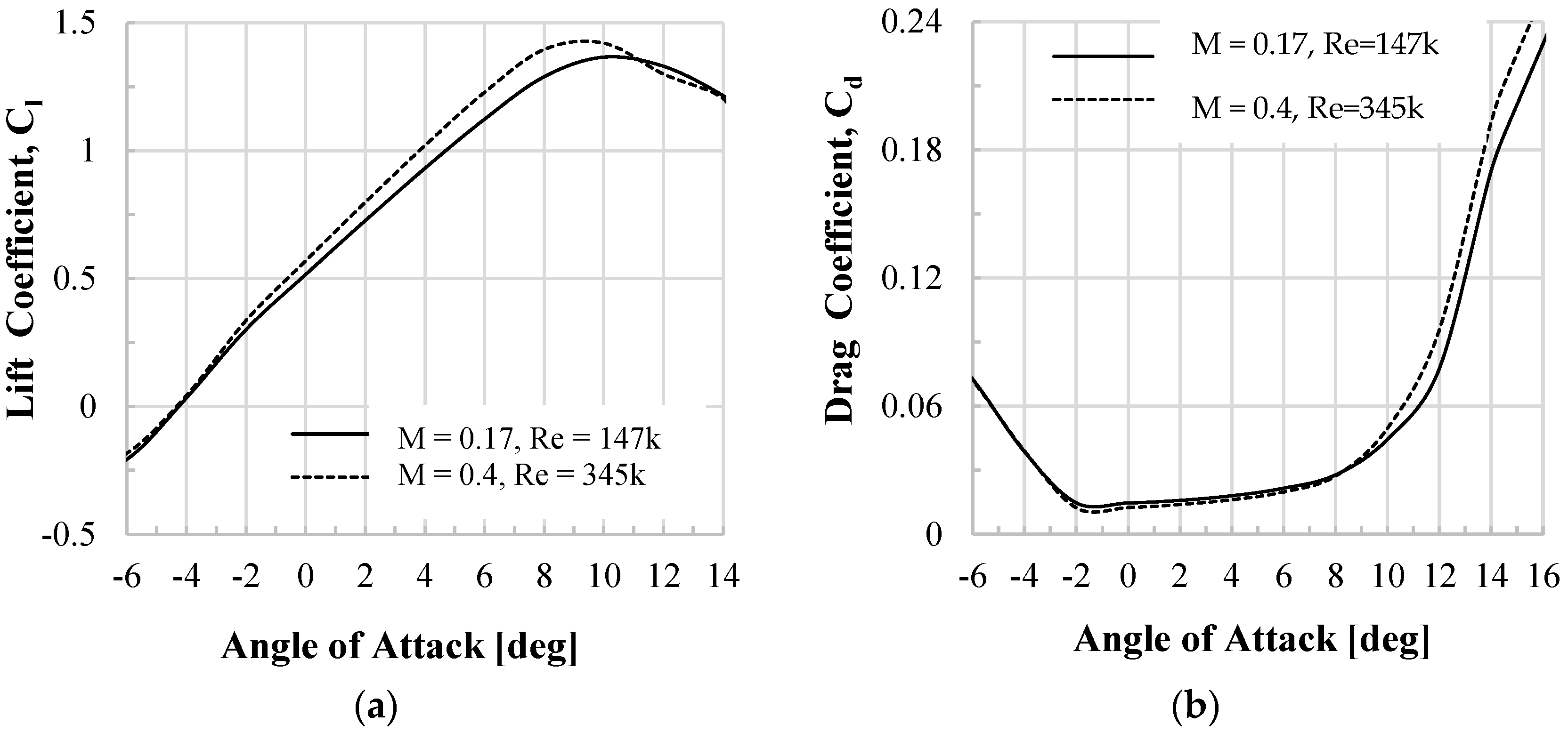
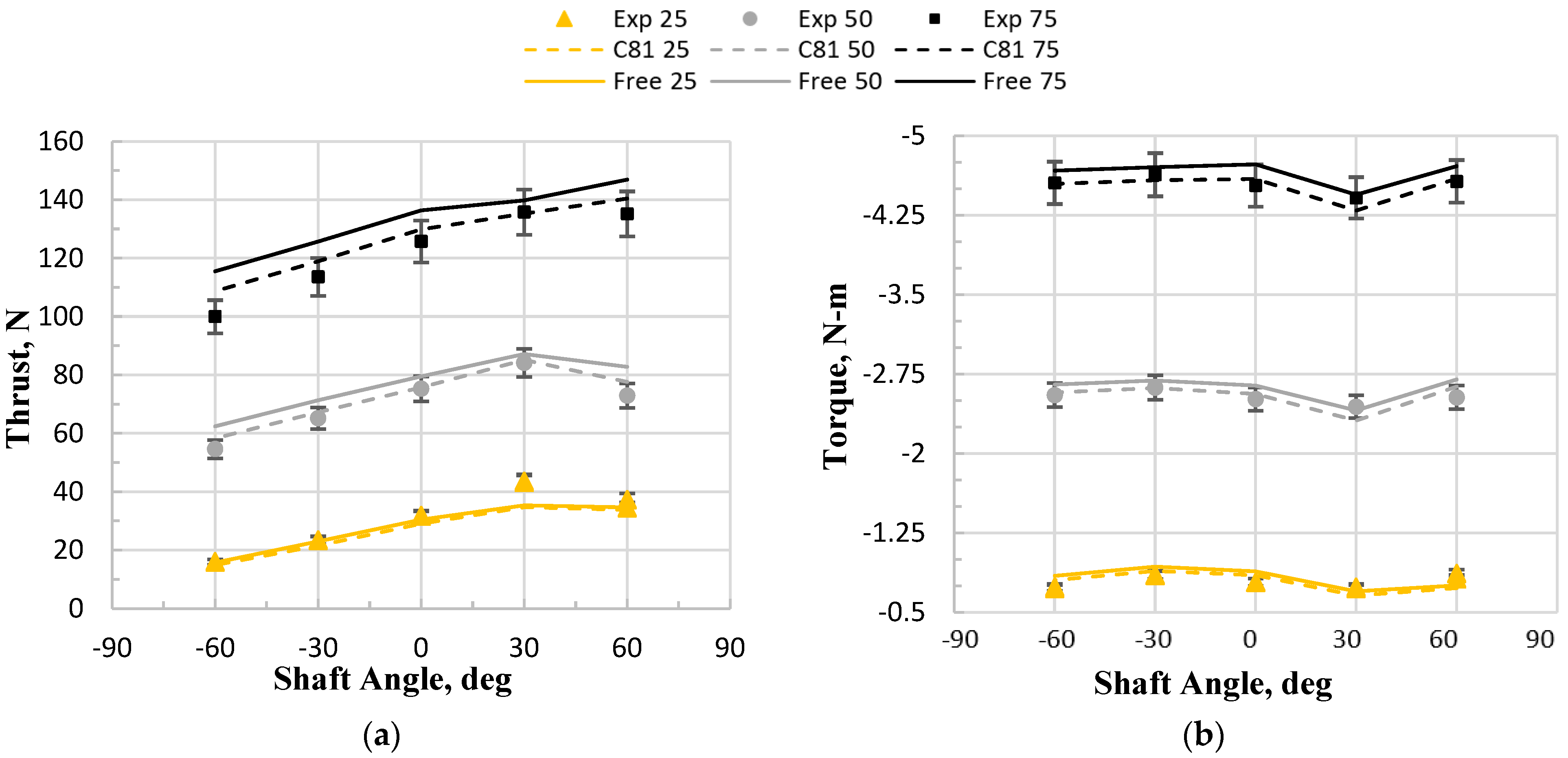
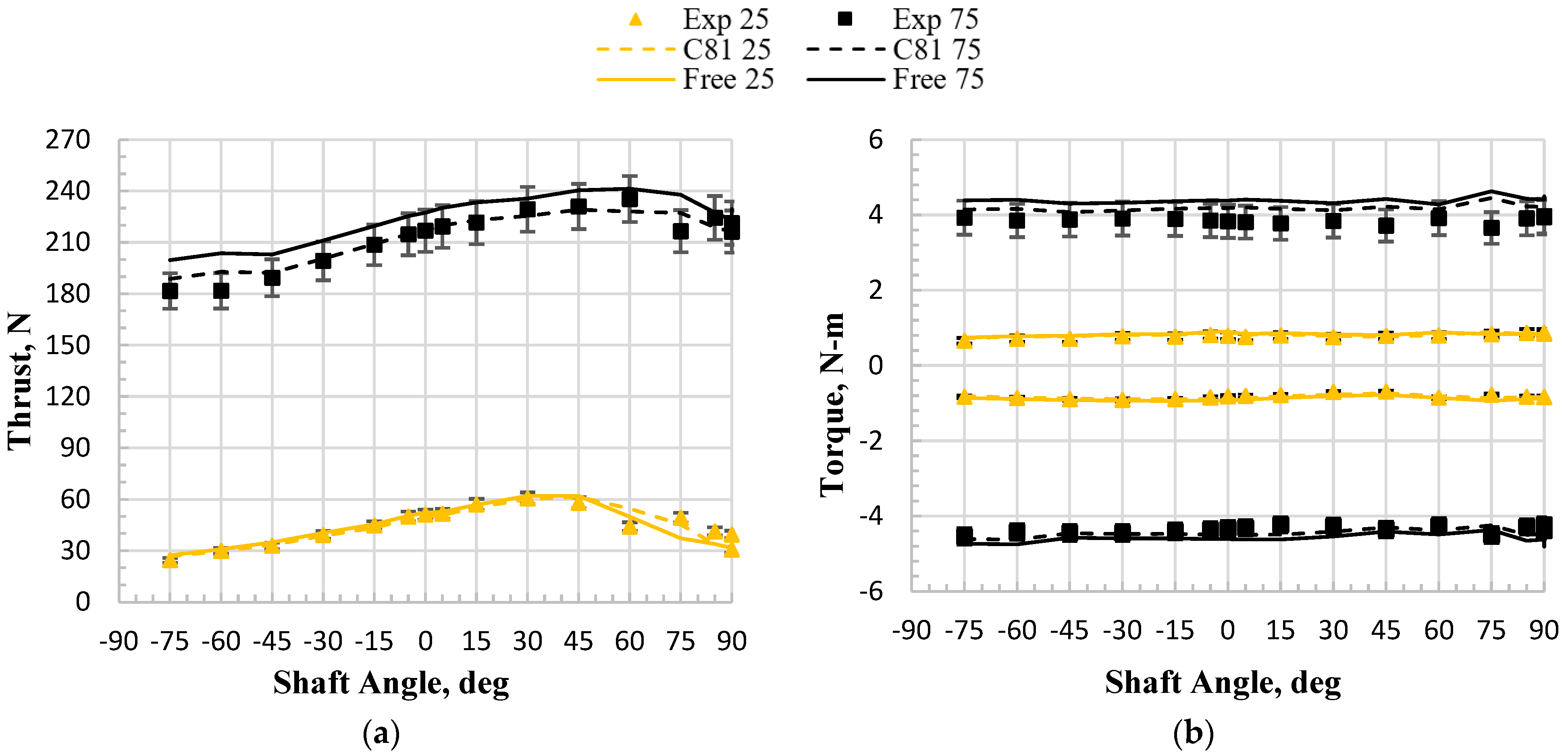
5.1. Discussion of the Experimental Data
5.2. Comparison of the Experimental Data to RotCFD Predictions
5.2.1. Single Rotor: Free-Transition vs. Fully Turbulent Airfoil Tables
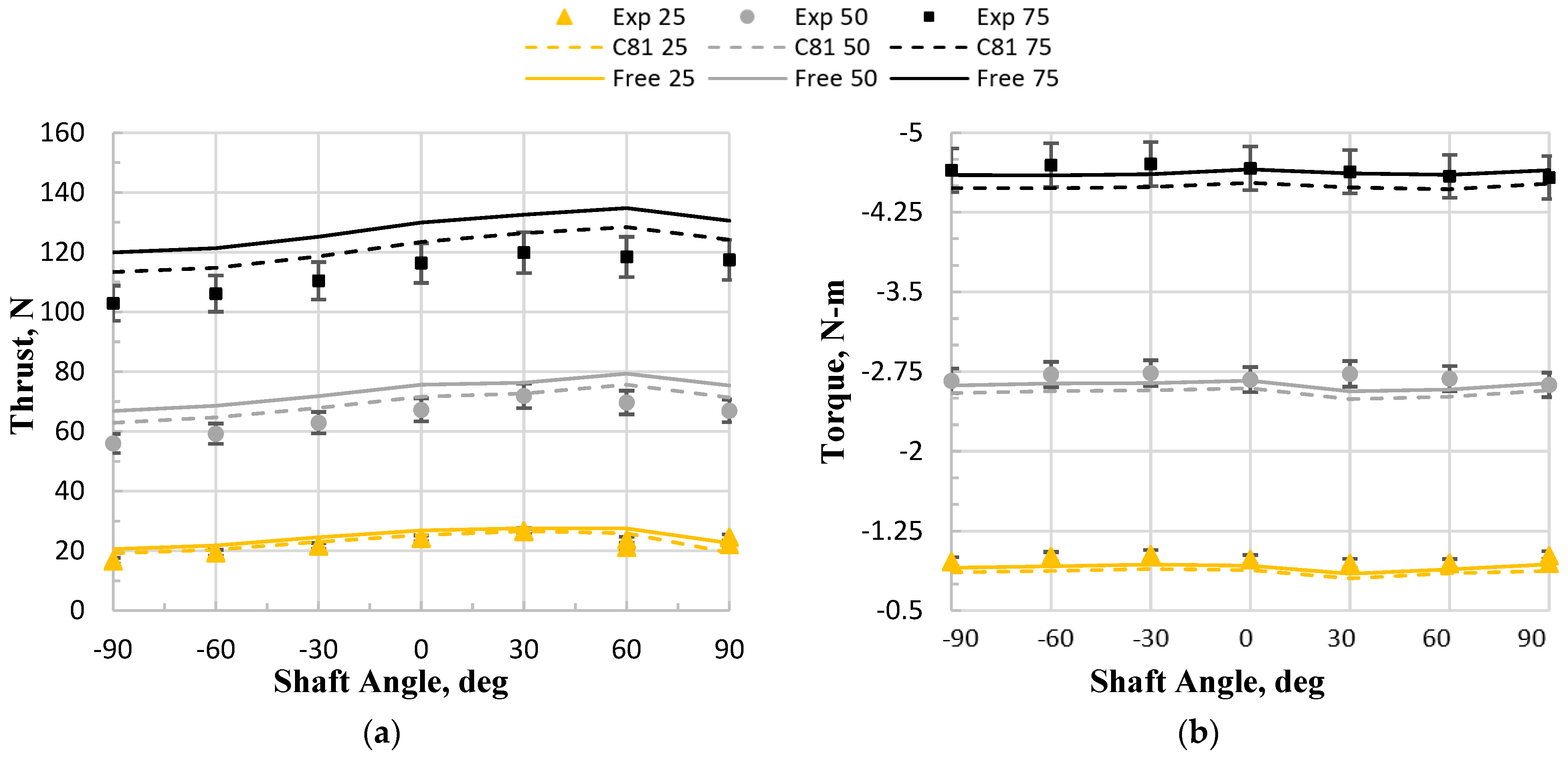
5.2.2. Coaxial Rotor: Free-Transition vs. Fully Turbulent Airfoil Tables
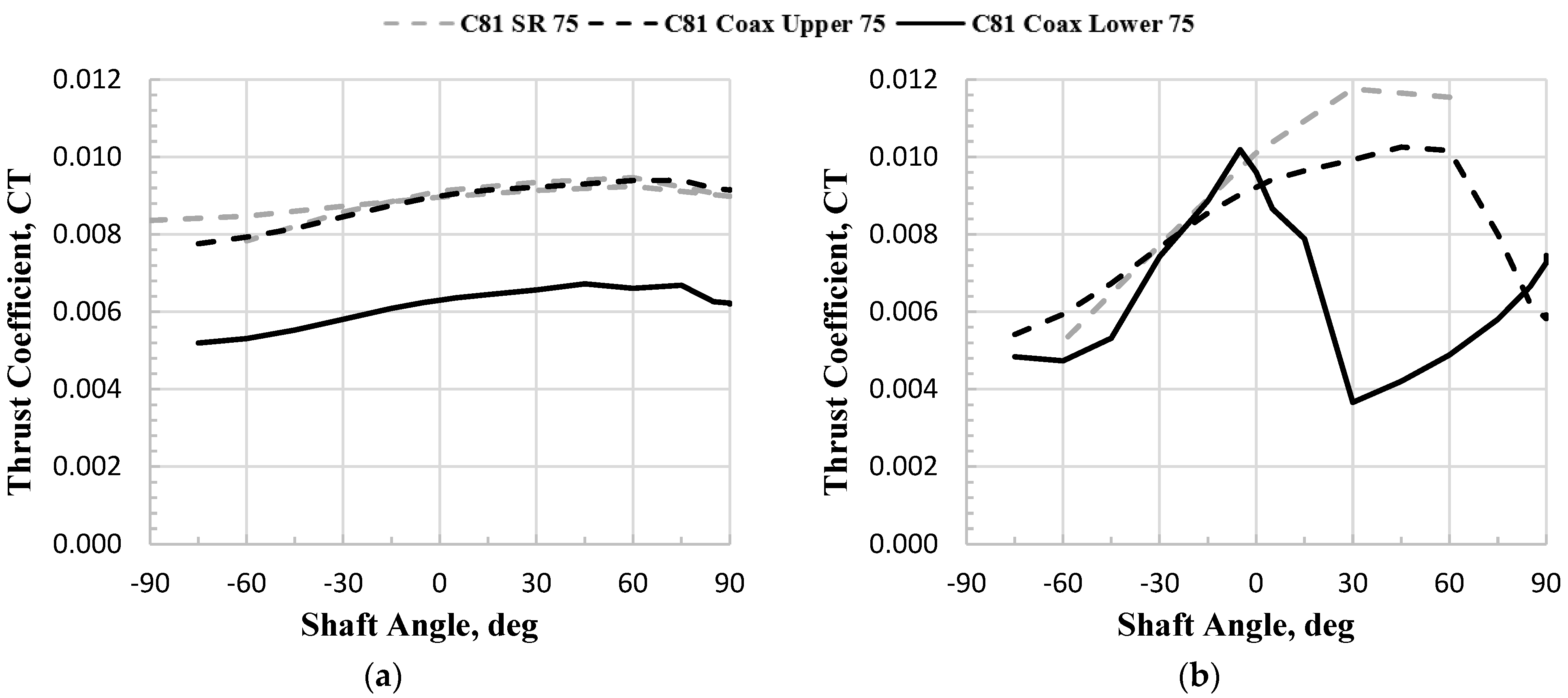
5.2.3. Single vs. Coaxial Rotor: Fully Turbulent Airfoil Tables
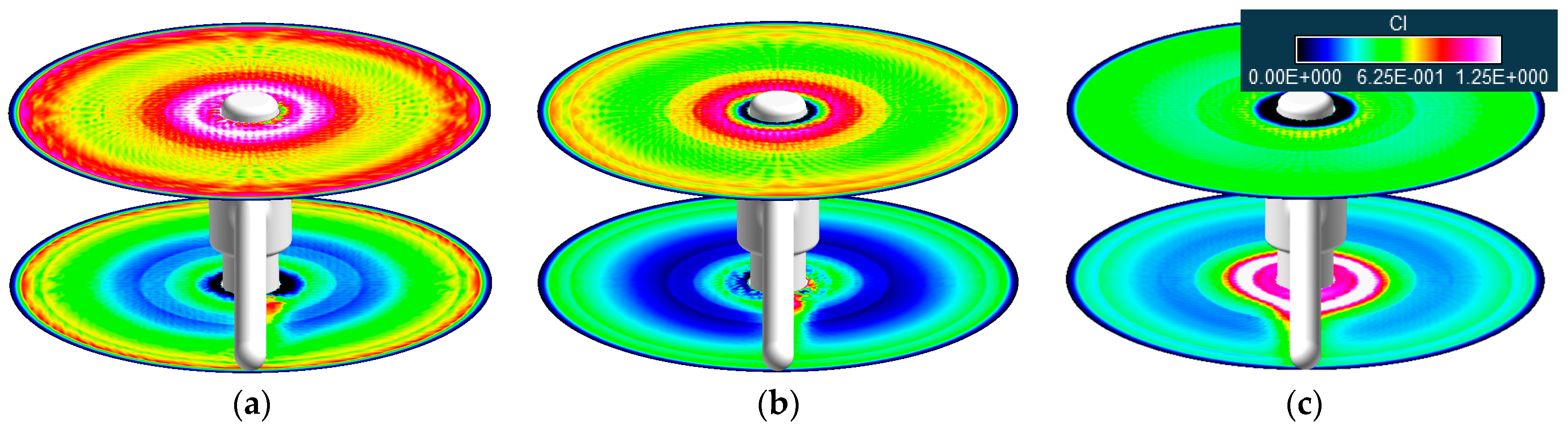
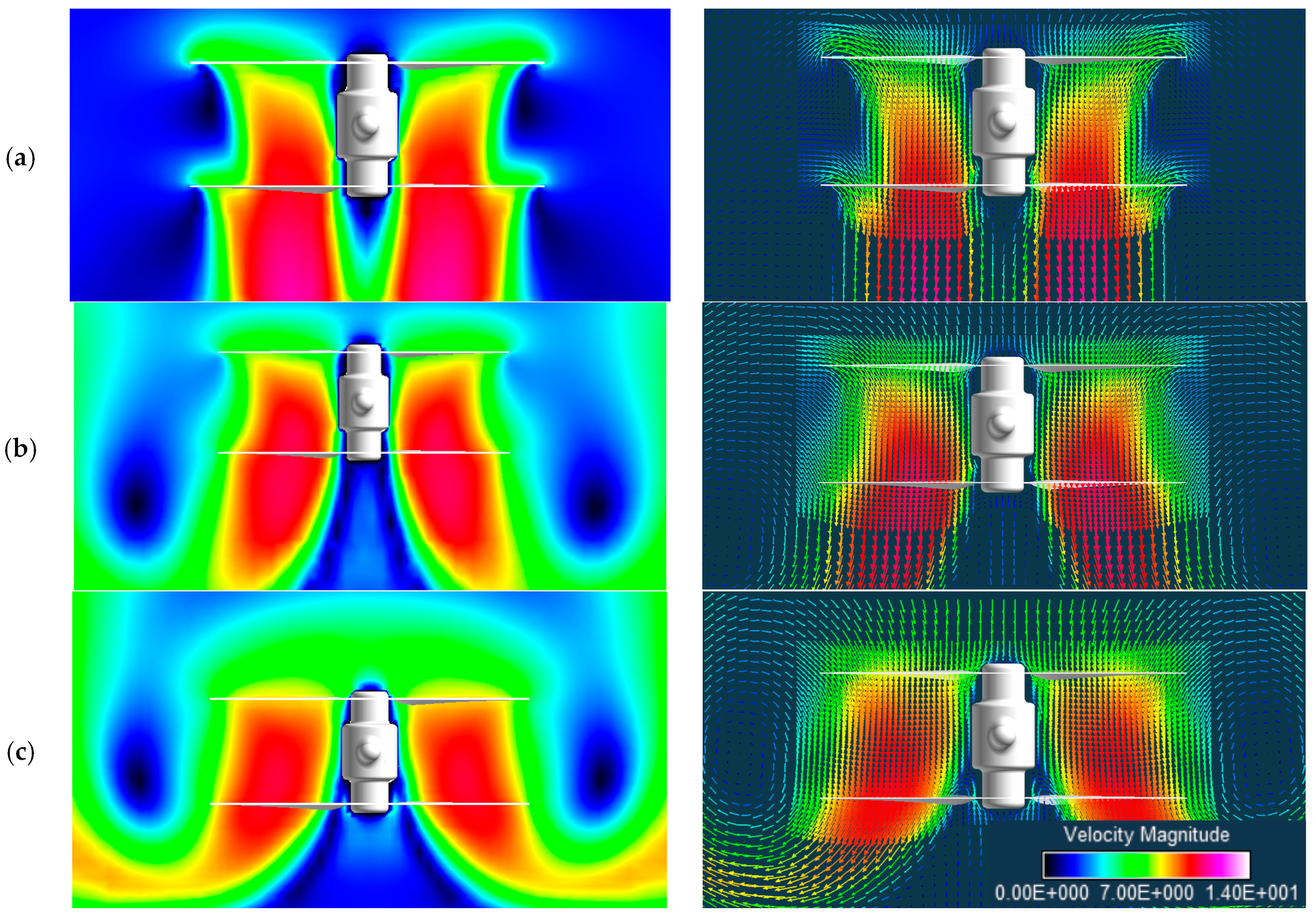
5.3. Axial Descent and Continued Discussion on the Vortex Ring State
6. Conclusions
- Summarize a methodology for multirotor performance prediction using an efficient hybrid BEMT-URANS CFD approach with a high-resolution model of the rotor.
- Document the effects of using fully turbulent versus free-transition airfoil performance tables on CFD rotor performance predictions.
- Compare single versus coaxial rotor performance across a wide range of flight conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Rotor disk area [m2] |
| a | Speed of sound [m/s] |
| CT | [non-dimensional] |
| Cd | [non-dimensional] |
| Cl | [non-dimensional] |
| Chord length at radial position, r [m] | |
| Verification comparison error [non-dimensional] | |
| M | [non-dimensional] |
| Q | Rotor torque [N-m] |
| R | Rotor blade radius [m] |
| Re | [non-dimensional] |
| r | Radial position [m] |
| SA | Shaft angle [deg], angle between free-stream velocity and rotor disk plane, negative nose-down |
| T | Rotor thrust [N] |
| Wind-tunnel speed [m/s] | |
| Density [kg/m3] | |
| Rotor rotational velocity [radians/s] | |
| µ | Dynamic viscosity [kg/(m-s)] or [Pa-s] |
| adv | [non-dimensional] |
| [non-dimensional] | |
| Uncertainty [non-dimensional] (used for multiple parameters in Section 2.3) | |
| δ | Error (used for multiple parameters in Section 2.3) |
| AAM | Advanced air mobility |
| BEMT | Blade Element Momentum Theory |
| CAD | Computer-aided design |
| CFD | Computational fluid dynamics |
| CPU | Central Processing Unit |
| D | Rotor diameter [m] |
| eVTOL | Electric vertical take-off and landing |
| GPU | Graphics Processing Unit |
| NACA | National Advisory Committee for Aeronautics |
| PAV | Planetary aerial vehicle |
| PWM | Pulse width modulation |
| RANS | Reynolds averaged Navier–Stokes |
| URANS | Unsteady Reynolds averaged Navier–Stokes |
| RotCFD | Rotorcraft Computational Fluid Dynamics Program |
| RPM | Revolutions per minute |
| SA | Shaft angle [deg] |
| TWS | Turbulent wake state |
| VRS | Vortex ring state |
| UAM | Urban air mobility |
| WBS | Windmill brake state |
References
- Cheney, M.C. The ABC Helicopter. In Proceedings of the VTOL Research, Design, and Operations Meeting, Atlanta, GA, USA, 17–19 February 1969; pp. 10–19. [Google Scholar] [CrossRef]
- Ruddell, A.J. Advancing Blade Concept (ABC) Development. AHS J. 1977, 22, 13–23. [Google Scholar] [CrossRef]
- Fegely, C.; Juhasz, O.; Xin, H.; Tischler, M. Flight Dynamics and Control Modeling with System Identification Validation of the Sikorsky X2 Technology Demonstrator. In Proceedings of the AHS 72nd Annual Forum, West Palm Beach, FL, USA, 17–19 May 2016; Available online: https://www.usna.edu/Users/aero/juhasz/_files/documents/Flight_Dynamics_and_Control_Modeling_with_System_ID_Validation_of_the_Sikorsky_X2TD_Submitted.pdf (accessed on 30 January 2024).
- Feil, R.; Eble, D.; Hajek, M. Comprehensive Analysis of a Coaxial Ultralight Rotorcraft and Validation with Full-Scale Fligth Test Data. J. Am. Helicopter Soc. 2018, 63, 1–12. [Google Scholar] [CrossRef]
- Feil, R.; Hajek, M. Aeromechanics of a Coaxial Ultralight Rotorcraft During Turn, Climb, and Descent Flight. J. Aircr. 2021, 58, 43–52. [Google Scholar] [CrossRef]
- Diaz, P.V.; Rubio, R.C.; Yoon, S. Simulations of Ducted and Coaxial Rotors for Air Taxi Operations. In Proceedings of the Aviation Forum, AIAA2019-2825, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Brown, A.; Harris, W. Vehicle Design and Optimization Model for Urban Air Mobility. J. Aircr. 2020, 57, 1003–1013. [Google Scholar] [CrossRef]
- Shrestha, R.; Benedict, M.; Hrishikeshavan, V.; Chopra, I. Hover Performance of a Small-Scale Helicopter Rotor for Flying on Mars. J. Aircr. 2016, 53, 1160–1167. [Google Scholar] [CrossRef]
- Grip, H.; Johnson, W.; Malpica, C.; Scharf, D.; Mandic, M.; Young, L.; Allan, B.; Mettler, B.; Martin, M.; Lam, J. Modeling and Identification of Hover Flight Dynamics for NASA’s Mars Helicopter. J. Guid. Control Dyn. 2020, 43, 179–194. [Google Scholar] [CrossRef]
- Gessow, A. Effect of Rotor-Blade Twist and Plan-Form Taper on Helicopter Hovering Performance, NACA TN-1542. 1948. Available online: https://ntrs.nasa.gov/citations/19930082219 (accessed on 30 January 2024).
- Harrington, R. Full-Scale Investigation of the Static-Thrust Performance of a Coaxial Helicopter Rotor, NACA TN-2318. 1951. Available online: https://ntrs.nasa.gov/citations/19930083001 (accessed on 30 January 2024).
- Dingeldein, R. Wind-Tunnel Studies of the Performance of Multirotor Configurations, NACA TN-3236. 1954. Available online: https://ntrs.nasa.gov/citations/19930083899 (accessed on 30 January 2024).
- Coleman, C. A Survey of Theoretical and Experimental Coaxial Rotor Aerodynamic Research, NASA TP-3675. 1997. Available online: https://ntrs.nasa.gov/citations/19970015550 (accessed on 30 January 2024).
- Ramasamy, M. Hover Performance Measurements Toward Understanding Aerodynamic Interference in Coaxial, Tandem, and Tilt Rotors. J. Am. Helicopter Soc. 2015, 60, 1–17. [Google Scholar] [CrossRef]
- Yeo, H. Design and Aeromechanics Investigation of Compound Helicopters. Aerosp. Sci. Technol. 2019, 88, 158–173. [Google Scholar] [CrossRef]
- Strawn, R.C.; Caradonna, F.X.; Duque, E.P.N. 30 Years of Rotorcraft Computational Fluid Dynamics Research and Development. J. Am. Helicopter Soc. 2006, 51, 5–21. [Google Scholar] [CrossRef]
- Russell, C.; Willink, G.; Theodore, C.; Jung, J.; Glasner, B. Wind Tunnel and Hover Performance Test Results for Multicopter UAS Vehicles, NASA/TM02018-219758. 2018. Available online: https://rotorcraft.arc.nasa.gov/Publications/files/Russell_1180_Final_TM_022218.pdf (accessed on 30 January 2024).
- Gregory, D.; Cornelius, J.; Waltermire, S.; Loob, C.; Schatzman, N. Acoustic Testing of Five Multicopter UAS in the U.S. Army 7- by 10-Foot Wind Tunnel. NASA/TM-2018-219894. May 2018. Available online: https://rotorcraft.arc.nasa.gov/Publications/files/Schatzman_TM_2018_219894_Final.pdf (accessed on 30 January 2024).
- Schatzman, N. Aerodynamics and Aeroacoustic Sources of a Coaxial Rotor, NASA/TM-2018-219895. November 2018. Available online: https://rotorcraft.arc.nasa.gov/Publications/files/Schatzman_TM_2018_219895_Final.pdf (accessed on 30 January 2024).
- Yoon, S.; Lee, H.; Pulliam, T. Computational Analysis of Multi-Rotor Flows. In Proceedings of the AIAA 2016-0812, AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Yoon, S.; Lee, H.; Pulliam, T. Computational Study of Flow Interactions in Coaxial Rotors. In Proceedings of the AHS Technical Meeting on Aeromechanics Design for Vertical Lift, San Francisco, CA, USA, 20–22 January 2016; Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20160001149.pdf (accessed on 30 January 2024).
- Yoon, S.; Chan, W.; Pulliam, T. Computations of Torque-Balanced Coaxial Rotor Flows. In Proceedings of the AIAA 2017-0052, AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Yoon, S.; Diaz, P.; Boyd, D.; Chan, W.; Theodore, C. Computational Aerodynamic Modeling of Small Quadcopter Vehicles. In Proceedings of the AHS 73rd Annual Forum, Fort Worth, TX, USA, 9–11 May 2017; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/73_2017_0015.pdf (accessed on 30 January 2024).
- Xu, H.; Ye, Z. Coaxial Rotor Helicopter in Hover Based on Unstructured Dynamic Overset Grids. AIAA J. Aircr. 2010, 47, 1820–1824. [Google Scholar] [CrossRef]
- Singh, P.; Friedmann, P. Application of Vortex Methods to Coaxial Rotor Wake and Load Calculations in Hover. AIAA J. Aircr. 2018, 55, 373–381. [Google Scholar] [CrossRef]
- Singh, P.; Friedmann, P. A Computational Fluid Dynamics-Based Viscous Vortex Particle Method for Coaxial Rotor Interaction Calculations in Hover. AHS J. 2018, 63, 1–13. [Google Scholar] [CrossRef]
- Singh, P.; Friedmann, P. Dynamic Stall Modeling Using Viscous Vortex Particle Method for Coaxial Rotors. AHS J. 2021, 66, 1–16. [Google Scholar] [CrossRef]
- Singh, P.; Friedmann, P.; Jeong, M.-S.; Lee, I.; Yoo, S.-J.; Yun, C.Y.; Kim, D.-K.; Hodges, D.H.; Hathaway, E.; Gandhi, F.; et al. Aeroelastic Stability Analysis of Coaxial Rotors using Viscous Vortex Particle Method. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Cornelius, J.; Kinzel, M.; Schmitz, S. Efficient Computational Fluid Dynamics Approach for Coaxial Rotor Simulations in Hover. AIAA J. Aircr. 2021, 58, 197–202. [Google Scholar] [CrossRef]
- Ho, J.; Yeo, H.; Bhagwat, M. Validation of Rotorcraft Comprehensive Analysis Performance Predictions for Coaxial Rotors in Hover. J. Am. Helicopter Soc. 2017, 62, 1–13. [Google Scholar] [CrossRef]
- Silva, C.; Johnson, W.; Solis, E. Concept Vehicles for VTOL Air Taxi Operations. In Proceedings of the AHS Technical Meeting on Aeromechanics Design for Vertical Lift, Holiday Inn at Fisherman’s Wharf, San Francisco, CA, USA, 16–18 January 2018; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/Johnson_2018_TechMx.pdf (accessed on 30 January 2024).
- Silva, C.; Johnson, W.; Antcliff, K.R.; Patterson, M.D. VTOL Urban Air Mobility Concept Vehicles for Technology Development, 2018 Aviation Technology, Integration, and Operations Conference. In Proceedings of the AIAA Aviation Forum, AIAA 2018-3847, Dallas, TX, USA, 17–21 June 2018. [Google Scholar] [CrossRef]
- Antcliff, K.; Whiteside, S.; Kohlman, L.; Silva, C. Baseline Assumptions and Future Research Areas for Urban Air Mobility Vehicles. In Proceedings of the AIAA SciTech, AIAA-2019-0528, San Diego, CA, USA, 28 May 2019. [Google Scholar] [CrossRef]
- Silva, C.; Johnson, W. Practical Conceptual Design of Quieter Urban VTOL Aircraft. In Proceedings of the Vertical Flight Society’s 77th Annual Forum & Technology Display, Virtual, 10–14 May 2021; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/77-2021-0202_Silva.pdf (accessed on 30 January 2024).
- Johnson, W.; Silva, C. NASA concept vehicles and the engineering of advanced air mobility aircraft. Aeronaut. J. 2022, 126, 59–91. [Google Scholar] [CrossRef]
- Wright, S.J. Fundamental Aeroelastic Analysis of an Urban Air Mobility Rotor. In Proceedings of the Vertical Flight Society’s 9th Biennial Autonomous VTOL Technical Meeting, Virtual, 26–28 January 2021; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/WRIGHT_EVTOL_2021_FINAL_REVISED2.pdf (accessed on 30 January 2024).
- Conley, S.; Shirazi, D. Comparing Simulation Results from CHARM and RotCFD to the Multirotor Test Bed Experimental Data. In Proceedings of the 2021 AIAA Aviation Forum, Virtual Event, 2–6 August 2021; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/CHARM_RotCFD_Test_Bed_Data_AIAA_Conley_Shirazi.pdf (accessed on 30 January 2024).
- Withrow-Maser, S.; Malpica, C.; Nagami, K. Impact of Handling Qualities on Motor Sizing for Multirotor Aircraft with Urban Air Mobility Missions. In Proceedings of the Vertical Flight Society’s 77th Annual Forum & Technology Display, Virtual, 10–14 May 2021; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/Impact_of_Handling_Qualities_on_Motor_Sizing_for_Multirotor_Aircraft_with_Urban_Air_Mobility_Missions_final.pdf (accessed on 30 January 2024).
- Beiderman, P.R.; Darmstadt, C.D.; Silva, C. Hazard Analysis Failure Modes, Effects, and Criticality Analysis for NASA Revolutionary Vertical Lift Technology Concept Vehicles. In Proceedings of the Vertical Flight Society’s 77th Annual Forum And Technology Display, Virtual, 10–14 May 2021; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/77-2021-0287_Beiderman.pdf (accessed on 30 January 2024).
- Cummings, H.; Willink, G.; Silva, C. Mechanical Design of the Urban Air Mobility Side-by-Side Test Stand. In Proceedings of the Vertical Flight Society’s 9th Biennial Autonomous VTOL Technical Meeting, Virtual, 26–28 January 2021; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/MechanicalDesignoftheUAMSBSTestStand_Cummings_AutonomousVTOLMeeting_.pdf (accessed on 30 January 2024).
- Orazio, P.; Oberai, A.; Healy, R.; Niemiec, R.; Gandhi, F. Multi-Fidelity Surrogate Model for Interactional Aerodynamics of a Multicopter. In Proceedings of the Vertical Flight Society Annual Forum 77, Virtual, 11–13 May 2021. [Google Scholar]
- Walter, A.; Niemiec, R.; Gandhi, F. Effects of Disk Loading on Handling Qualities of Large-Scale. In Proceedings of the Variable-RPM Quadcopters, Vertical Flight Society Annual Forum 77, West Palm Beach, FL, USA, 10–14 May 2021. [Google Scholar]
- Healy, R.; Gandhi, F.; Mistry, M. Computational Investigation of Multirotor Interactional Aerodynamics with Hub Lateral and Longitudinal Canting. AIAA J. 2022, 60, 872–882. [Google Scholar] [CrossRef]
- Healy, R.; Misiorowski, M.; Gandhi, F. A CFD-Based Examination of Rotor-Rotor Separation Effects on Interactional Aerodynamics for eVTOL Aircraft. J. Am. Helicopter Soc. 2022, 67, 1–12. [Google Scholar] [CrossRef]
- Bahr, M.; McKay, M.; Niemiec, R.; Gandhi, F. Handling qualities of fixed-pitch, variable-speed multicopters for urban air mobility. Aeronaut. J. 2022, 126, 951–972. [Google Scholar] [CrossRef]
- Tugnoli, M.; Montagnani, D.; Syal, M.; Droandi, G.; Zanotti, A. Mid-fidelity Approach to Aerodynamic Simulations of Unconventional VTOL Aircraft Configurations. Aerosp. Sci. Technol. 2021, 115, 106804. [Google Scholar] [CrossRef]
- Ruiz, M.; Scanavino, M.; D’Ambrosio, D.; Guglieri, G.; Vilardi, A. Experimental and Numerical Analysis of Hovering Multicopter Performance in Low-Reynolds Number Conditions. Aerosp. Sci. Technol. 2022, 128, 107777. [Google Scholar] [CrossRef]
- Cornelius, J.; Opazo, T.; Schmitz, S.; Langelaan, J.; Villac, B.; Adams, D.; Rodovskiy, L.; Young, L. Dragonfly—Aerodynamics during Transition to Powered Flight. In Proceedings of the VFS 77th Annual Forum, Virtual, 10–14 May 2021; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/77-2021-0264_Cornelius.pdf (accessed on 30 January 2024).
- Opazo, T.; Langelaan, J. Longitudinal control of transition to powered flight for a parachute dropped multi-copter. In Proceedings of the AIAA SciTech Forum, AIAA 2020-2072, Virtual, 10–14 May 2021. [Google Scholar] [CrossRef]
- Kinzel, M.P.; Cornelius, J.K.; Schmitz, S.; Palacios, J.L.; Langelaan, J.W.; Adams, D.S.; Lorenz, R.D. An Investigation of the Behavior of a Coaxial Rotor in Descent and Ground Effect. In Proceedings of the AIAA-2019-1098, AIAA SciTech Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Deluane, J.; Izraelevitz, J.; Sklyanskiy, E.; Schutte, A.; Fraeman, A.; Scott, V.; Leake, C.; Ballesterost, E.; Aaron, K.; Young, L.; et al. Motivations and Preliminary Design for Mid-Air Deployment of a Science Rotorcraft on Mars. In Proceedings of the AIAA Ascend Conference, Virtual, 16–18 November 2020; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/Mid_Air_Deployment_Delaune.pdf (accessed on 30 January 2024).
- Veismann, M.; Wei, S.; Conley, S.; Young, L.; Delaune, J.; Burdick, J.; Gharib, M.; Izraelevitz, J. Axial Descent of Variable-Pitch Multirotor Configurations: An Experimental and Computational Study for Mars Deployment Applications. In Proceedings of the Vertical Flight Society’s 77th Annual Forum & Technology Display, Virtual, 10–14 May 2021; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/77-2021-0193_Veismann.pdf (accessed on 30 January 2024).
- Enconniere, J.; Ortiz-Carretero, J.; Pachidis, V. Mission Performance Analysis of a Conceptual Coaxial Rotorcraft for Air Taxi Applications. Aerosp. Sci. Technol. 2017, 69, 1–14. [Google Scholar] [CrossRef]
- Zhu, H.; Nie, H.; Zhang, L.; Wei, X.; Zhang, M. Design and Assessment of Octocopter Drones with Improved Aerodynamic Efficiency and Performance. Aerosp. Sci. Technol. 2020, 106, 106206. [Google Scholar] [CrossRef]
- Lim, D.; Kim, H.; Yee, K. Uncertainty Propagation in Flight Performance of Multirotor with Parametric and Model Uncertainties. Aerosp. Sci. Technol. 2022, 122, 107398. [Google Scholar] [CrossRef]
- Balaram, J.; Canham, T.; Duncan, C.; Golombek, M.; Grip, H.; Johnson, W.; Maki, J.; Quon, A.; Stern, R.; Zhu, D. Mars Helicopter Technology Demonstrator. In Proceedings of the AIAA SciTech Forum, AIAA-2018-0023, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Koning, W.; Johnson, W.; Grip, H. Improved Mars Helicopter Aerodynamic Rotor Model for Comprehensive Analyses. AIAA J. 2019, 57, 3969–3979. [Google Scholar] [CrossRef]
- Koning, W. Generation of Performance Model for the Aeolian Wind Tunnel (AWT) Rotor at Reduced Pressure, NASA/CR–2018–219737. 2018. Available online: https://ntrs.nasa.gov/citations/20180008699 (accessed on 30 January 2024).
- Lorenz, R.D.; Turtle, E.P.; Barnes, J.W.; Trainer, M.G.; Adams, D.S.; Hibbard, K.E.; Sheldon, C.Z.; Zacny, K.; Peplowski, P.N.; Lawrence, D.J.; et al. Dragonfly: A rotorcraft lander concept for scientific exploration at Titan. Johns Hopkins APL Tech. Dig. 2018, 34, 374–387. Available online: https://dragonfly.jhuapl.edu/News-and-Resources/docs/34_03-Lorenz.pdf (accessed on 30 January 2024).
- Young, L.A.; Chen, R.T.N.; Aiken, E.W.; Briggs, G.A. Design Opportunities and Challenges in the Development of Vertical Lift Planetary Aerial Vehicles. In Proceedings of the American Helicopter Society International Vertical Lift Aircraft Design Specialist’s Meeting, San Francisco, CA, USA, 16–18 January 2000. [Google Scholar]
- Young, L.A. Vertical Lift—Not Just for Terrestrial Flight. In Proceedings of the AHS/AIAA/RaeS/SAE International Powered Lift Conference, Arlington, VA, USA, 30 October–1 November 2000. [Google Scholar]
- Lorenz, R.D. Post-Cassini exploration of Titan: Science rationale and mission concepts. J. Br. Interplanet. Soc. 2000, 53, 218–234. [Google Scholar]
- Lorenz, R.D. Flexibility for Titan Exploration: The Titan Helicopter. In Proceedings of the Forum on Innovative Approaches to Outer Planetary Exploration 2001–2020, Houston, TX, USA, 21–22 February 2001. [Google Scholar]
- Young, L.A. Exploration of Titan Using Vertical Lift Aerial Vehicles. In Proceedings of the Forum on Innovative Approaches to Outer Planetary Exploration 2001–2020, Houston, TX, USA, 21–22 February 2001. [Google Scholar]
- Lorenz, R.D. Flight power scaling of airplanes, airships, and helicopters: Application to planetary exploration. J. Aircr. 2001, 38, 208–214. [Google Scholar] [CrossRef]
- Barnes, J.; Lemke, L.; Foch, R.; McKay, C.; Beyer, R.; Radebaugh, J.; Atkinson, D.; Lorenz, R.; Le Mouelic, S.; Rodriguez, S.; et al. AVIATR—Aerial Vehicle for In-Situ and Airborne Titan Reconnaissance. Exp. Astron. 2012, 33, 55–127. [Google Scholar] [CrossRef]
- Stofan, E.; Lorenz, R.; Lunine, J.; Bierhaus, E.; Clark, B.; Mahaffy, P.; Ravine, M. TiME—The Titan Mare Explorer. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013. [Google Scholar]
- Young, L.; Pascal, L.; Aiken, E.; Briggs, G.; Withrow–Maser, S.; Pisanich, G.; Cummings, H. The Future of Rotorcraft and other Aerial Vehicles for Mars Exploration. In Proceedings of the Vertical Flight Society’s 77th Annual Forum & Technology Display, Virtual, 10–14 May 2021; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/77-2021-0064_Young.pdf (accessed on 30 January 2024).
- Radotich, M.; Withrow–Maser, S.; deSouza, Z.; Gelhar, S.; Gallagher, H. A Study of Past, Present, and Future Mars Rotorcraft. In Proceedings of the Vertical Flight Society’s 9th Biennial Autonomous VTOL Technical Meeting, Virtual, 26–28 January 2021; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/Radotich_aVTOL_Tech_Meeting_Final_Revised_012521.pdf (accessed on 30 January 2024).
- Young, L.; Deluane, J.; Johnson, W.; Withrow-Maser, S.; Cummings, H.; Sklyanskiy, E.; Izraelevitz, J.; Schutte, A.; Fraeman, A.; Bhagwat, R.T. Design Considerations for a Mars Highland Helicopter. In Proceedings of the AIAA Ascend Conference, AIAA-2020-4027, Virtual, 16–18 November 2020; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/Mars_Highlands_Helicopter_AIAA_ASCEND_Final.pdf (accessed on 30 January 2024).
- Withrow-Maser, S.; Johnson, W.; Young, L.; Koning, W.; Kuang, W.; Malpica, C.; Balaram, J.; Tzanetos, T. Mars Science Helicopter: Conceptual Design of the Next Generation of Mars Rotorcraft. In Proceedings of the AIAA Ascend Conference, AIAA-2020-4029, Virtual, 16–18 November 2020; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/MSH_summary_AIAA_ASCEND_final.pdf (accessed on 30 January 2024).
- Withrow-Maser, S.; Koning, W.; Kuang, W.; Johnson, W. Recent Efforts Enabling Future Mars Rotorcraft Missions. In Proceedings of the VFS Aeromechanics for Advanced Vertical Flight Technical Meeting, San Jose, CA, USA, 21–23 January 2020; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/Shannah_Withrow_TVF_2020.pdf (accessed on 30 January 2024).
- Johnson, W.; Withrow-Maser, S.; Young, L.; Malpica, C.; Koning, W.J.F.; Kuang, W.; Fehler, M.; Tuano, A.; Chan, A.; Datta, A.; et al. Mars Science Helicopter Conceptual Design, NASA/TM–2020–220485. Available online: https://rotorcraft.arc.nasa.gov/Publications/files/MSH_WJohnson_TM2020rev.pdf (accessed on 30 January 2024).
- Helitek, S. RotCFD: Rotor Computational Fluid Dynamics Integrated Design Environment, Software Package, Ver. 0.9.15 Build 402, Ames, IA, USA. 2020. Available online: http://sukra-helitek.com/ (accessed on 30 January 2024).
- Rajagopalan, G.; Baskaran, V.; Hollingsworth, A.; Lestari, A.; Garrick, D.; Solis, E.; Hagerty, B. RotCFD—A Tool for Aerodynamic Interference of Rotors: Validation and Capabilities. In Proceedings of the AHS Future Vertical Lift Aircraft Design Conference, San Francisco, CA, USA, 18–20 January 2012; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/A-5-D_rajagopalan.pdf (accessed on 30 January 2024).
- Mathur, S.R.; Murthy, J.Y. A Pressure-based Method for Unstructured Meshes. J. Numer. Heat Transf. 1997, 31, 195–215. [Google Scholar] [CrossRef]
- Conley, S.; Russell, C.; Kallstrom, K.; Koning, W.; Romander, E. Comparing RotCFD Predictions of the Multirotor Test Bed with Experimental Results. In Proceedings of the VFS Forum 76, Virtual, 5–8 October 2020. [Google Scholar]
- Koning, W.; Russell, C.; Solis, E.; Theodore, C. Mid-Fidelity Computational Fluid Dynamics Analysis of the Elytron 4S UAV Concept, NASA/TM-2018-219788. Available online: https://ntrs.nasa.gov/citations/20180008703 (accessed on 30 January 2024).
- Rajagopalan, G.; Thistle, J.; Polzin, W. The Potential of GPU Computing for Design in RotCFD. In Proceedings of the AHS Technical Meeting on Aeromechanics Design for Transformative Vertical Lift, San Francisco, CA, USA, 16–18 January 2018; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/Rajagopalan_2018_TechMx.pdf (accessed on 30 January 2024).
- Cornelius, J.; Schmitz, S. Massive Graphical Processing Unit Parallelization for Multirotor Computational Fluid Dynamics. AIAA J. Aircr. 2023, 60, 2010–2016. [Google Scholar] [CrossRef]
- Yeo, D. A Summary of Industrial Verification, Validation, and Uncertainty Quantification Procedures in Computational Fluid Dynamics; National Institute of Standards and Technology Interagency Report 8298; U.S. Department of Commerce, National Institute of Standards and Technology Interagency: Gaithersburg, MD, USA, 2020. [Google Scholar] [CrossRef]
- KDE Direct. KDE-CF305 Design Geometry Dimensions Specification Sheet, Bend, OR. 2021. Available online: https://cdn.shopify.com/s/files/1/0496/8205/files/KDE_Direct_CF305_Propeller_Blades_-_PRS.pdf?3912052235145003093 (accessed on 30 January 2024).
- ATI Industrial Automation Inc. F/T Sensor: Delta Calibration, Apex, NC. 2021. Available online: https://www.ati-ia.com/products/ft/ft_models.aspx?id=delta (accessed on 30 January 2024).
- C81 Airfoil Table Generator Using ARC2D (Efficient Two-Dimensional Solution Methods for The Navier-Stokes Equations), Software Package, Build, Ames, IA. 2018. Available online: https://software.nasa.gov/software/ARC-12112-1 (accessed on 30 January 2024).
- Baldwin, B.; Lomax, H. Thin-layer Approximation and Algebraic Model for Separated Turbulent Flows. In Proceedings of the AIAA 16th Aerospace Sciences Meeting, Huntsville, AL, USA, 16–18 January 1978. [Google Scholar] [CrossRef]
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils, Low Reynolds Number Aerodynamics; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–12. Available online: https://web.mit.edu/drela/Public/web/xfoil/ (accessed on 30 January 2024).
- MSES Multielement Airfoil Design/Analysis System, Software Package, Build: 3.11, Massachusetts Institute of Technology. 2015. Available online: https://web.mit.edu/drela/Public/web/mses/ (accessed on 30 January 2024).
- Critzos, C.; Heyson, H.; Boswinkle, R. Aerodynamic Characteristics of NACA 0012 Airfoil Section at Angles of Attack From 0-180 Degrees, NACA TN-3361. 1955. Available online: https://ntrs.nasa.gov/citations/19930084501 (accessed on 30 January 2024).
- Viterna, L.; Corrigan, R. Fixed Pitch Rotor Performance of Large Horizontal Axis Wind Turbines, DOE/NASA Workshop on Large Horizontal Axis Wind Turbines. 1982. Available online: https://ntrs.nasa.gov/citations/19830010962 (accessed on 30 January 2024).
- Tangler, J.; Kocurek, D. Wind Turbine Post-Stall Airfoil Performance Characteristics Guidelines for Blade-Element Momentum Methods. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, AIAA-2005-591, Reno, NV, USA, 10–13 January 2005. [Google Scholar] [CrossRef]
- Leishman, J.G.; Bhagwat, M.J.; Ananthan, S. The Vortex Ring State as a Spatially and Temporally Developing Wake Instability. J. Am. Helicopter Soc. 2004, 49, 160–175. [Google Scholar] [CrossRef]
- Johnson, W. Model for Vortex Ring State Influence on Rotorcraft Flight Dynamics, NASA/TP-2005-213477. 2005. Available online: https://ntrs.nasa.gov/citations/20060024029 (accessed on 30 January 2024).
- Brand, A.; Dreier, M.; Kisor, R.; Wood, T. The Nature of Vortex Ring State. J. Am. Helicopter Soc. 2001, 56, 22001–2200114. [Google Scholar] [CrossRef]
- Brown, R. Are eVTOL Aircraft Inherently More Susceptible to the Vortex Ring State than Conventional Helicopters. In Proceedings of the 48th European Rotorcraft Forum, Winterthur, Switzerland, 6–8 September 2022; Available online: https://sophrodyne-aerospace.com/static/soph_aerospace/files/downloads/Sophrodyne_eVTOL_VRS.pdf (accessed on 30 January 2024).




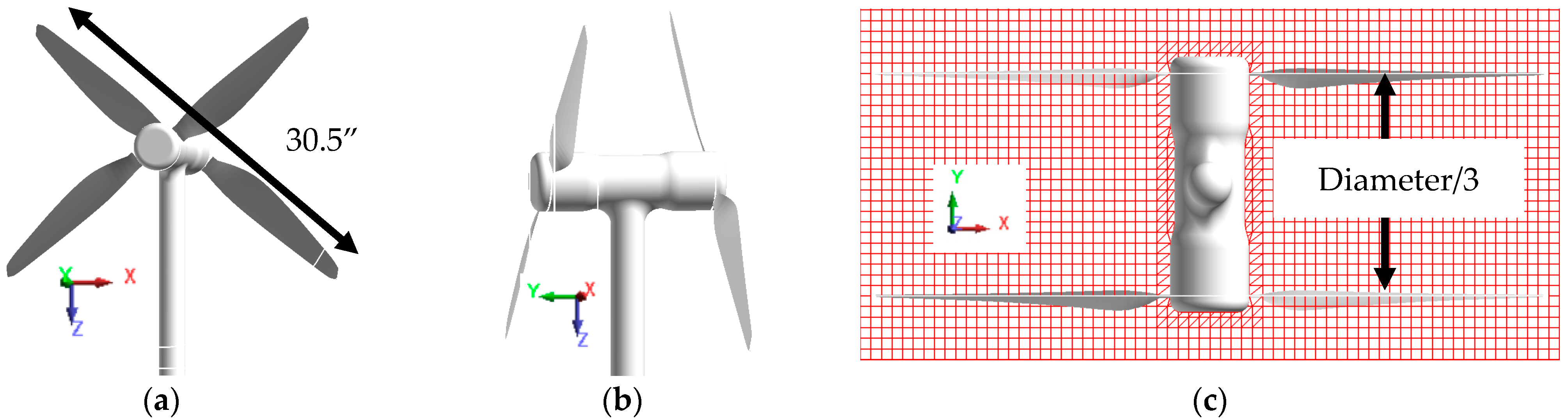

| Variable, Units (if Applicable) | Value |
|---|---|
| Diameter (D), in | 30.5 |
| Inter-Rotor Spacing, in | D/3 |
| RPM Range | ~1600–4515 |
| Cut-Out Radius, r/R | 0.117 |
| Reynolds Range at 25% R (thousands) | 65–180 |
| Mach Range at 25% R | 0.05–0.13 |
| Reynolds Range at 75% R (thousands) | 162–441 |
| Mach Range at 75% R | 0.15–0.40 |
| Fx, Fy | Fz | Tx, Ty | Tz | Fx, Fy | Fz | Tx, Ty | Tz |
|---|---|---|---|---|---|---|---|
| 667 N (150 lbf) | 2000 N (450 lbf) | 67.8 N-m (600 lbf-in) | 67.8 N-m (600 lbf-in) | 0.14 N (1/32 lbf) | 0.28 N (1/16 lbf) | 0.011 N-m (3/32 lbf-in) | 0.007 N-m (1/16 lbf-in) |
| Sensing Ranges | Resolution | ||||||
| (Turbulent Free)/Free | Upper Rotor Thrust | Upper Rotor Torque | Lower Rotor Thrust | Lower Rotor Torque |
|---|---|---|---|---|
| Forward Flight, SA = −15 deg | −3.6% | 0.7% | −3.5% | −1.0% |
| Climb, SA = −75 deg | −4.1% | −0.1% | −4.0% | −2.4% |
| Descent, SA = 90 deg | −3.4% | 1.5% | −3.5% | −0.7% |
| Maximum Uncertainty | −4.1% | 1.5% | −4.0% | −2.4% |
| Metric | Upper Rotor Thrust | Upper Rotor Torque | Lower Rotor Thrust | Lower Rotor Torque |
|---|---|---|---|---|
| Maximum Numerical Uncertainty | 1.0% | 1.0% | 3.3% | 3.3% |
| Flight Condition | C81 Thrust | C81 Torque | Free Thrust | Free Torque |
|---|---|---|---|---|
| Total | 3.6% | −3.9% | 9.5% | −0.5% |
| Climb | 6% | −3.5% | 12.6% | −0.2% |
| Edgewise | 2.2% | −0.8% | 7.6% | 2.7% |
| Descent | 1.8% | −5.5% | 7.1% | −1.9% |
| Flight Condition | C81 Thrust | C81 Torque | Free Thrust | Free Torque |
|---|---|---|---|---|
| Total | 1.4% | 4.5% | 3.0% | 7.9% |
| Climb | 2.3% | 2.8% | 7.4% | 7.1% |
| Edgewise | 0.0% | 4.9% | 3.5% | 11.5% |
| Descent | 2.0% | 5.1% | 0.4% | 7.8% |
| Upper Rotor Thrust | Upper Rotor Torque | Lower Rotor Thrust | Lower Rotor Torque | |
|---|---|---|---|---|
| Hover | 5.7% | 4.4% | 12.0% | 8.0% |
| Forward Flight, SA = −5, −15 deg | 5.7% | 4.4% | 12.0% | 8.0% |
| Axial Climb, SA = −90 deg | 5.7% | 4.4% | 12.0% | 7.9% |
| Descent, SA = 85, 90 deg | 7.2% | 5.3% | 14.7% | 10.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cornelius, J.; Schmitz, S.; Palacios, J.; Juliano, B.; Heisler, R. Rotor Performance Predictions for Urban Air Mobility: Single vs. Coaxial Rigid Rotors. Aerospace 2024, 11, 244. https://doi.org/10.3390/aerospace11030244
Cornelius J, Schmitz S, Palacios J, Juliano B, Heisler R. Rotor Performance Predictions for Urban Air Mobility: Single vs. Coaxial Rigid Rotors. Aerospace. 2024; 11(3):244. https://doi.org/10.3390/aerospace11030244
Chicago/Turabian StyleCornelius, Jason, Sven Schmitz, Jose Palacios, Bernadine Juliano, and Richard Heisler. 2024. "Rotor Performance Predictions for Urban Air Mobility: Single vs. Coaxial Rigid Rotors" Aerospace 11, no. 3: 244. https://doi.org/10.3390/aerospace11030244
APA StyleCornelius, J., Schmitz, S., Palacios, J., Juliano, B., & Heisler, R. (2024). Rotor Performance Predictions for Urban Air Mobility: Single vs. Coaxial Rigid Rotors. Aerospace, 11(3), 244. https://doi.org/10.3390/aerospace11030244






