Variational Method-Based Trajectory Optimization for Hybrid Airships
Abstract
:1. Introduction
2. Time and Energy Path Functionals for Hybrid Airship
3. Time and Energy Optimal Path Analysis for a Hybrid Airship under a Known Wind Field
3.1. Weak Wind Field
3.2. Uniform Wind Field
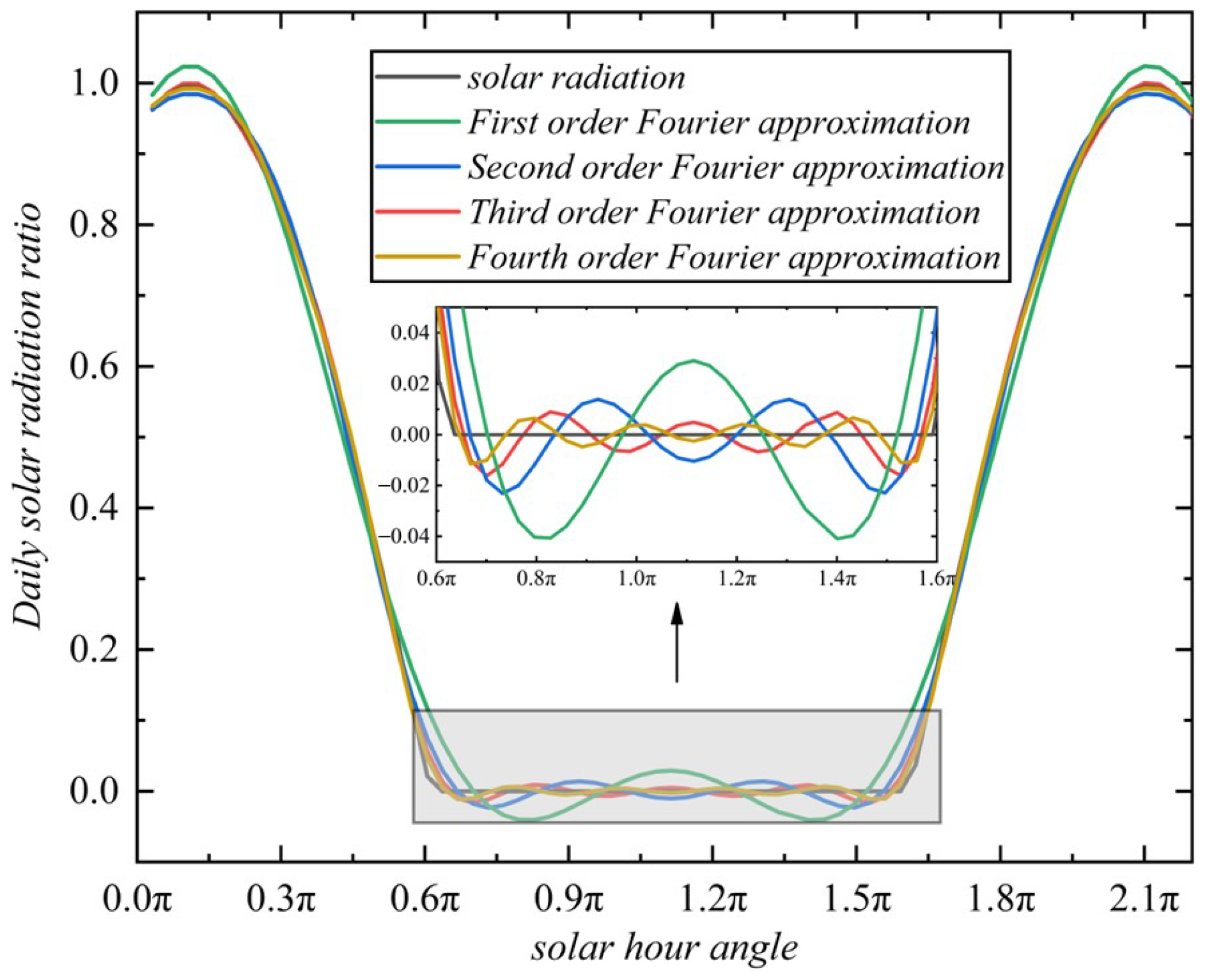
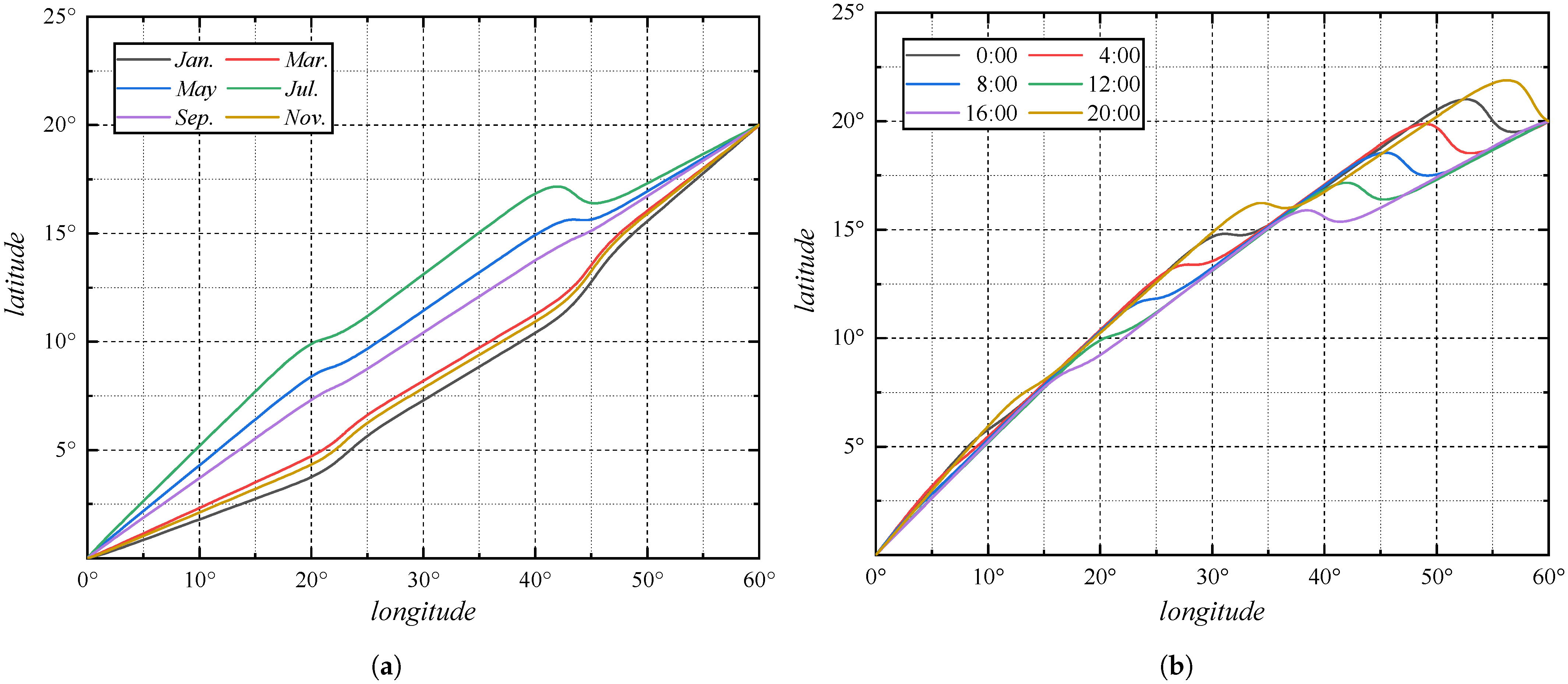
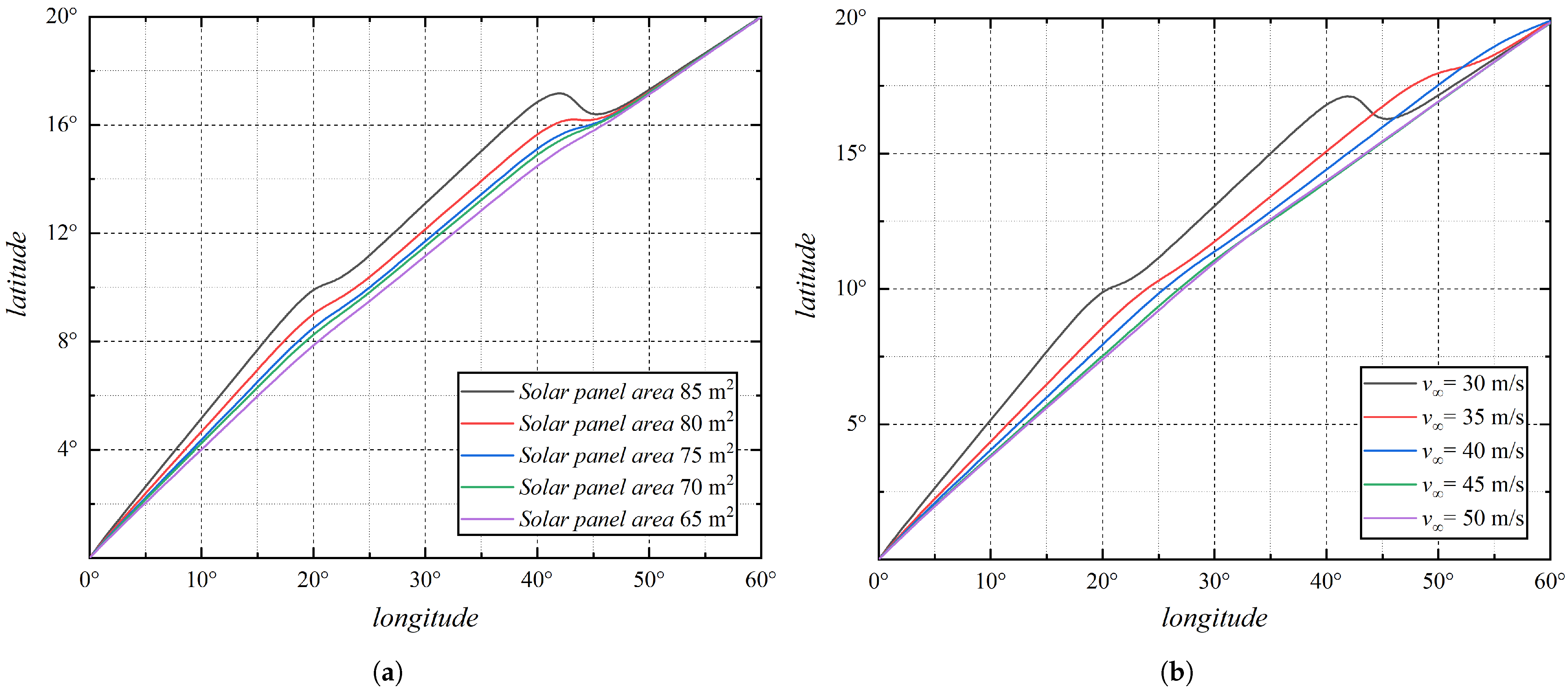
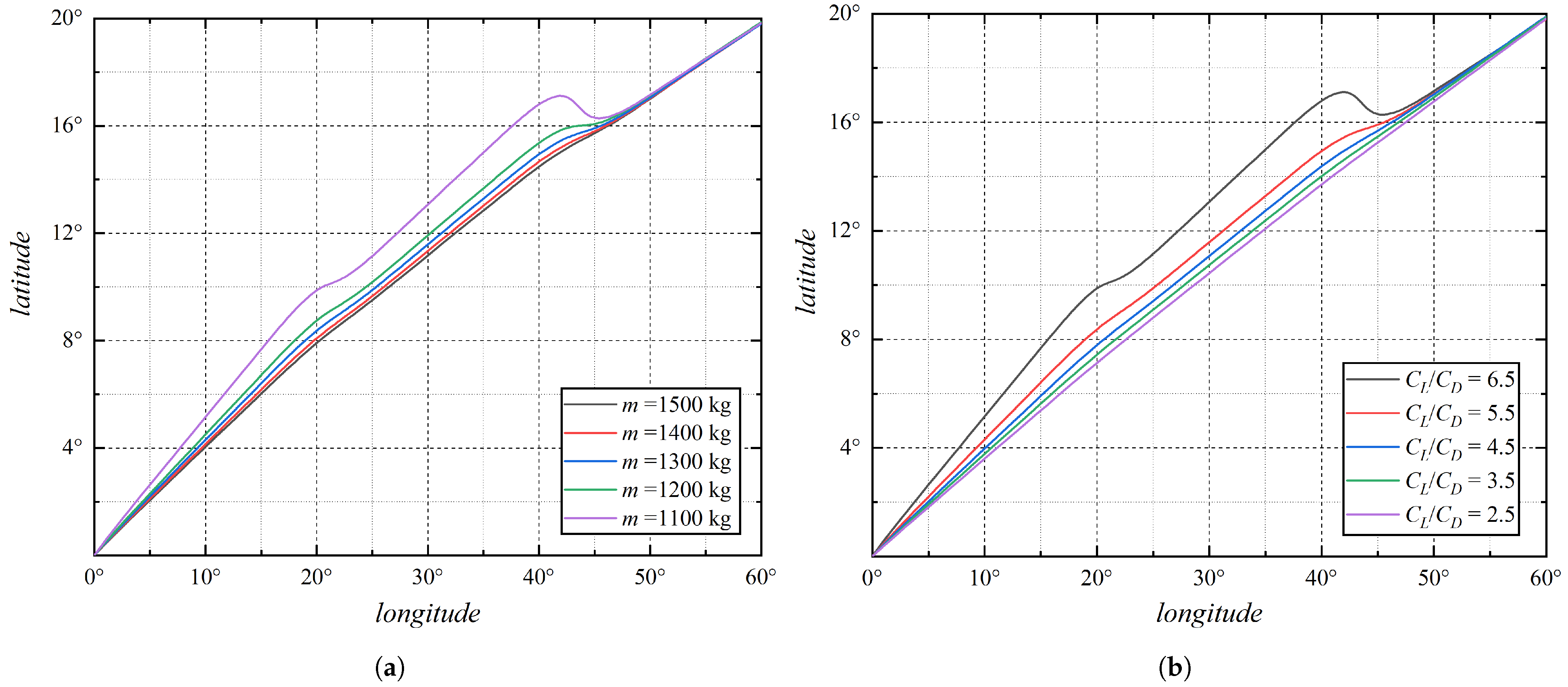
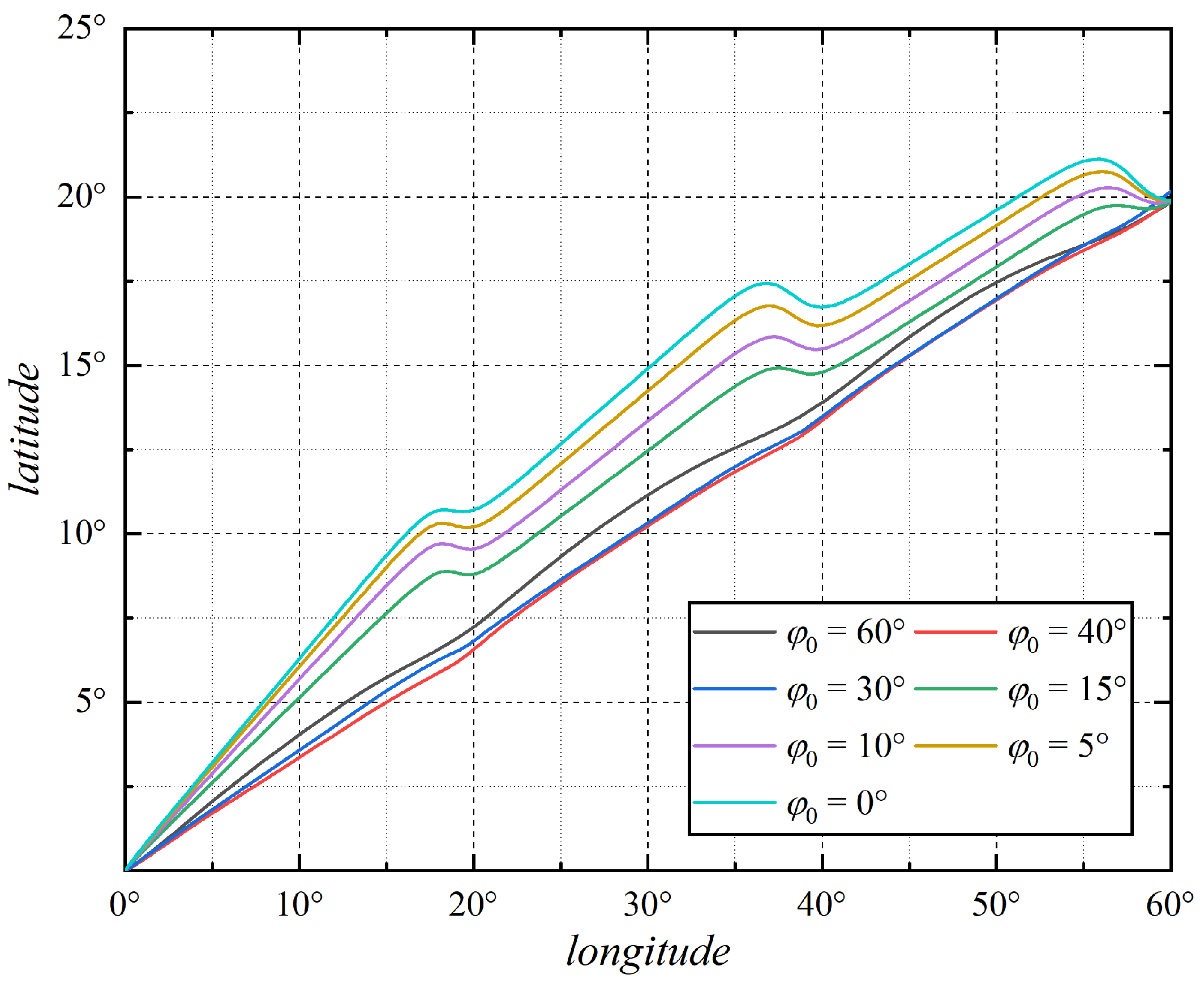
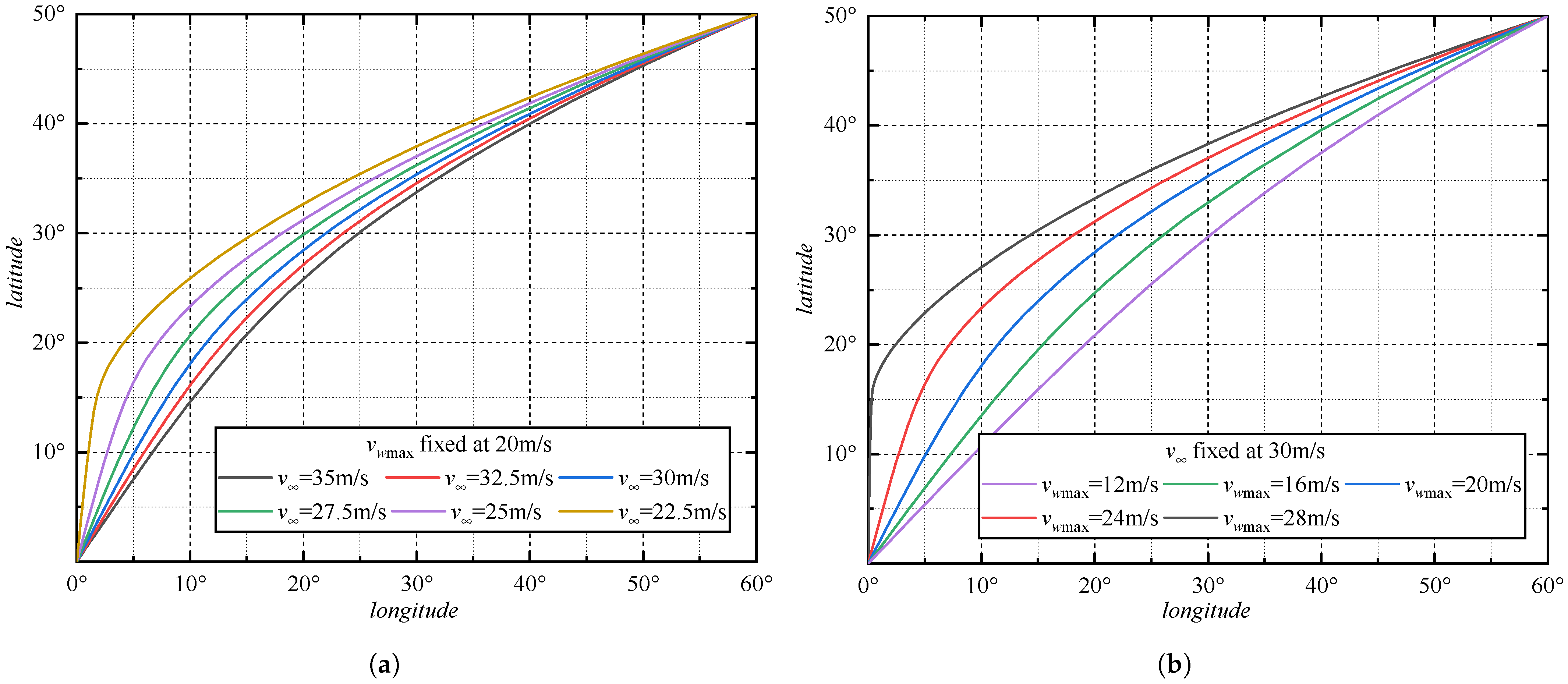
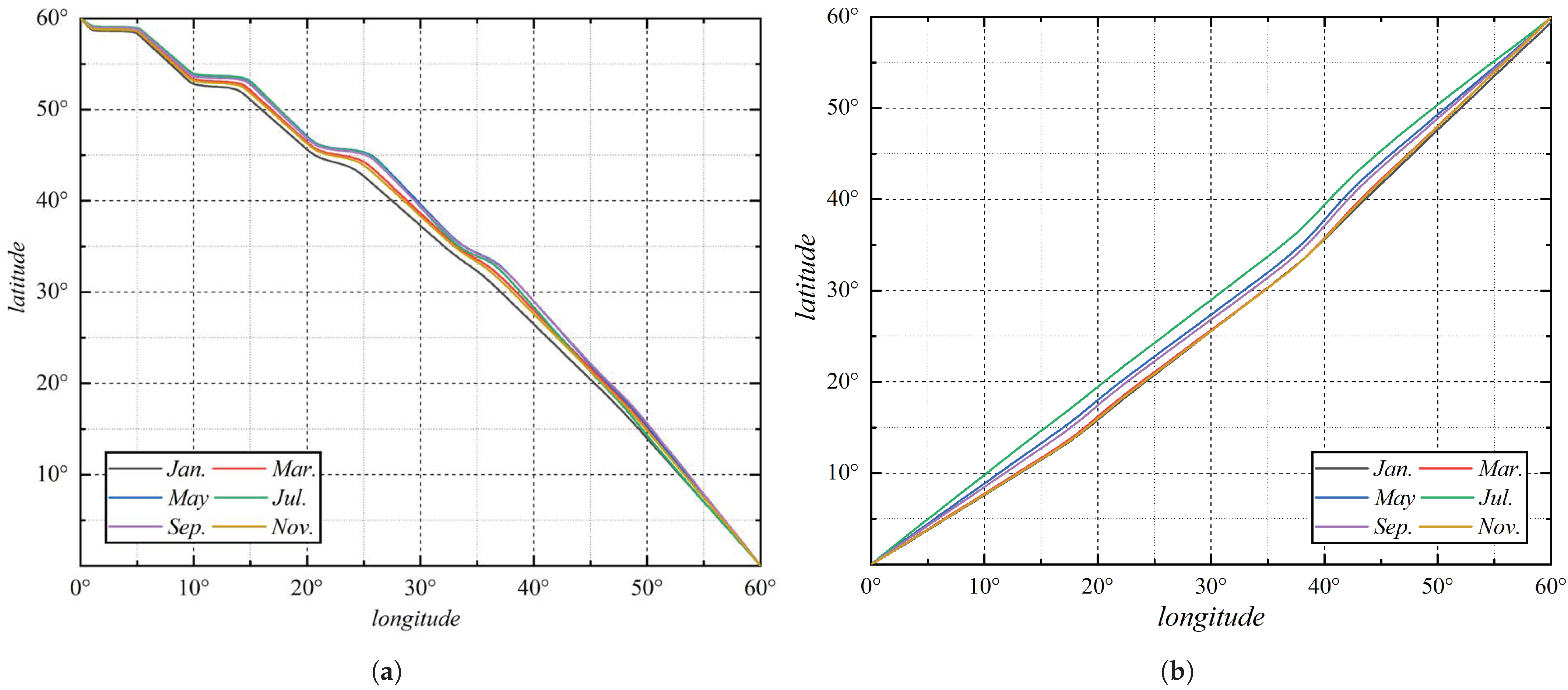
3.3. Latitudinal Linear Wind Field
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- D’Oliveira, F.A.; de Melo, F.C.L.; Devezas, T.C. High-Altitude Platforms—Present Situation and Technology Trends. J. Aerosp. Technol. Manag. 2016, 8, 249–262. [Google Scholar] [CrossRef]
- Manikandan, M.; Pan, R.S. Research and advancements in hybrid airships—A review. Prog. Aerosp. Sci. 2021, 127, 100741. [Google Scholar]
- Yang, B.; Yang, J.; Li, X. The operating environment of near-space and its effects on the airship. Spacecraft Environ. Eng. 2008, 25, 555–557. [Google Scholar]
- Akshay, G.; Murugaiah, M.; Dushhyanth, R.; Dimitri, M. Conceptual Design and Feasibility Study of Winged Hybrid Airship. Aerospace 2022, 9, 8. [Google Scholar]
- Stockbridge, C.; Ceruti, A.; Marzocca, P. Airship Research and Development in the Areas of Design, Structures, Dynamics and Energy Systems. Int. J. Aeronaut. Space Sci. 2012, 13, 170–187. [Google Scholar] [CrossRef]
- Carichner, G.E.; Nicolai, L.M. Fundamentals of Aircraft and Airship Design; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013; Volume 2—Airship Design and Case Studies, pp. 1–24. [Google Scholar]
- Ardema, M.D. Feasibility of Modern Airships: Preliminary Assessment. J. Aircr. 1977, 14, 1140–1148. [Google Scholar] [CrossRef]
- Mitchell, R. Effectiveness of Hybrid Airships as Cargo Airlifters. In Proceedings of the 11th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Virginia Beach, VA, USA, 20–22 September 2011. [Google Scholar]
- Pisarevskiy, Y.V.; Fursov, V.B.; Pisarevskiy, A.Y.; Tatarnikov, P.N.; Sitnikov, N.V.; Goremykin, S.A. Electric hybrid airship with unlimited flight time. In Proceedings of the Sustainable Energy Systems: Innovative Perspectives (SES-2020), Saint-Petersburg, Russia, 29–30 October 2020. [Google Scholar]
- Carrin, M.; Biava, M.; Steijl, R.; Barakos, G.N.; Stewart, D. Computational fluid dynamics challenges for hybrid air vehicle applications. Adv. AeroSpace Sci. 2017, 9, 43–84. [Google Scholar]
- Carrion, M.; Biava, M.; Steijl, R.; Barakos, G.N.; Stewart, D. CFD Studies of Hybrid Air Vehicles. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Pshikhopov, V.K.; Medvedev, M.Y.; Gaiduk, A.R.; Fedorenko, R.V.; Krukhmalev, V.A.; Gurenko, B.V. Position-Trajectory Control System for Unmanned Robotic Airship. In Proceedings of the 19th IFAC World Congress, Cape Town, South Africa, 24 August 2014. [Google Scholar]
- Prakash, O. Multibody Dynamics of winged Hybrid Airship Payload delivery System. In Proceedings of the AIAA Aviation 2020 Forum, Virtual, 15–19 June 2020. [Google Scholar]
- Anwar, U.H.; Waqar, A.; Erwin, S.; Jaffar, S.M.A.; Ali, O.A. Power-off static stability analysis of a clean configuration of a hybrid buoyant aircraft. In Proceedings of the 8th Ankara International Aerospace Conference 2015, Ankara, Turkey, 10–12 September 2015. [Google Scholar]
- Ceruti, A.; Marzocca, P. Conceptual Approach to Unconventional Airship Design and Synthesis. J. Aerosp. Eng. 2014, 27, 04014035. [Google Scholar] [CrossRef]
- Zhang, L.; Lv, M.; Meng, J.; Du, H. Conceptual design and analysis of hybrid airships with renewable energy. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 2144–2159. [Google Scholar] [CrossRef]
- Zhang, L.; Lv, M.; Zhu, W.; Du, H.; Meng, J.; Li, J. Mission-based multidisciplinary optimization of solar-powered hybrid airship. Energy Convers. Manag. 2019, 185, 44–54. [Google Scholar] [CrossRef]
- Jiwei, T.; Weicheng, X.; Pingfang, Z.; Hui, Y.; Tongxin, Z.; Quanbao, W. Multidisciplinary Optimization and Analysis of Stratospheric Airships Powered by Solar Arrays. Aerospace 2023, 10, 43. [Google Scholar]
- Junhui, M.; Moning, L.; Nuo, M.; Li, L. Multidisciplinary design optimization of a lift-type hybrid airship. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 72–83. [Google Scholar]
- Manikandan, M.; Pant, R.S. Conceptual Design Optimization of High-Altitude Airship Having a Tri-Lobed Envelope. In Advances in Multidisciplinary Analysis and Optimization; Springer: Singapore, 2022. [Google Scholar]
- Banavar, S.; Ng, H.K.; Chen, N.Y. Aircraft Trajectory Optimization and Contrails Avoidance in the Presence of Winds. J. Guid. Control. Dyn. 2011, 34, 1577–1584. [Google Scholar]
- Zhu, B.J.; Yang, X.-X.; Deng, X.-L.; Ma, Z.-Y.; Hou, Z.-X.; Jia, G.-W. Trajectory optimization and control of stratospheric airship in cruising. J. Numer. Math. 2019, 233, 1329–1339. [Google Scholar] [CrossRef]
- Hedin, A.E. Horizontal wind model (HWM) (1990). Planet. Space Sci. 1992, 40, 556–557. [Google Scholar] [CrossRef]
- Drob, D.P.; Emmert, J.T.; Meriwether, J.W.; Makela, J.J.; Doornbos, E.; Conde, M.; Hernandez, G.; Noto, J.; Zawdie, K.A.; McDonald, S.E.; et al. An update to the Horizontal Wind Model (HWM): The quiet time thermosphere. Earth Space Sci. 2014, 2, 301–319. [Google Scholar] [CrossRef]
- Shampine, L.F. Solving 0 = F(t, y(t), y’(t)) in Matlab. J. Numer. Math. 2002, 10, 291–310. [Google Scholar] [CrossRef]




| Design Parameter | Value | Unit |
|---|---|---|
| 30 | m/s | |
| m | 1200 | kg |
| V | 9545 | m3 |
| S | 85 × 0.12 | m2 |
| I | 1367 | W/m2 |
| 6.5 | unitless |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Bi, Y.; Li, X.; Dong, A.; Wang, J.; Yang, X. Variational Method-Based Trajectory Optimization for Hybrid Airships. Aerospace 2024, 11, 250. https://doi.org/10.3390/aerospace11040250
Gao W, Bi Y, Li X, Dong A, Wang J, Yang X. Variational Method-Based Trajectory Optimization for Hybrid Airships. Aerospace. 2024; 11(4):250. https://doi.org/10.3390/aerospace11040250
Chicago/Turabian StyleGao, Wen, Yanqiang Bi, Xiyuan Li, Apeng Dong, Jing Wang, and Xiaoning Yang. 2024. "Variational Method-Based Trajectory Optimization for Hybrid Airships" Aerospace 11, no. 4: 250. https://doi.org/10.3390/aerospace11040250
APA StyleGao, W., Bi, Y., Li, X., Dong, A., Wang, J., & Yang, X. (2024). Variational Method-Based Trajectory Optimization for Hybrid Airships. Aerospace, 11(4), 250. https://doi.org/10.3390/aerospace11040250





